Coupled-Cluster Computations of Optical Potential for Medium-Mass Nuclei

Recent progress in the numerical solution of the nuclear many-body problem and in the development of nuclear Hamiltonians rooted in Quantum Chromodynamics, has opened the door to first-principle computations of nuclear reactions. In this article, we discuss the current status of ab initio calculations of nucleon-nucleus optical potentials for medium-mass systems, with a focus on results obtained with the coupled-cluster method.

1. Introduction

Understanding the structure and dynamics of atomic nuclei in terms of nucleons and their mutual interactions is one of the main goals of nuclear physics. At the typical energy scale of nuclear phenomena, the quarks and gluons degrees of freedom are not resolved. As a consequence, in this context, nucleons can be treated as point-like particles and the nuclear problem with protons and neutrons can be viewed as a low-energy effective approximation to QCD. Within the framework of Effective Field Theory (EFT), inter-nucleon interactions consistent with the chiral symmetry can nowadays be derived systematically in terms of nucleon-nucleon, three-nucleon, and higher many-nucleon forces [1–6]. Starting with a given Hamiltonian, ab initio calculations of nuclei aim at solving the many-body Schrödinger equation without any uncontrolled approximations. Within the last decades, the increase in computing power and the development of powerful many-body methods, combined with the use of chiral-EFT interactions, have enabled a quantitative description of light and medium-mass nuclei ab initio [7–12]. With the inclusion of continuum effects in many-body methods, ab-initio calculations have also reached parts of the nuclear chart far from stability where the coupling to continuum states and decay channels plays an important part in the structure of nuclei [13–21].

A lot of progress has been made as well in the development of ab initio methods for nuclear reactions. The No-Core Shell Model with the Resonating Group Method (NCSM/RGM) or with continuum (NCSMC) have successfully described scattering and transfer reactions for light targets [22–24], the Green's Function Monte Carlo [25, 26] has recently been applied to nucleon-alpha scattering using chiral NN, 3N forces [27], and lattice-EFT computations of alpha-alpha scattering have recently been reported [28]. For medium-mass nuclei, nucleon-nucleus optical potentials and elastic scattering cross sections have been computed with chiral forces within the Self Consistent Green's Function (SCGF) approach [9, 29–31] and the coupled-cluster method [32–34].

The optical potential plays an important role in reaction theory. It is usual (and practical) in this context to reduce the many-body problem into a few-body one where only the most relevant degrees of freedom are retained [35]. Correspondingly, the many-body Hamiltonian is replaced by a few-body Hamiltonian expressed in terms of optical potentials, i.e., effective interactions between the particles considered at the few-body level. Traditionally, optical potentials have been constructed by fitting to data, particularly data on β-stable isotopes [36, 37]. For instance, global phenomenological nucleon-nucleus potentials enable the description of scattering processes for a large range of nuclei and projectile energies. However, extrapolation of these phenomenological potentials to exotic regions of the nuclear chart are unreliable and have uncontrolled uncertainties. Moreover, since fitting to two-body elastic scattering data (as it is most often done) does not constrain the off-shell behavior of potentials¹, a dependence on the choice of potentials may arise in transfer reactions observables (and other reactions) as shown in e.g., [38–40]. It is then critical, in order to advance the field of nuclear reactions and notably for reactions with exotic nuclei undertaken at rare-isotope-beam facilities [41, 42], to connect the optical potentials to an underlying microscopic theory of nuclei. Since potentials derived from ab initio approaches are built up from fundamental nuclear interactions without tuning to data, they may have a greater predictive power in regions of the nuclear chart that are unexplored experimentally. Furthermore, they can guide new parametrization of phenomenological potentials by providing insights on form factors, energy-dependence and dependence on the isospin-asymmetry of the target.

It is useful for pedagogical purpose and the introduction of key concepts, to start with the derivation of the optical potential within the Feshbach projection formalism [43, 44]. Let us consider the process of scattering of a nucleon on a target A. One can partition the Hilbert space for this A + 1 system into ${P}$ the subspace of elastic scattering states and ${Q}$ the complementary subspace. Denoting P and Q the projectors operators on respectively ${P}$ and ${Q}$, by construction one has P + Q = Id. We introduce H the Hamiltonian of the system and E its energy. The optical potential describing the elastic scattering process can be identified with the effective Hamiltonian $H_P^{eff}(E)$ acting in P, which by construction, reproduces the eigenvalues of H with a model wavefunction in ${P}$. One can show that

$\begin{array}{ll}{H}_P^{eff}(E)=H_{PP}+H_{PQ}\frac{1}{E-H_{QQ}+i\eta }{H}_{QP}& (1)\end{array}$

where H_PP ≡ PHP, H_PQ ≡ PHQ, …  and η → 0⁺. The optical potential $H_P^{eff}(E)$ is non-local and from Equation (1), it is clear that it is also energy-dependent and complex. The imaginary (absorptive) component of the potential represents the loss of flux in the elastic channel due to the opening of other channels, for instance, the excitation of the target to a state of energy $E_i^A$ for $E>E_i^A$ or breakup channels. By adding the Hilbert space of the A − 1 system (hole states in the target) in the formalism, it has been shown that the resulting optical potential corresponds to the self-energy defined in Green's function theory [45]. The particle part of the self-energy is equivalent to the optical potential (1), whereas the hole part describes the structure of the target. By including information on both the (A + 1)- and (A − 1)-system in the formalism, the Green's function approach, which will be used in this paper, provides a consistent treatment of scattering and structure.

In this article, we present some recent results for the ab-initio computation of nucleon-nucleus optical potential for medium-mass nuclei, constructed by combining the Green's function approach with the coupled-cluster method [10]. The coupled-cluster method is an efficient tool for the computation of ground- and low-lying excited states in nuclei with a closed (sub-)shell structure and in their neighbors with ±2 nucleons. By including complex continuum basis states in the formalism, it also provides a versatile framework to consistently compute bound, resonant states and scattering processes [13, 15–17, 32]. In our approach, the optical potential is obtained by solving the Dyson equation after a direct computation of the Green's function with the coupled-cluster method. As we will see in section 2, the inclusion of complex continuum basis states enables also a precise computation of Green's functions and optical potentials.

We want to point out here that there has been a lot of work over the years to compute optical potentials from various microscopic approaches. In the following, we mention some of the most recent works dedicated to that goal (for a more exhaustive review we refer the reader to, e.g., [46]). The authors in [47] have computed optical potentials for neutron and proton elastic scattering on ⁴⁰Ca based on the application of the self-consistent Hartree-Fock and Random-Phase Approximations to account for collective states in the target. Using the phenomenological Gogny interaction, a good reproduction of data for scattering at E ≤ 30 MeV has been reported in [47]. In Whitehead et al. [48, 49], nucleon-nucleus potentials are computed for finite nuclei from a folding of optical potentials obtained by many-body perturbation theory calculations in nuclear matter with chiral forces. In these papers, several calcium isotopes are considered and an overall satisfactory agreement with data is achieved. For the scattering of nucleons at intermediate and high energy (E ≳ 100 MeV) optical potentials can be derived within the multiple scattering formalism [50, 51] where the optical potential is obtained based on the folding of the nucleon-nucleon T-matrix or G-matrix with the nuclear density [52–54]. Recent applications of this approach, in which the nucleon-nucleus T-matrix and the density are computed consistently starting from the same chiral-EFT interaction, have been reported and shown a successful reproduction of data [55, 56]. In the Dispersive Optical Model [46, 57–59], a (semi-) phenomenological potential is constructed by exploiting formal properties of the Green's function, such as the dispersion relation, which connects the real part and imaginary part of the potential [60]. Applications of this data-driven approach have been made using local and non-local form factors of the potential for Ca and Pb isotopes.

This paper is organized as follows. In section 2, we will briefly review the formalism to construct optical potentials by combining the Green's function approach and the coupled-cluster method. In section 3, recent results for neutron-^40,48Ca optical potentials at negative and positive energies are presented. In section 4, we will discuss challenges and possible solutions for the construction of fully predictive optical potentials with the coupled-cluster method. Finally, we will conclude in section 5.

2. Coupled Cluster Green's Function

In this part, we will briefly review the formalism for deriving ab-initio nucleon-nucleus optical potentials by combining the Green's function approach and the coupled-cluster method. We start first by introducing below, key quantities of the Green's function formalism.

2.1. Green's Function and Dyson Equation

Given a single-particle basis {|α〉, |β〉, …}, the Green's function [61] of a nucleus A has matrix elements

$\begin{array}{l}G(\alpha ,\beta ,E)=\langle {\text{Ψ}}_0|a_{\alpha }\frac{1}{E-(H-E_{gs}^A)+i\eta }{a}_{\beta }^{†}|{\text{Ψ}}_0\rangle \\ +\langle {\text{Ψ}}_0|a_{\beta }^{†}\frac{1}{E-(E_{gs}^A-H)-i\eta }{a}_{\alpha }|{\text{Ψ}}_0\rangle .& (2)\end{array}$

Here, H is the Hamiltonian and |Ψ₀〉 the ground state of A with the energy $E_{gs}^A$ and by definition η → 0⁺. The operators $a_{\alpha }^{†}$ and a_β create and annihilate a fermion in the single-particle state α and β, respectively. α is shorthand for the quantum numbers α = (n, l, j, j_z, τ_z)². By inserting completeness relations expressed with the eigenstates of the A ± 1 systems in (2), one obtains the Lehmann representation of the Green's function:

$\begin{array}{l}G(\alpha ,\beta ,E)={\displaystyle \sum _i}\frac{\langle {\text{Ψ}}_0|a_{\alpha }|{\text{Ψ}}_i^{A+1}\rangle \langle {\text{Ψ}}_i^{A+1}|a_{\beta }^{†}|{\text{Ψ}}_0\rangle }{E-(E_i^{A+1}-E_{gs}^A)+i\eta }\\ +{\displaystyle \sum _j}\frac{\langle {\text{Ψ}}_0|a_{\beta }^{†}|{\text{Ψ}}_j^{A-1}\rangle \langle {\text{Ψ}}_j^{A-1}|a_{\alpha }|{\text{Ψ}}_0\rangle }{E-(E_{gs}^A-E_j^{A-1})-i\eta },& (3)\end{array}$

where $|{\text{Ψ}}_i^{A+1}\rangle$ ($|{\text{Ψ}}_j^{A-1}\rangle$) is an eigenstate of H for the A + 1 (A − 1) system with energy $E_i^{A+1}$ ($E_j^{A-1}$). To simplify the notation, the completeness relations are written in (3) as discrete summations over the states in the A ± 1 systems. The Lehmann representation has the merit to reveal somewhat more clearly some of the information content of the Green's Function. As one can see from (3), the poles of the Green's function correspond to the energies of the eigenstates of H in the A ± 1 systems.

The Green's function fulfills the Dyson equation

$\begin{array}{ll}G(E)=G^{(0)}(E)+G^0(E){\Sigma }^{*}(E)G(E),& (4)\end{array}$

where G⁰(E) is the Green's function associated with a single-particle potential U and Σ^*(E) the irreducible self energy. The optical potential is given by

$\begin{array}{ll}{V}^{opt}(E)\equiv {\Sigma }^{*}(E)+U.& (5)\end{array}$

The potential U is usually taken as the Hartree-Fock (HF) potential since the corresponding Green's function is a first-order approximation to G(E) in Equation (4). In our approach, since the Green's function is directly computed with the coupled-cluster method and is input of Equation 4, the resulting optical potential is independent of the choice of U.

For $E^{+}\equiv E-E_{gs}^A\ge 0$, V^opt(E) corresponds to the optical potential for the elastic scattering from the A-nucleon ground state [61]. In other words, the scattering amplitude ${\xi }_{E^{+}}(\text{r})=\langle {\text{Ψ}}_0|a_{\text{r}}|{\text{Ψ}}_{E+}\rangle$ (here $|{\text{Ψ}}_{E^{+}}\rangle$ is the elastic scattering state of a nucleon on the target with the energy E⁺ and a_r is the annihilation operator of a particle at the position r) fulfills the Schrödinger equation

$\begin{array}{ll}-\frac{{\hslash }^2}{2\mu }{\nabla }^2\xi (\text{r})+{\displaystyle \int }d{r}^{\prime }{V}^{opt}(\text{r},{\text{r}}^{\prime },E)\xi ({\text{r}}^{\prime })=E^{+}\xi (\text{r}),& (6)\end{array}$

where μ is the reduced mass of the nucleus-nucleon system. For simplicity, we have suppressed any spin and isospin labels. The optical potential is non-local, energy-dependent and complex [61] and for E⁺ ≥ 0, its imaginary component describes the loss of flux in the elastic channels to other channels. For E⁺ < 0, Equation (6) admits a discrete number of physical solution at $E_n=E_n^{A+1}-E_{gs}^A$, which corresponds to the bound states energies in A + 1. In that case, the solutions are given by the overlap ${\xi }_n(\text{r})=\langle {\text{Ψ}}_0|a_r|{\text{Ψ}}_n^{A+1}\rangle$ where $|{\text{Ψ}}_n^{A+1}\rangle$ is a bound state of energy $E_n^{A+1}$ in the A + 1 system³.

In the following section, we present the main steps involved in the computation of the Green's function with the coupled-cluster method.

2.2. Coupled-Cluster Green's Function

We start with the computation of the ground state |Ψ₀〉 of the A-nucleon system. Working in the laboratory frame, the intrinsic Hamiltonian reads

$\begin{array}{ll}H={\displaystyle \sum _{i=1}^A}\frac{{\overrightarrow{p_i}}^2}{2m}-\frac{{\overrightarrow{P}}^2}{2mA}+{\displaystyle \sum _{i<j}}{V}_{ij}+{\displaystyle \sum _{i<j<k}}{V}_{ijk},& (7)\end{array}$

with $\overrightarrow{p_i}$ the momentum of nucleon i of mass m and $\overrightarrow{P}=\sum _{i=1}^A\overrightarrow{p_i}$ the momentum associated with the center of mass motion. The terms V_ij and V_ijk are nucleon-nucleon (NN) and three-nucleon forces (3NFs), respectively. It is useful to rewrite the Hamiltonian as

$\begin{array}{ll}H={\displaystyle \sum _{i=1}^A}\frac{{\overrightarrow{p}}_i^2}{2m}\left(1-\frac{1}{A}\right)+{\displaystyle \sum _{i<j}}\left(V_{ij}-\frac{{\overrightarrow{p}}_i{\overrightarrow{p}}_j}{mA}\right)+{\displaystyle \sum _{i<j<k}}{V}_{ijk},& (8)\end{array}$

where one separates the one-body and two- (three-)body contributions. The single-particle basis solution of the HF potential generated by H in Equation (8) is a good starting point for coupled-cluster calculations. Denoting by |Φ₀〉 the HF state, the ground state of the target is represented as

$\begin{array}{ll}|{\text{Ψ}}_0\rangle =e^T|{\Phi }_0\rangle ,& (9)\end{array}$

where T denotes the cluster operator

$\begin{array}{ll}T=T_1+T_2+\cdots ={\displaystyle \sum _{i,a}}{t}_i^a{a}_a^{†}{a}_i+\frac{1}{4}{\displaystyle \sum _{ijab}}{t}_{ij}^{ab}{t}_{ijab}{a}_a^{†}{a}_b^{†}{a}_j{a}_i+\dots & (10)\end{array}$

The operators T₁ and T₂ induce 1p − 1h and 2p − 2h excitations of the reference state, respectively. Here, the single-particle states i, j, … refer to hole states occupied in the reference state |Φ₀〉 while a, b, … denote valence states above the reference state. In practice, the expansion (10) is truncated. In the coupled cluster method with singles and doubles (CCSD) all operators T_i with i > 2 are neglected. In that case, the ground-state energy and the amplitudes $t_i^a,t_{ij}^{ab}$ are obtained by projecting the state (9) on the reference state and on all 1p-1h and 2p-2h configurations for which

$\begin{array}{l}\langle {\Phi }_0|\overline{H}|{\Phi }_0\rangle =E,\\ \langle {\Phi }_i^a|\overline{H}|{\Phi }_0\rangle =0,\\ \langle {\Phi }_{ij}^{ab}|\overline{H}|{\Phi }_0\rangle =0.& (11)\end{array}$

Here,

$\begin{array}{ll}\overline{H}\equiv e^{-T}H{e}^T=H+\left[H,T\right]+\frac{1}{2!}\left[\left[H,T\right],T\right]+\dots & (12)\end{array}$

denotes the similarity transformed Hamiltonian, which is computed by making use of the Baker-Campbell-Hausdorff expansion [10]. For two-body forces and in the CCSD approximation, this expansion terminates at 4-fold nested commutators⁴. The CCSD equations (11) show that the CCSD ground state is an eigenstate of the similarity-transformed Hamiltonian $\bar{H}=e^{-T}H{e}^T$ in the space of 0p − 0h, 1p − 1h, 2p − 2h configurations. The operator e^T being not unitary, $\bar{H}$ is not Hermitian. As a consequence, its left- and right-eigenvectors form a bi-orthonormal set [10].

Denoting 〈Φ_{0, L}| the left eigenvector for the ground state of A, we can now write the matrix elements of the coupled cluster Green's function G^cc as

$\begin{array}{l}{G}^{CC}(\alpha ,\beta ,E)\equiv \langle {\Phi }_{0,L}|\overline{a_{\alpha }}\frac{1}{E-(\overline{H}-E_{gs}^A)+i\eta }\overline{a_{\beta }^{†}}|{\Phi }_0\rangle \\ +\langle {\Phi }_{0,L}|\overline{a_{\beta }^{†}}\frac{1}{E-(E_{gs}^A-\overline{H})-i\eta }\overline{a_{\alpha }}|{\Phi }_0\rangle .& (13)\end{array}$

Here, $\overline{a_{\alpha }}=e^{-T}{a}_{\alpha }{e}^T$ and $\overline{a_{\beta }^{†}}=e^{-T}{a}_{\beta }^{†}{e}^T$ are the similarity-transformed annihilation and creation operators, respectively. These are computed with the Baker-Campbell-Hausdorff expansion (12).

In principle, the Green's function could be computed from the Lehman decomposition (3) with the solutions of the particle-attached equation of-motion (PA-EOM) and particle-removed equation-of motion (PR-EOM) for the A + 1 and A − 1 systems, respectively [10]. However, as the sum over all states in Equation (3) involves also eigenstates in the continuum, this approach is difficult to pursue in practice. Instead, we make use of the Lanczos continued fraction technique, which allows for an efficient and numerically stable computation of the Green's function [33, 62–66].

By definition of the Green's function, the parameter η in the matrix elements (2) is such that η → 0⁺. However, in this limit, because of the appearance of poles at energies $E=(E_i^{A+1}-E_{gs}^A)$ in the Green's function (see Equation 3), the calculation of optical potential for elastic scattering becomes numerically unstable. In order to resolve this issue, we compute an analytic continuation of the Green's function in the complex-energy plane by working in a Berggren basis [17, 67–73] (generated by the HF potential) that includes bound, resonant, and complex-continuum states. The solutions of the (PA-EOM) and (PR-EOM) in the Berggren basis, i.e., the eigenstates of the A ± 1 systems, are either bound, resonant or complex-scattering states. In other words, the poles of the analytically continued Green's function are located either at negative real or complex energy. As a result, the Green's function matrix elements for E ≥ 0 smoothly converge to a finite value as η → 0⁺ (this is illustrated below in Figure 1).

FIGURE 1

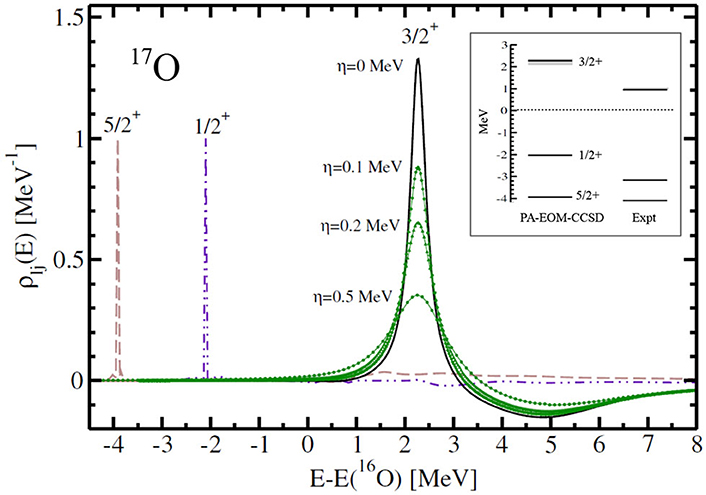
Figure 1. Computed level densities in ¹⁷O. For the J^π = 3/2⁺ level density, results are shown for several values of the parameter η to illustrate the smooth convergence pattern for η → 0. The inset shows the energies of the ground state, first excited and 3/2⁺ resonant states in ¹⁷O calculated at the PA-EOM-CCSD truncation level (see text for details).

The scattering states entering the Berggren basis are defined along a contour L⁺ in the fourth quadrant of the complex momentum plane, below the resonant single-particle states. According to the Cauchy theorem, the shape of the contour L⁺ is not important, under the condition that all resonant states lie between the contour and the real momentum axis. The Berggren completeness reads

$\begin{array}{ll}{\displaystyle \sum _i}|u_i\rangle \langle \widetilde{u_i}|+{\displaystyle {\int }_{L^{+}}}dk|u(k)\rangle \langle \widetilde{u(k)}|=\widehat{1},& (14)\end{array}$

where |u_i〉 are discrete states corresponding to bound and resonant solutions of the single-particle potential, and |u(k)〉 are complex-energy scattering states along the complex-contour L⁺. In practice, the integral along the complex continuum is discretized yielding a finite discrete basis set.

In Figure 1, we illustrate the numerical stability provided by the use of the Berggren basis for the computation of the Green's function. We are interested in the level density [74, 75]

$\begin{array}{ll}{\rho }_{lj}(E)=-\frac{1}{\pi }Tr\left[Im(G_{lj}(E)-G_{lj}^{(0)}(E))\right],& (15)\end{array}$

where G_lj(E) and $G_{lj}^0(E)$ are respectively the component of the Green's functions and the HF Green's function in the (l, j) partial wave⁵. We show in Figure 1, the J^π = 3/2⁺ level density in ¹⁷O calculated with the NNLO_sat interaction. The ground state in ¹⁶O is computed at the CCSD level while the Green's function is computed with the PA-EOM and PR-EOM Lanczos vectors truncated at the 2p − 1h and 1p − 2h excitation level, respectively (other details of the calculation are also the same as in section 3). As η approaches 0, the level density smoothly converges, and the position of the peak at η = 0 corresponds, as expected, to the position of the J^π = 3/2⁺ resonance in ¹⁷O (see inset in Figure 1, which shows the PA-EOM-CCSD energies in ¹⁷O). For completeness, we also show the J^π = 5/2⁺, 1/2⁺ level densities. In these cases, the level density at negative energies are equal to a Dirac delta function peaked at respectively the ground state and first excited state energies in ¹⁷O (see inset in Figure 1). For purpose of illustration in Figure 1, we have used a finite value of η for the J^π = 5/2⁺, 1/2⁺ densities and set the height of the corresponding peaks to 1.

3. Selected Results

We now show in this section a few results of the computation of neutron optical potentials for the double-magic nuclei ⁴⁰Ca and ⁴⁸Ca.

All calculations presented here are performed using the NNLO_sat chiral interaction [5], which reproduces the binding energy and charge radius of both systems [76, 77]. We want to point out here that a proper reproduction of the distribution of nuclear matter, and, more specifically, nuclear radii is critical in order to obtain an accurate account of reactions observables. All results are obtained from coupled-cluster calculations truncated at the CCSD level, while the Lanczos vectors in the PA-EOM (PR-EOM) have been truncated at the 2p − 1h (1p − 2h) excitation level. Since the computation of the Green's function is performed using the laboratory coordinates [the Hamiltonian H in Equation (8) is defined with these coordinates], the calculated optical potential is identified with the optical potential in the relative coordinates of the n −^A Ca system. This identification will result in a small error, which is a decreasing function of the target mass number A [33, 34] (see also section 4).

The HF calculations are performed in a mixed basis of harmonic oscillator and Berggren states, depending on the partial wave. The NNLO_sat interaction contains two-body and three-body terms. Denoting N₂ and N₃ the cutoffs in the harmonic oscillator (HO) basis of respectively, the two-body and three-body part of the interaction, we set N₂ = N₃ = N_max except for the most extensive calculations where N₂ = 14 and N₃ = 16. Finally, we truncate the three-nucleon forces at the normal-ordered two-body level in the HF basis. This approximation has been shown to work well in light- and medium mass nuclei [78, 79]. The harmonic oscillator frequency is kept fixed at ℏω = 16 MeV (for more details see [33, 34]).

We start with the computation of the n +⁴⁰ Ca optical potentials associated with the bound states in ⁴¹Ca. At the PA-EOM-CCSD level of truncation considered here, there are only three bound states supported by the NNLO_sat Hamiltonian. In order to show the convergence pattern of the potentials, we present in Figure 2 results at several values of N_max with the corresponding bound state energies. We present the diagonal part of the potentials, and for comparison the HF potential [for (N_max, N₃) = (14, 16)] in each partial wave is also shown in Figure 2. The energies are shown in the table in Figure 2 along with the experimental values. As expected, the convergence of energies is slower for higher-energy states. The difference between the ⁴¹Ca energies at (N_max, N₃) = (14,14) and (14,16) is ~220 keV in the case of the ground-state, whereas it is ~350 keV in the case of the J^π = 1/2⁻ second excited state. Even though the absolute binding energy is underestimated in the CCSD approximation, when compared to experiment [the CCSD binding energy of ⁴⁰Ca is 299.28 MeV for (N_max, N₃) = (14, 16), whereas the experimental value is 342.05 MeV], the neutron separation energies are consistently within 600 keV of the experimental values for ^40,48Ca⁶. The eigenenergies of these potentials are equal, by construction, to the bound states energies when using the effective mass mA/(A − 1) instead of the actual reduced mass. This can be traced to Equation (8) where the effective mass associated with the one-body kinetic operator is equal to mA/(A − 1) (see also section 4).

FIGURE 2

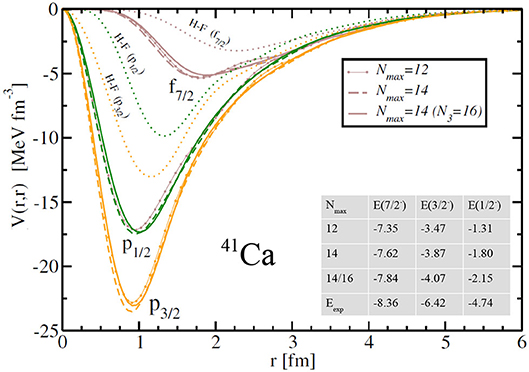
Figure 2. Diagonal part of the n +⁴⁰ Ca optical potential for the bound states in ⁴¹Ca computed with the NNLO_sat interaction. Results are shown for several values of N_max and the corresponding bound state energies (with respect to the ⁴⁰Ca ground state) are shown in the table (in MeV). The components of the HF potential in the associated partial waves are shown for (N_max, N₃) = (14, 16) (see text for details).

We now consider the neutron elastic scattering on ⁴⁰Ca and ⁴⁸Ca. The phase shift is computed in each partial wave with the optical potential calculated in the largest space (N_max, N₃) = (14, 16). The angular distributions are then obtained by summing the contributions from each partial wave. Figure 3 shows the resulting differential elastic cross section for ⁴⁰Ca(n, n)⁴⁰Ca at 5.2 MeV and ⁴⁸Ca(n, n)⁴⁸Ca at 7.8 MeV. We find that at these energies the inclusion of partial waves with angular momentum L ≤ 5 and L ≤ 6 is sufficient for ⁴⁰Ca and ⁴⁸Ca, respectively, the contribution of partial waves with higher L being negligible (see also the computations of elastic scattering on ^40,48Ca at other energies in Rotureau et al. [34]). The angular distributions obtained with the phenomenological Koning Delaroche (KD) potential [36] and the measured cross sections are also shown in Figure 3 for comparison. As Figure 3 indicates, the data at small angle where the cross section is larger, are well-reproduced for ⁴⁸Ca whereas the computed cross section is slightly above the data for ⁴⁰Ca. Overall, the shape of the experimental cross sections and the positions of the minima are well-reproduced for both nuclei, as expected from the correct reproduction of matter densities in ^40,48Ca by the NNLO_sat interaction.

FIGURE 3

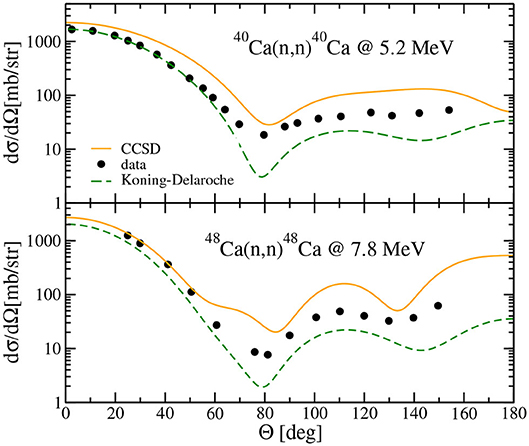
Figure 3. Differential elastic cross section for ⁴⁰Ca(n, n)⁴⁰Ca at 5.2 MeV (top) and ⁴⁸Ca(n, n)⁴⁸Ca at 7.8 MeV (bottom) calculated with the NNLO_sat interaction. Results obtained with the phenomenological Koning-Delaroche potential potential are shown (dashed line) for comparison. Data points are taken from Koning and Delaroche[36] (errors on the data are smaller than the symbols).

The experimental energy of the first two excited-states in ⁴⁰Ca, namely E(0⁺) = 3.35 MeV and E(3⁻) = 3.74 MeV are below the scattering energy E_scat = 5.2 MeV of the elastic process ⁴⁰Ca(n, n)⁴⁰Ca shown in Figure 3. In other words, the channels for excitation of the ⁴⁰Ca target are open at this scattering energy. This should result in a loss of flux in the initial elastic channel and the corresponding occurrence of an absorptive imaginary part in the phase shifts. The first excited 0⁺ state, which has a strong 4p − 4h components, cannot be properly reproduced at the truncation level considered here: its computed energy, solution of the EOM-CCSD equations, is ~16 MeV above the ground state. On the other hand, the 3⁻ excited state is well-reproduced with $E_{EOM-CCSD}(3^{-})$ = 3.94 MeV. Nevertheless, we have found that the computed absorption is practically negligible and none of the computed phase shifts at E_scat = 5.2 MeV have a significant imaginary part. A similar pattern happens for ⁴⁸Ca(n, n)⁴⁸Ca at 7.8 MeV: in that case, the first excited state E(2⁺) = 3.83 MeV is fairly well-reproduced, the computed value is $E_{EOM-CCSD}(2^{+})$ = 4.65 MeV, but again the absorption in that case is negligible too.

Although some excited states below the scattering energy are reproduced by the EOM-CCSD calculations, the absorption is negligible in both situations. This suggests that at the level of truncation considered here, namely 2p − 1h above the CCSD ground state, the computed wavefunctions are not correlated enough (in the perturbative expansion of the Dyson equation Equation (4), the absorption appears at second-order, beyond the HF contribution [61]). In other words, at these energies, the computed level density (15) in the n +^A Ca system is too small. We have observed that only at higher energy E ≳ 20 MeV the absorption starts to increase significantly (a similar pattern can be seen in Figure 4 of Rotureau et al. [33] for the CCSD computation of n +¹⁶ O optical potential). It is possible to increase artificially the absorption by using a finite value of η in Equation (13). This amounts to increasing the correlations content of the coupled-cluster wavefunctions and as shown in Rotureau et al. [33, 34], the computed elastic cross section in that case will decrease. In section 4, we will return to this lack of absorption in the computed potential.

FIGURE 4

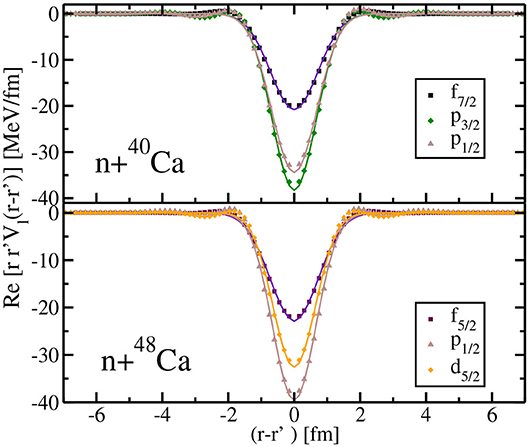
Figure 4. Real part of the neutron potential in several partial waves for ^40,48Ca at respectively 5.2 and 7.8 MeV. The potentials are shown at fixed values of R (equal to the charge radius in both nuclei) and as a function of r − r′. Symbols corresponds to the calculated potentials and the lines are the results of a fit with a Gaussian form factor (see text for details).

We should emphasize here that the computation of the optical potential with the coupled-cluster method is carried out without any free parameter. It is then not surprising that it does not allow for the same quality of reproduction of data as a phenomenological potential, such as the KD interaction (see Figure 3). But still, since microscopic optical potentials are built up from fundamental nuclear interactions without tuning to data, they may yield guidance for parameterizations of phenomenological potential, by providing information on the form factor, energy dependence and dependence on the isospin asymmetry of the targets. A recent series of studies has shown that non-locality can affect transfer reaction observables (e.g., [38–40]) and it is expected that it can equally affect other reaction channels. Microscopic potential can provide guidance on this aspect of the optical potential. Keeping in mind that a potential is not an observable and is not uniquely defined (for a given potential, it is possible to modify its high-energy component with a unitary transformation without affecting experimental predictions [80, 81]), we focus in the following on the non-locality of the CCSD optical potential.

We plot in Figure 4, the n +^40,48 Ca potentials in several partial waves, at a fixed value of R = (r + r′)/2 and as a function of r − r′. We fix R to be equal to the charge radius in both nuclei, namely 3.48 and 3.46 fm for respectively ⁴⁰Ca and ⁴⁸Ca [5]. We consider the same energy as previously, namely 5.2 MeV for ⁴⁰Ca and 7.8 MeV for ⁴⁸Ca. A fit of the potential using a Gaussian form factor, is also shown in Figure 4. As one can see, the shape of potentials in Figure 4 are well-reproduced by the fit. For ⁴⁰Ca, the values of the range β of the fitted Gaussian somehow varies slightly with the partial wave: we obtain β = 1.02, 0.94, 0.98 fm for the f_7/2, p_3/2 and p_1/2 component of the potentials, respectively. For ⁴⁸Ca, β = 1.04, 0.93, 0.91 fm for the f_5/2, p_1/2 and and d_5/2 partial waves, respectively. We have observed even smaller variations of the range with the energies although a more exhaustive study would be required to draw definitive conclusion about the dependence of β on the value of R and the energy. Nevertheless, in all cases, the non-local pattern of the optical potential display a Gaussian dependence, which corresponds to the choice made for the non-local form factor in the phenomenological potentials by Perey and Buck [82]. Note that due to the non-hermiticity of the Coupled Cluster Hamiltonian (see section 2.2) the potential is slightly non-symmetric in r and r′. However, since this effect is small [33, 34], it is hardly noticeable in Figure 4.

4. Challenges

In this section, we discuss some challenges and possible solutions for the development of fully predictive ab-initio optical potentials with the coupled-cluster method.

We saw in the previous section that with the ab-initio optical potentials computed at the CCSD level, one can arrive at an overall fair reproduction of data for medium-mass nuclei. However, the absorptive part of the potential was shown to be negligible at low energy. This lack of absorption was linked to neglected configurations in the computed Green's function.

Currently, ab-initio computation of optical potentials for medium-mass nuclei using chiral NN and 3NFs, have only been performed with the coupled-cluster method and the Self Consistent Green's Function (SCGF) method [31]. The SCGF is based on an iterative solution of the Dyson equation performed until a self-consistency between the input Green's function and the result of the Dyson equation has been reached [9]. In Idini et al. [31], the authors compute neutron optical potential for ¹⁶O and ⁴⁰Ca with the NNLO_sat interaction and include up to 2p − 1h configurations in the Green's function. In that work, the minima in the elastic cross sections are well-reproduced for both systems, and as in the CCSD computation of the potential, an overall lack of absorption was observed and attributed to neglected configurations in the model space.

The natural next step to address the lack of absorption at the CCSD level would be to include higher-order correlations in the Green's function by considering next order excitations in the coupled-cluster calculations, namely triple corrections. One should expect in that case an increased level density in the A + 1 system and as a result, a larger absorptive part of the optical potential. Coupled-cluster calculations with triple corrections are routinely used for nuclear spectroscopy [10] and have recently been implemented in the computation of the dipole polarizability of ⁴⁸Ca [83]. In that paper, the authors show that by including 3p − 3h excitations in the computation of the nuclear response function to an electromagnetic probe (the Green's function is a similar object since it is the response function to the addition/removal of a nucleon), the results improve over previous computations at CCSD.

For most nuclei, and particularly for heavier systems, there are many compound-nucleus resonances above the particle threshold. Since these states consist of a high number of particle-hole excitations they cannot be reproduced accurately by ab-initio methods and are usually best described by a stochastic approach [84]. In order to account for the formation of the compound nucleus and the resulting loss of flux in the elastic channel, one could add a polarization term to the ab-initio potential. A possible way to compute this term would be to use Random Matrix Theory to generate an effective Hamiltonian belonging to a Gaussian Orthogonal Ensemble [85].

Since the coupled-cluster Green's function is computed in the laboratory frame, the optical potential solution of the Dyson equation is defined with respect to the origin of that frame O. As mentioned in section 3, we have identified this potential with the potential in the relative n − A coordinate. For the medium-mass nuclei considered here, this prescription creates a small error, which decreases with A [33, 34, 86]. For light systems, a correction to the optical potential becomes necessary to account for the identification between laboratory and relative coordinates. It has been demonstrated that the coupled cluster wavefunction factorizes to a very good approximation into a product of an intrinsic wave function and a Gaussian in the center-of-mass coordinate [87]. Since both the potential and the center-of-mass wavefunction of the target are computed in the laboratory frame, it seems reasonable to suggest that such a correction could be introduced in the form of a folding of the potential with the center-of-mass wavefunction (nevertheless, such a prescription would have to be worked out and checked). Another possible way to introduce a correction of the potential could be to use the integral method utilized in the GFMC approach (see e.g., [88]) for computation of overlap functions (see also e.g., [89, 90]).

5. Summary

In this article, we have presented recent developments in the computation of nucleon-nucleus optical potential constructed by combining the Green's function and the coupled-cluster method. A key element in this approach is the use of the Berggren basis, which enables a consistent description of bound, resonant states and scattering process of the (nucleon-target) system and at the same time, allows to properly deal with the poles of the Green's function on the real energy axis.

We have shown results for optical potentials at negative and positive energy for the double magic systems ⁴⁰Ca and ⁴⁸Ca using a chiral NN and 3NFs that reproduces the binding energy and charge radii in both systems. We pointed out that a proper reproduction of the distribution of nuclear matter, and, more specifically, nuclear radii, by the Hamiltonian, is essential to give an accurate account of reaction observables. At the truncation level considered here, namely 2p − 2h and 2p − 1h / 2h − 1p in the computation of the target and the Green's function, respectively, an overall fair agreement with data was obtained. Nevertheless, in that case, the optical potential at positive energy suffers from a lack of absorption, which stems from the neglect of higher-order configurations. In (near) future development, higher-order excitations in the coupled-cluster expansion will be included to address this issue.

In the future, the Green's function formalism and coupled-cluster method could be combined for applications to other reaction channels, such as transfer, capture, breakup, and charge-exchange. Another possible approach toward the ab-initio computation of transfer reactions with medium-mass nuclei is the Green's Function Transfer (GFT) method [91]. Using the optical potential and Green's function computed with the coupled-cluster method as input of the GFT equations, as well as phenomenological ingredients, a very good reproduction of data for populating the ground states in ^41,49Ca was obtained with this approach. Although the current implementations of the GFT method require phenomenological inputs, future extensions of the formalism should allow ab-initio computation of transfer reactions [91].

Author Contributions

JR wrote this manuscript.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author would like to thank his collaborators P. Danielewicz, G. Hagen, G. R. Jansen, F. M. Nunes, and T. Papenbrock for their contributions to the studies presented in this work.

Footnotes

1. ^Two phase-equivalent potentials will reproduce the same elastic two-body scattering data but may have different off-shell behavior.

2. ^n, l, j, j_z, τ_z label the radial quantum number, the orbital angular momentum, the total orbital momentum, its projection on the z-axis, and the isospin projection, respectively.

3. ^Similarly, for $E=E_{gs}^A-E_n^{A-1}$, the solution of the optical potential V^opt(E) are the radial overlap ${\xi }_n^{-}(\text{r})=\langle {\text{Ψ}}_0|a_r^{†}|{\text{Ψ}}_n^{A-1}\rangle$ [61].

4. ^The 3NFs component V_ijk of the Hamiltonian in (8) is truncated at the normal-ordered two-body level in the HF basis (see section 3).

5. ^Since the Green's functions are here defined by adding (and removing) a nucleon from the 0⁺ ground state in the target A, the quantum number (l, j) are conserved.

6. ^By including both perturbative triple excitations and perturbative estimates for the neglected residual 3NFs (3NF terms beyond the normal-ordered two-body approximation), a good agreement with experimental binding energies can be obtained for ^40,48Ca [76].

References

1. Beane SR, Bedaque PF, Savage MJ, van Kolck U. Towards a perturbative theory of nuclear forces. Nucl Phys A. (2002) 700:377–402. doi: 10.1016/S0375-9474(01)01324-0

CrossRef Full Text | Google Scholar

2. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

3. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

5. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

6. Nogga A, Bogner SK, Schwenk A. Low-momentum interaction in few-nucleon systems. Phys Rev C. (2004) 70:061002. doi: 10.1103/PhysRevC.70.061002

CrossRef Full Text | Google Scholar

7. Barrett BR, Navratil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

8. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067–118. doi: 10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

9. Dickhoff WH, Barbieri C. Self-consistent Green's function method for nuclei and nuclear matter. Prog Part Nucl Phys. (2004) 52:377. doi: 10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

10. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rep Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hergert H, Bogner SK, Morris TD, Schwenk A, Tsukiyama K. The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys Rep. (2016) 621:165–222. doi: 10.1016/j.physrep.2015.12.007

CrossRef Full Text | Google Scholar

12. Lee D. Lattice simulations for few- and many-body systems. Prog Part Nucl Phys. (2009) 63:117–54. doi: 10.1016/j.ppnp.2008.12.001

CrossRef Full Text | Google Scholar

13. Hagen G, Dean DJ, Hjorth-Jensen M, Papenbrock T. Complex coupled-cluster approach to an ab-initio description of open quantum systems. Phys Lett B. (2007) 656:169–73. doi: 10.1016/j.physletb.2007.07.072

CrossRef Full Text | Google Scholar

14. Papadimitriou G, Rotureau J, Michel N, Płoszajczak M, Barrett BR. Ab initio no-core Gamow shell model calculations with realistic interactions. Phys Rev C. (2013) 88:044318. doi: 10.1103/PhysRevC.88.044318

CrossRef Full Text | Google Scholar

15. Hagen G, Papenbrock T, Dean DJ, Hjorth-Jensen M, Asokan BV. Ab initio computation of neutron-rich oxygen isotopes. Phys Rev C. (2009) 80:021306. doi: 10.1103/PhysRevC.80.021306

CrossRef Full Text | Google Scholar

16. Hagen G, Papenbrock T, Hjorth-Jensen M. Tuning spin-orbit coupling and superconductivity at the SrTiO₃/LaAlO₃ Interface: a magnetotransport study. Phys Rev Lett. (2010) 104:18250. doi: 10.1103/PhysRevLett.104.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hagen G, Jansen GR, Papenbrock T. Structure of ⁷8Ni from first-principles computations. Phys Rev Lett. (2016) 117:172501. doi: 10.1103/PhysRevLett.117.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Baroni S, Navrátil P, Quaglioni S. Unified ab initio approach to bound and unbound states: no-core shell model with continuum and its application to ⁷He. Phys Rev C. (2013) 87:034326. doi: 10.1103/PhysRevC.87.034326

CrossRef Full Text | Google Scholar

19. Langhammer J, Navrátil P, Quaglioni S, Hupin G, Calci A, Roth R. Continuum and three-nucleon force effects on ⁹Be energy levels. Phys Rev C. (2015) 91:021301. doi: 10.1103/PhysRevC.91.021301

CrossRef Full Text | Google Scholar

20. Vorabbi M, Calci A, Navrátil P, Kruse MKG, Quaglioni S, Hupin G. Structure of the exotic ⁹He nucleus from the no-core shell model with continuum. Phys Rev C. (2018) 97:034314. doi: 10.1103/PhysRevC.97.034314

CrossRef Full Text | Google Scholar

21. Hu BS, Wu Q, Sun ZH, Xu FR. Ab initio Gamow in-medium similarity renormalization group with resonance and continuum. Phys Rev C. (2019) 99:061302. doi: 10.1103/PhysRevC.99.061302

CrossRef Full Text | Google Scholar

22. Navrátil P, Roth R, Quaglioni S. Ab initio many-body calculations of nucleon scattering on ⁴He, ⁷Li, ⁷Be, ¹2C, and ¹6O. Phys Rev C. (2010) 82:034609. doi: 10.1103/PhysRevC.82.034609

CrossRef Full Text | Google Scholar

23. Baroni S, Navrátil P, Quaglioni S. Ab initio description of the exotic unbound ⁷He nucleus. Phys Rev Lett. (2013) 110:022505. doi: 10.1103/PhysRevLett.110.022505

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Raimondi F, Hupin G, Navrátil P, Quaglioni S. Deuteron-induced nucleon transfer reactions within an ab initio framework: first application to p-shell nuclei. Phys Rev C. (2016) 93:054606. doi: 10.1103/PhysRevC.93.054606

CrossRef Full Text | Google Scholar

25. Varga K, Pieper SC, Suzuki Y, Wiringa RB. Monte Carlo integration in Glauber model analysis of reactions of Halo nuclei. Phys Rev C. (2002) 66:034611. doi: 10.1103/PhysRevC.66.034611

CrossRef Full Text | Google Scholar

26. Nollett KM, Pieper SC, Wiringa RB, Carlson J, Hale GM. Quantum Monte Carlo calculations of neutron-α scattering. Phys Rev Lett. (2007) 99:022502. doi: 10.1103/PhysRevLett.99.022502

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha-alpha scattering. Nature. (2015) 528:111–4. doi: 10.1038/nature16067

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Waldecker SJ, Barbieri C, Dickhoff WH. Microscopic self-energy calculations and dispersive optical-model potentials. Phys Rev C. (2011) 84:034616. doi: 10.1103/PhysRevC.84.034616

CrossRef Full Text | Google Scholar

30. Barbieri C, Jennings BK. Nucleon-nucleus optical potential in the particle-hole approach. Phys Rev C. (2005) 72:014613. doi: 10.1103/PhysRevC.72.014613

CrossRef Full Text | Google Scholar

31. Idini A, Barbieri C, Navrátil P. Ab initio optical potentials and nucleon scattering on medium mass nuclei. Phys Rev Lett. (2019) 123:092501. doi: 10.1103/PhysRevLett.123.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Hagen G, Michel N. Elastic proton scattering of medium mass nuclei from coupled-cluster theory. Phys Rev C. (2012) 86:021602. doi: 10.1103/PhysRevC.86.021602

CrossRef Full Text | Google Scholar

33. Rotureau J, Danielewicz P, Hagen G, Nunes FM, Papenbrock T. Optical potential from first principles. Phys Rev C. (2017) 95:024315. doi: 10.1103/PhysRevC.95.024315

CrossRef Full Text | Google Scholar

34. Rotureau J, Danielewicz P, Hagen G, Jansen GR, Nunes FM. Microscopic optical potentials for calcium isotopes. Phys Rev C. (2018) 98:044625. doi: 10.1103/PhysRevC.98.044625

CrossRef Full Text | Google Scholar

35. Thompson IJ, Nunes FM. Nuclear Reactions for Astrophysics. Cambridge: Cambridge University Press (2009).

Google Scholar

36. Koning AJ, Delaroche JP. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl Phys A. (2003) 713:231–310. doi: 10.1016/S0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

37. Achterberg E, Capurro OA, Marti GV. Nuclear data sheets for A = 178. Nucl Data Sheets. (2009) 110:1473–688. doi: 10.1016/j.nds.2009.05.002

CrossRef Full Text | Google Scholar

38. Titus LJ, Nunes FM. Testing the Perey effect. Phys Rev C. (2014) 89:034609. doi: 10.1103/PhysRevC.89.034609

CrossRef Full Text | Google Scholar

39. Ross A, Titus LJ, Nunes FM, Mahzoon MH, Dickhoff WH, Charity RJ. Effects of nonlocal potentials on (p, d) transfer reactions. Phys Rev C. (2015) 92:044607. doi: 10.1103/PhysRevC.92.044607

CrossRef Full Text | Google Scholar

40. Titus LJ, Nunes FM, Potel G. Explicit inclusion of nonlocality in (d, p) transfer reactions. Phys Rev C. (2016) 93:014604. doi: 10.1103/PhysRevC.93.014604

CrossRef Full Text | Google Scholar

41. Bollen G. FRIB–facility for rare isotope beams. AIP Conf Proc. 1224:432–41. doi: 10.1063/1.3431449

CrossRef Full Text | Google Scholar

42. Kester O, Stöcker H. FAIR Project at GSI. Singapore: World Scientific Publishing Co. (2016).

Google Scholar

43. Feshbach H. Unified theory of nuclear reactions. Ann Phys. (1958) 5:357. doi: 10.1016/0003-4916(58)90007-1

CrossRef Full Text | Google Scholar

44. Feshbach H. A unified theory of nuclear reactions, II. Ann Phys. (1962) 19:287. doi: 10.1016/0003-4916(62)90221-X

CrossRef Full Text | Google Scholar

45. Capuzzi F, Mahaux C. Projection operator approach to the self-energy. Ann Phys. (1996) 245:147–208. doi: 10.1006/aphy.1996.0006

CrossRef Full Text | Google Scholar

46. Dickhoff WH, Charity RJ. Recent developments for the optical model of nuclei. Prog Part and Nucl Phys. (2019) 105:252–99. doi: 10.1016/j.ppnp.2018.11.002

CrossRef Full Text | Google Scholar

47. Blanchon G, Dupuis M, Arellano HF, Vinh Mau N. Microscopic positive-energy potential based on the Gogny interaction. Phys Rev C. (2015) 91:014612. doi: 10.1103/PhysRevC.91.014612

CrossRef Full Text | Google Scholar

48. Whitehead TR, Lim Y, Holt JW. Proton elastic scattering on calcium isotopes from chiral nuclear optical potentials. Phys Rev C. (2019) 100:014601. doi: 10.1103/PhysRevC.100.014601

CrossRef Full Text | Google Scholar

49. Whitehead TR, Lim Y, Holt JW. Neutron elastic scattering on calcium isotopes from chiral nuclear optical potentials. Phys Rev C. (2020) 100:064613. doi: 10.1103/PhysRevC.101.064613

CrossRef Full Text | Google Scholar

50. Amos K, Dortmans PJ, von Geramb HV, Karataglidis S, Raynnal J. Nucleon-nucleus scattering: a microscopic nonrelativistic approach. Adv Nucl Phys. (2002) 25:276–536. doi: 10.1007/0-306-47101-9_3

CrossRef Full Text | Google Scholar

51. Kerman AK, McManus H, Thaler RM. The scattering of fast nucleons from nuclei. Ann Phys. (1959) 8:551–635. doi: 10.1016/0003-4916(59)90076-4

CrossRef Full Text | Google Scholar

52. Yamaguchi N, Nagata S, Matsuda T. Optical model potential in the lowest order Brueckner theory and complex effective N-N interaction. Prog Theor Phys. (1983) 70:459–77. doi: 10.1143/PTP.70.459

CrossRef Full Text | Google Scholar

53. Furumoto T, Sakuragi Y, Yamamoto Y. New complex G-matrix interactions derived from two- and three-body forces and application to proton-nucleus elastic scattering. Phys Rev C. (2008) 78:044610. doi: 10.1103/PhysRevC.78.044610

CrossRef Full Text | Google Scholar

54. Vorabbi M, Finelli P, Giusti C. Theoretical optical potential derived from nucleon-nucleon chiral potentials. Phys Rev C. (2016) 93:034619. doi: 10.1103/PhysRevC.93.034619

CrossRef Full Text | Google Scholar

55. Gennari M, Vorabbi M, Calci A, Navrátil P. Microscopic optical potentials derived from ab initio translationally invariant nonlocal one-body densities. Phys Rev C. (2018) 97:034619. doi: 10.1103/PhysRevC.97.034619

CrossRef Full Text | Google Scholar

56. Burrows M, Elster C, Weppner SP, Launey KD, Maris P, Nogga A, et al. Ab initio folding potentials for nucleon-nucleus scattering based on no-core shell-model one-body densities. Phys Rev C. (2019) 99:044603. doi: 10.1103/PhysRevC.99.044603

CrossRef Full Text | Google Scholar

57. Mahzoon MH, Charity RJ, Dickhoff WH, Dussan H, Waldecker SJ. Forging the link between nuclear reactions and nuclear structure. Phys Rev Lett. (2014) 112:162503. doi: 10.1103/PhysRevLett.112.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Charity RJ, Sobotka LG, Dickhoff WH. Asymmetry dependence of proton correlations. Phys Rev Lett. (2006) 97:162503. doi: 10.1103/PhysRevLett.97.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Dickhoff WH, Charity RJ, Mahzoon MH. Novel applications of the dispersive optical model. J Phys G. (2017) 44:033001. doi: 10.1088/1361-6471/44/3/033001

CrossRef Full Text | Google Scholar

60. Mahaux C, Sartor R. Calculation of the shell-model potential from the optical-model potential. Phys Rev Lett. (1986) 57:3015–8. doi: 10.1103/PhysRevLett.57.3015

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Dickhoff WH, Neck DV. Many-Body Theory Exposed! Singapore: World Scientific (2007).

Google Scholar

62. Efros VD, Leidemann W, Orlandini G, Barnea N. The Lorentz integral transform (LIT) method and its applications to perturbation-induced reactions. J Phys G. (2007) 34:R459. doi: 10.1088/0954-3899/34/12/R02

CrossRef Full Text | Google Scholar

63. Bacca S, Barnea N, Hagen G, Miorelli M, Orlandini G, Papenbrock T. Giant and pigmy dipole resonances in ⁴He, ^16,22O, and ⁴⁰Ca from chiral nucleon-nucleon interactions. Phys Rev C. (2014) 90:064619. doi: 10.1103/PhysRevC.90.064619

CrossRef Full Text | Google Scholar

64. Dagotto E. Correlated electrons in high-temperature superconductors. Rev Mod Phys. (1994) 66:763–840. doi: 10.1103/RevModPhys.66.763

CrossRef Full Text | Google Scholar

65. Hallberg KA. Density-matrix algorithm for the calculation of dynamical properties of low-dimensional systems. Phys Rev B. (1995) 52:R9827–30. doi: 10.1103/PhysRevB.52.R9827

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Haxton WC, Nollett KM, Zurek KM. Piecewise moments method: generalized Lanczos technique for nuclear response surfaces. Phys Rev C. (2005) 72:065501. doi: 10.1103/PhysRevC.72.065501

CrossRef Full Text | Google Scholar

67. Berggren T. On the use of resonant states in eigenfunction expansions of scattering and reaction amplitudes. Nucl Phys A. (1968) 109:265–87. doi: 10.1016/0375-9474(68)90593-9

CrossRef Full Text | Google Scholar

68. Michel N, Nazarewicz W, Płoszajczak M, Bennaceur K. Gamow shell model description of neutron-rich nuclei. Phys Rev Lett. (2002) 89:042502. doi: 10.1103/PhysRevLett.89.042502

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Id Betan R, Liotta RJ, Sandulescu N, Vertse T. Two-particle resonant states in a many-body mean field. Phys Rev Lett. (2002) 89:042501. doi: 10.1103/PhysRevLett.89.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Hagen G, Vaagen JS, Hjorth-Jensen M. The contour deformation method in momentum space, applied to subatomic physics. J Phys A. (2004) 37:8991. doi: 10.1088/0305-4470/37/38/006

CrossRef Full Text | Google Scholar

71. Hagen G, Vaagen JS. Study of resonant structures in a deformed mean field by the contour deformation method in momentum space. Phys Rev C. (2006) 73:034321. doi: 10.1103/PhysRevC.73.034321

CrossRef Full Text | Google Scholar

72. Rotureau J, Michel N, Nazarewicz W, Płoszajczak M, Dukelsky J. Density matrix renormalization group approach for many-body open quantum systems. Phys Rev Lett. (2006) 97:110603. doi: 10.1103/PhysRevLett.97.110603

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Fossez K, Rotureau J, Nazarewicz W. Energy spectrum of neutron-rich helium isotopes: complex made simple. Phys Rev C. (2018) 98:061302. doi: 10.1103/PhysRevC.98.061302

CrossRef Full Text | Google Scholar

74. Shlomo S. Energy level density of nuclei. Nucl Phys A. (1992) 539:17–36. doi: 10.1016/0375-9474(92)90233-A

CrossRef Full Text | Google Scholar

75. Mizuyama K, Colò G, Vigezzi E. Continuum particle-vibration coupling method in coordinate-space representation for finite nuclei. Phys Rev C. (2012) 86:034318. doi: 10.1103/PhysRevC.86.034318

CrossRef Full Text | Google Scholar

76. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the ⁴8Ca nucleus. Nat Phys. (2016) 12:186. doi: 10.1038/nphys3529

CrossRef Full Text | Google Scholar

77. Garcia Ruiz RF, Bissell ML, Blaum K, Ekström A, Frömmgen N, Hagen G, et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat Phys. (2016) 12:594–8. doi: 10.1038/nphys3645

CrossRef Full Text | Google Scholar

78. Hagen G, Papenbrock T, Dean DJ, Schwenk A, Nogga A, Włoch M, et al. Coupled-cluster theory for three-body Hamiltonians. Phys Rev C. (2007) 76:034302. doi: 10.1103/PhysRevC.76.034302

CrossRef Full Text | Google Scholar

79. Roth R, Binder S, Vobig K, Calci A, Langhammer J, Navrátil P. Medium-mass nuclei with normal-ordered chiral NN+3N interactions. Phys Rev Lett. (2012) 109:052501. doi: 10.1103/PhysRevLett.109.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Bogner SK, Furnstahl RJ, Schwenk A. From low-momentum interactions to nuclear structure. Prog Part Nucl Phys. (2010) 65:94–147. doi: 10.1016/j.ppnp.2010.03.001

CrossRef Full Text | Google Scholar

81. Arellano HF, Blanchon G. Irreducible nonlocality of optical model potentials based on realistic NN interactions. Phys Rev C. (2018) 98:054616. doi: 10.1103/PhysRevC.98.054616

CrossRef Full Text | Google Scholar

82. Perey F, Buck B. A non-local potential model for the scattering of neutrons by nuclei. Nucl Phys. (1962) 32:353. doi: 10.1016/0029-5582(62)90345-0

CrossRef Full Text | Google Scholar

83. Miorelli M, Bacca S, Hagen G, Papenbrock T. Computing the dipole polarizability of ⁴8Ca with increased precision. Phys Rev C. (2018) 98:014324. doi: 10.1103/PhysRevC.98.014324

CrossRef Full Text | Google Scholar

84. Mitchell GE, Richter A, Weidenmüller HA. Random matrices and chaos in nuclear physics: nuclear reactions. Rev Mod Phys. (2010) 82:2845–901. doi: 10.1103/RevModPhys.82.2845

CrossRef Full Text | Google Scholar

85. Fanto P, Bertsch GF, Alhassid Y. Neutron width statistics in a realistic resonance-reaction model. Phys Rev C. (2018) 98:014604. doi: 10.1103/PhysRevC.98.014604

CrossRef Full Text | Google Scholar

86. Johnson RC. Translation invariance and antisymmetry in the theory of the nucleon optical model. Phys Rev C. (2017) 95:064610. doi: 10.1103/PhysRevC.95.064610

CrossRef Full Text | Google Scholar

87. Hagen G, Papenbrock T, Dean DJ. Solution of the center-of-mass problem in nuclear structure calculations. Phys Rev Lett. (2009) 103:062503. doi: 10.1103/PhysRevLett.103.062503

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Nollett KM. Ab initio calculations of nuclear widths via an integral relation. Phys Rev C. (2012) 86:044330. doi: 10.1103/PhysRevC.86.044330

CrossRef Full Text | Google Scholar

89. Pinkston WT, Satchler GR. Form factors for nuclear stripping reactions. Nucl Phys. (1965) 72:641–56. doi: 10.1016/0029-5582(65)90417-7

CrossRef Full Text | Google Scholar

90. Timofeyuk NK. One nucleon overlap integrals for light nuclei. Nucl Phys A. (1998) 632:19–38. doi: 10.1016/S0375-9474(98)00810-0

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Rotureau J, Potel G, Li W, Nunes F. Merging ab initio theory and few-body approach for (d, p) reactions. J Phys G. (2020) 47:065103. doi: 10.1088/1361-6471/ab8530

CrossRef Full Text | Google Scholar