Time Operators Determined by Cylindrical Processes

1. Introduction

The paper is devoted to extensions of internal time operators on the spaces of functions with values in topological vector spaces and on the spaces of generalized functions of this type associated with K-systems. The main reason of the introduction of time operators was the Lambda transformation theory formulated by I. Prigogine and his collaborators (see [1–3]) as a new approach to the theory of irreversibility in statistical physics. Precisely, to the problem of the relation between the reversible laws of dynamics and the observed irreversible (stochastic) evolution. Let us remind, that the classical view point was that irreversible behavior of the observed time evolution in a dynamical system can only arise from deterministic dynamics as the result of averaging (coarse-graining). The new approach can be formulated, in simplified terms, as a task to relate a given unitary evolution group {U_t}_t∈ℝ acting on a Hilbert space of Gibbs' square integrable densities with an entropy increasing evolution semigroup {W_t}_t∈ℝ+ through a similarity transformation called the transformation Λ (Lambda) (see [3]) as follows:

$\begin{array}{ll}{W}_t\Lambda =\Lambda U_t,t\in {ℝ}_{+}.& (1)\end{array}$

Almost all known constructions of Λ transformations have been done so far for the dynamical systems which admit time operators (see [4] for another approach). Such dynamical systems allow the existence of Lyapunov variables, defined as functions of time operators, representing non-equilibrium entropy [1]. This is also a possible way to the task of defining time operator in quantum mechanics which in turn could allow to determine entropy operator. However, the class of dynamical systems for which time operators can be defined is very narrow, in fact, it is limited to K-systems.

Time operators were initially defined on the Hilbert space of square integrable functions. The problem of an extension of the concept of time operator was motivated by a need to extend the Λ transformation theory beyond square integrable probability densities. Indeed, it is natural to ask about a possibility to extend Λ and W_t on a larger class of states, including probability measures. Particularly interesting, from the physical point of view, is the possibility of extension on singular measures concentrated at single points of the phase space [2, 5–7].

Another motivation for the introduction and study of time operators is due to the recently discovered fact that time operators can be also associated with non-invertible dynamics and used as a new tool in the spectral analysis of evolution semigroups of unstable dynamical systems (see e.g., [8–13]). In this case time operators and evolution semigroups are defined on various topological vector spaces. The relation between the time operator T and the evolution semigroup {U_t} is such that each U_t preserves the domain of T and satisfies the relation

$\begin{array}{ll}T{U}_t=U_{t}T+t{U}_t.& (2)\end{array}$

The idea behind the spectral analysis of the evolution semigroup {U_t} on a Hilbert space with the help of the time operator T is to decompose T in terms of a complete system of its eigenvectors {e_n,k}, Te_n,k = ne_n,k, such that U_te_n,k = e_n+t,k, as follows

$\begin{array}{l}T={\displaystyle \sum _n}n{\displaystyle \sum _k}(·,e_{n,k})e_{n,k}.\end{array}$

Similar spectral decompositions but in terms of Schauder bases or frames can be obtained in other topological vector spaces.

In this paper we will focus on the construction of time operators associated with K-systems acting on the spaces of cylindrical elements. A cylindrical element is an object which is a generalization of an E valued function, where E is a locally convex space. More precisely, p-cylindrical element, which will be defined in the next section, is a generalization of a weakly p-integrable function with values in E.

Although such extensions of time operators concern various topological vector spaces we will elaborate a unified approach based on the idea of stochastic integral with respect to cylindrical martingales (see [14]). We will also study the related problem of decomposability of cylindrical elements. It can happen that the action of a time operator or even a conditional expectation does not leave the space of vector valued functions invariant but leads to cylindrical elements instead. The decomposability of cylindrical elements allows to represent them again as measurable functions.

The paper is organized as follows. In section 2, we gathered the basic facts on cylindrical elements, cylindrical measures and cylindrical martingales. We focus on the Pettis integrability of vector valued functions and cylindrical elements. We also characterize vector spaces of Pettis integrable cylindrical elements. Section 3 is devoted to the construction of time operators with respect to cylindrical processes and to the solution of the problem of decomposability in two particular cases.

2. Cylindrical Elements and Cylindrical Martingales

Throughout this paper, by a locally convex space (l.c.s.) or a topological vector space (t.v.s) we mean a Hausdorff l.c.s. (respectively t.v.s.) not equal to {0} over the field of real or complex scalars. If E is an l.c.s. then E′ denotes its topological dual and 〈x, x′〉 stands for the value of a functional x′ ∈ E′ at x ∈ E. For subsets A ⊂ E and B ⊂ E′ the symbols A^◦ and B^◦ denote the polars with respect to the duality 〈E, E′〉 and 〈E′, E〉 respectively, i.e., A^◦ = {x′ ∈ E^′:|〈x, x′〉| ≤ 1, for each x ∈ A} and B^◦ = {x ∈ E:|〈x, x′〉| ≤ 1, for each x′ ∈ B}. By σ(E′, E) we shall denote the weak topology on E′ and by τ(E′, E) the Mackey topology, i.e., is the topology of uniform convergence on all σ(E, E′)–compact, convex, circled subsets of E. $E_{\tau }^{\prime }$ will denote the space E′ with the Mackey topology. An l.c.s. E is quasi-complete if each bounded closed subset of E is complete.

Let $(\Omega ,{A},P)$ be a probability space, $L^p=L^p(\Omega ,{A},P)$, p ≥ 0, and let E be an l.c.s. By a p-cylindrical element, or simply cylindrical element, we mean a linear operator X : E′ → L^p. Notice that any function x(·) : Ω → E such that 〈x(·), x′〉 ∈ L^p determines the cylindrical element

$\begin{array}{l}X{x}^{\prime }=X_{x(·)}{x}^{\prime }=\langle x(·),x^{\prime }\rangle .\end{array}$

Let us now introduce the concept of Pettis integrability of cylindrical elements. The reason of doing this is the following. In statistical physics the main object of interest is the time evolution of statistical ensembles, represented mathematically as probability distributions. However, for technical reasons we often take only some classes of probability distributions as the states of the system. In our case we confine to those probability measures which are absolutely continuous with respect to some reference measure. This allows to replace measures by their densities (Radon-Nikodyn derivatives) or by classes of integrable functions in general. Nevertheless, for a given integrable function f we can recover the corresponding measure μ_f putting

$\begin{array}{ll}{\mu }_f(A)={\displaystyle {\int }_{A}f}dP,A\in {A}.& (3)\end{array}$

Replacing f by a vector valued function $\overrightarrow{f}:\Omega \to E$ we should be able to recover the corresponding measure ${\mu }_{\overrightarrow{f}}$ like in (3) but this is not always possible. For example, if E is a Banach space and $\overrightarrow{f}$ a measurable function such that $\Vert \overrightarrow{f}\Vert$ is integrable then (3) holds and defines E-valued measure. However this is not true, in general, under the weaker assumption of integrability of $\left|\langle \overrightarrow{f},x^{\prime }\rangle \right|$, for all x′ ∈ E. Additional assumptions have to be imposed on $\overrightarrow{f}$ such as the Pettis integrability defined below. The same can happen when we replace vector valued functions by cylindrical elements.

We say that a cylindrical element X : E′ → L⁰ is Pettis integrable if X(E′) ⊂ L¹ and for each $A\in {A}$ there exists x_A ∈ E such that

$\begin{array}{ll}\langle x_A,x^{\prime }\rangle ={\displaystyle {\int }_A}X{x}^{\prime }dP\text{ for each }{x}^{\prime }\in E^{\prime }.& (4)\end{array}$

We write

$\begin{array}{ll}{\displaystyle {\int }_A}XdP=x_A.& (5)\end{array}$

and call it the Pettis integral of the cylindrical element X. Replacing in (4) and (5) X by a vector valued function $\overrightarrow{f}$ we obtain the classical definition of the Pettis integral (see [15]).

General properties of Pettis integrable cylindrical elements are in ref. ([16]). Here we will show relations between Pettis integrability and continuity of cylindrical elements.

We have

Proposition 1. ([16, 17]) Let E be a sequentially complete l.c.s. space and X : E′ → L¹ a cylindrical element. Then the following conditions are equivalent

(1) T is Pettis integrable

(2) T is $(\tau (E^{\prime },E),\Vert ·{\Vert }_{L^1})$ continuous.

Actually, the implication (2) ⇒ (1) in the above Proposition is valid without the assumption of sequential completeness (see [17]).

Let us also mention about two properties of Pettis integrable cylindrical elements which will be used later:

Proposition 2. If E and F are l.c.s., S : E → F is a continuous linear operator and X : E′ → L¹ is a Pettis integrable cylindrical element, then the linear operator X ◦ S^* : F′ → L¹ is Pettis integrable and

$\begin{array}{l}S\left({\displaystyle {\int }_A}XdP\right)={\displaystyle {\int }_A}X◦S^{*},\text{ for each }A\in {A}.\end{array}$

Proposition 3. If X is a Pettis integrable cylindrical element then for each absolutely convex neighborhood of 0 in E

$\begin{array}{l}{\displaystyle \underset{x^{\prime }\in U^{◦}}{\text{sup}}}{\displaystyle {\int }_{\Omega }}\left|X{x}^{\prime }\right|dP<\infty \end{array}$

The proofs of the above properties can be found in [17].

It follows from Proposition 3 that if E is a normed space then X is a bounded linear operator form E′ to L¹ with the operator norm

$\begin{array}{l}\Vert X\Vert ={\displaystyle \underset{\Vert x^{\prime }\Vert \le 1}{\text{sup}}}{\displaystyle {\int }_{\Omega }}\left|X{x}^{\prime }\right|dP\end{array}$

Notice that σ(L¹, L^∞) compactness of a family of functions in L¹ is equivalent to its uniform integrability (Dunford-Pettis Theorem) thus using the Vallèe-Poussin Theorem (see e.g., [18]) we obtain

Corollary. If p > 1, E is a reflexive Banach space and X : E′ → L^p a continuous cylindrical element then X is Pettis integrable.

Let E be an l.c.s. and let ${{L}}^p(E)$, p ≥ 1, denote the space of all separably valued and weakly p-integrable functions x(·) : Ω → E with the topology generated by the family of seminorms

$⦀x(·){⦀}_{U^{◦}}=\underset{x^{\prime }\in U^{◦}}{\text{sup}}{\displaystyle {\int }_{\Omega }|}\langle x(·),x^{\prime }\rangle {|}^{p}dP<\infty ,$

where U are convex and circled neighborhoods of zero in E.

It follows from ([16], Prop. 3.2, Th. 3.1 and Th. 3.2) that if E is a locally convex Fréchet space and p = 1 then the completion ${\hat{{L}}}^1(E)$ consists of all cylindrical elements X : E′ → L¹ which are $(\tau (E^{\prime },E),\Vert ·{\Vert }_{L^1})$ continuous and compact linear maps. In general, we will denote by ${\hat{{L}}}^p(E)$ the completion of ${{L}}^p(E)$.

If $X\in {\hat{{L}}}^p$ then for each fixed g ∈ L^q, $\frac{1}{p}+\frac{1}{q}=1$, the map

$\begin{array}{l}{x}^{\prime }\mapsto gX{x}^{\prime }\end{array}$

from E′ to L¹ is a Pettis integrable cylindrical element.

Let us also recall some relations between cylindrical elements and cylindrical measures on a locally convex space E. Denote by ${C}(E)$ the σ-field generated by cylindrical sets in E, i.e., the sets of the form

$\begin{array}{l}\{x|\in E:(\langle x,x_1^{\prime }\rangle ,\dots ,\langle x,x_n^{\prime }\rangle )\in B\},\end{array}$

where n ∈ ℕ, $x_1^{\prime },\dots ,x_n^{\prime }\in E^{\prime }$, $B\in {{B}}_{{ℝ}^n}$ (${{B}}_{{ℝ}^n}$ denotes the Borel σ-field in ℝⁿ).

Let μ be a finitely additive measure on ${C}(E)$ and let

${\mu }_{x_1^{\prime },\dots ,x_n^{\prime }}(B)\stackrel{\text{df}}{=}\mu \{x\in E:(\langle x,x_1^{\prime }\rangle ,\dots ,\langle x,x_n^{\prime }\rangle )\in B\}.$

The measure μ is called cylindrical if for each n ∈ ℕ and $x_1^{\prime },\dots ,x_n^{\prime }\in E^{\prime }$ ${\mu }_{x_1^{\prime },\dots ,x_n^{\prime }}$ is a probability measure on $({ℝ}^n,{{B}}_{{ℝ}^n})$.

Each cylindrical element X determines a cylindrical measure μ defined as

$\begin{array}{l}\mu (\{x\in E:(\langle x,x_1^{\prime }\rangle ,\dots ,\langle x,x_n^{\prime }\rangle )\in B\})=P\{(X{x}_1^{\prime },\dots ,X{x}_n^{\prime })\in B\}.\end{array}$

Conversely, if μ is a cylindrical measure on ${C}(E)$ then there exist a probability space $(\Omega ,{A},P)$ and a cylindrical element $X:E^{\prime }\to L^0(\Omega ,{A},P)$ satisfying the above equality (see [19]). The correspondence between cylindrical measures and cylindrical elements is one-to-one.

If μ is a cylindrical measure and X_μ the corresponding cylindrical element such that

$\begin{array}{l}{\displaystyle {\int }_{\Omega }}|X_{\mu }{x}^{\prime }{|}^{p}d\mu <\infty ,\text{ for each }{x}^{\prime }\in E^{\prime },\end{array}$

and some p > 0, then we say that μ has a weak p-order.

An important property of a cylindrical measure is its concentration on some families of sets. Namely, let 𝔖 be a family of subsets of E and μ a cylindrical measure on ${C}(E)$. We say that μ is scalarly concentrated on 𝔖 if for each ε > 0 there is A ∈ 𝔖 such that

$\begin{array}{l}{({\mu }_{x^{\prime }})}_{*}(x^{\prime }(A))\ge 1-\epsilon ,\end{array}$

for each x′ ∈ E′, where ∗ denotes the inner measure.

Assume that 𝔖 is the family of all compact circled subsets of E and denote by $E_{𝔖}^{\prime }$ the space E′ with the topology of uniform convergence on the sets from 𝔖. One of the basic relations between Pettis integrable cylindrical elements and the corresponding cylindrical measures is contained in the following Proposition.

Proposition 4. Let E be a complete l.c.s., 𝔖 the family of all compact circled subsets of E and X a cylindrical element. If $X\in {\hat{{L}}}^p(E)$, p ≥ 1, then the corresponding cylindrical measure μ is scalarly concentrated on 𝔖.

The proof of this Proposition is based on the fact that X is $(\tau (E^{\prime },E),\Vert ·{\Vert }_{L^p})$ continuous cylindrical element from E′ to L^p which transforms equicontinuous subsets of E′ into relatively compact sets in L^p, p > 1 (see also the proof of Th.4.1 in [16]).

The converse implication is not true in general even for Radon measures but is true for cylindrical Gaussian measures and corresponding L²–valued cylindrical elements (see [16] for details).

3. Time Operator

Before defining time operator acting on cylindrical elements let us remind the classical construction which is based on the idea of Misra-Prigogine-Courbage [3]. Let us consider an abstract dynamical system given by the quadruple $(\Omega ,{A},\mu ,\{S_t\})$, where {S_t} is a group of one-to-one μ invariant transformations of Ω and either t ∈ ℤ or t ∈ ℝ.

A K-flow (we will say K-system) is a probability space $(\Omega ,{A},P)$ with a group of measure preserving transformations S_t, t ∈ ℝ, of Ω. We assume that there exists a σ-algebra ${{A}}_0\subset {A}$ such that the family ${\{{{A}}_t\}}_{t\in ℝ}$, ${{A}}_t\stackrel{\text{df}}{=}{S}_t({{A}}_0)$has the properties

(i) ${{A}}_s\subset {{A}}_t$, for s < t

(ii) $\sigma ({\bigcup }_{t\in ℝ}{{A}}_t)={A}$

(iii) ${\bigcap }_{t\in ℝ}{{A}}_t={{A}}_{-\infty }$ – the trivial σ-algebra, i.e., the algebra of sets of measure 0 or 1.

where $\sigma ({\cup }_{t\in ℝ}{{A}}_t)$ stands for σ-algebra generated by ${{A}}_t$, t ∈ ℝ.

We replace deterministic evolution of phase space points by the Liouville evolution of probability density functions putting

$\begin{array}{ll}{U}_t\rho (\omega )=\rho (S_{-t}\omega ),& (6)\end{array}$

where ρ is ${A}$ measurable function on Ω. The invariance of the measure μ implies that the transformations U_t considered as operators on $L^2=L^2(\Omega ,{A},\mu )$ form a unitary group.

In this setting a possible approach to the problem of irreversibility can be formulated as in section 1. Namely it is constructed the Lambda operator connecting the reversible group {U_t}_t∈ℝ with an entropy increasing evolution semigroup {W_t}_t≥0. It is assumed that Λ is a bounded linear operator on $L^2(\Omega ,{A},\mu )$ with densely defined inverse Λ⁻¹ such that $W_t=\Lambda U_t{\Lambda }^{-1}$ defines, for t ≥ 0, a continuous one-parameter group of contractions. For physical reasons it is also additionally assumed that Λ is positivity preserving, Λ1 = 1 and ||W_t(ρ − 1)|| decreases strictly monotonically to 0, as t → +∞, for all densities ρ ≢ 1. The last condition means that the entropy of the system tends strictly monotonically to zero when the system approaches equilibrium.

In classical dynamical systems Lambda transformations have been constructed on the L^p spaces associated with K-systems as functions of time operators. The main idea of such construction is ([3] see also [20–22]) that each K-system determines the family {E_t}_t∈ℝ of conditional expectations,

$\begin{array}{l}{\text{E}}_t={\text{E}}^{{{A}}_t},\end{array}$

which in turn defines the operator T on each space $L^p=L^p(\Omega ,{A},P)$, p ≥ 1,

$\begin{array}{ll}T={\displaystyle {\int }_{-\infty }^{+\infty }}td{\text{E}}_t,& (7)\end{array}$

which is called the time operator.

In the case of discrete time, t ∈ ℤ, we consider the group {S_n}_n∈ℤ generated by a single measure preserving transformation S, i.e., $S_n=S^n$, for n ≠ 0, and S⁰ = I. The time operator T is then defined as

$\begin{array}{l}T={\displaystyle \sum _{n=-\infty }^{\infty }}n{E}_n.\end{array}$

If p = 2 then the above integral, or sum, defining T is just the spectral resolution of a selfadjoint operator. In this case {U_t}_t∈ℝ defined in (6) is a unitary group on L² satisfying the following relation with T

$\begin{array}{ll}{U}_{t}T{U}_{-t}=T+tI,& (8)\end{array}$

which is equivalent to (2).

The transformation Λ is defined, up to constants, as an operator function Λ = Λ(T). Namely

$\begin{array}{l}\Lambda =f(T)+E_{-\infty }\end{array}$

where E_−∞ is the projection on the space $L^2({{A}}_{-\infty })=ℝ$. The function f is assumed to be positive, decreasing on ℝ, f (−∞) = 1, f (+∞) = 0 and such that ln f is concave on ℝ. Then, for any such function f the corresponding operator Λ is injective on L², one-to-one with densely defined inverse (see ref. [21]). Moreover the semigroup

$\begin{array}{ll}{W}_t\stackrel{\text{df}}{=}\Lambda U_t{\Lambda }^{-1},t\ge 0,& (9)\end{array}$

is Markovian and $\Vert W_{t}p-1{\Vert }_{L^2}$ decreases to 0, for each density ρ ≠ 1 and together with {U_t} satisfies the relation (1).

The time operator as defined in (7) uses the family of conditional expectations {E_t} which can be treated as a spectral family of projectors on the Hilbert space L² which defines a selfadjoint operator or, for a given ρ ∈ L², {E_tρ} can be considered as a martingale with respect to the filtration $\{{{A}}_t\}$. In the latter case the integral defining T can be understood as a stochastic integral with respect to a martingale. Such approach allows to define time operators on larger classes of function, for example on L¹. Moreover the stochastic integral technique allows to replace the family of projectors {E_t} by a family of operators {M_t} such that for a given ρ {M_tρ} is a martingale with respect to $\{{{A}}_t\}$. In fact, such a generalization of the definition of time operators has been proposed in [22]. The extension of the definition of T on L¹ spaces can be found in [23].

It should be stressed that the above mentioned extension of the time operator concerns such states (probability measures) which have densities. However, in statistical physics the class of states can be larger and contain, for example, singular measures. There were successful attempts of such extension of the domain of time operators (see [2, 5, 6]).

We will define now a time operator acting on p-cylindrical elements. As we have seen in section 2 p-cylindrical element is actually a generalization of a weakly p-integrable function with values in a topological vector space. Equivalently, time operators will act on cylindrical measures on a topological vector spaces. This is a significant step beyond the classical L^p space.

We have to define first the conditional expectation of a cylindrical element. Let ${\text{E}}^{{B}}:L^1({A})\to L^1({B})$ denote the usual operator of the conditional expectation (see [18]), and let $Y:E_{\tau }^{\prime }\to L^p$, p ≥ 1, be a p-cylindrical element obtained as the composition of operators ${\text{E}}^{{B}}$ and X. Note that if $X:E_{\tau }^{\prime }\to L^p$ is continuous, then $Y={\text{E}}^{{B}}X$ is also continuous. Thus, if $X:E_{\tau }^{\prime }\to L^p$ is continuous, 1 ≤ p < ∞, then for each sub σ-field ${B}\subset {A}$ the 1-cylindrical element $Y={\text{E}}^{{B}}X:E_{\tau }^{\prime }\to L^1$ satisfies

$\begin{array}{l}{\displaystyle {\int }_B}YdP={\displaystyle {\int }_B}{\text{E}}^{{B}}XdP={\displaystyle {\int }_B}XdP,\end{array}$

for each $B\in {B}$.

The above definition of conditional expectation applies, in particular, to Banach space valued functions. Indeed, each function x(·) : Ω → E, where E is a Banach space, which has a weak p-order defines a cylindrical element $X:E_{\tau }^{\prime }\to L^p$. Thus we can define the conditional expectation of x(·)

$\begin{array}{l}{\text{E}}^{{B}}x(·)={\text{E}}^{{B}}X.\end{array}$

It should be noticed that it is not always possible to define the conditional expectation of a Banach space valued function which is not strongly integrable. Indeed one can find (see [24]) a Pettis integrable function x(·) with values in a reflexive Banach space E and a sub σ-algebra ${B}$ for which does not exist any ${B}$ measurable function y(·) : Ω → E such that

$\begin{array}{l}{\displaystyle {\int }_B}\langle y(·),x^{\prime }\rangle dP={\displaystyle {\int }_B}\langle x(·),x^{\prime }\rangle dP,\text{ for }B\in {B},x^{\prime }\in E^{\prime }.\end{array}$

However, we have shown above that this conditional expectation exists as a cylindrical element although not generated by a measurable function. Thus the replacement of Pettis integrable functions by the corresponding cylindrical elements allows to give a meaning to a generalization of the concept of conditional expectation.

Let us assume that E is a complete l.c.s. and ${I}$ a linear ordered set. A family ${\{X_t\}}_{t\in {I}}$ of cylindrical elements $X_t:E^{\prime }\to L^p$, $t\in {I}$, will be called the p-cylindrical process. If each X_t is Pettis integrable then the process will be also called Pettis integrable. Recall that Pettis integrability is equivalent $(\tau (E^{\prime },E),\Vert ·{\Vert }_{L^1})$ continuity - Proposition 1.

Let ${\{{{B}}_t\}}_{t\in {I}}$ be a family of σ-fields such that ${{B}}_t\subset {A}$ and ${{B}}_{t_1}\subset {{B}}_{t_2}$, for t₁ < t₂. A p-cylindrical process ${\{X_t\}}_{t\in {I}}$, where p ≥ 1, is called p-cylindrical martingale if it is adapted with respect to ${\{{{B}}_t\}}_{t\in {I}}$, each X_t is $(\tau (E^{\prime },E),\Vert ·{\Vert }_{L^p})$ continuous, and ${\text{E}}^{{{B}}_s}{X}_t=X_s$, for s < t.

It is easy to show that a τ-continuous p-cylindrical process ${\{X_t\}}_{t\in {I}}$ is p-cylindrical martingale if and only if ${\{X_t{x}^{\prime }\}}_{t\in {I}}$ is a real martingale for each x′ ∈ E′. The proposition below shows that for cylindrical martingales we have an analog of the classical convergence theorem (see [25]).

Proposition 5. Let ${\{X_t{x}^{\prime }\}}_{t\in {I}}$ be a discrete time p-cylindrical martingale with respect to ${\{{{B}}_t\}}_{t\in {I}}$, p > 1, and assume that $E_{\tau }^{\prime }$ is barreled Barreled space. If

$\begin{array}{l}{\displaystyle \underset{t\in {I}}{\text{sup }}}\text{E}|X_t{x}^{\prime }{|}^p<\infty ,\text{ for each }{x}^{\prime }\in E^{\prime },\end{array}$

then there exists a continuous cylindrical element $X:E_{\tau }^{\prime }\to L^p$ such that

$\begin{array}{l}{X}_t={\text{E}}^{{{B}}_t}X,\text{ for each }t\in {I},\end{array}$

and X_t converges to X in L^p norm.

This proposition is not true in the case p = 1. However assuming that

$\begin{array}{ll}\text{E }{\displaystyle \underset{t}{\text{sup}}}|X_t{x}^{\prime }|<\infty ,\text{ for each }{x}^{\prime }\in E^{\prime },& (10)\end{array}$

we obtain an analog of Proposition 5.

In the case of continuous time we can obtain similar results under the additional assumption of right continuity of the considered martingales. The assumption of right continuity of a martingale {m_t} allows to define the stochastic integral ∫f (t)dm_t, where f (t) is a Borel measurable function (see [26]).

The object of our interest will be the cylindrical martingales generated by a single cylindrical element, like in the thesis of Proposition 5, associated with the filtration ${\{{{B}}_t\}}_{t\in ℝ}$ determined by a given. K-flow.

Let $\{{{A}}_t\}$ be a family of σ-algebras of a given K-flow and {M_t} an associated operator valued martingale i.e., a family of bounded operators on L^p, p ≥ 1, such that {M_t} is a right continuous martingale with respect to $\{{{A}}_t\}$. In the classical approach (see [22] for the details) it was assumed that {M_t} acts on L², has orthogonal increments: for s₁ ≤ s₂ < t₁ ≤ t₂ (M_s2 − M_s1)(M_t2 − M_t1) = 0 and that M_∞ is a positive one-to-one operator satisfying

$\begin{array}{l}{M}_{\infty }1=1M_{\infty }{U}_t=U_t{M}_{\infty }\text{ for each }t\in ℝ,\end{array}$

where U_t is given by (6). It was shown that for a fixed monotonic function f on ℝ the transformation

$\begin{array}{ll}\rho \mapsto {\displaystyle \int }f(t)d{M}_t\rho +M_{-\infty }\rho ,\rho \in L^2.& (11)\end{array}$

is well-defined on the domain D_f which is dense in L². Taking f (t) = t we obtain the time operator. If we assume that f is a positive non-increasing function on ℝ with ${\text{lim}}_{t\to -\infty }f(t)=1$, ${\text{lim}}_{t\to \infty }f(t)=0$ and such that for each t ∈ ℝ the quotient f (s)/f (s − t) is a bounded and non-increasing function of s then (11) defines the discussed above similarity transformation Λ which in turn defines the Markov semigroup (9).

Note that taking M_t = E_t, where ${\text{E}}_t={\text{E}}^{{{A}}_t}$, we obtain an operator valued martingale satisfying the required properties. Moreover, a cylindrical element X with values in L^p defines the p-cylindrical martingale {E_tX}. Therefore, in the case p = 2 we can apply directly the above construction putting in (11) Xx′, x′ ∈ E′, instead of ρ. Replacing the space L² by L² ⊖ 1 we can omit the second component in (11) obtaining the following operator f (T) acting on cylindrical elements

$\begin{array}{ll}f(\text{T})(X)={\displaystyle \int }f(t)d{\text{E}}_{t}X.& (12)\end{array}$

We can not apply directly the above approach in the case p ≥ 1, p ≠ 2. Here we have to use a different approach to stochastic integration. The theory of integrals ∫f (t)dm_t, where {m_t} is a p-integrable martingale can be found in Bichteler's paper [26]. This integral is defined first for simple functions (or processes) f (t). Then it is said that {m_t} is an L^p-integrator if {m_t} is p-integrable and the linear operator f ↦ ∫f (t)dm_t from the space of elementary integrands to L^p has an extension satisfying the dominated convergence theorem (see Def.1 in [26]).

Theorem 1. Let E be an l.c.s. and $(\Omega ,{A},\mu ,\{S_t\})$ a K-flow. If 1 < p < ∞ then for any simple function f with a bounded support the linear operator on L(E′, L^p)

$\begin{array}{l}f(\text{T})(X)={\displaystyle \int }f(t)d{\text{E}}_{t}X.\end{array}$

is correctly defined, for each x ′ ∈ E′, the martingale $\{{\text{E}}_{t}X{x}^{\prime }\}$ is an L^p-integrator and we have

$\begin{array}{l}\Vert {\displaystyle \int }f(t)d{\text{E}}_{t}X{x}^{\prime }{\Vert }_{L^p}\le C_p\Vert {\text{E}}_{\tau }X{x}^{\prime }{\Vert }_{L^p},\end{array}$

where τ is such that f (t) = 0, for |t| > τ and C_p is a constant which depends only on p.

If p = 1 then the above integral exists and the martingale $\{{\text{E}}_{t}X{x}^{\prime }\}$ is an L¹-integrator under the additional assumption that

$\begin{array}{ll}\text{E}(|X{x}^{\prime }|\text{log}|X{x}^{\prime }|)<\infty ,\text{ for each }{x}^{\prime }\in E^{\prime },& (13)\end{array}$

Proof. If p > 1 we can apply (3.8) from [26] which says that a p-intergrable martingale is an L^p-integrator. If p = 1 we use Th. 7.2 from [26] and the additional assumption (13) to show that for each x′ ∈ E” the martingale $\{{\text{E}}_{t}X{x}^{\prime }\}$ is an L¹ integrator. Note that because the martingales satisfy the assumption (13), in the latter case, they are elements of the Hardy space H¹, i.e., (10) is satisfied.

It follows from Theorem 1 that f (T) can be defined for simple functions with bounded support. However, because of the dominated convergence theorem we can extend the class of functions taking, for example, f (t) = t to obtain the operator

$\begin{array}{l}\text{T}={\displaystyle \int }td{\text{E}}_t,\end{array}$

which acts on the space L(E′, L^p).

Let {U_t} be the evolution group on L(E′, L^p) associated with the transformations {S_t}, i.e., for X ∈ L(E′, L^p), U_tX is a cylindrical element of the form

$\begin{array}{l}({\text{U}}_{t}X)x^{\prime }(\omega )=X{x}^{\prime }(S_{-t}\omega ).\end{array}$

Using the relation E_s+tU_t = U_tE_s valid for conditional expectations associated with the K-system and the evolution {S_t} on the ordinary L^p-space (see e.g., [21]) we obtain that also

$\begin{array}{l}{\text{E}}_{s+t}{\text{U}}_t={\text{U}}_t{\text{E}}_s.\end{array}$

This leads to the following

Corollary. The operator T is a time operator on the space L(E′, L^p) associated with the evolution {U_t}.

We can also take as f a bounded monotonic function with the listed above properties to obtain an analog of the operator Lambda, Λ = f (T). An important example of applications the above construction of T is the possibility to define time operators on the spaces of weakly integrable E-valued functions. This is because the constructed above stochastic integral transforms cylindrical elements into cylindrical elements. If we take as an argument of T the cylindrical element generated by an E valued function then after the transformation it need not to remain a function (see remarks concerning the conditional expectation of Pettis integrable functions). However f (T) leaves the space L(E′, L^p) invariant.

An important question is: When a cylindrical element is generated by a measurable function defined on Ω with values in the vector space E? Similar question concerns martingales: When the integral transformation of a p-cylindrical martingale generated by a vector valued function will be still a function generated martingale? The rest of this section is devoted to an answer to these questions.

Let us introduce first the following definition:

We say that X is p-decomposable, p > 0, if there exists a measurable function x(·) : Ω → E such that

1⁰ Xx′ = 〈x(·), x′〉, for each x′ ∈ E′

2⁰ ${\int }_{\Omega }\Vert x(·){\Vert }^{p}dP<\infty$, for each continuous seminorm ||·|| on E.

Decomposability of a cylindrical element depends both on properties of X as a linear operator and on the topological properties of the vector space E. We will consider the problem of decomposability in both cases. We begin with the dependence of the decomposability of a cylindrical element X : E′ → L¹ on the properties of E. It is obvious that if E is finite dimensional then each 1-cylindrical element is 1-decomposable. If E is infinite dimensional then the space ${{L}}^1(E)$ of Pettis integrable functions on Ω with values in E, introduced in section 2, is not complete in general and its completion ${\hat{{L}}}^1(E)$ may contain cylindrical elements which are not associated with any measurable function. However, the transformations like conditional expectation or time operator leave ${\hat{{L}}}^1(E)$ invariant. Thus we can ask if there are locally convex spaces for which this completion remains a function space. The next theorem shows such a possibility.

Theorem 2. Let E be a locally convex nuclear Fréchet space. Then each element of ${\hat{{L}}}^1(E)$ is 1-decomposable.

Proof. In the proof we will use some results concerning tensor products of l.c.s. Let us first introduce the notation and remind the relevant facts (see [27]). Let E be an l.c.s., F a Banach space and E ⊗ F the algebraic tensor product. We define two basic topologies on E ⊗ F. First is the ε-topology generated by the seminorms

$\begin{array}{l}{\epsilon }_U(z)={\displaystyle \underset{x^{\prime }\in U^{◦}}{\text{sup}}}{\displaystyle \underset{y^{\prime }\in B^{◦}}{\text{sup}}}|\langle z,x^{\prime }\otimes y^{\prime }\rangle |,\text{ for }z\in E\otimes F,\end{array}$

where U runs over a basis of convex and circled neighborhoods of 0 in E and B is the unit ball in F. By $E{{\displaystyle \hat{\otimes }}}_{\epsilon }F$ we denote the completion of E ⊗ F in the ε-topology.

The second topology, called the projective topology, is generated by the seminorms

$\begin{array}{l}{\pi }_U(z)=\text{inf}{\displaystyle \sum _i}{p}_U(x_i)\Vert y_i\Vert \end{array}$

where the infinitum is taken over all representations of the element $z=\sum _{i=1}^n{x}_i\otimes y_i$ and U is an absolutely convex neighborhood of 0 in E. By $E{{\displaystyle \hat{\otimes }}}_{\pi }F$ we denote the completion of E ⊗ F in the projective topology.

Note that the ε-topology and the projective topology are respectively the weakest and the strongest topology on the tensor product of two l.c.s. which are generated by cross-seminorms (see [27]).

It is known that if E is a Banach space then $E{{\displaystyle \hat{\otimes }}}_{\pi }{L}^1$ is norm isomorphic to the space L¹(E) of all E valued Bochner integrable functions f on Ω endowed with the norm $\Vert f{\Vert }_{L^1(E)}={\int }_{\Omega }\Vert f(\omega )\Vert P(d\omega )$. If E is just an l.c.s. then $E{{\displaystyle \hat{\otimes }}}_{\pi }{L}^1$ is isomorphic with L¹(E) defined as the space of all strongly measurable functions f such that ||f (·)|| is integrable for each semi-norm ||·|| on E.

We have shown in [16] that if E is a separable l.c.s. Fréchet space then ${\hat{{L}}}^1(E)$ can be identified (is isomorhic) with $E{{\displaystyle \hat{\otimes }}}_{\epsilon }{L}^1$. However, when E is a complete nuclear l.c.s. the latter space is isomorphic to $E{{\displaystyle \hat{\otimes }}}_{\pi }{L}^1$ (see [27]). Therefore, each element from ${\hat{{L}}}^1(E)$ is represented by a Bochner integrable function which ends the proof.

It follows from the above theorem that for a nuclear space valued functions the Pettis integrability is equivalent to the Bochner integrability like in the finite dimensional case.

Let now consider the dependence between decomposability and operator properties of cylindrical elements. It is known that if E = H – is a Hilbert space then a 2-cylindrical martingale X : H′ → L² is 2-decomposable if and only if the mapping

$\begin{array}{l}{H}^{\prime }\ni h\mapsto X_{t}h\in L^2\end{array}$

is a Hilbert-Schmidt operator for any t (see [14]).

We can also decompose cylindrical elements by composing them with Hilbert-Schmidt operators or, more generally, with absolutely summing operators. The problem of decomposability of a cylindrical element acting on a Banach space through a composition with an absolutely summing operator has been already resolved (see [25, 28] and references therein). Here, we will resolve this problem in the case of cylindrical elements acting on locally convex spaces.

If E and F are normed spaces and 0 < p < ∞ then a linear operator S : E → F is said to be p-absolutely summing if there exists a constant C such that for each x₁, …, x_n ∈ E

$\begin{array}{l}{\displaystyle \sum _{i=1}^n}\Vert S{x}_i{\Vert }^p\le C{\displaystyle \underset{\Vert x^{\prime }\Vert \le 1}{\text{sup}}}{\displaystyle \sum _{i=1}^n}|\langle x_i,x^{\prime }\rangle {|}^p.\end{array}$

In the sequel we will use the following Pietsch Majorization Theorem:

Proposition 6. ([29], p. 232) Let E and F be normed spaces. An operator S : E → F is p-absolutely summing, 0 < p < ∞, if there exist a constant C and a Radon probability measure μ on the unit ball U^◦ of E′, where U^◦ is equipped with the σ(E′, E) - topology, such that

$\begin{array}{l}\Vert Sx{\Vert }^p\le C{\displaystyle {{\displaystyle \int }}_{U^{◦}}}|\langle x,x^{\prime }\rangle {|}^{p}d\mu (x^{\prime })\text{ for all }x\in E.\end{array}$

We shall now extend the definition of the p-absolutely summing operatoron operators acting on an l.c.s. with values in a t.v.s. Consider first the case of an operator S : E → F, where F is a quasi-normed space. Recall that a quasi-norm on F is a non-negative positively defined homogenous function ||·|| such that for some r, 0 < r ≤ 1, we have

$\begin{array}{l}\Vert x+y{\Vert }^r\le \Vert x{\Vert }^r+\Vert y{\Vert }^r,x,y\in E.\end{array}$

We then say that the space F is r-normed.

Remark:

(i) An r-normed space is s-normed for 0 < s ≤ r ≤ 1

(ii) If 0 < r ≤ 1 then the space L^r is r-normed.

The definition of a p-absolutely summing operator S : E → F, for E normed and F quasi-normed space, is the same as in the case of normed spaces. Moreover, the Proposition 6 remains true and we have

Proposition 7. ([29]) Let Ω be a compact Hausdorff space and ν a probability measure on Ω. Then the canonical embedding of the space C(Ω) (continuous functions on Ω) into L^p(Ω, ν) is p-absolutely summing for 0 < p < ∞.

Before we turn to the further generalization of the concept of p-absolutely summing operators we shall introduce first some auxiliary normed spaces and decompositions of bounded operators on topological vector spaces.

Let E be an l.c.s. and U an absolutely convex neighborhood of 0 in E. By E_U we denote the normed space $(E/p_U^{-1}(\{0\}),p_U(·))$ where p_U(·) is the Minkowski functional of U. Let Ê_U denotes the completion of E_U in the norm p_U(·) and Φ_U the canonical map from E into E_U (or into Ê_U). Of course Φ_U is continuous. Now, let F be a t.v.s. A subset B of F is said to be p-absolutely convex if whenever it contains x and y it contains all αx + βy with |α|^p + |β|^p ≤ 1. If p = 1 then B is absolutely convex. We put

$\Vert x{\Vert }_B=\text{inf}\{\lambda >0:x\in \lambda B\},$

and $F_B={\displaystyle \bigcup _{n=1}^{\infty }}nB$. Then (F_B, ||·||_B) is p-normed and the canonical injection

Ψ_B : F_B → F is continuous. Moreover, F_B is complete if B is complete.

A subset B of F is called quasi-absolutely convex if it is p-absolutely convex for some 0 < p ≤ 1.

Let E be an l.c.s., F be a t.v.s. and S : E → F a bounded linear operator, i.e., such that there exists a neighborhood U of 0 in E for which S(U) is bounded. Then S can be decomposed in the following way

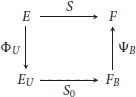
where U is an absolutely convex neighborhood of 0 in E and B is a bounded subset of F. If B can be chosen quasi-absolutely convex, then S₀ is a continuous linear operator from the normed space E_U into the quasi-normed space F_B. Moreover, if B is complete then S₀ has the continuous extension ${\overline{S}}_0$ from the Banach space Ê_U into F_B. Note that if F is an l.c.s. then F_B is a normed space.

We can now define p-absolutely summing operator on a locally convex space. Let E be an l.c.s. and F be a t.v.s. A linear operator S : E → F is p-absolutely summing, 0 < p < ∞, if there exist an absolutely convex neighborhood U of 0 in E and a bounded quasi-absolutely convex subset B of F such that S₀ : E_U → F_B is p-absolutely summing. This definition is analogous with the definition of nuclear operators on locally convex spaces (see [27]).

The next result gives sufficient conditions for p-decomposability of cylindrical elements. It is an extension of the Kwapien's Theorem ([28], Th. 2) as well as ([25], Th. 1.1) on the case of absolutely summing operators on locally convex spaces. Moreover, the method of absolutely summing operators on locally convex spaces allows to simplify the proof of ([28], Th. 2) and contains the case 0 < p < 1.

Theorem 3. Let E, F be a quasi-complete l.c.s. and let S : E → F be p-absolutely summing linear operator, p > 0. If $X:E_{\tau }^{\prime }\to L^p$ is a continuous cylindrical element and either p ≥ 1 or F′ has the approximation property then

(i) Y = X ◦ S^* is p-decomposable by an F valued function y(·)

(ii) If L^p is separable then for each absolutely convex neighborhood U of 0 in E and each continuous seminorm ||·|| on F we have

$\begin{array}{l}{\displaystyle {{\displaystyle \int }}_{\Omega }}\Vert y(·){\Vert }^{p}dP\le C{\displaystyle {{\displaystyle \int }}_{U^{◦}}}\Vert X{e}^{\prime }{\Vert }_{L^p}^{p}d\mu (e^{\prime })\end{array}$

where μ is a Radon measure on (U^◦, σ(E′, E)) and C is some constant.

Proof. Let U be an absolutely convex closed neighborhood of 0 in E and B an absolutely convex closed subset of F such that S₀ : E_U → F_B is p-absolutely summing. Because F is quasi-complete, F_B is a Banach space and S₀ extends to the map ${\bar{S}}_0:{Ê}_U\to F_B$, which is also p-absolutely summing. Since ${(E_U)}^{\prime }={({Ê}_U)}^{\prime }=E_{U^{◦}}^{\prime }$ and ${(F_B)}^{\prime }=F_{B^{◦}}^{\prime }$, ${({\bar{S}}_0)}^{*}=S_0^{*}:F_{B^{◦}}^{\prime }\to E_{U^{◦}}^{\prime }$. Moreover ${\Psi }_{V^{◦}}:F_{V^{◦}}^{\prime }\to F_{\tau }^{\prime }$ is continuous. Therefore applying Kwapien's Theorem ([28], Th.2) to the operators $S_0^{*}$ and $X◦{\Psi }_{V^{◦}}$ acting on Banach spaces, we obtain that that $S_0^{*}X{\Psi }_{V^{◦}}$ is p-decomposable by $y_B(·):\Omega \to {(F_B^{\prime })}^{\prime }=F_B$ (if F′ has the approximation property then also $F_{B^{◦}}^{\prime }$ has it (cf. [27] III, 9.2). Using the continuity of the cannonical injection Ψ_B : F_B → F we see that the function

$y(·)={\Psi }_B{y}_B(·):\Omega \to F$

decomposes X ◦ S^*. Furthermore, let us note that U^◦ is the unit ball in the space ${(E_U)}^{\prime }$ which is compact in σ(E′, E)-topology. Thus using ([25] Th.1.1 (ii) we obtain the inequality

${\displaystyle {{\displaystyle \int }}_{\Omega }}\Vert y(·){\Vert }_B^{p}dP\le C{\displaystyle {{\displaystyle \int }}_{U^{◦}}}\Vert X{e}^{\prime }{\Vert }_{L^p}^{p}d\mu (e^{\prime })$

where the measure μ is defined as in Proposition 6. If ||·|| is a continuous seminorm on F then $\Vert ·\Vert \le C_1\Vert ·{\Vert }_{B^{\prime }}$ for some constant C₁. This ends the proof of this theorem.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Misra B. Prigogine I. Lyapunov variable: entropy and measurement in quantum mechanics. Proc Natl Acad Sci USA. (1979) 76:4768–72.

PubMed Abstract | Google Scholar

2. Misra B, Prigogine I. Irreversibility and nonlocality. Lett Math Phys. (1983) 7:421–9.

Google Scholar

3. Misra B, Prigogine I, Courbage M. From deterministic dynamics to probabilistic descriptions. Phys A. (1979) 98 :1–26.

PubMed Abstract | Google Scholar

4. Gómez-Cubillo F. Solution of the MPC problem in terms of the Sz.-Nagy-Foias dilation theory. Infin Dimens Anal Quant Probab Relat Top. (2008) 11:73–96. doi: 10.1142/S0219025708002987

CrossRef Full Text | Google Scholar

5. Courbage M. Intrinsic irreversibility of Kolmogorov dynamical systems. Phys A. (1983) 122:459–82.

Google Scholar

6. Sorger U, Suchanecki Z. Nonlocalization properties of time operators transformations. Int J Theor Phys. (2015) 54:787–800. doi: 10.1007/s10773-014-2270-y

CrossRef Full Text | Google Scholar

7. Suchanecki Z, Antoniou I, Tasaki S. Nonlocality of the Misra-Prigogine-courbage semigroup. J Stat Phys. (1994) 75:919–28.

Google Scholar

8. Antoniou I, Suchanecki Z. Non-uniform time operator, chaos and wavelets on the interval. Chaos Solitons Fractals. (2000) 11:423–35. doi: 10.1016/S0960-0779(98)00310-5

CrossRef Full Text | Google Scholar

9. Gómez F. Unitary quasi-affine transforms of contractions. J Math Anal Appl. (2009) 351:84–96. doi: 10.1016/j.jmaa.2008.10.001

CrossRef Full Text | Google Scholar

10. Gómez-Cubillo F, Suchanecki Z. Breakdown of time-reversal symmetry: intrinsic randomness, time operator, scattering. J Geom Symmetry Phys. (2008) 11:33–40. doi: 10.7546/jgsp-11-2008-33-40

CrossRef Full Text | Google Scholar

11. Gómez-Cubillo F, Suchanecki Z, Villullas S. On lambda and time operators: the inverse intertwining problem revisited. Int J Theoret Phys. (2011) 50:2074–83. doi: 10.1007/s10773-010-0573-1

CrossRef Full Text | Google Scholar

12. Sorger U, Suchanecki Z. Time operators and approximation of continuous functions. Int J Theoret Phys. (2008) 47:1792–808. doi: 10.1007/s10773-007-9622-9

CrossRef Full Text | Google Scholar

13. Suchanecki Z, Gómez-Cubillo F. Evolution semigroups and time operators on Banach spaces. J Math Anal Appl. (2010) 371:454–64. doi: 10.1016/j.jmaa.2010.05.049

CrossRef Full Text | Google Scholar

14. Metivier M, Pellaumail J. Stochastic Integration. New York, NY: Academic Press (1980).

Google Scholar

15. Pettis BJ. On integration in vector spaces. Trans Am Math Soc. (1938) 44:277–304.

Google Scholar

16. Suchanecki Z. Cylindrical measures and cylindrical processes on locally convex spaces. Probability Math Stat. (1981) 2:71–81.

Google Scholar

17. Suchanecki Z. Remarks on Pettis integrability of cylindrical processes. Lecture Notes Math. (1980) 828:269–73.

Google Scholar

18. Meyer PA. Probability and Potentials. Waltham, MA; Toronto, ON; London: Blaisdell Publishing Company (1966).

19. Badrikian A. Séminaire sur les fonctions Aleatoires Linéaires et les Measures Cylindriques, Vol. 139. Lecture Notes in Math. Springer (1970).

Google Scholar

20. Gómez-Cubillo F, Suchanecki Z. On Lambda transformation approach to the theory of irreversibility. Bussei Kenkyu. (2011/12) 97:398–413. Available online at: http://hdl.handle.net/2433/169637

Google Scholar

21. Suchanecki Z. On lambda and internal time operators. Phys A. (1992) 187:249–66.

Google Scholar

22. Suchanecki Z, Weron A, Rybaczuk M, Weron K. An explicit approach to the Λ-operator and H-Theorem in the Prigogine's theory of irreversibility. Phys A. (1989) 155:385–400.

23. Suchanecki Z. An L¹ extension of stochastic dynamics for irreversible systems. Lecture Notes Math. (1989) 1391:367–74.

Google Scholar

24. Rybakov VI. On conditional expectations of Pettis integrable functions. Mat Zametki. (1971) 10:565–70.

Google Scholar

25. Suchanecki Z, Weron A. Decomposability of cylindrical martingales and absolutely summing operators. Math Z. (1984) 185:271–80.

Google Scholar

26. Bichteler K. Stochastic integration and L^p theory of semimartingales. Ann Prob. (1981) 9:49–89.

Google Scholar

27. Schaefer HH. Topological Vector Spaces. New York, NY: Springer (1970).

Google Scholar

28. S. Kwapień On a theorem of L. Schwartz and its applications to absolutely summing operators. Studia Math. (1970) 38:193–201.

Google Scholar

29. Pietsch A. Operators Ideals. Berlin: Deutscher Verlag der Wissenschatten (1978).

Google Scholar