Entropy Optimization of Third-Grade Nanofluid Slip Flow Embedded in a Porous Sheet With Zero Mass Flux and a Non-Fourier Heat Flux Model

The prime objective of this article is to explore the entropy analysis of third-order nanofluid fluid slip flow caused by a stretchable sheet implanted in a porous plate along with thermal radiation, convective surface boundary, non-Fourier heat flux applications, and nanoparticle concentration on zero mass flux conditions. The governing physical systems are modified into non-linear ordinary systems with the aid of similarity variables, and the outcomes are solved by a homotopy analysis scheme. The impression of certain governing flow parameters on the nanoparticle concentration, temperature, and velocity is illustrated through graphs, while the alteration of many valuable engineering parameters viz. the Nusselt number and Sherwood number are depicted in graphs. Entropy generation with various parameters is obtained and discussed in detail. The estimation of entropy generation using the Bejan number find robust application in power engineering and aeronautical propulsion to forecast the smartness of entire system.

Introduction

Nanoliquids are the type of liquids that have small volumetric quantities of nanoscale (10⁻⁹ − 10⁻⁷m) metallic (Cu, Ti, Hg, Fe, Ag, Au, etc.) or non-metallic particles (TiO₂, SiO₂, CuO, Al₂O₃, etc) taken as nano particles. Usually nanoliquids have a colloidal suspension of nanoparticles inside a base liquid for example water, oil, ethylene glycol, etc. Initially, Choi [1] proposed the “nanofluid” term. In general, the effective heat transfer enhancement has the reason of nanoliquids generally restrict up to volume fraction of nanoparticles. Therefore, in the latest technologies and engineering areas, nanoliquids receiving a phenomenal impact. Mushtaq et al. [2] attempted the numerical study of the nanoliquids induced by an exponentially stretchable sheet with rotating flow model. MHD nanoliquid flow toward a porous plate with internal heat generation effects was presented by Reddy and Chamka [3]. Shit et al. [4] studied the convective flow of hydromagnetic nanoliquid with entropy generation mechanism. Recently, Gireesha et al. [5] explained a Hall current effects of two-phase transient nanoliquid flow induced by a stretchable sheet. Reddy et al. [6] performed the combined convection flow of nanoliquid toward a semi-infinite vertical flat sheet with convectively heated boundary and Soret effect. Few more significant studies in this research area are seen in ref's [7–13].

Due to various applications in different technical and industrial areas, the fluid flow problems toward a stretching surface have developed. It finds application in rubber and plastic sheets production, melt-spinning, production of glass-fiber, and metallic plate cooling systems. Sakiadis [14] studied the uniform velocity of a magnetohydrodynamic flow past a solid medium. Magyari et al. [15] examined the first order chemical reaction and heat generation combination on micropolar fluid flow induced by a permeable stretching surface. Gupta [16] analyzed the heat and mass transfer effects of a boundary layer flow induced by a stretchy sheet with suction or blowing impact. Magyari and Keller [17] exposed the fluid flow over exponentially extending sheet with heat and mass transfer impacts. Significances of thermal boundary layer flow for a linearly stretchy sheet with viscous dissipation were examined by Cortell [18]. The cutting-edge research reports on stretching sheet flow are highlighted in these works of literature [19–24].

Fluid flow saturated in the porous surface have numerous applications in various fields like geothermal energy, fuel cell technologies, material processing, etc. Chamkha et al. [25] described the free convective flow past an inclined plate fitted in a porous medium of variable porosity with solar radiation. Khan and Aziz [26] studied the natural convective flow with double diffusion caused by a vertical porous sheet. Oyelakin et al. [27] analyzed the slip flow of unsteady radiative Casson nanofluid toward a stretchy surface. Gorla and Chamkha [28] studied the nanofluid flow toward a non-isothermal vertical plat entrenched in a porous sheet. The same research group extended their work for different models for various applications [29–32].

Heat transport problems in the flow of liquids have been examined by several researchers for the last decade. In 1822, Fourier [33] constructed the heat conduction law. This states that “the heat transfer in a medium with inertial rate.” A parabolic-type equation was used to state the heat conduction equation. The problem rising at this time is that there exists no such object or material that satisfies Fourier's law, as argued by Cattaneo [34] when using thermal relaxation time to customize Fourier's law. Later, Christov [35] developed and joined the upper convected Maxwell fluid. This developed model is called a Christov-Cattaneo heat flux model. Loganathan et al. [36] studied the thermal relaxation time effects on Oldroyd-B liquid with second-order slip and cross-diffusion impacts. The Christov-Cattaneo heat flux model for a third-grade liquid with chemical reaction effects was examined by Imtiaz et al. [37].

In the last decade, several scientists have researched entropy generation in the flow of fluids and heat transfer over a stretching surface. In various engineering and industrial divisions, the performance of heating and cooling are of massive importance in different electronic and energy issues. Aiboud and Saouli [38] examined the MHD viscoelastic fluid flow with the application of entropy analysis using Kummer's function. Makinde [39] presented the thermal radiation and Newtonian heating impacts of variable viscosity fluid caused by a semi-infinite plate using shooting quadrature and obtained the entropy generation number. Loganathan et al. [40, 41] verified the entropy analysis for the third grade and Williamson nanoliquid flow caused by a stretchable sheet with various effects. They employed HAM to solve the non-linear governing systems.

Based on our research in previously published works, entropy generation of third-grade nanofluid flow caused by a stretching sheet with a modified Fourier law has not been discussed with a high standard of scientific attention. As far as we noticed in literature, the studies taken for entropy generation are limited with some parameters viz the Brinkmann number, Reynolds number, Temperature difference parameter, and Hartmann number. We have extended our investigations to include thermal relaxation time, the Biot number, thermal radiation, slip parameter, porous parameter, etc. The effective collection and analysis of these results will open new gateways for diverse engineering application in various streams.

Problem Development

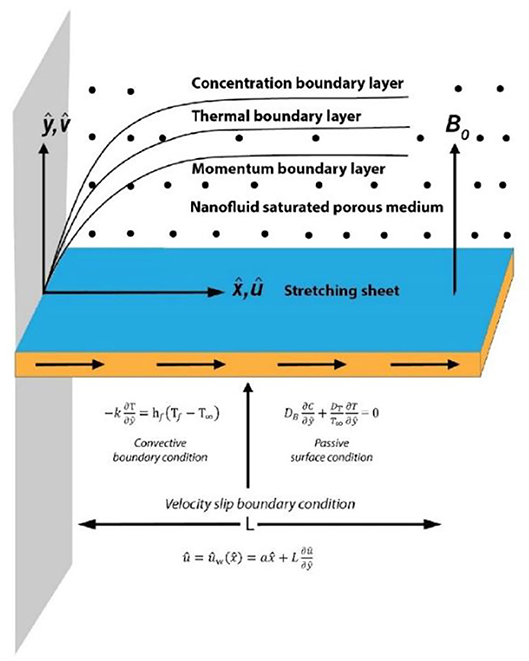
We were interested in analyzing the entropy and Bejan number of third-grade nanofluid saturated in a porous medium with Christov-Cattaneo heat flux. In Figure 1, the stretching parameter is taken along x direction where T_W and C_W are represented the wall temperature and concentration, respectively. T_∞ and C_∞ are used to index the ambient temperature and concentration, respectively. A convective heating temperature T_f is stimulated at the bottom of the sheet surface. The Buongiorno nanofluid [42] is used for the present case. Based on his consideration, the slip mechanisms, namely, the Brownian diffusion, inertia, Magnus effect, diffusiophoresis, thermophoresis, gravity, and fluid drainage, were analyzed. He recommended that the thermophoresis and Brownian diffusion are essential slip mechanism in low dimensional materials.

FIGURE 1

Figure 1. Flow diagram.

The following is an incompressible fluid model containing body forces with the equation of continuity and motion:

$\begin{array}{ll}divv=0& (1)\end{array}$

$\begin{array}{ll}\rho \frac{dv}{dt}=divT+\rho b+J+B& (2)\end{array}$

Here, ρ is the fluid density, which is taken as a constant, v is the velocity field, b indicates the body forces, J denotes the electric current, and T states the third-grade incompressible fluids Cauchy stress tensor [43]

$\begin{array}{l}T=-pI+\mu E_1+A_1^{*}{E}_2+A_2^{*}{E}_1^2+{\beta }_1{E}_3\\ \begin{array}{l}+{\beta }_2(E_1,E_2+E_2{E}_1)+{\beta }_3(tr{E}_1^2)E_1\end{array}& (3)\end{array}$

where μ, (E₁, E₂, E₃) and $A_1^{*},{\beta }_i$ indicate the viscosity coefficient, kinematics tensors, and material modulis as in

$\begin{array}{ll}{E}_1=L+{(L)}^T& (4)\end{array}$

$\begin{array}{ll}{E}_n=\frac{d}{dt}{E}_{n-1}+E_{n-1}L+{(L)}^T{E}_{n-1},n=2,3,\text{and}& (5)\end{array}$

$\begin{array}{ll}L=\nabla v.& (6)\end{array}$

$\frac{d}{dt}$ is expressed as the material time derivative

$\begin{array}{ll}\frac{d()}{dt}=\frac{\partial ()}{\partial t}+v.\nabla ().& (7)\end{array}$

The relationship between Clausius-Duhem inequality and thermodynamically compatible fluid is stated by Fosdick and Rajagopal [44]:

$\begin{array}{ll}\mu \ge 0,A_1^{*}\ge 0,{\beta }_1={\beta }_2=0,{\beta }_3\ge 0& (8)\end{array}$

$\begin{array}{ll}|A_1^{*}+A_2^{*}|\le 2\sqrt{6\mu {\beta }_3}& (9)\end{array}$

$\begin{array}{ll}T=-pI+\mu E_1+A_1^{*}{E}_2+A_2^{*}{E}_1^2+{\beta }_3\left(tr{E}_1^2\right)E_1& (10)\end{array}$

Boussinesq and normal boundary layer approximations were considered by Pakdemirli [45]. We made the following assumptions:

1. The nanoparticles are small and of equal size to the pores.

2. The zero-mass flux of the nanoparticles is included.

3. Christov-Cattaneo heat flux is considering instead of normal heat flux.

4. The magnetic field in the fluid flow is ignored due to a lower magnetic Reynolds number.

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0& (11)\end{array}$

$\begin{array}{l}u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\\ =\nu \frac{{\partial }^{2}u}{\partial y^2}+\frac{A_1^{*}}{\rho }\left(u\frac{{\partial }^{3}u}{\partial y^2\partial x}+v\frac{{\partial }^{3}u}{\partial y^3}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}+3\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}\right)\\ \begin{array}{l}+2\frac{A_2^{*}}{\rho }\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}+6\frac{{\beta }_1^{*}}{\rho }{\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B_0^2}{\rho }u-\frac{\nu }{k_p}u\end{array}& (12)\end{array}$

$\begin{array}{l}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{\rho c_p}\frac{\partial q_r}{\partial y}+\frac{Q_0}{\rho c_p}(T-T_{\infty })\\ \begin{array}{l}+\tau \left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right]\end{array}& (13)\end{array}$

$\begin{array}{ll}u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}& (14)\end{array}$

$\begin{array}{l}u=u_w(x)=ax+L\frac{\partial u}{\partial y},-k\frac{\partial T}{\partial y}=h_f(T_f-T_{\infty }),\\ D_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0aty=0\\ \begin{array}{l}u\to 0,T\to T_{\infty },c\to c_{\infty }asy\to \infty \end{array}& (15)\end{array}$

The energy equation with a Cattaneo-Christov heat flux model is stated as

$\begin{array}{l}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+{\lambda }_T(u^2\frac{{\partial }^{2}T}{\partial x^2}+v^2\frac{{\partial }^{2}T}{\partial y^2}+\left(u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}+v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}\right)\\ +2uv\frac{\partial T^2}{\partial x\partial y})+\left(u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y}+v\frac{\partial v}{\partial y}\frac{\partial T}{\partial y}\right)=\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial y^2}\\ -\frac{1}{\rho c_p}\frac{\partial q_r}{\partial y}+\frac{Q_0}{\rho c_p}\left(T-T_{\infty }\right)\\ +\tau \left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right].& (16)\end{array}$

Consider the transformation given below:

$\begin{array}{l}\psi =\sqrt{a\nu }xf(\eta ),u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},\eta =\sqrt{\frac{a}{\nu }}y,\\ v=-\sqrt{a\nu }f(\eta ),u=ax{f}^{\prime }(\eta ),\theta (\eta )=\frac{T-T_{\infty }}{T_f-T_{\infty }},\\ \begin{array}{l}\varphi (\eta )=\frac{C-C_{\infty }}{C_{\infty }}.\end{array}& (17)\end{array}$

The non-linear governing equations are:

$\begin{array}{ll}\begin{array}{l}{f}^{‴}+f{f}^{″}-{f^{\prime }}^2+{\alpha }_1(2f^{\prime }{f}^{‴}-f{f}^{iv})+(3{\alpha }_1+2{\alpha }_2){f^{″}}^2\hfill \\ \begin{array}{l}+6\beta Re{f}^{‴}{f^{″}}^2-(M{f}^{\prime }+K{f}^{\prime })=0\hfill \end{array}\hfill \end{array}& (18)\end{array}$

$\begin{array}{l}\left(1+\frac{4}{3}Rd\right){\theta }^{″}+Prf{\theta }^{\prime }+PrS\theta -Pr\gamma f^2{\theta }^{\prime \prime }-Pr\gamma f{f}^{\prime }{\theta }^{\prime }\\ \begin{array}{l}+PrNb{\theta }^{\prime }{\varphi }^{\prime }+PrNt{{\theta }^{\prime }}^2=0\end{array}& (19)\end{array}$

$\begin{array}{ll}{\varphi }^{\prime \prime }+Lef{\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{\prime \prime }=0& (20)\end{array}$

with the end points

$\begin{array}{l}f(0)=f_w,f^{\prime }(0)=1+\Gamma f^{″}(0),{\theta }^{\prime }(0)=-Bi(1-\theta (0)),\\ Nb{\varphi }^{\prime }(0)+Nt{\theta }^{\prime }(0)=1\\ \begin{array}{l}{f}^{\prime }(\infty )=0,\theta (\infty )=0,\varphi (\infty )=0\end{array}& (21)\end{array}$

The non-dimensional variables are

$\begin{array}{l}{\alpha }_1=\frac{a{A}_1^{*}}{\nu },{\alpha }_2=\frac{a{A}_2^{*}}{\nu },\beta =\frac{a{\beta }_1^{*}}{\nu },Re=\frac{u_{w}x}{\nu },Pr=\rho C_p/k,\\ M=\sigma B_0^2/\rho a,Rd=\left(4{\sigma }^{*}{T}_{\infty }^3\right)/\left(k{k}^{*}\right),S=\frac{Q_0}{\rho c_p},\gamma ={\lambda }_{T}a,\\ Bi=\frac{h_f}{k}\sqrt{{\text{}}^{\nu }{/}_a},Nb=\frac{\tau D_B}{\nu }(C_{\infty }),Nt=\frac{\tau D_T}{\nu }\left(T_f-T_{\infty }\right).\end{array}$

The application of physical entitles is such that

$\begin{array}{ll}R{e}^{\frac{1}{2}}{C}_f=f^{″}(0)+{\alpha }_1{f}^{\prime }(0)f^{‴}(0)+\beta Re{\left[f^{″}(0)\right]}^3& (22)\end{array}$

$\begin{array}{ll}R{e}^{-\frac{1}{2}}N{u}_x=-(1+\frac{4}{3}Rd){\theta }^{\prime }(0).& (23)\end{array}$

The local mass transfer rate becomes identically zero due to the zero mass flux state [46]

$\begin{array}{ll}R{e}^{-\frac{1}{2}}Sh=\frac{Nt}{Nb}{\theta }^{\prime }(0).& (24)\end{array}$

Entropy Optimization

The entropy minimization optimization for fluid friction, heat, and the irreversibility of mass transfer are given below:

$\begin{array}{l}{S}_{gen}^{{\text{}}^{‴}}=\frac{K_1}{T_{\infty }^2}\left[{\left(\frac{\partial T}{\partial x}\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}}{\left(\frac{\partial T}{\partial y}\right)}^2\right]\\ +\frac{\mu }{T_{\infty }}\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right]+{\left[\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right]}^2\\ +\frac{RD}{C_{\infty }}\left[{\left(\frac{\partial C}{\partial x}\right)}^2+{\left(\frac{\partial C}{\partial y}\right)}^2\right]+\frac{RD}{T_{\infty }}[\left(\frac{\partial T}{\partial x}\right)\left(\frac{\partial C}{\partial x}\right)\\ +\left(\frac{\partial T}{\partial y}\right)\left(\frac{\partial C}{\partial y}\right)]+\frac{\sigma B_0^2}{T_{\infty }} u^2+\frac{\nu }{k_p}{u}^2.& (25)\end{array}$

Using Equation (25) modified with the help of Equation (17),

$\begin{array}{l}{S}_{gen}^{{\text{}}^{‴}}=\frac{K_1}{T_{\infty }^2}\left[{\left(\frac{\partial T}{\partial y}\right)}^2+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}}{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{\mu }{T_{\infty }}{\left(\frac{\partial u}{\partial y}\right)}^2\\ \begin{array}{l}+\frac{RD}{C_{\infty }}{\left(\frac{\partial C}{\partial y}\right)}^2+\frac{RD}{T_{\infty }}\left(\frac{\partial T}{\partial y}\right)\left(\frac{\partial C}{\partial y}\right)+\frac{\sigma B_0^2}{T_{\infty }}{u}^2+\frac{\nu }{k_p}{u}^2.\end{array}& (26)\end{array}$

Dimensionless system of entropy generation is defined as:

$\begin{array}{ll}\begin{array}{l}{E}_G=Re(1+\frac{4}{3}Rd){{\theta }^{\prime }}^2+Re\frac{Br}{\Omega }{f^{″}}^2+Re{\left(\frac{\zeta }{\Omega }\right)}^2\lambda {{\varphi }^{\prime }}^2\hfill \\ \begin{array}{l}+Re\frac{\zeta }{\Omega }\lambda {\varphi }^{\prime }{\theta }^{\prime }+\frac{Br}{\Omega }(M+K){f^{\prime }}^2.\hfill \end{array}\hfill \end{array}& (27)\end{array}$

The Bejan number states

$\begin{array}{l}\text{Be}=\frac{\text{Entropy genration due to irrevesablity of heat and mass transfer}}{\text{Total entropy generated}}\end{array}$

$\begin{array}{ll}\begin{array}{l}Be=\hfill \\ \begin{array}{l}\frac{\left(Re\left(1+\frac{4}{3}\text{Rd}\right) {{\theta }^{\prime }}^2++Re{\left(\frac{\zeta }{\Omega }\right)}^2\lambda {{\varphi }^{\prime }}^2+Re\frac{\zeta }{\Omega }\lambda {\varphi }^{\prime }{\theta }^{\prime }\right)}{Re\left(1+\frac{4}{3}Rd\right){{\theta }^{\prime }}^2+Re\frac{Br}{\Omega }{f^{″}}^2+Re{\left(\frac{\zeta }{\Omega }\right)}^2\lambda {{\varphi }^{\prime }}^2+Re\frac{\zeta }{\Omega }\lambda {\varphi }^{\prime }{\theta }^{\prime }+\frac{Br}{\Omega }(M+K){f^{\prime }}^2}.\hfill \end{array}\hfill \end{array}& (28)\end{array}$

Homotopy Solutions

There are several techniques available to solve non-linear problems. The homotopy analysis method (HAM) is initially constructed by Liao [47]. Moreover, he altered a non-zero auxiliary parameter [48]. This parameter shows the way to calculate the convergence rate. It also offers great independence with which to make the initial guesses of the solutions.

The initial guesses for satisfying the boundary conditions

$\begin{array}{l}{f}_0=f_w+\left(\frac{1}{1+\Gamma }\right)1-e^{-\eta }\\ {\theta }_0=\frac{Bi*e^{-\eta }}{1+Bi}\\ {\varphi }_0=-\left(\frac{Nt}{Nb}\right)*\frac{Bi*e^{-\eta }}{1+Bi}.\end{array}$

L_f, L_θ, and L_ϕ are the linear operators

$\begin{array}{l}{L}_f=f^{‴}-f^{\prime }\\ L_{\theta }={\theta }^{\prime \prime }-\theta \\ L_{\varphi }={\varphi }^{\prime \prime }-\varphi \end{array}$

while obeying the resulting properties

$\begin{array}{l}{L}_f\left[E_1+E_2{e}^{\eta }+E_3{e}^{-\eta }\right]=0\\ L_{\theta }\left[E_4{e}^{\eta }+E_5{e}^{-\eta }\right]=0\\ L_{\varphi }\left[E_6{e}^{\eta }+E_7{e}^{-\eta }\right]\end{array}$

The zero^th order deformation is

$\begin{array}{l}\left(1-p\right)L_f\left[f\left(\eta ;p\right)-f(\eta )\right]=p{h}_f{{N}}_f\left[f\left(\eta ;p\right)\right]\end{array}$

$\begin{array}{l}\left(1-p\right)L_{\theta }\left[\theta \left(\eta ;p\right)-{\theta }_0(\eta )\right]\\ =p{h}_{\theta }{{N}}_{\theta }\left[\theta \left(\eta ;p\right),f\left(\eta ;p\right),\varphi \left(\eta ;p\right)\right]\end{array}$

$\begin{array}{l}\left(1-p\right)L_{\varphi }\left[\varphi \left(\eta ;p\right)-{\varphi }_0(\eta )\right]\\ =p{h}_{\varphi }{{N}}_{\varphi }\left[\varphi \left(\eta ;p\right),\theta \left(\eta ;p\right),f\left(\eta ;p\right)\right]\end{array}$

where p ϵ [0, 1]

h_f, h_θ, and h_ϕ are the non-zero auxiliary constants, and ${{N}}_f$, ${{N}}_{\theta }$, and ${{N}}_{\varphi }$ are the non-linear operators given by

$\begin{array}{l}{{N}}_f\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right)\right]=\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}-{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\\ +f\left(\eta ;p\right)\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\\ +{\alpha }_1\left(2\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}-f\left(\eta ;p\right)\frac{{\partial }^{4}f\left(\eta ;p\right)}{\partial {\eta }^4}\right)\\ +(3{\alpha }_1+2{\alpha }_2){\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\\ +6\beta Re\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\\ -(M+K)\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\end{array}$

$\begin{array}{l}{{N}}_{\theta }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right),\varphi \left(\eta ;p\right)\right]=\left(1+\frac{4}{3}Rd\right)\frac{{\partial }^2\theta \left(\eta ;p\right)}{\partial {\eta }^2}\\ +Prf\left(\eta ;p\right)\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }-Pr\gamma {\left[[f\left(\eta ;p\right)\right]}^2\frac{{\partial }^2\theta \left(\eta ;p\right)}{\partial {\eta }^2}\\ -Pr\gamma f\left(\eta ;p\right)\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }+PrS\theta \left(\eta ;p\right)\\ +PrNb\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\frac{\partial \varphi \left(\eta ;p\right)}{\partial \eta }+PrNt{\left[\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right]}^2\end{array}$

$\begin{array}{l}{{N}}_{\varphi }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right),\varphi \left(\eta ;p\right)\right]=\frac{{\partial }^2\varphi \left(\eta ;p\right)}{\partial {\eta }^2}\\ +Lef\left(\eta ;p\right)\frac{\partial \varphi \left(\eta ;p\right)}{\partial \eta }+\frac{Nt}{Nb}\frac{{\partial }^2\theta \left(\eta ;p\right)}{\partial {\eta }^2}\end{array}$

$\begin{array}{l}f\left(0;p\right)=f_w,f^{\prime }\left(0;p\right)=1+\Gamma f^{″}(0:p),f^{\prime }\left(\infty ;p\right)=0\\ {\theta }^{\prime }\left(0;p\right)=-Bi(1-\theta \left(0;p\right)),\theta \left(\infty ;p\right)=0\\ {\varphi }^{\prime }\left(0;p\right)=-\frac{Nt}{Nb}{\theta }^{\prime }\left(0;p\right),{\varphi }^{\prime }\left(\infty ;p\right)=0\end{array}$

The m^th order deformation equations are

$\begin{array}{l}{L}_f\left[f_m(\eta )-{\chi }_m{f}_{m-1}(\eta )\right]=h_f{R}_{f,m}(\eta )\\ L_{\theta }\left[{\theta }_m(\eta )-{\chi }_m{\theta }_{m-1}(\eta )\right]=h_{\theta }{R}_{\theta ,m}(\eta )\\ L_{\varphi }\left[{\varphi }_m(\eta )-{\chi }_m{\varphi }_{m-1}(\eta )\right]=h_{\varphi }{R}_{\varphi ,m}(\eta )\end{array}$

where

$\begin{array}{l}{\chi }_m=\{\begin{array}{c}0,m\le 1\hfill \\ 1,m>1\hfill \end{array},\hfill \end{array}$

$\begin{array}{l}{R}_{f,m}\left(\eta \right)=f_{m-1}^{‴}+{\displaystyle \underset{k=0}{\sum ^{m-1}}}[f_{m-1-k}{f}_k^{\prime \prime }-f_{m-1-k}^{\prime }{f}_k^{\prime }\\ +{\alpha }_1\left(2f_{m-1-k}^{\prime }{f}_k^{‴}-f_{m-1-k}{f}_k^{iv}\right)\\ +\left(3{\alpha }_1+2{\alpha }_2\right)f_{m-1-k}^{\prime \prime }{f}_k^{\prime \prime }\\ +6\beta Re{f}_{m-1-l}^{‴}{\displaystyle \underset{j=0}{\sum ^l}}{f}_{l-j}^{\prime \prime }{f}_j^{\prime \prime }-(M+K) \alpha f_{m-1-k^{\prime }}]\end{array}$

$\begin{array}{l}{R}_{\theta ,m}\left(\eta \right)=\left(1+\frac{4}{3}Rd\right){\theta }_{m-1}^{\prime \prime }+Pr{\displaystyle {\sum }_{k=0}^{m-1}}\left[{\theta }_{m-1-k}^{\prime }{f}_k\right]\\ -Pr\gamma [\left(f_{m-l-1}{\displaystyle {\sum }_{j=0}^l}{f}_{{{\text{}}_{1-j}}^{\prime }}{\theta }_j^{\prime }+f_{m-l-1}{\theta }_l^{\prime \prime }\right)]\\ +PrNb{\displaystyle {\sum }_{k=0}^{m-1}}{\theta }_{{\text{}}_{m-1-k}}^{\prime }{\varphi }_k+PrNt{\displaystyle {\sum }_{k=0}^{m-1}}{\theta }_{m-1-k^{\prime }}{\theta }_{k^{\prime }}\\ +PrS{\theta }_{m-1}\end{array}$

$\begin{array}{l}{R}_{\varphi ,m}\left(\eta \right)= {\varphi }_{m-1}^{\prime \prime }+Le{\displaystyle {\sum }_{k=0}^{m-1}}{\varphi }_{m-1-k^{\prime }}{f}_k\\ +\frac{Nt}{Nb}{\displaystyle {\sum }_{k=0}^{m-1}}{\theta }_{m-1-k^{\prime }}{\theta }_{k^{\prime }}\end{array}$

$\begin{array}{l}{f}_m(0)=0,{f_m}^{\prime }(0)-\Gamma {f_m}^{{\text{}}^{″}}(0)=0,{{\theta }_m}^{\prime }(0)-Bi{\theta }_m(0)=0,\\ {{\varphi }_m}^{\prime }(0)+\frac{Nt}{Nb}{{\theta }_m}^{\prime }(0)=0\\ {f_m}^{\prime }(\eta )\to 0,{{\theta }_m}^{\prime }(\eta )\to 0,{\varphi }_m(\eta )\to 0as\eta \to \infty .\end{array}$

with boundary conditions

$\begin{array}{l}{f}_{m^{\prime }}\left(0\right)=f_m\left(0\right)=f_{m^{\prime }}(\infty )={\theta }_m\left(0\right)={\theta }_m(\infty )={\varphi }_m\left(0\right)\\ ={\varphi }_m(\infty )=0.\end{array}$

The appropriate solutions $\left[f_m^{*},{\theta }_m^{*},{\varphi }_m^{*}\right]$ are

$\begin{array}{l}{f}_m(\eta )=f_m^{*}(\eta )+E_1+E_2{e}^{\eta }+E_3{e}^{-\eta },\\ {\eta }_m(\eta )={\eta }_m^{*}(\eta )+E_4{e}^{\eta }+E_5{e}^{-\eta },\\ {\eta }_m(\eta )={\eta }_m^{*}(\eta )+E_6{e}^{\eta }+E_7{e}^{-\eta }.\end{array}$

Convergence Analysis

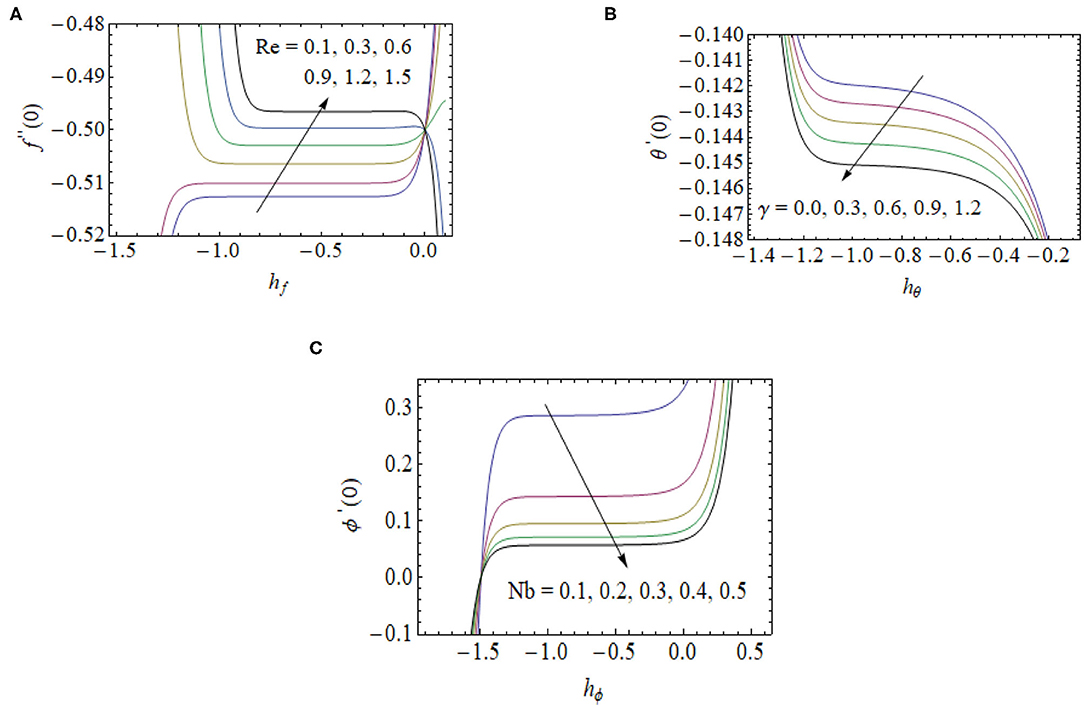
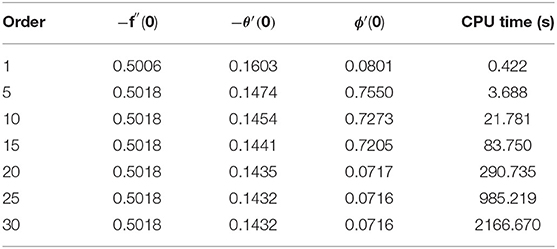
The auxiliary parameters h_f, h_θ, and h_ϕ act as a vital part of convergence series solutions. The h-charts of f″(0), θ′(0), and ϕ′(0) for Re, γ , and Nb are shown in Figure 2. From these curves, the straight line is referred as the h-curve. The convergent approximation is selected from this straight line of the curves. We note that h-curve of f″(0), θ′(0), and ϕ′(0) shrinks as we enhance the range of Re, γ , and Nb, which shows the larger order approximation will be needed if the larger value of Re, γ , and Nb is employed. Approximations values of HAM with CPU time is denoted in Table 1.

FIGURE 2

Figure 2. (A–C) h− curves for h_f, h_θ, h_ϕ.

TABLE 1

Table 1. Order of approximations of HAM.

Computational Results and Discussion

The numerical calculations of velocity, concentration, temperature, entropy generation, and the Bejan number are discussed in this section. The homotopy technique is used for solving the non-linear governing Equations (18)–(20) with boundary conditions (21). The graphical results of entropy, Bejan number, temperature, Nusselt number, nanoparticle concentration, Sherwood number, and velocity profiles are computed via different flow parameters included in this study with the fixed values of α₁ = α₂ = β = Bi = f_w = N_t = 0.2,Re = Pr = Le = Γ = 1.0, M = γ = 0.5, Rd = 0.3, Hg = −0.1, N_b = 0.4, Br = 5.0, and λ = Ω = ζ = 1.0.

Impact on Velocity

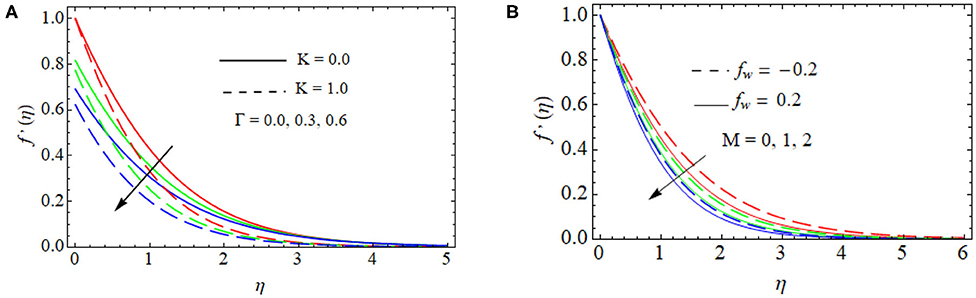
It is observed from Figure 3A that the velocity is reduced to increase the values of the velocity slip parameter due to the ratio of stretching velocity and the viscosity of the fluid. The effect of the slip parameter in velocity has had more impact in the absence of a porous medium. Figure 3B indicates that the velocity diminishes when the magnetic field (M) raises. Improved Lorentz force is observed because of the increasing the values of M that opposes the fluid motion. Thus, we conclude that the velocity profile diminishes.

FIGURE 3

Figure 3. (A,B) Impact of Γ and M on velocity profile f′(η).

Impact on Temperature

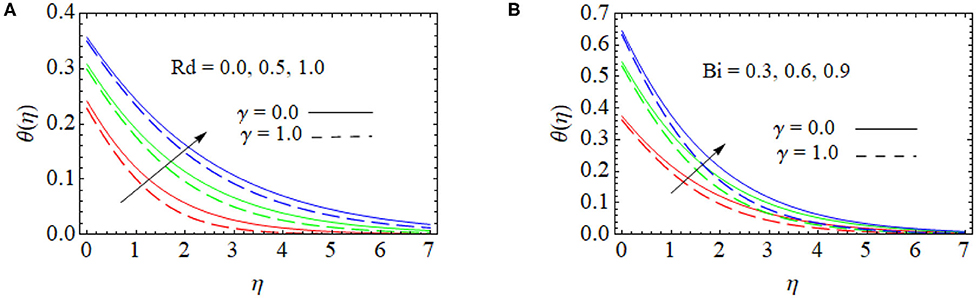
The impact of the radiation parameter Rd on the temperature profile is examined in Figure 4A. The temperature in the radiation parameter is high. Comparing the radiation effects with Christov-Cattaneo and normal heat flux, we observed that the radiation effect is quite low for Christov-Cattaneo heat flux. Figure 4B displays the influence of the Biot number on the temperature profile. From this figure, we observed that temperature is a rising function of Bi close to the sheet. Since Bi affects more temperature near the surface. Heat transfer resistance is higher within the body compared to the surface of the sheet for rising values Bi.

FIGURE 4

Figure 4. (A,B) Impact of Rd and Bi on temperature profile θ(η).

Impact on Nanoparticle Volume Concentration

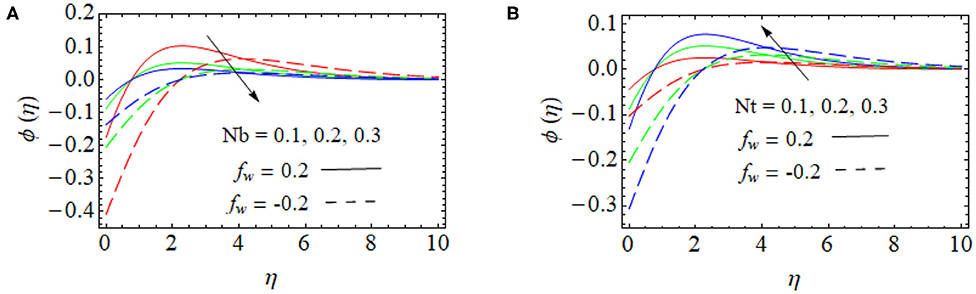
In Figure 5A, the effect of concentration profile with growing values of the Brownian motion parameter Nb is depicted. In suction cases, higher values of Nb increase the concentration profile close to that of the surface of the sheet, and, suddenly, the concentration begins to fall, stabilizing far away from the surface of the sheet. This is due to the appearance of passive surface conditions for the concentration profile. Moreover, the injection at the sheet shows the concentration is rising near the sheet, and it diminishes far away from the surface of the sheet. The influence of the thermophoresis parameter Nt in the concentration profile ϕ(η). is highlighted in Figure 5B. When there is suction in the sheet, with a rise in Nt, the concentration of the liquid decreases near to thsheet at certain stage starts to fall and stabilize away from the endpoints of the surface of the sheet. When there is an injection at the sheet, higher values of Nt decreases the concentration profile near the sheet, and it increases far away from the surface of the sheet.

FIGURE 5

Figure 5. (A,B) Impact of Nb and Nt on concentration profile ϕ(η).

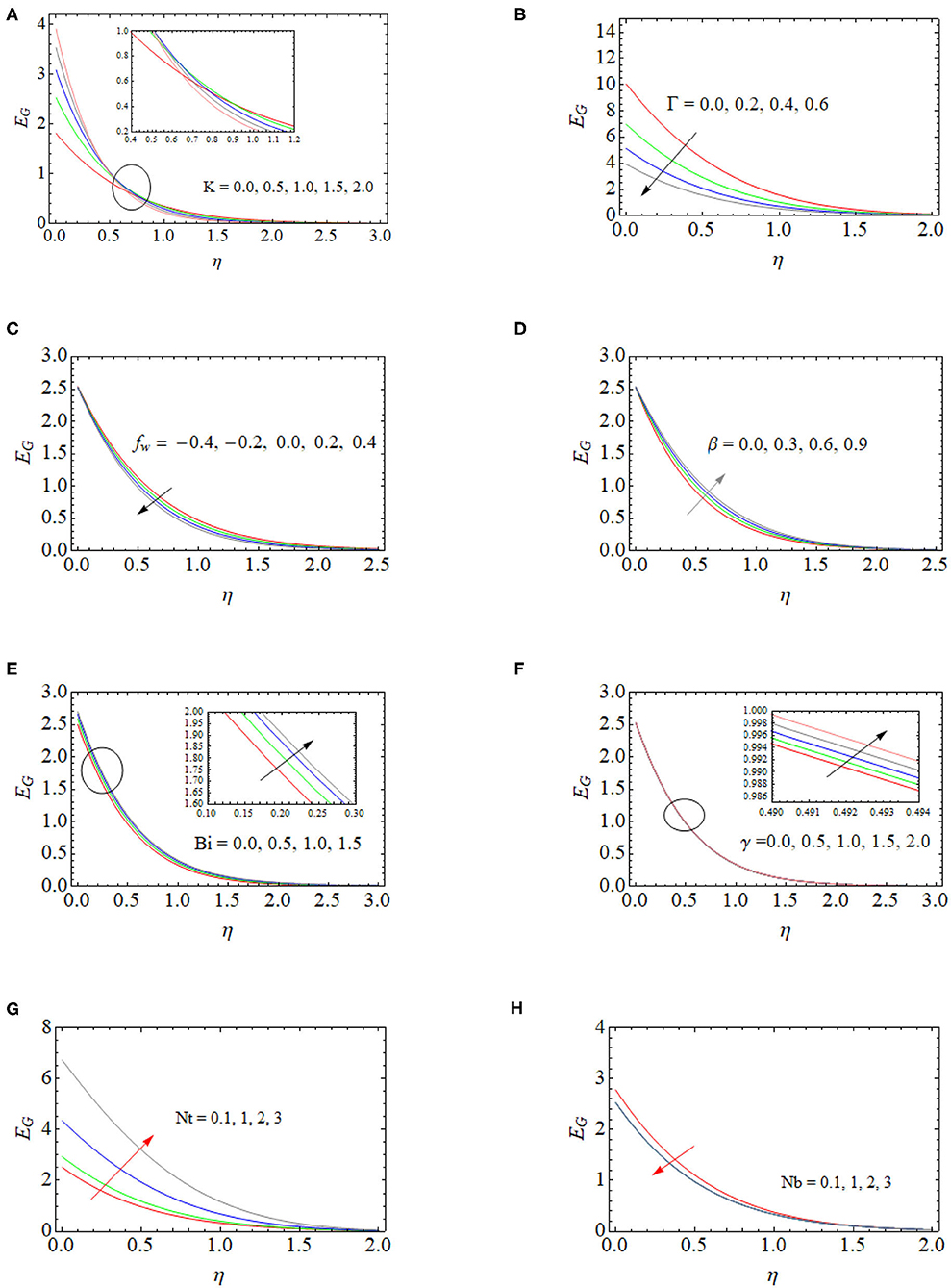
Impact on Entropy Generation

The Effects of distinct fluid parameters on the entropy generation profile are highlighted in Figures 6A–G. Figure 6A depicts the influence of porous parameter in entropy profile. Initially, the entropy rate increases for the porous parameter at a certain stage (η = 0.6) before it becomes to fall. The responses of the slip parameter on entropy generation were succinctly depicted in Figure 6B. From this figure, it was obviously noted that entropy generation was inversely proportional to slip parameter. This causes a decrease in large values of slip parameter and temperature gradients in the boundary layer when retaining the fluid friction as we proceed. This occurrence induces a suppression in entropy generation since heat transfer was committed. Figures 6C–E displayed the impact of the suction\ injection parameter (f_w.), material parameter (β) and Biot number (Bi) on the entropy profile (E_G). Our examination obtained that higher range of f_w, reduces the entropy generation profile, and the entropy generation rate is enhanced for higher β and Bi.

FIGURE 6

Figure 6. (A–H) Impacts of K, Γ, f_w, β, Bi, γ, Nt, and Nb on entropy generation E_G.

The effect of thermal relaxation time (γ) on the entropy genation profile is sketched in Figure 6F. It is obvious that thermal relaxation time is small for temperature and heat transfer rates. In addition, domination of the irreversibility in heat transfer affected the heat flux. Thus, we have seen a small increase in the entropy of the system. Performance of Nt and Nb on entropy generation profile (E_G) is shown in Figures 6G,H, which shows that entropy is increased with an increase of Nt, whereas E_G is inversely proportional to Nb. The Brownian motion induces the nanoparticles temperature, but it reduces the temperature gradient on wall. As a result, entropy generation parameter reduces where Nt is directly proportional to temperature gradient and creates ambient atmosphere for higher values of E_G.

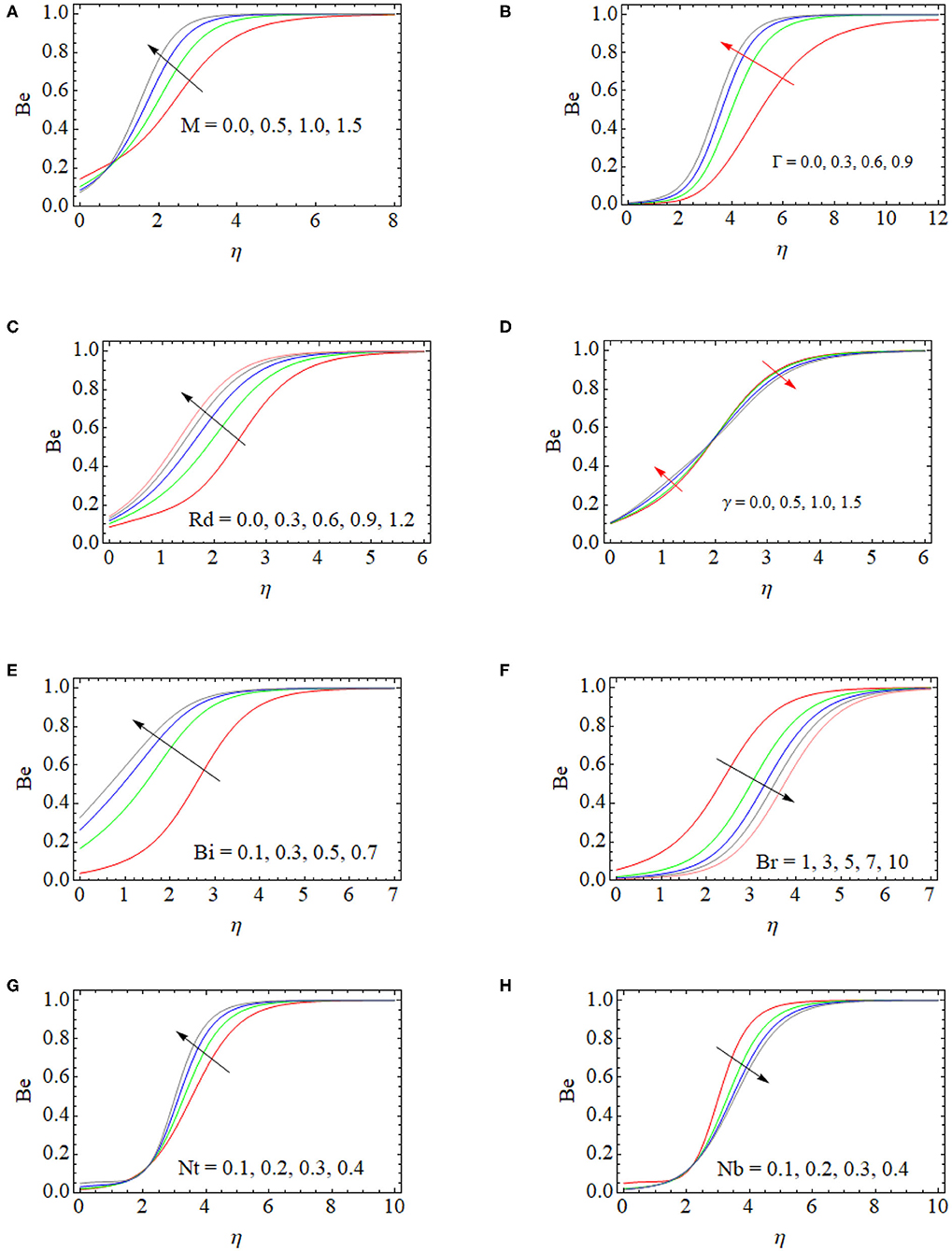
Impact on the Bejan Number

The Bejan number (Be) is a dimensionless quantity that specifies the ratio of entropy generation between heat transfer and the total entropy generation where Bejan numbers take values from 0 to 1. If Be is nearly equal to 1, the entropy generation will become more due to heat transfer. It is clear from Figure 7A that, with an escalation in the applied magnetic field, there is an augmentation in the Bejan number. The consequence of heat transfer entropy develops as we move up from the surface. The entropy effect has full domination because of the heat transfer while it is also outlying from the region. This is the reason behind how the augmenting value of M brings a stronger frictional effect, which leads to an increase in the liquid temperature. There is also a consequent development in the Be, as shown in Figure 7A. From Figure 7B, it is observed that the Be is increased for the increase in the slip parameter (Γ). Physically, larger values of (Γ) enhance the temperature gradient inside the regime, which induces the Bejan number and irreversibility of heat transfer.

FIGURE 7

Figure 7. (A–H) Impact of M, Γ, Rd, γ, Bi, Br, Nt, and Nb on the Bejan number B.

Figure 7C states that, with the rise of the radiation constant Rd, the Bejan number is boosted. This is due to the total entropy generation dominated by thermal irreversibility. Figure 7D shows the effect of the thermal relaxation time (γ) on the Be. At first, the Be is augmented for higher values of γ at a sudden point (η = 2.2). Consequently, the Bejan number profile reduces for the values of γ. Figure 7E shows that the Bi displays a trend of raising the Be. The demonstration of such an increasing trend of the Bejan number explains how the entropy production near the surface is large due to the liquid friction—at least relative to that of the heat transfer irreversibility. The variation of the Brinkmann number Br is sketched in Figure 7F. This figure shows that the Bejan number is reduced, as we have to enhance the Br. Figures 7G,H shows the influence of thermophoresis (Nt) and Brownian motion (Nb) parameters on the Bejan number. From these plots, we note that Nt and Nb have inverse effects on the Bejan number profile.

Impact on Physical Entities

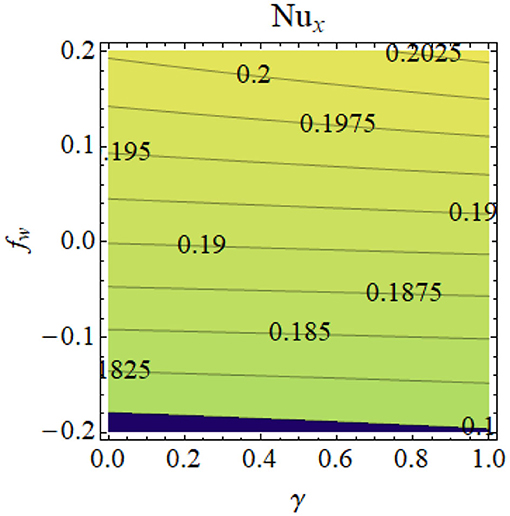
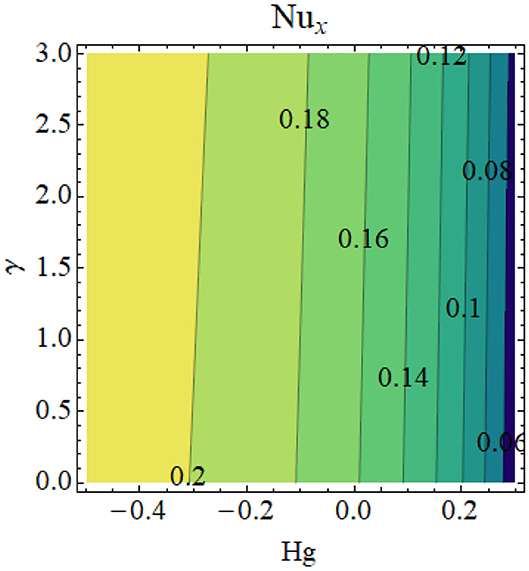
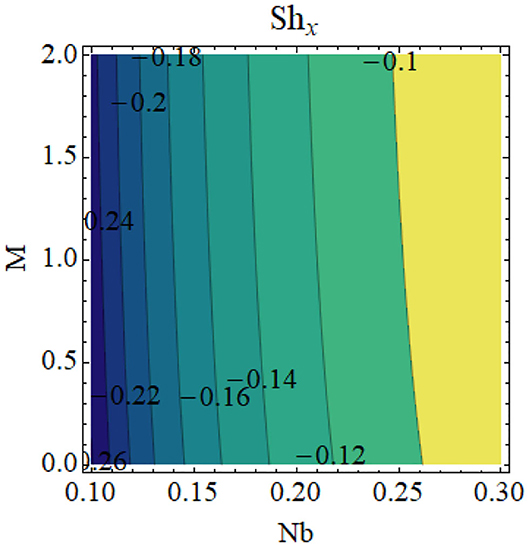
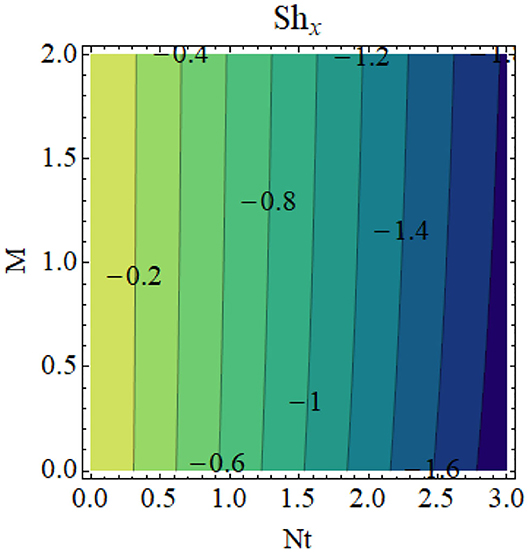
Figures 8–11 illustrate the effects of different physical parameters on the local Nusselt number and local Sherwood number. The influence of f_w andγ on Nu_x is shown in Figure 8: heat transfer decays for higher values of f_w and γ. The same phenomena can be observed for larger values Hg and γ on the Nusselt number profile, as presented in Figure 9. The combined effects of Nb and M as well as Nt and M are shown in Figures 10, 11, respectively. From these figures, we conclude that thermophoresis (Nt) and Brownian motion (Nb) parameters have produce the converse trend in the mass transfer rate.

FIGURE 8

Figure 8. Effects of γ and f_w on Nu_x.

FIGURE 9

Figure 9. Effects of Hg and γ on Nu_x.

FIGURE 10

Figure 10. Effects of Nb and M on Sh_x.

FIGURE 11

Figure 11. Effects of Nt and M on Sh_x.

Numerical Code Validation

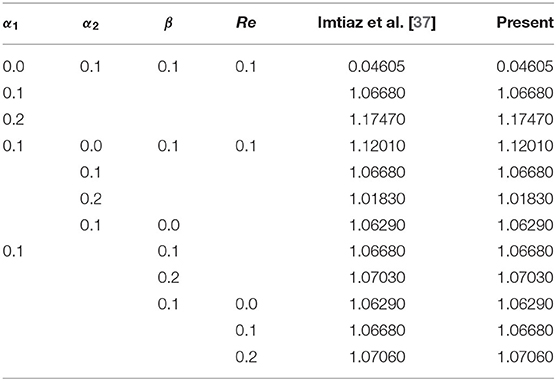
In this segment, we examine the code validation of early published works of literature. Table 2 validates the results of −f″(0) and −θ′(0) for the limiting case M = 0, K = 0, Nb = 0, Nt = 0, Rd = 0, S = 0, and Bi → ∞ with Imtiaz et al. [37]. Moreover, the skin friction rate is also validated by the same literature [37] when M = K = 0 (see Table 3). Table 4 exhibits the matching results of reduced Nusselt number with the references [20, 49–51]. From the above validation, results show that the current simulation is considered an efficient one.

TABLE 2

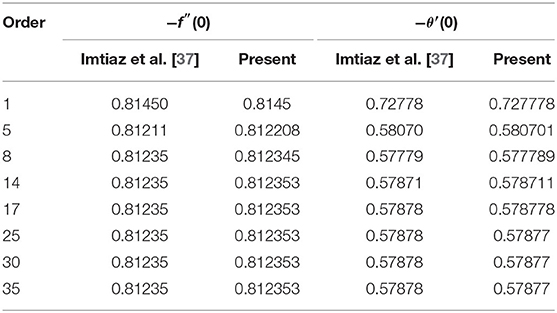
Table 2. Validation of −f″(0) and −θ′(0) for the limiting case M = 0, K = 0, Nb = 0, Nt = 0, Rd = 0, S = 0, and Bi → ∞.

TABLE 3

Table 3. Comparison of $R{e}^{0.5}{C}_f$ for different values when M = K = 0.

TABLE 4

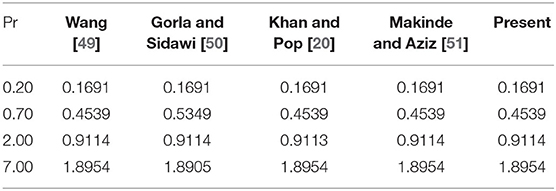
Table 4. Matching results of reduced Nusselt number with the restricting case Rd = Ec = M = Nt = Nb = γ = S = K = Γ = f_w = 0, and Bi → ∞.

Key Results

The present research work examines the entropy generation influence on third-grade nanoliquid flow caused by a stretching sheet in the appearance of Magnetic field, radiation, and convective heating effects. Christov-Cattaneo heat flux replaces ordinary heat flux. HAM is employed to validate the non-linear governing equations. Results of velocity, temperature, nanoparticle volume concentration, the system of entropy, the Bejan number, mass, and heat transfer rates are presented graphically. We obtained the following main upshots:

1. A falling tendency of the velocity profile is detectable while we keep increasing the values of the velocity slip and magnetic field parameter.

2. An augmentation in the range of radiation parameter and Biot number causes an increasing trend.

3. The concentration of the nanoparticle volume fraction is found to be a diminishing function of the thermophoretic parameter. On the other hand, a contrary impact is identified for the Brownian motion parameter.

4. The irreversibility of the system rises as we keep enhancing the values of the Biot number, thermal relaxation time, material parameter, and the Brinkmann number, but an inverse occurrence takes place as we increase the slip parameter and suction/injection parameter.

5. The Bejan number increases with greater values of the slip parameter, Biot number, thermophoresis parameter, magnetic parameter, and radiation parameter, whereas it reduces for larger values of the Brinkmann number and Brownian motion parameter.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research was supported by the Research Group Project (RGP), University of Tabuk, Tabuk 71491, Saudi Arabia, under Grant No. RGP-0207-14440.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Choi SUS, Eastman JA. Enhancing Thermal Conductivity of Fluids With Nanoparticles, Report No. ANL/MSD/CP 84938, Argonne National Laboratory, Lemont, IL, United States (1995). Available online at: https://ecotert.com/pdf/196525_From_unt-edu.pdf

PubMed Abstract | Google Scholar

2. Mushtaq A, Mustafa M, Hayat T, Alsaedi A. Numerical study for rotating flow of nanofluids caused by an exponentially stretching sheet. Adv Powder Technol. (2016) 27:2223–31. doi: 10.1016/j.apt.2016.08.007

CrossRef Full Text | Google Scholar

3. Reddy PS, Chamkha AJ. Soret and dufour effects on MHD convective flow of Al₂O₃-water and TiO₂-water nanofluids past a stretching sheet in porous media with heat generation/absorption. Adv Powder Technol. (2016) 27:1207–18. doi: 10.1016/j.apt.2016.04.005

CrossRef Full Text | Google Scholar

4. Shit GC, Haldar R, Mandal S. Entropy generation on MHD flow and convective heat transfer in a porous medium of exponentially stretching surface saturated by nanofluids. Adv Powder Technol. (2017) 28:1519–30. doi: 10.1016/j.apt.2017.03.023

CrossRef Full Text | Google Scholar

5. Gireesha BJ, Mahanthesh B, Thammanna GT, Sampathkumar P. Hall effects on dusty nanofluid two-phase transient flow past a stretching sheet using KVL model. J Mol Liq. (2018) 256:139–47. doi: 10.1016/j.molliq.2018.01.186

CrossRef Full Text | Google Scholar

6. RamReddy Ch, Murthy PVSN, Chamkha AJ, Rashad AM. Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int J Heat Mass Transfer. (2013) 64:384–92. doi: 10.1016/j.ijheatmasstransfer.2013.04.032

CrossRef Full Text | Google Scholar

7. Ghalambaz M, Behseresht A, Behseresht J, Chamkha AJ. Effects of nanoparticles diameter and concentration on natural convection of the Al₂O₃-water nanofluids considering variable thermal conductivity around a vertical cone in porous media. Adv Powder Technol. (2015) 26:224–35. doi: 10.1016/j.apt.2014.10.001

CrossRef Full Text | Google Scholar

8. Joshi PS, Mahapatra PS, Pattamatta A. Effect of particle shape and slip mechanism on buoyancy induced convective heat transport with nanofluids. Phys Fluids. (2017) 29:122001. doi: 10.1063/1.4996824

CrossRef Full Text | Google Scholar

9. Chamkha AJ, Abbasbandy S, Rashad AM, Vajravelu K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica. (2013) 48:275–85. doi: 10.1007/s11012-012-9599-1

CrossRef Full Text | Google Scholar

10. Reddy PS, Sreedevi P, Chamkha AJ. MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction. Powder Technol. (2017) 307:46–55. doi: 10.1016/j.powtec.2016.11.017

CrossRef Full Text | Google Scholar

11. Anitha S, Loganathan K, Pichumani M. Approaches for modelling of industrial energy systems: correlation of heat transfer characteristics between magnetohydrodynamics hybrid nanofluids and performance analysis of industrial length-scale heat exchanger. J Therm Anal Calorim. doi: 10.1007/s10973-020-10072-8

CrossRef Full Text | Google Scholar

12. Liu Z, Li D, Song Y, Pan X, Li D, Xuan X. Surface-conduction enhanced dielectrophoretic-like particle migration in electric-field driven fluid flow through a straight rectangular microchannel. Phys Fluids. (2017) 29:102001. doi: 10.1063/1.4996191

CrossRef Full Text | Google Scholar

13. Zargartalebi H, Ghalambaz M, Noghrehabadi A, Chamkha AJ. Natural convection of a nanofluid in an enclosure with an inclined local thermal non-equilibrium porous fin considering buongiorno's model. Numer Heat Transf A. (2016) 70:432–45. doi: 10.1080/10407782.2016.1173483

CrossRef Full Text | Google Scholar

14. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J. (1961) 7:26–28. doi: 10.1002/aic.690070108

CrossRef Full Text | Google Scholar

15. Magyari E, ChamkhaA J. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface: the full analytical solution. Int J Therm Sci. (2010) 49:1821–8. doi: 10.1016/j.ijthermalsci.2010.04.007

CrossRef Full Text | Google Scholar

16. Gupta PS, Gupta AS. Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng. (1977) 55:744–46. doi: 10.1002/cjce.5450550619

CrossRef Full Text | Google Scholar

17. Magyari E, Keller B. Heat mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D Appl Phys B. (1999) 32:577. doi: 10.1088/0022-3727/32/5/012

CrossRef Full Text | Google Scholar

18. Cortell R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl Math Comput. (2007) 184:864–73. doi: 10.1016/j.amc.2006.06.077

CrossRef Full Text | Google Scholar

19. Vajravelu K. Viscous flow over a nonlinearly stretching sheet. Appl Math Comput. (2001) 124:281–88. doi: 10.1016/S0096-3003(00)00062-X

CrossRef Full Text | Google Scholar

20. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transfer. (2010) 53:2477–83. doi: 10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

21. Rana P, Bhargava R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: a numerical study. Commun Nonlinear Sci Numer Simul. (2012) 17:212–26. doi: 10.1016/j.cnsns.2011.05.009

CrossRef Full Text | Google Scholar

22. Khedr MEM, Chamkha AJ, Bayomi M. MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Nonlinear Anal Model. (2009) 14:27–40. doi: 10.15388/NA.2009.14.1.14528

CrossRef Full Text | Google Scholar

23. Ghalambaz M, Izadpanahi E, Noghrehabadi A, Chamkha AJ. Study of the boundary layer heat transfer of nanofluids over a stretching sheet: passive control of nanoparticles at the surface. Can J Phys. (2014) 93:725–33. doi: 10.1139/cjp-2014-0370

CrossRef Full Text | Google Scholar

24. Al-Mudhaf A, Chamkha AJ. Similarity solutions for MHD thermosolutal marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat Mass Transfer. (2005) 42:112–21. doi: 10.1007/s00231-004-0611-8

CrossRef Full Text | Google Scholar

25. Chamkha AJ, Issa C, Khanafer K. Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation. Int J Therm Sci. (2002) 41:73–81. doi: 10.1016/S1290-0729(01)01305-9

CrossRef Full Text | Google Scholar

26. Khan WA, Aziz A. Double-diffusive natural convective boundary layer flow in a porous medium saturated with a nanofluid over a vertical plate: prescribed surface heat, solute and nanoparticle fluxes. Int J Therm Sci. (2011) 50:2154–60. doi: 10.1016/j.ijthermalsci.2011.05.022

CrossRef Full Text | Google Scholar

27. Oyelakin IS, Mondal S, Sibanda P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alexandria Eng J. (2016) 55:1025–35. doi: 10.1016/j.aej.2016.03.003

CrossRef Full Text | Google Scholar

28. Gorla RSR, Chamkha AJ. Natural convective boundary layer flow over a nonisothermal vertical plat embedded in a porous medium saturated with a nanofluid. Nanosc Microsc Therm. (2011) 15:81–94. doi: 10.1080/15567265.2010.549931

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Chamkha AJ, Mohamed RA, Ahmed SE. Unsteady MHD natural convection from a heated vertical porous plate in a micropolar fluid with joule heating, chemical reaction and radiation effects. Meccanica. (2011) 46:399–411. doi: 10.1007/s11012-010-9321-0

CrossRef Full Text | Google Scholar

30. Chamkha AJ. Hydromagnetic natural convection from an isothermal inclined surface adjacent to a thermally stratified porous medium. Int J Eng Sci. (1997) 35:975–86. doi: 10.1016/S0020-7225(96)00122-X

CrossRef Full Text | Google Scholar

31. Chamkha AJ. Solar radiation assisted natural convection in uniform porous medium supported by a vertical flat plate. ASME J Heat Transfer. (1997) 119:35–43. doi: 10.1115/1.2824104

CrossRef Full Text | Google Scholar

32. Chamkha AJ, Al-Mudhaf AF, Pop I. Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium. Int Commun Heat Mass. (2006) 33:1096–102. doi: 10.1016/j.icheatmasstransfer.2006.04.009

CrossRef Full Text | Google Scholar

33. Fourier J. Theorie analytique de la chaleur, par M. Fourier. Paris: Chez Firmin Didot, père et fils (1822).

34. Cattaneo C. Sulla conduzione del calore. In: Pignedoli A, editor. Some Aspects of Diffusion Theory. Berlin; Heidelberg: Springer (2011). doi: 10.1007/978-3-642-11051-1_5

CrossRef Full Text | Google Scholar

35. Christov CI. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech Res Commun. (2009) 36:481–86. doi: 10.1016/j.mechrescom.2008.11.003

CrossRef Full Text | Google Scholar

36. Loganathan K, Sivasankaran S, Bhuvaneshwari M, Rajan S. Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of oldroyd-B liquid using Cattaneo–Christov heat flux with convective heating. J Therm Anal Calorim. (2019) 136:401–9. doi: 10.1007/s10973-018-7912-5

CrossRef Full Text | Google Scholar

37. Imtiaz M, Alsaedi A, Shaq A, Hayat T. Impact of chemical reaction on third grade fluid flow with Cattaneo–Christov heat flux. J Mol Liq. (2017) 229:501–7. doi: 10.1016/j.molliq.2016.12.103

CrossRef Full Text | Google Scholar

38. Aiboud S, Saouli S. Entropy analysis for viscoelastic magnetohydrodynamic flow over a stretching surface. Int J Nonlinear Mech. (2010) 45:482–89. doi: 10.1016/j.ijnonlinmec.2010.01.007

CrossRef Full Text | Google Scholar

39. Makinde OD. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy. (2011) 13:1446–64. doi: 10.3390/e13081446

CrossRef Full Text | Google Scholar

40. Loganathan K, Mohana K, Mohanraj M, Sakthivel P, Rajan S. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: an approach to entropy optimization. J Therm Anal Calorim. (2020). doi: 10.1007/s10973-020-09751-3

CrossRef Full Text | Google Scholar

41. Loganathan K, Rajan S. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J Therm Anal Calorim. (2020) 141:2599–612. doi: 10.1007/s10973-020-09414-3

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Buongiorno J. Convective transport in nanofluids. J Heat Transfer. (2005) 128:240–50. doi: 10.1115/1.2150834

CrossRef Full Text | Google Scholar

43. Rivlin RS, Thomas AG. Large elastic deformations of isotropic materials. In: Barenblatt GI, Joseph DD, editors. Collected Papers of RS Rivlin. New York, NY: Springer (1997). doi: 10.1007/978-1-4612-2416-7_13

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Fosdick R, Rajagopal K. Thermodynamics and stability of fluids of third grade. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society (1980).

Google Scholar

45. Pakdemirli M. The boundary layer equations of third-grade fluids. Int J Nonlinear Mech. (1992) 27:785–93. doi: 10.1016/0020-7462(92)90034-5

CrossRef Full Text | Google Scholar

46. Halim NA, Rizwan Ul Haq, Noor NFM. Active and passive controls of nanoparticles in Maxwell stagnation point flow over a slipped stretched surface. Meccanica. (2017) 52:1527–39. doi: 10.1007/s11012-016-0517-9

CrossRef Full Text | Google Scholar

47. Liao SJ. The proposed homotopy analysis technique for the solution of nonlinear problems (Ph.D. thesis), Shanghai Jiao Tong University, Shanghai, China (1992).

48. Liao SJ. An explicit, totally analytic approximation of Blasius viscous flow problems. Int J Nonlinear Mech. (1999) 34:759–78. doi: 10.1016/S0020-7462(98)00056-0

CrossRef Full Text | Google Scholar

49. Wang CY. Free convection on a vertical stretching surface. ZAMM Z Angew Math Mech. (1989) 69:418–20. doi: 10.1002/zamm.19890691115

CrossRef Full Text | Google Scholar

50. Gorla RR, Sidawi I. Free convection on a vertical stretching surface with suction and blowing. Appl Sci Res. (1994) 52:247–57. doi: 10.1007/BF00853952

CrossRef Full Text | Google Scholar

51. Makinde OD, Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Therm Sci. (2011) 50:1326–32. doi: 10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

LIST OF SYMBOLS