- 1Amherst Center for Fundamental Interactions, Department of Physics, University of Massachusetts, Amherst, MA, United States
- 2RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York, NY, United States
- 3Institut für Theoretische Physik II, Fakultät für Physik und Astronomie, Ruhr-Universität Bochum, Bochum, Germany
- 4Department of Mathematics and Physics, University of Salento, Lecce, Italy
- 5Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Lecce, Lecce, Italy
- 6Gran Sasso Science Institute, L'Aquila, Italy
- 7Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, United States
- 8Istituto Nazionale di Fisica Nucleare, Sezione di Pisa, Pisa, Italy
Parity-violating and time-reversal conserving (PVTC) and parity-violating and time-reversal-violating (PVTV) forces in nuclei form only a tiny component of the total interaction between nucleons. The study of these tiny forces can nevertheless be of extreme interest because they allow one to obtain information on fundamental symmetries using nuclear systems. The PVTC interaction derives from the weak interaction between the quarks inside nucleons and nuclei, therefore the study of PVTC effects opens a window on the quark-quark weak interaction. The PVTV interaction is sensitive to more exotic interactions at the fundamental level, in particular to strong CP violation in the Standard Model Lagrangian, or even to exotic phenomena predicted in various beyond-the-Standard-Model scenarios. The presence of these interactions can be revealed either by studying various asymmetries in polarized scattering of nuclear systems, or by measuring the presence of non-vanishing permanent electric dipole moments of nucleons, nuclei and diamagnetic atoms and molecules. In this contribution, we review the derivation of the nuclear PVTC and PVTV interactions within various frameworks. We focus in particular on the application of chiral effective field theory, which allows for a more strict connection with the fundamental interactions at the quark level. We investigate PVTC and PVTV effects induced by these potentials on several few-nucleon observables, such as the longitudinal asymmetries in proton-proton scattering and the 3He()3H reaction, the radiative neutron-proton capture, and the electric dipole moments of the deuteron and the trinucleon system.
1. Introduction
The interaction between nucleons is at the heart of nuclear physics and has been a subject of great scientific interest for many decades. The strong nuclear forces have their origin in the residual interaction between quarks and gluons inside colorless nucleons and are described by quantum chromodynamics (QCD). The resulting parity-conserving, time-reversal-conserving (PCTC) nuclear interactions are known to exhibit a complicated pattern, involving a delicate interplay of strongly state-dependent repulsive and attractive pieces. While the nucleon-nucleon (NN) scattering data below the pion production threshold can nowadays be accurately described by modern NN potentials, the (weaker) three-nucleon (3N) forces and the electromagnetic interactions (EM) between the nucleons, known to play an important role in the nuclear structure and dynamics, are not so well-understood and represent a subject of active research. The current status of PCTC nuclear forces is reviewed in other contributions to this topical issue.
In addition to the bulk PCTC interactions mentioned above, nuclear forces also feature much tinier components, which originate from the weak forces between quarks and/or physics beyond the standard model (BSM) and whose strength is smaller than that of the strong and EM interactions by many orders of magnitude. These tiny components are, nevertheless, extremely interesting since investigation of their effects may shed new light on fundamental symmetries and BSM physics. While effects of such exotic PCTC components are, of course, completely overwhelmed by the strong and EM nuclear forces, parity- (P) violating and/or time-reversal- (T) violating nuclear interactions can be determined by measuring specific observables which would vanish if these symmetries were conserved. In this contribution, we review the theory of parity-violating, time-reversal-conserving (PVTC) and parity-violating, time-reversal-violating (PVTV) nuclear forces and discuss selected applications.
Starting from 1950s, a wide variety of phenomenological models have been developed to describe nuclear forces, the most prominent utilizing the one-boson exchange picture, see Machleidt [1] and references therein. More recently, the development of chiral effective field theory (χEFT) [2] has given a new impetus to the derivation of nuclear interactions [3–5]. The χEFT approach utilizes the spontaneously broken approximate SU(2)L×SU(2)R chiral symmetry of QCD1 in order to describe the low-energy dynamics of pions, the (pseudo-) Goldstone bosons of the spontaneously broken axial generators, in a systematic and model-independent fashion within the framework of the effective chiral Lagrangian [6–11], see [12–14] for review articles. Owing to the derivative nature of the Goldstone boson interactions, the scattering amplitude in the pion- and single-baryon sectors can be calculated via a perturbative expansion in powers of Q/Λχ, where Q refers to momenta of the order of the pion mass mπ and Λχ ~ mρ ~ 1 GeV denotes the chiral symmetry breaking scale, with mρ the ρ-meson mass. The effective Lagrangian involves (an infinite number of) all possible hadronic interactions compatible with the symmetries of QCD, which are naturally organized according to the number of derivatives and/or quark or pion mass insertions2. Every term in the effective Lagrangian is multiplied by a coefficient, whose strength is not fixed by the symmetry. These so-called low-energy constants (LECs) can be determined by fits to experimental data and/or obtained from lattice QCD simulations, see [13, 14] and references therein. At every order in the Q/Λχ-expansion, only a finite number of terms from the effective Lagrangian contributes to the scattering amplitude. The resulting framework, commonly referred to as chiral perturbation theory (χPT), is nowadays widely applied to analyze low-energy processes in the Goldstone boson and single-nucleon sectors. It has also been generalized to study few- and many-nucleon systems, where certain resummations beyond perturbation theory are necessary in order to dynamically generate the ultrasoft scale associated with nuclear binding. According to Weinberg [2], the breakdown of the perturbative expansion for the NN scattering amplitude is traced back to enhanced contributions of ladder diagrams, i.e., Feynman diagrams that become infrared divergent in the static limit of infinitely heavy nucleons. The simplest and natural way to resum enhanced ladder diagrams is provided by solving the nuclear Schrödinger equation. The framework therefore essentially reduces to the conventional quantum mechanical A-body problem. The corresponding nuclear forces and current operators are defined in terms of non-iterative parts of the scattering amplitude, which are free from the above mentioned enhancement. They can be derived from the effective chiral Lagrangian in a systematically improvable way via a perturbative expansion in powers of Q/Λχ [4, 5]. Assuming the scaling of few-nucleon contact operators according to naive dimensional analysis3, the PCTC interactions are dominated by the pairwise NN force, which receives its dominant contribution at order with ν = 0, defined to be the leading order (LO). Parity conservation forbids the appearance of nuclear forces at order ν = 1, so that the next-to-leading order (NLO) contribution to the PCTC NN potential appears at order ν = 2. Next-to-next-to-leading order (N2LO) has ν = 3 and so on. PCTC three- and four-nucleon forces are suppressed and start contributing at orders ν = 3 (N2LO) and ν = 4 (N3LO), respectively. Presently, the chiral expansion of the PCTC NN force has been pushed to order ν = 5 (N4LO) [16–19], while many-nucleon interactions have been worked out up through N3LO, see [4, 5] and references therein. We further emphasize that a number of alternative formulations of χEFT for nuclear systems have been proposed [20–25], see also [26–31] for a related discussion.
Another framework to analyze nuclear systems at very low energies is based on the so-called pionless formulation of EFT, see [31–33] for review articles. It is valid at momenta well below the pion mass, at which the pionic degrees of freedom can be integrated out. In the resulting picture, nucleons interact with each other solely through short-range contact two- and many-body forces. This formulation is considerably simpler than χEFT both at the conceptual and practical levels, and has been successfully applied to study e.g., Efimov physics and universality in few-body systems near the unitary limit, low-energy properties of halo-nuclei and reactions of astrophysical relevance, see [31–33] and references therein.
In this paper we focus on the PVTC and PVTV interactions in the frameworks of χEFT and pionless EFT. We also outline various meson-exchange models frequently adopted to analyze the results for some PVTC and PVTV observables. In the subsections below, we briefly discuss the origin of the PVTC and PVTV interactions and summarize the current experimental and theoretical status of research along these lines.
1.1. The PVTC Interaction
The PVTC component of the nuclear force is governed by the weak interaction between the quarks inside the nucleons (and pions). Studying such effects, therefore, opens a window on the so-called “pure” hadronic weak interaction (HWI) [34–38]. This part of the weak interaction is far less known experimentally.
A number of experiments aimed at studying PVTC in low-energy processes involving few-nucleon systems have been completed/are being planned at cold-neutron facilities, such as the Los Alamos Neutron Science Center (LANSCE), the National Institute of Standards and Technology (NIST) Center for Neutron Research, the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory, and the European Spallation Source (ESS) in Lund. The primary objective of this experimental program is to determine the LECs which appear in the PVTC nuclear potentials. For a recent review of the current status of experiments along this line and the impact of anticipated results, see ([39]).
PVTC nuclear forces have already been analyzed in the framework of χEFT [40–42]. The LO PVTC NN force is driven by the one-pion-exchange term with ν = −1, while the NLO terms with ν = 1 emerge from two-pion-exchange diagrams and NN contact interactions4. In Girlanda [44], it was shown that the PVTC NN potential involves only five independent contact operators at this order corresponding to five S-P transition amplitudes at low energies [45]. Including the PVTC pion-nucleon coupling constant , the NN potential at NLO thus contains six LECs which need to be determined from experimental data. At N2LO one has to take into account five additional LECs, which determine the strength of the subleading PVTC pion-nucleon interactions [46].
In pionless EFT, the LO PVTC NN potential is completely described in terms of the already mentioned five contact terms [36, 47]. The large-Nc scaling of PVTC NN contact interactions was analyzed in Phillips et al. [48] and Schindler et al. [47]. These studies suggest that three out of five PVTC contact interactions are suppressed by a factor of or by the factor , see also a related discussion in Vanasse [49]. If the large-Nc scaling persists to the physically relevant case of Nc = 3, the pionless potential at LO should be dominated by only 2 LECs [39]. Unfortunately, the currently available experimental data do not allow one to draw definitive conclusions on whether the suggested large-Nc hierarchy of PVTC contact interactions is indeed realized in Nature.
Regarding the various meson-exchange models developed to describe the PVTC interaction, we will mainly discuss the model proposed by Desplanques, Donoghue, and Holstein (DDH) [50] which includes pion and vector-meson exchanges with seven unknown meson-nucleon PVTC coupling constants.
1.2. The PVTV Interaction
PVTV nuclear forces originate from more exotic sources at the fundamental level, which include the so-called θ-term in the Standard Model (SM) Lagrangian [51], or even BSM interactions [52]. Due to the CPT theorem, any PVTV interaction also violates the CP symmetry, where C refers to charge conjugation. CP violation is a key ingredient for the dynamical generation of a matter-antimatter asymmetry in the Universe [53]. The SM with three generations of quarks has a natural source of CP-violation in the phase of the Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix. This mechanism is however not sufficient to explain the observed asymmetry [54].
The phase of the CKM matrix also does not contribute sizably to the nuclear PVTV interaction. For example, let us consider the electric dipole moment (EDM) of a system of particles. A non-zero permanent EDM of a particle or a system of particles necessarily involves the breaking of both parity and time-reflection symmetries. EDMs of the electron, nucleons and nuclei are mostly sensitive to P- and T-violating flavor-diagonal interactions. To induce a non-zero EDM, on the other hand, the phase of the CKM requires contributions from all three generations of quarks, including heavy quarks, leading to a large suppression [52, 55–57]. For example, the expected size of the nucleon EDM based on the CKM mechanism in the SM is fm [58, 59]. Therefore, any observed permanent EDM of an atomic or nuclear system larger in magnitude than the expected size within the SM would highlight PVTV effects beyond the CKM mixing matrix. The present experimental upper bounds on the EDMs of neutron and proton are fm [60, 61] and fm, where the proton EDM has been inferred from a measurement of the diamagnetic 199Hg atom [62] using a calculation of the nuclear Schiff moment [63]. For the electron, the most recent upper bound is fm [64], derived from the EDM of the ThO molecule. In all cases, the current experimental sensitivities are orders of magnitude away from the CKM predictions.
χEFT allows one to derive PVTV nuclear forces in a systematic and model independent way. To this aim, the PCTC effective chiral Lagrangian has to be extended to include all possible PVTV terms classified according to their chiral dimension. Some of these terms are induced, at the microscopic level, by the SM mechanisms discussed above. The effective chiral Lagrangian induced by the θ-term is discussed in Mereghetti et al. [65] and Bsaisou et al. [66]. BSM theories such as supersymmetry, multi-Higgs scenarios, left-right symmetric models, etc. would give rise to additional PVTV sources of dimension six (and higher) in the quark-gluon Lagrangian [67]. The χEFT Lagrangians originating from these sources were derived in de Vries et al. [68] and Bsaisou et al. [69]. Various terms in the resulting effective chiral Lagrangian possess different scaling with respect to the underlying microscopic PVTV sources. χEFT can thus be used to establish relations between the fundamental PVTV mechanisms and specific terms in the nuclear potentials and, accordingly, specific patterns in the corresponding nuclear observables [65, 68, 69]. In principle, this offers the possibility of identifying the fundamental sources of time-reversal violation and to shed light on some of the BSM scenarios, provided the corresponding LECs in the effective Lagrangian can be determined from Lattice QCD calculations or experimental data [70, 71].
In the framework of χEFT, the PVTV NN potential was derived up to N2LO including one- and two-pion exchange contributions and the corresponding contact interactions [72, 73]. Subsequent works showed the presence in the PVTV Lagrangian of a three-pion term [68], which was for the first time included in the calculations in Bsaisou et al. [66]. This term also generates a PVTV 3N force at NLO, which contributes to the 3H and 3He EDM. The calculation reported in Bsaisou et al. [66] was also the first one carried out using solely the interactions derived in χEFT. More precisely, the PVTV potential at NLO was used in combination with the N2LO PCTC potentials from Epelbaum et al. [74]. Finally, in Gnech and Viviani [75], the EDMs of deuteron and trinucleons were studied using the χEFT PVTV potential up to N2LO along with the N4LO PCTC potential of Entem et al. [18]. In this paper, it was also shown that the N2LO contribution to the PVTV 3N force generated by the three-pion interaction vanishes. The LO χEFT PVTV potential has also been applied in combination with many-body methods to calculate Schiff moments of heavy nuclei [76].
Currently, no direct limits on EDMs of light nuclei have been established. However, experiments are planned to measure the EDM of protons and light nuclei in dedicated storage rings [77–82]. This new approach could reach a precision of ~10−16 e fm, although this goal has to be established in practice. If successful, these experiments would lead to a great improvement in the hadronic sector of EDM searches. A measurement of a non-vanishing EDM of this magnitude would provide evidence of a PVTV source beyond the CKM mechanism. However, a single measurement would be insufficient to identify the specific source of PVTV. For this reason, experiments with various light nuclei such as 2H, 3H and 3He are planned. Such measurements would provide the complementary information needed to impose constraints on PVTV sources at the fundamental level.
A brief discussion of the PVTV potentials derived in the framework of the one-meson exchange model and in the pionless EFT approach will also be reported in this review.
1.3. Outline of the Article
Our paper is organized as follow. In section 2, we discuss the origins of PVTC and PVTV interactions at the fundamental level and list the relevant terms in the quark-gluon Lagrangian. In section 3, we give the corresponding terms in the effective chiral Lagrangian and discuss the derivation of the PVTC and PVTV potentials in χEFT. In section 4, we specifically focus on the contact few-nucleon interactions which enter the potentials in both the chiral and pionless EFT formulations. We also discuss the expected hierarchy of the corresponding LECs as suggested by the large-Nc analysis. Next, in section 5, the various meson-exchange models developed to describe the PVTC and PVTV interactions will be summarized. Then, in section 6, we report on a selected set of results for PVTC and PVTV observables in light nuclei up to A = 4. Finally, the main conclusions of this paper and future perspectives are summarized in section 7.
2. Parity Violation and Time-Reversal Violation at the Microscopic Level
Parity is violated in the SM of particle physics because of the different gauge interactions of left- and right-handed fermion fields. Only left-handed particles interact via SU(2)L gauge interactions such that this part of the SM violates parity maximally. The remaining color and electromagnetic interactions conserve parity modulo the QCD vacuum angle which is discussed below. Parity violation was first observed in semileptonic charged current interactions in 1957 [83]. Twenty years later, in the late ‘70s, PVTC was observed in neutral current electron-nucleus scattering [84], providing a strong confirmation of the SM. Subsequent PVTC electron scattering experiments have quantitatively confirmed the SM picture [85]. In addition to PVTC in β decays and semileptonic neutral current processes, the SM predicts PVTC in weak interactions between quarks. At energies smaller than the masses of the W and Z bosons, such interactions can be represented by four-fermion operators. Just below the electroweak (EW) scale, and limiting ourselves to the lightest u and d quarks, the four-fermion Lagrangian is
where GF is the Fermi coupling constant and , with θW the Weinberg mixing angle. qL and qR denote the left-handed and right-handed doublets and , and the dots denote terms that conserve parity5. Equation (1) was obtained assuming the CKM matrix to be the identity, that is Vud = 1. The three operators in Equation (1) all break parity, but have different transformation properties under chiral symmetry and isospin. We note that the isovector and isotensor terms (the second and third operators) given in Equation (1) are suppressed by a factor with respect to the isoscalar one.
The operators in Equation (1) need to be evolved using the renormalization group equations (RGE) from the EW scale down to the QCD scale, and in this process they mix with additional PVTC operators [86]. After the RGE evolution, the PVTC Lagrangian assumes the form
where in the SM, the coefficients are known functions of SM parameters as sw, the strong coupling constant gs, etc. Greek indices α and β appearing as superscripts in some of the quark fields in Equation (2) specify color indices. They are only shown for cases where the color contractions are not obvious. Notice that the QCD evolution does not remedy the suppression of the isospin-one and -two operators [86]. BSM physics that arises at scales well above the EW can be represented at the EW scale via gauge-invariant higher-dimensional operators [67, 87]. This framework is usually called the SM Effective Field Theory (SM-EFT). SM-EFT operators can induce new PVTC couplings of the W and Z bosons to left- and right-handed quarks, and new PVTC four-fermion operators. After evolving the effective operators from the EW to the QCD scale, the net effect of BSM PVTC SM-EFT operators is to modify the coefficients in Equation (2) with respect to their SM values, namely in Equation (2) one substitutes . We have focused so far on operators involving only the u and d quarks. Flavor-conserving (ΔF = 0) operators involving the s quark can also generate interesting contributions to hadronic P violation [86, 88], such as contributions to isospin-one operators that are not suppressed by .
While P and C are maximally broken by the V − A structure of the SM, the breaking of CP is much more delicate. In the SM with three generations of quarks, CP is broken by the phase of the CKM matrix, which explains all the observed CP violation in the kaon [89–91], and B meson systems [92, 93]. Theoretical uncertainties are at the moment too large to definitively conclude whether the recently discovered CP violation in D decays [94] is compatible with the SM. The phase of CKM gives, on the other hand, unobservable contributions to flavor-diagonal CP violation, in particular to the neutron [55, 59, 95] and electron EDMs [96–98].
The second source of CP violation in the SM is the QCD θ term [51, 99, 100]
where gs is the strong coupling constant and the gluon field tensors (a is a color index). The θ term is a total derivative, but it contributes to physical processes through extended, spacetime-dependent field configurations known as instantons. CP violation from the QCD θ term is intimately related to the quark masses. All phases of the quark mass matrix can be eliminated through non-anomalous SU(2) vector and axial rotations, except for a common phase ρ. The mass plus QCD θ terms which are left are
where . The parameters ρ and θ are not independent. In χEFT, it is convenient to rotate into a complex mass term with an anomalous U(1)A rotation, obtaining, after vacuum alignment [101],
where
nf = 2 is the number of light flavors, and the combinations of light quarks masses and ϵ are , ϵ = (md − mu)/(md+mu). Equations (5) and (6) can be easily generalized to include strangeness. is a free parameter in the QCD Lagrangian, and one would expect . This would however lead to a large neutron EDM e fm [102, 103], ten orders of magnitude larger than the current limits, e fm [61]. Therefore , which represents the so-called strong CP problem.
The phase of the CKM matrix and the QCD term are the only CP-violating parameters in the SM Lagrangian. They are however not sufficient to explain the observed matter-antimatter asymmetry of the Universe [104–107], and it is therefore natural to think about CP-violating sources induced by BSM physics. The low-energy CP-violating operators relevant for EDMs have been cataloged in several works (e.g., [52, 108–110]). de Vries et al. [68] considered all the low-energy operators that are induced by SM-EFT operators at tree level, retaining the two lightest quarks. Generalization to three flavors are given, for example, in Jenkins et al. [111] and Mereghetti [112]. The most relevant SU(3)c × U(1)em-invariant purely hadronic operators induced by dimension-six SM-EFT operators are
where fabc are the structure constants of the Lie algebra of the color SU(3) group, [dE] and [dCE] are matrices in flavor space, and . The coefficients , , and are dimensionless and scale as , where v = 246 GeV is the Higgs vacuum expectation value, and ΛX is the scale of new physics. The Weinberg three-gluon, the quark EDM (qEDM), and the chromo-EDM (qCEDM) operators (the first, second, and third term given in Equation (7), respectively) have received the most attention in the literature [52, 113]. They can be written directly in terms of SU(3)c × SU(2)L × U(1)Y-invariant operators at the EW scale, and receive corrections by a variety of CP-violating operators in the SM-EFT, involving heavy SM fields. The four-quark operators, given in the third and fourth lines of (7), can also be expressed in terms of gauge-invariant operators at the EW scale, and they arise, for example, in leptoquark models, see [114, 115]. The four-quark operators, given in the last line of Equation (7), are on the other hand induced by right-handed couplings of quarks to the W boson [68, 116], and are generated, for example, in left-right symmetric models.
While all operators in Equations (5) and (7) violate P and CP symmetry, they transform differently under isospin and chiral rotations. As such, the operators induce different χEFT Lagrangians at lower energies, and different hierarchies of CP-violating hadronic and nuclear observables such as EDMs or scattering observables.
3. PVTC and PVTV Chiral Potentials
In this section, we discuss the derivation of the PVTC and PVTV NN and 3N potentials within the framework of χEFT. In the first and second subsections we briefly review the properties of the PVTC and PVTV chiral Lagrangians. In section 3.3, we present briefly two methods used to derive the potentials starting from a Lagrangian. Finally, in the last two subsections, we present the PVTC and PVTV chiral potentials, respectively.
In order to discuss hadronic observables such as nuclear EDMs or PVTC asymmetries in pp scattering, the quark-level PVTC and PVTV Lagrangians of Equations (2) and (7) need to be matched onto nuclear EFTs, such as chiral EFT and pionless EFT. Due to the non-perturbative nature of QCD at low energy, this matching cannot be done in perturbation theory. Nevertheless, the approximate chiral and isospin symmetries of the QCD Lagrangian provide an organizing principle for low-energy interactions, see [12–14] for review articles.
Let us first introduce the nucleon and pion fields. The (relativistic) nucleon field N(x) is considered to be an isospin doublet
where p(x) (n(x)) is the proton (neutron) field. The pion fields are given in “Cartesian” coordinates πa, a = 1, 2, 3, where
π(+)(x), π(−)(x), and π(0)(x) being the fields associated to the three charge states of the pion. The pion fields in Cartesian coordinates are collectively denoted by . We use the 2 × 2 matrices τa, a = 0, …, 3, where τ0 is the identity matrix, while τa, a = 1, …, 3 are the Pauli matrices acting on the isospin degrees of freedom (often indicated cumulatively as ). For example, . Sometimes the a = 3 component will be denoted as the “z” component, i.e., π3 ≡ πz, etc., in our notation. Finally, we denote the nucleon (pion) mass by M (mπ).
In some cases, we will perform a non-relativistic reduction of the nucleon field N(x) and use Ns(x)
where ps(x) (ns(x)) is the two component Pauli spinor representing the static proton (neutron) field. Effects of the anti-nucleon degrees of freedom are taken into account in the form of 1/M relativistic corrections to the vertices. The coefficient of the annihilation operator reduces to χmexp(ip·x), where χm is a spinor describing a spin state with z-projection .
The main “building block” to construct the chiral Lagrangian is the SU(2) pionic matrix field U(x), often written as (but its definition is not unique) [12]
where fπ ≈ 92.4 MeV is the pion decay constant. Another low energy constant frequently entering the chiral Lagrangian is the axial coupling constant gA ≈ 1.29. Following the standard convention, we give here the effective value that takes into account the Goldberger-Treiman discrepancy and is extracted from the empirical value of the pion-nucleon coupling constant. The effective chiral Lagrangian is constructed in terms of N(x) and U(x) and therefore contains vertices with arbitrary number of pion fields. In the following, we will retain explicitly only relevant terms with the minimum number of pion fields, obtained by expanding U(x) in powers of the pion field. Additional terms with a larger number of pion fields will only contribute to the PVTC and PVTV potential at higher orders in the chiral expansion. For an introduction to the chiral Lagrangians and their building blocks, the reader is referred to Bernard et al. [12], Bernard [13], and Bijnens and Ecker [14] and references therein.
Each term of the chiral Lagrangian will be classified by the so-called “chiral order”. Each four-gradient of the pion matrix field or a multiplication by a pion mass increases the order of the term by one. Four-gradients acting on nucleon fields are more difficult to classify, since the time derivative brings down a factor proportional to the nucleon mass. An easier counting is obtained using the non-relativistic heavy baryon perturbation theory [12, 117], which was used in the derivation of the PVTC potential in de Vries et al. [46] and of the PVTV potential in Maekawa et al. [72]. In the following, we will use both the relativistic and non-relativistic nucleon fields.
For the sake of completeness, we report first of all the terms of the PCTC Lagrangian that contribute to the PVTC and PVTV potentials up to the order we are interested in. In SU(2) χPT, the PCTC Lagrangian can be conveniently organized in sectors with different numbers of pions and nucleons (below we give the explict expression for the relevant terms in the πN Lagrangian only).
where “⋯ ” in the previous expression denotes terms of higher order and/or more pions fields of no interest here. Above and . The parameters ci = 1−4 are LECs appearing in the Lagrangian of order Q2. They have dimension of mass−1. For a complete discussion of the terms appearing in the Lagrangians , , and , etc., see [12, 118].
3.1. The PVTC Chiral Lagrangian
The effective chiral Lagrangian that involves contributions from the weak sector of the SM was first discussed in the seminal paper by Kaplan and Savage [88] and subsequently revisited in Kaplan et al. [119], Zhu et al. [40], de Vries et al. [46], and Viviani et al. [42]. Also the PVTC Lagrangian can be conveniently organized in sectors with different numbers of pions and nucleons, explictly
where the superscript (n) denotes the chiral order of each piece. The pion-nucleon interaction terms are collected in and those entering the PVTC potential up to Q1 are the following [46, 88]
where
The parameters and are unknown LECs. The superscript ΔI labels the rank of the corresponding isospin tensor. The LECs can be estimated by naive dimensional analysis (NDA) [40, 42, 46, 88]
where Λχ = 4πfπ ~ 1.2 GeV is the typical scale of the strong interaction. Equation (21) shows the order-of-magnitude estimates of the PVTC interactions. These estimates do not take into account factors of and Nc that could modify the expected scaling of the LECs.
The contact terms entering the Lagrangian are products of a pair of bilinears of nucleon fields that are odd under P and even under CP. The most general bilinear product reads
where ΓA and ΓB are elements of the Clifford algebra with the possible addition of 4-gradients and Fab are unknown parameters. To violate P but conserve CP, at least one 4-gradient is required. We must build isoscalar, isovector and isotensor terms as discussed in section 2. The operators moreover have to conserve the electric charge and thus commute with the third component of the isospin operator. The terms with only one gradient operator are collected in (i.e., of chiral order 1). Only five independent terms can be written [44], corresponding to the five possible S ↔ P transitions in NN scattering [45]. It is more convenient to give the Lagrangian using the non-relativistic reduction of the nucleon fields Ns:
The factor has been chosen to ensure that the Ci are dimensionless and for convenience in the power counting. The construction of Equation (23) and the elimination of redundancies will be discussed in more details in section 4. The operators multiplying the LECs C1,2 are isoscalar, those multiplying C3,4 change isospin by one unit, while that multiplying C5 is an isotensor. The scaling of the LECs from naive dimensional analysis [120] is given by
which once again does not take into account the suppression by affecting, for example, the isovector operators. The operators in Equation (23) contribute to the PVTC potential at NLO (suppressed by with respect to LO), and we will give the potential derived from them in Equation (60). The terms appearing in contain two additional gradients and contribute to the PVTC potential at higher order. They have not been considered so far.
Finally, there are some terms with 3π vertices appearing in as discussed in Viviani et al. [42]. These terms would contribute to the Q2 PVTC potential, but their contributions at the end vanishes as discussed in section 3.4.
3.1.1. Connection to the Underlying PVTC Sources
Attempts to estimate the values of the coupling constants were performed mainly in the framework of the meson exchange models (which will be discussed in section 5). However, since in both χEFT and meson exchange frameworks the lowest order pion-nucleon Lagrangian term is the same as given in Equation (18), we can report here the values for estimated from the underlying fundamental theory also before the advent of χEFT [121–127]. One of the most comprehensive calculation including all previous results was performed in 1980 by Desplanques, Donoghue, and Holstein (DDH) [50] using the valence quark model. Additional calculations have been performed subsequently [128–130], using similar or other methods and finding qualitatively similar results. These estimates, however, are based on a series of rather uncertain assumptions (see, for example, [131]). For example, DDH presented not a single value for but rather a range inside of which it was extremely likely that this parameter would be found [50]. In addition they presented also a single number called the “best value” but this is described simply as an educated guess in view of all the uncertainties. The values of were [50]
Some years ago, a lattice QCD calculation of was also made [132], resulting in the estimate
where the theoretical uncertainty is related to the statistical Monte Carlo error. While the systematic errors are expected to be within the quoted statistical uncertainty [132], we stress that the calculation was performed at a heavy pion mass and not extrapolated to the physical point, disconnected diagrams were not included, and operator renormalization was neglected.
Regarding the other LECs entering the contact Lagrangian given in Equation (23), no direct estimates have been reported in literature. These LECs were estimated by comparing the expression of contact potential with the potential developed using the exchanges of heavy mesons, as for example, in the DDH potential [42, 46] (this issue will be considered in more detail in section 5). However, since also the DDH estimates are rather uncertain, we will not discuss this issue further.
3.2. The PVTV Lagrangian
The PVTV chiral Lagrangian taking into account the QCD term was first considered in the seminal paper by Crewther, di Vecchia, Veneziano and Witten [102], and consequently revisited in Cheng [133], Pich and de Rafael [134], Cho [135], Borasoy [136], and Ottnad et al. [137]. Subleading terms in the chiral expansion were systematically constructed in Mereghetti et al. [65] and Bsaisou et al. [69]. The chiral Lagrangian induced by the dimension-six operators in Equation (7) were derived in de Vries et al. [68] and Bsaisou et al. [69].
As before, in SU(2) χPT, the PVTV Lagrangian can be organized in sectors with different numbers of pions and nucleons
As in the previous subsection, we report here only the most important interactions for each sector, focusing on the terms with the minimum number of pion fields entering in the final expression of the potential. Terms with additional pions are not universal for the different PVTV sources at the quark level, but instead depend on their chiral-symmetry breaking pattern. These differences only enter at higher order in the potentials than we consider here.
In the PVTV case, the simultaneous violation of P, T, and isospin symmetry allows for a pion tadpole linear in the pion field ~π3 with a corresponding LEC proportional to the symmetry-violating source terms at the quark level. Such tadpoles can always be removed by appropriate field redefinitions of the pion and nucleon fields [65, 68, 69]. At LO in the chiral expansion, the tadpole removal is the same as the vacuum alignment procedure at the quark level [101]. While tadpoles can be removed, the corresponding field redefinitions affect other couplings in the chiral Lagrangian. In particular, for chiral-symmetry-breaking CP sources that do not transform as a quark mass term, a PVTV three-pion vertex of chiral order Q0 is left behind [68, 69].
where is a LEC. Other three-pion vertices will appear at N2LO, but they will contribute to high orders of the PVTV potential.
Arguably the most important interactions appear in the pion-nucleon sector. Simultaneous violation of P, T, and chiral symmetry allows for non-derivative single-pion-nucleon interactions, something which is not possible in the PCTC Lagrangian. In principle, three different interactions can be written
corresponding, respectively, to an isospin singlet, vector, and tensor interaction. As discussed below, the relative size of the LECs ḡ0, 1, 2 strongly depends on the quark-level PVTV source under consideration. In the case of CP-violation from chiral invariant operators, such as the three gluon term, ḡi are suppressed by powers of the pion masses, and the pion-nucleon Lagrangian contains chiral-invariant, derivative couplings as important as those in Equation (32) [68]. These can however always be absorbed into a shift of ḡ0 and of the ΔI = 0 NN operators discussed below.
The NLO Lagrangian contains several two-pion two-nucleon PVTV interactions [65, 68, 69, 75], but, for all CP-violating sources, they contribute to the two- and three-body PVTV potentials at N3LO and N2LO, respectively. We therefore ignore these couplings. Isospin-breaking sources also generate a single-pion-nucleon NLO coupling. The coupling involves a time derivative of the pion field, thus inducing a relativistic correction in the PVTV potential. At N2LO the number of interactions proliferates significantly and there are also new pure pionic interactions. These contributions can either be absorbed into LO LECs or appear at high orders in the PVTV potential considered here.
Apart from pionic and pion-nucleon interactions, there appear PVTV NN contact interactions. As in the PVTC case, at least one gradient is required such that these operators start at order Q. Terms with three or more gradients have not been considered so far. At order Q, only five independent interactions of this kind can be written, corresponding to the five possible S ↔ P transitions (see section 4 for a general discussion of this kind of interaction terms). Neglecting terms with multiple pions, the Lagrangian reads (again, it is convenient to write it in terms of the non-relativistic nucleon field Ns)
As suggested by the factor of which we pulled out of the definition of the LECs, in χEFT these operators contribute in general at N2LO and are suppressed with respect to the PVTV one-pion exchange (OPE) potential. The only exception, as discussed in section 3.2.1, are quark-level operators that do not break chiral symmetry, for which are as important as the contributions from ḡ0,1.
Finally, the calculation of EDMs or other PVTV electromagnetic moments requires the inclusion of electromagnetic currents. Nucleon EDMs are induced by pion loops involving the interactions in . The renormalization of these loops requires the inclusion of short-distance counter terms contributing to the nucleon EDMs. Such counter terms indeed appear in the chiral Lagrangian
where Fαβ is the electromagnetic field strength and and are LECs related to the proton and neutron EDMs, respectively. The above interactions are sufficient for calculations of hadronic and nuclear PVTV scattering observables and EDMs up to NLO in the chiral expansion. Calculations of higher PVTV moments, such as magnetic quadrupole moments, can depend on additional LECs [138].
3.2.1. Connection to the Underlying PVTV Sources
In the previous section we listed the PVTV hadronic interactions relevant for observables of experimental interest. However, for a given PVTV source at the quark-gluon level, a specific hierarchy among the various interactions appear. The relative importance of the LECs in Equations (31), (32), (33), and (34) for the different microscopic sources of CP violation is summarized in Table 1. These estimates are based on NDA [120]. NDA is valid in the regime in which the strong coupling gs is non-perturbative, and, as done for NDA estimates of the chiral-invariant PCTC interactions, we will take gs ≃ 4π. In addition, for dimension-six sources, we assumed that a Peccei-Quinn mechanism [139] relaxes to an induced , which depends on the coefficients and vacuum matrix elements of the operators in Equation (7) [52, 140, 141]. The scaling of the couplings without this assumption can be found in deVries et al. [68]. To make the power counting explicit, we introduced three ratios of scales
Numerically, ϵχ ~ ϵmπ, but we define two different parameters to track the dependence of the LECs on the quark masses. To assess the size of the contribution of different CP violating sources to the nucleon and nuclear EDMs, the scaling of the LECs in Table 1 can be combined with a naive estimate of these observables. As we will discuss in detail in sections 3.2.2 and 6.5, the nucleon EDM receives tree level contributions from and loop contributions by ḡ0 and ḡ1, leading to
where e is the electric charge and the coefficients of the loops α0,1 will be given explicitly in section 3.2.2. The additional suppression of ḡ1 is due to the fact that this coupling only involves neutral pions, which do not interact with a single photon at LO. Nuclear EDMs, on the other hand, receive tree level contributions from the single nucleon EDM, and from pion-nucleon and nucleon-nucleon couplings,
The coefficients an,p, aΔ,0,1,2 and A1,…,5 depend on the nucleus under consideration, and in section 6.5 we will present results for their calculation in chiral EFT for the deuteron, 3H and 3He. By power counting, they are expected to be (measured in units of fm in the case of the dimensionful aΔ,0,1,2 and A1,…,5), barring isospin selection rules, which for example suppress the contributions of the isoscalar operators ḡ0 and in nuclei with N = Z, such as the deuteron [142, 143] 6.

Table 1. Scaling of the LECs in the chiral Lagrangian in dependence of the microscopic CP violation sources.
The reader should be aware that the dimensionless Wilson coefficients of the dimension-six operators, , , , , and also come with intrinsic suppression factors. These arise from the typical loop and chiral factors that appear in BSM models. For example, quark and gluon dipole operators are typically induced at the one-loop level, and the quark EDM and chromo-EDM coefficients come with explicit factors of the quark mass (already included in Equation 7). This implies that one can expect , where . Of course this is just an estimate and certainly models exist where these operators appear only at the two- or higher-loop level. On the other hand, the four-quark operators Ξ and Σ can be induced at tree level, so that . Once the matching coefficients are calculated in a given model, Table 1 and Equations (36)-(37) allow identification of the dominant low-energy operator and to get a rough idea of the EDM constraints.
Table 1 highlights the feature that the chiral and isospin properties of the quark-level CP-violating sources induce very specific hierarchies between different low-energy couplings. These hierarchies in turn imply different relations between the EDMs of the nucleon, deuteron, and three-nucleon systems, which, if observed, would allow disentanglement of the various CP-violating sources. From Table 1, we see that chiral-symmetry-breaking sources, such as , , and , induce relatively large PVTV pion-nucleon couplings. These couplings appear in the table with entry 1, indicating no further suppression. In particular, the isoscalar term and isovector Ξ(u,d) predominantly induce, respectively, ḡ0 and ḡ1, while a qCEDM would yield both couplings with similar strengths. The consequence is that for these sources light nuclear EDMs are enhanced with respect to the nucleon EDM. For these chiral-symmetry-breaking sources, the contact nucleon interactions proportional to are suppressed in the chiral expansion because these operators involve an explicit derivative. The suppression can be explicitly seen combining the scaling in Table 1 with the explicit factor of ϵχ in Equations (33) and (37).
Chiral invariant sources such as the Weinberg operator and the four-quark operators , on the other hand, require additional chiral-symmetry breaking to generate ḡ0,1, as indicated by extra powers of ϵmπ. In this case, EDMs of light-nuclei are expected to be of similar size as the nucleon EDM. Furthermore, the contact nucleon operators proportional to now contribute to the PVTV potential at the same order as ḡ0,1. Finally, the qEDM mostly induces , all other couplings being suppressed by , where αem is the fine structure constant ~1/137. In this case one expects nuclear EDMs to be dominated by the constituent nucleon EDMs.
While most statements are source-dependent, there is an important general message hidden in Table 1. There is no PVTV source for which the couplings ḡ2 and appear at LO. For all sources they appear with a relative suppression of εϵmπ or ϵχ compared to other PVTV interactions. For most calculations one can simply neglect the associated interactions, reducing the number of LECs entering the expression of hadronic and nuclear observables. The suppression of the LECs ḡ2 and ultimately is a consequence of imposing gauge invariance on the dimension-six PVTV sources.
Table 1 relies on NDA estimates for hadronic matrix elements [120]. A more quantitative assessment of the discriminating power of EDM experiments necessitates to replace the NDA estimates in Table 1 with solid non-perturbative calculations of the LECs. At the moment, there exist controlled estimates only of a few LECs. The pion-nucleon couplings ḡ0 induced by the QCD term is related by chiral symmetry to modifications in the baryon spectrum [102]. In particular, in SU(2) χPT ḡ0 is related to the quark mass contribution to the nucleon mass splitting [65, 144], up to N2LO corrections. Using Lattice QCD evaluations of the nucleon mass splitting [145, 146], one finds
where the 15% error includes both the Lattice QCD error on mn−mp, and an estimate of the error from N2LO chiral corrections. Unfortunately, chiral-symmetry-based relations do not allow to extract ḡ1 and . ḡ1 has been estimated with resonance saturation leading to , somewhat larger than expected from NDA [73]. The LECs are usually estimated by naturalness arguments and considered to be of similar size to non-analytic contributions to the isoscalar and isovector nucleon EDM, see the section 3.2.2.
The relation between PVTV pion-nucleon couplings and corrections to the nucleon and pion masses is not specific to the QCD term, but can be generalized to all chiral-symmetry-breaking sources, such as for example the qCEDM [68, 147] and [141, 148]. Since corrections to spectroscopic quantities should be easier to compute on the lattice, these chiral relations allow a calculation of ḡ0,1 in Lattice QCD. While promising, this strategy has yet to lead to controlled results. The best estimate of ḡ0,1 induced by the qCEDM comes from QCD sum rules [52, 149]
These estimates agree with NDA, especially for ḡ1. However, ḡ0 seems to be slightly suppressed, in agreement with large-Nc expectations [150].
Only for the four quark operators proportional to of Equation (7) does the three-pion vertex with LEC appear at LO in the chiral Lagrangian. For this case, the LEC is related by SU(3) symmetry to K → ππ matrix elements and matrix elements that have been calculated on the lattice. We obtain
with
The matrix elements in Equation (41) are in good agreement with NDA. The value of also determines the tadpole component of ḡ1, which again is in line with NDA.
Most of the remaining LECs are undetermined at present. The focus of the Lattice QCD community has been on the matrix elements connecting the nucleon EDMs to the term [103, 151, 152], the qEDMs [153, 154], the qCEDMs [152, 155], and the Weinberg operator [156]. Some results are given in next subsection.
3.2.2. The Nucleon EDM in Chiral Perturbation Theory
The PVTV LECs defined in the previous section can be used to calculate the nucleon PVTV electric dipole form factor (EDFF). At zero momentum transfer, the EDFFs are identified with the nucleon EDMs. In dimensional regularization with modified minimal subtraction up to NLO in the chiral expansion, the EDMs are given by [137, 157]
where μ is the dimensional regularization scale. The leading loops proportional to ḡ0 are divergent and renormalized by the μ-dependent LECs . The NLO corrections proportional to mπ/M are finite. The LEC does not contribute at this order for any of the PVTV sources. As standard in χPT, the loops are associated to inverse powers of . Combined with the scaling of the LECs in Table 1, we conclude that for the term and the qCEDMs the leading loop proportional to ḡ0 and the counter terms appear at the same order. For all other PVTV sources, the short-range counter terms are expected to dominate the nucleon EDMs. In no scenario can the EDMs be calculated solely from the pion-nucleon LECs ḡ0,1 as is often assumed in the literature. Estimates for the nucleon EDMs are often obtained by setting μ = M and such that EDMs depend on the value of ḡ0,1, which for some PVTV sources is better known.
The separation between the short-range and loop contributions is scheme dependent and therefore not physical. Lattice QCD calculations can therefore only calculate the total nucleon EDMs dn and dp. In recent years, significant efforts have been made toward calculating the nucleon EDMs in terms of the underlying PVTV sources. Most efforts have focused on the QCD term and the qEDM. The most recent results for the term [103] give
in good agreement, but with sizeable uncertainties, with expectations from the chiral logarithm in Equation (42) using Equation (38). In the case of the qEDM, the nucleon EDM is related to the tensor charges, which have been computed with good accuracy [153, 154]. Using the FLAG average [154], we get
where Qu,d are the u and d-quark charges in units of the electric charge, and the u and d-quark tensor charges of the proton, and the error on the r.h.s. of Equation(45) is dominated by the uncertainty on the light quark masses.
On a longer time-scale, calculations of the qCEDMs and the Weinberg operator are also targeted. For now, the best results come from calculations using QCD sum rules [52, 158].
3.3. From the Lagrangian to the Potential
In this subsection, we briefly present two methods that have been used to derive nucleon-nucleon potentials starting from a Lagrangian. We first introduce the notation used here and in the next subsections.
The process under consideration is the scattering of two nucleons from an initial state |p1p2〉 to the final state (hereafter the dependence on the spin-isospin quantum numbers is understood). It is convenient to define the momenta
where pj and are the initial and the final momenta of the nucleon j. Furthermore it is useful to define
which are the spin (isospin) matrix element between the final state () and the initial state sj (tj) of the nucleon j.
Because k1 = −k2 ≡ k from the overall momentum conservation , the momentum-space potential V is a function of the momentum variables k, K1 and K2, namely
Moreover, we can write in general
where K = (K1 − K2)/2, P = p1 + p2 = K1 + K2, and the term V(P)(k, K) represents a boost correction to V(CM)(k, K), the potential in the center-of-mass frame (CM). Below we will ignore the boost correction and provide expressions for V(CM)(k, K) only. Note that in the CM we define also p1 = −p2 ≡ p and . So we have k = p′ − p and K = (p′ + p)/2, so in the following we also write V(CM) as V(CM)(p, p′). From now on, we will suppress the superscript “(CM)” for simplicity.
In order to derive the potential, two methods have been frequently used, the method of unitarity transformation (UT), and the method of the time-ordered perturbation theory (TOPT). They are briefly introduced below.
The time-ordered perturbation theory method. Let us consider the matrix element of the T-matrix, , the “amplitude” of a process of scattering of two nucleons. Its square modulus is directly related to the cross section of the process. The conventional perturbative expansion for this matrix element is given as
where Ei is the energy of the initial state, H0 is the Hamiltonian describing free pions and nucleons, and HI is the Hamiltonian describing interactions among these particles. These operators are defined to be in the Schrödinger picture and they can be derived from the Lagrangian constructed in terms of pions and nucleons as described, for example, in Epelbaum et al. [159] and Baroni et al.[118]. The evaluation of Tfi is carried out in practice by inserting complete sets of H0 eigenstates between successive HI factors. Power counting is then used to organize the expansion in powers of Q/Λχ ≪ 1, where Q stands for either an external momenta or the pion mass. We will use the “naive” Weinberg counting rules [2], namely, we will count simply the powers of both the external momenta and pion mass insertions (we will consider low energy processes only). Each term will be of some order . The terms with the lowest power of ν will be the LO, and so on.
In the perturbative series given in Equation (50), a generic contribution will be characterized by a certain number of vertices coming from the interaction Hamiltonian HI and energy denominators, and it can be visualized also as a diagram (hereafter referred to as a TOPT diagram). Each vertex will give a “vertex function” and a δ conservation of the momenta of the particles involved in the vertex. The vertex functions are the results of the matrix elements of terms appearing in HI and are given as products of Dirac four-spinors, momenta, etc. A sum over the momenta of the particles entering the intermediate states is also present. When a diagram includes one or more loops, the δ's are not sufficient to eliminate all the sums over the momenta of the intermediate states. The energy denominators come from the factors 1/(Ei − Eα + iϵ), where Eα is the (kinetic) energy of a specific intermediate state entering the calculation. The chiral order of each diagram can be calculated as follows. One needs to consider:
1. The chiral order of the vertex functions, which can be calculated from the non-relativistic (NR) expansion of the nucleon Dirac four-spinors (1/M expansion), and from various other factors. Typically, the powers of p/M coming from the NR expansion of the nucleon Dirac four-spinors are counted as ~Q2 [2, 4, 160]. In other approaches however they are considered to be of order Q [20, 161, 162]. In this paper, we will follow the first prescription.
2. The energy denominators. We note that typical momenta p of the nucleons are much smaller than the mass of the nucleons, so we can treat them non-relativistically. Namely . Regarding the pion energies, . Usually in the energy denominator all the nucleon masses M cancel out and therefore we have two cases:
• If there are no pions in the intermediate state, the energy denominator has only nucleon energy terms so it results of order 1/Q2.
• If there are pions in the intermediate states, the energy denominator reads
where the term ΔE = E1 + E2 + ⋯− Ei where E1, … are the energies of the nucleons in the intermediate state and Ei is the initial scattering energy. In the Taylor expansion the first term is of order Q−1, while the other terms are usually called “recoil corrections”. For the sake of consistency with the choice discussed above regarding the NR expansion of the Dirac 4-spinors, here we will count the p/M terms coming from recoil corrections as Q2 as well.
3. The number of loops, or better the number of the sums over the intermediate state momenta that remain after using the conservation δ's. Each loop at the end will give a contribution of order Q3.
4. The number of disconnected parts of the diagram. For each of these parts, a δ factor expressing the momentum conservation of each part is present. Then, if there are ND disconnected parts, one of the δ simply gives the total momentum conservation, a factor common to all diagrams and therefore not relevant. Each of the remaining ND − 1 δ's at the end will “block” a sum over an external three-momentum, each one therefore reducing the chiral order by 3 units.
Once the T-matrix has been calculated, one would obtain in general
where . In all cases the sum starts from a minimum value nmin, nmin = 0 for the PCTC and nmin = −1 for the PVTC and PVTV amplitudes. The idea now is to “define” the potential acting between the two nucleons so that it can reproduce the same amplitude Tfi, namely, so that (for more details, see [118])
where is the non-interacting Hamiltonian of two nucleons. Clearly, this procedure is not unique, since usually one imposes the relation TV = Tfi to hold “on shell,” namely by requiring the conservation of the energy between initial and final states. This induces an ambiguity, as discussed for example in Pastore et al. [162]. However, the obtained potentials are expected to be equivalent by means of a unitary or at least a similarity transformation [163].
Finally, to invert Equation (53), one assumes that V has the same Q expansion as the T matrix,
and Equation (53) can be solved for V(n) order-by-order (see, for example, Baroni et al. [118] for more details). This procedure can be generalized to the A = 3 case to define a three-nucleon potential and so on.
The method of unitarity transformation. The method of unitary transformation (MUT) has been pioneered in the 1950s to derive nuclear potentials in the framework of pion field theory [164, 165]. In the context of chiral EFT, this approach was formulated in Epelbaum et al. [166] and Epelbaum [167]. Similarly to TOPT, the MUT is applied to the pion-nucleon Hamiltonian which can be obtained from the effective Lagrangian in a straightforward way using the standard canonical formalism. Let η and λ denote the projection operators on the purely nucleonic subspace and the rest of the Fock space involving pion states with the usual properties η2 = η, λ2 = λ, ηλ = λη = 0 and η + λ = 1. To derive nuclear forces and/or current operators, the Hamiltonian needs to be brought into block-diagonal form with no coupling between the η- and λ-subspaces, which can be achieved via a suitably chosen unitary transformation U. Following Okubo, a unitary operator can be conveniently parametrized in terms of the operator A = λAη that mixes the two subspaces via
One then obtains the non-linear decoupling equation for the operator A:
The solution of the decoupling equation together with the calculation of the unitary operator U and the nuclear potential is carried out in perturbation theory by employing the standard chiral expansion. The resulting expressions for the operators A, U and have a form of a sequence of vertices from the pion-nucleon Hamiltonian H and energy denominators involving the kinetic energies of particles in the intermediate states with one or more virtual pions. They are thus similar to the expressions emerging in the context of TOPT, see e.g., the operator in Equation (50), and the corresponding matrix elements can also be interpreted in terms of TOPT-like diagrams. Notice that contrary to Equation (50), the expressions in the MUT do, per construction, not involve energy denominators that vanish in the static limit of infinitely heavy nucleons and correspond to iterative contributions to the scattering amplitude. As explained in Epelbaum [167], in order to implement the chiral power counting in the algebraic approach outlined above it is convenient to rewrite it in terms of different variables. Using the rules given in the description of the TOPT approach and counting the powers of the soft scale Q for a given irreducible (i.e., of non-iterative type) connected N-nucleon TOPT-like diagram without external sources, one obtains for the chiral order n [2, 167]
where L is the number of loops, Vi is the number of vertices of type i. Further, the vertex dimension Δi is given by Δi = di + 1/2ni − 2 with di and ni being the number of derivatives and/or mπ-insertions and the number of nucleon fields, respectively. The above expression is convenient to use for estimating the chiral dimension of TOPT-like diagrams. For the MUT, it is, however, advantageous to rewrite it in the equivalent form
where pi is the number of pionic fields. The parameter κi obviously corresponds to the inverse overall mass dimension of the coupling constant(s) accompanying a vertex of type i. In this form, the chiral expansion becomes formally equivalent to the expansion in powers of the coupling constants, and it is straightforward to employ perturbation theory for solving the decoupling equation (56) and deriving the nuclear potentials .
One non-trivial issue that emerges when applying chiral EFT to nuclear potentials concerns their renormalization. While on-shell scattering amplitudes, calculated in chiral EFT, can always be made finite by including the counterterms from the effective Lagrangian (provided one uses a chiral-symmetry preserving regularization scheme such as dimensional regularization), nuclear potentials represent scheme-dependent quantities, which correspond to non-iterative parts of the scattering amplitude. There is no a priori reason to expect all ultraviolet divergences emerging from TOPT-like diagrams, which give rise to nuclear forces, to be absorbable into a redefinition of the LECs. Indeed, it was found that the static PCTC three-nucleon force at order Q4 of the two-pion-one-pion exchange type cannot be renormalized if one uses the unitary transformation given in Equation (55) [168]. On the other hand, the employed parametrization of the operator U is clearly not the most general one and represents just one possible choice. The freedom to change the off-shell behavior of the nuclear potentials, already mentioned in the context of TOPT, has been exploited in a systematic way in the PCTC sector in order to enforce renormalizability of nuclear forces (using dimensional regularization) [167, 169–172]. The MUT has also been successfully applied to the effective Lagrangian in the presence of external classical sources in order to derive the corresponding nuclear current operators, see [160] and references therein.
3.4. The PVTC Potential Up to Order Q2
In this subsection we will discuss in detail the derivation of the PVTC potential up to N2LO using the TOPT approach. We consider diagrams contributing to the T-matrix with one vertex coming from the PVTC Lagrangian, with all other vertices coming from the PCTC interaction. Diagrams with two or more PVTC vertices can be safely neglected.
The TOPT diagrams contributing to the PVTC T-matrix up to N2LO are shown in Figure 1.
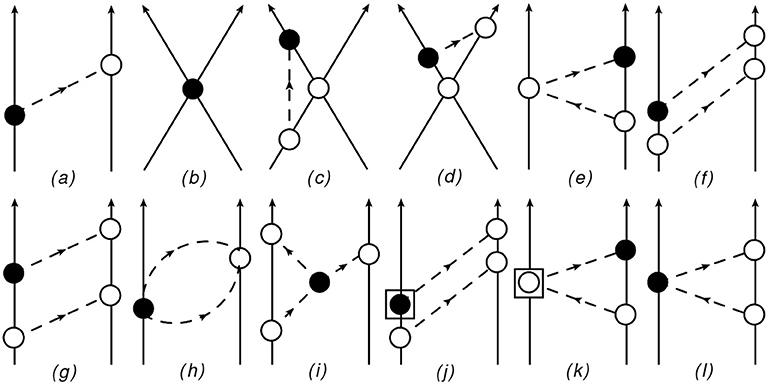
Figure 1. TOPT diagrams contributing up to N2LO to the PVTC amplitude. Nucleons and pions are denoted by solid and dashed lines, respectively. The open (solid) circles represent LO PCTC (PVTC) vertices. The vertex depicted by a square sourrounding a solid circle denotes the contribution of the subleading PVTC πNN terms coming from the Lagrangian given in Equation (19). The vertex depicted by a square surrounding an open circle denotes the contribution of the subleading PCTC ππNN (PVTC πNN) terms coming from the Lagrangian given in Equation (13).
The one pion exchange diagram (a) gives a contribution to the T-matrix of order Q−1 (that will be our LO). The diagram (b) represents a PVTC contact interaction of order Q; also the diagrams (c) and (d) with the PCTC contact vertex and one pion exchange are of order Q. The triangle diagram (e) with a PCTC ππNN vertex is of order Q, while if we consider the PVTC ππNN vertex as in panel (l) the diagram is of order Q2. The box diagrams (f) and (g) includes contribution of order Q0 and Q; the contribution of order Q0 is exactly canceled when inverting Equation (53). Finally, the “bubble” diagram (h), the three-pion vertex diagram (i), the box diagram (j) with the πNN vertex coming from the subleading PVTC Lagrangian terms proportionals to the LECs , and also the diagram (k) with the ππNN vertex coming from the subleading PCTC Lagrangian terms proportionals to the LECs ci, are of order Q2. These latter diagrams were considered for the first time in de Vries et al. [173] using the MUT, and using TOPT in [174].
Contributions proportional to 1/M coming from the NR expansion of the vertex functions or from recoil corrections in this work are considered to be at least of order N3LO.
Other types of diagrams like those shown in Figure 2(1–3) simply contribute to a renormalization of the coupling constants and masses, see Viviani et al. [42] for more details. In the following, we will disregard these diagrams, but it should be taken into account that the formulas below are given in terms of the renormalized (physical) LECs and masses. The contribution of diagram (4) is canceled when inverting Equation (53).
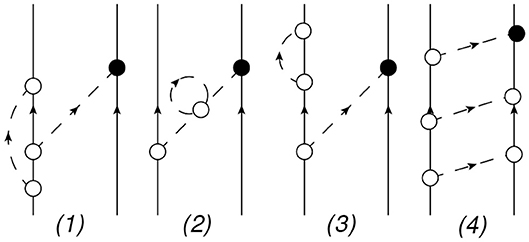
Figure 2. Other diagrams that would contribute at NLO. These diagrams contribute to the renormalization of the LECs (1–3) or give a vanishing contribution to the potential (4) due to the inversion of Equation (53). Notation as in Figure 1.
Let us now consider each kind of diagram separately:
• One pion exchange (OPE) diagram. Diagram (a) of Figure 1 gives the LO contribution (Q−1) to the potential
where and arises directly from the LO expansion of the vertices and energy denominators. Derived from the same diagram, there are terms coming from the NR expansion of the vertices, the first correction being of order (p/M)2. However, as discussed previously, they are counted to be of order Q4, and thus the corresponding terms are considered to be suppressed by four orders with respect to .
• Contact terms (CT) diagrams. The diagrams (b) depicted in Figure 1 derive from the interaction terms appearing in . They give a contribution to the potential of order Q1. As discussed in Chapter 4, this contribution can be written in various equivalent forms due to the Fierz identities [44]. We have chosen to write this part as follows [42]
where Λχ = 4πfπ ≈ 1.2 GeV. The parameters Ci, i = 1, …, 5 are LECs. Different (but equivalent) forms of this part were used in de Vries et al. [41] and de Vries et al. [173].
• Contact plus OPE diagrams. The diagrams (c) and (d) in Figure 1 are representative of diagrams containing a contact term and an OPE. However all these diagrams vanish after the integration over the loop variable.
• NLO two pions exchange: triangle diagrams. There are 6 different time-orderings of diagrams (e) given in Figure 1. After summing them, the total contribution from these diagrams results to be [40, 175]
where . The integral is singular and must be somehow regularized. We will discuss this issue later.
• NLO two pions exchange: box diagrams. There are 48 diagrams represented by the diagrams of type (f) and (g) of Figure 1 when we consider all possible time orderings. The final contribution is [40, 175]
and is of order Q1. Again the integral is singular. In this case, in the amplitude Tfi there appears a term of order Q0 coming from diagram (g), but it cancels out when inverting Equation (53).
• Bubble diagrams. We now turn to the diagrams contributing at order Q2, that is at N2LO. The sum of “bubble” diagrams (h) depicted in Figure 1 mutually cancel and these diagrams do not give any contribution to the PVTC potential.
• Diagrams with three pion vertices. The expansion of the PVTC Lagrangian in terms of pions gives rise to two terms proportional to which would contribute to Tfi via the diagram (i) depicted in Figure 1. However, after summing over all possible time orderings, the corresponding final contribution vanishes.
• N2LO two pion exchanges: box diagrams. The box diagrams (j) contributes also at N2LO, where the PVTC vertex comes from the subleading Lagrangian terms proportional to the LECs , , and in Equation (19). We have [75, 173]
• N2LO two pion exchanges: triangle diagrams. The diagram depicted in panel (k) derives from subleading ππNN vertices in the PCTC Lagrangians [75, 173], see Equation (13),
Note in Equation (64) the presence of the LEC c4, which belong to the PCTC sector [12].
The expression for the diagrams (l) comes from the LO PCTC and PVTC vertex functions. The final result is [75, 173]
where and are two of the LECs that appear in the Lagrangian terms given in Equation (19).
Finally, we conclude this section by mentioning that at N2LO, one should also include PVTC 3N forces. Examples of diagrams contributing to this 3N force are shown in Figure 3. The chiral order of diagrams with more than two nucleons is discussed in detail in Epelbaum [167]. The diagram depicted in panel (a) with a LO PCTC ππNN vertex would contribute at NLO, but vanishes when summed over all time orderings. The other three diagrams (the one in panel (b) has a subleading PCTC ππNN vertex proportional to ci, i = 1, …, 4 [12]) are N2LO and therefore they must be considered in order to perform fully consistent calculations in A ≥ 3 systems. However, these kind of diagrams have not yet been considered in literature. Note that diagrams with a 3N PVTC contact vertex are highly suppressed, so no new LEC needs to be introduced.
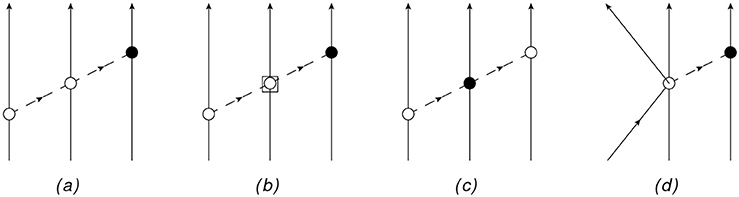
Figure 3. TOPT diagrams that would contribute to the PVTC 3N force For the notation see Figure 1.
3.4.1. Regularization of the PVTC Potential
In this section we deal with the divergences in the loop diagrams. We will briefly present three methods frequently used in literature, namely the dimensional regularization (DR) method used e.g., in [161], the spectral function regularization (SFR) [176], and the novel (semi-)local momentum-space regularization approach of Reinert et al. [19].
• Dimensional regularization method. This technique is well-known for dealing with divergences of loop integrals present in Feynman diagrams, where the integration is performed over four-momenta. In case of time-ordered diagrams, the loops involve integration over three-momenta. To deal with the singularities, the integrals are re-defined in d dimensions and successively one takes the limit d → 3. The singular part is singled out by terms ~1/(3 − d), which then can be reabsorbed in some of the LECs. As usual, we define ϵ = 3 − d, and we assume that ϵ → 0. When we use the DR, it is better to “rescale” all the dimensional quantities with an energy scale μ. Therefore we define , , etc., where the “tilde” quantities are dimensionless. We can now go to d dimensions and manipulate the integrals as discussed in detail in Pastore et al. [161], see also Friar [177]. Here we limit ourselves to listing the results needed to regularize the loop integrals we have encountered. Regarding the loop integrals appearing at NLO in Equations (61) and (62), we have
where
and
which contains the divergent part, where γ is the Euler–Mascheroni constant.
The loop integrals appearing in the N2LO diagrams as in Equations (64) and (65) are of the form
The first integral is finite, but the second integrand diverges linearly as q → ∞. The finite contribution can be obtained using the DR method. Alternatively, one can impose an ultraviolet cut-off ΛC on the integrals. The integrals then yield divergent pieces as ΛC → ∞, which can be again reabsorbed in some LECs, finite parts independent on ΛC that are exactly the same as obtained using the DR method, and a number of other terms which can be expressed in terms of a power series of Q/ΛC, where Q is either k or mπ. Taking the limit ΛC to infinity these latter parts would disappear. Since, in general we must fix ΛC at a value greater than the typical energies of the χEFT, then these additional terms carry at least an additional power of Q which means they give contributions at N3LO (or beyond) to the potential. Therefore, for the integral in Equation (71), we have followed the prescription to absorb the divergent parts in some LEC's, to disregard the parts depending on Q/ΛC, and to retain the finite parts as given by the DR method. Explicitly, the two integrals are given by
where
• Spectral function regularization method. Pion loop integrals appearing in the two-pion exchange contributions discussed in the previous subsection can be generally expressed using a dispersive representation. Writing the momentum-space potentials in the general form with Oi being spin-isospin-momentum operators and Wi the corresponding structure functions that depend only on the momentum transfer k ≡ |k|, the unsubtracted dispersion relations for the functions Wi(k) have the form [178]
where the spectral functions ρi(μ) are given by . Notice that the spectral integrals in Equation (75) do not converge for potentials derived in chiral EFT since ρi(μ) generally grow with μ, and must be subtracted the appropriate number of times. The subtractions introduce terms which are polynomial in k2 and can be absorbed into the corresponding contact interactions. It was shown in Epelbaum et al. [176] that even at fairly large internucleon distances, the potentials receive significant contributions from the spectral function in the region of μ ≳ Λχ, where the chiral expansion cannot be trusted. It was, therefore, proposed in that paper to employ an ultraviolet cutoff Λ in the spectral integrals. This can be shown to be equivalent to introducing a particular ultraviolet cutoff in the loop integrals over the momentum q. Using a sharp cutoff Λ in the spectral integrals over μ leads to the following modification of the loop functions L(k) and A(k):
where we have introduced . The resulting approach is referred to as the spectral function regularization. The limit of an infinitely large cutoff Λ corresponds to the previously considered case of dimensional regularization with L∞(k) = L(k) and A∞(k) = A(k). The spectral function regularization approach with a finite value of Λ was employed in the PCTC potentials of Epelbaum et al. [74] and the more recent work [18], as well as in the derivation of the N2LO PVTC potential in de Vries et al. [46].
• Local regularization in momentum space. The previously introduced spectral function regularization approach has the unpleasant feature of inducing long-range finite-Λ artifacts as can be seen by expanding the functions LΛ(k) and AΛ(k) in inverse powers of Λ. This feature may affect the applicability of chiral EFT for softer cutoff choices. Recently, local regulators in coordinate [17, 179] and momentum space [19] were introduced, which do not affect the analytic structure of the pion-exchange interactions and thus maintain the long-range part of the nuclear force. The approach of Reinert et al. [19] amounts to replacing the static propagators of pions exchanged between different nucleons via
with q ≡ |q|. Such a regulator obviously does not induce any long-range artifacts at any order in the 1/Λ-expansion. This regularization approach can be easily implemented for two-pion exchange NN potentials with no need to recalculate the various loop integrals. Using the feature that the regulator does not affect long-range interactions, it is easy to show that the regularization of a generic two-pion exchange contribution simply amounts to introducing a specific cutoff in the dispersive representation (modulo short-range interactions), namely [19]
In Reinert et al. [19], the regularized two-pion exchange contributions were defined using the requirement (i.e., a convention) that the corresponding potentials in coordinate space and derivatives thereof vanish at the origin. This is achieved by adding to the right-hand side of Equation (78) a specific combination of (locally regularized) contact interactions allowed by the power counting. For more details and explicit expressions see Reinert et al. [19]. This local regularization scheme has not been used for PVTC or PVTV nuclear potentials.
3.4.2. The Regularized PVTC Potential
Once the loop integrals have been manipulated as discussed previously, we can now write the PVTC potential up to N2LO derived from χEFT. In the following, some of the LEC's have been further redefined to absorb the singular parts coming from the loop integrals. If one has chosen to regularize the loop integral using the SFR method, then the functions L(k) and A(k) below have to be substituted with LΛ(k) and AΛ(k), the spectral regularized functions, see Equation (76). In summary,
where
The NLO term derives from the regularized parts of and , while the N2LO term from , , and . Let us note that we have in total 11 LECs that must be determined from the experimental data: one in the LO term, five in the subleading order and five at N2LO. This potential is the same as the one derived using the MUT in de Vries et al. [173].
Finally, the potential to be used in calculation of PVTC observables has to be regularized for large values of p, p′. The frequently used procedure is to multiply by a cutoff function containing a parameter ΛC
Typical choices for fΛC are [74]
where usually n = 6, adopted for example in de Vries et al. [173], or
adopted in Viviani et al. [42]. The value of the cutoff ΛC is chosen to be around 400–600 MeV, and consistent with the analogous parameter used to regularize the PCTC potential.
The currently most accurate and precise PCTC NN potentials of Reinert et al. [19] employ the local momentum-space regularization approach for pion-exchange contributions as described in section 3.4.1 in combination with a non-local Gaussian regulator given in Equation (85) with n = 2 and ΛC = Λ for contact interactions [Λ is the cutoff used in the local regulator in Equations (77), (78)]. The superior performance of the momentum-space regulator in Equation (78), as compared with both the spectral-function regularization and a local multiplicative regularization as defined in Equation (86), manifests itself in exponentially small distortions at large distances as visualized in Figure 5 of [19].
Last but not least, we emphasize that using different regulators when calculating loop integrals in the nuclear potentials/currents and solving the Schrödinger equation to compute observables is generally incorrect. This issue becomes relevant at the chiral order, at which one encounters the first loop contributions to the 3N potentials and to the NN exchange current operators (i.e., at order Q4 or N3LO in the PCTC sector) [180, 181], which is beyond the accuracy of the calculations described in this review article. For more details and a discussion of a possible solution to this problem see [182].
3.4.3. Relevant PCTC and PVTC Electromagnetic Currents
Electromagnetic currents can be calculated in the χEFT expansion. For our purposes we require currents for the longitudinal asymmetry in radiative neutron capture on a proton target at thermal energies. As we deal with a real outgoing photon, the LO PCTC current is induced by the nucleon magnetic moment. At NLO there are contributions from the convection currents and one-pion-exchange currents proportional to . At NLO the relevant currents become
where κ0 = −0.12 and μv = 3.71 are the isoscalar and isovector anomalous nucleon magnetic moments. pj and denote the incoming and outgoing momenta of nucleon j interacting with a photon of outgoing momentum q. The intermediate pions carry momenta or . de Vries et al. [173] used these currents in combination with N3LO χEFT potentials from Epelbaum et al. [17] to calculate the total np → dγ capture cross section. Using just the LO currents gives a cross section of 305 ± 4 mb, which grows to 319 ± 5 at NLO. The remaining 4% discrepancy to the experimental cross section 334.2 ± 0.5, indicates that N2LO currents should probably be included.
A consistent calculation of PVTC observables such as the photon asymmetry in the radiative capture also requires the inclusion of PVTC currents. There is no one-body current in this case, as the anapole moment vanishes for on-shell photons [183]. As such, the leading PVTC currents arises from one-pion-exchange currents
where we stress the dependence on the PVTC pion-nucleon LEC . Higher-order PVTC currents have not been developed.
3.5. The PVTV Potential Up to Order Q
In this section, we discuss the derivation of the PVTV NN and 3N potentials at N2LO. The final expressions are given in terms of a sum of diagrams, which can be obtained either using the MUT [4, 166, 184], standard dimensional regularization [72] or the TOPT method [75]. In the following, we briefly report the derivation of the PVTV potential in the framework of TOPT approach.
The TOPT diagrams that give contribution to the NN PVTV potential up to N2LO (order Q1) are shown in Figure 4. We do not consider diagrams which give contributions only to the renormalization of the LECs. In this section we write the final expression of the NN PVTV potential VPVTV having already taken into account the singular parts coming from loops. Note that for the PVTV potential the LO term is of order Q−1 as for the PVTC case. However, now there will be terms of order Q0, which will be denoted as NLO terms, etc. We have
namely coming from OPE diagrams at LO, TPE at N2LO, three-pion vertices (3π) at NLO and at N2LO, and contact contributions (CT). From now on we define . In this case, we report here the final form of the potential, namely, the LECs appearing in the expressions below are the physical ones, having reabsorbed the various infinities generated by loops and diagrams like those shown in Figure 2(1–3).
• One pion exchange diagram. The OPE term, depicted in diagram (a) of Figure 4, gives a contribution at LO, namely of order Q−1, coming from the NR expansion of the vertices
where there are an isoscalar, an isovector and an isotensor components. Contributions coming from the 1/M expansion are considered to be suppressed at least by four orders with respect to .
• Contact term diagrams. The potential , derived from the NN contact diagrams (b) of Figure 4, reads
Notice that the above LECs , , , , and have been redefined to absorb various singular terms coming from the TPE and 3π diagrams. It is possible to write ten operators which can enter at order Q but only five of them are independent as discussed in Chapter 4. In this work we have chosen to write the operators in terms of k, so that the r-space version of will assume a simple local form with no gradients.
• Contact terms with an OPE. Diagrams like (c) and (d) of Figure 4 vanish directly due to the integration over the loop momentum.
• Two pions exchange diagrams. The TPE term comes from the non-singular contributions of diagrams (e-h) in Figure 4. This term has no isovector component, as shown for the first time in Bsaisou et al. [73]. It reads
where the loop functions L(k) and H(k) are defined in Equation (68).
• Diagrams with three pion vertices The 3π-exchange term gives a NLO contribution through the diagram (i) of Figure 4,
where A(k) is given in Equation (74). Additional contributions coming from diagram (i) deriving from the 1/M expansion of the energy denominators and vertex functions are here neglected since they are counted as N3LO.
• The diagram (j) in Figure 4 contributes to at N2LO,
Note in Equation (94) the presence of the c1, c2, and c3 LECs, which belong to the PCTC Lagrangian given in Equation (13). In Equations (93) and (94), is a renormalized LEC.
The 3π PVTV vertex gives rise to a three body interaction through the diagram (k) in Figure 4. The lowest contribution appears at NLO while at N2LO the various time orderings cancel out [75]. The final expression for the NLO of the 3N PVTV potential is,
where . This expression is in agreement with that reported in deVries et al. [68] and Bsaisou et al. [69].
Figure 4. Time-ordered diagrams contributing to the PVTV potential (only a single time ordering is shown). Nucleons and pions are denoted by solid and dashed lines, respectively. The open (solid) circle represents a PCTC (PVTV) vertex.
3.5.1. The PVTV Current
The PVTV current up to now has been considered to arise from the LO one-body contribution
where dp (dn) is the proton (neutron) EDM. In nuclear physics applications, it is customary to consider dp and dn as unknown parameters, although they in principle can be estimated in terms of the LECs entering the χEFT, as we have seen in section 3.2.2. The complete derivation of PVTV two-body currents has not been completed, though partial results have been given in de Vries et al. [143] and Bsaisou et al. [73].
4. PVTC and PVTV Potentials in Pionless EFT
In this section, we specifically focus on the few-nucleon contact interactions which enter the potentials in both chiral and pionless EFT formulations. We also discuss the expected hierarchy of the corresponding LECs as suggested by the large-Nc analysis.
4.1. Effective Lagrangians
At distances much larger than the range of the interactions mediated by pions, the pionic degrees of freedom can be integrated out of the effective theory, and the relevant effective Lagrangian can be written in terms of nucleon fields only, interacting through contact vertices.
At leading order these vertices involve a single spatial derivative of fields, responsible for parity violation. Time derivatives can be eliminated recursively, using the equations of motion order by order in the low-energy expansion. This reflects our freedom in choosing the nucleon interpolating field, and amounts to a definite choice of the off-shell behavior of amplitudes. The theory can be formulated in terms of non-relativistic nucleon fields represented by two-component Pauli spinors Ns(x). The relativistic 1/M corrections, which can in principle be worked out (see e.g., [185]) will be of no interest here. Relativistic covariance requires that the interactions depend on the relative momenta only (momentum-dependent “drift” corrections, which vanish in the center-of-mass frame of two nucleon systems, are part of the above mentioned relativistic corrections). Thus, gradients of nucleon fields in two-nucleon contact operators may only enter in the combinations
where and the factor i, meant to ensure the hermiticity, makes it odd under time-reversal.
Since the underlying mechanism of parity violation in the SM may induce ΔI = 0, 1, 2 transitions (at least to order ), the effective Lagrangian will contain contact operators which transform as isoscalars or the neutral components of isovector and isotensors. In the two-nucleon case all these flavor structures are real, and therefore unaffected by the time-reversal operation, except for , which changes sign.
4.2. PVTC Lagrangian
Following the general considerations outlined above, there are ten possible structures entering the two-nucleon contact Lagrangian in the PVTC case,
The Fermi statistics of nucleon fields, together with Fierz's reshuffling of spin-isospin indices allow to establish linear relations between primed and unprimed operators,
thus reducing the number of independent operators to five, so that the effective Lagrangian can be written as
where Ci are LECs. This Lagrangian is identical to that reported in Equation (23). From this Lagrangian, one can derive the potential given in Equation (60).
The five LECs are in a one-to-one correspondence with the possible S-P transitions in two-nucleon systems [45], namely 1S0-3P0 (ΔI = 0, 1, 2), 3S1-1P1 (ΔI = 0) and 3S1-3P1 (ΔI = 1). This may be shown explicitly by using the spin-isospin projection operators [45, 186–188]
normalized according to
such that the operator creates a correctly normalized two-nucleon state with the appropriate spin-isospin quantum numbers. The relevant operators [188]
are related to the original basis via Fierz's transformations as follows,
whence one can read the relation between the partial-waves projected LECs and the Ci. The potential derived from the operators given in Equation (103) has been often used in studies of PVTC observables. It is given explicitly as [37, 39]
where the five LECs are in one-to-one correspondence with C1−5. Explicitly
where .
4.3. PVTV Lagrangian
The T-odd sector is very similar (see also [189]): one starts with a list of 10 redundant operators,
and uses Fierz's identities to establish the linear relations,
so that the Lagrangian only depends on five LECs,
from which one can derive the potential given in Equation (91).
The five S-P transition operators only differ from the T-even case by a factor i,
related to the original basis as follows,
4.4. Constraints From the Large-Nc Limit
In 1974 't Hooft combined the large-Nc and the small coupling limit, with fixed [190], and showed that QCD considerably simplifies, while maintaining many of the features of the actual theory, becoming a theory of stable hadrons. The baryons emerge as dense systems of many quarks, subjected to a mean field potential [191]. Nucleon-nucleon interactions exhibit in this limit a spin-flavor symmetry [192–194]. Indeed, due to the fact that nucleons carry definite spin and isospin of O(1), interactions inducing a change in either spin or isospin are suppressed relative to the dominant O(Nc) ones, that are either spin-isospin independent (~1) or dependent on both (~στ). The large-Nc counting of momenta follows from the observation that the nucleon-nucleon scattering amplitude is in this limit a sum of meson exchange poles, each one depending only on the relative momentum transfer. The average relative momenta can only appear as relativistic corrections, which are suppressed by inverse powers of M ~ O(Nc).
Apparently the resulting scaling laws do not conform with the operator identities (99) and (108) and seem to imply a dependence on the choice of operator basis. However, one can start with the redundant set of operators, pertinent to a theory of distinguishable nucleons, since the large-Nc arguments outlined above are completely general and do not rely on the statistics of the interacting baryons (the only assumption is that they both carry spin and isospin of O(1)). As a result one obtains the large-Nc scaling of the LECs in the PVTV contact potential,
and in the PVTV one,
Therefore we have only two leading LECs in the PVTC potential (C2 and C5 corresponding to ΔI = 0, 2 respectively) and only one in the PVTV potential ( with ΔI = 1) [47, 150]. This feature largely increases the predictive power for low-energy hadronic parity violation, and allows one to put more severe constraints on the forthcoming experimental results. Notice however that the above results are obtained by simply projecting the Hartree Hamiltonian in the nucleon-nucleon sector. A consistent treatment would require consideration of the induced effect on NN contact vertices of Δ exchanges, since the latter are enhanced, in the large-Nc limit, due to the degeneracy between nucleon and delta masses implied by the spin-flavor symmetry.
Moreover, for the PVTV case, this picture is obscured by the fact that the magnitude of the five contact LECs depends strongly on the particular type of the CP-violating source at the quark level. For example, the QCD term conserves isospin symmetry such that are suppressed by powers of εϵmπ compared to (see Table 1). Despite the possible 1/Nc suppression of compared to the former are still expected to dominate.
5. One-Meson Exchange Models
In the past, a simple and rather efficient description of the strong PCTC NN interaction was obtained in terms of a sum of single meson exchanges [195, 196]. These models began to be popular on account of the discovery of various meson resonances during the sixties. The potentials were generally constructed taking into account the exchanges of pions (JP = 0−, mπ = 138 MeV), η-mesons (JP = 0−, mη = 550 MeV), and ρ- and ω-mesons (JP = 1−, mρ, ω = 770, 780 MeV), but clearly, the number of mesons to be included is somewhat arbitrary. This picture has been extended also to describe PVTC and PVTV interactions, simply considering single meson exchanges where one vertex is strong and PCTC, while the other violates P and conserves T or violates both P and T. Then, all the dynamics of such interactions is contained in a number of PVTC and PVTC nucleon-nucleon-meson (NNM) coupling constants.
One starts by writing the Lagrangian consistent of Yukawa-like NNM vertices, invariant under the proper Lorentz transformations, and either conserving or violating the discrete P, C, T symmetries. The building blocks of the Lagrangian are therefore nucleon bilinears multiplied by a meson field arranged so that Lorentz symmetry is satisfied. For the construction of the PCTC Lagrangian, one usually includes only isospin-conserving terms. However, for the PVTC and PVTV Lagrangians, isospin-changing terms must be included since the underlying operators at the quark level are not necessarily isospin symmetric. A summary of the transformation properties of nucleon bilinears with different elements of the Clifford algebra and the various meson fields under hermitian conjugation (H), parity P, and charge conjugation C are reported in Table 2.

Table 2. Transformation properties of fermion bilinears with different elements of the Clifford algebra and various meson fields under hermitian conjugation (H), parity (P), and charge conjugation (C).
Using these properties it is not difficult to write the Lagrangians. For example, the strong Lagrangian constructed with these mesons is given by (here we list only isospin -conserving terms)
where qμ is the meson momentum7, πa, , η, and ωμ are meson fields and gπ, … PCTC coupling constants. Above, χV and χS are the ratios of the tensor to vector coupling constant for ρ and ω, respectively. Assuming vector-meson dominance [197], they can be related to the iso-vector and iso-scalar magnetic moments of a nucleon (χV = 3.70 and χS = −0.12). Note that the pion and rho-meson are isospin triplets, therefore the fields have the isospin index a = 1, …, 3. Moreover, the rho- and omega-mesons have spin 1, and their fields correspondingly are vector fields with index μ = 0, …, 3.
Let us now consider the PVTC Lagrangian constructed in terms of the same mesons. In this case one has to take into account Barton's theorem [198], which asserts that exchange of neutral and spinless mesons between on-shell nucleons is forbidden by CP invariance, and therefore they cannot enter in a PVTC Lagrangian. Therefore only π±, ρ, and ω vertices need to be considered and the form of the PVTC effective Lagrangian is [131]
where , … are PVTC coupling constants to be determined. As discussed also in section 3, where we focused in particular on the pion-nucleon PVTC constant , attempts to estimate the magnitude of these couplings from the fundamental theory were reported in several papers [121–127]. In particular, in the DDH paper [50], the authors presented reasonable ranges inside of which these parameters were extremely likely to be found, together with a set of “best values” (see Table 3). Clearly, these values have to be considered as educated guesses in view of all the uncertainties of their evaluation. Of the seven unknown weak couplings , there are estimates that indicate that is quite small [199] and this term was generally omitted, leaving PVTC observables to be described in terms of six constants. Notice further that the DDH parameters were also considered using a soliton description of the nucleon in [200] and [130].
In the same manner, we can write the PVTV Lagrangian composed of NNM vertices [142, 201]
where , i = 0, 1, 2, are PVTV meson-nucleon coupling constants. In this case, there were no attempts to obtain the values of these coupling constants from the fundamental theory, as also the magnitude of the parameters entering the underlying theory is unknown.
From these Lagrangians, the PVTC and PVTV interactions are obtained as a sum of single-meson exchange diagrams. Regarding PVTC, below we report the potential in the form obtained by DDH [50]
where k and K are defined in Equation (46). Often the potential is regularized for large values of k, modifying the meson propagators so that , where x = π, ρ, and ω. For example, in Schiavilla et al. [202] the following regularization was chosen
For example, the parameters Λπ, Λρ, and Λω were chosen to have the same value 2.4 GeV in Schiavilla et al. [203] and Schiavilla et al. [202]. However, the cutoff functions were not always applied and also their form can vary.
Several PVTC observables have been studied using the DDH potential, with the aim to identify the values of the six or seven coupling constants, see for example [34, 36, 37]. Up to now the lack of accurate experimental values has prevented the completion of this task.
Usually, the experiments are analyzed in terms of the DDH parameters. In the next Section, we will present a discussion of the experimental values within the χEFT framework. In order to make contact between the two approaches, we briefly discuss the relation between DDH and χEFT PVTC potentials. The OPE term is clearly the same, while in the DDH approach all the TPE terms are missing. They can be considered effectively included via the heavy-meson exchanges, however the ρ and ω masses are larger than 2mπ, which is the range of the TPE contributions. More precisely, the heavy meson exchange terms should be considered as equivalent to the five contact terms in the chiral potential multiplied by the LECs Ci. Keeping this in mind, we can match the components of the DDH potential mediated by ρ and ω exchanges to those of , and obtain in the limit k ≪ mρ, mω [42, 46]
where
Using the “best” values for the DDH parameters given in Table 3 (the other coupling constants and parameters have been taken from Schiavilla et al. [203]), we obtain, for example, the following estimates (in units of 10−7):
The large value of is due to the tensor coupling constant χV ≃ 3.7 of the ρ-meson to the nucleon. Clearly, these values should be taken only as indicative, since terms in the DDH vector-meson potential implicitly also account for TPE components, which in the χEFT PVTC potential are included explicitly. Relations where the TPE contributions are subtracted from the results above and the estimations of the LECs Ci within the soliton picture of the nucleon are given in de Vries et al. [46].

Table 3. Weak NNM couplings as estimated in Desplanques et al. [50].
The PVTV potential was derived in Haxton and Henley [204], Gudkov et al. [205], Towner and Hayes [206], and Liu and Timmermans [142]. The momentum space version reads
Also in this case, cut off functions can be applied in order to regularize the large k behavior of VPVTV. It is worthwhile to stress that the PVTV meson-exchange potential involves significantly more parameters than the LO PVTV chiral potential which depends in principle only on 4 LECs ḡ0,1 and , with ḡ2, , and appearing at subleading orders. While the meson-exchange potential can be mapped onto the short-distance operators, the dynamics from the 3-pion interaction is not captured in this way.
6. Selected Results for Various PVTC and PVTV Observables
In this section we present a selection of results obtained with the chiral EFT potentials and currents described in section 3 for various PVTC and PVTV observables. We will discuss first in the next four subsections the parity violation in (i) the radiative neutron capture on the proton, (ii) the longitudinal asymmetry in scattering, (iii) the longitudinal asymmetry in the 3He()3H reaction, and (iv) the -p and -d spin rotations, respectively. Finally, in the last subsection, we present some results for the EDM of light nuclei. Our motivation to include these results in the review is mainly to establish benchmarks to help future applications. We include also a “minimum” analysis how the current experimental data constrain some of the values of the LECs entering the χEFT interactions.
Results obtained using the pionless EFT can be found, for example, in Schindler and Springer [36], Haxton and Holstein [37], and Gardner et al. [39]. The meson-exchange potentials (in particular the DDH model) were used to analyze the results of several experiments of PVTC observables also in medium and heavy nuclei. For a summary of the obtained results, see, for example, [34, 39, 131]. Calculations of the EDM of light nuclei using the meson exchange potential were performed in Liu and Timmermans [142], Song et al. [207], and Yamanaka [208].
6.1. Parity Violation in Radiative Neutron Capture on the Proton
The radiative neutron capture on the proton , where d denotes the deuteron and a longitudinally polarized neutron, represents a very interesting process wherein to study PVTC effects in nuclear physics. The longitudinal analyzing power for this process is defined as
where dσ±(θ) is the differential cross section for positive/negative helicity neutrons, and θ is defined as the angle between the neutron spin and the outgoing photon momentum. aγ has been measured by several experiments during the past decades. The first non-zero signal was reported last year for incoming neutrons of thermal energies [209],
although this number is only two standard deviations away from a null result.
The theoretical asymmetry is given by
where are reduced matrix elements (RMEs) either of electric (X = E) or magnetic (X = M) type, of multipolarity ℓ, and describing the EM transition from the n − p system in the scattering state 2S+1SJ [203].
Compared to the PVTC longitudinal analyzing power in proton-proton scattering discussed later, aγ carries a significant advantage. The initial neutron-proton system can be in the 3S1 state, so that the process is sensitive to the 3S1 ↔ 3P1 transition and thus depends on the LO PVTC NN potential. In chiral EFT, the LO potential depends only on the LEC , meaning that measurements of aγ provide a unique chance to pin down the value of this LEC – something that is much more difficult to achieve in proton-proton scattering, where the contribution of the LO potential vanishes. The disadvantage is that is an electromagnetic process and therefore depends on P-conserving and P-violating electromagnetic currents.
As can be seen from Equation (130), a non-zero value of aγ requires interference between electric and magnetic dipole currents. As such, including only the leading magnetic moment current in the presence of the LO PVTC NN potential leads to a vanishing result and NLO currents are necessary. There are then three relevant contributions that consist of interference between the isovector nucleon magnetic moment and
1. The one-body convection current in combination with the PVTC NN potential,
2. The two-body PCTC currents in combination with the PVTC NN potential,
3. The two-body PVTC currents.
Each of these contributions is sizeable: , , and where the theoretical error bands are obtained from cut-off variations in the strong NN potential and do not reflect uncertainties from higher-order contributions [173]. While these uncertainties are small on the individual contributions, they lead to a sizeable uncertainty in the total analyzing power [173]
The cancellations between the different contributions are related to gauge invariance [173, 203, 210] and this explains the relatively large total theoretical uncertainty. While the electromagnetic currents given above are explicitly gauge invariant as they result from the gauge-invariant χEFT Lagrangian, explicit gauge invariance is lost due to applied regulator when solving the NN scattering and bound-state equations. Future calculations can probably reduce the uncertainty by using regulators that do not violate explicit gauge invariance, but such schemes have not been applied to PVTC processes. Alternatively, it is possible to apply the Siegert theorem to relate part of the electric dipole currents to the one-body charge density. Schiavilla et al. [211] applied the Siegert theorem in combination with phenomenological strong potentials to calculate aγ finding a result in good agreement with the central value in Equation (131). Such calculations however do not include an uncertainty estimate, for instance from missing transverse currents that are not included when applying the Siegert theorem. In this light, Equation (131) can be interpreted as a conservative result. It would be interesting to redo the calculation of aγ in an updated framework to reduce the theoretical uncertainty.
The contribution to aγ from the short range components of the potential is considered to be negligible. For example, using the meson-exchange model, the calculations have shown that aγ is essentially unaffected by short-range contributions [203, 212–214], represented in this case by ρ and ω exchanges. Within χEFT, a resonance saturation estimate of the short-distance LECs contributing to the asymmetry led to short-distance contributions to aγ of roughly 5·10−9 and is thus very small [173]. Therefore, considering the theoretical expression given in Equation (130) and the experimental value given in Equation (129), we obtain an estimate for the LEC
Note that the large experimental error and the large theoretical uncertainty only allow one to establish the positive sign and that the magnitude of this LEC is consistent with the preliminary Lattice QCD evaluation reported in Equation (26) [132].
6.2. Parity Violation in Scattering
PVTC effects in proton-proton scattering can be studied by looking at the longitudinal analyzing power Az(E, θ) defined as,
where θ is the scattering angle and E the energy of the protons in the laboratory frame, and σ+(θ, E)(σ−(θ, E)) the cross section when the polarization of the incoming proton is parallel (anti-parallel) to the beam direction. Actually the experiments detect the particles scattered in angular range [θ1, θ2] and the measured quantity is an “average” of the asymmetry over the total cross-section in this range, explicitly
where
is the unpolarized differential cross-section for the process. There exist several measurements of the angle-averaged longitudinal asymmetry , see Equation (134), obtained at different laboratory energies E [215–218]. The measurements and the angle ranges included in our analysis are reported in Table 4. The other “non-zero” measurement reported in the literature but not included in our analysis was performed at E = 15 MeV, with the result [216].
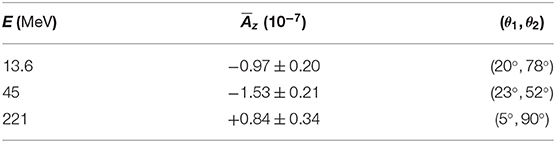
Table 4. Values of and angle ranges for the three measurements of the longitudinal analyzing power [215, 217, 218].
The isospin state of two proton system is |pp〉 ≡ |T = 1, Tz = 1〉, implying that the LO contribution that comes from the OPE vanishes and the LEC will contribute to the observable only via the TPE box diagrams that appear at NLO and N2LO. Taking into account the isospin selection rules, the longitudinal asymmetry can be written as
where the first two terms are NLO contributions and the third term enters at N2LO. We have defined
and , , are numerical coefficients independent of the LEC values (but depending on the energy). The values of the coefficients , , and calculated with the χEFT N2LO PVTC potential described in section 3.4 and the N4LO PCTC potential derived in Entem et al. [18] are reported in Table 5. The only coefficient which receives contributions from both the NLO and N2LO potentials is . In the table, we report separately the two contributions and also the total contribution, given simply as
The value of has been obtained assuming a value c4 = 3.56 GeV−1 [219]. This correction to is of the order of ~50% with respect to the NLO value, somewhat larger than expected. This is related by the unnaturally large value of the πNN LEC c4 appearing in the PCTC Lagrangian (13). This value has been obtained from the Roy-Steiner analysis of πN scattering data at N2LO performed in Hoferichter et al. [219].
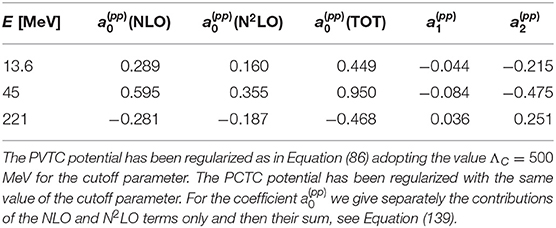
Table 5. Values of the coefficients calculated with the χEFT N2LO PVTC potential described in section 3.4 and the N4LO PCTC potential derived in Entem et al. [18] at three energies corresponding to the experimental data points.
Unfortunately, of the performed measurements, the two at the lowest energy do not give independent information. In fact, the observable at low energy scales as , since its energy dependence in this energy range is driven solely by that of the S-wave (strong interaction) phase shift [220]. Because of this scaling, it is not possible to fit from these data all three LECs , C, and at the same time. If we fix the value from the central value as extracted from the observable, see Equation (132), then we can perform a χ2 analysis of the three data points listed in Table 4 in order to fix the values of C and . Note that this value of was obtained from the calculation performed in de Vries et al. [173] using a different PCTC potential than that one used compute the coefficients. However, since the experiment depends mainly on the peripheral regions of the process, the value of aγ is not very sensitive to the PCTC interaction (see also the calculations reported in [221]).
First of all, if we restrict ourselves to an NLO analysis, using we would obtain C = (49±2)·10−7. If we take into account also the N2LO LEC, we report in Figure 5 the C and values for which χ2 ≤ 2, which form an elliptic region. As can be seen, there appears to be a strong correlation between C and and the range of allowed values of the LECs is rather large 5 × 10−7 < C < 67 × 10−7 and . Note that the ellipse is rather narrow and almost coincides with a straight line. See also de Vries et al. [46], Viviani et al. [42] for a similar analysis performed at NLO for the LECs and C only.
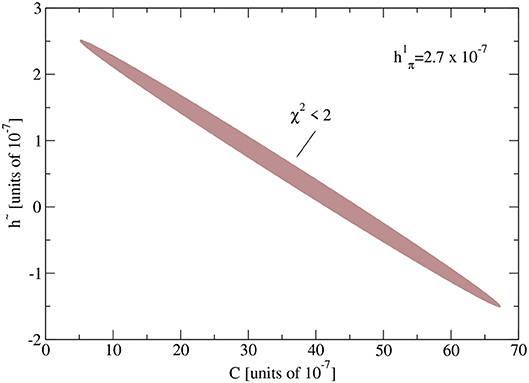
Figure 5. Region of C and values for which χ2 ≤ 2 for the -p longitudinal asymmetry. The calculation is based on the coefficients , , and reported in Table 5 assuming the value .
The previous discussion did not take into account the large uncertainty of the coupling constant after the fit of the -p radiative capture asymmetry. In Table 6, we report representative values of C and giving the minimum value of χ2 corresponding to range of values for as given in Equation (132). In the fourth column we report values for C if we neglect the N2LO contributions (setting ). We conclude that the combination of the and asymmetries allows for a rough extraction of the LO and NLO LECs and C, but is insufficient to also pinpoint the N2LO LEC . The uncertainty of the extractions of and C is dominated by theoretical and experimental uncertainties related to the PVTC asymmetry in the radiative neutron capture process.
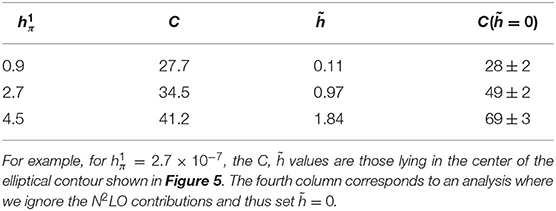
Table 6. Values for C and corresponding to different values of (all LECs are given in units of 10−7) giving the minimum value of the χ2 in the fit of the three experimental -p data points.
6.3. The 3He()3H Longitudinal Asymmetry
Very recently, a measurement of the longitudinal asymmetry for the reaction 3He()3H induced by ultracold neutrons was successfully completed at ORNL [222]. This quantity is given by [223], where θ is the angle between the outgoing proton momentum and the neutron beam direction. The measured value for az is given by az = (1.58±0.97 (stat) ±0.24 (sys) ) ×10−8 [224].
So far, this observable has been calculated using the NLO χEFT PVTC potential [42] (and also the DDH potential in [223]). The expression for the coefficient az is given as usual as
where the various coefficients are given as products of T-matrix elements involving three PCTC and three PVTC transitions [see [223] for details]. These T-matrix elements have been calculated by means of the HH method [225]. The resulting coefficients are listed in Table 7.

Table 7. Values of the coefficients entering the 3He()3H longitudinal asymmetry calculated for the χEFT NLO PVTC potential described in section 3.4 and the N3LO PCTC potential derived in Machleidt and Entem [5] at vanishing neutron beam energy.
First of all, if we restrict ourselves to LO (namely, setting all Ci = 0), using , one obtains , a value that is not compatible with the reported experimental value. Therefore, large contributions from NLO terms are expected. The values of become more negative at NLO. At present, we only have the combination , therefore we cannot proceed any further. Assuming, for example, , we would obtain a contribution to az from this term of ≈ +2.26 × 10−8. Therefore, this observable is very sensitive to the LECs Ci, and can be used to fit a linear combination of Ci that is independent of the combination appearing in scattering. Calculations at N2LO are planned. However, we recall that one should also include the PVTC 3N interaction terms for completeness.
6.4. The -p and -d Spin Rotation
The spin rotation of neutron traversing a slab of matter in a plane transverse to the beam direction induced by the PVTC potential is given by
where ρ is the density of hydrogen or deuterium nuclei for X = p or d, are the n-X scattering states with outgoing-wave (+) and incoming-wave (−) boundary conditions and relative momentum taken along the spin-quantization axis (the -axis), SX is the X spin, and vrel = p/μ is the magnitude of the relative velocity, μ being the n-X reduced mass. The expression above is averaged over the spin projections mX; however, the phase factor is ±1 depending on whether the neutron has mn = ±1/2. We consider the n-p and n-d spin rotations for vanishing incident neutron energy (measurements of this observable are performed using ultracold neutron beams). In the following, we assume ρ = 0.4 × 1023 cm−3. The rotation angle depends linearly on the PVTC LECs, as higher-order weak corrections are negligible. We write
where the for i = 0, …, 5 and for i = 1, …, 5 are numerical coefficients. The coefficient receives contributions from different chiral orders, in particular
The values of these coefficients for the n-p case and the cut-off value Λ = 500 MeV are listed in Table 8. From that table, it is possible to appreciate the chiral convergence for the coefficients . The NLO correction is ~10% of the LO result. In this case, the N2LO contribution vanishes since the LEC in multiplies the operator (τ1z + τ2z). The -p spin rotation is sensitive to all the LECs except for the LECs C4 and multiplying again the isospin term (τ1z + τ2z); in particular, there is a large sensitivity to C5 and , which multiply the isotensor terms of the PVTC potential.

Table 8. Values of the coefficients entering the expression of the -p spin rotation in units of Rad m−1 calculated for the χEFT N2LO PVTC potential described in section 3.4 and the N4LO PCTC potential derived in Entem et al. [18] at vanishing neutron beam energy.
Regarding the -d spin rotation, the coefficients, as reported in Table 9, are calculated by using only the NLO PVTC potential. We note the large sensitivity to (this fact is well-known [202, 226]), and to the LEC's C2 and C3.

Table 9. The same as in Table 8 but for the -d spin rotation and using the χEFT NLO PVTC potential and the N3LO PCTC potential derived in Machleidt and Entem [5].
At present there are no measurements of these quantities, however their experimental knowledge could be very useful in isolating certain combinations of LECs.
6.5. EDM of Light Nuclei
The EDM operator is composed by two parts,
is the electric dipole operator derived from the current JPCTC given in Equation (87), after using the long wavelength approximation and the continuity equation [227], explicitly
where e > 0 is the electric unit charge, τz(i) and ri are the z component of the isospin and the position of the i-th particle. This operator implicitly takes into account also the main part of the two-body PCTC currents. The contribution comes from the PVTV current at LO given in Equation (96) and it reads
where dp and dn are the EDM of proton and neutron, respectively and σi is the spin operator which act on the i-th particle. As discussed in section 3.5.1 and in de Vries et al. [143] and Bsaisou et al. [73] the should also include contributions from transition currents at N2LO. These are not considered in this review.
The EDM of an A nucleus can be expressed as
where is defined to be the even-parity (odd-parity) component of the wave function. In general, due to the smallness of the LECs, the EDM depends linearly on the PVTV LECs
where the ai for i = 0, 1, 2, Ai for i = 1, …, 5, aΔ, and ap, an are coefficients independent on the LEC values (all coefficients except ap and an have the unit of a length). For the deuteron, is dominated by one-body components, proportional to the neutron and proton EDM. The coefficients ap and an multiplying the intrinsic neutron and proton EDM, as already pointed out first in Yamanaka and Hiyama [228] and then in Bsaisou et al. [66], are given by,
where PD is the percentage of D-wave present in the deuteron wave function. , in the case of the deuteron, receives contribution only from the LECs ḡ1, , , and . The coefficients calculated with the χEFT N2LO PVTV potential described in section 3.5 and the N4LO PCTC potential derived in Entem et al. [18] are reported in Table 10. The cutoff for both the PCTC and PVTV potentials has been chosen to be ΛC = 500 MeV. The coefficients a1, A3, and A4 agree well with the power counting expectation in Equation (37). The slight suppression of a1 compared with the naive estimate a1 ~ 1 is in very good agreement with the perturbative pion power counting [70]. The LO perturbative pion calculation of a1 agrees with the value in Table 10 at the 20% level [70]. Results obtained in chiral EFT with N2LO PCTC potentials [66], and with “hybrid” approaches [143, 228] based on chiral PVTV and phenomenological PCTC potentials, also agree well with the results reported in Table 10. The contribution of the three-pion coupling aΔ is a bit more problematic. We find in this case that the contribution of the N2LO term is of the order of ~60% of the NLO term. We will discuss the issue of these large N2LO corrections more in detail below.

Table 10. Values of the coefficients entering the expression of the deuteron EDM calculated for the χEFT N2LO PVTV potential described in section 3.5 and the N4LO PCTC potential derived in Entem et al. [18].
Depending on the source of CP violation at the quark level, the deuteron EDM can be dominated by different LECs. For sources such as quark chromo-EDMs and four-quark operators Ξ, for which ḡ1 is induced without any chiral suppression, the pion-exchange contribution proportional to ḡ1 is expected to dominate the deuteron EDM. For sources such as quark EDMs or the Weinberg operator, however, the deuteron EDM is well-approximated by the sum of the nucleon EDMs. For the θ-term, the pion-exchange contributions are expected to be minor as well. Given measurements of the deuteron and nucleon EDMs, one can, therefore, identify the underlying source of CP violation [70, 229].
As regarding the 3H and 3He EDMs, the results are summarized in Table 11. The coefficients a0 and a1 are again a bit smaller than the expectation. Note that the value for a0 reported in Table 10 is approximately 50% smaller than that reported in Bsaisou et al. [66]. This difference can be traced back to the contribution of the TPE, which was not included in that work. Performing the calculations at LO, namely including only the OPE term, the a0 coefficient results to agree with that reported in Bsaisou et al. [66]. The values of the numerical coefficients are mostly equal in modulus between 3H and 3He except ap and an. The coefficients associated to isovector terms have the same sign while all the others are opposite. Again the contribution of the N2LO potential term to aΔ is significant, about 60%. This issue is discussed below.
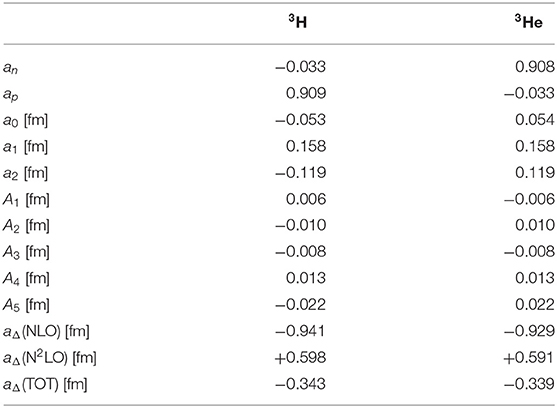
Table 11. The same as in Table 10 but for the 3H and 3He EDM.
Let us now consider in more detail the issue of the NLO and N2LO contributions to aΔ. We have seen that in all cases the N2LO correction to aΔ is of the order of 60%, a bit larger than expected. Explicitly, the coefficient aΔ can be written as [75]
where aΔ(0) comes from the NLO potential given in Equation (93) and aΔ(3N) from the 3N potential given in Equation (95). The N2LO terms come from , where the LECs c1, c2 and c3 appear. The values for the various components of coefficient aΔ for different nuclei are reported in Table 12. To calculate the values reported in Tables 10, 11, the following values were adopted: c1 = −1.10 GeV−1, c2 = +3.57 GeV−1, and c3 = −5.54 GeV−1 as reported in Hoferichter et al. [219] and Hoferichter et al. [230]. The large N2LO corrections are caused by the large values of these LECs8. For more detail, see [75]. For the trinucleon systems, the values of aΔ(3N) give a correction to aΔ(NLO) of the order of ~25%, which is in line with the chiral perturbation theory prediction because these contributions appear at the same order.
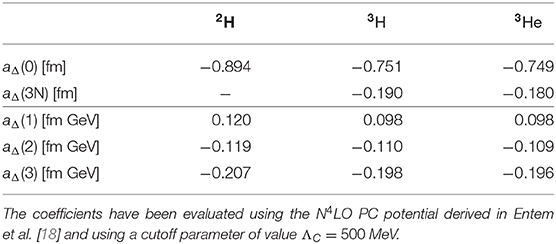
Table 12. Values of the various components of coefficient aΔ as given in Equation (151) in units of e fm for the different nuclei.
Similarly to the deuteron EDM, the trinucleon EDMs can be dominated by different terms. As the isoscalar interaction proportional to ḡ0 and now gives a sizable contribution, the trinucleon EDMs are noticeably different from the nucleon EDMs for the QCD θ-term, the quark chromo-EDMs, the four-quark operators Ξ, and potentially the Weinberg operator and the four-quark operators Σ. These EDMs therefore provide complementary information to the deuteron and nucleon EDMs. Combined measurements of all these EDMs would allow one to unravel various BSM models of new CP violation [71].
7. Conclusions and Perspectives
In this paper we have discussed the current status of the PVTC and PVTV nuclear interactions using the traditional approach based on phenomenological boson exchange models and as well as utilizing the modern frameworks of pionless and chiral EFT. The study of PVTC signals in nuclei is interesting since it derives from the non-leptonic weak interactions between quarks. Furthermore, a solid understanding of the manifestation of PVTC interactions at the nuclear level would give us confidence in the analysis of the more exotic PVTV case and other BSM nuclear observables. In fact, PVTV observables provide very valuable information since they are sensitive to interactions originating from the θ-term in the SM and even to more exotic mechanisms appearing in BSM theories.
As discussed in this review, the theoretical understanding of the PVTC and PVTV interactions is already rather advanced. Interactions in χEFT have been developed up to N2LO. The convergence of the χEFT appears to be problematic only for the contributions proportional to the ππNN LECs ci, due to the large values of those coefficients as measured in πN scattering [219]. Given that the LECs c2,3,4 are largely driven by the Δ(1232) [231], one may expect a better convergence in a formulation of chiral EFT that includes the Δ as an explicit degree of freedom. Furthermore, large Nc analysis may help in reducing the number of contact LECs. Also Lattice QCD calculations start to give valuable information [132, 232].
We have also reported the results of the theoretical calculations of several observables performed using the potentials derived within the χEFT framework. The PVTC observables considered include (i) the longitudinal asymmetry in -p radiative capture, (ii) the longitudinal asymmetry in proton-proton elastic scattering, (iii) the longitudinal asymmetry in the 3He()3H reaction, and (iv) the spin rotation of a neutron beam passing through a hydrogen and deuterium gas. As an example of a PVTV observable, we have studied the EDMs of some light nuclei. The main motivation to study these observables is that for such light systems, the theoretical analysis can be carried out without invoking any uncontrolled approximations. Thus, comparison with the experimental data can be performed unambiguously. The analyses of PVTC and PVTV observables using meson exchange models can be found in other review articles [34, 39, 131] and are not reported here.
As discussed previously, there exists a first measurement of the parameter aγ of the radiative neutron capture on the proton . The large error derives from the smallness of this parameter which makes this measurement very challenging [209]. This observable is directly connected to the LO pion-nucleon PVTC coupling constant . However, as we have seen, the theoretical estimate of the proportionality coefficient has been obtained with a relatively large theoretical uncertainty due to sizeable cancellations between different contributions. Therefore, to infer information from this observable, it will be necessary to make progress in both the experimental and theoretical analyses.
Other important information is brought forth by the three measurements at different energies of the -p longitudinal asymmetry. This observable is sensitive to via the TPE component of the PVTC potential and also to other LECs. In fact, owing to the isospin quantum numbers T = 1, Tz = 1 of the p-p system, the LO contribution vanishes. Moreover, at NLO (N2LO), this observable depends on two (three) combinations of the LECs. Unfortunately, only two of the performed measurements give independent information. These two data have not been obtained with enough accuracy, so the constraints to the (combinations of) LECs which can be obtained are not so stringent [42, 46], as discussed in section 6.2. For this observable the wave functions are easily obtained. However, the vanishing of the LO contribution makes the χPT convergence more uncertain. On the other hand, it would be very useful to have more accurate experimental measurements.
Very recently, a measurement of the -3He longitudinal asymmetry at the SNS facility was reported [222]. For this A = 4 system it is possible to perform accurate calculations of the wave functions, and therefore this observable can give valuable information in particular on the LECs Ci. A complete calculation, however, should also include the PVTC 3N interaction terms.
Regarding the spin rotation observables, no experiments to measure the -p and -d spin rotation angles, which could provide useful information on some of the contact term LECs, are planned at present. The experimental detection of a non-vanishing -p spin rotation would be rather important for two reasons: i) the theoretical treatment of the two-nucleon system does not present any difficulty numerically, while ii) this observable is sensitive to the LO term and therefore the chiral expansion of the potential is well under control, as discussed in section 6.4. Regarding the -d spin rotation, the same is not completely true since, as discussed in section 3.4 one has to include also the PVTC 3N interaction terms which start to appear at N2LO. This is an interesting extension of χEFT which will be considered in the future. From the experimental point of view, we note that there is an existing experiment trying to measure the -4He spin rotation at NIST [233]. Some years ago there was a measurement of the longitudinal asymmetry in -4He scattering, but this experiment was performed at a rather high energy of the proton beam (46 MeV) [234] and this makes the theoretical treatment very difficult and impossible without some approximations. From the theoretical point of view, recently there has been a rapid progress in solving accurately the A = 5 nuclear problem. In particular, the solution of A = 5 Faddeev-Yakubovsky equations [235, 236] has allowed a first study of the -4He spin rotation [237]. Also accurate applications using the so called “No-Core-Shell-Model with Continuum” technique have been reported [238, 239]. Therefore, we expect that, once the experimental value for the -4He spin rotation becomes available, it can be readily analyzed in the χEFT, pionless, and DDH frameworks.
To have the possibility to pin down all the LECs (6 LECs at NLO and 5 more at N2LO) more experimental information will be necessary in any case. In particular, an interesting possibility would be to measure PVTC observables in the A = 3 system, such as the longitudinal asymmetry of -d elastic scattering and the photon asymmetry in -d radiative capture. For both reactions, the theoretical treatment would be straightforward, once the PVTC 3N force has been taken into account. Experimental activities for the A = 3 systems were already attempted some years ago [240] (see also [39]). After the success of the recent PVTC observable measurements in A = 2 and A = 4 systems discussed previously, a successful experimental investigation of A = 3 observables appears to be possible. Actually, the measurement of the longitudinal photon asymmetry in -d radiative capture is currently being planned [241]. Therefore, a new campaign of measurements of PVTC observables in the A = 3 systems, in addition to the measure of the -4He spin rotation, would furnish enough information to fix (at least, some of) the LECs of the potentials in the different frameworks.
It would be clearly very interesting to take into account also PVTC measurements in medium-mass and heavy-systems. In particular, it is worth to mention that there exist fairly accurate measurements of the gamma angular asymmetry in 19F gamma decay and the gamma circular polarization in 18F gamma decay [242–244]. The mixing induced by the PVTC interaction in the matrix elements can be calibrated by the corresponding analog β decays of Ne isotopes [242]. Despite the large number of nucleons involved, the theoretical analysis can still be reliably performed. Calculations for these transitions have been performed only using the DDH interaction [37, 245].
Regarding the PVTV observables, the measurement of EDMs of particles is the most promising observable for studying CP violation beyond CKM mixing matrix effects. Currently, there are proposals for the direct measurement of EDMs of electrons, single nucleons and light nuclei in dedicated storage rings [77, 78, 81, 82, 246]. This new approach plans to reach an accuracy of ~10−16 e fm, improving the sensitivity in particular in the hadronic sector. Any measurement of a non-vanishing EDM of this magnitude would provide evidence of PVTV beyond CKM effects [52, 55–57]. However, a single measurement will be insufficient to identify the source of PVTV, only the availability of the measurement of EDM of various light nuclei such as 2H, 3H, and 3He can impose constrains on all the LECs. Other light nuclear EDMs have been discussed in Yamanaka [208] and Yamanaka et al. [247]. EDMs of heavy diamagnetic systems provide very important information as well, but such systems are too large for chiral EFT calculations.
Other observables sensitive to PVTV effects are the transmission of polarized neutrons through a polarized target [248, 249]. In particular, for heavy nuclei the PVTV effects can be enhanced by factors as large as 106 [250, 251], see also [252]. In order to exploit this enhancement, some experiments are being planned, such as the NOPTREX experiment at RIKEN [253, 254]. Also polarized nucleon—polarized deuteron scattering has been proposed as a way to detect PVTV signals [226, 255]. Finally, searching for large P- and T-violations in polarized β-decay of 8Li via measurement of the triple vector correlation is under consideration [256]. Clearly, it would be important to be able to detect a non-zero PVTV signal in all these experiments in order to pin down the values of all the LECs.
From the theoretical point of view, calculations of the EDM of 2H, 3H, and 3He can be performed very accurately, including taking into account the contributions of the PVTV 3N force. The robustness of the calculation has been checked by evaluating the EDMs of the nuclei to different chiral orders in the PCTC potential. The discrepancy between the use of the N2LO and the N4LO PCTC potential has been found to be approximately 5% [75].
Currently, the only missing ingredient is the two-body PVTV N2LO currents [73, 143]. Once this problem is solved, one can achieve a fully consistent calculation of the EDM of light nuclei up to N2LO. There are also plans to perform theoretical studies of PVTV observables in - and - scattering in order to have independent and complementary information about PVTV effects.
The PVTV χEFT interaction developed in the previous sections depends on 11 coupling constants that need to be determined by comparing with experimental data. As already pointed out by many authors [65, 68, 69] and discussed in section 3.2.1, the LECs ḡ2, , , and are suppressed for all CP-violation sources. However, for certain sources, this suppression is not too severe. For example, in Bsaisou et al. [66], an analysis of the nuclear EDM in the minimal left-right scenario is presented in which the Lagrangian terms with LECs and appear at N2LO. In any case, since the CP-violation sources are not known, the only way to determine them is to fit all possible LECs and compare the results with predictions for various scenarios.
Most of the observables discussed so far were obtained (or they are planned to be studied) at low energies, where also the pionless EFT framework is valid. The advantage of this framework is related to the fact that the resulting potentials depends on only five LECs. Then, assuming the validity of the large Nc analysis [47, 49], the number of dominant LECs could be further reduced. This new paradigm is advocated for the PVTC case in Gardner et al. [39]. For this case, only two LECs are expected to be dominant, the other three demoted to be subleading. Unfortunately, the photon asymmetry of depends on the subleading LECs (this could explain its relative smallness) and therefore cannot be used to give information on the two leading LECs. Moreover, only the low energy -p longitudinal asymmetry measurement may be used to test if this hierarchy is realized in Nature (the other measurement is taken at too high energy to be used in the pionless EFT framework). The other observable which can give valuable information is the -3He longitudinal asymmetry, for which the experimental result was just published. However, no theoretical calculations of this observable performed in the framework of pionless EFT are available at present. Additional information could be obtained by calculations of these LECs using Lattice QCD, presently in progress. Regarding the PVTV observables in pionless EFT, here the large Nc analysis predicts that only one of the LECs should be dominant, the other four being suppressed. However, this picture is partially obscured by the fact that the magnitude of the five contact LECs would depend very much on the particular type of the CP-violating source.
In conclusions, the study of PVTC and PVTV observables is an active area of research that provide important tests of the SM and hopefully future evidence for BSM physics.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
JV was supported by the RHIC Physics Fellow Program of the RIKEN BNL Research Center. EE was supported by BMBF (Grant No. 05P18PCFP1) and by DFG through funds provided to the Sino-German CRC 110 Symmetries and the Emergence of Structure in QCD (Grant No. TRR110). EM was supported in part by the LDRD program at Los Alamos National Laboratory, the DOE topical collaboration on Nuclear Theory for Double-Beta Decay and Fundamental Symmetries, the US DOE, Office of Science, Office of Nuclear Physics, under award numbers DE-AC52-06NA25396. LG, AG, and MV were supported by INFN through the National Initiative FBS.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer BH declared a shared affiliation, with no collaboration, with one of the authors, JV, to the handling editor at time of review.
Footnotes
1. ^Here and in what follows, we restrict ourselves to the two-flavor case of the light up and down quarks unless specified otherwise.
2. ^In the isospin limit, the quark and pion masses are related to each other via , where B is a constant proportional to the quark condensate .
3. ^Notice that for systems near the unitary limit corresponding to the infinitely large scattering length (such as e.g., the NN systems in the S-waves), the scattering amplitude exhibits a certain amount of fine tuning beyond naive dimensional analysis. The expansion of the scattering amplitude does, therefore, not necessarily coincide with the expansion of nuclear potentials [15].
4. ^Notice that PVTC hadronic interactions involve a typical suppression factor of as compared to PCTC vertices [43].
5. ^Here u and d denote the u- and d-quark Dirac fields, respectively. Moreover , etc.
6. ^ḡ0 and contribute to the deuteron EDM in conjunction with isospin breaking in the strong interaction, or via the spin-orbit coupling of the photon to the nucleons [143]. Both contributions are beyond the accuracy we work at in this paper.
7. ^More appropriately, these Lagrangian terms should be written in terms of four-gradients. For example
where [,] denotes the commutator.
8. ^Notice that the values of the LECs ci obtained from the pion-nucleon amplitude at NLO, which would be appropriate for , are considerably smaller in magnitude. We, however, decided to adopt the larger values to be consistent with the employed PCTC potential.
References
1. Machleidt R. Historical perspective and future prospects for nuclear interactions. Int J Mod Phys E. (2017) 26:1730005. doi: 10.1142/S0218301317300053
2. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3
3. Ordonez C, Ray L, van Kolck U. The Two nucleon potential from chiral Lagrangians. Phys Rev C. (1996) 53:2086–105. doi: 10.1103/PhysRevC.53.2086
4. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
5. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
6. Weinberg S. Pion scattering lengths. Phys Rev Lett. (1966) 17:616–21. doi: 10.1103/PhysRevLett.17.616
7. Weinberg S. Nonlinear realizations of chiral symmetry. Phys Rev. (1968) 166:1568–77. doi: 10.1103/PhysRev.166.1568
8. Weinberg S. Phenomenological Lagrangians. Physica A. (1979) 96:327–40. doi: 10.1016/0378-4371(79)90223-1
9. Coleman SR, Wess J, Zumino B. Structure of phenomenological Lagrangians. 1. Phys Rev. (1969) 177:2239–47. doi: 10.1103/PhysRev.177.2239
10. Callan CG Jr., Coleman SR, Wess J, Zumino B. Structure of phenomenological Lagrangians. 2. Phys Rev. (1969) 177:2247–50. doi: 10.1103/PhysRev.177.2247
11. Gasser J, Leutwyler H. Chiral perturbation theory to one loop. Ann Phys. (1984) 158:142. doi: 10.1016/0003-4916(84)90242-2
12. Bernard V, Kaiser N, Meißner UG. Chiral dynamics in nucleons and nuclei. Int J Mod Phys E. (1995) 4:193–346. doi: 10.1142/S0218301395000092
13. Bernard V. Chiral perturbation theory and baryon properties. Prog Part Nucl Phys. (2008) 60:82–60. doi: 10.1016/j.ppnp.2007.07.001
14. Bijnens J, Ecker G. Mesonic low-energy constants. Ann Rev Nucl Sci. (2014) 64:149–74. doi: 10.1146/annurev-nucl-102313-025528
15. Epelbaum E, Gegelia J, Meißner UG. Wilsonian renormalization group versus subtractive renormalization in effective field theories for nucleon–nucleon scattering. Nucl Phys. (2017) B925:161–85. doi: 10.1016/j.nuclphysb.2017.10.008
16. Entem DR, Kaiser N, Machleidt R, Nosyk Y. Peripheral nucleon-nucleon scattering at fifth order of chiral perturbation theory. Phys Rev C. (2015) 91:014002. doi: 10.1103/PhysRevC.91.014002
17. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301
18. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004
19. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A. (2018) 54:86. doi: 10.1140/epja/i2018-12516-4
20. Kaplan DB, Savage MJ, Wise MB. A New expansion for nucleon-nucleon interactions. Phys Lett B. (1998) 424:390–6. doi: 10.1016/S0370-2693(98)00210-X
21. Nogga A, Timmermans RGE, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev C. (2005) 72:054006. doi: 10.1103/PhysRevC.72.054006
22. Birse MC. Power counting with one-pion exchange. Phys Rev C. (2006) 74:014003. doi: 10.1103/PhysRevC.74.014003
23. Valderrama MP. Perturbative renormalizability of chiral two pion exchange in nucleon-nucleon scattering. Phys Rev C. (2011) 83:024003. doi: 10.1103/PhysRevC.83.024003
24. Long B, Yang CJ. Short-range nuclear forces in singlet channels. Phys Rev C. (2012) 86:024001. doi: 10.1103/PhysRevC.86.024001
25. Epelbaum E, Gegelia J. Weinberg′s approach to nucleon–nucleon scattering revisited. Phys Lett B. (2012) 716:338–44. doi: 10.1016/j.physletb.2012.08.025
26. Lepage GP. How to renormalize the Schrodinger equation. In: Nuclear Physics. Proceedings, 8th Jorge Andre Swieca Summer School, Sao Jose dos Campos, Campos do Jordao. Brazil (1997). p. 135–80.
27. Epelbaum E, Meißner UG. On the renormalization of the one-pion exchange potential and the consistency of Weinberg's power counting. Few Body Syst. (2013) 54:2175–90. doi: 10.1007/s00601-012-0492-1
28. Epelbaum E, Gegelia J. Regularization, renormalization and ‘peratization’ in effective field theory for two nucleons. Eur Phys J. (2009) A41:341–54. doi: 10.1140/epja/i2009-10833-3
29. Valderrama MP. Power counting and Wilsonian Renormalization in Nuclear Effective Field Theory. Int J Mod Phys E. (2016) 25:1641007. doi: 10.1142/S021830131641007X
30. Epelbaum E, Gasparyan AM, Gegelia J, Meißner UG. How (not) to renormalize integral equations with singular potentials in effective field theory. Eur Phys J A. (2018) 54:186. doi: 10.1140/epja/i2018-12632-1
31. Hammer HW, König S, van Kolck U. Nuclear effective field theory: status and perspectives. arXiv:1906 [Preprint].12122 (2019).
32. Bedaque PF, van Kolck U. Effective field theory for few nucleon systems. Ann Rev Nucl Sci. (2002) 52:339–96. doi: 10.1146/annurev.nucl.52.050102.090637
33. Hammer HW, Platter L. Efimov States in Nuclear and Particle Physics. Ann Rev Nucl Sci. (2010) 60:207–36. doi: 10.1146/annurev.nucl.012809.104439
34. Ramsey-Musolf MJ, Page SA. Hadronic parity violation: a new view through the looking glass. Ann Rev Nucl Sci. (2006) 56:1–52. doi: 10.1146/annurev.nucl.54.070103.181255
35. Hertzog D, Ramsey-Musolf MJ. Parity- and time-reversal tests in nuclear physics. In: Henley EM, Ellis SD, editors. 100 Years of Subatomic Physics. Singapore: World Scientific (2013) p. 155–70. doi: 10.1142/9789814425810_0006
36. Schindler MR, Springer RP. The theory of parity violation in few-nucleon systems. Prog Part Nucl Phys. (2013) 72:1–43. doi: 10.1016/j.ppnp.2013.05.002
37. Haxton WC, Holstein BR. Hadronic parity violation. Prog Part Nucl Phys. (2013) 71:185–203. doi: 10.1016/j.ppnp.2013.03.009
38. de Vries J, Meißner UG. Violations of discrete space–time symmetries in chiral effective field theory. Int J Mod Phys E. (2016) 25:1641008. doi: 10.1142/S0218301316410081
39. Gardner S, Haxton WC, Holstein BR. A new paradigm for hadronic parity nonconservation and its experimental implications. Ann Rev Nucl Sci. (2017) 67:69–95. doi: 10.1146/annurev-nucl-041917-033231
40. Zhu SL, Maekawa CM, Holstein BR, Ramsey-Musolf MJ, van Kolck U. Nuclear parity-violation in effective field theory. Nucl Phys A. (2005) 748:435–98. doi: 10.1016/j.nuclphysa.2004.10.032
41. de Vries J, Meißner UG, Epelbaum E, Kaiser N. Parity violation in proton-proton scattering from chiral effective field theory. Eur Phys J. (2013) A49:149. doi: 10.1140/epja/i2013-13149-9
42. Viviani M, Baroni A, Girlanda L, Kievsky A, Marcucci LE, Schiavilla R. Chiral effective field theory analysis of hadronic parity violation in few-nucleon systems. Phys Rev C. (2014) 89:064004. doi: 10.1103/PhysRevC.89.064004
43. Adelberger EG, Haxton WC. Parity violation in the nucleon-nucleon interaction. Ann Rev Nucl Part Sci. (1985) 35:501–58. doi: 10.1146/annurev.ns.35.120185.002441
44. Girlanda L. On a redundancy in the parity-violating 2-nucleon contact Lagrangian. Phys Rev. (2008) C77:067001. doi: 10.1103/PhysRevC.77.067001
45. Danilov GS. Circular polarization of γ quanta in absorption of neutrons by protons and isotopic structure of weak interactions. Phys Lett. (1965) 18:40–41. doi: 10.1016/0031-9163(65)90024-7
46. de Vries J, Li N, Meißner UG, Kaiser N, Liu XH, Zhu SL. A study of the parity-odd nucleon-nucleon potential. Eur Phys J A. (2014) 50:108. doi: 10.1140/epja/i2014-14108-8
47. Schindler MR, Springer RP, Vanasse J. Large-Nc limit reduces the number of independent few-body parity-violating low-energy constants in pionless effective field theory. Phys Rev C. (2016) 93:025502. doi: 10.1103/PhysRevC.93.025502
48. Phillips DR, Samart D, Schat C. Parity-violating nucleon-nucleon force in the 1/Nc expansion. Phys Rev Lett. (2015) 114:062301. doi: 10.1103/PhysRevLett.114.062301
49. Vanasse J. Parity-violating three-nucleon interactions at low energies and large NC. Phys Rev C. (2019) 99:054001. doi: 10.1103/PhysRevC.99.054001
50. Desplanques B, Donoghue JF, Holstein BR. Unified treatment of the parity violating nuclear force. Annals Phys. (1980) 124:449. doi: 10.1016/0003-4916(80)90217-1
51. 't Hooft G. Symmetry breaking through Bell-Jackiw anomalies. Phys Rev Lett. (1976) 37:8–11. doi: 10.1103/PhysRevLett.37.8
52. Pospelov M, Ritz A. Electric dipole moments as probes of new physics. Ann Phys. (2005) 318:119–69. doi: 10.1016/j.aop.2005.04.002
53. Sakharov AD. Violation of CP Invariance, C asymmetry, and baryon asymmetry of the universe. Pisma Zh Eksp Teor Fiz. (1967) 5:32–5.
54. Cohen AG, Kaplan DB, Nelson AE. Progress in electroweak baryogenesis. Ann Rev Nucl Sci. (1993) 43:27–70. doi: 10.1146/annurev.ns.43.120193.000331
55. Czarnecki A, Krause B. Neutron electric dipole moment in the standard model: valence quark contributions. Phys Rev Lett. (1997) 78:4339–42. doi: 10.1103/PhysRevLett.78.4339
56. Mannel T, Uraltsev N. Loop-less electric dipole moment of the nucleon in the standard model. Phys Rev D. (2012) 85:096002. doi: 10.1103/PhysRevD.85.096002
57. Mannel T, Uraltsev N. Charm CP Violation and the electric dipole moments from the charm scale. J High Energy Phys. (2013) 03:64. doi: 10.1007/JHEP03(2013)064
58. Wirzba A, Bsaisou J, Nogga A. Permanent electric dipole moments of single-, two-, and three-nucleon systems. Int J Mod Phys E. (2017) 26:1740031. doi: 10.1142/S0218301317400316
59. Seng CY. Reexamination of the standard model nucleon electric dipole moment. Phys Rev C. (2015) 91:025502. doi: 10.1103/PhysRevC.91.025502
60. Baker CA, Doyle DD, Geltenbort P, Green K, van der Grinten MGD, Harris PG, et al. An improved experimental limit on the electric dipole moment of the neutron. Phys Rev Lett. (2006) 97:131801. doi: 10.1103/PhysRevLett.97.131801
61. Pendlebury JM, Afach S, Ayres NJ, Baker CA, Ban G, Bison G, et al. Revised experimental upper limit on the electric dipole moment of the neutron. Phys Rev D. (2015) 92:092003. doi: 10.1103/PhysRevD.92.092003
62. Graner B, Chen Y, Lindahl EG, Heckel BR. Reduced limit on the permanent electric dipole moment of Hg199. Phys Rev Lett. (2016) 116:161601. doi: 10.1103/PhysRevLett.116.161601
63. Dmitriev VF, Sen'kov RA. Schiff moment of the mercury nucleus and the proton dipole moment. Phys Rev Lett. (2003) 91:212303. doi: 10.1103/PhysRevLett.91.212303
64. Andreev V, Ang DG, DeMille D, Doyle JM, Gabrielse G, Haefner J, et al. Improved limit on the electric dipole moment of the electron. Nature. (2018) 562:355–60. doi: 10.1038/s41586-018-0599-8
65. Mereghetti E, Hockings WH, van Kolck U. The effective chiral Lagrangian from the theta term. Ann Phys. (2010) 325:2363–409. doi: 10.1016/j.aop.2010.03.005
66. Bsaisou J, de Vries J, Hanhart C, Liebig S, Meißner UG, Minossi D, et al. Nuclear electric dipole moments in chiral effective field theory. J High Energy Phys. (2015) 03:104. doi: 10.1007/JHEP05(2015)083
67. Grzadkowski B, Iskrzynski M, Misiak M, Rosiek J. Dimension-six terms in the standard model Lagrangian. J High Energy Phys. (2010) 10:085. doi: 10.1007/JHEP10(2010)085
68. de Vries J, Mereghetti E, Timmermans RGE, van Kolck U. The effective chiral Lagrangian from dimension-six parity and time-reversal violation. Annals Phys. (2013) 338:50–96. doi: 10.1016/j.aop.2013.05.022
69. Bsaisou J, Meißner UG, Nogga A, Wirzba A. P- and T-violating Lagrangians in chiral effective field theory and nuclear electric dipole moments. Ann Phys. (2015) 359:317–70. doi: 10.1016/j.aop.2015.04.031
70. de Vries J, Mereghetti E, Timmermans RGE, van Kolck U. Parity- and time-reversal-violating form factors of the deuteron. Phys Rev Lett. (2011) 107:091804. doi: 10.1103/PhysRevLett.107.091804
71. Dekens W, de Vries J, Bsaisou J, Bernreuther W, Hanhart C, Meißner UG, et al. Unraveling models of CP violation through electric dipole moments of light nuclei. J High Energy Phys. (2014) >07: 69. doi: 10.1007/JHEP07(2014)069
72. Maekawa CM, Mereghetti E, de Vries J, van Kolck U. The time-reversal- and parity-violating nuclear potential in chiral effective theory. Nucl Phys A. (2011) 872:117–60. doi: 10.1016/j.nuclphysa.2011.09.020
73. Bsaisou J, Hanhart C, Liebig S, Meißner UG, Nogga A, Wirzba A. The electric dipole moment of the deuteron from the QCD θ-term. Eur Phys J A. (2013) 49:31. doi: 10.1140/epja/i2013-13031-x
74. Epelbaum E, Glockle W, Meißner UG. The Two-nucleon system at next-to-next-to-next-to-leading order. Nucl Phys A. (2005) 747:362–424. doi: 10.1016/j.nuclphysa.2004.09.107
75. Gnech A, Viviani M. Time reversal violation in light nuclei. Phys Rev C. (2020) 101:024004 doi: 10.1103/PhysRevC.101.024004
76. Dobaczewski J, Engel J, Kortelainen M, Becker P. Correlating Schiff moments in the light actinides with octupole moments. Phys Rev Lett. (2018) 121:232501. doi: 10.1103/PhysRevLett.121.232501
77. Orlov YF, Morse WM, Semertzidis YK. Resonance method of electric-dipole-moment measurements in storage rings. Phys Rev Lett. (2006) 96:214802. doi: 10.1103/PhysRevLett.96.214802
78. Semertzidis YK. A storage ring proton electric dipole moment experiment: most sensitive experiment to CP-violation beyond the standard model. In: Particles and Fields. Proceedings, Meeting of the Division of the American Physical Society, DPF 2011. Providence, RI (2011).
79. Lehrach A, Lorentz B, Morse W, Nikolaev N, Rathmann F. Precursor experiments to search for permanent electric dipole moments (EDMs) of protons and deuterons at COSY. arXiv preprint arXiv:1201.5773 (2012).
80. Pretz J. Measurement of permanent electric dipole moments of charged hadrons in storage rings. Hyperfine Interact. (2013) 214:111–117. doi: 10.1007/s10751-013-0799-4
81. Rathmann F, Saleev A, Nikolaev NN. The search for electric dipole moments of light ions in storage rings. J Phys Conf Ser. (2013) 447:012011. doi: 10.1088/1742-6596/447/1/012011
82. Abusaif F, Aggarwal A, Aksentev A, Alberdi-Esuain B, Atanasov A, Barion L, et al. Storage ring to search for electric dipole moments of charged particles-feasibility study. arXiv preprint arXiv:1912.07881 (2019).
83. Wu CS, Ambler E, Hayward RW, Hoppes DD, Hudson RP. Experimental test of parity conservation in beta decay. Phys Rev. (1957) 105:1413–4. doi: 10.1103/PhysRev.105.1413
84. Prescott CY, Atwood WB, Leslie Cottrell R, DeStaebler HC, Garwin EL, Gonidec A, et al. Parity nonconservation in inelastic electron scattering. Phys Lett B. (1978) 77:347–52. doi: 10.2172/5786614
85. Androić D, Armstrong DS, Asaturyan A, Averett T, Balewski J, Bartlett K, et al. Precision measurement of the weak charge of the proton. Nature. (2018) 557:207–11. doi: 10.1038/s41586-018-0096-0
86. Tiburzi BC. Hadronic parity violation at next-to-leading order. Phys Rev D. (2012) 85:054020. doi: 10.1103/PhysRevD.85.054020
87. Buchmuller W, Wyler D. Effective lagrangian analysis of new interactions and flavor conservation. Nucl Phys B. (1986) 268:621–53. doi: 10.1016/0550-3213(86)90262-2
88. Kaplan DB, Savage MJ. An analysis of parity violating pion - nucleon couplings. Nucl Phys A. (1993) 556:653–71. doi: 10.1016/0375-9474(93)90475-D
89. Christenson JH, Cronin JW, Fitch VL, Turlay R. Evidence for the 2π decay of the meson. Phys Rev Lett. (1964) 13:138–40. doi: 10.1103/PhysRevLett.13.138
90. Abouzaid E, Arenton M, Barker AR, Barrio M, Bellantoni L, Blucher E, et al. Precise measurements of direct CP violation, CPT symmetry, and other parameters in the neutral kaon system. Phys Rev D. (2011) 83:092001. doi: 10.1103/PhysRevD.83.092001
91. Batley JR, Dosanjh RS, Gershon TJ, Kalmus GE, Lazzeroni C, Munday DJ, et al. A Precision measurement of direct CP violation in the decay of neutral kaons into two pions. Phys Lett B. (2002) 544:97–112. doi: 10.1016/S0370-2693(02)02416-4
92. Aubert B, Boutigny D, Gaillard JM, Hicheur A, Karyotakis Y, Lees JP, et al. Observation of CP violation in the B0 meson system. Phys Rev Lett. (2001) 87:091801. doi: 10.1103/PhysRevLett.87.091801
93. Abe K, Abe K, Abe R, Adachi I, Ahn BS, Aihara H, et al. Observation of large CP violation in the neutral B meson system. Phys Rev Lett. (2001) 87:091802. doi: 10.1103/PhysRevLett.87.091802
94. Aaij R, Abellan Beteta C, Adeva B, Adinolfi M, Aidala CA, Ajaltouni Z, et al. Observation of CP violation in charm decays. Phys Rev Lett. (2019) 122:211803. doi: 10.1103/PhysRevLett.122.211803
95. Khriplovich IB, Zhitnitsky AR. What is the value of the neutron electric dipole moment in the Kobayashi-Maskawa model? Phys Lett B. (1982) 109:490–2. doi: 10.1016/0370-2693(82)91121-2
96. Pospelov ME, Khriplovich IB. Electric dipole moment of the W Boson and the electron in the Kobayashi-Maskawa model. Sov J Nucl Phys. (1991) 53:638–40.
97. Booth MJ. The Electric dipole moment of the W and electron in the Standard Model. arXiv preprint arXiv:hep-ph/9301293 (1993).
98. Pospelov M, Ritz A. CKM benchmarks for electron electric dipole moment experiments. Phys Rev D. (2014) 89:056006. doi: 10.1103/PhysRevD.89.056006
99. Callan CG Jr., Dashen RF, Gross DJ. The structure of the gauge theory vacuum. Phys Lett B. (1976) 63:334–40. doi: 10.1016/0370-2693(76)90277-X
100. 't Hooft G. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys Rev D. (1976) 14:3432–50. doi: 10.1103/PhysRevD.14.3432
101. Baluni V. CP Violating effects in QCD. Phys Rev D. (1979) 19:2227–30. doi: 10.1103/PhysRevD.19.2227
102. Crewther RJ, Di Vecchia P, Veneziano G, Witten E. Chiral estimate of the electric dipole moment of the neutron in quantum chromodynamics. Phys Lett B. (1979) 88:123. doi: 10.1016/0370-2693(79)90128-X
103. Dragos J, Luu T, Shindler A, de Vries J, Yousif A. Confirming the existence of the strong CP problem in lattice QCD with the gradient flow. arXiv preprint arXiv:1902.03254 (2019).
104. Gavela MB, Hernandez P, Orloff J, Pene O. Standard model CP violation and baryon asymmetry. Mod Phys Lett A. (1994) 9:795–810. doi: 10.1142/S0217732394000629
105. Gavela MB, Lozano M, Orloff J, Pene O. Standard model CP violation and baryon asymmetry. Part 1: Zero temperature. Nucl Phys B. (1994) 430:345–81. doi: 10.1016/0550-3213(94)00409-9
106. Gavela MB, Hernandez P, Orloff J, Pene O, Quimbay C. Standard model CP violation and baryon asymmetry. Part 2: Finite temperature. Nucl Phys B. (1994) 430:382–426. doi: 10.1016/0550-3213(94)00410-2
107. Huet P, Sather E. Electroweak baryogenesis and standard model CP violation. Phys Rev D. (1995) 51:379–94. doi: 10.1103/PhysRevD.51.379
108. Khriplovich IB, Lamoreaux SK. CP Violation Without Strangeness: Electric Dipole Moments of Particles, Atoms, and Molecules. Berlin: Springer. (1997). doi: 10.1007/978-3-642-60838-4
109. Dekens W, de Vries J. Renormalization group running of dimension-six sources of parity and time-reversal violation. J High Energy Phys. (2013) 05:149. doi: 10.1007/JHEP05(2013)149
110. Engel J, Ramsey-Musolf MJ, van Kolck U. Electric dipole moments of nucleons, nuclei, and atoms: the standard model and beyond. Prog Part Nucl Phys. (2013) 71:21–74. doi: 10.1016/j.ppnp.2013.03.003
111. Jenkins EE, Manohar AV, Stoffer P. Low-energy effective field theory below the electroweak scale: operators and matching. J High Energy Phys. (2018) 03:016. doi: 10.1007/JHEP03(2018)016
112. Mereghetti E. Electric dipole moments: a theory overview. In: 13th Conference on the Intersections of Particle and Nuclear Physics (CIPANP 2018). Palm Springs, CA (2018).
113. Weinberg S. Larger Higgs exchange terms in the neutron electric dipole moment. Phys Rev Lett. (1989) 63:2333. doi: 10.1103/PhysRevLett.63.2333
114. Fuyuto K, Ramsey-Musolf M, Shen T. Electric dipole moments from CP-violating scalar Leptoquark interactions. Phys Lett B. (2019) 788:52–7. doi: 10.1016/j.physletb.2018.11.016
115. Dekens W, de Vries J, Jung M, Vos KK. The phenomenology of electric dipole moments in models of scalar leptoquarks. J High Energy Phys. (2019) 01:69. doi: 10.1007/JHEP01(2019)069
116. Ng J, Tulin S. D versus d: CP violation in beta decay and electric dipole moments. Phys Rev D. (2012) 85:033001. doi: 10.1103/PhysRevD.85.033001
117. Jenkins EE, Manohar AV. Baryon chiral perturbation theory using a heavy fermion Lagrangian. Phys Lett B. (1991) 255:558–62. doi: 10.1016/0370-2693(91)90266-S
118. Baroni A, Girlanda L, Pastore S, Schiavilla R, Viviani M. Nuclear axial currents in chiral effective field theory. Phys Rev C. (2016) 93:015501. doi: 10.1103/PhysRevC.93.015501
119. Kaplan DB, Savage MJ, Springer RP, Wise MB. An Effective field theory calculation of the parity violating asymmetry in . Phys Lett B. (1999) 449:1–5. doi: 10.1016/S0370-2693(99)00032-5
120. Manohar A, Georgi H. Chiral quarks and the nonrelativistic quark model. Nucl Phys B. (1984) 234:189–212. doi: 10.1016/0550-3213(84)90231-1
121. Michel FC. Parity Nonconservation in nuclei. Phys Rev. (1964) 133:B329-B349. doi: 10.1103/PhysRev.133.B329
122. Donoghue JF, Golowich E, Holstein BR. Dynamics of the standard model. Camb Monogr Part Phys Nucl Phys Cosmol. (1992) 2:1–540.
123. McKellar BHJ. The one pion exchange contribution to the weak parity violating nucleon-nucleon potential. Phys Lett B. (1967) 26:107–8. doi: 10.1016/0370-2693(67)90561-8
124. Fischbach E. Application of current algebra and partially conserved axial-vector current to the weak BBpi vertex. Phys Rev. (1968) 170:1398–400. doi: 10.1103/PhysRev.170.1398
125. Tadic D. Weak parity-nonconserving potentials. Phys Rev. (1968) 174:1694–703. doi: 10.1103/PhysRev.174.1694
126. Kummer W, Schweda M. An SU(6) estimate of the effective nonleptonic parity-violating coupling in strangeness-conserving weak processes. Acta Phys Austriaca. (1968) 28:303–8.
127. Mckellar BHJ, Pick P. Pion-pole dominance of the divergence of the weak parity-nonconserving NN rho amplitude. Phys Rev D. (1972) 6:2184–8. doi: 10.1103/PhysRevD.6.2184
128. Dubovik VM, Zenkin SV. Formation of parity nonconserving nuclear forces in the standard model SU(2)(l) X U(1) X SU(3)(c). Ann Phys. (1986) 172:100–35. doi: 10.1016/0003-4916(86)90021-7
129. Feldman GB, Crawford GA, Dubach J, Holstein BR. Delta contributions to the parity violating nuclear interaction. Phys Rev C. (1991) 43:863–74. doi: 10.1103/PhysRevC.43.863
130. Meißner UG, Weigel H. The Parity violating pion nucleon coupling constant from a realistic three flavor Skyrme model. Phys Lett B. (1999) 447:1–7. doi: 10.1016/S0370-2693(98)01569-X
131. Haeberli W, Holstein BR. Parity violation and the nucleon-nucleon system. arXiv preprint arXiv:nucl-th/9510062 (1995). doi: 10.1142/9789812831446_0002
132. Wasem J. Lattice QCD calculation of nuclear parity violation. Phys Rev C. (2012) 85:022501. doi: 10.1103/PhysRevC.85.022501
133. Cheng HY. Reanalysis of strong CP violating effects in chiral perturbation theory. Phys Rev D. (1991) 44:166–74. doi: 10.1103/PhysRevD.44.166
134. Pich A, de Rafael E. Strong CP violation in an effective chiral Lagrangian approach. Nucl Phys B. (1991) 367:313–33. doi: 10.1016/0550-3213(91)90019-T
135. Cho PL. Chiral estimates of strong CP violation revisited. Phys Rev D. (1993) 48:3304–9. doi: 10.1103/PhysRevD.48.3304
136. Borasoy B. The Electric dipole moment of the neutron in chiral perturbation theory. Phys Rev D. (2000) 61:114017. doi: 10.1103/PhysRevD.61.114017
137. Ottnad K, Kubis B, Meißner UG, Guo FK. New insights into the neutron electric dipole moment. Phys Lett B. (2010) 687:42–7. doi: 10.1016/j.physletb.2010.03.005
138. Liu CP, de Vries J, Mereghetti E, Timmermans RGE, van Kolck U. Deuteron magnetic quadrupole moment from chiral effective field theory. Phys Lett B. (2012) 713:447–52. doi: 10.1016/j.physletb.2012.06.024
139. Peccei RD, Quinn HR. CP conservation in the presence of instantons. Phys Rev Lett. (1977) 38:1440–3. doi: 10.1103/PhysRevLett.38.1440
140. Mereghetti E, van Kolck U. Effective field theory and time-reversal violation in light nuclei. Ann Rev Nucl Sci. (2015) 65:215–43. doi: 10.1146/annurev-nucl-102014-022344
141. Cirigliano V, Dekens W, de Vries J, Mereghetti E. An ϵ′ improvement from right-handed currents. Phys Lett B. (2017) 767:1–9. doi: 10.1016/j.physletb.2017.01.037
142. Liu CP, Timmermans RGE. P- and T-odd two-nucleon interaction and the deuteron electric dipole moment. Phys Rev C. (2004) 70:055501. doi: 10.1103/PhysRevC.70.055501
143. de Vries J, Higa R, Liu CP, Mereghetti E, Stetcu I, Timmermans RGE, et al. Electric dipole moments of light nuclei from chiral effective field theory. Phys Rev C. (2011) 84:065501. doi: 10.1103/PhysRevC.84.065501
144. de Vries J, Mereghetti E, Walker-Loud A. Baryon mass splittings and strong CP violation in SU(3) chiral perturbation theory. Phys Rev C. (2015) 92:045201. doi: 10.1103/PhysRevC.92.045201
145. Borsanyi S, Durr S, Fodor Z, Hoelbling C, Katz SD, Krieg S, et al. Ab initio calculation of the neutron-proton mass difference. Science. (2015) 347:1452–5. doi: 10.1126/science.1257050
146. Brantley DA, Joo B, Mastropas EV, Mereghetti E, Monge-Camacho H, Tiburzi BC, et al. Strong isospin violation and chiral logarithms in the baryon spectrum. arXiv preprint arXiv:1612.07733 (2016).
147. de Vries J, Mereghetti E, Seng CY, Walker-Loud A. Lattice QCD spectroscopy for hadronic CP violation. Phys Lett B. (2017) 766:254–62. doi: 10.1016/j.physletb.2017.01.017
148. Seng CY, Ramsey-Musolf M. Parity-violating and time-reversal-violating pion-nucleon couplings: Higher order chiral matching relations. Phys Rev C. (2017) 96:065204. doi: 10.1103/PhysRevC.96.065204
149. Pospelov M, Ritz A. Neutron EDM from electric and chromoelectric dipole moments of quarks. Phys Rev D. (2001) 63:073015. doi: 10.1103/PhysRevD.63.073015
150. Samart D, Schat C, Schindler MR, Phillips DR. Time-reversal-invariance-violating nucleon-nucleon potential in the 1/Nc expansion. Phys Rev C. (2016) 94:024001. doi: 10.1103/PhysRevC.94.024001
151. Guo FK, Horsley R, Meißner UG, Nakamura Y, Perlt H, Rakow PEL, et al. The electric dipole moment of the neutron from 2+1 flavor lattice QCD. Phys Rev Lett. (2015) 115:062001. doi: 10.1103/PhysRevLett.115.062001
152. Abramczyk M, Aoki S, Blum T, Izubuchi T, Ohki H, Syritsyn S. Lattice calculation of electric dipole moments and form factors of the nucleon. Phys Rev D. (2017) 96:014501. doi: 10.1103/PhysRevD.96.014501
153. Gupta R, Jang YC, Yoon B, Lin HW, Cirigliano V, Bhattacharya T. Isovector charges of the nucleon from 2+1+1-flavor Lattice QCD. Phys Rev D. (2018) 98:034503. doi: 10.1103/PhysRevD.98.034503
154. Aoki S, Aoki Y, Bečirevic D, Blum T, Colangelo G, Collins S, et al. FLAG review 2019: Flavour lattice averaging group (FLAG). Eur. Phys. J. C. (2020) 80:113. doi: 10.1140/epjc/s10052-019-7354-7
155. Kim J, Dragos J, Shindler A, Luu T, de Vries J. Towards a determination of the nucleon EDM from the quark chromo-EDM operator with the gradient flow. PoS LATTICE2018. (2019) 260. doi: 10.22323/1.334.0260
156. Rizik M, Monahan C, Shindler A. Renormalization of CP-Violating Pure Gauge Operators in Perturbative QCD Using the Gradient Flow. PoS LATTICE2018 (2018) 215. doi: 10.22323/1.334.0215
157. Mereghetti E, de Vries J, Hockings WH, Maekawa CM, van Kolck U. The electric dipole form factor of the nucleon in chiral perturbation theory to sub-leading order. Phys Lett B. (2011) 696:97–102. doi: 10.1016/j.physletb.2010.12.018
158. Haisch U, Hala A. Sum rules for CP-violating operators of Weinberg type. arXiv preprint arXiv:1909.08955 (2019). doi: 10.1007/JHEP11(2019)154
159. Epelbaum E, Meißner UG, Glöckle W. Nuclear forces in the chiral limit. Nucl Phys A. (2003) 714:535–74. doi: 10.1016/S0375-9474(02)01393-3
160. Krebs H, Epelbaum E, Meißner UG. Nuclear axial current operators to fourth order in chiral effective field theory. Ann Phys. (2017) 378:317–95. doi: 10.1016/j.aop.2017.01.021
161. Pastore S, Schiavilla R, Goity JL. Electromagnetic two-body currents of one- and two-pion range. Phys Rev C. (2008) 78:064002. doi: 10.1103/PhysRevC.78.064002
162. Pastore S, Girlanda L, Schiavilla R, Viviani M. The two-nucleon electromagnetic charge operator in chiral effective field theory (χEFT) up to one loop. Phys Rev C. (2011) 84:024001. doi: 10.1103/PhysRevC.84.024001
163. Krebs H, Epelbaum E, Meißner UG. Box diagram contribution to the axial two-nucleon current. arXiv preprint arXiv: 2001.03904 (2020). doi: 10.1103/PhysRevC.101.055502
164. Fukuda N, Sawada K, Taketani M. On the construction of potential in field theory. Prog Theor Phys. (1954) 12:156. doi: 10.1143/PTP.12.156
165. Okubo S. Diagonalization of Hamiltonian and Tamm-Dancoff equation. Prog Theor Phys. (1954) 12:603. doi: 10.1143/PTP.12.603
166. Epelbaum E, Glöckle W, Meißner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation. 1. Formalism. Nucl Phys A. (1998) 637:107–34. doi: 10.1016/S0375-9474(98)00220-6
167. Epelbaum E. Four-nucleon force using the method of unitary transformation. Eur Phys J A. (2007) 34:197–214. doi: 10.1140/epja/i2007-10496-0
168. Epelbaum E. Four-nucleon force in chiral effective field theory. Phys Lett B. (2006) 639:456–61. doi: 10.1016/j.physletb.2006.06.046
169. Bernard V, Epelbaum E, Krebs H, Meißner UG. Subleading contributions to the chiral three-nucleon force. I. Long-range terms. Phys Rev C. (2008) 77:064004. doi: 10.1103/PhysRevC.77.064004
170. Bernard V, Epelbaum E, Krebs H, Meißner UG. Subleading contributions to the chiral three-nucleon force II: short-range terms and relativistic corrections. Phys Rev C. (2011) 84:054001. doi: 10.1103/PhysRevC.84.054001
171. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO I: longest-range contributions. Phys Rev C. (2012) 85:054006. doi: 10.1103/PhysRevC.85.054006
172. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO II: intermediate-range contributions. Phys Rev C. (2013) 87:054007. doi: 10.1103/PhysRevC.87.054007
173. de Vries J, Li N, Meißner UG, Nogga A, Epelbaum E, Kaiser N. Parity violation in neutron capture on the proton: Determining the weak pion–nucleon coupling. Phys Lett B. (2015) 747:299–304. doi: 10.1016/j.physletb.2015.05.074
174. Gnech A. Parity and Time Reversal Violation in Two Nucleons Systems. University of Pisa, Pisa. (2016).
175. Kaiser N. Parity-violating two-pion exchange nucleon-nucleon interaction. Phys Rev C. (2007) 76:047001. doi: 10.1103/PhysRevC.76.047001
176. Epelbaum E, Glöckle W, Meißner UG. Improving the convergence of the chiral expansion for nuclear forces. 1. Peripheral phases. Eur Phys J A. (2004). 19:125–37. doi: 10.1140/epja/i2003-10096-0
177. Friar JL. Dimensional regularization and nuclear potentials. Mod Phys Lett A. (1996) 11:3043–8. doi: 10.1142/S0217732396003027
178. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys A. (1997) 625:758–88. doi: 10.1016/S0375-9474(97)00586-1
179. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8
180. Krebs H. Electroweak current operators in chiral effective field theory. In: 9th International Workshop on Chiral Dynamics (CD18). Durham, NC (2019). doi: 10.22323/1.317.0098
181. Epelbaum E. Towards high-precision nuclear forces from chiral effective field theory. In: 6th International Conference Nuclear Theory in the Supercomputing Era (NTSE-2018). Daejeon (2019).
182. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral EFT: State-of-the-art, challenges and outlook. Front Phys. (2020) 8:98. doi: 10.3389/fphy.2020.00098
183. Maekawa CM, Veiga JS, van Kolck U. The Nucleon anapole form-factor in chiral perturbation theory to subleading order. Phys Lett B. (2000) 488:167–74. doi: 10.1016/S0370-2693(00)00851-0
184. Epelbaum E, Glöckle W, Meißner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation. 2. The two nucleon system. Nucl Phys A. (2000) 671:295–331. doi: 10.1016/S0375-9474(99)00821-0
185. Girlanda L, Pastore S, Schiavilla R, Viviani M. Relativity constraints on the two-nucleon contact interaction. Phys Rev C. (2010) 81:034005. doi: 10.1103/PhysRevC.81.034005
186. Kaplan DB, Savage MJ, Wise MB. A Perturbative calculation of the electromagnetic form-factors of the deuteron. Phys Rev C. (1999) 59:617–29. doi: 10.1103/PhysRevC.59.617
187. Savage MJ, Springer RP. Parity violation in effective field theory and the deuteron anapole moment. Nucl Phys A. (1998) 644:235–44. doi: 10.1016/S0375-9474(98)80013-4
188. Phillips DR, Schindler MR, Springer RP. An Effective-field-theory analysis of low-energy parity-violation in nucleon-nucleon scattering. Nucl Phys A. (2009) 822:1–19. doi: 10.1016/j.nuclphysa.2009.02.011
189. Vanasse J, David A. Time-reversal-invariance violation in the Nd system and large-NC. arXiv preprint arXiv:1910.03133 (2019).
190. 't Hooft G. A planar diagram theory for strong interactions. Nucl Phys B. (1974) 72:461. doi: 10.1016/0550-3213(74)90154-0
191. Witten E. Baryons in the 1/n Expansion. Nucl Phys B. (1979) 160:57–115. doi: 10.1016/0550-3213(79)90232-3
192. Dashen RF, Jenkins EE, Manohar AV. Spin flavor structure of large N(c) baryons. Phys Rev D. (1995) 51:3697–727. doi: 10.1103/PhysRevD.51.3697
193. Kaplan DB, Savage MJ. The Spin flavor dependence of nuclear forces from large n QCD. Phys Lett B. (1996) 365:244–51. doi: 10.1016/0370-2693(95)01277-X
194. Kaplan DB, Manohar AV. The Nucleon-nucleon potential in the 1/N(c) expansion. Phys Rev C. (1997) 56:76–83. doi: 10.1103/PhysRevC.56.76
195. Nagels MM, Rijken TA, de Swart JJ. Baryon Baryon scattering in an OBEP approach. 1. Nucleon-nucleon scattering. Phys Rev D. (1975) 12:744. doi: 10.1103/PhysRevD.12.744
196. Nagels MM, Rijken TA, de Swart JJ. Baryon Baryon scattering in a one boson exchange potential approach. 2. Hyperon-nucleon scattering. Phys Rev D. (1977) 15:2547. doi: 10.1103/PhysRevD.15.2547
197. Sakurai JJ. Theory of strong interactions. Ann Phys. (1960) 11:1–48. doi: 10.1016/0003-4916(60)90126-3
198. Barton G. Notes on the static parity nonconserving internucleon potential. Nuovo Cim. (1961) 19:512–27. doi: 10.1007/BF02733247
199. Holstein BR. Nuclear parity violation parameter . Phys Rev D. (1981) 23:1618–23. doi: 10.1103/PhysRevD.23.1618
200. Kaiser N, Meissner UG. The Weak Pion - nucleon vertex revisited. Nucl Phys A. (1988) 489:671–82. doi: 10.1016/0375-9474(88)90115-7
201. Herczeg P. T violating effects in neutron physics and CP violation in gauge models. In: Workshop on Time Reversal Invariance in Neutron Physics. Chapel Hill, NC (1987).
202. Schiavilla R, Viviani M, Girlanda L, Kievsky A, Marcucci LE. Neutron spin rotation in n-polarized - d scattering. Phys Rev C. (2008) 78:014002. doi: 10.1103/PhysRevC.78.014002
203. Schiavilla R, Carlson J, Paris MW. Parity violating interaction effects in the NP system. Phys Rev C. (2004) 70:044007. doi: 10.1103/PhysRevC.70.044007
204. Haxton WC, Henley EM. Enhanced T violating nuclear moments. Phys Rev Lett. (1983) 51:1937. doi: 10.1103/PhysRevLett.51.1937
205. Gudkov VP, He XG, McKellar BHJ. On the CP odd nucleon potential. Phys Rev. (1993) C47:2365-2368. doi: 10.1103/PhysRevC.47.2365
206. Towner IS, Hayes AC. P, T violating nuclear matrix elements in the one meson exchange approximation. Phys Rev C. (1994) 49:2391–7. doi: 10.1103/PhysRevC.49.2391
207. Song YH, Lazauskas R, Gudkov V. Nuclear electric dipole moment of three-body systems. Phys Rev C. (2013) 87:015501. doi: 10.1103/PhysRevC.87.015501
208. Yamanaka N. Review of the electric dipole moment of light nuclei. Int J Mod Phys E. (2017) 26:1730002. doi: 10.1142/S0218301317300028
209. Blyth D, Fry J, Fomin N, Alarcon R, Alonzi L, Askanazi E, et al. First observation of P-odd γ asymmetry in polarized neutron capture on hydrogen. Phys Rev Lett. (2018) 121:242002. doi: 10.1103/PhysRevLett.121.242002
210. Hyun CH, Park TS, Min DP. Asymmetry in polarized n + p –> d + gamma. Phys Lett B. (2001) 516:321–6. doi: 10.1016/S0370-2693(01)00917-0
211. Schiavilla R, Carlson J, Paris MW. Parity violating interactions and currents in the deuteron. Phys Rev C. (2003) 67:032501. doi: 10.1103/PhysRevC.67.032501
212. Desplanques B. Study of parity-violating effects in the neutron capture n+p→d+γ. Nucl Phys A. (1975) 242:423–8. doi: 10.1016/0375-9474(75)90105-0
213. McKellar BHJ. Parity Nonconservation in the low-energy nucleon-nucleon system: evidence for an isotensor weak interaction? Nucl Phys A. (1975) 254:349–52. doi: 10.1016/0375-9474(75)90221-3
214. Desplanques B. Parity nonconserving nuclear forces. Nucl Phys A. (1980) 335:147–67. doi: 10.1016/0375-9474(80)90174-8
215. Eversheim PD, Schmitt W, Kuhn S, Hinterberger F, von Rossen P, Chlebek J, et al. Parity violation in proton proton scattering at 13.6-MeV. Phys Lett B. (1991) 256:11–4. doi: 10.1016/0370-2693(91)90209-9
216. Nagle DE, Bowman JD, Hoffman C, McKibben J, Mischke R, Potter JM, et al. Parity violation in the scattering of 15 MeV protons by hydrogen. AIP Conf Proc. (1979) 51:224–30. doi: 10.1063/1.31768
217. Kistryn S, Lang J, Liechti J, Maier T, Muller R, Nessi-Tedaldi F, et al. Precision measurement of parity violation in proton proton scattering at 45-MeV. Phys Rev Lett. (1987) 58:1616. doi: 10.1103/PhysRevLett.58.1616
218. Berdoz AR, Birchall J, Bland JB, Bowman JD, Campbell JR, Coombes GH, et al. Parity violation in proton proton scattering at 221-MeV. Phys Rev C. (2003) 68:034004. doi: 10.1103/PhysRevC.68.034004
219. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Matching pion-nucleon Roy-Steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301
220. Carlson J, Schiavilla R, Brown VR, Gibson BF. Parity violating interaction effects 1: the Longitudinal asymmetry in pp elastic scattering. Phys Rev C. (2002) 65:035502. doi: 10.1103/PhysRevC.65.035502
221. Desplanques B. About the parity nonconserving asymmetry in n+p→d+γ. Phys Lett B. (2001) 512:305–13. doi: 10.1016/S0370-2693(01)00713-4
222. McCrea M, Kabir ML, Birge N, Coppola CE, Hayes C, Plemons E, et al. The n3He experiment: parity violation in polarized neutron capture on 3He. arXiv preprint arXiv:2004.10889 (2020).
223. Viviani M, Schiavilla R, Girlanda L, Kievsky A, Marcucci LE. The Parity-violating asymmetry in the 3He(n, p)3H reaction. Phys Rev C. (2010) 82:044001. doi: 10.1103/PhysRevC.82.044001
224. Gericke MT, Baeßler S, Barrón-Palos L, Birge N, Bowman JD, Britton C Jr., et al. First precision measurement of the parity violating asymmetry in cold neutron capture on 3He. arXiv preprint arXiv:2004.11535 (2020).
225. Kievsky A, Rosati S, Viviani M, Marcucci LE, Girlanda L. A High-precision variational approach to three- and four-nucleon bound and zero-energy scattering states. J Phys G. (2008) 35:063101. doi: 10.1088/0954-3899/35/6/063101
226. Song YH, Lazauskas R, Gudkov V. Parity violation in low energy neutron deuteron scattering. Phys Rev C. (2011) 83:015501. doi: 10.1103/PhysRevC.83.015501
227. Walecka JD. Theoretical Nuclear and Subnuclear Physics. Vol. 16. Cambridge, UK: Cambridge University Press (1995).
228. Yamanaka N, Hiyama E. Enhancement of the CP-odd effect in the nuclear electric dipole moment of 6Li. Phys Rev C. (2015) 91:054005. doi: 10.1103/PhysRevC.91.054005
229. Lebedev O, Olive KA, Pospelov M, Ritz A. Probing CP violation with the deuteron electric dipole moment. Phys Rev D. (2004) 70:016003. doi: 10.1103/PhysRevD.70.016003
230. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Roy-Steiner-equation analysis of pion–nucleon scattering. Phys Rep. (2016) 625:1–88. doi: 10.1016/j.physrep.2016.02.002
231. Siemens D, Ruiz de Elvira J, Epelbaum E, Hoferichter M, Krebs H, Kubis B, et al. Reconciling threshold and subthreshold expansions for pion-nucleon scattering. Phys Lett B. (2017) 770:27–34. doi: 10.1016/j.physletb.2017.04.039
232. Guo FK, Seng CY. Effective field theory in the study of long range nuclear parity violation on lattice. Eur Phys J C. (2019) 79:22. doi: 10.1140/epjc/s10052-018-6529-y
233. Bass CD, Bass TD, Heckel BR, Huffer CR, Luo D, Markoff DM, et al. A Liquid helium target system for a measurement of parity violation in neutron spin rotation. Nucl Instrum Methods A. (2009) 612:69–82. doi: 10.1016/j.nima.2009.10.055
234. Lang J, Maier T, Muller R, Nessi-Tedaldi F, Roser T, Simonius M, et al. Parity nonconservation in elastic p alpha scattering and the determination of the weak meson - nucleon coupling constants. Phys Rev Lett. (1985) 54:170–3. doi: 10.1103/PhysRevLett.54.170
235. Lazauskas R. Solution of the n−4He elastic scattering problem using the Faddeev-Yakubovsky equations. Phys Rev C. (2018) 97:044002. doi: 10.1103/PhysRevC.97.044002
236. Lazauskas R, Carbonell J. Description of four- and five-nucleon systems by solving Faddeev-Yakubovsky equations in configuration space. Front Phys. (2020) 7:251. doi: 10.3389/fphy.2019.00251
237. Lazauskas R, Song YH. Parity-violating neutron spin rotation in 4He. Phys Rev C. (2019) 99:054002. doi: 10.1103/PhysRevC.99.054002
238. Hupin G, Quaglioni S, Navratil P. Ab initio predictions for polarized deuterium-tritium thermonuclear fusion. Nat Commun. (2019) 10:351. doi: 10.1038/s41467-018-08052-6
239. Kravvaris K, Quinlan KR, Quaglioni S, Wendt KA, Navratil P. Quantifying uncertainties in neutron-alpha scattering with chiral nucleon-nucleon and three-nucleon forces. (2020).
240. Avenier M, Cavaignac JF, Koang DH, Vignon B, Hart R, Wilson R. Parity violation in n d capture. Phys Lett B. (1984) 137:125–128. doi: 10.1016/0370-2693(84)91119-5
242. Adelberger EG, Hindi MM, Hoyle CD, Swanson HE, Von Lintig RD, Haxton WC. Beta decays of Ne-18 and Ne-19 and their relation to parity mixing in F-18 and F-19. Phys Rev C. (1983) 27:2833–56. doi: 10.1103/PhysRevC.27.2833
243. Elsener K, Grubler W, Konig V, Schmelzbach PA, Ulbricht J, Singy D, et al. Constraints on weak meson nucleon coupling from parity nonconservation in F-19. Phys Rev Lett. (1984) 52:1476–9. doi: 10.1103/PhysRevLett.52.1476
244. Elsener K, Grubler W, Konig V, Schmelzbach PA, Ulbricht J, Vuaridel B, et al. Parity nonconservation in 19F nuclei. Nucl Phys A. (1987) 461:579–602. doi: 10.1016/0375-9474(87)90411-8
245. Haxton WC. Parity Nonconservation in 18F and meson exchange contributions to the axial charge operator. Phys Rev Lett. (1981) 46:698. doi: 10.1103/PhysRevLett.46.698
246. Guidoboni G, Stephenson E, Andrianov S, Augustyniak W, Bagdasarian Z, Bai M, et al. How to reach a thousand-second in-plane polarization lifetime with 0.97-GeV/c deuterons in a storage ring. Phys Rev Lett. (2016) 117:054801. doi: 10.1103/PhysRevLett.117.054801
247. Yamanaka N, Yamada T, Funaki Y. Nuclear electric dipole moment in the cluster model with a triton: 7Li and 11B. Phys Rev C. (2019) 100:055501. doi: 10.1103/PhysRevC.100.055501
248. Kabir PK. Test of T invariance in neutron optics. Phys Rev D. (1982) 25:2013. doi: 10.1103/PhysRevD.25.2013
249. Stodolsky L. Parity violation in threshold neutron scattering. Nucl Phys B. (1982) 197:213–27. doi: 10.1016/0550-3213(82)90287-5
250. Bunakov VE, Gudkov VP. Parity violation and related effects in neutron induced reactions. Nucl Phys A. (1983) 401:93–116. doi: 10.1016/0375-9474(83)90338-X
251. Gudkov VP. On CP violation in nuclear reactions. Phys Rept. (1992) 212:77–105. doi: 10.1016/0370-1573(92)90121-F
252. Bowman JD, Gudkov V. Search for time reversal invariance violation in neutron transmission. Phys Rev C. (2014) 90:065503. doi: 10.1103/PhysRevC.90.065503
253. Shimizu H, Gudkov V, Curole J, Harada H, Hautle P, Hino M, et al. Discrete symmetry tests in neutron-induced compound states. PoS INPC2016. (2017) 187. doi: 10.22323/1.281.0187
254. Gudkov V, Shimizu HM. Nuclear spin dependence of time reversal invariance violating effects in neutron scattering. Phys Rev C. (2018) 97:065502. doi: 10.1103/PhysRevC.97.065502
255. Uzikov YN, Haidenbauer J. Polarized proton-deuteron scattering as a test of time-reversal invariance. Phys Rev C. (2016) 94:035501. doi: 10.1103/PhysRevC.94.035501
Keywords: fundamental symmetries in nuclei, nuclear forces, effective field theory, chiral perturbation theory, few-body systems
Citation: de Vries J, Epelbaum E, Girlanda L, Gnech A, Mereghetti E and Viviani M (2020) Parity- and Time-Reversal-Violating Nuclear Forces. Front. Phys. 8:218. doi: 10.3389/fphy.2020.00218
Received: 21 January 2020; Accepted: 22 May 2020;
Published: 21 July 2020.
Edited by:
Nunzio Itaco, University of Campania Luigi Vanvitelli, ItalyReviewed by:
Barry R. Holstein, University of Massachusetts Amherst, United StatesRimantas Lazauskas, UMR7178 Institut Pluridisciplinaire Hubert Curien (IPHC), France
Copyright © 2020 de Vries, Epelbaum, Girlanda, Gnech, Mereghetti and Viviani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michele Viviani, bWljaGVsZS52aXZpYW5pQHBpLmluZm4uaXQ=
 Jordy de Vries1,2
Jordy de Vries1,2 Alex Gnech
Alex Gnech Emanuele Mereghetti
Emanuele Mereghetti Michele Viviani
Michele Viviani