Towards a Unitary, Renormalizable, and Ultraviolet-Complete Quantum Theory of Gravity

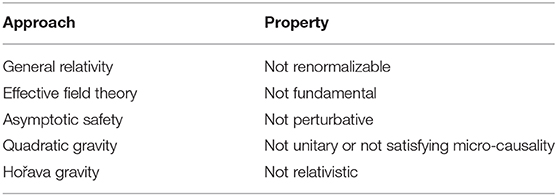
For any fundamental quantum field theory, unitarity, renormalizability, and relativistic invariance are considered to be essential properties. Unitarity is inevitably connected to the probabilistic interpretation of the quantum theory, while renormalizability guarantees its completeness. Relativistic invariance, in turn, is a symmetry that derives from the structure of spacetime. So far, the perturbative attempt to formulate a fundamental local quantum field theory of gravity based on the metric field seems to be in conflict with at least one of these properties. In quantum Hořava gravity, a quantum Lifshitz field theory of gravity characterized by an anisotropic scaling between space and time, unitarity and renormalizability can be retained while Lorentz invariance is sacrificed at high energies and must emerge only as approximate symmetry at low energies. This article reviews various approaches to perturbative quantum gravity, with a particular focus on recent progress in the quantization of Hořava gravity, supporting its theoretical status as a unitary, renormalizable, and ultraviolet-complete quantum theory of gravity.

1. Introduction

The search for a consistent quantum theory of gravity can be dated back almost 90 years to the work of Rosenfeld [1]. Since then, many different approaches have been suggested, each with its own assumptions, predictions (if any), and limitations; see [2] for an overview. Prominent roads to quantum gravity include canonical approaches, such as quantum geometrodynamics [3, 4] and loop quantum gravity [5–8], discrete approaches, such as causal dynamical triangulations [9–11], and unified approaches, such as string theory [12–16].

In this review, I restrict the discussion to local field theories, in which gravity is fundamentally described by the metric field. For non-local (infinite-derivative) theories of gravity, (see e.g. [17–26]), and for non-metric theories of gravity, (see e.g. [27–32]). In view of the tremendous success of perturbative quantum field theory in different areas of physics, including the standard model of particle physics, it seems natural to quantize gravity within this highly developed and strongly tested unified framework along with the fundamental interactions between the matter fields. For most of this review, I will focus on the covariant perturbative approach to quantum gravity. Much of the progress in this direction can be attributed to Bryce S. DeWitt, who pioneered the field and set the standards for most of its developments in the subsequent decades [33–35].

While the direct approach to quantizing general relativity perturbatively is considered a failure because of its non-renormalizability in the strict sense [36, 37], the perturbative quantization and renormalization can be consistently carried out when general relativity is treated as an effective field theory [38–40]. However, by construction the effective description breaks down at a finite energy scale and therefore does not extend to the arbitrarily high energies required for a fundamental theory of quantum gravity. In this respect, the non-perturbative asymptotic safety program towards quantum gravity might offer a solution in providing a consistent ultraviolet completion [41–44]. A different strategy, which retains the perturbative treatment, is based on the quantization of modifications of general relativity. Quadratic gravity, the extension of the Einstein-Hilbert action by all quadratic curvature invariants, is a perturbatively renormalizable quantum theory of gravity [45]. While the higher derivatives in quadratic gravity improve the ultraviolet behavior, relativistic invariance necessarily implies the inclusion of higher time derivatives, which in turn results in an enlarged particle spectrum, including a massive spin-2 ghost. At the classical level, the presence of the ghost leads to runaway solutions, known as Ostrogradsky instability [46]. At the quantum level, within the usual quantization prescription, the ghost was found to lead to a violation of unitarity [45]. Recent proposals, which involve different quantization prescriptions for the ghost, preserve unitarity but instead lead to a violation of micro-causality [47, 48].

In view of these problems, it has been suggested to explore the consequences of the assumption that Lorentz invariance is not a fundamental symmetry but only emerges as an approximate symmetry at low energies. In this way, higher spatial derivatives can be introduced to tame the ultraviolet divergences, while retaining only second-order time derivatives to avoid the problems associated with the occurrence of higher-derivative ghosts. The breaking of relativistic invariance at a fundamental level is naturally realized in Lifshitz theories by an anisotropic scaling between space and time [49, 50].

After a brief overview of various relativistic covariant approaches to quantum gravity, I will review several aspects of the Lifshitz theory of gravity, Hořava gravity [50], in D = 2 + 1 and D = 3 + 1 dimensions, including the consequences of the reduced invariance group of foliation-preserving diffeomorphisms, the geometrical formulation in terms of Arnowitt-Deser-Misner variables, the phenomenological implications of the additional propagating gravitational scalar degree of freedom, and the current status of the experimental constraints. I discuss the quantization of projectable Hořava gravity, a particular version of Hořava gravity in which the lapse function is not a propagating degree of freedom. I will also sketch the proof that projectable Hořava gravity is a perturbatively renormalizable quantum theory of gravity [51, 52] and report recent results on its renormalization group flow [53, 54].

The article is structured as follows. In section 2, I introduce the general formalism for the perturbative quantization of local field theories. In section 3, I summarize the essential properties of general relativity and the major drawback of its perturbative quantization: non-renormalizability. In section 4, I briefly comment on the status of general relativity as an effective field theory. In section 5, I discuss several aspects of the asymptotic safety conjecture in the context of gravity and its status as a possible ultraviolet-complete scenario for a quantum theory of gravity. In section 6, I review the perturbatively renormalizable theory of quadratic gravity and discuss the ghost problem. In section 7, I present various aspects of the classical theory of Hořava gravity in D = 2 + 1 and D = 3 + 1 dimensions. In section 8, I discuss the perturbative quantization of projectable Hořava gravity, its perturbative renormalizability, and its status as an ultraviolet-complete theory. Finally, I conclude in section 10 with a short summary and a brief outlook on important further steps towards a unitary, renormalizable, and ultraviolet-complete quantum theory of gravity in D = 3 + 1 dimensions.

2. Perturbative Quantum Field Theory: General Formalism

Consider a local field theory, which is defined by the action functional S,

$\begin{array}{ll}S\left[\varphi \right]={\displaystyle \sum _n}{\displaystyle \int }{\text{d}}^{D}X{c}_n{{O}}_n(\varphi ,\partial ).& (1)\end{array}$

Locality means that the operators ${{O}}_n(\varphi ,\partial )$ are functions of a finite number of derivatives (including no derivative) of the generalized field(s) ϕⁱ = ϕ^A(x) evaluated at the same point x. The operators ${{O}}_n$ are restricted by the symmetries of S. The c_n are coupling constants characterizing the strength of the interaction associated with the operator ${{O}}_n$¹. The main object in the quantum field theory (QFT) is the quantum effective action Γ.

2.1. Perturbation Theory

The starting point for the formal derivation of the Euclidean effective action is the partition function Z, which is defined by the functional integral over the field configurations ϕⁱ and is a functional of the external source J_i,

$\begin{array}{ll}Z\left[J\right]:=e^{-W\left[J\right]}={\displaystyle \int }{D}\varphi e^{-(S[\varphi ]+J_i{\varphi }^i)}.& (2)\end{array}$

The mean field φⁱ is defined as the quantum average in the presence of the source J_i,

$\begin{array}{ll}{\phi }^i:={\langle {\varphi }^i\rangle }_J=\frac{\delta W\left[J\right]}{\delta J_i}.& (3)\end{array}$

The quantum effective action Γ is defined as the functional Legendre transformation of the Schwinger functional W,

$\begin{array}{ll}\Gamma \left[\phi \right]:=W\left[J\right]-{\phi }^i{J}_i.& (4)\end{array}$

Combining (2) and (3) yields the functional integro-differential equation²

$\begin{array}{ll}{e}^{-\Gamma \left[\phi \right]}={\displaystyle \int }{D}\varphi e^{-\left\{S\left[\varphi \right]-({\phi }^i-{\varphi }^i){\Gamma }_{,i}\left[\phi \right]\right\}}.& (5)\end{array}$

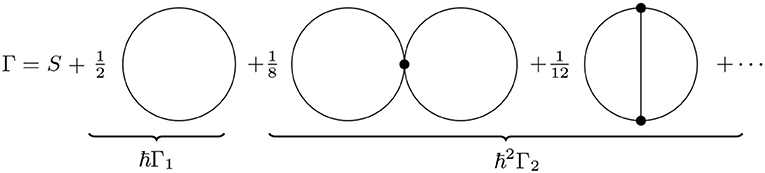
Equation (5) provides the starting point for the perturbative expansion of Γ (reinserting powers of ℏ),

$\begin{array}{ll}\Gamma \left[\phi \right]=S\left[\phi \right]+\hslash {\Gamma }_1\left[\phi \right]+{\hslash }^2{\Gamma }_2\left[\phi \right]+{O}({\hslash }^3).& (6)\end{array}$

The diagrammatic representation of the expansion (6) is given in terms of vacuum diagrams in which the number of loops corresponds to the power of ℏ in (6), as shown in Figure 1.

FIGURE 1

Figure 1. The diagrammatic expansion of the quantum effective action in powers of loops.

In the background field method (BFM), ϕⁱ is decomposed into a background field ${\bar{\varphi }}^i$ and a linear perturbation δϕⁱ,

$\begin{array}{ll}{\varphi }^i={\bar{\varphi }}^i+\delta {\varphi }^i.& (7)\end{array}$

The first two orders of the expansion (6) correspond to the vacuum diagrams shown in Figure 1:

$\begin{array}{l}{\Gamma }_1=\frac{1}{2}\text{Tr}ln{F}_{ij},\\ {\Gamma }_2=\frac{1}{8}{G}^{ij}{S}_{,ijk\ell }{G}^{k\ell }+\frac{1}{12}{S}_{,ijk}{G}^{i\ell }{G}^{jm}{G}^{kn}{S}_{,\ell mn}.& (8)\end{array}$

Here, Tr is the functional trace, F_ij is the fluctuation operator, and the Green's function G^ij (propagator) is its inverse, such that

$\begin{array}{ll}{F}_{ij}{G}^{ik}=-{\delta }_i^k.& (9)\end{array}$

The operator F_ij, which propagates the linear perturbations δϕⁱ on the background ${\bar{\varphi }}^i$, is defined as the Hessian of S,

$\begin{array}{ll}{F}_{ij}(\bar{\nabla }):=S_{,ij}{|}_{\varphi =\bar{\varphi }}.& (10)\end{array}$

The covariant derivative ∇_μ defines the commutator (“bundle”) curvature

$\begin{array}{ll}{{R}}_{\mu \nu }{{}^i}_j{\varphi }^j:=[{\nabla }_{\mu },{\nabla }_{\nu }]{\varphi }^i.& (11)\end{array}$

The effective action is the generating functional of off-shell one-particle-irreducible (1PI) n-point correlation functions

$\begin{array}{ll}\langle {\varphi }_{i_1},\dots ,{\varphi }_{i_n}\rangle ={\Gamma }_{,i_1,\dots ,i_n}.& (12)\end{array}$

In particular, for J_i = 0, the mean field φⁱ = 〈ϕ〉 is the solution of the quantum effective equations of motion

$\begin{array}{ll}{\Gamma }_{,i}=0.& (13)\end{array}$

Physical observables that derive from the S-matrix of scattering amplitudes are calculated from the off-shell correlation functions (12) via the Lehmann-Symanzik-Zimmermann (LSZ) reduction formula [55].

2.2. Gauge Theories

In gauge theories, different field configurations that correspond to the same physical state are related by an infinitesimal gauge transformation

$\begin{array}{ll}{\varphi }_{\epsilon }^i:={\delta }_{\epsilon }{\varphi }^i=R_{\alpha }^i{\epsilon }^{\alpha }.& (14)\end{array}$

The $R_{\alpha }^i(\varphi )$ are the generators of the gauge transformations, and ε^α is the infinitesimal gauge parameter³. For linearly realized symmetries (considered here), $R_{i,jk}^{\alpha }=0$. For gauge algebras that close off-shell, the generators satisfy

$\begin{array}{ll}\begin{array}{l}{R}^i{}_{\alpha ,j}{R}^j{}_{\beta }-R^i{}_{\beta ,j}{R}^j{}_{\alpha }=R^i{}_{\gamma }{C}^{\gamma }{}_{\alpha \beta }.\hfill \end{array}& (15)\end{array}$

The C^γ_αβ are the structure functions (here assumed to be field independent, C^γ_αβ,i = 0) and satisfy the Jacobi identity

$\begin{array}{ll}{C}_{\alpha \beta }^{ϵ}{C}_{ϵ\gamma }^{\delta }+C_{\gamma \alpha }^{ϵ}{C}_{ϵ\beta }^{\delta }+C_{\beta \gamma }^{ϵ}{C}_{ϵ\alpha }^{\delta }=0.& (16)\end{array}$

Gauge invariance δ_εS = 0 of the action (1) implies the Noether identity

$\begin{array}{ll}{S}_{,i}{R}_{\alpha }^i=0.& (17)\end{array}$

Differentiation of (17) shows that the fluctuation operator (10) for gauge theories is degenerate (on shell S_{, i} = 0),

$\begin{array}{ll}{F}_{ij}{R}_{\alpha }^i=0.& (18)\end{array}$

The gauge degeneracy Det(F_ij) = 0 prevents the construction of the inverse (F⁻¹)^ij, and the associated Green's function G^ij does not exist. In order to break the gauge degeneracy, a gauge-breaking action must be added:

$\begin{array}{ll}{S}_{\text{gb}}={\chi }^{\alpha }{O}_{\alpha \beta }(\bar{\nabla }){\chi }^{\beta }.& (19)\end{array}$

The background covariant gauge condition ${\chi }^{\alpha }(\bar{\varphi };\delta \varphi )$ depends linearly on the difference $\delta {\varphi }^i-{\bar{\varphi }}^i$ between the “quantum field” δϕⁱ, i.e., the variable that is integrated over in the path integral, and the background field ${\bar{\varphi }}^i$. But, like the operator $O_{\alpha \beta }(\bar{\varphi };\bar{\nabla })$, it may have an arbitrary (non-linear) parametric dependence on the background field ${\bar{\varphi }}^i$. In this way, invariance of the effective action under background gauge transformations is realized. For the linear split (7), an infinitesimal, linearly realized gauge transformation (14) can be distributed in different ways, in particular by

$\begin{array}{l}{\delta }_{\epsilon }^Q{\bar{\phi }}^i=0,{\delta }_{\epsilon }^Q\delta {\varphi }^i=R_{\alpha }^i(\bar{\varphi }+\delta \varphi ){\epsilon }^{\alpha },\end{array}$

or

$\begin{array}{ll}{\delta }_{\epsilon }^B{\bar{\phi }}^i=R_{\alpha }^i(\bar{\varphi }){\epsilon }^{\alpha },{\delta }_{\epsilon }^B\delta {\varphi }^i=R_{\alpha }^i(\delta \varphi ){\epsilon }^{\alpha }.& (20)\end{array}$

While the linearity of the generators ensures that in both cases ${\delta }_{\epsilon }{\varphi }^i={\delta }_{\epsilon }^Q({\bar{\varphi }}^i+\delta {\varphi }^i)={\delta }_{\epsilon }^B({\bar{\varphi }}^i+\delta {\varphi }^i)=R_{\alpha }^i(\varphi ){\epsilon }^{\alpha }$, the “quantum gauge transformation” ${\delta }_{\epsilon }^Q$ does not affect the background field ${\bar{\varphi }}^i$ but only the “quantum” field δφⁱ, whereas for the background gauge transformations ${\delta }_{\epsilon }^B$, the transformation (14) is split between the background field and the quantum field according to (7). The gauge-breaking action (19) must be compensated for by the ghost action

$\begin{array}{ll}{S}_{\text{gh}}=c_{\alpha }^{*}{Q}_{\beta }^{\alpha }{c}^{\beta }.& (21)\end{array}$

The anticommuting independent ghost field c^α and anti-ghost field $c_{\alpha }^{*}$ have fermionic statistics. The ghost operator Q^α_β is defined as the variation of the gauge-transformed gauge condition,

$\begin{array}{ll}{Q}^{\alpha }{}_{\beta }(\stackrel{-}{\nabla }):=\frac{\delta {\chi }^{\alpha }[{\varphi }_{\epsilon }^i]}{\delta {\epsilon }^{\beta }}.\hfill & (22)\end{array}$

Summarizing, for gauge theories the partition function (2) generalizes to

$\begin{array}{ll}Z\left[J\right]=\text{Det }{(O_{\alpha \beta })}^{1/2}{\displaystyle \int }{D}\left[\varphi ,c,c^{*}\right]e^{-\{S_{\text{tot}}[\varphi ,c,c^{*}]+J_i{\varphi }^i\}},& (23)\end{array}$

with the total action S_tot defined as the sum of (1), (19) and (21),

$\begin{array}{ll}{S}_{\text{tot}}\left[\varphi ,c,c^{*}\right]=S\left[\varphi \right]+S_{\text{gb}}\left[\bar{\varphi };\varphi \right]+S_{\text{gh}}\left[\bar{\varphi },c,c^{*}\right].& (24)\end{array}$

In particular, the gauge-fixed fluctuation operator is no longer degenerate and can be inverted:

$\begin{array}{ll}{F_{ij}^{\text{gb}}(\bar{\nabla }):={(S+S_{\text{gb}})}_{ij}|}_{\varphi =\bar{\varphi }}.& (25)\end{array}$

The structure of the effective action and the proof of perturbative renormalizability of a local gauge theory are described in more general terms by exploiting the residual non-linearly realized Becchi-Rouet-Stora-Tyutin (BRST) symmetry of the gauge-fixed action [56, 57]. For the application of these methods in the context of general relativity and Yang-Mills theories, (see [58]); for a generalization to non-relativistic theories, (see [52]).

2.3. Functional Traces and the Heat-Kernel Technique

In addition to the abstract formalism presented in section 2, explicit calculations in the perturbative expansion (6) require the evaluation of functional traces, for which the combination of the BFM with heat-kernel techniques provides a manifest covariant and efficient tool⁴. For the connection between the heat-kernel technique and position space Feynman diagrams in curved spacetime (see e.g., [60, 61]). For an introduction to the background field method, (see [62–64]). For an overview of flat-space Feynman-diagrammatic calculations in momentum space, see e.g., [65], as well as [66] for an introduction to modern on-shell methods. An explicit illustration of the connection between the different techniques is given section 9 in the context of the one-loop divergences for projectable Hořava gravity.

The heat-kernel technique, originally developed in mathematics in the context of asymptotic expansions, partial differential equations, and geometric analysis of the Laplace operator [67–72], has turned out to be a very useful tool in physics also, especially in the context of renormalization in Quantum Field Theory (QFT) on a curved background [33, 60, 73, 74]. Recalling the ultra-condensed DeWitt notation, the (gauge-fixed) fluctuation operator (25) takes the general form $F_{ij}(\bar{\nabla })=F_{AB}({\bar{\nabla }}_{X_A})\delta (X_A,X_B)$. The operator with proper index positions F^A_B, acting on the fluctuation field δϕ^A(X), is obtained from F_AB by raising the bundle index A with the (ultra-local) configuration space metric C_AB⁵,

$\begin{array}{ll}F(\nabla ):=F^A{}_B(\nabla )=C^{AC}{F}_{CB}(\nabla ).\hfill & (26)\end{array}$

Inverse powers and the logarithm of the operator (26), which appear in the perturbative expansion (6), are conveniently expressed in terms of the Schwinger integral representation⁶ over “proper time” s,

$\begin{array}{ll}\frac{1}{F^n}={\displaystyle {\int }_0^{\infty }}\frac{\text{d}s}{(n-1)!}{s}^{n-1}{e}^{-s\text{F}},ln\text{F}=-{\displaystyle {\int }_0^{\infty }}\frac{\text{d}s}{s}{e}^{-s\text{F}}.& (27)\end{array}$

The heat kernel K_F(s|X, Y) associated with the operator F formally satisfies the heat equation

$\begin{array}{l}{\text{K}}_F(s|X,Y):=e^{-s\text{F}({\nabla }_X)}\delta (X,Y),\\ \left[\frac{\partial }{\partial s}+\text{F}(\nabla )\right]{\text{K}}_F(s|X,Y)=0.& (28)\end{array}$

In terms of the heat kernel (28), the one-loop contribution to the effective action (8) takes the form

$\begin{array}{l}{\Gamma }_1=-\frac{1}{2}{\displaystyle {\int }_0^{\infty }}\frac{\text{d}s}{s}\text{Tr}{\text{ K}}_F(s|X,Y)\\ =-\frac{1}{2}{\displaystyle {\int }_0^{\infty }}\frac{\text{d}s}{s}{\displaystyle \int }{\text{d}}^{d}x\text{ tr}{\left[K_F\right]}_B^A(s|,X,X).& (29)\end{array}$

Equation (29) can be viewed as the definition of the functional trace Tr and requires evaluation of the spacetime integral over the internal trace tr of the coincidence limit y → x of the matrix-valued two-point kernel ${\left[K_F\right]}^A{}_B(s|,X,Y)$. Ultraviolet (UV) divergences arise from the lower integration bound in (29), i.e., the s → 0 limit.

For a minimal second-order operator with (positive-definite) Laplacian $\Delta =-g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }\mathbf{\text{1}}$ and potential P,

$\begin{array}{ll}\text{F}(\nabla )=\Delta +\text{P},& (30)\end{array}$

there is an ansatz for the associated heat kernel at non-coincident points, introduced in [33]:

$\begin{array}{ll}\text{K}(s|X,Y)=\frac{g^{1/2}(y)}{{(4\pi s)}^{d/2}}{𝔇}^{1/2}(X,Y)e^{-\frac{\sigma (X,Y)}{2s}}\Omega (s|X,Y).& (31)\end{array}$

Synge's world function σ(X, Y) is a bi-scalar [75], which measures one-half of the geodesic distance squared between the points X and Y, and 𝔇(X, Y) is the de-densitized Van Vleck determinant, a bi-scalar defined as

$\begin{array}{ll}𝔇(X,Y):=g^{-1/2}(X)det\left(\frac{{\partial }^2\sigma (X,Y)}{\partial X^{\mu }\partial Y^{\nu }}\right)g^{-1/2}(Y).& (32)\end{array}$

The bi-tensor Ω can be obtained in the form of an asymptotic expansion in proper time,

$\begin{array}{l}\Omega (s|X,Y):={\displaystyle \sum _{n=0}^{\infty }}{\text{a}}_n(X,Y)s^n,\\ {\text{a}}_n(X,X)\propto {\displaystyle \underset{2p}{{\displaystyle \underbrace{{\nabla }_X\dots {\nabla }_X}}}}{\displaystyle \underset{m}{{\displaystyle \underbrace{\Re \dots \Re }}}},n=p+m.& (33)\end{array}$

The Schwinger-DeWitt (SDW) coefficients at coincidence points a_n(X, X) are local functions of the background fields, and the generalized curvature ℜ encompasses three different types of background curvature, ℜ = {R_μνρσ1, ${R}$_μν, P}.

For the minimal second-order operators (30), a closed-form algorithm for calculating the one-loop divergences ${\Gamma }_1^{\text{div}}$ is available. In general, dimensional regularization annihilates all power-law divergences and is sensitive only to logarithmic divergences, which are isolated as poles in dimension ϵ⁻¹ = 2/(4 − D). In D = 4, the logarithmically UV-divergent part of the one-loop contributions to the effective action (29) for the minimal second-order operator (30) is determined by the coincidence limit of a₂(x, x) [33],

$\begin{array}{ll}{\Gamma }_1^{\text{div}}=-\frac{1}{ϵ}\frac{1}{32{\pi }^2}{\displaystyle \int }{\text{d}}^{4}X{g}^{1/2}\text{tr }{\text{a}}_2(X,X).& (34)\end{array}$

The coincidence limits of the SDW coefficients a_n(x, x) can be calculated iteratively by inserting the ansatz (31) into the heat Equation (28), leading to the recurrence relation (for n ≥ 0),

$\begin{array}{ll}\left[(n+1)+{\sigma }^{\mu }{\nabla }_{\mu }\right]{\text{a}}_{n+1}={𝔇}^{-1/2}\text{F}(\nabla )\left({𝔇}^{1/2}{\text{a}}_n\right)=0.& (35)\end{array}$

In order to obtain a₂(X, X) in this way, the coincidence limits of σ, 𝔇, a₀, a₁, and their derivatives must be calculated. The successive pattern of this calculation is illustrated in Table 1.

TABLE 1

Table 1. Coincidence limits required for the calculation of a₂(X, X).

The coincidence limits of σ, 𝔇, a₀, and their derivatives can be obtained by successive differentiation of the “defining equations” for σ, 𝔇, and a₀,

$\begin{array}{ll}{\sigma }^{\mu }{\sigma }_{\mu }=2\sigma ,{𝔇}^{-1}{\nabla }^{\mu }(𝔇{\sigma }_{\mu })=d,{\sigma }^{\mu }{\nabla }_{\mu }{\text{a}}_0=0,& (36)\end{array}$

with the “initial conditions” $\sigma {|}_{y=x}=0$, $𝔇{|}_{y=x}=1$, and ${\mathbf{\text{a}}}_0{|}_{y=x}=\mathbf{\text{1}}$. In this way, the coincidence limit of a₂(X, Y) is found as [33, 60],

$\begin{array}{l}{\text{a}}_2(X,X)=\frac{1}{180}\left(R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }-R_{\mu \nu }{R}^{\mu \nu }-6\Delta R\right)1\\ +\frac{1}{2}{\left({\text{P}}^2-\frac{1}{6}R1\right)}^2+\frac{1}{12}{{R}}_{\mu \nu }{{R}}^{\mu \nu }+\frac{1}{6}\Delta \text{P}.& (37)\end{array}$

For higher-order and non-minimal operators there is no closed-form expression for the one-loop divergences (34) in terms of a single SDW coefficient as for the minimal second-order operator (30). Nevertheless, in [60] a closed algorithm was developed, which reduces the calculation of the one-loop divergences for higher-order and non-minimal operators to the heat kernel of the second-order minimal operator (31) and a few universal functional traces,

$\begin{array}{ll}{{{U}}_{{\mu }_1\dots {\mu }_p}^{(p,n)}:={\nabla }_{{\mu }_1}\dots {\nabla }_{{\mu }_p}\frac{1}{{\Delta }^n}|}_{Y=X}^{\text{div}}.& (38)\end{array}$

The perturbative algorithm underlying the generalized SDW technique relies on the non-degeneracy of the principal symbol D of the operator F. There are, however, important physical theories for which the principal symbol of the fluctuation operator is degenerate so that the (generalized) SDW algorithm is not directly applicable. In such cases, more general methods are required; see [76–78] for heat-kernel calculations involving operators with degenerate principal part and [79, 80] for operators with Laplacians constructed from an effective (background field-dependent) metric. In the context of Lifshitz theories, the development of heat-kernel techniques for anisotropic operators has recently been initiated [81–83].

3. Perturbative Quantum General Relativity

3.1. Classical General Relativity

In the theory of general relativity (GR), the gravitational interaction manifests itself geometrically as curvature of spacetime and couples universally to all fields, which, combined with the attractive nature of gravity, implies that it cannot be shielded. In Einstein's theory, the dynamical character of the spacetime geometry is encoded in the dynamics of the metric field g_μν(X). The action functional of GR is the Einstein-Hilbert action

$\begin{array}{ll}{S}_{\text{EH}}=\frac{M_{\text{P}}^2}{2}{\displaystyle \int }{\text{d}}^{D}X\sqrt{-g}(R-2\Lambda ).& (39)\end{array}$

The action (39) involves the invariant volume element with determinant g = det(g_μν), the Ricci scalar $R=g^{\mu \nu }{R}_{\mu \nu }$, and the cosmological constant Λ⁷. The dynamics of g_μν is determined by Einstein's field equations, obtained from extremizing the total action S[g, Ψ] = S_EH[g] + S_M[g, Ψ] with respect to g_μν,

$\begin{array}{ll}{R}_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R+\Lambda g_{\mu \nu }=M_{\text{P}}^{-2}{T}_{\mu \nu }.& (40)\end{array}$

The energy momentum tensor T_μν derives from the “matter” action S_M[Ψ], with all non-geometrical “matter” fields collectively denoted by Ψ:

$\begin{array}{ll}{T}_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta S_{\text{M}}\left[g,\text{Ψ}\right]}{\delta g^{\mu \nu }}.& (41)\end{array}$

Infinitesimal spacetime distances ds measured by the metric field g_μν are defined by the line element

$\begin{array}{ll}\text{d}{s}^2=g_{\mu \nu }(X)\text{d}{X}^{\mu }\text{d}{X}^{\nu }.& (42)\end{array}$

Denoting the mass dimension by [·]_M and assigning coordinates X^μ the dimension of a length, [X]_M = −1, implies that

$\begin{array}{l}{[{\partial }_{\mu }]}_{\text{M}}=1,{[g_{\mu \nu }]}_{\text{M}}=0,{[R_{\mu \nu \rho \sigma }]}_{\text{M}}=2,\\ {[G_{\text{N}}]}_{\text{M}}=-(D-2),{[\Lambda ]}_{\text{M}}=2.& (43)\end{array}$

The Ricci scalar R is the only curvature invariant involving exactly two spacetime derivatives. Except for the cosmological constant, all other curvature invariants necessarily contain higher derivatives. In D = 4, these are the only two classically relevant local curvature operators⁸.

The metric field transforms as a rank-(0, 2) tensor under D-dimensional coordinate transformations $X^{\mu }\to {\tilde{X}}^{\mu }(X)$,

$\begin{array}{ll}{g}_{\mu \nu }(X)\mapsto {\tilde{g}}_{\mu \nu }(\tilde{X})=g_{\alpha \beta }(X)\frac{\partial X^{\alpha }}{\partial {\tilde{X}}^{\mu }}\frac{\partial X^{\beta }}{\partial {\tilde{X}}^{\nu }}.& (44)\end{array}$

The invariance group of GR consists of the D-dimensional diffeomorphisms $\text{Diff}({M})$. The change of the metric field under an infinitesimal diffeomorphism δ_ξ generated by the vector field ξ^μ is given by the Lie derivative of g_μν along ξ^μ:

$\begin{array}{ll}{\delta }_{\xi }{g}_{\mu \nu }={\left({{L}}_{\xi }g\right)}_{\mu \nu }={\xi }^{\rho }{\partial }_{\rho }{g}_{\mu \nu }+2g_{\rho (\nu }{\partial }_{\mu )}{\xi }^{\rho }=2{\nabla }_{(\mu }{\xi }_{\nu )}.& (45)\end{array}$

Round brackets in (45) denote symmetrization among the enclosed indices with unit weight and ${\xi }_{\mu }=g_{\mu \rho }{\xi }^{\rho }$. Since the gravitational field equations (40) relate geometry with matter, consistency requires that S_M[g, Ψ] must also be invariant under $\text{Diff}({M})$, which implies the “on-shell” covariant conservation of the energy-momentum tensor, ${\nabla }^{\mu }{T}_{\mu \nu }=0$.

3.2. Quantum GR

In order to establish a connection with the general formalism of perturbative QFT reviewed in section 2, the generalized field ϕⁱ in GR is identified with the metric field, ${\varphi }^i\mapsto g_{\mu \nu }(X)$. Comparison of (1) with the Einstein-Hilbert action (39) implies that the operators ${{O}}_i(g,\partial )$ and the coupling constants c_i should be identified as follows:

$\begin{array}{l}{{O}}_1(g)\mapsto \sqrt{-g},c_1\mapsto -M_{\text{P}}^2\Lambda ,\\ {{O}}_2(g,\partial )\mapsto \sqrt{-g}R,c_2\mapsto \frac{M_{\text{P}}^2}{2}.& (46)\end{array}$

The particle spectrum of GR is derived by expanding the action (39) to quadratic order in the linear perturbations

$\begin{array}{ll}{h}_{\mu \nu }=g_{\mu \nu }-{ḡ}_{\mu \nu }& (47)\end{array}$

around a flat background ḡ_μν = η_μν⁹. Absorbing a factor of M_P/2 in the definition of h_μν, i.e., h_μν ↦ 2h_μν/M_P, and defining $h={\eta }^{\mu \nu }{h}_{\mu \nu }$ and ${\partial }^2:={\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }$, upon integration by parts the result reads

$\begin{array}{l}{S}_{\text{EH}}^{(2)}{|}_{ḡ=\eta }={\displaystyle \int }{\text{d}}^{D}X[h^{\mu \nu }{\partial }^2{h}_{\mu \nu }-h{\partial }^{2}h-2h^{\mu \nu }{\partial }_{\nu }{\partial }_{\rho }{h_{\mu }}^{\rho }\\ +2h^{\mu \nu }{\partial }_{\nu }{\partial }_{\mu }h].& (48)\end{array}$

After Fourier transformation ∂_μ ↦ iP_μ with four momentum P^μ and square $P^2={\eta }_{\mu \nu }{P}^{\mu }{P}^{\nu }$, the fluctuation operator (10) in momentum space can be expressed in terms of spin-projection operators as

$\begin{array}{ll}{F}^{\mu \nu ,\rho \sigma }(-P^2)=[{\Pi }^{(2)\mu \nu \rho \sigma }-(D-2){\Pi }^{(0,ss)\mu \nu \rho \sigma }]\left(-P^2\right).& (49)\end{array}$

The spin-projection operators acting on the symmetric rank-two tensor h_μν read

$\begin{array}{l}{\Pi }^{(2)}{{}_{\mu \nu }}^{\rho \sigma }=\frac{1}{2}\left({\Pi }^{(\text{T})}{{}_{\mu }}^{\rho }{\Pi }^{(\text{T})}{{}_{\nu }}^{\sigma }+{\Pi }^{(\text{T})}{{}_{\mu }}^{\sigma }{\Pi }^{(\text{T})}{{}_{\nu }}^{\rho }\right)\\ -\frac{1}{D-1}{\Pi }^{(\text{T})}{}_{\mu \nu }{\Pi }^{(\text{T})}{}^{\rho \sigma },& (50)\end{array}$

$\begin{array}{l}{\Pi }^{(1)}{{}_{\mu \nu }}^{\rho \sigma }=\frac{1}{2}({\Pi }^{(\text{T})}{{}_{\mu }}^{\rho }{\Pi }^{(\text{L})}{{}_{\nu }}^{\sigma }+{\Pi }^{(\text{T})}{{}_{\mu }}^{\sigma }{\Pi }^{(\text{L})}{{}_{\nu }}^{\rho }+\\ {\Pi }^{(\text{T})}{{}_{\nu }}^{\rho }{\Pi }^{(\text{L})}{{}_{\mu }}^{\sigma }+{\Pi }^{(\text{T})}{{}_{\nu }}^{\sigma }{\Pi }^{(\text{L})}{{}_{\mu }}^{\rho }),& (51)\end{array}$

$\begin{array}{ll}{\Pi }^{(0,ss)}{{}_{\mu \nu }}^{\rho \sigma }=\frac{1}{D-1}{\Pi }^{(\text{T})}{}_{\mu \nu }{\Pi }^{(\text{T})}{}^{\rho \sigma },& (52)\end{array}$

$\begin{array}{ll}{\Pi }^{(0,ww)}{{}_{\mu \nu }}^{\rho \sigma }={\Pi }^{(\text{L})}{}_{\mu \nu }{\Pi }^{(\text{L})}{}^{\rho \sigma },& (53)\end{array}$

$\begin{array}{ll}{\Pi }^{(0,sw)}{{}_{\mu \nu }}^{\rho \sigma }=\frac{1}{\sqrt{D-1}}{\Pi }^{(\text{T})}{}_{\mu \nu }{\Pi }^{(\text{L})}{}^{\rho \sigma },& (54)\end{array}$

$\begin{array}{ll}{\Pi }^{(0,ws)}{{}_{\mu \nu }}^{\rho \sigma }=\frac{1}{\sqrt{D-1}}{\Pi }^{(\text{L})}{}^{\rho \sigma }{\Pi }^{(\text{T})}{}_{\mu \nu }.& (55)\end{array}$

Here, Π^(T) and Π^(L) are the transversal and longitudinal vector field projectors

$\begin{array}{ll}{\Pi }^{(\text{T})}{{}_{\mu }}^{\nu }={\delta }_{\mu }^{\nu }-\frac{P_{\mu }{P}^{\nu }}{P^2},{\Pi }^{(\text{L})}{{}_{\mu }}^{\nu }=\frac{P_{\mu }{P}^{\nu }}{P^2}.& (56)\end{array}$

Note that the scalar sector (52–55) is non-diagonal, such that apart from the diagonal projection operators P^(0,ss) and P^(0,ww) there are the two intertwining operators Π^(0,sw) and Π^(0,ws) which connect the two spin-0 representations s and w. The operators satisfy the algebra (orthogonality and idempotency relations)

$\begin{array}{ll}{\Pi }^{(I,ij)}{{}_{\mu \nu }}^{\alpha \beta }{\Pi }^{(J,kl)}{{}_{\alpha \beta }}^{\rho \sigma }={\delta }^{IJ}{\delta }^{ik}{\Pi }^{(J,jl)}{{}_{\mu \nu }}^{\rho \sigma },& (57)\end{array}$

with J = 2, 1, 0 labeling the spin of the representation and i, j, k, l = s, w labeling the different spin-0 operators. In addition, the diagonal operators (50–53) satisfy the completeness relation

$\begin{array}{ll}{\Pi }^{(2)}{{}_{\mu \nu }}^{\rho \sigma }+{\Pi }^{(1)}{{}_{\mu \nu }}^{\rho \sigma }+{\Pi }^{(0,ss)}{{}_{\mu \nu }}^{\rho \sigma }+{\Pi }^{(0,ww)}{{}_{\mu \nu }}^{\rho \sigma }={\delta }_{\mu \nu }^{\rho \sigma },& (58)\end{array}$

with ${\delta }_{\mu \nu }^{\rho \sigma }=({\delta }_{\mu }^{\rho }{\delta }_{\nu }^{\sigma }+{\delta }_{\nu }^{\rho }{\delta }_{\mu }^{\sigma })/2$ denoting the identity in the space of symmetric rank-two tensors. Finally, the traces of the operators (50–53) yield the dimensions of the invariant subspaces, which, according to (58), add up to the D(D + 1)/2 components of a symmetric rank-two tensor h_μν,

$\begin{array}{l}\text{ tr}{\Pi }^{(2)}=\frac{1}{2}(D+1)(D-2),\text{\hspace{1em} tr}{\Pi }^{(1)}=D-1,\\ \text{tr}{\Pi }^{(0,ss)}=1,\text{\hspace{1em} tr}{\Pi }^{(0,ww)}=1.& (59)\end{array}$

Despite the appearance of the spin-0 projector in (49), the spectrum of propagating particles in GR in D dimensions encompasses only the massless spin-2 graviton; the scalar mode can be eliminated by a residual gauge transformation and is not a physical degree of freedom. As explained in (18), the operator (49) is degenerate and a gauge-fixing is required for its inversion. Choosing O_μν = −η_μνδ(x − y) for the operator in (19) and the DeDonder gauge condition on a flat background,

$\begin{array}{ll}{\chi }^{\mu }\left[\eta ,g\right]=\left({\eta }^{\mu \rho }{\eta }^{\nu \sigma }-\frac{1}{2}{\eta }^{\rho \sigma }{\eta }^{\mu \nu }\right){\partial }_{\nu }{h}_{\rho \sigma },& (60)\end{array}$

the flat gauge-fixed fluctuation operator (25) of GR in momentum space reads

$\begin{array}{ll}{F}_{gf}^{\mu \nu ,\rho \sigma }(-P^2)=\frac{1}{2}\left[{\eta }^{\mu \rho }{\eta }^{\nu \sigma }+{\eta }^{\mu \sigma }{\eta }^{\nu \rho }-{\eta }^{\mu \nu }{\eta }^{\rho \sigma }\right]\left(-P^2\right).& (61)\end{array}$

Inversion of (61) leads to the spin-2 propagator on a flat background¹⁰,

$\begin{array}{ll}{{P}}_{\mu \nu ,\rho \sigma }(-P^2)=\frac{1}{2}\left({\eta }_{\mu \rho }{\eta }_{\nu \sigma }+{\eta }_{\mu \rho }{\eta }_{\nu \sigma }-\frac{2}{D-2}{\eta }_{\mu \nu }{\eta }_{\rho \sigma }\right)\frac{1}{(-P^2)}.& (62)\end{array}$

The propagator ${{P}}_{\mu \nu ,\rho \sigma }$ defines the free theory and hence the particle spectrum in perturbation theory. The massless graviton in D dimensions has D(D − 3)/2 polarization states, obtained by subtracting the 2D components of the independent ghost fields in (21) from the D(D + 1)/2 independent components of the symmetric rank-two tensor h_μν.

The interactions in momentum space are defined by the higher n-point functions ${{V}}_{{\mu }_1{\nu }_1\dots {\mu }_n{\nu }_n}^{(n)}(P_1,\dots ,P_n)$, which derive from the Fourier transforms of the nth functional derivative of the action

$\begin{array}{ll}{{V}}_{{\mu }_1{\nu }_1\cdots {\nu }_n{\mu }_n}^{(n)}(X_1,\dots ,X_n):=\frac{{\delta }^n{S}_{\text{EH}}\left[g\right]}{\delta g_{{\mu }_1{\nu }_1}(X_1)\dots \delta g_{{\mu }_n{\nu }_n}(X_n)},n>2.& (63)\end{array}$

The essential non-linearity of GR [i.e., the non-polynomial dependence of (39) on g_μν] is the origin of the infinite tower of interaction vertices (63) with an increasing number of legs n. The diagrammatic representation of the propagator and the interaction vertices in GR are shown in Figure 2¹¹.

FIGURE 2

Figure 2. Diagrammatic representation of the propagator and the interaction vertices in GR.

The fact that the Einstein-Hilbert action is linear in the scalar curvature implies that GR is a second-order derivative theory, such that (suppressing the index structure) the propagators have a momentum scaling of ${P}\propto P^{-2}$, while all n-point vertices in momentum space scale as ${{V}}^{(n)}\propto P^2$. Feynman diagrams with loops, such as in Figure 1, correspond to a momentum space integral ${I}$ that could diverge in UV. A generic Feynman integral ${I}$ in GR with L-loops, I internal propagators, and V vertices has the momentum scaling

$\begin{array}{ll}{I}\propto {\displaystyle \int }{\left({\text{d}}^{D}P\right)}^L\frac{1}{{\left(P^2\right)}^I}{\left(P^2\right)}^V.& (64)\end{array}$

The superficial degree of divergence $D^{\text{div}}({I})$ provides a simple way of estimating the leading divergence of ${I}$ by power counting. Scaling each loop momentum by a constant factor b, taking the limit b → ∞, and counting powers of b defines $D^{\text{div}}({I})$. If $D^{\text{div}}({I})<0$, the associated diagram is superficially finite (i.e., finite modulo subdivergences); and if $D^{\text{div}}({I})\ge 0$, it is divergent. Using the topological relation I − V = L − 1, valid on an abstract graph level (i.e., independent of the underlying physical theory), the superficial degree of divergence of quantum GR reads

$\begin{array}{ll}{D}_{\text{GR}}^{\text{div}}=DL-2(L-1).& (65)\end{array}$

This equality shows that in D = 4, the degree of divergence grows with the number of loops L as $D_{\text{GR}}^{\text{div}}=2(L+1)$ and signals the perturbatively non-renormalizable character of GR, which in D = 4 is directly connected to the negative mass dimension (43) of the gravitational coupling constant $G_N=M_{\text{P}}^{-2}$.

In addition to this simple power-counting argument, the UV divergences of GR and its coupling to matter fields have been calculated in various approximations. For GR with and without a scalar field, the one-loop divergences were first derived in [36]. In subsequent works, the one-loop divergences were extended, including to GR coupled to abelian and non-abelian gauge fields [91, 92], GR coupled to fermions [93], GR with a cosmological constant [94, 95], GR with non-minimal gauges [60], and GR coupled non-minimally to a scalar field [96–98]. At the two-loop order, the calculations of the UV divergences for pure gravity were first performed in [37, 99] and later confirmed in [100]; see also [59].

In order to make connections with the general formalism outlined in section 2, I briefly illustrate the calculation of the one-loop divergences for the Euclidean version of the Einstein-Hilbert action (39) in D = 4,

$\begin{array}{ll}{S}_{\text{EH}}\left[g\right]=-\frac{M_{\text{P}}^2}{2}{\displaystyle \int }{\text{d}}^{4}X\sqrt{g}(R-2\Lambda ).& (66)\end{array}$

The gauge-breaking action (19) for the second-order theory (66) is given by

$\begin{array}{ll}{S}_{\text{gb}}[{ḡ}_{\mu \nu };h_{\mu \nu }]=-\frac{1}{2}{\displaystyle \int }{\text{d}}^{4}X{\chi }^{\mu }{g}_{\mu \nu }{\chi }^{\nu },& (67)\end{array}$

where the ultra-local operator O_αβ and De Donder gauge condition χ^α are

$\begin{array}{l}{O}_{\alpha \beta }=-\frac{\sqrt{ḡ}}{2}{ḡ}_{\mu \nu }{\delta }^{(4)}(X,Y),\\ {\chi }^{\mu }[{ḡ}_{\mu \nu };h_{\mu \nu }]=\left({ḡ}^{\mu \rho }{ḡ}^{\nu \sigma }-\frac{1}{2}{ḡ}^{\rho \sigma }{ḡ}^{\mu \nu }\right){\bar{\nabla }}_{\nu }{h}_{\rho \sigma }.& (68)\end{array}$

Adding (67) to (66) results in a gauge-fixed fluctuation operator (25), which is of the minimal second-order type (30),

$\begin{array}{ll}{F}^{\mu \nu ,\rho \sigma }={\bar{{G}}}^{\mu \nu ,\tau \lambda }{F}_{\tau \lambda }^{\rho \sigma }={\bar{{G}}}^{\mu \nu ,\tau \lambda }\left(\bar{\Delta }{\delta }_{\tau \lambda }^{\rho \sigma }+{\bar{P}}_{\tau \lambda }^{\rho \sigma }\right),& (69)\end{array}$

where $\bar{\Delta }=-{ḡ}^{\mu \nu }{\bar{\nabla }}_{\mu }{\bar{\nabla }}_{\nu }$ is the positive-definite background Laplacian and the background values of the DeWitt metric ${{G}}^{\mu \nu ,\rho \sigma }$ and the potential $P_{\tau \lambda }{}^{\rho \sigma }$ are defined as

$\begin{array}{ll}{{G}}^{\mu \nu ,\rho \sigma }:=\frac{g^{1/2}}{4}\left(g^{\mu \rho }{g}^{\nu \sigma }+g^{\mu \sigma }{g}^{\nu \rho }-g^{\mu \nu }{g}^{\rho \sigma }\right),& (70)\end{array}$

$\begin{array}{l}{P}_{\mu \nu }{}^{\rho \sigma }:=-2R^{\rho }{}_{\left(\mu \nu \right)}^{\sigma }-2{\delta }_{(\mu }^{(\rho }{R}_{\nu )}^{\sigma )}+g_{\mu \nu }{R}^{\rho \sigma }+g^{\rho \sigma }{R}_{\mu \nu }\hfill \\ -\frac{1}{2}{g}_{\mu \nu }{g}^{\rho \sigma }R+(R-2\Lambda ){\delta }_{\mu \nu }^{\rho \sigma }.\hfill & (71)\end{array}$

According to (22), the ghost operator derives from (68) and reads

$\begin{array}{ll}{Q}_{\mu }{}^{\nu }={\delta }_{\mu }^{\nu }\bar{\Delta }-{\bar{R}}_{\mu }^{\nu }.& (72)\end{array}$

The divergent part of the one-loop approximation (8) reduces to the evaluation of the two functional traces

$\begin{array}{ll}{\Gamma }_1^{\text{div}}=\frac{1}{2}\text{Tr}\ln (F^{\mu \nu }{}_{\rho \sigma }){|}^{\text{div}}-\text{Tr}\ln (Q_{\mu }{}^{\nu }){|}^{\text{div}}.\hfill & (73)\end{array}$

Terms proportional to δ⁽⁴⁾(0) that arise from $\text{Tr}ln({{G}}_{\mu \nu \rho \sigma })$ are zero in dimensional regularization. The divergent parts of the functional traces (73) are most efficiently evaluated by the heat-kernel techniques presented in section 2.3. The operators (69) and (72) in (73) are both of the form (30), for which the divergent part is given by (34). The final result for the one-loop divergences (73) reads

$\begin{array}{l}{\Gamma }_1^{\text{div}}=\frac{1}{16{\pi }^2\epsilon }{\displaystyle \int }{\text{d}}^{4}X\sqrt{ḡ}[-\frac{53}{90}\overline{𝔊}-\frac{7}{20}{\bar{R}{}_{\mu }}_{\nu }{\bar{R}{}^{\mu }}^{\nu }\\ -\frac{1}{120}{\bar{R}}^2+\frac{13}{6}\Lambda \bar{R}-\frac{5}{2}{\Lambda }^2].& (74)\end{array}$

The Euler characteristic $\chi ({M})$ is a topological invariant, defined in terms of the quadratic Gauss-Bonnet invariant 𝔊 as

$\begin{array}{l}\chi ({M}):=\frac{1}{32{\pi }^2}{\displaystyle {\int }_{{M}}}{\text{d}}^{4}X\sqrt{-g}𝔊,\\ 𝔊:=R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }-4R_{\mu \nu }{R}^{\mu \nu }+R^2.& (75)\end{array}$

This allows us to eliminate squares of the Riemann tensor in (74) in favor of squares of the Ricci tensor and squares of the Ricci scalar. For gravity with a cosmological constant in vacuum, the field equations (40) imply R_μν = Λg_μν. Therefore, on-shell, quantum Einstein gravity with a cosmological constant at the one-loop order can be expressed in terms of the Euler characteristic (75) and the volume ${V}({M}):=\int {\text{d}}^{D}X\sqrt{ḡ}$ as

$\begin{array}{ll}{\Gamma }_{1,\text{on-shell}}^{\text{div}}=\frac{1}{\epsilon }\left[-\frac{53}{45}\chi ({M})+\frac{87}{20}\frac{{\Lambda }^2}{12{\pi }^2}{V}({M})\right].& (76)\end{array}$

As discussed in [95], the result (76) shows that, within the one-loop approximation, pure Einstein gravity in D = 4 is on-shell renormalizable, as the divergences in (76) can be absorbed by adding the topological term $\chi ({M})$ (which does not affect the field equations) with some coefficient to the action (66) and renormalizing this coefficient as well as the cosmological constant Λ. For the case of a vanishing cosmological constant, the fact that Einstein gravity is on-shell one-loop finite was first found in [36]. However, as soon as matter fields are coupled, the one-loop divergences remain even on-shell [36]. For example, the one-loop divergences of GR with a minimally coupled scalar field φ with quartic self-interaction induce a non-minimal coupling to gravity proportional to Rφ², an operator not present in the original action [36, 96–98]. At the two-loop order, even for a vanishing cosmological constant Λ = 0, a divergent contribution of a single operator among the cubic curvature invariants survives the on-shell reduction [37, 99, 100],

$\begin{array}{ll}{\Gamma }_{2,\text{on-shell}}^{\text{div}}=\frac{1}{\epsilon }\frac{1}{{(16{\pi }^2)}^2}\frac{209}{1470}\frac{1}{M_{\text{P}}^2}{{\displaystyle \int }}^{\text{}}{\text{d}}^{4}X\sqrt{-g}{\stackrel{-}{C}}_{\mu \nu }{}^{\rho \sigma }{\stackrel{-}{C}}_{\rho \sigma }{}^{\alpha \beta }{\stackrel{-}{C}}_{\alpha \beta }{}^{\mu \nu },\hfill & (77)\end{array}$

thereby showing explicitly that GR is perturbatively non-renormalizable¹². In (77), the cubic Riemann curvature invariant is expressed in terms of the Weyl tensor C_μνρσ, which on-shell coincides with the Riemann tensor R_μνρσ in view of the vacuum on-shell identity R_μν = 0,

$\begin{array}{l}{C}_{\mu \nu \rho \sigma }=R_{\mu \nu \rho \sigma }\\ -\frac{2}{D-2}\left(R_{\mu \rho }{g}_{\nu \sigma }+R_{\nu \rho }{g}_{\mu \sigma }+R_{\mu \sigma }{g}_{\nu \rho }+R_{\nu \sigma }{g}_{\nu \rho }\right)\\ -\frac{R}{(D-1)(D-2)}\left(g_{\mu \rho }{g}_{\nu \sigma }-g_{\nu \rho }{g}_{\mu \sigma }\right).& (78)\end{array}$

In a perturbatively renormalizable QFT, finitely many free parameters (fields, masses, and coupling constants) are sufficient to absorb all UV divergences to all orders in the perturbative expansion. As demonstrated in (65) based on power-counting arguments and in (77) based on explicit calculations, GR is not of that form. New higher-dimensional operators with divergent coefficients are induced at every loop order and have to be renormalized by introducing the corresponding counterterms, each of which introduces a new coupling constant with a finite part that needs to be determined by a measurement. In this way, more and more free parameters are introduced at each order in the perturbative expansion, and the theory ultimately loses its predictive power.

4. Effective Field Theory of Gravity

For many physical systems, an effective coarse-grained description is sufficient to accurately describe phenomena at low energies by the relevant degrees of freedom [38]. Such an effective description might arise in two complementary ways, often referred to as the top-down and bottom-up approaches. In the case where a (more) fundamental theory is known at high energy scales, a top-down approach leads to an effective low-energy theory by “integrating out” the heavy degrees of freedom¹³. Denoting the heavy degrees of freedom collectively by Φ, with characteristic mass scale M_Φ, and denoting the light degrees of freedom by ϕ, with characteristic mass scale M_ϕ, in a “top-down” scenario there is a natural mass hierarchy M_Φ ≫ M_ϕ. Integrating out the Φ-fields from the combined action S[Φ, ϕ] in the path integral defines the effective action S_eff[ϕ] for the ϕ-fields,

$\begin{array}{l}{\displaystyle \int }{D}\left[\varphi \right]e^{-S_{\text{eff}}\left[\varphi \right]}:={\displaystyle \int }{D}\left[\Phi ,\varphi \right]e^{-S\left[\varphi ,\Phi \right]}.\end{array}$

In general, the process of integrating out Φ-fields results in a non-local effective action S_eff[ϕ]. Within an energy expansion E/M_Φ ≪ 1, it can be expanded in terms of local operators ${{O}}_n(\varphi ,\partial )$ for the ϕ-fields as

$\begin{array}{l}{S}_{\text{eff}}\left[\varphi \right]=S\left[\varphi \right]+{\displaystyle \sum _n}{\displaystyle \int }{\text{d}}^{D}X{w}_n\frac{{{O}}_n(\varphi ,\partial )}{M_{\Phi }^{n-D}},\\ {\left[{{O}}_n(\varphi ,\partial )\right]}_M=n,{\left[w_n\right]}_{\text{M}}=0.& (79)\end{array}$

The higher-dimensional local operators ${{O}}_n(\varphi ,\partial )$ parameterize the impact of the heavy degrees of freedom Φ on the effective low-energy theory for the light degrees of freedom ϕ, and their interacting strength is characterized by the dimensionless Wilson coefficients w_n. In terms of momentum space Feynman integrals, this expansion is associated with an expansion of the Φ-propagators in inverse powers of the heavy mass scale M_Φ,

$\begin{array}{ll}\frac{1}{(-P^2)-M_{\Phi }^2}=-\frac{1}{M_{\Phi }^2}-\frac{1}{(-M_{\Phi })}(-P^2)\frac{1}{(-M_{\Phi }^2)}+\cdots .& (80)\end{array}$

For example, in this way, a ϕϕ-ϕϕ interaction from a trivalent vertex ∝gΦϕ² in S[Φ, ϕ] leads to an effective quartic contact interaction between the ϕ-fields $\propto (g^2/M_{\Phi }^2){\varphi }^4$ in S_eff[ϕ], as illustrated in Figure 3.

FIGURE 3

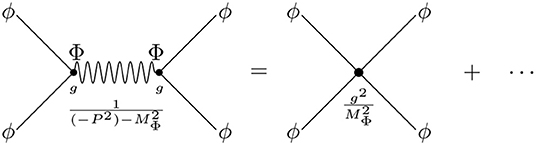
Figure 3. In the diagrammatic representation, to first order in the expansion (80), the Φ-propagator is shrunk to a point, leading to an effective four-point contact interaction between the ϕ-fields.

Since in the top-down approach calculations can be performed both ways, i.e., in the more fundamental theory as well as in the effective theory, scattering amplitudes can be compared at some scale below (but usually close to) M_Φ in order to fix the Wilson coefficients in terms of the parameters of the more fundamental theory, a procedure called matching. Assuming $w_n={O}(1)$, the accuracy of the effective description is limited only by the ratio E/M_Φ, which controls the energy expansion, and completely breaks down for energies E ≈ M_Φ, where the propagation of the Φ particles is no longer suppressed.

Importantly, the effective field theory (EFT) description is still applicable, even if no (more) fundamental theory in the UV is known. This is the situation for GR, i.e., the EFT approach to gravity is necessarily a bottom-up one [39, 40]. In this case, the cutoff scale M that limits the range of validity of the effective description is not known a priori. Assuming no new physics at scales in between the electroweak (EW) scale of the standard model (SM) of particle physics and the scale at which gravity becomes comparable to the other interactions (see Figure 4), the Planck scale might be the natural cutoff scale, M = M_P¹⁴.

FIGURE 4

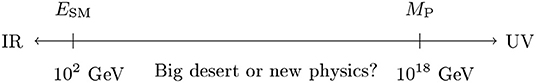
Figure 4. Different energy scales. Is there new physics beyond the EW scale and the Planck scale or a “big desert”?

It could be considered a particular strength of the bottom-up approach that it is agnostic about the gravitational degrees of freedom in the UV: the low-energy limit of the EFT defines the field variables, symmetries, and particle spectrum. In the case of GR, these are the metric field, the diffeomorphisms, and the massless spin-2 graviton. The ignorance of a more fundamental theory in the UV is parameterized by the systematic inclusion of higher-dimensional operators, which are compatible with the symmetries of the defining low-energy theory and suppressed by inverse powers of the cutoff scale. In the case of gravity, diffeomorphism invariance requires that the higher-dimensional purely gravitational operators ${O}(g,\partial )$ have the form of curvature invariants proportional to g^1/2∇²ⁿR^m/M^2(n+m)−D. For energy scales well below the cutoff ∇/M ≪ 1, R/M² ≪ 1, these higher-dimensional operators are strongly suppressed and the expansion can be truncated at a finite order determined by the required accuracy of the EFT. In contrast to a fundamental theory, the higher-dimensional operators in an EFT are viewed merely as correction terms, i.e., they lead to additional interaction vertices but do not modify the propagators of the theory and hence do not affect the particle spectrum, which is defined by the relevant operators at low energy¹⁵. While the higher-dimensional operators in an EFT are included in a controlled way, the precise way in which such an expansion scheme is realized can differ. Depending on the requirements of the underlying physical model, such an expansion could be realized as a derivative expansion, as a vertex expansion, as the aforementioned combined “energy expansion,” or according to a different scheme.

In principle, the presence of the infinite tower of operators ∇²ⁿR^m/M^2(n+m)−D is required in an EFT to absorb all UV divergences by renormalizing the w_i. However, according to the GR power counting (65), the Lth loop correction in D = 4 induces divergent operators of the form ∇²ⁿR^m/M^2(n+m)−D with n + m = L + 1. Thus, within a finite truncation, the EFT of gravity can be perturbatively renormalized in the standard way, and only finitely many renormalized parameters w_i have to be measured, ultimately rendering the EFT predictive¹⁶.

However, ultimately absorbing the UV divergences within a finite truncation provides a consistency condition rather than a prediction. In contrast to the local but unphysical UV divergences, true predictions of the quantum theory are connected with infrared (IR) effects that arise from long-range interactions dominated by massless particles. These contributions are connected to the non-analytic parts in scattering amplitudes. The most prominent example of how such IR effects can be extracted from QFT scattering amplitudes within the EFT of GR concerns the corrections to the Newtonian potential for two point masses M₁ and M₂, which after Fourier transformation read [111]

$\begin{array}{ll}V(r)=-\frac{G_{\text{N}}{M}_1{M}_2}{r}\left[1+3\frac{G_{\text{N}}(M_1+M_2)}{r{c}^2}+\frac{41}{10\pi }\frac{G_{\text{N}}\hslash }{r^2{c}^3}+\cdots \right].& (81)\end{array}$

The second term is a purely classical relativistic correction related to the $\sqrt{P^2}$ part, while the third term is of genuine quantum origin and related to the P²log(P²) part of the one-loop contribution [111]. Both contributions correspond to those parts of the scattering amplitude that have a non-analytic momentum dependence. They are independent of the higher curvature terms in the EFT expansion and therefore do not depend on a UV completion. While the general structure of the correction terms in (81) follows from dimensional analysis, the coefficients (in particular the signs) have to be calculated and provide a true prediction of quantum gravity.

While the quantum gravitational corrections are accompanied by powers of G_Nℏ and are therefore very hard to measure, classical post-Minkowskian (PM) corrections are in powers of G_N. High-order PM corrections have been calculated with classical techniques [112–115]. Since the advent of gravitational wave astronomy, there have been increasing efforts to extract the classical PM corrections within an EFT framework from QFT scattering amplitudes, which, in turn, can be efficiently calculated using modern on-shell techniques (see e.g., [116–122]).

The EFT of GR is a powerful and universal approach that yields universal quantum gravitational predictions from long-range effects of massless particles, but its scope of applicability is limited by construction. Therefore, certain questions cannot be addressed within this framework but require a fundamental quantum theory of gravity.

5. Asymptotic Safety

Although the question about a fundamental theory of gravity cannot be addressed in the framework of the perturbative EFT approach, the asymptotic safety (AS) program, initiated in [123, 124], might offer a UV-complete theory of quantum gravity. The basic underlying idea is that the renormalization group (RG) flow drives the (dimensionless) essential couplings g_n of a theory toward a UV fixed point $g_n^{*}$¹⁷. In this way, the AS scenario prevents the couplings from running into divergences at finite energy scales (Landau poles) and allows the RG flow to be extrapolated to arbitrary energy scales k → ∞. However, in contrast to the asymptotic freedom scenario corresponding to a free (i.e., non-interacting or “Gaussian”) UV fixed point $g_n^{*}=0$, the AS scenario only requires the weaker condition $g_n^{*}=\mathrm{\text{const.}}$, which includes the possibility of an interacting fixed point for $g_n^{*}\ne 0$ [123]. In particular, the couplings g_n are not required to remain within the perturbative regime g_n ≪ 1 and consequently allow for a strongly interacting UV fixed point at which (at least some of) the couplings $g_n^{*}\gg 1$. Clearly such a strongly interacting UV fixed point cannot be found within a perturbative approach. Thus, the AS scenario is an inherently non-perturbative approach, which can be addressed with the Wilsonian approach to the RG [125].

The main object is the averaged effective action Γ_k, which defines the full quantum theory at a given RG scale k. The sliding scale k interpolates between the bare action Γ_∞ = S in the UV, corresponding to k = ∞, and the full effective action Γ₀ = Γ in the IR, corresponding to k = 0. Once the propagating degrees of freedom ϕⁱ and their symmetries are identified, Γ_k can be expressed in terms of symmetry-compatible operators ${{O}}_n(\varphi ,\partial )$ with coupling strengths g_n(k) as

$\begin{array}{ll}{\Gamma }_k={\displaystyle \sum _{i=1}^{\infty }}{\displaystyle \int }{\text{d}}^{D}X{g}_i(k){{O}}_n(\varphi ,\partial ).& (82)\end{array}$

The space of all coupling constants g_i is called theory space. A suitable tool for a non-perturbative analysis is the Wetterich equation [126–128], which describes the exact functional RG flow of the averaged effective action Γ_k,

$\begin{array}{ll}k{\partial }_k{\Gamma }_k=\frac{1}{2}\text{Tr}\left(\frac{k{\partial }_k{{R}}_k}{{\Gamma }_k^{(2)}+{{R}}_k}\right).& (83)\end{array}$

Here, Tr is the functional trace, ${{R}}_k$ is a scale-dependent regulator and ${\Gamma }_k^{(2)}$ is the Hessian of the averaged effective action Γ_k. The Wetterich equation (83) has a similar structure to the one-loop approximation (8) but involves the scale-dependent regulator function ${{R}}_k$ defined such that it acts as an effective mass term of the full propagator for quantum fluctuations with momenta P² ≤ k² and vanishes for momenta P² ≫ k². Together with the factor ${\partial }_k{R}$ in (83), which cuts off fluctuations with momenta P² ≥ k², the presence of the regulator ensures that only fluctuations with momenta peaked around P² ≈ k² contribute to the trace in (83), thereby realizing the Wilsonian “shell-by-shell” integration¹⁸. Owing to the presence of the regulator, no divergences occur. In general, the Wetterich equation cannot be solved exactly. Instead of a semiclassical expansion in powers of loops, such as in (6), a finite truncation of the (in general infinite) set of operators included in Γ_k is performed:

$\begin{array}{ll}{\Gamma }_k={\displaystyle \sum _{n=1}^N}{\displaystyle \int }{\text{d}}^{D}X{g}_n(k){{O}}_n(\varphi ,\partial ).& (84)\end{array}$

According to which criteria such a truncation is chosen practically may depend on the underlying physical problem. In most applications the operators are organized in terms of an energy expansion, i.e., ordered by increasing canonical mass dimension. There are, however, cases where a derivative expansion or a vertex expansion is more appropriate. In the case of gravity, diffeomorphism invariance requires that the ${O}(g,\partial )$ be curvature invariants, schematically ${O}(g,\partial )=\sqrt{g}{(\nabla )}^{2p}{R}^m$. By substituting the ansatz (84) into (83), choosing a regulator ${{R}}_k$, and evaluating the functional trace on the right-hand side of (83), the RG flow of the couplings g_n(k) can be extracted by “projecting” to the operator basis ${{O}}_n(\varphi ,\partial )$. Contributions of operators that are induced by the flow and lead out of the truncation (84) are neglected¹⁹.

For a successful realization of the AS scenario, the existence of a UV fixed point $g_i^{*}$ is only a necessary condition, not a sufficient one. In addition, an appropriate fixed point must have a finite-dimensional UV critical surface²⁰. The finiteness of the UV critical surface lies at the very heart of the AS scenario, as it implies that only a finite subset of the (in general infinitely many) coupling constants have to be measured, rendering the theory predictive. It is this feature that might qualify the AS scenario in providing a UV-complete quantum theory of gravity²¹. Therefore, in principle, if all UV-relevant couplings were measured (and thus a particular RG trajectory emanating from the UV fixed point selected), all other UV-irrelevant couplings would be fixed. They therefore constitute predictions that could be falsified by additional measurements of these couplings. In practice, however, calculations are limited to finite truncations, and one must ensure that the properties of the fixed point (and hence any prediction derived from them) remain stable under an enlargement of the truncation. In principle, if a reliable measure of the quality of a given truncation were to exist, one could try to ultimately prove convergence; but as so far no such measure exists, this is hard to realize in practice and one has to rely on systematic step-by-step enlargements of finite truncations. Nevertheless, as for the perturbative approach (fundamental or EFT), a particular strength of the AS approach to quantum gravity is its universality, i.e., gravity and matter fields are treated within one and the same formalism. This not only allows for a unification but also enables one to test the techniques used in the context of quantum gravity in more controlled environments, for which experimental data are also available.

The functional RG flow in the context of gravity [41–43, 129, 130] has been studied in various truncations, starting with the Einstein-Hilbert truncation [131], encompassing higher curvature invariants [132–137] and matter fields [138–143] as well as closed flow equations for f(R) gravity [144, 145], and general scalar-tensor theories [146, 147]. A pattern that emerges from most of these truncations is that an interacting UV fixed point can be found and the dimension of the associated UV critical surface does not grow upon enlarging the truncation beyond the classically marginal operators. Since this program has been pushed to high orders in various truncations, it might provide some confidence that the observed pattern is a generic feature and not an artifact of the truncation.

Despite these interesting results, there are a number of open questions associated with this program (see e.g., [148]). In general, the off-shell flow defined by Γ_k suffers from a number of ambiguities related to the choice of regulator as well as to the gauge dependence and field parametrization dependence of the beta functions. Since different regulator choices, different gauges, and different field parameterizations can even affect qualitative features, such as the existence of a fixed point, a satisfying resolution of these ambiguities seems to be crucial for establishing the reliability of the predictions following from the AS conjecture.

In connection with the gauge and parameter dependence, a unique off-shell extension of the averaged effective action along the lines of the construction proposed in [149] might offer an interesting option. But even without such a construction, the gauge and parametrization dependence should be absent in an on-shell scheme (see e.g., [150]). However, making use of the equations of motion in general leads to degeneracies among different operators in a given truncation and therefore the individual RG flow of the couplings for these on-shell degenerate operators cannot be disentangled and resolved²². Nevertheless, extracting, for example, physical observables from the S-matrix will anyway involve an on-shell reduction. By definition only essential couplings span the theory space. In this sense, the “on-shellness” is already built into the formalism of the AS conjecture from the very beginning. However, especially in the context of gravity, the situation is more complicated. For example, the question of whether Newton's constant is an essential or inessential coupling is not so clear and leads to conceptional intricacies (see e.g., the discussion in [151]).

In any case, the starting point for the derivation of observables should be the effective action at k = 0, which is independent of the regulator and is formally obtained by integrating out all quantum fluctuations, i.e., integrating the functional flow all the way down to the IR. One might be tempted to extract information from the averaged effective action Γ_k at non-zero k by performing an “RG-improvement” based on a heuristic identification of the abstract coarse-graining RG scale k with some characteristic physical scale. However, aside from the fact that such an identification is typically only possible in highly symmetric backgrounds where a single scale is present, such as the radius in the context of spherically symmetric black hole backgrounds, the Hubble parameter in the context of an isotropic and homogeneous cosmological Friedmann-Lemaître-Robertson-Walker background, the value of the scalar field in the Coleman-Weinberg-like radiatively induced symmetry breaking in a classically scale-invariant theory, or the momentum transfer in the context of scattering amplitudes—it does not seem that such a naive identification can be based on a more general solid theoretical ground. However, even when working with the effective action at k = 0, another problem arises: the effective action is non-local (and non-analytic) and therefore not appropriately described by the finite number of local operators in a given truncation that do not capture essential IR contributions. In this context, the introduction of form factors in the AS program provides a more promising route. Including form factors in the truncation goes beyond a finite derivative expansion, as it captures the full momentum dependence of propagators and vertices, which can be studied either using a flat-space vertex expansion [152–154] or in a general background by an expansion of the effective action in powers of external fields (curvatures in the context of gravity) [155, 156]. The manifest covariant calculations of these non-local form factors are technically challenging and require heat-kernel-based methods developed in [108, 109, 157–159].

The analysis of form factors in the AS program may also shed light on the status of the particle content, a problem shared by higher-derivative theories of gravity, discussed in section 6. Any truncation based on a finite derivative expansion will in general lead to additional propagating degrees of freedom in the particle spectrum (defined by the quadratic action expanded around a flat background) and will almost always include higher-derivative ghosts among them. Having access to the pole structure of the propagators, including the full momentum dependence carried by the form factors, may ultimately reveal the status of the ghost degrees of freedom as an artifact of the finite truncation (realized, for example, when the full propagators have only a single pole with positive residue). Technically, this program is closely related to the (ghost-free) non-local approach to quantum gravity (see e.g., [18, 20–22, 25, 26]).

6. Higher-Derivative Gravity

Before giving up on finding a fundamental theory of quantum gravity or abandoning the framework of perturbative QFT, another obvious approach to try is to modify the underlying classical theory of gravity and investigate the impact of these modifications on the resulting quantum theory. Adding higher-dimensional curvature invariants to the action might be the most natural generalization of GR. In contrast to the EFT treatment, when treating the modified theory as fundamental, the higher-dimensional operators are no longer considered as perturbations, and so they not only modify the interaction vertices but also the propagators. Ultimately, this leads to new additional propagating degrees of freedom. There are many ways to modify GR. A simple and phenomenologically important extension of GR is f(R) gravity, allowing for an arbitrary function f of the Ricci scalar R,

$\begin{array}{ll}{S}_f\left[g\right]={\displaystyle \int }{\text{d}}^{4}X\sqrt{g}f(R).& (85)\end{array}$

In particular, (85) encompasses the Starobinsky model [160], which is highly relevant for inflationary cosmology,

$\begin{array}{ll}{f}_{\text{Star}}=\frac{M_{\text{P}}^2}{2}\left[R+\frac{1}{6M_0^2}{R}^2\right].& (86)\end{array}$

In fact, (86) was the first model of inflation and is strongly favored by the latest Planck data [161]. The one-loop divergences for f(R) gravity (85) have recently been calculated on an arbitrary background [76], thereby essentially generalizing previous calculations obtained for spaces of constant curvature [144, 145, 162],

$\begin{array}{l}{\Gamma }_1^{\text{div}}=\frac{1}{32{\pi }^2\epsilon }{{\displaystyle \int }}^{\text{}}{\text{d}}^{4}X\sqrt{g}[-\frac{71}{60}𝔊-\frac{259}{180}{R}_{\mu }{}_{\nu }{R}^{\mu }{}^{\nu }-\frac{9}{2}{\left(\frac{f}{f_1}\right)}^2\hfill \\ -\frac{1}{18}{\left(\frac{f_1}{f_2}\right)}^2+\frac{9}{2}\frac{f}{f_1}R+\frac{1}{3}\frac{f}{f_2}-\frac{59}{360}{R}^2+\frac{21}{2}\frac{f}{f_1}\left({{\rm Y}}_{\mu }{}^{;\mu }\right)\hfill \\ -\frac{33}{4}R\left({{\rm Y}}_{\mu }{}^{;\mu }\right)-\frac{371}{72}R\left({{\rm Y}}_{\mu }{{\rm Y}}^{\mu }\right)+\frac{27}{4}\frac{f}{f_1}\left({{\rm Y}}_{\mu }{{\rm Y}}^{\mu }\right)\hfill \\ +\frac{20}{9}{R}_{\mu }{}_{\nu }{{\rm Y}}^{\mu }{{\rm Y}}^{\nu }-\frac{137}{24}{\left({{\rm Y}}_{\mu }{}^{;\mu }\right)}^2-\frac{9}{8}\left({{\rm Y}}_{\mu }{{\rm Y}}^{\mu }\right)\left({{\rm Y}}_{\nu }{}^{;\nu }\right)\hfill \\ -\frac{769}{96}{\left({{\rm Y}}_{\mu }{{\rm Y}}^{\mu }\right)}^2].\hfill & (87)\end{array}$

The derivatives of the function f are defined by $f_n:={\partial }^{n}f/\partial R^n$, and the vector Υ_μ is defined as Υ_μ: = R_{; μ}f₂/f₁. Even for a general function f, the result (87) shows that f(R) gravity is perturbatively non-renormalizable on a general background. Although divergences accompanied by arbitrary functions of R can be absorbed by renormalizing f(R), due to the absence of the derivative structures Υ_μ and the quadratic curvature structure $R_{\mu \mu }{R}^{\mu \nu }$ in (85), the associated divergences cannot be absorbed²³. The higher derivatives in (85) lead to a fourth-order fluctuation operator and imply the presence of an additional propagating scalar degree of freedom, the scalaron. In the context of the cosmological model (86), the scalaron drives the accelerated expansion of the early universe, and its mass $M_0\approx 10^{-5}{M}_{\text{P}}$ is fixed by the observed anisotropy spectrum in the cosmic microwave background radiation [161].

What is the required extension of GR that qualifies as a candidate for a perturbatively renormalizable quantum theory of gravity? The power counting performed in (65) for GR can easily be generalized to higher-derivative theories of gravity. Diffeomorphism invariance requires that all higher curvature invariants have a schematic structure $\sqrt{-g}{\nabla }^{2n}{R}^m$ (suppressing indices) with a total number of derivatives p = 2(n + m). The natural candidate higher-derivative gravity (HDG) theory is the one which includes all classically relevant and marginal operators, i.e., in the D = 4 case all operators with p ≤ 4. Aside from the relevant operators (46) that are already present in the Einstein-Hilbert action (39), the marginal operators with p = 4 have either m = 2 and n = 0 or m = 1 and n = 1. For the latter case, there is only one scalar invariant ${{O}}_3(g,\partial )=\sqrt{-g}{\nabla }_{\mu }{\nabla }^{\mu }R$, which is a total derivative. For the former case there are three possible scalar invariants that are quadratic in the curvature,

$\begin{array}{l}{{O}}_4(g,\partial )=\sqrt{-g}{R}_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma },\\ {{O}}_5(g,\partial )=\sqrt{-g}{R}_{\mu \nu }{R}^{\mu \nu },\\ {{O}}_6(g,\partial )=\sqrt{-g}{R}^2.& (88)\end{array}$

The three curvature invariants in (88) can be more conveniently parameterized in a different basis of quadratic curvature invariants involving the Gauss-Bonnet term, the Weyl tensor, and the Ricci scalar, as the latter two are more directly related to the particle content:

$\begin{array}{l}{S}_{\text{QDG}}\left[g\right]=S_{\text{EH}}\left[g\right]+{\displaystyle \int }{\text{d}}^{4}X\sqrt{-g}\\ \times \left[c_1𝔊+c_2{C}_{\mu \nu \rho \sigma }{C}^{\mu \nu \rho \sigma }+c_3{R}^2\right].& (89)\end{array}$

The power counting in the UV is dominated by the marginal quadratic curvature operators, and the momentum scaling of the propagator is ${P}\propto P^{-4}$, while that of the vertices is ${{V}}^{(n)}\propto P^4$. Consequently, the superficial degree of divergence in quadratic gravity (QDG) in D = 4 is

$\begin{array}{ll}{D}_{\text{QDG}}^{\text{div}}=4L-4(L-1)=4.& (90)\end{array}$

Hence, in D = 4, QDG is power-counting renormalizable, suggesting that QDG is indeed the required extension of GR. Going beyond this simple power-counting argument requires more advanced methods; a strict proof that the QDG (89) is a perturbatively renormalizable quantum theory of gravity was given in [45].

However, even if the perturbative renormalizability of QDG has been established, it remains to show that QDG is UV-complete, i.e., that the theory can be extended to an arbitrary energy scale. To answer this question requires studying the RG flow determined by the divergence structure of the theory. In particular, for a UV-complete theory the absence of Landau poles, where couplings diverge at finite energies, must be assured. The one-loop divergences of QDG were first calculated in [163] and later corrected in [164]. The authors of [164] considered the Euclidean version of (89) with a different parametrization and basis for the quadratic curvature invariants,

$\begin{array}{l}{S}_{\text{QDG}}\left[g\right]={\displaystyle \int }{\text{d}}^{4}X\sqrt{g}[\frac{2}{k^4}\lambda -\frac{1}{k^2}R+\frac{1}{{\nu }^2}𝔊\\ +\frac{1}{f^2}\left(R_{\mu \nu }{R}^{\mu \nu }-\frac{1}{3}{R}^2\right)-\frac{\omega }{3f^2}{R}^2],& (91)\end{array}$

with $1/k^2=M_{\text{P}}^2/2$ and the dimensionless cosmological constant $\lambda =2\Lambda /M_{\text{P}}^2$. The beta functions can directly be read off from the one-loop divergences and determine the running of the coupling constants with the logarithmic parameter $t:=1/(4{\pi }^2)ln(\mu /{\mu }_0)$. Here μ is the sliding scale and μ₀ an arbitrary renormalization point. Within the standard framework with the “ordinary” definition of the effective action as in (5), it was found in [164] that the essential couplings 1/ν²(t), 1/f²(t), and ω/f²(t) are asymptotically free, provided that 1/ν² > 0, 1/f² > 0, and ω/f² < 0, while λ grows in the UV limit t → ∞. Note, however, that in [165] it was found that ω/f² > 0 is required in the Lorentzian regime to avoid a tachyonic instability of the scalaron. Fixing the correct sign, the running is no longer asymptotically free.

Newton's constant, or k² in terms of the parametrization in (91), is an inessential coupling and does not run. In order to access the running of all couplings separately, including the running of k², an off-shell extension is required, which renders the effective action gauge-independent and parametrization-invariant²⁴. Such an off-shell extension was proposed in [149] by a geometrically defined (field-covariant) “unique” effective action. At the one-loop level, the difference between the “ordinary” definition of the effective action and the “unique” effective action is a correction term proportional to the equations of motion. The “unique” off-shell one-loop beta functions for (91) were calculated in [164] and the running of 1/k²(t) was extracted, with the result that ${lim}_{t\to \infty }1/k^2(t)=0$ and ${lim}_{t\to \infty }\Lambda (t)=0$. Thus, the UV limit t → ∞ found in this way corresponds to the induced gravity scenario $M_{\text{P}}^2\to 0$ (i.e., G_N → ∞) with vanishing (dimensional) cosmological constant Λ → 0²⁵.

While the above quoted results support the status of QDG in D = 4 as a perturbative renormalizable theory of quantum gravity, the reason QDG is not usually regarded as a consistent theory of quantum gravity relates to its problem with the additional propagating spin-2 ghost degrees of freedom. In analogy to (49), the momentum space fluctuation operator of QDG defined in the parametrization (89) for arbitrary D on a flat background can be expressed in terms of the projectors (50) and (53) and reads [171]

$\begin{array}{ll}\begin{array}{l}{F}^{\mu \nu ,\rho \sigma }(-P^2)=\frac{(-P^2)}{2}\left[1+8c_2\frac{D-3}{D-2}\frac{(-P^2)}{M_{\text{P}}^2}\right]P^{(2)}{}^{\mu \nu \rho \sigma }\\ -(D-2)\frac{(-P^2)}{2}\left[1-8c_3\frac{D-1}{D-2}\frac{(-P^2)}{M_{\text{P}}^2}\right]P^{(0,ss)}{}^{\mu \nu \rho \sigma }.\end{array}\hfill & (92)\end{array}$

Clearly, this reduces to (49) for c₂ = c₃ = 0. Moreover, because of the topological nature of the GB term 𝔊, c₁ does not enter (92). Just as in GR, the diffeomorphism invariance of QDG renders the fluctuation operator (92) degenerate, and a gauge-fixing is required to obtain the propagators. Nevertheless, the tree-level particle spectrum of QDG can already be analyzed on the basis of the pole structure in (92). Defining the two effective masses for D > 3,

$\begin{array}{ll}{M}_2^2:=-\frac{1}{8c_2}\frac{D-2}{D-3}{M}_{\text{P}}^2,M_0^2:=\frac{1}{8c_3}\frac{D-2}{D-1}{M}_{\text{P}}^2,& (93)\end{array}$

the pole structure of the propagators in the spin-2 and spin-0 sectors becomes more transparent [45]:

$\begin{array}{ll}{{P}}_{(2)}\propto \frac{-M_2^2}{(-P^2)\left[(-P^2)-M_2^2\right]}=\frac{1}{(-P^2)}-\frac{1}{(-P^2)-M_2^2},& (94)\end{array}$

$\begin{array}{ll}{{P}}_{(0)}\propto \frac{M_0^2}{(-P^2)\left[(-P^2)-M_0^2\right]}=-\frac{1}{(-P^2)}+\frac{1}{(-P^2)-M_0^2}.& (95)\end{array}$

The partial fraction in the second equality reveals that, compared to GR, in QDG there are two additional propagating particles with masses M₂ and M₀. The first term in (94) corresponds to a massless spin-2 particle and, just as in GR, combines with the first term in (95) to become the massless graviton. The second term of (94) indicates the presence of a propagating massive spin-2 particle originating from the $C_{\mu \nu \rho \sigma }{C}^{\mu \nu \rho \sigma }$ term in (89), while the second term in (95) indicates the presence of a massive spin-0 particle originating from the R² term in (89). Excluding tachyons requires $M_2^2>0$ (c₂ < 0) and $M_0^2>0$ (c₃ > 0). The massive spin-0 particle, which can be identified with the scalaron in model (86), is “healthy” (neither a ghost nor a tachyon), while the overall minus sign in the second term of (94) shows that the massive spin-2 particle is a higher-derivative ghost. The presence of ghosts corresponds to states of negative norm, leading to a violation of unitarity [45] (see also [172–175]).

Within an effective low-energy treatment $P^2/M_2^2\ll 1$, the propagation of the massive spin-2 ghost is strongly suppressed. Whether such an EFT, which still includes the scalaron as a propagating degree of freedom (since the R² would not be treated as a perturbation compared to the R term), can be realized depends strongly on the characteristic mass scales M₂ and M₀, i.e., the values of c₂ and c₃, respectively. It requires that $M_2^2$ be large enough that the effective description is valid up to energy scales at which the additional propagating scalaron has interesting phenomenology, such as in the inflationary model (86), but at the same time $M_0^2\ll 1$ must be sufficiently small that the scalaron can be considered a propagating degree of freedom; see e.g., [176] for discussion of such a scenario in the context of the scalaron-Higgs model. Solar system-based experimental constraints on both c₂ and c₃ are extremely weak. However, while c₂ is practically unconstrained, a large $c_3=M_{\text{P}}^2/(12M_0^2)\approx 10^9$ is required in (86) if the scalaron is supposed to drive inflation. But even if the problem with the spin-2 ghost can effectively be neglected at sufficiently “low” energies, without a mechanism that prevents the occurrence of the higher-derivative ghost at arbitrarily high energy scales, QDG cannot be considered a fundamental theory.

Recently, the negative conclusion about the ghost-related loss of unitarity in QDG at the fundamental level has been questioned. The questions are related to early proposals about different quantization prescriptions, which modify the pole structure of the propagators in higher-derivative theories [177, 178]. In [47, 179] a new quantization prescription was proposed which turns higher-derivative ghosts into “fakeons” at the expense of a loss of micro-causality. Another resolution of the unitarity problem was suggested in [48, 180]. A key point in this proposal is that the coupling of light matter particles to gravity renders the heavy spin-2 ghost unstable, such that the ghost is not part of the asymptotic particle spectrum. Extending the conclusion that unstable particles must be excluded from the sum of the unitarity relation [181] to the case of unstable ghost particles (which are nevertheless identified as such by the free-particle spectrum), it is concluded in [48] that there is no violation of unitarity in QDG. Nevertheless, in [48, 180] it is also found that the ghosts “propagate backwards in time,” leading to a violation of micro-causality. While this effect can in principle be tested experimentally, it becomes unobservably small for sufficiently heavy ghost masses, such as in QDG if M₂ ≈ M_P.

Summarizing, the proposals [47, 179] and [48, 180] about the correct treatment of higher-derivative ghost particles both led to the conclusion that the unitarity violation can be avoided at the expense of violating micro-causality, but it seems that a conclusive agreement on this controversially debated issue has not yet been reached. For related work on higher-derivative ghosts (see also [182–194]). For a discussion of the ghost problem in the context of the non-perturbative AS program for quantum gravity, see e.g., [135, 195–199]. For the non-local approach to a ghost-free quantum theory of gravity (see [17–26]).

7. Hořava Gravity

The picture emerging from the previously described approaches to providing a consistent fundamental local quantum theory of gravity suggests that the basic principles of relativistic invariance, renormalizability, and unitarity are incompatible in the context of the perturbative quantization of the gravitational interaction: quantum GR is a relativistic and unitary but perturbatively non-renormalizable QFT, while quantum QDG is a relativistic and perturbatively renormalizable but non-unitary QFT. Therefore, in [49, 50], Petr Hořava suggested exploring the consequences of abandoning relativistic invariance while trying to preserve unitarity and perturbative renormalizability.

One of the key motivations for Hořava's proposal comes from the discussion of QDG. While the higher derivatives help to improve the UV behavior of the theory, the higher time derivatives are responsible for the occurrence of the additional higher-derivative ghost degrees of freedom and the associated problems with unitarity. The desire to keep the UV-improving effect of the higher derivatives, but at the same time avoid the ghost problem, leads to the idea of allowing higher spatial derivatives but restricting to second-order time derivatives. Obviously, such a proposal is not compatible with relativistic invariance. It is clear that “sacrosanct” principles, such as relativistic invariance should not be recklessly sacrificed—not only because this changes the fundamental structure of spacetime but also since there are very strong experimental constraints on Lorentz-violating effects.

With this proviso, I first review how the above idea can be formalized by the notion of an anisotropic Lifshitz scaling between space and time and how it can be incorporated into a consistent mathematical framework by formulating the resulting anisotropic theory of gravity in terms of the geometric Arnowitt-Deser-Misner (ADM) variables, giving rise to the Lifshitz theory of gravity, Hořava gravity (HG). Within the ADM formulation, the main difference between GR and HG is the weaker invariance group underlying HG, the foliation-preserving diffeomorphisms $\text{Dif}{\text{f}}_{{F}}$, which form a subgroup of the full diffeomorphisms.

Important consequences of the anisotropic scaling and the less restrictive invariance group in HG are the modified dispersion relations and the presence of an additional propagating gravitational scalar degree of freedom. After a brief discussion of their phenomenological consequences in D = 2 + 1 and D = 3+1 dimensions, I review the quantum properties of HG. I first discuss the gauge and propagator structure of the theory and then review the essential steps in the proof of perturbative renormalizability of the projectable version of HG.

Finally, I discuss the UV properties of quantum HG based on the RG flow of the projectable theory in D = 2 + 1 dimensions, which requires explicit calculation of the one-loop divergences within a Lifshitz theory of gravity [53]. I close with a brief summary and an outlook on future perspectives of quantum HG. For earlier reviews of HG with a different focus, especially on the phenomenological constraints and the cosmological applications (see [200–203]).

7.1. Anisotropic Scaling and Modified Propagators

As briefly outlined before, the basic idea of Hořava gravity is to allow higher spatial derivatives but restrict to second-order time derivatives. Obviously, such a proposal implies that relativistic invariance will be lost at the fundamental level. How precisely Lorentz invariance is broken in a manner compatible with this proposal can be made concrete by introducing the anisotropic Lifshitz scaling between time and space [49, 50, 204],

$\begin{array}{ll}t\to b^{-z}t,x^i\to b^{-1}{x}^i.& (96)\end{array}$

Here, b is a constant scaling parameter and z a dynamical scaling exponent. In analogy to the mass dimension [·]_M introduced in section 3.1, the anisotropic scaling dimension is denoted by [·]_S. According to the anisotropic scaling law (96), the scaling dimensions of time and space are [t]_S = −z and [x]_S = −1. This implies the scaling relations

$\begin{array}{ll}{\left[{\partial }_t\right]}_{\text{S}}=z,{\left[{\partial }_i\right]}_{\text{S}}=1,{\left[\omega \right]}_{\text{S}}=z,{\left[k_i\right]}_{\text{S}}=1,& (97)\end{array}$

where ω and k_i are the frequency and spatial momentum, Fourier conjugates to ∂_t and ∂_i. The dynamical scaling exponent z can be thought of as measuring the degree of anisotropy between space and time, with z = 1 restoring relativistic invariance. In view of (97), the (Euclidean) anisotropic propagator takes the form

$\begin{array}{ll}{P}\propto \frac{1}{{\omega }^2+k^2+\cdots +G(k^2{)}^z}\simeq \{\begin{array}{cc}\frac{1}{{\omega }^2+k^2}=\frac{1}{p^2}& \text{in the IR,}\\ \frac{1}{{\omega }^2+G(k^2{)}^z}& \text{in the UV,}\\ \end{array}& (98)\end{array}$

with some coupling constant G such that [G]_M = −2(z − 1) and [G]_S = 0. This propagator illustrates the basic idea that Lorentz invariance is completely broken by the anisotropic scaling exponent z for G(k²)^z ≫ k² in the UV limit and is effectively restored in a natural way for k² ≫ G(k²)^z in the IR limit [50]²⁶.

7.2. Geometrical Formulation in Terms of ADM Variables

The anisotropic Lifshitz theory of gravity can be consistently formulated within a geometrical framework when described in terms of ADM variables. Following the presentation in [205], I briefly review the ADM formulation in the context of GR, and highlight the differences in HG when the full diffeomorphism invariance $\text{Diff}({M})$ is reduced to the foliation-preserving diffeomorphism $\text{Dif}{\text{f}}_{{F}}({M})$.

7.2.1. ADM Variables and GR

A point $X\in {M}$ in the D-dimensional ambient spacetime ${M}$ can be described by local coordinates X^μ. For a globally hyperbolic ambient space, ${M}$ can be foliated by a one-parameter family of d-dimensional spatial hypersurfaces Σ_t of constant time t, where d = D − 1. The hypersurfaces Σ_t can be thought of as level surfaces of a time field t. The gradient of t defines a natural unit covector field

$\begin{array}{l}{n}_{\mu }:=-\frac{{\nabla }_{\mu }t}{\sqrt{-g^{\mu \nu }{\nabla }_{\mu }t{\nabla }_{\nu }t}},\\ n^{\mu }=g^{\mu \nu }{n}_{\nu },n^{\mu }{n}_{\mu }=-1.& (99)\end{array}$

By construction, at each point, the normal vector field n^μ(x, t) is orthogonal to Σ_t and therefore allows an orthogonal decomposition of tensor fields with respect to n^μ. In particular, the ambient metric decomposes as

$\begin{array}{ll}{g}_{\mu \nu }={\gamma }_{\mu \nu }-n_{\mu }{n}_{\nu }.& (100)\end{array}$

Here, γ_μν is the tangential part of g_μν, i.e., ${\gamma }_{\mu \nu }{n}^{\mu }=0$. The hypersurfaces Σ_t can be viewed as embeddings of an intrinsically d-dimensional manifold ${\tilde{\Sigma }}_t$ into the ambient space ${M}$. A point $x\in {\tilde{\Sigma }}_t$ can be described by the local coordinates xⁱ, i = 1, …, d. The D-dimensional coordinates X^μ = X^μ(t, x) can be parameterized in terms of the time field t and the spatial coordinates xⁱ. The change of X^μ with respect to t and xⁱ is given by the coordinate one-form

$\begin{array}{ll}\text{d}{X}^{\mu }=t^{\mu }\text{ d}t+e^{\mu }{}_i\text{ d}{x}^i.& (101)\end{array}$

The time vector field t^μ and the soldering form e^μ_i appearing in (101) are defined as

$\begin{array}{ll}{t}^{\mu }:=\frac{\partial X^{\mu }(t,x)}{\partial t},e^{\mu }{}_i:=\frac{\partial X^{\mu }(t,x)}{\partial x^i}.\hfill & (102)\end{array}$

As illustrated in Figure 5, the lapse function N(t, x) and the shift vector N^μ(t, x) are defined as the coefficients of the orthogonal decomposition of t^μ: = Nn^μ + N^μ in the directions normal and tangential to Σ_t, respectively.

FIGURE 5

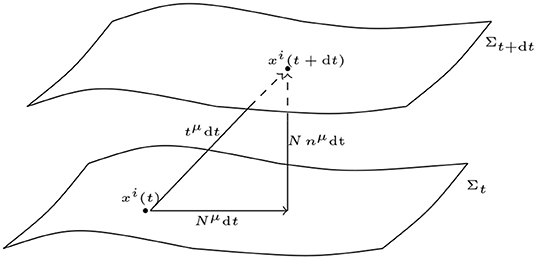
Figure 5. Foliation of D-dimensional spacetime into hypersurfaces of dimension d = D − 1 at constant time t.

The soldering form e^μ_i transforms like a D-dimensional tangential vector with respect to the μ index, i.e., e^μ_in_μ = 0, and a d-dimensional vector with respect to the i index. It defines the pullback of tangential tensors in ${M}$ to tensors in ${\tilde{\Sigma }}_t$:

$\begin{array}{ll}{e}^{\mu }{}_i{e}_{\nu }{}^i={\delta }_{\nu }^{\mu },e^i{}_{\mu }{e}^{\mu }{}_j={\delta }_j^i.\hfill & (103)\end{array}$

The pullbacks of γ_μν and N^μ define the spatial metric γ_ij and the spatial shift-vector Nⁱ,

$\begin{array}{ll}{\gamma }_{ij}:=e^{\mu }{}_i{e}^{\nu }{}_j{\gamma }_{\mu \nu },N^i:=e_{\mu }{}^i{N}^{\mu }.\hfill & (104)\end{array}$

In terms of dt and dxⁱ, the ambient space coordinate one-form is expressed as

$\begin{array}{ll}d{X}^{\mu }=N{n}^{\mu }\text{ d}t+e_i^{\mu }\left(N^i\text{ d}t+\text{d}{x}^i\right).& (105)\end{array}$

Inserting this into (42), the ambient space line element takes the familiar ADM form [206]

$\begin{array}{ll}d{s}^2=-N^2\text{ d}{t}^2+{\gamma }_{ij}\left(N^i\text{ d}t+\text{d}{x}^i\right)\left(N^j\text{ d}t+\text{d}{x}^j\right).& (106)\end{array}$

On ${\tilde{\Sigma }}_t$, the commutator of the (torsion-free and metric-compatible ∇_kγ_ij = 0) spatial covariant derivative ∇_i defines the d-dimensional spatial curvature tensor by its action on a spatial vector field v^k,

$\begin{array}{ll}[{\nabla }_i,{\nabla }_j]v^k=R_l^k{{}_i}_j(\gamma )v^l.& (107)\end{array}$

The relation between the scalar curvature of the D-dimensional ambient space R(g) and the scalar curvature R(γ) of the d-dimensional embedded space is given by the Gauss-Codazzi relation (see e.g., [207])

$\begin{array}{l}R(g)=R(\gamma )-\left(K^2-K_{ij}{K}^{ij}\right)\\ -2({\nabla }_i+a_i)a^i+2(D_t+K)K.& (108)\end{array}$

Here, $K:={\gamma }^{ij}{K}_{ij}$ is the trace of the extrinsic curvature K_ij, defined via the covariant time derivative D_t as

$\begin{array}{l}{K}_{ij}:=\frac{1}{2}{D}_t{\gamma }_{ij}=\frac{1}{2N}\left({\partial }_t{\gamma }_{ij}-{\nabla }_i{N}_j-{\nabla }_i{N}_j\right),\\ D_t:=\frac{1}{N}({\partial }_t-{{L}}_{\text{N}}),& (109)\end{array}$

where ${{L}}_{\mathbf{\text{N}}}$ is the Lie derivative along the spatial shift vector Nⁱ. The acceleration vector aⁱ in (108) is defined as

$\begin{array}{ll}{a}_i:={\partial }_{i}lnN.& (110)\end{array}$

Note that the D-dimensional diffeomorphisms $\text{Diff}({M})$ completely fix the structure and the numerical coefficients of the individual terms in (108). In terms of the ADM variables (106), the volume element of ${M}$ reads $\sqrt{-g}=N\sqrt{\gamma }$, and, modulo surface terms, the Einstein-Hilbert action (39) takes the ADM form

$\begin{array}{ll}{S}_{\text{EH}}=\frac{M_{\text{P}}^2}{2}{\displaystyle \int }\text{d}t{\text{ d}}^{3}xN\sqrt{\gamma }\left[K_{ij}{K}^{ij}-K^2+R(\gamma )\right].& (111)\end{array}$

It is natural to think of the first two terms in (111), which involve the square of the “velocities” ∂_tγ_ij, as the “kinetic term” for γ_ij, and to view R(γ) as the “potential,” which involves only spatial derivatives ∂_kγ_ij. In particular, the invariance of the action (39) under $\text{Diff}({M})$ implies that only the very specific combination of ADM operators in (111) is $\text{Diff}({M})$-invariant. This illustrates how strongly the underlying $\text{Diff}({M})$ invariance in GR restricts the possible operators allowed in the Einstein-Hilbert action when expressed in terms of ADM variables.

7.2.2. Symmetry in GR and HG

In GR, the ADM variables derive from the decomposition of the D-dimensional ambient space metric g_μν. Consequently, in this case, the symmetry group acting on the ADM variables consists of the full D-dimensional spacetime diffeomorphisms $\text{Diff}({M})$, or general coordinate transformations,

$\begin{array}{ll}{x}^i\mapsto {\tilde{x}}^i(t,x),t\mapsto \tilde{t}(t,x).& (112)\end{array}$

In general, operators ${O}(g_{\mu \nu },{\partial }_{\nu })$, invariant under $\text{Diff}({M})$, are constructed by scalar contractions of covariant derivatives ∇_μ and curvature tensors R_μνρσ. While the action of $\text{Diff}({M})$ on the D-dimensional ambient metric g_μν is realized linearly as in (45), in view of (106), the action of $\text{Diff}({M})$ on the ADM variables N, Nⁱ, and γ_ij is non-linearly realized. Thus, only very particular combinations of $\text{Diff}({M})$-invariant operators ${O}(N,N^i,{\gamma }_{ij},{\partial }_i,{\partial }_t)$ constructed by scalar contractions of the time and space derivatives ∂_t and ∂_i of the ADM variables N, Nⁱ, and γ_ij are allowed.

In contrast to the general coordinate transformations (112), the coordinate transformations that preserve the foliation include the d-dimensional time-dependent spatial diffeomorphisms and the reparameterizations of time,

$\begin{array}{ll}{x}^i\mapsto {\tilde{x}}^i(t,x),t\mapsto \tilde{t}(t).& (113)\end{array}$

Under (113), the ADM fields N, Nⁱ, and γ_ij transform as

$\begin{array}{l}N\mapsto Ñ=N\frac{\text{d}t}{\text{d}\tilde{t}},\\ N^i\mapsto {Ñ}^i=\left(N^j\frac{\partial {\tilde{x}}^i}{\partial x^j}-\frac{\partial {\tilde{x}}^i}{\partial t}\right)\frac{\text{d}t}{\text{d}\tilde{t}},\\ {\gamma }_{ij}\mapsto {\tilde{\gamma }}_{ij}={\gamma }_{k\ell }\frac{\partial x^k}{\partial {\tilde{x}}^i}\frac{\partial x^{\ell }}{\partial {\tilde{x}}^j}.& (114)\end{array}$

Combining the action of an infinitesimal diffeomorphism (45) on the ambient metric g_μν, its decomposition in ADM variables (100), and the decomposition of the generator of infinitesimal diffeomorphisms ε^μ = (ε, εⁱ) with ${\epsilon }^i(t,x)={\epsilon }^{\mu }{e}_{\mu }^i$ and $\epsilon (t,x)=t_{\mu }{\epsilon }^{\mu }$ the action of an infinitesimal $\text{Diff}({M})$ on the ADM fields γ_ij, Nⁱ, and N is derived as

$\begin{array}{ll}{\delta }_{\epsilon }N={\partial }_t(\epsilon N)+{{L}}_{\mathit{\epsilon }}N-N{N}^i{\partial }_i\epsilon ,& (115)\end{array}$

$\begin{array}{ll}{\delta }_{\epsilon }{N}^i={\partial }_t\left(\epsilon N^i\right)+{\partial }_t{\epsilon }^i+{({{L}}_{\mathit{\epsilon }}N)}^i-\left(N^i{N}^j+N^2{\gamma }^{ij}\right){\partial }_j\epsilon ,& (116)\end{array}$

$\begin{array}{ll}{\delta }_{\epsilon }{\gamma }_{ij}=\epsilon {\partial }_t{\gamma }_{ij}+{\left({{L}}_{\mathit{\epsilon }}\gamma \right)}_{ij}+2N_{(i}{\partial }_{j)}\epsilon .& (117)\end{array}$

Here ${{L}}_{\mathit{\epsilon }}$ denotes the Lie derivative along εⁱ. The transformation law for the shift vector with covariant index position $N_i={\gamma }_{ij}{N}^j$ can be obtained by combining the transformation laws (116) and (117), giving

$\begin{array}{ll}{\delta }_{\epsilon }{N}_i={\partial }_t(\epsilon N_i)+{({{L}}_{\mathit{\epsilon }}N)}_i+{\gamma }_{ij}{\partial }_{\tau }{\epsilon }^j+\left(N_j{N}^j-N^2\right){\partial }_i\epsilon .& (118)\end{array}$

In contrast to the linear transformation (45) of the ambient metric g_μν, the transformations (115–117) of the ADM variables under an infinitesimal $\text{Diff}({M})$ is not linear. The transformations of the ADM variables under $\text{Dif}{\text{f}}_{{F}}({M})$, for which the time component ε of the generator ε^μ = (ε, εⁱ) is a function of time only, ε(t, x) = ε(t), are derived from (115–117) by neglecting terms involving ∂_iε, and the action of an infinitesimal $\text{Dif}{\text{f}}_{{F}}({M})$ on the ADM variables is given by

$\begin{array}{ll}{\delta }_{\epsilon }N={\partial }_t(\epsilon N)+{{L}}_{\mathit{\epsilon }}N,& (119)\end{array}$

$\begin{array}{ll}{\delta }_{\epsilon }{N}^i={\partial }_t\left(\epsilon N^i\right)+{\partial }_t{\epsilon }^i+{({{L}}_{\mathit{\epsilon }}N)}^i,& (120)\end{array}$

$\begin{array}{ll}{\delta }_{\epsilon }{\gamma }_{ij}=\epsilon {\partial }_t{\gamma }_{ij}+{({{L}}_{\mathit{\epsilon }}\gamma )}_{ij}.& (121)\end{array}$

Likewise, the transformation (118) reduces to

$\begin{array}{ll}{\delta }_{\epsilon }{N}_i={\partial }_t(\epsilon N_i)+{({{L}}_{\mathit{\epsilon }}N)}_i+{\gamma }_{ij}{\partial }_{\tau }{\epsilon }^j.& (122)\end{array}$

Hence, the $\text{Dif}{\text{f}}_{{F}}({M})$ form a subgroup of the $\text{Diff}({M})$, and the absence of terms proportional to ∂_iε has the effect that the transformations (119–122) act linearly on the ADM variables [50, 208].

Mathematically, the $\text{Dif}{\text{f}}_{{F}}({M})$ are diffeomorphisms that respect the preferred codimension-one foliation ${F}$ of (d + 1)-dimensional spacetime ${M}$ into spatial d-dimensional leaves [50]. On such a foliation, two classes of functions can be defined: functions that depend on all coordinates (t, xⁱ) and functions that are constant on each spatial leaf, i.e., which depend only on time t. The latter are called “projectable.” From a canonical perspective with a fundamental dynamical field γ_ij, the shift vector Nⁱ can be viewed as the gauge field associated with the time-dependent spatial diffeomorphisms with infinitesimal generator εⁱ(t, x), and the lapse function N can be viewed as the gauge field of the reparameterizations of time with infinitesimal generator ε(t). It therefore seems natural to restrict N(x, t) to be a function of time only, although the versions N(t, x) and N(t) are both compatible with the $\text{Dif}{\text{f}}_{{F}}({M})$ symmetry, essentially leading to two variants of HG.

 i) Projectable HG:

The lapse function depends only on time, i.e., N(t), and is not considered a dynamical field. By choosing a global time slicing corresponding to the gauge in which N(t) = 1, the foliation-preserving diffeomorphisms reduce to the time-dependent spatial diffeomorphisms.

ii) Non-projectable HG:

The lapse function depends on space and time, and N(t, x) is a propagating degree of freedom, i.e., an integration variable in the path integral. Compared to the projectable theory, the main technical challenge is the enlarged set of $\text{Dif}{\text{f}}_{{F}}({M})$-invariants that involve the acceleration vector (110).

Since the two possibilities lead to two different theories with different particle content and different phenomenology, they have to be investigated separately. In particular, the quantization of the non-projectable theory is complicated due to the presence of the fluctuating lapse function, which leads to non-regular propagators [51]. In this paper I mainly focus on the projectable theory but will highlight at several places important differences from the non-projectable theory.

7.3. Projectable HG in D = 2 + 1 and D = 3 + 1 Dimensions

The action functional of projectable HG in D = d + 1 dimensions can be formulated in terms of the ADM variables. The natural assignment of the anisotropic scaling dimensions to the ADM variables follows from (105) and (106):

$\begin{array}{ll}{[{\gamma }_{ij}]}_{\text{S}}=0,{[N^i]}_{\text{S}}=z-1,{[N]}_{\text{S}}=0.& (123)\end{array}$

Compared with the stringent constraints on the ADM operators in GR following from the invariance under $\text{Diff}({M})$, the less restrictive invariance under $\text{Dif}{\text{f}}_{{F}}({M})$ allows for a richer structure and hence more ADM invariants. Nevertheless, there are a number of conditions which limit the possible $\text{Dif}{\text{f}}_{{F}}({M})$-invariants in the projectable HG:

1. Formulated in a manifest $\text{Dif}{\text{f}}_{{F}}$-invariant way, the shift vector can only arise in combination with a time derivative of the metric γ_ij in the form of the covariant time derivative (109). Thus, the invariants in projectable HG can only be constructed by scalar contractions of covariant time derivatives of the metric field D_tγ_ij (or, equivalently, extrinsic curvatures K_ij), covariant space derivatives ∇_i, and spatial curvature tensors R_ijkl.

2. Invariance under time-reversal and parity allows only invariants with an even number of time and space derivatives. Writing $S_{\text{HG}}=\int \text{d}t{\text{ d}}^{d}x{{L}}_{\text{HG}}$ and ${{L}}_{\text{HG}}=\sum _n{c}_{(n)}{{O}}_{(n)}(D_t,{\nabla }_i,{\gamma }_{ij})$ implies that the operators have the general schematic structure (suppressing the summation index n)

$\begin{array}{ll}{O}(D_t,{\nabla }_i,{\gamma }_{ij})=\sqrt{\gamma }{(D_t{\gamma }_{ij})}^{2k}{({\nabla }_i)}^{2n}{(R_{ijkl})}^m.& (124)\end{array}$

3. For HG to be power-counting renormalizable, the action can only include relevant and marginal operators with respect to the anisotropic scaling [50]. Combining the scaling [S_HG]_S = 0 with ${\left[\int \text{d}t{\text{ d}}^{d}x\right]}_{\text{S}}=-(d+z)$ implies that ${\left[{{L}}_{\text{HG}}\right]}_{\text{S}}=d+z$. Relevant and marginal operators have scaling ${\left[{{O}}_{(j)}(D_t,{\nabla }_i,{\gamma }_{ij})\right]}_{\text{S}}\le d+z$. Combining this with the structure (124) yields the constraint

$\begin{array}{ll}2(kz+n+m)\le d+z.& (125)\end{array}$

4. The original motivation of HG as a means of solving the problems with unitarity caused by higher-derivative ghosts is to restrict the invariants in the action to include time derivatives of the metric only up to second-order. In view of the structure (124), this leaves the two possibilities of k = 1 and k = 0. For the kinetic term with k = 1 and n = m = 0 to scale marginally under (96), equality in (125) has to be satisfied and implies the critical scaling condition

$\begin{array}{ll}z=d.& (126)\end{array}$

The operators with k = 0 correspond to the potential ${{V}}^d$ and, for the critical scaling (126), are restricted by the condition 2(n + m) ≤ 2d.

The action of projectable HG in D = d + 1 dimensions (in the gauge N = 1), including all relevant and marginal terms with respect to the critical anisotropic scaling, reads

$\begin{array}{ll}{S}_{\text{HG}}=\frac{1}{2G}{\displaystyle \int }\text{d}t{\text{ d}}^{d}x\sqrt{\gamma }\left(K_{ij}{K}^{ij}-\lambda K^2-{{V}}^{(d)}\right).& (127)\end{array}$

As a consequence of (126), the structure of the kinetic term is universal, i.e., independent of d:

$\begin{array}{ll}\sqrt{\gamma }(K_{ij}{K}^{ij}-\lambda K^2)=\frac{1}{4}(D_t{\gamma }_{ij}){{G}}^{ij,kl}(D_t{\gamma }_{kl}).& (128)\end{array}$

Here, ${{G}}^{ij,kl}$ is the one-parameter λ-family of “generalized DeWitt metrics”

$\begin{array}{ll}{{G}}^{ij,kl}:=\frac{\sqrt{\gamma }}{2}\left({\gamma }^{ik}{\gamma }^{jl}+{\gamma }^{il}{\gamma }^{jk}-2\lambda {\gamma }^{ij}{\gamma }^{kl}\right).& (129)\end{array}$

There are two special values of λ. The first is the “relativistic” value λ = 1, which leads to an enhanced symmetry [50]. The second is the “conformal” value λ_c = 1/d, where ${{G}}^{ij,kl}$ is degenerate, which also leads to an enhanced symmetry, namely local anisotropic Weyl invariance [49]. For non-singular values λ ≠ λ_c, the inverse is given by

$\begin{array}{ll}{{G}}_{ij,kl}=\frac{1}{\sqrt{\gamma }}\left({\gamma }_{ik}{\gamma }_{jl}+{\gamma }_{il}{\gamma }_{jk}-\frac{2\lambda }{d\lambda -1}{\gamma }_{ij}{\gamma }_{kl}\right).& (130)\end{array}$

For λ < λ_c (129) is positive definite, and for λ > λ_c it is indefinite. In the context of GR, this property was found in [209] to be directly related to the attractive or repulsive nature of gravity.

Note the difference between (127) and the Einstein-Hilbert action (111) in ADM variables, where the $\text{Diff}({M})$ invariance completely fixed the structure of the action, i.e., the relative coefficient between the two terms $K_{ij}{K}^{ij}$ and K² in the kinetic terms as well as the coefficient of the potential R. In HG, $K_{ij}{K}^{ij}$, K², and the terms in ${{V}}^d$ are separately invariant under $\text{Dif}{\text{f}}_{{F}}({M})$. In particular, λ is a free parameter of the theory.

The potential ${{V}}^{(d)}$ of projectable HG is defined in terms of d-dimensional curvature invariants and, according to (3), includes all relevant and marginal operators with respect to the critical anisotropic scaling. In contrast to the kinetic term, the potential is not universal and the number and complexity of invariants in the potential grows with increasing d. Restricting to d = 2 and d = 3, up to total derivatives the possible curvature invariants read [210]

$\begin{array}{ll}{{V}}^{(d=2)}=2\Lambda +\mu R^2,& (131)\end{array}$

$\begin{array}{l}{{V}}^{(d=3)}=2\Lambda -\eta R+{\mu }_1{R}^2+{\mu }_2{R}_{ij}{R}^{ij}+{\nu }_1{R}^3+{\nu }_{2}R{R}_{ij}{R}^{ij}\\ +{\nu }_3{R}_j^i{R}_k^j{R}_i^k+{\nu }_4{\nabla }_{i}R{\nabla }^{i}R+{\nu }_5{\nabla }_i{R}_{jk}{\nabla }^i{R}^{jk}.& (132)\end{array}$

Note that in d = 2 and d = 3 all invariants involving the Riemann tensors are absent. In addition, in d = 2, the linear Einstein-Hilbert term $\sqrt{\gamma }R$ is a total derivative. In general, the Riemann tensor in d dimensions has d²(d² − 1)/12 independent components. Hence, in d = 2, there is only one independent component associated with the Ricci scalar,

$\begin{array}{ll}{R}_{ijkl}^{(d=2)}=\frac{R}{2}\left({\gamma }_{ik}{\gamma }_{jl}-{\gamma }_{il}{\gamma }_{jk}\right).& (133)\end{array}$

Likewise, in d = 3, there are only six independent components of the Riemann curvature tensors that are associated with the six components of the Ricci tensor R_ij. This can also be seen from the fact that in d = 3, the Weyl tensor C_ijkl ≡ 0 vanishes identically, which allows all curvature tensors R_ijkl to be expressed in terms of R_ij and R via

$\begin{array}{ll}{R}_{ijkl}^{(d=3)}=R_{ik}{\gamma }_{jl}+R_{il}{\gamma }_{jk}+R_{jk}{\gamma }_{il}+R_{jl}{\gamma }_{ik}-\frac{R}{2}\left({\gamma }_{ik}{\gamma }_{jl}-{\gamma }_{il}{\gamma }_{jk}\right).& (134)\end{array}$

The mass dimensions of the coupling constants follow from [S_HG]_M = 0, [γ_ij]_M = 0, and ${\left[{\partial }_i\right]}_{\text{M}}={\left[{\partial }_t\right]}_{\text{M}}={\left[N^i\right]}_{\text{M}}=1$:

$\begin{array}{l}{\left[G\right]}_{\text{M}}=1-d,{\left[\Lambda \right]}_{\text{M}}=2,{\left[\lambda \right]}_{\text{M}}={\left[\eta \right]}_{\text{M}}=0,\\ {\left[\mu \right]}_{\text{M}}={\left[{\mu }_1\right]}_{\text{M}}={\left[{\mu }_2\right]}_{\text{M}}=-2,\\ {\left[{\nu }_1\right]}_{\text{M}}={\left[{\nu }_2\right]}_{\text{M}}={\left[{\nu }_3\right]}_{\text{M}}={\left[{\nu }_4\right]}_{\text{M}}={\left[{\nu }_5\right]}_{\text{M}}=-4.& (135)\end{array}$

A new set of dimensionless couplings ${[\tilde{G}]}_{\text{M}}={[\tilde{\Lambda }]}_{\text{M}}={[\widetilde{{\mu }_i}]}_{\text{M}}={[\widetilde{{\nu }_i}]}_{\text{M}}=0$ is trivially defined by expressing the couplings in units of a common, a priori unspecified, mass scale M_∗:

$\begin{array}{l}\tilde{G}:=\frac{G}{M_{*}^{1-d}},\tilde{\Lambda }:=\frac{\Lambda }{M_{*}^2},\\ {\tilde{\mu }}_i:=M_{*}^2{\mu }_i,{\tilde{\nu }}_i=M_{*}^4{\nu }_i.& (136)\end{array}$

The parametrization (136) is useful when discussing phenomenological bounds on HG.

7.4. Particle Spectrum, Dispersion Relations, and Phenomenological Constraints

The particle spectrum of projectable HG in d = 2 and d = 3 is derived along the same lines as for GR by expanding the action around flat space ${\bar{\gamma }}_{ij}={\delta }_{ij}$, ${\bar{N}}^i=0$ to quadratic order in the linear perturbations²⁷

$\begin{array}{ll}{h}_{ij}:={\gamma }_{ij}-{\bar{\gamma }}_{ij},n^i:=N^i-{\bar{N}}^i.& (137)\end{array}$

Substituting the irreducible decomposition of the perturbations,

$\begin{array}{l}{n}^i=n_{\text{T}}^i+{\partial }^{i}B,\\ h_{ij}=h_{ij}^{\text{TT}}+2{\partial }_{(i}{v}_{j)}^{\text{T}}+\left({\delta }_{ij}-\frac{{\partial }_i{\partial }_j}{{\partial }^2}\right)\Psi +\frac{{\partial }_i{\partial }_j}{{\partial }^2}E& (138)\end{array}$

with the three scalars Ψ, E, and B, the differentially constrained transversal vector fields ${\partial }_i{v}_T^i=0$ and ${\partial }_i{n}_T^i=0$, and the transversal traceless tensor field $h_{ij}^{\text{TT}}{\delta }^{ij}={\partial }^i{h}_{ij}^{\text{TT}}=0$ into the quadratic action, “integrating out” the non-dynamical modes $v_i^{\text{T}}$ and E, fixing the gauges B = 0 and $n_{\text{T}}^i=0$, yields after Fourier transformation to momentum space the dispersion relations for the physical propagating degrees of freedom $h_{ij}^{\text{TT}}$ and Ψ. As discussed in the previous section, in D = 2 + 1 there are no transversal traceless (TT) modes $h_{ij}^{\text{TT}}$. However, in contrast to GR, which has no local degrees of freedom in D = 2 + 1 dimensions, in HG there is an additional propagating scalar degree of freedom, which is a consequence of the reduced $\text{Dif}{\text{f}}_{{F}}({M})$ invariance of HG; cf. the discussion in section 3.2. The additional scalar mode persists even for low energies such that there is no smooth limit of HG to GR.

In d = 2, the additional gravitational scalar has the following non-relativistic dispersion relation expressed in terms of the dimensionless couplings (136):

$\begin{array}{ll}{\omega }_{\text{S}}^2=4\tilde{\mu }\frac{1-\lambda }{1-2\lambda }\frac{k^4}{M_{*}^2}.& (139)\end{array}$

Clearly, the dispersion relation for the additional scalar does not reduce to the linear relativistic form at low energies $k^2/M_{*}^2\ll 1$, which again is a consequence of the absence of the relevant linear curvature invariant in the potential (131).

In d = 3, aside from the additional scalar mode, the spectrum encompasses a propagating TT mode. Both modes have non-relativistic dispersion relations,

$\begin{array}{l}{\omega }_{\text{TT}}^2=k^2\left[\eta +{\tilde{\mu }}_2\frac{k^2}{M_{*}^2}+{\tilde{\nu }}_5\frac{k^4}{M_{*}^4}\right],\\ {\omega }_{\text{S}}^2=\frac{1-\lambda }{1-3\lambda }{k}^2\left[-\eta +(8{\tilde{\mu }}_1+3{\tilde{\mu }}_2)\frac{k^2}{M_{*}^2}+(8{\tilde{\nu }}_4+3{\tilde{\nu }}_5)\frac{k^4}{M_{*}^4}\right].& (140)\end{array}$

Before discussing experimental constraints on HG, I briefly review several theoretical restrictions:

1. Despite the critical scaling (126), which guarantees that the non-relativistic dispersion relations depend only quadratically on the frequency ω, it is essential to make sure that no unitarity-violating propagating ghost degrees of freedom enter in HG. Demanding the absence of ghosts leads to the condition G > 0, which ensures the positivity of the TT kinetic term, and the requirement that λ must lie in the gapped interval λ < 1/d or λ > 1, bounded by the points of enhanced symmetry, to ensure the positivity of the scalar kinetic term.

2. In contrast to the situation in D = 2 + 1, thanks to the presence of the relevant operator ∝R in (132), for low energies $k^2/M_{*}^2\ll 1$ both dispersion relations (140) in D = 3 + 1 reduce to the linear relativistic relations

$\begin{array}{l}{\omega }_{\text{TT}}^2=\eta k^2+{O}(k^2/M_{*}^2),\\ {\omega }_{\text{S}}^2=-\eta \frac{1-\lambda }{1-3\lambda }{k}^2+{O}(k^2/M_{*}^2).& (141)\end{array}$

However, because of the requirement that (1 − 3λ)/(1 − λ) > 0, there is no value of η ≠ 0 at which both of the relations in (141) are simultaneously positive, and for η = 0 the linear relativistic dispersion relation is lost, just as in D = 2 + 1. For η > 0, this leads to a tachyonic instability of the scalar mode at low energies $k^2/M_{*}^2\ll 1$. An obvious attempt to circumvent this problem is to keep η > 0 and tune λ very close to 1, in order to suppress the IR instability of the scalar mode. Unfortunately, this leads to strong coupling for the scalar mode at low energies [212–215], invalidating the perturbative treatment that underlies the power-counting renormalizability [216]; see, however [200, 217–220]. In summary, without a mechanism by which this IR problem can be avoided, the projectable theory seems to be excluded on phenomenological grounds.

3. The IR instability problem can be remedied in the non-projectable version of HG in which the potential (132) involves invariants including the acceleration vector (110), thanks to the propagating lapse function. To illustrate the difference from the projectable case, I present the potential and the dispersion relation for the non-projectable theory in d = 2. In the non-projectable case, the action (127) acquires a modified volume element $\text{d}t{\text{ d}}^{d}x\sqrt{\gamma }\mapsto \text{d}t{\text{ d}}^{d}xN\sqrt{\gamma }$, and the potential (131) for the non-projectable theory in d = 2 dimensions is enlarged by additional invariants,

$\begin{array}{ll}\begin{array}{l}{{V}}_{\text{np}}^{(2)}=2\Lambda -\eta R-\alpha a_i{a}^i+\mu R+{\rho }_1\Delta R+{\rho }_{2}R{a}_i{a}^i\\ +{\rho }_3{(a_i{a}^i)}^2+{\rho }_4{a}_i{a}^i{\nabla }_j{a}^j+{\rho }_5{({\nabla }_i{a}^i)}^2+{\rho }_6{\nabla }_i{a}_j{\nabla }^i{a}^j.\end{array}& (142)\end{array}$

Defining the perturbation of the lapse function ϕ: = N − 1 (with the choice $\bar{N}=1$ for the background value of the lapse function), expansion of the action around the flat background (Λ = 0) up to quadratic order in the linear perturbations leads to the dispersion relation for the single scalar propagating degree of freedom [51],

$\begin{array}{l}{\omega }_{\text{S}}^2=\left(\frac{1-\lambda }{1-2\lambda }\right)({\eta }^2{k}^2+(4\alpha \mu +2\eta {\rho }_1)k^4\\ +[{\rho }_1^2-4\mu ({\rho }_5+{\rho }_6)]k^6{)}^{-\alpha -({\rho }_5+{\rho }_6)k^2}.& (143)\end{array}$

In particular, among the additional invariants in (142), there is a relevant operator proportional to $\alpha N\sqrt{\gamma }{a}^i{a}_i$ that leads to the required modifications of the low-energy limit. The freedom in tuning the additional coupling constant α can be used to avoid the IR instability. In [221] it was found that for 0 < α < 2 the instability can be avoided in non-projectable HG. However, as already anticipated in [50] and supported by different arguments in [51, 214, 222], the presence of the propagating lapse function N in the non-projectable version leads to essential complications with the quantization, which I briefly comment on in section 8.

Aside from these theoretical restrictions, there are phenomenological constraints stemming from experimental bounds on Lorentz violation (LV) (see e.g., [223–228]). In the context of HG, these can be divided into two regimes:

1. LV in the IR:

Despite the suppression of higher-order terms in the dispersion relations (140) for low energies $k^2/M_{*}^2\ll 1$, HG does not smoothly connect to GR in the IR, but rather to a modified theory of gravity with an additional propagating gravitational scalar degree of freedom. Deviations from GR can be quantified by a variety of experiments and mainly lead to restrictions on the couplings of the relevant operators in the IR. Experimental constraints come from deviations of the observed helium abundance during Big Bang nucleosynthesis [221, 229, 230] from post-Newtonian parameters [214, 231, 232], binary pulsars [233], and black holes [234–236]. The most stringent constraint, however, comes from the recent detection of gravitational waves from the binary neutron star merger event GW170817 [237]. The inferred speed of propagation of the TT mode strongly constrains the parameter, |η − 1| ≲ 10⁻¹⁵, but the propagation speed of the scalar mode remains largely unconstrained (cf., [238]).

2. LV in the UV:

LV effects in the gravitational sector at high energies are not as strongly restricted as in the matter sector provided by the SM particles. In particular, the scale M_* might naturally be identified with the LV scale in the gravitational sector. Observations sensitive to the higher-order corrections in the dispersion relations (140) provide a lower bound on M_∗. However, LV effects in the SM are constrained much more tightly, and a mechanism is needed that would prevent LV effects percolating from the gravitational sector to the matter sector [227]. While several such mechanisms have been suggested (see e.g., [239–246]), it remains an open question as to whether they can ultimately be realized in HG [247, 248]. In the case of there being a universal LV scale (i.e., when the LV scale in the matter sector can be identified with the LV scale M_∗ in the gravitational sector), the observation of synchrotron radiation from the crab nebula would provide a lower bound on M_∗ around the grand unification scale $M_{*}>10^{16}$ GeV [130].

Summarizing, the “healthy extension” of the non-projectable model is still phenomenologically viable [221, 238], but stronger constraints on the IR parameter, as well as on M_∗, have the potential to rule out the theory. Moreover, regarding the quantum theory, these properties will rely on the IR limit of the RG flow for the couplings of the relevant operators, as briefly discussed in section 9 for projectable HG in d = 2 + 1 dimensions.

8. Quantum Hořava Gravity

So far, all considerations in HG have been purely classical. However, the main motivations for proposing a Lifshitz theory of gravity are its unitarity and perturbative renormalizability, which was originally conjectured based on power-counting arguments [50]. While this conjecture has stimulated a vast amount of research devoted to specific applications of HG in various scenarios, the question of whether HG is indeed perturbatively renormalizable beyond power counting remained open for a long time. It was ultimately answered in the affirmative for the projectable version of HG in [51]. Furthermore, for HG to qualify as a UV-complete theory, its RG structure must also be investigated, which in turn requires explicit loop calculations. In this section, I discuss both these aspects. In order to establish a connection with the general formalism in section 2, in the remaining sections I use Euclidean signature by the Wick rotation t ↦ it and Nⁱ ↦ −iN^j, which effectively leads to a sign flip of the potential in (127).

8.1. Non-local Gauge-Fixing and Propagators

Since HG is a gauge theory with invariance group $\text{Dif}{\text{f}}_{{F}}({M})$, its fluctuation operator (10) is degenerate and its perturbative quantization requires a gauge-fixing. In contrast to relativistic theories, in Lifshitz theories the situation is more complicated because of the anisotropic scaling between space and time: a standard local gauge-fixing causes the propagators of the theory to behave in an irregular way, ultimately leading to spurious non-local divergences [51]. Even if, on general grounds, it might be expected that these non-local divergences ultimately cancel order by order in the perturbative expansion, their presence would greatly complicate the general analysis of renormalizability as well as the intermediate calculations. Therefore, a new type of non-local gauge-fixing was proposed in [51], which leads to regular propagators.

In the background field method, the geometric fields γ_ij and Nⁱ are decomposed according to (137). As in the general case for relativistic theories (19), the gauge-breaking action in HG is quadratic in the gauge condition χⁱ,

$\begin{array}{ll}{S}_{\text{gb}}=\frac{\sigma }{2G}{\displaystyle \int }\text{d}t{\text{ d}}^d{x}^i\sqrt{\gamma }{\chi }^i{O}_{ij}{\chi }^j,& (144)\end{array}$

where σ is a gauge parameter. Guidance for finding a suitable gauge condition χⁱ can be obtained by looking at the spatial part of the relativistic gauges of type (68), which expressed in terms of ADM variables (106), with the background covariant derivatives ${\bar{D}}_t$ and ${\bar{\nabla }}_i$ and the gauge parameter c₁, have the general structure

$\begin{array}{ll}{\chi }^i\left[\bar{\gamma },\bar{N};h,n\right]={\bar{D}}_t{n}^i+\left({\bar{\gamma }}^{ij}{\bar{\gamma }}^{k\ell }-c_1{\bar{\gamma }}^{ik}{\bar{\gamma }}^{j\ell }\right){\bar{\nabla }}_k{h}_{j\ell }.& (145)\end{array}$

A characteristic feature of these “quasi-relativistic gauge conditions” is that they artificially render the shift perturbation nⁱ propagating, owing to the time derivative ${\bar{D}}_t{n}^i$. However, the gauge condition in the form (145) is not adequate, as it does not scale homogeneously under (96), which can be seen by comparing ${\left[{\bar{D}}_t{n}^i\right]}_{\text{S}}=2d-1$ with ${\left[{\bar{\gamma }}^{ij}{\bar{\gamma }}^{kl}{\bar{\nabla }}_k{h}_{jl}\right]}_{\text{S}}=1$. A possible solution is to omit the term ${\bar{D}}_t{n}^i$ from (145), but this would lead precisely to the aforementioned irregular propagators [51]. Therefore, keeping the ${\bar{D}}_t{n}^i$ term, the only option is to increase the scaling dimension of the remaining terms by decorating them with additional spatial derivatives:

$\begin{array}{ll}{\chi }^i\left[\bar{\gamma },\bar{N};h,n\right]={\bar{D}}_t{n}^i+B^{ij}{\bar{\gamma }}^{k\ell }({\bar{\nabla }}_k{h}_{j\ell }-c_1{\bar{\nabla }}_j{h}_{k\ell }).& (146)\end{array}$

Here, $B^{ij}(\bar{\gamma };\bar{\nabla })$ is a differential operator of order 2(d − 1), which apart from ${\bar{\nabla }}_i$ involves only the background metric ${\bar{\gamma }}_{ij}$. Without introducing any new dimensional parameter, S_gb should have a marginal anisotropic scaling [S_gb]_S = 0, which in view of the critical scaling (126) and ${\left[\text{d}t{\text{ d}}^d{x}^i\right]}_{\text{S}}=2d$ implies ${\left[{\chi }^i{O}_{ij}{\chi }^j\right]}_{\text{S}}=-2d$. Therefore, while (146) with ${\left[B^{ij}\right]}_{\text{S}}=2(d-1)$ ensures a homogeneous scaling ${\left[{\chi }^i\right]}_{\text{S}}=2d-1$, it requires a scaling of [O_ij]_S = −2(d − 1). Consequently, if the operator $O_{ij}(\bar{\gamma };\bar{\nabla })$ includes only powers of γ_ij and ∇_i, it must be of the non-local form²⁸

$\begin{array}{ll}{O}_{ij}={(-1)}^{d-1}{\left({\bar{\Delta }}^{(d-1)}{\bar{\gamma }}^{ij}+\xi {\bar{\nabla }}^i{\bar{\Delta }}^{(d-2)}{\bar{\nabla }}^j\right)}^{-1},\xi \ne -1.& (147)\end{array}$

For the particularly useful choice of B^ij = (O⁻¹)^ij/2σ and c₁ = λ, the metric and shift fluctuations in the quadratic action of projectable HG decouple, leading to the two-parameter family of (ξ, σ) gauge conditions [51],

$\begin{array}{ll}{\chi }^i\left[\bar{\gamma },\bar{N};h,n\right]={\bar{D}}_t{n}^i+\frac{1}{2\sigma }{\left(O^{-1}\right)}^{ij}{\bar{\gamma }}^{k\ell }\left({\bar{\nabla }}_k{h}_{j\ell }-\lambda {\bar{\nabla }}_j{h}_{k\ell }\right).& (148)\end{array}$

The gauge-fixing given by (147) and (148) leads to the aforementioned regular propagators, discussed in more detail in the next subsection. Unfortunately, the same gauge-fixing does not seem to work in the non-projectable theory; it leads to irregular terms in the propagators involving the lapse function, which is absent in the projectable theory [51].

8.2. Regular Propagators, Superficial Degree of Divergence, and Renormalizability

In the context of Lifshitz theories with anisotropic scaling (96), an important concept is the notion of a regular propagator, which also plays a central role in the proof of perturbative renormalizability of HG. A propagator for two generalized fields ϕ₁ and ϕ₂ with anisotropic scaling [ϕ₁]_S = s₁ and [ϕ₂]_S = s₂ is of the regular form

$\begin{array}{l}\langle {\varphi }_1,{\varphi }_2\rangle ={\displaystyle \sum }\frac{P(\omega ,k)}{D(\omega ,k)},\\ D={\displaystyle \prod _{m=1}^M}\left[A_m{\omega }^2+B_m{k}^{2d}+\cdots \right],& (149)\end{array}$

if and only if P(ω, k) is a polynomial in ω and kⁱ with leading anisotropic scaling [P]_S ≤ s₁ + s₂ + 2d(M − 1) and A_m > 0 and B_m > 0 are strictly positive constants. The ellipsis represents terms with subleading scaling dimensions, which generically originate from relevant operators in the action. The scaling properties ensure that the propagator has the right fall-off properties at small distances and time intervals, i.e., it scales as [〈ϕ₁, ϕ₂〉]_S ≤ s₁ + s₂ − 2d in the UV limit for high frequencies and momenta in momentum space.

With the choice (148), the propagators of projectable HG in D = 2 + 1 and D = 3 + 1 dimensions are derived on a flat background ${\bar{\gamma }}_{ij}={\delta }_{ij}$ and ${\bar{N}}^i=0$. Upon inserting the decomposition (138) for the fluctuations h_ij and n_i into the gauge-fixed quadratic action, the gauge-fixed fluctuation operator (25) has a block-diagonal form in the scalar, vector, and tensor sectors and can be inverted algebraically in momentum space. The propagators for the original h_ij and n_i fields are recovered by using (138) again. In D = 2 + 1 the propagators read [51],

$\begin{array}{ll}\langle h_{ij},h_{kl}\rangle =2G\left[{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jl}+\frac{2\lambda }{1-2\lambda }{\delta }_{ij}{\delta }_{kl}\right]{{P}}_{\text{S}}(\omega ,k),& (150)\end{array}$

$\begin{array}{ll}\langle n_i,n_j\rangle =4\mu G{k}^2\left[\frac{2(1-\lambda )}{(1-2\lambda )}{\delta }_{ij}-\frac{k_i{k}_j}{k^2}\right]{{P}}_{\text{S}}(\omega ,k).& (151)\end{array}$

The tensor combination in (150) is just the inverse DeWitt metric (130) in d = 2 flat space. In order to arrive at the final forms (150) and (151), the gauge parameters (ξ, σ) have to be chosen such that there is a single pole

$\begin{array}{l}{{P}}_{\text{S}}(\omega ,k)={\left[{\omega }^2+4\mu \frac{1-\lambda }{1-2\lambda }{k}^4\right]}^{-1},\\ \sigma =\frac{1-2\lambda }{8\mu (1-\lambda )},\xi =-\frac{1-2\lambda }{2(1-\lambda )}.& (152)\end{array}$

Clearly, the propagators (150) and (151) are both of the regular form (149)²⁹.

In D = 3 + 1 dimensions the analogous procedure yields the propagators for the h_ij and n_i fields [51],

$\begin{array}{l}\langle h_{ij},h_{kl}\rangle =2G\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right){{P}}_{\text{TT}}-2G{\delta }_{ij}{\delta }_{kl}\left[{{P}}_{\text{TT}}-\frac{1-\lambda }{1-3\lambda }{{P}}_{\text{S}}\right]\\ +2G\left({\delta }_{ij}\frac{k_k{k}_l}{k^2}+{\delta }_{kl}\frac{k_i{k}_j}{k^2}\right)\left[{{P}}_{\text{TT}}-{{P}}_{\text{S}}\right]\\ +2G\frac{k_i{k}_j{k}_k{k}_l}{k^4}\left[\frac{7\lambda -5}{1-\lambda }{{P}}_{\text{TT}}+\frac{1-3\lambda }{1-\lambda }{{P}}_{\text{S}}\right],& (153)\end{array}$

$\begin{array}{ll}\langle n_i,n_j\rangle =G\frac{{\nu }_5}{1-\lambda }{k}^4\left[2(1-\lambda ){\delta }_{ij}-(1-2\lambda )\frac{k_i{k}_j}{k^2}\right]{{P}}_{\text{S}}.& (154)\end{array}$

Again, in order to arrive at the final forms (153) and (154), the gauge parameters (ξ, σ) have been chosen in such a way that there are only the two physical poles³⁰

$\begin{array}{l}{{P}}_{\text{TT}}={\left[{\omega }^2+{\nu }_5{k}^6\right]}^{-1},\\ {{P}}_{\text{S}}={\left[{\omega }^2+\frac{(1-\lambda )(8{\nu }_4+3{\nu }_5)}{1-3\lambda }{k}^6\right]}^{-1},\\ \sigma =\frac{1}{2{\nu }_5},\xi =-\frac{1-2\lambda }{2(1-\lambda )}.& (155)\end{array}$

The additional second pole in D = 3 + 1 is due to the TT mode, which is absent in D = 2 + 1 dimensions. Again, the propagators (153) and (154) are of the regular form (149).

The superficial degree of divergence in HG is obtained along the same lines as in (65), but with the anisotropic scaling of loop frequencies and momenta (97). Provided the propagators are of the regular form, it reads [51]

$\begin{array}{ll}{D}_{\text{HG}}^{\text{div}}=2d-dT-X-(d-1)l_N,& (156)\end{array}$

where T and X are the numbers of time derivatives and spatial derivatives, respectively, acting on external legs and l_n is the number of external n-legs. Due to the $\text{Dif}{\text{f}}_{{F}}$ invariance of the counterterms it is sufficient to focus on diagrams with l_n = 0³¹. From (156) it follows that $D_{\text{HG}}^{\text{div}}<0$ with more than two time derivatives or d space derivatives on external h_ij-legs. If $D_{\text{HG}}^{\text{div}}<0$ were indeed to imply the absence of divergences, only local operators with at most two time derivatives or d spatial derivatives acting on h_ij would have to be renormalized and HG would be perturbatively renormalizable. However, there are two complications that prevent us from immediately drawing this conclusion. The first is the problem of (overlapping) subdivergences, which is also present in non-relativistic theories, i.e., a diagram might diverge despite $D_{\text{HG}}^{\text{div}}<0$. However, in [249] it was shown that the combinatorics of the recursive order-by-order subtraction of the Bogoliubov-Parasiuk-Hepp-Zimmermann (BPHZ) scheme [250–252] works essentially the same as in relativistic theories.

The second problem is similar but inherently related to the non-relativistic nature of the theory. It can be illustrated by considering a generic L-loop Feynman integral that is free of subdivergences and has $D_{\text{HG}}^{\text{div}}({I})<0$:

$\begin{array}{ll}{I}={\displaystyle \int }\text{d}{\omega }_{(L)}{\text{d}}^d{k}_{(L)}f\left({\omega }_{(L)},k_{(L)}\right),& (157)\end{array}$

$\begin{array}{ll}f\left({\omega }_{(L)},k_{(L)}\right)={\displaystyle \int }{\displaystyle \prod _{\ell =1}^{L-1}}\text{d}{\omega }_{(\ell )}{\text{d}}^d{k}_{(\ell )}\tilde{f}\left(\{{\omega }_{(\ell )}\},\{k_{(\ell )}\};{\omega }_{(L)},l_{(L)}\right).& (158)\end{array}$

The absence of subdivergences implies that the integrations over the L − 1 loop integrals converge and result in a function f(ω_(L), k_(L)) which, upon suppressing the dependence on the external momenta, depends only on the Lth loop frequency ω_(L) and spatial momentum k_(L). The anisotropic scalings [ω]_S = d and [k]_S = 1 imply that ${\left[f\right]}_{\text{S}}=D^{\text{div}}({I})-2d$. However, in contrast to relativistic theories, in which f(ω_(L), k_(L)) can depend only on the relativistic combination $p_{(L)}^2={\omega }_{(L)}^2-k_{(L)}^2$, in Lifshitz theories the anisotropic scaling is less restrictive and f(ω_(L), k_(L)) can take different forms, such as

$\begin{array}{ll}f({\omega }_{(L)},k_{(L)})=\{\begin{array}{l}{\omega }_{(L)}^{-1+n}{k}_{(L)}^{D^{\text{div}}({I})-d(1+n)},\\ {\omega }_{(L)}^{-1-n}{k}_{(L)}^{D^{\text{div}}({I})-d(1-n)}.\end{array}& (159)\end{array}$

The problem is that, despite the fact that $D^{\text{div}}({I})<0$, the total integral ${I}$ may diverge as the individual integrals over the frequency [as in the first case of (159)] or the spatial momentum [as in the second case of (159)] diverge. In [51] it was shown that this problem is absent if the propagators are of the regular form (156), in which case $D_{\text{HG}}^{\text{div}}({I})<0$ really implies convergence of ${I}$. As shown earlier, all propagators in projectable HG can be brought into the regular form (149) by the non-local gauge-fixing (147) and (148). Combined with the $\text{Dif}{\text{f}}_{{F}}({M})$ invariance of the counterterms shown in [52], this completes the proof of perturbative renormalizability of projectable HG [51]. Unfortunately, the proof does not extend to the non-projectable theory, as not all propagators can be brought into the regular form (149) for the gauge-fixing (147) and (148), because of the propagating lapse function. This, of course, does not imply that the non-projectable theory is perturbatively non-renormalizable; it simply means that other methods are needed to investigate the renormalization structure of the non-projectable theory.

8.3. Auxiliary Field, Local Formulation, and Path Integral

The Euclidean path integral (2) for projectable HG has the form

$\begin{array}{ll}{Z}_{\text{HG}}={\left(\text{Det }{O}_{ij}\right)}^{1/2}{\displaystyle \int }{D}[N^i,{\gamma }_{ij},c^i,c_i^{*}]e^{-S_{\text{tot}}[N^i,{\gamma }_{ij},c^i,c_i^{*}]}& (160)\end{array}$

with the total action

$\begin{array}{ll}{S}_{\text{tot}}=S_{\text{HG}}+S_{\text{gb}}+S_{\text{gh}},& (161)\end{array}$

including the HG action (127), the gauge-breaking action (144), and the ghost action S_gh, which derives from the gauge condition (148) according to the general definition (21) with the ghost operator (22).

Because of the gauge condition (148) with the non-local operator O_ij defined in (147), the gauge-breaking action S_gb introduces a non-locality in S_tot. However, this non-locality only persists in the shift-shift sector of S_gb,

$\begin{array}{ll}{S}_{\text{gb}}=\frac{\sigma }{2G}{\displaystyle \int }\text{d}t{\text{ d}}^{d}x\sqrt{\bar{\gamma }}\left({\bar{D}}_t{n}^i{O}_{ij}{\bar{D}}_t{n}^j+\text{local terms}\right).& (162)\end{array}$

The non-local part can be rendered local by “integrating in” the auxiliary field π_i via the Gaussian functional integral:

$\begin{array}{ll}\begin{array}{l}{(\text{Det }{O}_{ij})}^{1/2}exp\left[-{\displaystyle \int }\text{d}t{\text{ d}}^{d}x\frac{\sigma \sqrt{\bar{\gamma }}}{2G}{\bar{D}}_t{n}^i{O}_{ij}{\bar{D}}_t{n}^j\right]\\ ={\displaystyle \int }{D}\left[{\pi }_i\right]exp\left[-{\displaystyle \int }\text{d}t{\text{ d}}^{d}x\frac{\sqrt{\bar{\gamma }}}{G}\left(\frac{1}{2\sigma }{\pi }_i{(O^{-1})}^{ij}{\pi }_j-i{\pi }_i{\bar{D}}_t{n}^i\right)\right].\end{array}& (163)\end{array}$

The Hubbard-Stratonovich-type transformation (163) reveals the role of π_i as momentum canonically conjugated to nⁱ. The field π_i also shares similarities with the Nakanishi-Lautrup field used in the BRST formalism to ensure the off-shell nilpotency of the Slavnov operator (see e.g., [52]).

The field π_i has mass dimensionality [π_i]_M = 1 and scaling dimensionality [π_i]_S = 1 (for arbitrary d). In [51] it was verified that the 〈π_i, π_j〉 and 〈π_i, n_j〉 propagators are also of the regular form (149) and that the presence of the π_i field does not affect the regularity of the h_ij and n_i propagators. Therefore, within the perturbative quantization, the procedure (163) is well-defined such that the apparent non-locality in the shift sector, induced by the gauge-fixing, does not lead to any problems. Moreover, (163) has the effect of absorbing the functional determinant ${(\text{Det }{O}_{ij})}^{1/2}$ in (160), such that the partition function takes the simple form

$\begin{array}{ll}{Z}_{\text{HG}}={\displaystyle \int }{D}[N^i,{\pi }_i,{\gamma }_{ij},c^i,c_i^{*}]e^{-S_{\text{tot}}[N^i,{\pi }_i,{\gamma }_{ij},c^i,c_i^{*}]},& (164)\end{array}$

with a local action functional $S_{\text{tot}}[N^i,{\pi }_i,{\gamma }_{ij},c^i,c_i^{*}]$ that includes the auxiliary π_i field.

9. Explicit Calculations and Renormalization Group Flow

The proof that projectable HG is perturbatively renormalizable beyond power counting [51, 52] is an important step toward a unitary quantum theory of gravity. However, for this theory to qualify as a fundamental theory, it must be extendable to arbitrarily high energy scales. In other words, perturbative renormalizability does not yet ensure the UV completeness, as the RG flow could drive one or more coupling constants into a Landau pole, leading to divergent interaction strengths at finite energy scales. Another aspect of the RG flow in HG is connected to the IR and the question of whether relativistic invariance can effectively be restored dynamically as an emergent symmetry at low energies. The RG analysis and the logarithmic running of the coupling constants requires calculation of the beta functions determined by the UV divergences of the theory.

Various quantum aspects of Lifshitz theories, in particular in the context of HG, have been considered in [49–51, 81, 83, 208, 253–273]. Here, I focus on the calculation of the beta functions in HG in D = 2 + 1 dimensions. Previous work in this context includes the contributions of Lifshitz scalars to the gravitational beta functions [82, 274], the one-loop beta functions for conformally reduced projectable HG in D = 2 + 1 dimensions [275], and the renormalization of the cosmological constant in D = 2 + 1 projectable HG [276]. In this section I report on the full RG flow of all couplings in projectable HG in D = 2 + 1 dimensions, which was derived in [53]. The analogous calculation in D = 3 + 1 dimensions is technically much more challenging and has not yet been completed. However, recent partial results provide an important first step in this direction [277].

The Euclidean action for projectable HG in D = 2 + 1 dimensions reads³²

$\begin{array}{ll}{S}_{\text{HG}}^{(d=2)}=\frac{1}{2G}{\displaystyle \int }\text{d}t{\text{ d}}^{2}x\sqrt{\gamma }(K_{ij}{K}^{ij}-\lambda K^2+\mu R^2).& (165)\end{array}$

The background covariant gauge condition (148) and the non-local operator (147) in D = 2 + 1 dimensions take the forms

$\begin{array}{l}{\chi }^i={\bar{D}}_t{n}^i+\frac{1}{2\sigma }{\left(O^{-1}\right)}^{ij}{\bar{\gamma }}^{k\ell }\left({\bar{\nabla }}_k{h}_{j\ell }-\lambda {\bar{\nabla }}_j{h}_{k\ell }\right),\\ O_{ij}=-{\left(\bar{\Delta }{\bar{\gamma }}^{ij}+\xi {\bar{\nabla }}^i{\bar{\nabla }}^j\right)}^{-1},\xi \ne -1.& (166)\end{array}$

In the background field method the “quantum fields” h_ij, nⁱ, π_i, $c_i^{*}$, and cⁱ are integrated out in the path integral, which, within the one-loop approximation, means performing the functional Gaussian integration (8). Therefore, only the part of the total action S_tot = S_HG+S_gf+S_gh that is quadratic in the perturbations $S_{\text{tot}}^{(2)}$ is required. In view of (21) and (22), this means that only the “affine” parts of the gauge transformations on h_ij and n_i are required to derive the quadratic part of S_gh. In the projectable version of HG in the gauge N = 1, the $\text{Dif}{\text{f}}_{{F}}$ reduce to the time-dependent spatial diffeomorphisms [corresponding to ε = 0 in (120) and (121)], and the required gauge transformations in terms of the background covariant time derivative ${\bar{D}}_t$ and the background covariant spatial derivative ${\bar{\nabla }}_i$ are given by

$\begin{array}{ll}{\delta }_{\epsilon }{h}_{ij}=2{\overline{\nabla }}_{(i}{\epsilon }_{j)},{\delta }_{\epsilon }{n}^i={\overline{D}}_t{\epsilon }^i.& (167)\end{array}$

The vector-ghost operator $Q_j^i$ is derived from (166) according to the general formula (22), and its quadratic part reads

$\begin{array}{l}{Q}_j^i={\delta }^i{}_j{\overline{D}}_t^2+\frac{1}{4\sigma }\{-2{\delta }^i{}_j{\overline{\Delta }}^2+2\left[1+2\xi -2\lambda (1+\xi )\right]{\overline{\nabla }}^i\overline{\Delta }{\overline{\nabla }}_j\\ +{\delta }^i{}_j\overline{R}\overline{\Delta }-(1-2\lambda +2\xi )\overline{R}{\overline{\nabla }}^i{\overline{\nabla }}_j-2\xi {\overline{R}}_{;j}{\overline{\nabla }}^i\\ -2\xi {\overline{R}}^{;i}{\overline{\nabla }}_j-2{\delta }^i{}_j{\overline{R}}_{;k}{\overline{\nabla }}^k-{\delta }^i{}_j{\overline{R}}_{;k}{}^k-2\xi {\overline{R}}^{;i}{}_j\}.& (168)\end{array}$

A virtue of the manifest background covariant treatment in the background field method is that, owing to the background $\text{Dif}{\text{f}}_{{F}}$ invariance, the shift vector ${\bar{N}}^i$ appears only in combination with the time derivative ∂_tγ_ij in the form of the extrinsic curvature or, equivalently, in the form of the covariant time derivative of the metric D_tγ_ij = 2K_ij. When performing variations of the total action S_tot = S_HG + S_gf + S_gh, factors of the shift perturbations nⁱ arise only from the variation of the covariant time derivative, as can be seen from the operator relation

$\begin{array}{ll}\left[\delta ,D_t\right]=-{{L}}_{\delta \text{N}}.& (169)\end{array}$

Moreover, a canonical ordering among mixed covariant time derivatives and covariant space derivatives could be chosen in such a way that the covariant time derivatives act first. This requires repeated use of the basic commutator³³

$\begin{array}{ll}\left[D_t,{\nabla }_m\right]T_{i_1\dots i_s}^{j_1\dots j_r}={\displaystyle \sum _{j_{\ell }}}{{K}}_{mn}^{j_{\ell }}{T}_{i_1\dots i_s}^{j_1\dots n\dots j_r}-{\displaystyle \sum _{i_{\ell }}}{{K}}_{m{i}_{\ell }}^n{T}_{i_1\dots n\dots i_s}^{j_1\dots j_r},& (170)\end{array}$

with the “anisotropic commutator curvature” tensor defined in terms of derivatives of the extrinsic curvature,

$\begin{array}{ll}{{K}}_{ij}^k:={\nabla }_i{K}_j^k+{\nabla }_j{K}_i^k-{\nabla }^k{K}_{ij}.& (171)\end{array}$

Upon introducing the auxiliary field π_i according to (163), making use of (169), integrating by parts, sorting derivatives with (170), reducing curvature tensors by the dimension-dependent identity (133), and arranging the fluctuations of the fields h_ij, nⁱ, and π_i in a multiplet ${\varphi }^A={(h_{ij},n^i,{\pi }_i)}^T$, the gauge-fixed fluctuation operator acquires a block matrix structure and can be represented in the form

$\begin{array}{l}{F}_{AB}(\overline{D_t},\bar{\nabla })=C_{AB}{\bar{D}}_t^2+D_{AB}^{ijkl}{\bar{\nabla }}_i{\bar{\nabla }}_j{\bar{\nabla }}_k{\bar{\nabla }}_l+T_{AB}{\bar{D}}_t+W_{AB}^{ij}{\bar{\nabla }}_i{\bar{\nabla }}_j\\ +{\Gamma }_{AB}^i{\bar{\nabla }}_i+P_{AB}.& (172)\end{array}$

The principal part of (172) is split into a temporal part C_AB and a spatial part $D_{AB}^{ijkl}$ for which the derivatives have been made explicit. For brevity, I do not give explicit expressions for the matrices C_AB, $D_{AB}^{ijkl}$, T_AB, $W_{AB}^{ij}$, ${\Gamma }_{AB}^i$, and P_AB, which are functions of the background fields. The one-loop renormalization requires calculation of the divergent part of the functional traces for the operators (172) and (168),

$\begin{array}{ll}{\Gamma }_1^{\text{div}}=\frac{1}{2}\text{Tr}ln{F}_{AB}{|}^{\text{div}}-\text{Tr}ln{Q}_i^j{|}^{\text{div}}.& (173)\end{array}$

In contrast to the relativistic case, standard heat-kernel techniques are not available for the anisotropic case; in particular, there is no closed algorithm based on an SDW representation (31) for the off-diagonal kernel of (172). In addition to the anisotropic character of these operators, they suffer from further complications. First, the matrices in the principal parts C_AB and D_AB are degenerate, as nⁱ and πⁱ enter F_AB only with lower derivatives and the h-h block of $D_{AB}^{ijkl}$ is a non-minimal fourth-order operator³⁴.

Nevertheless, initial attempts to deal with anisotropic operators using the heat-kernel technique were suggested in [81, 274]. A general algorithm for anisotropic operators, based on the resolvent method, was proposed in [83]. In the most general case, however, this algorithm requires the evaluation of a large number of products of nested multi-commutators as well as non-trivial parameter integrals, which is technically challenging.

Therefore, an alternative way of calculating the one-loop divergences might be more suitable, especially since the number of invariants in HG in D = 2 + 1 dimensions is reasonably small and the one-loop calculation using Feynman-diagrammatic techniques is still manageable, particularly when combined with the background field method. After integrating out the “quantum fields” h_ij and nⁱ as well as π_i, $c_i^{*}$, and cⁱ in the path integral, the effective action becomes a functional of the mean fields, which at the one-loop level can be identified with the background fields. In particular, the divergent part of the effective action is a sum of local operators of the background fields ${\bar{\gamma }}_{ij}$ and ${\bar{N}}^i$ together with their time and space derivatives, which, owing to the renormalizability of projectable HG, are of the same form as the manifestly ${\mathrm{\text{Diff}}}_{{F}}({M})$-invariant operators already present in the bare action (165). This allows us to extract the one-loop renormalization of G, λ, and μ in a simpler way by expanding the general background field ${\bar{\gamma }}_{ij}$ around a flat background in which ${\bar{N}}^i=0$:

$\begin{array}{ll}{\bar{\gamma }}_{ij}={\delta }_{ij}+H_{ij}.& (174)\end{array}$

Evaluating the bare action (165) on the background (174) and expanding up to quadratic order in H_ij yields

$\begin{array}{l}{S}_{\text{HG}}\left[{\bar{\gamma }}_{ij},{\bar{N}}^i\right]=\frac{1}{2G}{\displaystyle \int }\text{d}t{\text{ d}}^{2}x\{\frac{1}{4}({Ḣ}_{ij}{Ḣ}^{ij}-\lambda ḢḢ)+\mu [{\partial }^{2}H{\partial }^{2}H\\ -{\partial }_k{\partial }_l{H}^{kl}(2{\partial }^{2}H-{\partial }_j{\partial }_i{H}^{ij})]+{O}(H^3)\},& (175)\end{array}$

with ${\partial }^2:={\delta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }$. The divergent part of the effective action can be expanded in the same way:

$\begin{array}{l}{\Gamma }^{\text{div}}[{\bar{\gamma }}_{ij},{\bar{N}}^i]={\displaystyle \int }\text{d}t{\text{ d}}^{2}x\{c_1^{\text{div}}{Ḣ}_{ij}{Ḣ}^{ij}+c_2^{\text{div}}ḢḢ+c_3^{\text{div}}[{\partial }^{2}H{\partial }^{2}H\\ -\mu {\partial }_k{\partial }_l{H}^{kl}(2{\partial }^{2}H-{\partial }_j{\partial }_i{H}^{ij})]+{O}(H^3)\}.& (176)\end{array}$

In order to obtain the renormalizations of the couplings G, λ, and μ, it is sufficient to calculate the divergent coefficients $c_1^{\mathrm{\text{div}}}$, $c_2^{\mathrm{\text{div}}}$, and $c_3^{\mathrm{\text{div}}}$ of the operators quadratic in H_ij. The renormalization of G is extracted from $c_1^{\mathrm{\text{div}}}$, the renormalization of λ/G from $c_2^{\mathrm{\text{div}}}$, and the renormalization of μ/G by any of the three operators in (176). Disentangling this system enables extraction of the individual renormalizations of G, λ, and μ. Diagrammatically, the background fields H_ij appear only at external legs, while the quantum fields h_ij and nⁱ, as well as π_i, $c_i^{*}$, and cⁱ, propagate in the loops. Hence, according to (175) and (176), the one-loop renormalization of G, λ, and μ requires one to calculate the divergent part of the 1PI diagrams with two external H_ij-legs, shown in Figure 6.

FIGURE 6

Figure 6. One-loop two-point 1PI diagrams in projectable HG in D = 2 + 1 dimensions (from [53]).

For the regular gauge (166) with gauge parameters (ξ, σ) and pole ${{P}}_{\text{S}}$ as in (152), the propagators of the quantum fields h_ij and nⁱ are the same as in (150) and (151), while those including the π_i, $c_i^{*}$, and cⁱ fields read [51],

$\begin{array}{l}\langle {\pi }_i,n^j\rangle =G\omega {\delta }_i^j{{P}}_{\text{S}}(\omega ,k),\\ \langle {\pi }_i,{\pi }_j\rangle =\frac{G{k}^2}{2}\left[{\delta }_{ij}+(1-2\lambda )\frac{k_i{k}_j}{k^2}\right]{{P}}_{\text{S}}(\omega ,k),\\ \langle c_i^{*},c^j\rangle =G{\delta }_i^j{{P}}_{\text{S}}(\omega ,k).& (177)\end{array}$

The required three-point and four-point vertices in the gauge ${\bar{N}}^i=0$ are obtained by expanding the background fields in ${{L}}^{(2)}=\delta {\varphi }^A{F}_{AB}\delta {\varphi }^B$, with F_AB given in (172), according to (174) up to second order in H_ij. The explicit results for the vertices are rather lengthy and therefore not presented here. Within dimensional regularization, the divergent part of the one-loop diagrams in Figure 6 can be extracted by expanding the propagators in the corresponding integrals around vanishing external frequency and momenta, resulting in a sum of vacuum diagrams from which the logarithmically divergent contributions can easily be extracted by power counting³⁵. The one-loop beta functions β_G, β_λ, and β_μ, which determine the RG running of the couplings G, λ, and μ, are obtained directly from the logarithmic one-loop divergences, i.e., from the corresponding coefficient of the pole 1/ε in dimension.

Finally, in order to discuss the physical implications of the RG flow, it is important to extract the gauge-independent physical information from the RG system. In general, the off-shell effective action is parametrization- and gauge-dependent. On the one hand, a change of the gauge-fixing induces a change ${\Gamma }^{\text{div}}\mapsto {\Gamma }^{\text{div}}+{E}\delta {\Gamma }^{\text{div}}$, which is proportional to the equations of motion $\delta {\Gamma }^{\text{div}}=S_{,i}{X}^i$ with an arbitrary constant ${E}$ [34, 279, 280]. On the other hand, this change could be compensated for by the change δΓ^div = (∂Γ^div/∂G)δG + (∂Γ^div/∂λ)δλ + (∂Γ^div/∂μ)δμ, which is induced by a change in the couplings. The combinations of couplings for which the corresponding beta function is gauge-independent are called essential; all other couplings are called inessential and do not enter physical observables. The problem is therefore to tell apart and disentangle the essential from the inessential couplings. In order to find Xⁱ explicitly, one could exploit power counting, as $S_{,i}{X}^i$ must be a local functional with the same scaling as Γ^div; that is, in the context of D = 2 + 1 projectable HG, $S_{,i}{X}^i$ can only involve marginal operators with respect to the anisotropic scaling. Since the scaling and the index structure of the S_{, i} are known, this corresponds to a strong constraint on the possible structure of the Xⁱ. In [53], it was found that the unique combination $X^i{S}_{,i}$ that vanishes on-shell is

$\begin{array}{ll}\delta {\Gamma }^{\text{div}}={E}{\displaystyle \int }\text{d}t{\text{ d}}^{2}x\left[K_{ij}{K}^{ij}-\lambda K^2-\mu R^2\right].& (178)\end{array}$

The variation of Γ^div with respect to the couplings reads

$\begin{array}{l}\delta {\Gamma }^{\text{div}}=\frac{1}{2G}{\displaystyle \int }\text{d}t{\text{ d}}^{2}x\sqrt{\gamma }[-\frac{\delta G}{G}{K}_{ij}{K}^{ij}-\lambda \left(\frac{\delta \lambda }{\lambda }-\frac{\delta G}{G}\right)K^2\\ +\mu \left(\frac{\delta \mu }{\mu }-\frac{\delta G}{G}\right)R^2].& (179)\end{array}$

Equating (178) and (179) yields the desired transformations of the couplings [53],

$\begin{array}{ll}\delta G=-2G^2{E},\delta \lambda =0,\delta \mu =-4G\mu {E}.& (180)\end{array}$

Thus, only λ and the combination ${G}=G/\sqrt{\mu }$ are essential couplings $(\delta \lambda =\delta {G}=0)$, with beta functions [53]

$\begin{array}{l}{\beta }_{\lambda }=\frac{15-14\lambda }{64\pi }\sqrt{\frac{1-2\lambda }{1-\lambda }}{G},\\ {\beta }_{{G}}=-\frac{(16-33\lambda +18{\lambda }^2)}{64\pi {(1-\lambda )}^2}\sqrt{\frac{1-\lambda }{1-2\lambda }}{{G}}^2.& (181)\end{array}$

The RG flow driven by the beta functions (181) is shown in Figure 7. There are two UV fixed points at

$\begin{array}{ll}\left({\lambda }_1^{*},{{G}}_1^{*}\right)=(1/2,0),\left({\lambda }_2^{*},{{G}}_2^{*}\right)=(15/14,0).& (182)\end{array}$

The first fixed point $({\lambda }_1^{*},{{G}}_1^{*})$ lies exactly on the lower boundary of the non-unitary interval 1/2 < λ < 1 for which the gravitational scalar degree of freedom behaves like a ghost; cf. the discussion in section 7.4. For fixed ${G}$, the beta function ${\beta }_{{G}}$ develops a divergence in the limit λ → 1/2. At the same time, however, the limit λ → 1/2 is accompanied by ${G}\to 0$, implying that the relevant expansion parameter in this limit is $\tilde{{G}}={G}{(1-2\lambda )}^{-1/2}$. The beta function ${\beta }_{\tilde{{G}}}$ vanishes for λ → 1/2, which means that there is a one-parameter family of UV fixed points parameterized by the asymptotic value of $\tilde{{G}}$. Summarizing, the status of this fixed point remains inconclusive and higher loop corrections or contributions from matter loops are required to resolve the situation and to decide whether the fixed point is merely an artifact of the approximation or has physical significance.

FIGURE 7

Figure 7. RG flow of essential couplings in HG in D = 2 + 1 dimensions; arrows point from the UV to the IR (from [53]).

In contrast, the second fixed point $({\lambda }_2^{*},{{G}}_2^{*})$ is regular, lies in the unitary region λ > 1, and is asymptotically free [53]. Although projectable HG in D = 2 + 1 dimensions only has the status of a toy model without propagating spin-2 particles, it provides the first unitary, perturbatively renormalizable, and UV-complete quantum theory of gravitational propagating degrees of freedom. In previous calculations of the one-loop divergences in D = 2 + 1 projectable HG, the dynamical content of the metric field was restricted to the conformal mode [275]. In this conformally reduced model, only the fixed point at (1/2, 0) has been found. This shows that the formation of the regular fixed point at (15/14, 0) requires the full theory [53].

Another interesting feature of the RG flow is that there are RG trajectories which emanate from the regular UV fixed point and asymptotically approach the “relativistic value” λ → 1 in the IR. In addition to the problems with the IR λ → 1 limit discussed in section 7.4, the “gravitational coupling” ${G}$ becomes strongly coupled along these trajectories, necessitating a non-perturbative analysis in this regime. Nevertheless, the observed flow toward λ = 1 suggests that the possibility of a dynamical mechanism for an emergent restoration of relativistic symmetry at low energies should be investigated in more detail. First, the phenomenon that a theory which is asymptotically free in the UV develops a strong coupling in the IR is well-known. Second, the strong coupling of ${G}$ in the IR could just be an artifact of the absence of relevant curvature operators in D = 2 + 1. In D = 3 + 1 dimensions relevant deformations might be expected to naturally cut off the strong coupling of ${G}$.

All these interesting and encouraging results justify the hope that the RG flow of the more realistic and physically relevant theory in D = 3 + 1 dimensions exhibits similar features. Although there are no conceptual problems associated with the analogous calculation in D = 3 + 1 dimensions, in view of the increased number and complexity of the independent curvature invariants, it is technically much more challenging. A first step toward the RG flow of projectable HG in D = 3 + 1 dimensions has been taken in [54], where the one-loop beta functions of G and λ were derived with Feynman-diagrammatic methods in a similar way to (175) and (176), by exploiting the gauge invariance of counterterms, which allows one to restrict to a flat metric background and focus only on diagrams with background shift fields at the external legs. However, the gauge-invariant beta functions for the essential coupling constants and the fixed point structure of the theory can only be derived by having access to the renormalizations of all couplings, including those in the potential sector. Thus, the complete calculation of the one-loop divergences in D = 3 + 1 projectable HG is an important task.

10. Conclusions and Outlook

In this article I have reviewed various attempts to quantize gravity within the framework of perturbative quantum field theory, with a particular focus on Hořava gravity. I have highlighted the merits and difficulties that come with each of the approaches. The different approaches to quantum gravity discussed in this work might best be characterized by the property that each does not share with the other approaches, as shown in Table 2.

TABLE 2

Table 2. Approaches to quantum gravity characterized by properties that they do not have.

The status of HG with critical anisotropic scaling can be roughly summarized by dividing the discussion into “projectable” vs. “non-projectable” and “phenomenology of the classical theory” vs. “properties of the quantum theory.”

From a phenomenological point of view, projectable HG does not seem to qualify as a viable theory, mainly because it suffers from an IR instability of the additional scalar gravitational mode [212–215]. Although other proposals with a more optimistic conclusion for this problem have been made [200, 217, 218], they are based on non-perturbative effects which are outside the scope of the weak coupling regime where perturbation theory is applicable.

In contrast, the non-projectable model does not suffer from an IR instability because additional relevant operators that include powers of the acceleration vector (spatial derivatives of the lapse function) can remedy the IR instability [221]. Even if the low-energy sector of the non-projectable model is strongly constrained by observational data and a mechanism to avoid percolation of LV effects from the gravitational sector to the matter sector seems necessary to avoid conflicts with bounds on LV in the matter sector [227], the non-projectable model is still phenomenologically viable [238].

From a theoretical point of view, regarding the status of HG as a consistent quantum theory of gravity, the situation is somewhat opposite to that of the phenomenological assessment. The projectable theory has been proven to be perturbatively renormalizable (for any dimension D = d + 1) in the strict sense [51, 52]. Moreover, the model in D = 2 + 1 dimensions has been shown to be asymptotically free, and its RG flow features interesting RG trajectories which emanate from the UV fixed point and asymptotically approach the relativistic value λ = 1 in the IR [53]. Even if the model in D = 2 + 1 dimensions must be considered a toy model without propagating TT modes, it is a unitary, perturbatively renormalizable, and UV-complete quantum theory of non-trivial propagating degrees of freedom and captures essential features of HG, which are expected to carry over to the physically relevant D = 3 + 1 case. The situation in D = 3 + 1 dimensions has not yet been conclusively clarified and requires calculation of the one-loop beta functions. A first step in this direction has been taken in [54], but in order to extract the gauge-independent physical information about the running of the essential couplings, the renormalization of all couplings is needed. While there are no new conceptual difficulties, the analogous calculation is technically much more complex than in the D = 2 + 1 case and requires more efficient methods, such as newly developed heat-kernel techniques for anisotropic operators [81, 83, 274]. In any case, the calculation of the one-loop divergences of projectable HG in D = 3 + 1 dimensions is certainly a very important endeavor that will provide new insights into the structure of the theory.

The situation with the quantization of the non-projectable model is less clear. Unfortunately, the proof of perturbative renormalizability for the projectable theory [51, 52] does not extend to the non-projectable theory, mainly because it relies on the regular form of all propagators and no gauge-fixing could be found in the non-projectable model that would render all propagators regular. In particular, there seems to be no gauge-fixing that could remove all irregular contributions to the propagator involving the lapse function—interpreted in [51] as a reflection of the instantaneous interaction induced by the lapse function [214]. Therefore new ideas seem to be necessary for dealing with the perturbative quantization of the non-projectable theory.

In summary, HG is an interesting proposal, but, closing with the words of Bryce DeWitt, the theory does not yet seem to have been “pushed to its logical conclusion” [281]. Further important calculations in D = 3 + 1 dimensions are required and may decide the fate of Hořava's proposal for a unitary, perturbatively renormalizable, and UV-complete quantum theory of gravity.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Benjamin Bahr, Antonio Duarte Pereira, and Astrid Eichhorn for inviting me to contribute this article to the Frontiers Research Topic Coarse Graining in Quantum gravity: Bridging the Gap between Microscopic Models and Spacetime-Physics. I would also like to thank those collaborators with whom I had the pleasure to work in various constellations on different topics that have found their way into this contribution, especially Andrei Barvinsky, Diego Blas, Anirudh Gundhi, Lavinia Heisenberg, Mario Herrero-Valea, Alexander Kamenshchik, Claus Kiefer, Dmitry Nesterov, Guillem Pérez-Nadal, Michael Ruf, Sergey Sibiryakov, Alexei Starobinsky, and Matthijs van der Wild. Part of this work was done during a stay at SISSA (Trieste) in the framework of the Young Investigator Training Program 2018, and it is my pleasure to thank Roberto Percacci and SISSA (Trieste) for their warm hospitality and INFN/ACRI for financial support. I also acknowledge financial support for the article-processing charge, funded by the Baden-Württemberg Ministry of Science, Research and Art and the University of Freiburg through the funding program Open Access Publishing.

Footnotes

1. ^I use the ultra-condensed DeWitt notation, in which the generalized index i = {A, X} of a generalized field ϕⁱ = ϕ^A(X) encompasses the discrete bundle index A and the continuous spacetime point X. Summation over i implies summation over A as well as integration over X, i.e., ${\varphi }_i{\varphi }^i=\int {\text{d}}^{D}X{\varphi }_A(X){\varphi }^A(X)$.

2. ^Post-fix notation with indices separated by a comma is used to denote functional derivatives with respect to the argument, e.g., ${\Gamma }_{,i}=\delta \Gamma \left[\phi \right]/\delta {\phi }^i$.

3. ^The generalized DeWitt gauge index α = (a, X) is taken from the beginning of the Greek alphabet and not to be confused with indices μ, ν, … from the tangent bundle.

4. ^The heat kernel is in particular very efficient for the extraction of the one-loop divergences. For calculations involving higher loop orders, it is not so well-developed, but see [59].

5. ^If the configuration space of fields ${C}$ is viewed as a differentiable manifold, the configuration space metric defines the invariant line element $\text{d}{S}^2={{C}}_{ij}\text{d}{\varphi }^i\text{d}{\varphi }^j$. Ultra-locality means that ${{C}}_{ij}=C_{AB}\delta (X_A,X_B)$ with ${{C}}_{AB}$ involving no derivatives. For 2kth-order derivative theories, defined by an action functional (1), the configuration space metric C_AB could be defined by the coefficient of the (minimal part of the) highest derivative term in the fluctuation operator $F_{AB}=C_{AB}{\Delta }^k+\dots .$ The inverse is defined via $C^{AC}{C}_{CB}={\delta }_B^A=\mathbf{\text{1}}$. The boldface notation is exclusively reserved for matrix-valued operators with proper index positions. Since the content of this section holds for general operators F, no background tensors appear in what follows.

6. ^The inverse F⁻¹ of the operator F is denoted by 1/F. It is assumed that F is positive definite. In the integral relation for the logarithm (27), an (infinite) constant has been neglected. The precise relation can be defined by a regularizing mass damping factor, i.e., by defining $\mathbf{\text{G}}(m^2):={\int }_0^{\infty }\text{d}s{e}^{-s{m}^2}{e}^{-s\mathbf{\text{F}}}$, with the logarithm of F obtained as a limit, $ln\mathbf{\text{F}}=\underset{m^2\to \infty }{lim}[ln{m}^2\mathbf{\text{1}}-{\int }_0^{m^2}\text{d}{\mu }^2\mathbf{\text{ G}}({\mu }^2)]$.

7. ^I work on a D-dimensional (pseudo)-Riemannian manifold ${M}$ with local coordinates X^μ, μ = 0, 1, 2, 3, a metric structure g_μν with inverse g^μν defined by $g^{\mu \rho }{g}_{\rho \nu }={\delta }_{\nu }^{\mu }$, and the torsion-free metric-compatible Christoffel connection ${\Gamma }_{\mu \nu }^{\rho }=g^{\rho \sigma }({\partial }_{\mu }{g}_{\sigma \nu }+{\partial }_{\nu }{g}_{\mu \sigma }-{\partial }_{\sigma }{g}_{\mu \nu })/2$, which defines the covariant derivative ∇_μ. I use the following conventions for the Lorentzian signature sig(g) = diag(−1, 1, 1, …, 1), the Riemann curvature tensor $R_{\mu \sigma \nu }^{\rho }={\partial }_{\sigma }{\Gamma }_{\mu \nu }^{\rho }-{\partial }_{\nu }{\Gamma }_{\mu \sigma }^{\rho }+{\Gamma }_{\mu \nu }^{\lambda }{\Gamma }_{\lambda \sigma }^{\rho }-{\Gamma }_{\mu \sigma }^{\lambda }{\Gamma }_{\lambda \nu }^{\rho }$, and the Ricci tensor $R_{\mu \nu }=R_{\mu \rho \nu }^{\rho }$. I use natural units in which the speed of light c and Planck's constant ℏ are set to one, c = ℏ = 1, and Newton's constant G_N can be expressed in terms of the reduced Planck mass, $M_{\text{P}}:=1/\sqrt{8\pi G_{\text{N}}}$.

8. ^I call an operator O classically relevant if ${\left[{O}\right]}_{\text{M}}<D$, classically marginal if ${\left[{O}\right]}_{\text{M}}=D$, and classically irrelevant if ${\left[{O}\right]}_{\text{M}}>D$.

9. ^The particle spectrum of a QFT is usually derived by expanding the action up to quadratic order in the linear perturbation around the vacuum. In relativistic QFTs, the natural vacuum is Minkowski space, which, even in the presence of gravity, could be justified locally by the equivalence principle. Minkowski space is a maximal symmetric space whose isometries are generated by the D(D + 1)/2 linearly independent Killing vectors, which correspond to the generators of infinitesimal transformations of the Poincaré group. In this way, the Minkowski vacuum is connected to the representation theory of the Poincaré group, ultimately giving rise to Wigner's classification [84], in which particles are classified according to their mass and their spin, i.e., the eigenvalues of the Casimir operators of the Poincaré group. A positive cosmological constant Λ > 0 suggests, however, that the global vacuum is De Sitter space rather than Minkowski space. De Sitter space is also a maximally symmetric space, whose Killing vectors are the generators of the De Sitter group. More generally, this also suggests that for an arbitrary spacetime without any symmetry, the very concept of a particle is not really well-defined.

10. ^I reserve the symbol G for the general Green's function in position space defined in (9), and use ${P}$ instead for the flat-space Green's function in momentum space.

11. ^This can also be seen as follows: Starting from a spin-2 particle freely propagating in flat spacetime with a linear field equation, locality and diffeomorphism invariance require non-linear self-interactions to be added iteratively in a consistent way such that, when summed, the full non-linear theory of GR is recovered (see [85]). The explicit expressions for the vertices in momentum space are rather lengthy and not very illuminating. The expressions for the three-point and four-point vertices can be found in [35], for example. For these calculations computer-algebra programs, such as FORM or the Mathematica-based xAct bundle (in particular, the core package xTensor and the extension packages xPert and xTras) are indispensable [86–90].

12. ^In a recent calculation of the two-loop divergences with modern on-shell methods, it was found that by using dimensional regularization, evanescence operators (such as the Gauss-Bonnet term) in divergent subdiagrams can alter the coefficient of the pole term [101].

13. ^Only when the more fundamental theory is valid up to arbitrarily high energy scales does it qualify as UV-complete theory. Instead of integrating out certain heavy particles, in the Wilsonian approach the effective action is defined at a given energy scale E by integrating out all particles with momenta P² > E.

14. ^This naive estimate might be modified in the presence of matter; see e.g., the discussion in the context of scalar-tensor theories with a strong non-minimal coupling, such as in the model of Higgs inflation [102–107].

15. ^Note, however, that a summation of operators with a fixed number of external fields but an arbitrary number of derivatives results in non-local form factors that lead to IR modifications of the propagator. For a discussion of these non-local form factors in the context of gravity and the heat kernel (see e.g., [108, 109]).

16. ^An important technical requirement for the consistent renormalization is that the counterterms have the same structure as the operators in the EFT expansion. Since the latter are restricted by symmetry, the process of renormalization is required to preserve this symmetry; see e.g., the discussion in [110]. This property is non-trivial to show and has been proven for GR and Yang-Mills theory in [58]. Recently, the proof was extended to effective and non-relativistic theories by combining the BRST cohomology with the background field method [52].

17. ^In this section, I denote the coupling constants by g_n to contrast with the c_n in (1) and the ω_n in (79), although when put in the right context they are all the same objects. The RG flow g_n(k) is defined as the solution to the RG system k∂_kg_n = β_gn, with the abstract RG scale k and beta functions β_gn. A fixed point $g_n^{*}$ is defined by the condition ${\beta }_{g_n}(g_m^{*})=0$ for all n. The couplings ${\tilde{g}}_n$, which carry a canonical physical dimension ${\left[{\tilde{g}}_n\right]}_{\text{M}}={\alpha }_n$, are made dimensionless by rescaling with the appropriate power of the RG scale [k]_M = 1, i.e., $g_n={\tilde{g}}_n{k}^{-{\alpha }_n}$, such that [g_n]_M = 0. Moreover, since only essential couplings enter physical observables, only they are required to take finite values in the UV. In contrast, inessential couplings, which can be changed by a field redefinition, do not enter physical observables and so may diverge in the UV.

18. ^In particular, once a cutoff is introduced, it does not matter whether the underlying theory is perturbatively renormalizable in the strict sense or not. All operators compatible with the symmetries of the theory have to be considered. This is similar to the EFT case, but in contrast to the EFT treatment, the particle content and the symmetries are not necessarily defined by the relevant operators of the low-energy approximation, but rather are defined along with the averaged effective action (82). In general the theory space is infinite, but if the symmetry restriction is so strong that it only allows for a finite number of operators, the theory space could be finite.

19. ^This is a consistency requirement of the truncation. If no operators that lead out of the truncation are induced, the flow closes and (83) is really an exact equation.

20. ^The UV critical surface can be thought of as a subspace of the tangent space at $g_i^{*}$, consisting of those RG trajectories which are attracted toward the fixed point. In general there can be more than just one fixed point, and the RG flow may also allow for more exotic phenomena, such as limit cycles. It could also happen that some of the fixed points can be discarded on physical grounds.

21. ^Compare this with the perturbative quantization of GR, discussed in section 3. The perturbatively non-renormalizable character requires the measurements of an infinite number of couplings, thereby leading to a loss of predictive power. Compare this also with the EFT approach to GR, discussed in section 4. While only a finite number of couplings have to be measured within a finite truncation, the EFT cannot be extrapolated beyond a certain energy scale and therefore does not qualify as a UV-complete theory.

22. ^A similar problem occurs when working on special (in general highly symmetric) backgrounds, even if they do not correspond to on-shell configurations.

23. ^Even on-shell, there remain divergences associated with operators involving derivatives of the Ricci scalar, which are not total derivatives and cannot be absorbed into the function f(R) [76]. On a constant-curvature background $g_{\mu \nu }^0$, for which $R_{\mu \nu \rho \sigma }^0=R_0(g_{\mu \rho }^0{g}_{\nu \sigma }^0-g_{\mu \sigma }^0{g}_{\nu \rho }^0)$, Υ_μ = 0, $\int {\text{d}}^{4}X\sqrt{g^0}=384{\pi }^2/R_0^2$, and the equations of motion reduce to the algebraic equation 2f − R₀f₁ = 0, the one-loop divergences ${\Gamma }_1^{\text{div}}{|}_0^{\mathrm{\text{on-shell}}}=(1/\epsilon )\left[\frac{97}{20}+4f/R_0^2{f}_2-8f^2/3{(R_0{f}_2)}^2\right]$ can be absorbed by a renormalization of f(R₀).

24. ^See also [166–170] for a discussion of the quantum parametrization dependence of the effective action in cosmology.

25. ^Since Newton's constant $G_{\text{N}}(t)~1/k^2(t)$ exceeds the perturbative regime, a perturbative treatment does not seem reliable in the asymptotic limit t → ∞. However, because Newton's coupling is an inessential coupling in the ordinary perturbative approach (even if it runs in the covariant Vilkovisky off-shell extension), it should never enter an on-shell observable in an isolated way, but only via a dimensionless combination with other couplings [including Λ(t)] whose beta function is gauge-independent. Thus, independently of whether G_N itself grows beyond perturbative control in the limit t → ∞, the question should then rather be whether the RG running of this dimensionless combination stays under perturbative control.

26. ^In general, relevant deformations also lead to different coupling constants in front of different powers of k² in the propagator (98), which, as discussed in the context of HG in section 7.4, might prevent a direct restoration of Lorentz invariance in the IR.

27. ^This implies Λ = 0. For a discussion of the cosmological constant in HG, see e.g. [211].

28. ^The order of the covariant derivatives in (147) is a matter of choice, as different orders differ only in curvature terms that do not affect the principal part of the fluctuation operator. When lower-derivative parts are included in the operator (147), there may be “preferred choices” that simplify the lower-derivative parts of the fluctuation operator. In (147), a symmetric ordering has been chosen. Another natural symmetric choice is $O_{ij}=-{\left({\bar{\nabla }}_{i_1}{\bar{\nabla }}_{i_2}\dots {\bar{\nabla }}_{i_{(d-2)/2}}(\bar{\Delta }{\gamma }^{kl}+\xi {\bar{\nabla }}^k{\bar{\nabla }}^l){\bar{\nabla }}^{i_{(d-2)/2}}\dots {\bar{\nabla }}^{i_2}{\bar{\nabla }}^{i_1}\right)}^{-1}.$

29. ^The ghost field propagator $\langle c_i^{*},c^i\rangle =G{\delta }_i^j{{P}}_{\text{S}}(\omega ,k)$, which is derived from the gauge-fixing (148) according to the general rule (22), also has the regular form [51].

30. ^The propagators (153) and (154) with the poles (155) are derived by taking into account only those operators in the potential (132) that have a marginal anisotropic scaling. If the relevant operators in (132) were taken into account, they would lead to relevant deformations in the propagators, i.e., additional terms with lower k-dependence. Positive definiteness of O_ij requires ξ > − 1, which is not satisfied for λ > 1 in the gauge (155). This, however, does not seem to lead to difficulties in the perturbative approach, at least as far as gauge-independent on-shell quantities are concerned, such as the beta functions of the essential couplings in (2 + 1)-dimensional HG discussed in section 9.

31. ^This statement also relies on the $\text{Dif}{\text{f}}_{{F}}$-invariant structure of the counterterms proven in [52], as factors of the shift vector in $\text{Dif}{\text{f}}_{{F}}$-invariant operators can only occur in the form of the covariant time derivative (109).

32. ^Note the flipped sign of the μR² term compared to (127).

33. ^The relations (169) and (170) hold for any d, but only in the projectable version of HG. In the non-projectable theory the operator version of (169) reads $\left[\delta ,D_t\right]=-N^{-1}(\delta N{D}_t+{{L}}_{\delta \mathbf{\text{N}}})$. Likewise, (170) yields an additional term $a_m{D}_t{T}_{i_1\dots i_s}^{j_1\dots j_r}$ on the right-hand side, and the covariant spatial derivatives in the definition (171) must be shifted by the acceleration vector ∇_i ↦ ∇_i + a_i.

34. ^The degeneracy is a consequence of the anisotropic scaling: in contrast to [h_ij]_S = 0, the fields nⁱ and πⁱ carry non-zero scaling dimension ${\left[{\pi }_i\right]}_{\mathrm{\text{S}}}={\left[n^i\right]}_{\mathrm{\text{S}}}$, such that the overall homogeneous scaling [F_AB]_S = 4 only allows for lower derivatives of nⁱ and πⁱ.

35. ^See e.g., [278] for an application of this method with a particular focus on the combinatorial aspects in the context of relativistic higher-derivative theories.

References

1. Rosenfeld L. Über die Gravitationswirkungen des Lichts. Z Phys. (1930) 65:589–99. doi: 10.1007/BF01391161

CrossRef Full Text | Google Scholar

2. Kiefer C. Quantum Gravity. New York, NY: Oxford University Press (2007). doi: 10.1093/acprof:oso/9780199212521.001.0001

CrossRef Full Text | Google Scholar

3. DeWitt BS. Quantum theory of gravity. 1. The canonical theory. Phys Rev. (1967) 160:1113–48. doi: 10.1103/PhysRev.160.1113

CrossRef Full Text | Google Scholar

4. Hartle JB, Hawking SW. Wave function of the universe. Adv Ser Astrophys Cosmol. (1987) 3:174–89.

Google Scholar

5. Rovelli C, Smolin L. Discreteness of area and volume in quantum gravity. Nucl Phys B. (1995) 442:593–622. doi: 10.1016/0550-3213(95)00150-Q

CrossRef Full Text | Google Scholar

6. Rovelli C. Loop quantum gravity. Living Rev Rel. (1998) 1:1. doi: 10.12942/lrr-1998-1

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ashtekar A, Lewandowski J. Background independent quantum gravity: a status report. Class Quant Grav. (2004) 21:R53. doi: 10.1088/0264-9381/21/15/R01

CrossRef Full Text | Google Scholar

8. Thiemann T. Modern Canonical Quantum General Relativity. arXiv preprint. arXiv:gr-qc/0110034 (2001).

Google Scholar

9. Ambjorn J, Jurkiewicz J, Loll R. Emergence of a 4-D world from causal quantum gravity. Phys Rev Lett. (2004) 93:131301. doi: 10.1103/PhysRevLett.93.131301

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ambjorn J, Jurkiewicz J, Loll R. Spectral dimension of the universe. Phys Rev Lett. (2005) 95:171301. doi: 10.1103/PhysRevLett.95.171301

PubMed Abstract | CrossRef Full Text

11. Loll R. Quantum gravity from causal dynamical triangulations: a review. Class Quant Grav. (2020) 37:013002. doi: 10.1088/1361-6382/ab57c7

CrossRef Full Text | Google Scholar

12. Lust D, Theisen S. Lecture Notes in Physics. Vol. 346 Berlin; Heidelberg: Springer (1989).

Google Scholar

13. Polchinski J. String Theory. Vol. 1: An Introduction to the Bosonic String. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press (2007).

Google Scholar

14. Polchinski J. String Theory. Vol. 2: Superstring Theory and Beyond. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press (2007).

Google Scholar

15. Kiritsis E. String Theory in a Nutshell. Princeton, NJ: Princeton University Press (2019).

Google Scholar

16. Schomerus V. A Primer on String Theory. Cambridge: Cambridge University Press (2017). doi: 10.1017/9781316672631

CrossRef Full Text

17. Krasnikov NV. Nonlocal gauge theories. Theor Math Phys. (1987) 73:1184–90. doi: 10.1007/BF01017588

CrossRef Full Text | Google Scholar

18. Gorbar EV, Shapiro IL. Renormalization group and decoupling in curved space. JHEP. (2003) 2:021. doi: 10.1088/1126-6708/2003/02/021

CrossRef Full Text | Google Scholar

19. Smilga AV. Ghost-free higher-derivative theory. Phys Lett B. (2006) 632:433–8. doi: 10.1016/j.physletb.2005.10.014

CrossRef Full Text | Google Scholar

20. Shapiro IL. Counting ghosts in the “ghost-free” non-local gravity. Phys Lett B. (2015) 744:67–73. doi: 10.1016/j.physletb.2015.03.037

CrossRef Full Text | Google Scholar

21. Biswas T, Gerwick E, Koivisto T, Mazumdar A. Towards singularity and ghost free theories of gravity. Phys Rev Lett. (2012) 108:031101. doi: 10.1103/PhysRevLett.108.031101

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Modesto L. Super-renormalizable quantum gravity. Phys Rev D. (2012) 86:044005. doi: 10.1103/PhysRevD.86.044005

CrossRef Full Text | Google Scholar

23. Tomboulis ET. Renormalization and unitarity in higher derivative and nonlocal gravity theories. Mod Phys Lett A. (2015) 30:1540005. doi: 10.1142/S0217732315400052

CrossRef Full Text | Google Scholar

24. Tomboulis ET. Nonlocal and quasilocal field theories. Phys Rev D. (2015) 92:125037. doi: 10.1103/PhysRevD.92.125037

CrossRef Full Text | Google Scholar

25. Edholm J, Koshelev AS, Mazumdar A. Behavior of the Newtonian potential for ghost-free gravity and singularity-free gravity. Phys Rev D. (2016) 94:104033. doi: 10.1103/PhysRevD.94.104033

CrossRef Full Text | Google Scholar

26. Modesto L, Rachwał La. Nonlocal quantum gravity: a review. Int J Mod Phys D. (2017) 26:1730020. doi: 10.1142/S0218271817300208

CrossRef Full Text | Google Scholar

27. Sezgin E, van Nieuwenhuizen P. New ghost free gravity lagrangians with propagating torsion. Phys Rev D. (1980) 21:3269. doi: 10.1103/PhysRevD.21.3269

CrossRef Full Text | Google Scholar

28. Sezgin E. Class of ghost free gravity Lagrangians with massive or massless propagating torsion. Phys Rev D. (1981) 24:1677–80. doi: 10.1103/PhysRevD.24.1677

CrossRef Full Text | Google Scholar

29. Hehl FW, McCrea JD, Mielke EW, Ne'eman Y. Metric affine gauge theory of gravity: field equations, Noether identities, world spinors, and breaking of dilation invariance. Phys Rept. (1995) 258:1–171. doi: 10.1016/0370-1573(94)00111-F

CrossRef Full Text | Google Scholar

30. Shapiro IL. Physical aspects of the space-time torsion. Phys Rept. (2002) 357:113. doi: 10.1016/S0370-1573(01)00030-8

CrossRef Full Text | Google Scholar

31. Pagani C, Percacci R. Quantum gravity with torsion and non-metricity. Class Quant Grav. (2015) 32:195019. doi: 10.1088/0264-9381/32/19/195019

CrossRef Full Text | Google Scholar

32. Percacci R, Sezgin E. A new class of ghost and tachyon free metric affine gravities. Phys. Rev. D. (2020) 8:084040. doi: 10.1103/PhysRevD.101.084040

CrossRef Full Text | Google Scholar

33. DeWitt BS. Dynamical Theory of Groups and Fields. London: Blackie & Son (1965).

PubMed Abstract

34. DeWitt BS. Quantum theory of gravity. 2. The manifestly covariant theory. Phys Rev. (1967) 162:1195–239. doi: 10.1103/PhysRev.162.1195

CrossRef Full Text | Google Scholar

35. DeWitt BS. Quantum theory of gravity. 3. Applications of the covariant theory. Phys Rev. (1967) 162:1239–56. doi: 10.1103/PhysRev.162.1239

CrossRef Full Text | Google Scholar

36. 't Hooft G, Veltman MJG. One loop divergencies in the theory of gravitation. Ann Inst H Poincare Phys Theor A. (1974) 20:69–94.

Google Scholar

37. Goroff MH, Sagnotti A. Quantum gravity at two loops. Phys Lett B. (1985) 160:81–6. doi: 10.1016/0370-2693(85)91470-4

CrossRef Full Text | Google Scholar

38. Weinberg S. Phenomenological Lagrangians. Phys A. (1979) 96:327–40. doi: 10.1016/0378-4371(79)90223-1

CrossRef Full Text | Google Scholar

39. Donoghue JF. General relativity as an effective field theory: the leading quantum corrections. Phys Rev D. (1994) 50:3874–88. doi: 10.1103/PhysRevD.50.3874

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Burgess CP. Quantum gravity in everyday life: general relativity as an effective field theory. Living Rev Rel. (2004) 7:5–56. doi: 10.12942/lrr-2004-5

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Reuter M. Nonperturbative evolution equation for quantum gravity. Phys Rev D. (1998) 57:971–85. doi: 10.1103/PhysRevD.57.971

CrossRef Full Text | Google Scholar

42. Codello A, Percacci R, Rahmede C. Investigating the ultraviolet properties of gravity with a Wilsonian renormalization group equation. Ann Phys. (2009) 324:414–69. doi: 10.1016/j.aop.2008.08.008

CrossRef Full Text | Google Scholar

43. Reuter M, Saueressig F. Quantum Einstein gravity. New J Phys. (2012) 14:055022. doi: 10.1088/1367-2630/14/5/055022

CrossRef Full Text | Google Scholar

44. Litim DF. Renormalisation group and the Planck scale. Phil Trans Roy Soc Lond A. (2011) 369:2759–78. doi: 10.1098/rsta.2011.0103

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Stelle KS. Renormalization of higher derivative quantum gravity. Phys Rev D. (1977) 16:953–69. doi: 10.1103/PhysRevD.16.953

CrossRef Full Text | Google Scholar

46. Ostrogradsky M. Mmoires sur les quations diffrentielles, relatives au problme des isoprimtres. Mem Acad St Petersbourg. (1850) 6:385–517.

47. Anselmi D, Piva M. Quantum gravity, Fakeons and microcausality. JHEP. (2018) 11:021. doi: 10.1007/JHEP11(2018)021

CrossRef Full Text | Google Scholar

48. Donoghue JF, Menezes G. Unitarity, stability and loops of unstable ghosts. Phys Rev D. (2019) 100:105006. doi: 10.1103/PhysRevD.100.105006

CrossRef Full Text | Google Scholar

49. Horava P. Membranes at quantum criticality. JHEP. (2009) 3:020. doi: 10.1088/1126-6708/2009/03/020

CrossRef Full Text | Google Scholar

50. Horava P. Quantum gravity at a Lifshitz point. Phys Rev D. (2009) 79:084008. doi: 10.1103/PhysRevD.79.084008

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Barvinsky AO, Blas D, Herrero-Valea M, Sibiryakov SM, Steinwachs CF. Renormalization of Hořava gravity. Phys Rev D. (2016) 93:064022. doi: 10.1103/PhysRevD.93.064022

CrossRef Full Text | Google Scholar

52. Barvinsky AO, Blas D, Herrero-Valea M, Sibiryakov SM, Steinwachs CF. Renormalization of gauge theories in the background-field approach. JHEP. (2018) 7:035. doi: 10.1007/JHEP07(2018)035

CrossRef Full Text | Google Scholar

53. Barvinsky AO, Blas D, Herrero-Valea M, Sibiryakov SM, Steinwachs CF. Hořava gravity is asymptotically free in 2 + 1 dimensions. Phys Rev Lett. (2017) 119:211301. doi: 10.1103/PhysRevLett.119.211301

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Barvinsky AO, Herrero-Valea M, Sibiryakov SM. Towards the renormalization group flow of Horava gravity in (3+1) dimensions. Phys Rev D. (2019) 100:026012. doi: 10.1103/PhysRevD.100.026012

CrossRef Full Text | Google Scholar

55. Lehmann H, Symanzik K, Zimmermann W. On the formulation of quantized field theories. Nuovo Cim. (1955) 1:205–25. doi: 10.1007/BF02731765

CrossRef Full Text | Google Scholar

56. Becchi C, Rouet A, Stora R. Renormalization of Gauge theories. Ann Phys. (1976) 98:287–321. doi: 10.1016/0003-4916(76)90156-1

CrossRef Full Text | Google Scholar

57. Tyutin IV. Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. Lebedev Institute (1975).

Google Scholar

58. Barnich G, Brandt F, Henneaux M. Local BRST cohomology in Einstein Yang-Mills theory. Nucl Phys B. (1995) 455:357–408. doi: 10.1016/0550-3213(95)00471-4

CrossRef Full Text | Google Scholar

59. Barvinsky AO, Vilkovisky GA. The effective action in quantum field theory: two loop approximation. In: Isham A, Batalin CJ, Vilkovisky GA, editors. Quantum Field Theory and Quantum Statistics, Vol. 1. Bristol: IOP Publishing (1987). p. 245–75.

Google Scholar

60. Barvinsky AO, Vilkovisky GA. The generalized Schwinger-Dewitt technique in Gauge theories and quantum gravity. Phys Rept. (1985) 119:1–74. doi: 10.1016/0370-1573(85)90148-6

CrossRef Full Text | Google Scholar

61. Vilkovisky GA. Heat kernel: rencontre entre physiciens et mathematiciens. In: Proceedings of the Strasbourg Meeting between Physicists and Mathematicians Institut de Recherche Mathematique Avancee, Universite Louis Pasteur Strasbourg (1992). Available online at: http://cds.cern.ch/record/234641/files/CM-P00057033.pdf

Google Scholar

62. Abbott LF. Introduction to the background field method. Acta Phys Polon B. (1982) 13:33.

Google Scholar

63. Abbott LF. The background field method beyond one loop. Nucl Phys B. (1981) 185:189–203. doi: 10.1016/0550-3213(81)90371-0

CrossRef Full Text | Google Scholar

64. Abbott LF, Grisaru MT, Schaefer RK. The background field method and the S matrix. Nucl Phys B. (1983) 229:372–80. doi: 10.1016/0550-3213(83)90337-1

CrossRef Full Text | Google Scholar

65. Ellis RK, Kunszt Z, Melnikov K, Zanderighi G. One-loop calculations in quantum field theory: from Feynman diagrams to unitarity cuts. Phys Rept. (2012) 518:141–250. doi: 10.1016/j.physrep.2012.01.008

CrossRef Full Text | Google Scholar

66. Dixon LJ. Calculating scattering amplitudes efficiently. In: QCD and Beyond. Proceedings, Theoretical Advanced Study Institute in Elementary Particle Physics, TASI-95. Boulder, CO (1996). p. 539–84.

Google Scholar

67. Hadamard J. Lectures on Cauchy's Problem in Linear Partial Differential Equations. New Haven, CT: Yale University Press (1923).

68. Minakshisundaram S, Pleijel A. Some properties of the eigenfunctions of the Laplace operator on Riemannian manifolds. Can J Math. (1949) 1:242–56. doi: 10.4153/CJM-1949-021-5

CrossRef Full Text | Google Scholar

69. Minakshisundaram S. Eigenfunctions on Riemannian manifolds. J Indian Math Soc. (1953) 17:158–65.

70. Atiyah M, Bott R, Patodi VK. On the Heat equation and the index theorem. Invent Math. (1973) 19:279–330. doi: 10.1007/BF01425417

CrossRef Full Text | Google Scholar

71. Atiyah MF, Patodi VK, Singer IM. Spectral asymmetry and Riemannian geometry. I. In: Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 77. Berlin; Heidelberg: Cambridge University Press; Springer (2000). p. 43–69. doi: 10.1017/S0305004100049410

CrossRef Full Text | Google Scholar

72. Gilkey PB. The spectral geometry of a Riemannian manifold. J Diff Geom. (1975) 10:601–18. doi: 10.4310/jdg/1214433164

CrossRef Full Text | Google Scholar

73. Avramidi IG. Heat Kernel and Quantum Gravity. Vol. 64. Springer Science & Business Media (2000).

Google Scholar

74. Vassilevich DV. Heat kernel expansion: user's manual. Phys Rept. (2003) 388:279–360. doi: 10.1016/j.physrep.2003.09.002

CrossRef Full Text | Google Scholar

75. Synge JL. Relativity: The General Theory. Amsterdam: Elsevier Science Publishing Co Inc. (1960).

Google Scholar

76. Ruf MS, Steinwachs CF. One-loop divergences for f(R) gravity. Phys Rev D. (2018) 97:044049. doi: 10.1103/PhysRevD.97.044049

CrossRef Full Text | Google Scholar

77. Ruf MS, Steinwachs CF. Renormalization of generalized vector field models in curved spacetime. Phys Rev D. (2018) 98:025009. doi: 10.1103/PhysRevD.98.025009

CrossRef Full Text | Google Scholar

78. Ruf MS, Steinwachs CF. Quantum effective action for degenerate vector field theories. Phys Rev D. (2018) 98:085014. doi: 10.1103/PhysRevD.98.085014

CrossRef Full Text | Google Scholar

79. Heisenberg L, Steinwachs CF. One-loop renormalization in Galileon effective field theory. JCAP. (2020) 2001:014. doi: 10.1088/1475-7516/2020/01/014

CrossRef Full Text | Google Scholar

80. Heisenberg L, Steinwachs CF. Geometrized quantum Galileons. JCAP. (2020) 02:031. doi: 10.1088/1475-7516/2020/02/031

CrossRef Full Text | Google Scholar

81. Nesterov D, Solodukhin SN. Gravitational effective action and entanglement entropy in UV modified theories with and without Lorentz symmetry. Nucl Phys B. (2011) 842:141–71. doi: 10.1016/j.nuclphysb.2010.08.006

CrossRef Full Text | Google Scholar

82. D'Odorico G, Saueressig F, Schutten M. Asymptotic freedom in Hořava-Lifshitz gravity. Phys Rev Lett. (2014) 113:171101. doi: 10.1103/PhysRevLett.113.171101

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Barvinsky AO, Blas D, Herrero-Valea M, Nesterov DV, Pérez-Nadal G, Steinwachs CF. Heat kernel methods for Lifshitz theories. JHEP. (2017) 6:063. doi: 10.1007/JHEP06(2017)063

CrossRef Full Text | Google Scholar

84. Wigner EP. On unitary representations of the inhomogeneous Lorentz group. Ann Math. (1939) 40:149–204. doi: 10.2307/1968551

CrossRef Full Text | Google Scholar

85. Deser S. Selfinteraction and gauge invariance. Gen Rel Grav. (1970) 1:9–18. doi: 10.1007/BF00759198

CrossRef Full Text | Google Scholar

86. Vermaseren JAM. New features of FORM. arXiv preprint arXiv:math-ph/0010025 (2000).

Google Scholar

87. Martin-Garcia JM, García-Parrado A, Stecchina A, Wardell B, Pitrou C, Brizuela D, et al. xAct: Efficient Tensor Computer Algebra for Mathematica. (2002–2020). Available online at: http://www.xact.es/

88. Martin-Garcia JM. xTensor: Fast Abstract Tensor Computer Algebra. (2002–2020). Available online at: http://www.xact.es/xTensor/

89. Brizuela D, Martin-Garcia JM, Mena Marugan GA. xPert: computer algebra for metric perturbation theory. Gen Rel Grav. (2009) 41:2415–31. doi: 10.1007/s10714-009-0773-2

CrossRef Full Text | Google Scholar

90. Nutma T. xTras: a field-theory inspired xAct package for mathematica. Comput Phys Commun. (2014) 185:1719–38. doi: 10.1016/j.cpc.2014.02.006

CrossRef Full Text | Google Scholar

91. Deser S, van Nieuwenhuizen P. One loop divergences of quantized Einstein-Maxwell fields. Phys Rev D. (1974) 10:401. doi: 10.1103/PhysRevD.10.401

CrossRef Full Text | Google Scholar

92. Deser S, Tsao HS, van Nieuwenhuizen P. One loop divergences of the Einstein Yang-Mills system. Phys Rev D. (1974) 10:3337. doi: 10.1103/PhysRevD.10.3337

CrossRef Full Text | Google Scholar

93. Deser S, van Nieuwenhuizen P. Nonrenormalizability of the quantized Dirac-Einstein system. Phys Rev D. (1974) 10:411. doi: 10.1103/PhysRevD.10.411

CrossRef Full Text | Google Scholar

94. Gibbons GW, Perry MJ. Quantizing gravitational instantons. Nucl Phys B. (1978) 146:90–108. doi: 10.1016/0550-3213(78)90434-0

CrossRef Full Text | Google Scholar

95. Christensen SM, Duff MJ. Quantizing gravity with a cosmological constant. Nucl Phys B. (1980) 170:480–506. doi: 10.1016/0550-3213(80)90423-X

CrossRef Full Text | Google Scholar

96. Barvinsky AO, Kamenshchik A Yu, Karmazin IP. The Renormalization group for nonrenormalizable theories: Einstein gravity with a scalar field. Phys Rev D. (1993) 48:3677–94. doi: 10.1103/PhysRevD.48.3677

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Shapiro IL, Takata H. One loop renormalization of the four-dimensional theory for quantum dilaton gravity. Phys Rev D. (1995) 52:2162–75. doi: 10.1103/PhysRevD.52.2162

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Steinwachs CF, Kamenshchik A Yu. One-loop divergences for gravity non-minimally coupled to a multiplet of scalar fields: calculation in the Jordan frame. I. The main results. Phys Rev D. (2011) 84:024026. doi: 10.1103/PhysRevD.84.024026

CrossRef Full Text | Google Scholar

99. Goroff MH, Sagnotti A. The ultraviolet behavior of Einstein gravity. Nucl Phys B. (1986) 266:709–36. doi: 10.1016/0550-3213(86)90193-8

CrossRef Full Text | Google Scholar

100. van de Ven AEM. Two loop quantum gravity. Nucl Phys B. (1992) 378:309–66. doi: 10.1016/0550-3213(92)90011-Y

CrossRef Full Text | Google Scholar

101. Bern Z, Cheung C, Chi HH, Davies S, Dixon L, Nohle J. Evanescent effects can alter ultraviolet divergences in quantum gravity without physical consequences. Phys Rev Lett. (2015) 115:211301. doi: 10.1103/PhysRevLett.115.211301

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Burgess CP, Lee HM, Trott M. Power-counting and the validity of the classical approximation during inflation. JHEP. (2009) 9:103. doi: 10.1088/1126-6708/2009/09/103

CrossRef Full Text | Google Scholar

103. Barbon JLF, Espinosa JR. On the naturalness of Higgs inflation. Phys Rev D. (2009) 79:081302. doi: 10.1103/PhysRevD.79.081302

CrossRef Full Text | Google Scholar

104. Burgess CP, Lee HM, Trott M. Comment on Higgs inflation and naturalness. JHEP. (2010) 7:007. doi: 10.1007/JHEP07(2010)007

CrossRef Full Text | Google Scholar

105. Bezrukov F, Magnin A, Shaposhnikov M, Sibiryakov S. Higgs inflation: consistency and generalisations. JHEP. (2011) 1:016. doi: 10.1007/JHEP01(2011)016

CrossRef Full Text | Google Scholar

106. Barvinsky AO, Kamenshchik A Yu, Kiefer C, Starobinsky AA, Steinwachs CF. Higgs boson, renormalization group, and naturalness in cosmology. Eur Phys J C. (2012) 72:2219. doi: 10.1140/epjc/s10052-012-2219-3

CrossRef Full Text | Google Scholar

107. Steinwachs CF. Higgs field in cosmology. In: 678th WE Heraeus-Seminar: Hundred Years of Gauge Theory. Bad Honnef (2019).

Google Scholar

108. Barvinsky AO, Vilkovisky GA. Covariant perturbation theory. 2: second order in the curvature. General algorithms. Nucl Phys B. (1990) 333:471–511. doi: 10.1016/0550-3213(90)90047-H

CrossRef Full Text | Google Scholar

109. Barvinsky AO, Gusev YuV, Vilkovisky GA, Zhytnikov VV. Asymptotic behaviors of the heat kernel in covariant perturbation 19 theory. J Math Phys. (1994) 35:3543–59. doi: 10.1063/1.530428

CrossRef Full Text | Google Scholar

110. Gomis J, Weinberg S. Are nonrenormalizable gauge theories renormalizable? Nucl Phys B. (1996) 469:473–87. doi: 10.1016/0550-3213(96)00132-0

CrossRef Full Text | Google Scholar

111. Bjerrum-Bohr NEJ, Donoghue JF, Holstein BR. Quantum gravitational corrections to the nonrelativistic scattering potential of two masses. Phys Rev D. (2003) 67:084033. doi: 10.1103/PhysRevD.67.084033

CrossRef Full Text | Google Scholar

112. Jaranowski P, Schaefer G. Third postNewtonian higher order ADM Hamilton dynamics for two-body point mass systems. Phys Rev D. (1998) 57:7274–91. doi: 10.1103/PhysRevD.57.7274

CrossRef Full Text | Google Scholar

113. Buonanno A, Damour T. Effective one-body approach to general relativistic two-body dynamics. Phys Rev D. (1999) 59:084006. doi: 10.1103/PhysRevD.59.084006

CrossRef Full Text | Google Scholar

114. Damour T. Gravitational scattering, post-Minkowskian approximation and effective one-body theory. Phys Rev D. (2016) 94:104015. doi: 10.1103/PhysRevD.94.104015

CrossRef Full Text | Google Scholar

115. Schäfer G, Jaranowski P. Hamiltonian formulation of general relativity and post-Newtonian dynamics of compact binaries. Living Rev Rel. (2018) 21:7. doi: 10.1007/s41114-018-0016-5

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Goldberger WD, Rothstein IZ. An Effective field theory of gravity for extended objects. Phys Rev D. (2006) 73:104029. doi: 10.1103/PhysRevD.73.104029

CrossRef Full Text | Google Scholar

117. Bjerrum-Bohr NEJ, Donoghue JF, Vanhove P. On-shell techniques and universal results in quantum gravity. JHEP. (2014) 2:111. doi: 10.1007/JHEP02(2014)111

CrossRef Full Text | Google Scholar

118. Porto RA. The effective field theorist's approach to gravitational dynamics. Phys Rept. (2016) 633:1–104. doi: 10.1016/j.physrep.2016.04.003

CrossRef Full Text | Google Scholar

119. Bern Z, Cheung C, Roiban R, Shen CH, Solon MP, Zeng M. Scattering amplitudes and the conservative Hamiltonian for binary systems at third post-Minkowskian order. Phys Rev Lett. (2019) 122:201603. doi: 10.1103/PhysRevLett.122.201603

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Bern Z, Ita H, Parra-Martinez J, Ruf MS. Universality in the Classical Limit of Massless Gravitational Scattering. arXiv preprint arXiv:hep-th/2002.02459 (2020).

Google Scholar

121. Blümlein J, Maier A, Marquard P, Schäfer G. Testing binary dynamics in gravity at the sixth post-Newtonian level. Phys. Lett. B. (2020) 807:135496. doi: 10.1016/j.physletb.2020.135496

CrossRef Full Text | Google Scholar

122. Blümlein J, Maier A, Marquard P, Schäfer G. Fourth post-Newtonian Hamiltonian dynamics of two-body systems from an effective field theory approach. Nucl. Phys. B. 955:115041. doi: 10.1016/j.nuclphysb.2020.115041

CrossRef Full Text | Google Scholar

123. Weinberg S. Critical phenomena for field theorists. In: 14th International School of Subnuclear Physics: Understanding the Fundamental Constitutents of Matter. Erice (1976). p. 1. Available online at: https://www.quantamagazine.org/why-an-old-theory-of-everything-is-gaining-new-life-20180108

Google Scholar

124. Weinberg S. Ultraviolet divergences in quantum theories of gravitation. In: Hawking SW, Israel W, editors. General Relativity: An Einstein Centenary Survey. Cambridge: Cambridge University Press (1980). p. 790–831.

Google Scholar

125. Wilson KG, Kogut JB. The Renormalization group and the epsilon expansion. Phys Rept. (1974) 12:75–199. doi: 10.1016/0370-1573(74)90023-4

CrossRef Full Text | Google Scholar

126. Wetterich C. Exact evolution equation for the effective potential. Phys Lett B. (1993) 301:90–4. doi: 10.1016/0370-2693(93)90726-X

CrossRef Full Text | Google Scholar

127. Morris TR. The exact renormalization group and approximate solutions. Int J Mod Phys A. (1994) 9:2411–50. doi: 10.1142/S0217751X94000972

CrossRef Full Text | Google Scholar

128. Reuter M, Wetterich C. Effective average action for gauge theories and exact evolution equations. Nucl Phys B. (1994) 417:181–214. doi: 10.1016/0550-3213(94)90543-6

CrossRef Full Text | Google Scholar

129. Niedermaier M, Reuter M. The asymptotic safety scenario in quantum gravity. Living Rev Rel. (2006) 9:5–173. doi: 10.12942/lrr-2006-5

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Liberati S, Maccione L, Sotiriou TP. Scale hierarchy in Horava-Lifshitz gravity: a strong constraint from synchrotron radiation in the Crab nebula. Phys Rev Lett. (2012) 109:151602. doi: 10.1103/PhysRevLett.109.151602

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Reuter M, Saueressig F. Renormalization group flow of quantum gravity in the Einstein-Hilbert truncation. Phys Rev D. (2002) 65:065016. doi: 10.1103/PhysRevD.65.065016

CrossRef Full Text | Google Scholar

132. Lauscher O, Reuter M. Is quantum Einstein gravity nonperturbatively renormalizable? Class Quant Grav. (2002) 19:483–92. doi: 10.1088/0264-9381/19/3/304

CrossRef Full Text | Google Scholar

133. Lauscher O, Reuter M. Flow equation of quantum Einstein gravity in a higher derivative truncation. Phys Rev D. (2002) 66:025026. doi: 10.1103/PhysRevD.66.025026

CrossRef Full Text | Google Scholar

134. Codello A, Percacci R. Fixed points of higher derivative gravity. Phys Rev Lett. (2006) 97:221301. doi: 10.1103/PhysRevLett.97.221301

PubMed Abstract | CrossRef Full Text | Google Scholar

135. Benedetti D, Machado PF, Saueressig F. Asymptotic safety in higher-derivative gravity. Mod Phys Lett A. (2009) 24:2233–41. doi: 10.1142/S0217732309031521

CrossRef Full Text | Google Scholar

136. Falls K, Litim DF, Nikolakopoulos K, Rahmede C. Further evidence for asymptotic safety of quantum gravity. Phys Rev D. (2016) 93:104022. doi: 10.1103/PhysRevD.93.104022

CrossRef Full Text | Google Scholar

137. Gies H, Knorr B, Lippoldt S, Saueressig F. Gravitational two-loop counterterm is asymptotically safe. Phys Rev Lett. (2016) 116:211302. doi: 10.1103/PhysRevLett.116.211302

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Eichhorn A. Quantum-gravity-induced matter self-interactions in the asymptotic-safety scenario. Phys Rev D. (2012) 86:105021. doi: 10.1103/PhysRevD.86.105021

CrossRef Full Text | Google Scholar

139. Don P, Eichhorn A, Percacci R. Matter matters in asymptotically safe quantum gravity. Phys Rev D. (2014) 89:084035. doi: 10.1103/PhysRevD.89.084035

CrossRef Full Text | Google Scholar

140. Don P, Eichhorn A, Labus P, Percacci R. Asymptotic safety in an interacting system of gravity and scalar matter. Phys Rev D. (2016) 93:044049. doi: 10.1103/PhysRevD.93.044049

CrossRef Full Text | Google Scholar

141. Eichhorn A, Held A. Viability of quantum-gravity induced ultraviolet completions for matter. Phys Rev D. (2017) 96:086025. doi: 10.1103/PhysRevD.96.086025

CrossRef Full Text | Google Scholar

142. Eichhorn A. Status of the asymptotic safety paradigm for quantum gravity and matter. Found Phys. (2018) 48:1407–29. doi: 10.1007/s10701-018-0196-6

CrossRef Full Text | Google Scholar

143. Christiansen N, Litim DF, Pawlowski JM, Reichert M. Asymptotic safety of gravity with matter. Phys Rev D. (2018) 97:106012. doi: 10.1103/PhysRevD.97.106012

CrossRef Full Text | Google Scholar

144. Machado PF, Saueressig F. On the renormalization group flow of f(R)-gravity. Phys Rev D. (2008) 77:124045. doi: 10.1103/PhysRevD.77.124045

CrossRef Full Text | Google Scholar

145. Codello A, Percacci R, Rahmede C. Ultraviolet properties of f(R)-gravity. Int J Mod Phys A. (2008) 23:143–50. doi: 10.1142/S0217751X08038135

CrossRef Full Text | Google Scholar

146. Narain G, Percacci R. Renormalization group flow in scalar-tensor theories. I. Class Quant Grav. (2010) 27:075001. doi: 10.1088/0264-9381/27/7/075001

CrossRef Full Text | Google Scholar

147. Narain G, Rahmede C. Renormalization group flow in scalar-tensor theories. II. Class Quant Grav. (2010) 27:075002. doi: 10.1088/0264-9381/27/7/075002

CrossRef Full Text | Google Scholar

148. Donoghue JF. A critique of the asymptotic safety program. Front Phys. (2020) 8:56. doi: 10.3389/fphy.2020.00056

CrossRef Full Text | Google Scholar

149. Vilkovisky GA. The unique effective action in quantum field theory. Nucl Phys B. (1984) 234:125–37. doi: 10.1016/0550-3213(84)90228-1

CrossRef Full Text | Google Scholar

150. Benedetti D. Asymptotic safety goes on shell. New J Phys. (2012) 14:015005. doi: 10.1088/1367-2630/14/1/015005

CrossRef Full Text | Google Scholar

151. Percacci R, Perini D. Should we expect a fixed point for Newton's constant? Class Quant Grav. (2004) 21:5035–41. doi: 10.1088/0264-9381/21/22/002

CrossRef Full Text | Google Scholar

152. Christiansen N, Knorr B, Pawlowski JM, Rodigast A. Global flows in quantum gravity. Phys Rev D. (2016) 93:044036. doi: 10.1103/PhysRevD.93.044036

CrossRef Full Text | Google Scholar

153. Christiansen N, Knorr B, Meibohm J, Pawlowski JM, Reichert M. Local quantum gravity. Phys Rev D. (2015) 92:121501. doi: 10.1103/PhysRevD.92.121501

CrossRef Full Text | Google Scholar

154. Eichhorn A, Labus P, Pawlowski JM, Reichert M. Effective universality in quantum gravity. SciPost Phys. (2018) 5:031. doi: 10.21468/SciPostPhys.5.4.031

CrossRef Full Text | Google Scholar

155. Bosma L, Knorr B, Saueressig F. Resolving spacetime singularities within asymptotic safety. Phys Rev Lett. (2019) 123:101301. doi: 10.1103/PhysRevLett.123.101301

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Knorr B, Ripken C, Saueressig F. Form factors in asymptotic safety: conceptual ideas and computational toolbox. Class Quant Grav. (2019) 36:234001. doi: 10.1088/1361-6382/ab4a53

CrossRef Full Text | Google Scholar

157. Barvinsky AO, Gusev YV, Vilkovisky GA, Zhytnikov VV. The basis of nonlocal curvature invariants in quantum gravity theory. (Third order). J Math Phys. (1994) 35:3525–42. doi: 10.1063/1.530427

CrossRef Full Text | Google Scholar

158. Barvinsky AO, Vilkovisky GA. Covariant perturbation theory. 3: spectral representations of the third order form-factors. Nucl Phys B. (1990) 333:512–24. doi: 10.1016/0550-3213(90)90048-I

CrossRef Full Text | Google Scholar

159. Codello A, Zanusso O. On the non-local heat kernel expansion. J Math Phys. (2013) 54:013513. doi: 10.1063/1.4776234

CrossRef Full Text | Google Scholar

160. Starobinsky AA. A new type of isotropic cosmological models without singularity. Phys Lett B. (1980) 91:99–102. doi: 10.1016/0370-2693(80)90670-X

CrossRef Full Text

161. Akrami Y, Arroja F, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. X. Constraints on inflation. arXiv. (2018) 1807.06211.

Google Scholar

162. Cognola G, Elizalde E, Nojiri S, Odintsov SD, Zerbini S. One-loop f(R) gravity in de Sitter universe. JCAP. (2005) 2:010. doi: 10.1088/1475-7516/2005/02/010

CrossRef Full Text | Google Scholar

163. Fradkin ES, Tseytlin AA. Renormalizable asymptotically free quantum theory of gravity. Nucl Phys B. (1982) 201:469–91. doi: 10.1016/0550-3213(82)90444-8

CrossRef Full Text | Google Scholar

164. Avramidi IG, Barvinsky AO. Asymptotic freedom in higher derivative quantum gravity. Phys Lett B. (1985) 159:269–74. doi: 10.1016/0370-2693(85)90248-5

CrossRef Full Text | Google Scholar

165. Salvio A, Strumia A. Agravity. JHEP. (2014) 6:080. doi: 10.1007/JHEP06(2014)080

CrossRef Full Text

166. Yu. Kamenshchik A, Steinwachs CF. Question of quantum equivalence between Jordan frame and Einstein frame. Phys Rev D. (2015) 91:084033. doi: 10.1103/PhysRevD.91.084033

CrossRef Full Text | Google Scholar

167. Ruf MS, Steinwachs CF. Quantum equivalence of f(R) gravity and scalar-tensor theories. Phys Rev D. (2018) 97:044050. doi: 10.1103/PhysRevD.97.044050

CrossRef Full Text | Google Scholar

168. Ohta N. Quantum equivalence of f(R) gravity and scalar tensor theories in the Jordan and Einstein frames. PTEP. (2018) 2018:033B02. doi: 10.1093/ptep/pty008

CrossRef Full Text | Google Scholar

169. Falls K, Herrero-Valea M. Frame (In)equivalence in quantum field theory and cosmology. Eur Phys J C. (2019) 79:595. doi: 10.1140/epjc/s10052-019-7070-3

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Finn K, Karamitsos S, Pilaftsis A. Grand Covariance in Quantum Gravity. arXiv preprint arXiv:hep-th/1910.06661 (2019).

Google Scholar

171. Stelle KS. Classical gravity with higher derivatives. Gen Rel Grav. (1978) 9:353–71. doi: 10.1007/BF00760427

CrossRef Full Text | Google Scholar

172. Pais A, Uhlenbeck GE. On Field theories with nonlocalized action. Phys Rev. (1950) 79:145–65. doi: 10.1103/PhysRev.79.145

CrossRef Full Text | Google Scholar

173. Barth NH, Christensen SM. Quantizing fourth order gravity theories. 1. The functional integral. Phys Rev D. (1983) 28:1876. doi: 10.1103/PhysRevD.28.1876

CrossRef Full Text | Google Scholar

174. Hawking SW. Who' s afraid of (higher derivative) ghosts? In: Batalin CJ, Isham A, editors. Quantum Field Theory and Quantum Statistics, Vol. 2. Bristol: Hilger (1987). p. 129–39.

Google Scholar

175. Woodard RP. Avoiding dark energy with 1/r modifications of gravity. Lect Notes Phys. (2007) 720:403–33. doi: 10.1007/978-3-540-71013-4_14

CrossRef Full Text | Google Scholar

176. Gundhi A, Steinwachs CF. Scalaron-Higgs inflation. Nucl Phys B. (2020) 954:114989. doi: 10.1016/j.nuclphysb.2020.114989

CrossRef Full Text | Google Scholar

177. Lee TD, Wick GC. Negative metric and the unitarity of the S matrix. Nucl Phys B. (1969) 9:209–43. doi: 10.1016/0550-3213(69)90098-4

CrossRef Full Text | Google Scholar

178. Tomboulis E. 1/N expansion and renormalization in quantum gravity. Phys Lett B. (1977) 70:361–64. doi: 10.1016/0370-2693(77)90678-5

CrossRef Full Text | Google Scholar

179. Anselmi D, Piva M. The ultraviolet behavior of quantum gravity. JHEP. (2018) 05:027. doi: 10.1007/JHEP05(2018)027

CrossRef Full Text | Google Scholar

180. Donoghue JF, Menezes G. Arrow of causality and quantum gravity. Phys Rev Lett. (2019) 123:171601. doi: 10.1103/PhysRevLett.123.171601

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Veltman MJG. Unitarity and causality in a renormalizable field theory with unstable particles. Physica. (1963) 29:186–207. doi: 10.1016/S0031-8914(63)80277-3

CrossRef Full Text | Google Scholar

182. Coleman S. Acausality. In: Zichichi A, editor. 7th International School of Subnuclear Physics (Ettore Majorana): Subnuclear Phenomena. New York, NY: Academic Press Inc. (1970). p. 282–327. doi: 10.1016/B978-0-12-780580-1.50016-4

CrossRef Full Text | Google Scholar

183. Cutkosky RE, Landshoff PV, Olive DI, Polkinghorne JC. A non-analytic S matrix. Nucl Phys B. (1969) 12:281–300. doi: 10.1016/0550-3213(69)90169-2

CrossRef Full Text | Google Scholar

184. Salam A, Strathdee JA. Remarks on high-energy stability and renormalizability of gravity theory. Phys Rev D. (1978) 18:4480. doi: 10.1103/PhysRevD.18.4480

CrossRef Full Text | Google Scholar

185. Tomboulis E. Renormalizability and asymptotic freedom in quantum gravity. Phys Lett B. (1980) 97:77–80. doi: 10.1016/0370-2693(80)90550-X

CrossRef Full Text | Google Scholar

186. Boulware DG, Gross DJ. Lee-Wick indefinite metric quantization: a functional integral approach. Nucl Phys B. (1984) 233:1–23. doi: 10.1016/0550-3213(84)90167-6

CrossRef Full Text | Google Scholar

187. Hawking SW, Hertog T. Living with ghosts. Phys Rev D. (2002) 65:103515. doi: 10.1103/PhysRevD.65.103515

CrossRef Full Text | Google Scholar

188. Mannheim PD. Solution to the ghost problem in fourth order derivative theories. Found Phys. (2007) 37:532–71. doi: 10.1007/s10701-007-9119-7

CrossRef Full Text | Google Scholar

189. Bender CM, Mannheim PD. No-ghost theorem for the fourth-order derivative Pais-Uhlenbeck oscillator model. Phys Rev Lett. (2008) 100:110402. doi: 10.1103/PhysRevLett.100.110402

PubMed Abstract | CrossRef Full Text | Google Scholar

190. Grinstein B, O'Connell D, Wise MB. Causality as an emergent macroscopic phenomenon: the Lee-Wick O(N) model. Phys Rev D. (2009) 79:105019. doi: 10.1103/PhysRevD.79.105019

CrossRef Full Text | Google Scholar

191. Denner A, Lang JN. The complex-mass scheme and unitarity in perturbative quantum field theory. Eur Phys J C. (2015) 75:377. doi: 10.1140/epjc/s10052-015-3579-2

CrossRef Full Text | Google Scholar

192. Salvio A, Strumia A. Quantum mechanics of 4-derivative theories. Eur Phys J C. (2016) 76:227. doi: 10.1140/epjc/s10052-016-4079-8

PubMed Abstract | CrossRef Full Text | Google Scholar

193. Accioly A, Giacchini BL, Shapiro IL. Low-energy effects in a higher-derivative gravity model with real and complex massive poles. Phys Rev D. (2017) 96:104004. doi: 10.1103/PhysRevD.96.104004

CrossRef Full Text | Google Scholar

194. Mannheim PD. Unitarity of loop diagrams for the ghostlike $1/(k^2-M_1^2)-1/(k^2-M_2^2)$ propagator. Phys Rev D. (2018) 98:045014. doi: 10.1103/PhysRevD.98.045014

CrossRef Full Text | Google Scholar

195. Floreanini R, Percacci R. The Renormalization group flow of the Dilaton potential. Phys Rev D. (1995) 52:896–911. doi: 10.1103/PhysRevD.52.896

PubMed Abstract | CrossRef Full Text | Google Scholar

196. Niedermaier MR. Gravitational fixed points from perturbation theory. Phys Rev Lett. (2009) 103:101303. doi: 10.1103/PhysRevLett.103.101303

PubMed Abstract | CrossRef Full Text | Google Scholar

197. Becker D, Ripken C, Saueressig F. On avoiding Ostrogradski instabilities within asymptotic safety. JHEP. (2017) 12:121. doi: 10.1007/JHEP12(2017)121

CrossRef Full Text | Google Scholar

198. Narain G. Exorcising ghosts in induced gravity. Eur Phys J C. (2017) 77:683. doi: 10.1140/epjc/s10052-017-5249-z

CrossRef Full Text | Google Scholar

199. Narain G. Signs and stability in higher-derivative gravity. Int J Mod Phys A. (2018) 33:1850031. doi: 10.1142/S0217751X18500318

CrossRef Full Text | Google Scholar

200. Mukohyama S. Horava-Lifshitz cosmology: a review. Class Quant Grav. (2010) 27:223101. doi: 10.1088/0264-9381/27/22/223101

CrossRef Full Text | Google Scholar

201. Sotiriou TP. Horava-Lifshitz gravity: a status report. J Phys Conf Ser. (2011) 283:012034. doi: 10.1088/1742-6596/283/1/012034

CrossRef Full Text | Google Scholar

202. Wang A. Hořava gravity at a Lifshitz point: a progress report. Int J Mod Phys D. (2017) 26:1730014. doi: 10.1142/S0218271817300142

CrossRef Full Text | Google Scholar

203. Blas D. Hořava gravity: motivation and status. J Phys Conf Ser. (2018) 952:012002. doi: 10.1088/1742-6596/952/1/012002

CrossRef Full Text | Google Scholar

204. Lifshitz EM. On the theory of second-order phase transitions I & II. Zh Eksp Teor Fiz. (1941) 11:255–69.

205. Steinwachs CF, van der Wild ML. Quantum gravitational corrections from the Wheeler-DeWitt equation for scalar-tensor theories. Class Quant Grav. (2018) 35:135010. doi: 10.1088/1361-6382/aac587

CrossRef Full Text | Google Scholar

206. Arnowitt RL, Deser S, Misner CW. Canonical variables for general relativity. Phys Rev. (1960) 117:1595–602. doi: 10.1103/PhysRev.117.1595

CrossRef Full Text | Google Scholar

207. Kuchař K. Kinematics of tensor fields in hyperspace. 2. J Math Phys. (1976) 17:792–800. doi: 10.1063/1.522977

CrossRef Full Text | Google Scholar

208. Rechenberger S, Saueressig F. A functional renormalization group equation for foliated spacetimes. JHEP. (2013) 3:010. doi: 10.1007/JHEP03(2013)010

CrossRef Full Text | Google Scholar

209. Giulini D, Kiefer C. Wheeler-DeWitt metric and the attractivity of gravity. Phys Lett A. (1994) 193:21–4. doi: 10.1016/0375-9601(94)00651-2

CrossRef Full Text | Google Scholar

210. Sotiriou TP, Visser M, Weinfurtner S. Quantum gravity without Lorentz invariance. JHEP. (2009) 10:033. doi: 10.1088/1126-6708/2009/10/033

CrossRef Full Text | Google Scholar

211. Appignani C, Casadio R, Shankaranarayanan S. The cosmological constant and horava-lifshitz gravity. JCAP. (2010) 4:006. doi: 10.1088/1475-7516/2010/04/006

CrossRef Full Text | Google Scholar

212. Charmousis C, Niz G, Padilla A, Saffin PM. Strong coupling in Horava gravity. JHEP. (2009) 8:070. doi: 10.1088/1126-6708/2009/08/070

CrossRef Full Text | Google Scholar

213. Blas D, Pujolas O, Sibiryakov S. On the extra mode and inconsistency of Horava gravity. JHEP. (2009) 10:029. doi: 10.1088/1126-6708/2009/10/029

CrossRef Full Text | Google Scholar

214. Blas D, Pujolas O, Sibiryakov S. Models of non-relativistic quantum gravity: the Good, the bad and the healthy. JHEP. (2011) 4:018. doi: 10.1007/JHEP04(2011)018

CrossRef Full Text | Google Scholar

215. Koyama K, Arroja F. Pathological behaviour of the scalar graviton in Horava-Lifshitz gravity. JHEP. (2010) 3:061. doi: 10.1007/JHEP03(2010)061

CrossRef Full Text | Google Scholar

216. Papazoglou A, Sotiriou TP. Strong coupling in extended Horava-Lifshitz gravity. Phys Lett B. (2010) 685:197–200. doi: 10.1016/j.physletb.2010.01.054

CrossRef Full Text | Google Scholar

217. Izumi K, Mukohyama S. Nonlinear superhorizon perturbations in Horava-Lifshitz gravity. Phys Rev D. (2011) 84:064025. doi: 10.1103/PhysRevD.84.064025

CrossRef Full Text | Google Scholar

218. Gümrükçüoğlu AE, Mukohyama S, Wang A. General relativity limit of Horava-Lifshitz gravity with a scalar field in gradient expansion. Phys Rev D. (2012) 85:064042. doi: 10.1103/PhysRevD.85.064042

CrossRef Full Text | Google Scholar

219. Cognola G, Myrzakulov R, Sebastiani L, Vagnozzi S, Zerbini S. Covariant Hořava-like and mimetic Horndeski gravity: cosmological solutions and perturbations. Class. Quant. Grav. 33:225014. doi: 10.1088/0264-9381/33/22/225014

CrossRef Full Text | Google Scholar

220. Casalino A, Rinaldi M, Sebastiani L, Vagnozzi S. Alive and well: mimetic gravity and a higher-order extension in light of GW170817. Class. Quant. Grav. (2019) 36:017001. doi: 10.1088/1361-6382/aaf1fd

CrossRef Full Text | Google Scholar

221. Blas D, Pujolas O, Sibiryakov S. Consistent extension of Horava gravity. Phys Rev Lett. (2010) 104:181302. doi: 10.1103/PhysRevLett.104.181302

PubMed Abstract | CrossRef Full Text | Google Scholar

222. Henneaux M, Kleinschmidt A, Lucena Gómez G. A dynamical inconsistency of Horava gravity. Phys Rev D. (2010) 81:064002. doi: 10.1103/PhysRevD.81.064002

CrossRef Full Text | Google Scholar

223. Colladay D, Kostelecky VA. Lorentz violating extension of the standard model. Phys Rev D. (1998) 58:116002. doi: 10.1103/PhysRevD.58.116002

CrossRef Full Text | Google Scholar

224. Mattingly D. Modern tests of Lorentz invariance. Living Rev Rel. (2005) 8:5. doi: 10.12942/lrr-2005-5

PubMed Abstract | CrossRef Full Text | Google Scholar

225. Jacobson T, Liberati S, Mattingly D. Lorentz violation at high energy: concepts, phenomena and astrophysical constraints. Ann Phys. (2006) 321:150–96. doi: 10.1016/j.aop.2005.06.004

CrossRef Full Text | Google Scholar

226. Kostelecky AV, Tasson JD. Matter-gravity couplings and Lorentz violation. Phys Rev D. (2011) 83:016013. doi: 10.1103/PhysRevD.83.016013

CrossRef Full Text | Google Scholar

227. Liberati S. Tests of Lorentz invariance: a 2013 update. Class Quant Grav. (2013) 30:133001. doi: 10.1088/0264-9381/30/13/133001

CrossRef Full Text | Google Scholar

228. Eichhorn A, Platania A, Schiffer M. Lorentz invariance violations in the interplay of quantum gravity with matter. arXiv preprint arXiv:hep-th/1911.10066 (2019).

Google Scholar

229. Carroll SM, Lim EA. Lorentz-violating vector fields slow the universe down. Phys Rev D. (2004) 70:123525. doi: 10.1103/PhysRevD.70.123525

CrossRef Full Text | Google Scholar

230. Aver E, Olive KA, Skillman ED. The effects of He I λ 10830 on helium abundance determinations. JCAP. (2015) 1507:011. doi: 10.1088/1475-7516/2015/07/011

CrossRef Full Text | Google Scholar

231. Will CM. The Confrontation between general relativity and experiment. Living Rev Rel. (2006) 9:3. doi: 10.12942/lrr-2006-3

PubMed Abstract | CrossRef Full Text | Google Scholar

232. Blas D, Sanctuary H. Gravitational radiation in Horava gravity. Phys Rev D. (2011) 84:064004. doi: 10.1103/PhysRevD.84.064004

CrossRef Full Text | Google Scholar

233. Yagi K, Blas D, Barausse E, Yunes N. Constraints on Einstein-ther theory and Hořava gravity from binary pulsar observations. Phys Rev D. (2014) 89:084067. doi: 10.1103/PhysRevD.89.084067

CrossRef Full Text | Google Scholar

234. Barausse E, Jacobson T, Sotiriou TP. Black holes in Einstein-aether and Horava-Lifshitz gravity. Phys Rev D. (2011) 83:124043. doi: 10.1103/PhysRevD.83.124043

CrossRef Full Text | Google Scholar

235. Barausse E, Sotiriou TP. Slowly rotating black holes in Horava-Lifshitz gravity. Phys Rev D. (2013) 87:087504. doi: 10.1103/PhysRevD.87.087504

PubMed Abstract | CrossRef Full Text | Google Scholar

236. Barausse E, Sotiriou TP. Black holes in Lorentz-violating gravity theories. Class Quant Grav. (2013) 30:244010. doi: 10.1088/0264-9381/30/24/244010

CrossRef Full Text | Google Scholar

237. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys J. (2017) 848:L13. doi: 10.3847/2041-8213/aa920c

CrossRef Full Text | Google Scholar

238. Emir Gümrükçüoğlu A, Saravani M, Sotiriou TP. Hořava gravity after GW170817. Phys Rev D. (2018) 97:024032. doi: 10.1103/PhysRevD.97.024032

CrossRef Full Text | Google Scholar

239. Chadha S, Nielsen HB. Lorentz invariance as a low-energy phenomenon. Nucl Phys B. (1983) 217:125–44. doi: 10.1016/0550-3213(83)90081-0

CrossRef Full Text | Google Scholar

240. Groot Nibbelink S, Pospelov M. Lorentz violation in supersymmetric field theories. Phys Rev Lett. (2005) 94:081601. doi: 10.1103/PhysRevLett.94.081601

PubMed Abstract | CrossRef Full Text | Google Scholar

241. Bolokhov PA, Groot Nibbelink S, Pospelov M. Lorentz violating supersymmetric quantum electrodynamics. Phys Rev D. (2005) 72:015013. doi: 10.1103/PhysRevD.72.015013

CrossRef Full Text | Google Scholar

242. Anber MM, Donoghue JF. The emergence of a universal limiting speed. Phys Rev D. (2011) 83:105027. doi: 10.1103/PhysRevD.83.105027

CrossRef Full Text | Google Scholar

243. Pospelov M, Shang Y. On Lorentz violation in Horava-Lifshitz type theories. Phys Rev D. (2012) 85:105001. doi: 10.1103/PhysRevD.85.105001

CrossRef Full Text | Google Scholar

244. Kiritsis E. Lorentz violation, gravity, dissipation and holography. JHEP. (2013) 1:030. doi: 10.1007/JHEP01(2013)030

CrossRef Full Text | Google Scholar

245. Bednik G, Pujols O, Sibiryakov S. Emergent Lorentz invariance from strong dynamics: holographic examples. JHEP. (2013) 11:064. doi: 10.1007/JHEP11(2013)064

CrossRef Full Text | Google Scholar

246. Kharuk I, Sibiryakov SM. Emergent Lorentz invariance with chiral fermions. Theor Math Phys. (2016) 189:1755–74. doi: 10.1134/S0040577916120084

CrossRef Full Text | Google Scholar

247. Colombo M, Gümrükçüoğlu AE, Sotiriou TP. Hořava gravity with mixed derivative terms. Phys Rev D. (2015) 91:044021. doi: 10.1103/PhysRevD.91.044021

CrossRef Full Text | Google Scholar

248. Coates A, Colombo M, Gümrükçüoğlu AE, Sotiriou TP. Uninvited guest in mixed derivative Hořava gravity. Phys Rev D. (2016) 94:084014. doi: 10.1103/PhysRevD.94.084014

CrossRef Full Text | Google Scholar

249. Anselmi D, Halat M. Renormalization of Lorentz violating theories. Phys Rev D. (2007) 76:125011. doi: 10.1103/PhysRevD.76.125011

CrossRef Full Text | Google Scholar

250. Bogoliubow NN, Parasiuk OS. Über die Multiplikation der Kausalfunktionen in der Quantentheorie der Felder. Acta Math. (1957) 97:227–66. doi: 10.1007/BF02392399

CrossRef Full Text | Google Scholar

251. Hepp K. Proof of the Bogoliubov-Parasiuk theorem on renormalization. Commun Math Phys. (1966) 2:301–26. doi: 10.1007/BF01773358

CrossRef Full Text | Google Scholar

252. Zimmermann W. Convergence of Bogoliubov's method of renormalization in momentum space. Commun Math Phys. (1969) 15:208–34. doi: 10.1007/BF01645676

CrossRef Full Text

253. Orlando D, Reffert S. On the renormalizability of Horava-Lifshitz-type gravities. Class Quant Grav. (2009) 26:155021. doi: 10.1088/0264-9381/26/15/155021

CrossRef Full Text | Google Scholar

254. Iengo R, Russo JG, Serone M. Renormalization group in Lifshitz-type theories. JHEP. (2009) 11:020. doi: 10.1088/1126-6708/2009/11/020

CrossRef Full Text | Google Scholar

255. Orlando D, Reffert S. On the perturbative expansion around a Lifshitz point. Phys Lett B. (2010) 683:62–8. doi: 10.1016/j.physletb.2009.11.053

CrossRef Full Text | Google Scholar

256. Giribet G, Nacir DL, Mazzitelli FD. Counterterms in semiclassical Horava-Lifshitz gravity. JHEP. (2010) 09:009. doi: 10.1007/JHEP09(2010)009

CrossRef Full Text | Google Scholar

257. Ambjorn J, Gorlich A, Jordan S, Jurkiewicz J, Loll R. CDT meets Horava-Lifshitz gravity. Phys Lett B. (2010) 690:413–9. doi: 10.1016/j.physletb.2010.05.054

CrossRef Full Text | Google Scholar

258. Baggio M, de Boer J, Holsheimer K. Anomalous breaking of anisotropic scaling symmetry in the quantum Lifshitz model. JHEP. (2012) 07:099. doi: 10.1007/JHEP07(2012)099

CrossRef Full Text | Google Scholar

259. Gomes PRS, Gomes M. On ward Iidentities in Lifshitz-like field theories. Phys Rev D. (2012) 85:065010. doi: 10.1103/PhysRevD.85.065010

CrossRef Full Text | Google Scholar

260. Griffin T, Horava P, Melby-Thompson CM. Conformal Lifshitz gravity from holography. JHEP. (2012) 5:010. doi: 10.1007/JHEP05(2012)010

PubMed Abstract | CrossRef Full Text | Google Scholar

261. Lopez Nacir DL, Mazzitelli FD, Trombetta LG. Lifshitz scalar fields: one loop renormalization in curved backgrounds. Phys Rev D. (2012) 85:024051. doi: 10.1103/PhysRevD.85.024051

CrossRef Full Text | Google Scholar

262. Griffin T, Hořava P, Melby-Thompson CM. Lifshitz gravity for Lifshitz holography. Phys Rev Lett. (2013) 110:081602. doi: 10.1103/PhysRevLett.110.081602

PubMed Abstract | CrossRef Full Text | Google Scholar

263. Nakayama Y. Holographic renormalization of foliation preserving gravity and trace anomaly. Gen Rel Grav. (2012) 44:2873–89. doi: 10.1007/s10714-012-1427-3

CrossRef Full Text | Google Scholar

264. Contillo A, Rechenberger S, Saueressig F. Renormalization group flow of Hořava-Lifshitz gravity at low energies. JHEP. (2013) 12:017. doi: 10.1007/JHEP12(2013)017

CrossRef Full Text | Google Scholar

265. Arav I, Chapman S, Oz Y. Lifshitz scale anomalies. JHEP. (2015) 02:078. doi: 10.1007/JHEP02(2015)078

CrossRef Full Text | Google Scholar

266. Arav I, Chapman S, Oz Y. Non-relativistic scale anomalies. JHEP. (2016) 6:158. doi: 10.1007/JHEP06(2016)158

CrossRef Full Text | Google Scholar

267. Arav I, Oz Y, Raviv-Moshe A. Lifshitz anomalies, ward identities and split dimensional regularization. JHEP. (2017) 3:088. doi: 10.1007/JHEP03(2017)088

CrossRef Full Text | Google Scholar

268. Taylor M. Lifshitz holography. Class Quant Grav. (2016) 33:033001. doi: 10.1088/0264-9381/33/3/033001

CrossRef Full Text | Google Scholar

269. Keranen V, Sybesma W, Szepietowski P, Thorlacius L. Correlation functions in theories with Lifshitz scaling. JHEP. (2017) 5:033. doi: 10.1007/JHEP05(2017)033

CrossRef Full Text | Google Scholar

270. Pal S, Grinstein B. Heat kernel and Weyl anomaly of Schrödinger invariant theory. Phys Rev D. (2017) 96:125001. doi: 10.1103/PhysRevD.96.125001

CrossRef Full Text | Google Scholar

271. Mohammadi Mozaffar MR, Mollabashi A. Entanglement in Lifshitz-type quantum field theories. JHEP. (2017) 7:120. doi: 10.1007/JHEP07(2017)120

CrossRef Full Text | Google Scholar

272. Knorr B. Lorentz symmetry is relevant. Phys Lett B. (2019) 792:142–8. doi: 10.1016/j.physletb.2019.01.070

CrossRef Full Text | Google Scholar

273. Angel-Ramelli J, Puletti VGM, Thorlacius L. Entanglement entropy in generalised quantum Lifshitz models. JHEP. (2019) 8:072. doi: 10.1007/JHEP08(2019)072

CrossRef Full Text | Google Scholar

274. D'Odorico G, Goossens JW, Saueressig F. Covariant computation of effective actions in Hořava-Lifshitz gravity. JHEP. (2015) 10:126. doi: 10.1007/JHEP10(2015)126

CrossRef Full Text | Google Scholar

275. Benedetti D, Guarnieri F. One-loop renormalization in a toy model of Hořava-Lifshitz gravity. JHEP. (2014) 3:078. doi: 10.1007/JHEP03(2014)078

CrossRef Full Text | Google Scholar

276. Griffin T, Grosvenor KT, Melby-Thompson CM, Yan Z. Quantization of Hořava gravity in 2 + 1 dimensions. JHEP. (2017) 6:004. doi: 10.1007/JHEP06(2017)004

CrossRef Full Text | Google Scholar

277. Barvinsky AO, Pronin PI, Wachowski W. Heat kernel for higher-order differential operators and generalized exponential functions. Phys Rev D. (2019) 100:105004. doi: 10.1103/PhysRevD.100.105004

CrossRef Full Text | Google Scholar

278. Steinwachs CF. Combinatorial aspects in the one-loop renormalization of higher derivative theories. arXiv preprint arXiv:hep-ph/1909.00810 (2019).

Google Scholar

279. Kallosh RE, Tyutin IV. The Equivalence theorem and gauge invariance in renormalizable theories. Yad Fiz. (1973) 17:190–209.

Google Scholar

280. Kallosh RE. The renormalization in Nonabelian gauge theories. Nucl Phys B. (1974) 78:293–312. doi: 10.1016/0550-3213(74)90284-3

CrossRef Full Text | Google Scholar

281. DeWitt-Morette C. The Pursuit of Quantum Gravity: Memoirs of Bryce DeWitt From 1946 to 2004. Berlin; Heidelberg: Springer (2011).

Google Scholar