Ab initio Calculations of Lepton-Nucleus Scattering

The advent of high precision measurements of neutrinos and their oscillations calls for accurate predictions of their interactions with nuclear targets utilized in the detectors. Over the past decade, ab initio methods based on realistic nuclear interactions and current operators were able to provide accurate description of lepton-nucleus scattering processes. Achieving a comprehensive description of the different reaction mechanisms active in the broad range of energies relevant for oscillation experiments required the introduction of controlled approximations of the nuclear many-body models. In this review, we give an overview of recent developments in the description of electroweak interactions within different approaches and discuss the future perspectives to support the experimental effort in this new precision era.

1. Introduction

Understanding neutrino properties and interactions is the main focus of the world-wide accelerator-based neutrino-oscillation program. The new generation of short [1] and long-baseline [2] neutrino experiments—such as the Deep Underground Neutrino Experiment (DUNE)—will address fundamental questions and play a key role in the search of physics beyond the Standard Model. In particular, the absolute scale of neutrino masses and the presence of charge parity (CP) violation in the leptonic sector, which may contribute to our understanding of the matter-antimatter asymmetry of the universe, will be determined. The existence of a fourth (sterile) neutrino will be investigated, this could explain the excess of electron neutrinos from charged current quasi-elastic events reported by the MiniBooNe collaboration [3].

Studying neutrino-nucleus interactions in the energy region of interest for oscillation experiments is a multi-scale problem. In fact, the experiments [4–9] are sensitive to a broad range of energy where different reaction mechanisms contribute [10, 11]. Quasielastic scattering is dominant for energies of hundreds of MeVs, in this case the lepton interacts with individual bound nucleons. In addition to this, there are corrections accounting for coupling of the probe to interacting nucleons, belonging to a correlated pairs on connected via two-body currents. For larger values of the energy, a struck nucleon can be excited to a baryon resonance state and subsequently decays into pions, or give rise to deep-inelastic scattering (DIS) processes. Constructing a framework able to describe these diverse reaction mechanisms on the same footing is a formidable nuclear-theory challenge. Nuclear effective field theory (EFT) provides a systematic way to construct nuclear interactions and currents performing a low-momentum expansion. In addition, an estimate of the theoretical uncertainty–which will be crucial for the neutrino data analyses– can be properly assessed. In the last decade there has been a tremendous progress in the field of nuclear ab initio methods made possible by the increasing availability of computing resources and the development of new algorithms. Within these approaches the nucleus is treated as a collection of nucleons interacting with each other via two- and three-body forces obtained within nuclear EFTS. The interaction with external electroweak probes is described by one- and two-body effective currents that are consistent with the nuclear potentials [12–17].

Among these ab initio many-body methods, the Green's Function Monte Carlo (GFMC) method utilizes quantum Monte Carlo (QMC) techniques [18] to perform first-principle calculations of nuclei up to ¹²C [19, 20]. More recently the GFMC method has also been applied to the calculation of the electroweak sum rules and response functions of ⁴He and ¹²C, including one and two-body currents [21–23]. In order to do that, integral transform techniques have been utilized. The accuracy of the inversion procedure adopted within the GFMC to obtain the response function from its integral transform has been compared and benchmarked with the Lorentz Integral Transform method [24]. The GFMC electroweak responses computed in the quasielastic sector are virtually exact for low and moderate values of the momentum transfer. Initial and final state correlations are fully retained within this approach [25, 26]. In order to extend the predictive power of this approach, relativistic effects in nuclear kinematics were included [24] leading to an excellent agreement with electron scattering data off ⁴He. However, within this approach it is not possible to access more exclusive channels, the calculations are fully inclusive. The inclusion of explicit pion degrees of freedom in the nuclear wave function [27], necessary to describe the resonance production region, is extremely complicated and its achievement is still a long way ahead.

The short-time approximation (STA) method has been recently proposed to overcome some of the limitations of GFMC [28]. In particular, this approach allows to compute both the inclusive and exclusive response of nuclei in the high-energy (short-time) limit–corresponding to the Fermi energy and above– utilizing realistic nuclear interactions and currents. In the STA the full ground-state dynamics is retained while the hadronic final state is factorized at the two-nucleon level, this approximation is expected to be valid at high-energy and momentum transfer. It allows to account for the final state interactions of the pairs involved in the interaction vertex and to incorporate two-nucleon correlations and currents as well as their interference, which are known be sizable in the GFMC results [22–26]. While keeping consistently two-body physics and ensuing quantum interference contributions, the STA is not expected to accurately model the correct physics for low-lying excitations or collective behavior like giant resonances. A good agreement with the GFMC electromagnetic responses of ⁴He is observed after enforcing the correct threshold behavior. Since the STA involves only two active nucleons, it suitable to be improved and include relativistic currents and kinematics as well pion production channels.

In the past years, the framework based on the impulse approximation (IA) and realistic spectral-functions (SFs) has been largely utilized to describe electron-nucleus scattering data in the limit of moderate and high momentum transfer [29, 30]. This scheme combines a realistic description of the initial target state with a fully-relativistic interaction vertex and kinematics. This is achieved factorizing the hadronic final state in terms of a free nucleon state and enclosing all the information on nuclear structure in the SF. The latter does not depend on the momentum transfer and can be computed within non-relativistic nuclear many-body approaches. In this review we consider two nuclear SFs, derived within the correlated basis function (CBF) formalism [31] and the self-consistent Green's function (SCGF) theory [32, 33]. These two approaches utilize different nuclear forces and involve different approximations in each of the SF calculations. Within the factorization scheme lepton-nucleus scattering is rewritten as an incoherent sum of elementary processes involving individual nucleons. This framework has been extended and generalized to include two-nucleon emission processes induced by relativistic meson-exchange currents [34] and applied to calculate the electroweak inclusive cross sections of carbon and oxygen [35, 36]. In order to tackle the resonance production region, the electroweak pion production amplitudes generated within the dynamical coupled-channel (DCC) model [37–39] have been included in the IA formalism. The results obtained convoluting the DCC elementary amplitudes with the CBF SF will also be reported.

In this review, we present lepton-nucleus interaction results obtained within different many-body methods. In section 2 we outline the formalism and define the electroweak cross sections, nuclear interactions and currents. In section 3 we discuss the integral transform techniques utilized in the GFMC to obtain the nuclear response functions. Sections 4 and 5 are devoted to the STA and extended factorization scheme, respectively. We present recent results obtained within each of the aforementioned approaches for different nuclei. In section 6 we state out conclusions and discuss future directions.

2. Formalism

We consider the scattering of an initial electron of four-momentum k = (E, k) off a nucleus A at rest; in the final state only the outgoing electron with momentum k = (E′, k′) is detected. The inclusive double differential cross section for this process can be written in Born Approximation as

$\begin{array}{ll}(\frac{d^2\sigma }{d{E}^{\prime }d{\Omega }^{\prime }}{)}_e=\frac{{\alpha }^2}{Q^4}\frac{E^{\prime }}{E}{L}_{\mu \nu }{R}^{\mu \nu }& (1)\end{array}$

where α ≃ 1/137 is the fine structure constant and Ω′ is the scattering solid angle in the direction specified by k′. The energy and the momentum transfer are denoted by ω and q, respectively, with Q² = −q² = q² − ω². The lepton tensor is fully determined by the lepton kinematical variables. It can be written neglecting the electron mass as

$\begin{array}{ll}{L}_{\mu \nu }=\frac{1}{E{E}^{\prime }}(k_{\mu }{k}_{\nu }^{\prime }+k_{\mu }^{\prime }{k}_{\nu }-g_{\mu \nu }k·k^{\prime }).& (2)\end{array}$

The hadronic tensor describes the transition between the initial and final nuclear states |Ψ₀〉 and |Ψ_f〉, with energies E₀ and E_f. For nuclei of spin-zero, it can be written as

$\begin{array}{l}{R}^{\mu \nu }(\text{q},\omega )=\\ {\displaystyle \sum _f}\langle {\text{Ψ}}_0|J^{\mu †}(\text{q},\omega )|{\text{Ψ}}_f\rangle \langle {\text{Ψ}}_f|J^{\nu }(\text{q},\omega )|{\text{Ψ}}_0\rangle \delta (E_0+\omega -E_f).& (3)\end{array}$

where we sum over all hadronic final states and J^μ(q, ω) is the nuclear current operator whose structure will be discussed in detail in section 2.1. For inclusive processes, the cross section of Equation (1) only depends on the two response functions, R_L(q, ω) and R_T(q, ω), which describe the interactions with a virtual photon longitudinally (L) and transversely (T) polarized. It is given by

$\begin{array}{ll}(\frac{d^2\sigma }{d{E}^{\prime }d{\Omega }^{\prime }}{)}_e={\left(\frac{d\sigma }{d{\Omega }^{\prime }}\right)}_{\text{M}}{\displaystyle [A_L{R}_L(\left|\text{q}\right|,\omega )+A_T{R}_T(\left|\text{q}\right|,\omega )]},& (4)\end{array}$

where the lepton kinematical factors are given by

$\begin{array}{ll}{A}_L=(\frac{q^2}{{\text{q}}^2}{)}^2,A_T=-\frac{1}{2}\frac{q^2}{{\text{q}}^2}+{tan}^2\frac{\theta }{2},& (5)\end{array}$

and

$\begin{array}{ll}{\left(\frac{d\sigma }{d{\Omega }^{\prime }}\right)}_{\text{M}}={\left[\frac{\alpha cos(\theta /2)}{2E^{\prime }{sin}^2(\theta /2)}\right]}^2& (6)\end{array}$

is the Mott cross section depending on the scattering angle θ.

The extension to neutral- and charge-current electroweak processes is straightforward. Let us consider the scattering of a neutrino (ν_ℓ) or an anti-neutrino (${\stackrel{-}{\nu }}_{\ell }$) off a nuclear target. In analogy with the electromagnetic case, we denote by k = (E, k) and k = (E′, k′) the momentum of the initial and outgoing lepton; the double-differential cross section can be written as [40, 41]

$\begin{array}{ll}(\frac{d\sigma }{d{E}^{\prime }d{\Omega }^{\prime }}{)}_{{\nu }_{\ell }/{\stackrel{-}{\nu }}_{\ell }}=\frac{G^2}{4{\pi }^2}{k}^{\prime }{E}^{\prime }{L}_{\mu \nu }{R}^{\mu \nu },& (7)\end{array}$

where G = G_F and G = G_F cos θ_c for neutral current (NC) and charge current (CC) processes, respectively, with cos θ_c = 0.97425 [42] and for the Fermi coupling constant we use $G_F=1.1803\times 10^{-5}$ [43]. The leptonic tensor contains an extra-contribution proportional to the Levi Civita

$\begin{array}{ll}{L}_{\mu \nu }=\frac{1}{E{E}^{\prime }}(k_{\mu }{k}_{\nu }^{\prime }+k_{\mu }^{\prime }{k}_{\nu }-g_{\mu \nu }k·k^{\prime }\pm i{ϵ}_{\mu \rho \nu \sigma }{k}^{\rho }{k}^{\prime \sigma }),& (8)\end{array}$

where the + (−) sign is for ν_ℓ ($\stackrel{-}{{\nu }_{\ell }}$) initiated reactions. The hadronic tensor is the same as Equation (3) but the current operator will have a vector and axial component, its explicit expression will be given in section 2.1. We perform the Lorentz contraction of the leptonic and hadronic tensor of Equation (7), yielding

$\begin{array}{l}{\left(\frac{d\sigma }{d{E}^{\prime }d{\Omega }^{\prime }}\right)}_{\nu /\overline{\nu }}=\frac{G_F^2{\text{ cos}}^2{\theta }_c}{4{\pi }^2}\frac{k^{\prime }}{2E_{\nu }}[{\widehat{L}}_{CC}{R}_{CC}+2{\widehat{L}}_{CL}{R}_{CL}\\ +{\widehat{L}}_{LL}{R}_{LL}+{\widehat{L}}_T{R}_T\pm 2{\widehat{L}}_{T^{\prime }}{R}_{T^{\prime }}].& (9)\end{array}$

Taking the three-momentum transfer along the z axis and the total three-momentum in the x − z plane, we can define q and Q as

$\begin{array}{l}q=k-k^{\prime }=(\omega ,\text{q}),\text{q}=(0,0,q_z)\\ Q=k+k^{\prime }=(\Omega ,\text{Q}),\text{Q}=(Q_x,0,Q_z),& (10)\end{array}$

and write the leptonic kinematical factors as

$\begin{array}{l}{\widehat{L}}_{CC}={\Omega }^2-q_z^2-m_{\ell }^2,{\widehat{L}}_{CL}=(-\Omega Q_z+\omega q_z)\\ {\widehat{L}}_{LL}={Q_z}^2-{\omega }^2+m_{\ell }^2,{\widehat{L}}_T=\frac{{Q_x}^2}{2}-q^2+m_{\ell }^2\\ {\widehat{L}}_{T^{\prime }}=\Omega q_z-\omega Q_z,& (11)\end{array}$

with $m_{\ell }^2=k^{\prime 2}$ the mass of the outgoing lepton. The five electroweak response functions correspond to different components of the hadro tensor

$\begin{array}{l}{R}_{CC}=R^{00},R_{CL}=-\frac{1}{2}(R^{03}+R^{30})\\ R_{LL}=R^{33},R_T=R^{11}+R^{22}\\ R_{T^{\prime }}=-\frac{i}{2}(R^{12}-R^{21}).& (12)\end{array}$

Note that electron and neutrino scattering cross sections are written in a similar fashion as a contraction of the leptonic and the hadronic tensor. This analogy will become even more apparent in section 2.1 where we introduce the explicit expression of the current operators and use the conserved vector current (CVC) hypothesis to connect the vector part of the electroweak current with the electromagnetic one. For this reason, any model of neutrino-nucleus scattering has to be capable of describing electron-scattering cross sections first [44].

2.1. Nuclear Hamiltonian and Current Operator

The internal structure of nuclei and their reactions can be described within non-relativistic many body approaches utilizing an Hamiltonian in which the nucleons are the only active degrees of freedom. Its general expression is given by

$\begin{array}{ll}H={\displaystyle \sum _i}\frac{{\text{p}}_i^2}{2m_N}+{\displaystyle \sum _{i<j}}{v}_{ij}+{\displaystyle \sum _{i<j<k}}{V}_{ijk},& (13)\end{array}$

where p_i is the momentum of the i-th nucleon having mass m_N, while the potentials v_ij and V_ijk model the nucleon-nucleon (NN) and three-nucleon (3N) interactions, respectively. A model of NN interaction has to be constrained by the large number of NN scattering data available. Currently, very accurate results have been obtained from both phenomenological approaches and chiral effective field theory able to accurately fit these data.

The Argonne v18 is a finite, coordinate space NN potential that has been fit to the full Nijmegen phase-shift database and to low energy scattering parameters and deuteron properties. It can be written as a product of radial functions and spin-isospin operator

$\begin{array}{ll}{v}_{ij}={\displaystyle \sum _{p=1,\dots ,18}}{v}_p(r_{ij})O_{ij}^p& (14)\end{array}$

where r_ij = |r_i − r_j|. The first 14 operators are charge independent (corresponding to the older Argonne v14 model)

$\begin{array}{l}{O}_{ij}^{p=1,\dots ,14}=[1,{\sigma }_i·{\sigma }_j,S_{ij},\text{L}·\text{S},{\text{L}}^2,{\text{L}}^2{\sigma }_i·{\sigma }_j,{(\text{L}·\text{S})}^2],\\ \times [1,{\tau }_i·{\tau }_j]& (15)\end{array}$

where σ and τ are the Pauli matrices operating over the nucleon spin and isospin degrees of freedom, respectively, $S_{ij}=3{\sigma }_i·{\widehat{r}}_{ij}{\sigma }_j·{\widehat{r}}_{ij}-{\sigma }_i·{\sigma }_j$ is the tensor operator, ${\text{L}}_{ij}=\frac{1}{2i}({\text{r}}_i-{\text{r}}_j)\times ({\nabla }_i-{\nabla }_j)$ is the relative angular momentum, and ${\text{S}}_{ij}=\frac{1}{2}({\sigma }_i+{\sigma }_j)$ is the total spin. The terms p = 15…18 are included in the formulation of the Argonne potential to account for small violations of charge symmetry [45]. In addition to the NN interactions, also phenomenological 3N interactions have been developed. In particular the Illinois 7 (IL7) interaction is expressed as a sum of a two-pion-exchange P-wave term (Fujita-Miyazawa), a two-pion-exchange S-wave contribution, a three-pion-exchange contribution, and a 3N central interaction [46]. These phenomenological NN and 3N interactions were successfully utilized in QMC calculations of nuclear properties, neutron drops, and neutron-star matter [18, 47–50].

In the last decades there has been a tremendous progress in development of chiral EFT interactions as proven by the availability of a number of different potentials [13, 51–54]. However, it is only recently with their formulation in coordinate space that the application of chiral forces within QMC approaches became possible. These new local potentials have been computed up to N²LO with consistent 3N terms in Gezerlis et al. [55, 56], the Δ-isobar degrees of freedom were fully accounted for in the derivation of Piarulli et al. [57, 58].

In analogy with the nuclear Hamiltonian, the current operator can be expressed as a sum of one- and two-body terms

$\begin{array}{ll}{J}^{\mu }={\displaystyle \sum _i}{j}^{\mu }(i)+{\displaystyle \sum _{i<j}}{j}^{\mu }(ij)+\dots & (16)\end{array}$

The one-body electromagnetic current is given by

$\begin{array}{ll}{j}_{\text{EM}}^{\mu }=ū({\text{p}}^{\prime })[{{F}}_1{\gamma }^{\mu }+i{\sigma }^{\mu \nu }{q}_{\nu }\frac{{{F}}_2}{2m_N}]u(\text{p}),& (17)\end{array}$

where p and p′ are the initial and final nucleon momentum. The isoscalar (S) and isovector (V) form factors, ${{F}}_1$ and ${{F}}_2$, are given by combination of the Dirac and Pauli ones, F₁ and F₂, as

$\begin{array}{ll}{{F}}_{1,2}=\frac{1}{2}\left[F_{1,2}^S+F_{1,2}^V{\tau }_z\right]& (18)\end{array}$

where τ_z is the is the isospin operator and

$\begin{array}{ll}{F}_{1,2}^S=F_{1,2}^p+F_{1,2}^n,F_{1,2}^V=F_{1,2}^p-F_{1,2}^n.& (19)\end{array}$

The Dirac and Pauli form factors can be expressed in terms of the electric and magnetic form factors of the proton and neutron as

$\begin{array}{lll}{F}_1^{p,n}=& \frac{G_E^{p,n}+\tau G_M^{p,n}}{1+\tau },F_2^{p,n}=\frac{G_M^{p,n}-G_E^{p,n}}{1+\tau }& (20)\end{array}$

with $\tau =Q^2/4m_N^2$. Therefore, the electromagnetic current can be schematically written as $J_{\text{EM}}^{\mu }=J_{\gamma ,S}^{\mu }+J_{\gamma ,z}^{\mu }$ where the first is the isoscar term and the second is the isovector multiplied by the isospin operators τ_z. The one-body charge and current operator are obtained from the non-relativistic reduction of the covariant operator of Equation (17) including all the terms up to $1/m_N^2$ in the expansion. It leads to the following expression for isoscalar charge, transverse (⊥) and longitudinal (∥) to q component of the current operator

$\begin{array}{l}{j}_{\gamma ,S}^0=\frac{G_E^S}{2\sqrt{1+Q^2/4m_N^2}}-i\frac{2G_M^S-G_E^S}{8m_N^2}\text{q}·({\sigma }_i\times {\text{p}}_i)\\ {\text{j}}_{\gamma ,S}^{\perp }=\frac{G_E^S}{2m_N}{\text{p}}_i^{\perp }-i\frac{G_M^S}{4m_N}{(\text{q}\times \sigma )}_i\\ j_{\gamma ,S}^{\parallel }=\frac{\omega }{\left|\text{q}\right|}{j}_{\gamma ,S}^0.& (21)\end{array}$

Note that the last relation has been obtained from current conservation relation discussed in Equation (30). Analogously to Equation (19), the isoscalar and isovector component of the electric and magnetic form factors are written as

$\begin{array}{ll}{G}_{E,M}^S=G_{E,M}^p+G_{E,M}^n,G_{E,M}^V=G_{E,M}^p-G_{E,M}^n.& (22)\end{array}$

The isovector contribution to the current $J_{\gamma ,z}^{\mu }$ is obtained by replacing $G_{E,M}^S\to G_{E,M}^V{\tau }_z$. The electroweak interactions of a neutrino or anti-neutrino with the hadronic target can be induced by both CC and NC transitions. The current operator is written as a different combination of vector and axial terms. Note that in both cases the Conserved Vector Current (CVC) hypothesis allows to relate the vector form factor to the electromagnetic ones

$\begin{array}{l}{J}_{CC}^{\mu }=J_{\gamma ,z}^{\mu }+J_{a,z}^{\mu }\\ J_{NC}^{\mu }=-2{sin}^2{\theta }_W{J}_{\gamma ,S}^{\mu }+(1-2{sin}^2{\theta }_W)J_{\gamma ,z}^{\mu }+J_{a,z}^{\mu },& (23)\end{array}$

where θ_W is the Weinberg angle (${sin}^2{\theta }_W=0.2312$ [42]). The fully relativistic expression of the axial one-body current operator reads

$\begin{array}{ll}{j}_A^{\mu }=ū({\text{p}}^{\prime })[-{\gamma }^{\mu }{\gamma }_5{{F}}_A-q^{\mu }{\gamma }_5\frac{{{F}}_P}{m_N}]u(\text{p}).& (24)\end{array}$

For CC processes the axial and pseudo-scalar form factors can be written as

$\begin{array}{ll}{{F}}_A=F_A{\tau }_{\pm },{{F}}_P=F_P{\tau }_{\pm },& (25)\end{array}$

with τ_i,± = (τ_i,x ± τ_i,y)/2 being the isospin raising-lowering operator.

The dipole parametrization for the axial form factor is routinely adopted in most of the calculations, it reads

$\begin{array}{ll}{F}_A=\frac{g_A}{{(1+Q^2/m_A^2)}^2},& (26)\end{array}$

where the nucleon axial-vector coupling constant is assumed to be g_A = 1.2694. The impact of the Q² dependence of the axial form factor on neutrino-nucleus cross-section predictions has been discussed in Aguilar-Arevalo et al. [59] and Bernard et al. [60]. The validity of the dipole parametrization has been questioned and in these regards both lattice-QCD calculations [61] and the so called “z-expansion” analysis [62] has been recently proposed. The pseudo-scalar form factor is obtained by using Partially Conserved Axial Current (PCAC) arguments to write it in terms of the axial one

$\begin{array}{ll}{F}_P=\frac{2m_N^2}{(m_{\pi }^2+Q^2)}{F}_A.& (27)\end{array}$

For NC transitions, we report the non-relativistic reduction of the charge- and axial-current operator [63] (for brevity we neglect order $1/m_N^2$ terms)

$\begin{array}{ll}{j}_{a,z}^0(i)=-\frac{G_A}{4m_N}{\tau }_{i,z}{\sigma }_i·(\text{q}+{\text{p}}_i),{\text{j}}_{a,z}(i)=-\frac{G_A}{4m_N}{\sigma }_i{\tau }_{i,z}.& (28)\end{array}$

The CC non-relativistic current is obtained by substituting in the non-relativistic isovector term $j_{\gamma ,z}^{\mu }$ and $j_{a,z}^{\mu }$ of Equation (28), τ_i,z/2 → τ_i,± and adding a pseudoscalar contribution

$\begin{array}{ll}{j}_{a,PS}^{\mu }=\frac{G_A}{m_{\pi }^2+Q^2}{\tau }_{i,\pm }{q}^{\mu }{\sigma }_i·\text{q}.& (29)\end{array}$

The electromagnetic current must satisfy the continuity equation

$\begin{array}{ll}\nabla ·\text{J}+i[H,J^0]=0& (30)\end{array}$

which links the two-body exchange current operator to the NN interaction and leads to separate continuity equations for the one- and two-body current operators. Chiral EFT formulations allow to construct electroweak currents which are fully consistent with the nuclear forces entering the hamiltonian. The gauge invariance of the theory implies that the nuclear current operators satisfy the continuity equation with the potentials order by order of the chiral expansion. The calculation of the two-body electromagnetic currents has been the subject of extensive study carried out by different groups [64–68]. Another important advantage of chiral EFT consists on having connected three-nucleon interaction and the two-nucleon axial current; their derivation up to one-loop is reported in Krebs et al. [69] and Baroni et al. [70] while the Δ-full expression obtained consistently with the nuclear forces of Piarulli et al. [57, 58] can be found in Baroni et al. [71].

The majority of the results that will be presented in this review have been obtained utilizing the aforementioned AV18 potential and related semi-phenomenological currents. The spin and isospin dependence of the NN potential leads to a non-vanishing commutator with the non-relativistic one-body charge operator. In order to satisfy the continuity equation, the so-called “model-independent” two-body currents j_MI(ij) have to be introduced; their longitudinal part is directly constrained by the NN interaction while their transverse components are not uniquely defined. The main contributions comes from the one-pion and one-rho exchange current operator, their expression is well-known and reported in Rocco et al. [72], Dekker et al. [36] and Schiavilla et al. [73] both in their relativistic and non-relativistic formulation.

In addition to the model-independent two body currents a significant contribution comes from model dependent terms in which the exchange of a pion is followed by the excitation of a Δ-resonance in the intermediate state. Due to the transverse nature of this current, its expression is model dependent. In fact, the form of the vector part is not determined from current-conservation constraints [74].

Analogously to the one-body case, the two-body CC operator is the sum of a vector and axial component. The relativistic expression of the two-body current operator we present in this work has been obtained following the parametrization of Ruiz Simo et al. [75] where the pion-production amplitudes of Hernandez et al. [76] are coupled to a second nucleonic line. Starting from the vector component of $j_{\text{CC}}^{\mu }$, the electromagnetic current operators can be obtained using the CVC hypothesis. Adopting the momentum variables specified in Figure 1, the expression of the CC Δ-current reads

$\begin{array}{l}{(j_{\Delta }^{\mu })}_{\text{CC}}=\frac{3}{2}\frac{f_{\pi NN}{f}^{*}}{m_{\pi }^2}{\displaystyle \{}\Pi {(k_2)}_{(2)}\left[\right(-\frac{2}{3}{\tau }^{(2)}\\ +\frac{I_V}{3}{\displaystyle {)}_{\pm }}{F}_{\pi NN}(k_2)F_{\pi N\Delta }(k_2){(j_a^{\mu })}_{(1)}-{\displaystyle (\frac{2}{3}{\tau }^{(2)}+\frac{I_V}{3}{)}_{\pm }}\\ \times F_{\pi NN}(k_2)F_{\pi N\Delta }(k_2){(j_b^{\mu })}_{(1)}]+(1\leftrightarrow 2)\}& (31)\end{array}$

where $k_2=p^{\prime }-k^{\prime }$ is the momentum of the π exchanged in the two depicted diagrams, f^* = 2.14 and

$\begin{array}{ll}\Pi (k)=\frac{{\gamma }_5\cancel{k}}{k^2-m_{\pi }^2},& (32)\end{array}$

$\begin{array}{ll}{F}_{\pi N\Delta }(k)=\frac{{\Lambda }_{\pi N\Delta }^2}{{\Lambda }_{\pi N\Delta }^2-k^2},& (33)\end{array}$

$\begin{array}{ll}{F}_{\pi NN}(k)=\frac{{\Lambda }_{\pi }^2-m_{\pi }^2}{{\Lambda }_{\pi }^2-k^2},& (34)\end{array}$

with Λ_πNΔ = 1150 MeV and Λ_π = 1300 MeV. In the above equations, Π(k) describes the pion propagation and absorption, while the πNN and πNΔ couplings depend on the form factors F_πNΔ(k) and F_πNN(k), respectively, accounting for the off-shellness of the π and Δ. The operator ${(I_V)}_{\pm }={({\tau }^{(1)}\times {\tau }^{(2)})}_{\pm }$ with ± → x ± iy raises-lowers the isospin components. In Equation (31), $j_a^{\mu }$ and $j_b^{\mu }$ denote the N → Δ transition vertices of the left and right diagrams, respectively. They are expressed as

$\begin{array}{l}{j}_a^{\mu }={(j_a^{\mu })}_V+{(j_a^{\mu })}_A,\\ {(j_a^{\mu })}_V=\frac{C_3^V}{m_N}\left[k_2^{\alpha }{G}_{\alpha \beta }(p_{\Delta })(g^{\beta \mu }\cancel{q}-q^{\beta }{\gamma }^{\mu })\right]{\gamma }_5,\\ {(j_a^{\mu })}_A=C_5^A\left[k_2^{\alpha }{G}_{\alpha \beta }(p_{\Delta })g^{\beta \mu }\right]& (35)\end{array}$

where k is the momentum of the initial nucleon, q is the momentum transfer and p_Δ = q+k, yielding $p_{\Delta }^0=e(\text{k})+\omega$. For the left diagram we have

$\begin{array}{l}{j}_b^{\mu }={(j_b^{\mu })}_V+{(j_b^{\mu })}_A,\\ {(j_b^{\mu })}_V=\frac{C_3^V}{m_N}{\gamma }_5\left[(g^{\alpha \mu }\cancel{q}-q^{\alpha }{\gamma }^{\mu })G_{\alpha \beta }(p_{\Delta })k_2^{\beta }\right],\\ {(j_b^{\mu })}_A=C_5^A\left[g^{\alpha \mu }{G}_{\alpha \beta }(p_{\Delta })k_2^{\beta }\right].& (36)\end{array}$

where p is the outgoing nucleon four-momentum and p_Δ = p − q. The vector and axial form factors, denoted by $C_3^V$ and $C_5^A$, are obtained from general principles and experimental results as discussed in Hernandez et al. [76] where their explicit expressions is also reported. In the above equations all nucleons are on the mass-shell with the time component $p^0=\sqrt{m_N^2+{\overrightarrow{p}}^2}$. For the Δ-propagator we adopted the Rarita-Schwinger convention where $G^{\alpha \beta }(p_{\Delta })=P^{\alpha \beta }(p_{\Delta })/(p_{\Delta }^2-M_{\Delta }^2)$ is proportional to the spin 3/2 projection operator

$\begin{array}{l}{P}^{\alpha \beta }(p_{\Delta })=({\cancel{p}}_{\Delta }+M_{\Delta })[g^{\alpha \beta }-\frac{1}{3}{\gamma }^{\alpha }{\gamma }^{\beta }-\frac{2}{3}\frac{p_{\Delta }^{\alpha }{p}_{\Delta }^{\beta }}{M_{\Delta }^2}\\ +\frac{1}{3}\frac{p_{\Delta }^{\alpha }{\gamma }^{\beta }-p_{\Delta }^{\beta }{\gamma }^{\alpha }}{M_{\Delta }}].& (37)\end{array}$

In order to account for the possible decay of the Δ into a physical πN we replace its real mass M_Δ = 1,232 MeV entering the denominator of the free propagator, i.e., $p_{\Delta }^2-M_{\Delta }^2$, by M_Δ − iΓ(p_Δ)/2 [72, 77]. The decay width Γ(p_Δ)/2 is not a constant but explicitly depends upon the energy, its expression can be found in Dekker et al. [72].

FIGURE 1

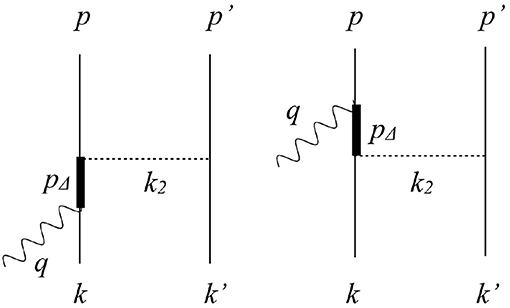
Figure 1. Feynman diagrams of the Δ contribution to two-body currents. Solid, thick, and dashed lines represent nucleons, deltas, pions, respectively while the wavy line correspond to the vector boson.

3. Integral Transform Techniques

Evaluating the hadronic tensor of Equation (3) is highly non-trivial as it requires to sum over the entire excitation spectrum of the nucleus and to include one- and two-body current operators. Integral transform techniques are extremely useful in reducing the problem to a ground-state one instead of explicitly evaluating each transition amplitude |Ψ₀〉 → |Ψ_f〉. We consider the convolution of the response function with a smooth kernel

$\begin{array}{l}{E}_{\alpha \beta }(\text{q},\sigma )={\displaystyle \int }d\omega K(\sigma ,\omega )R_{\alpha \beta }(\text{q},\omega )=\\ {\displaystyle \sum _f}\langle {\text{Ψ}}_0\left|J_{\alpha }^{†}(\text{q})\right|{\text{Ψ}}_f\rangle K(\sigma ,E_f-E_0)\langle {\text{Ψ}}_f\left|J_{\beta }(\text{q})\right|{\text{Ψ}}_0\rangle ,& (38)\end{array}$

using the closure property $\sum _f\left|{\text{Ψ}}_f\rangle \langle {\text{Ψ}}_f\right|=1$ a generalized sum rule depending on a continuous parameter σ can be obtained

$\begin{array}{ll}{E}_{\alpha \beta }(\text{q},\sigma )=\langle {\text{Ψ}}_0\left|J^{†}(\text{q})K(\sigma ,H-E_0)J_{\beta }(\text{q})\right|{\text{Ψ}}_0\rangle .& (39)\end{array}$

With an appropriate choice of the kernel K, the right-hand side of the above equation can be accurately computed within different ab-initio methods. In order to retrieve the energy dependence of the response function, the integral transform has to be accurately inverted.

3.1. Lorentz Integral Transform Technique

The kernel used to compute the integral transform is a Lorentzian

$\begin{array}{ll}K(\sigma ,\omega )=\frac{1}{(\omega -{\sigma }^{*})(\omega -\sigma )}& (40)\end{array}$

where σ is a complex parameter, generally defined for convenience as

$\begin{array}{ll}\sigma =E_0+{\sigma }_R+i{\sigma }_I.& (41)\end{array}$

For simplicity we leave the Lorentz indices implicit and rewrite Equation (39) substituting the Lorentz kernel as

$\begin{array}{l}E(\text{q},{\sigma }_I,{\sigma }_R)=\langle {\text{Ψ}}_0|J^{†}(\text{q})\frac{1}{H-E_0-{\sigma }_R+i{\sigma }_i}\\ \frac{1}{H-E_0-{\sigma }_R-i{\sigma }_i}J(\text{q})|{\text{Ψ}}_0\rangle =\langle \widetilde{\text{Ψ}}|\widetilde{\text{Ψ}}\rangle ,& (42)\end{array}$

implying that the Lorentz Integral Transform (LIT) of the response function is given by the norm of the $|\widetilde{\text{Ψ}}\rangle$ state. This state is determined by solving a Schrödinger-like equation for a quantum mechanical bound system

$\begin{array}{ll}(H-E_0-{\sigma }_R-i{\sigma }_I)|\widetilde{\text{Ψ}}\rangle =J(\text{q})|{\text{Ψ}}_0\rangle & (43)\end{array}$

for different values of σ_I and σ_R. In order to obtain the response function, one first computes Ē(q, σ_I, σ_R) and then inverts it numerically. This second step is highly non-trivial and belongs to the class of so-called “ill-posed” problems. The devised method consists on: (i) making an ansatz to write down the expression of the response function as a function of a set of parameters c_i (ii) the corresponding LIT is computed using this parametrization of the nuclear response function (iii) the parameters c_i are determined from a least-squares fit of the LIT computed in (ii) with the one calculated at the beginning, Ē(q, σ_I, σ_R). A more detailed discussion of the inversion procedures utilized can be found in Efros et al. [78] and Reiss et al. [79].

A very accurate determination the electromagnetic responses of light nuclei has been achieved, for different values of q, combining the LIT method with the hyperspherical harmonic (HH) formalism [80–82]. This expansion method has been successfully utilized to study nuclear, atomic and molecular few-body systems; the wave function of the system is expanded in a series of products of HH basis functions and hyperradial basis functions allowing for a correct description of the large distance components. The predictive power of the HH approach is limited to relatively light mass number, to overcome this limitation the Couple Cluster (CC) theory has been recently combined with the LIT approach to tackle medium and large mass nuclei [83, 84]. The photoabsorption cross sections of ^16,22 O and ⁴⁰ Ca and electromagnetic sum rules have been recently computed using the LIT-CC approach in Simonis et al. [85].

3.2. Green's Function Monte Carlo

The Green's Function Monte Carlo (GFMC) is an ab-initio method that allows to predict with high accuracy the structure and low-energy transitions of A ≤ 12 nuclei [19]. This method is utilized to project out the ground state starting from a trial wave function |Ψ_T〉

$\begin{array}{l}|{\text{Ψ}}_0\rangle \propto {\displaystyle \underset{\tau \to \infty }{lim}}exp\left[-(H-E_0)\tau \right]|{\text{Ψ}}_T\rangle ,\end{array}$

where E₀ is a parameter used to control the normalization and τ is the imaginary time. Recently, exploiting integral transform techniques accurate predictions for the electromagnetic response functions of ⁴He and ¹²C in the quasielastic sector have been obtained. The inclusion of two-body currents yields to a very good agreement between GFMC predictions and experimental data [23, 25]. The integral transform of Equation (38) is evaluated using a Laplace kernel and denoted as Euclidean response. Its inelastic contribution is obtained as

$\begin{array}{ll}{E}_{\alpha \beta }(\text{q},\sigma )={\displaystyle {\int }_{{\omega }_{el}^{+}}^{\infty }}d\omega R_{\alpha \beta }(\text{q},\omega )e^{-\omega \sigma },& (44)\end{array}$

where ω_el is the energy of the recoiling ground state. Using the closure property, the sum over the final states can be removed, the inelastic Euclidean responses can be written as the following ground-state expectation value

$\begin{array}{ll}{E}_{\alpha }(\left|\text{q}\right|,\sigma )=\langle {\text{Ψ}}_0\left|J_{\alpha }^{†}(\text{q})e^{-(H-E_0)\tau }{J}_{\beta }(\text{q})\right|{\text{Ψ}}_0\rangle -|F_{\alpha }(q){|}^2{\text{e}}^{-\sigma {\omega }_{\text{el}}}& (45)\end{array}$

where F_α(q) is the longitudinal elastic form factor and the nucleon form factors entering in the current operator are evaluated at the quasielastic peak $Q_{qe}^2={\text{q}}^2-{\omega }_{qe}^2$.

In order to obtain the response function the Laplace transform has to be inverted. This is achieved exploiting maximum entropy techniques, as described in Lovato et al. [25] and in the supplemental material of Lovato et al. [86]. The LIT-HH and GFMC results for the longitudinal electromagnetic responses of ⁴He have been recently compared to benchmark the inversion procedure used in the two approaches. The calculations presented are based on the AV18 and IL7 combination of two- and three-nucleon potential for the GFMC method and AV18 and UIX for the LIT-HH [45, 87]. The results are displayed in Figure 2 for |q| = 300 and 500 MeV, the (red) dashed and solid (blue) lines corresponding to the LIT-HH and GFMC predictions, respectively, are found in good agreement and correctly reproduce the experimental data taken from Carlson et al. [88]. The small discrepancies between the two curves have been discussed in Rocco et al. [24] and they do not originate from the inversion techniques utilized in the two approaches.

FIGURE 2

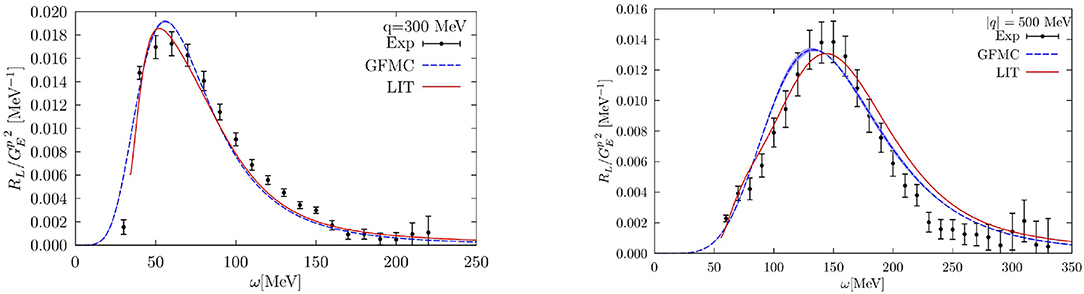
Figure 2. Longitudinal electromagnetic response functions of ⁴He at |q| = 300 MeV (left) and |q| = 500 MeV (right) obtained inverting the Laplace and Lorentz integral transforms compared to the experimental data of Carlson et al. [88].

Because of the non-relativistic nature of the GFMC approach, it can be safely applied to compute electroweak responses in the high momentum transfer region relevant for neutrino-nucleus scattering. Relativistic corrections are in both one- and two-body current operators up to order $1/m_N^2$ as discussed in Carlson and Schiavilla [63] for the one-body case. However, the quantum mechanical framework is non-relativistic; an attempt of including relativistic corrections in the kinematics has been recently carried out in Rocco et al. [24]. The strategy consists on performing the calculation in a reference frame that minimizes nucleon momenta in the final state.

In electron-nucleus scattering processes, the quasielastic region is dominated by a one-nucleon knock-out and this condition is satisfied by the active nucleon Breit (ANB) frame in which the target nucleus has a momentum −Aq/2. In this reference frame the momentum of the nucleons in the initial state is about −q/2 while the one of the emitted particle is ≃ q/2. The momentum of the final state is higher in all the other reference frames like for example the laboratory (LAB) system where the emitted knocked-out nucleon has a momentum of about q. Therefore, the ANB system can be utilized to minimize relativistic corrections.

In order to compare with experimental data measured in the LAB system, the results from the ANB need to be boosted back to the LAB frame. The solid blue and red curves in Figure 3 performing the calculation of the longitudinal electromagnetic response of ⁴He at |q| = 700 MeV in the LAB and ANB frame, respectively, and boosting back to the LAB frame using Lorentz transformation. The two curves peak in different positions and have different strengths, this frame dependence of the results is a clear indication that relativistic effects are sizable for these values of q.

FIGURE 3

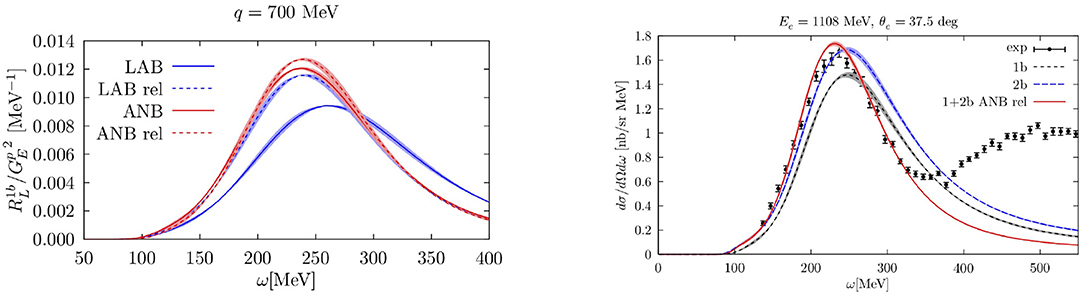
Figure 3. (Left) Longitudinal electromagnetic response functions of ⁴He at |q| = 700 MeV computed in the LAB and in the ANB frame are displayed by the blue and red solid curves, respectively. The dashed curves have been obtained by applying the two-fragment model to consider two-body relativistic kinematics for the final state energy. (Right) Double-differential electron-⁴He cross sections for E_e = 1108 MeV and θ = 37.5. The short-dashed red and dashed blue curves are the GFMC calculation were only one- body and one- plus two-body contributions in the electromagnetic currents are accounted for. The results obtained in the ANB frame corrected by the two-fragment model are displayed by the red solid line. The experimental data are taken from Benhar et al. [44].

Relativistic effects in the kinematics can be included employing the two-fragment model of Efros et al. [89] which presents strong analogies with the procedure used to determine NN potentials. In this case, the relative momentum of the two-nucleon system p₁₂ is determined in a relativistic fashion and utilized to solve the Schrödinger equation with a non-relativistic kinetic energy $E_{12}=p_{12}^2/2{\mu }_{12}$, μ₁₂ being the reduced mass.

The two-fragment model relies on the assumption that the dominant reaction in the quasielastic region consists on the break-up of the nucleus into a knocked-out nucleon with momentum ${\text{p}}_N^{\text{fr}}$ and a remaining (A − 1) system in its ground state ${\text{p}}_X^{\text{fr}}$, respectively. The relative and center-of-mass momenta of the nucleon and spectator system are obtained as

$\begin{array}{ll}{\text{p}}_{\text{f}}^{\text{fr}}=\mu (\frac{{\text{p}}_N^{\text{fr}}}{m}-\frac{{\text{p}}_X^{\text{fr}}}{M_X}),{\text{P}}_f^{\text{fr}}={\text{p}}_N^{\text{fr}}+{\text{p}}_X^{\text{fr}},& (46)\end{array}$

where M_X and μ are the mass of the residual nucleus and the reduced mass, respectively. The relative momentum $p_f^{\text{fr}}$ can be computed in a relativistic way utilizing the correct definition of the final hadronic energy

$\begin{array}{l}{E}_f^{fr}=\sqrt{m^2+{({\text{p}}_f^{\text{fr}}+(\mu /M_{A-1}){\text{P}}_f^{\text{fr}})}^2}\\ +\sqrt{M_{A-1}^2+{({\text{p}}_f^{\text{fr}}-(\mu /m){\text{P}}_f^{\text{fr}})}^2};\end{array}$

and used to determine the relativistically “fake” kinetic energy ${(p_f^{\text{fr}})}^2/2\mu$ entering in the energy conserving δ-function of Equation (3). A more detailed discussion of the approach can be found in Rocco et al. [89] and Efros et al. [24].

The results computed within the two-fragment model are displayed by the dashed curves in Figure 3. Note that, now the position and the strength of the LAB rel and ANB rel curves are the same. This implies that the position of the quasielastic peak in the electromagnetic responses no longer depends upon the reference frame and coincides with that of the ANB frame (solid blue curve).

In order to compute the inclusive electromagnetic cross section of Equation (4), R_L and R_T have to be evaluated for several values of ω and |q|. Hence, due to the sizable computational effort associated with the inversion of the Euclidean response for a given value of |q|, the direct evaluation of Equation (4) is not feasible within GFMC. In order to overcome this limitation, an interpolation procedure based on the concept of scaling was devised in Rocco et al. [24] and used for an accurate and efficient interpolation of the GFMC responses. The right panel of Figure 3 displays the double-differential electron-⁴He cross sections for E_e = 1108 MeV and θ = 37.5. The red and blue lines have been obtained including the one- body and one- plus two-body contributions in the electromagnetic currents. The inclusion of the meson exchange current leads to a substantial enhancement in the quasielastic region. The same feature is present in the results of Lovato et al. [23, 25] where the electromagnetic responses of ⁴He and ¹²C have been calculated and compared with the experimental data. Separating the longitudinal and transverse channel it has been observed that the two-body term has a predominantly transverse nature; its contribution is almost vanishing in the longitudinal channel when electromagnetic processes are considered. The red solid line indicates one plus two-body current results obtained in the ANB frame, employing the two-body fragment model to account for relativistic kinematics. The inclusion of relativistic effects leads to a shift of the peak position toward lower values of ω and to a reduction of its width.

Recently, GFMC calculations of the neutral-current responses and cross sections for neutrino scattering off ¹²C have also been performed [26]. A description of the two-body charge and current operators used in this work is provided in Lovato et al. [23] and Shen et al. [40] and references therein. The left panel of Figure 4 shows the different spatial components of the neutral-current response functions in ¹²C at momentum transfer |q| = 570 MeV. The vector and axial contributions are shown separately in all cases but for R_xy the entire strength is given by the axial-vector interference. The dashed and solid lines have been obtained including the one-body and one- and two-body currents, respectively. Note that also in this case the two-body term significantly increases in magnitude the response functions in the quasielastic region. At variance with the electromagnetic results, the axial component of the two-body operator in the weak neutral charge produce substantial excess strength in the longitudinal channels as clearly visible in the upper figure. While in the transverse response, shown in the middle panel, we have a two-body enhancement both from the axial and vector terms. The xy response function in the lower panel which arises solely on account of this interference is also modified by the two-body contribution. In the right panel of Figure 4 the CC responses in ⁴He at momentum transfer |q| = 600 MeV are displayed. In analogy the NC case, we see that the enhancement given by the inclusion of two-body currents is present in all the different channels. However, in the longitudinal one it is not as significant as for the NC scattering. This has to be ascribed to the relative strength of the axial contribution to the total response which in this case is much smaller than the vector one.

FIGURE 4

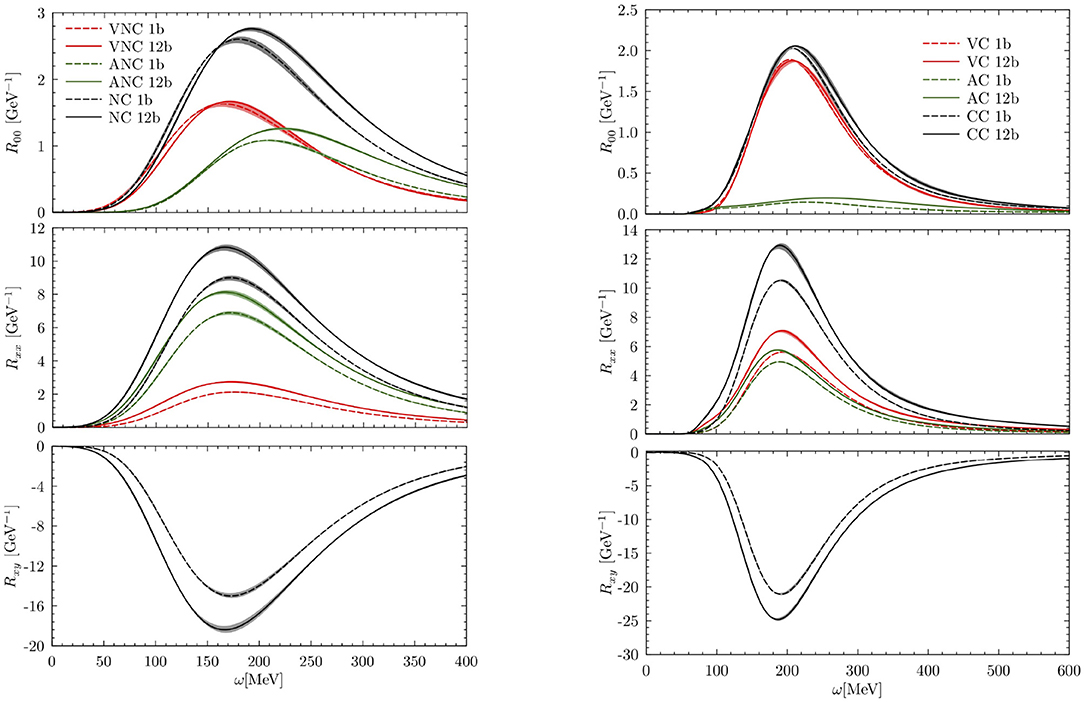
Figure 4. (Left) Adapted from Lovato et al. [26] under the Creative Commons CCBY license. Neutral-current response functions in ¹²C at momentum transfer |q| = 570 MeV obtained with one-body only (dashed lines) and one- and two-body (solid lines) currents. The vector and axial contribution corresponds to the red and green curves, the black curves display the full result in which the axial-vector interference is accounted for. The upper, middle, and lower panel corresponds to the charge, transverse and xy component of the response function. (Right) Charge-current response functions in ⁴He at momentum transfer |q| = 600 MeV. The different lines are the same as for the left panel.

4. Short Time Approximation

A novel approach to calculate the short-time propagation resulting from two- nucleon dynamics has been recently developed [28]. The STA method utilizes QMC techniques to evaluate path integrals of one- and two-nucleon currents in real time and predict the response function of nuclei in the quasielastic region. The expression of this response is reported in Equation (3) and can be rewritten as

$\begin{array}{l}{R}^{\mu \nu }(\text{q},\omega )={\displaystyle {\int }_{-\infty }^{\infty }}\frac{dt}{2\pi }{e}^{i(\omega +E_0-E_f)t}\\ {\displaystyle \sum _f}\langle {\text{Ψ}}_0\left|J^{\mu †}(\text{q},\omega )\right|{\text{Ψ}}_f\rangle \langle {\text{Ψ}}_f\left|J^{\nu }(\text{q},\omega )\right|{\text{Ψ}}_0\rangle \\ ={\displaystyle {\int }_{-\infty }^{\infty }}\frac{dt}{2\pi }{e}^{i(\omega +E_0)t}\langle {\text{Ψ}}_0\left|J^{\mu †}(\text{q},\omega )e^{-iHt}{J}^{\nu }(\text{q},\omega )\right|{\text{Ψ}}_0\rangle & (47)\end{array}$

where the sum over final states has been replaced with a real-time propagator. In the following, we drop the Lorentz indices to simplify the notation and replace J(q, ω) → J(q) with ω = ω_qe, the one- and two-body current operators utilized are the same as for the GFMC results [40]. The main assumption underlying the STA is that only the active pair of nucleons propagate, this qualitatively amounts to rewrite the final state as $\sum _f|{\text{Ψ}}_f\rangle \to \sum _{f^{\prime }{f}^{″}}|{\varphi }_{f^{\prime }}^2\rangle |{\text{Ψ}}_{f^{″}}^{A-2}\rangle$ where $|{\varphi }_{f^{\prime }}^2\rangle$ is the correlated two-nucleon state. To evaluate the response function, two completeness relations on the coordinate states are inserted, yielding

$\begin{array}{l}\langle {\text{Ψ}}_0\left|J^{\mu †}{e}^{-iHt}{J}^{\nu }\right|{\text{Ψ}}_0\rangle ={\displaystyle \int }d{r}_1\dots d{r}_{A}d{r}_1^{\prime }\dots d{r}_A^{\prime }\langle {\text{Ψ}}_0\left|J^{\mu †}\right|r_1\dots r_A\rangle \\ \times \langle r_1\dots r_A\left|e^{-iHt}\right|r_1^{\prime }\dots r_A^{\prime }\rangle \langle r_1^{\prime }\dots r_A^{\prime }\left|J^{\nu }\right|{\text{Ψ}}_0\rangle .& (48)\end{array}$

In the STA the current-current correlator is rewritten keeping the one- and two-body terms

$\begin{array}{l}{J}^{\mu †}{e}^{-iHt}{J}^{\nu }=({\displaystyle \sum _i}{j}^{\mu †}(i)+{\displaystyle \sum _{i<j}}{j}^{\mu †}(ij))e^{-iHt}({\displaystyle \sum _{i^{\prime }}}{j}^{\nu }(i^{\prime })\\ +{\displaystyle \sum _{i^{\prime }<j^{\prime }}}{j}^{\nu }(i^{\prime }{j}^{\prime }))\\ ={\displaystyle \sum _i}{j}^{\mu †}(i)e^{-iHt}{j}^{\nu }(i)+{\displaystyle \sum _{i\ne j}}{j}^{\mu †}(i)e^{-iHt}{j}^{\nu }(j)\\ +{\displaystyle \sum _{i\ne j}}(j^{\mu †}(i)e^{-iHt}{j}^{\nu }(ij)+j^{\mu †}(ij)e^{-iHt}{j}^{\nu }(i)\\ +j^{\mu †}(ij)e^{-iHt}{j}^{\nu }(ij))& (49)\end{array}$

the contributions with three or more active nucleons have been neglected. This amounts to include only two-nucleon interactions in the Hamiltonian; the A-nucleon particle propagator is approximated as

$\begin{array}{l}\langle r_1\dots r_A\left|e^{-iHt}\right|r_1^{\prime }\dots r_A^{\prime }\rangle =\langle r_1\dots r_A\left|e^{-i(H_{ij}^{\text{cm}}+H_{ij}^{\text{rel}}+H_{A-2})t}\right|r_1^{\prime }\dots r_A^{\prime }\rangle \\ =\langle R_{ij}\left|e^{-i{H}_{ij}^{\text{cm}}t}\right|R_{ij}^{\prime }\rangle \langle r_{ij}\left|e^{-i{H}_{ij}^{\text{rel}}t}\right|r_{ij}^{\prime }\rangle e^{-i{Ē}_{A-2}t}\\ {\displaystyle \prod _{k\ne i,j}^A}\delta (r_k-r_k^{\prime })& (50)\end{array}$

where $H_{ij}^{\text{cm}}={\text{P}}_{ij}^2/(4m_N)$ and $H_{ij}^{\text{rel}}={\text{p}}_{ij}^2/m_N+v_{ij}$. The A − 2 nucleons are treated as static spectators and their energy is assumed to be peaked around a constant value Ē_A−2.

We put the two equations together and define $j_L^{\mu †}{j}_R^{\nu }=\left(j^{\mu †}(i)j^{\nu }(j)+j^{\mu †}(i)j^{\nu }(ij)+j^{\mu †}(j)j^{\nu }(ij)\right)$ yielding

$\begin{array}{l}{R}^{\mu \nu }(\text{q},\omega )=\frac{A(A-1)}{2}{\displaystyle \int }dt{e}^{i(\omega +E_0-{Ē}_{A-2})t}\\ {\displaystyle \int }d{r}_{12}d{R}_{12}d{r}_{12}^{\prime }d{R}_{12}^{\prime }d{R}_{A-2}\langle {\text{Ψ}}_0\left|j_L^{\mu †}\right|r_{12}{R}_{12};R_{A-2}\rangle \\ \times \langle R_{12}\left|e^{-i{H}_{12}^{\text{cm}}t}\right|R_{12}^{\prime }\rangle \langle r_{12}\left|e^{-i{H}_{12}^{\text{rel}}t}\right|r_{12}^{\prime }\rangle \langle r_{12}^{\prime }{R}_{12}^{\prime };R_{A-2}\left|j_R^{\nu }\right|{\text{Ψ}}_0\rangle .& (51)\end{array}$

The two-nucleon propagator $\langle r_{12}\left|e^{-i{H}_{12}^{\text{rel}}t}\right|r_{12}^{\prime }\rangle$ is obtained by summing over the bound and continuum eigenstates of $H_{12}^{\text{rel}}$. Note that the interaction effects in the active pair are exactly accounted for. It is convenient to rewrite the STA response in terms of an integral over the relative- and center-of-mass energy of the pair as

$\begin{array}{ll}{R}^{\mu \nu }(\text{q},\omega )={\displaystyle {\int }_0^{\infty }}de{\displaystyle {\int }_0^{\infty }}d{E}_{\text{cm}}\delta (\omega +E_0-e-E_{\text{cm}})D^{\mu \nu }(e,E_{\text{cm}}).& (52)\end{array}$

Within the factorization scheme outlined above, interaction effects at the two-nucleon level are fully retained, and the interference between one- and two-body terms in the electromagnetic current operator are consistently accounted for. The low-energy properties of the system (discrete transition and collective excitation of the nucleus) and the correct energy threshold for the quasielastic region can not be described within the STA. For this reason, some corrections have to be introduced in order to recover the exact value of the threshold for the quasielastic scattering. In particular, the response density is folded with a gaussian kernel

$\begin{array}{ll}\tilde{D}(e^{\prime },E_{\text{cm}})={\displaystyle {\int }_0^{\infty }}deD(e,E_{\text{cm}})Nexp\{-[\frac{e^{\prime }-\omega (e)}{{\omega }_{\text{th}}}{]}^2\}& (53)\end{array}$

where $\omega (e)=\sqrt{e^2+{\omega }_{\text{th}}^{2}exp-e/\stackrel{-}{\omega }}$ and N is defined requiring that the sum rules are preserved

$\begin{array}{ll}{\displaystyle {\int }_0^{\infty }}deNexp\{-[\frac{e^{\prime }-\omega (e)}{{\omega }_{\text{th}}}{]}^2\}=1.& (54)\end{array}$

The two parameters controlling the shift and width of the gaussian folding are ω_th and $\stackrel{-}{\omega }$, respectively. The values chosen to reproduce the physical threshold of ~ 20 MeV of ⁴He are ω_th = 35 MeV and a 15 MeV width.

A comparison between the STA and GFMC electromagnetic response function of ⁴He is shown in Figure 5 for |q| = 300 and 500 MeV. The dashed line displays the STA results without any knowledge of the threshold while in the full red line the correct behavior at threshold has been enforced as explained in Equation (53). Including these corrections leads to a shift of the response toward larger values of the energy transfer and a redistribution of the strength; while for |q| = 300 MeV this effect is sizable the results at |q| = 500 are only slightly modified. In both configurations the STA results which include the shift accurately reproduce the GFMC ones.

FIGURE 5

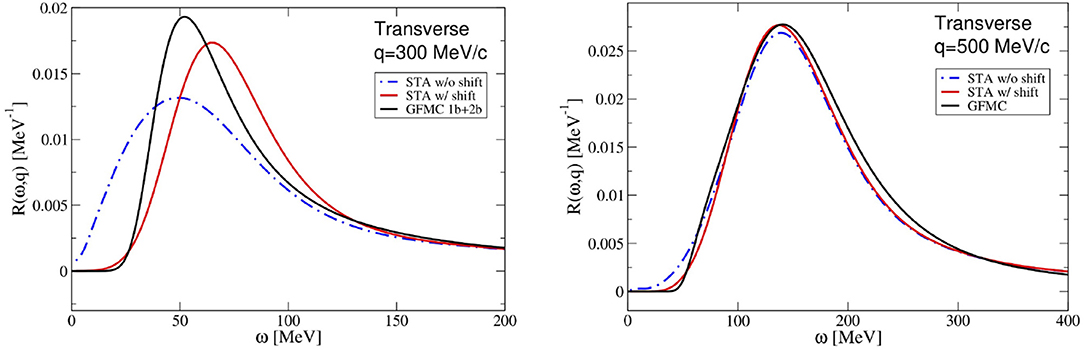
Figure 5. Transverse electromagnetic response of ⁴He obtained within the STA and GFMC approaches. The left and right panel corresponds to |q| = 300 and 500 MeV, respectively. The dashed (blue) and solid (red) lines are STA calculations prior and including the shift; the solid (black) line displays the GFMC results. Figure adapted from Pastore et al. [28].

The role played by final-state interactions within the pair is analyzed in the left panel of Figure 6 where the solid and dashed lines correspond to the transverse electromagnetic response of ⁴He obtained with and without interactions effects, respectively. Their inclusion leads to a visible shift in the position of the quasielastic peak toward left. The breakdown of the response into one-body current diagonal and off-diagonal terms, interference between one- and two-body currents, and two-body currents only, is also shown. It is interesting to note that the off-diagonal terms, routinely neglected in the IA scheme, provide a negative contribution depleting the response strength. In analogy with the GFMC findings, the interference between one-and two-body currents provides an important enhancement in the quasielastic region; contrary to the pure two-body current which does not provide a significant contribution to the response function in this kinematics. This is likely to be ascribed to the static limit adopted in both the GFMC and STA approaches to derive the non-relativistic expression of the Δ current. As discussed in Dekker et al. [72] in the static limit all energy dependence of the Δ propagator disappears and the resonance behavior in the dip region is not present.

FIGURE 6

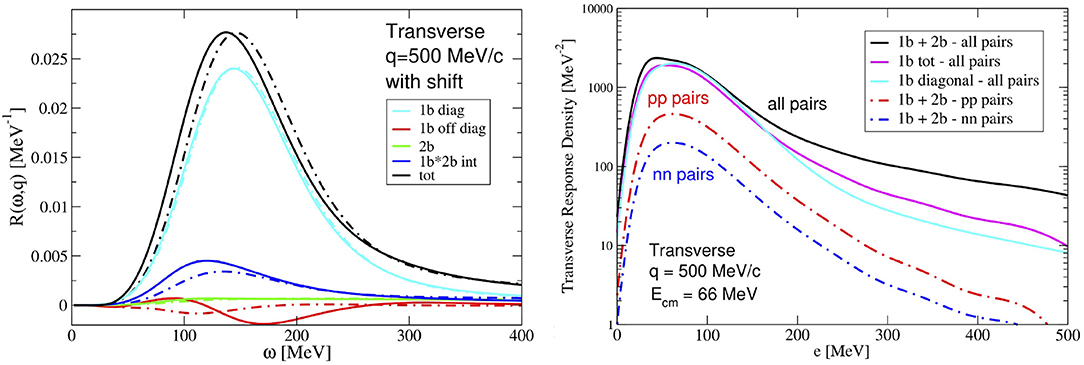
Figure 6. (Left) Transverse electromagnetic response of ⁴He at |q| = 500 MeV without (dashed lines) and with (solid lines) interacting two-nucleons in the final state. The different contributions corresponding to one-body current diagonal terms, one-body current off-diagonal terms, interference between one- and two-body currents, and two-body currents only are separately shown. (Right) Transverse response densities of ⁴He at |q| = 500 MeV and final center of mass energy $E_{\text{cm}}=|\text{q}{|}^2/(2m_N)$. The solid cyan and magenta solid line display the diagonal only and diagonal plus off-diagonal one-body term, respectively. The solid black curve corresponds to the total one- plus two-body current result while in the blue dashed and red dashed isolate the contribution of the nn and pp pairs is singled-out. Figure adapted from Pastore et al. [28].

The isospin dependence of pairs in the back-to-back kinematics, i.e., pairs with low initial center-of-mass momentum and high relative momentum, is studied in the right panel of Figure 6. These pairs can be singled-out in the response densities by requiring the pair center-of-mass momentum P being close to |q| and the relative momentum in the final state being large. Figure 6 displays the response densities at fixed energy $E_{\text{cm}}\simeq |\text{q}{|}^2/(4m_N)$ as a function of the relative energy of the pair e. The solid and dot-dashed curves have been obtained with and without interactions within the pair. The comparison between the full results (black line) and the one-body total (magenta line) shows that the two-nucleon currents do not provide a large contribution at low relative energies. While, the full result becomes substantially larger than the one-body current term for e ≥ 250 MeV. The back-to-back momentum distributions of np pairs are known to dominate over pp or nn pairs at high relative momenta because of tensor correlations as discussed in Schiavilla et al. [90]. In addition to that, the two-nucleon currents are almost entirely in the np pairs, and increase the response by roughly a factor of ~ 2 around at e = 300 MeV.

5. Extended Factorization Scheme

For large values of ω and |q|, a non-relativistic calculation of the hadron tensor is no longer reliable. Since both the final state and the transition currents depends upon the momentum transfer, relativity has to be properly accounted for. Factorizing the hadronic final state allows one to overcome these difficulties by providing a relativistic description of |Ψ_f〉 and of the current operator. In addition to that, realistic spectral functions are used to accurately model the dynamics of the target nucleus and account for correlation effects. We start by only retaining the one-body current terms and rewriting the hadronic final state as

$\begin{array}{ll}{J}^{\mu }={\displaystyle \sum _i}{j}^{\mu }(i),|{\text{Ψ}}_f\rangle \to |p\rangle \otimes |{\psi }_f^{A-1}\rangle & (55)\end{array}$

where |p〉 is a plane wave describing the propagation of the final-state nucleon with momentum |p| and energy $e(\text{p})=\sqrt{|\text{p}{|}^2+m_N^2}$, while $|{\psi }_f^{A-1}\rangle$ describes the (A − 1)-body spectator system. The energy and momentum of the latter are obtained by energy and momentum conservation relations

$\begin{array}{ll}{E}_f^{A-1}=\omega +E_0-e(\text{p}),{\text{P}}_f^{A-1}=\text{q}-\text{p}.& (56)\end{array}$

The incoherent contribution to the one-body hadron tensor can be easily obtained from Equation (55) and by inserting a single-nucleon completeness relation

$\begin{array}{l}{R}_{1\text{b}}^{\mu \nu }={\displaystyle \int }\frac{d^{3}k}{{(2\pi )}^3}dE{P}_h(\text{k},E)\frac{m_N^2}{e(\text{k})e(\text{k}+\text{q})}{\displaystyle \sum _i}\langle k\left|{j_i^{\mu }}^{†}\right|k+q\rangle \\ \langle k+q\left|j_i^{\nu }\right|k\rangle \delta (\tilde{\omega }+e(\text{k})-e(\text{k}+\text{q})),& (57)\end{array}$

where m_N is the rest mass of the initial nucleon. We introduced $\tilde{\omega }$ defined as $\tilde{\omega }=\omega -E+m_N-e(\text{k})$. To describe the scattering off a bound nucleon with momentum k, the four-momentum transfer employed in the hadronic tensor is replaced by $q=(\omega ,\text{q})\to \tilde{q}=(\tilde{\omega },\text{q})$. The factors m_N/e(k) and m_N/e(k + q) ensures the implicit covariant normalization of the nucleon quadri-spinors. The hole-spectral function P_h(k, E) provides the probability distribution of removing a nucleon with momentum k from the target nucleus, leaving the residual (A − 1)-nucleon system with an excitation energy E. The calculation of the spectral function of finite nuclei is a challenging problem that has seen the endeavor of multiple theory groups. In this work we will focus on the results obtained within the Correlated Basis Function and the Self Consistent Green's Function many-body methods, shortly outlined in section 5.1.

For low and moderate values of |q|, interactions between the struck particle and the spectator system become relevant. For this reason, the IA results must be modified to include them [30]. This is achieved by including in the energy spectrum of the propagating nucleon the real part of the optical potential U of Cooper et al. [91] which accounts for its interactions with the mean-field created by the residual system. This potential has to be evaluated for a given kinetic energy of the nucleon $t_{kin}(\text{p})=\sqrt{{\text{p}}^2+m^2}-m$, and modifies its energy as

$\begin{array}{ll}ẽ(\text{k}+\text{q})=e(\text{k}+\text{q})+U(t_{\text{kin}}(\text{k}+\text{q})).& (58)\end{array}$

The rescattering processes of the propagating nucleon are described by a convolution scheme which amounts to fold the IA responses with a function f_k+q, normalized as

$\begin{array}{ll}{\displaystyle {\int }_{-\infty }^{+\infty }}d\omega f_{\text{k}+\text{q}}(\omega )=1.& (59)\end{array}$

The one-body hadron tensor then reads

$\begin{array}{l}{R}_{1\text{b}}^{\mu \nu }{(q,\omega )}^{\text{FSI}}={\displaystyle \int \frac{d^{3}k}{{(2\pi )}^3}}dE{P}_h(k,E){\displaystyle \int d}{\omega }^{\prime }{f}_{k+q}(\omega -{\omega }^{\prime })\\ \frac{m_N^2}{e(k)e(k+q)}{\displaystyle \sum _i}\langle k\left|{j_i^{\mu }}^{†}\right|k+q\rangle \langle k+q\left|j_i^{\nu }\right|k\rangle \\ \times \delta ({\omega }^{\prime }+E-\tilde{e}(k+q))\theta (|k+q|-p_F).& (60)\end{array}$

where a generalization of the Glauber theory is utilized to derive the folding function [92]

$\begin{array}{l}{f}_{\text{p}}(\omega )=\delta (\omega )\sqrt{T_{\text{p}}}+{\displaystyle \int }\frac{dt}{2\pi }{e}^{i\omega t}\left[{Ū}_{\text{p}}^{FSI}(t)-\sqrt{T_{\text{p}}}\right]\\ =\delta (\omega )\sqrt{T_{\text{p}}}+(1-\sqrt{T_{\text{p}}})F_{\text{p}}(\omega ).& (61)\end{array}$

A more detailed discussion on how to obtain the nuclear transparency T_p and the finite width function F_p(ω) can be found in Benhar et al. [29] and Benhar et al. [93].

The inclusion of two body-currents requires an extension of the factorization ansatz of Equation (55). In Benhar et al. [34] and Rocco et al. [35, 36] the amplitudes involving two-nucleon currents have been included by rewriting the hadronic final state as

$\begin{array}{ll}|{\psi }_f^A\rangle \to |p{p}^{\prime }{\rangle }_a\otimes |{\psi }_f^{A-2}\rangle & (62)\end{array}$

where $|p{p}^{\prime }{\rangle }_a=|p{p}^{\prime }\rangle -|p^{\prime }p\rangle$ is the anti-symmetrized two-nucleon plane wave state. The two-body current component of the hadron tensor reads [34]

$\begin{array}{l}{W}_{\text{2b}}^{\mu \nu }(q,\omega )=\frac{V}{4}{\displaystyle \int d}E\frac{d^{3}k}{{(2\pi )}^3}\frac{d^3{k}^{\prime }}{{(2\pi )}^3}\frac{d^{3}p}{{(2\pi )}^3}\frac{m_N^4}{e(k)e(k^{\prime })e(p)e(p^{\prime })}{P}_h(k,k^{\prime },E)\\ \times 2{\displaystyle \sum _{ij}}{\langle k{k}^{\prime }\left|{j_{ij}^{\mu }}^{†}\right|p{p}^{\prime }\rangle }_a\langle p{p}^{\prime }\left|j_{ij}^{\nu }\right|k{k}^{\prime }\rangle \delta (\omega -E+2m_N-e(p)-e(p^{\prime })).& (63)\end{array}$

where $P_h(\text{k},{\text{k}}^{\prime },E)$ is a two-hole spectral function which in Benhar et al. [34] and Rocco et al. [35, 36] has been approximated as the product of the one-nucleon ones. Note that, while this is correct for infinite nuclear matter, its application to medium mass nuclei such as ¹²C is questionable and should be further investigated.

The production of real pions in the final state will be crucial for the correct understanding of the DUNE results. In order to include this reaction mechanism, we can write the hadronic final state as

$\begin{array}{ll}|{\psi }_f^A\rangle \to |p_{\pi }p\rangle \otimes |{\psi }_f^{A-1}\rangle ,& (64)\end{array}$

where p_π denotes both the four-momentum $(p_{\pi }^0,{\text{p}}_{\pi })$ and the isospin t_π of the emitted pion. In analogy with the one-body case reported in Equation (57), the one-body one-pion (1b1π) incoherent contribution to the hadron tensor is given by

$\begin{array}{l}{W}_{\text{1b1}\pi }^{\mu \nu }(q,\omega )={\displaystyle \int \frac{d^{3}k}{{(2\pi )}^3}}dE{P}_h(k,E)\frac{d^3{p}_{\pi }}{{(2\pi )}^3}\frac{m_N^2}{e(k)e(k+q-p_{\pi })}\\ {\displaystyle \sum _i}\langle k\left|{j_i^{\mu }}^{†}\right|p_{\pi }p\rangle \langle p_{\pi }p\left|j_i^{\nu }\right|k\rangle {|}_{p=k+q-p_{\pi }}\\ \times \delta (\omega -E+m_N-e(k+q-p_{\pi })-e_{\pi }(p_{\pi })),& (65)\end{array}$

where $e_{\pi }({\text{p}}_{\pi })=\sqrt{{\text{p}}^2+m_{\pi }^2}$ is the energy of the outgoing pion. The expression of $\tilde{\omega }$ is the same as for the one-body current process. In order to describe the real emission of a pion we need the transition amplitude between the initial one-nucleon state |k〉 to the pion-nucleon |p_πp〉 final state. These matrix elements have been obtained within the sophisticated dynamical couple-channel (DCC) model able to describe the πN → πN, γN → πN, and N(e, e′π)N reactions accounting for meson-baryon channels and nucleon resonances up to an invariant of W= 2 GeV. About 26,000 data points of the πN, γN → πN, ηN, KΛ, KΣ data from the channel thresholds to W ≤ 2.1 GeV have been fitted to obtain the parameters adopted within the DCC model. The extension to the electroweak sector has been recently performed [38].

Within the DCC model the following Hamiltonian is defined

$\begin{array}{ll}{H}_{\text{AO}}=H_0+{\displaystyle \sum _{c,c^{\prime }}}{v}_{c,c^{\prime }}+{\displaystyle \sum _{N^{*}}}{\displaystyle \sum _c}\left[{\Gamma }_{N^{*},c}+{\Gamma }_{N^{*},c}^{†}\right],& (66)\end{array}$

to generate the matrix element $\langle p_{\pi }p\left|j_i^{\nu }\right|k\rangle$ of Equation (65). In the above equation H₀ is the free Hamiltonian while the production of an N^* state from a meson-baryon channel c is described by the vertex ${\Gamma }_{N^{*},c}$. The energy independent meson-exchange potentials $v_{c,c^{\prime }}$–where c, c′ = γN, πN, ηN, KΛ, KΣ–are derived from phenomenological Lagrangians by using the unitary transformation method [94, 95]. This hamiltonian is used to generate $\langle p_{\pi }p\left|j_i^{\nu }\right|k\rangle$ of Equation (65). Convoluting the DCC elementary current matrix elements for π-production with the spectral function formalism allows to predict electroweak interactions of finite nuclei in large energy transfer region presented in section 5.2.

5.1. Determination of the Hole Spectral Function of Finite Nuclei

The accurate determination of SFs suitable to encompass both single-particle aspects and short-range dynamics is crucial for the theoretical description of lepton-nucleus scattering. Its definition can be given either in terms of nuclear overlaps or as the imaginary part of a two-point hole Green's Function

$\begin{array}{l}{P}_h(\text{k},E)={\displaystyle \sum _f}\left|\langle {\psi }_0^A\right|\left[|k\rangle \otimes |{\psi }_f^{A-1}\rangle \right]{|}^2\delta (E+E_f^{A-1}-E_0^A)\\ =\frac{1}{\pi }\text{Im}\langle {\psi }_0^A\left|a_{\text{k}}^{†}\frac{1}{E-(H-E_0^A)-iϵ}{a}_{\text{k}}\right|{\psi }_0^A\rangle .& (67)\end{array}$

Within the CBF, the hole SF of finite nuclei is written as a sum of two terms [31], $P_h(\text{k},E)=P_h^{\text{MF}}(\text{k},E)+P_h^{\text{corr}}(\text{k},E)$ displaying distinctly different energy and momentum dependences. The first term is associated to the low momentum and removal-energy region. The spectroscopic factor obtained from (e, e′p) scattering measurements are utilized to obtain the first term within a modified mean field (MF) picture. The correlated contribution $P_h^{\text{corr}}(\text{k},E)$ includes the unbound states of the A − 1 spectator system in which at least one of the spectator nucleons is in a continuum state. The local density approximation (LDA) is adopted to compute this term for finite nuclei

$\begin{array}{ll}{P}_h^{\text{corr}}(\text{k},E)={\displaystyle \int }{d}^{3}R{\rho }_A(\text{R})P_{h,NM}^{\text{corr}}(\text{k},E;{\rho }_A(\text{R})).& (68)\end{array}$

where the correlation component of the SF obtained within the CBF theory for isospin-symmetric nuclear matter for a given density ρ is convoluted with the density profile of the nucleus ρ_A(R). The applicability of the LDA in obtaining the correlation part of the SF in finite nuclei relies on the observation that short-range nuclear dynamics is not affected by surface and shell effects. This strength of $P_h^{\text{corr}}(\text{k},E)$ is concentrated in the high momentum and removal energy region as opposed to $P_h^{\text{MF}}(\text{k},E)$. For momenta larger than the Fermi one, the spectral function coincides with the correlation term.

The SCGF approach is a many-body approach which scales polynomially with the number of particle and allows reach nuclei with A up to ~100. The spectral function is determined within an ab initio theory starting from individual interactions among the nucleons. The central quantity of the SCGF formalism is the one-body Green's function which is directly related to the spectral function through $P_h(\text{k},E)=-\frac{1}{\pi }\text{Im}\left[G_h(\text{p},\text{p};\mu -E)\right]$, as expressed in the last equality in Equation (67). This is obtained by adopting an iterative procedure to solve the associated Dyson equation [96, 97] where the irreducible self-energy –which encodes nuclear medium effects in the particle [98]– explicitly depends on the propagator itself. To extend the predictive power of the approach to open shell nuclei, the SCGF has been recently reformulated within Gorkov's theory. The particle number is no longer conserved in this new formulation of the propagator in which a grand canonical Hamiltonian is utilized. Breaking of the particle-number symmetry allows one to include pairing correlations and eliminate the degeneracies that would otherwise prevent microscopic calculations for open-shell systems.

The results obtained for the neutron and proton spectral functions of ⁴⁰Ar, ⁴⁰Ca, and ⁴⁸Ti isotopes have been recently presented in Barbieri et al. [99]. The SCGF calculations are performed employing a spherical harmonic oscillator basis in a model space of 14 major shells and varying the frequency ℏΩ to study the uncertainties resulting from the truncation of the model space. The saturating chiral interactions at next to next to leading order (NNLO_sat) are utilized in order to correctly reproduce radii as well as charge density distributions of nuclei. In the left panel of Figure 7 the charge density profiles computed within the SCGF (solving the Gorkov's equations) or ⁴⁰Ca and ⁴⁰Ar are compared to experimental data from Emrich et al. [100] and Ottermann et al. [101]. The shaded area in the theoretical curves has been obtained by performing the calculation at the extremes of the range ℏΩ = 14 − 20 MeV–which from the analysis of Somá et al. [102] turns out to be the optimal one for the convergence of radii and energies– and taking the differences between the results. The authors of Barbieri et al. [99] interpreted this band as a conservative estimate for the theoretical errors due to model space convergence. The right panel of Figure 7 displays the computed hole (particle) P_h(p)(p, E) spectral function for neutron removal (addition) from ⁴⁰Ar.

FIGURE 7

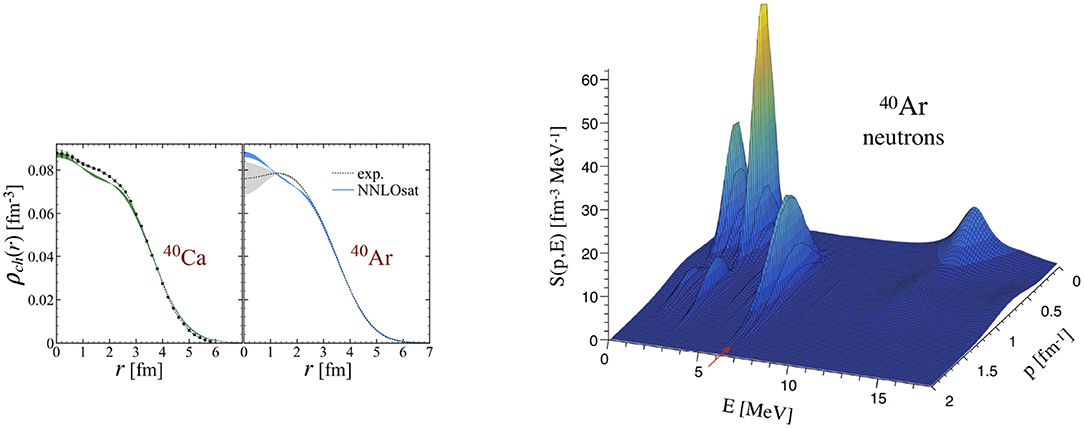
Figure 7. (Left) Results obtained SCGF approach are compared to experimental data (dotted lines and square points) from references Emrich et al. [100] and Ottermann et al. [101] for the charge density distributions of ⁴⁰Ca (left) and ⁴⁰Ar (right). The shaded areas represent the total experimental error, while the colored bands displays the theoretical uncertainties due to model-space convergence. (Right) Neutron spectral function of ⁴⁰Ar computed within the SCGF. The particle and hole spectral function corresponds to the region above and below the Fermi level E = 6.3 MeV, respectively, indicated by the red arrow.

In analogy with $P_h^{\text{MF}}(\text{k},E)$ introduced in the discussion of the CBF results, the peaks present at low E and k correspond to nucleons that occupy the valence shell close to the Fermi surface. In the high momentum and removal energy region, which is typically associated with short range correlation physics, the SCGF spectral function presents a mild tail (not shown in Figure 7). In this regards, it has to be noted that the CBF spectral function relies on the semi-phenomenological AV18 Hamiltonian, which naturally encompass short-range correlations. On the other hand, the NNLO_sat interaction is a relatively soft interaction, with a cutoff of 450 MeV which is able to produce tails for large values of the momentum. However, the strength in that region is significantly smaller than the one obtained using AV18 [103].

5.2. Results

In this section we present different scattering results obtained using the CBF and SCGF spectral function. In the left panel of Figure 8 we gauge the differences between the two spectral functions by comparing the results obtained for the double-differential cross section of electron-¹²C scattering at E_e = 620 MeV and ${\theta }_e=36^{°}$. In the theoretical results we focused on the quasielastic region, including only the one-body current operator of Equation (17). The dashed and solid curve correspond to the CBF and SCGF SFs, the blue and red lines have been obtained with and without including FSI effects. Calculations carried out employing the two different many-body approaches are in very nice agreement, although they are obtained from different nuclear interactions. FSI effects have been introduced following the procedure discussed in Equation (60). The overall effect is a shift in the position of the quasielastic peak to the left and a redistribution of the strength which leads to a correct reproduction of the experimental data. The right panel of Figure 8 shows the inclusive electron scattering on ⁴⁰Ar at the energy and kinematics of the E12-14-012 JLab experiment compared with the SCGF results with and without FSI displayed by the dot-dashed blue and solid red curve, respectively. The real part of the ⁴⁰Ca optical potential taken from Cooper et al. [106]–the one of Ar in not available in the literature–and the folding function of Benhar et al. [93] were adopted to obtain the FSI corrections. The prediction based on the NNLO _sat interaction and SCGF spectral function slightly underestimates the experimental data at the quasielastic peak. Overall, there is a small discrepancy which is compatible with the errors associated to the nuclear forces [54].

FIGURE 8

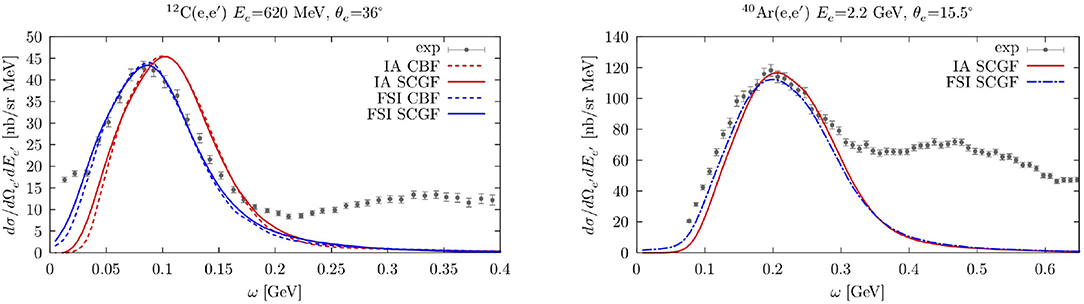
Figure 8. (Left) Inclusive ¹²C(e,e') cross sections at 620 MeV and 36° scattering angle. The solid and dashed curves correspond to the SCGF and CBF SF calculations, respectively. The red lines correspond to the IA calculation in which the outgoing nucleon is free while in the blue ones FSI corrections have been taken into account. (Right) Inclusive Ar(e,e') cross section at 2.2 GeV and 15.5° scattering angle. The solid (dashed) line shows the quasielastic cross section without (with) the inclusion of FSI obtained utilizing the SCGF spectral function calculations. Experimental data are taken from Dai et al. [104, 105] and show both the quasielastic peak and the contribution from meson production at larger missing energies.

The left panel of Figure 9 shows the double-differential electron-¹²C cross sections for E_e = 730 MeV, ${\theta }_e=37^{°}$. The theoretical results have been obtained using the CBF spectral function and correcting for FSI effects in the quasielastic region. The solid black line corresponds to the total cross section obtained summing up the contributions associated with the different reaction mechanisms. The dashed blue line displays the one-body current contribution while MEC leading to two-nucleon emission are given by the short-dashed red line. The dot-dashed magenta line corresponds to the emission of a real pion and a nucleon. A good agreement between theory and data is observed for the different kinematics analyzed. Note that, the strength associated with pion production is necessary to correctly reproduce the peak in the Δ-production region.

FIGURE 9

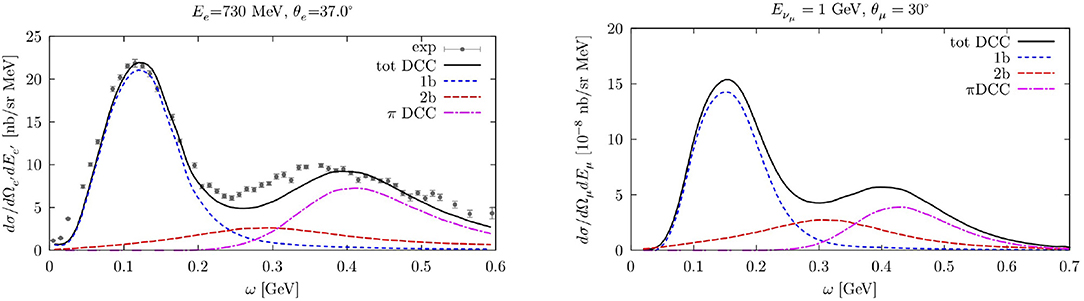
Figure 9. (Left) Inclusive ¹²C(e,e') cross sections at 730 MeV and 37° scattering angle. The short-dashed (blue) line and dashed (red) line correspond to one- and two-body current contributions, respectively. The dash-dotted (magenta) lines represent π production contributions. The solid (black) line is the total results obtained summing the three different terms. (Right) Same as left panel but for CC ν_μ scattering on ¹²C. The energy of the ν_μ is 1 GeV and the scattering angle is 30°.

The interference between one- and two-body currents has not yet been included. Although the authors of Benhar et al. [34] argue that the inclusion of this contribution within the factorization scheme leads to a small enhancement the dip region, the GFMC and STA calculations presented in sections 3 and 4 display a significant increase in the transverse response due to the interference contribution. Therefore, the consistent implementation of this term within the spectral function formalism is a necessary step to be undertaken in order to properly compare with the GFMC and STA results.

The results obtained for the double-differential CC ν_μ-¹²C scattering cross sections are shown in the right panel of Figure 9 for E_ν = 1 GeV, ${\theta }_{\mu }=30^{°}$. The calculations have been carried out within the same framework employed in the electromagnetic case, utilizing the CBF spectral function and including an axial term in all the current operators. In order to compare with experimental data a folding with the energy distribution of a given neutrino flux is needed.

6. Conclusions

The success of current- and next- generation of neutrino-oscillation experiments strongly depend on the availability of accurate nuclear physics calculations of the dynamics and electroweak interactions of nuclei with quantified theoretical uncertainties. This motivated the advent of many recent theoretical works focused on improving the description of lepton interactions with nuclei. In this review we outlined the main features of three different many-body approaches.

The GFMC is an ab-initio method which provides extremely accurate predictions for the electroweak response functions of nuclei up to ¹²C in which correlations are fully retained. In these results the strength and energy-dependence of two-nucleon processes induced by correlation effects and interaction currents provide a sizable contribution in the quasielastic region. The main limitations of this method come from its non-relativistic and fully inclusive nature, i.e., the transition to a given hadronic final state can not be easily identified. Choosing a reference frame that minimizes nucleon momenta allows to extend the applicability of GFMC to larger lepton energies, correctly reproducing experimental data for a large set of kinematics. For moderate values of momentum transfers, comparing the predictions based on more approximate schemes of nuclear dynamics with the accurate GFMC results in the quasielastic region is extremely important in order to test and validate them.

In the STA, two-nucleon physics is fully accounted for including ground-state correlations and final state interactions among the pair. Within this approach the interference between one- and two-nucleon current is included. When the physical threshold is enforced in the STA calculations, a very good agreement with the GFMC quasi-elastic response of light nuclei is observed for momentum transfers near and above the Fermi momentum.

The formalism based on IA and realistic SF combines a non-relativistic description of the target nucleus including realistic interactions with relativistic currents and kinematics. The results obtained utilizing two-different spectral functions corresponding to the CBF and SCGF calculations have been compared in the quasielastic region. The original formulation of the factorization scheme utilized in the IA only included one-nucleon matrix elements, its recent generalization allowed to include meson-exchange currents and pion-production mechanisms. The elementary amplitudes corresponding to pion-production processes were computed capitalizing on the sophisticated DCC model [37–39], which provides robust predictions up to an invariant mass of W ≤ 2.1 GeV. Theoretical calculations that include different reaction mechanisms are in good agreement with inclusive electron-scattering off ¹²C.

Over the last decade, we witnessed a great progress in the development of many-body techniques aimed at studying nuclear properties and interactions. These methods rely on nuclear EFT to consistently derive the nuclear Hamiltonian and many-body currents. Despite this success, their application on the broad energy region explored by oscillation experiments involves non-trivial difficulties that have to be explored and understood, such as how to transition to regions where resonance-production occur and how to correctly include relativistic effects. To address these points, models based on a factorization of the hadronic final state have been developed. Benchmark these models with the low-energy description provided by correct many-body calculations and understand the limit of validity of the approximations done will play a crucial role in providing robust predictions of neutrino-nucleus interactions.

Author Contributions

The author made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work has been supported by the U.S. DOE, Office of Science, 1811 Office of Nuclear Physics, under contract DE-AC02-06CH11357 1812, by the NUCLEI SciDAC program and by Fermi Research Alliance, LLC, under Contract No. DE- 1813 AC02-07CH11359 with the U.S. Department of Energy, Office of 1814 Science, Office of High Energy Physics.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author would like to thank her collaborators C. Barbieri, O. Benhar, T. S. H. Lee, W. Leidemann, A. Lovato, S. Nakamura, G. Orlandini, S. Pastore, and V. Soma' for their contributions to the studies presented in this work and for many valuable discussions.

References

1. Acciarri R, Adams C, An R, Andreopoulos C, Ankowski AM, Antonello M, et al. A Proposal for a Three Detector Short-Baseline Neutrino Oscillation Program in the Fermilab Booster Neutrino Beam. (2015).

Google Scholar

2. Abi B, Acciarri R, Acero MA, Adamowski M, Adams C, Adams D, et al. The DUNE Far Detector Interim Design Report Volume 1: Physics, Technology and Strategies. (2018). Available online at: https://lss.fnal.gov/archive/design/fermilab-design-2018-02.pdf

Google Scholar

3. Aguilar-Arevalo AA, Brown BC, Bugel L, Cheng G, Conrad JM, Cooper RL, et al. Significant excess of electronlike events in the MiniBooNE short-baseline neutrino experiment. Phys Rev Lett. (2018) 121:221801. doi: 10.1103/PhysRevLett.121.221801

PubMed Abstract | CrossRef Full Text | Google Scholar

4. The MicroBooNE Experiment. Available online at: http://www-microboone.fnal.gov

Google Scholar

5. The NOvA Experiment. Available online at: http://www-nova.fnal.gov

Google Scholar

6. The T2K Experiment. Available online at: http://t2k-experiment.org

Google Scholar

7. The MINERvA Experiment. Available online at: http://minerva.fnal.gov

Google Scholar

8. The Deep Underground Neutrino Experiment. Available online at: http://www.dunescience.org

Google Scholar

9. Hyper-Kamiokande. Available online at: http://www.hyperk.org

Google Scholar

10. Katori T, Martini M. Neutrino–nucleus cross sections for oscillation experiments. J Phys G. (2018) 45:013001. doi: 10.1088/1361-6471/aa8bf7

CrossRef Full Text | Google Scholar

11. Benhar O, Huber P, Mariani C, Meloni D. Neutrino–nucleus interactions and the determination of oscillation parameters. Phys Rept. (2017) 700:1–47. doi: 10.1016/j.physrep.2017.07.004

CrossRef Full Text | Google Scholar

12. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

13. Epelbaum E, Hammer HW, Meissner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

14. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

15. Machleidt R, Sammarruca F. Chiral EFT based nuclear forces: achievements and challenges. Phys Scripta. (2016) 91:083007. doi: 10.1088/0031-8949/91/8/083007

CrossRef Full Text | Google Scholar

16. Epelbaum E, Krebs H, Meiner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

17. van Kolck U. Few nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932–41. doi: 10.1103/PhysRevC.49.2932

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067. doi: 10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

19. Carlson J. Green's function Monte Carlo study of light nuclei. Phys Rev C. (1987) 36:2026–33. doi: 10.1103/PhysRevC.36.2026

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Carlson J. Alpha particle structure. Phys Rev C. (1988) 38:1879–85. doi: 10.1103/PhysRevC.38.1879

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lovato A, Gandolfi S, Butler R, Carlson J, Lusk E, Pieper SC, et al. Charge form factor and sum rules of electromagnetic response functions in ¹²C. Phys Rev Lett. (2013) 111:092501. doi: 10.1103/PhysRevLett.111.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Neutral weak current two-body contributions in inclusive scattering from ¹²C. Phys Rev Lett. (2014) 112:182502. doi: 10.1103/PhysRevLett.112.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Electromagnetic and neutral-weak response functions of ⁴He and ¹²C. Phys Rev C. (2015) 91:062501. doi: 10.1103/PhysRevC.91.062501

CrossRef Full Text | Google Scholar

24. Rocco N, Leidemann W, Lovato A, Orlandini G. Relativistic effects in ab-initio electron-nucleus scattering. Phys Rev C. (2018) 97:055501. doi: 10.1103/PhysRevC.97.055501

CrossRef Full Text | Google Scholar

25. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Electromagnetic response of ¹2C: a first-principles calculation. Phys Rev Lett. (2016) 117:082501. doi: 10.1103/PhysRevLett.117.082501

CrossRef Full Text | Google Scholar

26. Lovato A, Gandolfi S, Carlson J, Lusk E, Pieper SC, Schiavilla R. Quantum Monte Carlo calculation of neutral-current ν − ¹²C inclusive quasielastic scattering. Phys Rev C. (2018) 97:022502. doi: 10.1103/PhysRevC.97.022502

CrossRef Full Text | Google Scholar

27. Madeira L, Lovato A, Pederiva F, Schmidt KE. Quantum Monte Carlo formalism for dynamical pions and nucleons. Phys Rev C. (2018) 98:034005. doi: 10.1103/PhysRevC.98.034005

CrossRef Full Text | Google Scholar

28. Pastore S, Carlson J, Gandolfi S, Schiavilla R, Wiringa RB. Quasielastic Lepton Scattering and Back-to-Back Nucleons in the Short-Time Approximation. (2019).

Google Scholar

29. Benhar O, Day D, Sick I. Inclusive quasi-elastic electron-nucleus scattering. Rev Mod Phys. (2008) 80:189–224. doi: 10.1103/RevModPhys.80.189

CrossRef Full Text | Google Scholar

30. Ankowski AM, Benhar O, Sakuda M. Improving the accuracy of neutrino energy reconstruction in charged-current quasielastic scattering off nuclear targets. Phys Rev D. (2015) 91:033005. doi: 10.1103/PhysRevD.91.033005

CrossRef Full Text | Google Scholar

31. Benhar O, Fabrocini A, Fantoni S, Sick I. Spectral function of finite nuclei and scattering of GeV electrons. Nucl Phys A. (1994) 579:493–517. doi: 10.1016/0375-9474(94)90920-2

CrossRef Full Text | Google Scholar

32. Dickhoff WH, Barbieri C. Selfconsistent Green's function method for nuclei and nuclear matter. Prog Part Nucl Phys. (2004) 52:377–496. doi: 10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

33. Barbieri C, Carbone A. 11. In: Hjorth-Jensen M, Lombardo MP, van Kolck U, , editors. Self-Consistent Green's Function Approaches. Vol. 936 of Lect. Notes Phys. Cham: Springer International Publishing (2017). p. 571–644. doi: 10.1007/978-3-319-53336-0_11

CrossRef Full Text | Google Scholar

34. Benhar O, Lovato A, Rocco N. Contribution of two-particle–two-hole final states to the nuclear response. Phys Rev C. (2015) 92:024602. doi: 10.1103/PhysRevC.92.024602

CrossRef Full Text | Google Scholar

35. Rocco N, Lovato A, Benhar O. Unified description of electron-nucleus scattering within the spectral function formalism. Phys Rev Lett. (2016) 116:192501. doi: 10.1103/PhysRevLett.116.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rocco N, Barbieri C, Benhar O, De Pace A, Lovato A. Neutrino-nucleus cross section within the extended factorization scheme. Phys Rev C. (2019) 99:025502. doi: 10.1103/PhysRevC.99.025502

CrossRef Full Text | Google Scholar

37. Kamano H, Nakamura SX, Lee TSH, Sato T. Nucleon resonances within a dynamical coupled-channels model of πN and γN reactions. Phys Rev C. (2013) 88:035209. doi: 10.1103/PhysRevC.88.035209

CrossRef Full Text | Google Scholar

38. Nakamura SX, Kamano H, Sato T. Dynamical coupled-channels model for neutrino-induced meson productions in resonance region. Phys Rev D. (2015) 92:074024. doi: 10.1103/PhysRevD.92.074024

CrossRef Full Text | Google Scholar

39. Kamano H, Nakamura SX, Lee TSH, Sato T. Isospin decomposition of γN→N^* transitions within a dynamical coupled-channels model. Phys Rev C. (2016) 94:015201. doi: 10.1103/PhysRevC.94.015201

CrossRef Full Text | Google Scholar

40. Shen G, Marcucci LE, Carlson J, Gandolfi S, Schiavilla R. Inclusive neutrino scattering off the deuteron from threshold to GeV energies. Phys Rev C. (2012) 86:035503. doi: 10.1103/PhysRevC.86.035503

CrossRef Full Text | Google Scholar

41. Benhar O, Meloni D. Total neutrino and antineutrino nuclear cross-sections around 1-GeV. Nucl Phys A. (2007) 789:379–402. doi: 10.1016/j.nuclphysa.2007.02.015

CrossRef Full Text | Google Scholar

42. Nakamura K, Particle Data Group. Review of particle physics. J Phys G. (2010) 37:075021. doi: 10.1088/0954-3899/37/7A/075021

CrossRef Full Text | Google Scholar

43. Herczeg P, Hoffman CM, Klapdor-Kleingrothaus HV. In: Physics Beyond the Standard Model. (1999). p. 1–802. Available online at: https://www.worldscientific.com/doi/abs/10.1142/9789814527514

Google Scholar

44. Benhar O, Day D, Sick I. An Archive for Quasi-Elastic Electron-Nucleus Scattering Data. (2006). Available online at: https://arxiv.org/pdf/nucl-ex/0603032.pdf

Google Scholar

45. Wiringa RB, Stoks VGJ, Schiavilla R. An Accurate nucleon-nucleon potential with charge independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Pieper SC, Pandharipande VR, Wiringa RB, Carlson J. Realistic models of pion exchange three nucleon interactions. Phys Rev C. (2001) 64:014001. doi: 10.1103/PhysRevC.64.014001

CrossRef Full Text | Google Scholar

47. Gandolfi S, Carlson J, Pieper SC. Cold neutrons trapped in external fields. Phys Rev Lett. (2011) 106:012501. doi: 10.1103/PhysRevLett.106.012501

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Maris P, Vary JP, Gandolfi S, Carlson J, Pieper SC. Properties of trapped neutrons interacting with realistic nuclear Hamiltonians. Phys Rev C. (2013) 87:054318. doi: 10.1103/PhysRevC.87.054318

CrossRef Full Text | Google Scholar

49. Gandolfi S, Lovato A, Carlson J, Schmidt KE. From the lightest nuclei to the equation of state of asymmetric nuclear matter with realistic nuclear interactions. Phys Rev C. (2014) 90:061306. doi: 10.1103/PhysRevC.90.061306

CrossRef Full Text | Google Scholar

50. Buraczynski M, Gezerlis A. Ab initio and phenomenological studies of the static response of neutron matter. Phys Rev C. (2017) 95:044309. doi: 10.1103/PhysRevC.95.044309

CrossRef Full Text | Google Scholar

51. Epelbaum E, Krebs H, Meissner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Ekstrom A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

53. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004

CrossRef Full Text | Google Scholar

54. Hebeler K, Holt JD, Menéndez J, Schwenk A. Nuclear forces and their impact on neutron-rich nuclei and neutron-rich matter. Annu Rev Nucl Part Sci. (2015) 65:457–84. doi: 10.1146/annurev-nucl-102313-025446

CrossRef Full Text | Google Scholar

55. Gezerlis A, Tews I, Epelbaum E, Gandolfi S, Hebeler K, Nogga A, et al. Quantum Monte Carlo calculations with chiral effective field theory interactions. Phys Rev Lett. (2013) 111:032501. doi: 10.1103/PhysRevLett.111.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev C. (2014) 90:054323. doi: 10.1103/PhysRevC.90.054323

CrossRef Full Text | Google Scholar

57. Piarulli M, Girlanda L, Schiavilla R, Pérez RN, Amaro JE, Arriola ER. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C. (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

58. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C. (2016) 94:054007. doi: 10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

59. Aguilar-Arevalo AA, Anderson CE, Bazarko AO, Brice SJ, Brown BC, Bugel L, et al. First measurement of the muon neutrino charged current quasielastic double differential cross section. Phys Rev D. (2010) 81:092005. doi: 10.1103/PhysRevD.81.092005

CrossRef Full Text | Google Scholar

60. Bernard V, Elouadrhiri L, Meissner UG. Axial structure of the nucleon: topical review. J Phys G. (2002) 28:R1–35. doi: 10.1088/0954-3899/28/1/201

CrossRef Full Text | Google Scholar

61. Gupta R, Jang YC, Lin HW, Yoon B, Bhattacharya T. Axial vector form factors of the nucleon from lattice QCD. Phys Rev D. (2017) 96:114503. doi: 10.1103/PhysRevD.96.114503

CrossRef Full Text | Google Scholar

62. Meyer AS, Betancourt M, Gran R, Hill RJ. Deuterium target data for precision neutrino-nucleus cross sections. Phys Rev D. (2016) 93:113015. doi: 10.1103/PhysRevD.93.113015

CrossRef Full Text | Google Scholar

63. Carlson J, Schiavilla R. Structure and dynamics of few-nucleon systems. Rev Mod Phys. (1998) 70:743–841. doi: 10.1103/RevModPhys.70.743

CrossRef Full Text | Google Scholar

64. Pastore S, Schiavilla R, Goity JL. Electromagnetic two-body currents of one- and two-pion range. Phys Rev C. (2008) 78:064002. doi: 10.1103/PhysRevC.78.064002

CrossRef Full Text | Google Scholar

65. Pastore S, Girlanda L, Schiavilla R, Viviani M, Wiringa RB. Electromagnetic currents and magnetic moments in (chi)EFT. Phys Rev C. (2009) 80:034004. doi: 10.1103/PhysRevC.80.034004

CrossRef Full Text | Google Scholar

66. Pastore S, Girlanda L, Schiavilla R, Viviani M. The two-nucleon electromagnetic charge operator in chiral effective field theory (χEFT) up to one loop. Phys Rev C. (2011) 84:024001. doi: 10.1103/PhysRevC.84.024001

CrossRef Full Text | Google Scholar

67. Kolling S, Epelbaum E, Krebs H, Meissner UG. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys Rev C. (2009) 80:045502. doi: 10.1103/PhysRevC.80.045502

CrossRef Full Text | Google Scholar

68. Kolling S, Epelbaum E, Krebs H, Meissner UG. Two-nucleon electromagnetic current in chiral effective field theory: one-pion exchange and short-range contributions. Phys Rev C. (2011) 84:054008. doi: 10.1103/PhysRevC.84.054008

CrossRef Full Text | Google Scholar

69. Krebs H, Epelbaum E, Meissner UG. Nuclear axial current operators to fourth order in chiral effective field theory. Ann Phys. (2017) 378:317–95. doi: 10.1016/j.aop.2017.01.021

CrossRef Full Text | Google Scholar

70. Baroni A, Schiavilla R. Inclusive neutrino scattering off the deuteron at low energies in chiral effective field theory. Phys Rev C. (2017) 96:014002. doi: 10.1103/PhysRevC.96.014002

CrossRef Full Text | Google Scholar

71. Baroni A, Schiavilla R, Marcucci LE, Girlanda L, Kievsky A, Lovato A, et al. Local chiral interactions, the tritium Gamow-Teller matrix element, and the three-nucleon contact term. Phys Rev C. (2018) 98:044003. doi: 10.1103/PhysRevC.98.044003

CrossRef Full Text | Google Scholar

72. Dekker MJ, Brussaard PJ, Tjon JA. Relativistic meson exchange and isobar currents in electron scattering: Noninteracting Fermi gas analysis. Phys Rev C. (1994) 49:2650–70. doi: 10.1103/PhysRevC.49.2650

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Schiavilla R, Pandharipande VR, Riska DO. Magnetic form factors of the trinucleons. Phys Rev C. (1989) 40:2294–309. doi: 10.1103/PhysRevC.40.2294

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Bacca S, Pastore S. Electromagnetic reactions on light nuclei. J Phys G. (2014) 41:123002. doi: 10.1088/0954-3899/41/12/123002

CrossRef Full Text | Google Scholar

75. Ruiz Simo I, Amaro JE, Barbaro MB, De Pace A, Caballero JA, Donnelly TW. Relativistic model of 2p-2h meson exchange currents in (anti)neutrino scattering. J Phys G. (2017) 44:065105. doi: 10.1088/1361-6471/aa6a06

CrossRef Full Text | Google Scholar

76. Hernandez E, Nieves J, Valverde M. Weak pion production off the nucleon. Phys Rev D. (2007) 76:033005. doi: 10.1103/PhysRevD.76.033005

CrossRef Full Text | Google Scholar

77. De Pace A, Nardi M, Alberico WM, Donnelly TW, Molinari A. The 2p-2h electromagnetic response in the quasielastic peak and beyond. Nucl Phys A. (2003) 726:303–26. doi: 10.1016/S0375-9474(03)01625-7

CrossRef Full Text | Google Scholar

78. Efros VD, Leidemann W, Orlandini G. Electromagnetic few-body response functions with the Lorentz integral transform method. Few Body Syst. (1999) 26:251–69. doi: 10.1007/s006010050118

CrossRef Full Text | Google Scholar

79. Reiss C, Leidemann W, Orlandini G, Tomusiak EL. Application of the Lorentz transform technique to meson photoproduction. Eur Phys J A. (2003) 17:589–94. doi: 10.1140/epja/i2003-10027-1

CrossRef Full Text | Google Scholar

80. Leidemann W. Electromagnetic reactions of few-body systems with the Lorentz integral transform method. Nucl Phys A. (2007) 790:24–9. doi: 10.1016/j.nuclphysa.2007.03.052

CrossRef Full Text | Google Scholar

81. Yuan L, Leidemann W, Efros VD, Orlandini G, Tomusiak EL. Transverse electron scattering response function of ³He in the quasi-elastic peak region and beyond with—isobar degrees of freedom. Phys Lett B. (2011) 706:90–3. doi: 10.1016/j.physletb.2011.10.066

CrossRef Full Text | Google Scholar

82. Bacca S, Barnea N, Leidemann W, Orlandini G. Role of final state interaction and of three-body force on the longitudinal response function of He-4. Phys Rev Lett. (2009) 102:162501. doi: 10.1103/PhysRevLett.102.162501

CrossRef Full Text | Google Scholar

83. Bacca S, Miorelli M, Hagen G. Electromagnetic reactions from coupled-cluster theory. J Phys Conf Ser. (2018) 966:012019. doi: 10.1088/1742-6596/966/1/012019

CrossRef Full Text | Google Scholar

84. Xu T, Miorelli M, Bacca S, Hagen G. A theoretical approach to electromagnetic reactions in light nuclei. EPJ Web Conf . (2016) 113:04016. doi: 10.1051/epjconf/201611304016

CrossRef Full Text | Google Scholar

85. Simonis J, Bacca S, Hagen G. First principles electromagnetic responses in medium-mass nuclei. Eur Phys J A. (2019) 55:241. doi: 10.1140/epja/i2019-12825-0

CrossRef Full Text | Google Scholar

86. Lovato A, Rocco N, Schiavilla R. Muon capture in nuclei: An ab initio approach based on Green's function Monte Carlo methods. Phys Rev C. (2019) 100:035502. doi: 10.1103/PhysRevC.100.035502

CrossRef Full Text | Google Scholar

87. Pieper SC. The Illinois extension to the Fujita-Miyazawa three-nucleon force. AIP Conf Proc. (2008) 1011:143–52. doi: 10.1063/1.2932280

CrossRef Full Text | Google Scholar

88. Carlson J, Jourdan J, Schiavilla R, Sick I. Longitudinal and transverse quasielastic response functions of light nuclei. Phys Rev C. (2002) 65:024002. doi: 10.1103/PhysRevC.65.024002

CrossRef Full Text | Google Scholar

89. Efros VD, Leidemann W, Orlandini G, Tomusiak EL. Improved (e, e′) response functions at intermediate momentum transfers: the ³He case. Phys Rev C. (2005) 72:011002. doi: 10.1103/PhysRevC.72.011002

CrossRef Full Text | Google Scholar

90. Schiavilla R, Wiringa RB, Pieper SC, Carlson J. Tensor forces and the ground-state structure of nuclei. Phys Rev Lett. (2007) 98:132501. doi: 10.1103/PhysRevLett.98.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Cooper ED, Hama S, Clark BC, Mercer RL. Global Dirac phenomenology for proton nucleus elastic scattering. Phys Rev C. (1993) 47:297–311. doi: 10.1103/PhysRevC.47.297

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Benhar O, Fabrocini A, Fantoni S, Miller GA, Pandharipande VR, Sick I. Scattering of GeV electrons by nuclear matter. Phys Rev C. (1991) 44:2328–42. doi: 10.1103/PhysRevC.44.2328

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Benhar O. Final state interactions in the nuclear response at large momentum transfer. Phys Rev C. (2013) 87:024606. doi: 10.1103/PhysRevC.87.024606

CrossRef Full Text | Google Scholar

94. Sato T, Lee TSH. Meson exchange model for pi N scattering and gamma N –> pi N reaction. Phys Rev C. (1996) 54:2660–84. doi: 10.1103/PhysRevC.54.2660

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Kobayashi M, Sato T, Ohtsubo H. Effective interactions for mesons and baryons in nuclei. Prog Theor Phys. (1997) 98:927–51. doi: 10.1143/PTP.98.927

CrossRef Full Text | Google Scholar

96. Barbieri C, Hjorth-Jensen M. Quasiparticle and quasihole states of nuclei around Ni-56. Phys Rev C. (2009) 79:064313. doi: 10.1103/PhysRevC.79.064313

CrossRef Full Text | Google Scholar

97. Cipollone A, Barbieri C, Navratil P. Isotopic chains around oxygen from evolved chiral two- and three-nucleon interactions. Phys Rev Lett. (2013) 111:062501. doi: 10.1103/PhysRevLett.111.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Dickhoff WH, Van Neck D. Many-Body Theory Exposed! 2nd ed. London: World Scientific Publishing (2008).

Google Scholar

99. Barbieri C, Rocco N, Soma V. Lepton scattering from ⁴0Ar and Ti in the quasielastic peak region. Phys Rev C. (2019) 100:062501. doi: 10.1103/PhysRevC.100.062501

CrossRef Full Text | Google Scholar

100. Emrich HJ, Fricke G, Mallot G, Miska H, Sieberling HG, Cavedon JM, et al. Radial distribution of nucleons in the isotopes 48,40ca. Nucl Phys A. (1983) 396:401–8. doi: 10.1016/0375-9474(83)90034-9

CrossRef Full Text | Google Scholar

101. Ottermann CR, Schmitt C, Simon GG, Borkowski F, Walther VH. Elastic electron scattering from 40Ar. Nucl Phys A. (1982) 379:396–406. doi: 10.1016/0375-9474(82)90004-5

CrossRef Full Text | Google Scholar

102. Somá V, Navrátil P, Raimondi F, Barbieri C, Duguet T. Novel chiral Hamiltonian and observables in light and medium-mass nuclei. Phys Rev C. (2019) 101:014318. doi: 10.1103/PhysRevC.101.014318

CrossRef Full Text | Google Scholar

103. Rocco N, Barbieri C. Inclusive electron-nucleus cross section within the self-consistent Green's function approach. Phys Rev C. (2018) 98:025501. doi: 10.1103/PhysRevC.98.025501

CrossRef Full Text | Google Scholar

104. Dai H, Murphy M, Pandey V, Abrams D, Nguyen D, Aljawrneh B, et al. First measurement of the Ti(e, e′)X cross section at Jefferson Lab. Phys Rev C. (2018) 98:014617. doi: 10.1103/PhysRevC.98.014617

CrossRef Full Text | Google Scholar

105. Dai H, Murphy M, Pandey V, Abrams D, Nguyen D, Aljawrneh B, et al. First measurement of the Ar(e, e′)X cross section at Jefferson Laboratory. Phys Rev C. (2019) 99:054608. doi: 10.1103/PhysRevC.99.054608

CrossRef Full Text | Google Scholar

106. Cooper ED, Clark BC, Kozack R, Shim S, Hama S, Johansson JI, et al. Global optical potentials for elastic P+⁴ 0Ca scattering using the Dirac equation. Phys Rev C. (1987) 36:2170–2. doi: 10.1103/PhysRevC.36.2170

PubMed Abstract | CrossRef Full Text | Google Scholar