Heat Transfer Analysis for Non-linear Boundary Driven Flow Over a Curved Stretching Sheet With a Variable Magnetic Field

A 2-D boundary-layer flow induced by non-linear (quadratic) stretching of a curved surface of an incompressible MHD viscous fluid is investigated. Heat transfer analysis is presented including viscous dissipation and thermal radiation. A radially variable magnetic field is applied that satisfies Maxwell's equation and incorporates the curvature effects. A new similarity variable and similarity transformation are introduced to reduce the governing PDE's into ODE's. A numerical procedure is adopted to find the solution of momentum and energy equations. The numerical scheme is validated with the existing data. The results are illustrated graphically and discussed physically. Comparison with the literature shows a significant improvement compared to existing studies.

Introduction

Stretching is one of the most important mechanisms for boundary driven flows. Crane [1] was the first to present an exact analytical solution for linear stretching on a flat plate. Since then a lot of theoretical and numerical studies have been conducted with applications in the polymer industry and engineering processes. Linear stretching was extended to non-linear and exponential stretching velocities for plane surfaces and tubes in Newtonian and non-Newtonian fluids [2–13]. The stretching of curved surfaces is now being studied for its mathematical interest as a method for solving non-linear governing equations in curvilinear coordinates and for understanding boundary driven flow behavior and generalized flow geometry. As the body of literature about stretching is so large it cannot be cited here, we will focus on curved surfaces only. Sajid et al. [14] was first to introduce the concept of flow due to the linear stretching of the curved surface in a Newtonian fluid. They concluded that the velocity decreases as the radius of curvature increases, or the velocity and the boundary layer thickness increase for the curved surface in comparison with the flat surface. In addition, the pressure gradient is variable contrary to the constant pressure gradient for the flat surface. Sanni et al. [15] discussed non-linear power law stretching velocity. Magnetohydrodynamic (MHD) flow over a curved linear stretching surface with heat transferred to an electrically conducting fluid in the presence of a transversely applied magnetic field was presented by Abbas et al. [16]. We observe that the studies for MHD flow in the curvilinear geometry are normally undertaken using a uniform magnetic field [17–24]. However, we find that the magnetic field must be such that it satisfies the solenoidal property (div B = 0). Hence, the assumption of a uniform magnetic field is valid for a rectangular coordinate system but not for curvilinear coordinates. Variable magnetic fields are used for the treatment of peptic ulcers, medical diagnosis and in medical therapeutic techniques. In industry, the growing of pure crystal semiconductors can be controlled using a variable magnetic field [25, 26]. Some other papers about curved structures also include: Reddy et al. [27] which analyzed a dual solution of nanofluid flow due to a curved stretching surface under the influence of non-linear radiation. The flow of a nanofluid with carbon nanotubes caused by a curved stretching surface, with internal heat generation, is examined by Saba et al. [28]. Naveed et al. [29] documented dual solutions of MHD viscous fluid flow past a shrinking curved surface. Hayat et al. [30] discussed a numerical solution for hydromagnetic fluid flow under Soret and Dufour effects. In the presence of variable viscosity and carbon nanotubes, Nadeem et al. [31] investigated an MHD nanofluid over a curved stretching surface. For the solution methodology, new similarities have been defined which take into account the effects of both linear and non-linear stretching velocities. In the literature, the similarity for the non-linear stretching velocity is defined in a way that takes care of the linear part only. We believe that it results in incomplete governing equations and incomplete results missing out the effects of the non-linear part. This motivates us to define a new similarity transformation, resulting in the complete set of governing equations and improved results which addresses the non-linear part of the velocity as well. Mathematically, the objective of the present study has been to formulate the Lorentz force for variable magnetic field in the curvilinear coordinates and to redefine the similarity transformation to improve upon the results of the non-linear stretching velocity for a flat surface. This is accomplished for the flow and heat transfer analysis over the non-linear stretching of a curved surface in an electrically conducting viscous fluid in the presence of a variable magnetic field. The important observations are that the velocity induced by the boundary decreases as the the magnetic field and the radius of curvature increases. Thus, the flow field and the boundary layer thickness can be maintained with the help of these parameters. The non-linear contribution of the boundary velocity has more significant effect than the linear part. Detailed consequences of this study are discussed in the last section.

Problem Formulation

Consider the steady two-dimensional boundary-layer flow and heat transfer for an incompressible hydromagnetic viscous fluid moving over a curved surface. The flow is induced by a non-linear (quadratic) stretching velocity of the form ax + bx² (a and b being the dimensional constants), and the energy equation includes the viscous dissipation and thermal radiation. A variable applied magnetic field, given as $B(r)=R{B}_o(R+r{)}^{-1}{\widehat{e}}_r$, is acting in the radial direction compared to the curved surface. The variable magnetic field is taken on purpose to make it consistent with Maxwell's equation (∇.B = 0). The governing equations are modeled using curvilinear coordinates. The Lorentz force F = J × B and the current density J in the absence of an electrical current (E = 0) are expressed as:

$\begin{array}{ll}J=\sigma (\text{V }\times \text{ B})& (1)\end{array}$

$\begin{array}{ll}F=(-\sigma R{B}_o(R+r{)}^{-1}u,0,0).& (2)\end{array}$

We observe that an electrically conducting fluid transverses a curved path along the stretching surface (instead of in a linear direction), and the magnetic field is perpendicular to the flow direction. Using Equaion (1), the Lorentz force takes the form $F=(-\sigma R{B}_o(R+r{)}^{-1}u,0,0)$ which takes a constant value as R goes to infinity. In the above equation, σ is the electrical conductivity of the fluid, ${\widehat{e}}_r$ is the unit vector in the radial direction and B_o is the strength of the applied magnetic field; whereas u and v are the components of velocity field in the x− and r−directions. The geometry of the flow is given in Figure 1.

FIGURE 1

Figure 1. Physical geometry of the problem.

The boundary layer equations [16] in the presence of a variable magnetic field can be given as follows:

$\begin{array}{ll}{\partial }_r\left[(R+r)v\right]=-R{\partial }_{x}u& (3)\end{array}$

$\begin{array}{c}v{\partial }_{r}u+\frac{Ru}{R+r}{\partial }_{x}u+\frac{uv}{R+r}=-\frac{1}{\rho }\frac{R}{R+r}{\partial }_{x}P\\ +\upsilon \left\{\left(\frac{1}{R+r}{\partial }_r\left[(R+r){\partial }_{r}u\right]\right)-\frac{u}{{(R+r)}^2}\right\}-\frac{\sigma B_0^2{R}^2}{\rho {(R+r)}^2}u& (4)\end{array}$

$\begin{array}{ll}\frac{u^2}{R+r}=\frac{1}{\rho }{\partial }_{r}P& (5)\end{array}$

$\begin{array}{l}v{\partial }_{r}T+\frac{Ru}{R+r}{\partial }_{x}T=\frac{K}{\rho C_p}\{\frac{1}{R+r}{\partial }_r[(R+r){\partial }_{r}T\}\\ +\frac{u}{\rho C_p}{\left({\partial }_{r}u-\frac{u}{R+r}\right)}^2-\frac{1}{\rho C_p}{\partial }_r{q}_w+\frac{\sigma R^2}{\rho C_p{(R+r)}^2}{u}^2,& (6)\end{array}$

where u is the viscosity of the fluid, ρ is the fluid density, p is the pressure, T_w is the temperature of the surface at γ = 0, T_∞ is the ambient temperature, K is the thermal conductivity of the fluid, C_p is specific heat of the fluid at constant pressure, and q_w is the heat flux.

The boundary conditions for all $a,b\in {R}$ satisfied by the velocity and the temperature fields are:

$\begin{array}{ll}{u}_w=ax+b{x}^2,v=v_w=0,T=T_{w}atr=0& (7)\end{array}$

$\begin{array}{ll}u=0,{\partial }_{r}u=0,T\to T_{\infty }asr\to \infty .& (8)\end{array}$

In Equation (7), a and b determine the strength of the linear and non-linear parts of the stretching velocity, respectively.

The similarity variables given in [2–4] are revisited and modified for generalized curvilinear coordinates to include both a linear and non-linear part. These are now defined as:

$\begin{array}{r}\gamma =r{\left\{\frac{a+bx}{\upsilon }\right\}}^{\frac{1}{2}},=ax{g}^{\prime }\left(\gamma \right)+b{x}^2{h}^{\prime }\left(\gamma \right),\\ R=k{\left\{\frac{\upsilon }{a+bx}\right\}}^{\frac{1}{2}},p=\rho u_w^{2}P\left(\eta \right)& (9)\end{array}$

$\begin{array}{r}v=-\frac{R}{R+r}{\left\{\frac{\upsilon }{a+bx}\right\}}^{\frac{1}{2}}\{\left[ag\left(\gamma \right)+2bxh\left(\gamma \right)\right]\\ +\frac{d}{2\left(a+bx\right)}\{[\gamma \left[ax{g}^{\prime }\left(\gamma \right)+b{x}^2{h}^{\prime }\left(\gamma \right)\right]\\ -\left[axg\left(\gamma \right)+b{x}^{2}h\left(\gamma \right)\right]]\}\}.& (10)\end{array}$

Equation (3) is identically satisfied; however, Equations (4) and (5) together with Equations (9) and (10) yield

$\begin{array}{l}{a}^{2}x\{--\frac{k\left[g{g}^{″}-{\left(g^{\prime }\right)}^2-2p_1\left(\gamma \right)\right]}{k+\gamma }-\frac{k(g{g}^{\prime }-\frac{1}{k}{g}^{\prime })}{{\left(k+\gamma \right)}^2}\\ -\frac{g^{″}}{k+\gamma }-g^{‴}+\frac{Ha{k}^2{g}^{\prime }}{{(k+\gamma )}^2}\}\\ +ab{x}^2\{-\frac{k\left[h^{″}g+2h{g}^{″}-3h^{\prime }{g}^{\prime }-6p_2\left(\gamma \right)\right]}{k+\gamma }\\ -\frac{k\left(2h{g}^{\prime }+h^{\prime }g\right)}{{\left(k+\gamma \right)}^2}-\frac{h^{″}+g^{″}}{k+\gamma }+\frac{h^{\prime }+g^{\prime }}{{\left(k+\gamma \right)}^2}-(h^{‴}+g^{‴})\\ +\frac{Ha{k}^2{h}^{\prime }}{{(k+\gamma )}^2}\}+b^2{x}^3\{-\frac{2k\left[h{h}^{″}-{\left(g^{\prime }\right)}^2+\frac{1}{k}{h}^{″}-2p_3\left(\gamma \right)\right]}{k+\gamma }\\ -\frac{k\left[h{h}^{\prime }-\frac{1}{k}{h}^{\prime }\right]}{{\left(k+\gamma \right)}^2}-h^{‴}\}=0& (11)\end{array}$

$\begin{array}{l}{a}^{2}x\left[\frac{{\left(g^{\prime }\right)}^2}{k+\gamma }-p_{i^{\prime }}(\gamma )\right]+ab{x}^2\left[\frac{2h^{\prime }{g}^{\prime }}{k+\gamma }-2p_{j^{\prime }}(\gamma )\right]\\ +b^2{x}^3\left[\frac{{\left(h^{\prime }\right)}^2}{k+\gamma }-p_k{}^{\prime }\left(\gamma \right)\right]=0& (12)\end{array}$

where $\left(Ha=\sqrt{\sigma {B_0}^2{a}^2/\mu }\right)$ is the Hartman number.

The boundary conditions in the dimensionless form are:

$\begin{array}{ll}g(0)=0,g^{\prime }(0)=1,h(0)=0,h^{\prime }(0)=1at\gamma =0& (13)\end{array}$

$\begin{array}{ll}{h}^{\prime }(\infty )=0,h^{″}(\infty )=0,g^{\prime }(\infty )=0,g^{″}(\infty )=0as\gamma \to \infty .& (14)\end{array}$

Equation (12) along with Equation (11) gives

$\begin{array}{l}{\frac{2k}{k+\gamma }P}_1(\gamma )=g^{‴}+\frac{g^{″}}{k+\gamma }-\frac{g^{\prime }}{{(k+\gamma )}^2}+\frac{kg{g}^{″}}{k+\gamma }\\ +\frac{kg{g}^{\prime }}{{(k+\gamma )}^2}-\frac{k{(g^{\prime })}^2}{k+\gamma }-\frac{Ha{k}^2}{{(k+\gamma )}^2}{g}^{\prime }& (15)\end{array}$

$\begin{array}{l}{\frac{6k}{k+\gamma }P}_2(\gamma )=g^{‴}+h^{‴}+\frac{h^{″}+g^{″}}{k+\gamma }-\frac{h^{\prime }+g^{\prime }}{{(k+\gamma )}^2}\\ +\frac{k{h}^{″}g}{(k+\gamma )}+\frac{2kh{g}^{″}}{(k+\gamma )}-\frac{3k{h}^{\prime }{g}^{\prime }}{k+\gamma }\\ +\frac{2kh{g}^{\prime }}{{(k+\gamma )}^2}+\frac{k{h}^{\prime }g}{{(k+\gamma )}^2}-\frac{Ha{k}^2}{{(k+\gamma )}^2}{h}^{\prime }& (16)\end{array}$

$\begin{array}{l}{\frac{4k}{k+\gamma }P}_3(\gamma )=h^{‴}+\frac{h^{″}}{k+\gamma }-\frac{h^{\prime }}{{(k+\gamma )}^2}+\frac{2kh{h}^{″}}{k+\gamma }\\ +\frac{2kh{h}^{\prime }}{{(k+\gamma )}^2}-\frac{2k{(h^{\prime })}^2}{k+\gamma }.& (17)\end{array}$

The pressure inside the boundary layer is now expressed as:

$\begin{array}{ll}P(\gamma )={a^{2}p}_1(\gamma )+ab{p}_2(\gamma )+b{p}_3(\gamma ).& (18)\end{array}$

Using the limit ξ → ∞, Equations (15)−(17) reduce to

$\begin{array}{ll}{g}^{‴}+g{g}^{″}-{(g^{\prime })}^2-H{a}^2{g}^{\prime }=0& (19)\end{array}$

$\begin{array}{ll}{h}^{‴}+g^{‴}{+h}^{″}g+2h{g}^{″}-3h^{\prime }{g}^{\prime }-H{a}^2{h}^{\prime }=0& (20)\end{array}$

$\begin{array}{ll}{h}^{‴}+2h{h}^{″}-{2(h^{\prime })}^2=0& (21)\end{array}$

At this point, we make some observations of vital importance. One, the similarity transformation as defined in this paper considers the contribution of both linear and non-linear parts of the stretching velocity through the terms “a” and “b.” The similarity used in the literature for non-linear stretching $(\eta =y\sqrt{\frac{a}{\upsilon }})$ is deficient in that its only involves a which only corresponds to the linear part of the stretching velocity [2–4]. This omission leads to the omission of terms in the momentum equations and consequently results in an incomplete solution.

Eliminating the pressure from Equations (15), (16), and (17), we obtain self-similar equations as given below:

$\begin{array}{l}{g}^{{}^{\prime }v}+\frac{2g^{‴}}{k+\gamma }-\frac{g^{″}}{{(k+\gamma )}^2}+\frac{g^{\prime }}{{(k+\gamma )}^3}+\frac{kg{g}^{‴}}{k+\gamma }-\frac{k{g}^{\prime }{g}^{″}}{k+\gamma }\\ +\frac{kg{g}^{″}}{{(k+\gamma )}^2}-\frac{k{(g^{\prime })}^2}{{(k+\gamma )}^2}-\frac{kg{g}^{\prime }}{{(k+\gamma )}^3}-\frac{{Ha}^2{k}^2{g}^{″}}{{(k+\gamma )}^2}\\ +\frac{H{a}^2{k}^2{g}^{\prime }}{{(k+\gamma )}^3}=0& (22)\end{array}$

$\begin{array}{l}{h}^{{}^{\prime }v}+g^{{}^{\prime }v}+\frac{2(h^{‴}+g^{‴})}{k+\gamma }-\frac{h^{″}+g^{″}}{{(k+\gamma )}^2}+\frac{h^{\prime }+g^{\prime }}{{(k+\gamma )}^3}\\ +\frac{k(g{h}^{‴}+2h{g}^{‴}-2h^{″}{g}^{\prime }-h^{\prime }{g}^{″})}{k+\gamma }-\frac{k(2h{g}^{\prime }+h^{\prime }g)}{{(k+\gamma )}^3}\\ +\frac{k(g{h}^{″}-3h^{\prime }{g}^{\prime }+2h{g}^{″})}{{(k+\gamma )}^2}-\frac{{Ha}^2{k}^2{h}^{″}}{{(k+\gamma )}^2}+\frac{H{a}^2{k}^2{h}^{\prime }}{{(k+\gamma )}^3}=0& (23)\end{array}$

$\begin{array}{l}{h}^{{}^{\prime }v}+\frac{2h^{‴}}{k+\gamma }-\frac{h^{″}}{{(k+\gamma )}^2}+\frac{h^{\prime }}{{(k+\gamma )}^3}+\frac{2kh{h}^{‴}}{k+\gamma }-\frac{2k{h}^{\prime }{h}^{″}}{k+\gamma }\\ +\frac{2kh{h}^{″}}{{(k+\gamma )}^2}-\frac{2k{(h^{\prime })}^2}{{(k+\gamma )}^2}-\frac{2kh{h}^{\prime }}{{(k+\gamma )}^3}=0.& (24)\end{array}$

Heat Transfer Analysis

The thermal boundary layer Equation (6) is solved for a constant surface temperature and variable surface temperature, in sequence.

Constant Surface Temperature (CST)

In this case, T = T(r) and the Equation (6) reduces to

$\begin{array}{l}v{\partial }_{r}T=\frac{K}{\rho C_p}\left\{\frac{1}{R+r}{\partial }_r\left[(R+r){\partial }_{r}T\right]\right\}\\ +\frac{\text{u}}{\rho C_p}{\left({\partial }_{r}u-\frac{u}{R+r}\right)}^2-\frac{1}{\rho C_p}{\partial }_r{q}_w\\ +\frac{\sigma R^2}{\rho C_p{(R+r)}^2}{u}^2& (25)\end{array}$

The boundary conditions are

$\begin{array}{ll}T=T_{w{|}_{r=0}}\text{and }{T}_{|r\to \infty }=0& (26)\end{array}$

and the dimensionless temperature distributions is of the form,

$\begin{array}{ll}\theta (\gamma )=\frac{T-T_{\infty }}{T_w-T_{\infty }}.& (27)\end{array}$

Variable Surface Temperature (PSVT)

Expressing T = T(x, r) in the form

$\begin{array}{ll}T(x,r)=T_{\infty }+A{\left(\frac{x}{l}\right)}^n\theta (\gamma )& (28)\end{array}$

and the boundary conditions

$\begin{array}{ll}{T}_{w{|}_{r=0}}=T_{\infty }+A{\left(\frac{x}{l}\right)}^n\text{and }{T}_{|r\to \infty }=0& (29)\end{array}$

in which $n\in {R}$ is the index of wall temperature parameter, and A is the dimensional wall constant.

The radiative heat flux q_w under Rosseland's approximation is given by

$\begin{array}{ll}{q}_w=-\frac{4{\sigma }^{*}}{3k^{*}}{\partial }_r{T}^4& (30)\end{array}$

where k^* and σ^* are the mean absorption coefficient and the Stefan-Boltzmann constant, respectively.

Taylor's series is employed in the expansion of the temperature variation (T⁴) about T_∞, and we get

$\begin{array}{ll}{T}^4\approx 4T_{\infty }^{3}T-3T_{\infty }^4.& (31)\end{array}$

Substituting Equation (31) in Equation (30), we have

$\begin{array}{ll}{\partial }_r{q}_w=-\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}{\partial }_{rr}T.& (32)\end{array}$

After using Equation (32), the energy Equation (25) and (6) for CST and PSVT cases reduce to

$\begin{array}{l}v{\partial }_{r}T=\frac{K}{\rho C_p}\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}K}\right){\partial }_{rr}T\\ +\frac{\mu }{\rho C_p}{\left({\partial }_{r}u-\frac{u}{R+r}\right)}^2+\frac{K}{\rho C_p}{\partial }_{r}T+\frac{\sigma R^2}{\rho C_p{(R+r)}^2}{u}^2& (33)\end{array}$

$\begin{array}{l}v{\partial }_{r}T+\frac{Ru}{R+r}{\partial }_{x}T=\frac{K}{\rho C_p}\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}K}\right){\partial }_{rr}T\\ +\frac{\mu }{\rho C_p}{\left({\partial }_{r}u-\frac{u}{R+r}\right)}^2+\frac{K}{\rho C_p}{\partial }_{r}T+\frac{\sigma R^2}{\rho C_p{(R+r)}^2}{u}^2.& (34)\end{array}$

Equations (33) and (34) after using Equation (9), (10), (27), and (28) give

$\begin{array}{l}(1+Rd){\theta }^{″}+\frac{{\theta }^{\prime }}{(k+\gamma )}+\frac{Prk(g+2h){\theta }^{\prime }}{(k+\gamma )}\\ +\text{EcPr}{\left(h^{″}+g^{″}-\frac{h^{\prime }+g^{\prime }}{k+\gamma }\right)}^2+\frac{w{k}^2{(h^{\prime }+g^{\prime })}^2}{{(k+\gamma )}^2}=0& (35)\end{array}$

$\begin{array}{l}(1+Rd){\theta }^{″}+\frac{{\theta }^{\prime }}{(k+\gamma )}+\frac{Prk\left[(g+2h){\theta }^{\prime }-n(h^{\prime }+g^{\prime })\theta \right]}{(k+\gamma )}\\ +\text{EcPr}{\left(h^{″}+g^{″}-\frac{h^{\prime }+g^{\prime }}{k+\gamma }\right)}^2+\frac{w{k}^2{(h^{\prime }+g^{\prime })}^2}{{(k+\gamma )}^2}=0& (36)\end{array}$

The boundary conditions become

$\begin{array}{ll}\theta {|}_{\gamma =0}=1\text{and }\theta {|}_{\gamma \to \infty }=0& (37)\end{array}$

where Pr (= C_pμ/k_o), $\mathrm{\text{Ec}}(=U^2/(C_p(T_w-T_{\infty })))$, $\mathrm{\text{Ec}}(=U^2/C_{p}A{(x)}^n)$, $\mathrm{\text{Rd}}(=16{\sigma }^{*}{T}_{\infty }^3/3k^{*}K)$ and $w(=H_a^{2}EcPr)$ are Prandtl's number, Eckert's number, the modified Eckert number, Radiation and Joule heating parameters, respectively. Equation (36) is locally similar and corresponds to CST if n = 0.

The surface frictional drag and other important quantities experienced by the fluid flow at the surface are the skin-friction coefficients C_f, Nusselt number Nu and Local Nusselt Nu^*. These are defined as follows:

$\begin{array}{ll}{C}_f=\frac{{\tau }_{rx}{|}_{r=0}}{\frac{1}{2}\rho u_w^2},Nu=\frac{x{q}_w}{k^{*}(T-T_w)}\text{and }N{u}^{*}=\frac{x{q}_w}{k^{*}B{(x)}^{\omega }}& (38)\end{array}$

such that

$\begin{array}{r}{\tau }_{rx}{|}_{r=0}={\mu \left({\partial }_{r}u-\frac{u}{R+r}\right)}_{r=0};R_{e_x}^{\frac{1}{2}}=\sqrt{\left(\frac{c+dx}{\upsilon }\right)x^2};\\ q_w=-k^{*}{\partial }_{r}T{|}_{r=0}& (39)\end{array}$

Equations (38) and (39) give

$\begin{array}{ll}-\frac{1}{2}{R}_{e_x}^{\frac{1}{2}}{C}_f=\left(f^{″}(0)+g^{″}(0)-\frac{2}{k}\right)& (40)\end{array}$

$\begin{array}{ll}Nu{R}_e^{\frac{1}{2}}={-\theta }^{\prime }(0),N{u}^{*}{R}_{e_x}^{\frac{1}{2}}& (41)\end{array}$

We notice that Equation (41) is subjected to the heat conditions defined in Equation (37).

Computational Methodology

In this present work, our focus is to present physical and plausible solutions for the three momentum equations in response to a curved structure through a numerical approach. Substituting Equation (22) into Equation (23), differentiating the resulting equation and accommodating Equation (24) gives

$\begin{array}{l}{g}^{{}^{\prime }v}+\frac{2g^{‴}+kg{g}^{‴}-k{g}^{\prime }{g}^{″}}{(k+\gamma )}-\frac{g^{″}-kg{g}^{″}+k{(g^{\prime })}^2+{(Ha)}^2{k}^2{g}^{″}}{}\\ {(k+\gamma )}^2+\frac{g^{\prime }-kg{g}^{\prime }-{(Ha)}^2{k}^2{g}^{\prime }}{{(k+\gamma )}^3}=0& (42)\end{array}$

$\begin{array}{l}{h}^v-\frac{7h^{‴}}{{(k+\gamma )}^2}+\frac{5h^{″}}{{(k+\gamma )}^3}-\frac{5h^{\prime }}{{(k+\gamma )}^4}\\ +\frac{4kh{h}^{\prime }}{{(k+\gamma )}^4}-\frac{2k({2hh}^{‴}-2h^{\prime }{h}^{″})}{{(k+\gamma )}^2}\\ -\frac{2k\left[2h{h}^{″}-2{(h^{\prime })}^2\right]}{{(k+\gamma )}^3}+\frac{k\left[3g{g}^{″}-{(g^{\prime })}^2\right]}{{(k+\gamma )}^3}\\ -\frac{3kg{g}^{\prime }}{{(k+\gamma )}^4}-\frac{k\left[g{g}^{iv}-{(g^{″})}^2\right]}{(k+\gamma )}\\ +\frac{k(2h{g}^{iv}+h^{\prime }{g}^{‴}-h^{‴}{g}^{\prime }-3h^{″}{g}^{″})}{(k+\gamma )}+\frac{kg{h}^{iv}}{(k+\gamma )}\\ -\frac{k(3h^{″}g+6h{g}^{″}-3h^{\prime }{g}^{\prime })}{{(k+\gamma )}^3}+\frac{3k(2h{g}^{\prime }+h^{\prime }g)}{{(k+\gamma )}^4}\\ -\frac{{(Ha)}^2{k}^2(h^{‴}+g^{‴})}{{(k+\gamma )}^2}-\frac{{(Ha)}^2{k}^2(h^{″}+g^{″})}{{(k+\gamma )}^3}\\ +\frac{{(Ha)}^2{k}^2(3h^{\prime }+g^{\prime })}{{(k+\gamma )}^4}=0& (43)\end{array}$

At this point, the solution of the non-linear coupled system of differential Equations (35), (36), (42), and (43) as subject to boundary conditions from Equations (13), (14), and (37), is obtained by using the shooting method with Runge-Kutta algorithms in MATLAB. The initial expression of the higher order system into first order differential equations are transformed into an initial value problem by considering ${(g,g^{\prime },g^{″},g^{‴},h,h^{\prime },h^{″},h^{‴},h^{\prime }v,\theta ,{\theta }^{\prime })}^T={(s_1,s_2,s_3,s_4,s_5,s_6{s}_7,s_8,s_9,s_{10},s_{11})}^T.$ The implementation of our numerical technique into the above system of equations gives the following.

$\begin{array}{ll}\left(\begin{array}{l}{s}_1\prime \\ \begin{array}{c}{s}_2\prime \\ s_3\prime \\ s_4\prime \\ s_5\prime \\ s_6\prime \\ s_7\prime \\ s_8\prime \\ s_9\prime \\ s_{10}\prime \\ s_{11}\prime \end{array}\end{array}\right)=\left\{\begin{array}{c}{s}_2\\ s_3\\ s_4\\ -\left[\begin{array}{c}z\left(2s_4+k{s}_1{s}_4-k{s}_2{s}_3\right)-z^2\left(s_3-k{s}_1{s}_3+k{s}_2^2+{\left(Ha\right)}^2{k}^2{s}_3\right)\\ +z^3\left(s_2-k{s}_1{s}_2-{\left(Ha\right)}^2{k}^2{s}_2\right)\end{array}\right]\\ s_6\\ s_7\\ s_8\\ s_9\\ \left[\begin{array}{c}-7z^2{s}_8+5z^3{s}_7-5z^4{s}_6+4k{z}^4{s}_5{s}_6-4k{z}^2{s}_5{s}_8+4k{z}^2{s}_6{s}_7\\ -4k{z}^3{s}_5{s}_7+4k{z}^3{s}_6^2+3k{z}^3{s}_1{s}_3-k{z}^3{s}_2^2-3k{z}^4{s}_1{s}_2-kz{s}_1{s}_4\prime \\ -kz{s}_3^2+2kz{s}_1{s}_4\prime +kz{s}_6{s}_4-kz{s}_2{s}_8-3kz{s}_3{s}_7+kz{s}_1{s}_9\prime -3k{z}^3{s}_1{s}_7\\ -6k{z}^3{s}_3{s}_5+3k{z}^3{s}_2{s}_6+6k{z}^4{s}_2{s}_5+3k{z}^4{s}_1{s}_6-{\left(Ha\right)}^2{k}^2{z}^2\left(s_8+s_4\right)\\ -{\left(Ha\right)}^2{k}^2{z}^3\left(s_7+s_3\right)+{\left(Ha\right)}^2{k}^2{z}^4\left(3s_6+s_2\right)\end{array}\right]\\ s_{11}\\ -\left[\begin{array}{c}z{s}_{11}+kzPr\left(s_1{s}_{10}+2s_5{s}_{10}-n{s}_{10}\left[s_6+s_2\right]\right)+EcPr\left(s_7+s_3-z\left[s_6+s_2\right]\right)\\ +w{k}^2{z}^2(s_6+s_2)\end{array}\right]\end{array}\right\}& (44)\end{array}$

$\begin{array}{ll}\left(\begin{array}{c}{s}_1(0)\\ s_2(0)\\ s_3(0)\\ s_4(0)\\ s_5(0)\\ s_6(0)\\ s_7(0)\\ s_8(0)\\ s_9(0)\\ s_{10}(0)\\ s_{11}(0)\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ N_1\\ N_2\\ 0\\ 1\\ N_3\\ N_4\\ N_5\\ 1\\ N_6\end{array}\right),& (45)\end{array}$

where $z=\frac{1}{(k+\gamma )}$ and $z_k=\frac{1}{(1+Rd)}$. The unknown initial values N₁, N₂, N₃, N₄, N₅ and N₆ are approximated with the help of Newton's method till the required conditions (h′(γ) = 0, h″(gamma) = 0, g′(γ) = 0, g″(γ) = 0, g^‴(γ) = 0, θ′(γ) = 0) are satisfied as γ → ∞. The initial guesses are given by

$\begin{array}{ll}\begin{array}{c}{g}^{″}=N_1\\ g^{‴}=N_2\\ h^{″}=N_3\\ h^{‴}=N_4\\ h^{\prime }v=N_5\\ {\theta }^{\prime }=N_6\\ \end{array}{\}}_{\eta =0}.& (46)\end{array}$

Expanding Equation (46) about γ = ∞

$\begin{array}{r}{g}^{″}(\gamma ,N_1+\Delta N_1,N_2+\Delta N_2,N_3+\Delta N_3,N_4\\ +\Delta N_4,N_5+\Delta N_5,N_6+\Delta N_6)\\ =g^{″}(\gamma ,N_1,N_2,N_3,N_4,N_5,N_6)+\frac{\partial g^{″}}{\partial N_1}\Delta N_1+\frac{\partial g^{″}}{\partial N_2}\Delta N_2\\ +\frac{\partial g^{″}}{\partial N_3}\Delta N_3+\frac{\partial g^{″}}{\partial N_4}\Delta N_4+\frac{\partial g^{″}}{\partial N_5}\Delta N_5+\frac{\partial g^{″}}{\partial N_6}\Delta N_6.& (47)\end{array}$

The remaining conditions (g‴, h″, h‴, h′v, θ′) are subsequently expressed in the form of Equation (47). The required Jacobian Matrix computed (for γ = ∞) after several processes is given as

$\begin{array}{ll}Â\widehat{X}=\widehat{B},& (48)\end{array}$

where $\widehat{X}={(N_1,N_2,N_3,N_4,N_5,N_6)}^T$, $\widehat{B}={(B_1,B_2,B_3,B_4,B_5,B_6)}^T$ and the iterations that generate the above Matrix takes the form:

$\begin{array}{ll}\text{For}\begin{array}{c}i=1\left(1\right)6\\ j=1(1)6\end{array}\}& (49)\end{array}$

$\begin{array}{r}Â(i,j)=s(11i+3)\\ \times s(11j+3)+s(11i+4)\times s(11j+4)\\ +s(11i+7)\times s(11j+7)\\ +s(11i+8)\times s(11j+8)+s(11i+9)\\ \times s(11j+9)+s(11i+11)\times s(11j+11)& (50)\end{array}$

$\begin{array}{r}\widehat{B}(i)=-(s(3)\times s(11i+3)+s(4)\\ \times s(11i+4)+s(7)\times s(11i+7)+s(8)\\ \times s(11i+8)+s(9)\times s(11i+9)+s(11)\times s(11i+11)).& (51)\end{array}$

The final point of the boundary layer region is determined successfully when no changes occur at s = 1 to a tolerance value of 10⁻⁸. Our interest focuses in investigating the flow characteristics: velocity, temperature, momentum and thermal boundary layer thickness over a curved surface under certain physical parameters.

Result and Discussion

In this section, we present the effects of characterizing parameters on flow and thermal behavior. Table 1 gives the surface drag force and heat transfer rate for CST/PSVT cases. Figures 2A,B establish the patterns of fluid trajectory which decreases as the radius of curvature, k, increases. Figures 3A,B examine the behavior of the velocity, u(γ), and momentum boundary layer for an increasing radius of curvature, k, and the Lorentz force. The fluid velocity and the momentum boundary layer are found to decrease as these parameters increase. This helps to control the fluid flow by means of curvature (Figure 3A) and the Lorentz force (Figure 3B). Thus, besides the well-known behavior of the Lorentz force, the curvature plays an important role in reducing the velocity. This alternate way of reducing the velocity field through the radius of curvature (for curved structures) has been established for the first time. The effects of the linear, a, and non-linear, b, parts of the stretching velocity are presented in Figures 3C,D. It is noted that fixing either a or b and varying the other parameter increases the velocity field and the boundary layer thickness; inferring that both parameters are indispensable and equally important. The temperature profile is found to decrease/increase for increasing/decreasing Prandtl/Eckert numbers for both CST (Figure 4A) and PSVT (Figure 4B) according to the physics of heat flow. Increasing the radiation parameter, Rd, increases the fluid temperature and the thermal boundary layer thickness (radiation servers as additional source for heat generation) as shown in Figure 4C. This effect is more significant in CST than PSVT. Figure 4D gives a comparison of the temperature distribution between CST (n = 0) and PSVT (n > 0). It is observed that the thermal kinetics profile is maintained over the surface for CST. However, the temperature and thermal boundary layer decreases as the temperature index, n, increases. Figure 4E expresses the effect of Lorentz force in the generation of surface heating. Thus, the application of Lorentz force increases the heat flow characteristic in both CST/PSVT. The effects of a magnetic parameter on the temperature and thermal boundary layer thickness are presented in Figure 4F and show a slight increase with Ha. It is further observed that heat transfer from the surface to the fluid is more significant for a constant surface temperature than a variable surface temperature. This shows an additional effect of magnetic fields (hitherto unknown) is raising the temperature of the fluid flow over the curved surface. The pressure gradient P(γ) in the boundary layer region for the curved surface cannot be neglected; whereas it is neglected for the straight surface. However, the effect of increasing curvature, k, and Ha on the pressure is shown in Figures 5A,B. We observe from Figure 5A that the pressure rises from the start of the curved surface and decreases subsequently. The observation conforms with the velocity behavior which decreases for large k, while the pressure approaches zero for the flat surface as (k → ∞). In Figure 5B the pressure decreases significantly along the curved surface due to an opposing Lorentz force that suppresses the bulk movement of the fluid. This agrees with the behavior of the velocity as explained in the figure above. Figures 5C,D show the effects of stretching strengths a and b on the pressure. The pressure increases when either a (Figure 5C) or b (Figure 5D) is increased. This increase is more significant at the start of the curved surface for b, proving that the strength of non-linear stretching contributes more effectively compared to the linear strength of the stretching velocity. This phenomenal observation is presented for the first time. We further notice that the flow field characteristic decreases for linear stretching in Figure 5C while it increases for non-linear stretching in Figure 5D. The surface drag force for varying curvature and magnetic field parameters is shown in Figures 6A,B. Figure 6A shows that the drag force increases with k for increasing Ha, while in Figure 6B it decreases with Ha as a consequence of increasing k. Table 1 is presented to show the impacts of a variable magnetic field in comparison with the constant magnetic input on surface drag force and heat transfer rate in view of possible engineering applications. The differences raise a slight concern due to improvements in the geometry (curvilinear) of the magnetic field rather that using a constantly applied field as in the existing literature. Table 2 is computed to tabulate the numerical values of the skin friction coefficient and the heat transfer rate (Nusselt/local Nusselt numbers) for CST/PSVT under varying values of the characterizing parameters.

TABLE 1

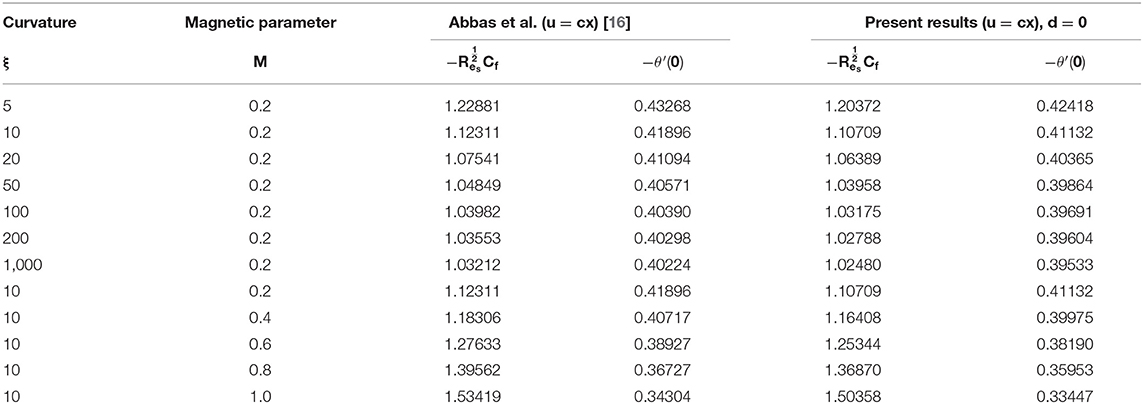
Table 1. Comparison of the present results of the Skin-friction coefficient and the Local Nusselt number.

FIGURE 2

Figure 2. (A) Effects of k on stream function f (γ). (B) Effects of k on stream function g(γ).

FIGURE 3

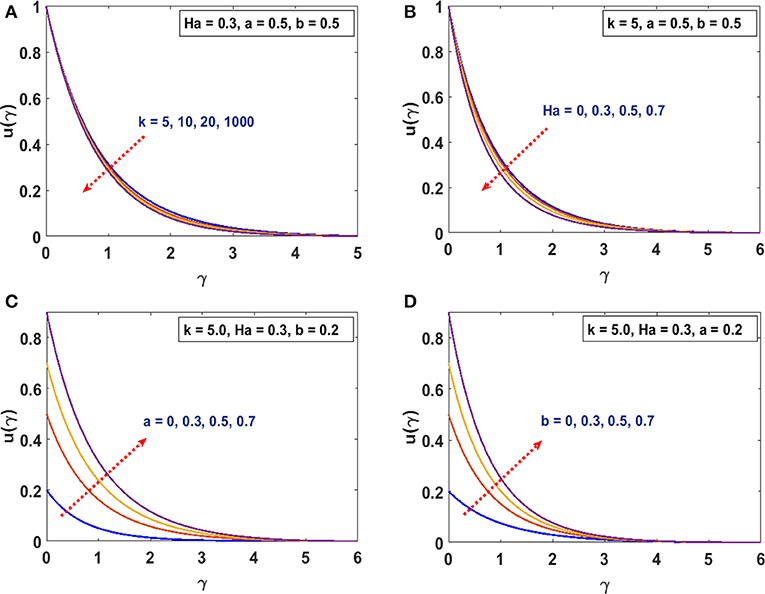
Figure 3. (A) Effects of k on velocity field u(γ). (B) Effects of Ha on velocity field u(γ). (C) Effects of a on velocity field u(γ). (D) Effects of b on velocity field u(γ).

FIGURE 4

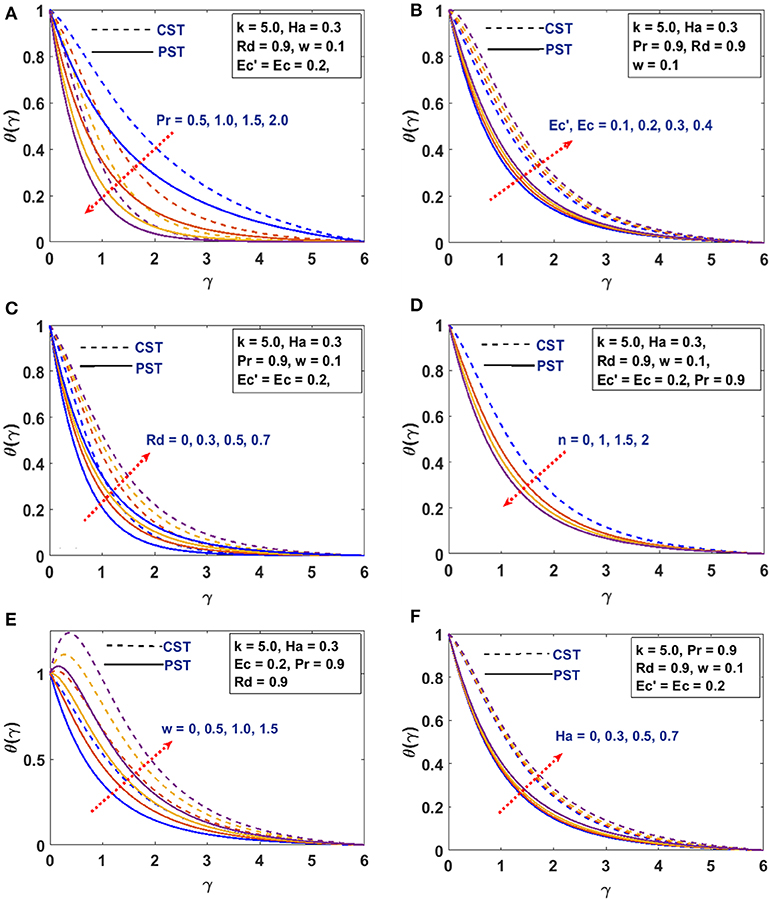
Figure 4. (A) Effects of Pr on temperature field θ(γ). (B) Effects of Ec′, Ec on temperature field θ(γ). (C) Effects of Rd on temperature field θ(γ). (D) Effects of n on temperature field θ(γ). (E) Effects of w on temperature field θ(γ). (F) Effects of Ha on temperature field θ(γ).

FIGURE 5

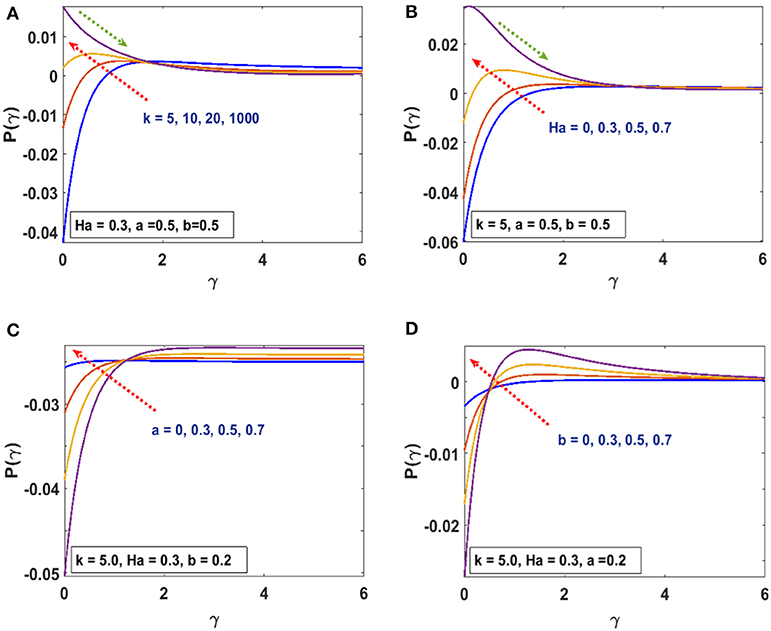
Figure 5. (A) Effects of k on pressure profile P(γ). (B) Effects of Ha on pressure profile P(γ). (C) Effects of a on pressure profile P(γ). (D) Effects of b on pressure profile P(γ).

FIGURE 6

Figure 6. (A) Effects of k on surface drage force. (B) Effect of Ha on surface drag force.

TABLE 2

Table 2. Numerical values of ${-R}_{e_x}^{\frac{1}{2}}{C}_f$ and rate of heat transfer at fixed a = 0.5, and b = 0.5.

Conclusion

The flow and heat transfer analysis of a two-dimensional steady hydromagnetic viscous fluid flow due to non-linear (quadratic) stretching of the curved surface is investigated. The energy equation contains viscous dissipation, linear radiation and joule heating effects. The similarity transformation is improved to contain both the effects of the linear and non-linear parts of the stretching velocity on the velocity field. The expression of Lorentz force is modified for the curved surface. The heat flow is discussed for the cases of constant surface temperature (CST) and variable surface temperature (PSVT). The reduced boundary layer equations are solved numerically using Runge-Kutta (RK) fourth order algorithms. The salient features of this work are: (i) Correct modeling of the quadratic stretching is presented by redefining the similarity transformation (ii) An accurate expression of the Lorentz force is obtained for an applied magnetic field on the curved structure by considering the variable magnetic field that depends on the radial direction. (iii) The velocity field and the momentum boundary layer thickness can be maintained by the curvature and the Lorentz force (iv) The effects of the strengths of the linear and non-linear parts of the stretching velocity are investigated for controlling the flow over the curved surface. (v) For both CST/PSVT cases the magnetic field increases slightly due to quantum heat generation caused by the Lorentz force, (vi) A decrease of the dimensionless radius of curvature (increasing the curvature) gives a decrease in the heat transfer from the curved surface to the fluid as compared to a flat surface, (vii) Increasing the Eckert/Local Eckert number enhances the temperature field and thermal boundary layer thickness, (viii) Low thermal conductivity due to an increasing Prandtl number consequently diminishes the temperature field and thermal boundary layer thickness, (ix) A high radiation parameter increases the heat flow from the surface to the fluid, (x) Variation of the wall temperature (PSVT) index reduces the heat flow characteristics, consequently it helps in regulating the heat flow rate generated over a curved sheet. (xi) The pressure decreases for a large radius of curvature, k, and Ha and increases due to the non-linear part of the stretching velocity.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The corresponding author is a PhD student under supervision of SA and co-guidance QH. All authors work and mediated on, the technicality, physical intuition, and mathematical significance contributions of the manuscript content to the research world.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Crane LJ. Flow past a stretching plate. Z Angew Math Phys. (1970) 7:645–7. doi: 10.1007/BF01587695

CrossRef Full Text

2. Kumaran V, Ramanaiah G. A note on the flow over stretching sheet. Acta Mech. (1996) 116:229–33. doi: 10.1007/BF01171433

CrossRef Full Text | Google Scholar

3. Raptis AA, Perdikis C. Viscous flow over a nonlinear stretching sheet in the presence of a chemical reaction and magnetic field. Int. J. Nonlinear Mech. (2006) 41:527–9. doi: 10.1016/j.ijnonlinmec.2005.12.003

CrossRef Full Text | Google Scholar

4. Cortell R. Further results on nonlinearly stretching permeable sheets. analytic solution for MHD flow and mass transfer. Math Probl Eng. (2012) 2012:18. doi: 10.1155/2012/743130

CrossRef Full Text | Google Scholar

5. Takhar HS, Raptis AA, Perdikis CP. MHD asymmetric flow past note a semi-infinte moving plate. Acta Mech. (1986) 65:287–90. doi: 10.1007/BF01176888

CrossRef Full Text | Google Scholar

6. Kelson NA. Note on similarity solutions for viscous flow over an impermeable and non-linearly (quadratic) stretching sheet. Int J Nonlinear Mech. (2011) 46:1090–1. doi: 10.1016/j.ijnonlinmec.2011.04.025

CrossRef Full Text | Google Scholar

7. Cortel R. MHD (magneto-hydrodynamic) flow and radiative nonlinear heat transfer of a viscoelastic fluid over a stretching sheet with heat generation/absorption. Energ J. (2014) 74:896–905. doi: 10.1016/j.energy.2014.07.069

CrossRef Full Text | Google Scholar

8. Magyari E, Keller B. Heat and mass transfer in the boundary layer on an exponentially stretching continuous surface. J Phys D Appl Phys. (1999) 32:577–85. doi: 10.1088/0022-3727/32/5/012

CrossRef Full Text | Google Scholar

9. Partha MK, Murthy PN, Rajasekhar GP. Effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. Heat Mass Transfer. (2005) 41:360–6. doi: 10.1007/s00231-004-0552-2

CrossRef Full Text | Google Scholar

10. Abd-El-Aziz M. Viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Can J Phys. (2009) 57:359–3678. doi: 10.1139/P09-047

CrossRef Full Text | Google Scholar

11. Ishak A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays. (2011) 40:391–5. Available online at: http://journalarticle.ukm.my/2406/1/17_Anuar_Ishak.pdf

Google Scholar

12. Zeeshan A, Ellahi R. Series solutions for nonlinear partial differential equations with slip boundary conditions for non-Newtonian MHD fluid in porous space. Appl Math Inform Sci. (2013) 7:257–65. doi: 10.12785/amis/070132

CrossRef Full Text | Google Scholar

13. Magyari E, Ali ME, Keller B. Heat and mass transfer characteristics of self-similar boundary-layer flows induced continuous surface stretched with rapidly decreasing velocities. Heat Mass Transfer. (2010) 38:65–74. doi: 10.1007/s002310000126

CrossRef Full Text | Google Scholar

14. Sajid M, Ali N, Javed T, Abbas Z. Stretching a curved surface in a viscous fluid. Chinese Phys Lett. (2010) 27:024703. doi: 10.1088/0256-307X/27/2/024703

CrossRef Full Text | Google Scholar

15. Sanni KM, Asghar S, Jalil M, Okechi NF. Flow of viscous fluid along a nonlinearly stretching curved surface. Results Phys. (2017) 7:1–7. doi: 10.1016/j.rinp.2016.11.058

CrossRef Full Text | Google Scholar

16. Abbas Z, Naveed M, Sajid M. Heat transfer analysis for stretching flow over a curved surface with magnetic field. J Eng Thermophys. (2013) 22:337–45. doi: 10.1134/S1810232813040061

CrossRef Full Text | Google Scholar

17. Naveed M, Abbas Z, Sajid M. Hydromagnetic flow over an unsteady curved stretching surface. Eng Sci Technol Int J. (2016) 19:841–5. doi: 10.1016/j.jestch.2015.11.009

CrossRef Full Text | Google Scholar

18. Imtiaz M, Hayat T, Alsaedi A, Hobiny A. Homogeneous-heterogeneous reaction in MHD flow due to an unsteady curved stretching surface. J Mol Liq. (2016) 221:245–53. doi: 10.1016/j.molliq.2016.05.060

CrossRef Full Text | Google Scholar

19. Imtiaz M, Hayat T, Alsaedi A. MHD convective flow of jeffrey fluid due to a curved stretching surface with homogeneous-heterogeneous reactions. PLoS ONE. (2016) 11:e0161641. doi: 10.1371/journal.pone.0161641

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Imtiaz M, Hayat T, Alsaedi A. Convective flow of ferrofluid due to a curved stretching surface with homogeneous-heterogeneous reaction. Powder Technol. (2017) 310:154–62. doi: 10.1016/j.powtec.2017.01.029

CrossRef Full Text | Google Scholar

21. Abbas Z, Naveed M, Sajid M. Hydromagnetic Slip flow of nanofluid Over a Curved Surface with heat generation and thermal radiation. J Mol Liq. (2016) 215:756–62. doi: 10.1016/j.molliq.2016.01.012

CrossRef Full Text | Google Scholar

22. Hayat T, Rashid M, Imtiaz M, Alsaedi A. MHD Convective flow due to a curved surface with thermal radiation and chemical reaction. J Mol Liq. (2016) 225:482–9. doi: 10.1016/j.molliq.2016.11.096

CrossRef Full Text | Google Scholar

23. Hayat T, Sajjad R, Ellahi R, Alsaedi A, Muhammad T. Homogeneous-heterogeneous reaction in MHD flow of micropolar fluid by a curved stretching surface. J Mol Liq. (2017) 240:209–20. doi: 10.1016/j.molliq.2017.05.054

CrossRef Full Text | Google Scholar

24. Hayat T, Saif RS, Ellahi R, Muhammad T, Ahmad B. Numerical study of boundary layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions. Results Phys. (2017) 7:2601–6. doi: 10.1016/j.rinp.2017.08.030

CrossRef Full Text | Google Scholar

25. Aleksander S, Grzegorz C. Application of variable magnetic fields in medicine−15 years' experience. Wiad Lek (Warsaw, Poland: 1960). (2003) 56:9–10. Available online at: https://europepmc.org/article/med/15049208

Google Scholar

26. Hurley DP, Coey JMD. Device for Generating a Variable Magnetic Field. United State Patent US 6535092B1 (2003). Dublin: Magnetic Solution (Holdings) Limited.

Google Scholar

27. Reddy JVR, Sugunamma V, Sandeep N. Dual solutions for nanofluid past a curved surface with nonlinear radiation, soret and Dufour effects. IOP Conf Series J Phys Conf Series. (2018) 1000:012152. doi: 10.1088/1742-6596/1000/1/012152

CrossRef Full Text | Google Scholar

28. Saba F, Ahmed N, Hussain S, Khan U, Mohyd-Din ST. Thermal analysis of nanofluid flow over a curved stretching surface suspended by carbon nanotubes with internal heat generation. Appl Sci. (2018) 8:395. doi: 10.3390/app8030395

CrossRef Full Text | Google Scholar

29. Naveed M, Abbas Z, Sajid M. Dual solutions in hydromagnetic viscous fluid flow past a shrinking curved surface. Arab J Sci Eng. (2018) 43:1189–94. doi: 10.1007/s13369-017-2772-z

CrossRef Full Text | Google Scholar

30. Hayat T, Nasir T, Ijaz MK, Alsaedi A. Numerical investigation of MHD flow with Soret and Dufour effect. Results Phys. (2018) 8:1017–22. doi: 10.1016/j.rinp.2018.01.006

CrossRef Full Text | Google Scholar

31. Nadeem S, Ahmed Z, Saleem S. Carbon nanotubes effect in magneto nanofluid flow over a curved stretching surface with variable viscosity. Microsyst Technol. (2019) 25:2881–8. doi: 10.1007/s00542-018-4232-4

CrossRef Full Text | Google Scholar