- 1College of Information and Statistics, Guangxi University of Finance and Economics, Nanning, China
- 2Guangxi Key Laboratory Cultivation Base of Cross-Border E-Commerce Intelligent Information Processing, Nanning, China
- 3Guangxi (ASEAN) Research Center of Finance and Economics, Guangxi University of Finance and Economics, Nanning, China
The backstepping technique is greatly effective for the integer-order triangular non-linear systems. Nevertheless, it is dramatically challenging to implement backstepping technique in the manipulation of fractional-order permanent magnet synchronous motors (FOPMSMs), since the fractional derivatives of the composite functions are deeply complex. In this paper, adaptive neural network (NN) backstepping-based control scheme for FOPMSMs on the basis of fractional Lyapunov stability criterion is established. First, we propose a novel adaptive synchronous controller for FOPMSMs by coupling with NNs and backstepping technique. Then, we present a detailed stability analysis in terms of FOPMSMs via the proposed controller. Finally, a simulation example is given to reveal that the proposed controller can effectively eliminate or restrain the chaos of FOPMSMs, and keep the tracking signals synchronous with the reference signals.
1. Introduction
In late decades, fractional-order non-linear systems (FONSs) [1] have been widely studied, not only owing to their accurate performance in modeling physical phenomena (e.g., chaos, oscillations, impulses, diffusions, see [2–5]), but also owing to their successful applications in a variety of fields, such as chemistry, medicine, biology, electronics, robotics, fuel cells, and so on [6–11]. Stability analysis [12] is regarded as a fundamental and crucial task in the development of cybernetics. Recently, more and more scholars have paid attention to stability analysis of fractional-order non-linear systems [13–16]. It is not exaggerated to say that stability analysis of FONSs along with their robust control have become a hot and promising research topic.
The researches on the control of chaotic systems are widely concerned due to its valuable significance in both theoretical and practical aspects [17, 18]. Since Kuroe and Hayashi [19] originally discovered chaotic phenomenon from the motor drive system in the late 1980's, chaos control has been one of the most popular research topics in cybernetics. There are several types of chaotic motor drivers that capture widespread interests. For instance, DC motor drivers [20], step motor drivers [21], single-phase induction motor drivers [22], synchronous reluctance motor drivers [23], switched reluctance motor drivers [24] and so on. The extensive utilization of permanent magnet synchronous motors (PMSMs) in industries mainly benefits from their merits of high speed, high efficiency, high power, low loss and low temperature rise. Chaotic non-linear systems are very complex due to the irregular and unpredictable behaviors. A remarkable feature of chaotic systems is that they are very sensitive to the initial conditions. The small change of initial state will lead to great distinction. On the other hand, they have many other desired properties, such as information processing, secure communication and mechanical system. However, it may cause unexpected oscillations and even destroy the system stability. Therefore, such oscillations should be effectively suppressed. For this reason, various methods have been developed to stabilize non-linear chaotic systems, in which fractional order chaos control has also been focused, such as OGY type [25], feedback type [26–28], dynamic surface type [29], sliding mode type [30–33], backstepping type [34, 35], etc.
Neural network (NN) control technique [36, 37] is an intelligent method for controlling non-linear systems with uncertainties. Analogizing to fuzzy control approach [38, 39], the idea of NN control technique is to approximate unknown non-linear functions by using radial basis function neural networks (RBFNNs), which is a type of neuron-modeled structure formed by the computation of some adjustable parameter vectors and some specific continuous functions. As one of the most powerful tools to realizing approximation of functions, NN control technique is popular because it facilitates to control most of many non-linear systems in which the data are too imprecise or too complex to construct mathematical modeling. It provides an available way for the control designs, and it is considerably applicable in the field of control engineering.
Backstepping technique has engaged much attention due to its efficient performance in handling mismatched uncertainties of integer-order non-linear systems [40, 41]. Unfortunately, this control method has an inherent drawback, namely “explosion of complexity,” triggered by iteratively differentiating virtual control inputs [42]. Additionally, it requires complicated analysis to compute a so-called “regression matrix” [43]. Dawson et al. [44] pointed out that the size of the regression matrix displays too large when backstepping technique was applied to manipulate DC motors in a conventional manner. Such complexities might be augmented remarkably for fractional-order non-linear systems.
It is well-known that the design of NN control is rarely systematic, which is difficult to work for the control of complex systems. It is also challenging to establish a systematic NN control theory to solve a series of problems, such as the mechanism of NN control, stability analysis, systematic design, etc. Backstepping control usually leads to the problem of “complexity explosion” when it is applied in the processing of unknown functions, so the methods of adaptive NN control [36], adaptive fuzzy control [45] and adaptive NN backstepping control [35] are put forward to address such a problem. These techniques enable systems to be greatly adaptive and robust obeying the required performance criteria for the control. However, the control performance is not desired for the non-linear systems with triangular structures, and the problem of “complexity explosion” will occur during the control proceeding. Based on the above discussion, this paper proposes an adaptive neural network control method of chaotic fractional-order permanent magnet synchronous motors using backstepping technique, which can improve the control performance of non-linear systems.
To deal with the synchronization issue of fractional-order permanent magnet synchronous motor (FOPMSM) with triangular structure, we expect to construct an adaptive NN controller combined with backstepping technique. This enables every uncertain complex non-linear functions being approximated by a radial basis function neural network (RBFNN) during each control step. The main contributions of this work can be summarized as follows:
The synchronization control scheme design and the stability analysis of FOPMSMs are investigated. In order to analyze the stability of the controlled systems, firstly, some basic results related to fractional calculus and RBFNN are recalled, including a fractional differential inequality, which lays the foundation for the application of the fractional Lyapunov function method. Meanwhile, it lays a foundation for the stability analysis of other types of FONSs. Secondly, an adaptive NN backstepping recursive control method is proposed for a class of uncertain FOPMSMs. The stability of FOPMSMs is analyzed based on fractional Lyapunov criterion. NN control technique is employed when dealing with the approximation of uncertain functions of FOPMSMs, and the fractional adaptive law is designed to update the parameters of NNs. The relevant properties of Mittag-Leffler function and Laplace transform are applied when the fractional Lyapunov function is defined to implement the system control. Our proposed control method fully averts the superfluous terms which are aroused by repeated derivation on virtual control inputs, and facilitates to overcome the so-called “complexity explosion” inherent drawback of the traditional backstepping technique. Finally, we present a numerical example to verify the main results. The simulation results show that our method embodies a perfect control effect. This also reveals the effectiveness of our control algorithm in another way.
The remainder of this work is arranged as below: In section 2, we recall several fundamental preliminaries of fractional calculus and RBFNN. Then, a brief overview of a class of FOPMSMs is provided. In section 3, we propose a RBFNN-based control scheme in three steps and present stability analysis. In section 4, we illustrate the effectiveness of the proposed synchronous controller via a simulation example. Finally, in section 5, we summarize the results of this work and put forward the prospect for our further investigation.
2. Preliminaries and Model Description
Some basic concepts, notations and lemmas, involved with fractional calculus and radial basis function neural network (RBFNN), need to be stated in this section before used. For convenience, we adopt the symbol ℝ (resp. ℝn, ℂ) to represent the collection of all real numbers (resp. n-dimensional real vectors, complex numbers). Ω ⊆ ℝn is always assumed to be compact. T = [0, +∞) means the time-variable domain. The notation C1(T, Ω) stands for the collection of all continuous functions from T to Ω with continuous derivatives. Given a vector x ∈ ℝn, xT denotes its transpose, ∥x∥ denotes its Euclidean norm.
Definition 1 ([8]). Let α ≥ 0. For a given function f :[0, ∞) → ℝ, its α-th order integral is written as
where .
Definition 2 ([8]). Let α ≥ 0. For a given function f :[0, ∞) → ℝ, its α-th order Caputo derivative is expressed by
where α ∈ [n − 1, n), n = 1, 2, ⋯ .
Definition 3 ([8]). Let α, γ > 0. The Mittag-Leffler function Eα,γ on ℂ is expressed as
Moreover, taking the Laplace transform on Eα,γ generates
Lemma 1 ([1]). Let 0 < α < 1, γ ∈ ℂ and ν ∈ ℝ fulfilling the following:
If |ζ| → ∞, ν ≤ |arg(ζ)| ≤ π, then the following statement holds:
where n is a non-zero natural number.
Lemma 2 ([1]). Let α ∈ (0, 2), β ∈ ℝ. If μ is a constant fulfilling
then there exists C > 0 such that
with |arg(ζ)| ∈ [μ, π].
Lemma 3 ([35]). Let z(t) be a smooth function. Then
Lemma 4 ([34, 46]). Let z = 0 be the equilibrium point of a FONS, which is given by
where f : T × Ω → ℝ is a function with the Lipschitz condition. Suppose there exist a Lyapunov function V(t, z(t)) and a family of class-K functions1 ĝi (i = 1, 2, 3) satisfying
Then system (10) is asymptotical stable, i.e., .
Next, let us introduce some basic notions and notations about the radial basis function NN (RBFNN) [43, 47]. The goal of the control procedure is to establish a adaptive NN control scheme, which enables the tracking signal x1(t) and the given reference signal xd(t) are synchronized.
A RBFNN can be formed as
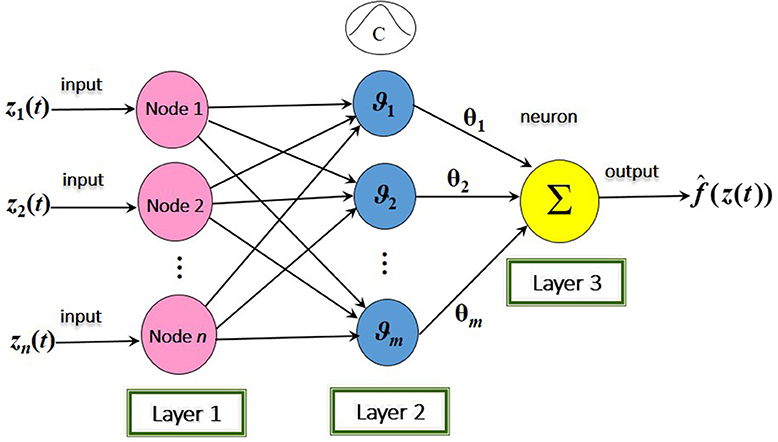
where and are the input-variable and the output-variable, respectively, is an adjustable parameter vector, with (j = 1, 2, ⋯ , m) being a continuous function, called the regressor variable. To illustrate its structure, we refer to Figure 1.
Suppose that all of the continuous functions ϑ1(z(t)), ϑ2(z(t)), ⋯ , ϑm(z(t)) in the above RBFNN are chosen as Gaussian functions, that is, for j = 1, 2, ⋯ , m,
where is the center vector and σj > 0 is the width of the Gaussian function ϑj(z(t)). Then the next lemma is obtained.
Lemma 5 ([35]). Let f :Ω → ℝ be a Lipschitz function. For each z ∈ C1(T, Ω) and for each ε > 0, there is a RBFNN fulfilling Equation (13) and the following property:
It is well-known that non-linear theory has yet been widely applied in the stability analysis of integer-order non-linear PMSMs. Yu et al. [48] investigated a type of classical PMSMs, which are described as follows:
Yu et al. [48] also studied that when the parameters σ, γ of a PMSM decrease in a certain range, chaos will appear in the PMSM. To eliminate chaos in PMSM drive systems, they treated ud as an adjustable variable, and proposed an adaptive NN control method based on backstepping control technique. It is well-known that backstepping technique usually makes great efforts to the effective control of integer-order triangular non-linear systems. Nevertheless, it is difficult to incorporate backstepping control technique into FONSs because of the complexities of fractional derivatives of composite functions. Moreover, the applications of FONSs broadly cover a great deal of fields, such as physics, chemistry, mathematics, etc., which suggests that the mathematical structures modeled by FONSs are more accurate and more practical.
Based on the aforementioned facts, this paper concerns a class of FOPMSMs. For simplicity, denote ω = x1, iq = x2, id = x3 in system (15), and extend system (15) into the next fractional-order form:
where 0 < α < 1, is a measurable state-variable, x1(t) ∈ ℝ is an output-variable, ud(t) ∈ ℝ is an input-variable, σ and γ are positive constants, both of them represent system operating parameters.
3. Adaptive Neural Network Backstepping Control of FOPMSMs
In this section, we will improve the conventional control method combined with backstepping technique, by which the chaos of FOPMSMs realizes to be eliminated or restrained in a high effective manner. The design process includes three steps. Each of them will construct a virtual control variable based on a proper Lyapunov function. At the end, a controller in real sense will be produced to manipulate FOPMSM. Assume that xd(t) is a given reference signal. Our goal is to establish an appropriate controller ud(t), ensuring that the tracking error e(t): = x1(t) − xd(t) will ultimately converge to an arbitrarily small neighborhood of the origin. Next, we present a recursive backstepping procedure to reach our goal in three steps:
Step 1: From (16), we obtain
The virtual control input α1(e(t), x1(t), xd(t)) is adopted as
where k11 > 0, k21 > 0 are design parameters, sign(·) denotes a signum function.
Denote α1(t) = α1(e(t), x1(t), xd(t)). Let
Introduce Equations (18) and (19) into Equation (17) yields
Multiplying e(t) with Equation (20) generates
Let the Lyapunov function candidate V1(t) be taken as
By Lemma 3 and Equation (21), one obtains
where κ1 = 2k11 is a positive constant.
Step 2: From Equations (16) and (19), we have
where is an unknown function. To approximate F1(x1(t)), we adopt a RBFNN formulated by
Suppose is the optimal parameter, which is represented as
Here, is presented for the purpose of analysis, in other words, it is not required in the controller design procedure.
Define the parameter estimation error as
Also, formulate the optimal approximate error ϵ1(x1(t)) by
According to Tong and Li [49], we know that ϵ1(x1(t)) is bounded. Therefore,
where is a known constant. Consequently,
Define the virtual control input by
where k12 > 0 and are design parameters.
Implement the following fractional-order adaptation law:
where ρ1 is a positive design parameters. Noting that the α-th order derivatives of constants are equal to 0, by Equation (27), we immediately get
Put
Then Equations (24), (30), and (31) lead to
By multiplying e1(t) with (35), we obtain
Adopt the next Lyapunov function candidate V2(t):
Applying Lemma 3 and Equation (23), ont gets
Substituting Equations (36) and (32) into Equation (38) derives
where κ2 = min{κ1, 2k12, ρ1} and are positive constants.
Step 3: Using Equation (34), one has
where is unknown. We approximate F2(x1(t), x2(t)) via RBFNN as follows:
Furthermore, Equation (40) can be reformulated by
Let the virtual control input be expressed by
Design the fractional-order adaptation law as
where k13 > 0, ( are design parameters with ), ρ2 > 0. Substitute it into Equation (43). By multiplying e2(t) with Equation (42), we get
Choose the Lyapunov function V3(t) as
Employing Lemma 3 with Equations (39), (44), and (45) together gives
where κ3 = min{κ2, 2k13, ρ2} and are positive constants.
Theorem 1. In system (16), if the control outputs are formulated by Equations (18), (31), and (43), and the adaptation law is designed as Equations (32) and (44), then the tracking error e(t) must tend to a sufficiently small neighborhood of the equilibrium point.
Proof. Applying (47), one gets
where . By the implementation of the Laplace transform on Equation (48), we obtain
where V3(s) and M(s) are given by the Laplace transform on V3(t) and , respectively.
By Equations (4), (49), V3(t) can be rearranged as
where * denotes the convolution between functions. Since and are non-negative,
Additionally, we have
Note that , for any t ≥ 0 and α ∈ (0, 2). Employing Lemma 2, we deduce that there is a positive constant C with
It follows from Equation (52) that
Therefore, for an arbitrary positive constant ε, there exists a positive constant t1 fulfilling that
On the other hand, by employing Lemma 1, we get
From Equation (55), for an arbitrary ε > 0, there is a positive constant t2 with
Note that the design parameter can be adjusted with . Thus, coupling of Equations (51), (54), and (56) yields
In view of Equation (57) and the definition of V3(t), we conclude that all signals and estimation errors are bounded in the closed-loop system. Further, the tracking signal e(t) will ultimately tend toward a sufficiently small neighborhood of the equilibrium point with radius for every t > min{t1, t2}.□
Remark 1. Theorem 1 can be extended to the stability analysis of many other FONSs. Employing fractional-order Lyapunov stability criterion. we know that if there are two positive constants ϕ1, ϕ2 such that , where is a Lyapunov function, then y(t) ∈ ℝn is globally bounded and holds whenever the time variable t is sufficiently large.
Remark 2. In practice, the system parameters σ and γ for the model of FOPMSM are uncertain in general. Thereby, we can take advantage of the RBFNNs and adopt the corresponding adaptation law to estimate the unknown system parameters, analogizing to our proposed estimation formula (25). For the sake of simplicity, we assume that the system parameters are constants.
Remark 3. In the proposed adaptive NN backstepping control scheme, the designed controller determined by Equations (20), (31), and (43) is apparently simpler than the ones without using NN backstepping technique. Meanwhile, it is able to avert superfluous terms aroused by repeated derivation on virtual control inputs. This is beneficial especially for FONSs, in which there are a larger amount of complicated terms of fractional derivatives. For the detail, the readers may refer to Appendix B of the literature [48].
4. Numerical Simulation Example
Let us consider the next non-linear FOPMSM by setting σ = 5.6, γ = 230 and xi(t) = yi(t) (i = 1, 2, 3) in system (16):
system is proceeded under the initial condition y0 = (−2, −0.8, 0.6). Given a reference signal yd(t) = sin t. The chosen parameters k1i (i = 1, 2, 3) should be >0. However, if k1i are too large, the control gain will increase, which will consume more control energy. Therefore, in the simulation, the selected parameters k1i are very small such that the synchronization control performs perfectly. This also shows the effectiveness of our control algorithm from another viewpoint. The adaptive parameters change much faster when the parameters are selected much larger. Based on the above considerations, The control parameters are selected as k11 = k12 = 1, k13 = 3, ρ1 = ρ2 = 0.5, then we have κ1 = κ2 = κ3 = 0.5.
In the aforementioned settings, there are two RBFNNs:
The first one, endowed with the input y1(t), relies on the Gaussian radial basis functions expressed by
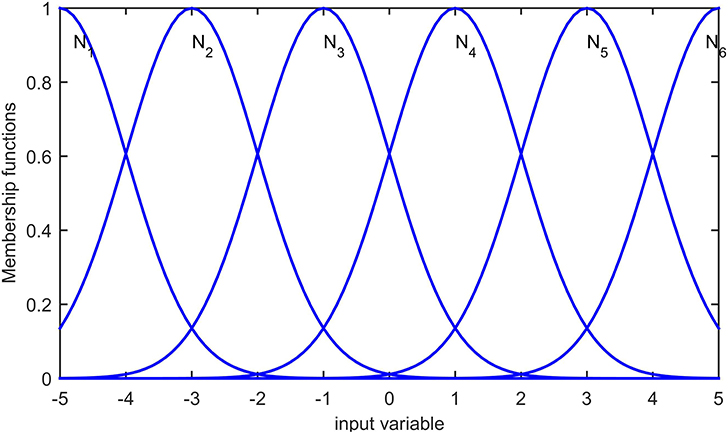
respectively. The radial basis functions are shown in Figure 2. The initial condition is taken as , uniformly distributed on [−5, 5].
Another RBFNN utilizes y1(t) and y2(t) as its inputs. Choose the Gaussian radial basis functions to be the same as that of the previous RBFNN for every input. The initial condition is fixed as .
On the basis of the above settings, the drive system of FOPMSM is simulated as follows:
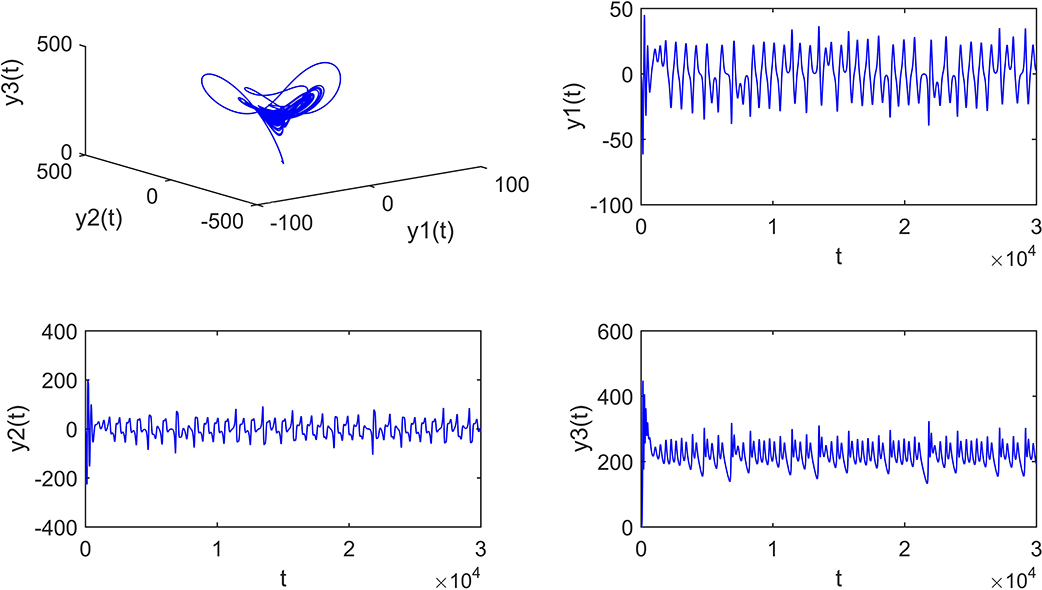
Firstly, when α = 0.98 and ud(t) = 0, the chaotic phenomenon of the FOPMSM drive system is tested, demonstrating that system (58) is not stable, as illustrated in Figure 3.
Secondarily, we apply the proposed adaptive RBFNN backstepping method in the control procedure of chaotic FOPMSM, which is depicted in Figure 4.
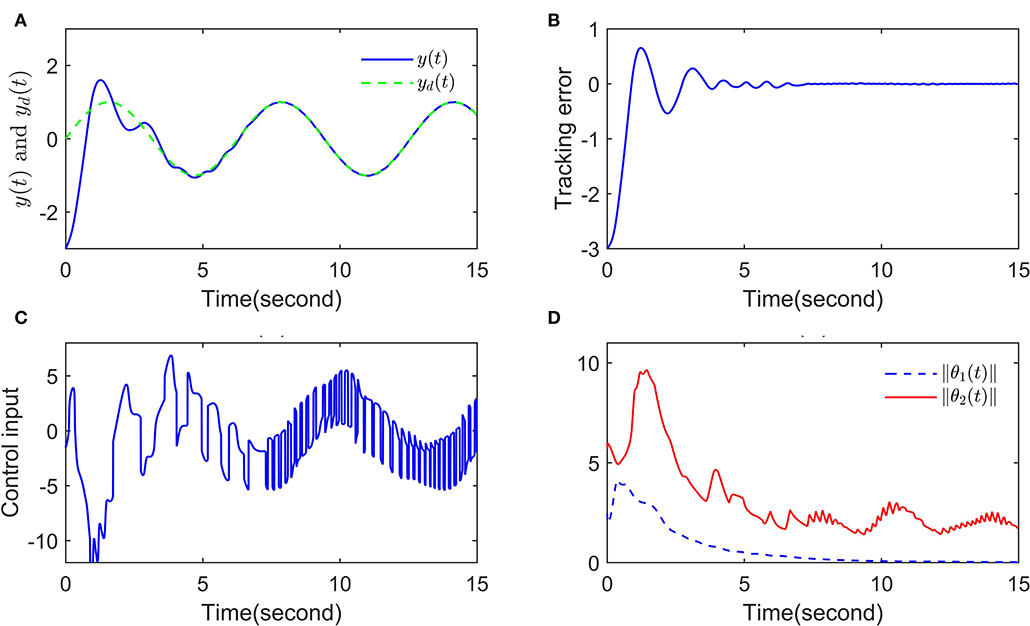
Figure 4. The simulation diagrams, (A) The signals y(t) and yd(t), (B) The tracking error, (C) The control input, (D) The parameter norms of RBFNN.
Finally, as a summary, it is evident that the proposed controller makes an effective effort to restrain the chaos of FOPMSM drive system, and it embodies desirable performance during the signal tracking.
5. Conclusion
This work provides a framework to study stabilization control of chaotic FOPMSMs on the basis of extended Lyapunov stability criterion. Our results as well as numerical simulations indicate that when the proposed adaptive NN backstepping-based control scheme is employed to control chaotic FOPMSMs, it indeed facilitates to overcome the inherent drawback “explosion of complexity.” It is demonstrated that chaos and oscillation may appear apparently in the system when the system is uncontrolled. Through the control proceeding, the variables become regular, the chaos oscillation is suppressed, and the task of signal tracking is perfectly accomplished. The problem about how to further construct an adaptive NN backstepping control scheme for generalized FOPMSMs with more input uncertainties and non-linearities is open, which is one task of our future works.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
GX, FL, and BQ contributed the conception and design of the study. GX organized the literature. FL performed the design of figures. GX wrote the first draft of the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.
Funding
This work was supported the Basic Ability Promotion Project for Young and Middle-aged Teachers of Guangxi Colleges and Universities (Grant No. 2019KY0669), the Scientific Research Development Fund of Young Researchers of Guangxi University of Finance and Economics (Grant No. 2019QNB18).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to express their sincere gratitude to the reviewers and the editors for their careful reviews and constructive recommendations.
Footnote
1. ^A function ĝ :[0, ∞) → T is said to belong to class-K if it is strictly increasing, continuous and ĝ(0) = 0.
References
2. Bagley RL, Torvik PJ. Fractional calculus–a different approach to the analysis of viscoelastically damped structures. AIAA J. (1983) 21:741–8. doi: 10.2514/3.8142
3. Chen W, Ye L, Sun H. Fractional diffusion equations by the Kansa method. Comput Math Appl. (2010) 59:1614–20. doi: 10.1016/j.camwa.2009.08.004
4. Radwan AG, Elwakil AS, Soliman AM. Fractional-order sinusoidal oscillators: design procedure and practical examples. IEEE Trans Circuits Syst I Reg Pap. (2008) 55:2051–63. doi: 10.1109/TCSI.2008.918196
5. Wang J, Ibrahim AG, Fečkan M. Nonlocal impulsive fractional differential inclusions with fractional sectorial operators on Banach spaces. Appl Math Comput. (2015) 257:103–18. doi: 10.1016/j.amc.2014.04.093
6. Podlubny I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract Calculus Appl Anal. (2002) 5:367–86. doi: 10.1016/j.sigpro.2014.05.026
7. Baleanu D, Golmankhaneh AK, Golmankhaneh AK. On electromagnetic field in fractional space. Nonlin Anal Real World Appl. (2010) 11:288–92. doi: 10.1016/j.nonrwa.2008.10.058
8. Kilbas AAA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Vol. 204. Amsterdam: Elsevier Science Limited (2006).
9. Tsirimokou G, Psychalinos C, Elwakil AS. Fractional-order electronically controlled generalized filters. Int J Circuit Theory Appl. (2017) 45:595–612. doi: 10.1002/cta.2250
10. Tsirimokou G, Psychalinos C, Elwakil A. Design of CMOS Analog Integrated Fractional-Order Circuits: Applications in Medicine and Biology. Cham: Springer (2017).
11. Zhou Y, Liu H, Cao J, Li S. Composite learning fuzzy synchronization for incommensurate fractional-order chaotic systems with time-varying delays. Int J Adapt Control. (2019) 33:1739–58. doi: 10.1002/acs.2967
12. Wang LX. Adaptive Fuzzy Systems and Control: Design and Stability Analysis. Englewood Cliffs, NJ: Prentice-Hall, Inc. (1994).
13. Radwan AG, Soliman A, Elwakil AS, Sedeek A. On the stability of linear systems with fractional-order elements. Chaos Solit Fract. (2009) 40:2317–28. doi: 10.1016/j.chaos.2007.10.033
14. You X, Song Q, Zhao Z. Global Mittag-Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. (2020) 122:382–94. doi: 10.1016/j.neunet.2019.11.004
15. You X, Song Q, Zhao Z. Existence and finite-time stability of discrete fractional-order complex-valued neural networks with time delays. Neural Netw. (2020) 123:248–60. doi: 10.1016/j.neunet.2019.12.012
16. Liu H, Pan Y, Cao J, Zhou Y, Wang H. Positivity and stability analysis for fractional-order delayed systems: a T-S fuzzy model approach. IEEE Trans Fuzzy Syst. (2020). doi: 10.1109/TFUZZ.2020.2966420. [Epub ahead of print].
17. Kurths J, Boccaletti S, Grebogi C, Lai YC. Introduction: control and synchronization in chaotic dynamical systems. Chaos. (2003) 13:126–7. doi: 10.1063/1.1554606
18. Radwan AG, Moaddy K, Salama KN, Momani S, Hashim I. Control and switching synchronization of fractional order chaotic systems using active control technique. J Adv Res. (2014) 5:125–32. doi: 10.1016/j.jare.2013.01.003
19. Kuroe Y, Hayashi S. Analysis of bifurcation in power electronic induction motor drive systems. In: 20th Annual IEEE Power Electronics Specialists Conference. Milwaukee, WI: IEEE (1989). p. 923–30.
20. Chen J, Chau K, Siu S, Chan C. Experimental stabilization of chaos in a voltage-mode DC drive system. IEEE Trans Circuits Syst I Fundam Theory Appl. (2000) 47:1093–5. doi: 10.1109/81.855466
21. Robert B, Alin F, Goeldel C. Aperiodic and chaotic dynamics in hybrid step motor-new experimental results. In: ISIE 2001. 2001 IEEE International Symposium on Industrial Electronics Proceedings (Cat. No. 01TH8570). Vol. 3. Pusan: IEEE (2001). p. 2136–41.
22. Gao Y, Chau K, Ye S. A novel chaotic-speed single-phase induction motor drive for cooling fans. In: Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, 2005. Vol. 2. IEEE (2005). p. 1337–41.
23. Wei D, Luo X. Passive adaptive control of chaos in synchronous reluctance motor. Chin Phys B. (2008) 17:92–7. doi: 10.1088/1674-1056/17/1/017
24. Chau K, Chen J. Modeling, analysis, and experimentation of chaos in a switched reluctance drive system. IEEE Trans Circuits Syst I Fundam Theory Appl. (2003) 50:712–6. doi: 10.1109/TCSI.2003.811030
25. Ott E, Grebogi C, Yorke JA. Controlling chaos. Phys Rev Lett. (1990) 64:1196. doi: 10.1103/PhysRevLett.64.1196
26. Ren H, Liu D. Nonlinear feedback control of chaos in permanent magnet synchronous motor. IEEE Trans Circuits Syst II Express Briefs. (2006) 53:45–50. doi: 10.1109/TCSII.2005.854592
27. Pan Y, Sun T, Yu H. On parameter convergence in least squares identification and adaptive control. Int J Robust Nonlin. (2019) 29:2898–911. doi: 10.1002/rnc.4527
28. Liu H, Wang H, Cao J, Alsaedi A, Hayat T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J Franklin Inst. (2019) 356:9580–99. doi: 10.1016/j.jfranklin.2019.02.042
29. Luo XS, Wang BH, Fang JQ, Wei DQ. Robust adaptive dynamic surface control of chaos in permanent magnet synchronous motor. Phys Lett A. (2007) 363:71–7. doi: 10.1016/j.physleta.2006.10.074
30. Balasubramaniam P, Muthukumar P, Ratnavelu K. Theoretical and practical applications of fuzzy fractional integral sliding mode control for fractional-order dynamical system. Nonlin Dyn. (2015) 80:249–67. doi: 10.1007/s11071-014-1865-4
31. Li H, Wang J, Wu L, Lam HK, Gao Y. Optimal guaranteed cost sliding-mode control of interval type-2 fuzzy time-delay systems. IEEE Trans Fuzzy Syst. (2018) 26:246–57. doi: 10.1109/TFUZZ.2017.2648855
32. Harb AM. Nonlinear chaos control in a permanent magnet reluctance machine. Chaos Solit Fract. (2004) 19:1217–24. doi: 10.1016/S0960-0779(03)00311-4
33. Stotsky A, Hedrick J, Yip P. The use of sliding modes to simplify the backstepping control method. In: Proceedings of the 1997 American Control Conference (Cat. No. 97CH36041). Vol. 3. Albuquerque, NM: IEEE (1997). p. 1703–8. doi: 10.1109/ACC.1997.610875
34. Liu H, Pan Y, Li S, Chen Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybern Syst. (2017) 47:2209–17. doi: 10.1109/TSMC.2016.2640950
35. Liu H, Pan Y, Jinde C, Hongxing W, Yan Z. Adaptive neural network backstepping control of fractionial-order nonlinear systems with actuator faults. IEEE Trans Neural Netw Learn Syst. (2020). doi: 10.1109/TNNLS.2020.2964044. [Epub ahead of print].
36. Gao H, Song Y, Wen C. Event-triggered adaptive neural network controller for uncertain nonlinear system. Inform Sci. (2020) 506:148–60. doi: 10.1016/j.ins.2019.08.015
37. Bai W, Li T, Tong S. NN reinforcement learning adaptive control for a class of nonstrict-feedback discrete-time systems. IEEE Trans Cybern. (2020). doi: 10.1109/TCYB.2020.2963849. [Epub ahead of print].
38. Boulkroune A, Tadjine M, M'Saad M, Farza M. Fuzzy adaptive controller for MIMO nonlinear systems with known and unknown control direction. Fuzzy Sets Syst. (2010) 161:797–820. doi: 10.1016/j.fss.2009.04.011
39. Boulkroune A, Bouzeriba A, Bouden T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing. (2016) 173:606–14. doi: 10.1016/j.neucom.2015.08.003
40. Shukla MK, Sharma BB. Backstepping based stabilization and synchronization of a class of fractional order chaotic systems. Chaos Solit Fract. (2017) 102:274–84. doi: 10.1016/j.chaos.2017.05.015
41. Zhou J, Wen C, Wang W, Yang F. Adaptive backstepping control of nonlinear uncertain systems with quantized states. IEEE Trans Autom Control. (2019) 64:4756–63. doi: 10.1109/TAC.2019.2906931
42. Yip PP, Hedrick JK. Adaptive dynamic surface control: a simplified algorithm for adaptive backstepping control of nonlinear systems. Int J Control. (1998) 71:959–79. doi: 10.1080/002071798221650
43. Kwan C, Lewis FL. Robust backstepping control of induction motors using neural networks. IEEE Trans Neural Netw. (2000) 11:1178–87. doi: 10.1109/72.870049
44. Dawson DM, Carroll JJ, Schneider M. Integrator backstepping control of a brush DC motor turning a robotic load. IEEE Trans Control Syst Technol. (1994) 2:233–44. doi: 10.1109/87.317980
45. Fateh S, Fateh MM. Adaptive fuzzy control of robot manipulators with asymptotic tracking performance. J Control Autom Electric Syst. (2020) 31:52–61. doi: 10.1007/s40313-019-00496-5
46. Li Y, Chen Y, Podlubny I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica. (2009) 45:1965–9. doi: 10.1016/j.automatica.2009.04.003
47. Li Y, Tong S. Adaptive neural networks decentralized FTC design for nonstrict-feedback nonlinear interconnected large-scale systems against actuator faults. IEEE Trans Neural Netw Learn Syst. (2016) 28:2541–54. doi: 10.1109/TNNLS.2016.2598580
48. Yu J, Chen B, Yu H, Gao J. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping. Nonlin Anal Real World Appl. (2011) 12:671–81. doi: 10.1016/j.nonrwa.2010.07.009
Keywords: adaptive control, backstepping technique, neural network, fractional-order chaotic system, permanent magnet synchronous motor
Citation: Xue G, Lin F and Qin B (2020) Adaptive Neural Network Control of Chaotic Fractional-Order Permanent Magnet Synchronous Motors Using Backstepping Technique. Front. Phys. 8:106. doi: 10.3389/fphy.2020.00106
Received: 18 February 2020; Accepted: 20 March 2020;
Published: 21 April 2020.
Edited by:
Muhammad Javaid, University of Management and Technology, PakistanReviewed by:
Mohd Ariffanan Mohd Basri, Universiti Teknologi Malaysia, MalaysiaShengda Zeng, Jagiellonian University, Poland
Xianghu Liu, Guizhou University, China
Copyright © 2020 Xue, Lin and Qin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Funing Lin, dG9wbGluNTE4QDEyNi5jb20=
 Guangming Xue
Guangming Xue Funing Lin1*
Funing Lin1*