- Fakultät für Physik und Astronomie, Institut für Theoretische Physik II, Ruhr-Universität Bochum, Bochum, Germany
We review a new generation of nuclear forces derived in chiral effective field theory using the recently proposed semilocal regularization method. We outline the conceptual foundations of nuclear chiral effective field theory, discuss all steps needed to compute nuclear observables starting from the effective chiral Lagrangian and consider selected applications in the two- and few-nucleon sectors. We highlight key challenges in developing high-precision three-body forces, such as the need to maintain consistency between two- and many-body interactions and constraints placed by the chiral and gauge symmetries after regularization.
1. Introduction
Almost 30 years ago, Weinberg put forward his groundbreaking idea to apply chiral perturbation theory (ChPT), the low-energy effective field theory (EFT) of QCD, to the derivation of nuclear interactions [1, 2]. This seminal work has revolutionized the whole field of nuclear physics by providing a solid theoretical basis and offering a systematically improvable approach to low-energy nuclear structure and reactions.
So where do we stand today in the implementation of the program initiated by Weinberg? Much has been learned about specific features of the nuclear interactions and currents and about the role of many-body forces from the point of view of the effective chiral Lagrangian, see Epelbaum [3], Epelbaum et al. [4], Machleidt and Entem [5], and Hammer et al. [6] for review articles covering different research areas, while some issues are still under debate [6, 7]. Meanwhile, the interactions derived in chiral EFT, sometimes referred to as “chiral forces,” have largely replaced phenomenological potentials developed in the nineties of the last century. They are nowadays commonly used in ab initio nuclear structure calculations, see Epelbaum et al. [8], Piarulli et al. [9], Lonardoni et al. [10], Hagen et al. [11], Gebrerufael et al. [12], and Cipollone et al. [13] for recent examples using a variety of continuum ab initio methods and Epelbaum et al. [14], Elhatisari et al. [15], and Lähde and Meißner [16] for selected highlights from nuclear lattice simulations. With the most recent chiral nucleon-nucleon (NN) potentials [17] providing a nearly perfect description of the mutually consistent neutron-proton (np) and proton-proton (pp) scattering data below pion production threshold from the Granada-2013 database [18], the two-nucleon sector is already in a very good shape. On the other hand, three-nucleon forces (3NF) are much less understood at the quantitative level [19] and constitute an important frontier in nuclear physics [20].
In this article we focus on the latest generation of chiral nuclear forces based on an improved regularization approach [17, 21, 22], which allows one to maintain the long-range part of the interaction as will be described in section 4.1. We review our recent work along these lines in the two-nucleon sector, describe the ongoing efforts by the Low-Energy Nuclear Physics International Collaboration (LENPIC) toward developing consistent1 many-body forces and solving the structure and reactions of nuclei, and discuss selected applications. For selected recent studies along these lines by other groups, see Entem et al. [23], Gezerlis et al. [24], Piarulli et al. [25], Ekström et al. [26, 27], Li et al. [28], Lynn et al. [29], and Girlanda et al. [30], and references therein.
Our paper is organized as follows. In section 2, we outline the foundations of the employed theoretical framework. Section 3 gives an overview of various methods to derive nuclear forces and currents from the effective chiral Lagrangian. It also summarizes the available results for nuclear potentials derived using dimensional regularization (DR). In section 4, we present the improved semilocal regularization approach, which is utilized in the most accurate and precise NN potentials of Reinert et al. [17]. We also discuss the challenges that need to be addresses to construct consistently regularized 3NFs and exchange current operators beyond tree level, which are not restricted to any particular type of cutoff regularization. Section 5 is devoted to uncertainty quantification in chiral EFT. Selected results for the NN system, three-nucleon scattering and light nuclei are presented in section 6. We conclude with a short summary and outlook in section 7.
2. The Framework in a Nutshell
Throughout this work, we restrict ourselves to the two-flavor case of the light up- and down-quarks and employ the simplest version of the effective chiral Lagrangian with pions and nucleons as the only active degrees of freedom. Contributions of the Δ(1232) isobar to the nuclear potentials are discussed in Ordonez et al. [31], Kaiser et al. [32], Krebs et al. [33], Epelbaum et al. [34, 35], and Krebs et al. [36]. The effective Lagrangian involves all possible interactions between pions and nucleons compatible with the symmetries of QCD and is organized in powers of derivatives and quark (or equivalently pion) masses. Pions correspond to the (pseudo) Nambu-Goldstone bosons of the spontaneously broken axial generators and thus transform nonlinearly with respect to chiral SU(2)L × SU(2)R transformations. The effective Lagrangian can be constructed in a straightforward way using covariantly transforming building blocks defined in terms of the pion fields [37, 38]. All applications reviewed in this paper rely on a non-relativistic treatment of the nucleon fields and make use of the heavy-baryon formalism to eliminate the nucleon mass m from the leading-order Lagrangian. The individual terms in the effective Lagrangian are multiplied by the corresponding coupling constants, commonly referred to as low-energy constants (LECs), which are not fixed by the symmetry and typically need to be determined from experimental data. The most accurate currently available nuclear potentials at fifth order in the chiral expansion, i.e., at N4LO, require input from the following effective Lagrangians (with each line containing the contributions with a fixed number of the nucleon fields)
where Mπ and Fπ are the pion mass and decay constant2, gA is the nucleon axial-vector coupling while li, ci, di, ei, Ci, D, Di, E, and Ei are further LECs. The superscript n of denotes the number of derivatives and/or Mπ-insertions and is sometimes referred to as the chiral dimension. Notice that we only show new LECs that appear in the corresponding Lagrangians and suppress the dependence on the LECs appearing at lower orders. The pionic Lagrangian can be found in Gasser and Leutwyler [39], is given in Bernard et al. [40], and Fettes et al. [41], was introduced in Weinberg [1, 2], can be found in Epelbaum et al. [42], and Girlanda et al. [43], the minimal form of is given in Reinert et al. [17], and are discussed in Epelbaum et al. [44] while was constructed in Girlanda et al. [45]. Notice further that the chiral symmetry breaking terms are not shown explicitly in and . For calculations at the physical value of the quark masses, their contributions are absorbed into the LECs listed in Equation (1). We have, furthermore, restricted ourselves in this equation to isospin-invariant terms for the Lagrangians involving two and three nucleons. The single-nucleon Lagrangian does involve isospin-breaking contributions due to the quark mass difference and can be extended to include virtual photon effects [46, 47]. The ellipses in the second-to-last line of Equation (1) refer to higher-order Lagrangians , which have not been worked out yet and would be needed to finalize the derivation of the 3NF at N4LO.
The long-range parts of the nuclear forces emerge from pion exchange diagrams and can be derived from and . Fortunately, only a very restricted set of (linear combinations of) LECs from these Lagrangians contributes to the πN → πN and πN → ππN scattering amplitudes, which enter as subprocesses when deriving the long-range nuclear interactions up to N4LO, namely c1, …, 4 from , d1 + d2, d3, 5, 18, and d14 − d15 from and e14, …, 18 from . Here, we made use of the fact that the contributions from the LECs l3, e19, …, 22, and e35, …, 38 can be absorbed into the appropriate shifts of the LECs ci [48]. All these πN LECs can nowadays be reliably extracted by matching the πN scattering amplitude from the recent Roy-Steiner equation analysis [49] with ChPT at the subthreshold point [50], see also Siemens et al. [51] for an alternative strategy. Thus, the long-range nuclear interactions are completely determined by the spontaneously broken approximate chiral symmetry of QCD and experimental/empirical information on the πN system in a parameter-free way. The two- and three-nucleon interactions in the last two lines of Equation (1) parameterize the short-range part of the nuclear forces, and the corresponding LECs have to be determined from NN scattering and three- or more-nucleon observables.
In the single-nucleon sector, the effective Lagrangian can be used to systematically compute the scattering amplitude in perturbation theory by applying the chiral expansion, a simultaneous expansion in particles' external three-momenta and around the chiral limit Mπ → 0. The importance of every Feynman diagram is estimated by counting powers of the soft scales and applying the rules of naive dimensional analysis (NDA). The expansion parameter Q ∈ {p/Λb, Mπ/Λb} is determined by the breakdown scale Λb, which may (optimistically) be expected to be of the order of the ρ-meson mass3. At every order in the chiral expansion only a finite number of Feynman diagrams need to be evaluated. For more details on ChPT in the 1N sector see the review article [53].
Contrary to the 1N case, the NN S-wave scattering amplitude exhibits poles in the near-threshold region corresponding to the bound state (deuteron) and the virtual state in the 1S0 channel, which signal the breakdown of perturbation theory. In this context, it was pointed out by Weinberg that the contributions of multi-nucleon ladder diagrams are enhanced compared to the estimation based on the chiral power counting due to the appearance of pinch singularities (in the m → ∞ limit) [1, 2]. Weinberg also argued that the nucleon mass needs to be counted as in order to formally justify the need to perform a non-perturbative resummation of the ladder contributions. Given that the ladder diagrams are automatically resummed by solving the few-nucleon Schrödinger equation, Weinberg's chiral EFT approach to low-energy nuclear systems, perhaps not surprisingly, resembles the quantum mechanical A-body problem
where Δi is the Laplace operator acting on the nucleon i. The nuclear potentials V2N, V3N, … receive contributions from diagrams that cannot be reduced to ladder iterations and are calculable in a systematically improvable way within ChPT.
Among the many attractive features, the approach outlined above allows one to maintain consistency between nuclear forces and exchange current operators which are scheme-dependent quantities. To illustrate the meaning and importance of consistency consider the Feynman diagram on the left-hand side (l.h.s.) of the equality shown in Figure 1 as an example. The corresponding (on-shell) contribution to the scattering amplitude features both a reducible (i.e., of a ladder-type) and irreducible pieces as visualized in the figure. Reducible contributions to the amplitude are resummed up to an infinite order when solving the Faddeev equation corresponding to Equation (2). In doing so, the diagrams corresponding to its zeroth and first iterations shown in the figure must match the result obtained from the Feynman diagram when taken on the energy shell. The iterative contribution from the first graph on the right-hand side of the depicted equality, however, involves NN and 3N potentials, whose off-shell behavior is scheme dependent. Also the 3NF corresponding to the last diagram is scheme dependent (even on the energy shell) [54], and only a consistent choice of the involved two- and three-nucleon potentials guarantees the validity of matching for the scattering amplitude. This can indeed be verified explicitly using the expressions for the 3NFs from Equations (4.9) to (4.11) of Bernard et al. [55] and from Equations (2.16) to (2.20) of Bernard et al. [54] and employing DR to evaluate loop integrals4.
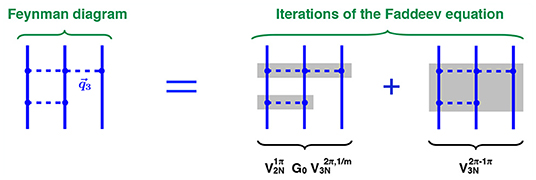
Figure 1. Representation of the on-shell scattering amplitude from the one-pion-two-pion-exchange Feynman diagram (left) in terms of iterations of the Faddeev equation (right). Gray-shaded rectangles visualize the corresponding two- and three-nucleon potentials , , and while G0 denotes the free resolvent operator for non-relativistic nucleons.
Clearly, DR is impractical for a numerical solution of the A-body problem and is usually replaced by cutoff regularization. Renormalization of the Schrödinger equation in the context of chiral EFT is a controversial and heavily debated topic, see Lepage [56], Pavon Valderrama and Ruiz Arriola [57], Nogga et al. [58], Birse [59], Epelbaum and Meißner, [60], Epelbaum and Gegelia [61], Long and Yang [62], Valderrama [63], Epelbaum et al. [7], and Hammer et al. [6] for a range of opinions. The essence of the problem is related to the non-renormalizable nature of the Lippmann-Schwinger (LS) equation for NN potentials truncated at a finite order in the chiral expansion. Except for a few cases, such as the leading-order (LO) equation in pionless EFT and in chiral EFT in spin-singlet channels, ultraviolet (UV) divergences emerging from the loop expansion of the scattering amplitude cannot be absorbed into redefinitions of parameters appearing in the truncated potentials [7, 64]. The problem can be avoided by treating the one-pion exchange (OPE) and higher-order contributions to the potential in perturbation theory using e.g., the systematic power counting scheme proposed by Kaplan et al. [65], but the resulting approach unfortunately fails to converge (at least) in certain spin-triplet channels [66, 67] (see also [68] for a recent discussion). A renormalizable framework with the one-pion exchange potential (OPEP) treated non-perturbatively was proposed in Epelbaum and Gegelia [69] (see also [70]), based on a manifestly Lorentz invariant form of the effective Lagrangian. This approach requires a perturbative inclusion of higher-order contributions to the potential in order to maintain renormalizability (which may lead to convergence issues in some channels [71]) but has not been systematically explored beyond LO yet.
Throughout this work we employ a finite-cutoff version of nuclear chiral EFT in the formulation of Lepage [56], which is utilized in most of the applications available today. This is so far the only scheme, that has been advanced to high chiral orders and successfully applied to a broad range of few- and many-nucleon systems. Below, we briefly summarize the basic steps involved in the calculation of nuclear observables within this framework. In the following sections, all four steps outlined below will be discussed in detail.
i. Derivation of nuclear forces and current operators from the effective chiral Lagrangian. This can be achieved by separating out irreducible contributions to the A-nucleon scattering amplitude that cannot be generated by iterations of the dynamical equation using various methods outlined in section 3. The derivations are carried out in perturbation theory using the standard chiral power counting. In contrast to ChPT for the scattering amplitude, special efforts are needed to arrive at renormalized nuclear potentials. This requires that all UV divergences from irreducible loop diagrams are canceled by the corresponding counter terms. The renormalizability requirement imposes strong constraints on the unitary ambiguity of nuclear forces and currents [48, 72–75].
ii. Introduction of a regulator for external (off-shell) momenta of the nucleons in order to make the A-body Schrödinger equation well-behaved. Given the lack of counter terms needed to absorb all UV divergences from iterations of the dynamical equation with a truncated potential, the (momentum-space) cutoff Λ must not be set to arbitrarily high values but should be kept of the order of the breakdown scale, Λ ~ Λb [7, 56, 61]. The accessible cutoff window is, in practice, further restricted by the need to avoid the appearance of spurious deeply bound states which provide a severe complication for applications beyond the NN system [76] and a preference for soft interactions in order to optimize convergence of ab initio many-body methods. Given the rather restricted available cutoff window, it is important to employ regulators that minimize the amount of finite-cutoff artifacts, see section 4 for discussion. While the regulator choice for V2N still features a high degree of ambiguity, maintaining the relevant symmetries and consistency with regularized many-body forces and exchange currents beyond tree level represents a highly nontrivial task [77, 78] (see section 4 for an example and discussion).
iii. Renormalization of the few-nucleon amplitude by fixing the short-range multi-nucleon interactions from low-energy experimental data (see section 6 for details). This allows one to express the calculated scattering amplitude in terms of observable quantities instead of the bare LECs CS, T(Λ), Ci(Λ), Di(Λ), D(Λ), E(Λ), Ei(Λ), …, and amounts to implicit renormalization of the amplitude. Notice that in the pion and 1N sectors of ChPT, renormalization is usually carried out explicitly by splitting the bare LECs li, di, ei, …, into the (finite) renormalized ones and counter terms, e.g., . Here, μ denotes the renormalization scale while Ri are the corresponding counter terms, which diverge in the limit of a removed regulator (i.e., Λ → ∞ in the cutoff regularization or the number of dimensions d → 4 in DR). Such a splitting is not unique as reflected by the scale μ, and the appropriate choice of renormalization conditions is essential to maintain the desired power counting, i.e., to ensure the appropriate scaling behavior of renormalized contributions to the amplitude leading to a systematic and self-consistent scheme (see e.g., [79, 80]). In the few-nucleon sector, the non-perturbative resummation of pion-exchange potentials via Equation (2) can only be carried out numerically5, which leaves the implicit renormalization outlined above as the only available option. Notice that contrary to the renormalized LECs , , …, the bare LECs CS, T(Λ), Ci(Λ), …, must be re-determined at every order in the expansion.
iv. Estimation of the truncation uncertainty and a-posteriori consistency checks of the obtained results. These include, among others, testing the naturalness of the extracted LECs [17], making error plots for phase shifts as suggested in Lepage [56], and Grießhammer [81], verifying a reduced residual Λ-dependence of observables (within a specified cutoff range) upon including higher-order short-range interactions, see e.g., Figure 4 of Epelbaum [82], and confronting the contributions of many-body interactions and/or exchange currents with estimations based on the assumed power counting [83, 84]. Our approach to error analysis is outlined in section 5, while selected consistency checks are discussed in section 6.
Before closing this section, several remarks are in order. First, we emphasize that the approach outlined above is applicable at the physical quark masses. Quark mass dependence of nuclear observables can be studied more efficiently in the renormalizable chiral EFT framework of Epelbaum and Gegelia [69, 85], see also Baru et al. [86, 87], and Lähde et al. [88] for an alternative method. Secondly, the validity (in the EFT sense) of the finite-cutoff EFT formulation outlined above has been demonstrated numerically by means of the error plots [56, 89] and analytically [61] for toy-models with long-range interactions. It can also be easily verified in pionless EFT. For the case of exactly known non-singular long-range potentials, the employed approach reduces in the NN sector to the well-known modified effective range expansion [90]. The relation between the choice of renormalization conditions and power counting is discussed within pionless EFT in Epelbaum et al. [91]6. That paper provides an explicit example of the choice of subtraction scheme (i.e., renormalization conditions), which leads to a self-consistent EFT approach for two particles with both a natural and unnaturally large scattering length, while respecting the NDA scaling of renormalized LECs. Notice that in all applications reviewed in this article, few-nucleon short-range interactions are counted according to NDA. A number of authors advocate alternative approaches, in particular by inferring the importance of short-range operators from the requirement of Λ-independence of the scattering amplitude at arbitrarily large values of Λ as articulated in detail in Hammer et al. [6]. However, performing the loop expansion of the solution of the LS equation in spin-triplet channels for the resummed OPEP shows that the scattering amplitude is only partially renormalized in spite of the fact that it admits, in some cases, a finite Λ → ∞ limit at a fixed energy [7]. The danger of choosing Λ≫Λb in such partially renormalized non-perturbative expressions is demonstrated using an exactly solvable model in Epelbaum and Gegelia [61].
3. Chiral Perturbation Theory for Nuclear Potentials
One method to decouple pion-nucleon and purely nucleonic subspaces of the Fock space, thereby reducing a quantum field theoretic problem to a quantum mechanical one, is the unitary transformation (UT) technique. Let η and λ be the projection operators onto the purely nucleonic subspace of the Fock space and the rest, respectively. The time-independent Schrödinger equation can be written in the form
where E denotes the eigenenergy of the πN system. The idea is to apply a UT to the Hamilton operator H in order to block diagonalize the matrix on the l.h.s. of Equation (3) leading to
The decoupling requirement is given by
To construct the UT U we first introduce a Møller operator Ω [92], which is defined by
with the requirement
Here, |Ψ〉 refers to few-nucleon scattering states below pion production threshold. See Lindgre [93] for a discussion of the properties of the operator Ω. The Møller operator reproduces the original low-energy state out of projected state. By projecting Equation (6) onto the model space η one obtains the identity
Using Equation (6), we can write the time-independent Schrödinger equation in the form
where H0 denotes a free Hamiltonian. On the other hand, projecting the original Schrödinger equation Equation (3) onto the model space and applying on the resulting equation the operator Ω, we obtain
Subtracting Equation (10) from Equation (9) leads to
This way we obtain a non-linear equation for the Møller operator Ω
Defining the operator A via Ω =:η+A with A = λAη, as follows from Equations (7) and (8), we rewrite Equation (12) in the form
The UT U was parameterized by Okubo [94] in terms of the operator A via
The resulting transformed Hamiltonian
leads to the effective potential defined via
Obviously, the Okubo transformation in Equation (14) is not the only possibility to obtain a block-diagonalized Hamiltonian. On top of the transformation U one can always apply e.g., a UT acting nontrivially on the η-space, thus leaving the Hamiltonian block-diagonal. This freedom has been exploited in a systematic manner to construct renormalizable/factorizable 3NFs and four-nucleon forces (4NFs) in chiral EFT in Epelbaum [72], Bernard et al. [54, 55], and Krebs et al. [48, 95].
To derive the potential from the effective chiral Lagrangian in Equation (1) one needs to solve the non-linear decoupling Equation (13) for the operator A. This can be done perturbatively using NDA [3] to count powers of three-momenta and pion masses, denoted collectively by Q. For the sake of definiteness, we restrict ourselves in the following to nuclear potentials in the absence of external sources. The extension to the current operators is straightforward and discussed in details in Krebs et al. [75]. The irreducible contributions of any connected Feynman diagram scale as Qν with , where Vi denotes the number of vertices of type i and κi is the inverse mass dimension of the corresponding coupling constant, . Here, di is the number of derivatives and/or Mπ-insertions, while ni and pi denote the number of nucleon and pion fields, respectively7. This particular form of the power counting allows one to formulate the chiral expansion in the form that is completely analogous to the expansion in powers of coupling constants. It is thus particularly well suited for algebraic approaches such as the method of UT. Once the operator A is available, one can perform the chiral expansion of Equation (15) to construct the effective potential order-by-order.
The chiral expansion of the nuclear forces is visualized in Figure 2. Below, we briefly discuss isospin symmetric contributions starting from the leading order (LO) Q0. The only contributions at this order emerge from the OPEP and two contact interactions ∝CS, T [1, 2]. The first corrections at order Q2 (NLO) involve the leading two-pion exchange potential (TPEP) [31, 96, 97] and 7 short range interactions ∝Ci. At order Q3 (N2LO), further corrections to the TPEP ∝ci need to be taken into account [96]. At the same order one has the first non-vanishing contributions to the 3NF. They are given by the two-pion exchange diagram involving the LECs ci and two shorter-range tree-level diagrams involving the LECs D and E [44, 98]. At order Q4 (N3LO), the NN potential receives the contributions from the leading three-pion exchange [99–101], further corrections to the TPEP [102, 103] and 12 new short-range interactions ∝Di [17]. At the same order, there are various one-loop corrections to the 3NF [54, 55, 104] and the first contributions to the 4NFs [72, 73], which do not involve unknown parameters. Finally, at order Q5 (N4LO), the NN potential receives corrections to the three-pion exchange ∝ ci [101] and further contributions to the TPEP [105]. No additional unknown parameters appear in the isospin-conserving part of the NN force at this order. The 3NF also receives corrections at N4LO, most of which have already been worked out using DR [45, 48, 95]. Notice that the 3NF involves at this order a number of new short-range operators. Work is still in progress to derive the remaining 3NF and 4NF at N4LO. We further emphasize that all calculations mentioned above are carried out using DR or equivalent schemes.
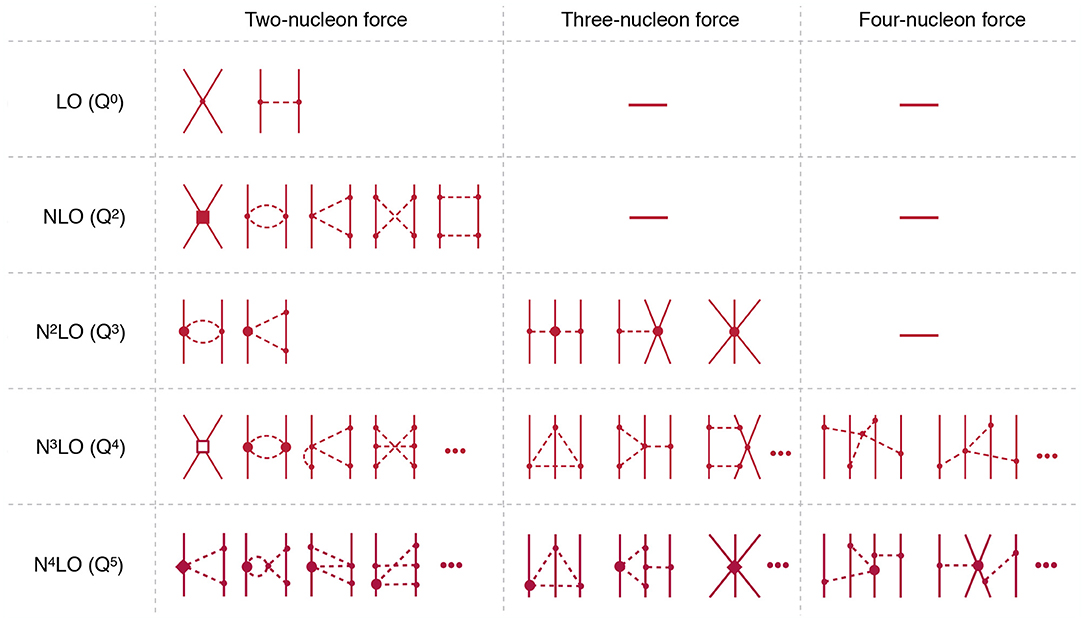
Figure 2. Hierarchy of nuclear forces at increasing orders in chiral expansion in the Weinberg scheme. Solid and dashed lines refer to nucleons and pions, respectively. Solid dots, filled circles, filled squares, filled diamonds, and open squares refer to vertices from the Lagrangian in Equation (1) of dimension Δ = 0, 1, 2, 3, and 4, respectively.
The effective potential leads, by construction, to the same spectrum and on-shell scattering matrix as the original untransformed potential V [106, 107]. There are, however, other possibilities to define the effective potential without changing on-shell physics. One example is an energy-independent potential defined by
The proof that of Equation (17) leads to the same spectrum is trivial:
where we used Equations (6) and (8) in the first and second lines, respectively. Note that the potential is manifestly non-hermitian. However, due to its simplicity, it is widely used in the literature [92]. This example shows that there is a considerable freedom to define nuclear potentials. Nuclear forces and current operators constructed by the Bochum-Bonn group (see e.g., [17, 21, 22, 48, 54, 55, 73–75, 95, 97]), are obtained using the method of UT. The JLab-Pisa group utilizes a different approach by starting with the on-shell transfer matrix T and “inverting” it to obtain the effective potential (see e.g., [108–111]). This is carried out in perturbation theory by counting the nucleon mass via m ~ Λb
where the superscripts indicate the chiral order Qn. The same counting scheme is used to organize the contributions to effective potential:
The inversion of the LS equation is carried out iteratively to yield
Obviously, the knowledge of the on-shell transfer matrix is insufficient to perform the inversion, and one needs to specify its off-shell extension. Notice that the potentials constructed in this way are not necessarily hermitian, and thus there is no guarantee that they are unitarily equivalent to the ones derived using the UT technique. It should, however, always be possible to find a similarity transformation that relates one potential to another. This is exemplified with the potential in Equation (20) of Pastore et al. [109], where ν is an arbitrary phase, which is manifestly non-hermitian. Using the similarity transformation in Equation (28) of that paper8, it can be transformed to the hermitian potential , that is actually employed in the current version of the interactions developed by the JLab-Pisa group. With this choice, their potentials are unitarily equivalent to the ones of the Bochum-Bonn group.
4. Regularization
4.1. Semilocal Momentum-Space Regularization of the NN Potential
In this review article we focus on the semilocal regularization approach of the chiral nuclear potentials carried out in momentum space [17]. For the purpose of regularization we will consider the two-nucleon interaction consisting of two distinct parts: the short-range contact interaction part and the long-range pion-exchange part. In this context, the term “semilocal” refers to the application of a nonlocal regulator for the former and a local regulator for the latter. In particular, the momentum-space matrix elements of the contact potential are multiplied by a simple nonlocal Gaussian regulator
Here and in what follows, and . Such kinds of nonlocal regulators (albeit with different powers of p, p′, and Λ) have been and still are employed as the main method of regularization for the entire potential including the long-range interactions (see e.g., [23, 27, 112–115])9.
However, in Epelbaum et al. [21, 22] it was shown that the amount of long-range cutoff artifacts can be significantly reduced by employing a local regulator for pion-exchange potentials. Notice that pion-exchange contributions, except for some relativistic corrections, give rise to local potentials. We require the regulator to preserve the long-range part of the interaction, which is unambiguously determined in chiral EFT. More precisely, for Λ≫Mπ, the regulator is required not to affect the large-distance behavior of the n-pion exchange potential Vnπ(r) ~ exp(−nMπr)f(r), with f(r) being an irrational function, up to exponentially small corrections that vanish in the limit Λ → ∞. Inspired by Rijken [118], this is achieved in our momentum-space approach by regularizing the static propagators of pions exchanged between different nucleons with a local Gaussian cutoff via
with and denoting the three-momentum of the exchanged pion. The introduction of the Gaussian form factor in the pion propagators leads to properly regularized long-range potentials that are finite at short distances in coordinate space. In order to have a clean separation of the long-range pion-exchange potential from the short-range contact interactions, we made use of the available contact interactions to subtract out the remaining (finite) admixtures of short-range interactions [17]. The fixed coefficients of these subtractions are determined from the requirement that the corresponding coordinate-space potential and as many derivatives thereof as allowed by power counting vanish at the origin. This convention leads to a qualitatively similar regularization as the coordinate-space regulator previously employed in Epelbaum et al. [21, 22].
Application of these ideas to the OPEP is straightforward and leads, in the limit of exact isospin symmetry, to
where and (τi) are the Pauli spin (isospin) matrices of the i-th nucleon. Here, the static pion propagator has been regularized according to Equation (23) and a likewise-regularized LO contact interaction has been added to the OPEP. Its coefficient C(Mπ),
with erfc(z) denoting the complementary error function, is fixed by the requirement that the spin-spin part of the OPEP in coordinate space vanishes at the origin. For the regularization of the TPEP, we start with a generic three-dimensional loop integral arising in the derivation of the TPEP using e.g., the method of unitary transformation as detailed in the previous section or comparable approaches like time-ordered perturbation theory or S-matrix-based methods [96]. As discussed in Rijken [118], the pion energy denominators in the corresponding 1-loop expressions can always be rewritten into an integral over a mass parameter λ involving a product of two static pion propagators with mass
where and denote the three-momenta of the exchanged pions and the ellipses refer to additional momentum-spin-isospin structures arising from the vertices of a particular diagram. With the pion propagators factorized in this a way, we can regularize them by applying the prescription specified in Equation (23) to each of them. Although the introduction of the regulator obviously affects the resulting expression for the TPEP, there is no need to rederive them explicitly. Indeed, the scalar functions accompanying the spin-isospin operators in the unregularized TPEP can be expressed using the dispersive representation
with the spectral functions which are readily available up to N4LO. For the explicit expressions of the TPEP, additional subtractions of short-range terms have to be performed to arrive at a convergent spectral integral in Equation (27) whose number depends on the chiral order of the contribution at hand. Introducing the pion propagator regulators in Equation (26), the regularized generic spectral integral of Equation (27) is replaced by
see Reinert et al. [17] for more details. The resulting potential coinsides with the one obtained by explicitly evaluating the loop integral with regularized pion propagators up to a short-range function.
Expanding the exponentials in inverse powers of the cutoff in either Equation (24) or Equation (28), one observes that the regulator indeed does not affect the long-range part of the potential to any order, but generates an infinite series of short-range terms polynomial in q2. Since an increasing number of contact interactions of this form with freely adjustable LECs become available with increasing chiral order, the perturbative restoration of cutoff-independence is also obvious in this scheme.
The expressions of the regularized and subtracted TPEP can be found in Reinert et al. [17]. Here we restrict ourselves to the example of the isospin-independent central part of the leading TPEP at NLO which is given by
with the spectral function
Two subtractions have been performed in order to render the unregularized spectral integral in Equation (29) convergent and according to our convention, we have additionally fixed the subtraction coefficients and by the requirement that . [The first derivative of vanishes at the origin regardless of the subtraction coefficients]. Figure 3 shows the ratio of the regularized and unregularized expressions in Equation (29) in coordinate space. As one can see, the behavior of the regularized potential is smoother when fixing the subtraction coefficients by the convention explained above. Also note that the potential with does not vanish at the origin10.
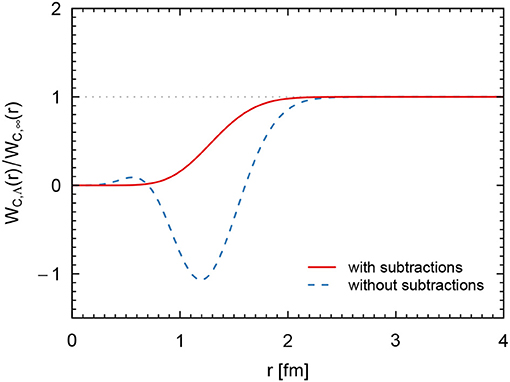
Figure 3. Ratio of the regularized and unregularized central part of the leading TPEP in coordinate space for , fixed as discussed in the text and .
4.2. Regularization and Consistency of Nuclear Forces
Having defined the regularization scheme in the NN sector, we now turn to regularization of the 3NF. The expressions for the 3NFs described in section 3 have been worked out completely through N3LO using DR. They are off-shell consistent with the unregularized NN interactions reviewed in that section in the way explained in section 2. To arrive at regularized 3NFs, it is tempting to apply some kind of multiplicative regulators to the expressions of the 3NF derived using DR. Such a naive approach, however, leads to a violation of the chiral symmetry at N3LO and destroys the consistency between two- and three-nucleon forces after regularization.
To illustrate the problem consider the diagrams shown in Figure 1, which have already been discussed in section 2. The 3NF entering the first graph on the right-hand side (r.h.s.) is given by Bernard et al. [55]
with , , and , () the initial (final) momenta of the i-th nucleon. The complete expression for the relativistic corrections to the 3NF at N3LO can be found in Bernard et al. [55]. We now consider the first iteration of with the static OPEP
as shown by the first diagram on the r.h.s. of Figure 1. By simply counting the powers of momenta in the loop integration one observes that the loop integral is linearly divergent, which leads to a finite result in DR. As already pointed out in section 2, adding the DR expression for the 3NF from Equations (2.16) to (2.20) of Bernard et al. [54] yields (on-shell) the same result as obtained from calculating the Feynman diagram on the l.h.s. of Figure 1 as expected for consistent two- and three-nucleon forces.
We now repeat this exercise using the semilocally regularized nuclear potentials
in the calculation of the first diagram on the r.h.s. of Figure 2. This leads to
where the ellipses refer to all permutations of the nucleon labels and terms finite in the Λ → ∞-limit. The linear divergence is canceled by the D counter term in the second 3NF diagram at N2LO in Figure 2. To cancel the linearly divergent contribution one would, however, need to introduce a vertex in corresponding to a derivative-less coupling of the pion to the NN systems. Such vertices violate the chiral symmetry and, being suppressed by powers of , cannot appear in . As a consequence, this linear divergence can not be absorbed into redefinition of the LECs, and the amplitude on the r.h.s. of Figure 1 can seemingly not be renormalized (i.e., made finite in the Λ → ∞ limit). The r.h.s. of the shown equation, therefore, apparently cannot match the (renormalizable) on-shell scattering amplitude from the Feynman diagram on the l.h.s. The problem can be traced back to mixing the DR when calculating the 3NF with a cutoff regularization for the iterative contributions in Equation (34), see Krebs [77] for another example with the NN axial vector current operator at N3LO. Indeed, recalculating the loop integral in using the cutoff-regularized pion propagators leads to
where the ellipses refer to the finite terms in the Λ → ∞-limit. The problematic linear divergence cancels exactly and the agreement with the on-shell amplitude from the Feynman diagram is restored when both consistently regularized contributions on the r.h.s. of Figure 1 are added together.
One may worry whether the regularization issues discussed above could also be relevant for NN interactions. Fortunately, this is not the case since the momentum structure of the NN contact interactions is not restricted by the chiral symmetry. UV divergences emerging from iterations of the LS equation can, therefore, always be absorbed into redefinition of the bare LECs CS, T(Λ), Ci (Λ), ….
In the considered example with the 3N amplitude, the consistently regularized 3NF could be obtained by simply recalculating with all pion propagators being regularized according to Equation (23). This would indeed solve the problem with the cancelation of linear divergencies at N3LO, but it would still lead to a violation of the chiral symmetry in diagrams involving three- and four-pion vertices, which depend on the parametrization of the pion field. For vertices involving up to four pion fields, this freedom is represented by a single real parameter α. In the effective chiral Lagrangian, all pion fields are collected in an SU(2) matrix U(π), whose most general expression, expanded in powers of the pion fields, takes the form
Clearly, the on-shell amplitude must be independent of the arbitrary parameter α. Evaluating the 3NF and 4NF with the regularized pion propagators, however, leads to α-dependent expressions (for finite values of Λ). This shows, perhaps not surprisingly, that the simplistic approach by regularizing all pion propagators as described above violates the chiral symmetry. A possible solution of this problem is provided by the symmetry preserving higher derivative regularization method introduced by Slavnov [119], see also Djukanovic et al. [120] and Long and Mei [121] for recent applications in chiral EFT.
To summarize, we have shown that a naive regularization of the three- and more-nucleon forces by multiplying the expressions derived in DR with regulator functions leads to inconsistencies starting from N3LO, see Krebs [77] for the same conclusion for two- and more-nucleon charge and current operators. This problem is by no means restricted to semilocal cutoffs. To derive many-body forces and currents regularized consistently with the NN potentials of Reinert et al. [17], the expressions for the 3NF of Bernard et al. [54, 55] and Krebs et al. [48], 4NF of Epelbaum [73], and exchange charge and current operators of Kölling et al. [74, 122] and Krebs et al. [75, 123] need to be recalculated using e.g., an appropriately chosen higher derivative regulator at the level of the effective Lagrangian.
5. Truncation Error Analysis
Estimating the uncertainty associated with truncations of the EFT expansion, which typically dominates the error budget (see section 6), is an important task – in particular since chiral EFT is being developed into a precision tool. In the past, truncation errors were often estimated in few-nucleon calculations from a residual cutoff dependence. This approach, however, suffers from several drawbacks and does not allow for a reliable estimation of truncation errors [113]. In Epelbaum et al. [21], we have formulated a simple algorithm to estimate the size of neglected higher-order terms based on the available information about the EFT expansion pattern for any given observable. To be specific, consider an arbitrary NN scattering observable X at the center of mass momentum p, which is calculated in chiral EFT up to the order Qk
The corrections ΔX(i), , are assumed to be known explicitly up to the order i = k. The goal is to estimate the size of neglected higher-order terms . We, furthermore, assume that the expansion parameter Q is given by
This simple ansatz is motivated by the expectation that at very low energies, the errors are dominated by the expansion around the chiral limit. The scale , which will be specified below, is related to the pion mass and controls the convergence rate of the expansion around the chiral limit. At higher energies one would, on the other hand, expect the expansion to be dominated by powers of momenta. This simple picture is in qualitative agreement with the error plots for NN phase shifts [21], which show clearly the two different regimes mentioned above, see Epelbaum [82] for a discussion. It is less clear how to estimate the relevant momentum scale in bound-state observables.
The algorithm proposed by Epelbaum, Krebs and Meißner (EKM) in Epelbaum et al. [21] employs and Λb = 600 MeV based on the estimation from the error plots. It also assumes the truncation error δX(k) to be dominated by the first neglected term. The truncation errors at orders Qi, 0 ≤ i ≤ k, are then estimated via
subject to the additional constraint
which ensures that the estimated errors cannot be smaller than the known actual higher-order contributions. Notice that this relation leads, per construction, to overlapping errors at different orders. In Binder et al. [83], the method was adjusted to make it applicable to incomplete calculations of few-body observables based on NN interactions only. The EKM approach was applied to a broad range of low-energy reactions in the single-baryon [51, 124–126] as well as few- and many-nucleon [8, 22, 127–129] sectors. The robustness of this method and some alternative algorithms are discussed in Binder et al. [130]. The obvious drawback of the EKM approach is that the estimated uncertainties do not offer a statistical interpretation.
In Furnstahl et al. [131] and Melendez et al. [132, 133], a more general and statistically well-founded Bayesian approach was developed to calculate the probability distribution function (pdf) for truncation errors in chiral EFT. The EKM approach was then shown to correspond to one particular choice of prior probability distribution for the coefficients in the chiral expansion of X(p). In Furnstahl et al. [131], the EKM uncertainties for the np total cross section were found to be consistent with 68% degree-of-belief (DoB) intervals. The authors of that paper, furthermore, found using the semilocal coordinate-space regularized (SCS) potentials of Epelbaum et al. [21, 22] the assumed value of the breakdown scale of Λb = 600 MeV to be statistically consistent for not too soft regulator values, see also Melendez et al. [132] for a related discussion. Recently, a slightly modified version of the Bayesian approach developed in Furnstahl et al. [131] and Melendez et al. [132] was applied by the LENPIC Collaboration to study NN and 3N scattering [84]. Below, we briefly outline the Bayesian model proposed in that paper, which will be employed throughout section 6. For more details on the Bayesian approach the reader is referred to the original publications [131, 132].
We begin with rewriting Equation (37) in terms of dimensionless expansion coefficients ci by introducing a (generally dimensionfull) scale Xref via
where11
This choice of the reference scale was found in Epelbaum et al. [84] to be more robust for observables that depend on continuously varying parameters, as compared with the choice of adopted in Melendez et al. [132]. Alternatively, correlations between observables (and thus the coefficients ci) evaluated at different values of continuously varying parameters can be taken into account using Gaussian processes [133]. Except for the coefficient cm = 1, m ∈ {0, 2, 3}, used to set the scale Xref, the expansion coefficients ci are assumed to be distributed according to some common pdf with a hyperparameter . Performing marginalization over h chiral orders k + 1, …, k + h, which are assumed to dominate the truncation error, the probability distribution for the dimensionless residual to take a value Δk = Δ, given the knowledge of {ci ≤ k}, is given by Melendez et al. [132]
where the set A is defined as A = {n ∈ ℕ0|n ≤ k ∧ n ≠ 1 ∧ n ≠ m} and
The model utilizes the Gaussian prior of “set C” from Melendez et al. [132],
for which the integrals in Equation (43) can be performed analytically [132], and uses the values of h = 10, and . Following Epelbaum [134], the scales that control the expansion parameter are set to MeV and Λb = 650 MeV. The sensitivity of the estimated uncertainties to the choice of prior pdf is discussed in Epelbaum et al. [84], Furnstahl et al. [131], and Melendez et al. [132]. One generally finds minor dependence on the prior pdf if a sufficient amount of information on the coefficients ci is available.
6. Selected Results
6.1. The Two-Nucleon System
We now turn to the calculation of phase shifts and observables in the two-nucleon system. While the derivation and regularization of the nuclear forces have been outlined in the previous sections, we also need to specify the numerical values of all relevant physical quantities and LECs to perform actual calculations. For pion-exchange contributions to the potential, all LECs can be extracted from processes involving at most one nucleon, making it parameter-free. In the TPEP, we use the values of the πN LECs as determined recently by matching the πN scattering amplitude from chiral perturbation theory to a Roy-Steiner equations analysis of πN scattering data at the subthreshold point [50].
We account for the isospin-breaking effects due to the different pion masses in the OPEP and employ the physical masses of the charged and neutral pions MeV and MeV, while we use the isospin-averaged value of Mπ = 138.03 MeV in the TPEP. We adopt an effective value of gA = 1.29 for the nucleon axial coupling constant which is slightly larger than the current experimental average value of gA = 1.2723(23) [135] because it already accounts for the Goldberger-Treiman discrepancy (see [136] for a related discussion). The employed value of the pion decay constant is Fπ = 92.4 MeV.
In contrast to the parameter-free long-range potential, the short-range contact interactions in the two-nucleon force have to be determined from experimental NN data. In order to achieve a proper reproduction of pp and, to a lesser extent, np scattering data, it is crucial to also include electromagnetic interactions between the nucleons. Although these interactions are accompanied by powers of a numerically small coupling constant α ~ 1/137, they are enhanced at low energies and/or forward angles due to the infrared singularity of the photon propagator or, equivalently, due to their long-range nature. Here, we follow the treatment of the Nijmegen group [137] and include the so-called improved Coulomb potential [138], the magnetic-moment interaction [139] as well as the vacuum-polarization potential [140] in the calculation of proton-proton observables. The magnetic moment interaction is also taken into account in neutron-proton scattering. To the best of our knowledge, these effects have been included in every partial-wave analysis (PWA) of or fit of a high-quality potential model from NN data since the Nijmegen PWA of Stoks et al. [137], so that differences in their predictions stem from modeling the strong interaction, the experimental input and/or details of the fitting procedure itself.
For scattering data we use the Granada-2013 database [18] which consists of experimental data for NN elastic scattering up to Elab = 350 MeV from 1950 up to 201312. The database contains the data that have been found to be mutually compatible by means of a 3σ rejection criterion in the corresponding phase shift analysis of Navarro Pérez et al. [18]. The presence of very precisely measured proton-proton data in the database, such as those of Cox et al. [142], motivated us to introduce the N4LO+ version of the potential. As the proper description of these data requires a precise reproduction of F-waves, the N4LO+ potential adds the four leading F-wave contact interactions
formally appearing at N5LO and entering the 3F2, 1F3, 3F3, and 3F4 partial waves, to the N4LO potential.
The fits have been performed for all cutoffs Λ = 400, 450, 500, and 550 MeV as well as for all orders from LO up to N4LO+13. When determining the values of the contact LECs, one has to decide up to which energy Elab the experimental data should be taken into account. One is faced with the two competing features: on the one hand, the inclusion of as many data as possible is desirable from a data fitting point of view. On the other hand, the truncation errors for the chiral interactions become larger at high energies. We therefore chose the maximum energy Elab of data to be included to be Emax = 260 MeV for N4LO and N4LO+, while we reduced the energy to Emax = 25, 100, 125, and 200 MeV at the orders LO, NLO, N2LO, and N3LO, respectively. Notice that balancing the tradeoff between these two competing features can be handled using Bayesian methods (see e.g., [143]). From N3LO on, we also adjust the deuteron binding energy Bd and the coherent neutron-proton scattering length bnp to reproduce their experimental values of Bd = 2.224575(9) MeV [144] and bnp = −3.7405(9) fm [145].
Table 1 shows the reproduction of neutron-proton and proton-proton scattering data in terms of χ2/datum values at all considered orders for the cutoff Λ = 450 MeV14. We employ a standard definition of the objective function in terms of a sum of squared residuals as detailed in Reinert et al. [17]. As expected, a clear order-by-order improvement in the description of the scattering data can be seen. Table 1 also gives the number of adjustable parameters at each order which also includes isospin-breaking LECs contributing to the 1S0 partial wave. It should be noted that no new contact interactions are added when going from NLO to N2LO and that the observed improvement of the χ2/datum values is entirely due to the N2LO contributions to the parameter-free TPEP. A similar situation occurs when going from N3LO to N4LO, although here we also allow for additional isospin-breaking of the C1S0 contact LEC splitting it into two independently adjustable parameters for the neutron-proton and proton-proton/neutron-neutron systems. These improvements demonstrate both the importance of the chiral TPEP in the nuclear force and the predictive power of chiral perturbation theory, which allows to use LECs extracted in one process for making parameter-free predictions for (parts of) another.
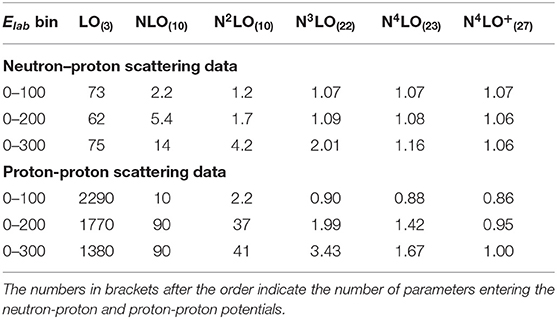
Table 1. χ2/datum for the description of the neutron-proton and proton-proton scattering data at various orders in the chiral expansion for Λ = 450 MeV.
Starting from N3LO, a satisfactory description of the neutron-proton data in the energy range of Elab = 0 − 200 MeV and the proton-proton data for Elab = 0−100 MeV is achieved. Although the N4LO potential improves on this, especially at intermediate and higher energies, it does not achieve a χ2/datum ~ 1 description of the proton-proton data for Elab ≥ 100 MeV. In the intermediate region, this value is significantly affected by the already mentioned high-precision data which requires an accurate description of F-waves. At N4LO the differential cross section data set of Cox et al. [142] at Elab = 144.1 MeV, although well described within the Bayesian truncation errors, yields a χ2/datum value of 27.88.
The situation is much improved once we switch to the N4LO+ potential and short-range interactions in F-waves are added. The description of scattering data at higher energies is generally improved and also the high-precision proton-proton data at intermediate energies is accurately reproduced leading to a χ2/datum ~ 1 description of the complete scattering database. Throughout the orders LO − N4LO the χ2/datum value for proton-proton scattering up to 200 or 300 MeV has been larger than the one for neutron-proton scattering. This is plausible as proton-proton data is in general more precise than neutron-proton data and because only isovector partial waves contribute to it and hence only roughly half of the total number of parameters. However, at N4LO+, the reproduction of proton-proton data becomes very accurate while the slightly larger χ2/datum values for the neutron-proton data as compared to proton-proton data reflect the larger statistical fluctuations among different data sets. This can be seen as an indication for reaching the threshold where the model accuracy approaches the precision of the data. In fact, the description of the scattering data at N4LO+ and Λ = 450 MeV is comparable to or exceeds that of the high-quality semi-phenomenological potentials such as CD-Bonn [146], Nijm I, II [147], and Reid93 [147]. Thanks to the parameter-free effects of the TPEP this is achieved with only 27 adjustable short-range parameters instead of the ~ 40 − 50 parameters used in those potentials.
Indeed, due to the excellent description of the data, the obtained results at Λ = 450 MeV qualify to be considered a partial-wave analysis. In Figures 4, 5, we show the obtained N4LO+ neutron-proton and proton-proton phase shifts for Λ = 450 MeV, respectively. We compare them to the 2013 Granada analysis [18] and in the case of neutron-proton scattering also to the corresponding 2008 analysis by Gross and Stadler [148]. Furthermore, we also show the predictions from the N4LO+ potential of Entem et al. [23] at the intermediate cutoff Λ = 500 MeV.
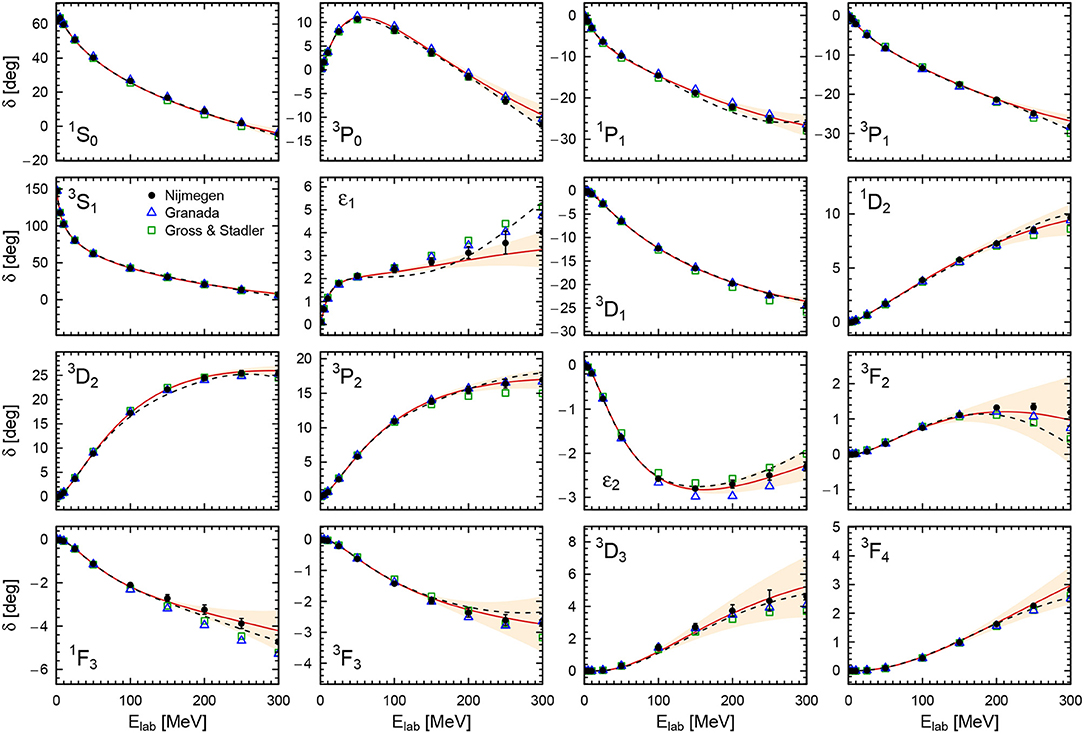
Figure 4. Neutron-proton phase shifts with respect to Riccati-Bessel functions in comparison with the Nijmegen [137] (solid dots), the Granada [149] (blue open triangles), and Gross-Stadler [148] (green open squares) PWA. Red solid lines and peach-colored bands denote the central results and 68% DoB truncation errors at the order N4LO+ for the cutoff Λ = 450 MeV. Black dashed lines denote the result of the nonlocal N4LO+ potential of Entem et al. [23] for the cutoff Λ = 500 MeV. The shown uncertainties of the Nijmegen PWA correspond to systematic errors defined in Equation (32) of Epelbaum et al. [21].
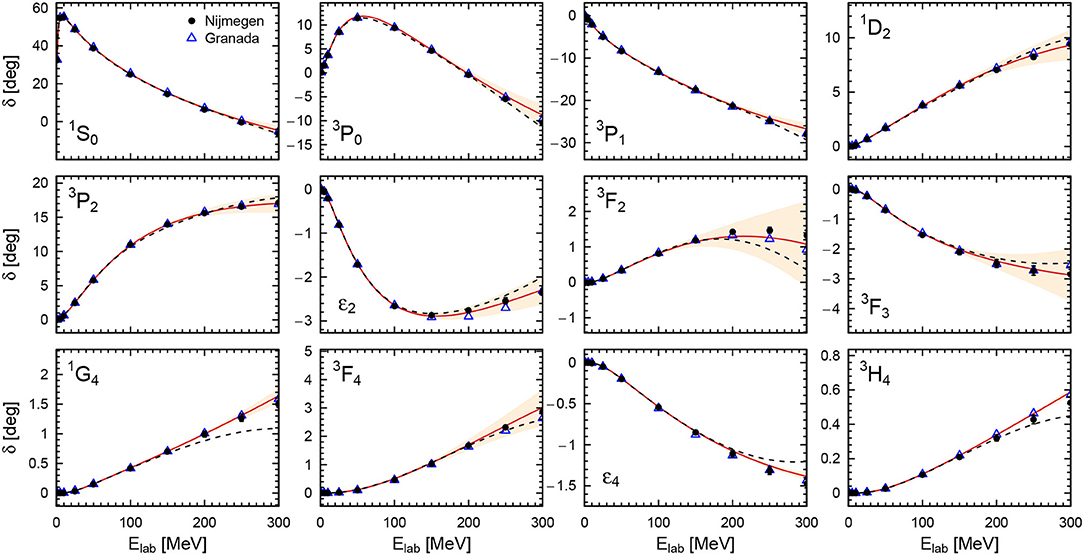
Figure 5. Proton-proton phase shifts with respect to Coulomb wave functions in comparison with the Nijmegen [137] (solid dots) and the Granada [149] (blue open triangles) PWA. Red solid lines and peach-colored bands denote the central result and 68% DoB truncation errors at the order N4LO+ for the cutoff Λ = 450 MeV. Black dashed lines denote the result of the nonlocal N4LO+ potential of Entem et al. [23] for the cutoff Λ = 500 MeV. The shown uncertainties of the Nijmegen PWA correspond to systematic errors defined in Equation (32) of Epelbaum et al. [21].
In general, there is good agreement between the shown N4LO+ phase shifts and the results obtained by the considered phase shift analyses. This is especially true for the case of proton-proton phase shifts which are more strongly constrained by the precise experimental data. Some discrepancies among the different results remain e.g., around the maximum of the 3P0 phase shift where the N4LO+ prediction for the proton-proton phase is slightly larger than the ones of the Nijmegen and Granada PWAs, resulting in a ~ 3σ deviation from the former at Elab = 50 MeV. On the other hand, our neutron-proton phase shifts fall in between the results of the two PWAs. The study of isospin-breaking effects in P-waves beyond the ones included in the two PWAs and the current version of the semilocal momentum-space regularized (SMS) interaction of Reinert et al. [17] is expected to shed some light on this issue. We can also compare our results at N4LO+ to the ones of Entem et al. [23]. Similar to the comparison with the PWAs, agreement with proton-proton phases is better than with neutron-proton ones. There are, however, notable differences in the 3P0, 3P2, and 3D2 waves starting at low or intermediate energies. At higher energies around Elab = 250 − 300 MeV, a change in curvature of the phase shift as a function of energy is visible e.g., in the 1P1 and 3P1 waves, which is presumably caused by the regulator employed in Entem et al. [23]. The effects of regulator artifacts can be observed particularly well in the 1G4, 3H4, and ϵ4 phase shifts and mixing angle shown in Figure 5 since they do not involve any adjustable short-range parameters at N4LO+ but are solely determined by the long-range pion-exchange potential. Here, the local regulator of Equation (23) leads to an undistorted reproduction of the peripheral phase shifts.
Selected proton-proton scattering observables and their estimated truncation error at various orders are shown in Figure 6 for Elab around ~ 143 MeV. In particular, we show our predictions for the differential cross section at Elab = 144.1 MeV and compare them with two high-precision data sets, most notably the one of Cox et al. [142], which motivated the introduction of the N4LO+ potential as discussed above. The data are well described within the given truncation error for all considered orders, but the N4LO+ clearly allows for a proper quantitative description. Likewise, the reproduction of the spin observables in Figure 6 is excellent already at N3LO with a good convergence pattern. Notice however, that the error bands at lower orders for D (A) at the minimum (maximum) around do not overlap with the ones for N≥3LO and are indeed underestimating the uncertainty. Here we find that the value of the observable in that particular angular region is notably shifted starting at N3LO while lower-order corrections are small, such that the overall scale in Equation (42) is still underestimated. Using a more sophisticated Bayesian approach of Melendez et al. [133] would likely allow for a more reliable estimation of the truncation errors at LO-N2LO in these particular cases.
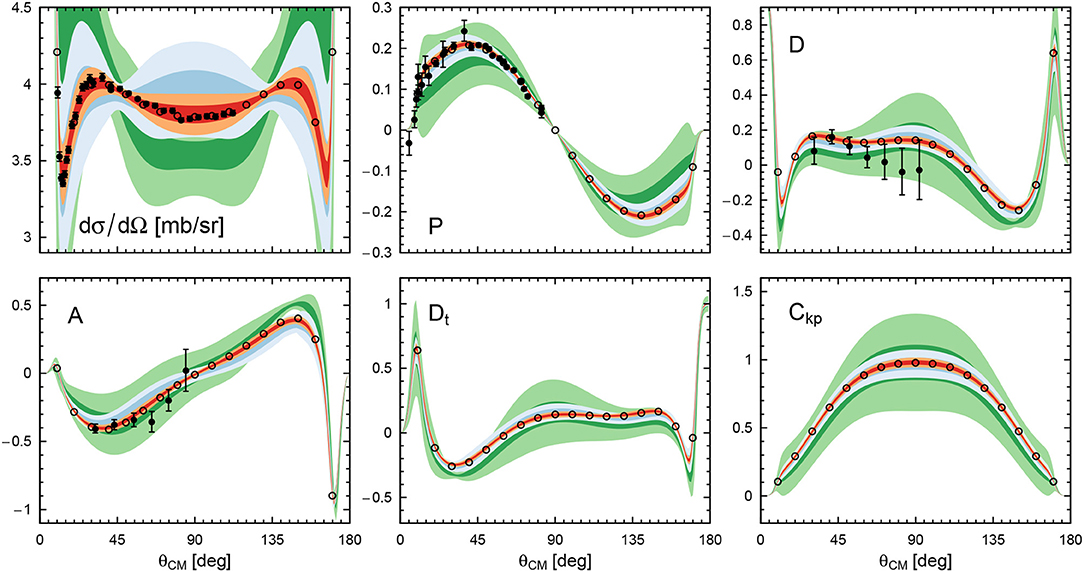
Figure 6. Selected proton-proton observables around Elab = 143 MeV: Differential cross section dσ/dΩ at Elab = 144.1 MeV with experimental data taken from Cox et al. [142] and Jarvis et al. [150]. The data sets have been corrected for their estimated norms of 0.988 and 1.001, respectively. Analyzing power P at Elab = 142 MeV with experimental data taken from Taylor et al. [151]. The data have been floated and multiplied by an estimated norm of 0.942. Depolarization D, rotation parameter A, polarization transfer coefficient Dt, and spin-correlation parameter Ckp at Elab = 143 MeV with experimental data taken from Bird et al. [152] and Jarvis et al. [153]. The light- (dark-) shaded green, blue, and red bands depict the 68% (95%) DoB truncation errors at N2LO, N3LO, and N4LO+, respectively. Open circles show the predictions of the Nijmegen partial-wave analysis [137].
There are various a posteriori checks that can be performed to test the self-consistency and quality of the fit. First, the values of the LECs have to be of natural size assuming the cutoff is kept below the hard scale. The expected sizes of the spectroscopic contact LECs can be estimated to be [21]
where the LECs , Ci, Di, and Ei start to contribute at order Q0, Q2, Q4, and Q6, respectively. Λb is the breakdown scale of the chiral expansion discussed in section 5. Furthermore, the factor of 4π emerges from the angular integration of the partial-wave decomposition and has been included in the definition of the spectroscopic LECs. If we now divide the contact LECs obtained in the fit by their expected sizes in Equation (47), we consequently should obtain values of unit magnitude. Figure 7 shows the absolute values of the LECs at N4LO+ in these natural units for all considered values of the cutoff Λ using Λb = 650 MeV. As can be seen, all LECs are indeed of natural size with D1S0 and D3S1 being among the largest in magnitude. This is especially true for the softest cutoff Λ = 400 MeV, for which also most of the other-Q4 LECs turn out to be slightly larger than at higher values of the cutoff. This indicates that at Λ = 400 MeV and below, finite-cutoff artifacts start to increase, leading to a lower effective breakdown scale compared to the other considered cutoffs. Notice further that the values for the Q6 LECs Ei included at N4LO+ turn out to be of a perfectly natural size. Therefore, even though we have emphasized their importance in describing some high-precision proton-proton data and achieving a χ2/datum ~ 1 description of the database, their actual contributions agree with the expectations from naive dimensional analysis (i.e., Weinberg) power counting, and there is no need to promote them to a lower order.
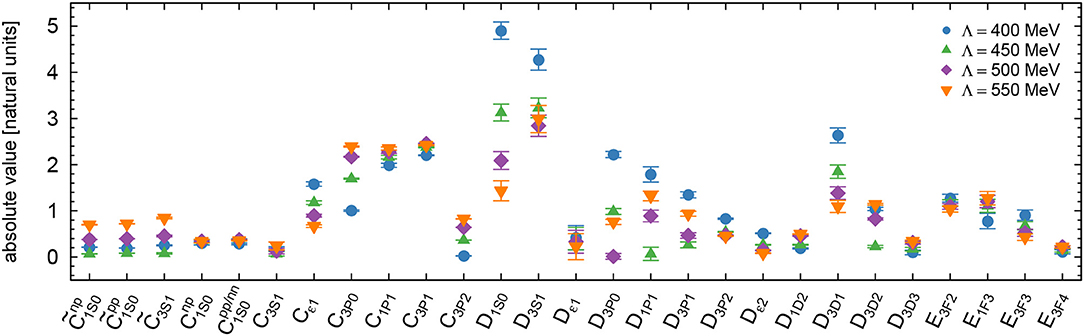
Figure 7. Absolute values of the contact interaction LECs in natural units at the order N4LO+ for all considered cutoffs. Error bars represent the statistical errors of the LECs.
In addition to the absolute of the central values, Figure 7 also shows the statistical uncertainties of the contact LECs as determined from the covariance matrix of the fit (expressed in their natural units). When going from , Ci, Di to Ei the statistical relative errors tend to increase. This is in accordance with the decreasing importance of higher-order contributions as predicted by power counting. One also notices that errors are smaller for LECs entering isovector partial waves, because these parameters are mainly constrained by the more precise proton-proton data. Since we perform a combined fit of neutron-proton and proton-proton data, the isovector partial waves are not only constrained by more precise data but also by more data in general compared to the isoscalar partial waves which have to be extracted from neutron-proton data alone. The covariance matrix also gives access to the correlations among the LECs. As to be expected, correlations mostly occur among LECs entering the same partial waves with the largest ones arising in the channels with the most parameters, namely in the 1S0 and 3S1 − 3D1 channels. Nevertheless, all LECs are well-constrained as can already be seen by looking at the errors in Figure 7. We can further look at the largest eigenvalue of the covariance matrix of the natural LECs as a measure of how well-determined the parameters are. Throughout the considered range of the cutoff Λ = 400 − 550 MeV, the largest eigenvalue of the covariance matrix does not exceed 0.1 and is ~ 0.08 for Λ = 450 MeV.
From the point of view of data fitting, another check concerns the statistical assumptions underlying a χ2 fit. One usually assumes that the residuals follow a normal distribution with zero mean and unit standard deviation. Here and ΔOi are the experimental value and its error of an observable and is its calculated “theoretical” value. If the assumptions on the normally-distributed residuals can be verified, this confirms that the data are described sufficiently well by the theoretical model. An easy and often employed check is the value of χ2 per degree of freedom. For the N4LO+ fit with Λ = 450 MeV we get χ2 = 4708.65 in the fitting range of Elab = 0 − 260 MeV with the number of data Ndat = 4616 and the number of parameters Npar = 27. Consequently, we obtain χ2/ν = 1.026 with ν = Ndat − Npar. If the residuals are indeed normal-distributed then χ2/ν should follow the χ2-distribution and yields as the 68% confidence interval.
We can go one step beyond this simple check and plot the quantiles of the empirical distribution of residuals ri that we obtain against the quantiles of the assumed normal distribution . If they are the same, they should lie on the diagonal line x = y. In order to statistically quantify deviations from the diagonal, confidence bands have been derived with one of the most recent and most sensitive being the ones of the “tail-sensitive test” by Aldor-Noiman et al. [154]. This graphical test for normal-distributed residuals has been first applied to the analysis of nucleon-nucleon scattering by Navarro Pérez et al. [155]. Figure 8 shows a rotated quantile-quantile plot for the N4LO+ residuals at Λ = 450 MeV where the theoretical quantiles have been subtracted from the empirical ones on the y-axis, turning the diagonal line into a horizontal one. As evident from the figure, the empirical distribution of residuals lies within the 68% confidence region of the tail-sensitive test signaling that the residuals are indeed normal-distributed. The quantile-quantile plot for the other values of the cutoff turn out to be overall similar, but perform slightly worse. For Λ = 500 MeV and Λ = 550 MeV the quantiles that are already close to the edge of the 68% confidence region in Figure 8 cross these limits but still stay well within the 95% confidence region. The increased cutoff-artifacts at Λ = 400 MeV manifest themselves in a stronger deviation from normality as the plotted quantiles also cross the 95% confidence limits at the spike at Qth = 2 in Figure 8.
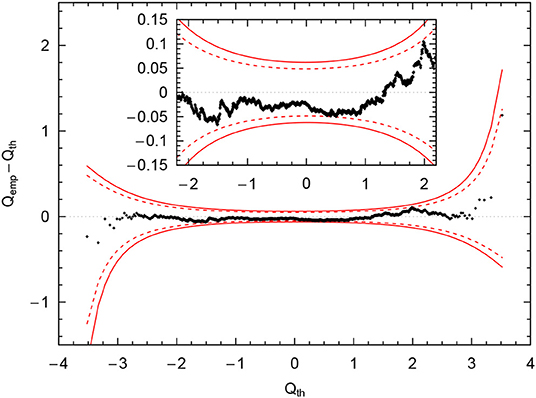
Figure 8. Rotated Quantile–Quantile plot of the empirical quantiles at N4LO+ and Λ = 450 MeV vs. the quantiles of the normal distribution Dotted (solid) red bands denote the 68% (95%) confidence bands of the tail-sensitive test by Aldor-Noiman et al. [154].
We now turn to the extended error analysis for observable predictions. While the truncation of the chiral expansion is clearly the dominant source of uncertainty at higher energies, other sources of uncertainty can become relevant at N4LO+. In particular we account for the following sources of uncertainty:
• Statistical uncertainties of NN LECs: As already mentioned, Figure 7 shows the statistical errors of the contact LECs as determined from the covariance matrix of the fit. The uncertainties of the parameters can then be propagated from the covariance matrix to the observable of interest. While it is always possible to do this via a Monte Carlo sampling of the corresponding multivariate Gaussian probability distribution, it is computationally much more convenient to do a Taylor expansion of the desired observable with respect to the LECs and evaluate the moments of the LECs analytically. While a linear expansion is commonly employed, it has been argued in Carlsson et al. [114], that some observables require a second order expansion for an accurate reproduction of their uncertainties. In the case of large second-order contributions, the error bars become asymmetric and we usually give both the upper and lower error to accommodate for this possibility. Notice that in such a case, the probability density of the observable is not Gaussian and the quoted uncertainties do not necessarily correspond to a 68% degree-of-belief.
• Statistical uncertainties of πN LECs: In addition to the central values, the authors of Hoferichter et al. [50] also give the covariance matrix as determined from πN scattering data. Propagation of these uncertainties to NN observables is, however, less straightforward, because the values of the NN contact interactions depend on the values of πN LECs. We thus resort to some Monte Carlo sampling of the multivariate Gaussian probability distribution of the πN LECs given by their central values and their covariance matrix. For each of the sampled sets of LECs, we refit the NN contact LECs before calculating any observables. The uncertainty of a given observable can then be estimated in a standard way from the variance of the results calculated with different πN LEC sets. Due to the need to refit the contact interactions for each sampled set of πN LECs and the computational overhead related to it, we have restricted the total number of such sets to 50. Although this is a quite low statistics for a Monte Carlo approach, it should give an idea of the order of magnitude of the uncertainty. It indeed turns out that the uncertainty related to the statistical error of the πN LECs is small compared to the other sources of uncertainty. However, the aforementioned approach does not probe the systematic errors in the determination of the πN LECs emerging from the truncation of the chiral expansion and thus does not represent the full uncertainty related to these LECs.
• Uncertainty due to the choice of the maximum fit energy: The extracted values of the contact LECs also depend on details of the fitting protocol. In particular, we probe the impact of the choice for the maximum laboratory energy Emax = 260 MeV up to which scattering data is included in the N4LO+ fit. This is achieved by performing additional fits with Emax = 220 MeV and Emax = 300 MeV and determining the maximum deviation of the observables from the Emax = 260 MeV predictions. Unlike the aforementioned uncertainties, the error estimated via this simple procedure does not reflect any particular degree-of-belief.
As an example, Figure 9 shows the neutron-proton total cross section and the corresponding uncertainties in the energy range Elab = 0 − 300 MeV. The plot on the left in Figure 9 shows the ratio of our predictions using the N4LO+ potential at Λ = 450 MeV and the result of the Nijmegen partial-wave analysis [137]. In the right panel, the different relative errors stemming from the various sources discussed above are shown. For the case of the statistical errors of the NN contact interactions, second order effects and resulting asymmetries in the error bands turn out to be small for the total cross section, and the plotted uncertainty corresponds to the average of upper and lower statistical errors. As expected, the dominant contribution to the uncertainty at higher energies (Elab>100 MeV) arises from the truncation of the chiral expansion. At lower energies, however, other sources of uncertainty become relevant and indeed both the statistical errors of the NN contact LECs and the uncertainty due to the maximum fitting energy are larger than the truncation error in the range of Elab = 30 − 100 MeV. When quantitatively comparing the different errors, one has to keep in mind that the uncertainty due to the maximum fitting energy does not correspond to a particular degree-of-belief. The uncertainty arising from the statistical errors of the πN LECs is found to be significantly smaller throughout the whole considered energy range and is negligible for the total cross section. Finally, we would like to comment on the origin of the existing kinks in the right-hand-side plot of Figure 9. In particular, the kink in the Emax-error at around 200 MeV arises because of the maximum operation. Below 200 MeV, the error is dominated by the deviation of the Emax = 220 MeV fit while it is given by the deviation of the Emax = 300 MeV fit above 200 MeV. The second kink present in the truncation error, on the other hand, is caused by the transition of Q from to p/Λb.
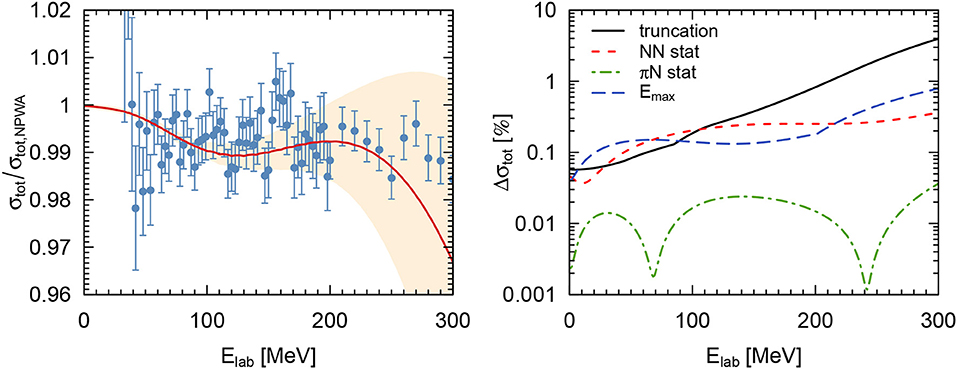
Figure 9. Neutron-proton total cross section in the range of Elab = 0 − 300 MeV. The plot on the left shows the results divided by the predictions of the Nijmegen PWA. The red line and peach-colored band show the central values and truncation errors (the 68% DoB interval) at the order N4LO+ and for Λ = 450 MeV. The experimental data are taken from Lisowski et al. [156] and have been corrected for their estimated norm of 0.999. The plot on the right shows the relative uncertainties as discussed in the text.
Table 2 shows the deuteron properties as predicted by various high-quality potentials. Clearly, the error analysis can also be applied to the bound state properties of Table 2. However, the obtained uncertainties are only meaningful for a complete calculation of an unconstrained observable. This excludes the deuteron binding energy Bd (as it is a fitted quantity), the quadrupole moment Q and deuteron radius rd (as meson exchange currents and relativistic corrections are not taken into account) as well as the D-state probability PD (which is not observable). On the other hand, we can perform the uncertainty quantification for the asymptotic S-state normalization AS and the asymptotic D/S-state ratio η for which we obtain at N4LO+ and for Λ = 450 MeV the values of and , respectively. Here the first, second, third, and fourth error refer to the NN statistical, truncation, πN statistical, and Emax uncertainty, respectively. Notice that the quoted truncation errors estimated using the Bayesian model of section 5 are fairly similar to the ones given in Reinert et al. [17], which were obtained using the EKM method. On the other hand, the πN statistical uncertainties are much smaller than the corresponding errors quoted in Reinert et al. [17], where an attempt was made to also include systematic effects by using the values of these LECs determined in the physical region of πN scattering.
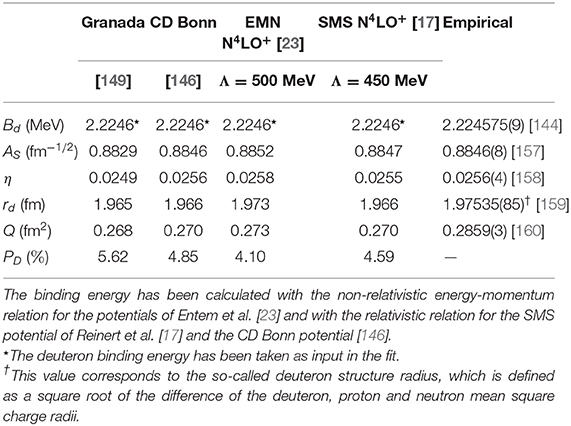
Table 2. Deuteron binding energy Bd, asymptotic S-state normalization AS, asymptotic D/S-state ratio η, radius rd, quadrupole moment Q, and D-state probability PD as predicted by various high-quality potentials.
Finally, let us discuss the treatment of isospin-breaking effects in the two-nucleon interaction. Like all modern high-precision potentials, the SMS interactions include isospin-breaking in the OPEP due to the different physical pion masses and and charge dependence of the short-range potential in the 1S0 partial wave. These are the dominant and well-understood isospin-breaking effects necessary to arrive at e.g. a correct description of the charge-dependence of the 1S0 scattering length. For the calculation of scattering observables in the two-nucleon system, the isospin-breaking due to long-range electromagnetic interactions is taken into account as discussed at the beginning of this section. This treatment of strong and electromagnetic isospin-breaking effects is identical to the Nijmegen PWA [137]. On the other hand, chiral EFT allows for a systematic inclusion of isospin-breaking effects beyond the ones previously considered. In fact, expressions for the leading isospin-breaking TPEP [161, 162], the subleading isospin-breaking TPEP [163], and irreducible πγ exchange [164], which are (mostly) parameter-free in the two-nucleon system, have been available for some time. The long-standing question regarding the charge-dependence of the πNN coupling constant also re-emerges in a systematic treatment of isospin-breaking effects in the framework of chiral EFT. While the Nijmegen group did not find evidence for charge-dependence, the issue does not seem to be settled (see [165] for a recent determination). Last but not least, charge-dependence in the short-range potential entering P-waves should also be taken into account starting from N4LO [163].
6.2. Three-Nucleon Scattering
As discussed in the previous subsection, the N4LO+ SMS potentials of Reinert et al. [17] lead to excellent and in fact a nearly perfect description of np and pp scattering data below pion production threshold. Moreover, an order-by-order comparison of the results for various observables along with the Bayesian error analysis indicate a generally good convergence of the chiral expansion in the NN sector. On the other hand, a description of nucleon-deuteron elastic and breakup scattering data at a comparable level of accuracy is not available yet. Extensive calculations performed in the last decades using high-precision phenomenological NN potentials and 3NF models in the framework of the Faddeev equations [166] and using other ab initio methods [167] have revealed the following picture (see [19] and references therein):
– Calculations based on high-precision NN potentials alone (including the N4LO+ ones of [17]) tend to underestimate the 3H and 3He binding energy by ~ 0.5 MeV and generally lead to similar predictions in Nd scattering observables.
– At low energies, the resulting description of Nd data appears to be rather good apart from a few exceptions such as the underprediction of the nucleon analyzing power Ay, known as the Ay puzzle [168], and the discrepancy for the cross section for the symmetric space star deuteron breakup configuration [169]. 3NF effects in this energy range are found to be small in agreement with qualitative arguments based on the chiral power counting as explained below.
– Starting from Elab ~ 50 MeV, discrepancies between theory and experimental data set in and become large at Elab ~ 200 MeV and above. Except for the cross section, the inclusion of the phenomenological 3NFs like the Tucson-Melbourne (TM99) [170] and Urbana-IX [171] models does not globally reduce the discrepancies between theory and data [19]. Relativistic effects have also been studied, see Witała et al. [172] and references therein, and found to be small at energies below the pion production threshold.
Assuming that the discrepancies between theory and experimental data in the 3N system are to be resolved by 3NFs, these findings demonstrate that the currently available phenomenological models do not provide an appropriate description of the 3NF. This should not come as a surprise given the enormously rich and complex spin-isospin-momentum structure of a most general 3NF [95, 173–175]. Here, chiral EFT offers a decisive advantage over more phenomenological approaches by predicting the long-range part of the 3NF in a model-independent way, establishing a clear importance hierarchy of short-range terms and providing a solid theoretical framework for maintaining consistency between two- and three-nucleon forces and ensuring scheme independence of the calculated observables.
As already mentioned in section 3, three-body contributions to the nuclear Hamiltonian first appear at N2LO in the chiral expansion and are, therefore, suppressed by Q3 relative to the dominant pairwise NN interaction. It is instructive to estimate the expected magnitude of 3NF effects for various observables solely on the basis of the chiral power counting (i.e., using NDA). For 3H and 4He, one can use the typical expectation values of the NN potential energy of MeV and MeV [83], along with the estimation of the expansion parameter with MeV and Λb = 650 MeV, in order to estimate the expected 3NF contributions to the binding energy to be MeV and MeV. These qualitative estimations agree well with the actual underprediction of the 3H and 4He by the NN interactions alone which, using the AV18 [176], CD Bonn [146], N2LO [113], and Idaho N3LO [112] potentials as representative examples, amounts to 0.5…0.9 MeV and 2.1…4.1 MeV, respectively. The shallow nature of few-nucleon bound states indicates that there are large cancelations between the kinetic and potential energies. Because of this fine tuning, 3NF contributions to the binding energies are enhanced beyond the naive estimation of Q3 ~ 3% and actually reach 10…15%. On the other hand, there is generally no reason to expect a similar enhancement for Nd scattering observables at low energy except for some fine-tuned polarization observables such as Ay. It is well known that tiny changes of the NN interaction in the triplet P-waves amount to large relative changes in the Nd Ay [168]. On the other hand, starting from EN ~ 60 MeV, the expansion parameter Q in Equation (38) is dominated by the momentum scale [84]. At e.g. the energies of EN ~ 100 MeV and EN ~ 200 MeV, the expansion parameter becomes Q ~ 0.40 and Q ~ 0.55, and the relative contributions of the 3NF to a generic scattering observable are expected to increase to ~ 6 and ~ 16%, respectively. Clearly, these simplistic back-of-envelope estimations only yield qualitative insights into the role of the 3NF. Nevertheless, they agree remarkably well with the observed trend of discrepancies between theoretical predictions based solely on the NN interactions and experimental data, which tend to increase with energy. For further examples and a more quantitative analysis along this line of Nd scattering, selected properties of light and medium-mass nuclei and the equation of state of nuclear matter (see [83, 127, 130, 177]). We further emphasize that it is not entirely clear how to estimate the relevant momentum scale, that determines the expansion parameter in heavy nuclei, and how to quantify truncation errors for excited states (see [130] for an extended discussion).
As discussed in section 3 and visualized in Figure 2, the leading contributions to the 3NF at N2LO emerge from the two-pion exchange, one-pion-exchange-contact and purely contact tree-level diagrams, leading to the well-known expressions [44, 98]
where with and being the final and initial momenta of the nucleon i. The LECs D and E are usually expressed in terms of the corresponding dimensionless coefficients cD and cE via and [44]. In Epelbaum et al. [8] and [84], semilocal coordinate- and momentum-space regularized 3NF expressions in combination with the corresponding chiral NN potentials from Epelbaum et al. [21, 22] and Reinert et al. [17], respectively, were employed by the LENPIC Collaboration to analyze Nd scattering observables at N2LO. The numerical implementation of the 3NF in the Faddeev equations is carried out in the partial wave basis. Partial wave decomposition (PWD) of a general 3NF can be carried out numerically using the machinery developed in Golak et al. [178] by performing five-dimensional angular integrations. Given the required number of partial waves and grid points for the four Jacobi momenta to reach converged results for Nd scattering observables, such a numerical PWD requires substantial computational resources. In Hebeler et al. [179], a more efficient approach was introduced, that exploits the local nature of the bulk of the 3NF.
To make predictions for few-nucleon observables, one first needs to determine the LECs cD and cE entering the 3NF. A broad range of few- and many-body observables including the binding energies and radii of 3H, 4He, and heavier nuclei, nucleon-deuteron doublet scattering length 2a, n-α scattering, triton β-decay, and the saturation properties of nuclear matter have been proposed and employed in the past to determine these two LECs [9, 27, 29, 44, 180, 181]. A reliable determination of cD, cE is complicated by the existence of strong correlations between some of the low-energy observables (see e.g.,[182]), which originate from the large S-wave scattering lengths in the NN system. Furthermore, going beyond the 3N system may require, depending on the observable and the chiral order, the inclusion of 4NF and exchange current contributions. In Epelbaum et al. [8], we therefore, restricted ourselves to 3N observables in the determination of cD, cE. Specifically, we employed the 3H binding energy of B3H MeV to fix the LECs cE for a given value of cD. The remaining LEC cD was determined by considering a number of observables including 2a = 0.645±0.008 fm [145], nd total cross section data from [183] and precisely measured pd differential cross section in the minimum region at EN = 70 MeV [184], 108 MeV [185], and 135 MeV [184]. In the left panel of Figure 10, we show the extracted values of cD for the SCS interactions with the cutoff R = 0.9 fm. It is reassuring to see that the considered 3N observables lead to consistent values of cD. In addition, these results show that the strongest constraint on cD, given the experimental and the estimated truncation uncertainty, is imposed by the pd differential cross section data at EN = 70 MeV from Sekiguchi et al. [184] as visualized in the right panel of Figure 10. We also found no correlations between this observable and the 3H binding energy. In particular, the resulting value of the LEC cD is largely determined by the differential cross section and almost insensitive to a variation of the triton binding energy.
Figure 10. (Left) Determination of the LEC cD at N2LO from selected Nd scattering observables. The smaller (blue) error bars correspond to the experimental uncertainty while the larger (orange) error bars also take into account the truncation error at N2LO estimated using the EKM approach of Epelbaum et al. [21]. The green (violet) bands show standard error intervals of cD resulting from a combined least squares single-parameter fit to all observables (to observables up to EN = 108 MeV) using the orange error bars. (Right) Nd cross section in the minimum region (θ = 130°) at EN = 70 MeV as function of the LEC cD. For each cD value, the LEC cE is adjusted to the 3H binding energy. Dotted lines show the statistical uncertainty of the experimental data from Sekiguchi et al. [184], while the yellow band also takes into account the quoted systematic uncertainty of 2%. All results are obtained using the N2LO SCS NN potential from Epelbaum et al. [21] in combination with the N2LO SCS 3NF for the coordinate-space cutoff R = 0.9 fm.
In Epelbaum et al. [84], we have analyzed Nd scattering observables using the most recent SMS NN potentials from Reinert et al. [17] in combination with the N2LO 3NF regularized in the same way. Motivated by the experience with the SCS interactions [8], the LECs cD and cE were determined from the 3H binding energy and the pd cross section minimum at EN = 70 MeV. In Figure 11, we show, as a representative example, our N2LO predictions for selected Nd scattering observables at EN = 135 MeV, along with the experimental data and calculations based on the CD Bonn NN potential with and without the TM99 3NF model. As an important internal consistency check of the calculations, we have verified that the predictions obtained using different cutoff values are consistent with each other (within errors) (see Figure 5 of [84]).
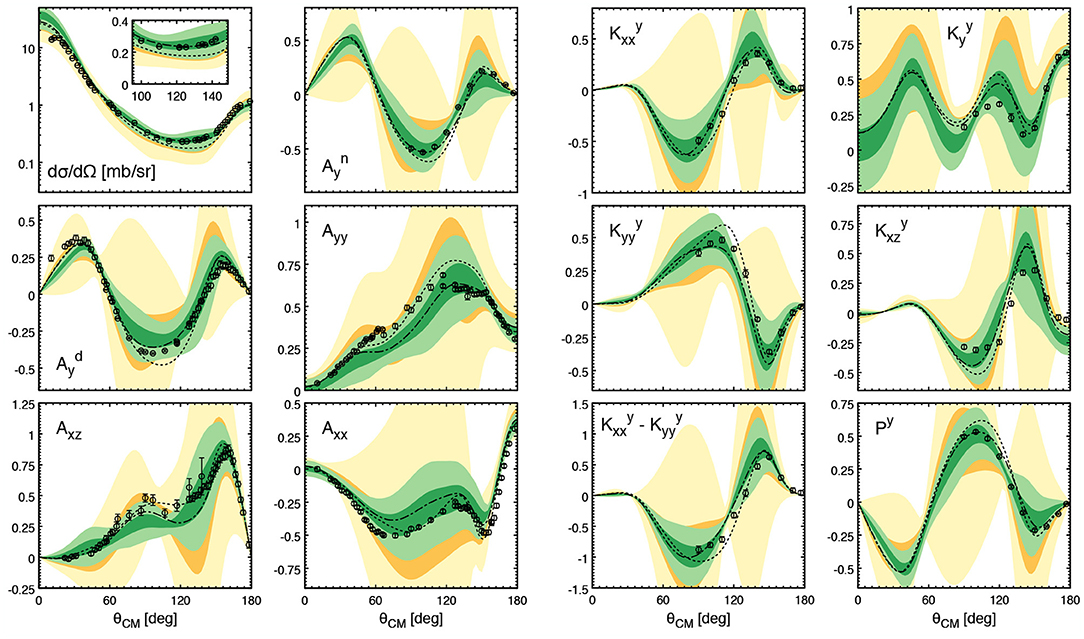
Figure 11. Predictions for the differential cross section, nucleon and deuteron analyzing powers and , deuteron tensor analyzing powers Ayy, Axz, Axx, polarization transfer coefficients , , , , , and the induced polarization Py in elastic Nd scattering at laboratory energy of EN = 135 MeV at NLO (yellow bands) and N2LO (green bands). The light- (dark-) shaded bands indicate 95% (68%) DoB intervals using the Bayesian model introduced in section 5. Open circles are proton-deuteron data from Sekiguchi et al. [184]. The dotted (dashed-dotted) lines show the results based on the CD Bonn NN potential [146] (CD Bonn NN potential in combination with the Tucson-Melbourne 3NF [170]). All results are obtained using the N2LO SMS NN potential from Reinert et al. [17] in combination with the N2LO SMS 3NF for the momentum-space cutoff Λ = 500 MeV.
It is reassuring to see that the experimental data are generally well described by the theory. On the other hand, while accurate, our predictions at N2LO have obviously rather low precision at this energy. In fact, the N2LO truncation errors are comparable with or even larger than the observed deviations between experimental data and calculations based on phenomenological high-precision NN and 3NF models, see the dotted and dashed-dotted lines in Figure 11. Based on the experience in the NN sector as discussed in section 6.1, it is conceivable that a high-precision description of Nd scattering data will require the chiral expansion of the 3NF to be pushed to (at least) N4LO. At the energy of EN = 135 MeV, the uncertainty bands at N4LO are expected to become 4-5 times more narrow as compared with the N2LO ones shown in Figure 11.
So where do we stand in terms of efforts to include 3NF corrections beyond N2LO? As explained in section 4.2, the main obstacle for the inclusion of higher order contributions to the 3NF is the lack of their consistently regularized expressions. Starting from N3LO, it is not sufficient anymore to naively regularize the available expressions for the 3NF from Bernard and Epelbaum [54, 55] and Krebs et al. [48, 95] derived using DR, since such an approach violates constraints imposed by the chiral symmetry. Rather, the N3LO and N4LO corrections to the 3NF need to be re-derived using the consistent finite-cutoff regularization approach. Work along these lines is in progress. Another challenge, that will have to be addressed at N4LO, is the determination of the LECs appearing in the 3NF at this order. While the N3LO contributions do not involve free parameters, the short-range part of the 3NF at N4LO depends on 10 unknown LECs [45], from which 9 contribute to the isospin-1/2 channel and thus can, in principle, be determined in Nd scattering. Furthermore, the yet-to-be-derived one-pion-exchange-contact contributions to the 3NF at N4LO will also involve unknown LECs. Given the still rather significant computational cost of solving the Faddeev equations in the 3N continuum, the complicated treatment of the Coulomb interaction [186] and the lack of partial wave analyses in the 3N sector, the determination of these LECs from 3N scattering data will certainly be a challenging task.
While a complete analysis of Nd scattering is currently not available beyond N2LO, it is instructive to explore the role of subleading short-range 3NF interactions. In Girlanda et al. [30], it was shown within a hybrid phenomenological approach that the 3N contact operators at N4LO can be tuned to reproduce the 3H binding energy, nd scattering lengths, cross section and polarization observables of pd scattering at 2 MeV center-of-mass energy. The resulting models were shown to lead to a satisfactory description of pd polarization observables below the deuteron breakup. On the other hand, 3NF effects are expected to be much more visible at intermediate and higher energies. In Epelbaum et al. [84], we explored the impact of the short-range 3NF operators of the central and spin-orbit types proportional to the LECs E1 and E7, respectively,
where . Parameterizing the dimension-full LECs E1, E7 in terms of the corresponding dimensionless parameters via with Λχ = 700 MeV, we studied the impact of these N4LO terms on selected Nd scattering observables for the fixed values of the LECs of cEi = ±2. Based on the experience in the NN sector and with the N2LO 3NF, we expect the actual values of these LECs to lie well within this range. The expectation values of various contributions to the 3NF in the triton state indicate that the employed values cE7 = ±2 may already overestimate the expected natural range of this LEC.
In order to compute the contributions of the cEi-terms to 3N observables in a meaningful way, one needs to perform (implicit) renormalization as explained in section 2. This was achieved in Epelbaum et al. [84] by simultaneously adjusting the values of the N2LO LECs cD, cE to the triton binding energy and the cross section minimum at EN = 70 MeV for all considered values of the LECs cEi. The calculations have been performed using the N4LO+ SMS NN potential from Reinert et al. [17] in combination with the SMS N2LO 3NF. In Figure 12, we show the resulting predictions at the lowest considered energy of EN = 10 MeV. The blue bands show the estimated truncation error at N3LO, obtained by rescaling the N2LO Bayesian truncation uncertainty with the expansion parameter Q15, and visualize the expected impact of N4LO terms. In agreement with the expectations, 3NF effects generally appear to be rather small at such low energies. This figure also provides a nice illustration of the fine tuned nature of the nucleon vector analyzing power Ay, which shows a strong sensitivity to small changes in the Hamiltonian. What has been traditionally referred to as the Ay-puzzle thus appears to be just a consequence of the fine-tuned nature of this observable, and the “puzzle” may be expected to be resolved by 3NF contributions beyond N2LO (see also [30, 45] for a similar conclusion). While the Ay is well-known to be particularly sensitive to spin-orbit types of 3NFs [191] such as the one proportional to cE7, our results also show an unexpectedly strong sensitivity to the subleading central interaction of the cE1-type.
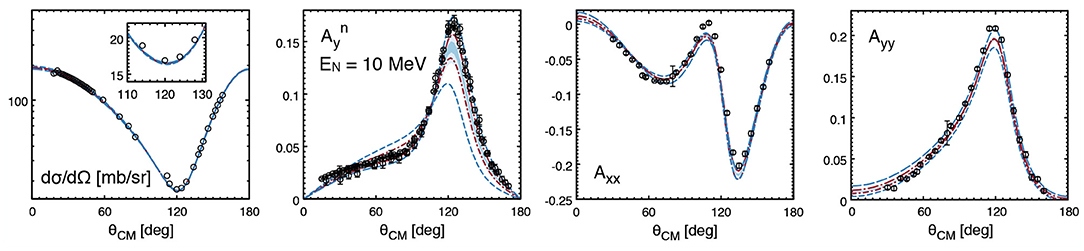
Figure 12. Results for the differential cross section, nucleon analyzing powers as well as deuteron tensor analyzing powers Axx and Axx in elastic nucleon-deuteron scattering at laboratory energy of MeV based on the SMS NN potentials of Reinert et al. [17] at N4LO+ in combination with the SMS 3NF at N2LO using Λ = 450 MeV. Blue light- (dark-) shaded bands show the expected truncation uncertainty for a complete N3LO calculation and are obtained by multiplying the N2LO truncation error corresponding to 95% (68%) DoB intervals for the model with the corresponding value of the expansion parameter Q. Short-dashed-dotted and long-dashed-dotted red lines show the impact of the N4LO central short-range 3NF ∝ cE1 with cE1 = − 2 and cE1 = 2, respectively. Similarly, short-dashed and long-dashed blue lines show the impact of the N4LO spin-orbit short-range 3NF ∝ cE7 with cE7 = − 2 and cE7 = 2, respectively. Open circles are neutron-deuteron data from Howell et al. [187] and proton-deuteron data from Sagara et al. [188], Rauprich et al. [189], and Sperisen et al. [190], corrected for the Coulomb effects (see [44] for details).
At higher energies, the effects of the considered N4LO 3NF terms become more significant as visualized in Figure 13 for the case of selected spin-correlation parameters. More results for the cross section, vector and tensor analyzing powers and polarization transfer coefficients at EN = 135 MeV can be found in Epelbaum et al. [84]. It is comforting to see that the impact of the cEi-terms on Nd scattering observables is, in general, consistent with the estimated N3LO truncation errors. One should, however, keep in mind that the employed Bayesian approach may, under certain circumstances, become unreliable. This is, in particular, the case for observables that depend on a continuously varying parameter in the kinematical regions where the LO results and higher-order corrections change sign (see [84] for a detailed discussion). One such failure of the Bayesian model is shown in Figure 13 for the spin-correlation coefficient Cx, z at EN = 200 MeV around θ = 120°. In such problematic cases, the approach proposed in Melendez et al. [133] and based on Gaussian processes is expected to provide more reliable estimations of the truncation uncertainty.
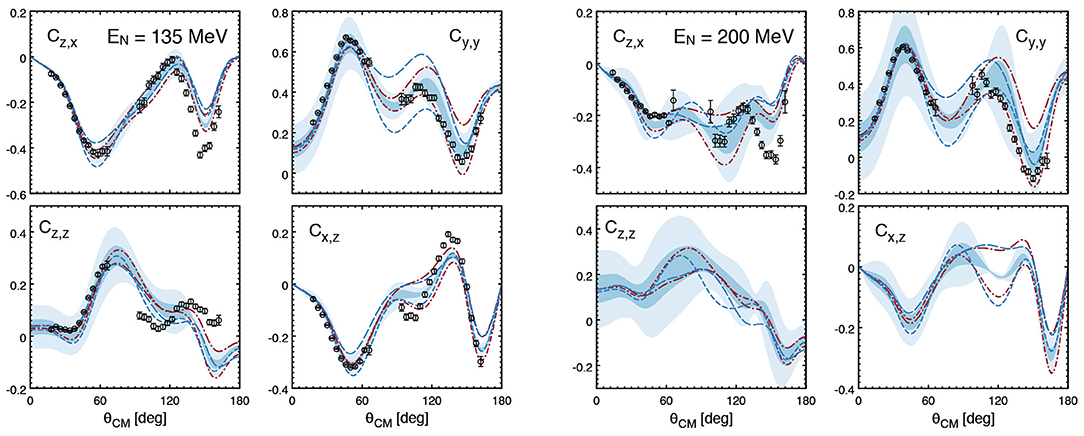
Figure 13. Same as Figure 12 but for the deuteron-nucleon spin-correlation parameters Cz, x, Cy, y, Cz, z, and Cx, z for Nd elastic scattering at EN = 135 MeV (left) and EN = 200 MeV (right). Open circles are proton-deuteron data from von Przewoski et al. [192].
6.3. Light Nuclei
While no results for light nuclei using SMS chiral interactions are available yet, we briefly review here some recent highlights obtained by the LENPIC Collaboration using the SCS NN potentials of Epelbaum et al. [21, 22] with and without the corresponding 3NFs at N2LO. In Binder et al. [83, 130], we have calculated the ground state energies and selected properties of light and medium-mass nuclei up to 48Ca using the SCS NN interactions at various chiral orders. Specifically, A = 3, 4 nuclei were analyzed in the framework of the Faddeev-Yakubovsky equations while light p-shell nuclei were calculated using the No-Core Configuration Interaction (NCCI) method [193–195] and employing Similarity Renormalization Group (SRG) transformed interactions [196–199] to improve the convergence. The results for 16, 24O and 40, 48Ca were obtained within the coupled cluster and in-medium SRG group frameworks (see [12, 200–203] and references therein). A qualitatively similar convergence pattern was observed in all considered cases, namely a significant overbinding at LO, results close to the experimental values at NLO and N2LO and underbinding at N3LO and N4LO. Notice that the strongly repulsive nature of the N3LO contributions to the SCS NN interactions of Epelbaum et al. [21, 22] was shown to be caused by the employed unnaturally large values of the redundant short-range operators [17]. The SMS interactions of Reinert et al. [17] utilize a soft choice for these contact terms, which leads to more perturbative interactions at and beyond N3LO. No large gap between the N2LO and N3LO results for the ground state energies is, therefore, expected for the new SMS NN interactions. The calculated charge radii of the considered medium-mass nuclei were found to show a systematic improvement with the chiral order, but remain underestimated using the NN interaction at the highest available order N4LO+.
In Epelbaum et al. [8], a complete N2LO analysis of p-shell nuclei was presented by the LENPIC Collaboration using the SCS NN and 3N interactions. In Figure 14, we show the NLO and N2LO results from that paper for nuclei up to A = 16. We emphasize that since the Hamiltonian has been completely determined in the NN and 3N system as described in sections 6.1 and 6.2, the ground-state energies shown in that figure are parameter-free predictions. In Figure 14, we have updated the corresponding figure from Epelbaum et al. [8] by replacing the truncation errors, that have been estimated in that paper using the EKM approach of Epelbaum et al. [21] and Binder et al. [130], with the Bayesian uncertainties calculated as described in section 5. The 68% DoB Bayesian truncation errors are similar to those quoted in Epelbaum et al. [8] at N2LO but appear to be significantly larger at NLO. We also calculated in that paper the excitation energies for selected states of A = 6 − 12 nuclei and the point-proton radius of 4He. For almost all considered cases, adding the 3NF to the NN interaction was found to lead to a significant improvement in the description of experimental data. The predicted ground state energies of p-shell nuclei show a good agreement with the data except for 16O, which appears to be overbound. Notice that the deviation between the predicted and experimental values of the 16O binding energy is comparable to the 95% DoB Bayesian error at N2LO. It will be very interesting to repeat the calculations for the newest SMS interactions and to extend them to higher orders and heavier nuclei.
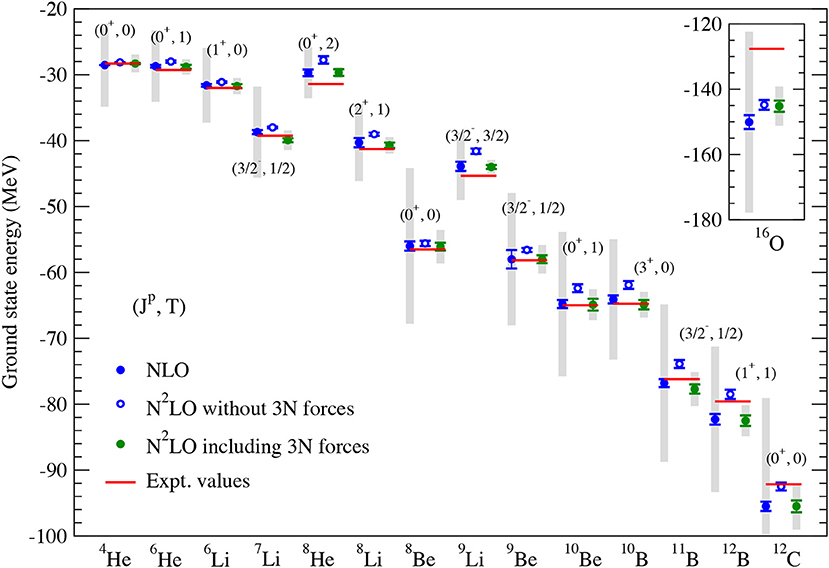
Figure 14. Calculated ground state energies in MeV using chiral SCS NN interactions from Epelbaum et al. [8] in combination with the SCS 3NF at R = 1.0 fm (open and solid dots) in comparison with experimental values (red levels). For each nucleus the NLO and N2LO results are the left and right symbols and bars, respectively. The open blue symbols correspond to incomplete calculations at N2LO using NN-only interactions. Blue and green error bars indicate the NCCI extrapolation uncertainty and, where applicable, an estimate of the SRG dependence. The shaded bars indicate the truncation error at each chiral order corresponding to 68% DoB intervals using the Bayesian model with the expansion parameter .
7. Summary and Outlook
In this review article we have presented a snapshot of the current state-of-the-art in low-energy nuclear theory with a focus on the latest generation of semilocal nuclear potentials from chiral EFT. We now summarize some of the key conclusions of our paper.
• We have presented a concise and self-contained introduction to the conceptual foundations of chiral effective field theory in the few-nucleon sector and described in some detail all steps needed to compute low-energy observables from the effective chiral Lagrangians (including error analysis). Special emphasis was given to clarify the notion of consistency of nuclear forces and current operators in terms of a perturbative matching to the unambiguously defined on-shell scattering amplitude. In particular, few-nucleon potentials from Epelbaum [73], Bernard et al. [54, 55], Krebs et al. [48, 95] and electroweak current operators from Kölling et al. [74, 122] and Krebs et al. [75, 123] at N3LO and beyond, derived using DR, are off-shell consistent with each other provided DR is also used to compute loop integrals arising from iterations of the dynamical equations.
• We have reviewed the semilocal momentum-space regularized potentials of Reinert et al. [17], which are currently the most precise chiral EFT NN forces on the market. These are the only NN interactions derived in chiral EFT, which—from the statistical point of view—qualify to be regarded as PWA of NN data below pion production threshold (see section 6.1 for details). At the highest considered order N4LO+, these interactions describe the np and pp data from the self-consistent Granada-2013 database with a precision that is at least comparable to the one reached by modern phenomenological potentials with a much larger number of adjustable parameters. The significantly better description of the scattering data by the SMS N4LO+ interactions of Reinert et al. [17] as compared to the nonlocal potentials of Entem et al. [23] at the same chiral order, and their much smaller residual cutoff dependence (see Figure 17 of Reinert et al. [17]), can presumably be traced back to the improved semilocal regulator, which maintains the long-range part of the interaction as described in section 4.1. We also addressed in detail the issue of uncertainty quantification in the NN sector. In particular, we discussed statistical uncertainties of NN and πN LECs and their propagation to selected observables as well as uncertainty introduced by fixing the maximum fit energy in the determination of the NN LECs. We also estimated truncation errors at various chiral orders using the Bayesian model specified in section 5.
• Beyond the NN sector, calculations based on the SMS interactions have so far been carried out up to N2LO [84]. The LECs cD and cE, which enter the 3NF at this order, have been determined from the 3H binding energy and the very precise pd cross section data at MeV from Sekiguchi et al. [184]. Using the employed Bayesian model to estimate truncation uncertainties, the predicted ground state energies of p-shell nuclei up to A = 16 are generally in a good agreement with the data. Also the predicted Nd scattering observables including the vector analyzing power Ay are consistent with experimental data within errors. We performed an additional test of the employed Bayesian model for truncation errors by exploring the impact of selected short-range 3NF terms at N4LO on observables in Nd elastic scattering. Our results suggest that a high-precision description of Nd scattering data will likely require the chiral expansion of the 3NF to be pushed to N4LO.
• The novel semilocal nuclear forces, derived in the finite-cutoff formulation of chiral EFT with short-range interactions counted according to NDA (i.e., the Weinberg scheme), have already been successfully confronted with few-nucleon data and passed a number of a-posteriori consistency checks as briefly summarized below:
– Using the minimal basis of the order-Q4 NN contact interactions as detailed in section 6, the LECs determined from the np and pp scattering data come out of a natural size (see Figure 7). The same is true for the LECs cD and cE entering the leading 3NF, as can be seen e.g., from the corresponding expectation values in the 3H state [84].
– The residual cutoff-dependence of NN phase shifts is strongly reduced at N3, 4LO as compared to N1, 2LO within the considered Λ-range (see e.g., Figure 4 of [82]).
– There is a clear systematic improvement in the description of np and pp data with increasing chiral orders (see Table 1). At order Q3 (i.e., N2LO), this improvement results solely from taking into account the parameter-free subleading TPEP contributions. Notice that certain alternative power counting schemes suggest that some of the contact interactions that appear at order Q4 in the Weinberg scheme are enhanced and should yield contributions to observables larger than the order-Q3 TPEP (see e.g., Table 1 of [81]). The clear evidence of the chiral TPEP at orders Q3 and Q5 observed in Epelbaum et al. [21, 22] and Reinert et al. [17] does, however, not support such alternative scenarios.
– The resulting convergence pattern of the EFT expansion for selected NN observables was scrutinized using Bayesian statistical methods (see section 5 for details). For not too soft cutoffs, the assumed breakdown scale of the EFT expansion of Λb ~ 600 MeV [21] was found to be statistically consistent [131] (see also [84, 132] for a related discussion).
– Scheme-dependence of nuclear potentials offers yet another way to perform nontrivial consistency checks of the theoretical framework by explicitly verifying (approximate) scheme-independence of observables. In the formulation we employ, scheme dependence of the nuclear forces first appears at N3LO and manifests itself in their dependence on arbitrary real phases , , which parameterize the unitary ambiguity of the leading relativistic corrections [21, 74], and the appearance of three off-shell short-range operators in the 1S0 and 3S1-3D1 channels proportional to the LECs , , and [17, 204, 205]. The SMS potentials of Reinert et al. [17] make use of the standard choice for namely , which minimizes the amount of 1/m2-corrections to the OPEP, and employ . Different choices of these parameters lead to different off-shell behaviors of the potential. They are related to each other by unitary transformations which, however, also induce an infinite tower of higher-order terms beyond the order one is working. The residual dependence of observables on and , therefore, probes the impact of neglected higher-order terms and should lie within the estimated truncation errors. We have redone the fits at N4LO+ for Λ = 450 MeV using alternative choices of [17] and also developed a version of the potential with [206]. The letter choice is motivated by the vanishing isoscalar exchange charge density operator at N3LO. In all considered cases, we found negligibly small changes in observables in spite of strong changes at the interaction level.
– Calculations of three- and more-nucleon observables based on solely NN interactions are incomplete beyond second order. They do, however, provide information about the magnitude of the missing 3NF contributions by assessing the spread in results at different orders Q≥3 and via a comparison of such incomplete predictions with experimental data. In Binder et al. [83], such an analysis was performed for Nd scattering observables and selected properties of light nuclei using the SCS NN interactions of Epelbaum et al. [21, 22]. The sizes of the 3NF contributions required to bring such incomplete results in agreement with experimental data were found to agree well with expectations based on Weinberg's power counting. Furthermore, recent calculations by the LENPIC Collaboration which include the leading 3NF [8, 84] show that the resulting N2LO predictions for observables that have not been used in the determination of the LECs cD, cE are generally in a good agreement with the data (see section 6). No indications are found for enhanced contributions of the 3NF in general and of the cD-term in particular as suggested in Birse [207].
To summarize, major progress has been achieved in recent years toward developing chiral EFT into a precision tool for low-energy nuclear physics. In the NN sector, the latest SMS interactions at fifth chiral order have already reached the accuracy at or even below permille level for low-energy observables such as e.g., the deuteron asymptotic S-state normalization AS (see section 6.1 for details and further examples). The only essential missing step in the NN sector concerns the inclusion of isospin-breaking interactions up to fifth chiral order. Work along this line is in progress.
Pushing the precision frontier beyond the NN system opens exciting perspectives for low-energy nuclear theory and will allow one to confront chiral EFT with currently unsolved problems, such as a quantitative description of 3N scattering observables [19]. This, however, will require to address the two core challenges:
(i) Derivation of consistent regularized three- and four-nucleon forces and exchange charge and current operators at and beyond N3LO as detailed in section 4.2. This issue has not been paid attention to in the recent calculations involving the 3NFs [208–211] and exchange electroweak currents [110, 212, 213] at N3LO. As explained in section 4.2, using ad hoc regularization approaches at N3LO and beyond generally leads to incorrect results for the scattering amplitude and other observables due to the appearance of uncontrolled short-range artifacts, which violate chiral symmetry and are not suppressed by inverse powers of Λ. This puts the findings of these studies into question.
(ii) Determination of the LECs in the 3NF at N4LO. While the N3LO contributions to the 3NF and 4NF do not involve unknown parameters, the N4LO corrections to the 3NF involve 10 LEC accompanying purely short-range operators [45] and one or more LECs entering the one-pion-exchange-contact topology, which has not been worked out yet. As discussed in section 6.2, the determination of these LECs from 3N data will require a computationally challenging analysis.
As a first example of a precision calculation not restricted to NN scattering, we have recently determined the deuteron structure radius with an accuracy below the permille level, fm, by pushing the chiral expansion of the electromagnetic exchange charge density beyond N3LO and performing a thorough analysis of various types of uncertainty [206]. By combining the predicted value for rstr with the very accurate atomic data from isotope shift measurements, it was, for the first time, possible to extract the neutron charge radius from experimental data on light nuclei. This study was facilitated by the absence of loop contributions in the isoscalar exchange charge density at N3LO [74, 122], which allowed for a trivial construction of the corresponding consistently regularized expressions for the charge operator. Rederivation of the contributions to 3NFs, 4NFs and exchange currents at and beyond N3LO using a regulator, consistent with the one employed in Reinert et al. [17], would open the way for performing similar precision calculations for a broad class of low-energy few-nucleon reactions.
Author Contributions
EE has lead the development of this review. All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported by BMBF (Grant No. 05P18PCFP1) and by DFG through funds provided to the Sino-German CRC 110 110 Symmetries and the Emergence of Structure in QCD (Grant No. TRR110).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Ashot Gasparyan, Jambul Gegelia, and Ulf-G. Meißner for a careful reading of the manuscript and useful comments and to all members of the LENPIC Collaboration for sharing their insights into the topics addressed in this review article. We also thank Pieter Maris for providing us with a source file of Figure 8 from Epelbaum et al. [8].
Footnotes
1. ^The precise meaning of consistency of many-body forces is defined in sections 2 and 4.2.
2. ^Strictly speaking, Mπ is to be understood as the pion mass to leading order in the chiral expansion while Fπ and other parameters in the effective Lagrangian refer to the corresponding LECs in the chiral limit of vanishing light quark masses.
3. ^An upper bound for Λb is set by the scale 4πFπ emerging from pion loops [52].
4. ^Notice that the contributions from diagrams shown in Figure 1 are finite in DR.
5. ^See, however, Kaplan [68] for analytical results in the chiral limit.
6. ^For pionless EFT or chiral EFT with perturbative pions, the NN amplitude can be calculated analytically, and renormalization can be carried out explicitly.
7. ^Alternatively (but equivalently), the chiral order ν of a connected, N-nucleon irreducible diagram with L loops can be expressed as with Δi = di + ni/2 − 2.
8. ^The claim in Pastore et al. [109] that the transformation eiU in Equation (28) of that paper is unitary is incorrect since the operator iU(1)(ν) from Equation (28) is not antihermitian.
9. ^Notice that the aforementioned potentials (except the one of [112]) additionally employ spectral function regularization (SFR) [116, 117] of the TPEP in the form of a sharply cut-off spectral integral in order to suppress its remaining unphysical short-distance behavior. Notice, however, that the application of a nonlocal regulator exp(−(p2n + p′2n)/Λ2n) with suitably chosen n is sufficient to arrive at UV-finite iterations of the potential.
10. ^This is not visible in Figure 3 since the unregularized potential WC, ∞(r) is singular at r = 0.
11. ^No meaningful uncertainty estimation can be carried out within the Bayesian approach at LO.
12. ^Strictly speaking, our database differs from the one of Navarro Pérez [18] by the omission of the data set from Daub et al. [141] (see [17] for more details).
13. ^In our paper Reinert et al. [17], also the cutoff Λ = 350 MeV was considered. Given the sizable finite-Λ artifacts for this very soft cutoff choice, we do not consider this case in the following discussion.
14. ^We have corrected the last figures in the values for χ2/datum for np data in the Elab bins of 0–100 and 0–200 MeV at N3LO and N4LO+ quoted in Table 3 of Reinert et al. [17].
15. ^We cannot estimate the N3LO truncation error using the Bayesian approach described in section 5 since no complete N3LO results are available for Nd scattering.
References
1. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288. doi: 10.1016/0370-2693(90)90938-3
2. Weinberg S. Effective chiral Lagrangians for nucleon - pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3. doi: 10.1016/0550-3213(91)90231-L
3. Epelbaum E. Few-nucleon forces and systems in chiral effective field theory. Prog Part Nucl Phys. (2006) 57:654. doi: 10.1016/j.ppnp.2005.09.002
4. Epelbaum E, Hammer HW, Meißner U-G. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773. doi: 10.1103/RevModPhys.81.1773
5. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1. doi: 10.1016/j.physrep.2011.02.001
6. Hammer H-W, König S, van Kolck U. Nuclear effective field theory: status and perspectives. arXiv: [preprint] arXiv:1906.12122 [nucl-th].
7. Epelbaum E, Gasparyan AM, Gegelia J, Meißner U-G. How (not) to renormalize integral equations with singular potentials in effective field theory. Eur Phys J A. (2018) 54:186. doi: 10.1140/epja/i2018-12632-1
8. Epelbaum E, Golak J, Hebeler K, Hüther T, Kamada H, Krebs H, et al. Few- and many-nucleon systems with semilocal coordinate-space regularized chiral two- and three-body forces. Phys Rev C. (2019) 99:024313. doi: 10.1103/PhysRevC.99.024313
9. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lus E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503
10. Lonardoni D, Carlson J, Gandolfi S, Lynn JE, Schmidt KE, Schwenk A, Wang X. Properties of nuclei up to A = 16 using local chiral interactions. Phys Rev Lett. (2018) 120: 122502 doi: 10.1103/PhysRevLett.120.122502
11. Hagen G, Jansen GR, Papenbrock T. Structure of 78Ni from first principles computations. Phys Rev Lett. (2016) 117: 172501 doi: 10.1103/PhysRevLett.117.172501
12. Gebrerufael E, Vobig K, Hergert H, Roth R. Ab initio description of open-shell nuclei: merging no-core shell model and in-medium similarity renormalization group. Phys Rev Lett. (2017) 118:152503. doi: 10.1103/PhysRevLett.118.152503
13. Cipollone A, Barbieri C, Navratil P. Chiral three-nucleon forces and the evolution of correlations along the oxygen isotopic chain. Phys Rev C. (2015) 92:014306. doi: 10.1103/PhysRevC.92.014306
14. Epelbaum E, Krebs H, Lee D, Meißner UG. Ab initio calculation of the Hoyle state. Phys Rev Lett. (2011) 106:192501. doi: 10.1103/PhysRevLett.106.192501
15. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha-alpha scattering. Nature. (2015) 528:111. doi: 10.1038/nature16067
16. Lähde TA, Meißner UG. Nuclear lattice effective field theory : an introduction. Lect Notes Phys. (2019) 957:1. doi: 10.1007/978-3-030-14189-9
17. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A. (2018) 54:86. doi: 10.1140/epja/i2018-12516-4
18. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse-grained potential analysis of neutron-proton and proton-proton scattering below the pion production threshold. Phys Rev C. (2013) 88:064002. doi: 10.1103/PhysRevC.88.064002
19. Kalantar-Nayestanaki N, Epelbaum E, Messchendorp JG, Nogga A. Signatures of three-nucleon interactions in few-nucleon systems. Rept Prog Phys. (2012) 75:016301. doi: 10.1088/0034-4885/75/1/016301
20. Hammer HW, Nogga A, Schwenk A. Three-body forces: from cold atoms to nuclei. Rev Mod Phys. (2013) 85:197. doi: 10.1103/RevModPhys.85.197
21. Epelbaum E, Krebs H, Meißner U-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8
22. Epelbaum E, Krebs H, Meißner U-G. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301
23. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004
24. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev C. (2014) 90:054323. doi: 10.1103/PhysRevC.90.054323
25. Piarulli M, Girlanda L, Schiavilla R, Navarro Perez R, Amaro JE, Ruiz Arriola E. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C. (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003
26. Ekström A, Baardsen G, Forssén C, Hagen G, Hjorth-Jensen M, Jansen GR, et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys Rev Lett. (2013) 110:192502. doi: 10.1103/PhysRevLett.110.192502
27. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301
28. Li N, Elhatisari S, Epelbaum E, Lee D, Lu BN, Meißner U-G. Neutron-proton scattering with lattice chiral effective field theory at next-to-next-to-next-to-leading order. Phys Rev C. (2018) 98:044002. doi: 10.1103/PhysRevC.98.044002
29. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, Schwenk A. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev C. (2017) 96:054007. doi: 10.1103/PhysRevC.96.054007
30. Girlanda L, Kievsky A, Viviani M, Marcucci LE. Short-range three-nucleon interaction from A=3 data and its hierarchical structure. Phys Rev C. (2019) 99:054003. doi: 10.1103/PhysRevC.99.054003
31. Ordonez C, Ray L, van Kolck U. The two nucleon potential from chiral Lagrangians. Phys Rev C. (1996) 53:2086. doi: 10.1103/PhysRevC.53.2086
32. Kaiser N, Gerstendorfer S, Weise W. Peripheral NN scattering: role of delta excitation, correlated two pion and vector meson exchange. Nucl Phys A. (1998) 637:395. doi: 10.1016/S0375-9474(98)00234-6
33. Krebs H, Epelbaum E, Meißner U-G. Nuclear forces with Delta-excitations up to next-to-next-to-leading order. I. Peripheral nucleon-nucleon waves, Eur Phys J A. (2007) 32:127. doi: 10.1140/epja/i2007-10372-y
34. Epelbaum E, Krebs H, Meißner U-G. Delta-excitations and the three-nucleon force. Nucl Phys A. (2008) 806:65. doi: 10.1016/j.nuclphysa.2008.02.305
35. Epelbaum E, Krebs H, Meißner U-G. Isospin-breaking two-nucleon force with explicit Delta-excitations. Phys Rev C. (2008) 77:034006. doi: 10.1103/PhysRevC.77.034006
36. Krebs H, Gasparyan AM, Epelbaum E. Three-nucleon force in chiral EFT with explicit Δ(1232) degrees of freedom: longest-range contributions at fourth order. Phys Rev C. (2018) 98:014003. doi: 10.1103/PhysRevC.98.014003
37. Coleman SR, Wess J, Zumino B. Structure of phenomenological Lagrangians. 1. Phys Rev. (1969) 177:2239 doi: 10.1103/PhysRev.177.2239
38. Callan CG Jr, Coleman SR, Wess J, Zumino B. Structure of phenomenological Lagrangians. 2. Phys Rev. (1969) 177:2247. doi: 10.1103/PhysRev.177.2247
39. Gasser J, Leutwyler H. Chiral perturbation theory to one loop. Ann Phys. (1984) 158:142. doi: 10.1016/0003-4916(84)90242-2
40. Bernard V, Kaiser N, Meißner U-G. Chiral dynamics in nucleons and nuclei. Int J Mod Phys E. (1995) 4:193. doi: 10.1142/S0218301395000092
41. Fettes N, Meißner U-G, Mojzis M, Steininger S. The Chiral effective pion nucleon Lagrangian of order p4. Ann Phys. (2000) 283:273. doi: 10.1006/aphy.2000.6059
42. Epelbaum E, Meißner U-G, Glöckle W, Elster C. Resonance saturation for four nucleon operators. Phys Rev C. (2002) 65:044001. doi: 10.1103/PhysRevC.65.044001
43. Girlanda L, Pastore S, Schiavilla R, Viviani M. Relativity constraints on the two-nucleon contact interaction. Phys Rev C. (2010) 81:034005. doi: 10.1103/PhysRevC.81.034005
44. Epelbaum E, Nogga A, Glöckle W, Kamada H, Meißner U-G, Witała H. Three nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001
45. Girlanda L, Kievsky A, Viviani M. Subleading contributions to the three-nucleon contact interaction. Phys Rev C. (2011) 84:014001. doi: 10.1103/PhysRevC.84.014001
46. Müller G, Meißner U-G. Virtual photons in baryon chiral perturbation theory. Nucl Phys B. (1999) 556:265. doi: 10.1016/S0550-3213(99)00339-9
47. Gasser J, Ivanov MA, Lipartia E, Mojzis M, Rusetsky A. Ground state energy of pionic hydrogen to one loop. Eur Phys J C. (2002) 26:13. doi: 10.1007/s10052-002-1013-z
48. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO I: Longest-range contributions. Phys Rev C. (2012) 85:054006. doi: 10.1103/PhysRevC.85.054006
49. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner U-G. Roy-Steiner-equation analysis of pion-nucleon scattering. Phys Rept. (2016) 625:1. doi: 10.1016/j.physrep.2016.02.002
50. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner U-G. Matching pion-nucleon Roy-Steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301
51. Siemens D, Bernard V, Epelbaum E, Gasparyan AM, Krebs H, Meißner U-G. Elastic and inelastic pion-nucleon scattering to fourth order in chiral perturbation theory. Phys Rev C. (2017) 96:055205. doi: 10.1103/PhysRevC.96.055205
52. Manohar A, Georgi H. Chiral quarks and the nonrelativistic Quark model. Nucl Phys B. (1984) 234:189. doi: 10.1016/0550-3213(84)90231-1
53. Bernard V. Chiral perturbation theory and baryon properties. Prog Part Nucl Phys. (2008) 60:82. doi: 10.1016/j.ppnp.2007.07.001
54. Bernard V, Epelbaum E, Krebs H, Meißner U-G. Subleading contributions to the chiral three-nucleon force. I. Long-range terms. Phys Rev C. (2008) 77:064004. doi: 10.1103/PhysRevC.77.064004
55. Bernard V, Epelbaum E, Krebs H, Meißner U-G. Subleading contributions to the chiral three-nucleon force II: short-range terms and relativistic corrections. Phys Rev C. (2011) 84:054001. doi: 10.1103/PhysRevC.84.054001
57. Pavon Valderrama M, Ruiz Arriola E. Renormalization of NN-scattering with one pion exchange and boundary conditions. Phys Rev C. (2004) 70:044006. doi: 10.1103/PhysRevC.70.044006
58. Nogga A, Timmermans RGE, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev C. (2005) 72:054006. doi: 10.1103/PhysRevC.72.054006
59. Birse MC. Power counting with one-pion exchange. Phys Rev C. (2006) 74:014003. doi: 10.1103/PhysRevC.74.014003
60. Epelbaum E, Meißner UG. On the renormalization of the one-pion exchange potential and the consistency of Weinberg's power counting. Few Body Syst. (2013) 54:2175. doi: 10.1007/s00601-012-0492-1
61. Epelbaum E, Gegelia J. Regularization, renormalization and 'peratization' in effective field theory for two nucleons. Eur Phys J A. (2009) 41:341. doi: 10.1140/epja/i2009-10833-3
62. Long B, Yang CJ. Renormalizing chiral nuclear forces: triplet channels. Phys Rev C. (2012) 85:034002. doi: 10.1103/PhysRevC.85.034002
63. Valderrama MP. Power counting and wilsonian renormalization in nuclear effective field theory. Int J Mod Phys E. (2016) 25:1641007. doi: 10.1142/S021830131641007X
64. Savage MJ. Including pions *Pasadena 1998, Nuclear physics with effective field theory. arXiv: nucl-th/9804034. p. 247–67.
65. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett B. (1998) 424:390 doi: 10.1016/S0370-2693(98)00210-X
66. Cohen TD, Hansen JM. Testing low-energy theorems in nucleon-nucleon scattering. Phys Rev C. (1999)59:3047 doi: 10.1103/PhysRevC.59.3047
67. Fleming S, Mehen T, Stewart IW. NNLO corrections to nucleon-nucleon scattering and perturbative pions. Nucl Phys A. (2000) 677:313. doi: 10.1016/S0375-9474(00)00221-9
68. Kaplan DB. On the convergence of nuclear effective field theory with perturbative pions. arXiv: [preprint] arXiv:1905.07485 [nucl-th].
69. Epelbaum E, Gegelia J. Weinberg's approach to nucleon-nucleon scattering revisited. Phys Lett B . (2012)716:338. doi: 10.1016/j.physletb.2012.08.025
70. Baru V, Epelbaum E, Gegelia J, Ren XL. Towards baryon-baryon scattering in manifestly Lorentz-invariant formulation of SU(3) baryon chiral perturbation theory. Phys Lett B. (2019)798:134987. doi: 10.1016/j.physletb.2019.134987
71. Epelbaum E, Gasparyan AM, Gegelia J, Krebs H. 1S0 nucleon-nucleon scattering in the modified Weinberg approach. Eur Phys J A. (2015)51:71. doi: 10.1140/epja/i2015-15071-6
72. Epelbaum E. Four-nucleon force in chiral effective field theory. Phys Lett B. (2006)639:456. doi: 10.1016/j.physletb.2006.06.046
73. Epelbaum E. Four-nucleon force using the method of unitary transformation. Eur Phys J A. (2007)34:197. doi: 10.1140/epja/i2007-10496-0
74. Kölling S, Epelbaum E, Krebs H, Meißner U-G. Two-nucleon electromagnetic current in chiral effective field theory: one-pion exchange and short-range contributions. Phys Rev C. (2011) 84:054008. doi: 10.1103/PhysRevC.84.054008
75. Krebs H, Epelbaum E, Meißner UG. Nuclear axial current operators to fourth order in chiral effective field theory. Ann Phys. (2017) 378:317. doi: 10.1016/j.aop.2017.01.021
76. Epelbaum E, Nogga A, Glöckle W, Kamada H, Mei UGßner, Witała H. Few nucleon systems with two nucleon forces from chiral effective field theory. Eur Phys J A. (2002) 15:543. doi: 10.1140/epja/i2002-10048-2
77. Krebs H. Electroweak current operators in chiral effective field theory. PoS CD. (2019) 2018:098 doi: 10.22323/1.317.0098
78. Epelbaum E. Towards high-precision nuclear forces from chiral effective field theory. arXiv:1908.09349 [nucl-th].
79. Gegelia J, Japaridze G, Wang XQ. Is heavy baryon approach necessary?. J Phys G. (2003) 29:2303. doi: 10.1088/0954-3899/29/9/322
80. Fuchs T, Gegelia J, Japaridze G, Scherer S. Renormalization of relativistic baryon chiral perturbation theory and power counting. Phys Rev D. (2003) 68:056005. doi: 10.1103/PhysRevD.68.056005
81. Grießhammer HW. Assessing theory uncertainties in EFT power countings from residual cutoff dependence. PoS CD. (2016) 15:104. doi: 10.22323/1.253.0104
82. Epelbaum E. Nuclear chiral EFT in the precision era. PoS CD. (2016) 15:014. doi: 10.22323/1.253.0014
83. Binder S, Calci A, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Few-nucleon systems with state-of-the-art chiral nucleon-nucleon forces. Phys Rev C. (2016) 93:044002. doi: 10.1103/PhysRevC.93.044002
84. Epelbaum E, Golak J, Hebeler K, Kamada H, Krebs H, Meißner UG, et al. Towards high-order calculations of three-nucleon scattering in chiral effective field theory. Eur Phys J A. (2020) 56:92. doi: 10.1140/epja/s10050-020-00102-2
85. Epelbaum E, Gegelia J. The two-nucleon problem in EFT reformulated: Pion and nucleon masses as soft and hard scales. PoS CD. (2013) 12:090. doi: 10.22323/1.172.0090
86. Baru V, Epelbaum E, Filin AA, Gegelia J. Low-energy theorems for nucleon-nucleon scattering at unphysical pion masses. Phys Rev C. (2015) 92:014001. doi: 10.1103/PhysRevC.92.014001
87. Baru V, Epelbaum E, Filin AA. Low-energy theorems for nucleon-nucleon scattering at Mπ = 450 MeV. Phys Rev C. (2016) 94:014001. doi: 10.1103/PhysRevC.94.014001
88. Lahde TA, Meißner UG, Epelbaum E. An update on fine-tunings in the triple-alpha process. Eur Phys J A. (2020) 56:89. doi: 10.1140/epja/s10050-020-00093-0
89. Epelbaum E. Nuclear forces from chiral effective field theory: a primer. arXiv: 1001.3229 [nucl-th].
90. van Haeringen H, Kok LP. Modified effective range function. Phys Rev A. (1982) 26:1218. doi: 10.1103/PhysRevA.26.1218
91. Epelbaum E, Gegelia J‘, Meißner UG. Wilsonian renormalization group versus subtractive renormalization in effective field theories for nucleon-nucleon scattering. Nucl Phys B. (2017) 925:161. doi: 10.1016/j.nuclphysb.2017.10.008
92. Suzuki K, Okamoto R. Degenerate perturbation theory in quantum mechanics. Prog Theor Phys. (1983) 70:439.
93. Lindgren I. The Rayleigh-Schrödinger perturbation and the linked-diagram theorem for a multi-configurational model space. J Phys B. (1974) 7:2441.
94. Okubo S. Diagonalization of Hamiltonian and Tamm-Dancoff equation. Prog Theor Phys. (1954) 12:603. doi: 10.1143/PTP.12.603
95. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO II: intermediate-range contributions. Phys Rev C. (2013) 87:054007. doi: 10.1103/PhysRevC.87.054007
96. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys A. (1997) 625:758. doi: 10.1016/S0375-9474(97)00586-1
97. Epelbaum E, Glöckle W, Meißner U-G. Nuclear forces from chiral Lagrangians using the method of unitary transformation. 1. Formalism. Nucl Phys A. (1998) 637:107. doi: 10.1016/S0375-9474(98)00220-6
98. van Kolck U. Few nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932. doi: 10.1103/PhysRevC.49.2932
99. Kaiser N. Chiral three pi exchange N N potentials: results for diagrams proportional to and . Phys Rev C. (2000) 62:024001. doi: 10.1103/PhysRevC.62.024001
100. Kaiser N. Chiral 3π exchange NN potentials: results for representation invariant classes of diagrams. Phys Rev C. (2000) 61:014003. doi: 10.1103/PhysRevC.61.014003
101. Kaiser N. Chiral 3π exchange NN potentials: results for dominant next-to-leading order contributions. Phys Rev C. (2001) 63:044010. doi: 10.1103/PhysRevC.63.044010
102. Kaiser N. Chiral 2π exchange NN potentials: two loop contributions. Phys Rev C. (2001) 64:057001. doi: 10.1103/PhysRevC.64.057001
103. Kaiser N. Chiral 2π exchange NN potentials: relativistic 1/M2 corrections. Phys Rev C. (2002) 65:017001. doi: 10.1103/PhysRevC.65.017001
104. Ishikawa S, Robilotta MR. Two-pion exchange three-nucleon potential: chiral expansion. Phys Rev C. (2007) 76:014006. doi: 10.1103/PhysRevC.76.014006
105. Entem DR, Kaiser N, Machleidt R, Nosyk Y. Peripheral nucleon-nucleon scattering at fifth order of chiral perturbation theory. Phys Rev C. (2015) 91:014002. doi: 10.1103/PhysRevC.91.014002
106. Epelbaum E, Glöckle W, Krüger A, Meißner U-G. Effective theory for the two nucleon system. Nucl Phys A. (1999) 645:413. doi: 10.1016/S0375-9474(98)00585-5
107. Polyzou WN. Equivalent hamiltonians. Phys Rev C. (2010) 82:014002. doi: 10.1103/PhysRevC.82.014002
108. Pastore S, Girlanda L, Schiavilla R, Viviani M, Wiringa RB. Electromagnetic currents and magnetic moments in (χ)EFT. Phys Rev C. (2009) 80:034004. doi: 10.1103/PhysRevC.80.034004
109. Pastore S, Girlanda L, Schiavilla R, Viviani M. The two-nucleon electromagnetic charge operator in chiral effective field theory (χEFT) up to one loop. Phys Rev C. (2011) 84:024001. doi: 10.1103/PhysRevC.84.024001
110. Piarulli M, Girlanda L, Marcucci LE, Pastore S, Schiavilla R, Viviani M. Electromagnetic structure of A = 2 and 3 nuclei in chiral effective field theory. Phys Rev C. (2013) 87:014006. doi: 10.1103/PhysRevC.87.014006
111. Baroni A, Girlanda L, Pastore S, Schiavilla R, Viviani M. Nuclear axial currents in chiral effective field theory. Phys Rev C. (2016) 93:015501. doi: 10.1103/PhysRevC.93.015501
112. Entem DR, Machleidt R. Accurate charge dependent nucleon nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001
113. Epelbaum E, Glöckle W, Meißner U-G. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl Phys A. (2005) 747:362. doi: 10.1016/j.nuclphysa.2004.09.107
114. Carlsson BD, Ekström A, Forssén C, Fahlin Strömberg D, Jansen GR, Lija O, et al. Uncertainty analysis and order-by-order optimization of chiral nuclear interactions. Phys Rev X. (2016) 6:011019. doi: 10.1103/PhysRevX.6.011019
115. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys Rev C. (2018) 97:024332. doi: 10.1103/PhysRevC.97.024332
116. Epelbaum E, Glöckle W, Meißner U-G. Improving the convergence of the chiral expansion for nuclear forces. 1. Peripheral phases. Eur Phys J A. (2004) 19:125. doi: 10.1140/epja/i2003-10096-0
117. Epelbaum E, Glöckle W, Meißner U-G. Improving the convergence of the chiral expansion for nuclear forces. 2. Low phases and the deuteron. Eur Phys J A. (2004) 19:401. doi: 10.1140/epja/i2003-10129-8
118. Rijken TA. Soft two pion exchange nucleon-nucleon potentials. Ann Phys. (1991) 208:253. doi: 10.1016/0003-4916(91)90296-K
119. Slavnov AA. Invariant regularization of nonlinear chiral theories. Nucl Phys B. (1971) 31:301. doi: 10.1016/0550-3213(71)90234-3
120. Djukanovic D, Schindler MR, Gegelia J, Scherer S. Improving the ultraviolet behavior in baryon chiral perturbation theory. Phys Rev D. (2005) 72:045002. doi: 10.1103/PhysRevD.72.045002
121. Long B, Mei Y. Cutoff regulators in chiral nuclear effective field theory. Phys Rev C. (2016) 93:044003. doi: 10.1103/PhysRevC.93.044003
122. Kölling S, Epelbaum E, Krebs H, Meißner U-G. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys Rev C. (2009) 80:045502. doi: 10.1103/PhysRevC.80.045502
123. Krebs H, Epelbaum E, Meißner U-G. Nuclear electromagnetic currents to fourth order in chiral effective field theory. Few Body Syst. (2019) 60:31. doi: 10.1007/s00601-019-1500-5
124. Siemens D, Bernard V, Epelbaum E, Gasparyan A, Krebs H, Meißner U-G. Elastic pion-nucleon scattering in chiral perturbation theory: a fresh look. Phys Rev C. (2016) 94:014620. doi: 10.1103/PhysRevC.94.014620
125. Yao DL, Siemens D, Bernard V, Epelbaum E, Gasparyan AM, Gegelia J, et al. Pion-nucleon scattering in covariant baryon chiral perturbation theory with explicit Delta resonances. JHEP. (2016) 1605:038. doi: 10.1007/JHEP05(2016)038
126. Hiller Blin AN, Sun ZF, Vicente Vacas MJ. Electromagnetic form factors of spin 1/2 doubly charmed baryons. Phys Rev D. (2018) 98:054025. doi: 10.1103/PhysRevD.98.054025
127. Hu J, Zhang Y, Epelbaum E, Meißner U-G, Meng J. Nuclear matter properties with nucleon-nucleon forces up to fifth order in the chiral expansion. Phys Rev C. (2017) 96:034307. doi: 10.1103/PhysRevC.96.034307
128. Skibiński R, Golak J, Topolnicki K, Witała H, Epelbaum E, Krebs H, et al. Testing semi-local chiral two-nucleon interaction in selected electroweak processes. Phys Rev C. (2016) 93:064002. doi: 10.1103/PhysRevC.93.064002
129. Nevo Dinur N, Hernandez OJ, Bacca S, Barnea N, Ji C, Pastore S, et al. Zemach moments and radii of 2, 3H and 3, 4He. Phys Rev C. (2019) 99:034004. doi: 10.1103/PhysRevC.99.034004
130. Binder S, Calci A, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Few-nucleon and many-nucleon systems with semilocal coordinate-space regularized chiral nucleon-nucleon forces. Phys Rev C. (2018) 98:014002. doi: 10.1103/PhysRevC.98.014002
131. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev C. (2015) 92:024005. doi: 10.1103/PhysRevC.92.024005
132. Melendez JA, Wesolowski S, Furnstahl RJ. Bayesian truncation errors in chiral effective field theory: nucleon-nucleon observables. Phys Rev C. (2017) 96:024003. doi: 10.1103/PhysRevC.96.024003
133. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys Rev C. (2019) 100:044001. doi: 10.1103/PhysRevC.100.044001
134. Epelbaum E. High-precision nuclear forces: where do we stand?. In: To Appear in Proceedings of the 9th International Workshop on Chiral Dynamics. Durham, NC (2018).
135. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takashi F, et al. Review of particle physics. Phys Rev D. (2018) 98:030001. doi: 10.1103/PhysRevD.98.030001
136. Fettes N, Meißner U-G, Steininger S. Pion-nucleon scattering in chiral perturbation theory. 1. Isospin symmetric case. Nucl Phys A. (1998) 640:199. doi: 10.1016/S0375-9474(98)00452-7[hep-ph/9803266].
137. Stoks VGJ, Klomp RAM, Rentmeester MCM, de Swart JJ. Partial wave analaysis of all nucleon-nucleon scattering data below 350 MeV. Phys Rev C. (1993) 48:792. doi: 10.1103/PhysRevC.48.792
138. Austen GJM, de Swart JJ. An improved coulomb potential. Phys Rev Lett. (1983) 50:2039. doi: 10.1103/PhysRevLett.50.2039
139. Stoks VGJ, De Swart JJ. The magnetic moment interaction in nucleon-nucleon phase shift analyses. Phys Rev C. (1990) 42:1235. doi: 10.1103/PhysRevC.42.1235
140. Durand L. Vacuum polarization effects in proton-proton scattering. Phys Rev. (1957) 108:1597. doi: 10.1103/PhysRev.108.1597
141. Daub BH, Henzl V, Kovash MA, Matthews JL, Miller ZW, Shoniyozov K, Yang H. Measurements of the neutron-proton and neutron-carbon total cross section from 150 to 800 keV. Phys Rev C. (2013) 87:014005. doi: 10.1103/PhysRevC.87.014005
142. Cox GF, Eaton GH, Van Zyl CP, Jarvis ON, Rose B. Measurements of the differential cross section and polarization in proton-proton scattering at about 143 MeV. Nucl Phys B. (1968) 4:353. doi: 10.1016/0550-3213(68)90115-6
143. Wesolowski S, Furnstahl RJ, Melendez JA, Phillips DR. Exploring Bayesian parameter estimation for chiral effective field theory using nucleon–nucleon phase shifts. J Phys G. (2019) 46:045102. doi: 10.1088/1361-6471/aaf5fc
144. Van Der Leun C, Alderliesten C. The deuteron binding energy. Nucl Phys A. (1982) 380:261. doi: 10.1016/0375-9474(82)90105-1
145. Schoen K, Jacobson DL, Arif M, Huffman PR, Black TC, Snow WM, et al. Precision neutron interferometric measurements and updated evaluations of the np and nd coherent neutron scattering lengths. Phys Rev C. (2003) 67:044005. doi: 10.1103/PhysRevC.67.044005
146. Machleidt R. The high precision, charge dependent Bonn nucleon-nucleon potential (CD-Bonn). Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001
147. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high quality N N potential models. Phys Rev C. (1994) 49:2950 doi: 10.1103/PhysRevC.49.2950
148. Gross F, Stadler A. Covariant spectator theory of np scattering: phase shifts obtained from precision fits to data below 350-MeV. Phys Rev C. (2008) 78:014005. doi: 10.1103/PhysRevC.78.014005
149. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Partial wave analysis of nucleon-nucleon scattering below pion production threshold. Phys Rev C. (2013) 88:024002. doi: 10.1103/PhysRevC.88.024002
150. Jarvis ON, Whitehead C, Shah M. Small-angle proton - proton scattering cross-sections at 144 MeV. Phys Lett. (1971) 36B:409. doi: 10.1016/0370-2693(71)90737-4
151. Taylor AE, Wood E, Bird L. Proton-proton scattering at 98 and 142 MeV. Nucl Phys. (1960) 16:320.
152. Bird L, Christmas P, Taylor A, Wood E. De-polarization parameter in p-p scattering at 143 MeV. Nucl Phys. (1961) 27:586.
153. Jarvis O, Rose B, Scanlon J, Wood E. A measurement of the Wolfenstein A parameter in p-p scattering at 143 MeV. Nucl Phys. (1963) 42:294.
154. Aldor-Noiman S, Brown LD, Buja A, Rolke W, Stine RA. The power to see: a new graphical test of normality. Am Stat. (2013) 67:249. doi: 10.1080/00031305.2013.847865
155. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Statistical error analysis for phenomenological nucleon-nucleon potentials. Phys Rev C. (2014) 89:064006. doi: 10.1103/PhysRevC.89.064006
156. Lisowski PW, Shamu RE, Auchampaugh GF, King NSP, Moore MS, Morgan GL, Singleton TS. Search for resonance structure in np total cross-section below 800 MeV. Phys Rev Lett. (1982) 49:255. doi: 10.1103/PhysRevLett.49.255
157. Ericson TEO, Rosa-Clot M. The deuteron asymptotic D state as a probe of the nucleon-nucleon force. Nucl Phys A. (1983) 405:497.
158. Rodning NL, Knutson LD. Asymptotic D-state to S-state ratio of the deuteron. Phys Rev C. (1990) 41:898.
159. Huber A, Udem T, Gross B, Reichert J, Kourogi M, Pachucki K, et al. Hydrogen-deuterium S-1- S-2 isotope shift and the structure of the deuteron. Phys Rev Lett. (1998) 80:468.
160. Bishop DM, Cheung LM. Quadrupole moment of the deuteron from a precise calculation of the electric field gradient in D-2. Phys Rev A. (1979) 20:381.
161. Friar JL, van Kolck U. Charge independence breaking in the two pion exchange nucleon-nucleon force. Phys Rev C. (1999) 60:034006.
162. Friar JL, van Kolck U, Payne GL, Coon SA. Charge symmetry breaking and the two pion exchange two nucleon interaction, Phys Rev C. (2003) 68:024003. doi: 10.1103/PhysRevC.68.024003
163. Epelbaum E, Meißner U-G. Isospin-violating nucleon-nucleon forces using the method of unitary transformation. Phys Rev C. (2005) 72:044001. doi: 10.1103/PhysRevC.72.044001
164. van Kolck U, Rentmeester MCM, Friar JL, Goldman JT, de Swart JJ. Electromagnetic corrections to the one pion exchange potential. Phys Rev Lett. (1998) 80:4386. doi: 10.1103/PhysRevLett.80.4386
165. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Precise determination of charge dependent pion-nucleon-nucleon coupling constants. Phys Rev C. (2017) 95:064001. doi: 10.1103/PhysRevC.95.064001
166. Glöckle W, Witała H, Hüber D, Kamada H, Golak J. The three nucleon continuum: achievements, challenges and applications. Phys Rept. (1996) 274:107.
167. Kievsky A, Viviani M, Rosati S, Huber D, Glöckle W, Kamada H, et al. Benchmark calculations for polarization observables in three nucleon scattering. Phys Rev C. (1998) 58:3085. doi: 10.1103/PhysRevC.58.3085
168. Witała H, Glöckle W. The analysing power in elastic nucleon-deuteron scattering. Nucl Phys A. (1991) 528:48.
169. Witała H, Glöckle W. On the discrepancies in the low energy neutron-deuteron breakup. J Phys G. (2010) 37:064003. doi: 10.1088/0954-3899/37/6/064003
170. Coon SA, Han HK. Reworking the Tucson-Melbourne three nucleon potential. Few Body Syst. (2001) 30:131. doi: 10.1007/s006010170022
171. Pudliner BS, Pandharipande VR, Carlson J, Wiringa RB. Quantum Monte Carlo calculations of A < = 6 nuclei. Phys Rev Lett. (1995) 74:4396. doi: 10.1103/PhysRevLett.74.4396
172. Witała H, Golak J, Skibiński R, Glöckle W, Kamada H, Polyzou WN. Three-nucleon force in relativistic three-nucleon Faddeev calculations. Phys Rev C. (2011) 83:044001. doi: 10.1103/PhysRevC.83.044001
173. Phillips DR, Schat C. Three-nucleon forces in the 1/Nc expansion. Phys Rev C. (2013) 88:034002. doi: 10.1103/PhysRevC.88.034002
174. Epelbaum E, Gasparyan AM, Krebs H, Schat C. Three-nucleon force at large distances: Insights from chiral effective field theory and the large-Nc expansion. Eur Phys J A. (2015) 51:26. doi: 10.1140/epja/i2015-15026-y
175. Topolnicki K. General operator form of the non-local three-nucleon force. Eur Phys J A. (2017) 53:181. doi: 10.1140/epja/i2017-12376-4
176. Wiringa RB, Stoks VGJ, Schiavilla R. An accurate nucleon-nucleon potential with charge independence breaking. Phys Rev C. (1995) 51:38. doi: 10.1103/PhysRevC.51.38
177. Hu J, Wei P, Zhang Y. Bayesian truncation errors in equations of state of nuclear matter with chiral nucleon-nucleon potentials. Phys Lett B. (2019) 798:134982. doi: 10.1016/j.physletb.2019.134982
178. Golak J, Rozpedzik D, Skibinski R, Topolnicki K, Witała H, Glöckle W, et al. A new way to perform partial wave decompositions of few-nucleon forces. Eur Phys J A. (2010) 43:241. doi: 10.1140/epja/i2009-10903-6
179. Hebeler K, Krebs H, Epelbaum E, Golak J, Skibiński R. Efficient calculation of chiral three-nucleon forces up to N3LO for ab initio studies. Phys Rev C. (2015) 91:044001. doi: 10.1103/PhysRevC.91.044001
180. Navratil P, Gueorguiev VG, Vary JP, Ormand WE, Nogga A. Structure of A=10-13 nuclei with two plus three-nucleon interactions from chiral effective field theory. Phys Rev Lett. (2007) 99:042501. doi: 10.1103/PhysRevLett.99.042501
181. Gazit D, Quaglioni S, Navratil P. Three-Nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502
182. Platter L, Hammer H-W, Meißner U-G. On the correlation between the binding energies of the triton and the alpha-particle. Phys Lett B. (2005) 607:254. doi: 10.1016/j.physletb.2004.12.068
183. Abfalterer WP, Bateman FB, Dietrich FS, Finlay RW, Haight RC, Morgan GL. Measurement of neutron total cross-sections up to 560-MeV. Phys Rev C. (2001) 63:044608. doi: 10.1103/PhysRevC.63.044608
184. Sekiguchi K, Sakai H, Witała H, Glöckle W, Golak J, Hatano M, et al. Complete set of precise deuteron analyzing powers at intermediate energies: comparison with modern nuclear force predictions. Phys Rev C. (2002) 65:034003. doi: 10.1103/PhysRevC.65.034003
185. Ermisch K, Amir-Ahmadi HR, van den Berg AM, Castelijns R, Davids B, Epelbaum E, et al. Systematic investigation of the elastic proton deuteron differential cross-section at intermediate-energies. Phys Rev C. (2003) 68:051001. doi: 10.1103/PhysRevC.68.051001
186. Deltuva A, Fonseca AC, Sauer PU. Momentum-space treatment of coulomb interaction in three-nucleon reactions with two protons. Phys Rev C. (2005) 71:054005. doi: 10.1103/PhysRevC.71.054005
187. Howell CR, Tornow W, Murphy K, Pfützner HG, Roberts ML, Anli L, et al. Comparisons of vector analyzing-power data and calculations for neutron-deuteron elastic scattering from 10 to 14 MeV. Few Body Syst. (1987) 2:19.
188. Sagara K, Oguri H, Shimizu S, Maeda K, Nakamura H, Nakashima T, Morinobu S. Energy dependence of analyzing power Ay and cross section for p+d scattering below 18 MeV. Phys Rev C. (1994) 50:576.
189. Rauprich G, Hähn HJ, Karus M, Nießen P, Nyga KR, Oswald H, et al. Measurement of elastic scattering at 10.0, 12.0, 14.1 and 16.5 MeV especially for small forward and extreme backward scattering angles. Few Body Syst. (1988) 5:67.
190. Sperisen F, Grüebler W, König V, Schmelzbach PA, Elsener K, Jenny B, et al. Comparison of a nearly complete pd elastic scattering data set with Faddeev calculations. Nucl Phys. (1984) A422:81.
191. Kievsky A. Phenomenological spin orbit three-body force. Phys Rev C. (1999) 60:034001. doi: 10.1103/PhysRevC.60.034001
192. von Przewoski B, Meyer HO, Balewski JT, Daehnick WW, Doskow J, Haeberli W, et al. Analyzing powers and spin correlation coefficients for p+d elastic scattering at 135-MeV and 200-MeV. Phys Rev C. (2006) 74:064003. doi: 10.1103/PhysRevC.74.064003
193. Barrett BR, Navratil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131. doi: 10.1016/j.ppnp.2012.10.003
194. Maris P, Vary JP, Shirokov AM. Ab initio no-core full configuration calculations of light nuclei. Phys Rev C. (2009) 79:014308. doi: 10.1103/PhysRevC.79.014308
195. Maris P, Vary JP. Ab initio nuclear structure calculations of p-shell nuclei with JISP16. Int J Mod Phys E. (2013) 22:1330016. doi: 10.1142/S0218301313300166
196. Glazek SD, Wilson KG. Renormalization of Hamiltonians. Phys Rev D. (1993) 48:5863. doi: 10.1103/PhysRevD.48.5863
197. Wegner F. Flow equations for Hamiltonians. Ann Phys. (1994) 506:77. doi: 10.1002/andp.19945060203
198. Bogner SK, Furnstahl RJ, Maris P, Perry RJ, Schwenk A, Vary JP. Convergence in the no-core shell model with low-momentum two-nucleon interactions. Nucl Phys A. (2008) 801:21. doi: 10.1016/j.nuclphysa.2007.12.008
199. Bogner SK, Furnstahl RJ, Schwenk A. From low-momentum interactions to nuclear structure. Prog Part Nucl Phys. (2010) 65:94. doi: 10.1016/j.ppnp.2010.03.001
200. Hagen G, Papenbrock T, Dean DJ, Schwenk A, Nogga A, Wloch M, Piecuch P. Coupled-cluster theory for three-body Hamiltonians. Phys Rev C. (2007) 76:034302. doi: 10.1103/PhysRevC.76.034302
201. Roth R, Binder S, Vobig K, Calci A, Langhammer J, Navratil P. Ab initio calculations of medium-mass nuclei with normal-ordered chiral NN+3N interactions. Phys Rev Lett. (2012) 109:052501. doi: 10.1103/PhysRevLett.109.052501
202. Binder S, Piecuch P, Calci A, Langhammer J, Navratil P, Roth R. Extension of coupled-cluster theory with a noniterative treatment of connected triply excited clusters to three-body Hamiltonians. Phys Rev C. (2013) 88:054319. doi: 10.1103/PhysRevC.88.054319
203. Stroberg SR, Calci A, Hergert H, Holt JD, Bogner SK, Roth R, Schwenk A. A nucleus-dependent valence-space approach to nuclear structure. Phys Rev Lett. (2017) 118:032502. doi: 10.1103/PhysRevLett.118.032502
204. Beane SR, Savage MJ. Rearranging pionless effective field theory. Nucl Phys A. (2001) 694:511. doi: 10.1016/S0375-9474(01)01088-0
205. Furnstahl RJ, Hammer HW, Tirfessa N. Field redefinitions at finite density. Nucl Phys A. (2001) 689:846. doi: 10.1016/S0375-9474(00)00687-4
206. Filin AA, Baru V, Epelbaum E, Krebs H, Möller D, Reinert P. Extraction of the neutron charge radius from a precision calculation of the deuteron structure radius. Phys Rev Lett. (2020) 124:082501.
207. Birse MC. More effective theory of nuclear forces. PoS CD (2009) 09:078. doi: 10.22323/1.086.0078
208. Golak J, Skibinski R, Topolnicki K, Witała H, Epelbaum E, Krebs H, et al. Low-energy neutron-deuteron reactions with N3LO chiral forces. Eur Phys J A. (2014) 50:177. doi: 10.1140/epja/i2014-14177-7
209. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501
210. Hoppe J, Drischler C, Hebeler K, Schwenk A, Simonis J. Probing chiral interactions up to next-to-next-to-next-to-leading order in medium-mass nuclei. Phys Rev C. (2019) 100:024318. doi: 10.1103/PhysRevC.100.024318
211. Hüther T, Vobig K, Hebeler K, Machleidt R, Roth R. Family of chiral two- plus three-nucleon interactions for accurate nuclear structure studies. arXiv: [preprint]. arXiv:1911.04955 [nucl-th].
212. Baroni A, Girlanda L, Kievsky A, Marcucci LE, Schiavilla R, Viviani M. Tritium β-decay in chiral effective field theory. Phys Rev C. (2016) 94:024003. doi: 10.1103/PhysRevC.94.024003
Keywords: nuclear forces, effective field theory, chiral perturbation theory, regularization, few-body systems
Citation: Epelbaum E, Krebs H and Reinert P (2020) High-Precision Nuclear Forces From Chiral EFT: State-of-the-Art, Challenges, and Outlook. Front. Phys. 8:98. doi: 10.3389/fphy.2020.00098
Received: 29 November 2019; Accepted: 16 March 2020;
Published: 17 April 2020.
Edited by:
Ruprecht Machleidt, University of Idaho, United StatesReviewed by:
David Rodriguez Entem, University of Salamanca, SpainAndreas Ekström, Chalmers University of Technology, Sweden
Copyright © 2020 Epelbaum, Krebs and Reinert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Evgeny Epelbaum, ZXZnZW55LmVwZWxiYXVtQHJ1Yi5kZQ==
 Evgeny Epelbaum
Evgeny Epelbaum Hermann Krebs
Hermann Krebs Patrick Reinert
Patrick Reinert