TDHF and a Macroscopic Aspect of Low-Energy Nuclear Reactions

Time-dependent Hartree–Fock (TDHF) method has been applied to various low-energy nuclear reactions, such as fusion, fission, and multinucleon transfer reactions. In this Mini Review, we summarize recent attempts to bridge a microscopic nuclear reaction theory, TDHF, and a macroscopic aspect of nuclear reactions through nucleus–nucleus potentials and energy dissipation from macroscopic degrees of freedom to microscopic ones obtained from TDHF in various colliding systems from light to heavy mass regions.

1. Introduction

Time-dependent Hartree–Fock (TDHF) method has been widely used in analyzing low-energy nuclear reactions since Bonche and his coworkers applied TDHF to collision of slabs in one-dimensional space as the first application of TDHF to nuclear physics [1]. Since then TDHF has been improved in several respects, e.g., including all terms in recent energy density functionals (EDF) such as Skyrme [2] and Gogny [3] functionals and breaking symmetries such as space (from one-dimensional to three-dimensional space).

It is well-known that the coupling between relative motions of colliding nuclei (macroscopic degrees of freedom) and internal excitations of them (microscopic degrees of freedom) plays an important role for describing low-energy nuclear reactions at energies around the Coulomb barrier. To include such couplings, coupled-channel models [4–7] have been developed and widely used. TDHF automatically includes couplings between relative motion and internal excitations since TDHF describes the dynamics of single particles. Moreover, TDHF provides an intuitive picture of nuclear dynamics through the time evolution of one-body densities constructed from single-particle wave functions in nuclei. Recently, TDHF has been applied to nuclear collective excitations [3, 8–15] and to nuclear reactions such as fusion [16–22], quasifission [23–25], fission [26–29], and multinucleon transfer reactions [30–34], some of which include pairing correlations.

In this Mini Review, however, we do not discuss the development of TDHF itself (see recent review articles on the development of TDHF in [35–40]). Instead, we focus on a macroscopic aspect of low-energy nuclear reactions described by TDHF. To this end, we show various applications of the method called “dissipative-dynamics TDHF” (DD-TDHF) developed in Washiyama and Lacroix [19], Washiyama et al. [20], and Washiyama [41].

2. Dissipative-Dynamics TDHF

The basic idea of DD-TDHF is to combine microscopic dynamics of nuclear reactions described by TDHF and a macroscopic aspect of nuclear reactions through a mapping from microscopic TDHF evolution to a set of macroscopic equations of motion. We briefly summarize DD-TDHF by the following steps: (1) We first solve the TDHF equation to obtain time evolution of single-particle wave functions for nuclear reactions:

$\begin{array}{ll}i\hslash \frac{\partial {\varphi }_i(t)}{\partial t}=ĥ\left[\rho (t)\right]{\varphi }_i(t),& (1)\end{array}$

where ϕ_i(t) is the single-particle wave functions with index i (including spin and isospin degrees of freedom), and ĥ[ρ(t)] is the single-particle Hamiltonian as a functional of one-body density ρ(t), obtained from an EDF E[ρ] by an appropriate functional derivative ĥ[ρ(t)] = δE/δρ. (2) The next step is to define macroscopic two-body dynamics from microscopic TDHF simulations. Macroscopic two-body dynamics can be constructed once collective coordinate is defined from TDHF simulations. To do so in TDHF, we introduce a separation plane which divides the density ρ(r, t) of a colliding system to two subsystems, ρ₁(r, t) and ρ₂(r, t), corresponding to projectile-like and target-like densities. This separation plane is perpendicular to the collision axis, and at the position where the two densities ρ_P(r, t) and ρ_T(r, t) constructed from the single-particle wave functions initially in the projectile and in the target, respectively, cross (see Figure 1 of [19] for an illustrative example). We then compute the coordinate R_i and its conjugated momentum P_i for each subsystem i = 1, 2 from ρ₁(r, t) and ρ₂(r, t). Also, we compute the masses of the two subsystems by m_i = P_i/Ṙ_i. From these, two-body dynamics for the relative distance R as a collective coordinate and its conjugated momentum P, and reduced mass μ that may depend on R is constructed. (3) For the case of central collisions, we assume that the trajectory of the two-body dynamics obtained from TDHF follows a one-dimensional equation of motion for relative motions,

$\begin{array}{ll}\frac{dR}{dt}=\frac{P}{\mu },& (2)\end{array}$

$\begin{array}{ll}\frac{dP}{dt}=-\frac{dV}{dR}-\frac{d}{dR}\left(\frac{P^2}{2\mu }\right)-\gamma \frac{P}{\mu },& (3)\end{array}$

where V(R) and γ(R) denote the nucleus–nucleus potential and friction coefficient expressing energy dissipation from the relative motion of colliding nuclei to internal excitations in nuclei, respectively. An important point is that these two quantities V(R) and γ(R) are unknown in TDHF simulations. (4) To obtain those two unknown quantities we prepare a system of two equations from two trajectories at slightly different energies. Then, we solve the system of two equations at each R to obtain V(R) and γ(R). The details of numerical procedures for the calculations described above can be found in Washiyama and Lacroix [19], Washiyama et al. [20], and Washiyama [41]. In the following results, we used the SLy4d Skyrme EDF [16] without pairing interactions.

3. Nucleus–Nucleus Potential and Energy Dissipation

3.1. Light and Medium-Mass Systems

In light and medium-mass systems, whose charge product Z₁Z₂ is smaller than ≈ 1, 600, it is known that fusion occurs once two nuclei contact each other after passing the Coulomb barrier. Indeed, TDHF simulations for head-on collisions at energies above the Coulomb barrier lead to fusion, keeping a compound system compact for sufficiently long time. We first provide selected results of nucleus–nucleus potential and energy dissipation obtained from DD-TDHF and discuss their properties.

In Figure 1A, we show obtained nucleus–nucleus potentials as a function of relative distance R near the Coulomb barrier radius for ⁴⁰Ca + ⁴⁰Ca. The lines show the nucleus–nucleus potentials at different center-of-mass energies (E_c.m.) by DD-TDHF, while the filled circles show the potential obtained by the frozen-density approximation, where the energy of the system is calculated with the same EDF except that the dynamical effect during the collision is neglected and the density of each fragment is fixed to be its ground-state one. Moreover, in the frozen-density approximation, the Pauli principle is neglected between nucleons in the projectile and in the target, leading to worse approximation as the overlap of projectile and target nuclei becomes significant. Important remarks from this figure are: (1) Potentials obtained at higher energies (E_c.m. = 90, 100 MeV) agree with the frozen-density one, indicating the convergence of the potentials obtained by DD-TDHF at higher energies. (2) DD-TDHF potentials express an E_c.m. dependence at lower energies E_c.m. = 55, 57 MeV. (3) The height of DD-TDHF potential decreases with decreasing E_c.m.. The Coulomb barrier height decreases from ≈54.5 MeV at E_c.m. = 90, 100 MeV of DD-TDHF and of the frozen-density approximation to ≈53.4 MeV at E_c.m. = 55 MeV of DD-TDHF. The above remarks can be understood by the dynamical reorganization of the TDHF density profile of each TDHF trajectory. Figure 1B shows the TDHF density ρ(x, y, z = 0, t) at each R for E_c.m. = 55 (top panels) and 90 MeV (bottom panels). At E_c.m. = 90 MeV, the shape of each ⁴⁰Ca density keeps its shape spherical, while at E_c.m. = 55 MeV the shape of each ⁴⁰Ca density deviates from its ground-state spherical shape as R becomes smaller. This is a dynamical reorganization of density during fusion reactions. This dynamical reorganization changes the shape of each nucleus when two nuclei approach sufficiently, then reduces the height of the nucleus–nucleus potential obtained by DD-TDHF. This dynamical reduction of the nucleus–nucleus potential is seen in various light- and medium-mass systems in Washiyama and Lacroix [19].

FIGURE 1

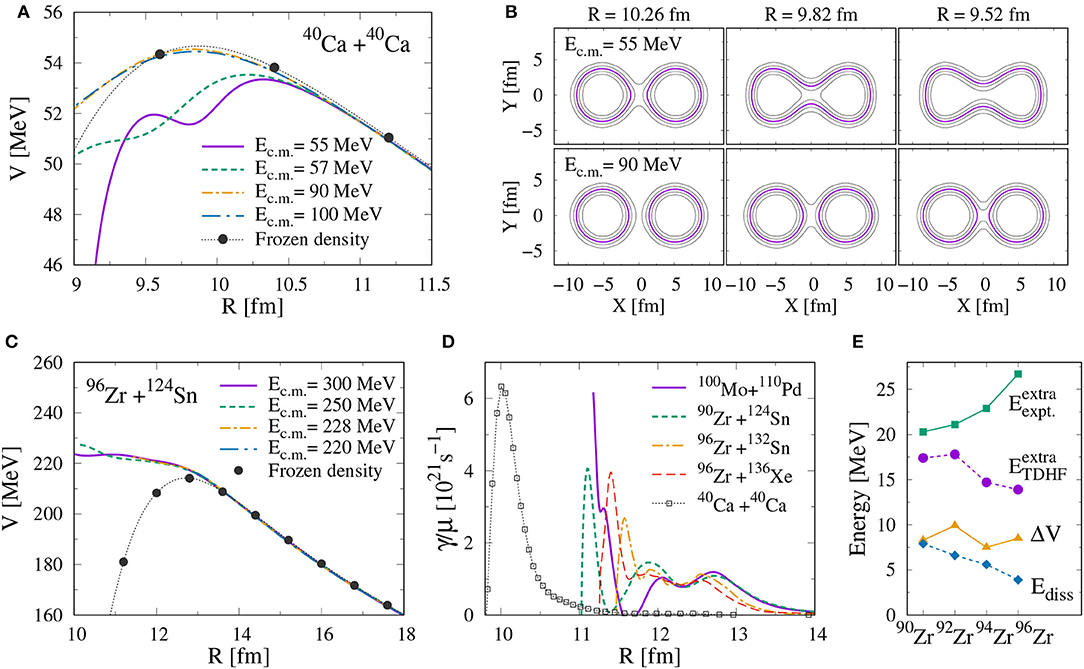
Figure 1. (A) Nucleus–nucleus potentials denoted by lines obtained by DD-TDHF at different energies and by the frozen-density approximation by filled circles with the dotted line as a function of R in ⁴⁰Ca + ⁴⁰Ca. (B) Contour plots of density profile ρ(X, Y, 0) obtained from TDHF at E_c.m. = 55 MeV (upper panels) and at E_c.m. = 90 MeV (lower panels), at R = 10.26 fm (left panels), 9.82 fm (middle), and 9.52 fm (right) in ⁴⁰Ca + ⁴⁰Ca. The isodensities (contour lines) are plotted at each 0.025 fm⁻³. (C) Same as (A) but for ⁹⁶Zr + ¹²⁴Sn. (D) Friction coefficient divided by reduced mass, γ/μ, from DD-TDHF. (E) Extra-push energy from experiments ($E_{\mathrm{\text{expt.}}}^{\mathrm{\text{extra}}}$) and from TDHF ($E_{\mathrm{\text{TDHF}}}^{\mathrm{\text{extra}}}$) together with potential increase ΔV and dissipated energy E_diss for ^{90, 92, 94, 96}Zr + ¹²⁴Sn (see text for detail). (A,B) adopted from Washiyama and Lacroix [19], (C,D) adopted from Washiyama [41], and (E) adopted from Washiyama [41] with slight change with permission from APS and SciPris.

We would like to note that, in the density-constrained TDHF (DC-TDHF) method [17], in which constrained Hartree–Fock calculation is performed to obtain the nucleus–nucleus potential under the condition that the density is constrained to the density obtained from TDHF at each time, similar E_c.m. dependence of nucleus–nucleus potentials is seen in various colliding systems reported, e.g., in Umar and Oberacker [18], Umar et al. [42], Oberacker et al. [43], and Umar et al. [44]. Moreover, in the ⁴⁰Ca + ⁴⁰Ca system, we find no significant difference in the potential extracted by DD-TDHF and the one by DC-TDHF [44].

3.2. Heavy Systems

Contrary to light and medium-mass systems described in section Light and Medium-Mass Systems, it was experimentally observed that fusion probability at energies near the Coulomb barrier is strongly hindered in heavy systems (Z₁Z₂ ≥ 1, 600) [45, 46]. The main origin of this hindrance has been considered as the presence of the quasifission process, where a composite system of two colliding nuclei reseparates before forming an equilibrated compound nucleus. This fusion hindrance indeed has been observed in TDHF e.g., in Simenel [35], Washiyama [41], Simenel et al. [47], and Guo and Nakatsukasa [48]. Namely, TDHF simulations for head-on collisions at energies above the Coulomb barrier lead to touching configuration of a composite system, and then to reseparation after a while (several to tens of zeptoseconds). In Washiyama [41], the extra-push energy $E_{\mathrm{\text{extra}}}^{\mathrm{\text{TDHF}}}=E_{\mathrm{\text{thres}}}^{\mathrm{\text{TDHF}}}-V_B^{\mathrm{\text{FD}}}$ in TDHF was systematically obtained in heavy systems, where $E_{\mathrm{\text{thres}}}^{\mathrm{\text{TDHF}}}$ and $V_B^{\mathrm{\text{FD}}}$ denote the fusion threshold energy above which fusion occurs in TDHF and the Coulomb barrier energy obtained in the frozen-density approximation, respectively. We show in Figure 1E extra-push energies in TDHF for ^{90, 92, 94, 96}Zr + ¹²⁴Sn, compared with those deduced from experimental data, $E_{\mathrm{\text{expt.}}}^{\mathrm{\text{extra}}}$, taken from Schmidt and Morawek [49], where the Bass barrier V_Bass [50] was employed as the Coulomb barrier height. We found that the difference between $V_B^{\mathrm{\text{FD}}}$ and V_Bass in ^{90, 92, 94, 96}Zr + ¹²⁴Sn is at most ≈1 MeV. These obtained extra-push energies in TDHF reasonably reproduce observations.

One may think why the fusion hindrance in heavy systems appears in both experiments and TDHF simulations. In Washiyama [41], we address this question and analyze where finite extra-push energies arise. For the analysis, we first derive the nucleus–nucleus potential and energy dissipation by DD-TDHF because we think that these two quantities are strongly related to the appearance of finite extra-push energy. In Figure 1C, we show an example of nucleus–nucleus potentials extracted in heavy systems, which is for the ⁹⁶Zr + ¹²⁴Sn system for three different energies in DD-TDHF and the frozen-density one. One can clearly see the difference between the potentials in ⁴⁰Ca + ⁴⁰Ca (Figure 1A) and ⁹⁶Zr + ¹²⁴Sn (Figure 1C): the potentials in ⁹⁶Zr + ¹²⁴Sn extracted by DD-TDHF monotonically increases as the relative distance decreases while the potentials in ⁴⁰Ca + ⁴⁰Ca and by the frozen-density approximation in ⁹⁶Zr + ¹²⁴Sn show a barrier structure at a certain relative distance. We have observed monotonic increase in potential in other heavy systems [41]. We consider the increase in potential in heavy systems as the transition from two-body dynamics of colliding nuclei to one-body dynamics of a composite system with strong overlap of the densities of colliding nuclei in TDHF and as the appearance of the conditional saddle point inside the Coulomb barrier in heavy systems [51–54].

We would like to note here that this is different property from the one obtained from the DC-TDHF method in the same colliding system in Oberacker et al. [43]. This difference comes from a different interpretation of the nucleus–nucleus potential between the two methods. In the DC-TDHF method energy minimization is carried out at a given density of a system obtained from TDHF to deduce a nucleus–nucleus potential that eliminates internal excitations in this system. In the DD-TDHF method the potential is deduced under the assumption that TDHF evolution is reduced to a one-dimensional equation of motion for relative motion. We consider that the DD-TDHF potential can include a part of the DC-TDHF internal excitation energy. We make a comment on the origin of the difference between the two potentials in the following: In heavy systems with larger Coulomb replusion, larger overlap of projectile and target densities during a collsion in TDHF is achieved at a short relative distance. In TDHF, diabatic level crossings can occur more in larger overlap region, leading to a part of internal excitations and to a transition from two-body to one-body picture of a system. This part of internal excitations is interpreted as potential energy in DD-TDHF, while this is treated as excitation energy in DC-TDHF. In the DC-TDHF method, the flattening of the potential at short distances inside the Coulomb barrier radius is seen in heavier systems leading to the synthesis of superheavy elements in Umar et al. [42].

In Figure 1D, reduced friction coefficient (γ/μ), the friction coefficient divided by the reduced mass extracted from Equation (2), are plotted for selected systems. The friction coefficient increases as R decreases, and shows oscillations in heavy systems. We consider that the fact that the friction coefficient becomes negative indicates breakdown of the assumption that the TDHF trajectory follows a macroscopic one-dimensional equation of motion for relative motion of a two-body colliding system.

Finally, we consider the origin of the fusion hindrance in heavy systems through the analysis with DD-TDHF. As mentioned above, nucleus–nucleus potential and energy dissipation are main contribution to the appearance of finite extra-push energy. We evaluate the potential increase at short distances and the accumulated dissipation energy from the friction coefficient using the formula [41],

$\begin{array}{ll}{E}_{\text{diss}}(t)={\displaystyle {\int }_0^t}d{t}^{\prime }\gamma \left[R(t^{\prime })\right]Ṙ{(t^{\prime })}^2,& (4)\end{array}$

up to time t when the kinetic energy of the relative motion of the system is completely dissipated. In Figure 1E, we also show the contribution of potential increase ΔV and dissipated energy E_diss to the extra-push energy in the ^{90, 92, 94, 96}Zr + ¹²⁴Sn systems. The result ΔV>E_diss indicates that the potential increase is a main origin for the appearance of the finite extra-push energy, i.e., fusion hindrance. Though the energy dissipation is known to play an important role in this fusion hindrance, it is not sufficient to explain the amount of the extra-push energy in the analysis with the DD-TDHF method.

3.3. Off-Central Collisions

So far, the applications of the DD-TDHF method has been limited to central collisions. Here we discuss a possible extension of the method to off-central collisions. Regarding (R, P) and (φ, L) as sets of canonical coordinates, where φ represents a rotation angle of the colliding system in the reaction plane and $L=\mu R^2\stackrel{\bullet }{\phi }$ is the angular momentum of the relative motion, we obtain a set of macroscopic equations of motion:

$\begin{array}{ll}\frac{\text{d}R}{\text{d}t}=\frac{P}{\mu },& (5)\end{array}$

$\begin{array}{ll}\frac{\text{d}\phi }{\text{d}t}=\frac{L}{\mu R^2},& (6)\end{array}$

$\begin{array}{ll}\frac{\text{d}P}{\text{d}t}=-\frac{\text{d}V}{\text{d}R}+\frac{1}{2}\left(\frac{P^2}{{\mu }^2}+\frac{L^2}{{\mu }^2{R}^2}\right)\frac{\text{d}\mu }{\text{d}R}+\frac{L^2}{\mu R^3}-{\gamma }_R\frac{P}{\mu },& (7)\end{array}$

$\begin{array}{ll}\frac{\text{d}L}{\text{d}t}=-{\gamma }_{\phi }\frac{L}{\mu }.& (8)\end{array}$

Here, γ_R(R) and γ_φ(R) denote the radial and tangential (or “sliding”) friction coefficients, respectively, where the former already appeared in Equation (3), the case of central collisions, and the latter governs the angular momentum dissipation (cf. Equation 8).

At first sight, there are three unknown quantities: the nucleus–nucleus potential V, the radial friction coefficient γ_R, and the tangential friction coefficient γ_φ. However, since time evolution of φ(t) and L(t) can be obtained from TDHF, a single TDHF simulation already provides the tangential friction coefficient by

$\begin{array}{ll}{\gamma }_{\phi }(R)=-\mu (t)\frac{\stackrel{\bullet }{L}(t)}{L(t)}.& (9)\end{array}$

Thus, there are only two unknown quantities in Equations (5)–(8), i.e., V(R) and γ_R(R), and we can apply the same procedure applied for central collisions.

In Figure 2, we show the results for the ¹⁶O+¹⁶O reaction at E/V_B = 1.4 including off-central collisions, as an illustrative example. In Figure 2A, the nucleus–nucleus potential is shown as a function of the relative distance, R. We also show the potential in the frozen-density approximation by open circles, for comparison. Figure 2A clearly shows that the method provides almost identical nucleus–nucleus potentials V(R) irrespective of the impact parameters. In Figure 2B, the effective potential V_eff(R), the sum of nuclear, Coulomb, and centrifugal potentials, is shown. It can be seen that, for b = 6 fm, the closest distance is achieved at around R = 10 fm, at which the effective potential coincides with the incident relative energy. In Figures 2C,D, the reduced radial and tangential friction coefficients, β_R = γ_R/μ and β_φ = γ_φ/μ, are shown as a function of the relative distance. We found no significant dependence of the friction coefficients on the impact parameters in this system. In this way, this approach enables us to access the angular momentum dissipation mechanism and a systematic calculation is in progress.

FIGURE 2

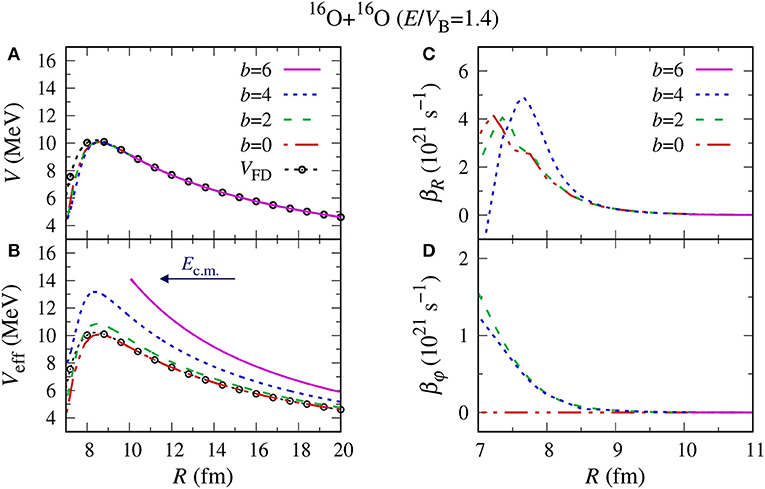
Figure 2. Results of DD-TDHF calculations for the ¹⁶O+¹⁶O reaction at E/V_B = 1.4 at various impact parameters. The nucleus–nucleus potentials and the effective potential $V_{\text{eff}}(R)=V(R)+L^2/2\mu R^2$ are shown in (A,B), respectively, as a function of the relative distance, R. The reduced radial friction coefficients, β_R = γ_R/μ, are shown in (C), while the reduced tangential friction coefficients, β_φ = γ_φ/μ, are shown in (D).

Note that non-central effects on nucleus–nucleus potentials and effective mass parameters in fusion reactions have been studied in TDHF and DC-TDHF in Jiang et al. [21]. It is interesting to make detailed comparison between those and our DD-TDHF in a future work.

4. Summary

The macroscopic aspect of TDHF dynamics for low-energy nuclear reactions at energies near the Coulomb barrier was discussed within the DD-TDHF method. We showed that the dynamical reorganization of single-particle wave functions inside the colliding nuclei affects the macroscopic nucleus–nucleus potential that leads to dynamical reduction of the potential around the Coulomb barrier radius in light- and medium-mass systems. In heavy systems, the dynamical reorganization leads to the fusion hindrance, increase in potential compared with the potential obtained from the frozen-density approximation in which the dynamical reorganization effect is neglected. By extending the DD-TDHF method to off-central collisions, the tangential friction coefficient was extracted in the ¹⁶O+¹⁶O reaction in addition to the nucleus–nucleus potential and the radial friction. As expected, the nucleus–nucleus potentials do not show a significant dependence of the initial angular momentum. The strength of the tangential friction is in the same order of magnitude as the radial one. From this extension, one can access the mechanism of angular momentum dissipation from microscopic reaction models. Possible future extension would be a systematic study of angular momentum dissipation mechanism in various systems, especially in heavy systems to address the fusion hindrance problem. Another possible extension would be a systematic study of collisions with deformed nuclei. It is interesting to study an orientation effect, a dependence of an angle between the collision axis and the principle axis of a deformed nucleus, on the nucleus–nucleus potential and the friction coefficient. It would be important to investigate how orbital angular momentum dissipation couples to a rotation of deformed nucleus during collision.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported in part by QR Program of Kyushu University, by JSPS-NSFC Bilateral Program for Joint Research Project on Nuclear mass and life for unravelling mysteries of r-process, and by JSPS Grant-in-Aid for Early-Career Scientists No. 19K14704.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge Denis Lacroix and Sakir Ayik for the collaboration to this work. This work used computational resources of the Oakforest-PACS Supercomputer System provided by Multidisciplinary Cooperative Research Program in Center for Computational Sciences (CCS), University of Tsukuba (Project ID: NUCLHIC), and computational resources of the HPCI system (Oakforest-PACS) provided by Joint Center for Advanced High Performance Computing (JCAHPC) through the HPCI System Project (Project ID: hp190002).

References

1. Bonche P, Koonin S, Negele JW. One-dimensional nuclear dynamics in the time-dependent Hartree-Fock approximation. Phys Rev C. (1976) 13:1226–58. doi: 10.1103/PhysRevC.13.1226

CrossRef Full Text | Google Scholar

2. Umar AS, Strayer MR, Reinhard PG. Resolution of the fusion window anomaly in heavy-ion collisions. Phys Rev Lett. (1986) 56:2793–6. doi: 10.1103/PhysRevLett.56.2793

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hashimoto Y. Linear responses in time-dependent Hartree-Fock-Bogoliubov method with Gogny interaction. Eur Phys J A. (2012) 48:55. doi: 10.1140/epja/i2012-12055-0

CrossRef Full Text | Google Scholar

4. Reisdorf W, Hessberger FP, Hildenbrand KD, Hofmann S, Münzenberg G, Schmidt KH, et al. Influence of collective surface motion on the threshold behavior of nuclear fusion. Phys Rev Lett. (1982) 49:1811–5. doi: 10.1103/PhysRevLett.49.1811

CrossRef Full Text | Google Scholar

5. Dasso CH, Landowne S, Winther A. Channel-coupling effects in heavy-ion fusion reactions. Nucl Phys A. (1983) 405:381–96.

Google Scholar

6. Balantekin AB, Takigawa N. Quantum tunneling in nuclear fusion. Rev Mod Phys. (1998) 70:77–100. doi: 10.1103/RevModPhys.70.77

CrossRef Full Text | Google Scholar

7. Hagino K, Takigawa N. Subbarrier fusion reactions and many-particle quantum tunneling. Prog Theor Phys. (2012) 128:1001–60. doi: 10.1143/PTP.128.1061

CrossRef Full Text | Google Scholar

8. Simenel C, Chomaz P, de France G. Quantum calculation of the dipole excitation in fusion reactions. Phys Rev Lett. (2001) 86:2971–4. doi: 10.1103/PhysRevLett.86.2971

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Simenel C, Chomaz P. Nonlinear vibrations in nuclei. Phys Rev C. (2003) 68:024302. doi: 10.1103/PhysRevC.68.024302

CrossRef Full Text | Google Scholar

10. Nakatsukasa T, Yabana K. Linear response theory in the continuum for deformed nuclei: Green's function vs. time-dependent Hartree-Fock with the absorbing boundary condition. Phys Rev C. (2005) 71:024301. doi: 10.1103/PhysRevC.71.024301

CrossRef Full Text | Google Scholar

11. Maruhn JA, Reinhard PG, Stevenson PD, Stone JR, Strayer MR. Dipole giant resonances in deformed heavy nuclei. Phys Rev C. (2005) 71:064328. doi: 10.1103/PhysRevC.71.064328

CrossRef Full Text | Google Scholar

12. Avez B, Simenel C, Chomaz P. Pairing vibrations study with the time-dependent Hartree-Fock-Bogoliubov theory. Phys Rev C. (2008) 78:044318. doi: 10.1103/PhysRevC.78.044318

CrossRef Full Text | Google Scholar

13. Ebata S, Nakatsukasa T, Inakura T, Yoshida K, Hashimoto Y, Yabana K. Canonical-basis time-dependent Hartree-Fock-Bogoliubov theory and linear-response calculations. Phys Rev C. (2010) 82:034306. doi: 10.1103/PhysRevC.82.034306

CrossRef Full Text | Google Scholar

14. Stetcu I, Bulgac A, Magierski P, Roche KJ. Isovector giant dipole resonance from the 3D time-dependent density functional theory for superfluid nuclei. Phys Rev C. (2011) 84:051309. doi: 10.1103/PhysRevC.84.051309

CrossRef Full Text | Google Scholar

15. Scamps G, Lacroix D. Systematics of isovector and isoscalar giant quadrupole resonances in normal and superfluid spherical nuclei. Phys Rev C. (2013) 88:044310. doi: 10.1103/PhysRevC.88.044310

CrossRef Full Text | Google Scholar

16. Kim KH, Otsuka T, Bonche P. Three-dimensional TDHF calculations for reactions of unstable nuclei. J Phys G. (1997) 23:1267.

Google Scholar

17. Umar AS, Oberacker VE. Heavy-ion interaction potential deduced from density-constrained time-dependent Hartree-Fock calculation. Phys Rev C. (2006) 74:021601. doi: 10.1103/PhysRevC.74.021601

CrossRef Full Text | Google Scholar

18. Umar AS, Oberacker VE. Density-constrained time-dependent Hartree-Fock calculation of ¹⁶O+²⁰⁸Pb fusion cross-sections. Eur Phys J A. (2009). 39:243–7. doi: 10.1140/epja/i2008-10712-5

CrossRef Full Text | Google Scholar

19. Washiyama K, Lacroix D. Energy dependence of the nucleus-nucleus potential close to the Coulomb barrier. Phys Rev C. (2008) 78:024610. doi: 10.1103/PhysRevC.78.024610

CrossRef Full Text | Google Scholar

20. Washiyama K, Lacroix D, Ayik S. One-body energy dissipation in fusion reactions from mean-field theory. Phys Rev C. (2009) 79:024609. doi: 10.1103/PhysRevC.79.024609

CrossRef Full Text | Google Scholar

21. Jiang X, Maruhn JA, Yan S. Microscopic study of noncentral effects in heavy-ion fusion reactions with spherical nuclei. Phys Rev C. (2014) 90:064618. doi: 10.1103/PhysRevC.90.064618

CrossRef Full Text | Google Scholar

22. Hashimoto Y, Scamps G. Gauge angle dependence in time-dependent Hartree-Fock-Bogoliubov calculations of ²⁰O+²⁰O head-on collisions with the Gogny interaction. Phys Rev C. (2016) 94:014610. doi: 10.1103/PhysRevC.94.014610

CrossRef Full Text | Google Scholar

23. Kedziora DJ, Simenel C. New inverse quasifission mechanism to produce neutron-rich transfermium nuclei. Phys Rev C. (2010) 81:044613. doi: 10.1103/PhysRevC.81.044613

CrossRef Full Text | Google Scholar

24. Wakhle A, Simenel C, Hinde DJ, Dasgupta M, Evers M, Luong DH, et al. Interplay between quantum shells and orientation in quasifission. Phys Rev Lett. (2014) 113:182502. doi: 10.1103/PhysRevLett.113.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer and quasifission processes in the ⁶⁴Ni+²³⁸U reaction. Phys Rev C. (2016) 93:054616. doi: 10.1103/PhysRevC.93.054616

CrossRef Full Text | Google Scholar

26. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601

CrossRef Full Text | Google Scholar

27. Scamps G, Simenel C, Lacroix D. Superfluid dynamics of ²⁵⁸Fm fission. Phys Rev C. (2015) 92:011602(R). doi: 10.1103/PhysRevC.92.011602

CrossRef Full Text | Google Scholar

28. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: Deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610

CrossRef Full Text | Google Scholar

29. Bulgac A, Magierski P, Roche KJ, Stetcu I. Induced fission of ²⁴⁰Pu within a real-time microscopic framework. Phys Rev Lett. (2016) 116:122504. doi: 10.1103/PhysRevLett.116.122504

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Simenel C. Particle transfer reactions with the time-dependent Hartree-Fock theory using a particle number projection technique. Phys Rev Lett. (2010) 105:192701. doi: 10.1103/PhysRevLett.105.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer processes in ^{40, 48}Ca+¹²⁴Sn, ⁴⁰Ca+²⁰⁸Pb, and ⁵⁸Ni+²⁰⁸Pb reactions. Phys Rev C. (2013) 88:014614. doi: 10.1103/PhysRevC.88.014614

CrossRef Full Text | Google Scholar

32. Scamps G, Lacroix D. Effect of pairing on one- and two-nucleon transfer below the Coulomb barrier: a time-dependent microscopic description. Phys Rev C. (2013) 87:014605. doi: 10.1103/PhysRevC.87.014605

CrossRef Full Text | Google Scholar

33. Wu Z, Guo L. Microscopic studies of production cross sections in multinucleon transfer reaction ⁵⁸Ni+¹²⁴Sn. Phys Rev C. (2019) 100:014612. doi: 10.1103/PhysRevC.100.014612

CrossRef Full Text | Google Scholar

34. Jiang X, Wang N. Probing the production mechanism of neutron-rich nuclei in multinucleon transfer reactions. Phys Rev C. (2020) 101:014604. doi: 10.1103/PhysRevC.101.014604

CrossRef Full Text | Google Scholar

35. Simenel C. Nuclear quantum many-body dynamics. Eur Phys J A. (2012) 48:152. doi: 10.1140/epja/i2012-12152-0

CrossRef Full Text | Google Scholar

36. Nakatsukasa T. Density functional approaches to collective phenomena in nuclei: Time-dependent density functional theory for perturbative and non-perturbative nuclear dynamics. Prog Theor Exp Phys. (2012) 2012:01A207. doi: 10.1093/ptep/pts016

CrossRef Full Text | Google Scholar

37. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys. (2016) 88:045004. doi: 10.1103/RevModPhys.88.045004

CrossRef Full Text | Google Scholar

38. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19–66. doi: 10.1016/j.ppnp.2018.07.002

CrossRef Full Text | Google Scholar

39. Sekizawa K. TDHF theory and its extensions for the multinucleon transfer reaction: a mini review. Front Phys. (2019) 7:20. doi: 10.3389/fphy.2019.00020

CrossRef Full Text | Google Scholar

40. Stevenson PD, Barton MC. Low-energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys. (2019) 104:142–64. doi: 10.1016/j.ppnp.2018.09.002

CrossRef Full Text | Google Scholar

41. Washiyama K. Microscopic analysis of fusion hindrance in heavy nuclear systems. Phys Rev C. (2015) 91:064607. doi: 10.1103/PhysRevC.91.064607

CrossRef Full Text | Google Scholar

42. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Entrance channel dynamics of hot and cold fusion reactions leading to superheavy elements. Phys Rev C. (2010) 81:064607. doi: 10.1103/PhysRevC.81.064607

CrossRef Full Text | Google Scholar

43. Oberacker VE, Umar AS, Maruhn JA, Reinhard PG. Microscopic study of the ^{132, 124}Sn+⁹⁶Zr reactions: Dynamic excitation energy, energy-dependent heavy-ion potential, and capture cross section. Phys Rev C. (2010). 82:034603. doi: 10.1103/PhysRevC.82.034603

CrossRef Full Text | Google Scholar

44. Umar AS, Simenel C, Oberacker VE. Energy dependence of potential barriers and its effect on fusion cross sections. Phys Rev C. (2014) 89:034611. doi: 10.1103/PhysRevC.89.034611

CrossRef Full Text | Google Scholar

45. Gäggeler H, Sikkeland T, Wirth G, Brüchle W, Bögl W, Franz G, et al. Probing sub-barrier fusion and extra-push by measuring fermium evaporation residues in different heavy ion reactions. Z Phys A. (1984) 316:291–307. doi: 10.1007/BF01439902

CrossRef Full Text | Google Scholar

46. Sahm CC, Clerc HG, Schmidt KH, Reisdorf W, Armbruster P, Heberger FP, et al. Hindrance of fusion in central collisions of heavy, symmetric nuclear systems. Z Phys A. (1984) 319:113–8. doi: 10.1007/BF01415623

CrossRef Full Text | Google Scholar

47. Simenel C, Avez B, Golabek C. Microscopic description of heavy ion collisions around the barrier (2009). arXiv: 0904.2653.

Google Scholar

48. Guo L, Nakatsukasa T. Time-dependent Hartree-Fock studies of the dynamical fusion threshold. EPJ Web Conf. (2012) 38:09003. doi: 10.1051/epjconf/20123809003

CrossRef Full Text | Google Scholar

49. Schmidt KH, Morawek W. The conditions for the synthesis of heavy nuclei. Rep Prog Phys. (1991) 54:949.

Google Scholar

50. Bass R. Fusion of heavy nuclei in a classical model. Nucl Phys A. (1974) 231:45–63.

Google Scholar

51. Swiatecki WJ. The Dynamics of Nuclear Coalescence or Reseparation. Phys Scr. (1981) 24:113–22.

PubMed Abstract | Google Scholar

52. Swiatecki WJ. The dynamics of the fusion of two nuclei. Nucl Phys A. (1982) 376:275–91.

Google Scholar

53. Bjornholm S, Swiatecki WJ. Dynamical aspects of nucleus-nucleus collisions. Nucl Phys A. (1982) 391:471–504.

Google Scholar

54. Swiatecki WJ, Siwek-Wilczynska K, Wilczynski J. Fusion by diffusion. II. Synthesis of transfermium elements in cold fusion reactions. Phys Rev C. (2005) 71:014602. doi: 10.1103/PhysRevC.71.014602

CrossRef Full Text | Google Scholar