Exact Soliton Solutions to the Cubic-Quartic Non-linear Schrödinger Equation With Conformable Derivative

The research paper aims to investigate the space-time fractional cubic-quartic non-linear Schrödinger equation in the appearance of the third, and fourth-order dispersion impacts without both group velocity dispersion, and disturbance with parabolic law media by utilizing the extended sinh-Gordon expansion method. This method is one of the strongest methods to find the exact solutions to the non-linear partial differential equations. In order to confirm the existing solutions, the constraint conditions are used. We successfully construct various exact solitary wave solutions to the governing equation, for example, singular, and dark-bright solutions. Moreover, the 2D, 3D, and contour surfaces of all obtained solutions are also plotted. The finding solutions have justified the efficiency of the proposed method.

1. Introduction and Motivation

Non-linear partial differential equations have different types of equations, one of them is the non-linear Schrödinger equation (NLSE) that relevant to the classical and quantum mechanics. The non-linear Schrödinger equation is a generalized (1 + 1)-dimensional version of the Ginzburg-Landau equation presented in 1950 in their study on supraconductivity and has been specifically reported by Chiao et al. [1] in their research of optical beams. In the past several years, various methods have been proposed to obtain the exact optical soliton solutions of the non-linear Schrödinger equation [2–12]. Dispersion and non-linearity are two of the essential components for the distribution of solitons across inter-continental regions. Usually, group velocity dispersion (GVD) level with self-phase modulation in a sensible manner allows these solitons to sustain tall range travel. In fact it might happen that the GVD is tiny and thus totally ignored, in this case the dispersion effect is determined by third and fourth order dispersion effects. Subsequently, this equation has been studied in a variety of ways, such as the Lie symmetry [13], both the $\left(m+\frac{G^{\prime }}{G}\right)$-improved expansion, and the exp(−φ(ξ))−expansion methods [14], and the semi-inverse variation principle method [4]. In this study, the extended sinh-Gordon expansion method (ShGEM) is applied to the non-linear cubic-quartic Schrödinger equations with the Parabolic law of fractional order, which is given by

$\begin{array}{ll}i{D}_t^{\alpha }u+i\beta D_{{}_x}^{3\alpha }u+\gamma D_{{}_x}^{4\alpha }u+cF\left({\left|u\right|}^2\right)u=0,& (1)\end{array}$

where u(x, t) is the complex valued wave function. The operator D^α of order α, where α ∈ (0, 1] is the fractional derivative, the parameters γ and β are real constants, a real-valued algebraic function F(|u|²) is p-times continuously differentiable, then

$\begin{array}{ll}F\left({\left|u\right|}^2\right)\in {\displaystyle \bigcup _{m,n=1}^{\infty }}{C}^p\left(\left(-n,n\right)\times \left(-m,m\right):R^2\right).& (2)\end{array}$

By using the relation of

$F(u)={\text{c}}_{1}u+c_2{u}^2,$

on Equation (1), we obtain the fractional non-linear Schrödinger equations with Parabolic law as follows:

$\begin{array}{ll}i{D}_t^{\alpha }u+i\beta D_{{}_x}^{3\alpha }u+\gamma D_{{}_x}^{4\alpha }u+\left(c_1{\left|u\right|}^2+c_2{\left|u\right|}^4\right)u=0.& (3)\end{array}$

The extended sinh-Gordon expansion method is intended to a generalization of the sine-Gordon expansion equation because it is based on an auxiliary equation namely the sine-Gordon equation (see previous studies [15, 16] for details). Moreover, different computational and numerical methods have been utilized to constructed new solutions to the non-linear partial differential equations, such as the variable separated method [17], the auxiliary parameters and residual power series method [18], the Bernoulli sub-equation method [19, 20], the modified auxiliary expansion method [21], the homotopy analysis transform method [22–26], the homotopy perturbation sumudu transform method [27], the shooting method with the explicit Runge-Kutta scheme [28, 29], and the Adomian decomposition method [30]. Recently, several fractional operators have been applied to the mathematical models in order to seek their exact solutions, such as the Laplace transform [31, 32], the Nabla operator [33–35].

The outline of paper are organize the paper as follows: A short review of the conformable derivative is presented in section 2. Section 3 deals with the analysis of the ShGEM. In section 4, the method is applied to solve the non-linear Schrödinger equation involving the fractional derivatives with the parabolic law. Eventually, in section 5, we presented our conclusion of this paper.

2. Basic Definitions

The basic definitions of the conformable derivative of order α are given as follows [36–41]:

Definition 2.1. Assume the function h : (0, ∞) → ℝ then, the conformable derivative of h of order α is defined as $D_t^{\alpha }h(t)=\underset{\epsilon \to 0}{\text{lim}}\frac{h(t+\epsilon t^{1-\alpha })-h(t)}{\epsilon }$, ∀t > 0, and 0 < α ≤ 1.

Definition 2.2. Assume that c ≥ 0 and t ≥ c, let h be a function defined on (c, t] as well as α ∈ ℝ. Then, the α-fractional integral of h is given by

$\begin{array}{ll}{}_t{I}_c^{\alpha }h\left(t\right)={\displaystyle \underset{c}{\overset{\alpha }{\int }}\frac{h\left(x\right)}{x^{1-\alpha }}dx},& (4)\end{array}$

if the Riemann improper integral exists.

Theorem 2.1. Let α ∈ (0, 1], and h = h(t), g = g(t) be α-conformable differentiable at a point t > 0, then:

$\begin{array}{l}{D}_t^{\alpha }\left(ah+bg\right)=a{D}_t^{\alpha }h+b{D}_t^{\alpha }g,forall\left(a,b\notin ℝ\right).\\ D_t^{\alpha }\left(t^{\lambda }\right)=\lambda t^{\lambda -\alpha },forall\left(\lambda \in ℝ\right).\\ D_t^{\alpha }\left(hg\right)=g{D}_t^{\alpha }\left(h\right)+h{D}_t^{\alpha }\left(g\right).\\ D_t^{\alpha }\left(\frac{h}{g}\right)=\frac{g{D}_t^{\alpha }\left(h\right)-h{D}_t^{\alpha }\left(g\right)}{g^2}.& (5)\end{array}$

Furthermore, if function h is differentiable, then $D_t^{\alpha }(h(t))=t^{1-\alpha }\frac{dh}{dt}$.

Theorem 2.2. (see for details pervious research [40]): Let h be a differentiable function and α is order of the conformable derivative. Let g be a differentiable function defined in the range of h, then

$\begin{array}{ll}{D}_t^{\alpha }(fog)(t)=t^{1-\alpha }g{(t)}^{\alpha -1}{g}^{\prime }(t)D_t^{\alpha }{(f(t))}_{t=g(t)},& (6)\end{array}$

here “prime” is the classical derivatives with respect to t.

3. The Extended ShGEM

In the current section, we presented the main steps of the e ShGEM (see previous study [42, 43]).

Consider the following fractional non-linear PDE:

$\begin{array}{ll}W(D_x^{\sigma }p,p^2{D}_x^{2\sigma }p,D_t^{\upsilon }p,D_t^{\upsilon }{D}_x^{\sigma }p,\dots )=0,& (7)\end{array}$

where p = p(x, t).

Consider the wave transformation

$\begin{array}{ll}p(x,t)=\psi (\zeta ),\zeta =\frac{x^{\sigma }}{\sigma }-c\frac{t^{\upsilon }}{\upsilon },& (8)\end{array}$

by substitute relation Equation (8) into Equation (7), we obtain the following non-linear ODE:

$\begin{array}{ll}P(\psi ,{\psi }^{\prime },\psi {,}^{″}{\psi }^2{\psi }^{\prime },.\; .\; .)=0.& (9)\end{array}$

Consider the trial solution of Equation (9) of the form

$\begin{array}{ll}\psi (\theta )={\displaystyle \sum _{j=1}^k}{\left[A_{j}sinh(\theta )+B_{j}cosh(\theta )\right]}^j+A_0.& (10)\end{array}$

The parameters A_j, B_j, for (j = 1, 2, …, k) and A₀ are real constants, and θ is a function of η that hold the following ODE:

$\begin{array}{ll}{\theta }^{\prime }=sinh(\theta ).& (11)\end{array}$

The homogeneous balance principle is applied on Equation (9) to find the value of k. From the space-time fractional the sinh-Gordon equation, we have (see previous study [15, 16]).

$\begin{array}{ll}{D_t}^{\nu }{D_x}^{\sigma }p=\lambda sinh(p).& (12)\end{array}$

The exact solutions of Equation (12) may be given as

$\begin{array}{ll}sinh(\theta )=\pm csch(\zeta )orsinh(\theta )=\pm isech(\zeta ),& (13)\end{array}$

and

$\begin{array}{ll}cosh(\theta )=\pm coth(\zeta )orcosh(\theta )=\pm tanh(\zeta ).& (14)\end{array}$

Letting solutions of Equation (10) along with Equations (13) and (14) as the form

$\begin{array}{ll}\psi (\zeta )={\displaystyle \sum _{j=1}^k}{\left[\pm i{A}_{j}sech(\zeta )\pm B_{j}tanh(\zeta )\right]}^j+A_0,& (15)\end{array}$

$\begin{array}{ll}\psi (\zeta )={\displaystyle \sum _{j=1}^k}{\left[\pm A_{j}csch(\zeta )\pm B_{j}coth(\zeta )\right]}^j+A_0.& (16)\end{array}$

Finding the value of k and then inserting Equations (10) and (12) into Equation (9), we get a system of terms of:

$\begin{array}{ll}sin{h}^i(\theta )cos{h}^j(\theta ),& (17)\end{array}$

we gather a group of over-defined non-linear algebraic equations in A₀, A_j, B_j, putting the coefficients of sinhⁱ(θ) cosh^j(θ) to zero, and finding the solutions of acquired system, we gain the values of A₀, A_j, B_j, c₁, c₂, κ, and ω. Putting the values of A₀, A_j, B_j, c₁, c₂, κ, and ω into Equations (15) and (16), we can find the solutions of Equation (7).

4. Implement of the Extended ShGEM

The implementation of the extended ShGEM to the cubic-quartic non-linear Schrödinger equation with conformable derivative is provided in this section.

Consider the wave transformation

$\begin{array}{ll}u(x,t)=U(\xi )e^{{}^{i\theta }},\xi =\frac{x^{\alpha }}{\alpha }-\nu \frac{t^{\alpha }}{\alpha },\theta =-\frac{\kappa x^{\alpha }}{\alpha }+\frac{\omega t^{\alpha }}{\alpha }.& (18)\end{array}$

In Equation (18), θ(x, t) represents the phase component of the soliton. The ω, κ, ν are the wave number, the soliton frequency, and the soliton velocity, respectively. Substituting wave transformation into Equation (2) and splitting the outcomes equation into real and imaginary parts, we gain

$\begin{array}{l}-(\beta {\kappa }^3-\gamma {\kappa }^4+\omega )U+c_1{U}^3+c_2{U}^5+3\beta \kappa U^{\prime \prime }\\ -6\gamma {\kappa }^2{U}^{\prime \prime }+\gamma U^{(4)}=0,& (19)\end{array}$

$\begin{array}{ll}-(3\beta {\kappa }^2-4\gamma {\kappa }^3+\nu )U^{\prime }+\beta U^{(3)}-4\gamma \kappa U^{(3)}=0.& (20)\end{array}$

Multiply both sides of Equation (19) by U′ and integrate it, we obtain

$\begin{array}{l}\gamma \left(-\frac{{\left(U^{″}\right)}^2}{2}+U^{‴}{U}^{\prime }\right)+\frac{c_1{U}^4}{4}+\frac{c_2{U}^6}{6}+3\gamma {\kappa }^2{\left(U^{\prime }\right)}^2\\ +\frac{1}{2}{U}^2\left(-4\gamma {\kappa }^4+\gamma {\kappa }^4-\omega \right)=0.& (21)\end{array}$

From Equation (20), we get constraint conditions ν = 4γκ³ − 3βκ² and β = 4γκ. Balancing the terms U^‴U′ and U⁶ yields κ = 1. With κ = 1, Equations (10), (16), and (17) change to

$\begin{array}{ll}\psi (\theta )=\left[A_{1}sinh(\theta )+B_{1}cosh(\theta )\right]+A_0,& (22)\end{array}$

$\begin{array}{ll}\psi (\zeta )=\left[\pm i{A}_{1}sech(\zeta )\pm B_{1}tanh(\zeta )\right]+A_0,& (23)\end{array}$

and

$\begin{array}{ll}\psi (\zeta )=\left[\pm m_{1}csch(\zeta )\pm n_{1}coth(\zeta )\right]+n_0,& (24)\end{array}$

respectively.

Inserting Equation (22) along with Equation (12) into Equation (21), and using constraint conditions provides a non-linear algebraic system. Equaling each coefficient of sinhⁱ(θ) cosh^j(θ) with the same power to zero, and finding the obtained system of algebraic equations, we gain the values of the parameters. Putting the obtained values of the parameters into Equations (23) and (24), give the solutions of Equation (3).

Set 1

$\begin{array}{l}{B}_1=\frac{2^{3/4}{3}^{1/4}{\omega }^{1/4}}{{\left(c_2\left(-1-6{\kappa }^2+3{\kappa }^4\right)\right)}^{1/4}},c_1=\frac{\sqrt{\frac{2}{3}}{c}_2\left(5+3{\kappa }^2\right)\sqrt{\omega }}{\sqrt{c_2\left(-1-6{\kappa }^2+3{\kappa }^4\right)}},\\ A_0=0,\gamma =\frac{\omega }{1+6{\kappa }^2-3{\kappa }^4},A_1=0,& (25)\end{array}$

we get

$\begin{array}{l}{u}_1\left(x,t\right)=\frac{2^{3/4}{3}^{1/4}{\omega }^{1/4}}{{\left(c_2\left(-1-6{\kappa }^2+3{\kappa }^4\right)\right)}^{1/4}}\\ csch\left(\frac{x^{\alpha }}{\alpha }+\frac{8t^{\alpha }{\kappa }^3\omega }{\alpha \left(1+6{\kappa }^2-3{\kappa }^4\right)}\right){\text{e}}^{\text{i}\left(-\frac{x^{\alpha }\kappa }{\alpha }+\frac{t^{\alpha }\omega }{\alpha }\right)}.& (26)\end{array}$

Set 2

$\begin{array}{l}{B}_1=\frac{(1+\text{i})6^{1/4}{\gamma }^{1/4}}{{c_2}^{1/4}},\omega =\gamma (1+6{\kappa }^2-3{\kappa }^4),\\ c_1=\text{i}\sqrt{\frac{2}{3}}\sqrt{\gamma }\sqrt{c_2}(5+3{\kappa }^2),A_1=0,A_0=0,& (27)\end{array}$

we get

$\begin{array}{l}{u}_2\left(x,t\right)=\frac{\left(1+\text{i}\right)6^{1/4}{a}_2^{1/4}}{{c_2}^{1/4}}\\ csch\left(\frac{x^{\alpha }}{\alpha }+\frac{8a_2{t}^{\alpha }{\kappa }^3}{\alpha }\right){\text{e}}^{\text{i}\left(-\frac{x^{\alpha }\kappa }{\alpha }+\frac{a2t^{\alpha }\left(1+6{\kappa }^2-3{\kappa }^4\right)}{\alpha }\right)}.& (28)\end{array}$

Set 3

$\begin{array}{l}{A}_0=0,A_1=\frac{4\sqrt{2}\sqrt{\gamma }}{\sqrt{c_1}},B_1=0,c_2=-\frac{3{c_1}^2}{128\gamma },\\ \kappa =-\sqrt{\frac{2}{3}},\omega =\frac{20\gamma }{3},& (29)\end{array}$

we get

$\begin{array}{ll}{u}_3\left(x,t\right)=-\frac{4\sqrt{2}\sqrt{\gamma }}{\sqrt{c_1}}coth\left(\frac{16\sqrt{\frac{2}{3}}\gamma t^{\alpha }}{3\alpha }-\frac{x^{\alpha }}{\alpha }\right){\text{e}}^{\text{i}\left(\frac{20\gamma t^{\alpha }}{3\alpha }+\frac{\sqrt{\frac{2}{3}}{x}^{\alpha }}{\alpha }\right)}.& (30)\end{array}$

Set 4

$\begin{array}{l}{A}_0=0,A_1=-\frac{\sqrt{2}\sqrt{\gamma }}{\sqrt{c_1}},B_1=\frac{\sqrt{2}\sqrt{\gamma }}{\sqrt{c_1}},c_2=-\frac{3{c_1}^2}{8\gamma },\\ \kappa =-\frac{1}{\sqrt{6}},\omega =\frac{5\gamma }{12},& (31)\end{array}$

we get

$\begin{array}{l}{u}_4\left(x,t\right)=-\frac{\sqrt{2}\sqrt{\gamma }}{\sqrt{c_1}}(\coth \left(\frac{2\sqrt{\frac{2}{3}}\gamma t^{\alpha }}{3\alpha }-\frac{x^{\alpha }}{\alpha }\right)\\ +\text{ csch}\left(\frac{2\sqrt{\frac{2}{3}}\gamma t^{\alpha }}{3\alpha }-\frac{x^{\alpha }}{\alpha }\right))\times {\text{e}}^{\text{i}\left(\frac{5a2t^{\alpha }}{12\alpha }+\frac{x^{\alpha }}{\sqrt{6}\alpha }\right)}.& (32)\end{array}$

Set 5

$\begin{array}{ll}\begin{array}{c}{B}_1=-\frac{2\sqrt{(5+3{\kappa }^2)\omega }}{\sqrt{c_1(-1-6{\kappa }^2+3{\kappa }^4)}},A_1=0,A_0=0,\\ c_2=\frac{3{c_1}^2(-1-6{\kappa }^2+3{\kappa }^4)}{2{(5+3{\kappa }^2)}^2\omega },\gamma =\frac{\omega }{1+6{\kappa }^2-3{\kappa }^4},\end{array}& (33)\end{array}$

we obtain

$\begin{array}{l}{u}_5\left(x,t\right)=\frac{2\sqrt{\left(5+3{\kappa }^2\right)\omega }}{\sqrt{c_1\left(-1-6{\kappa }^2+3{\kappa }^4\right)}}\\ csch\left(\frac{x^{\alpha }}{\alpha }+\frac{8t^{\alpha }{\kappa }^3\omega }{\alpha \left(1+6{\kappa }^2-3{\kappa }^4\right)}\right){\text{e}}^{\text{i}\left(-\frac{x^{\alpha }\kappa }{\alpha }+\frac{t^{\alpha }\omega }{\alpha }\right)}.& (34)\end{array}$

Set 6

$\begin{array}{l}{B}_1=A_1,A_0=0,c_1=-\frac{4{A_1}^2{c}_2}{3},\gamma =-\frac{2{A_1}^4{c}_2}{3},\\ \omega =-\frac{5{A_1}^4{c}_2}{18},\kappa =\frac{1}{\sqrt{6}},& (35)\end{array}$

we get

$\begin{array}{l}{u}_6\left(x,t\right)=(-A_1\text{ coth }\left(\frac{4\sqrt{\frac{2}{3}}{A}_1{}^4{c}_2{t}^{\alpha }}{9\alpha }-\frac{x^{\alpha }}{\alpha }\right)\\ +A_{1}csch\left(\frac{4\sqrt{\frac{2}{3}}{A}_1{}^4{c}_2{t}^{\alpha }}{9\alpha }-\frac{x^{\alpha }}{\alpha }\right))\\ \times {\text{e}}^{\text{i}\left(-\frac{5A_1{}^4{c}_2{t}^{\alpha }}{18\alpha }-\frac{x^{\alpha }}{\sqrt{6}\alpha }\right)}.& (36)\end{array}$

Set 7

$\begin{array}{ll}\begin{array}{c}{B}_1=\frac{\sqrt{6}\sqrt{c_1}}{\sqrt{c_2(5+3{\kappa }^2)}},\gamma =-\frac{3{c_1}^2}{2c_2{(5+3{\kappa }^2)}^2},\hfill \\ \omega =\frac{3{c_1}^2(-1-6{\kappa }^2+3{\kappa }^4)}{2c_2{(5+3{\kappa }^2)}^2},A_1=0,A_0=0,\end{array}& (37)\end{array}$

we get

$\begin{array}{c}{u}_7\left(x,t\right)=\frac{\sqrt{6}\sqrt{c_1}}{\sqrt{c_2\left(5+3{\kappa }^2\right)}}csch\left(\frac{x^{\alpha }}{\alpha }-\frac{12{c_1}^2{t}^{\alpha }{\kappa }^3}{c_2\alpha {\left(5+3{\kappa }^2\right)}^2}\right)\\ {\text{e}}^{\text{i}\left(-\frac{x^{\alpha }\kappa }{\alpha }+\frac{3{c_1}^2{t}^{\alpha }\left(-1-6{\kappa }^2+3{\kappa }^4\right)}{2c_2\alpha {\left(5+3{\kappa }^2\right)}^2}\right)}.& (38)\end{array}$

5. Conclusion

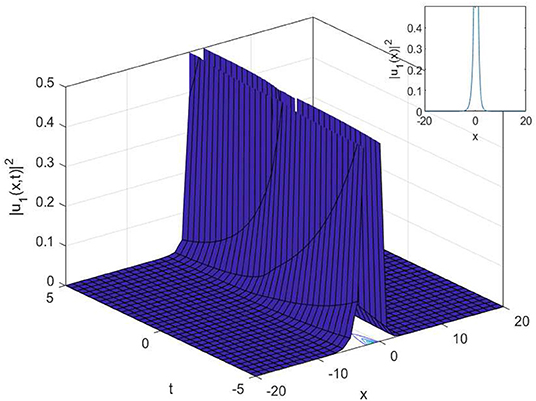
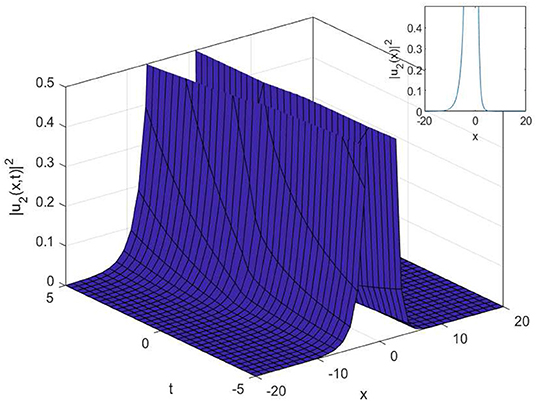
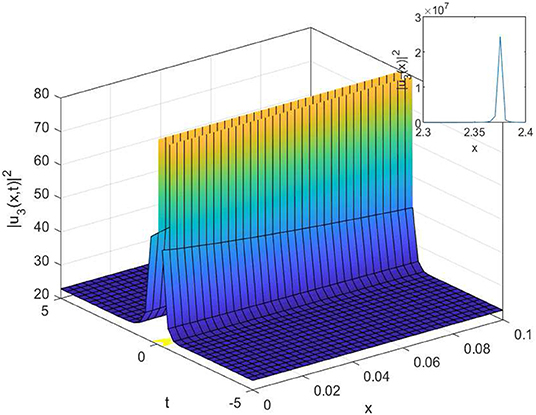
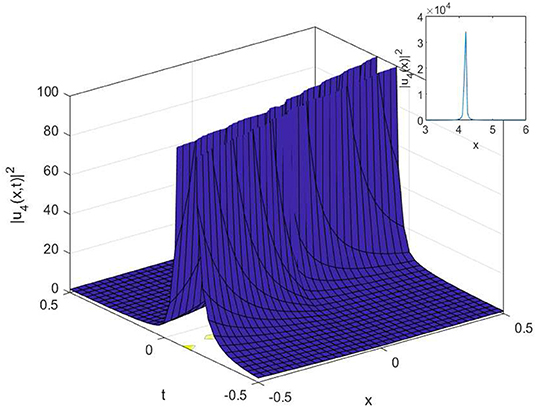
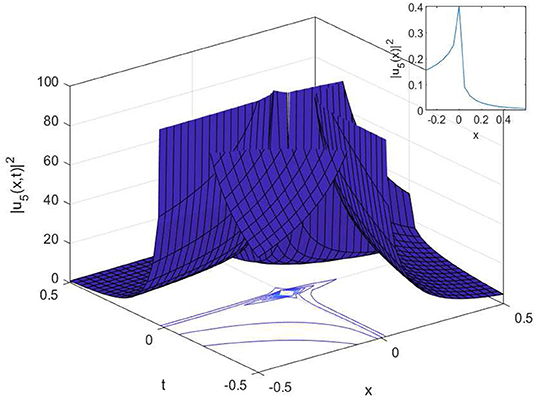
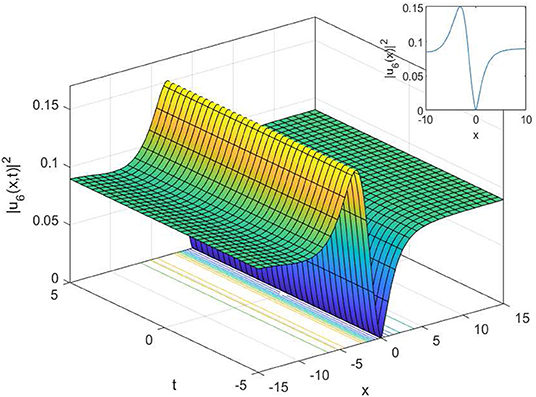
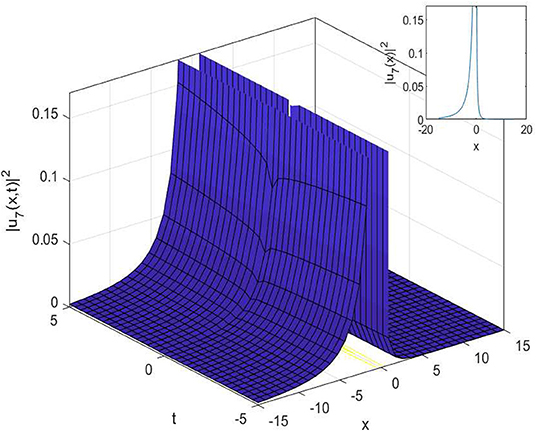
In this article, we have successfully used the extended sinh-Gordon expansion method to solve the problem for the non-linear cubic-quartic Schrödinger equations involving fractional derivatives with the Parabolic law. A traveling wave transforms in the sense of the comfortable derivative has been used to convert the governing equation into a NODE. The various optical solutions of the studied model have been constructed, for example, the singular soliton solutions as shown in Figures 1–6, and the dark-bright soliton solution as seen in Figure 7. Comparing our solutions to the results obtained in references [16–18], our findings solutions are new and different. To better analyze the dynamic attitude, and the characteristics of these solutions, the 2D, 3D and counter-surface of all obtained solutions are plotted. The study shows that this method is the effective and appropriate technique for finding the exact solution of the model considered in the paper.

FIGURE 1

Figure 1. 3D, 2D, and contour surfaces of Equation (26) where ω = 0.1, c₂ = 0.1, κ = 2, α = 0.8.

FIGURE 2

Figure 2. 3D, 2D, and contour surfaces of Equation (28) where γ = 0.5, c₂ = 0.2, κ = 0.4, α = 0.7.

FIGURE 3

Figure 3. 3D, 2D, and contour surfaces of Equation (30) where γ = 0.5, c₁ = 0.7, α = 0.9.

FIGURE 4

Figure 4. 3D, 2D, and contour surfaces of Equation (32) where γ = 5, c₁ = 7, α = 0.7.

FIGURE 5

Figure 5. 3D, 2D, and contour surfaces of Equation (34) where c₁ = 0.2, κ = 0.4, ω = 6, α = 0.4.

FIGURE 6

Figure 6. 3D, 2D, and contour surfaces of Equation (36) where c₂ = 0.2, A₁ = 0.3, α = 0.7.

FIGURE 7

Figure 7. 3D, 2D, and contour surfaces of Equation (38) where α = 0.3, c₁ = 0.5, c₂ = 0.2, κ = 0.4.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

HD contributed in developing the proofs and edited the article for possible improvement. HG, KA, and RY contributed in developing the main results and proofs. All authors read the final version and approved it.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Chiao RY, Garmire E, Townes CH. Self-trapping of optical beams. Phys Rev Lett. (1964) 13:479–82. doi: 10.1103/PhysRevLett.13.479

CrossRef Full Text | Google Scholar

2. Arshad M, Seadawy AR, Dianchen Lu. Exact bright–dark solitary wave solutions of the higher-order cubic–quintic nonlinear Schrödinger equation and its stability. Optik. (2017) 9:40–9. doi: 10.1016/j.ijleo.2017.03.005

CrossRef Full Text | Google Scholar

3. Biswas A, Triki H, Zhou Q, Moshokoa SP, Ullah MZ, Belic M. Cubic–quartic optical solitons in Kerr and power law media. Optik. (2017) 144:357–62. doi: 10.1016/j.ijleo.2017.07.008

CrossRef Full Text | Google Scholar

4. Biswas A, Arshed S. Application of semi-inverse variational principle to cubic-quartic optical solitons with kerr and power law nonlinearity. Optik. (2018) 172:847–50. doi: 10.1016/j.ijleo.2018.07.105

CrossRef Full Text | Google Scholar

5. Hosseini K, Samadani F, Kumar D, Faridi M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik. (2018) 157:1101–5. doi: 10.1016/j.ijleo.2017.11.124

CrossRef Full Text | Google Scholar

6. Houwe A, Hammouch Z, Bienvenue D, Nestor S, Betchewe G, DOKA SY. Nonlinear Schrödingers equations with cubic nonlinearity: M-derivative soliton solutions by exp(ϕ(ξ))-Expansion method. Preprints. (2019). 2019:2019030114 doi: 10.20944/preprints201903.0114.v1

CrossRef Full Text | Google Scholar

7. Li HM, Xu YS, Lin J. New optical solitons in high-order dispersive cubic-quintic nonlinear Schrödinger equation. Commun Theor Phys. (2004) 41:829–32. doi: 10.1088/0253-6102/41/6/829

CrossRef Full Text | Google Scholar

8. Nawaz B, Ali K, Oan Abbas S, Rizvi STR, Zhou Q. Optical solitons for non-Kerr law nonlinear Schrödinger equation with third and fourth order dispersions. Chin J Phys. (2019) 60:133–40. doi: 10.1016/j.cjph.2019.05.014

CrossRef Full Text | Google Scholar

9. Seadawy AR, Kumar D, Chakrabarty AK. Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur Phys J Plus. (2018) 133:182. doi: 10.1140/epjp/i2018-12027-9

CrossRef Full Text | Google Scholar

10. Xie Y, Yang Z, Li L. New exact solutions to the high dispersive cubic–quintic nonlinear Schrödinger equation. Phys Lett A. (2018) 382:2506–14. doi: 10.1016/j.physleta.2018.06.023

CrossRef Full Text | Google Scholar

11. Wang P, Shang T, Feng L, Du Y. Solitons for the cubic-quintic nonlinear Schrödinger equation with Raman effect in nonlinear optics. Opt Quant Electron. (2014) 46:1117–26. doi: 10.1007/s11082-013-9840-8

CrossRef Full Text | Google Scholar

12. Srivastava HM, Gnerhan H, Ghanbari B. Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Math Meth Appl Sci. (2019) 42:7210–21. doi: 10.1002/mma.5827

CrossRef Full Text | Google Scholar

13. Bansal A, Biswas A, Zhou Q, Babatin MM. Lie symmetry analysis for cubic–quartic nonlinear Schrödinger's equation. Optik. (2018) 169:12–5. doi: 10.1016/j.ijleo.2018.05.030

CrossRef Full Text | Google Scholar

14. Gao W, Ismael HF, Husien AM, Bulut H, Baskonus HB. Optical soliton solutions of the cubic-quartic nonlinear schrödinger and resonant nonlinear Schrödinger equation with the parabolic law. Appl Sci. (2020) 10:219. doi: 10.3390/app10010219

CrossRef Full Text | Google Scholar

15. Baskonus HM, Bulut H, Sulaiman TA. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl Math Nonlin Sci. (2019) 4:129–38. doi: 10.2478/AMNS.2019.1.00013

CrossRef Full Text | Google Scholar

16. Ali KK, Yilmazer R, Bulut H. Analytical solutions to the coupled Boussinesq–Burgers equations via Sine-Gordon expansion method. In: 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer. (2020). p. 233–40. doi: 10.1007/978-3-030-39112-6_17

CrossRef Full Text | Google Scholar

17. Al-Ghafri KS, Rezazadeh H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl Math Nonlin Sci. (2019) 4:289–304. doi: 10.2478/AMNS.2019.2.00026

CrossRef Full Text | Google Scholar

18. Kumar S, Kumar A, Momani S, Aldhaifallah M, Nisar KS. Numerical solutions of nonlinear fractional model arising in the appearance of the stripe patterns in two-dimensional systems. Adv Differ Equat. (2019) 2019:413. doi: 10.1186/s13662-019-2334-7

CrossRef Full Text | Google Scholar

19. Ismael HF, Bulut H. On the Solitary Wave Solutions to the (2 + 1)-Dimensional Davey-Stewartson Equations, 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, vol 1111. Springer, Cham. (2020). p. 156–65. doi: 10.1007/978-3-030-39112-6_11

CrossRef Full Text | Google Scholar

20. Abdulkareem HH, Ismael HF, Panakhov ES, Bulut H. Some novel solutions of the coupled Whitham-Broer-Kaup equations. In: 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer (2020). p. 200–8. doi: 10.1007/978-3-030-39112-6_14

CrossRef Full Text | Google Scholar

21. Gao W, Ismael HF, Bulut H, Baskonus HM. Instability modulation for the (2 + 1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media. Phys Scripta. (2019) 95. doi: 10.1088/1402-4896/ab4a50

CrossRef Full Text | Google Scholar

22. Kumar D, Singh J, Purohit SD, Swroop R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Modell Nat Phen. (2019) 14:304. doi: 10.1051/mmnp/2018063

CrossRef Full Text | Google Scholar

23. Bhatter S, Mathur A, Kumar D, Nisar KS, Singh J. Fractional modified Kawahara equation with Mittag–Leffler law. Chaos Solit Fract. (2019) 131:109508. doi: 10.1016/j.chaos.2019.109508

CrossRef Full Text | Google Scholar

24. Singh J, Kumar D, Baleanu D. New aspects of fractional Biswas–Milovic model with Mittag-Leffler law. Math Modell Nat Phen. (2019) 14:303. doi: 10.1051/mmnp/2018068

CrossRef Full Text | Google Scholar

25. Kumar D, Singh J, Baleanu D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math Methods Appl Sci. (2020) 43:443–57. doi: 10.1002/mma.5903

CrossRef Full Text | Google Scholar

26. Veeresha P, Prakasha DG, Baskonus HM. New numerical surfaces to the mathematical model of cancer chemotherapy effect in caputo fractional derivatives. AIP Chaos. (2019) 29:1–14. doi: 10.1063/1.5074099

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Goswami A, Singh J, Kumar D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys A. (2019) 524:563–75. doi: 10.1016/j.physa.2019.04.058

CrossRef Full Text | Google Scholar

28. Ismael HF. Carreau-Casson fluids flow and heat transfer over stretching plate with internal heat source/sink and radiation. Int J Adv Appl Sci. (2017) 4:11–5. doi: 10.21833/ijaas.2017.07.003

CrossRef Full Text | Google Scholar

29. Ismael HF, Arifin NM. Flow and heat transfer in a Maxwell liquid sheet over a stretching surface with thermal radiation and viscous dissipation. JP J Heat Mass Transf. (2018) 15:847–66. doi: 10.17654/HM015040847

CrossRef Full Text | Google Scholar

30. Ismael HF, Ali KK. MHD casson flow over an unsteady stretching sheet. Adv Appli Fluid Mech. (2017) 20:533–41. doi: 10.17654/FM020040533

CrossRef Full Text | Google Scholar

31. Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Differ Equat. (2019) 2019:278. doi: 10.1186/s13662-019-2199-9

CrossRef Full Text | Google Scholar

32. Singh J, Kumar D, Baleanu D, Rathore S. On the local fractional wave equation in fractal strings. Math Methods Appl Sci. (2019) 42:1588–95. doi: 10.1002/mma.5458

CrossRef Full Text | Google Scholar

33. Ali KK, Yilmazer R. Discrete fractional solutions to the effective mass Schrödinger equation by mean of Nabla operator. AIMS Math. (2020) 5:894–903. doi: 10.3934/math.2020061

CrossRef Full Text | Google Scholar

34. Ozturk O, Yilmazer R. Solutions of the radial Schrödinger equation in hypergeometric and discrete fractional forms. Commun Fac Sci Univ Ank Ser A1 Math Stat. (2019) 68:833–9. doi: 10.31801/cfsuasmas.481600

CrossRef Full Text | Google Scholar

35. Yilmazer R, Discrete fractional solution of a non-homogeneous non-Fuchsian differential equations. Therm Sci. (2019) 23:S121–7. doi: 10.2298/TSCI180917336Y

CrossRef Full Text | Google Scholar

36. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math. (2014) 264:65–70. doi: 10.1016/j.cam.2014.01.002

CrossRef Full Text | Google Scholar

37. Nisar KS, Rahman G, Khan A. Some new inequalities for generalized fractional conformable integral operators. Adv Differ Equat. (2019) 2019:427. doi: 10.1186/s13662-019-2362-3

CrossRef Full Text | Google Scholar

38. Nisar KS, Tassaddiq A, Rahman G, Khan A. Some inequalities via fractional conformable integral operators. J Inequal Appl. (2019) 2019:217. doi: 10.1186/s13660-019-2170-z

CrossRef Full Text | Google Scholar

39. Rahman G, Ullah Z, Khan A, Set E, Nisar KS. Certain Chebyshev-type inequalities involving fractional conformable integral operators. Mathematics. (2019) 7:364. doi: 10.3390/math7040364

CrossRef Full Text | Google Scholar

40. Abdeljawad T. On conformable fractional calculus. J Comput Appl Math. (2015) 279:57–66. doi: 10.1016/j.cam.2014.10.016

CrossRef Full Text | Google Scholar

41. Gao W, Yel G, Haci MB, Cattani C. Complex solitons in the conformable (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur Equation. AIMS Math. (2020) 5:507–21. doi: 10.3934/math.2020034

CrossRef Full Text | Google Scholar

42. Xian-Lin X, Jia-Shi T. Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion. Commun Theor Phys. (2008) 50:1047. doi: 10.1088/0253-6102/50/5/06

CrossRef Full Text | Google Scholar

43. Esen A, Sulaiman TA, Bulut H, Baskonus HM. Optical solitons to the space-time fractional (1 + 1)-dimensional coupled nonlinear Schrödinger equation. Optik. (2018) 167:150–6. doi: 10.1016/j.ijleo.2018.04.015

CrossRef Full Text | Google Scholar