Far Off Equilibrium Dynamics in Clusters and Molecules

This brief review illustrates on a few typical applications fully fledged dynamical simulations of finite electronic systems (atoms, molecules, clusters) using time-dependent density-functional theory (TDDFT). It concentrates on aspects which are different from nuclear applications. These are: the correct handling of electron emission, the self-interaction correction, the enormous versatility of laser excitation to probe systems properties, and with it the exploitation of detailed observables of electron emission as photo-electron angular distributions and photo-electron spectra (PES). Finally, we demonstrate the impact of electronic dissipation putting question marks on the reliability of TDDFT simulations over long times.

1. Introduction

Far-off equilibrium dynamics in quantum many-body systems is since numerous decades a challenging task much studied in experimental and theoretical investigations. In the realm of finite electronic systems, the availability of versatile laser pulses has given way to detailed analysis of the response of clusters and molecules [1–11]. In particular it allows one to explore the properties of electrons emitted after irradiation in correlation with the laser pulse. This has led to detailed analysis of angular- and energy-resolved electron spectra, e.g., their angular distributions and photoelectron spectra (PES) or both simultaneously as angular resolved PES (ARPES) recorded via Velocity Map Imaging techniques [12]. The theoretical description of such far-off equilibrium situations is also demanding. It requires large phase spaces and must cover vastly different time scales ranging from basic processes of excitation over collisional redistribution with subsequent relaxation to ionic motion and possible coupling to environment. They thus require dedicated fully time-dependent approaches, such as the widely used time-dependent density functional theory (TDDFT), often combined with molecular dynamics for the description of ionic motion (see e.g., [13]). This approach is both versatile and robust and allows one to simulate numerous dynamical scenarios with high degree of accuracy. The electronic part, TDDFT, is formally exactly the same as time-dependent Hartree-Fock (TDHF) in the nuclear domain [14]. The difference lies mainly in energy functionals which are constructed by very different strategies, see Dreizler and Gross [15] for electronic systems and Bender et al. [16] for nuclei.

In a typical laser irradiation, electrons immediately react to the external electro-magnetic field driving the system quickly far-off equilibrium long before ionic motion and thermal relaxation processes set on [17]. Thus, the system fully remains in the quantum regime for quite a while, as seen in recent experiments, exhibiting clear quantum and thermal pattern in photoelectron spectra [18–20]. The crucial first stage, i.e., the doorway to any photo-reaction, is predominantly quantum-mechanical electron dynamics which is (as in nuclear dynamics) well-described by TDDFT and we shall focus on this domain below.

Actual implementations of TDDFT are often based on the Time-Dependent Local Density Approximation (TDLDA) [8, 21, 22] which usually performs well at moderate excitation. However, TDLDA is plagued by a self-interaction error [23] which arises because the local approximation of Coulomb exchange spoils the subtle balance with the direct Coulomb term (which was still maintained in full Hartree-Fock calculations). This is particularly disastrous for simulation of emission properties because the ionization potentials in terms of the energy of the highest occupied single-electron orbital are underestimated. The problem is cured in ad hoc manner by augmenting TDLDA with a self-interaction correction (SIC). As this is an aspect which is less important in the nuclear domain and thus ignored, we will address it below. Another aspect which is missing in TDLDA and which becomes important in later stages of the dynamical evolution are dynamical correlations and associated dissipative features. Extensions beyond TDLDA which take dissipation into account are presently under development. We shall address also this question on one example.

The paper is organized as follows. Section 2 provides a brief summary of the formalism, TDDFT in real time with SIC and computation of observables, particularly ionization and PES. Section 3 presents a few selected application examples starting with the impact of SIC and basic features of optical responses as the latter plays a crucial role as doorway to any dynamical scenario. We then illustrate the capabilities of short laser pulses and finally discuss the impact of dissipation.

2. Theoretical Background

2.1. Electronic DFT

As in nuclear TDHF, the state of the electronic system is described in terms of single-particle (s.p.) Kohn-Sham (KS) wave functions φ_n(n = 1, …, N) from which the key ingredient in DFT, the total electronic density, is built as $\varrho (\text{r},t)=\sum _{n=1,\dots ,N}|{\phi }_n(\text{r},t){|}^2$. The total energy is composed as E_tot = E_kin + E_H + E_xc + E_ion + E_ext. The first three terms, namely kinetic energy, Coulomb Hartree energy, and exchange-correlation energy, constitute the purely electronic part and correspond to typical nuclear energy expressions. The last two terms, the ionic energy with its coupling to electrons and a possible external (laser) field, are specific to atoms/molecules. Hartree and exchange-correlation energies are approximated as functionals of ϱ: E_H + E_xc ≃ E_TDLDA[ϱ(r, t)]. This constitutes in the dynamic domain the Time-Dependent Adiabatic Local Density Approximation (TDLDA) [15, 24, 25], the electronic analog of nuclear TDHF. Variation with respect to ${\phi }_n^{*}$ yields the KS equations:

$\begin{array}{ll}\text{i}\hslash {\partial }_t{\phi }_n=\left\{-\frac{{\hslash }^2}{2m}{\nabla }^2+v_{\text{LDA}}\left[\varrho \right]+v_{\text{ion}}+v_{\text{ext}}\right\}{\phi }_n.& (1)\end{array}$

The LDA potential is obtained as a functional derivative with respect to the local density : $v_{\text{LDA}}\left[\varrho \right](\text{r},t)=\frac{\delta E_{\text{LDA}}}{\delta \varrho (\text{r},t)}{\displaystyle {|}_{\left[\varrho \right]}}$. The ionic background v_ion is described by pseudopotentials [26]. We use the particularly simple and efficient soft local [27] or Goedecker-type [28] pseudopotentials.

An external, coherent laser field is handled as a classical field in the long wavelength limit, adding to the mean-field Hamiltonian the potential

$\begin{array}{l}{v}_{\text{ext}}(\text{r},t)=e^2\text{r}·{\text{e}}_{\text{z}}{E}_{0}cos(\hslash {\omega }_{\text{las}}t+{\varphi }_{\text{CEP}})f(t)\text{\hspace{1em}with}\\ f(t)={cos}^2\left(\pi \frac{t}{T_{\text{pulse}}}\right)\theta (t)\theta (T_{\text{pulse}}-t),& (2)\end{array}$

θ being the Heaviside function. The laser characteristics are: linear polarization (here denoted by e_z), peak field strength E₀ related to laser intensity ($I\propto E_0^2$), photon frequency ℏω_las, and total pulse length T_pulse. The full width at half maximum of intensity (FWHM) is given as FWHM ≃T_pulse/3. The parameter ϕ_CEP, the so-called carrier-envelop phase, is the phase between the maximum of an oscillation at frequency ℏω_las and the maximum of the cos² envelope which plays a role particularly for short pulses [29].

2.2. Self-Interaction Correction

The KS equations introduce a self-interaction (SI) error because KS mean field v_LDA employs the total density which includes also the electron on which v_LDA acts. This is particularly disastrous for the long-range Coulomb term which produces thus a shifted single particle energy spectrum and, as a consequence, a wrong ionization potential (IP). To overcome the SI error, the energy-density functional is augmented by a SI correction (SIC) [30]

$\begin{array}{ll}{E}_{\text{LDA}}\to E_{\text{LDA}}[\varrho (\text{r},t)]-{\displaystyle \sum _n}{E}_{\text{LDA}}[{\varrho }_n(\text{r},t)].& (3)\end{array}$

The price to pay is to deal with a Hamiltonian that is now non-Hermitian and state-dependent, since the variation with respect to ${\phi }_n^{*}$ of the SI-corrected energy explicitly produces a functional of the s.p. density ϱ_n instead of the total electronic density (for a broad overview of orbital-dependent functionals, see Kümmel and Kronik [31]). This difficulty is particularly severe in the time domain and requires elaborate strategies to maintain unitary time evolution [32, 33].

Still, a full solution of dynamical SIC is expensive. Fortunately, there are many situations where one can employ a drastic simplification, namely the average density SIC (ADSIC) which was proposed already in the 1930s [34], and applied since then in clusters [35]. The idea is to assume that all electrons fill about the same region of space and thus contribute about equally to the SI error. This amounts to replace Equation (3) by

$\begin{array}{ll}{E}_{\text{LDA}}\to E_{\text{LDA}}[{\varrho }_{\uparrow }+{\varrho }_{\downarrow }]-{\displaystyle \sum _{\sigma \in \left\{\uparrow ,\downarrow \right\}}}{N}_{\sigma }{E}_{\text{LDA}}[{\varrho }_{\sigma }/N_{\sigma }],& (4)\end{array}$

where ϱ_σ and N_σ are the total electronic density and the total number of particles of spin σ, respectively. This is, again, a functional of the local spin-density only and thus can be treated in the same manner as any LDA scheme. This works nicely in a wide class of compact atomic/molecular systems [36] and particularly well for metal clusters. It is not applicable to situations with fragmented electron density and to bulk systems (the latter because the particle numbers N_σ grow infinite).

2.3. Observables

The KS equations are solved in real time on a 3D grid with standard techniques [13, 17, 37]. The predominantly local structure of the KS Hamiltonian allows one to use the very efficient time-splitting scheme for time propagation [38]. The Coulomb field is computed with successive over-relaxation [39] or Fast Fourier Transform techniques [37, 40]. To describe ionization dynamics, we use absorbing boundary conditions [17], which, when properly optimized [41], gently remove outgoing electron flow at the boundaries of the numerical grid. This is a crucial ingredient which is so far not much used in nuclear dynamics. But it is essential in atoms/molecules where observables from electron emission (explained below) are very important.

The analysis of electron dynamics is performed through a set of well-established observables [10, 17, 42, 43] that we briefly recall here. As the laser field couples to the electronic dipole, dipole response is the most prominent observable in many studies [10, 13, 42, 44]. We compute the dipole moment of electrons (with respect to ionic background) from the electronic density as:

$\begin{array}{ll}\text{D}(t)={\displaystyle \int }{\text{d}}^3\text{r}\text{r}\varrho (\text{r},t).& (5)\end{array}$

Spectral properties are then obtained from the time-frequency Fourier transform $\text{D}(t)\to \tilde{D}(\omega )$ after unfolding the spectrum of the exciting pulse [44]. Spectral analysis becomes particularly simple for excitation by an instantaneous dipole boost. The dipole strength becomes then $\Im \left\{\tilde{\text{D}}(\omega )\right\}$ and the dipole power spectrum $|\tilde{\text{D}}(\omega ){|}^2$.

For sufficiently strong excitation, electron emission becomes important. It can be analyzed at various levels of sophistication thanks to the use of absorbing boundary conditions mentioned above. Simplest is the global measure, the total ionization which can be computed from the given density as

$\begin{array}{ll}{N}_{\text{esc}}(t)=N-{\displaystyle \int }{\text{d}}^3\text{r}\varrho (\text{r},t)& (6)\end{array}$

where N is the initial electron number.

More detailed observables are Photo-Electron Spectra (PES), obtained from measuring the distribution of kinetic energies of the emitted electrons, or their angular distribution. Measuring both simultaneously yields Angular-Resolved PES (ARPES) for which often valuable experimental data exist to compare with [43]. The strategy to compute PES consists in defining a set of “measuring points” ${\text{r}}_{{M}}$ near the absorbing boundaries, and to record the time evolution of s.p. wave functions ${\phi }_n({\text{r}}_{{M}},t)$ at these points. The information thus gathered can be post-processed in two ways. Simple time integration of $|{\phi }_n({\text{r}}_{{M}},t){|}^2$ yields the amount of ionization at this measuring point. This together with properly accounting for the solid angle ${\Omega }_{{\text{r}}_{{M}}}$ associated with the vicinity of the measuring point direction yields the angular distribution of emitted electrons [42, 45]. The PES is obtained by Fourier transforming the s.p. wave functions at the measuring point from time to frequency ${\phi }_n({\text{r}}_{{M}},t)\to {\tilde{\phi }}_i({\text{r}}_{{M}},E_{\text{kin}})$ and identifying the kinetic energy as $E_{\text{kin}}=k^2/(2m)=\hslash \omega$. This delivers the PES from s.p. state i for emission in direction of the measuring point ${\text{r}}_{{M}}$. The total PES is then obtained by summing up the contributions from each s.p. state

$\begin{array}{ll}{{Y}}_{{\Omega }_{{\text{r}}_{{M}}}}(E_{\text{kin}})\propto {\displaystyle \sum _{n=1}^N}|{\tilde{\phi }}_i({\text{r}}_{{M}},E_{\text{kin}}){|}^2.& (7)\end{array}$

This simple Fourier transform applies to weak and moderate fields. For stronger field one still needs a phase correction which is explained in detail in [46].

3. Results

3.1. Impact of SIC

We illustrate the importance of SIC for TDDFT on the example of the Na₅ cluster irradiated by a femtosecond (fs) laser pulse with FWHM of 10 fs, intensity I = 2.2 × 10¹¹ W/cm², and frequency ω_las = 10.9 eV, well above ionization threshold (ionization potential IP = 4.1 eV) and far away from dominant eigenfrequencies of the system. We use the simple ADSIC approximation (which is found to be appropriate for Na systems [35, 36]) and compare it to LDA. Figure 1 collects the results. The top right part of the figure shows the (planar) ionic configuration. The lower right panel compares the sequence of s.p. energies for LDA and ADSIC. The latter produces a global down-shift of the s.p. levels as compared to those from LDA (by 1.2 eV for the HOMO) due to the enhanced Coulomb attraction (self-interaction neutralizes the asymptotic Coulomb field). The IP can be checked independently by comparing with the difference of energies of Na₅ and ${\text{Na}}_5^{+}$ (Koopman's theorem) and ADSIC matches this energy difference perfectly while LDA fails badly. As a consequence, the s.p. spectrum from ADSIC carries the correct information on the ionization threshold.

FIGURE 1

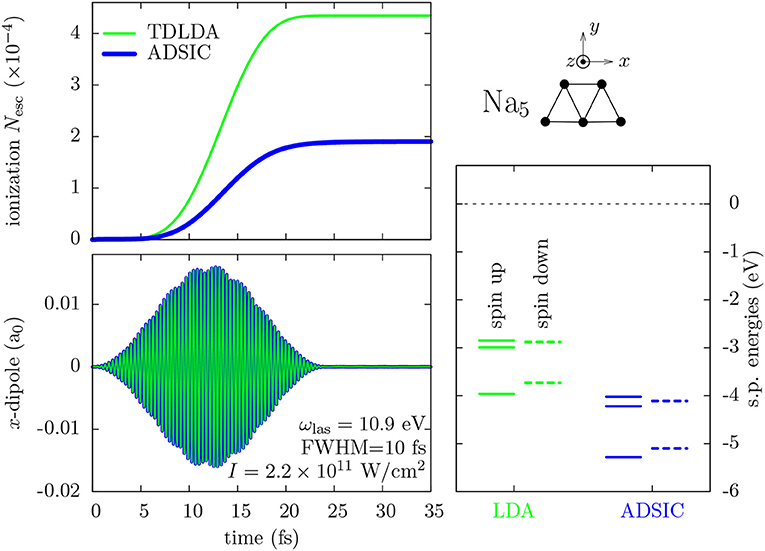
Figure 1. Comparison of (TD)LDA and ADSIC for the Na₅ cluster. (Top right) Sketch of ionic configuration of Na₅. (Bottom right) Single particle (s.p.) energies for spins up (full lines) and down (dashes). (Left) Time evolution of total ionization N_esc (top) and of the electronic dipole in the x direction (bottom) after irradiation by a laser pulse polarized along x with ω_las = 10.9 eV, T_pulse = 24 fs, and I = 2.2 × 10¹¹ W/cm².

The left panels show the dynamical response of the system to the laser pulse. The left lower panel displays the time evolution of the electronic dipole moment along laser polarization (x axis). There is almost no difference between LDA and ADSIC for the dipole signal. This is also found for the optical absorption strength (not shown here) which is no surprise because the optical absorption is another way to look at the dipole response. There is no urgent need to employ SIC when computing these quantities. This is plausible because the dipole signal is a global signal deduced from the density and density is, by construction, well-described in DFT.

The left upper panel shows the time evolution of the total ionization N_esc (see Equation 6). This signal reveals a dramatic difference between ADSIC and LDA. This is no surprise as ADSIC provides a larger IP than LDA (and altogether, more deeply bound levels, see bottom right panel). The reason is that, in TDDFT, ionization is mediated via the actual s.p. energies such that it is crucial to put the s.p. energies right within DFT.

3.2. Optical Response

Optical response is the most prominent observable for dynamical properties of a system. Its role in nuclear physics and in molecular or cluster physics is similarly important. The conceptually simplest way is to compute it by spectral analysis of a time-dependent simulation (see section 2.3). Traditionally, it has mostly been computed by linearized TDDFT which complicates coding, but simplifies calculations, particularly if a system has certain symmetries (see e.g., [47–49]). The pathway through spectral analysis is competitive in fully 3D calculations and it is more flexible as it also allows one to explore the transition to the non-linear regime [50]. We use that here.

Figure 2 shows optical absorption strengths for a nucleus, ²⁰⁸Pb, and three different electronic systems of different bond types, a metal cluster Na₄₀, a covalent molecule H₂O, and the noble gas Ar atom. The three electronic systems have significantly different spectra. For Ar and H₂O, the strength is heavily fragmented over many dipole states, most of them having predominantly the structure of one-particle-one-hole excitations. Quite different is the metallic Na₄₀, with one dominating and almost exhaustive peak, the highly collective Mie plasmon [54, 55]. The nuclear spectrum looks very similar to the cluster case. It is dominated by the a strong collective mode, the giant dipole resonance [56]. The similarity is not surprising as both, the metallic electron cloud and the nucleons, have the same bulk limit, namely a Fermi liquid [57].

FIGURE 2

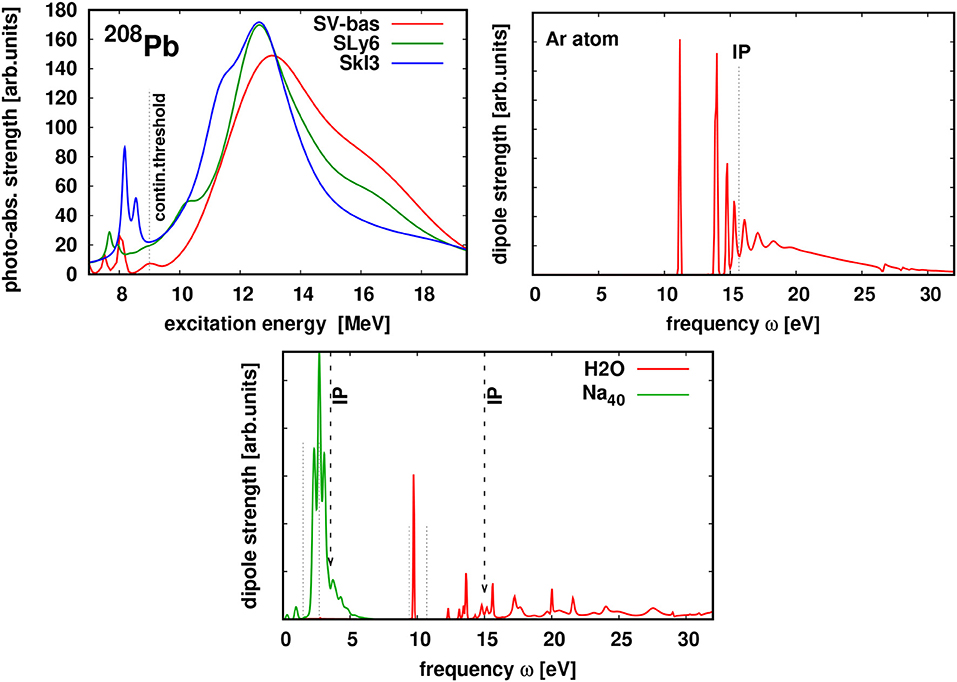
Figure 2. Optical absorption spectra for three electronic systems as indicated and the nucleus ²⁰⁸Pb. The electronic systems are computed with TDLDA + ADSIC as explained in section 2. The nucleus is computed with nuclear TDHF using the code of [37] (for details see Reinhard et al. [50]) and three different Skyrme parameterizations as indicated, SkI3 from [51], SLy6 from [52], and SV-bas from [53]. The vertical dashed lines indicate the particle continuum thresholds in each system, the electronic ionization potential (IP) and the neutron threshold in the nuclear case.

The nuclear dipole resonance and the cluster's plasmon resonance both have some width. However, the mechanisms producing these widths is different. The nuclear dipole resonance lies in the nucleon continuum and a large part of the width stems from limited lifetime due to nucleon emission. The remaining part is due to dissipative processes from nucleon-nucleon collisions. Both processes also play some role in metal clusters. But here the dominant broadening mechanism is given by thermal fluctuations of the underlying ionic configuration [58, 59].

3.3. Laser Excitation

Laser pulses offer a unique and extremely versatile tool for dedicated probing and switching of electronic systems. Coherent pulses in keV and MeV regime, as required for nuclear experiments, appear at the horizon [60–62], but deliver not yet sufficient field strengths to attain the most interesting multi-photon regime. This day will come and thus it is worth having a look at electronic applications and see what experiments with coherent pulses can reveal.

A great deal of information is gained when combining laser excitations with detailed analysis of the emitted electrons. The top panels of Figure 3 show as an example ARPES produced from the Ar atom (left) and the ${\text{Na}}_9^{+}$ cluster (right) after irradiation by a few-cycle laser pulse. Cuts along a fixed angle represent the PES and cuts along a fixed kinetic energy the angular distribution. The PES decrease with increasing E_kin because more photons have to cooperate to supply the higher emitted energy. And yet, one finds a plateau around 20 eV which is typical for above-threshold ionization spectra [63, 64]. The two different systems deliver different patterns, demonstrating that system properties form the signal which, in turn, can be used to analyze a system by ARPES studies.

FIGURE 3

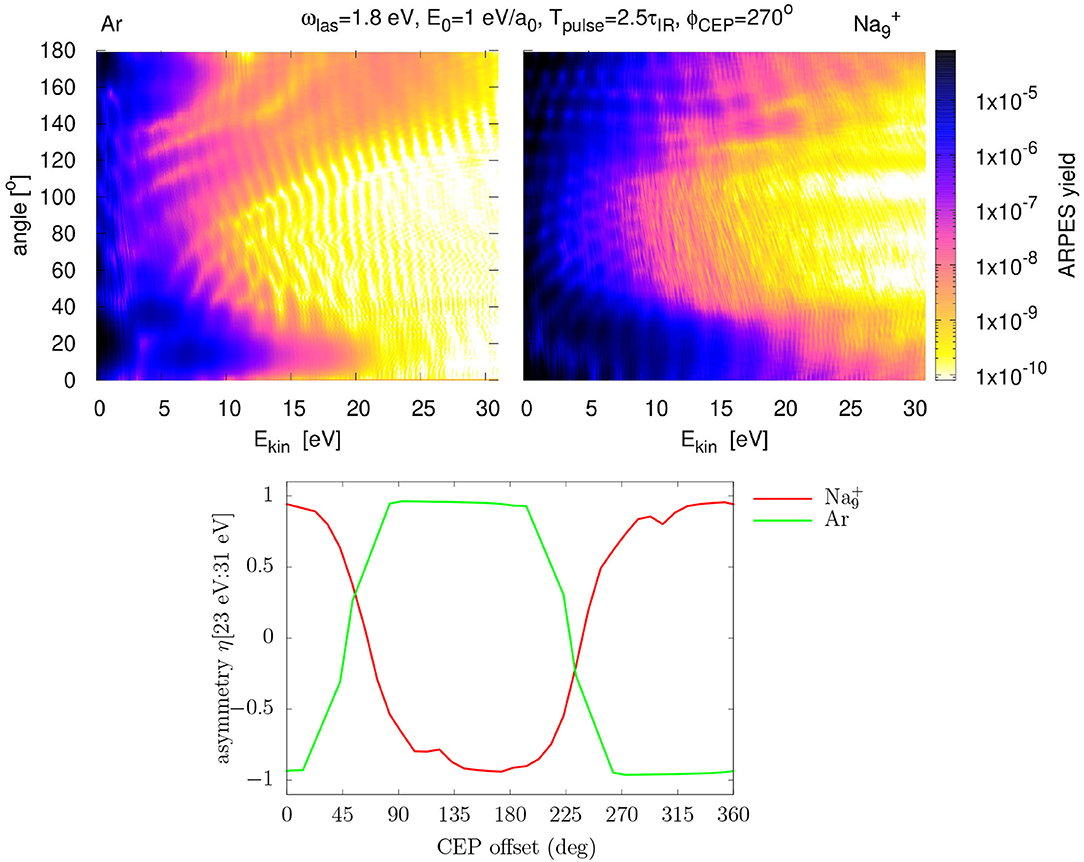
Figure 3. Ar atom and ${\text{Na}}_9^{+}$ cluster excited by a laser with ω_las = 1.8 eV, I = 6 × 10¹³ W/cm², pulse length T_pulse = 6 fs (corresponding to 2.5 optical cycles), and ${\varphi }_{\text{CEP}}=270^{\bullet }$. Upper panels: ARPES yield ${Y}$ in the plane of kinetic energy E_kin and emission angle θ, for Ar (left) and ${\text{Na}}_9^{+}$ (right). Lower panel: asymmetry parameter η(E_kin) integrated on the E_kin interval [23eV:31eV].

One of the interesting features in ARPES from very short pulses is the asymmetry of the angular distributions which appears in various energy bins for both systems. Indeed, in such laser pulses, the carrier-envelop phase ϕ_CEP, see Equation (2), becomes a decisive laser parameter because the CEP controls the net momentum exerted on the electron cloud and so impacts the pattern of the pulse dramatically which, in turn, can have a strong impact on laser-induced electron dynamics. For example, photo-electron emission induced by few-cycle laser fields can be controlled by the CEP, leading to a pronounced forward-backward (also called “right-left”) asymmetry in the PES. We can quantify this asymmetry by a simple number as

$\begin{array}{llll}\eta (E_{\text{kin}})& =& \frac{{\int }_0^{\Theta }d\theta {Y}(E_{\text{kin}},\theta )-{\int }_{180°-\Theta }^{180°}d\theta {Y}(E_{\text{kin}},\theta )}{{\int }_0^{\Theta }d\theta {Y}(E_{\text{kin}},\theta )+{\int }_{180°-\Theta }^{180°}d\theta {Y}(E_{\text{kin}},\theta )}& (8)\end{array}$

where ${Y}(E_{\text{kin}},\theta )$ is the ARPES strength at given kinetic energy and emission angle. For the opening angle in the integration, we take Θ = 15° in accordance with many experiments in that field (see e.g., [65]). A value of η = +1 indicates prevailing forward emission and η = −1 backward dominance. Condensing the angular distribution into one compact number η allows one to visualize trends with laser parameter. The lower panel of Figure 3 shows an energy-integrated asymmetry η as a function of ϕ_CEP. The effects are impressive. Tuning ϕ_CEP allows one to switch emission from forward to backward and vice versa. And we also see a significant system dependence of the trend. The marked difference between both systems can be explained by the difference in their optical response displayed in Figure 2. The 1.8 eV laser frequency lies far below any considerable dipole strength for Ar while it comes close to the strong Mie plasmon resonance for the Na cluster. For a detailed discussion with more material see Reinhard et al. [29].

3.4. Impact of Dissipation

So far, we have demonstrated the use of TDDFT in electronic systems on a few selected examples. TDDFT has shown to be a robust and versatile tool for simulating dynamical processes. However, the more energy comes into a system, the more likely come dynamical correlations beyond TDDFT into play. This is also well-known in nuclear physics and a variety of methods has been developed to deal with those correlations. They employ all semi-classical concepts and most of them are based on the Vlasov-Ühling-Uhlenbeck collision term [66] (for reviews see [67, 68]). This has also been applied to clusters [10, 69, 70]. But laser excitation processes sail often for a long initial time span through the quantum regime. There is thus a need for a quantum description of dynamical correlations from electron-electron collisions and associated dissipation. Just recently, there were promising moves to develop such approaches, one along the line of stochastic jumps (comparable to the collisions in semi-classical methods) [71–73] and another one with the more empirical relaxation-time approximation (RTA) [74, 75]. Both approaches are based on two-body collisions implying the in-medium electron-electron interaction and take care of the available phase space of final states. RTA, for which we will show an example here, maps cross-section and phase space into a collision rate with which the system relaxes toward local-instantaneous equilibrium, the latter being evaluated at each relaxation step by density- and current-constrained minimization of the free energy. By construction, RTA maintains the continuity equation and energy conservation.

Figure 4 exemplifies the consequences of the dissipation thus introduced with an application of RTA to resonant laser excitation of a Na₄₀ cluster. The lower left panel shows the effect on the dipole signal. The additional damping introduced by RTA is clearly visible. It is interesting to note that the TDLDA signal is also damped, although at lower rate. This damping stems from electron emission which is the dominant cooling mechanism in TDLDA. This is corroborated by the time evolution of ionization shown in the lower right panel. The trends agree up to about 100 fs, the same span where the dipole signals agree. But then the RTA curve levels off whereas TDLDA continues to emit. That happens because RTA has meanwhile converted much of the initial excitation energy into internal heat and so distracted it from moving into direct electron emission.

FIGURE 4

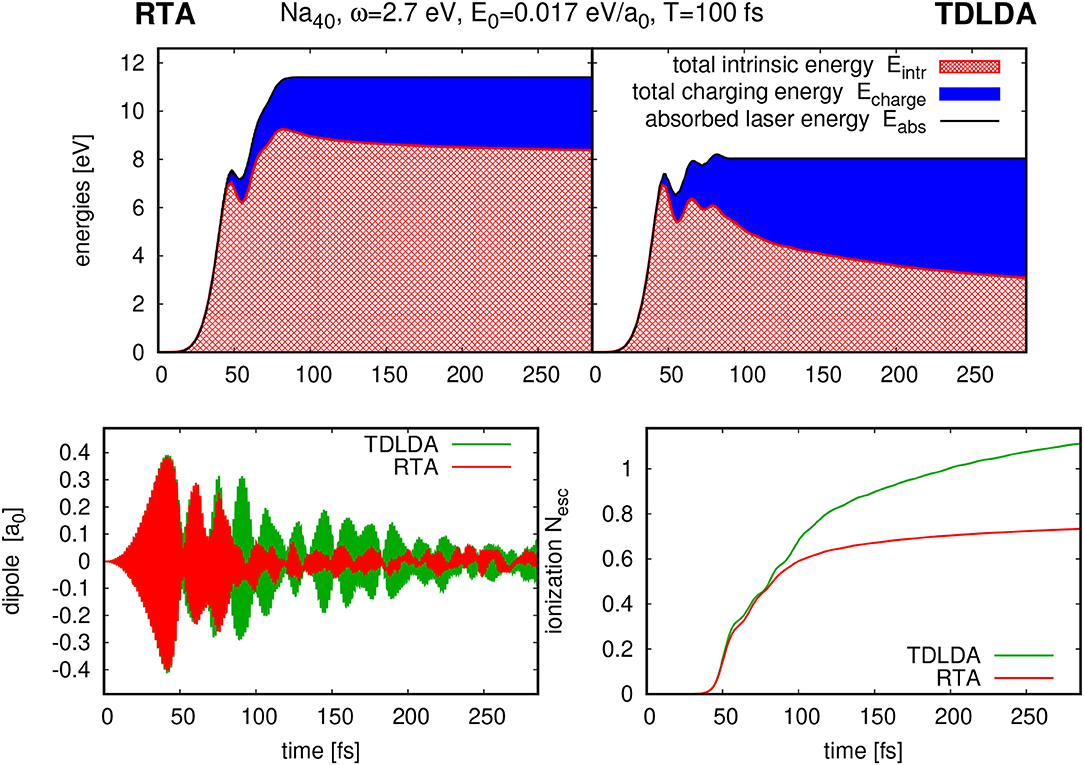
Figure 4. Time evolution of ionization (lower right), dipole moment (lower left), and the various contribution to the energy (upper panels) for the case of Na₄₀ excited by a laser with frequency ω = 2.7 eV, total pulse length T_pulse = 100 fs, and intensity I = 1.3 × 10¹⁰ W/cm². Left upper panels show results from RTA and right upper panels from TDLDA.

A comparison of energy balances is detailed in the upper panel of Figure 4. It shows the contributions from intrinsic energy and energy invested in electron emission for TDLDA and RTA (for details of the definition see [75]). It confirms what we have inferred from the ionization trends in the lower right panel. Most interesting is the large difference in the total energy absorbed from the laser pulse (black line). In pure TDLDA, the entrance channel for energy absorption, the dipole channel, has limited capacity as one can see from the onset of oscillations in the absorption signal. Dissipation in RTA clears the entrance channel and thus allows more energy to come in. Altogether, we see that dissipation can make a difference. Note, however, that this example deals with a considerable excitation energy and that deviations from TDLDA develop only slowly. In turn, we can conclude that TDDFT provides a pertinent description of dynamical processes in its early stages. The time scale of validity of TDDFT depends on excitation energy: the lower the excitation is, the longer TDDFT holds.

4. Conclusions

We have presented a couple of typical applications of time-dependent density functional theory (TDDFT) to electronic dynamics in clusters and molecules, as triggered by laser pulses. Basis of our description is TDDFT propagated in real time which delivers a versatile and robust tool for a great variety of dynamical situations. At the numerical side it is important to implement absorbing boundary conditions which then allow a detailed description of electron emission. We have addressed in detail two known defects of TDDFT in the local density approximation, namely the self-interaction error and the lack of dynamical correlations. The first problem is less important in nuclear physics, but highly relevant in electronic systems. It is solved by a self-interaction correction (SIC) which still can be formulated within a mean field theory (thus affordable) and which is particularly crucial if electron emission plays a role. The second problem, also important in nuclear dynamics, requires extensions beyond TDDFT for which manageable quantum mechanical approximations are presently being developed.

We have considered typical examples of applications in clusters and molecules excited by a laser pulses of different strengths. In all cases, the early response of the systems addresses predominantly the electrons and remains fully in the quantum mechanical regime (as properly described by TDDFT). In particular, we have focused on an analyzing tool which is not yet available in nuclear dynamics, namely widely tunable laser excitation in combination with detailed resolution of the distributions of the emitted electrons with respect to angles and kinetic energies. We have demonstrated that such a setup delivers valuable information on the system and its dynamical response.

Finally, the inclusion of dissipative features is a key step to address the long-time evolution of dynamics far off-equilibrium in which one observes, in addition to ionization, a thermalization of the electron cloud. Formerly, the problem was attacked with semi-classical approaches much similar as done in nuclear dynamics, particularly in heavy-ion collisions. This approach is less justified in connection with laser excitations for which the (electronic) system stays much longer in the quantum regime. Promising and manageable solutions to deal with dissipation in the quantum regime are just presently coming up. First results from treating dynamical correlations in the relaxation-time approximation (RTA) show that dissipation has a crucial impact on the energy balance in the system (internal energy vs. electron emission) and on the energy intake from the laser pulse. Proper treatment of dynamical correlations is still in its infancy and will attract much future development.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Institut Universitaire de France for support during the realization of this work. This work was also granted access to the HPC resources of CalMiP (Calcul en Midi-Pyrénées) under the allocation P1238, and of RRZE (Regionales Rechenzentrum Erlangen).

References

1. Caillat J, Zanghellini J, Kitzler M, Koch O, Kreuzer W, Scrinzi A. Correlated multielectron systems in strong laser fields: a multiconfiguration time-dependent Hartree-Fock approach. Phys Rev A. (2005) 71:012712. doi: 10.1103/PhysRevA.71.012712

CrossRef Full Text | Google Scholar

2. Ehrmaier J, Picconi D, Karsili TNV, Domcke W. Photodissociation dynamics of the pyridinyl radical: time-dependent quantum wave-packet calculations. J Chem Phys. (2017) 146:124304. doi: 10.1063/1.4978283

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Greenman L, Ho PJ, Pabst S, Kamarchik E, Mazziotti DA, Santra R. Implementation of the time-dependent configuration-interaction singles method for atomic strong-field processes. Phys Rev A. (2010) 82:023406. doi: 10.1103/PhysRevA.82.023406

CrossRef Full Text | Google Scholar

4. Hochstuhl D, Hinz C, Bonitz M. Time-dependent multiconfiguration methods for the numerical simulation of photoionization processes of many-electron atoms. Eur Phys J Spec Top. (2014) 223:177–336. doi: 10.1140/epjst/e2014-02092-3

CrossRef Full Text | Google Scholar

5. Lappas DG, van Leeuwen R. Electron correlation effects in the double ionization of He. J Phy B. (1998) 31:L249. doi: 10.1088/0953-4075/31/6/001

CrossRef Full Text | Google Scholar

6. Rohringer N, Peter S, Burgdörfer J. Calculating state-to-state transition probabilities within time-dependent density-functional theory. Phys Rev A. (2006) 74:042512. doi: 10.1103/PhysRevA.74.042512

CrossRef Full Text | Google Scholar

7. Sato T, Ishikawa KL, Brezinova I, Lackner F, Nagele S, Burgdoerfer J. Time-dependent complete-active-space self-consistent-field method for atoms: application to high-order harmonic generation. Phys Rev A. (2016) 94:023405. doi: 10.1103/PhysRevA.94.023405

CrossRef Full Text | Google Scholar

8. Haken H, Wolf HC. Time-Dependent Density-Functional Theory: Concepts and Applications. Oxford: Oxford University Press (2012).

Google Scholar

9. Wilken F, Bauer D. Momentum distributions in time-dependent density-functional theory: product-phase approximation for nonsequential double ionization in strong laser fields. Phys Rev A. (2007) 76:023409. doi: 10.1103/PhysRevA.76.023409

CrossRef Full Text | Google Scholar

10. Fennel T, Meiwes-Broer KH, Tiggesbäumker J, Dinh PM, Reinhard PG, Suraud E. Electro-magnetic signals for analyzing non-linear cluster dynamics. Rev Mod Phys. (2010) 82:1793. doi: 10.1103/RevModPhys.82.1793

CrossRef Full Text | Google Scholar

11. Gao CZ, Dinh PM, Reinhard PG, Suraud E. Towards the analysis of attosecond dynamics in complex systems. Phys Chem Chem Phys. (2017) 19:19784–93. doi: 10.1039/C7CP00995J

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Pinaré JC, Baguenard B, Bordas C, Broyer M. Angular distributions in photoelectron spectroscopy of small tungste n clusters: competition between direct and thermionic emission. Eur Phys J D. (1999) 9:21–4. doi: 10.1007/s100530050392

CrossRef Full Text | Google Scholar

13. Reinhard PG, Suraud E. Introduction to Cluster Dynamics. New York, NY: Wiley (2004).

Google Scholar

14. Reinhard PG, Suraud E. Comparison of resonance dynamics in metal clusters and nuclei. In: Ekardt W, editor. Resonance Dynamics in Metal Clusters and Nuclei. New York, NY: Wiley (1999). p. 211.

Google Scholar

15. Dreizler RM, Gross EKU. Density Functional Theory: An Approach to the Quantum Many-Body Problem. Berlin: Springer-Verlag (1990).

Google Scholar

16. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys. (2003) 75:121–80. doi: 10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

17. Calvayrac F, Reinhard PG, Suraud E, Ullrich CA. Nonlinear electron dynamics in metal clusters. Phys Rep. (2000) 337:493–578. doi: 10.1016/S0370-1573(00)00043-0

CrossRef Full Text | Google Scholar

18. Kjellberg M, Johansson O, Jonsson F, Bulgakov AV, Bordas C, Campbell EEB, et al. Momentum-map-imaging photoelectron spectroscopy of fullerenes with femtosecond laser pulses. Phys Rev A. (2010) 81:023202. doi: 10.1103/PhysRevA.81.023202

CrossRef Full Text | Google Scholar

19. Hansen K. Statistical Physics of Nanoparticles in the Gas Phase. Amsterdam: Springer (2013).

Google Scholar

20. Hansen K, Richter R, Alagia M, Stranges S, Schio L, Salen P, et al. Single Photon Thermal Ionization of C₆₀. Phys Rev Lett. (2017) 118:103001. doi: 10.1103/PhysRevLett.118.103001

CrossRef Full Text | Google Scholar

21. Marques MAL, Ullrich CA, Nogueira F, Rubio A, Burke K, Gross EKU. Time Dependent Density Functional Theory. Berlin: Springer (2006).

Google Scholar

22. Marques MAL, Maitra NT, Nogueira FMS, Gross EKU, Rubio A. Fundamentals of Time-Dependent Density Functional Theory. Vol. 837 of Lecture Notes in Physics. Berlin: Springer-Verlag (2012).

Google Scholar

23. Yelin S, Arimondo E, Lin CC. Advances in Atomic, Molecular, and Optical Physics. Vol. 64. Amsterdam: Elsevier (2015).

Google Scholar

24. Gross EKU, Kohn W. Time-dependent density-functional theory. Adv Quant Chem. (1990) 21:255–91. doi: 10.1016/S0065-3276(08)60600-0

CrossRef Full Text | Google Scholar

25. Gross EKU, Dobson JF, Petersilka M. Density functional of time-dependent phenomena. Top Curr Chem. (1996) 181:81–172. doi: 10.1007/BFb0016643

CrossRef Full Text | Google Scholar

26. Szasz L. Pseudopotential Theory of Atoms and Molecules. New York, NY: Wiley (1985).

Google Scholar

27. Kümmel S, Brack M, Reinhard PG. Ionic geometries and electronic excitations of ${\text{Na}}_9^{+}$ and ${\text{Na}}_{55}^{+}$. Eur Phys J D. (1999) 9:149–52. doi: 10.1007/s100530050416

CrossRef Full Text | Google Scholar

28. Goedecker S, Teter M, Hutter J. Separable dual-space Gaussian pseudopotentials. Phys Rev B. (1996) 54:1703. doi: 10.1103/PhysRevB.54.1703

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Reinhard PG, Suraud E, Meier C. The impact of the carrier envelope phase—dependence on system and laser parameters. J Phys B. (2018) 51:024007. doi: 10.1088/1361-6455/aa9a9c

CrossRef Full Text | Google Scholar

30. Perdew JP, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B. (1981) 23:5048. doi: 10.1103/PhysRevB.23.5048

CrossRef Full Text | Google Scholar

31. Kümmel S, Kronik L. Orbital-dependent density functionals: theory and applications. Rev Mod Phys. (2008) 80:3–60. doi: 10.1103/RevModPhys.80.3

CrossRef Full Text | Google Scholar

32. Messud J, Dinh PM, Reinhard PG, Suraud E. Time-dependent density-functional theory with self-interaction correction. Phys Rev Lett. (2008) 101:096404. doi: 10.1103/PhysRevLett.101.096404

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Messud J, Dinh PM, Reinhard PG, Suraud E. On the exact treatment of time dependent self-interaction correction. Ann Phys. (2008) 324:955–76. doi: 10.1016/j.aop.2008.12.001

CrossRef Full Text | Google Scholar

34. Fermi E, Amaldi E. Le Orbite Oos Degli Elementi. Accad Ital Rome. (1934) 6:117–49.

Google Scholar

35. Legrand C, Suraud E, Reinhard PG. Comparison of self-interaction-corrections for metal clusters. J Phys B. (2002) 35:1115. doi: 10.1088/0953-4075/35/4/333

CrossRef Full Text | Google Scholar

36. Klüpfel P, Dinh PM, Reinhard PG, Suraud E. Koopmans' condition in self-interaction corrected density functional theory. Phys Rev A. (2013) 88:052501. doi: 10.1103/PhysRevA.88.052501

CrossRef Full Text | Google Scholar

37. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The TDHF code Sky3D. Comp Phys Comm. (2014) 185:2195–216. doi: 10.1016/j.cpc.2014.04.008

CrossRef Full Text | Google Scholar

38. Feit MD, Fleck JA, Steiger A. J Comp Phys. (1982) 47:412–33. doi: 10.1016/0021-9991(82)90091-2

CrossRef Full Text | Google Scholar

39. Davies KTR, Koonin SE. Skyrme-force time-dependent Hartree–Fock calculations with axial symmetry. Phys Rev C. (1981) 23:2042–61. doi: 10.1103/PhysRevC.23.2042

CrossRef Full Text | Google Scholar

40. Lauritsch G, Reinhard PG. An FFT Solver for the Coulomb problem. Int J Mod Phys C. (1994) 5:65–75. doi: 10.1142/S0129183194000064

CrossRef Full Text | Google Scholar

41. Reinhard PG, Stevenson PD, Almehed D, Maruhn JA, Strayer MR. Role of boundary conditions in dynamic studies of nuclear giant resonances. Phys Rev E. (2006) 73:036709. doi: 10.1103/PhysRevE.73.036709

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Reinhard PG, Suraud E. Cluster dynamics in strong laser fields. In: Marques MAL, Ullrich CA, Nogueira F, editors. Time-Dependent Density Functional Theory. Vol. 706 of Lecture Notes in Physics. Berlin: Springer (2006). p. 391.

Google Scholar

43. Wopperer P, Dinh PM, Reinhard PG, Suraud E. Electrons as probes of dynamics in molecules and clusters: a contribution from time dependent density functional theory. Phys Rep. (2015) 562:1. doi: 10.1016/j.physrep.2014.07.003

CrossRef Full Text | Google Scholar

44. Calvayrac F, Reinhard PG, Suraud E. Spectral signals from electronic dynamics in sodium clusters. Ann Phys. (1997) 255:125–62. doi: 10.1006/aphy.1996.5654

CrossRef Full Text | Google Scholar

45. Pohl A, Reinhard PG, Suraud E. Angular distribution of electrons emitted from Na clusters. Phys Rev A. (2004) 70:023202. doi: 10.1103/PhysRevA.70.023202

CrossRef Full Text | Google Scholar

46. Dinh PM, Romaniello P, Reinhard PG, Suraud E. Calculation of photoelectron spectra: a mean-field-based scheme. Phys Rev A. (2013) 87:032514. doi: 10.1103/PhysRevA.87.032514

CrossRef Full Text | Google Scholar

47. Reinhard PG, Gambhir Y. RPA in wavefunction representation. Ann Phys. (1992) 504:598–631. doi: 10.1002/andp.19925040804

CrossRef Full Text | Google Scholar

48. Reinhard PG. From sum rules to RPA: 1. Nuclei. Ann Phys. (1992) 504:632–61. doi: 10.1002/andp.19925040805

CrossRef Full Text | Google Scholar

49. Reinhard PG, Genzken O, Brack M. From sum rules to RPA: 3. Metal clusters. Ann Phys. (1996) 508:576–607. doi: 10.1002/andp.2065080704

CrossRef Full Text | Google Scholar

50. Reinhard PG, Guo L, Maruhn JA. Nuclear giant resonances and linear response. Eur Phys J A. (2007) 32:19–23. doi: 10.1140/epja/i2007-10366-9

CrossRef Full Text | Google Scholar

51. Reinhard PG, Flocard H. Nuclear effective forces and isotope shifts. Nucl Phys A. (1995) 584:467–88. doi: 10.1016/0375-9474(94)00770-N

CrossRef Full Text | Google Scholar

52. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Syrme parametrization from subnuclear to neutron star densities. Nucl Phys A. (1997) 627:710–46. doi: 10.1016/S0375-9474(97)00596-4

CrossRef Full Text | Google Scholar

53. Klüpfel P, Reinhard PG, Bürvenich TJ, Maruhn JA. Variations on a theme by Skyrme. Phys Rev C. (2009) 79:034310.

Google Scholar

54. Mie G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann Phys. (1908) 25:377–445. doi: 10.1002/andp.19083300302

CrossRef Full Text | Google Scholar

55. Kreibig U, Vollmer M. Optical Properties of Metal Clusters. Vol. 25. New York, NY; Heidelberg; Berlin: Springer Series in Materials Science (1993).

Google Scholar

56. Ring P, Schuck P. The Nuclear Many-Body Problem. New York, NY: Heidelberg; Berlin: Springer-Verlag (1980).

Google Scholar

57. Pines D, Nozières P. The Theory of Quantum Liquids. New York, NY: W. A. Benjamin (1966).

Google Scholar

58. Montag B, Reinhard PG. Width of the plasmon resonance in metal clusters. Phys Rev B. (1995) 51:14686. doi: 10.1103/PhysRevB.51.14686

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Moseler M, Landman U, Yannouleas C. Controllable electrostatic surface guide for cold molecules with a single charged wire. Phys Rev A. (2001) 87:053401. doi: 10.1103/PhysRevLett.87.053401

CrossRef Full Text | Google Scholar

60. Esirkepov TZ, Bulanov SV, Zhidkov AG, Pirozkov AS, Kando M. High-power laser-driven source of ultra-short X-ray and gamma-ray pulses. Eur Phys J D. (2009) 55:457–63. doi: 10.1140/epjd/e2009-00172-y

CrossRef Full Text | Google Scholar

61. Kiefer D, Yeung M, Dzelzainis T, Foster PS, Rykovanov SG, Lewis CL, et al. Relativistic electron mirrors from nanoscale foils for coherent frequency upshift to the extreme ultraviolet. Nat Commun. (2013) 4:1763. doi: 10.1038/ncomms2775

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Li FY, Sheng ZM, Chen M, Wu HC, Liu Y, Meyer-ter Vehn J, et al. Coherent kilo-electron-volt backscattering from plasma-wave boosted relativistic electron mirrors. Appl Phys Lett. (2014) 105:161102. doi: 10.1063/1.4899136

CrossRef Full Text | Google Scholar

63. Paulus GG, Nicklich W, Xu H, Lambropoulos P, Walther H. Plateau in above threshold ionization spectra. Phys Rev Lett. (1994) 72:2851–54. doi: 10.1103/PhysRevLett.72.2851

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Wopperer P, Gao CZ, Barillot T, Cauchy C, Marciniak A, Despré V, et al. Progress towards a realistic theoretical description of C₆₀ photoelectron-momentum imaging experiments using time-dependent density-functional theory. Phys Rev A. (2015) 91:042514. doi: 10.1103/PhysRevA.91.042514

CrossRef Full Text | Google Scholar

65. Li H, Mignolet B, Wachter G, Skruszewicz S, Zherebtsov S, Süßmann F, et al. Coherent electronic wave packet motion in C₆₀ controlled by the waveform and polarization of few-cycle laser fields. Phys Rev Lett. (2015) 114:123004. doi: 10.1103/PhysRevLett.114.123004

CrossRef Full Text | Google Scholar

66. Uehling EA, Uhlenbeck GE. Theory of superconductivity. Phys Rev. (1932) 108:1175. doi: 10.1103/PhysRev.108.1175

CrossRef Full Text | Google Scholar

67. Bertsch GF, Das Gupta S. A guide to microscopic models for intermediate energy heavy ion collisions. Phys Rep. (1988) 160:190. doi: 10.1016/0370-1573(88)90170-6

CrossRef Full Text | Google Scholar

68. Abe Y, Ayik S, Reinhard PG, Suraud E. On stochastic approaches of nuclear dynamics. Phys Rep. (1996) 275:49–196. doi: 10.1016/0370-1573(96)00003-8

CrossRef Full Text | Google Scholar

69. Fennel T, Bertsch GF, Meiwes-Broer KH. Ionization dynamics of simple metal clusters in intense fields by the Thomas-Fermi-Vlasov method. Eur Phys J D. (2004) 29:367–78. doi: 10.1140/epjd/e2004-00035-1

CrossRef Full Text | Google Scholar

70. Domps A, Reinhard PG, Suraud E. Semi-classical electron dynamics in metal clusters beyond mean-field. Ann Phys. (2000) 280:211–35. doi: 10.1006/aphy.1999.5990

CrossRef Full Text | Google Scholar

71. Lacroix D. Stochastic mean-field dynamics for fermions in the weak coupling limit. Phys Rev C. (2006) 73:044311. doi: 10.1103/PhysRevC.73.044311

CrossRef Full Text | Google Scholar

72. Suraud E, Reinhard PG. Non equilibrium quantum dynamics with collisional correlations. New J Phys. (2014) 16:063066. doi: 10.1088/1367-2630/16/6/063066

CrossRef Full Text | Google Scholar

73. Slama N, Reinhard PG, Suraud E. On the inclusion of collisional correlations in quantum dynamics. Ann Phys. (2015) 355:182–203. doi: 10.1016/j.aop.2015.02.008

CrossRef Full Text | Google Scholar

74. Reinhard PG, Suraud E. A quantum relaxation-time approximation for finite fermion systems. Ann Phys. (2015) 354:183–202. doi: 10.1016/j.aop.2014.12.011

CrossRef Full Text | Google Scholar

75. Vincendon M, Suraud E, Reinhard PG. Dissipation and energy balance in electronic dynamics of Na clusters. Eur Phys J D. (2017) 71:179. doi: 10.1140/epjd/e2017-80067-0

CrossRef Full Text | Google Scholar