
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Phys. , 14 February 2020
Sec. Chemical Physics and Physical Chemistry
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00020
This article is part of the Research Topic Are There Common Origins in Heterogeneous Dynamics and Structures in Ionic and Non-Ionic Systems? View all 7 articles
Understanding the microscopic (molecular) mechanism of crystal nucleation remains intangible. For instance, it is still impossible to predict in which regions of a supercooled liquid nucleation will occur. Moreover, allegedly the Classical Nucleation Theory fails to describe the homogeneous crystal nucleation rates below the glass transition temperature. In this mini-review article, we revisit, critically comment, and link some highly selected recent studies using examples of an oxide glass-former, water, and a metallic alloy on the largely neglected effect of dynamic heterogeneities on crystal nucleation.
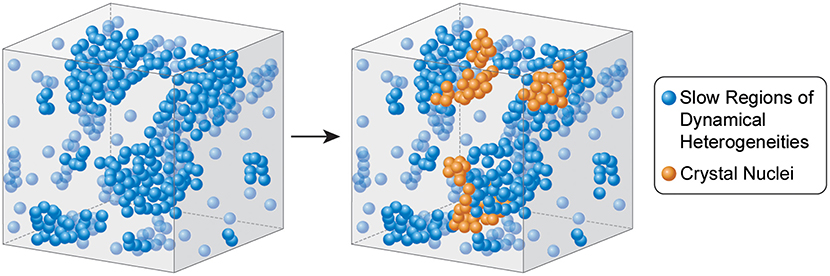
Graphical Abstract. Illustration of crystal nucleation inside the slowest regions of dynamic heterogeneity in a supercooled liquid.
- The effect of DHs on nucleation are revisited for water, an oxide, and a metallic glass-former.
- A link between crystal nucleation and dynamic heterogeneities (DHs) is reviewed.
- The dominant role of DHs on nucleation opens up new challenges to the physics of nucleation.
The formation of crystalline clusters or embryos in supercooled liquids (SCL) is stochastic; they statistically appear and disappear within the parent phase and only become sustainable when a critical size is reached. Ubiquitous examples of nucleation-induced crystallization are intracellular freezing, snow precipitation, mineralization, metal solidification, and glass-ceramic formation [1, 2]. On the other hand, the absence of nucleation on the cooling path is a necessary condition for glass formation [3]. However, despite the extraordinary relevance of crystal nucleation in materials and life sciences and technology, due to the extremely small size scales, and either very long or very short time scales, experimental assessment is very challenging, and comprehension of the microscopic details of crystal nucleation remains intangible. Many open questions remain. For instance, will glasses eventually crystallize after sufficiently long times? [3, 4]; is there a link between dynamic heterogeneities (DHs) and nucleation? In which regions of the supercooled liquid nucleation will occur? [5, 6]. We will address this issue here.
However, we will start with another prying opinion on nucleation in glass-forming substances, which has been a matter of vigorous debate. It is related to an alleged failure of the Classical Nucleation Theory (CNT) to describe the magnitudes of nucleation rates and the temperature-dependence of the crystal nucleation rates below the temperature of maximum, Tmax, which is close to the glass transition temperature, Tg [7–9]. Possible explanations for the failure at Tmax have been advanced by different authors (e.g., [9]). They include the (often neglected) effect of elastic stresses on the thermodynamic barrier for nucleation [10] and the variation of the size of the “structural units” with temperature [11], both with limited success.
The discovery and increasing understanding of dynamic heterogeneity—referring to the spatio-temporal fluctuations in local dynamics in supercooled liquids, i.e., the phenomenon of coexisting domains of widely different sizes and agility [12]—provides a promising approach to realize the slowdown of dynamics during vitrification as the temperature decreases toward the glass transition [13–15]. Furthermore, attention has been given to investigate the relationship between structural relaxation and dynamic heterogeneity in glass-forming liquids [16–18]. A recent publication on the possible role of dynamic heterogeneities in crystal nucleation kinetics is of particular interest to this article [19]. Therefore, we will also discuss here whether DH could be important in explaining this alleged breakdown of CNT.
Let us take homogeneous nucleation rate data in the stoichiometric Li2O·2SiO2 supercooled melt—which nucleates in the sample interior, homogeneously—to study the suspected failure of CNT at low temperatures. CNT fits nucleation rate data rather well for temperatures above Tmax ~ Tg; however, below this temperature, the measured rates allegedly drop off from the extrapolation of the high-temperature CNT fit. This CNT break is not related to the breakdown of the Stokes–Einstein expression, which considers diffusivity to be proportional to viscosity. The proposed explanations for this failure treat the SCL as being structurally and chemically homogeneous.
However, Gupta et al. [19] treated crystal nucleation in a heterogeneous medium using a concept proposed by Stevenson and Wolynes [5]. Grounded on the presence of dynamic heterogeneities in supercooled liquids, they anticipated the existence of a “cross-over” temperature, TX, which might regulate a lower limit for the validity of Classical Theory. TX is the temperature where the size scales become equal, ξ(TX) = rC(TX), with ξ being the (average) size of the CRR (cooperatively rearranging regions), which characterizes the size scale of relaxation in a dynamically heterogeneous liquid, and rC is the size of CNT's critical crystal nucleus, which defines the size scale of the nucleation process. The possible cross-over of these two sizes poses an intriguing question for the mechanism of nucleation below TX. Since interactions with the surrounding SCL environment configurationally constrain the structural rearrangements on a scale smaller than ξ(T), structural changes required for nucleation cannot take place in such cooperatively rearranging regions.
Stevenson and Wolynes [5] showed that the calculated values of TX are close to the glass transition temperatures, Tg, of o-terphenyl, and methanol. Using experimental data on the nucleation kinetics in lithium disilicate, Gupta et al. [19] reported for the first time values of TX for an oxide glass-former. Their findings indicate that TX is very close to Tmax, which, in turn, is close to Tg, Figure 1.
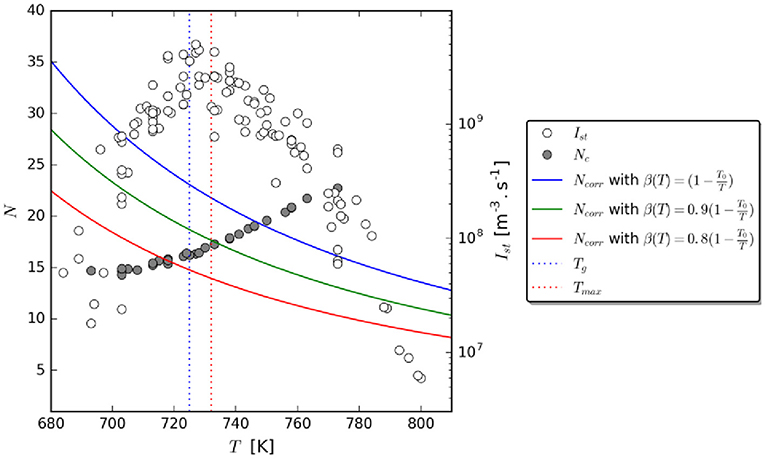
Figure 1. NC(T) and NCorr(T) vs. temperature. Upper, average, and lower boundaries for Ncorr are shown (solid lines). Ist = experimental steady-state nucleation rates for Li2O.2SiO2. The two vertical lines indicate the temperature Tmax (~732 K) of maximum nucleation rate, and the glass transition temperature, Tg (~725 K), where the viscosity is1012 Pa·s. NC = calculated number of atoms in the critical nucleus utilizing experimental nucleation rates and CNT. Ncorr = estimated number of correlated units in the CRR (reprinted from [19] with permission from AIP Publishing).
Based on this finding, Gupta et al. [19] proposed that the anomalous drop of nucleation rates below Tx in this regime is because the size of the CRR, NCorr, controls the critical nucleus size, NC, and the nucleation rate. Hence the mechanism changes around TX. Their discovery linked experimental nucleation kinetics to dynamic heterogeneities in a SCL, suggesting a new opportunity in terms of understanding crystal nucleation in glass-forming liquids.
In a related study, Abyzov et al. [20] proposed another idea, incorporating concepts of spatial heterogeneity of glass-forming liquids for the description of crystal nucleation. They assumed that nucleation takes place only in the high mobility, floppy regions and is suppressed in the solid-like parts of a SCL. They calculated the fraction of liquid-like and solid-like areas as a function of temperature, and thus achieved a satisfactory agreement between the predictions of the CNT and experimental data at temperatures above and below Tmax. This is a thought-provoking idea; however, it contradicts the Molecular Dynamic simulations of Fitzner et al. [21] and Puosi and Pasturel [22], to be reported in the following sessions, which demonstrated that nucleation takes place in the low mobility regions of the SCL.
Water crystallization is likely the most ubiquitous phase transition on Earth. It is known that SCL exhibits dynamical heterogeneity, however, the microscopic connection between the DH and crystal nucleation was not known until recently. Substantial effort has been focused on understanding the microscopic details of ice nucleation (e.g., [23–27]). While several studies have significantly improved our knowledge of the structural transformation during nucleation, the dynamics of ice nucleation have been scarcely addressed.
From a structural perspective, several investigations highlighted the differences between very mobile and very immobile regions within the liquid [28, 29]. Regarding bond-orientational order [30], have observed a higher degree of tetrahedrality in less mobile regions and 5-membered rings acting as locally preferential structures [31]. It has been under debate whether the immobile or mobile regions could be favored domains for nucleation. However, if there is any preference, it had not been proved for any supercooled liquid until recently. Fitzner et al. [21] filled this important gap through studying supercooled liquid water and ice nucleation by computer simulations to infer in which regions ice nucleation happens preferentially. Figure 2 shows regions of high and low mobility.
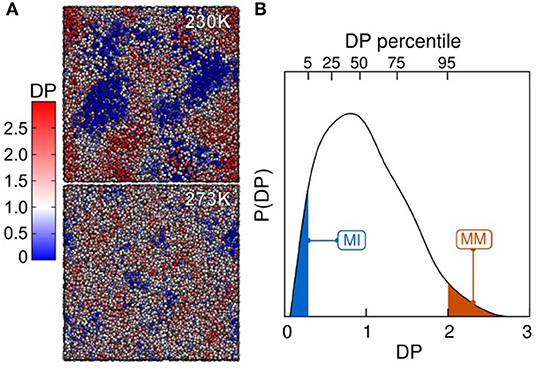
Figure 2. Dynamical heterogeneity in supercooled liquid water. (A) Spatial distribution of the dynamical propensity (DP, the tendency of each molecule to move) at 230 and 273 K. Molecules (only oxygen are shown) are colored based on the scale on the left. (B) Probability density distribution of the DP at 230 K. Shaded regions in blue and red underline the 5% most immobile (MI) and most mobile (MM) molecules (reprinted from [21] under the Creative Commons CC BY-NC-ND license).
The preliminary results of their simulations showed a strong propensity for the pre-critical ice nuclei to form within the most immobile domains. Then they studied the temporal correlation between immobility and clusters prior to their initial time of assembly. They showed that the mobility drops at 1,000 ps before the assembly at 240 K, which is significantly longer than the structural relaxation time of the liquid: τliq ≈ 70 ps. Besides, this drop takes place earlier than cluster formation and is not as abrupt as the change in structure, which can be related to the increase of an order parameter at about 400 ps before the assembly. This result confirmed that immobility precedes ice-cluster formation by a significant timespan.
The same authors also reported simulation results that allowed them to sample many nucleation events at high temperatures. Simulation details are given in the original article [21]. Figure 3A shows a snapshot before nucleation from a typical trajectory. While there are no domains recognized as ice-like, they show large immobile regions in the supercooled liquid. (Figures 3B,C) show similar trajectories after the start of nucleation. The formation of an ice nucleus commences in an immobile domain. Their study further demonstrated that the behavior shown in Figure 3 is typical for all nucleation snapshots.
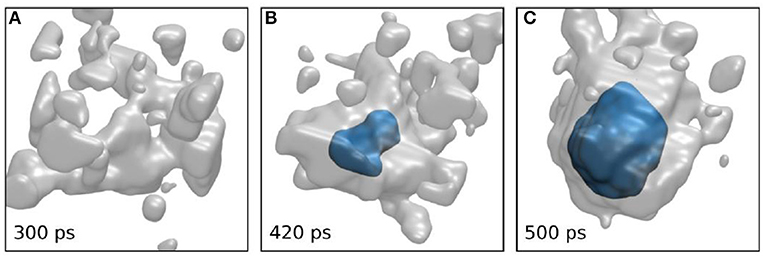
Figure 3. Evolution of the coarse-grained immobility (gray) and crystallinity (blue) fields from a particular trajectory. (A) Pre-nucleation stage, absence of crystalline order in the large immobile domains. (B,C) During nucleation, an ice nucleus forms (B) and grows (C) within the immobile domain. The diameter of the ice-like region in C is ~3.4 nm (reprinted from [21] under the Creative Commons CC BY-NC-ND license).
Fitzner et al. [21] have also analyzed the distribution of primitive rings in the regions of extreme mobility (MI and MM as defined in Figure 2B). The MI regions have a ring distribution sharped peaked around 6 ± 1 members, whereas the distribution for the MM domains is much broader. Moreover, the percentage of fully H-bonded rings is much higher in the MI region. In particular, an abundance of six 1-membered hydrogen-bonded rings can be considered as the critical structural characteristic of the MI domains in the liquid. Since, if regarded in isolation, most of the 6-membered rings in the MI domains are seen as ice-like, which is the sign of the relative orientation between rings that is different from the crystal, and therefore the missing component in forming ice. Since this was observed in the MI region, which shows a reduced diffusivity, the authors suggested that the mechanism of the initial formation of ice-like clusters is collective. This is consistent with a picture of ring reorientation rather than single-particle attachments through diffusive motion.
In conclusion, Fitzner et al. [21] have clearly shown that ice nuclei are born in immobile regions of the SCL water, and that there is an incubation time when the particle mobility drops before any structural change. Additionally, the ring distribution is the structural hallmark of DH.
Along the same line of thought, Puosi and Pasturel [22] used MD simulations to infer the mechanism underlying crystal nucleation in a supercooled metal, Cu5Zr, which is known to show crystal and non-crystalline (local) order based on icosahedral symmetry. Figure 4A shows a crossover temperature, Ts. They found that the supercooled liquid undergoes a breakdown of the Stokes-Einstein relation at this temperature that coincides with the emergence of spatially heterogeneous dynamics. This coincidence of Ts with the breakdown of the SE equation is also very relevant to condensed matter science.
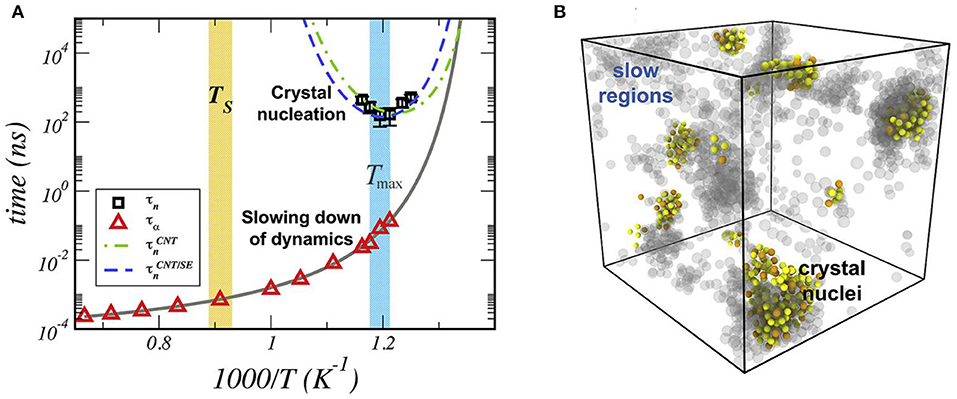
Figure 4. (A) Temperature dependence of the nucleation time (squares), τn, and relaxation time (triangles), τα, of Cu atoms. The solid line is a fit of relaxation data by the Vogel-Fulcher-Tammann equation. The dash-dotted and dashed lines show the CNT predictions of the nucleation time. The shaded regions mark the onset temperature, TS, and the temperature Tmax (with their uncertainty). (B) colored particles = crystal nuclei; gray particles = slow regions of dynamical heterogeneities for selected configurations at T = 837 K, close to Tmax, and t = 160 ns (adapted from Puosi and Pasturel [22] with permission from Elsevier).
They showed that the origin of these phenomena is related to an increase of icosahedral symmetry during cooling. They also revealed that crystal nucleation could be detected by MD near the glass transition temperature and occurs in domains of high icosahedral symmetry. The underlying nucleation mechanism was thus linked to the slow regions of DH. The crystallization pathways were described as follows: (i) formation of heterogeneities in the supercooled liquid below Ts (ii) slow regions of DH having a high degree of icosahedral symmetry act as nucleation ancestors (Figure 4B).
These findings corroborate those reported by Fitzner et al. [21] for nucleation of ice and allowed them to quantify how the non-uniform nature of supercooled liquids influences the theory.
In summary, the above-discussed research works on recent MD simulations show that homogeneous nucleation in Cu5Zr and H2O happens in the largest, most immobile regions that arise from heterogeneous dynamics in supercooled liquids. We are not aware of other studies on this particular topic; therefore, it could be educational and relevant to test these novel findings with other substances.
Using a different approach, the alleged breakdown of the CNT below Tmax could be explained for Li2O.2SiO2 by the fact that the (calculated) average size of the CRR becomes larger than the (calculated) critical nucleus size, and starts to control the nucleation process below this temperature. This hypothesis still needs to be confirmed for other materials that show homogeneous nucleation on laboratory time scales. Possible candidates are BaO.2SiO2, Na2O.2CaO.3SiO2, 2Na2O.1CaO.3SiO2, and Li2O.2B2O3 [32].
One suggestion for future research is that it could be extremely revealing to obtain by MD simulations the average CRR size and the critical nucleus size vs. temperature for other substances. Such work could contribute to generalize or not the predicted crossover. Possible substances could be, for instance, BaS [33] and Lennard-Jones [34], for which excellent potentials exist and spontaneous homogeneous nucleation and the critical nucleus size can be detected by MD at a wide range of supercoolings. In this way, one could perhaps link the findings resulting from calculations performed for lithium disilicate with the MD simulation results for Cu5Zr and H2O.
These three original articles connecting the crystal nucleation phenomenon to the non-uniform nature of supercooled liquids open up new questions to the physics of nucleation. We thus hope this mini-review article paves the way for future research on this most relevant topic.
EZ has written the first draft. Both authors have polished, reviewed, and prepared the final manuscript.
This study was financed by the CNPq, and the São Paulo State Research Foundation support (FAPESP) grant numbers 15/13314-9 and 2013/07793-6.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Neuville D, Cormier L, Caurant D, Montagne L, (eds). (2017). From Glass to Crystal. Nucleation, Growth and Phase Separation, From Research to Applications. London: EDP Science.
2. Kelton KF, Greer AL. Nucleation in Condensed Matter: Applications in Materials and Biology. 1st edn. Amsterdam: Pergamon (2010). doi: 10.1016/S1470-1804(09)01521-1
3. Zanotto ED, Mauro JC. The glassy state of matter: its definition and ultimate fate. J Non-Cryst Solids. (2017) 471:490–5. doi: 10.1016/j.jnoncrysol.2017.05.019
4. Zanotto ED, Cassar DR. The race within supercooled liquids - relaxation versus crystallization. J Chem Phys. (2018) 149:024503. doi: 10.1063/1.5034091
5. Stevenson JD, Wolynes PG. The ultimate fate of supercooled liquids. J Phys Chem A. (2011) 115:3713–9. doi: 10.1021/jp1060057
6. Morris DG. Crystallisation of the metglas 2826 amorphous alloy. Acta Metal. (1981) 29:1213–20. doi: 10.1016/0001-6160(81)90012-2
7. Zanotto ED, James PF. Experimental tests of the classical nucleation theory for glasses. J Non-Cryst Solids. (1985) 74:373–94. doi: 10.1016/0022-3093(85)90080-8.
8. Weinberg MC, Zanotto ED. Re-examination of the temperature dependence of the classical nucleation rate: homogeneous crystal nucleation in glass. J Non-Cryst Solids. (1989) 108:99–108. doi: 10.1016/0022-3093(89)90337-2.
9. Fokin VM, Zanotto ED, Yuritsyn NS, Schmelzer JWP. Homogeneous crystal nucleation in silicate glasses: a 40 years perspective. J Non-Cryst Solids. (2006) 352:2681–714. doi: 10.1016/j.jnoncrysol.2006.02.074
10. Abyzov AS, Fokin VM, Rodrigues AM, Zanotto ED, Schmelzer JWP. The effect of elastic stresses on the thermodynamic barrier for crystal nucleation. J Non-cryst Solids. (2016) 432:325–33. doi: 10.1016/j.jnoncrysol.2015.10.029.
11. Fokin VM, Abyzov AS, Zanotto ED, Cassar DR, Rodrigues AM, Schmelzer JWP. Crystal nucleation in glass-forming liquids: variation of the size of the “structural units” with temperature. J Non-cryst Solids. (2016) 447:35–44. doi: 10.1016/j.jnoncrysol.2016.05.017.
12. Ediger MD. Spatially heterogeneous dynamics in supercooled liquids. Ann Rev Phys Chem. (2000) 51:99–128. doi: 10.1146/annurev.physchem.51.1.99.
13. Lačević N, Starr FW, Schroder TB, Glotzer SC. Spatially heterogeneous dynamics investigated via a time-dependent four-point density correlation function. J Chem Phys. (2003) 119:7372–87. doi: 10.1063/1.1605094.
14. Berthier L, Biroli G, Bouchaud JP, Cipelletti L, El Masri D, L'Hôte D, et al. Direct experimental evidence of a growing length scale accompanying the glass transition. Science. (2005) 310:1797–800. doi: 10.1126/science.1120714
15. Flenner E, Szamel G. Dynamic heterogeneity in a glass forming fluid: susceptibility, structure factor, and correlation length. Phys Rev Lett. (2010) 105:217801. doi: 10.1103/PhysRevLett.105.217801.
16. Coslovich D, Roland CM. Density scaling in viscous liquids: from relaxation times to four-point susceptibilities. J Chem Phys. (2009) 131:151103. doi: 10.1063/1.3250938.
17. Henritzi P, Bormuth A, Klameth F, Vogel M. A molecular dynamics simulations study on the relations between dynamical heterogeneity, structural relaxation, and self-diffusion in viscous liquids. J Chem Phys. (2015) 143:164502. doi: 10.1063/1.4933208.
18. Wang L, Xu N, Wang WH, Guan P. Revealing the link between structural relaxation and dynamic heterogeneity in glass-forming liquids. Phys Rev Lett. (2018) 120:125502. doi: 10.1103/PhysRevLett.120.125502.
19. Gupta PK, Cassar DR, Zanotto ED. Role of dynamic heterogeneities in crystal nucleation kinetics in an oxide supercooled liquid. J Cheml Phys. (2016) 145:211920. doi: 10.1063/1.4964674.
20. Abyzov AS, Fokin VM, Yuritsyn NS, Rodrigues AM, Schmelzer JWP. The effect of heterogeneous structure of glass-forming liquids on crystal nucleation. J Non-cryst Solids. (2017) 462:32–40. doi: 10.1016/j.jnoncrysol.2017.02.004.
21. Fitzner M, Sosso GC, Cox SJ, Michaelides A. Ice is born in low-mobility regions of supercooled liquid water. Proc Natl Acad Sci USA. (2019) 116:2009–14. doi: 10.1073/pnas.1817135116
22. Puosi F, Pasturel A. Nucleation kinetics in a supercooled metallic glass former. Acta Mater. (2019) 174:387–97. doi: 10.1016/j.actamat.2019.05.057.
23. Bartels-Rausch T. Chemistry: ten things we need to know about ice and snow. Nature. (2013) 494:27–9. doi: 10.1038/494027a
24. Sellberg JA, Huang C, McQueen TA, Loh ND, Laksmono H, Schlesinger D, et al. Ultrafast X-ray probing of water structure below the homogeneous ice nucleation temperature. Nature. (2014) 510:381–4. doi: 10.1038/nature13266
25. Malkin TL, Murray BJ, Salzmann CG, Molinero V, Pickering SJ, Whale TF. Stacking disorder in ice I. Phys Chem Chem Phys. (2015) 17:60–76. doi: 10.1039/c4cp02893g
26. Kim KH, Späh A, Pathak H, Perakis F, Mariedahl D, Amann-Winkel K, et al. Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science. (2017) 358:1589–93. doi: 10.1126/science.aap8269
27. Palmer JC, Poole PH, Sciortino F, Debenedetti PG. Advances in computational studies of the liquid–liquid transition in water and water-like models. Chem Rev. (2018) 118:9129–51. doi: 10.1021/acs.chemrev.8b00228
28. Sciortino F, Geiger A, Stanley HE. Effect of defects on molecular mobility in liquid water. Nature. (1991) 354:218–21. doi: 10.1038/354218a0
29. Bullock G, Molinero V. Low-density liquid water is the mother of ice: on the relation between mesostructure, thermodynamics and ice crystallization in solutions. Faraday Discuss. (2013) 167:371–88. doi: 10.1039/c3fd00085k
30. Russo J, Akahane K, Tanaka H. Water-like anomalies as a function of tetrahedrality. Proc Natl Acad Sci USA. (2018) 115:E3333–E3341. doi: 10.1073/pnas.1722339115
31. Russo J, Tanaka H. Understanding water's anomalies with locally favoured structures. Nat Commun. (2014) 5:3556. doi: 10.1038/ncomms4556
32. Abyzov AS, Fokin VM, Zanotto ED. Predicting homogeneous nucleation rates in silicate glass-formers. J Non-cryst Solids. (2018) 500:231–4. doi: 10.1016/j.jnoncrysol.2018.08.002
33. Prado SCC, Rino JP, Zanotto ED. Successful test of the classical nucleation theory by molecular dynamic simulations of BaS. Comput Mater Sci. (2019) 161:99–106. doi: 10.1016/j.commatsci.2019.01.023
Keywords: nucleation, crystallization, dynamic heterogeneity, supercooled liquid, glass
Citation: Zanotto ED and Montazerian M (2020) Dominant Effect of Heterogeneous Dynamics on Homogenous Crystal Nucleation in Supercooled Liquids. Front. Phys. 8:20. doi: 10.3389/fphy.2020.00020
Received: 22 November 2019; Accepted: 23 January 2020;
Published: 14 February 2020.
Edited by:
Carlos Leon, Complutense University of Madrid, SpainReviewed by:
Dong Chen, Zhejiang University, ChinaCopyright © 2020 Zanotto and Montazerian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Edgar D. Zanotto, ZGVkekB1ZnNjYXIuYnI=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.