Self-Consistent Two-Gap Approach in Studying Multi-Band Superconductivity of NdFeAsO0.65F0.35

High quality single crystals of NdFeAsO_0.65F_0.35 (the superconducting transition temperature T_c ≃ 30.6 K) were studied in zero-field (ZF) and transverse-field (TF) muon-spin rotation/relaxation (μSR) experiments. An upturn in muon-spin depolarization rate at T ≲ 3 K was observed in ZF-μSR measurements and it was associated with the onset of ordering of Nd electronic moments. Measurements of the magnetic field penetration depth (λ) were performed in the TF geometry. By applying the external magnetic field B_ex parallel to the crystallographic c-axis (B_ex||c) and parallel to the ab-plane (B_ex||ab), the temperature dependencies of the in-plane component (${\lambda }_{ab}^{-2}$) and the combination of the in-plane and the out of plane components (${\lambda }_{ab,c}^{-2}$) of the superfluid density were determined, respectively. The out-of-plane superfluid density component (${\lambda }_c^{-2}$) was further obtained by combining the results of B_ex||c and B_ex||ab set of experiments. The temperature dependencies of ${\lambda }_{ab}^{-2}$, ${\lambda }_{ab,c}^{-2}$, and ${\lambda }_c^{-2}$ were analyzed within the framework of a self-consistent two-gap model despite of using the traditional α-model. Interband coupling was taken into account, instead of assuming it to be zero as it stated in the α-model. A relatively small value of the interband coupling constant Λ₁₂ ≃ 0.01 was obtained, thus indicating that the energy bands in NdFeAsO_0.65F_0.35 are only weakly coupled. In spite of their small magnitude, the coupling between the bands leads to the single value of the superconducting transition temperature T_c. The penetration depth anisotropy γ_λ = λ_c/λ_ab was found to increase upon cooling, consistent with most of Fe-based superconductors, and their behavior is attributed to the multi-band nature of superconductivity in NdFeAsO_0.65F_0.35.

1. Introduction

Iron-based superconductors (IBS's) remain a subject of intensive research due to a comparable large value of the transition temperature T_c. It reaches up to 55 K for the RFeAsO_1−xF_x IBS family (R corresponds to the lanthanides La, Sm, Ce, Nd, Pr, and Gd) [1–5] and approaches T_c ≃ 100 K in a single layer of FeSe on the SrTiO₃ substrate [6]. Emergence of superconductivity at such high temperatures raises a puzzling question about the gap symmetry, which can further determine the pairing mechanism for the superconducting state.

The superconductivity in IBS's appears in close proximity to the magnetism offered by d-orbitals of Fe, hence one can expect the unconventional nature of the superconducting state. The electronic band structure calculations manifest that superconductivity in IBS's originates from multiple disconnected Fermi surface sheets derived from Fe d-orbitals, thus reflecting the possibility of a complex nature of the superconducting gap structure [7, 8]. There are already different scenarios proposed for the gap structure in IBS's including two-gap, s-wave, d-wave, isotropic, anisotropic, and surprisingly, p-type wave symmetry of the superconducting order parameter [9–18]. Even after several years of discovery of IBS's, an unified picture of the gap structure is not reached, contradicting the case of cuprate high-temperature superconductors, where almost all superconducting families represent a nodal pairing state [19]. In the context of conflicting results, there is still a need of comprehensive tools to understand the gap symmetry of IBS's. The magnetic penetration depth and its anisotropy carry important information about the low lying quasiparticles and hence can shed light on the gap structure of IBS's.

This paper presents a detailed muon-spin rotation/relaxation (μSR) study of high quality single crystals of NdFeAsO_0.65F_0.35 grown with high pressure and high temperature cubic anvil technique. Very few investigations were carried out in the direction of exploring the symmetry of the order parameter for NdFeAsO_1−xF_x (Nd-1111). As an example, a single gap without nodes at the Γ hole pocket was revealed through angle resolved photoemission spectroscopy (ARPES) [20], a nodal type gap structure was concluded through the linear behavior of the lower critical field B_c1 at low temperatures [21]. A multi-band nature of superconductivity seems to be a more generic feature for Nd-1111 as most measurements point toward a two superconducting gaps without nodes as, e.g., magnetic penetration depth measured through Tunnel Diode Resonator (TDR) technique [22], ARPES [23], point contact Andreev reflection spectroscopy [24, 25], conductance [26], and B_c1 measurements [27]. In most cases, however, the analysis of the multiple gap behavior was performed within the framework of a phenomenological α-model [28–37], which assumes zero coupling between the energy bands. In fact, the zero-coupling requires that the temperature dependencies of the energy gaps, as well as the values of the superconducting transition temperatures can not be identical and should vary from one to another energy band. Speaking in a broader way, there is a clear need of different set of data and an analysis which takes in account the coupling between the bands. In the present paper we approach to a so-called self-consistent model [38–41], allowing to analyze the magnetic penetration depth data obtained in the transverse field μSR experiment. Within this model, the energy bands with two different superconducting order parameters were assumed to be coupled and the gap equations were solved self-consistently by considering the presence of the “interband” and “intraband” coupling strengths.

The paper is organized as follows: In section 2 the sample preparation procedure, the results of magnetization measurements and the details of μSR experiments are briefly discussed. The experimental results obtained in zero-field (ZF) and transverse-field (TF) μSR experiments are described in section 3. The subsection 3.1 comprises studies of the magnetic response of NdFeAsO_0.65F_0.35. The subsection 3.2 describes the results of the field-shift experiments and the measurements of the temperature dependencies of the magnetic field penetration depth. The self-consistent two-gap model and the temperature evolution of the penetration depth anisotropy are presented in section 4. The conclusions follow in section 5.

2. Experimental Techniques

2.1. Sample Preparation

Bulk single crystals of NdFeAsO_1−xF_x with nominal fluorine content x = 0.35 were synthesized at 3 GPa and ≃ 1, 450°C from NaAs/KAs flux by using the cubic anvil high-pressure and high-temperature technique. The detailed description of the sample preparation procedure is given in reference [42]. The individual crystals obtained after the sample grow had a typical size of ~0.5 × 0.5 × 0.03 mm³.

2.2. Magnetization Measurements

The magnetization measurements were carried out on a Quantum Design MPMS-5 system. Figure 1 shows the temperature variation of the normalized magnetic moment [M(T)/M(T = 5K)] measured simultaneously on about thirty NdFeAsO_0.65F_0.35 single crystals. These crystals were further used in μSR experiments. The external field B_ex = 0.5 mT was applied parallel to the ab plane of the crystals. Measurements were performed in the zero-field cooled (ZFC) mode. A sharp diamagnetic signal is seen across the superconducting transition which confirms the bulk nature of the superconductivity. The superconducting transition temperature T_c ≃ 30.6 K was determined from the cross point of the two lines extrapolated from the high temperature normal state and the low temperature superconducting state, respectively (see Figure 1).

FIGURE 1

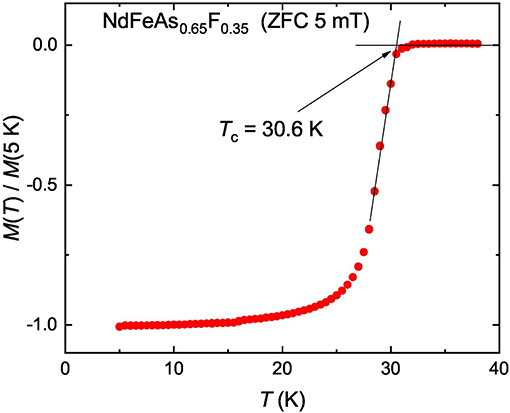
Figure 1. The zero-field cooled magnetization curve [M(T) curve] measured on about thirty NdFeAsO_0.65F_0.35 single crystals, which were further used in μSR experiments. The external magnetic field B_ex = 0.5 mT was applied along the ab-plane of the crystals. The M(T) data were normalized to their M(T = 5K) value.

2.3. Muon-Spin Rotation/Relaxation Experiments

Muon-spin rotation/relaxation (μSR) measurements were carried out in a temperature range of 1.5–50 K at the GPS (General Purpose Surface) (πM3 beam line) and DOLLY (πE1 beam line) spectrometers at the Paul Scherrer Institut (PSI), Villigen, Switzerland. In this technique, 100% spin-polarized muons are implanted uniformly through the sample volume, where they decay with the lifetime of 2.2 μs and the relevant decay positrons are detected successively. Muons act as sensitive magnetic probes. The spin of the muon precesses in the local magnetic field B_μ with a frequency ω_μ = γ_μB_μ (γ_μ is muon gyromagnetic ratio, γ_μ/2π = 135.53 MHz/T). The detailed description of μSR technique and its applications for studying the superconducting and magnetic samples can be found in references [43–50].

A specific sample holder was designed in order to perform μSR experiments on thin single crystals of NdFeAsO_0.65F_0.35. A mosaic of about 200 single crystals was sandwiched between two sheets made of several 0.125 nm thick Kapton layers [51]. The first few Kapton layers decelerate the muons from incoming beam and served the role of a degrader. The outgoing muons from the degrader were slow enough to stop inside the thin single crystals. The last few layers were used to stop the muons which still manage to pass through the sample. A schematic picture of the sample holder can be found in the reference [52]. The data were analyzed using the free software package MUSRFIT [53].

3. Experimental Results

3.1. The Magnetic Response of NdFeAsO_0.65F_0.35: ZF-μSR Experiments

The μSR experiments in zero-field (ZF-μSR) were performed in order to study the magnetic response of the NdFeAsO_0.65F_0.35 sample. In two sets of experiments the initial muon-spin polarization P(0) was applied parallel to the c-axis and the ab-plane, respectively. Few representative muon-time spectra for P(0)||c and P(0)||ab orientations are shown in Figures 2A,C, respectively.

FIGURE 2

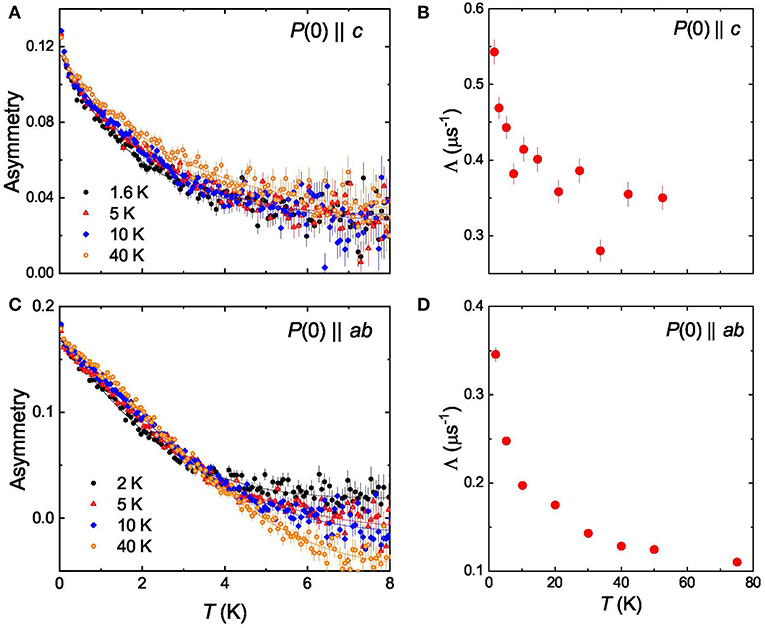
Figure 2. (A) ZF-μSR time-spectra of NdFeAsO_0.65F_0.35 measured at T = 1.6, 5, 10, and 40 K with the initial muon-spin polarization P(0) applied parallel to the crystallographic c−axis. (B) The temperature evolution of the exponential relaxation rate Λ obtained from the fit of Equation (1) to P(0)||c set of data. (C,D) —the same as in (A,B), but for P(0)||ab set of experiments and T = 2.0, 5, 10, and 40 K.

The experimental data were analyzed by separating the μSR response on the sample (s) and the background (bg) contributions:

$\begin{array}{ll}{A}_{0}P(t)=A_{\text{s}}{P}_{\text{s}}(t)+A_{\text{bg}}{P}_{\text{bg}}(t).& (1)\end{array}$

Here A₀ is the initial asymmetry of the muon-spin ensemble. A_s (A_bg) and P_s(t) [P_bg(t)] are the asymmetry and the time evolution of the muon-spin polarization of the sample (background), respectively. The background contribution accounts for muons missing the sample and/or stopped in Kapton layers [52].

In ZF-μSR experiments the sample contribution was described by assuming the presence of the nuclear and the electronic magnetic moments:

$\begin{array}{ll}{P}_{\text{s}}^{\text{ZF}}(t)=\left[\frac{1}{3}+\frac{2}{3}(1-{\sigma }_{\text{GKT}}^2{t}^2)e^{-{\sigma }_{\text{GKT}}^2{t}^2/2}\right]e^{-\Lambda t}.& (2)\end{array}$

Here the term within the square brackets is the Gaussian Kubo-Toyabe function with the relaxation rate σ_GKT, which is generally used to describe the nuclear magnetic moment contribution in ZF-μSR experiments (see e.g., references [43–49], and references therein). The exponential term with the relaxation parameter Λ represents the contribution of randomly distributed magnetic impurities and/or disordered magnetic moments [35, 54].

The temperature evolution of the exponential relaxation rate Λ for P(0)||c and P(0)||ab set of experiments are presented in Figures 2B,D. During fits the Gaussian Kubo-Toyabe relaxation σ_GKT entering Equation (2) was assumed to be dependent on the orientation, but independent on temperature, respectively. From the data presented in Figures 2B,D two important points emerges:

(i) No detectable change in the relaxation rates Λ is observed across the superconducting transition temperature, which rules out the possibility of any spontaneous magnetic field below T_c. This means that the time-reversal symmetry breaking is not an immanent feature of NdFeAsO_0.65F_0.35 studied here.

(ii) An increase in Λ is seen below 3 K for both orientations, which is probably associated with the onset of ordering of Nd magnetic moments. A similar upturn was seen in measured frequency shift [δf(T)] obtained by means of TDR technique and was explained with the ordering of the local magnetic moments of Nd below 4 K [22]. Further evidence comes form the powder Neutron diffraction experiment, where below ≃ 1.96 K a long range antiferromagnetic order was apparent and it was associated to the combined magnetic ordering of Fe and Nd magnetic moments in the parent compound NdFeAsO [55].

3.2. The Superconducting Response of NdFeAsO_0.65F_0.35: TF-μSR Experiments

3.2.1. The Homogeneity of the Superconducting State: Field-Shift Experiments

The homogeneity of the superconducting state and the effects of the flux-line lattice (FLL) pinning were probed by performing series of field-shift experiments in the transverse-field (TF) geometry. The measurements were carried out with the external magnetic field B_ex applied parallel to the c-axis (B_ex||c) and parallel to the ab-plane (B_ex||ab), respectively. The sample was initially cooled in B_ex ≃ 15 mT to the desired temperature (T ≃ 1.6 K for B_ex∥c and T ≃ 5 K for B_ex∥ab) where the first muon-time spectra were collected (red curves in Figures 3A,C). Then, by keeping the temperature constant, the field was decreased down to 12 mT and a new “field-shift” data sets were collected (black curves in Figures 3A,C). The corresponding Fast Fourier transform of the TF-μSR time-spectra, which reflects the internal field distribution P(B) inside the sample, are shown in Figures 3B,D.

FIGURE 3

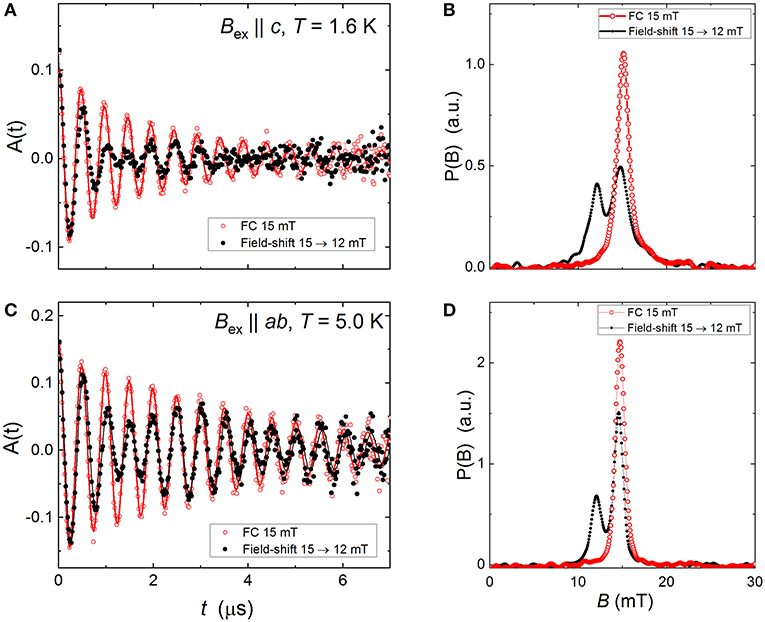
Figure 3. (A) TF-μSR time-spectra of NdFeAsO_0.65F_0.35 measured at T = 1.6 K with the external field B_ex applied parallel to the crystallographic c−axis. The TF-μSR time-spectra denoted by red points correspond to the direct cooling at B_ex = 15 mT from T above T_c down to 1.6 K. The black points correspond to time-spectra obtained after a subsequent field decrease to 12 mT without changing temperature. (B) The Fast Fourier transform of the TF-μSR time-spectra presented at (A). (C,D) —the same as in (A,B), but for B_ex||ab and at T = 5 K.

The data presented in Figures 3B,D reveal that for both field orientations the main part of the signal, accounting for ~70% of the total signal amplitude, remains unchanged within the experimental accuracy. Only the symmetric sharp peak follows exactly the applied field. It is attributed, therefore, to the residual background signal from muons missing the sample (see also reference [54], where the first μSR field-shift experiments were introduced). The field-shift measurements clearly demonstrate that for both, B_ex||c and B_ex||ab field orientations, the flux-line lattice in NdFeAsO_0.65F_0.35 sample is strongly pinned.

The field distribution caused entirely by the flux-line lattice was further obtained by subtracting the symmetric background peak. The corresponding P(B)′s are represented in Figure 4 by blue curves. It is worth noting that, for both field orientation P(B) distributions possess the basic features expected for an arranged flux-line lattice. The cutoff at low fields, the pronounced peak at the intermediate field and the long tail in the high field directions are clearly visible.

FIGURE 4

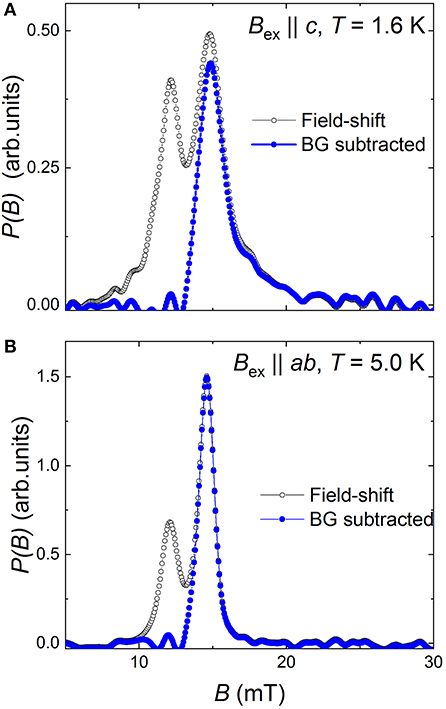
Figure 4. The magnetic field distribution P(B) caused by formation of the flux-line lattice in NdFeAsO_0.65F_0.35 sample in B_ex||c (A) and B_ex||ab (B) set of experiments. The blue curves are obtained by subtracting the symmetric background peak (see text for details).

3.2.2. Analysis of B_ex||c and B_ex||ab Set of TF-μSR Data

The distribution of the internal magnetic fields P(B) in the superconductor in the FLL state is uniquely determined by two characteristic lengths: the magnetic field penetration depth λ and the coherence length ξ. For an isotropic extreme type-II superconductor (λ ≫ ξ) and for fields much smaller than the upper critical field B_c2 (B_ex ≪ B_c2) the P(B) is almost independent on ξ and it could be calculated from the spatial variation of the internal magnetic field B(r) (r is the spatial coordinate) [56, 57]. In the present work the magnetic field distribution P(B), measured by means of TF-μSR, was analyzed assuming B(r) is being described within the framework of Ginzburg-Landau approach [56–59].

The spatial distribution of magnetic fields in the mixed state of a type-II superconductor is calculated via the Fourier expansion [56–59]:

$\begin{array}{ll}B(\text{r})=\langle B\rangle {\displaystyle \sum _{\text{G}}}exp(-i\text{G}\text{r})B_{\text{G}}(\lambda ,\xi ).& (3)\end{array}$

Here 〈B〉 is the average magnetic field inside the superconductor, G is the reciprocal vector, r represents the vector coordinate in a plane perpendicular to the applied magnetic field and B_G is the Fourier component. Within the Ginzburg-Landau model B_G is obtained via [58]:

$\begin{array}{ll}{B}_{\text{G}}=\frac{{\varphi }_0}{S}(1-b^4)\frac{u{K}_1(u)}{{\lambda }^2{G}^2}.& (4)\end{array}$

ϕ₀ is the magnetic flux quantum, S = ϕ₀/〈B〉 represents the area of the FLL unit cell, b = 〈B〉/B_c2, K₁(u) is the modified Bessel function, with u² = 2ξ²G²(1 + b⁴)[1 − 2b(1 − b)²]. For the hexagonal FLL, the reciprocal lattice is $G_{mn}=(2\pi /\sqrt{S})(m·\sqrt[4]{3}/\sqrt{2},(n-m/2)·\sqrt{2}/\sqrt[4]{3})$. m and n are the integer numbers.

The internal field distribution within the “ideal” flux-line lattice was obtained as:

$\begin{array}{ll}{P}_{id}(B)=\frac{\int \delta (B-B^{\prime })dA(B^{\prime })}{\int dA(B^{\prime })}.& (5)\end{array}$

Here dA(B′) is the elementary area of the FLL with a field B′ inside, and the integration is performed over a quarter of the flux-line lattice unit cell [60]. The FLL disorder, the broadening of the TF-μSR line due to the nuclear depolarization and the contribution of the electronic moments were considered by convoluting P_id(B) with Gaussian and Lorentzian functions [34, 35, 57, 61]. Finally, the following depolarization function was fitted to the measured TF-μSR data:

$\begin{array}{ll}{P}_{\text{s}}^{\text{TF}}(t)=e^{i\varphi }{e}^{-{\sigma }_g^2{t}^2/2-\Lambda t}{\displaystyle \int }{P}_{id}(B)e^{i{\gamma }_{\mu }Bt}dB.& (6)\end{array}$

Here ϕ is phase of the muon-spin ensemble, Λ represents the relaxation rate associated with the electronic moment, and σ_g is associated with the FLL disorder and the nuclear moment contributions, respectively. In our calculations Λ was fixed to the values obtained in ZF-μSR experiments (see section 3.1 and Figure 2).

The results of the fit of Equation (1) with the sample part described by Equation (6) to the B_ex||c and B||ab set of data are presented in Figure 5. Note that with the field applied parallel to the c-axis the screening current, flowing around the flux-line cores, remains within the ab-plane. This means that the field distribution P(B) in B_ex||c set of experiments is determined by the so-called in-plane component of the magnetic penetration depth λ_ab (Figure 5A). Note that in superconductors with the tetragonal layered crystal structure, as NdFeAsO_0.65F_0.35, the a- and b- components of the magnetic penetration depth are equal: λ_a = λ_b [31]. With the field applied parallel to the a(b)-axis, the screening current flows along the b(a) and c-axes, respectively. Consequently, in B_ex||ab set of experiments λ_{ab, c} is obtained (Figure 5B).

FIGURE 5

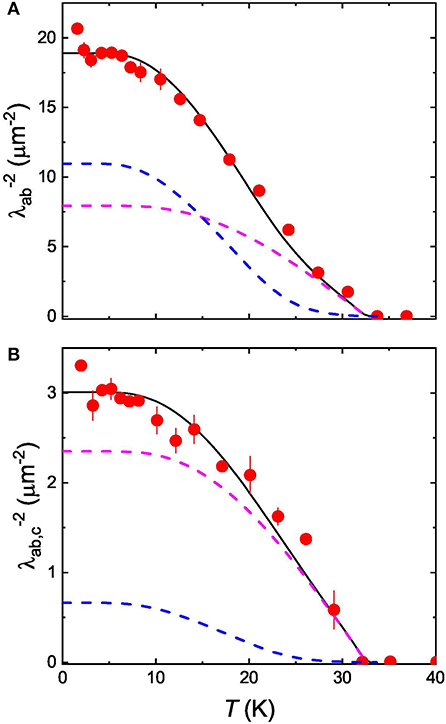
Figure 5. Temperature evolution of the inverse squared magnetic penetration depth of NdFeAsO_0.65F_0.35: (A) —${\lambda }_{ab}^{-2}$ and (B) —${\lambda }_{ab,c}^{-2}$. Black solid lines are theoretical curves obtained by analyzing the data within the self-consistent two-gap model. The dashed pink and blue lines are contributions of the larger (Δ₁), and the smaller (Δ₂) gaps to the magnetic penetration depth, respectively. See section 4.1 for details.

4. Discussions

4.1. Temperature Dependencies of ${\lambda }_{ab}^{-2}$ and ${\lambda }_{ab,c}^{-2}$

Temperature dependencies of ${\lambda }_{ab}^{-2}$ and ${\lambda }_{ab,c}^{-2}$, as they reported in section 3.2.2, are shown in Figures 5A,B, respectively. Due to a possible influence caused by ordering of Nd magnetic moments (see the discussion in section 3.1 and Figure 2), the data points below 5 K were excluded from consideration.

In order to elucidate the pairing states in NdFeAsO_0.65F_0.35, the experimental data were analyzed by means of a two-gap model, with both gaps having an s-wave symmetry. Despite of considering a similar BCS type temperature dependence for both the gaps, as in phenomenological α-model [28–33, 35–37], the temperature dependencies of the two gaps (Δ₁ and Δ₂) were obtained through a self-consistent coupled gap equations [38, 40, 41]:

$\begin{array}{lll}{\Delta }_1& =& {\displaystyle {\int }_0^{{\omega }_{D1}}}\frac{N_1(0)V_{11}{\Delta }_1}{\sqrt{E^2+{\Delta }_1^2}}\text{tanh}\frac{\sqrt{E^2+{\Delta }_1^2}}{2k_{B}T}dE\\ & & +{\displaystyle {\int }_0^{{\omega }_{D2}}}\frac{N_2(0)V_{12}{\Delta }_2}{\sqrt{E^2+{\Delta }_2^2}}\text{tanh}\frac{\sqrt{E^2+{\Delta }_2^2}}{2k_{B}T}dE,\\ {\Delta }_2& =& {\displaystyle {\int }_0^{{\omega }_{D1}}}\frac{N_1(0)V_{21}{\Delta }_1}{\sqrt{E^2+{\Delta }_1^2}}\text{tanh}\frac{\sqrt{E^2+{\Delta }_1^2}}{2k_{B}T}dE\\ & & +{\displaystyle {\int }_0^{{\omega }_{D2}}}\frac{N_2(0)V_{22}{\Delta }_2}{\sqrt{E^2+{\Delta }_2^2}}\text{tanh}\frac{\sqrt{E^2+{\Delta }_2^2}}{2k_{B}T}dE.& (7)\end{array}$

Here, N₁(0) and N₂(0) are the partial density of states for each band at the Fermi level. V₁₁ (V₂₂) and V₁₂ (V₂₁) are the intraband and the interband interaction potentials, respectively. ω_D1 (ω_D2) is the Debye (cut-off) phonon frequency of the band 1 (2).

A simplification of the above expressions can be done by using the notation for the coupling constant Λ_ij = N_j(0)V_ij, as is introduced by Kogan et al. [39]. Further simplification is made by assuming a similar Debye frequency for both the bands, i.e., ω_D1 = ω_D2 = ω_D. The gap equation becomes [40, 41]:

$\begin{array}{lll}{\Delta }_1& =& {\displaystyle {\int }_0^{{\omega }_D}}\frac{{\Lambda }_{11}{\Delta }_1}{\sqrt{E^2+{\Delta }_1^2}}tanh\frac{\sqrt{E^2+{\Delta }_1^2}}{2k_{B}T}dE\\ & & +{\displaystyle {\int }_0^{{\omega }_D}}\frac{{\Lambda }_{12}{\Delta }_2}{\sqrt{E^2+{\Delta }_2^2}}tanh\frac{\sqrt{E^2+{\Delta }_2^2}}{2k_{B}T}dE,\\ {\Delta }_2& =& {\displaystyle {\int }_0^{{\omega }_D}}\frac{{\Lambda }_{12}{\Delta }_1}{\sqrt{E^2+{\Delta }_1^2}}tanh\frac{\sqrt{E^2+{\Delta }_1^2}}{2k_{B}T}dE\\ & & +{\displaystyle {\int }_0^{{\omega }_D}}\frac{{\Lambda }_{22}{\Delta }_2}{\sqrt{E^2+{\Delta }_2^2}}tanh\frac{\sqrt{E^2+{\Delta }_2^2}}{2k_{B}T}dE.& (8)\end{array}$

The advantage the above mentioned simplifications is that: (i) in the notation of Kogan et al. [39] Λ₁₂ = Λ₂₁ and (ii) the number of the free parameters, which were initially eight in Equation (7), namely: ω_D1, ω_D2, N₁₍₀₎, and N₂₍₀₎, V₁₁, V₁₂, V₂₁, and V₂₂; reduces to four in Equation (8), namely: ω_D, Λ₁₁, Λ₁₂, and Λ₂₂ [40, 41].

With the known temperature variation of Δ₁(T) and Δ₂(T), a rigorous analysis of λ⁻² is carried out by separating it into two components [39, 41]:

$\begin{array}{ll}\frac{{\lambda }^{-2}(T)}{{\lambda }^{-2}(0)}=\omega \frac{{\lambda }_1^{-2}(T)}{{\lambda }_1^{-2}(0)}+(1-\omega )\frac{{\lambda }_2^{-2}(T)}{{\lambda }_2^{-2}(0)}.& (9)\end{array}$

ω is the weight factor for the larger gap Δ₁ and ${\lambda }_i^{-2}(T)/{\lambda }_i^{-2}(0)$ is the superfluid density component of the i−th band. The superfluid density component is related to the superconducting energy gap via the expression [62]:

$\begin{array}{ll}\frac{{\lambda }_i{(T)}^{-2}}{{\lambda }_i{(0)}^{-2}}=1+2{\displaystyle {\int }_{{\Delta }_i(T)}^{\infty }}\left(\frac{\partial f}{\partial E}\right)\times \frac{EdE}{\sqrt{E^2-{\Delta }_i{(T)}^2}},& (10)\end{array}$

where $f={\left[1+\text{exp}(E/k_{B}T)\right]}^{-1}$ is the Fermi distribution function.

For the analysis of the temperature evolution of magnetic penetration depths, the literature value of the Debye frequency, ω_D = 37 meV, obtained in Mössbauer experiments [63], was considered. The coupling constants: Λ₁₁, Λ₂₂, and Λ₁₂; the gaps: Δ₁(T), Δ₂(T) were kept identical during the analysis of ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$, but the weight factor ω was varied. The common parameters obtained with the analysis of ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$ are: Λ₁₁ ≃ 0.368, Λ₂₂ ≃ 0.315, Λ₁₂ ≃ 0.01, Δ₁(0) ≃ 5.2 meV, Δ₂(0) ≃ 3.5 meV, and T_c ≃ 33.7 K. The weighting factors (ω) and the zero-temperature values of the inverse squared magnetic penetration depth [λ⁻²(0)] are 0.42/0.85 and 18.9/3.0 μm⁻² for ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$, respectively.

Contribution of the penetration depths corresponding to the larger gap (Δ₁) and the smaller gap (Δ₂) are shown in Figures 5A,B by dashed pink and blue lines, respectively. The solid black lines are the theory curves obtained by means of two-gap model as described earlier. The temperature dependencies of the gaps [Δ₁(T) and Δ₂(T)] and the corresponding superfluid density components [${\lambda }_1^{-2}(T)/{\lambda }_1^{-2}(0)$ and ${\lambda }_2^{-2}(T)/{\lambda }_2^{-2}(0)$] are presented in Figure 6.

FIGURE 6

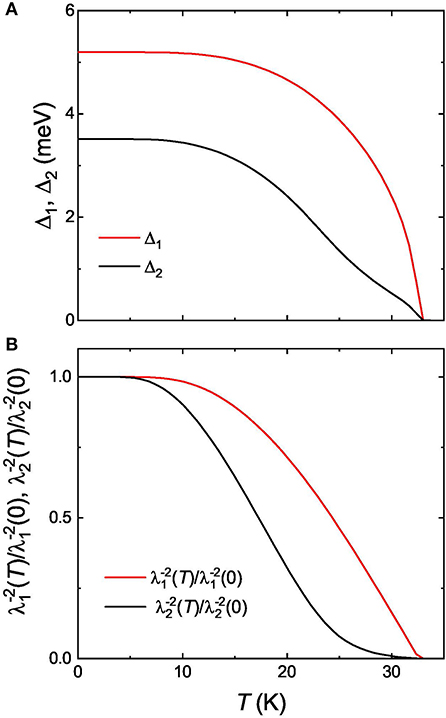
Figure 6. (A) Temperature evolution of the Δ₁ and Δ₂ superconducting energy gaps obtained within the framework of the self-consistent two-gap model. (B) Temperature evolution of the corresponding superfluid density contributions ${\lambda }_1^{-2}(T)/{\lambda }_1^{-2}(0)$ and ${\lambda }_2^{-2}(T)/{\lambda }_2^{-2}(0)$. See section 4.1 for details.

From the analysis of the magnetic penetration depths data by means of two-gap model three following important points emerge:

(i) The interband coupling constant Λ₁₂ ≃ 0.01 is relatively small, indicating the fact that the two bands are nearly decoupled. However, the value of Λ₁₂ is significant enough to assign a single T_c for each gap along both the planes.

(ii) The gap to T_c ratio for the bigger gap 2Δ₁/k_BT_c ≃ 3.58 is close to the universal BCS value 3.52. For the lower gap 2Δ₂/k_BT_c = 2.41 is found. This indicates the weak coupling regime for both the gaps.

(iii) The difference in the temperature variation of ${\lambda }_{ab}^{-2}$ and ${\lambda }_{ab,c}^{-2}$ arises because of much smaller contribution of larger gap to ${\lambda }_{ab}^{-2}$ compared to that to ${\lambda }_{ab,c}^{-2}$.

4.2. Out of Plane Magnetic Penetration Depth, ${\lambda }_c^{-2}$

This section describes the determination of the out of plane component of the magnetic penetration depth, ${\lambda }_c^{-2}(T)$, and its analysis based on self-consistent two-gap model.

According to the London model, the inverse squared magnetic field penetration depth for the isotropic superconductor is proportional to the superfluid density in terms of ${\lambda }^{-2}\propto {\rho }_s=n_s/m^{*}$ (ρ_s is the superfluid density, n_s is the charge carrier concentration and m^* is the effective mass of the charge carriers). For an anisotropic superconductor, as NdFeAsO_0.65F_0.35, the magnetic penetration depth is also anisotropic and is determined by an effective mass tensor [64]:

$\begin{array}{ll}{m}_{eff}=\left(\begin{array}{ccc}{m}_i^{*}& 0& 0\\ 0& m_j^{*}& 0\\ 0& 0& m_k^{*}\end{array}\right).& (11)\end{array}$

Here, $m_i^{*}$ is the effective mass of charge carrier flowing along i-th principal axis. For a magnetic field applied along i-th principal axis of the effective mass tensor, the effective penetration depth is given as [64]:

$\begin{array}{ll}{\lambda }_{jk}^{-2}=\frac{1}{{\lambda }_j{\lambda }_k}.& (12)\end{array}$

By using Equation (12) the out of plane component of the magnetic penetration depth, ${\lambda }_c^{-2}$, was further obtained from ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$ data shown in Figure 5 as:

$\begin{array}{ll}{\lambda }_c^{-2}=\frac{{\lambda }_{ab,c}^{-4}}{{\lambda }_{ab}^{-2}}.& (13)\end{array}$

The resulting dependence of ${\lambda }_c^{-2}$ on temperature is shown in Figure 7. The theoretical temperature variation of ${\lambda }_c^{-2}(T)$ was also obtained from the theory curves for ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$, as they are described in Figures 5A,B, and it is represented by solid black line. It is evident that the curve obtained by means of two-gap model replicates the experimental data very well, which indicates that the magnetic penetration depth along c-axis is well-analyzed with two-gap s + s-wave model. For the zero-temperature value of the out-of plane component the value ${\lambda }_c^{-2}(0)\simeq 0.48$ μm⁻² is obtained.

FIGURE 7

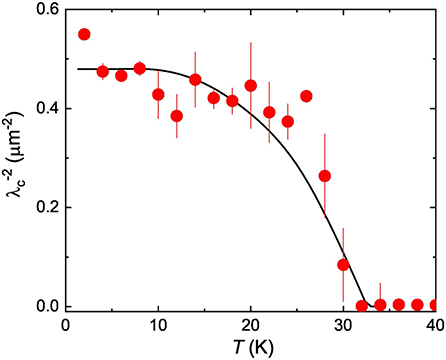
Figure 7. Temperature evolution of the inverse squared out of plane magnetic penetration depth ${\lambda }_c^{-2}(T)$. The solid line is obtained from the theoretical ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$ curves, as they presented in Figure 5, by using Equation (13).

4.3. The Magnetic Penetration Depth Anisotropy, γ_λ

Figure 8A shows the temperature evolution of the magnetic penetration depth anisotropy obtained with the experimental data presented in Figure 5 and Equation (12):

$\begin{array}{ll}{\gamma }_{\lambda }=\frac{{\lambda }_c}{{\lambda }_{ab}}=\frac{{\lambda }_{ab}^{-2}}{{\lambda }_{ab,c}^{-2}}.& (14)\end{array}$

γ_λ(T) increases with decreasing temperature from γ_λ ≃ 1.8 at T = T_c to γ_λ ≃ 6.3 close to T = 0 K. The theoretical curve obtained within the self-consistent two-band model is represented by the solid black line. The temperature variation of anisotropy is reproduced well with this theoretical curve, which further confirms the multi-band nature of superconductivity in the studied oxypnictide material. It is worth to mention, that ${\lambda }_{ab}^{-2}(T)$ and ${\lambda }_{ab,c}^{-2}(T)$, obtained within the present study, were measured on a mosaic of about 200 NdFeAsO_0.65F_0.35 single crystalline samples. For such a big number of simultaneously measured crystals a certain misalignment will definitively take place. Consequently, our results put a lower limit on the determination of γ_λ.

FIGURE 8

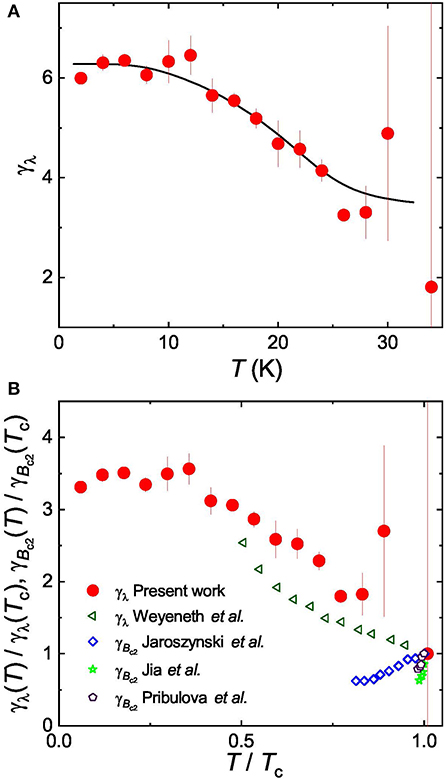
Figure 8. (A) Temperature dependence of the magnetic penetration depth anisotropy, γ_λ(T) = λ_c(T)/λ_ab(T). The solid curve is the result of the self-consistent two-gap model. (B) Comparison of γ_λ(T)/γ_λ(T_c) (from the present work and reference [65]) with the anisotropy of the upper critical field γ_Bc2(T)/γ_Bc2(T_c) from references [66–68].

Figure 8B compares γ_λ obtained in the present study with that measured by means of torque magnetometry by Weyeneth et al. [65]. In both cases λ_λ increases with decreasing T. A similar qualitative behavior of γ_λ(T) was observed in Sm- and Nd-1111 systems by means of torque magnetometry [65, 69]; in Ba(Fe_1−xCo_x)₂As₂ by means of TDR [70]; in Ba_1−xK_xFe₂As₂ [34], SrFe_1.75Co_0.25As₂ [35], FeSe_0.5Te_0.5 [71], CaKFe₄As₄ [37], by means of μSR, etc. In all these works the pronounced temperature dependence of γ_λ was attributed to the multiple gap nature of superconductivity.

As a further step, γ_λ is compared with the anisotropy of the upper critical field γ_Bc2 for NdFeAsO_1−xF_x, as obtained form resistivity [66, 67] and specific heat measurements [68]. According to the phenomenological Ginzburg-Landau theory, these two anisotropies should be equal for a single gap superconductor [62, 72]:

$\begin{array}{ll}{\gamma }_{\lambda }=\frac{{\lambda }_c}{{\lambda }_{ab}}=\sqrt{\frac{m_c^{*}}{m_{ab}^{*}}}={\gamma }_{B_{\text{c}2}}=\frac{B_{\text{c}2}^{\parallel ab}}{B_{\text{c}2}^{\parallel c}}=\frac{{\xi }_{ab}}{{\xi }_c}.& (15)\end{array}$

Figure 8B implies that the two anisotropies show opposite trends with temperature and violate the Ginzburg-Landau theory. This situation is reminiscent of well-known two-gap superconductor MgB₂, despite the reversed slope for both the anisotropies [73, 74].

5. Conclusions

To conclude, the magnetic and the superconducting properties of NdFeAsO_0.65F_0.35 single crystalline samples were studied by means of muon-spin rotation/relaxation technique. The results can be summarized as follows:

(i) No changes in the relaxation rate was observed in ZF-μSR spectra across the superconducting transition, thus ruling out the possibility of any spontaneous magnetic field below T_c.

(ii) An upturn in exponential muon-spin depolarization rate at T ≲ 3 K is detected in ZF-μSR measurements. It is most probably associated with the onset of ordering of Nd electronic moments.

(iii) Measurements of the magnetic field penetration depth (λ) were performed in the TF geometry. By applying the external magnetic field B_ex parallel to the crystallographic c-axis and parallel to the ab-plane, the temperature dependencies of the in-plane component ${\lambda }_{ab}^{-2}$ and the combination of the in-plane and the out of plane components ${\lambda }_{ab,c}^{-2}$ of the superfluid density were determined, respectively. The out-of-plane component ${\lambda }_c^{-2}$ was further obtained by combining the results of B_ex||c and B_ex||ab set of experiments.

(iv) The temperature dependencies of ${\lambda }_{ab}^{-2}$, ${\lambda }_{ab,c}^{-2}$, and ${\lambda }_c^{-2}$ were analyzed within the framework of a self-consistent two-gap model despite of using the traditional α-model. Interband coupling is taken into account instead of assuming it to be zero as is assumed in the α-model. The values of intraband and interband coupling constants were determined to be: Λ₁₁ ≃ 0.368, Λ₂₂ ≃ 0.315, Λ₁₂ ≃ 0.01. A relatively small value of the interband coupling constant Λ₁₂ indicates that the energy bands in NdFeAsO_0.65F_0.35 are nearly decoupled.

(v) The zero-temperature values of the inverse squared magnetic penetration depth and the superconducting energy gaps were estimated to be: ${\lambda }_{ab}^{-2}(0)\simeq 18.9$ μm⁻², ${\lambda }_c^{-2}(0)\simeq 0.48$ μm⁻², Δ₁(0) ≃ 5.2 meV, and Δ₂(0) ≃ 3.5 meV, respectively.

(vi) The magnetic penetration depth anisotropy, γ_λ = λ_ab/λ_c increases from γ_λ ≃ 1.8 at T = T_c to γ_λ ≃ 6.3 close to T = 0 K, while the upper critical field anisotropy γ_Bc2 demonstrates the opposite temperature behavior. This experimental situation is similar to MgB₂, a well-known two-gap superconductor, which further provides a strong evidence for multiple band superconductivity in the studied NdFeAsO_0.65F_0.35 compound.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

RK conceived the topic, conducted the experiment, analyzed the data, wrote and prepared the manuscript. RG analyzed the data and wrote the manuscript. AM analyzed the data and took part in physics discussions. NZ synthesized the single crystals of NdFeAsO_0.65F_0.35 and took part in physics discussions. HL and AA revised the manuscript. All authors participated in manuscript review.

Funding

The work of RG was supported by the Swiss National Science Foundation (SNF-Grant No. 200021-175935).

Conflict of Interest

NZ becomes an owner and is employed by the company CRYSTMAT.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was performed at Swiss Muon Source (SμS), Paul Scherrer Institute (PSI, Switzerland). RK, AM, and NZ thank Bertram Batlogg for fruitful discussions on the early stage of this study.

References

1. Ren ZA, Yang J, Lu W, Yi W, Che GC, Dong XL, et al. Superconductivity at 52 K in iron based F doped layered quaternary compound Pr[O_1−−xF_x]FeAs. Mater Res Innov. (2008) 12:105–6. doi: 10.1179/143307508X333686

CrossRef Full Text | Google Scholar

2. Yang J, Li ZC, Lu W, Yi W, Shen XL, Ren ZA, et al. Superconductivity at 53.5 K in GdFeAsO_1−δ. Supercond Sci Technol. (2008) 21:082001. doi: 10.1088/0953-2048/21/8/082001

CrossRef Full Text | Google Scholar

3. Ren ZA, Lu W, Yang J, Yi W, Shen XL, Zheng C, et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound Sm[O_1−xF_x]FeAs. Chin Phys Lett. (2008) 25:2215–6. doi: 10.1088/0256-307X/25/6/080

CrossRef Full Text | Google Scholar

4. Chen XH, Wu T, Wu G, Liu RH, Chen H, Fang DF. Superconductivity at 43 K in SmFeAsO_1−xF_x. Nature. (2008) 453:761–2. doi: 10.1038/nature07045

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chen GF, Li Z, Wu D, Li G, Hu WZ, Dong J, et al. Superconductivity at 41 K and its competition with spin-density-wave instability in layered CeO_1−xF_xFeAs. Phys Rev Lett. (2008) 100:247002. doi: 10.1103/PhysRevLett.100.247002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ge JF, Liu ZL, Liu C, Gao CL, Qian D, Xue QK, et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO₃. Nat Mater. (2015) 14:285–9. doi: 10.1038/nmat4153

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Singh DJ, Du MH. Density functional study of LaFeAsO_1−xF_x: a low carrier density superconductor near itinerant magnetism. Phys Rev Lett. (2008) 100:237003. doi: 10.1103/PhysRevLett.100.237003

CrossRef Full Text | Google Scholar

8. Yin ZP, Lebeǵue S, Han MJ, Neal BP, Savrasov SY, Pickett WE. Electron-hole symmetry and magnetic coupling in antiferromagnetic LaFeAsO. Phys Rev Lett. (2008) 101:047001. doi: 10.1103/PhysRevLett.101.047001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Daghero D, Tortello M, Gonnelli RS, Stepanov VA, Zhigadlo ND, Karpinski J. Evidence for two-gap nodeless superconductivity in SmFeAsO_1−xF_x from point-contact Andreev-reflection spectroscopy. Phys Rev B. (2009) 80:060502(R). doi: 10.1103/PhysRevB.80.060502

CrossRef Full Text | Google Scholar

10. Malone L, Fletcher JD, Serafin A, Carrington A, Zhigadlo ND, Bukowski Z, et al. Magnetic penetration depth of single-crystalline SmFeAsO_1−xF_y. Phys Rev B. (2009) 79:140501(R). doi: 10.1103/PhysRevB.79.140501

CrossRef Full Text | Google Scholar

11. Kuzmicheva TE, Kuzmichev SA, Pervakov KS, Pudalov VM, Zhigadlo ND. Evolution of superconducting gaps in Th-substituted Sm_1−xTh_xOFeAs studied by multiple Andreev reflection spectroscopy. Phys Rev B. (2017) 95:094507. doi: 10.1103/PhysRevB.95.094507

CrossRef Full Text | Google Scholar

12. Matano K, Ren ZA, Dong XL, Sun LL, Zhao ZX, Zheng GQ. Spin-singlet superconductivity with multiple gaps in PrFeAsO_0.89F_0.11. Eur Phys Lett. (2008) 83:57001. doi: 10.1209/0295-5075/83/57001

CrossRef Full Text | Google Scholar

13. Kuroki K, Onari S, Arita R, Usui H, Tanaka Y, Kontani H, et al. Unconventional pairing originating from the disconnected fermi surfaces of superconducting LaFeAsO_1−xF_x. Phys Rev Lett. (2008) 101:087004. doi: 10.1103/PhysRevLett.101.087004

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Patrick AL, Xiao-Gang W. Spin-triplet p-wave pairing in a three-orbital model for iron pnictide superconductors. Phys Rev B. (2008) 78:144517. doi: 10.1103/PhysRevB.78.144517

CrossRef Full Text | Google Scholar

15. Evtushinsky DV, Inosov DS, Zabolotnyy VB, Viazovska MS, Khasanov R, Amato A, et al. Momentum-resolved superconducting gap in the bulk of Ba_1−xK_xFe₂As₂ from combined ARPES and μSR measurements. New J Phys. (2009) 11:055069. doi: 10.1088/1367-2630/11/5/055069

CrossRef Full Text | Google Scholar

16. Borisenko SV, Evtushinsky DV, Liu ZH, Morozov I, Kappenberger R, Wurmehl S, et al. Direct observation of spin-orbit coupling in iron-based superconductors. Nat Phys. (2016) 12:311–7. doi: 10.1038/nphys3594

CrossRef Full Text | Google Scholar

17. Charnukha A, Thirupathaiah S, Zabolotnyy VB, Büchner B, Zhigadlo ND, Batlogg B, et al. Interaction-induced singular fermi surface in a high-temperature oxypnictide superconductor. Sci Rep. (2015) 5:10392. doi: 10.1038/srep10392

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Khasanov R, Meier WR, Wu Y, Mou D, Bud'ko SL, Eremin I, et al. In-plane magnetic penetration depth of superconducting CaKFe₄As₄. Phys Rev B. (2018) 97:140503(R). doi: 10.1103/PhysRevB.97.140503

CrossRef Full Text | Google Scholar

19. Tsuei CC, Kirtley JR. Pairing symmetry in cuprate superconductors. Rev Mod Phys. (2000) 72:969–1016. doi: 10.1103/RevModPhys.72.969

CrossRef Full Text | Google Scholar

20. Kondo T, Santander-Syro AF, Copie O, Liu C, Tillman ME, Mun ED, et al. Momentum dependence of the superconducting gap in NdFeAsO_0.9F_0.1 single crystals measured by angle resolved photoemission spectroscopy. Phys Rev Lett. (2008) 101:147003. doi: 10.1103/PhysRevLett.101.147003

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang XL, Dou SX, Ren ZA, Yi W, Li ZC, Zhao ZX, et al. Unconventional superconductivity of NdFeAsO_0.82F_0.18 indicated by the low temperature dependence of the lower critical field H_c1. J Phys Condens Matter. (2009) 21:205701. doi: 10.1088/0953-8984/21/20/205701

CrossRef Full Text | Google Scholar

22. Martin C, Tillman ME, Kim H, Tanatar MA, Kim SK, Kreyssig A, et al. Nonexponential london penetration depth of FeAs-based superconducting RFeAsO_0.9FP_0.1 (R=La, Nd) single crystals. Phys Rev Lett. (2009) 102:247002. doi: 10.1103/PhysRevLett.102.247002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Charnukha A, Evtushinsky DV, Matt CE, Xu N, Shi M, Büchner B, et al. High-temperature superconductivity from fine-tuning of Fermi-surface singularities in iron oxypnictides. Sci Rep. (2015) 5:18273. doi: 10.1038/srep18273

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Samuely P, Szabó P, Pribulová Z, Tillman ME, Bud'ko SL, Canfield PC. Possible two-gap superconductivity in NdFeAsO_0.9F_0.1 probed by point-contact Andreev-reflection spectroscopy. Supercond Sci Technol. (2009) 22:014003. doi: 10.1088/0953-2048/22/1/014003

CrossRef Full Text | Google Scholar

25. Kuzmicheva TE, Kuzmichev SA, Zhigadlo ND. Superconducting order parameter and bosonic mode in hydrogen-substituted NdFeAsO_0.6H_0.36 revealed by multiple-Andreev-reflection spectroscopy. Phys Rev B. (2019) 100:144504. doi: 10.1103/PhysRevB.100.144504

CrossRef Full Text | Google Scholar

26. Miyakawa N, Minematsu M, Kawashima S, Ogata K, Miyazawa K, Kito H, et al. Probing the superconducting gap from tunneling conductance on NdFeAsO_0.7 with T_c = 51 K. J Supercond Nov Mag. (2010) 23:575–8. doi: 10.1007/s10948-010-0689-9

CrossRef Full Text | Google Scholar

27. Adamski A, Krellner C, Abdel-Hafiez M. Signature of multigap nodeless superconductivity in fluorine-doped NdFeAsO. Phys Rev B. (2018) 96:100503(R). doi: 10.1103/PhysRevB.96.100503

CrossRef Full Text | Google Scholar

28. Bouquet F, Wang Y, Fisher RA, Hinks DG, Jorgensen JD, Junod A, et al. Phenomenological two-gap model for the specific heat of MgB₂. Europhys Lett. (2001) 56:856–62. doi: 10.1209/epl/i2001-00598-7

CrossRef Full Text | Google Scholar

29. Carrington A, Manzano F. Magnetic penetration depth of MgB₂. Phys C. (2003) 385:205–14. doi: 10.1016/S0921-4534(02)02319-5

CrossRef Full Text | Google Scholar

30. Guritanu V, Goldacker W, Bouquet F, Wang Y, Lortz R, Goll G, et al. Specific heat of Nb₃Sn: the case for a second energy gap. Phys Rev B. (2004) 70:184526. doi: 10.1103/PhysRevB.70.184526

CrossRef Full Text | Google Scholar

31. Prozorov R, Giannetta RW. Magnetic penetration depth in unconventional superconductors. Supercond Sci Technol. (2006) 19:R41–67. doi: 10.1088/0953-2048/19/8/R01

CrossRef Full Text | Google Scholar

32. Khasanov R, Shengelaya A, Maisuradze A, La Mattina F, Bussmann-Holder A, Keller H, et al. Experimental evidence for two gaps in the high-temperature La_1.83Sr_0.17CuO₄ superconductor. Phys Rev Lett. (2007) 98:057007. doi: 10.1103/PhysRevLett.98.057007

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Khasanov R, Shengelaya A, Karpinski J, Bussmann-Holder A, Keller H, Müller KA. s-Wave symmetry along the c-axis and s+d in-plane superconductivity in bulk YBa₂Cu₄O₈. J Supercond Nov Magn. (2008) 21:81–5. doi: 10.1007/s10948-007-0302-z

CrossRef Full Text | Google Scholar

34. Khasanov R, Evtushinsky DV, Amato A, Klauss HH, Luetkens H, Niedermayer Ch, et al. Two-gap superconductivity in Ba_1−xK_xFe₂As₂: a complementary study of the magnetic penetration depth by Muon-spin rotation and angle-resolved photoemission. Phys Rev Lett. (2009) 102:187005. doi: 10.1103/PhysRevLett.102.187005

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Khasanov R, Maisuradze A, Maeter H, Kwadrin A, Luetkens H, Amato A, et al. Superconductivity and field-induced magnetism in SrFe_1.75Co_0.25As₂. Phys Rev Lett. (2009) 103:067010. doi: 10.1103/PhysRevLett.103.067010

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Khasanov R, Amato A, Biswas PK, Luetkens H, Zhigadlo ND, Batlogg B. SrPt₃P: a two-band single-gap superconductor. Phys Rev B. (2014) 90:140507(R). doi: 10.1103/PhysRevB.90.140507

CrossRef Full Text | Google Scholar

37. Khasanov R, Meier WR, Bud'ko SL, Luetkens H, Canfield PC, Amato A. Anisotropy induced vortex lattice rearrangement in CaKFe₄As₄. Phys Rev B. (2019) 99:140507(R). doi: 10.1103/PhysRevB.99.140507

CrossRef Full Text | Google Scholar

38. Bussmann-Holder A, Micnas R, Bishop AR. Enhancements of the superconducting transition temperature within the two-band model. Eur Phys J B. (2004) 37:345–8. doi: 10.1140/epjb/e2004-00065-5

CrossRef Full Text | Google Scholar

39. Kogan VG, Martin C, Prozorov R. Superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. Phys Rev B. (2009) 80:014507. doi: 10.1103/PhysRevB.80.014507

CrossRef Full Text | Google Scholar

40. Bussmann-Holder A. Comment on: superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. arXiv:0909.3603.

Google Scholar

41. Khasanov R, Bendele M, Amato A, Conder K, Keller H, Klauss HH, et al. Evolution of two-gap behavior of the superconductor FeSe_1−x. Phys Rev Lett. (2010) 104:087004. doi: 10.1103/PhysRevLett.104.087004

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zhigadlo ND, Weyeneth S, Katrych S, Moll PJW, Rogacki K, Bosma S, et al. High-pressure flux growth, structural, and superconducting properties of LnFeAsO (Ln = Pr, Nd, Sm) single crystals. Phys Rev B. (2012) 86:214509. doi: 10.1103/PhysRevB.86.214509

CrossRef Full Text | Google Scholar

43. Schenck A. Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics. Bristol: Hilger (1985).

Google Scholar

44. Cox SFJ. Implanted muon studies in condensed matter science. J Phys C Solid State Phys. (1987) 20:3187–319. doi: 10.1088/0022-3719/20/22/005

CrossRef Full Text | Google Scholar

45. Dalmas de Réotier P, Yaouanc A. Muon spin rotation and relaxation in magnetic materials. J Phys Condens Matter. (1997) 9:9113–66. doi: 10.1088/0953-8984/9/43/002

CrossRef Full Text | Google Scholar

46. Yaouanc A, Dalmas de Réotier P. Muon Spin Rotation, Relaxation and Resonance: Applications to Condensed Matter. Oxford: Oxford University Press (2011).

Google Scholar

47. Blundell SJ. Spin-polarized muons in condensed matter physics. Contemp Phys. (1999) 40:175–92. doi: 10.1080/001075199181521

CrossRef Full Text | Google Scholar

48. Sonier JE, Brewer JH, Kiefl RF. μSR studies of the vortex state in type-II superconductors. Rev Mod Phys. (2000) 72:769–811. doi: 10.1103/RevModPhys.72.769

CrossRef Full Text | Google Scholar

49. Uemura YJ. Muon spin relaxation studies of unconventional superconductors: first-order behavior and comparable spin-charge energy scales. In: Avella A, Mancini F, editors. Strongly Correlated Systems, Springer Series Solid-State Science, Vol. 180. Berlin; Heidelberg: Springer (2015).

Google Scholar

50. Karl R, Burri F, Amato A, Donegà M, Gvasaliya S, Luetkens Hu, et al. Muon spin rotation study of type-I superconductivity: elemental β-Sn. Phys Rev B. (2019) 99:184515. doi: 10.1103/PhysRevB.99.184515

CrossRef Full Text | Google Scholar

51. Available, online at: https://www.dupont.com/electronic-materials/polyimide-films.html (accessed January 22, 2020).

Google Scholar

52. Khasanov R, Zhou H, Amato A, Guguchia Z, Morenzoni E, Dong X, et al. Proximity-induced superconductivity within the insulating (Li_0.84Fe_0.16)OH layers in (Li_0.84Fe_0.16)OHFe_0.98Se. Phys Rev B. (2016) 93:224512. doi: 10.1103/PhysRevB.93.224512

CrossRef Full Text | Google Scholar

53. Suter A, Wojek BM. Musrfit: a free platform-independent framework for μSR data analysis. Phys Proc. (2012) 30:69–73. doi: 10.1016/j.phpro.2012.04.042

CrossRef Full Text | Google Scholar

54. Sonier JE, Kiefl RF, Brewer JH, Bonn DA, Carolan JF, Chow KH, et al. New muon-spin-rotation measurement of the temperature dependence of the magnetic penetration depth in YBa₂Cu₃O_6.95. Phys Rev Lett. (1994) 72:744–7. doi: 10.1103/PhysRevLett.72.744

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Qiu Y, Bao W, Huang Q, Yildirim T, Simmons JM, Green MA, et al. Crystal structure and antiferromagnetic order in NdFeAsO_1−xF_x (x=0.0 and 0.2) superconducting compounds from neutron diffraction measurements. Phys Rev Lett. (2008) 101:257002. doi: 10.1103/PhysRevLett.101.257002

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Brandt EH. Flux distribution and penetration depth measured by muon spin rotation in high-T_c superconductors. Phys Rev B. (1988) 37:2349–52. doi: 10.1103/PhysRevB.37.2349

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Maisuradze A, Khasanov R, Shengelaya A, Keller H. Comparison of different methods for analyzing μSR line shapes in the vortex state of type-II superconductors. J Phys Condens Matter. (2009) 21:075701. doi: 10.1088/0953-8984/21/7/075701

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Yaouanc A, Dalmas de Reotier P, Brandt EH. Effect of the vortex core on the magnetic field in hard superconductors. Phys Rev B. (1997) 55:11107–10. doi: 10.1103/PhysRevB.55.11107

CrossRef Full Text | Google Scholar

59. Clem JR. Simple model for the vortex core in a type II superconductor. J Low Temp Phys. (1975) 18:427–34. doi: 10.1007/BF00116134

CrossRef Full Text | Google Scholar

60. Laulajainen M, Callaghan FD, Kaiser CV, Sonier JE. Muon spin rotation measurements of the vortex state in vanadium: a comparative analysis using iterative and analytical solutions of the Ginzburg-Landau equations. Phys Rev B. (2006) 74:054511. doi: 10.1103/PhysRevB.74.054511

CrossRef Full Text | Google Scholar

61. Sonier JE, Poon KF, Luke GM, Kyriakou P, Miller RI, Liang R, et al. Superconductivity and field-induced magnetism in Pr_2−xCe_xCuO₄ single crystals. Phys Rev Lett. (2003) 91:147002. doi: 10.1103/PhysRevLett.91.147002

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Tinkham M. Introduction to Supercondcutivity. Malabar, FL: Krieger Publishing Company (1975).

Google Scholar

63. Pissas M, Sanakis Y, Psycharis V, Simopoulos A, Devlin E, Ren ZA, et al. A Mössbauer study of the superconducting NdFeAsO_0.82F_0.18 oxypnictide compound. Supercond Sci Technol. (2008) 21:115015. doi: 10.1088/0953-2048/21/11/115015

CrossRef Full Text | Google Scholar

64. Thiemann SL, Radović Z, Kogan VG. Field structure of vortex lattices in uniaxial superconductors. Phys Rev B. (1989) 39:11406–12. doi: 10.1103/PhysRevB.39.11406

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Weyeneth S, Puzniak R, Zhigadlo ND, Katrych S, Bukowski Z, Karpinski J, et al. Evidence for two distinct anisotropies in the oxypnictide superconductors SmFeAsO_0.8F_0.2 and NdFeAsO_0.8F_0.2. J Supercond Nov Magn. (2009) 22:347–51. doi: 10.1007/s10948-009-0445-1

CrossRef Full Text | Google Scholar

66. Jaroszynski J, Hunte F, Balicas L, Jo Y, Raicević I, Gurevich A, et al. Upper critical fields and thermally-activated transport of NdFeAsO_0.7F_0.3 single crystal. Phys Rev B. (2008) 78:174523. doi: 10.1103/PhysRevB.78.174523

CrossRef Full Text | Google Scholar

67. Jia Y, Cheng P, Fang L, Luo H, Yang H, Ren C, et al. Critical fields and anisotropy of NdFeAsO_0.82F_0.18 single crystals. Appl Phys Lett. (2008) 93:032503. doi: 10.1063/1.2963361

CrossRef Full Text | Google Scholar

68. Pribulova Z, Klein T, Kacmarcik J, Marcenat C, Konczykowski M, Bud'ko SL, et al. Upper and lower critical magnetic fields of superconducting NdFeAsO_1−xF_x single crystals studied by Hall-probe magnetization and specific heat. Phys Rev B. (2009) 79:020508(R). doi: 10.1103/PhysRevB.79.020508

CrossRef Full Text | Google Scholar

69. Weyeneth S, Puzniak R, Mosele U, Zhigadlo ND, Katrych S, Bukowski Z, et al. Anisotropy of superconducting single crystal SmFeAsO_0.8F_0.2 studied by torque magnetometry. J Supercond Nov Magn. (2009) 22:325-9. doi: 10.1007/s10948-008-0413-1

CrossRef Full Text | Google Scholar

70. Prozorov R, Tanatar MA, Gordon RT, Martin C, Kim H, Kogan VG, et al. Anisotropic London penetration depth and superfluid density in single crystals of iron-based pnictide superconductors. Phys C. (2009) 469:582–9. doi: 10.1016/j.physc.2009.03.012

CrossRef Full Text | Google Scholar

71. Bendele M, Weyeneth S, Puzniak R, Maisuradze A, Pomjakushina E, Conder K, et al. Anisotropic superconducting properties of single-crystalline FeSe_0.5Te_0.5. Phys Rev B. (2010) 81:224520. doi: 10.1103/PhysRevB.81.224520

CrossRef Full Text | Google Scholar

72. Kogan VG. London approach to anisotropic type-II superconductors. Phys Rev B. (1981) 24:1572–5. doi: 10.1103/PhysRevB.24.1572

CrossRef Full Text | Google Scholar

73. Angst M, Puzniak R, Wisniewski A, Jun J, Kazakov SM, Karpinski J, et al. Temperature and field dependence of the anisotropy of MgB₂. Phys Rev Lett. (2002) 88:167004. doi: 10.1103/PhysRevLett.88.167004

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Fletcher JD, Carrington A, Taylor OJ, Kazakov SM, Karpinski J. Temperature-dependent anisotropy of the penetration depth and coherence length of MgB₂. Phys Rev Lett. (2005) 95:097005. doi: 10.1103/PhysRevLett.95.097005

PubMed Abstract | CrossRef Full Text | Google Scholar