
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys., 17 January 2020
Sec. Soft Matter Physics
Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00246
This article is part of the Research TopicNon-local Modeling and Diverging Lengthscales in Structured FluidsView all 6 articles
Many fluids undergo shear banding, in which two states of different apparent viscosity coexist for a given shear rate (or for a given stress). In the idealized case of an infinite gap between shearing plates the selection of the conditions for shear banding has been shown to depend on the spatial structure and shape of the interface between shear bands. With the advent of microfluidic design for processing and additive manufacturing, the processing of many complex fluids often occurs in situations where this idealized limit doesn't apply, and the gap between walls, in either shearing flow or more often for pressure driven flow, is no longer “infinite” compared to the structural scales. It is increasingly clear that the effective rheology and structure of flowing fluids in these conditions requires information about the entire sample size, i.e., that the rheology is intrinsically non-local. In this review we discuss some recent attempts (both theoretical and experimental) to address non-local rheology and its implications for shear-banding flows of polymeric fluids. This manifests itself in rheology extracted from velocity profiles, as well as the dependence of shear-banding conditions on the position of the interface between shear bands, as well as the system size.
Shear banding occurs when a fluid can support two different states of apparent viscosity for either the same shear rate (different local stresses) or the same shear stress (different local strain rates). It is expected when the relation between shear stress σ and shear rate [called the constitutive curve ] is non-monotonic. Shear banding, either steady or transient, is now well-established in many soft materials [1], including surfactant solutions (wormlike micelles [2], lamellar phases [3], associating polymers [4]), potentially in polymer solutions and melts [5, 6]; yield stress fluids, such as emulsions [7], colloidal suspensions [8], microgels [9], and star polymer solutions [10]; and liquid crystalline solutions [11, 12]. Banding is often initiated by an instability, but can also appear as if it is a “nucleated” event, in which, for example, a lower viscosity state appears somewhere in the system under certain conditions of either imposed global stress or average shear rate. Shear banding results in heterogenous flows (Figure 1), with the spatial organization determined by the nature of the multi-valued relation between shear stress and shear rate. In the most common situation two different shear rates coexist for a given stress, which corresponds to gradient banding, in which shear bands are organized along the flow gradient direction, with the interface between the bands lying in the velocity-vorticity plane. In parallel sliding plates this corresponds to bands parallel to the plates, while in cylindrical Couette flow the bands are arranged in concentric cylinders. In vorticity banding the bands are arranged in the vorticity direction such that the shear rate is the same in each band while the shear stress differs. In polymeric fluids, such as polymer solutions and melts, and surfactant solutions that self-assemble into long thread-like wormlike micelles, the shear banding is usually driven by the lower viscosity that results when the polymers are aligned more parallel to each other in flow. This is thought to be accompanied by a reduction in the degree of entanglement among the polymers (wormlike micelles have the additional complication that they can break and reform rapidly [16]). Breakage leads to a simpler relaxation spectrum than that of polymers in the fast-breaking limit, since all lengths of micelles relax together; but the effect of breakage on entanglement is unknown.
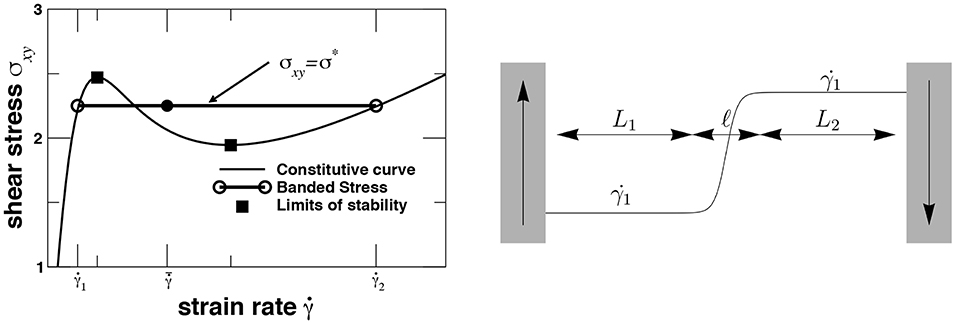
Figure 1. (Left) Constitutive curve showing shear-banding construction. For an imposed average shear rate satisfying shear rates and coexist at a selected shear stress σ*. The plateau stress σ* is measured for controlled average rates in the coexistence regime, while for controlled stress the lower shear rate branch is measured for σxy < σ*, and the upper shear rate branch measured for σxy > σ*. The square points mark shear rates between which the fluid is predicted to be absolutely unstable; at other shear rates it is either stable or metastable [13–15]. (Right) Configuration showing a shear-banding profile of the local shear rate, with an interface width ℓ and shear bands of sizes L1 and L2. The interfacial profile satisfies a version of Equation (9).
There are clear similarities between shear banding and equilibrium phase transitions, such as liquid-vapor coexistence. The non-monotonic constitutive curve is analogous to the non-monotonic pressure-density relation p(ρ) of an equilibrium liquid-vapor isotherm. The conditions of liquid-vapor equilibrium are equality of chemical potential (Gibbs free energy per particle) and pressure. For shear banding the shear stresses must balance, which is analogous to the pressure; but because the system is dissipative one cannot use equality of chemical potentials to determine which shear stress is “selected” as the coexisting stress. Instead, one can solve the steady-state inhomogeneous dynamics to find coexistence and determine stress selection, which is analogous to finding the shape and width of the liquid-vapor interface [17, 18]. Correspondingly, the steady-state shear-banding configuration contains three length scales: the sizes L1 and L2 of the two bands1 and the width ℓ of the interface between bands. In a very large system the width ℓ can be ignored compared to the distance L≫ℓ between the shearing surfaces, and the relative size of the two shear bands is determined to satisfy the applied average shear rate, such that (see Figure 1)
where the two bands have shear rates and . The width ℓ of the interface between bands is usually microns in size, which is negligible compared to the sizes of most processing devices (millimeters or centimeters).
This simple picture, which will be described below, has several complications and challenges. The value of ℓ is predicted to be determined by a constitutive parameter (or parameters) that is independent of the conditions of flow; typically in the form of a coefficient that governs the contributions of spatial gradients to the total shear stress and to the dynamics of microstructural order. A reliable theory for this parameter is lacking, despite much work in the area. Many modern processing methods based on microfluidic technologies use very small geometries to transport, mix, and deliver soft materials, with length scales ranging from microns to millimeters, and in some cases sub-micron in scale. Experiments on small gaps show that it is difficult to consistently model and describe the both small scale and larger scale rheologies [19, 20]. The simple shear-banding model predicts that the interfacial width ℓ is independent of the applied average shear rate . However, experiments show that this is not correct [21], as will be explained below.
In this brief review we focus on polymeric fluids, i.e., polymer and surfactant solutions. We outline some of the main phenomenology of non-local terms in models for shear-banding polymeric fluids, and discuss some of the implications for experiments, as well as challenges posed by recent experiments.
To physically model shear banding the stress tensor must incorporate stresses due to microstructural quantities, such as molecular or segmental orientation, micellar length, concentration fields in polymeric fluids. Other fluids could include degrees of association, fraction of frictional or non-frictional contacts in suspensions, structural (such as local icosahedral ordering) or crystalline order parameters, and many others. The principal guiding rules are to (1) include all non-negligible contributions to the total stress, and (2) incorporate variables that relax slowly compared to typical thermal or flow-induced noise (“slow” can unfortunately be used subjectively!). In polymeric fluids the total stress σ is often written in terms of a molecular configurational tensor W, or equivalently a polymeric stress tensor Σ, where
Here G is a characteristic modulus, I denotes the identity matrix, η is a Newtonian viscosity, is the symmetric velocity gradient tensor, and p is the isotropic pressure determined by incompressibility (∇·v = 0). The configurational tensor can be defined in a number of ways; as W = 〈rr〉 of the second moment of the normalized molecular end-to-end vector r = R/|R0|, where R0 is the equilibrium RMS end to end vector; as the right Cauchy-Green deformation tensor acting on the polymeric degrees of freedom [22]; or the average tangent-tangent correlation function along the chain , where Lc is the contour length. In most cases of interest we assume creeping flow, corresponding to small Reynolds numbers, for which
This condition holds for most, but not all, conditions under which shear banding is seen. The microstructure dynamics determines the non-monotonic behavior of the fluid; a finite strain rate induces molecular alignment, which in turn reduces the shear stress σ ≡ σxy below the Newtonian limit . For rapid shear rates the increasing alignment actually leads to a stress maximum, beyond a strain rate corresponding to the molecular relaxation time. For greater shear rates progressively fewer chains carry stress through a plane with normal vector in the flow gradient direction [23], and thus the shear stress is predicted to decrease [23, 24].
Numerous dynamical models have been proposed for W or equivalently Σ. They have the form
where denotes a covariant derivative that compares the time dependence of the tensor Σ to the manner in which the microstructure is expected to rotate in the least dissipative manner in a flow field parameterized by the velocity gradient tensor καβ = ∇βvα. Several models are collected in Table 1. The models shown do not accommodate concentration changes (so-called “two-fluid” models), and have been used to varying degrees of success in modeling banding behavior in wormlike micelles or polymer solutions. None of the models is an excellent fit to experimental data, so in the absence of better microscopically-derived models that are tractable for modeling inhomogeneous flows, the choice of model depends on the details of the calculations necessary, and the features required.

Table 1. Constitutive models that exhibit shear banding for polymeric fluids with no concentration variations from Olmsted et al. [15] [a], Giesekus [25] [b], Likhtman and Graham [26] [c], Yuan et al. [27] and Dhont [28] [d].
The “diffusion constant” is usually written to indicate that the stress variable Σ can “diffuse,” or more precisely, that spatial gradients in Σ relax. Hence, the diffusion term is actually a product of a mobility and a local free energy cost, and thus in this form has dimensions . Hence, the product is the square of a length, and we define
as the characteristic lengthscale corresponding to stress “diffusion.” In most cases this is also of order the length scale of the interface between shear bands [15, 33]. In practice the experiments described below extract from an experimental method in conjunction with a model, and then use the measured (longest) relaxation time τ of the fluid in equilibrium to estimate ℓ.
The Johnson-Segalman (JS, or d-JS with the diffusive term) model is a very simple model that exhibits a non-monotonic flow curve due to the slip parameter a, which parameterizes the degree to which polymers “slip” relative to the local flow field [34]. It has been used by many authors to model shear banding [15, 35]. The non-linear Giesekus (or d-Giesekus) model is another phenomenological model that can exhibit banding, due to a second-order non-linearity in the polymer stress Σ. The microscopically-inspired Rolie-Poly [26] model approximates the more detailed microscopic GLaMM model [36–38], which incorporates reptation, convected constraint release, retraction, and contour length fluctuations of entangled non-breakable polymers. By controlling the parameters one can tune continuously between shear-banding and non-shear banding fluids in the Rolie-Poly model [39].
In all cases an ad hoc “diffusive” term with coefficient has been added to the constitutive models in order to model the strongly inhomogeneous flow associated with shear banding [15]. The need for such a term to obtain physically and mathematically sensible models in polymeric solutions was recognized by El-Kareh and Leal [40], who demonstrated that diffusing polymers can carry a non-local stress. One simple motivation for such a term is the small, but non-zero, contribution from Frank elastic effects familiar from liquid crystals [1, 41]. Frank elasticity accounts for the free energy increase due to the average molecular orientation becoming inhomogeneous. Liquid crystalline polymers exhibit such free energies, with distortion energy controlled by the persistence length of the polymers. Nematic liquid crystals themselves are also predicted to exhibit shear banding between the higher viscosity isotropic phase and the lower viscosity nematic phase [17, 42–45]; in this case non-local contributions to the total stress and segment orientation dynamics arise naturally from Frank elasticity and lead to stress selection. Note that experimental liquid crystalline systems of rod-like molecules are often in the tumbling regime [11], so that the nematic state is often time-dependent and banding is not so clear. Pujolle-Robic and Noirez [46] presented experimental for shear banding in a side-chain liquid crystalline polymer system. The non-zero contribution of nematic effects to the segment orientation dynamics of polymers appears as non-local terms in the dynamics for the segment orientation tensor Q as well as in the total stress tensor. If the orientation dynamics are fast then the fluctuations can be integrated out at the level of the free energy [47, 48], which leads to non-local terms in the free energy penalizing W (or equivalently Σ). This will generate a diffusive term in the dynamics for W (or Σ) that, in a melt, scales as [41]
where ℓp is the persistence length of the polymer (of order 0.5 nm for synthetic polymers, 15–20 nm for wormlike micelles, and 25 nm for single-stranded DNA); one expects to acquire a concentration dependence for solutions. Note that the corresponding length scale for this contribution scales as , which is much smaller than the micron length scale estimated experimentally.
The non-local terms in the total stress arising from Frank-elastic effects are analogous to the Korteweg stresses suggested by Renardy [49] as a mechanism for stress selection. Korteweg stresses arise from an expansion of the free energy in gradients of W, where the expansion coefficients can, most generally, be functions of W. This leads to additional terms in the total stress tensor σ that are non-linear in W and its gradients:
where F is a free energy functional and the fourth rank tensors Ξ and Ψ depend on the formulation of the model.
Non-locality can also arise from long-range hydrodynamic coupling between polymer segments [18, 28]. Jin et al. [50] demonstrated that this non-locality enters as a so-called curvature viscosity κ, in addition to the usual viscosity, and has the form −2κ∇2D/τ in the dynamics for the polymeric contribution to the stress (Equation [d], Table 1). In steady state this gives a contribution to the total stress of the form −2κ∇2D, as proposed by [28]. Jin et al. [50] estimated this term as
where ηs is the solvent viscosity, am is a molecular size and is a numerical pre-factor. In this case the interfacial width is given by .
The d-JS model has been coupled to concentration degrees of freedom in several different guises [29, 30, 51–55], as has the Rolie-Poly model [32]. These models have non-local effects due to coupling of stress gradients to solvent or polymers concentrations [56].
There have been no simulations that we are aware of that study the interface between shear bands in polymeric or micellar fluids. Germano and Schmid [57] studied shear banding in nematic liquid crystals using molecular dynamics simulations of ellipsoidal particles, where the equilibrium interface width is set by Frank elasticity and is fairly well-understood. Micellar systems are still too complex to simulate large enough systems that can shear band; Mohagheghi and Khomami [58] observed transient shear banding in dissipative particle dynamics simulations of bead-spring polymers, but did not study the apparent diffusive or interfacial effects.
Non-locality in the form of a diffusive term in the microstructure dynamics can successfully model shear-banding behavior. The steady-state shear-banding configuration becomes a spatial differential equation that describes the shear-banding profile, for given imposed conditions, of the form [1, 15]
where σ is the uniform total shear stress that satisfies ∇·σ = 0. In the second equation the time derivative has been removed from the covariant derivative to lead to a steady-state condition (see Table 1). To solve this differential equation one requires boundary conditions. Many authors have assumed a so-called “zero flux” condition , where denotes the surface normal [15, 29]. There is no specific justification for such a boundary condition, since there is no specific conservation law on a “stress flux” governed solely by the polymer; the diffusive contribution derived by El-Kareh and Leal [40] is an exception to this.
In the limit of an infinite system undergoing shear flow between parallel plates the specific boundary conditions do not play an important role, and one finds that a shear-banding state is selected at a unique value of the total shear stress in the non-monotonic region of the constitutive curve [15, 18]. For other values of the stress the interface propagates until all of the fluid has been converted to either the high or low viscosity state. The interface has a width , and the infinite system limit corresponds to L ≫ ℓ. For imposed average shear rates in the non-monotonic part of shear bands will develop to satisfy Equation (1), and select the stress σ*. One then finds a stress plateau that extends from the low shear rate to high shear rate branch between coexisting shear rates and . For non-uniform stresses, which occurs for virtually all practical geometries (cylindrical Couette flow, cone and plate flow, pressure driven flows) the interface will migrate to the position within the cell at which the local total shear stress [15, 33]. In rheology experiments this leads to a measured average shear stress that has a slope, rather than a flat plateau, with a slope increasing with the stress gradient imposed by the flow geometry. This feature has been verified in cylindrical Couette flow [59, e.g.,]. In practice band formation develops via an instability or nucleation of an inhomogeneous shear rate profile [14, 28, 30, 60], which then develops into two (or sometimes more) shear bands, followed by migration of the shear band to the position in the shear cell at which the stress is equal to the selected stress [61].
For imposed average shear rates close to either or one of the shear bands will be very small; when the shear band size is of order the interfacial width ℓ, the shear band ceases to be well-defined, and the polymer stress will vary more or less smoothly from the edge of the wider shear band to the wall. This is predicted to give departures from the stress plateau at its extremities, by typically increasing (low shear branch) or decreasing (high shear rate branch) the stress σxy relative to σ* [15]. For small systems L ≳ ℓ the stress should depart more readily from σ*, and eventually one expects to suppress banding completely for ℓ > L.
There have been limited attempts to generalize the no-flux boundary condition . Adams et al. [41] introduced a generalized boundary condition inspired by the anchoring condition in liquid crystals,
The first term is a surface partner to the bulk diffusive term, and represents the surface contribution to the molecular torques that control the dynamics of the microstructure. The second term represents surface-specific interactions, controlled by an anchoring energy ωa and a preferred surface value for the stress Σ0. For polymer liquid crystals or charged polymers the wall chemistry will influence the preferred conformational state at the wall. For uncharged flexible polymers [62] showed that steric exclusion should lead to an oblate polymer conformation at the wall.
The limit of weak anchoring ωa → 0 reduces to the traditional no-flux boundary condition, while the wall will typically enforce surface stress with the symmetry of the wall (such as an oblate polymer conformation near the surface). Depending on the strength and direction of alignment one or the other of the shear bands (which have different directions and degrees of alignment) will be preferred near the walls. A preferred wall alignment (or misalignment) can also reduce (or increase) the degree of hysteresis found during increasing shear rate ramps, since the material near an aligning wall is closer in character to the high shear rate band [41]. Rossi et al. [54] studied the effects of similar boundary conditions on a two-fluid version of the d-JS model, and found standard shear banding with hysteresis at either side of the stress plateau for zero imposed gradient (ωa → 0); and hysteretic behavior at the high shear rate side of the stress plateau (where the molecules are also better aligned in bulk) when the walls specify alignment, analogous to ωa → ∞.
An outstanding experimental challenge is to impose different known boundary conditions on the polymer or micelle degrees of freedom, and measure the resulting effects on shear banding. These wall effects are expected to be more important in confined geometries, where the “anchoring length” competes with the interfacial width ℓ.
Experimental attempts to determine orders of magnitude of non-local terms in polymeric fluids have exclusively focused on shear-banding (semi-dilute and concentrated) wormlike micelles. The characteristic length scale ℓ has been estimated in both in macro- and micro-flows using various experimental techniques, either global (rheology) or local (velocimetry, optical visualizations), as summarized in Table 2. Essentially two types of experimental approaches have been used. The first one is based on the fact that the diffusive term, even vanishingly small is expected to control the stage of slow migration of the interface between bands toward its final stationary position [33]. The second one is based on direct comparison of the flow profiles (i.e., the velocity field) with predictions of non-monotonic constitutive models including spatial gradient terms (see Table 1).
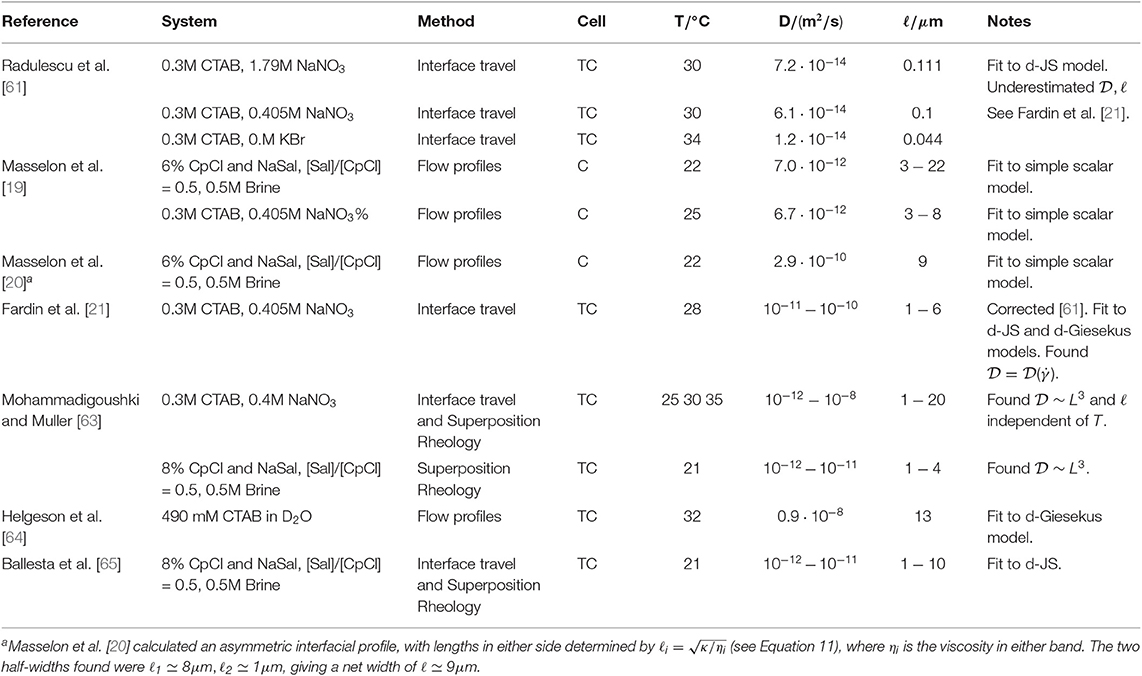
Table 2. Summary of measurements of the interface length ℓ, based on different techniques in channels flow (C) or Taylor Couette flow (TC) with a gap size L.
In shear-banding wormlike micelles, the shear stress response following a step shear rate exhibits transient features that are intimately related to the dynamics of the interface between bands (Figure 2). Successive relaxation regimes over well-separated time scales are commonly observed [66]. The last regime, which precedes steady state, is expected to be related to the migration of the interface that separates the shear bands. It is predicted to be the slowest relaxation and to be controlled by stress diffusive terms [61]. It starts when the interface between stable bands forms at a position corresponding to a stress value above or below the plateau stress and adopts a fully sharp profile. As the shear stress σ is different from the plateau value σ*, the front between bands has a non-zero velocity and propagates over a short distance to reach its final equilibrium position (σ = σ*) where its velocity becomes equal to zero. For a general non-local and non-monotonic constitutive equation of the reaction-diffusion type [67] the interface position during this stage was shown to follow, at first order, a single exponential evolution as a function of time. The characteristic time scale (or equivalently the characteristic velocity) associated with this slow migration process was found to depend on the flow geometry, the stress diffusion coefficient , and the local constitutive model. Hence, from the knowledge of the migration time scale (or the front velocity) and within the framework of a given constitutive model, the diffusion coefficient and the corresponding length scale ℓ can be computed. In practice, the effect of non-local terms on the transient evolution toward the steady shear-banded state has been mostly investigated in the framework of the d-JS model [61]. Predictions with the d-Giesekus model have also been tested [21] and a similar approach has been recently developed in the framework of the VCM model [68].
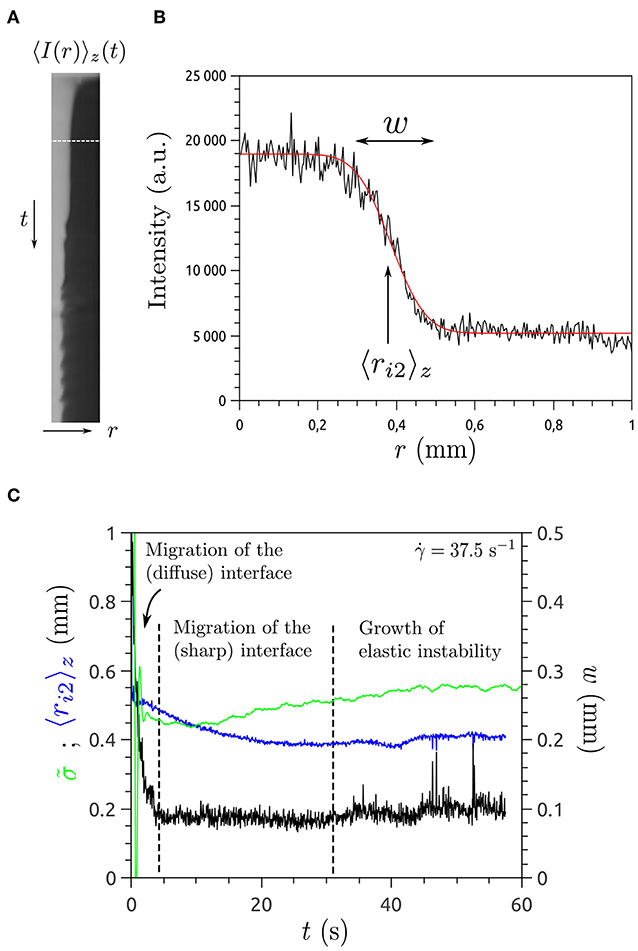
Figure 2. Sketch of measurement of interface properties during stress relaxation after strain rate step from a sample initially at rest. (A) Space-time plot showing shear band migration after a step, where the white band signifies turbidity in light transmission. (B) Spatial profile across shear band along the white line in (A) showing a well-formed interface. (C) Stress relaxation showing the region where a well-formed band migrates, from which the diffusion constant was inferred by fitting the relaxation to the predictions of the d-JS model. Here 〈ri2〉z is the position of the interface between band, w is its apparent width, and is the dimensionless shear stress. Adapted with permissions from Fardin et al. [21], copyright by American Institute of Physics.
Different experimental strategies have been implemented to access the slow interface migration process, namely transient rheology [61], direct visualizations [21, 63], ultrasonic velocimetry [65], and superposition rheology [63, 65], all performed on semi-dilute wormlike micelles sheared in a Taylor-Couette (TC) device. In all of these cases the diffusion coefficient was computed in the framework of the d-JS model.
The first estimate of the magnitude of non-local terms in shear-banding wormlike micelles was inferred from the transient stress response following a step shear rate between two banded states [61]: from the characteristic time scale of the longest stage preceding steady state, a stress diffusion coefficient was computed, leading to diffusion length scale or interface width ℓ around tens of nanometers, i.e., compatible with the mesh size of the micellar network. However, more recent experiments showed that the last and slowest regime preceding steady state in the transient stress relaxation of shear-banding wormlike micelles is not related to interface migration but to the subsequent development of an elastic instability [69], which is ubiquitous in these systems [2, 70]. The migration stage of interest occurs before the elastic instability and spreads over a shorter time scale. Consequently, the order of magnitude of the non-local terms established in the pioneering study by [61] was greatly underestimated. The original study was recently revisited using optical visualization of the interface between bands [21, 63]. By tracking the interface position as a function of time, the relevant migration stage has been identified. The corresponding time scale led to stress a diffusion coefficient in the range and corresponding diffusive lengths (or interface widths) ℓ≃1-20μm (see Table 2).
Mohammadigoushki and Muller [63] found that the stress diffusion coefficient increases linearly with increasing temperature, leading to a corresponding length scale ℓ independent of T. They also found a monotonic increase of with the gap size L as , for a given fixed curvature ratio (inner to outer radii), thus ensuring the same percentage stress drop across the gap [63]. This dependence cannot be understood from current theory. Finally, Fardin et al. [21] found a dependence of the migration time scale on the applied shear rate, also suggesting that a given micellar system is not characterized by a single value of . Assuming that the relaxation time of the system does not vary with , ℓ was thus found to decrease with increasing . Note that such a dependence on the shear rate was not observed by Mohammadigoushki and Muller [63]. This discrepancy may arise from insufficient spatial resolution in the experiments performed by Mohammadigoushki and Muller [63], a drawback that also limited the data from Fardin and Lerouge [71].
Non-local terms were also probed using parallel superposition rheology, which consists in adding a small-amplitude oscillatory shear parallel to a main steady shear [63, 65]. In that case, the stress diffusion coefficient was inferred from the velocity of the interface during the migration stage, by comparing with the d-JS model. The interface velocity was deduced from fitting the imaginary part of the complex viscosity within the framework of a two-fluid phenomenological model [65] combined with the reaction-diffusion model proposed by Radulescu et al. [67]. This method of determination of the interface velocity has been validated using ultrasonic velocimetry where the interface position was deduced from tracking the crossover between the two shear bands in the velocity profiles [65]. Stress diffusion coefficients and diffusive length were found in the range and ℓ≃1-10μm, respectively.
The diffusive terms have also been estimated through direct comparison between measured velocity profiles in the banding regime and predictions of non-local models. Helgeson et al. [64] measured the velocity profile using particle image velocimetry (PIV) at a given applied shear rate in Taylor-Couette geometry, and fitted to the non-homogeneous form of the d-Giesekus model with the stress diffusion coefficient as the only adjustable parameter. From the value of , a stress diffusion length ℓ≃13μm was inferred. Recently, a model-free experimental procedure was developed to distinguish shear banding from strong shear thinning using high-resolution PIV [72]. An appropriate statistical method was used to smooth the steady-state experimental velocity profiles and calculate their local numerical derivatives. This procedure was tested on semi-dilute wormlike micelles systems. From the third derivative of a shear-banding velocity profile, an effective thickness of the transition zone between bands, which can be interpreted as an upper bound for the interface width, has been inferred. A stress diffusion coefficient giving ℓ≃20μm was then deduced in the framework of the d-Giesekus model.
Another attempt to determine the order of magnitude of spatial gradient terms came from confined microfluidic flows in straight channel. Pressure-driven flows in channels have a linear shear stress gradient σxy = σwr/R, where σw is the wall stress and R is the half-width of the channel (or radius of a cylindrical channel)2. A shear-banded state would typically have a thin and fast flowing band near the wall, and plug-like flow in the middle where the stress is much smaller. Hence the stress drop across the interface between shear bands is δσxy≃ ℓσw/R. For small channels one expects a significant stress difference across the interface, so banding is expected to be influenced [33].
Experiments by Masselon et al. [19, 20] using μ-PIV in straight rectangular microchannels measured the local velocity of a shear-banding fluid across the channel, and by correlating this with the known wall stress (obtained from the driving pressure) they could reconstruct the local stress σloc(y) as a function of shear rate through the channel, as well as the velocity profile. should follow the flow curve (including the stress plateau) measured by bulk rheology. Masselon et al. [19] showed that for small channels (R ~ 60-100μm) this procedure doesn't work; the bulk and local flow curves deviated significantly. Some of this can be attributed to wall slip, and some is not well-accounted for by existing models. A simple model was devised to address this, based on a scalar version of Dhont's curvature stress:
where κ is the curvature-stress coefficient of Dhont (see Table 1). To fit this model to the measured velocity profiles a constitutive model was used based on bulk rheology, and a specific boundary condition was applied, where the experimentally determined velocity gradient at the wall was used. This allowed for an estimate of κ, as well as a successful fit to the measured local rheology and the velocity profile. From a large set of data obtained by systematically changing the imposed pressure drop, the level of confinement, and the boundary conditions for different semi-dilute shear-banding wormlike micelles, the correlation length was found to vary along the stress plateau from ℓ ≃ 1-20μm [19, 20]. Note that this work has some unsatisfactory points: wall slip was put in “by hand” rather than emerging from a detailed stress balance at the wall, and a scalar theory was used, rather than also incorporating normal stresses.
Several experimental methods used in combination with ad-hoc constitutive models have estimated the magnitude of non-local terms in shear-banding wormlike micelles, to thus determine an interfacial length ℓ of order a few microns, which is larger than the typical mesh size of the micellar network, and thus consistent with the models that depend on coarse-grained field, such as the average polymer conformation or stress. However, many challenges remain:
1. The diffusive length ℓ is not related in an obvious way to mesoscopic length scales of the quiescent samples. Systems of various compositions have been tested, mostly semi-dilute systems, at various concentrations (ranging between 6 and 11% wt). Whatever the experimental technique and the theoretical framework used, the emerging length scale is still around 1–20 microns. In all the systems investigated, the high shear rate band appears slightly turbid, suggesting micron scale concentration fluctuations. Such fluctuations might explain the order of magnitude of ℓ but more systematic studies are required to fully understand the connection between ℓ and the microstructure of the micellar systems.
2. In some cases (e.g., Fardin et al. [21]) the observed length scale ℓ does not seem to have a unique value but depends on the average imposed shear rates or the width of the shear band. This behavior is not captured by phenomenological models like the d-JS or d-Giesekus models, but conceivably could be taken into account by more complex fluidity models where the relaxation time has more complex dynamics [73]; or with non-linear diffusive terms in which is replace by a function .
3. No theory simultaneously treats boundary conditions on the polymeric degrees of freedom, shear banding, and wall slip consistently, despite progress on separate aspects of these issues. An ideal scenario would be to combine molecular theories of polymers slip [74, 75] with shear-banding calculations in which the wall boundary condition has been generalized to include the effects of the wall on polymer conformation tensor [41].
4. It would be very useful to have an experimental method for measuring the actual boundary conditions of the structural tensor at the wall (e.g., using Raman scattering, evanescent wave methods, or other techniques).
In this review we have limited ourselves to diffusion lengths extracted from non-local effects in wormlike micellar systems; non-local rheology has been shown to be important in other systems, notably dense yielding materials, such as emulsions and pastes [7]. We have not attempted to review these together, although there are certainly many parallels between the different classes of systems.
SL and PO conceived and wrote the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
PO was grateful to Georgetown University and the Ives Foundation for financial support. SL acknowledges funding from Institut Universitaire de France.
1. ^In practice many shear bands can form with shear rates , but in most situations these will coarsen to leave only two bands. This is usually driven by small stress gradients in rotational rheometers; for example, Taylor Couette and cone-and-plate geometries both have gradients in stress at steady state.
2. ^x and y refer to as the flow and flow gradient directions, respectively.
1. Olmsted PD. Perspectives on shear banding in complex fluids. Rheol Acta. (2008) 47:283–300. doi: 10.1007/s00397-008-0260-9
2. Divoux T, Fardin MA, Manneville S, Lerouge S. Shear banding of complex fluids. Ann Rev Fluid Mech. (2016) 48:81–103. doi: 10.1146/annurev-fluid-122414-034416
3. Diat O, Roux D, Nallet FN. Effect of shear on a lyotropic lamellar phase. J Phys B Atom Mol Phys. (1993) 3:1427–52. doi: 10.1051/jp2:1993211
4. Berret JF, Séréro Y, Winkelman B, Calvet D, Collet A, Viguier M. Nonlinear rheology of telechelic polymer networks. J Rheol. (2001) 45:477–92. doi: 10.1122/1.1339245
5. Tapadia P, Ravindranath S, Wang SQ. Banding in entangled polymer fluids under oscillatory shearing. Phys Rev Lett. (2006) 96:196001. doi: 10.1103/PhysRevLett.96.196001
6. Hu YT. Steady-state shear banding in entangled polymers? J Rheol. (2010) 54:1307–23. doi: 10.1122/1.3494134
7. Goyon J, Colin A, Ovarlez G, Ajdari A, Bocquet L. Spatial cooperativity in soft glassy flows. Nature. (2008) 454:84–7. doi: 10.1038/nature07026
8. Besseling R, Isa L, Ballesta P, Petekidis G, Cates ME, Poon WCK. Shear banding and flow-concentration coupling in colloidal glasses. Phys Rev Lett. (2010) 105:268301. doi: 10.1103/PhysRevLett.105.268301
9. Divoux T, Tamarii D, Barentin C, Manneville S. Transient shear banding in a simple yield stress fluid. Phys Rev Lett. (2010) 104:208301. doi: 10.1103/PhysRevLett.104.208301
10. Rogers SA, Vlassopoulos D, Callaghan PT. Aging, yielding, and shear banding in soft colloidal glasses. Phys Rev Lett. (2008) 100:128304. doi: 10.1103/PhysRevLett.100.128304
11. Dhont JKG, Lettinga MP, Dogic Z, Lenstra TAJ, Wang H, Rathgeber S, et al. Shear-banding and microstructure of colloids in shear flow. Faraday Discuss. (2003) 123:157–72. doi: 10.1039/b205039k
12. Kang K, Lettinga MP, Dogic Z, Dhont JKG. Vorticity banding in rodlike virus suspensions. Phys Rev E. (2006) 74:26307. doi: 10.1103/PhysRevE.74.026307
13. Grand C, Arrault J, Cates ME. Slow transients and metastability in wormlike micelle rheology. J Phys B Atom Mol Phys. (1997) 7:1071–86. doi: 10.1051/jp2:1997172
14. Berret JF. Transient rheology of wormlike micelles. Langmuir. (1997) 13:2227–34. doi: 10.1021/la961078p
15. Olmsted PD, Radulescu O, Lu CYD. Johnson–Segalman model with a diffusion term in cylindrical Couette flow. J Rheol. (2000) 44:257–75. doi: 10.1122/1.551085
16. Cates ME, Candau SJ. Statics and dynamics of worm-like surfactant micelles. J Phys Cond Mat. (1990) 2:6869–92.
17. Olmsted PD, Goldbart PM. Isotropic-nematic transition in shear flow: state selection, coexistence, phase transitions, and critical behavior. Phys Rev A. (1992) 46:4966–93. doi: 10.1103/PhysRevA.46.4966
18. Lu CYD, Olmsted PD, Ball RC. Effects of nonlocal stress on the determination of shear banding flow. Phys Rev Lett. (2000) 84:642–5. doi: 10.1103/PhysRevLett.84.642
19. Masselon C, Salmon JB, Colin A. Nonlocal effects in flows of wormlike micellar solutions. Phys Rev Lett. (2008) 100:038301. doi: 10.1103/PhysRevLett.100.038301
20. Masselon C, Colin A, Olmsted PD. Influence of boundary conditions and confinement on nonlocal effects in flows of wormlike micellar systems. Phys Rev E. (2010) 81:021502. doi: 10.1103/PhysRevE.81.021502
21. Fardin MA, Radulescu O, Morozov A, Cardoso O, Browaeys J, Lerouge S. Stress diffusion in shear banding wormlike micelles. J Rheol. (2015) 59:1335–62. doi: 10.1122/1.4930858
22. Larson RG. Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering. Boston, MA: Butterworths (1988).
24. Spenley NA, Cates ME, McLeish TCB. Nonlinear rheology of wormlike micelles. Phys Rev Lett. (1993) 71:939–42. doi: 10.1103/PhysRevLett.71.939
25. Giesekus H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J Non Newton Fluid Mech. (1982) 11:69–109.
26. Likhtman AE, Graham RS. Simple constitutive equation for linear polymer melts derived from molecular theory: Rolie–Poly equation. J Non Newton Fluid Mech. (2003) 114:1–12. doi: 10.1016/S0377-0257(03)00114-9
27. Yuan XF, Ball RC, Edwards SF. Dynamical modelling of viscoelastic extrusion flows. J Non Newton Fluid Mech. (1994) 54:423–35.
28. Dhont JKG. A constitutive relation describing the shear-banding transition. Phys Rev E. (1999) 60:4534–44.
29. Cook L, Rossi L. Slippage and migration in models of dilute wormlike micellar solutions and polymeric fluids. J Non Newton Fluid Mech. (2004) 116:347–69. doi: 10.1016/j.jnnfm.2003.09.005
30. Fielding SM, Olmsted PD. Flow phase diagrams for concentration-coupled shear banding. Eur Phys J E. (2003) 11:65–83. doi: 10.1140/epje/i2002-10128-7
31. Vasquez PA, McKinley GH, Cook LP. A network scission model for wormlike micellar solutions: I. Model formulation and viscometric flow predictions. J Non Newton Fluid Mech. (2007) 144:122–39. doi: 10.1016/j.jnnfm.2007.03.007
32. Cromer M, Villet MC, Fredrickson GH, Leal LG. Shear banding in polymer solutions. Phys Fluids. (2013) 25:051703. doi: 10.1063/1.4805089
33. Radulescu O, Olmsted PD. Matched asymptotic solutions for the steady banded flow of the diffusive Johnson–Segalman model in various geometries. J Non Newton Fluid Mech. (2000) 91:143–64. doi: 10.1016/S0377-0257(99)00093-2
34. Johnson MW, Segalman D. A model for viscoelastic fluid behavior which allows non-affine deformation. J Non Newton Fluid Mech. (1977) 2:255–70.
35. Greco F, Ball RC. Shear-band formation in a non-Newtonian fluid model with a constitutive instability. J Non Newton Fluid Mech. (1997) 69:195–206.
36. Milner ST, McLeish TCB, Likhtman AE. Microscopic theory of convective constraint release. J Rheol. (2001) 45:539–63. doi: 10.1122/1.1349122
37. Likhtman AE, Milner ST, McLeish TCB. Microscopic theory for the fast flow of polymer melts. Phys Rev Lett. (2000) 85:4550–3. doi: 10.1103/PhysRevLett.85.4550
38. Graham RS, Likhtman AE, McLeish TCB, Milner ST. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J Rheol. (2003) 47:1171–200. doi: 10.1122/1.1595099
39. Adams JM, Olmsted PD. Nonmonotonic models are not necessary to obtain shear banding phenomena in entangled polymer solutions. Phys Rev Lett. (2009) 102:067801. doi: 10.1103/PhysRevLett.102.067801
40. El-Kareh AW, Leal LG. Existence of solutions for all Deborah numbers for a non-Newtonian model modified to include diffusion. J Non Newton Fluid Mech. (1989) 33:257–87.
41. Adams JM, Fielding SM, Olmsted PD. The interplay between boundary conditions and flow geometries in shear banding: Hysteresis, band configurations, and surface transitions. J Non Newton Fluid Mech. (2008) 151:101–18. doi: 10.1016/j.jnnfm.2008.01.008
42. Hess S. Pre-transitional and post-transitional behavior of flow alignment and flow-induced phase-transition in liquid-crystals. Z Fur Naturforsch A. (1976) 31:1507–13.
43. See H, Doi M, Larson R. The effect of steady flow fields on the isotropic–nematic phase transition of rigid rod-like polymers. J Chem Phys. (1990) 92:792–800.
44. Olmsted PD, Goldbart P. Theory of the nonequilibrium phase transition for nematic liquid crystals under shear flow. Phys Rev A. (1990) 41:4578–81. doi: 10.1103/PhysRevA.41.4578
45. Olmsted PD, Lu CYD. Phase separation of rigid-rod suspensions in shear flow. Phys Rev E. (1999) 60:4397–415. doi: 10.1103/PhysRevE.60.4397
46. Pujolle-Robic C, Noirez L. Observation of shear-induced nematic–isotropic transition in side-chain liquid crystal polymers. Nature. (2001) 409:167–71. doi: 10.1038/35051537
47. Liu AJ, Fredrickson GH. Influence of nematic fluctuations on the phase separation of polymer blends. Macromolecules. (1992) 25:5551–3. doi: 10.1021/ma00046a071
48. Olmsted PD, Milner ST. Fluctuation corrections to mean-field theory for homopolymer-copolymer phase separation: sequence distribution effects. Macromolecules. (1994) 27:1964–7. doi: 10.1021/ma00085a047
49. Renardy M. Korteweg stresses and admissibility criteria for shear banded flows. J Non Newton Fluid Mech. (2014) 213:68–72. doi: 10.1016/j.jnnfm.2014.09.012
50. Jin H, Kang K, Ahn KH, Briels WJ, Dhont JKG. Non-local stresses in highly non-uniformly flowing suspensions: the shear-curvature viscosity. J Chem Phys. (2018) 149:014903. doi: 10.1063/1.5035268
51. Fielding SM, Olmsted PD. Early stage kinetics in a unified model of shear-induced demixing and mechanical shear banding instabilities. Phys Rev Lett. (2003) 90:224501. doi: 10.1103/PhysRevLett.90.224501
52. Fielding SM, Olmsted PD. Kinetics of the shear banding instability in startup flows. Phys Rev E. (2003) 68:036313. doi: 10.1103/PhysRevE.68.036313
53. Yuan XF, Jupp L. Interplay of flow-induced phase separations and rheological behavior of complex fluids in shearbanding flow. Eur Phys Lett. (2002) 60:691–7. doi: 10.1209/epl/i2002-00364-5
54. Rossi LF, McKinley G, Cook LP. Slippage and migration in Taylor–Couette flow of a model for dilute wormlike micellar solutions. J Non Newton Fluid Mech. (2006) 136:79–92. doi: 10.1016/j.jnnfm.2006.02.012
55. Zhou L, Vasquez PA, Cook LP, McKinley GH. Modeling the inhomogeneous response and formation of shear bands in steady and transient flows of entangled liquids. J Rheol. (2008) 52:591–623. doi: 10.1122/1.2829769
56. Fredrickson GH, Helfand E. Fluctuation effects in the theory of microphase separation in block copolymers. J Chem Phys. (1987) 87:697–705. doi: 10.1063/1.453566
57. Germano G, Schmid F. Nematic-isotropic interfaces under shear: a molecular-dynamics simulation. J Chem Phys. (2005) 123:214703. doi: 10.1063/1.2131065
58. Mohagheghi M, Khomami B. Molecular processes leading to shear banding in well entangled polymeric melts. ACS Macro Lett. (2015) 4:684–8. doi: 10.1021/acsmacrolett.5b00238
59. Salmon JB, Colin A, Manneville S, Molino F. Velocity profiles in shear-banding wormlike micelles. Phys Rev Lett. (2003) 90:228303. doi: 10.1103/PhysRevLett.90.228303
60. Fielding SM. Linear instability of planar shear banded flow. Phys Rev Lett. (2005) 95:134501. doi: 10.1103/PhysRevLett.95.134501
61. Radulescu O, Olmsted PD, Decruppe JP, Lerouge S, Berret JF, Porte G. Time scales in shear banding of wormlike micelles. Eur Phys Lett. (2003) 62:230–6. doi: 10.1209/epl/i2003-00351-x
62. Bitsanis I, Hadziioannou G. Molecular dynamics simulations of the structure and dynamics of confined polymer melts. J Chem Phys. (1989) 92:3827.
63. Mohammadigoushki H, Muller SJ. A flow visualization and superposition rheology study of shear-banding wormlike micelle solutions. Soft Matter. (2016) 12:1051–61. doi: 10.1039/C5SM02266E
64. Helgeson ME, Vasquez PA, Kaler EW, Wagner NJ. Rheology and spatially resolved structure of cetyltrimethylammonium bromide wormlike micelles through the shear banding transition. J Rheol. (2009) 53:727–56. doi: 10.1122/1.3089579
65. Ballesta P, Lettinga MP, Manneville S. Superposition rheology of shear-banding wormlike micelles. J Rheol. (2007) 51:1047–72. doi: 10.1122/1.2750665
66. Lerouge S, Berret JF. Shear-induced transitions and instabilities in surfactant wormlike micelles. In: Dusek K, Joanny JF, editors. Polymer Characterization: Rheology, Laser Interferometry, Electrooptics. Berlin; Heidelberg: Springer Berlin Heidelberg (2010). p. 1–71. doi: 10.1007/12_2009_13
67. Radulescu O, Olmsted PD, Lu CYD. Shear banding in reaction-diffusion models. Rheol Acta. (1999) 38:606–13. doi: 10.1007/s003970050211
68. Zhou L, McKinley GH, Cook LP. Wormlike micellar solutions: III. VCM model predictions in steady and transient shearing flows. J Non Newton Fluid Mech. (2014) 211:70–83. doi: 10.1016/j.jnnfm.2014.06.003
69. Lerouge S, Fardin MA, Argentina M, Grégoire G, Cardoso O. Interface dynamics in shear-banding flow of giant micelles. Soft Matter. (2008) 4:1808–19. doi: 10.1039/B804915G
70. Fardin MA, Casanellas L, Saint-Michel B, Manneville S, Lerouge S. Shear-banding in wormlike micelles: beware of elastic instabilities. J Rheol. (2016) 60:917–26. doi: 10.1122/1.4960333
71. Fardin MA, Lerouge S. Instabilities in wormlike micelle systems. Eur Phys J E. (2012) 35:1–29. doi: 10.1140/epje/i2012-12091-0
72. Cheng P, Burroughs MC, Leal LG, Helgeson ME. Distinguishing shear banding from shear thinning in flows with a shear stress gradient. Rheol Acta. (2017) 56:1007–32. doi: 10.1007/s00397-017-1051-y
73. Garcia-Sandoval JP, Bautista F, Puig JE, Manero O. The interface migration in shear-banded micellar solutions. Rheol Acta. (2017) 56:765–78. doi: 10.1007/s00397-017-1031-2
74. Graham MD. Wall slip and the nonlinear dynamics of large amplitude oscillatory shear flows. J Rheol. (1995) 39:697–712. doi: 10.1122/1.550652
Keywords: shear banding, microfluidics, confinement, constitutive modeling, non-linear dynamics, polymers, wormlike micelles, rheology
Citation: Lerouge S and Olmsted PD (2020) Non-local Effects in Shear Banding of Polymeric Flows. Front. Phys. 7:246. doi: 10.3389/fphy.2019.00246
Received: 01 August 2019; Accepted: 20 December 2019;
Published: 17 January 2020.
Edited by:
Joshua Albert Dijksman, Wageningen University & Research, NetherlandsReviewed by:
Martin Kröger, ETH Zürich, SwitzerlandCopyright © 2020 Lerouge and Olmsted. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter D. Olmsted, cGV0ZXIub2xtc3RlZEBnZW9yZ2V0b3duLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.