- 1School of Mathematics, Qilu Normal University, Jinan, China
- 2School of Control Science and Engineering, Shandong University, Jinan, China
- 3Department of Mathematics, Faculty of Science, Jiangsu University, Zhenjiang, China
- 4Department of Basic Science, Higher Technological Institute, 10th of Ramadan City, Egypt
This research paper studies the semi-analytical and numerical solutions of the non-linear long-short wave interaction system. This represents an optical field that does not change through multiplication due to a sensitive balance being struck between linear and non-linear impacts in an elastic medium, defined as a medium that can adjust its shape as a consequence of deforming stress and return to its original form when the force is eliminated. In this medium, a wave is produced by vibrations that are a consequence of acoustic power, known as a sound wave or acoustic wave. The Adomian decomposition method and the cubic and septic B-spline methods are applied to the suggested system to obtain distinct types of solutions that are used to explain the novel physical properties of this system. These novel features are described by different types of figures that show more of the physical properties of this model. Also, the convergence between the obtained solutions is discussed through tables that show the values of absolute error between them.
1. Introduction
Optical study is considered as one of the most important methodologies in this age due to its different and important applications in several fields. To develop a deeper understanding of this type of study, mathematicians have derived many analytical, semi-analytical, and numerical schemes to obtain distinct types of solutions that are used to characterize the physical properties of optical soliton waves. The optical soliton constitutes an optical field that does not alter through multiplication due to a sensitive balance being struck between linear and non-linear impacts in the medium [1–5]. Optical soliton can be of two types:
• Spatial solitons: the non-linear influence balances the diffraction. The electromagnetic field can alter the refraction index of the medium while propagating, thus establishing an architecture identical to a graded-index fiber [6–10].
• Temporal solitons: if the electromagnetic field is already spatially restricted, it is feasible to transmit pulses that will not alter their form, as the non-linear impacts will be in equilibrium with the dispersion [11–15].
The non-linear long-short wave interaction system describes the interaction between one short transverse wave and one long longitudinal wave propagating in a generalized elastic medium. This system has the following form:
where Φ(x, t) represents the slowly varying envelope of the short transverse wave, Ψ(x, t) discriminates the long longitudinal wave, (x) is the locational harmonization, and (t) is the time. Waves in plasmas are defined as an interrelated set of particles and fields that disseminate in a periodically duplicating fashion. A plasma is a quasi-neutral, electrically conductive fluid. Plasma waves have an EM character of two types, electrostatic and electromagnetic. Electrostatic and electromagnetic waves have oscillating species in electrons and ions. Some examples of the dispersion relationships of plasma waves in electrostatic and electromagnetic terms are as follows:
• Plasma oscillation: rapid oscillations of the electron intensity in conducting media such as plasmas or metals in the ultraviolet zone
• Upper hybrid oscillation: a form of oscillation of magnetized plasma
• Ion acoustic wave: one kind of longitudinal oscillation of the ions and electrons in a plasma
• Electrostatic ion cyclotron wave: a longitudinal wobble of the ions in a magnetized plasma, with dissemination nearly perpendicular to the magnetic field
• Langmuir wave
• Lower hybrid oscillation: a longitudinal fluctuation of ions and electrons in a magnetized plasma
• Light wave: a wave made of oscillating magnetic and electric fields; comprises radio waves, microwaves, ultraviolet, visible light, infrared, gamma rays, and X-rays
• O wave
• X wave
• R wave (whistler-mode)
• L wave
• Alfvén wave: a kind of magnetohydrodynamic wave in which ions oscillate in response to a restoration strength presented by an effective tension on the magnetic field lines; this kind of wave was named after Hannes Alfvén
• Magnetosonic wave: a longitudinal wave of ions in a magnetized plasma disseminating perpendicular to the stationary magnetic field.
All of the properties and abilities of the non-linear partial differential equations are used to describe these natural phenomena. According to these properties, many mathematicians have developed methods and are still trying to find new general methods to obtain exact and single traveling wave solutions for these models. For more details about these methods, please see [16–36].
The rest of this paper is arranged as follows. In section 2, the Adomian decomposition method [37–40] and Cubic and septic B-spline method [41–50] are used to obtain approximate solutions of the non-linear long-short wave interaction system. In section 4, the conclusion is given.
2. Application
This section applies the Adomian decomposition method as the semi-analytical scheme and the cubic & septic B–spline methods as numerical schemes to the non-linear long-short wave interaction system [51–55] that is given by:
Using the wave transformation Φ(x, t) = eiηΛ(ε), Ψ(x, t) = φ(ε) where η = (ρx + ct), ε = (ax + bt) transforms the non-linear partial differential equation (2) into the following ordinary differential equation:
Equating the complex term to zero leads to
Integrating the second equation of the system (3) with zero constant of integration yields:
Substituting (4) and (5) into the first equation in the system (3) yields:
According to the analytical solutions obtained in Raghda et al. [Submitted], the exact solution of Equation (6) takes the following formula
2.1. Semi-analytical Solution
This section applies the Adomian decomposition method to Equation (6) by using its exact solution (6) with the following conditions:
where . Implementation of the Adomian decomposition method on Equation (6) yields
According to (8–11), we get
2.2. Numerical Solutions
This section studies the numerical solutions of the modified BBM equation by applying the cubic and septic B-spline techniques, which are considered as the most accurate numerical tools for getting this type of solution.
2.2.1. Cubic-Spline
According to the cubic B–spline, the numerical solution of the modified BBM equation (6) is given by
where λi, βi fulfill the conditions:
and
where i ∈ [−2, n + 2], so that the numerical formula of the solution is given as
Substituting Equation (15) into (6), leads to a system of equations. Solving this system of equations gives the value of λi. Replacing the values of λi, βi into Equation (13) gives the data shown in Table 2.
2.2.2. Septic-Spline
Based on the septic B-spline, the suggested solution of the ordinary differential form of the modified BBM equation (6) is given as follows:
where λi, βi satisfies the conditions
and
where i ∈ [−3, n + 3]. Thus, the approximate solution is given by:
Substituting Equation (18) into Equation (6) produces a system of equations. Solving this system gives the data shown in Table 3.
3. Results and Discussion
This section details a comparison between the numerical solutions obtained in our paper to determine which one of them is the more accurate.
The comparison between the numerical solutions depends on showing which one of the schemes obtains the smallest value of the absolute value of error. To find these values, the obtained values of the total value of error in each method used are plotted in Figure 5, which shows that all the methods used are accurate and have almost the same amount of absolute failure.
4. Conclusion
This research paper succeeded in the application of the Adomian decomposition method and the cubic and septic B–spline method to the non-linear long-short wave interaction system and in obtaining semi-analytical and numerical solutions for this system. Moreover, a comparison between the distinct types of solutions obtained is detailed, and the absolute values of error between them are shown in Tables 1–3 and Figures 1–5. Both semi–computational and numerical schemes are shown to be powerful, effective, and able to be applied to many and various forms of non-linear evolution equations.
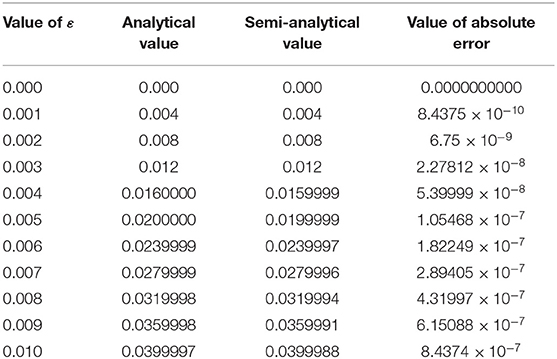
Table 1. Computational, semi-analytical, and absolute error values obtained by using the Adomian decomposition method.
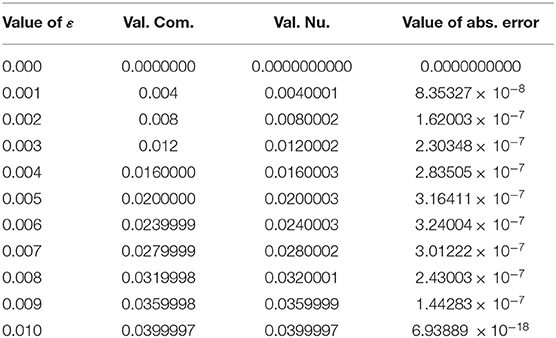
Table 2. Computational, numerical, and absolute error values obtained by using the cubic B–spline scheme.
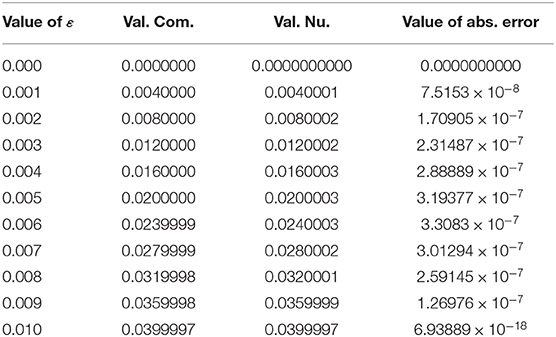
Table 3. Computational, numerical, and absolute error value obtained by using the septic B–spline scheme.
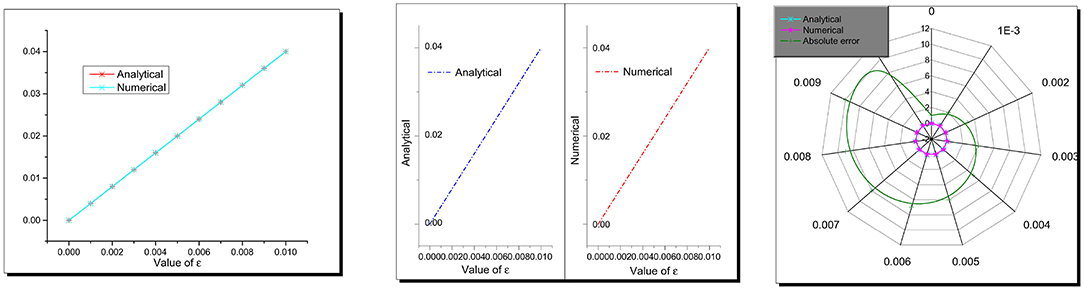
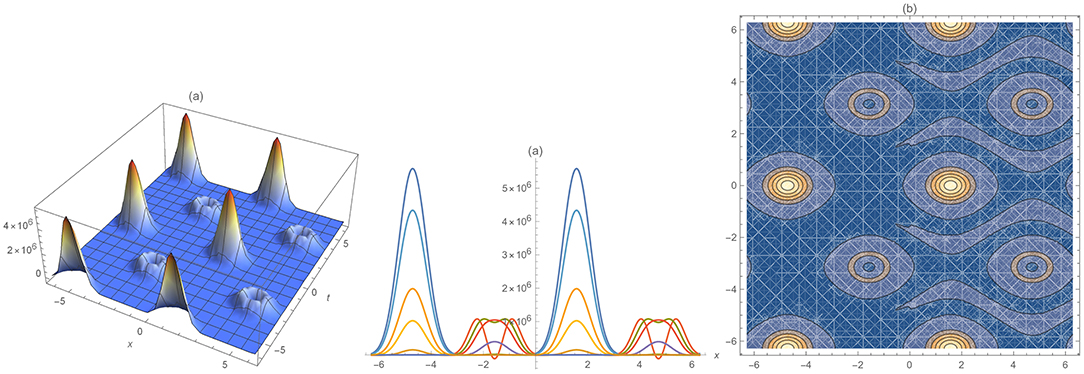
Figure 2. Combined, separated, and radar plots of analytical (7) and semi-analytical solutions (12) of Equation (6), respectively.
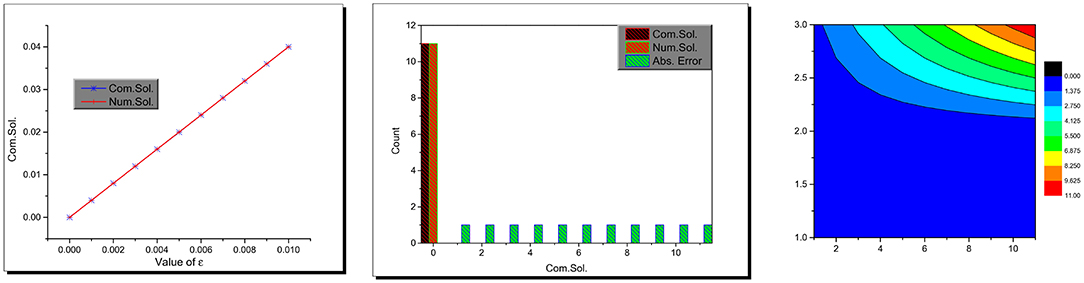
Figure 3. Combined, bar, and contour plots of the computational, numerical, and absolute error values.
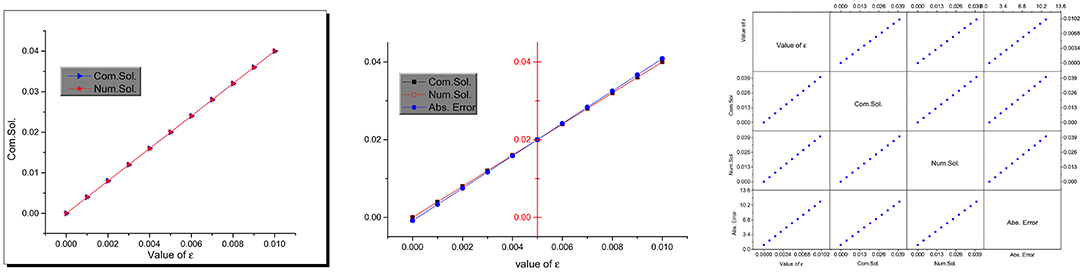
Figure 4. Combined and scattering matrix plots of the computational, numerical, and absolute error values.
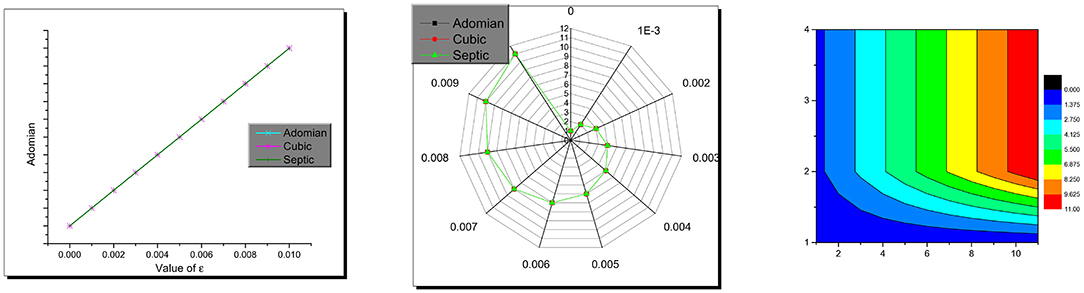
Figure 5. Combined, radar, and contour plots of the absolute value of error for the Adomian, cubic, and septic schemes.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research is supported by a Project of Shandong Province Higher Educational Science and Technology Program (Grant No. J17KB121), Shandong Provincial Natural Science Foundation (Grant No. ZR2016AB04), Foundation for Young Teachers of Qilu Normal University (Grant Nos. 2016L0605, 2015L0603, 2017JX2311, and 2017JX2312), Scientific Research Foundation for University Students of Qilu Normal University (Grant Nos. XS2017L01 and XS2017L05).
References
1. Mena-Contla A, Serkin V, Belyaeva T, Peña-Moreno R, Agüero M, Hernandez-Tenorio C, et al. Extreme nonlinear waves in external gravitational-like potentials: possible applications for the optical soliton supercontinuum generation and the ocean coast line protection. Optik. (2018) 161:187–95. doi: 10.1016/j.ijleo.2018.01.031
2. Kippenberg TJ, Gaeta AL, Lipson M, Gorodetsky ML. Dissipative Kerr solitons in optical microresonators. Science. (2018) 361:eaan8083. doi: 10.1126/science.aan8083
3. Trocha P, Karpov M, Ganin D, Pfeiffer MH, Kordts A, Wolf S, et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science. (2018) 359:887–91. doi: 10.1126/science.aao3924
4. Li BQ, Ma YL, Yang TM. Stable optical soliton in the ring-cavity fiber system with carbon nanotube as saturable absorber. Superlattices Microstruct. (2018) 113:366–72. doi: 10.1016/j.spmi.2017.11.016
5. Biswas A, Zhou Q, Triki H, Ullah MZ, Asma M, Moshokoa SP, et al. Resonant optical solitons with parabolic and dual-power laws by semi-inverse variational principle. J Mod Opt. (2018) 65:179–84. doi: 10.1080/09500340.2017.1382597
6. Cyprych K, Jung PS, Izdebskaya Y, Shvedov V, Christodoulides DN, Krolikowski W. Anomalous interaction of spatial solitons in nematic liquid crystals. Opt Lett. (2019) 44:267–70. doi: 10.1364/OL.44.000267
7. Jung PS, Karpierz M, Trippenbach M, Christodoulides D, Krolikowski W. Supermode spatial solitons via competing nonlocal nonlinearities. Photon Lett Pol. (2018) 10:33–5. doi: 10.4302/plp.v10i2.827
8. Rubin S, Fainman Y. Nonlocal and nonlinear surface plasmon polaritons and optical spatial solitons induced by the thermocapillary effect. Phys Rev Lett. (2018) 120:243904. doi: 10.1103/PhysRevLett.120.243904
9. Salgueiro JR, Ferrando A. Spatial solitons in nonlinear photonic crystal fibers. In: Nonlinear Systems, Vol. 2. Springer (2018). p. 139–71.
10. Perumbilavil S, Piccardi A, Kauranen M, Assanto G. Directional random laser by combining cavity-less lasing and spatial solitons in liquid crystals. In: Nonlinear Photonics. Optical Society of America (2018). p. NpW2C–4.
11. Obrzud E, Brasch V, Lecomte S, Herr T. Temporal cavity solitons in synchronously driven Fabry-Perot microresonators. In: Laser Resonators, Microresonators, and Beam Control XX. Vol. 10518. International Society for Optics and Photonics. (2018).
12. Lilienfein N, Hofer C, Högner M, Saule T, Trubetskov M, Pervak V, et al. Temporal solitons in free-space femtosecond enhancement cavities. Nat Photon. (2019) 13:214. doi: 10.1038/s41566-018-0341-y
13. Spiess C, Yang Q, Dong X, Bucklew VG, Renninger WH. Chirped temporal solitons in driven optical resonators. arXiv preprint arXiv:190612127 (2019).
14. Xue X, Zheng X, Zhou B. Super-efficient temporal solitons in mutually coupled optical cavities. Nat Photon. (2019) 13:616–22. doi: 10.1038/s41566-019-0436-0
15. Shtyrina O, Kivshar Y, Turitsyn S, Yarutkina I, Fedoruk M. Stability of spatio-temporal solitons in multi-mode fibers. In: Nonlinear Photonics. Optical Society of America (2018). p. JTu5A–45.
16. Rezazadeh H, Korkmaz A, Khater MM, Eslami M, Lu D, Attia RA. New exact traveling wave solutions of biological population model via the extended rational Sinh–Cosh method and the modified Khater method. Mod Phys Lett B. (2019) 33:1950338. doi: 10.1142/S021798491950338X
17. Khater M, Attia RA, Lu D. Explicit lump solitary wave of certain interesting (3+ 1)-dimensional waves in physics via some recent traveling wave methods. Entropy. (2019) 21:397. doi: 10.3390/e21040397
18. Khater MM, Lu D, Attia RA. Dispersive long wave of nonlinear fractional Wu–Zhang system via a modified auxiliary equation method. AIP Adv. (2019) 9:025003. doi: 10.1063/1.5087647
19. Khater MM, Lu D, Attia RA. Lump soliton wave solutions for the (2+ 1)-dimensional Konopelchenko–Dubrovsky equation and KdV equation. Mod Phys Lett B. (2019) 33:1950199. doi: 10.1142/S0217984919501999
20. Khater MM, Attia RA, Lu D. Numerical solutions of nonlinear fractional Wu–Zhang system for water surface versus three approximate schemes. J Ocean Eng Sci. (2019). doi: 10.1016/j.joes.2019.03.002
21. Attia RA, Lu D, Khater MMA. Chaos and relativistic energy-momentum of the nonlinear time fractional Duffing equation. Math Comput Appl. (2019) 24:10. doi: 10.3390/mca24010010
22. Khater M, Attia R, Lu D. Modified auxiliary equation method versus three nonlinear fractional biological models in present explicit wave solutions. Math Comput Appl. (2019) 24:1. doi: 10.3390/mca24010001
23. Elghobashi S. Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu Rev Fluid Mech. (2019) 51:217–44. doi: 10.1146/annurev-fluid-010518-040401
24. Nasiri H, Jamalabadi MYA, Sadeghi R, Safaei MR, Nguyen TK, Shadloo MS. A smoothed particle hydrodynamics approach for numerical simulation of nano–fluid flows. J Therm Anal Calorimetry. (2019) 135:1733–41. doi: 10.1007/s10973-018-7022-4
25. Knab O, Riedmann H, Ivancic B, Höglauer C, Frey M, Aichner T. Consequences of modeling demands on numerical rocket thrust chamber flow simulation tools. EUCASS Proc Ser. (2019) 11:317–46. doi: 10.1051/eucass/201911317
26. Khan U, Ellahi R, Khan R, Mohyud-Din ST. Extracting new solitary wave solutions of Benny–Luke equation and Phi-4 equation of fractional order by using (G'/G)-expansion method. Opt Quant Electron. (2017) 49:362. doi: 10.1007/s11082-017-1191-4
27. Sikander W, Khan U, Ahmed N, Mohyud-Din ST. Optimal solutions for homogeneous and non–homogeneous equations arising in physics. Results Phys. (2017) 7:216–24. doi: 10.1016/j.rinp.2016.12.018
28. Sikander W, Khan U, Mohyud-Din ST. Optimal solutions for the evolution of a social obesity epidemic model. Eur Phys J Plus. (2017) 132:257. doi: 10.1140/epjp/i2017-11512-y
29. Mohyud-Din ST, Irshad A, Ahmed N, Khan U. Exact solutions of (3+ 1)-dimensional generalized KP equation arising in physics. Results Phys. (2017) 7:3901–9. doi: 10.1016/j.rinp.2017.10.007
30. Mohyud-Din ST, Noor MA, Noor KI. Some relatively new techniques for nonlinear problems. Math Probl Eng. (2009) 2009:234849. doi: 10.1155/2009/234849
31. Tauseef Mohyud-Din S, Yildirim A, Demirli G. Analytical solution of wave system in R n with coupling controllers. Int J Numer. Methods Heat Fluid Flow. (2011) 21:198–205. doi: 10.1108/09615531111105399
32. Nazir A, Ahmed N, Khan U, Mohyud-din ST. On stability of improved conformable model for studying the dynamics of a malnutrition community. Physica A Stat Mech Appl. (2020) 537:122664. doi: 10.1016/j.physa.2019.122664
33. Shakeel M, Mohyud-Din ST, Iqbal MA. Modified extended exp-function method for a system of nonlinear partial differential equations defined by seismic sea waves. Pramana. (2018) 91:28. doi: 10.1007/s12043-018-1601-6
34. Tchier F, Yusuf A, Aliyu AI, Inc M. Soliton solutions and conservation laws for lossy nonlinear transmission line equation. Superlattices Microstruct. (2017) 107:320–36. doi: 10.1016/j.spmi.2017.04.003
35. Al Qurashi MM, Yusuf A, Aliyu AI, Inc M. Optical and other solitons for the fourth–order dispersive nonlinear Schrödinger equation with dual-power law nonlinearity. Superlattices Microstruct. (2017) 105:183–97. doi: 10.1016/j.spmi.2017.03.022
36. Yusuf A, Inc M, Bayram M. Invariant and simulation analysis to the time fractional Abrahams–Tsuneto reaction diffusion system. Phys Script. (2019) 94:125005. doi: 10.1088/1402-4896/ab373b
37. Keskin AÜ. Adomian Decomposition Method (ADM). In: Boundary Value Problems for Engineers. Springer (2019). p. 311–59.
38. Hamoud AA, Ghadle KP. Modified adomian decomposition method for solving fuzzy volterra-fredholm integral equation. J Indian Math Soc. (2018) 85:53–69. doi: 10.18311/jims/2018/16260
39. Ali N, Ahmad S, Aziz S, Zaman G. The adomian decomposition method for solving Hiv infection model of latently infected cells. Matrix Sci Math. (2019) 3:5–8. doi: 10.26480/msmk.01.2019.05.08
40. Moradweysi P, Ansari R, Hosseini K, Sadeghi F. Application of modified Adomian decomposition method to pull–in instability of nano–switches using nonlocal Timoshenko beam theory. Appl Math Model. (2018) 54:594–604. doi: 10.1016/j.apm.2017.10.011
41. Goss A, Schmidt M, Erdogan E, Görres B, Seitz F. High-resolution vertical total electron content maps based on multi-scale B-spline representations. Ann Geophys. (2019). 37. doi: 10.5194/angeo-2019-32
42. Penner A. ODF Using a 5-Point B-Spline. In: Fitting Splines to a Parametric Function. Springer (2019). p. 37–42.
43. Edwards MC, Meyer R, Christensen N. Bayesian nonparametric spectral density estimation using B-spline priors. Stat Comput. (2019) 29:67–78. doi: 10.1007/s11222-017-9796-9
44. Gavriil K, Schiftner A, Pottmann H. Optimizing B–spline surfaces for developability and paneling architectural freeform surfaces. Comput Aid Design. (2019) 111:29–43. doi: 10.1016/j.cad.2019.01.006
45. Hepson OE, Korkmaz A, Dag I. Exponential B–spline collocation solutions to the Gardner equation. Int J Comput Math. (2019) 1–14. doi: 10.1080/00207160.2019.1594791
46. Karakoc SBG, Ucar Y, Yağmurlu N. Numerical solutions of the MRLW equation by cubic B–spline Galerkin finite element method. Kuwait J Sci. (2019) 42:141–59.
47. Massarwi F, Elber G. A B–spline based framework for volumetric object modeling. Comput Aid Design. (2016) 78:36–47. doi: 10.1016/j.cad.2016.05.003
48. Qiao B, Zhang X, Luo X, Chen X. A force identification method using cubic B–spline scaling functions. J Sound Vibr. (2015) 337:28–44. doi: 10.1016/j.jsv.2014.09.038
49. Donatelli M, Garoni C, Manni C, Serra-Capizzano S, Speleers H. Symbol–based multigrid methods for Galerkin B–spline isogeometric analysis. SIAM J Numer Anal. (2017) 55:31–62. doi: 10.1137/140988590
50. Fey M, Eric Lenssen J, Weichert F, Müller H. SplineCNN: Fast geometric deep learning with continuous B–spline kernels. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2018). p. 869–77.
51. Baskonus HM, Bulut H, Belgacem FBM. Analytical solutions for nonlinear long–short wave interaction systems with highly complex structure. J Comput Appl Math. (2017) 312:257–66. doi: 10.1016/j.cam.2016.05.035
52. Aghdaei MF, Adibi H. On some new analytical solutions for the nonlinear long–short wave interaction system. Opt Quant Electron. (2018) 50:100. doi: 10.1007/s11082-018-1361-z
53. Chan HN, Ding E, Kedziora DJ, Grimshaw R, Chow KW. Rogue waves for a long wave–short wave resonance model with multiple short waves. Nonlinear Dyn. (2016) 85:2827–41. doi: 10.1007/s11071-016-2865-3
54. Inc M, Aliyu AI, Yusuf A, Baleanu D. On the classification of conservation laws and soliton solutions of the long short-wave interaction system. Mod Phys Lett B. (2018) 32:1850202. doi: 10.1142/S0217984918502020
Keywords: nonlinear long-short wave interaction system, adomian decomposition method, cubic B-spline method, septic B-spline method, semi-analytical and numerical solutions
Citation: Qin H, Khater MMA, Attia RAM and Lu D (2020) Approximate Simulations for the Non-linear Long-Short Wave Interaction System. Front. Phys. 7:230. doi: 10.3389/fphy.2019.00230
Received: 16 October 2019; Accepted: 10 December 2019;
Published: 23 January 2020.
Edited by:
Mustafa Inc, Firat University, TurkeyReviewed by:
Syed Tauseef Mohyud-Din, HITEC University, PakistanAbdullahi Yusuf, Federal University, Dutse, Nigeria
Copyright © 2020 Qin, Khater, Attia and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haiyong Qin, cWh5bWF0aEBob3RtYWlsLmNvbQ==; Mostafa M. A. Khater, bW9zdGFmYS5raGF0ZXIyMDI0QHlhaG9vLmNvbQ==
 Haiyong Qin
Haiyong Qin Mostafa M. A. Khater
Mostafa M. A. Khater Raghda A. M. Attia3,4
Raghda A. M. Attia3,4