Point Interactions With Bias Potentials

We develop an approach on how to define single-point interactions under the application of external fields. The essential feature relies on an asymptotic method based on the one-point approximation of multi-layered heterostructures that are subject to bias potentials. In this approach, the zero-thickness limit of the transmission matrices of specific structures is analyzed and shown to result in matrices connecting the two-sided boundary conditions of the wave function at the origin. The reflection and transmission amplitudes are computed in terms of these matrix elements as well as biased data. Several one-point interaction models of two- and three-terminal devices are elaborated. The typical transistor in the semiconductor physics is modeled in the “squeezed limit” as a δ- and a δ′-potential and referred to as a “point” transistor. The basic property of these one-point interaction models is the existence of several extremely sharp peaks as an applied voltage tunes, at which the transmission amplitude is non-zero, while beyond these resonance values, the heterostructure behaves as a fully reflecting wall. The location of these peaks referred to as a “resonance set” is shown to depend on both system parameters and applied voltages. An interesting effect of resonant transmission through a δ-like barrier under the presence of an adjacent well is observed. This transmission occurs at a countable set of the well depth values.

1. Introduction

One-dimensional quantum systems modeled by Schrödinger operators with singular zero-range potentials have been discussed widely in both the physical and mathematical literature [see books [1–3] for details and references]. Additionally, a whole body of literature beginning from the early publications [4–11] (to mention just a few) has been published, where the one-dimensional stationary Schrödinger equation

$\begin{array}{ll}-{\psi }^{″}\left(x\right)+V\left(x\right)\psi \left(x\right)=E\psi \left(x\right),& (1)\end{array}$

with the potential V(x) given in the form of distributions, where ψ(x) is the wave function and E the energy of an electron, was shown to exhibit a number of peculiar features with possible applications to quantum physics. Currently, because of the rapid progress in fabricating nanoscale quantum devices, of particular importance is the point modeling of different structures like quantum waveguides [12, 13], spectral filters [14, 15], or infinitesimally thin sheets [16, 17].

In the present paper we follow the traditional approach [see the work [7] by Albeverio et al. and references therein], according to which there exists a one-to-one correspondence between the full set of self-adjoint extensions of the one-dimensional free Schrödinger operator and the two families of boundary conditions: non-separated and separated. The non-separated extensions describe non-trivial four-parameter point interactions subject to the two-sided at x = ±0 boundary conditions on the wave function ψ(x) and its derivative ψ′(x) given by the connection matrix of the form

$\begin{array}{ll}\left(\begin{array}{c}\psi \left(+0\right)\\ {\psi }^{\prime }\left(+0\right)\end{array}\right)=\Lambda \left(\begin{array}{c}\psi \left(-0\right)\\ {\psi }^{\prime }\left(-0\right)\end{array}\right),\Lambda ={\text{e}}^{\text{i}\chi }\left(\begin{array}{c}{\lambda }_{11}{\lambda }_{12}\\ {\lambda }_{21}{\lambda }_{22}\end{array}\right),& (2)\end{array}$

where χ ∈ [0, π), λ_ij ∈ ℝ fulfilling the condition λ₁₁λ₂₂ − λ₁₂λ₂₁ = 1. The separated point interactions are described by the direct sum of the free Schrödinger operators defined on the half-lines (−∞, 0), (0, ∞) and subject to the following pair of boundary conditions:

$\begin{array}{ll}{\psi }^{\prime }\left(-0\right)=h^{-}\psi \left(-0\right)\text{and }{\psi }^{\prime }\left(+0\right)=h^{+}\psi \left(+0\right),& (3)\end{array}$

where h^± ∈ ℝ ∪ {∞}. For instance, if {h⁻, h⁺} = {∞, ∞}, Equation (3) describe the Dirichlet boundary conditions ψ(±0) = 0. In physical terms, a separated self-adjoint extension means that the corresponding point potential is completely opaque for an incident particle. Alternatively, the boundary conditions can be connected using the Asorey-Ibort-Marmo formalism [18] or the Cheon-Fülöp-Tsutsui approach [19, 20]. The advantage of both these connecting representations is that they enable to include all the self-adjoint extensions without treating the particular cases as any parameters tend to infinity. In other words, the relations (3) are excluded from the consideration.

Some particular examples of Equation (1) and the corresponding Λ-matrix (2) are important in applications. The most simple and widespread potential is Dirac's delta function δ(x), i.e., V(x) = αδ(x) where α is a strength constant (or intensity). The wave function ψ(x) for this interaction (called the δ-interaction or δ-potential) is continuous at the origin x = 0, whereas its derivative undergoes a jump, so that the boundary conditions read ψ(−0) = ψ(+0) = :ψ(0) and ψ′(+0) − ψ′(−0) = αψ(0) yielding the Λ-matrix in the form

$\begin{array}{ll}\Lambda =\left(\begin{array}{l}10\\ \alpha 1\end{array}\right).& (4)\end{array}$

In the simplest case, this point potential is constructed from constant functions defined on a squeezed interval.

The dual point interaction for which the derivative ψ′(x) is continuous at the origin, but ψ(x) discontinuous, is called a δ′-interaction (the notation adopted in the literature [2]). This point interaction with strength β defined by the boundary conditions ψ′(−0) = ψ′(+0) = :ψ′(0) and ψ(+0) = ψ(−0) = βψ′(0) has the Λ-matrix of the form

$\begin{array}{ll}\Lambda =\left(\begin{array}{l}1\beta \\ 01\end{array}\right).& (5)\end{array}$

As a particular example of the Cheon-Shigehara approach [21], the δ′-interaction can be constructed from the spatially symmetric configuration consisting of three separated δ-potentials having the intensities scaled in a non-linear way as the distances between the potentials tend to zero. Following this approach, Exner et al. [22] have approximated the δ-potentials by regular functions and realized rigorously the similar one-point limit in the norm resolvent topology. In particular, they have proved that the resulting limit takes place if the distances between the peaks of δ-like regularized potentials tend to zero sufficiently slow relative to shrinking these potentials to the origin. The other aspects of the δ′-interaction and its approximations by local and non-local potentials have been investigated, for instance, by Albeverio and Nizhnik [23–27], Fassari and Rinaldi [28] (see also references therein). The δ′-interaction can be used together with background potentials. Thus, Albeverio et al. [29] have rigorously defined the self-adjoint Hamiltonian of the harmonic oscillator perturbed by an attractive δ′-interaction of strength β centered at the origin x = 0 (the bottom of a confining parabolic potential), explicitly providing its resolvent. In a subsequent publication [30], their study has been extended for the perturbation by a triple of attractive δ′-interactions using the Cheon-Shigehara approximation. It is worth mentioning the recent publication [31], where Golovaty has constructed a new approximation to the δ′-interaction involving two parameters in the boundary conditions. Here the connection matrix

$\begin{array}{ll}\Lambda =\left(\begin{array}{c}\theta \beta \\ 0{\theta }^{-1}\end{array}\right)& (6)\end{array}$

describes the two-parametric family of point interactions being the generalization of the δ′-interaction with θ = 1.

It should be emphasized that the term “δ′-interaction” is somewhat misleading because the point interaction described by the Λ-matrix (5) does not correspond to Equation (1) in which the potential part is the derivative of the Dirac delta function in the distributional sense, i.e., V(x) = γδ′(x) with strength γ. Since the term δ′(x)ψ(x) is not defined for discontinuous ψ(x), Kurasov [5] has developed the distribution theory based on the space of discontinuous at x = 0 test functions. Within this theory, as a particular example, the point interaction that corresponds to the potential V(x) = γδ′(x) is given by the connection matrix

$\begin{array}{ll}\Lambda =\left(\begin{array}{c}\theta 0\\ 0{\theta }^{-1}\end{array}\right),& (7)\end{array}$

where θ = (2 + γ)/(2 − γ), γ ∈ ℝ \ {±2}. Since the term “δ′-interaction” is reserved for the case with the connection matrix of the type (5), Brasche and Nizhnik [32] suggested to refer the point interactions described by the matrices of the form (7) even if the element θ ≠ 1 does not correspond to the delta prime potential. We will follow this terminology in the present paper.

The Kurasov approach has been followed in many applications (see, e.g., [32–39]) including more general examples. Thus, in the context of this approach, Gadella et al. [33] have shown that Equation (1) with the potential V(x) = aδ(x) + bδ′(x), a < 0, b ∈ ℝ, has a bound state and calculated the energy of this state in terms of the parameters a and b. A new approach based on the integral form of the Schrödinger Equation (1) has been developed by Lange [35, 36] with some revision of Kurasov's theory. The potential V(x) = aδ(x) + bδ′(x) has also been used by Gadella and coworkers as a perturbation of some background potential, such as a constant electric field and the harmonic oscillator [34] or the infinite square well [37]. The spectrum of a one-dimensional V-shaped quantum well perturbed by three types of a point impurity as well as three solvable two-dimensional systems (the isotropic harmonic oscillator, a square pyramidal potential and their combination) perturbed by a point interaction centered at the origin has been studied by Fassari et al. in the recent papers [40–42].

On the other hand, as derived in the series of publications [43–47] for some particular cases and proved rigorously by Golovaty with coworkers [48–52] in a general case, the potential V(x) = γδ′(x) appears to be partially transparent at some discrete values forming a countable set {γ_n} in the γ-space. The corresponding Λ-matrix is diagonal, i.e., of the form (7) where the element θ = {θ_n} takes discrete values that depend on the sequence {γ_n}. Except the distribution δ′(x), which is obtained as a limit of regular δ′-like functions, the diagonal form of the Λ-matrix can be realized even if the squeezed limit of regular functions does not exist. Beyond the “resonance” set {γ_n}, the δ′-potential is fully opaque satisfying the boundary conditions of the type (3). However, this resonant-tunneling behavior contradicts with the Λ-matrix (7) where the element θ continuously depends on strength γ. It is remarkable that this controversy can be resolved using the one-dimensional model for the heterostructure consisting of two or three squeezed parallel homogeneous layers approaching to one point [53, 54]. Here a “splitting” effect of one-point interactions has been described.

As for two-point interactions in one dimension, one should mention the recent studies concerning quantum tunneling times and the associated questions such as, for instance, the Hartman effect and its generalized version [see, e.g., [55–59] and references therein]. Another important aspect regarding the application of double-point potentials is the Casimir effect that arises in the behavior of the vacuum energy between two homogeneous parallel plates. For the interpretation of this effect, Muñoz-Castañeda and coworkers [60–66] reformulated the theory of self-adjoint extensions of symmetric operators over bounded domains in the framework of quantum field theory. Particularly, they have calculated the vacuum energy and identified which boundary conditions generate attractive or repulsive Casimir forces between the plates. Bordag and Muñoz-Castañeda [67] have calculated the quantum vacuum interaction energy between two kinks of the sine-Gordon equation (for a review on non-linear localized excitations including topological solitons see, e.g., the work [68]) and shown that this interaction induces an attractive force between the kinks in parallel to the Casimir force between conducting mirrors. A rigorous mathematical model of real metamaterials has been suggested in Nieto et al. [69]. The resonant tunneling through double-barrier scatters is still an active area of research for the applications to nanotechnology. In the context of the Cheon-Fülöp-Tsutsui approach [19, 20], the conditions for the parameter space under which the perfect resonant transmission occurs through two point interactions, each of which is described by four parameters, have been found by Konno et al. [70, 71].

The pioneering studies [72–74] demonstrated that the resonant transmission through quantum multilayer heterostructures of electronic tunnel systems are of considerable general interest. These structures are not only important in micro- and nanodevices, but their study involves a great deal of basic physics. In recent years it has been realized that the study of the electron transmission through heterostructures can be investigated in the zero-thickness limit approximation materialized when their width shrinks to zero. Within such an approximation it is possible to produce various point interaction models, particularly those as described above which admit exact closed analytic solutions. These models are required to provide relatively simple configurations where an appropriate way of squeezing to the zero-width limit must be compatible with the original real structure. Additionally, as a rule, the nanodevices are subject to electric fields applied externally. In this regard, is of great interest to produce point interaction models with bias potentials. So far no models have been elaborated for such devices using one-point approximation methods.

The present paper is devoted to the investigation of planar heterostructures composed of extremely thin layers separated by small distances in the limit where both the layer thickness and the distance between the layers simultaneously tend to zero. The electron motion in the systems of this type is usually confined in the longitudinal direction (say, along the x-axis); the latter is perpendicular to the transverse planes where electronic motion is free. The three-dimensional Schrödinger equation of such a structure can be separated into longitudinal and transverse parts, writing the total electron energy as the sum of the longitudinal and transverse energies: $E_l+{\hslash }^2{\text{k}}_t^2/2m^{*}$, where m^* is an effective electron mass and k_t the transverse wave vector; for such additive Hamiltonian the wave function is expressed as a product, i.e. ψ = ψ_lψ_t. As a result, we arrive at the reduced one-dimensional Schrödinger equation with respect to the longitudinal component of the wave function ψ_l(x) and the electron energy E_l. For brevity of notations, in the following we omit the subscript “l” at both ψ_l(x) and E_l. Thus, in the units as ℏ²/2m^* = 1, the one-dimensional stationary Schrödinger equation reduces to the form (1) where V(x) is a potential for electrons. Concerning the dimensions of the longitudinal electron position x, the potential V(x) and the electron energy E, in the system ℏ²/2m^* = 1 we have [x] = nm and [V, E] = nm⁻². For computations we choose $m^{*}=0.1m_e$ and in this case, 1 eV = 2.62464 nm⁻².

2. Transmission characteristics of multi-layered structures

This introductory section generalizes the approach described in Lui and Fukuma [75]. We consider the Schrödinger Equation (1), where the potential V(x) is an arbitrary piecewise function defined on the interval (x₀, x_N) with N subsets (x_i−1, x_i), $i=\overline{1,N},N=1,2,\dots$. Each V_i(x) is a real bounded function defined on this interval, so that we have the set of functions: V₁(x), …, V_N(x). Next, we express the transmission matrix in terms of the interface values of the linearly independent solutions of the Schrödinger equation.

The solution of the Schrödinger equation across the interval (x_i−1, x_i), ψ_i(x), will be given as

$\begin{array}{ll}{\psi }_i\left(x\right)=C_i^{\left(1\right)}{u}_i\left(x\right)+C_i^{\left(2\right)}{v}_i\left(x\right),\overline{1,N},& (8)\end{array}$

where u_i(x) and v_i(x) are linearly independent solutions on the interval (x_i−1, x_i). At the interface x_i, $i=\overline{1,N-1}$, the particle conservation requires the continuity of the wave function ψ(x), while the momentum conservation demands the continuity of the first derivative of the wave function ψ′(x) resulting in the equations

$\begin{array}{ll}{\psi }_i\left(x_i\right)={\psi }_{i+1}\left(x_i\right),{\psi }_i^{\prime }\left(x_i\right)={\psi }_{i+1}^{\prime }\left(x_i\right),i=\overline{1,N-1},& (9)\end{array}$

where the prime denotes first derivative with respect to x.

2.1. Transmission Matrix

Using Equation (8), the boundary conditions (9) can be realized as a system of two linear equations with two unknowns such that

$\begin{array}{ll}{\text{M}}_i\left(x_i\right){\text{C}}_i={\text{M}}_{i+1}\left(x_i\right){\text{C}}_{i+1},i=\overline{1,N-1},N\ge 2,& (10)\end{array}$

where

$\begin{array}{ll}{\text{C}}_i:=\text{col}\left(C_i^{\left(1\right)},C_i^{\left(2\right)}\right)=\left(\begin{array}{c}{C}_i^{\left(1\right)}\\ C_i^{\left(2\right)}\end{array}\right)\text{and }{\text{M}}_i\left(x\right):=\left(\begin{array}{c}{u}_i\left(x\right)v_i\left(x\right)\\ u_i^{\prime }\left(x\right)v_i^{\prime }\left(x\right)\end{array}\right)& (11)\end{array}$

are Wronskian matrices. Next, using Equation (10), one can connect the column vectors C₁ and C_N as follows

$\begin{array}{l}{\text{C}}_N={\text{M}}_N^{-1}\left(x_{N-1}\right){\text{M}}_{N-1}\left(x_{N-1}\right){\text{M}}_{N-1}^{-1}\left(x_{N-2}\right)\dots {\text{M}}_2\left(x_2\right){\text{M}}_2^{-1}\left(x_1\right){\text{M}}_1\left(x_1\right){\text{C}}_1\\ ={\text{M}}_N^{-1}\left(x_{N-1}\right){\Lambda }_{N-1}\left(x_{N-2},x_{N-1}\right)\dots {\Lambda }_2\left(x_1,x_2\right){\text{M}}_1\left(x_1\right){\text{C}}_1,N\ge 2,& (12)\end{array}$

where we have introduced the following matrices:

$\begin{array}{ll}{\Lambda }_i\left(x_{i-1},x_i\right):={\text{M}}_i\left(x_i\right){\text{M}}_i^{-1}\left(x_{i-1}\right),i=\overline{2,N-1},N\ge 3.& (13)\end{array}$

Here each matrix Λ_i(x_i−1, x_i) connects the boundary values of the corresponding Wronskian matrix M_i(x) at x = x_i−1 and x = x_i. Yet, it is not obvious that the matrices Λ_i's are transmission matrices connecting the boundary conditions imposed on the wave functions ψ_i(x) at x = x_i−1 and x = x_i. To prove this fact, we compute the right-hand matrix product of (13) and obtain

$\begin{array}{ll}{\Lambda }_i\left(x_{i-1},x_i\right)=\left(\begin{array}{c}{\lambda }_{i,11}{\lambda }_{i,12}\\ {\lambda }_{i,21}{\lambda }_{i,22}\end{array}\right),& (14)\end{array}$

where

$\begin{array}{l}{\lambda }_{i,11}\left(x_{i-1},x_i\right)=\left[u_i\left(x_i\right)v_i^{\prime }\left(x_{i-1}\right)-u_i^{\prime }\left(x_{i-1}\right)v_i\left(x_i\right)\right]/W_i,\\ {\lambda }_{i,12}\left(x_{i-1},x_i\right)=\left[u_i\left(x_{i-1}\right)v_i\left(x_i\right)-u_i\left(x_i\right)v_i\left(x_{i-1}\right)\right]/W_i,\\ {\lambda }_{i,21}\left(x_{i-1},x_i\right)=\left[u_i^{\prime }\left(x_i\right)v_i^{\prime }\left(x_{i-1}\right)-u_i^{\prime }\left(x_{i-1}\right)v_i^{\prime }\left(x_i\right)\right]/W_i,\\ {\lambda }_{i,22}\left(x_{i-1},x_i\right)=\left[u_i\left(x_{i-1}\right)v_i^{\prime }\left(x_i\right)-u_i^{\prime }\left(x_i\right)v_i\left(x_{i-1}\right)\right]/W_i,& (15)\end{array}$

with the Wronskian

$\begin{array}{ll}{W}_i=W_i\left(x_{i-1}\right)=u_i\left(x_{i-1}\right)v_i^{\prime }\left(x_{i-1}\right)-u_i^{\prime }\left(x_{i-1}\right)v_i\left(x_{i-1}\right)& (16)\end{array}$

computed at x = x_i−1, which does not depend on x on the interval (x_i−1, x_i). Using Equations (15) and (16), one can check the equality

$\begin{array}{ll}\left|{\Lambda }_i\right|={\lambda }_{i,11}{\lambda }_{i,22}-{\lambda }_{i,12}{\lambda }_{i,21}=1.& (17)\end{array}$

There is an infinite number of the linearly independent solutions u_i(x) and v_i(x). The representation of the Λ_i-matrix elements can be simplified if we choose these solutions satisfying the initial conditions:

$\begin{array}{ll}{u}_i\left(x_{i-1}\right)=1,u_i^{\prime }\left(x_{i-1}\right)=0,v_i\left(x_{i-1}\right)=0,v_i^{\prime }\left(x_{i-1}\right)=1.& (18)\end{array}$

Inserting thus these conditions into Equations (15) and (16), we get that W_i = 1 and, as a result,

$\begin{array}{ll}{\Lambda }_i\left(x_{i-1},x_i\right)=\left(\begin{array}{c}{u}_i\left(x_i\right)v_i\left(x_i\right)\\ u_i^{\prime }\left(x_i\right)v_i^{\prime }\left(x_i\right)\end{array}\right).& (19)\end{array}$

The next step is to compute the product ${\Lambda }_i(x_{i-1},x_i)\mathrm{\text{col}}({\psi }_i(x_{i-1}),{\psi }_i^{\prime }(x_{i-1}))$. This computation immediately results in $\mathrm{\text{col}}({\psi }_i(x_i),{\psi }_i^{\prime }(x_i))$, so that we have the matrix relation

$\begin{array}{ll}\left(\begin{array}{c}{\psi }_i\left(x_i\right)\\ {\psi }_i^{\prime }\left(x_i\right)\end{array}\right)={\Lambda }_i\left(x_{i-1},x_i\right)\left(\begin{array}{c}{\psi }_i\left(x_{i-1}\right)\\ {\psi }_i^{\prime }\left(x_{i-1}\right)\end{array}\right),& (20)\end{array}$

confirming that Equation (13) indeed defines the transmission matrix Λ_i(x_i−1, x_i) expressed in terms of the matrices M_i(x_i−1) and M_i(x_i). Thus, each transmission matrix Λ_i(x_i−1, x_i) connects the boundary conditions at x = x_i−1 and x = x_i.

Equation (12) that connects the column vectors C₁ and C_N can be transformed to the equation connecting the boundary conditions at x = x₀ and x = x_N. To this end, we define the lateral transmission matrices Λ_i(x_i−1, x_i) with i = 0, N. Thus, on one side, one can write

$\begin{array}{ll}{\text{M}}_1\left(x_1\right){\text{C}}_1=\left(\begin{array}{c}{\psi }_1\left(x_1\right)\\ {\psi }_1^{\prime }\left(x_1\right)\end{array}\right)={\Lambda }_1\left(x_0,x_1\right)\left(\begin{array}{c}{\psi }_1\left(x_0\right)\\ {\psi }_1^{\prime }\left(x_0\right)\end{array}\right).& (21)\end{array}$

On the other hand, multiplying from the left Equation (12) by M_N(x_N) and using that

$\begin{array}{ll}{\text{M}}_N\left(x_N\right){\text{C}}_N=\left(\begin{array}{c}{\psi }_N\left(x_N\right)\\ {\psi }_N^{\prime }\left(x_N\right)\end{array}\right),& (22)\end{array}$

one finds the relation that connects the boundary conditions at x = x₀ and x = x_N:

$\begin{array}{ll}\left(\begin{array}{c}{\psi }_N\left(x_N\right)\\ {\psi }_N^{\prime }\left(x_N\right)\end{array}\right)=\Lambda \left(x_0,x_N\right)\left(\begin{array}{c}{\psi }_1\left(x_0\right)\\ {\psi }_1^{\prime }\left(x_0\right)\end{array}\right)& (23)\end{array}$

with

$\begin{array}{ll}\Lambda \left(x_0,x_N\right)={\Lambda }_N\left(x_{N-1},x_N\right)\dots {\Lambda }_1\left(x_0,x_1\right).& (24)\end{array}$

Thus, the transmission matrix for each layer defined on the interval (x_i−1, x_i) can be computed through the solutions u_i(x) and v_i(x) and their derivatives taken at the boundaries x = x_i−1 and x = x_i, resulting in the elements given by Equations (15) and (16).

2.2. Reflection-Transmission Coefficients

Consider now the solutions outside the interval (x₀, x_N). In the region x < x₀ and x > x_N where the potential is a constant, the wave function is the well-known free particle solution of the Schrödinger Equation (1) as follows

$\begin{array}{ll}{\psi }_0\left(x\right)=A_{1}exp\left[i{k}_L\left(x-x_0\right)\right]+A_{2}exp\left[-i{k}_L\left(x-x_0\right)\right]& (25)\end{array}$

for x < x₀ and

$\begin{array}{ll}{\psi }_{N+1}\left(x\right)=B_{1}exp\left[i{k}_R\left(x-x_N\right)\right]+B_{2}exp\left[-i{k}_R\left(x-x_N\right)\right]& (26)\end{array}$

for x > x_N, where $k_L:=\sqrt{E-V_L}$ and $k_R:=\sqrt{E-V_R}$. Then the continuity of the boundary conditions at x = x₀ and x = x_N leads to the following equations:

$\begin{array}{l}{\psi }_0\left(x_0\right)={\psi }_1\left(x_0\right),{\psi }_0^{\prime }\left(x_0\right)={\psi }_1^{\prime }\left(x_0\right),\\ {\psi }_N\left(x_N\right)={\psi }_{N+1}\left(x_N\right),{\psi }_N^{\prime }\left(x_N\right)={\psi }_{N+1}^{\prime }\left(x_N\right),& (27)\end{array}$

which can be represented in the matrix form as follows

$\begin{array}{ll}{\text{M}}_L\text{A}={\text{M}}_1\left(x_0\right){\text{C}}_1,{\text{M}}_N\left(x_N\right){\text{C}}_N={\text{M}}_R\text{B},& (28)\end{array}$

where A: = col(A₁, A₂), B: = col(B₁, B₂) and

$\begin{array}{ll}{\text{M}}_L:=\left(\begin{array}{c}11\\ i{k}_L-i{k}_L\end{array}\right),{\text{M}}_R:=\left(\begin{array}{c}11\\ i{k}_R-i{k}_R\end{array}\right).& (29)\end{array}$

Using these matrix equations in Equation (12), we obtain the following basic equation, which allows us to represent the reflection-transmission coefficients through the elements (15) of the transmission matrix Λ(x₀, x_N):

$\begin{array}{ll}\Lambda \left(x_0,x_N\right){\text{M}}_L\text{A}={\text{M}}_R\text{B}.& (30)\end{array}$

Thus, if there is no incidental particle coming from the right, one can set

$\begin{array}{ll}{A}_1=1,A_2=R_L,B_1=T_L,B_2=0,& (31)\end{array}$

so that in Equation (30) we have A = col(1, R_L) and B = col(T_L, 0). Similarly, if there is no incidental particle from the left, we put

$\begin{array}{ll}{A}_1=0,A_2=T_R,B_1=R_R,B_2=1,& (32)\end{array}$

hence A = col(0, T_R) and B = col(R_R, 1) in (30). Then Equation (29) becomes a set of two linear equations with respect to the pair {R_L, T_L} or {R_R, T_R}. Solving these equations and using the relation λ₁₁λ₂₂ − λ₁₂λ₂₁ = 1, we find

$\begin{array}{ll}{R}_L=-\frac{p+\text{i}q}{D},T_L=\frac{2k_L/k_R}{D},R_R=\frac{p-\text{i}q}{D},T_R=\frac{2}{D},& (33)\end{array}$

where

$\begin{array}{ll}p:={\lambda }_{11}-\left(k_L/k_R\right){\lambda }_{22},q:=k_L{\lambda }_{12}+k_R^{-1}{\lambda }_{21}& (34)\end{array}$

and

$\begin{array}{ll}D:={\lambda }_{11}+\left(k_L/k_R\right){\lambda }_{22}-\text{i}\left(k_L{\lambda }_{12}-k_R^{-1}{\lambda }_{21}\right).& (35)\end{array}$

The current $j(x)=(\text{i}/2)(\psi {\partial }_x{\psi }^{*}-{\psi }^{*}{\partial }_x\psi )$ has to be conserved across the transition region x₀ ≤ x ≤ x_N. Using the definition of the reflection-transmission coefficients given above, we find the left-to-right current $j_L(x_0)=k_L(1-|R_L{|}^2),$ $j_L(x_N)=k_R|T_L{|}^2$ and the right-to-left current $j_R(x_0)=-k_L|T_R{|}^2,$ $j_R(x_N)=-k_R(1-|R_R{|}^2)$. From the equations j_{L, R}(x₀) = j_{L, R}(x_N) we obtain the conservation law for both the directions of the current: ${R}$_{L, R} + ${T}$_{L, R} = 1, where

$\begin{array}{ll}{{R}}_L:=|R_L{|}^2,{{T}}_L:=\left(k_R/k_L\right)|T_L{|}^2,{{R}}_R:=|R_R{|}^2,{{T}}_R:=\left(k_L/k_R\right)|T_R{|}^2.& (36)\end{array}$

One can derive that $|D{|}^2=4k_L/k_R+p^2+q^2$ and, as a result, the reflection-transmission amplitudes can be represented in the form

$\begin{array}{ll}{{R}}_{L,R}=\frac{p^2+q^2}{4k_L/k_R+p^2+q^2},{{T}}_{L,R}=\frac{4k_L/k_R}{4k_L/k_R+p^2+q^2}.& (37)\end{array}$

In its turn, the scattering matrix can also be represented in terms of the elements of the transmission matrix Λ. Indeed, due to Equations (33) and (36), this representation reads

$\begin{array}{ll}S=\left(\begin{array}{c}{R}_L\sqrt{k_L/k_R}{T}_R\\ \sqrt{k_R/k_L}{T}_L{R}_R\end{array}\right)=\frac{1}{D}\left(\begin{array}{c}-p-\text{i}q2\sqrt{k_L/k_R}\\ 2\sqrt{k_L/k_R}p-\text{i}q\end{array}\right),& (38)\end{array}$

where p, q and D are defined by Equations (34) and (35).

3. Schrödinger equation and transmission matrix for the layer with a linear potential profile

Consider now the particular case of a linear potential profile for the layer defined on the interval (x_i−1, x_i). In this case the solutions u_i(x) and v_i(x) and thus the transmission matrix Λ_i(x_i−1, x_i) can be written explicitly. The Schrödinger Equation (1) for the ith layer, $i=\overline{1,N}$, can be rewritten as

$\begin{array}{ll}-{\psi }_i^{″}\left(x\right)+V_i\left(x\right){\psi }_i\left(x\right)=E{\psi }_i\left(x\right),& (39)\end{array}$

where the potential V_i(x) is a linear function defined on the interval x_i−1 < x < x_i of length l_i: = x_i − x_i−i, i.e.,

$\begin{array}{ll}{V}_i\left(x\right)={\eta }_i\left(x-x_i\right)+V_i\left(x_i\right),{\eta }_i:=\frac{V_i\left(x_i\right)-V_i\left(x_{i-1}\right)}{l_i}.& (40)\end{array}$

These equations can be transformed to the Airy equation

$\begin{array}{ll}\frac{d^2{\psi }_i\left(z_i\right)}{d{z}_i^2}-z_i{\psi }_i\left(z_i\right)=0,& (41)\end{array}$

by setting z_i(x) = σ_i(x − s_i), where the constants σ_i and s_i are given by

$\begin{array}{ll}{\sigma }_i={\eta }_i^{1/3},s_i=x_i+{\eta }_i^{-1}\left[E-V_i\left(x_i\right)\right].& (42)\end{array}$

According to the general expressions (15), we use the Airy functions of the first and the second order as linearly independent solutions to Equation (41), setting u_i(x) = Ai(z_i(x)) and v_i(x) = Bi(z_i(x)). On the interval −∞ < z_i < ∞, these solutions are real-valued. The interface (boundary) values of the (dimensionless) function z_i(x) at the edges of the ith layer, to be used in Equations (15) and (16), are

$\begin{array}{l}{z}_{i,i-1}:=z_i\left(x\right){|}_{x=x_{i-1}}=-{\eta }_i^{-2/3}{k}_{i,i-1}^2,\\ z_{i,i}:=z_i\left(x\right){|}_{x=x_i}=-{\eta }_i^{-2/3}{k}_{i,i}^2,& (43)\end{array}$

where

$\begin{array}{l}{k}_{i,i-1}:=\sqrt{E-V_{i,i-1}},k_{i,i}:=\sqrt{E-V_{i,i}},V_{i,i-1}\\ :=V_i\left(x_{i-1}\right),V_{i,i}:=V_i\left(x_i\right).& (44)\end{array}$

The Wronskian with respect to the variable z is W{Ai(z), Bi(z)} = 1/π, therefore with respect to x, it is W{Ai(z_i(x)), Bi(z_i(x))} = σ_i/π. Then the elements of the Λ_i-matrix are

$\begin{array}{l}{\lambda }_{i,11}\left(x_{i-1},x_i\right)=\pi \left[Ai\left(z_{i,i}\right)B{i}^{\prime }\left(z_{i,i-1}\right)-A{i}^{\prime }\left(z_{i,i-1}\right)Bi\left(z_{i,i}\right)\right],\\ {\lambda }_{i,12}\left(x_{i-1},x_i\right)=\left(\pi /{\sigma }_i\right)\left[Ai\left(z_{i,i-1}\right)Bi\left(z_{i,i}\right)-Ai\left(z_{i,i}\right)Bi\left(z_{i,i-1}\right)\right],\\ {\lambda }_{i,21}\left(x_{i-1},x_i\right)={\sigma }_i\pi \left[A{i}^{\prime }\left(z_{i,i}\right)B{i}^{\prime }\left(z_{i,i-1}\right)-A{i}^{\prime }\left(z_{i,i-1}\right)B{i}^{\prime }\left(z_{i,i}\right)\right],\\ {\lambda }_{i,22}\left(x_{i-1},x_i\right)=\pi \left[Ai\left(z_{i,i-1}\right)B{i}^{\prime }\left(z_{i,i}\right)-A{i}^{\prime }\left(z_{i,i}\right)Bi\left(z_{i,i-1}\right)\right],& (45)\end{array}$

where the prime denotes the differentiation with respect to z.

In the η_i → 0 limit as V_i(x_i−1) → V_i(x_i), we obtain

$\begin{array}{ll}{z}_i\left(x\right)\to -{\sigma }_i{s}_i={\sigma }_i\left[-x_i-\frac{E-V_i\left(x_i\right)}{{\sigma }_i^3}\right]\to {\sigma }_i^{-2}\left[V_i\left(x_i\right)-E\right],& (46)\end{array}$

yielding Equation (39) with a constant profile V_i(x) ≡ V_i. In this limit case, one can choose the linearly independent solutions to Equation (39) as

$\begin{array}{l}{u}_i\left(x\right)=cos\left[k_i\left(x-x_{i-1}\right)\right],\\ v_i\left(x\right)=k_i^{-1}sin\left[k_i\left(x-x_{i-1}\right)\right],k_i:=\sqrt{k^2-V_i},& (47)\end{array}$

satisfying the initial conditions (18). Therefore, due to Equations (19) and (47), the Λ_i-matrix becomes

$\begin{array}{ll}{\Lambda }_i\left(x_{i-1},x_i\right)=\left(\begin{array}{c}cos\left(k_i{l}_i\right)k_i^{-1}sin\left(k_i{l}_i\right)\\ -k_{i}sin\left(k_i{l}_i\right)cos\left(k_i{l}_i\right)\end{array}\right).& (48)\end{array}$

4. Asymptotic representations of the single-layer transmission matrix

Similarly to the previous section, here we also focus on one of the layers and for brevity of notations we replace for while in the above expressions the subscripts {i, i − 1} and {i, i} by “0” and “1”, respectively. Then, according to Equations (43) and (44), we write

$\begin{array}{l}{z}_0=-{\left(\frac{l}{V_1-V_0}\right)}^{2/3}{k}_0^2,z_1=-{\left(\frac{l}{V_1-V_0}\right)}^{2/3}{k}_1^2,\\ \sigma ={\left(\frac{V_1-V_0}{l}\right)}^{1/3},& (49)\end{array}$

where we have replaced V_{i, i−1}, V_{i, i}, k_{i, i−1}, k_{i, i} by V₀, V₁, k₀, k₁, respectively. Using next the two asymptotic expressions for the Airy functions and their derivatives known in the limit as z → 0 and z → ±∞, below we will derive the corresponding asymptotic representations of the elements (45) in the two limits as (i) z₀, z₁ → 0 and (ii) z₀, z₁ → ±∞. It is reasonable to assume that everywhere z₀ and z₁ are of the same sign. We omit for a while the subscript “i” for the matrix Λ_i and its elements.

4.1. Asymptotic Representation of the Λ-Matrix in the Limit as z₀, z₁ → 0

For the z₀, z₁ → 0 limit to be carried out in Equation (45), one can use the series representation of the Airy functions and their first derivatives in the neighborhood of the origin z = 0. It is sufficient to explore only the two first terms:

$\begin{array}{l}Ai\left(z\right)\to \frac{1}{3^{2/3}\Gamma \left(2/3\right)}-\frac{z}{3^{1/3}\Gamma \left(1/3\right)}+\dots ,\\ A{i}^{\prime }\left(z\right)\to -\frac{1}{3^{1/3}\Gamma \left(1/3\right)}+\frac{z^2}{2·3^{2/3}\Gamma \left(2/3\right)}+\dots ,\\ Bi\left(z\right)\to \frac{1}{3^{1/6}\Gamma \left(2/3\right)}+\frac{3^{1/6}z}{\Gamma \left(1/3\right)}+\dots ,\\ B{i}^{\prime }\left(z\right)\to \frac{3^{1/6}}{\Gamma \left(1/3\right)}+\frac{z^2}{2·3^{1/6}\Gamma \left(2/3\right)}+\dots .& (50)\end{array}$

As a result of applying these expansion formulae to Equation (45) and using Euler's reflection formula for the gamma function, Γ(1 − z)Γ(z) = π/sin(πz), z ∉ ℤ, we get the following asymptotic representation of the Λ-matrix elements:

$\begin{array}{l}{\lambda }_{11}\to 1-z_0^2{z}_1/2,{\lambda }_{22}\to 1-z_0{z}_1^2/2,\\ {\lambda }_{12}\to \frac{z_1-z_0}{\sigma }=l,{\lambda }_{21}\to \frac{\sigma }{2}\left(z_1^2-z_0^2\right)=-\frac{l}{2}\left(k_0^2+k_1^2\right)& (51)\end{array}$

as z₀, z₁ → 0.

4.2. Asymptotic Representation of the Λ-Matrix in the Limit as z₀, z₁ → ±∞

In the limit as z → −∞, for the Airy functions and their derivatives we have the following asymptotics:

$\begin{array}{ll}Ai\left(z\right)\to \frac{sin\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]}{\sqrt{\pi }{\left(-z\right)}^{1/4}},Bi\left(z\right)\to \frac{cos\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]}{\sqrt{\pi }{\left(-z\right)}^{1/4}},& (52)\end{array}$

$\begin{array}{l}A{i}^{\prime }\left(z\right)\to \frac{\frac{1}{4}{\left(-z\right)}^{-3/4}sin\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]-{\left(-z\right)}^{3/4}cos\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]}{\sqrt{\pi }{\left(-z\right)}^{1/2}},\\ B{i}^{\prime }\left(z\right)\to \frac{\frac{1}{4}{\left(-z\right)}^{-3/4}cos\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]+{\left(-z\right)}^{3/4}sin\left[\frac{2}{3}{\left(-z\right)}^{3/2}+\pi /4\right]}{\sqrt{\pi }{\left(-z\right)}^{1/2}}.& (53)\end{array}$

Using this asymptotic representation in Equations (45) as z₀, z₁ → −∞, we obtain

$\begin{array}{l}{\lambda }_{11}\to {(-z_0)}^{1/4}{(-z_1)}^{-1/4}cos{\chi }_{-}-{(4z_0)}^{-1}{(-z_0)}^{-1/4}{(-z_1)}^{-1/4}sin{\chi }_{-},\\ {\lambda }_{12}\to -{\sigma }^{-1}{(-z_0)}^{-1/4}{(-z_1)}^{-1/4}sin{\chi }_{-},\\ {\lambda }_{21}\to \sigma {(-z_0)}^{-1/2}{(-z_1)}^{-1/2}\\ \times \{\left[{(-z_0)}^{3/4}{(-z_1)}^{3/4}+4^{-2}{(-z_0)}^{-3/4}{(-z_1)}^{-3/4}\right]sin{\chi }_{-}\\ +4^{-1}\left[{(-z_0)}^{3/4}{(-z_1)}^{-3/4}-{(-z_1)}^{3/4}{(-z_0)}^{-3/4}\right]cos{\chi }_{-}\},\\ {\lambda }_{22}\to {(-z_1)}^{1/4}{(-z_0)}^{-1/4}cos{\chi }_{-}+{(4z_1)}^{-1}{(-z_0)}^{-1/4}{(-z_1)}^{-1/4}sin{\chi }_{-},& (54)\end{array}$

where

$\begin{array}{ll}{\chi }_{-}:=\frac{2}{3}\left[{(-z_1)}^{3/2}-{(-z_0)}^{3/2}\right].& (55)\end{array}$

One can check that |Λ| = λ₁₁λ₂₂ − λ₁₂λ₂₁ = 1. According to Equations (50), this representation corresponds to a well (V_j < 0, j = 0, 1). However, these formulae can be “continued” to positive values of z₀ and z₁ that correspond to a barrier with E < V_j. To prove this, we use the asymptotic representation of the Airy functions and their derivatives in the limit as z₀, z₁ → +∞:

$\begin{array}{ll}Ai(z)\to \frac{{\text{e}}^{-\frac{2}{3}{z}^{3/2}}}{2\sqrt{\pi }{z}^{1/4}},Bi(z)\to \frac{{\text{e}}^{\frac{2}{3}{z}^{3/2}}}{\sqrt{\pi }{z}^{1/4}},& (56)\end{array}$

$\begin{array}{ll}A{i}^{\prime }\left(z\right)\to -\frac{z^{3/4}+\frac{1}{4}{z}^{-3/4}}{2\sqrt{\pi }{z}^{1/2}}{\text{e}}^{-\frac{2}{3}{z}^{3/2}},B{i}^{\prime }\left(z\right)\to \frac{z^{3/4}-\frac{1}{4}{z}^{-3/4}}{\sqrt{\pi }{z}^{1/2}}{\text{e}}^{\frac{2}{3}{z}^{3/2}}& (57)\end{array}$

and, as a result, we find

$\begin{array}{l}{\lambda }_{11}\to {(z_0/z_1)}^{1/4}cosh{\chi }_{+}+{(4z_0)}^{-1}{(z_0{z}_1)}^{-1/4}sinh{\chi }_{+},\\ {\lambda }_{12}\to {\sigma }^{-1}{(z_0{z}_1)}^{-1/4}sinh{\chi }_{+},\\ {\lambda }_{21}\to \sigma {(z_0{z}_1)}^{-1/2}\{\left[{(z_0{z}_1)}^{3/4}-4^{-2}{(z_0{z}_1)}^{-3/4}\right]sinh{\chi }_{+}\\ +4^{-1}\left[{(z_1/z_0)}^{3/4}-{(z_0/z_1)}^{3/4}\right]cosh{\chi }_{+}\},\\ {\lambda }_{22}\to {(z_1/z_0)}^{1/4}cosh{\chi }_{+}-{(4z_1)}^{-1}{(z_0{z}_1)}^{-1/4}sinh{\chi }_{+},& (58)\end{array}$

where z₀ and z₁ are positive and

$\begin{array}{ll}{\chi }_{+}:=\frac{2}{3}\left(z_1^{3/2}-z_0^{3/2}\right).& (59)\end{array}$

Similarly, for the elements (58) one can also check that |Λ| = 1. In fact, Equations (58) with (59) appear to coincide with Equations (54) and (55) if we assume that in the latter equations z₀ and z₁ are positive. To show this, we note that (−z)^3/2 = i³z^3/2 = −iz^3/2 and, as a result, we get the relation χ₋ = −iχ₊ for positive z₀ and z₁ in both Equations (55) and (59). Next, the elements (58) are obtained from the representation (54) if we note that ${(-z_0)}^{1/4}{(-z_1)}^{1/4}=\text{i}{(z_0{z}_1)}^{1/4}$, ${(-z_0)}^{1/2}{(-z_1)}^{1/2}=-{(z_0{z}_1)}^{1/2}$ and ${(-z_0)}^{3/4}{(-z_1)}^{3/4}=-\text{i}{(z_0{z}_1)}^{3/4}$. Therefore, in the following it is sufficient to consider only the representation given by Equations (54) and (55), being valid for both negative and positive z₀ and z₁.

Using the explicit values for z₀ and z₁ given by Equations (49), the expression (55) for χ₋ can be transformed to

$\begin{array}{ll}{\chi }_{-}=\text{sgn}\left(V_0-V_1\right)k_{1,0}l,& (60)\end{array}$

where

$\begin{array}{ll}{k}_{1,0}:=\frac{2(k_0^2+k_1^2+k_0{k}_1)}{3\left(k_0+k_1\right)},k_j:=\sqrt{E-V_j}j=0,1.& (61)\end{array}$

Inserting next the expressions (49) and (60) into Equations (54), one can write the elements of the Λ-matrix in terms of k₀ and k₁ as follows

$\begin{array}{l}{\lambda }_{11}\to {\left(\frac{k_0}{k_1}\right)}^{1/2}cos\left(\kappa l\right)+\frac{k_1^2-k_0^2}{4l}{k}_0^{-5/2}{k}_1^{-1/2}sin\left(k_{1,0}l\right),\\ {\lambda }_{12}\to k_0^{-1/2}{k}_1^{-1/2}sin\left(k_{1,0}l\right),\\ {\lambda }_{21}\to \frac{3{\left(k_0^2-k_1^2\right)}^2{k}_{1,0}}{8l{k}_0^{5/2}{k}_1^{5/2}}cos\left(k_{1,0}l\right)\\ -k_0^{1/2}{k}_1^{1/2}\left[1+{\left(\frac{k_0^2-k_1^2}{4l}\right)}^2{k}_0^{-3}{k}_1^{-3}\right]sin\left(k_{1,0}l\right),\\ {\lambda }_{22}\to {\left(\frac{k_1}{k_0}\right)}^{1/2}cos\left(\kappa l\right)+\frac{k_0^2-k_1^2}{4l}{k}_0^{-1/2}{k}_1^{-5/2}sin\left(k_{1,0}l\right),& (62)\end{array}$

where k_{1, 0} is defined by Equation (61). One can check that the matrix elements (62) together with the argument (61) satisfy the condition |Λ| = 1. Note that the only restriction for the existence of the representation (62) are the asymptotics z₀, z₁ → ±∞. Both k₀ and k₁ are either real-valued or imaginary. In the particular case V₁ = V₀ (k₁ = k₀), Equations (61) and (62) reduce to the matrix representation (48).

5. Realization of point interactions in the zero-thickness limit for one layer

Keeping in the following the same notations with respect to the subscripts “0” and “1”, let us consider the linear potential (40) rewritten as

$\begin{array}{ll}V\left(x\right)=V_0+\frac{V_1-V_0}{l}x,V_0,V_1\in ℝ,& (63)\end{array}$

on the interval 0 < x < l, where V₀ and V₁ are the potential values at the left and right edges of the layer with width l. Consider first the case when this potential is constant, i.e., V₀ = V₁. A point interaction can be realized in the limit as the layer thickness l → 0, whereas V₀ → ±∞. To this end, one can use the parametrization of the potential V(x) ≡ V₀ introducing a dimensionless parameter ε > 0 that controls the shrinking of the layer to zero width as ε → 0. It is natural to consider the power parametrization setting

$\begin{array}{ll}{V}_0=a{\epsilon }^{-\mu },l=\epsilon d,a\in ℝ,\mu ,d>0.& (64)\end{array}$

In the squeezed limit (as ε → 0), a one-parameter family of point interactions at x = 0 is realized. It is determined by the power μ ∈ (0, ∞): the transmission is perfect for μ ∈ (0, 1), at μ = 1 the potential takes the form of Dirac's delta function αδ(x) with the transmission matrix (4), where α = ad is the strength of the δ-interaction, and for μ ∈ (1, ∞) the interaction acts as a fully reflecting wall satisfying the Dirichlet boundary condition ψ(±0) = 0 for the wave function ψ(x).

In the case when the difference V₁ − V₀ is non-zero, as shown in Figure 1, one deals with two potential values V₀ and V₁ at the layer edges that must tend to infinity in the zero-thickness limit. Both the potential values V₀ and V₁ are supposed to be of the same sign. In general, the rate of this divergence to infinity can differ and therefore the parametrization of the potential (63) should involve two parameters. We introduce the two powers μ and ν, where the parameters μ and ν describe how rapidly the potential V₀ at the left layer edge and the difference V₁ − V₀ tend (escape) to infinity as ε → 0, respectively. The particular case when this difference is a constant not depending on ε can also be included. Thus, we set

$\begin{array}{l}{V}_0=a{\epsilon }^{-\mu },\\ V_1=V_0+b{\epsilon }^{-\nu },0<\mu <\infty ,0\le \nu \le \mu ,a,b\in ℝ,l=\epsilon d,& (65)\end{array}$

including the following two situations in the squeezed limit: (i) V₁ − V₀ is constant (ν = 0) and (ii) the “escaping-to-infinity” rate of V₁ − V₀ does not exceed the rate of V₀ (ν ≤ μ). In the electronics domain the difference V₁ − V₀ or b may play the role of a bias voltage.

FIGURE 1

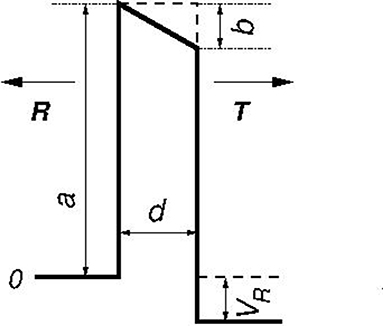
Figure 1. Schematics of one-layer potential (63) tilted by difference V₁ − V₀ (solid line) with notations given in (65) at ε = 1: V₁ − V₀ = b = V_R. The dashed line represents potential with b = 0.

Due to Equations (43), we have the asymptotics $z_0,z_1~{\epsilon }^{2(1+\nu )/3-\mu }$. Consequently, the line L_{0, ∞}: = {0 < μ ≤ 2, ν = 3μ/2 − 1} separates the asymptotic representations z₀, z₁ → 0 and z₀, z₁ → ±∞ on the (μ, ν)-plane as illustrated by the diagram depicted in Figure 2. Here, we have the two triangle sets:

$\begin{array}{l}{S}_0:=\left\{0<\mu <2,max\left\{0,3\mu /2-1\right\}<\nu \le \mu \right\}\\ \cup \left\{0<\mu <2/3,\nu =0\right\},\\ S_{\infty }:=\left\{2/3<\mu \le 2,0\le \nu <3\mu /2-1\right\},& (66)\end{array}$

where the asymptotic representations z₀, z₁ → 0 and z₀, z₁ → ±∞ take place, respectively. The corresponding angles are formed by the boundary lines: S₀ by L_{0, 1}: = {0 < μ < 2/3, ν = 0}, L_{0, 2}: = {0 < μ < 2, ν = μ} and S_∞ by L_{∞, 1}: = {2/3 < μ ≤ 2, ν = 0}, L_{∞, 2}: = {μ = 2, 0 < ν < 2}.

FIGURE 2

Figure 2. Regions of asymptotic representations z₀, z₁ → 0 (S₀) and z₀, z₁ → ±∞ (S_∞) with separating line L_0,∞. Three balls indicate characteristic points P_1,1 : = {μ = ν = 1} ∈ S₀, P_2,0 : = {μ = 2, ν = 0} ∈ S_∞ and P_2,1 : = {μ = 2, ν = 1} ∈ S_∞.

5.1. Point Interactions Realized in the Limit as z₀, z₁ → 0

Let us consider the boundary lines L_{0, 1} and L_{0, 2} of the angle S₀. On the line L_{0, 1}, we find that $z_0,z_1~{\epsilon }^{2/3-\mu }$, so that the z₀, z₁ → 0 limit takes place on the interval 0 < μ < 2/3. Next, we have $k_0^2,k_1^2~{\epsilon }^{-\mu }$ and according to Equations (51), λ₁₂ → 0 and ${\lambda }_{21}~{\epsilon }^{1-\mu }\to 0$, so that the Λ-matrix becomes the identity (Λ = I) because μ < 1.

Similarly, on the line L_{0, 2}, where $z_0,z_1~{\epsilon }^{(2-\mu )/3}$, from Equations (49) and (51) we get the asymptotics

$\begin{array}{l}{\lambda }_{11}\to 1-c_1{\epsilon }^{2-\mu },{\lambda }_{12}\to \epsilon d,\\ {\lambda }_{21}\to \left(a+b/2\right)d{\epsilon }^{1-\mu },{\lambda }_{22}\to 1-c_2{\epsilon }^{2-\mu }& (67)\end{array}$

with

$\begin{array}{ll}{c}_1:=\left(a^2/2\right)\left(a+b\right){\left(d/b\right)}^2,c_2:=\left(a/2\right){\left(a+b\right)}^2{\left(d/b\right)}^2.& (68)\end{array}$

Therefore, on the interval 0 < μ < 1 the transmission matrix is the identity I, while on the interval 1 < μ < 2 the transmission matrix does not exist. In this case the point interaction acts as a fully reflecting wall (the boundary conditions for this point interaction are of the Dirichlet type). The value μ = 1 describes the intermediate situation with a partial transmission through the system, namely the δ-interaction with bias b, which separates both these regimes. The limit transmission matrix (as ε → 0) corresponds to the δ-interaction described by the connection matrix (4) with the strength constant

$\begin{array}{ll}\alpha =\left(a+b/2\right)d.& (69)\end{array}$

This result also includes the constant case when V₀ = V₁, i.e., b = 0. This approximation is appropriate for modeling the δ-potential. Note that similar analysis can be done for μ and ν belonging to the interior of S₀. In this case in the above equations we have to set b = 0.

Using the second formula (37), one can compute the transmission amplitude for this δ-interaction. We get

$\begin{array}{ll}{T}=\frac{4k{k}_R}{{\left(k+k_R\right)}^2+{\alpha }^2},& (70)\end{array}$

where α is given by (69). In the unbiased case (b = 0, k_R = k) this formula reduces to ${T}$ = [1 + (α/2k)²]⁻¹ with α = ad, the well known expression for the constant potential. Equation (70) has been obtained for any a ∈ ℝ. However, for negative values of a, i.e., for a δ-like well, it does not describe the oscillating behavior with respect to the constant α that takes place under tunneling across a well with finite thickness l.

5.2. Point Interactions Realized in the Limit as z₀, z₁ → ±∞

Consider now the characteristic point P_{2, 1} ∈ S_∞ setting in Equation (62) μ = 2 and ν = 1. Here $k_0^2-k_1^2=V_1-V_0=b{\epsilon }^{-1}$ and $k_0,k_1,k_{1,0}\to \sqrt{-a}{\epsilon }^{-1}$, so that the asymptotic representation of Equation (62) in the limit as ε → 0 becomes

$\begin{array}{l}{\lambda }_{11}\to cos\left(\kappa d\right)-\epsilon gsin\left(\kappa d\right),\\ {\lambda }_{12}\to \epsilon {\kappa }^{-1}sin\left(\kappa d\right),\\ {\lambda }_{21}\to -{\epsilon }^{-1}\kappa sin\left(\kappa d\right)+{O}\left(\epsilon \right),\\ {\lambda }_{22}\to cos\left(\kappa d\right)+\epsilon gsin\left(\kappa d\right),& (71)\end{array}$

where

$\begin{array}{ll}\kappa :=\sqrt{-a},g:={\kappa }^{-3}\left(b/4d\right).& (72)\end{array}$

As follows from these asymptotic expressions derived at the point P_{2, 1}, in the limit as ε → 0, the transmission through a barrier is zero, while across a well (a < 0) it appears to be resonant. The resonance set consists of the roots of the equation sin(κd) = 0. At fixed d > 0, these roots form the countable set $\Sigma ={\cup }_{n=0}^{\infty }{\sigma }_n$ formed from the points ${\sigma }_n:=-{(n\pi /d)}^2$. On this resonance set, the discrete-valued matrix is ${\Lambda }_n:=\Lambda {|}_{\Sigma }={(-1)}^{n}I$. Beyond these resonance values, the δ-like well is opaque and, instead of the identity matrix I, the two-sided boundary conditions for the wave function are of the Dirichlet type: (ψ(±0) = 0).

6. Multi-layered heterostructures with bias

Now we are ready to apply the expressions obtained above for a single layer to the total structure consisting of an arbitrary number N of layers replacing μ → μ_i, ν → ν_i, b → b_i, d → d_i. Taking for account that the left boundary value for the potential of the ith layer a_i is shifted because of the biases b₁, …b_i−1 in the left-hand layers, we need to use the following replacement rule:

$\begin{array}{ll}a\to a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j,i=\overline{1,N},& (73)\end{array}$

where the sum vanishes if i = 1. Then Equation (65) are transformed to

$\begin{array}{l}{V}_0\to V_{i,i-1}=\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right){\epsilon }^{-{\mu }_i},\\ V_1\to V_{i,i}=V_{i,i-1}+b_i{\epsilon }^{-{\nu }_i}.& (74)\end{array}$

Next, all the other expressions derived above should be rewritten for the ith layer using the following replacement rules:

$\begin{array}{l}{z}_0\to z_{i,i-1}={\left(\frac{d_i}{b_i}\right)}^{2/3}\left[\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right){\epsilon }^{-{\mu }_i}-E\right]{\epsilon }^{2\left(1+{\nu }_i\right)/3},\\ z_1\to z_{i,i}={\left(\frac{d_i}{b_i}\right)}^{2/3}\left[\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right){\epsilon }^{-{\mu }_i}+b_i{\epsilon }^{-{\nu }_i}-E\right]{\epsilon }^{2\left(1+{\nu }_i\right)/3},\\ \alpha \to {\alpha }_i=\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j+b_i/2\right)d_i,\sigma \to {\sigma }_i=(\frac{b_i}{d_i}{)}^{1/3}{\epsilon }^{-\left(1+{\nu }_i\right)/3},\\ \kappa \to {\kappa }_i=\sqrt{-\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right)},g\to g_i=\frac{b_i}{4{\kappa }_i^3{d}_i},\\ c_1\to c_{i,1}=\frac{1}{2}{\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right)}^2\left(a_i+{\displaystyle \sum _{j=1}^i}{b}_j\right){\left(\frac{d_i}{b_i}\right)}^2,\\ c_2\to c_{i,2}=\frac{1}{2}\left(a_i+{\displaystyle \sum _{j=1}^{i-1}}{b}_j\right){\left(a_i+{\displaystyle \sum _{j=1}^i}{b}_j\right)}^2{\left(\frac{d_i}{b_i}\right)}^2.& (75)\end{array}$

In the following we will consider some particular examples of multi-layered structures with N = 2, 3. It will be shown that in some cases two- and three-lateral quantum devices can be approximated by one-point interactions.

6.1. Two-Layered Structures

Consider now the structure consisting of two layers (N = 2). The piecewise linear potential of a barrier-well form is shown in Figure 3. For an arbitrary two-layered structure, the limit transmission matrix is the product Λ = Λ₂Λ₁, where the matrices Λ_i's can be constructed from the asymptotic approximations (67) and (71) by applying the replacement rules (73)–(75). Applying these rules in Equations (67), (68) and (71), (72) to the matrices Λ₁ and Λ₂, below we compute their product for two different situations. Note that due to the presence of the factor ε⁻¹ in the expression λ₂₁ [see Equation (71)], the terms of order ${O}$(ε) must be kept in the product Λ₂Λ₁ because $\underset{\epsilon \to 0}{lim}{\Lambda }_2·\underset{\epsilon \to 0}{lim}{\Lambda }_1\ne \underset{\epsilon \to 0}{lim}({\Lambda }_2{\Lambda }_1)$.

FIGURE 3

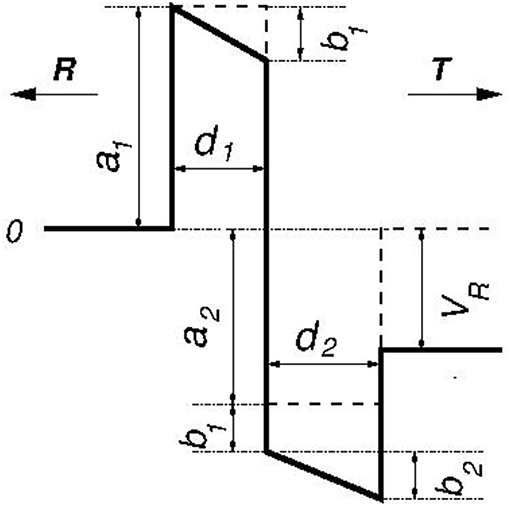
Figure 3. Schematics of tilted (solid line) and piecewise constant (dashed line) barrier-well potential, where notations correspond to Equations (73) and (74) for N = 2 and ε = 1. Potential values at layer edges are V_1,0 = a₁, V_1,1 = a₁ + b₁ (barrier, a₁ > 0) and V_2,1 = a₂ + b₁, V_2,2 = a₂ + b₁ + b₂ (well, a₂ < 0). Polarity is shown positive (left-to-right electron flow, b₁, b₂ < 0). Dashed lines show unbiased potential (b₁ = b₂ = 0).

Point interactions of a δ′-type: Consider the zero-thickness limit determined by the powers μ₁ = μ₂ = 2 and ν₁ = ν₂ = 1. Then, the product Λ = Λ₂Λ₁ yields the following asymptotic representation of the Λ-matrix elements for the total double-layer system:

$\begin{array}{l}{\lambda }_{11}\to cos\left({\kappa }_1{d}_1\right)cos\left({\kappa }_2{d}_2\right)-\left({\kappa }_1/{\kappa }_2\right)sin\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right),\\ {\lambda }_{12}\to 0,\\ {\lambda }_{21}\to \alpha -{\epsilon }^{-1}\left[{\kappa }_{1}sin\left({\kappa }_1{d}_1\right)cos\left({\kappa }_2{d}_2\right)+{\kappa }_{2}cos\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right)\right],\\ {\lambda }_{22}=cos\left({\kappa }_1{d}_1\right)cos\left({\kappa }_2{d}_2\right)-\left({\kappa }_2/{\kappa }_1\right)sin\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right),& (76)\end{array}$

where the ε → 0 limit has been performed and

$\begin{array}{ll}\alpha =\left({\kappa }_2{g}_1-{\kappa }_1{g}_2\right)sin\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right).& (77)\end{array}$

The second term in the element λ₂₁ diverges as ε → 0 and it vanishes if the equation

$\begin{array}{ll}{\kappa }_{1}tan\left({\kappa }_1{d}_1\right)+{\kappa }_{2}tan\left({\kappa }_2{d}_2\right)=0& (78)\end{array}$

takes place. Using this equation in the elements λ₁₁ and λ₂₂ [see Equation (76)], we find the total transmission matrix

$\begin{array}{ll}\Lambda =\left(\begin{array}{c}cos\left({\kappa }_1{d}_1\right)/cos\left({\kappa }_2{d}_2\right)0\\ \alpha cos\left({\kappa }_2{d}_2\right)/cos\left({\kappa }_1{d}_1\right)\end{array}\right).& (79)\end{array}$

Equation (78) admits a countable set of solutions if at least one of the layer potential has a well profile. In particular, if a₁ > 0 (barrier) and a₂ + b₁ < 0 (well), Equation (78) reduces to

$\begin{array}{ll}\sqrt{a_1}tanh(\sqrt{a_1}{d}_1)=\sqrt{|a_2+b_1|}tan(\sqrt{|a_2+b_1|}{d}_2).& (80)\end{array}$

It is reasonable to assume that −b₁ < a₁ (otherwise the right-edge barrier potential becomes negative), so that on the interval (−a₁, 0), under appropriate values of the layer parameters, only a finite set of discrete (resonance) values of b₁ can be found. According to the classification of point interactions given in Brasche and Nizhnik [32], the interactions described by the connection matrix with diagonal elements λ₁₁, λ₂₂ ≠ 1 may be referred to as a family of (resonant) δ′-potentials, despite the distribution δ′(x) in general does not exist. Similarly to the single δ-well potential, beyond the resonance set, the two-sided boundary conditions are of the Dirichlet type: ψ(±0) = 0.

On the resonance set Σ = ∪_nσ_n, the explicit expressions for the Λ-matrix (79) and the element (77) become

$\begin{array}{ll}\Lambda {|}_{\Sigma }=\left(\begin{array}{c}{\theta }_{n}0\\ {\alpha }_n{\theta }_n^{-1}\end{array}\right),& (81)\end{array}$

where

$\begin{array}{l}{\theta }_n=\frac{cosh(\sqrt{a_1}{d}_1)}{cos(\sqrt{|a_2+b_{1,n}|}{d}_2)}\ne \pm 1,\\ {\alpha }_n=\frac{1}{4}\left[\frac{\sqrt{a_1}{b}_2}{|a_2+b_{1,n}{|}^{3/2}{d}_2}-\frac{\sqrt{|a_2+b_{1,n}|}{b}_{1,n}}{a_1^{3/2}{d}_1}\right]\\ \times sinh(\sqrt{a_1}{d}_1)sin(\sqrt{|a_2+b_{1,n}|}{d}_2).& (82)\end{array}$

The transmission amplitude on the resonance set Σ is

$\begin{array}{ll}{{T}}_n=\frac{4k{k}_{R,n}}{{\left(k{\theta }_n^{-1}+k_{R,n}{\theta }_n\right)}^2+{\alpha }_n^2},& (83)\end{array}$

where $k_{R,n}=\sqrt{k^2-b_{1,n}}$.

Resonant transmission through a δ-barrier: Let us consider now the two-layered structure in which the potential of one of the layers in the squeezed limit has a δ-like form. We specify this situation by the power parameters μ₁ = ν₁ = 1 (point P_{1, 1} ∈ S₀) for the barrier, and μ₂ = 2 and ν₂ = 1 (point P_{2, 1} ∈ S_∞) for the well. Even in the unbiased case this potential has no distributional limit, however the transmission matrix does exist. Applying the replacement rules (73)-(75) in the asymptotics (67) with μ = 1 yielding the Λ₁-matrix, and in the representation (71) creating the Λ₂-matrix, we obtain the ε → 0 limit for the elements of the total matrix Λ = Λ₂Λ₁ in the form

$\begin{array}{l}{\lambda }_{11}\to cos\left({\kappa }_2{d}_2\right),\\ {\lambda }_{12}\to 0,\\ {\lambda }_{21}\to {\alpha }_{1}cos\left({\kappa }_2{d}_2\right)+c_{1,1}{\kappa }_{2}sin\left({\kappa }_2{d}_2\right)-{\epsilon }^{-1}{\kappa }_{2}sin\left({\kappa }_2{d}_2\right),\\ {\lambda }_{22}\to cos\left({\kappa }_2{d}_2\right)-{\kappa }_2{d}_{1}sin\left({\kappa }_2{d}_2\right).& (84)\end{array}$

While the first and the second terms in λ₂₁ are finite, the third one diverges as ε → 0. However, it vanishes at the values satisfying the equation sin(κ₂d₂) = 0, i.e., for

$\begin{array}{ll}{a}_2+b_{1,n}=-{\left(n\pi /d_2\right)}^2,& (85)\end{array}$

where the integer n = n₀, n₀ + 1, … with some n₀. These values form the countable resonance set Σ on which the transmission matrix Λ corresponds to the δ-interaction, whereas beyond this set the interaction acts as a fully reflecting wall. The limit transmission matrix is

$\begin{array}{ll}\Lambda {|}_{\Sigma }={\left(-1\right)}^n\left(\begin{array}{c}10\\ {\alpha }_{n}1\end{array}\right),& (86)\end{array}$

where α_n = α_{1, n} = (a₁ + b_{1, n})/2)d₁. Note that the effect of the resonant transmission through a δ-barrier keeps to be valid in the unbiased case when b₁ = b₂ = 0.

Thus, we have realized the resonant δ-interaction, due to the presence of an adjacent well with depth a₂ < 0. In the case when the system parameters a₁, a₂, d₁, d₂ are supposed to be fixed, the biased potential b₁ may be considered as a tunable parameter. The transmission is resonant on the set given by (85). The potential at the right edge of the first layer keeps to be positive for all values of b₁ satisfying the inequality −b₁ < a₁. Therefore, this is a constraint that limits the resonance set to a finite number of resonances.

The existence of the resonant tunneling through a δ-like barrier can be supported numerically calculating the transmission amplitude ${T}$ according to Equations (37) and (34), where the matrix elements are given by Equation (45). For different values of the squeezing parameter ε, the result of these calculations is illustrated by Figure 4.

FIGURE 4

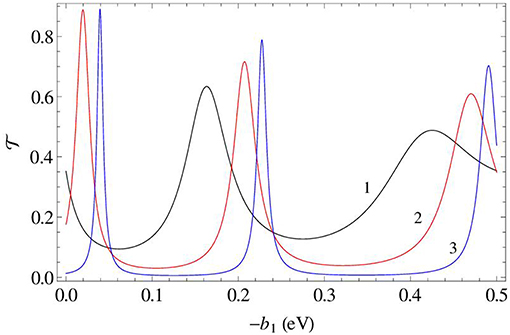
Figure 4. Transmission amplitude ${T}$ as a function of bias −b₁ plotted for parameter values: E = 0.1 eV, a₁ = 0.5 eV, a₂ = −0.1 eV, d₁ = 2 nm, d₂ = 10 nm. Computations have been carried out with powers μ₁ = ν₁ = 1 (point P_1,1) and μ₂ = 2, ν₂ = 1 (point P_2,1). Squeezing scenario is displayed for ε = 0.5 (curve 1, black), 0.25 (curve 2, red), and 0.1 (curve 3, blue). Location of all three peaks converges to set {−b_1,n} defined by Equation (85) with n = 2, 3, 4.

6.2. Modeling of Point Transistors

It is of interest to give an interpretation for a semiconductor transistor in the limit as its dimensions are extremely tiny. This is a three-terminal device [76] described by a tilted double-barrier potential profile as illustrated by Figure 5. Here the potential between the barriers is constant depending on the emitter-to-base voltage V_EB as a parameter tuned externally. The other external parameter V_CB is the collector-to-base voltage being fixed. For the description of this device by a one-point interaction model, we assume that in the zero-thickness limit both the barriers as well as the distance between them tend to the point x = 0.

FIGURE 5

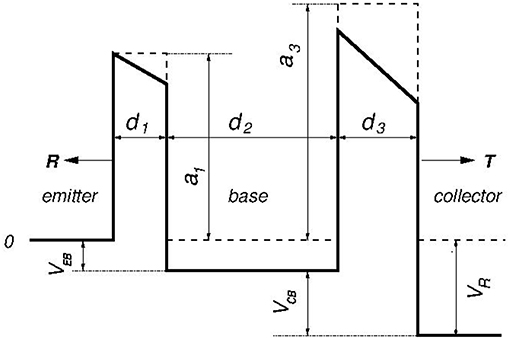
Figure 5. Schematics of typical transistor, where notations correspond to Equations (73) and (74) for N = 3 and ε = 1 with replacement: b₁ → −V_EB (emitter-to-base voltage) and b₃ → −V_CB (collector-to-base voltage). Potential values at layer edges are V_1,0 = a₁, V_1,1 = a₁ − V_EB (a₁ > 0), V_2,1 = V_2,2 = −V_EB and V_3,2 = a₃ − V_EB, V_3,3 = a₃ + V_R (a₃ > 0). Polarity is shown to be positive (left-to-right electron flow, V_EB, V_CB > 0).

Similarly to the double-layer structure [see the general formula (24)], the transmission matrix for the total system is the product Λ = Λ₃Λ₂Λ₁, where the matrices Λ₁ and Λ₃ correspond to the barriers and the Λ₂-matrix to the space between the barriers. Setting b₁ ≡ −V_EB, b₂ = 0 and b₃ ≡ −V_CB, according to (73), we replace: a → a₁ for Λ₁, a → −V_EB (a₂ = 0) for Λ₂ and a → a₃ − V_EB for Λ₃. In the case of positive polarity, as shown in the figure, both the voltages are non-negative parameters. Applying next the replacement rules (75) in the terms (68), (69), and (72), we write the following explicit expressions for the matrices Λ₁ and Λ₃:

$\begin{array}{l}{\kappa }_1=\sqrt{-a_1},{\kappa }_2=\sqrt{V_{EB}},{\kappa }_3=\sqrt{V_{EB}-a_3},\\ {\alpha }_1=(a_1-V_{EB}/2)d_1,{\alpha }_3=(a_3-V_{EB}-V_{CB}/2)d_3,\\ c_{1,1}=(a_1^2/2)(a_1-V_{EB}){(d_1/V_{EB})}^2,\\ c_{1,2}=(a_1/2){(a_1-V_{EB})}^2{(d_1/V_{EB})}^2,\\ c_{3,1}=[{(a_3-V_{EB})}^2/2](a_3-V_{EB}-V_{CB}){(d_3/V_{CB})}^2,\\ c_{3,2}=[(a_3-V_{EB})/2]{(a_3-V_{EB}-V_{CB})}^2{(d_3/V_{CB})}^2,\\ g_1=-{\kappa }_1^{-3}(V_{EB}/4d_1),g_3=-{\kappa }_3^{-3}(V_{CB}/4d_3).& (87)\end{array}$

The Λ₂-matrix is defined by (48) for i = 2, where $k_2={\kappa }_2{\epsilon }^{-1}$ and l₂ = εd₂.

Below we examine the following two zero-thickness limits: (i) μ₁ = μ₃ = ν₁ = ν₃ = 1 (points P_{1, 1}) and (ii) μ₁ = μ₃ = 2, ν₁ = ν₃ = 1 (points P_{2, 1}).

(i) δ-potential model: The matrix multiplication yields the asymptotic representation in the limit as ε → 0:

$\begin{array}{l}{\lambda }_{11}\to cos\left({\kappa }_2{d}_2\right)-{\kappa }_2{d}_{3}sin\left({\kappa }_2{d}_2\right),\\ {\lambda }_{12}\to 0,\\ {\lambda }_{21}\to \left({\alpha }_1+{\alpha }_3\right)cos\left({\kappa }_2{d}_2\right)+\left(c_{1,1}+c_{3,2}\right){\kappa }_{2}sin\left({\kappa }_2{d}_2\right)-\\ {\epsilon }^{-1}{\kappa }_{2}sin\left({\kappa }_2{d}_2\right),\\ {\lambda }_{22}\to cos\left({\kappa }_2{d}_2\right)-{\kappa }_2{d}_{1}sin\left({\kappa }_2{d}_2\right).& (88)\end{array}$

Here, the element λ₂₁ diverges as ε → 0 and it will be finite if sin(κ₂d₂) = 0, resulting in the resonance set

$\begin{array}{ll}{V}_{EB,n}={\left(n\pi /d_2\right)}^2,n=\overline{1,n_0},& (89)\end{array}$

where the integer n₀ depends on the interval of admissible values of the bias potential V_EB. This interval is determined by the requirement that the barrier potential values V_{1, 1} and V_{3, 3} must be positive, leading to the inequalities 0 < V_EB < a₁ and 0 < V_EB + V_CB < a₃. Therefore, the potential V_EB is allowed to tune within the interval 0 < V_EB < min{a₁, a₃ − V_CB}.

Thus, the limit transmission matrix is of the form (86) with

$\begin{array}{ll}{\alpha }_n={\alpha }_{1,n}+{\alpha }_{3,n}=(a_1-V_{EB,n}/2)d_1+(a_3-V_{EB,n}-V_{CB}/2)d_3>0.& (90)\end{array}$

realizing the δ-potential defined on the resonance set described by Equation (89).

According to the general expressions (37) and (34), the transmission amplitude, being non-zero on this resonance set, is given by the formula (83), where θ_n = 1 and $k_{R,n}=\sqrt{k^2+V_{EB,n}+V_{CB}}$. The transmission amplitude ${T}$ displayed in Figure 6 illustrates the convergence of the location of the peaks to the roots of Equation (89).

FIGURE 6

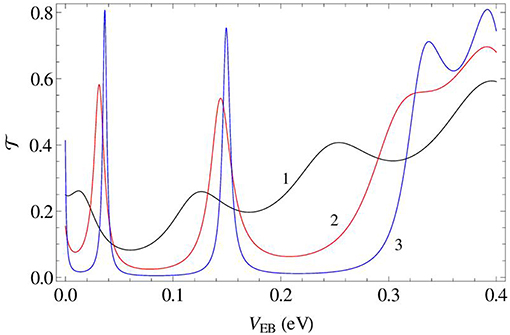
Figure 6. Transmission amplitude ${T}$ as a function of emitter-to-base voltage V_EB for parameter values: E = 0.1 eV, a₁ = a₃ = 0.5 eV, a₂ = 0, V_CB = 0.2 eV, d₁ = d₃ = 2 nm, d₂ = 10 nm. Computations have been carried out with powers μ₁ = ν₁ = μ₃ = ν₃ = 1 (points P_1,1) and μ₂ = 2, ν₂ = 0. Squeezing scenario is displayed for ε = 0.5 (curve 1, black), 0.25 (curve 2, red), and 0.1 (curve 3, blue). Location of all three peaks approaches set {V_EB,n} given by Equation (89) with n = 1, 2, 3.

(ii) δ′-potential model: The three-lateral device can also be approximated by a δ′-interaction with a bias if we choose for the zero-thickness limit the powers μ₁ = μ₂ = μ₃ = 2 and ν₁ = ν₃ = 1. The multiplication of the matrices yields

$\begin{array}{l}{\lambda }_{11}\to cos({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ -({\kappa }_1/{\kappa }_2)sin({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ -({\kappa }_1/{\kappa }_3)sin({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)sin({\kappa }_3{d}_3)\\ -({\kappa }_2/{\kappa }_3)cos({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)sin({\kappa }_3{d}_3),\\ {\lambda }_{12}\to 0,\\ {\lambda }_{21}\to {\kappa }_2[g_{1}sin({\kappa }_1{d}_1)cos({\kappa }_3{d}_3)\\ -g_{3}cos({\kappa }_1{d}_1)sin({\kappa }_3{d}_3)]sin({\kappa }_2{d}_2)\\ +({\kappa }_3{g}_1-{\kappa }_1{g}_3)sin({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)sin({\kappa }_3{d}_3)\\ -{\epsilon }^{-1}[{\kappa }_{1}sin({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ +{\kappa }_{2}cos({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ +{\kappa }_{3}cos({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)sin({\kappa }_3{d}_3)\\ -({\kappa }_1{\kappa }_3/{\kappa }_2)sin({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)sin({\kappa }_3{d}_3)],\\ {\lambda }_{22}\to cos({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ -({\kappa }_2/{\kappa }_1)sin({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)cos({\kappa }_3{d}_3)\\ -({\kappa }_3/{\kappa }_1)sin({\kappa }_1{d}_1)cos({\kappa }_2{d}_2)sin({\kappa }_3{d}_3)\\ -({\kappa }_3/{\kappa }_2)cos({\kappa }_1{d}_1)sin({\kappa }_2{d}_2)sin({\kappa }_3{d}_3),& (91)\end{array}$

where the notations for κ₁, κ₂, κ₃, and g₁, g₃ can be found in Equation (87). The arguments of the trigonometric functions are finite and the element λ₂₁ diverges as ε → 0 because of the presence of the factor ε⁻¹. Therefore, the only opportunity to define properly a point interaction is a full cancelation of all the terms at this factor, so that λ₂₁ becomes finite. As a result, this cancelation yields the following equation:

$\begin{array}{ll}\frac{{\kappa }_1{\kappa }_3}{{\kappa }_2}{\displaystyle \prod _{i=1}^3}tan({\kappa }_i{d}_i)={\displaystyle \sum _{i=1}^3}{\kappa }_{i}tan({\kappa }_i{d}_i).& (92)\end{array}$

Using the resonance equation (92), we derive that the pair {λ₁₁, λ₂₂} admits the following sixteen representations:

$\begin{array}{ll}\left\{{\lambda }_{11},{\lambda }_{22}\right\}=\left\{I_1,I_2,J_1^{-1},J_2^{-1}\right\}\times \left\{I_1^{-1},I_2^{-1},J_1,J_2\right\},& (93)\end{array}$

where

$\begin{array}{l}{I}_1=\frac{cos\left({\kappa }_1{d}_1\right)cos\left({\kappa }_2{d}_2\right)-\left({\kappa }_1/{\kappa }_2\right)sin\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right)}{cos\left({\kappa }_3{d}_3\right)},\\ I_2=-\frac{{\kappa }_{1}sin\left({\kappa }_1{d}_1\right)cos\left({\kappa }_2{d}_2\right)+{\kappa }_{2}cos\left({\kappa }_1{d}_1\right)sin\left({\kappa }_2{d}_2\right)}{{\kappa }_{3}sin\left({\kappa }_3{d}_3\right)},\\ J_1=\frac{cos\left({\kappa }_2{d}_2\right)cos\left({\kappa }_3{d}_3\right)-\left({\kappa }_3/{\kappa }_2\right)sin\left({\kappa }_2{d}_2\right)sin\left({\kappa }_3{d}_3\right)}{cos\left({\kappa }_1{d}_1\right)},\\ J_2=-\frac{{\kappa }_{2}sin\left({\kappa }_2{d}_2\right)cos\left({\kappa }_3{d}_3\right)+{\kappa }_{3}cos\left({\kappa }_2{d}_2\right)sin\left({\kappa }_3{d}_3\right)}{{\kappa }_{1}sin\left({\kappa }_1{d}_1\right)}.& (94)\end{array}$

These representations follow from the equations I₁ = I₂, J₁ = J₂, and I₁J₁ = 1, which can be checked using the condition (92). As a result, we have |Λ| = λ₁₁λ₂₂ = 1 if Equation (92) is fulfilled.

Equation (92) can be rewritten in the explicit form as follows

$\begin{array}{l}\sqrt{a_1/V_{EB}}tanh(\sqrt{a_1}{d}_1)+\sqrt{a_3/V_{EB}-1}tanh(\sqrt{a_3-V_{EB}}{d}_3)\\ =\left[1-\sqrt{a_1/V_{EB}}\sqrt{a_3/V_{EB}-1}tanh(\sqrt{a_1}{d}_1)tanh(\sqrt{a_3-V_{EB}}{d}_3)\right]\\ \times tan(\sqrt{V_{EB}}{d}_2).& (95)\end{array}$

This form shows the existence of the roots forming a resonance set Σ = {V_{EB, n}}. Inserting next these roots into Equation (94), one can get the discrete values of the diagonal elements λ_{11, n} and λ_{22, n} of the matrix set Λ|_Σ. One can write then ${\theta }_n:={\lambda }_{11,n}={\lambda }_{22,n}^{-1}=I_{1,n}=I_{2,n}=J_{1,n}^{-1}=J_{2,n}^{-1}$. Finally, one can represent the off-diagonal element λ_{21, n} = α_n as

$\begin{array}{l}{\alpha }_n=a_1^{-3/2}(V_{EB,n}/4d_1)sinh(\sqrt{a_1}{d}_1)\\ \times [\sqrt{V_{EB,n}}cosh(\sqrt{a_3-V_{EB,n}}{d}_3)sin(\sqrt{V_{EB,n}}{d}_2)\\ -\sqrt{a_3-V_{EB,n}}sinh(\sqrt{a_3-V_{EB,n}}{d}_3)cos(\sqrt{V_{EB,n}}{d}_2)]\\ -{(a_3-V_{EB,n})}^{-3/2}(V_{CB}/4d_3)sinh(\sqrt{a_3-V_{EB,n}}{d}_3)\\ \times [\sqrt{V_{EB,n}}cosh(\sqrt{a_1}{d}_1)sin(\sqrt{V_{EB,n}}{d}_2)\\ -\sqrt{a_1}sinh(\sqrt{a_1}{d}_1)cos(\sqrt{V_{EB,n}}{d}_2)].& (96)\end{array}$

Similarly to the double-layer structure with the limit transmission matrix (81), we refer this one-point interaction to as the δ′-potential because λ_{11, n}, λ_{22, n} ≠ 1. The transmission amplitude is given by the same formula (83) in which θ_n = λ_{11, n} and α_n = λ_{21, n} is given by the expression (96).

7. Concluding remarks

In the present work we addressed the family of point interactions as the zero-thickness limit of heterostructures composed of several layers. The latter have energy diagrams stemming from tilted linear potentials that arise as a result of the application of external electric fields. The analysis starts from the solution of the one-dimensional stationary Schrödinger equation for the structure with finite size using the transfer matrix approach. Within this approach, we find the transmission matrices for each layer; their product quantifies the penetration amplitude of electrons through the whole system. In order to realize point interactions we introduce a squeezing parameter ε > 0 in the structural parameters of the system (layer width, potentials at layer edges, etc.) leading to shrinking the thickness of the system as ε → 0. In this limit the potential values at the interfaces of layers must go to infinity if we wish to create a point interaction in the squeezed limit. At ε = 1, the structural parameters correspond to realistic values of the device.

One of interesting features discovered in the previous publications [17, 43–45, 48, 49, 51] is the appearance of electron tunneling through one-point barriers that occurs at some discrete values of system parameters, whereas beyond these values the system behaves as a fully reflecting wall. The origin of this phenomenon is an oscillating behavior of particle transmission. Surprisingly, as the system shrinks to a point, the oscillating regular function that describes the transmission amplitude, converges pointwise to the function with non-zero finite values only at some discrete points in the space of system parameters, whereas beyond this (resonance) set, the system acts a fully reflecting wall (see, e.g., Figure 1 in Zolotaryuk and Zolotaryuk [17]). In other words, the maxima of the oscillating amplitude correspond in the squeezing limit to the set of extremely sharp peaks. On the other hand, in many devices the oscillating behavior of transmitted particles appears as a function of tuning some controllable (not system) parameters. For instance, in the typical point transistor, an emitter-to-base voltage may be served as such a parameter. Indeed, the electron flow across this device is an oscillating function of this voltage. In this regard, it is of interest to construct the point interactions with a resonance set controllable by parameters applied externally and this is the main goal of the present paper.

In conclusion, in the present paper we have tried to develop the general approach on how to realize the point interactions as a zero-thickness limit of structures composed of an arbitrary number of layers with biased potentials. This approach is specified by the examples describing one layer, the double- and three-layer systems. The piecewise linear potentials are not required to have any distributional limit as ε → 0. Despite this, the ε → 0 limit of the transmission matrices has been shown to exist enable us to compute analytically the transmission amplitude. The most interesting phenomenon discussed in the present paper is the appearance of the resonant transmission through a δ-like barrier in the presence of an adjacent well. The origin of this effect emerges from the fact that the particle transmission across a well has an oscillating behavior. This behavior keeps to be of the same nature after tunneling through a barrier. Therefore, in the squeezed limit this oscillating transforms into the function with non-zero values only at discrete points, whereas on the intervals between these points, this function converges pointwise to zero resulting in blocking the tunneling trough the barrier.

Data Availability

The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

AZ, GT, and YZ contributed equally in all stages of this work. YZ contributed to calculations of transmission amplitudes.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

One of us (AZ) acknowledges partial financial support from the National Academy of Sciences of Ukraine (project No. 0117U000238). GT acknowledges support by the European Commission under project NHQWAVE (MSCA-RISE 691209). YZ acknowledges support from the Department of Physics and Astronomy of the National Academy of Sciences of Ukraine under project No. 0117U000240. The authors are indebted to both the Referees for their suggestions and corrections resulting in the significant improvement of the paper.

References

1. Demkov YN, Ostrovskii VN. Zero-Range Potentials and Their Applications in Atomic Physics. New York, NY: Plenum Press (Leningrad University Press, Leningrad, 1975) (1988).

Google Scholar

2. Albeverio S, Gesztesy F, Høegh-Krohn R, Holden H. Solvable Models in Quantum Mechanics. 2nd ed. With appendix by P. Exner. Providence, RI: AMS Chelsea (2005).

Google Scholar

3. Albeverio S, Kurasov P. Singular Perturbations of Differential Operators: Solvable Schrödinger-Type Operators. Cambridge: Cambridge University Press (1999).

Google Scholar

4. Šeba P. Some remarks on the δ′-interaction in one dimension. Rep Math Phys. (1986) 24:111–20.

Google Scholar

5. Kurasov P. Distribution theory for discontinuous test functions and differential operators with generalized coefficients. J Math Anal Appl. (1996) 201:297–323. doi: 10.1006/jmaa.1996.0256

CrossRef Full Text | Google Scholar

6. Coutinho FAB, Nogami Y, Perez JF. Generalized point interactions in one-dimensional quantum mechanics. J Phys A Math Gen. (1997) 30:3937–45. doi: 10.1088/0305-4470/30/11/021

CrossRef Full Text | Google Scholar

7. Albeverio S, Da̧browski L, Kurasov P. Symmetries of Schrödinger operators with point interactions. Lett Math Phys. (1998) 45:33–47. doi: 10.1023/A:1007493325970

CrossRef Full Text | Google Scholar

8. Coutinho FAB, Nogami Y, Tomio L. Many-body system with a four-parameter family of point interactions in one dimension. J Phys A Math Gen. (1999) 32:4931–42. doi: 10.1088/0305-4470/32/26/311

CrossRef Full Text | Google Scholar

9. Albeverio S, Nizhnik L. On the number of negative eigenvalues of a one-dimensional Schrödinger operator with point interactions. Lett Math Phys. (2003) 65:27–35. doi: 10.1023/A:1027396004785

CrossRef Full Text | Google Scholar

10. Nizhnik LP. A Schrödinger operator with δ′-interaction. Funct Anal Appl. (2003) 37:72–4. doi: 10.1023/A:1022932229094

CrossRef Full Text | Google Scholar

11. Nizhnik LP. A one-dimensional Schrödinger operator with point interactions on Sobolev spaces. Funct Anal Appl. (2006) 40:143–7. doi: 10.1007/s10688-006-0022-3

CrossRef Full Text | Google Scholar

12. Albeverio S, Cacciapuoti C, Finco D. Coupling in the singular limit of thin quantum waveguides. J Math Phys. (2007) 48:032103. doi: 10.1063/1.2710197

CrossRef Full Text | Google Scholar

13. Cacciapuoti C, Exner P. Nontrivial edge coupling from a Dirichlet network squeezing: the case of a bent waveguide. J Phys A Math Theor. (2007) 40:F511–23. doi: 10.1088/1751-8113/40/26/F02

CrossRef Full Text | Google Scholar

14. Turek O, Cheon T. Threshold resonance and controlled filtering in quantum star graphs. Europhys Lett. (2012) 98:50005. doi: 10.1209/0295-5075/98/50005

CrossRef Full Text | Google Scholar

15. Turek O, Cheon T. Potential-controlled filtering in quantum star graphs. Ann Phys. (2013) 330:104–41. doi: 10.1016/j.aop.2012.11.011

CrossRef Full Text | Google Scholar

16. Zolotaryuk AV, Zolotaryuk Y. Controllable resonant tunnelling through single-point potentials: a point triode. Phys Lett A. (2015) 379:511–7. doi: 10.1016/j.physleta.2014.12.016

CrossRef Full Text | Google Scholar

17. Zolotaryuk AV, Zolotaryuk Y. A zero-thickness limit of multilayer structures: a resonant-tunnelling δ′-potential. J Phys A Math Theor. (2015) 48:035302. doi: 10.1088/1751-8113/48/3/035302

CrossRef Full Text | Google Scholar

18. Asorey M, Ibort A, Marmo G. Global theory of quantum boundary conditions and topology change. Int J Mod Phys A. (2005) 20:1001–26. doi: 10.1142/S0217751X05019798

CrossRef Full Text | Google Scholar

19. Cheon T, Fülöp T, Tsutsui I. Symmetry, duality, and anholonomy of point interactions in one dimension. Ann Phys. (2001) 294:1–23. doi: 10.1006/aphy.2001.6193

CrossRef Full Text | Google Scholar

20. Tsutsui I, Fülöp T, Cheon T. Möbius structure of the special space of Schrödinger operators with point interaction. J Math Phys. (2001) 42:5687–97. doi: 10.1063/1.1415432

CrossRef Full Text | Google Scholar

21. Cheon T, Shigehara T. Realizing discontinuous wave functions with renormalized short-range potentials. Phys Lett A. (1998) 243:111–6.

Google Scholar

22. Exner P, Neidhardt H, Zagrebnov VA. Potential Approximations to δ′: an inverse Klauder phenomenon with norm-resolvent convergence. Commun Math Phys. (2001) 224:593–612. doi: 10.1007/s002200100567

CrossRef Full Text | Google Scholar

23. Albeverio S, Nizhnik L. Approximation of general zero-range potentials. Ukr Mat Zh. (2000) 52:582–9.

Google Scholar

24. Albeverio S, Nizhnik L. Approximation of general zero-range potentials. Ukr Math J. (2001) 52:664–72. doi: 10.1007/BF02487279

CrossRef Full Text | Google Scholar

25. Albeverio S, Nizhnik L. A Schrödinger operator with a δ′-interaction on a Cantor set and Krein-Feller operators. Math Nachrichten. (2006) 279:467–76. doi: 10.1002/mana.200310371

CrossRef Full Text | Google Scholar

26. Albeverio S, Nizhnik L. Schrödinger operators with nonlocal point interactions. J Math Anal Appl. (2007) 332:884–95. doi: 10.1016/j.jmaa.2006.10.070

CrossRef Full Text | Google Scholar

27. Albeverio S, Nizhnik L. Schrödinger operators with nonlocal potentials. Methods Funct Anal Topol. (2013) 19:199–210.

Google Scholar

28. Fassari S, Rinaldi F. On the spectrum of the Schrödinger Hamiltonian with a particular configuration of three one-dimensional point interactions. Rep Math Phys. (2009) 64:367–93. doi: 10.1016/S0034-4877(10)00004-2

CrossRef Full Text | Google Scholar

29. Albeverio S, Fassari S, Rinaldi F. A remarkable spectral feature of the Schrödinger Hamiltonian of the harmonic oscillator perturbed by an attractive δ′-interaction centred at the origin: double degeneracy and level crossing. J Phys A Math Theor. (2013) 46:385305. doi: 10.1088/1751-8113/46/38/385305

CrossRef Full Text | Google Scholar

30. Albeverio S, Fassari S, Rinaldi F. The Hamiltonian of the harmonic oscillator with an attractive δ′-interaction centred at the origin as approximated by the one with a triple of attractive δ-interactions. J Phys A Math Theor. (2016) 49:025302. doi: 10.1088/1751-8113/49/2/025302

CrossRef Full Text | Google Scholar

31. Golovaty Y. Two-parametric δ′-interactions: approximation by Schrödinger operators with localized rank-two perturbations. J Phys A Math Theor. (2018) 51:255202. doi: 10.1088/1751-8121/aac110

CrossRef Full Text | Google Scholar

32. Brasche JF, Nizhnik LP. One-dimensional Schrödinger operators with general point interactions. Methods Funct Anal Topol. (2013) 19:4–15.

33. Gadella M, Negro J, Nieto LM. Bound states and scattering coefficients of the −aδ(x)+bδ′(x) potential. Phys Lett A. (2009) 373:1310–3. doi: 10.1016/j.physleta.2009.02.025

CrossRef Full Text | Google Scholar

34. Gadella M, Glasser ML, Nieto LM. One dimensional models with a singular potential of the type −aδ(x)+bδ′(x). Int J Theor Phys. (2011) 50: 2144–52. doi: 10.1007/s10773-010-0641-6

CrossRef Full Text | Google Scholar

35. Lange RJ. Potential theory, path integrals and the Laplacian of the indicator. J High Energy Phys. (2012) 2012:1-32. doi: 10.1007/JHEP11(2012)032

CrossRef Full Text | Google Scholar

36. Lange RJ. Distribution theory for Schrödinger's integral equation. J Math Phys. (2015) 56:122105. doi: 10.1063/1.4936302

CrossRef Full Text | Google Scholar

37. Gadella M, García-Ferrero MA, González-Martín S, Maldonado-Villamizar FH. The infinite square well with a point interaction: a discussion on the different parameterizations. Int J Theor Phys. (2014) 53:1614–27. doi: 10.1007/s10773-013-1959-7

CrossRef Full Text | Google Scholar

38. Kulinskii VL, Panchenko DY. Physical structure of point-like interactions for one-dimensional Schrödinger operator and the gauge symmetry. Physica B (2015) 472:78–83. doi: 10.1016/j.physb.2015.05.011

CrossRef Full Text | Google Scholar

39. Gadella M, Mateos-Guilarte J, Muñoz-Castañeda JM, Nieto LM. Two-point one-dimensional δ-δ′ interactions: non-abelian addition law and decoupling limit. J Phys A Math Theor. (2016) 49:015204. doi: 10.1088/1751-8113/49/1/015204

CrossRef Full Text | Google Scholar

40. Fassari S, Gadella M, Glasser ML, Nieto LM. Spectroscopy of a one-dimensional V-shaped quantum well with a point impurity. Ann Phys. (2018) 389:48–62. doi: 10.1016/j.aop.2017.12.006

CrossRef Full Text | Google Scholar

41. Fassari S, Gadella M, Glasser ML, Nieto LM. Level crossings of eigenvalues of the Schrödinger Hamiltonian of the isotropic harmonic oscillator perturbed by a central point interaction in different dimensions. Nanosyst Phys Chem Math. (2018) 9:179–86. doi: 10.17586/2220-8054-2018-9-2-179-186

CrossRef Full Text | Google Scholar

42. Fassari S, Gadella M, Glasser ML, Nieto LM, Rinaldi F. Spectral properties of the two-dimensional Schrödinger Hamiltonian with various solvable confinements in the presence of a central point perturbation. Phys Script. (2019) 94:055202. doi: 10.1088/1402-4896/ab0589

CrossRef Full Text | Google Scholar

43. Christiansen PL, Arnbak NC, Zolotaryuk AV, Ermakov VN, Gaididei YB. On the existence of resonances in the transmission probability for interactions arising from derivatives of Dirac's delta function. J Phys A Math Gen. (2003) 36:7589–600. doi: 10.1088/0305-4470/36/27/311

CrossRef Full Text | Google Scholar

44. Zolotaryuk AV, Christiansen PL, Iermakova SV. Scattering properties of point dipole interactions. J Phys A Math Gen. (2006) 39:9329–38. doi: 10.1088/0305-4470/39/29/023

CrossRef Full Text | Google Scholar

45. Toyama FM, Nogami Y. Transmission-reflection problem with a potential of the form of the derivative of the delta function. J Phys A Math Theor. (2007) 40:F685–90. doi: 10.1088/1751-8113/40/29/F05

CrossRef Full Text | Google Scholar

46. Zolotaryuk AV. Boundary conditions for the states with resonant tunnelling across the δ′-potential. Phys Lett A. (2010) 374:1636–41. doi: 10.1016/j.physleta.2010.02.005

CrossRef Full Text | Google Scholar

47. Zolotaryuk AV, Zolotaryuk Y. Intrinsic resonant tunneling properties of the one-dimensional Schrödinger operator with a delta derivative potential. Int J Mod Phys B. (2014) 28:1350203. doi: 10.1142/S0217979213502032

CrossRef Full Text | Google Scholar

48. Golovaty YD, Man'ko SS. Solvable models for the Schrödinger operators with δ′-like potentials. Ukr Math Bull. (2009) 6:169–203.

49. Golovaty YD, Hryniv RO On norm resolvent convergence of Schrödinger operators with δ′-like potentials. J Phys A Math Theor. (2010) 43:155204. doi: 10.1088/1751-8113/43/15/155204

CrossRef Full Text | Google Scholar

50. Golovaty Y. Schrödinger operators with (αδ′+βδ)-like potentials: Norm resolvent convergence and solvable models. Methods Funct Anal Topol. (2012) 18:243–55.

Google Scholar

51. Golovaty YD, Hryniv RO. Norm resolvent convergence of singularly scaled Schrödinger operators and δ′-potentials. Proc R Soc Edinb. (2013) 143A:791–816. doi: 10.1017/S0308210512000194

CrossRef Full Text | Google Scholar

52. Golovaty Y. 1D Schrödinger operators with short range interactions: two-scale regularization of distributional potentials. Integr Equat Oper Theor. (2013) 75:341–62. doi: 10.1007/s00020-012-2027-z

CrossRef Full Text | Google Scholar

53. Zolotaryuk AV. Families of one-point interactions resulting from the squeezing limit of the sum of two- and three-delta-like potentials. J Phys A Math Theor. (2017) 50:225303. doi: 10.1088/1751-8121/aa6dc2

CrossRef Full Text | Google Scholar

54. Zolotaryuk AV. A phenomenon of splitting resonant-tunneling one-point interactions. Ann Phys. (2018) 396:479–94. doi: 10.1016/j.aop.2018.07.030

CrossRef Full Text | Google Scholar

55. Calçada M, Lunardi JT, Manzoni LA. Salecker-Wigner-Peres clock and double-barrier tunneling. Phys Rev A. (2009) 79:012110. doi: 10.1103/PhysRevA.79.012110

CrossRef Full Text | Google Scholar

56. Lunardi JT, Manzoni LA, Monteiro W. Remarks on point interactions in quantum mechanics. J Phys Conf Ser. (2013) 410:012072. doi: 10.1088/1742-6596/410/1/012072

CrossRef Full Text | Google Scholar

57. Calçada M, Lunardi JT, Manzoni LA, Monteiro W. Distributional approach to point interactions in one-dimensional quantum mechanics. Front Phys. (2014) 2:23. doi: 10.3389/fphy.2014.00023

CrossRef Full Text | Google Scholar

58. Lee MA, Lunardi JT, Manzoni LA, Nyquist EA. On the generalized Hartman effect for symmetric double-barrier point potentials. J Phys Conf Ser. (2015) 574:012066. doi: 10.1088/1742-6596/574/1/012066

CrossRef Full Text | Google Scholar

59. Lee MA, Lunardi JT, Manzoni LA, Nyquist EA. Double general point interactions: symmetry and tunneling times. Front Phys. (2016) 4:10. doi: 10.3389/fphy.2016.00010

CrossRef Full Text | Google Scholar

60. Asorey M, Garciá-Alvarez D, Muñoz-Castañeda JM. Casimir effect and global theory of boundary conditions. J Phys A Math Theor. (2006) 39:6127–36. doi: 10.1088/0305-4470/39/21/S03

CrossRef Full Text | Google Scholar

61. Asorey M, Muñoz-Castañeda JM. Vacuum boundary effects. J Phys A Math Theor. (2008) 41:304004. doi: 10.1088/1751-8113/41/30/304004

CrossRef Full Text | Google Scholar

62. Guilarte JM, Muñoz-Castañeda JM. Double-delta potentials: one dimensional scattering. The Casimir effect and kink fluctuations. Int J Theor Phys. (2011) 50:2227–41. doi: 10.1007/s10773-011-0723-0

CrossRef Full Text | Google Scholar

63. Asorey M, Muñoz-Castañeda JM. Attractive and repulsive Casimir vacuum energy with general boundary conditions. Nucl Phys B. (2013) 874:852–76. doi: 10.1016/j.nuclphysb.2013.06.014

CrossRef Full Text | Google Scholar

64. Muñoz-Castañeda JM, Guilarte JM, Mosquera AM. Quantum vacuum energies and Casimir forces between partially transparent δ-function plates. Phys Rev D. (2013) 87:105020. doi: 10.1103/PhysRevD.87.105020

CrossRef Full Text | Google Scholar

65. Muñoz-Castañeda JM, Kirsten K, Bordag M. QFT over the finite line. Heat kernel coefficients, spectral zeta functions and selfadjoint extensions. Lett Math Phys. (2015) 105:523549. doi: 10.1007/s11005-015-0750-5

CrossRef Full Text | Google Scholar

66. Muñoz-Castañeda JM, Guilarte JM. δ-δ′ generalized Robin boundary conditions and quantum vacuum fluctuations. Phys Rev D. (2015) 91:025028. doi: 10.1103/PhysRevD.91.025028

CrossRef Full Text | Google Scholar

67. Bordag M, Muñoz-Castañeda JM. Quantum vacuum interaction between two sine-Gordon kinks. J Phys A Math Theor. (2012) 45:374012. doi: 10.1088/1751-8113/45/37/374012

CrossRef Full Text | Google Scholar

68. Hennig D, Tsironis GP. Wave transmission in nonlinear lattices. Phys. Rep. (1999) 307:333–432. doi: 10.1016/S0370-1573(98)00025-8

CrossRef Full Text | Google Scholar

69. Nieto LM, Gadella M, Guilarte JM, Muñoz-Castañeda JM, Romaniega C. Towards modelling QFT in real metamaterials: singular potentials and self-adjoint extensions. J Phys Conf Ser. (2017) 839:012007. doi: 10.1088/1742-6596/839/1/012007

CrossRef Full Text | Google Scholar

70. Konno K, Nagasawa T, Takahashi R. Effects of two successive parity-invariant point interactions on one-dimensional quantum transmission: resonance conditions for the parameter space. Ann Phys. (2016) 375:91–104. doi: 10.1016/j.aop.2016.09.012

CrossRef Full Text | Google Scholar

71. Konno K, Nagasawa T, Takahashi R. Resonant transmission in one-dimensional quantum mechanics with two independent point interactions: full parameter analysis. Ann Phys. (2017) 385:729–43. doi: 10.1016/j.aop.2017.08.031

CrossRef Full Text | Google Scholar

72. Tsu R, Esaki L. Tunneling in a finite superlattice. Appl Phys Lett. (1973) 22:562–4.

Google Scholar

73. Chang LL, Esaki L, Tsu R. Resonant tunneling in semiconductor double barriers. Appl Phys Lett. (1974) 24:593–5.

Google Scholar

74. Esaki L, Chang LL. New transport phenomenon in a semiconductor “superlattice”. Phys Rev Lett. (1974) 33:495–8.

Google Scholar

75. Lui WW, Fukuma M. Exact solution of the Schrödinger equation across an arbitrary one-dimensional piecewise-linear potential barrier. J Appl Phys. (1986) 60:1555–9. doi: 10.1063/1.337788

CrossRef Full Text | Google Scholar

76. Jogai B, Wang KL. Dependence of tunneling current on structural variations of superlattice devices. Appl Phys Lett. (1985) 46:167–8. doi: 10.1063/1.95671

CrossRef Full Text | Google Scholar