New Physics Suggested by Atomki Anomaly

We consider several extensions of the Standard Model (SM) which can explain the anomalies observed by the Atomki collaboration in the decay of excited states of Beryllium via a new boson with a mass around 17 MeV yielding e⁺e⁻ pairs. We show how both spin-0 and 1 solutions are possible and describe the Beyond the SM (BSM) scenarios that can accommodate these. They include BSM frameworks with either an enlarged Higgs, or gauge sector, or both.

1. Introduction

The quest for New Physics (NP) above and Beyond the Standard Model (BSM) has always seen a 2-fold approach. On the one hand, the high energy frontier has been pursued, typically through multi-purpose experiments at hadron accelerators, like the $Sp\bar{p}S$, Tevatron, and LHC. On the other hand, the high precision frontier has been exploited, typically at lepton collider experiments, like LEP and SLC. Alongside this time honored two-prong pursuit, over the years, a transversal dimension, covering both hadron and lepton colliders, centered on flavor physics, has also developed. So that, presently, the attention of the particle physics community in unveiling some NP has mainly been concentrated upon these three research strands. However, surprises may arise in other contexts, notably from (much) lower energy experiments. In this respect, results from (g − 2) of the muon are prototypical. Another interesting result which has recently been reported is the one in Krasznahorkay et al. [1] (see also [2–5]), by the Atomki experiment [6]. The latter is a pair spectrometer for measuring multi-polarities of nuclear transitions, specifically, using a multi-detector array designed and constructed for the simultaneous measurement of energy and angular correlations of electron-positron pairs, in turn emerging via internal pair creation from a variety of nuclear transitions in various isotopes, such as ¹⁶O, ¹²C, and ⁸Be. The intriguing result reported in Krasznahorkay et al. [1] concerns e⁺e⁻ correlations measured for the isovector magnetic dipole 17.64 MeV state (with spin-parity and isospin, J^P = 1⁺, T = 1, respectively), and the isoscalar magnetic dipole 18.15 MeV state (J^P = 1⁺, T = 0) in their transitions to the ground state (J^P = 0⁺, T = 0) for the Beryllium case. Significant deviations from the internal pair creation rate were observed at large angles in the angular correlation for the isoscalar transition with a confidence level of more than 5σ. This observation may indicate that, in an intermediate step, a (light) neutral boson with a mass of 16.70 ± 0.35 (stat) ± 0.5 (sys) MeV has been created. In fact, also the 17.64 MeV transition eventually appeared to present a similar anomaly, albeit less significant, with a boson mass broadly compatible with the above one, i.e., 17.0 ± 0.5 (stat) ± 0.5 (sys) MeV¹.

The purpose of this review is to discuss possible solutions to these results, assuming that the neutral boson could be either a spin-1 or spin-0 object, belonging to a variety of BSM scenarios. The plan is as follows. In the next section we consider the characteristics of the results reported by the Atomki experiment. Then we describe possible candidate particles for such a light bosonic state. Finally, we illustrate the embedding of such solutions in possible theoretical models, in presence of a variety of experimental constraints emerging from both low and high energy experiments. We finally conclude.

2. The Atomki Experiment and 17 MeV Beryllium Anomaly

The Atomki pair spectrometer experiment [6] was set up for searching e⁺e⁻ internal pair creation in the decay of excited ⁸Be nuclei (henceforth, ⁸Be*), the latter being produced with the help of a beam of protons directed on a ⁷Li target. The proton beam was tuned in such a way that the different ⁸Be excitations could be separated in energy with high accuracy.

In the data collection stage, a clear anomaly was observed in the decay of ⁸Be* with J^P = 1⁺ into the ground state ⁸Be with spin-parity 0⁺ (both with T = 0), where ⁸Be* had an excitation energy of 18.15 MeV [1]. Upon analysis of the electron-positron properties, the spectra of both their opening angle θ and invariant mass M presented the characteristics of an excess consistent with an intermediate boson (henceforth, X) being produced on-shell in the decay of the ⁸Be* state, with the X object subsequently decaying into e⁺e⁻ pairs. As mentioned, the best fit to the mass M_X of X was given as M_X = 16.7 ± 0.35 (stat) ± 0.5 (sys) MeV, [1] in correspondence of a ratio of Branching Ratios (BRs) obtained as

$\begin{array}{ll}B\equiv \frac{\text{BR}({}^8\text{B}{\text{e}}^{*}\to X+{}^8\text{B}\text{e})}{\text{BR}({}^8\text{B}{\text{e}}^{*}\to \gamma +{}^8\text{B}\text{e})}\times \text{BR}(X\to e^{+}{e}^{-})=5.8\times {10}^{-6}.& (1)\end{array}$

The signal appeared as a bump over the monotonically decreasing background from pure Quantum Electro-Dynamics (QED) interactions, i.e., internal pair creation via γ* → e⁺e⁻ splittings. This excess appeared only for symmetric energies of e⁺e⁻, as expected from an on-shell non-relativistic particle. In addition, the opening angle of electron-positron pair and their invariant mass distributions presented the characteristics of an excess consistent with an intermediate boson. The measurements yielded the mentioned value M_X from the invariant mass $m_{e^{+}{e}^{-}}$, in correspondence of an angular excess around ~ 135°, as shown in Figure 1. The best fit to data was obtained for a new particle interpretation, in which case the statistical significance of the excess is 6.8 sigma. The aforementioned result from the 17.64 MeV transition yielded M_X = 17.0 ± 0.5 (stat) ± 0.5 (sys) as best fit, in correspondence of an angular peak around 155° with ${B}=4.0\times 10^{-6}$. The corresponding significance is nowhere near discovery though.

FIGURE 1

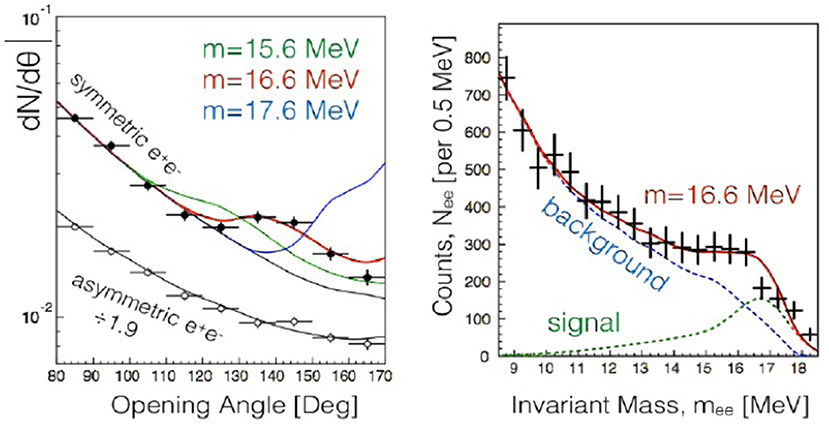
Figure 1. Angular and invariant mass distributions of the internal conversion electron-positron pairs measured by the Atomki spectrometer (from Feng et al. [7]).

3. Candidates for the New Boson

An explanation of the nature of the intermediate particle, X, decaying to electron-positron pairs, was attempted by considering it as boson either with spin zero (scalar or pseudoscalar) or with spin one (vector or axial-vector). We introduce all possible combinations in turn.

3.1. Scalar Particle

If the intermediate particle X is a scalar, ϕ (J^P = 0⁺), then the decay ⁸Be*(1⁺) → ⁸Be(0⁺) + ϕ implies, due to angular momentum conservation, that ϕ should have L = 1. Also, from parity conservation, it must have a parity equal to (−1)^L, which is −1 and this contradicts the assumption that ϕ is scalar with even parity. Therefore, one can conclude that a scalar intermediate particle is ruled out.

3.2. Pseudoscalar Particle

The situation is different if the intermediate particle is a pseudoscalar, A (J^P = 0⁻) [8]. In this case, given the quantum numbers of the ⁸Be* and ⁸Be states, the intermediate boson can indeed be a J^P = 0⁻ pseudoscalar particle if it was emitted with L = 1 orbital momentum. It was in fact shown in Ellwanger and Moretti [8] that A can account for the Atomki results if its Yukawa couplings with the SM fermions are of order of the Yukawa couplings of the SM Higgs.

3.3. Vector Particle

A neutral vector boson is the most common example considered for explaining this signal [7, 9–18]. It was emphasized that it can be a valid candidate if its coupling is constrained as g′ ~ 10⁻³.

3.4. Axial-Vector Particle

The pure axial-vector boson is also considered and it was shown that it can be a candidate if its coupling satisfies g′ ~ 10⁻⁴, as done in Kozaczuk et al. [19], Feng et al. [7], and Kahn et al. [20]. The case of general spin-one boson, with no definite parity, i.e., it is a mix of vector and axial-vector, could be a possible candidate after taking care of stringent constraints from atomic parity violation.

The couplings of these new light bosons with the SM particles remain an open question and subject to severe constraints from several experiments.

4. Experimental Constraints on the Pseudoscalar Explanation

The reduced couplings ξ_q of a pseudoscalar A to quarks is defined as

$\begin{array}{ll}{L}_{Aqq}={\xi }_q\frac{m_q}{v}A\bar{q}i{\gamma }_{5}q,& (2)\end{array}$

with v ~ 246 GeV. Assuming such fundamental interactions and adopting the nuclear shell model wave functions with definite isospin T = 0 of Ellwanger and Moretti [8], one finds that

$\begin{array}{ll}{\xi }_u+{\xi }_d\approx 0.6& (3)\end{array}$

or, for ξ_u = ξ_d ≡ ξ, ξ ≈ 0.3. Furthemore, if A has Yukawa couplings to quarks and leptons which are proportional to the Yukawa couplings of the SM Higgs boson rescaled by generation independent factors ξ_d ≈ ξ_u ≈ ξ_e (or ξ_u ≪ ξ_d), and the Yukawa couplings to BSM fermions are not much larger than the electric charge e, A has a BR of about 99% into e⁺e⁻ and only about 1% into γγ. Its total width is then dominated by A → e⁺e⁻ and given by

$\begin{array}{ll}\Gamma (A)={\xi }_e^2\frac{m_e^2}{8\pi v^2}{M}_A={\xi }_e^2·2.9\times 10^{-15}\text{ GeV}& (4)\end{array}$

for M_A = 17 MeV. Its decay length is

$\begin{array}{ll}{l}_A=\frac{p_A}{M_A\Gamma (A)}.& (5)\end{array}$

For the decay ⁸Be* → ⁸Be + A with M(⁸Be*) − M(⁸Be) = 18.15 MeV we obtain

$\begin{array}{ll}{l}_A~\frac{1}{{\xi }_e^2}·2.5\text{ cm}.& (6)\end{array}$

(For M_A = 17.9 MeV, 2σ above the central value in M_X from the 18.15 MeV transition, we obtain $l_A~\frac{1}{{\xi }_e^2}\times 1.1\mathrm{\text{cm}}$.) In order to explain the observed anomaly in the Atomki pair spectrometer experiment [1], l_A should then not be much larger than 1 cm leading to

$\begin{array}{ll}{\xi }_e\gtrsim 1,& (7)\end{array}$

depending somewhat on the precise value of M_A.

Light pseudoscalars are subject to constraints from searches for axions or axion-like particles. For recent summaries of constraints relevant for light pseudoscalars decaying dominantly into e⁺e⁻, see [21–25]. However, since we allow for different Yukawa type couplings rescaled by ξ_u, ξ_d, and ξ_e with respect to SM Higgs couplings, at least some experimental constraints studied therein have to be reconsidered. Constraints from π⁰ → γ + X from the NA48/2 experiment, which play a major role for the Z′ scenario [7, 9], do not apply here since the decay π⁰ → γ + A would violate parity.

Constraints also originate from flavor violating meson decays, analyzed recently in Dolan et al. [21], and are mainly due to the following decays: K⁺ → π⁺ + A [constrained by the K_μ2 experiment [26]], K⁺ → π⁺ + invisible (measured by the experiments E787 [27] and BNL-E949 [28]), $B_s\to {\mu }^{+}{\mu }^{-}$ [measured by the LHCb collaboration [29] and the CMS collaboration [30], see [31] for a LHCb/CMS combination] and $B^0\to K_S^0+invisible$ [measured by CLEO [32]]. It turns out that the most stringent Flavor Changing Neutral Current (FCNC) constraint is due to K⁺ → π⁺ + A from the K_μ2 experiment [26]. This process depends on a loop-induced Asd vertex (with W bosons and up-type quarks in the loop) which depends, in turn, on the couplings of A to d- and u-type quarks. Constraints from Yamazaki et al. [26] can lead to

$\begin{array}{ll}{\xi }_d\lesssim 2\times 10^{-2}.& (8)\end{array}$

A similar constraint can be obtained from the process B → K + A.

Constraints from searches for K⁺ → π⁺ + invisible from E787 and BNL-E949 [27, 28] apply only if A decays outside the detectors, i.e., if ξ_e is small enough. According to Andreas et al. [22], identifying now C_Aff in Andreas et al. [22] with ξ_e, this is not the case for ξ_e ≳ 0.3.

According to Dolan et al. [21], the constraints from $B_s\to {\mu }^{+}{\mu }^{-}$ (through an off-shell A) rule out any ξ ≳ 0.7 which is weaker than the constraint (8) from K⁺ → π⁺ + A. Again, the loop contributions to the Asb vertex considered in Dolan et al. [21] are incomplete within an Ultra-Violet (UV) complete extension of the Higgs sector, and could again be canceled by additional BSM contributions as in the case of the Asd vertex.

The constraints from $B^0\to K_S^0+invisible$ measured by CLEO [32] apply only if the pseudoscalar A produced in $B^0\to K_S^0+A$ decays outside the detector. Accordingly these constraints depend both on the BR$(B^0\to K_S^0+A)$, hence on the Asb vertex or on ξ_u, ξ_d, and on the A decay length which depends on ξ_e. These quantities are identified in Dolan et al. [21] where a limit ξ ≳ 3.5 on all flavors satisfies the constraints, since then the A decay length becomes short enough despite the large production rate. Using this constraint only for ξ_e is conservative, if ξ_u, ξ_d < ξ_e is assumed.

Finally, ξ_e ≳ 3.5 satisfies also bounds on A production in radiative ϒ decays ϒ → γ + invisible interpreted as ϒ → γ + A from CLEO [33] and BaBar [34], which apply only if A decays outside the detectors. For M_A ~ 17 MeV, following [22], this is not the case for ξ_e ≳ 1.5.

Other important constraints on light pseudoscalars originate from beam dump experiments. From the Orsay experiment of Davier and Nguyen Ngoc [35], lifetimes τ_A in the range $5\times 10^{-12}\mathrm{\text{s}}\lesssim {\tau }_A\lesssim 2\times 10^{-9}$ s are ruled out for M_A ~ 17 − 18 MeV. This has already been translated into constraints on a reduced pseudoscalar-fermion Yukawa coupling C_Aff in Andreas et al. [22], where C_Aff = ξ_e in our notation. Following Andreas et al. [22], 0.4 ≲ C_Aff ≲ 4 is ruled out by this constraint. Since ξ_e < 0.4 is incompatible with (7), one is left with

$\begin{array}{ll}{\xi }_e\gtrsim 4.& (9)\end{array}$

This constraint leads automatically to the satisfaction of the lower bound ξ_e ≳ 3.5 from $B^0\to K_S^0+invisible$, as well as to a short enough decay length (7) for the Atomki pair spectrometer experiment. It is also compatible with the exclusion from the NA64 experiment [36] provided that ξ_e ≲ 15.

Another potentially relevant experiment is the proton beam dump on copper CHARM experiment [37]. In Bergsma et al. [37] constraints were derived assuming that the production cross section and decay length of light pseudoscalars correspond to those of axions, which is not the case here. Relevant is the analysis in Dolan et al. [21] which uses the production of light pseudoscalars in K → π + A and B → X + A decays. For universally rescaled Yukawa couplings the region ξ ≳ 1 satisfies the constraints, since then the decay length of A is too short to reach the decay region of the CHARM experiment. This constraint does not supersede the one in Equation (9).

5. Explanation of the Beryllium Anomaly With a Pseudoscalar

One of the less well-studied solutions is that of the pseudoscalar, but this has been done in Ellwanger and Moretti [8]. It was initially dismissed by Feng et al. [7, 9] and subsequent authors by the argument that for such axion-like pseudoscalars A, fermion loops generate couplings of the form $g_{A\gamma \gamma }A{F}^{\mu \nu }(\gamma ){\tilde{F}}_{\mu \nu }(\gamma )$ which are strongly constrained by axion searches. However, light pseudoscalars in this mass range with tree level Yukawa couplings to electrons decay dominantly into electron-positron pairs, unless Yukawa couplings to other charged fermions f with mass m_f are much larger than m_f/m_e compensating g_Aγγ ≈ 1/(8π m_f). For solutions to the Atomki anomaly, we require such couplings to electrons and hence one should dismiss the pseudoscalar solution.

To summarize the previous section investigating the constraints, couplings of the form ξ_u + ξ_d ~ 0.6 and ξ_e > 4 should satisfy all aforementioned constraints and provide an explanation to the Atomki anomaly, with the caveat that FCNCs must be suppressed by loop contributions at the level of at least 10%.

Ultimately, it will be the Atomki experiment itself which will be in a position to either confirm or disprove the light pseudoscalar hypothesis. In fact, the experiment is currently planning to study the γγ decays of the 17 MeV particle, also in 4He → γγ [3], in order to distinguish between a vector boson and pseudoscalar boson scenario. According to the Landau-Yang theorem, the (on-shell) decay of a vector boson by double γ-emission is forbidden, however, the decay of a pseudoscalar one is allowed [38]. The angular correlation of the γ-rays will be measured by using 15 large (3″ × 3″) LaBr₃ detectors. If the A boson with a mass of 17 MeV is created in the decay of the J^P = 0⁻ state and in turn decays into two γ-rays, their angular correlation θ should peak at

$\begin{array}{ll}cos\theta =1-\frac{M_A^2}{2E_{\gamma }{E}_{{\gamma }^{\prime }}},& (10)\end{array}$

where M_A is the mass of the A boson (17 MeV) and $E_{\gamma ,{\gamma }^{\prime }}$ are the energies of the two photons. However, it should be kept in mind that a light pseudoscalar with tree level coupling to electrons would have a loop-induced BR to di-photons of only one percent or so, hence hardly visible with current Atomki data sets. At any rate, results in this respect, are eagerly awaited.

6. Experimental Constraints on the Spin-1 Explanation

Let us assume that the generic coupling of a new vector boson, Z′, to the SM fermions is given by the following interaction Lagrangian

$\begin{array}{ll}-L_{\text{int}}=Z_{\mu }^{\prime }{\displaystyle \sum _f}{\bar{\psi }}_f{\gamma }^{\mu }(C_{f,V}+{\gamma }_5{C}_{f,A}){\psi }_f.& (11)\end{array}$

Experimental Constraints on the Lepton Couplings

We have not seen a Z′ in the electron beam dump experiment SLAC E141. Therefore, a Z′ has not been produced, hence

$\begin{array}{ll}{C}_{e,V}^2+C_{e,A}^2<10^{-17}& (12)\end{array}$

or, else, a Z′ has been caught in the dump, hence

$\begin{array}{ll}\frac{C_{e,V}^2+C_{e,A}^2}{\text{BR}(Z^{\prime }\to e^{+}{e}^{-})}\gtrsim 3.7\times 10^{-9}.& (13)\end{array}$

We have not seen a Z′ either in the electron beam dump experiment NA64 [36]. If a Z′ has been caught in the dump, this places the (stronger than E141) condition

$\begin{array}{ll}\frac{C_{e,V}^2+C_{e,A}^2}{\text{BR}(Z^{\prime }\to e^{+}{e}^{-})}\gtrsim 1.6\times 10^{-8}.& (14)\end{array}$

The parity-violating Møller scattering measured at the SLAC E158 experiment [39] imposes a constraint on the product C_e,VC_e,A of the Z′, namely

$\begin{array}{ll}\left|C_{e,V}{C}_{e,A}\right|\lesssim 10^{-8},& (15)\end{array}$

for $M_{Z^{\prime }}\simeq 17$ MeV [20].

Furthermore, there could be contributions of a Z′ to the magnetic moments of electron and muon. The one-loop ones δa_l, mediated by a Z′, lead to

$\begin{array}{ll}\delta a_l=\frac{r_{m_l}}{4{\pi }^2}\left[C_{l,V}^2{g}_V(r_{m_l})-C_{l,A}^2{g}_A(r_{m_l})\right],& (16)\end{array}$

where $r_{m_l}\equiv {(m_l/M_{Z^{\prime }})}^2$ and g_V, g_A are given by

$\begin{array}{l}{g}_V(r)={\displaystyle {\int }_0^1}dz\frac{z^2(1-z)}{1-z+r{z}^2},\\ g_A(r)={\displaystyle {\int }_0^1}dz\frac{(z-z^2)(4-z)+2r{z}^3}{1-z+r{z}^2}.& (17)\end{array}$

The light boson contribution to the anomalous magnetic moment of the electron is required to be within the 2σ uncertainty of the departure of the SM prediction from the experimental result [40]. Concerning the muon anomalous magnetic moment [41], which has been measured at Brookhaven National Laboratory (BNL) to a precision of 0.54 parts per million, the current average of the experimental results is given by Bennett et al. [42], Blum et al.[43], and Lindner et al. [44]

$\begin{array}{ll}{a}_{\mu }^{\text{exp}}=11659208.9(6.3)\times 10^{-10},& (18)\end{array}$

which is different from the SM prediction by 3.3 to 3.6σ: $\Delta a_{\mu }=a_{\mu }^{\text{exp}}-a_{\mu }^{\text{SM}}=(28.3\pm 8.7\text{ to }28.7\pm 8.0)\times 10^{-10}.$ We require again that the contribution of a Z′ to (g − 2)_μ, which is mainly due to its axial-vector component, is less than the 2σ uncertainty of the discrepancy between the SM result and the experimental measure. For $M_{Z^{\prime }}\simeq 17$ MeV, one then finds

$\begin{array}{l}\delta a_e=7.6\times 10^{-6}{C}_{e,V}^2-3.8\times 10^{-5}{C}_{e,A}^2\simeq -10.5(8.1)\\ \times 10^{-13},& (19)\end{array}$

$\begin{array}{ll}\delta a_{\mu }=0.009C_{\mu ,V}^2-C_{\mu ,A}^2\le 2.9(90)\times 10^{-9}.& (20)\end{array}$

Electron-positron colliders (like KLOE2) would be sensitive to a new spin-1 gauge boson via the channel e⁺e⁻ → γ, Z, Z′ → e⁺e⁻. From this process one finds

$\begin{array}{ll}(C_{e,V}^2+C_{e,A}^2)\text{BR}(Z^{\prime }\to e^{+}{e}^{-})\lesssim 3.7\times 10^{-7}.& (21)\end{array}$

Similarly, Z′ contributions to neutrino-electron scattering implies a bound on the product of the electron and neutrino couplings to the Z′ [45, 46].

Experimental Constraints on the Quark Couplings

The couplings of a light Z′ state with quarks are, in general, strongly constrained from π⁰ → Z′ + γ searches at the NA48/2 experiment [47]. The process is proportional to the anomaly factor $N_{\pi }=\frac{1}{2}{(2C_{u,V}+C_{d,V})}^2$. Therefore, one gets the following limit:

$\begin{array}{ll}|2C_{u,V}+C_{d,V}|\lesssim \frac{3.6\times 10^{-4}}{\sqrt{\text{BR}(Z^{\prime }\to e^{+}{e}^{-})}}& (22)\end{array}$

for $M_{Z^{\prime }}\simeq 17$ MeV. The contribution of the axial components is induced by chiral symmetry breaking effects and is, therefore, suppressed by the light quark masses.

Furthermore, atomic parity violation in Cesium (Cs) must be considered. In fact, very strong constraints on a light Z′ can be extracted from the measurement of the effective weak charge of the Cs atom [48, 49]:

$\begin{array}{l}\Delta Q_w=\frac{-2\sqrt{2}}{G_F}{C}_{e,A}\left[C_{u,V}(2Z+N)+C_{d,V}(Z+2N)\right]\\ \left(\frac{0.8}{{(17\text{ MeV})}^2}\right)\lesssim 0.71& (23)\end{array}$

at 2σ [50].

7. A U(1)′ Extension of the SM With a Light and Weakly Interacting Z′

We consider a generic extension to the SM described by a new Abelian group U(1)′ [51–57]. Due to the presence of two such Abelian symmetries, $U{(1)}_Y\times U{(1)}^{\prime }$, the most general kinetic Lagrangian of the corresponding fields, ${\widehat{B}}_{\mu }$ and ${\widehat{B}}_{\mu }^{\prime }$, allows for a gauge invariant operator mixing the two field strengths. In particular, the quadratic Lagrangian for the two gauge fields is given by

$\begin{array}{ll}{L}_{\text{kin}}=-\frac{1}{4}{\widehat{F}}_{\mu \nu }{\widehat{F}}^{\mu \nu }-\frac{1}{4}{\widehat{F}}_{\mu \nu }^{\prime }{\widehat{F}}^{{ }^{\prime }\mu \nu }-\frac{\kappa }{2}{\widehat{F}}_{\mu \nu }^{\prime }{\widehat{F}}^{\mu \nu },& (24)\end{array}$

with κ being the kinetic mixing parameter. Since the parameterizations above may be inconvenient for practical computations, it is often useful to recast the kinetic Lagrangian into a diagonal form by removing the mixing operator through a rotation and rescaling of the Abelian fields. This transformation, while diagonalizing Equation (24), introduces a non-diagonal term in the interactions such that the covariant derivative may be written as

$\begin{array}{ll}{D}_{\mu }={\partial }_{\mu }+\dots +i{g}_{1}Y{B}_{\mu }+i(\tilde{g}Y+g^{\prime }z)B_{\mu }^{\prime },& (25)\end{array}$

where Y and z are, respectively, the hypercharge and the U(1)′ charge, and $B_{\mu },B_{\mu }^{\prime }$ are the rotated fields. The parameter $\tilde{g}$ replaces κ and describes the mixing between the two Abelian groups while g′ is the usual gauge coupling associated to the extra Abelian symmetry U(1)′.

Due to the mixing term in the gauge covariant derivative, after spontaneous symmetry breaking, the EW Vacuum Expectation Value (VEV) contributes to the U(1)′ breaking even if the Higgs sector is neutral under the new Abelian symmetry. For instance, in a scenario with only one Higgs doublet, the neutral gauge boson mass matrix can be extracted from the Higgs Lagrangian and reads as

$\begin{array}{ll}-L_{\text{Higgs}}=\frac{v^2}{8}{(g_2{W}_{\mu }^3-g_1{B}_{\mu }-g_{\Phi }{B}_{\mu }^{\prime })}^2+\frac{m_{B^{\prime }}^2}{2}{B}_{\mu }^{{ }^{\prime }2}+\dots ,& (26)\end{array}$

where $g_{\Phi }=\tilde{g}+2z_{\Phi }{g}^{\prime }$ with z_Φ being the U(1)′ charge of the SM Higgs or a combination of charges in multi-Higgs doublet scenarios. As stated above, a non-vanishing g_Φ can be achieved either by the non-zero U(1)′ charges of the Higgs sector, z_Φ ≠ 0, or by the presence of the kinetic mixing $\tilde{g}\ne 0$. Both of them contribute to a Z − Z′ mass mixing. The mass term $m_{B^{\prime }}^2$ represents a possible source for the Z′ mass from a SM neutral sector. This can be realized, for instance, by the VEV v′ of a SM-singlet complex scalar χ, with a z_χ charge under U(1)′. In this case $m_{B^{\prime }}=g^{\prime }{z}_{\chi }{v}^{\prime }$. We remark here that, for our purposes, it is not necessary to specify the origin of the B′ mass term and other mechanisms, beside Spontaneous Symmetry Breaking (SSB) with a complex scalar, can be also envisaged. Moreover, the mixing in the neutral gauge sector is only triggered by the g_Φ parameter and, as such, is unaffected by the details of the scalar sector in which the B′ mass term is generated.

The diagonalization of the mass matrix provides the relation between the interaction and the mass eigenstates and is described by the rotation matrix

$\begin{array}{ll}\left(\begin{array}{c}{B}^{\mu }\\ W_3^{\mu }\\ {B{ }^{\prime }}^{\mu }\end{array}\right)=\left(\begin{array}{ccc}cos{\theta }_w& -sin{\theta }_{w}cos{\theta }^{\prime }& sin{\theta }_{w}sin{\theta }^{\prime }\\ sin{\theta }_w& cos{\theta }_{w}cos{\theta }^{\prime }& -cos{\theta }_{w}sin{\theta }^{\prime }\\ 0& sin{\theta }^{\prime }& cos{\theta }^{\prime }\end{array}\right)\left(\begin{array}{c}{A}^{\mu }\\ Z^{\mu }\\ {Z{ }^{\prime }}^{\mu }\end{array}\right)& (27)\end{array}$

where θ_w is the usual weak mixing angle and θ′ is a new mixing angle, with −π/4 ≤ θ′ ≤ π/4, defined as Accomando et al. [58]

$\begin{array}{ll}tan2{\theta }^{\prime }=\frac{2g_{\Phi }{g}_Z}{g_{{\Phi }^2}+4m_{B^{\prime }}^2/v^2-g_Z^2},& (28)\end{array}$

where $g_Z=\sqrt{g_1^2+g_2^2}$ is the EW coupling, $g_{\Phi }=\tilde{g}+2z_{\Phi }{g}^{\prime }$ and $g_{{\Phi }^2}=g_{\Phi }^2$. The masses of the Z and Z′ gauge bosons are then given by

$\begin{array}{ll}{M}_{Z,Z^{\prime }}=g_Z\frac{v}{2}{\left[\frac{1}{2}\left(\frac{g_{{\Phi }^2}+4m_{B^{\prime }}^2/v^2}{g_Z^2}+1\right)\mp \frac{g_{\Phi }}{\sin 2{\theta }^{\prime }{g}_Z}\right]}^{\frac{1}{2}}.& (29)\end{array}$

For a light and weakly interacting Z′, namely $g^{\prime },\tilde{g}\ll g_Z$ and $m_{B^{\prime }}^2\ll v^2$, the mixing angle and the masses can be expanded at leading order as

$\begin{array}{ll}{M}_Z^2\simeq \frac{1}{4}{g}_Z^2{v}^2,M_{Z^{\prime }}^2\simeq m_{B^{\prime }}^2,tan2{\theta }^{\prime }\simeq -2\frac{g_{\Phi }}{g_Z}.& (30)\end{array}$

While the SM Z mass is correctly reproduced by the EW VEV, the mass of the Z′ is controlled by the $m_{B^{\prime }}$ parameter or, equivalently, by the VEV v′ of the SM-singlet χ which is then given by $v^{\prime }=M_{Z^{\prime }}/(g^{\prime }{z}_{\chi })$. The Z′ massless limit for $m_{B^{\prime }}=0$ is naively expected since if SSB is turned off in the scalar sector, no scalar degrees of freedom can provide the longitudinal component of a massive Z′. For a 17 MeV Z′ with g′ ~ 10⁻³ the VEV of χ is v′ ~ 10 GeV.

The expansions in Equation (30) are applicable if the Higgs sector is populated by only one SU(2) doublet, as in the SM. This assumption can be obviously relaxed and more Higgs doublets can be implemented. We show, indeed, in the following sections that this possibility leads to an interesting phenomenology in the Z′ sector and provides alternative solutions to the ⁸Be anomaly.

For instance, in a scenario with two SU(2) doublet scalars, Φ₁ and Φ₂ with the same hypercharge Y = 1/2 and two different charges z_Φ1 and z_Φ2 under the extra U(1)′, the diagonalization of the neutral gauge mass matrix is obtained through the mixing angle θ′ in Equation (28) with

$\begin{array}{l}{g}_{\Phi }=(\tilde{g}+2g^{\prime }{z}_{{\Phi }_1}){cos}^2\beta +(\tilde{g}+2g^{\prime }{z}_{{\Phi }_2}){sin}^2\beta ,\\ g_{{\Phi }^2}={(\tilde{g}+2g^{\prime }{z}_{{\Phi }_1})}^2{cos}^2\beta +{(\tilde{g}+2g^{\prime }{z}_{{\Phi }_2})}^2{sin}^2\beta .& (31)\end{array}$

The angle β is defined as usual as tan β = v₂/v₁ with $v^2=v_1^2+v_2^2$. In the small coupling limit the Z′ mass is given by

$\begin{array}{ll}{M}_{Z^{\prime }}^2\simeq m_{B^{\prime }}^2+\frac{v^2}{4}{g^{\prime }}^2{(z_{{\Phi }_1}-z_{{\Phi }_2})}^2{sin}^2(2\beta ),& (32)\end{array}$

which, differently from the previous case, is non-vanishing even when $m_{B^{\prime }}\simeq 0$ due to mismatch between z_Φ1 and z_Φ2. In the limit in which there is no contribution from the dark scalar sector, one finds for $M_{Z^{\prime }}\simeq 17$ MeV and v ≃ 246 GeV, $\tilde{g}~g^{\prime }~10^{-4}$. Interestingly, as we will show below, the same order of magnitude of the gauge couplings is required to explain the ⁸Be anomaly with a Z′ gauge boson characterized by axial-vector couplings.

In summary, for the case of one Higgs doublet, we showed that the limit $m_{B^{\prime }}\ll v$ leads to $M_{Z^{\prime }}\simeq m_{B^{\prime }}$ with the SM Higgs sector playing no role in the generation of the Z′ mass. In contrast, in a multi-Higgs scenario, like in a 2-Higgs Doublet Model (2HDM), if z_Φ1 ≠ z_Φ2, the symmetry breaking of the U(1)′ can actually be realized without any contribution from the dark scalar sector, namely with v′ = 0. In fact, the longitudinal degree of freedom of the Z′ is provided by the typical CP-odd state of the 2HDM spectrum which, differently from standard constructions, is characterized by a missing pseudoscalar field among the physical states. Before moving to this 2HDM realization, though, we ought to discuss the Z′ interactions with the SM fermions emerging from the present construct.

7.1. The Z′ Interactions With the SM Fermions

The interactions between the SM fermions and the Z′ gauge boson are described by the Lagrangian ${{L}}_{\mathrm{\text{int}}}=-J_{Z^{\prime }}^{\mu }{Z}_{\mu }^{\prime }$ where the gauge current is given by

$\begin{array}{ll}{J}_{Z^{\prime }}^{\mu }={\displaystyle \sum _f}{\bar{\psi }}_f{\gamma }^{\mu }(C_{f,L}{P}_L+C_{f,R}{P}_R){\psi }_f& (33)\end{array}$

with coefficients

$\begin{array}{l}{C}_{f,L}=-g_Z{s}^{\prime }\left(T_f^3-s_w^2{Q}_f\right)+(\tilde{g}{Y}_{f,L}+g^{\prime }{z}_{f,L})c^{\prime },\\ C_{f,R}=g_Z{s}_w^2{s}^{\prime }{Q}_f+(\tilde{g}{Y}_{f,R}+g^{\prime }{z}_{f,R})c^{\prime }.& (34)\end{array}$

In the previous equations we have adopted the shorthand notation s_w ≡ sin θ_w, c_w ≡ cos θ_w, s′ ≡ sin θ′ and c′ ≡ cos θ′ and introduced Y_f the hypercharge, z_f the U(1)′ charge, $T_f^3$ the third component of the weak isospin and Q_f the electric charge. Analogously, the vector and axial-vector components of the Z′ interactions are [57]

$\begin{array}{l}{C}_{f,V}=\frac{C_{f,R}+C_{f,L}}{2}=\frac{1}{2}[-g_Z{s}^{\prime }(T_f^3-2s_w^2{Q}_f)+c^{\prime }\tilde{g}(2Q_f-T_f^3)\\ +c^{\prime }{g}^{\prime }(z_{f,L}+z_{f,R})],\\ C_{f,A}=\frac{C_{f,R}-C_{f,L}}{2}=\frac{1}{2}\left[(g_Z{s}^{\prime }+\tilde{g}{c}^{\prime })T_f^3-c^{\prime }{g}^{\prime }(z_{f,L}-z_{f,R})\right]& (35)\end{array}$

The vector and axial-vector coefficients simplify considerably in the limit $g^{\prime },\tilde{g}\ll g_Z$. By noticing that $s^{\prime }\simeq -g_{\Phi }/g_Z$, we get

$\begin{array}{l}{C}_{f,V}\simeq \tilde{g}{c}_w^2{Q}_f+g^{\prime }\left[z_{\Phi }(T_f^3-2s_w^2{Q}_f)+z_{f,V}\right],\\ C_{f,A}\simeq g^{\prime }\left[-z_{\Phi }{T}_f^3+z_{f,A}\right],& (36)\end{array}$

where we have introduced the vector and axial-vector U(1)′ charges z_f,V/A = 1/2(z_f,R ± z_f,L) and z_Φ can be either the U(1)′ charge of the Higgs or $z_{{\Phi }_1}{cos}^2\beta +z_{{\Phi }_2}{sin}^2\beta$ in a 2HDM scenario.

The Z′ couplings are characterized by the sum of three different contributions. The kinetic mixing $\tilde{g}$ induces a vector-like term proportional to the Electro-Magnetic (EM) current which is the only source of interactions when all the SM fields are neutral under U(1)′. In this case the Z′ is commonly dubbed dark photon. The second term is induced by the z_Φ, the U(1)′ charge in the Higgs sector, and leads to a dark Z, namely a gauge boson mixing with the SM Z boson. Finally there is the standard gauge interaction proportional to the fermionic U(1)′ charges z_f,V/A.

We can delineate different scenarios depending on the structure of the axial-vector couplings of the Z′ boson. In particular, the C_f,A coefficients can be suppressed with respect to the vector-like counterparts (see also [20]). This is realized, for instance, when only one SU(2) doublet is considered and the gauge invariance of the Yukawa Lagrangian under the new Abelian symmetry is enforced. Indeed, the latter requires the U(1)′ charge of the Higgs field to satisfy the conditions

$\begin{array}{ll}{z}_{\Phi }=z_Q-z_d=-z_Q+z_u=z_L-z_e.& (37)\end{array}$

Inserting the previous relations into Equation (36), we find C_f,A ≃ 0 which describes a Z′ with only vector interactions with charged leptons and quarks. We stress again that the suppression of the axial-vector coupling is only due to the structure of the scalar sector, which envisions only one SU(2) doublet, and the gauge invariance of the Yukawa Lagrangian. This feature is completely unrelated to the U(1)′ charge assignment of the fermions, the requirement of anomaly cancelation and the matter content potentially needed to account for it.

In contrast, in the scenario characterized by two Higgs doublets, the axial-vector couplings of the Z′ are, in general, of the same order of magnitude of the vector ones and the cancelation between the two terms of C_f,A in Equation (36) is not achieved regardless of the details of the Yukawa Lagrangian (such as which type 2HDM). The same result can be achieved if a single Higgs doublet is considered but the conditions in Equation (37) are not satisfied as in scenarios in which the fermion masses are generated radiatively or through horizontal symmetries.

To summarize, we can identify three different situations that can provide a light Z′ with interactions potentially explaining the Beryllium anomaly. In all of them, the SM is extended by an additional Abelian gauge group.

1. The SM scalar sector is unchanged, being characterized by only one Higgs doublet. In this case the mass of the Z′ is entirely generated in the dark sector. The Yukawa Lagrangian preserves the SM structure and its gauge invariance under the U(1)′ necessary implies that the Z′ has only vector interactions with the SM fermions at leading order in the couplings $\tilde{g},g^{\prime }$.

2. The SM scalar sector is extended by an additional Higgs doublet. Even though the Yukawa Lagrangian is invariant under the local U(1)′ symmetry, the cancelation between the two terms in C_f,A in Equation (36) does not occur and both the vector and axial-vector couplings of the Z′ are non-vanishing. The mass of the Z′ acquires contribution from both the dark and the EW sectors.

3. The SM scalar sector is characterized by a single Higgs doublet but the constraints in Equation (37) are avoided by relying on more complicated Yukawa structures. As such, the cancelation providing C_f,A ≃ 0 is not realized and the vector and axial-vector interactions of the Z′ are of the same order of magnitude.

We will discuss the three scenarios in the following sections focusing on their implications in the interpretation of the ⁸Be anomaly.

Before concluding this section we briefly go through the conditions required by the cancelation of gauge and gravitational anomalies which strongly constrain the charge assignment of the SM spectrum under the extra U(1)′ gauge symmetry. These conditions can be eventually combined with the requirement of gauge invariance of the Lagrangian responsible for the generation of the fermion masses which may also involve non-renormalisable operators. We will also allow for extra SM-singlet fermions which can be easily interpreted as right-handed neutrinos. We assign the charges z_Q and z_L for the SU(2) quark and lepton doublets, z_u, z_d, z_e for the corresponding right-handed components and z_ν for the n_R right-handed neutrinos. We obtain the following gauge and gravitational anomaly cancelation conditions:

$\begin{array}{ll}U{(1)}^{\prime }SU(3)SU(3):& {\displaystyle \sum _i^3}(2z_{Q_i}-z_{u_i}-z_{d_i})=0,\\ U{(1)}^{\prime }SU(3)SU(3):& {\displaystyle \sum _i^3}(3z_{Q_i}+z_{L_i})=0,\\ U{(1)}^{\prime }U{(1)}_{Y}U{(1)}_Y:& {\displaystyle \sum _i^3}\left(\frac{z_{Q_i}}{6}-\frac{4}{3}{z}_{u_i}-\frac{z_{d_i}}{3}+\frac{z_{L_i}}{2}-z_{e_i}\right)=0,\\ U{(1)}^{\prime }U{(1)}^{\prime }U{(1)}_Y:& {\displaystyle \sum _i^3}\left(z_{Q_i}^2-2z_{u_i}^2+z_{d_i}^2-z_{L_i}^2+z_{e_i}^2\right)=0,\\ U{(1)}^{\prime }U{(1)}^{\prime }U{(1)}^{\prime }:& {\displaystyle \sum _i^3}\left(6z_{Q_i}^3-3z_{u_i}^3-3z_{d_i}^3+2z_{L_i}^3-z_{e_i}^3\right)+{\displaystyle \sum _i^{n_R}}{z}_{{\nu }_i}=0,\\ U{(1)}^{\prime }GG:& {\displaystyle \sum _i^3}\left(6z_{Q_i}-3z_{u_i}-3z_{d_i}+2z_{L_i}-z_{e_i}\right)+{\displaystyle \sum _i^{n_R}}{z}_{{\nu }_i}=0.& (38)\end{array}$

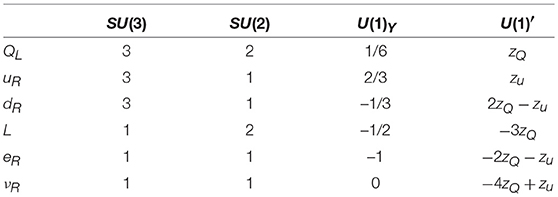
A simple solution is found for instance in the family universal case with n_R = 3 and z_νi = z_ν and it is defined in terms of only two U(1)′ charges, z_Q and z_u as shown in Table 1. As an example, the U(1)_B−L is reproduced by z_Q = z_u = 1/3 while the sequential U(1)′ is obtained for z_Q = 1/6 and z_u = 2/3.

TABLE 1

Table 1. Family universal charge assignment in the U(1)′ extension of the SM.

7.2. Z′ With Vector Couplings

The simplest U(1)′ extension of the SM, which may account for an extra neutral light gauge boson potentially explaining the ⁸Be anomaly, is characterized by a single Higgs doublet. As already explained above, the gauge invariance of the Yukawa interactions fixes the U(1)′ charge of the Higgs to satisfy the restrictions in Equation (37) thus leading to a suppression of the Z′ axial-vector couplings to the quarks and charged leptons with respect to the vector ones.

In this scenario, the anomalous internal pair creation transition of the excited stated of the Beryllium described by the normalized BR is given by

$\begin{array}{ll}\frac{\text{BR}({}^8\text{B}{\text{e}}^{*}\to X+{}^8\text{B}\text{e})}{\text{BR}({}^8\text{B}{\text{e}}^{*}\to \gamma +{}^8\text{B}\text{e})}=\frac{1}{e^2}{(C_{p,V}+C_{n,V})}^2\frac{|{\overrightarrow{k}}_{Z^{\prime }}{|}^3}{|{\overrightarrow{k}}_{\gamma }{|}^3}& (39)\end{array}$

in which any dependence from the nuclear matrix elements factors out in the ratio of BRs. Moreover, the partial decay width of the Z′ into SM fermions is

$\begin{array}{ll}\Gamma (Z^{\prime }\to f\bar{f})=\frac{M_{Z^{\prime }}}{12\pi }\sqrt{1-\frac{4m_f^2}{M_{Z^{\prime }}^2}}\left[C_{f,V}^2+C_{f,A}^2+2(C_{f,V}^2-2C_{f,A}^2)\frac{m_f^2}{M_{Z^{\prime }}^2}\right].& (40)\end{array}$

Since $M_{Z^{\prime }}\simeq 17$ MeV, the light Z′ can only decay into electrons and active neutrinos (assuming heavier right-handed neutrinos, if any).

While C_f,A ≃ 0, the explicit expressions of the vector couplings of the Z′ are

$\begin{array}{l}{C}_{p,V}=\tilde{g}{c}_w^2-2g^{\prime }{z}_H{s}_w^2+g^{\prime }(z_H+3z_Q),\\ C_{n,V}=-g^{\prime }(z_H-3z_Q),\\ C_{e,V}=-\tilde{g}{c}_w^2+2g^{\prime }{z}_H{s}_w^2-g^{\prime }(z_H-z_L),\\ C_{\nu ,V}=-C_{\nu ,A}=\frac{g^{\prime }}{2}(z_H+z_L),& (41)\end{array}$

where we have introduced the proton and neutron couplings C_p,V = 2C_u,V + C_d,V, C_n,V = C_u,V + 2C_d,V and we have exploited the gauge invariance of the Yukawa Lagrangian. Moreover, the cancelation of the anomaly in the U(1)′SU(2)SU(2) triangle diagram given in Equation (38) leads to 3z_Q + z_L = 0, namely C_ν,V = −2C_n,V.

The acceptable range of couplings is Feng et al. [7, 9]

$\begin{array}{l}\left|C_{p,V}\right|\lesssim 1.2\times 10^{-3}e,\\ \left|C_{n,V}\right|=(2-10)\times 10^{-3}e,\\ \left|C_{e,V}\right|=(0.2-1.4)\times 10^{-3}e,\\ \sqrt{\left|C_{\nu ,V}{C}_{e,V}\right|}\lesssim 3\times 10^{-4}e,& (42)\end{array}$

where BR(Z′ → e⁺e⁻) = 1 has been assumed. The first two conditions ensure that the Atomki anomaly is correctly reproduced while avoiding, at the same time, the strong constraint from the π⁰ → Z′γ decay. As the coupling to proton is smaller than the corresponding one to neutron, the Z′ realizing this particular configuration has been dubbed protophobic. The bound on the electron coupling is mainly obtained from KLOE2, (g−2)_e and beam dump experiments, while the neutrino coupling is constrained by neutrino scattering off electrons at the Taiwan EXperiment On Neutrinos (TEXONO) [45]. Reinterpreting the bounds obtained in Bilmis et al. [46], where a B − L scenario without mixing has been considered, for a general vector-like Z′, one can show that the C_ν coupling must be much smaller than the typical value of C_n,V required to explain the ⁸Be anomaly, thus invalidating the C_ν,V = −2C_n,V condition required by the consistency of this simple model.

A possible way to suppress the neutrino coupling, without affecting the neutron one, could be to invoke the presence of additional neutral fermionic degrees of freedom, charged under the U(1)′ symmetry and mixed to the left-handed neutrinos, so that the effective coupling of the Z′ to the physical neutrino mass eigenstate would be significantly reduced. This mixing is commonly realized in the seesaw mechanism, which is naturally envisaged in the Abelian extension considered here since right-handed neutrinos are required to cancel the gauge anomalies, but it can hardly account for the bounds determined by the neutrino-electron scattering experiments. Such a strategy has been discussed in Feng et al. [7], however, here we show two alternative solutions based on the exploitation of the Z′ axial-vector interactions.

8. Explanation of the Beryllium Anomaly With a Family Universal U(1)′

In this section we investigate the explanation of the Atomki anomaly in a scenario characterized by an extra U(1)′ model and two Higgs doublets.

One possibility studied as a solution to the Atomki anomaly is a well-known realization of the scalar potential and Yukawa interactions with two scalar doublets is the so-called type-II in which the up-type quarks couple to one Higgs (conventionally chosen to be Φ₂) while the down-type quarks couple to the other (Φ₁). The constraint from anomaly cancelation arising from the U(1)′SU(3)SU(3) triangle diagram together with the gauge invariance of the Yukawa Lagrangian require 2z_Q − z_d − z_u = z_Φ1 − z_Φ2 = 0, in the type-II scenario. In order to satisfy this condition with z_Φ1 ≠ z_Φ2, extra colored states are necessarily required which will bring additional terms into the anomaly cancelation conditions and so the equation above will be modified and no longer require equal Higgs charges under the new gauge group. These states must be vector-like under the SM gauge group and chiral under the extra U(1)′. This option has been explored in detail in Kahn et al. [20]. In this work, the constraints on new vector bosons with axial vector couplings in a family-universal scenario which includes extra colored states to cancel anomaly conditions is considered. In this review focus on a different, more minimal scenario than this, which does not require additional states, but modifies the scalar theory to affect the condition of anomaly cancelation.

The gauge invariance condition above is modified when the scalar sector reproduces the structure of the type-I 2HDM in which only one (Φ₂) of the two Higgs doublets participates in the Yukawa interactions. In this theory, the corresponding Lagrangian is the same as the SM one and its gauge invariance simply requires z_Φ2 = −z_Q + z_u = z_Q − z_d = z_L − z_e, without constraining the U(1)′ charge of Φ₁, in the type-I scenario. In this way, we allow for gauge invariance even when z_Φ1 ≠ z_Φ2. Differently from the type-II scenario in which extra colored states are required to build an anomaly-free model, in the type-I case the UV consistency of the theory can be easily satisfied introducing only SM-singlet fermions as demanded by the anomaly cancelation conditions of the U(1)′U(1)′U(1)′ and U(1)′GG correlators. Nevertheless, the mismatch between z_Φ and z_f,A = ±z_Φ2/2 (for up-type and down-type quarks, respectively) prevents C_f,A to be suppressed and the Z′ interactions are given by Delle Rose et al. [57],

$\begin{array}{l}{C}_{u,V}=\frac{2}{3}\tilde{g}{c}_w^2+g^{\prime }\left[z_{\Phi }\left(\frac{1}{2}-\frac{4}{3}{s}_w^2\right)+z_{u,V}\right],\\ C_{u,A}=-\frac{g^{\prime }}{2}{cos}^2\beta (z_{{\Phi }_1}-z_{{\Phi }_2}),\\ C_{d,V}=-\frac{1}{3}\tilde{g}{c}_w^2+g^{\prime }\left[z_{\Phi }\left(-\frac{1}{2}+\frac{2}{3}{s}_w^2\right)+z_{d,V}\right],\\ C_{d,A}=\frac{g^{\prime }}{2}{cos}^2\beta (z_{{\Phi }_1}-z_{{\Phi }_2}),\\ C_{e,V}=-\tilde{g}{c}_w^2+g^{\prime }\left[z_{\Phi }\left(-\frac{1}{2}+2s_w^2\right)+z_{e,V}\right],\\ C_{e,A}=\frac{g^{\prime }}{2}{cos}^2\beta (z_{{\Phi }_1}-z_{{\Phi }_2}),\\ C_{\nu ,V}=-C_{\nu ,A}=\frac{g^{\prime }}{2}(z_{\Phi }+z_L).& (43)\end{array}$

As pointed out in Feng et al. [7], the contribution of the axial-vector couplings to the ⁸Be* → ⁸Be Z′ decay is proportional to $\left|{\overrightarrow{k}}_{Z^{\prime }}\right|/M_{Z^{\prime }}\ll 1$, where ${\overrightarrow{k}}_{Z^{\prime }}$ is the momentum of the Z′, while the vector component is suppressed by $|{\overrightarrow{k}}_{Z^{\prime }}{|}^3/M_{Z^{\prime }}^3$. Therefore, in our case, being C_f,V ~ C_f,A, we can neglect the effects of the vector couplings of the Z′ and their interference with the axial counterparts. For a Z′ with only axial-vector couplings to quarks, the transition ⁸Be* → ⁸Be Z′ is described by the partial width [19]

$\begin{array}{ll}\Gamma =\frac{k}{18\pi }\left(2+\frac{E_k^2}{M_{Z^{\prime }}^2}\right)|a_n\langle 0\left|\right|{\sigma }^n\left|\right|1\rangle +a_p\langle 0\left|\right|{\sigma }^p\left|\right|1\rangle {|}^2,& (44)\end{array}$

where the neutron and proton coefficients a_n = (a₀ − a₁)/2 and a_p = (a₀ + a₁)/2 are defined in terms of

$\begin{array}{l}{a}_0=(C_{u,A}+C_{d,A})\left(\Delta u^{(p)}+\Delta d^{(p)}\right)+2C_{s,A}\Delta s^{(p)},\\ a_1=(C_{u,A}-C_{d,A})\left(\Delta u^{(p)}-\Delta d^{(p)}\right),& (45)\end{array}$

with Δu^(p) = 0.897(27), Δd^(p) = −0.367(27) and Δs^(p) = −0.026(4) [59]. The reduced nuclear matrix elements of the spin operators have been computed in Kozaczuk et al. [19] and are given by 〈0||σⁿ||1〉 = −0.132 ± 0.033, 〈0||σ^p||1〉 = −0.047 ± 0.029 for the isoscalar ⁸Be* → ⁸Be transition and 〈0||σⁿ||1〉 = −0.073 ± 0.029, 〈0||σ^p||1〉 = 0.102 ± 0.028 for the isovector ⁸Be^*′ → ⁸Be transition.

Notice that the axial couplings of the quarks and, therefore, the width of the ⁸Be* → ⁸Be Z′ decay are solely controlled by the product g ′cos² β while the kinetic mixing $\tilde{g}$ only affects the BR(Z′ → e⁺e⁻) since the Z′ → νν decay modes are allowed (we assume that the $Z^{\prime }\to {\nu }_R{\nu }_R$ decays are kinematically closed). For definiteness, we consider a U(1)_B-L charge assignment with z_QL = z_uR = 1/3, with other charges defined using Table 1, and z_Φ2 = 0, z_Φ1 = 1 and tan β = 1. Analog results may be obtained for different U(1)′ charge assignments and values of tan β. We show in Figure 2 the parameter space explaining the Atomki anomaly together with the most constraining experimental results.

FIGURE 2

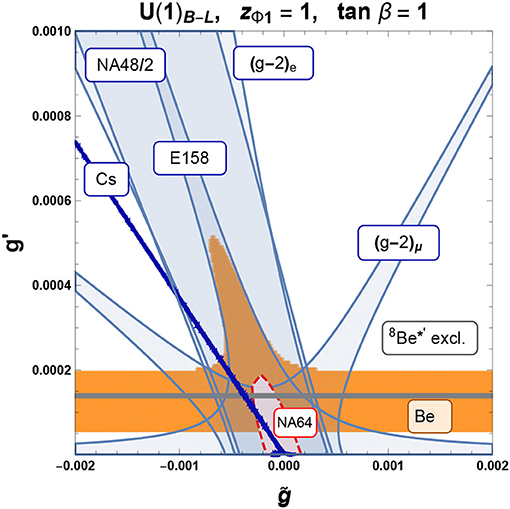
Figure 2. Allowed parameter space (orange region) explaining the anomalous ⁸Be* decay. The white region above is excluded by the non-observation of the same anomaly in the ⁸Be^*′ transition. Also shown (shaded regions) is the allowed parameter space by the g − 2 of electrons and muons and the Møller scattering at SLAC E158 and pion decay from NA48/2. The beam dump experiment NA64 allows parameter space outside the red shaded region with dashed line. Finally, the blue line selects values of g′ and $\tilde{g}$ compatible with the weak nuclear charge measurement of Cesium. The horizontal gray band delineates values of g′ for which the Z′ mass is solely generated by the SM vev.

The orange region, where the Z′ gauge couplings comply with the best-fit of the ⁸Be* decay rate in the mass range $M_{Z^{\prime }}=16.7\text{ MeV}-17.6\text{ MeV}$ [1, 7], encompasses the uncertainties on the computation of the nuclear matrix elements [19]. The region above it is excluded by the non-observation of the same transition in the isovector excitation ⁸Be^*′ [1]. The horizontal gray band selects the values of g′ accounting for the Z′ mass in the negligible $m_{B^{\prime }}$ case in which the U(1)′ symmetry breaking is driven by the two Higgs doublets. Furthermore, among all other experimental constraints involving a light Z′ that may be relevant for this analysis we have shown the most restrictive ones.

The strongest bound comes from the atomic parity violation in Cs and it represents a constraint on the product of C_e,A and a combination of C_u,V and C_d,V. This bound can be avoided if the Z′ has either only vector or axial-vector couplings but in the general scenario considered here, it imposes severe constraints on the gauge couplings $g^{\prime },\tilde{g}$ thus introducing a fine-tuning in the two gauge parameters.

We finally comment on the constraints imposed by neutrino-electron scattering processes [45, 60, 61], the strongest one being from ${\bar{\nu }}_{e}e$ scattering at the TEXONO experiment [45], which affect a combination of C_e,V/A and C_ν,V. As discussed above, in the protophobic scenario, in which the Z′ has only vector interactions, the constrained ν coupling to the Z′ boson is in high tension with the measured ⁸Be* decay rate since C_ν,V = −2C_n,V and a mechanism to suppress the neutrino coupling must be envisaged [7]. This bound is, in general, alleviated if one attempts to explain the Atomki anomaly with a Z′ boson with axial-vector interactions since the required gauge couplings $g^{\prime },\tilde{g}$ are smaller than the ones needed in the protophobic case. Neutrino couplings are also constrained by meson decays, like, for instance K^± → π^±νν which has been studied in Davoudiasl et al. [62] and where it has been shown that the corresponding constraint is relaxed by a destructive interference effect induced by the charged Higgs. As the results presented in Davoudiasl et al. [62] relies on the Goldstone boson equivalence approximation, we have computed the full one-loop corrections to the K^± → π^±Z′ process in the U(1)′-2HDM scenario. The results are in agreement with the estimates in Davoudiasl et al. [62]. In our setup, for g′ ~ 10⁻⁴ and tan β = 1, $M_{H^{\pm }}~600$ GeV can account for the destructive interference quoted above between the W^± and H^± loops. For instance, we find $\mathrm{\text{BR}}(K^{\pm }\to {\pi }^{\pm }{Z}^{\prime }\to {\pi }^{\pm }\nu \nu )\simeq 0.1\mathrm{\text{ BR}}{(K^{\pm }\to {\pi }^{\pm }\nu \nu )}_{\mathrm{\text{exp}}}$ for $M_{H^{\pm }}~615$ GeV with BR(Z′ → νν) ≃ 30% which is the maximum value for the invisible Z′ decay rate in the allowed region (orange and gray shaded area) shown in Figure 2. A similar constraint arises from the B meson decay to invisible but is less severe than the one discussed above [63]. The B^± → K^±Z′ process is characterized by the same loop corrections appearing in K^± → π^±Z′, with the main difference being the dependence on the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements. Therefore, the suppression effect induced by the charge Higgs mass affects both processes in the same region of the parameter space, thus ensuring that the bound from the invisible B decays is satisfied once the constraint from the analogous K meson decay is taken into account.

9. Explanation of the Beryllium Anomaly With a Family Non-universal U(1)′

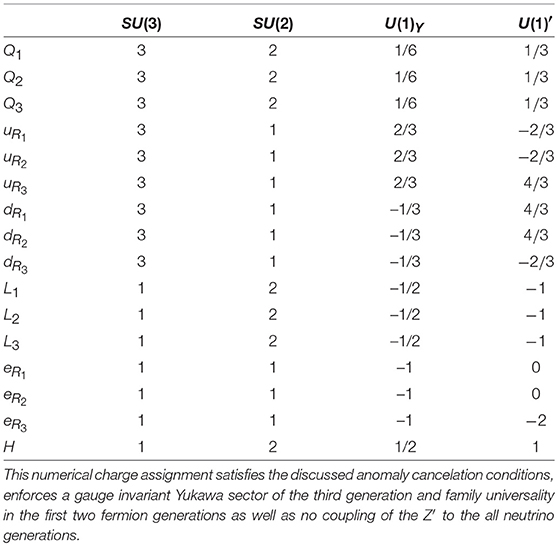
The final alternative is to consider a single Higgs doublet, as with the SM, but non-standard Yukawa interactions, to allow axial couplings through the violation of Equation (37), as done in Delle Rose et al. [64]. This is done for the first two generations of fermions and the third has SM-like gauge-invariance, motivated by ${O}(1)$ couplings. We begin by modifying the Yukawa couplings for the first two generations as follows,

$\begin{array}{l}-L_{Yuk}={\Gamma }^u\frac{{\chi }^{n_{ij}}}{M^{n_{ij}}}{\overline{Q}}_{L,i}\tilde{H}{u}_{R,j}+{\Gamma }^d\frac{{\chi }^{l_{ij}}}{M^{l_{ij}}}{\overline{Q}}_{L,i}H{d}_{R,j}\\ +{\Gamma }^e\frac{{\chi }^{m_{ij}}}{M^{m_{ij}}}{\overline{L}}_{i}H{e}_{R,j}+h.c.,& (46)\end{array}$

where the exponent, n_ij, of the non-renormalisable scale, M, is defined by the U(1)′ charges of the fields, such that these new Yukawa terms are gauge invariant. Subsequently, one may obtain fermion masses either at tree-level or radiatively by the method of Ref. Froggatt and Nielsen [65]². There are several models which motivate radiative mass generation for the lighter generations, as done in Demir et al. [66], alternatively, there exist mass generation dynamics by horizontal symmetries, as in Froggatt and Nielsen [65]. We do not specify these dynamics, and simply leave an effective approach. We finally enforce that the first two generations are flavor universal, differing from the third, z_i1 = z_i2 for i = {Q, u_R, d_R, L, e_R}, where the condition (37) is not applied to z_i1,2. We now consider further constraints on the charge assignment. We also enforce the chiral anomaly cancelation conditions in Equation (38), which will be satisfied by solely the fermionic content of the SM, supplemented by two right-handed neutrinos.

Our remaining constraints on the charge assignment are motivated by the non-observation of BSM physics. As discussed above, there are strong constraints on coupling to neutrinos, which would enhance processes such as K^± → π^±νν [62], as well as electron-neutrino interactions, measured by the TEXONO experiment [7, 45, 46, 67]. To avoid these stringent constraints, we therefore impose no couplings to the neutrinos, i.e., C_V,ν = C_A,ν = 0. This subsequently yields a relation between the neutrino and Higgs charges,

$\begin{array}{ll}{z}_{L_1}=z_{L_2}=z_{L_3}=-z_H.& (47)\end{array}$

Another constraint is to require that one indeed does have axial couplings for the up/down quarks to the Z′, as required to explain the anomaly,

$\begin{array}{ll}-z_{Q_{1,2}}-z_H+z_{u_{1,2}}\ne 0,& (48)\end{array}$

$\begin{array}{ll}-z_{Q_{1,2}}+z_H+z_{d_{1,2}}\ne 0.& (49)\end{array}$

Our final constraint is from the atomic parity violation in Cs. As can be seen from other solutions, this provides a stringent bound on models with axial couplings for electrons. We thus also forbid interactions of this kind, and due to requiring universality for the first two generations, this will also forbid axial couplings for the muon,

$\begin{array}{ll}{C}_{e,A}=C_{\mu ,A}=0.& (50)\end{array}$

Preventing the appearance of these axial couplings will also help to avoid bounds from both (g − 2)_e and avoid worsening the discrepancy in (g − 2)_μ.

Combining all these constraints yields a single, unique charge assignment. We have a normalization choice, and choose to set z_H = 1. This unique choice is shown in Table 2.

TABLE 2

Table 2. Charge assignment of the SM particles under the family-dependent (non-universal) U(1)′.

Now, we consider constraints on the new gauge coupling, and gauge-kinetic mixing parameters $(g^{\prime },\tilde{g})$, given this charge selection. Unlike the previous scenarios considered, since this is family non-universal, one finds tree level FCNCs, which should be analyzed. In diagonalizing the quarks into the mass basis, off-diagonal couplings are generated, due to different coupling strengths between the first two and third quark generations. We now discuss the consequences of this on experimental observables. We begin with K → πe⁺e⁻ through a tree-level exchange of an on-shell Z′. There are no contributions to the μ⁺μ⁻ decay as $M_{Z^{\prime }}~17$ MeV < 2m_μ. There are stringent limits from LHCb [68], though these are inapplicable in our case due to the small invariant mass of the e⁺e⁻ pair. There is only sensitivity to energies above 20 MeV, due to photon conversion in the detector, and so energy resolution strongly degrades around these invariant masses. It is possible that future upgrades will lower this threshold and thus act as a discovery tool, or to disprove this scenario.

Another flavor observable is from meson mixing measurements. We begin with $B^0-{\bar{B}}^0$, following the procedure as done in Bečirević et al. [69], but now assuming a much lighter propagator than their scenario, $P\equiv {(m_B^2-M_{Z^{\prime }}^2)}^{-1}\simeq m_B^{-2}$, as opposed to their $P\simeq M_{Z^{\prime }}^{-2}$. One subsequently finds the requirement

$\begin{array}{ll}\left|g_{sb}^{L(R)}\right|\lesssim 10^{-6},& (51)\end{array}$

where (assuming Minimal Flavor Violation (MFV) in the quark sector and using CKM matrix elements),

$\begin{array}{ll}{g}_{sb}^L=g^{\prime }(V_{\text{CKM}}^T\text{ Diag}(z_{Q_1},z_{Q_1},z_{Q_3})V_{\text{CKM}}{)}_{23},& (52)\end{array}$

$\begin{array}{ll}{g}_{sb}^R=g^{\prime }(V_{\text{CKM}}^T\text{ Diag}(z_{u_{R_1}},z_{u_{R_1}},z_{u_{R_3}})V_{\text{CKM}}{)}_{23},& (53)\end{array}$

Since our charge assignment is family universal for LH quarks, $g_{sb}^L=0$, see Table 2, only the right-handed sector will contribute to the FCNC. This is suppressed by CKM factors, $g_{sb}^R\propto V_{tb}{V}_{ts}$, and so one finds a condition on the couplings, $g^{\prime },\tilde{g}\lesssim 10^{-4}$.

Proceeding in a similar faction but for $K-\bar{K}$ oscillations will yield a weaker constraint on the couplings. Although the propagator suppression is less severe, $P\simeq m_K^{-2}>m_B^{-2}$, the CKM suppression is much stronger, $g_{sd}^R\propto V_{td}{V}_{ts}$, and one finds the constraint $g^{\prime },\tilde{g}\lesssim 10^{-3}$. In this review, we do not perform a full flavor analysis, but require these approximate constraints.

Finally, we present the allowed parameter space in Figure 3 for this scenario with one Higgs doublet extended by a U(1)′, with a charge assignment shown in Table 2. The red, purple and green bands show regions which can explain the Atomki anomaly for 16.7, 17.3 and 17.6 MeV Z′ masses, respectively. These overlap in places and are independent of $\tilde{g}$ as the axial coupling depends solely on g′ and BR(Z′ → e⁺e⁻) = 1 everywhere. These bands have upper bounds due to the non-observation of the ⁸Be^*′ anomaly. Also shown on the plot are the bounds from (g − 2)_μ, where the allowed region is inside the dashed line and (g − 2)_e, where the allowed region is shaded in blue inside the dotted lines. In addition, the allowed region from NA64 is also shown, where one should be outside the red shaded region. The overall allowed region is therefore between the NA64 and (g − 2)_e lines, in the overlap shaded in blue. The other experimental constraints (electron positron collider (KLOE2), Moller scattering (E158), pion decay (NA48/2), E141, and atomic parity violation of Cs), similar to (g − 2)_μ, do not limit the allowed parameter space in blue, and are not shown on the plot.

FIGURE 3

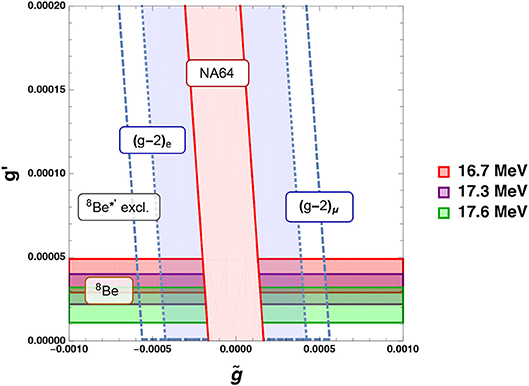
Figure 3. Allowed parameter space mapped on the $(g^{\prime },\tilde{g})$ plane explaining the anomalous ⁸Be* decay for Z′ solutions with mass 16.7 (red), 17.3 (purple), and 17.6 (green) MeV. The white regions are excluded by the non-observation of the same anomaly in the ⁸Be^*′ transition. Also shown are the constraints from (g − 2)_μ, to be within the two dashed lines; (g − 2)_e, to be inside the two dotted lines (shaded in blue) and the electron beam dump experiment, NA64, to be outside the shaded red region, which lies between the two solid lines. The surviving parameter space lies at small positive and negative $\tilde{g}$ (though not at $\tilde{g}=0$), inside the shaded blue region which overlaps the Atomki anomaly solutions.

Figure 4 shows the quantity ${B}$, as defined in Equation (1), over a range of Z′ masses. For each fixed mass value, a scan is performed over $(g^{\prime },\tilde{g})$, in a range compatible with other experimental constraints, and the Atomki anomaly (i.e., over the dark blue and colored regions in Figure 3). For each scanned point in $\left\{M_{Z^{\prime }},g^{\prime }.\tilde{g}\right\}$, there is a range of branching ratios, due to uncertainties in the Nuclear Matrix Elements (NMEs). This lower limit for all points is lower than the Atomki branching ratios, so only the upper ${B}$ is of importance, and this is plotted. Also drawn, in orange, is the required branching ratio, as published by the Atomki collaboration, see Table 3. A given point is then allowed if the upper ${B}$ limit lies above the orange dots. For larger $M_{Z^{\prime }}$ values, the largest ${B}$ decreases, and a larger number of the scanned points lie above the Atomki points. This suggests that at higher masses, there is slightly more parameter space available for the 17.6 MeV solution, in comparison to the 16.7 MeV one. This is reflected in the slightly different widths shown in Figure 3.

FIGURE 4

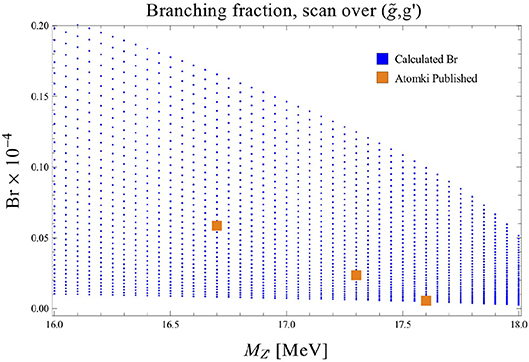
Figure 4. Values of the upper limit ${B}$ (lower limits are smaller than the scale of the plot), as defined in Equation (1), vs. the mass of the Z′ obtained scanning over the allowed parameter space in $(g^{\prime },\tilde{g})$, obtained from Figure 3 for each mass step taken (in blue). The Atomki collaboration solutions are also shown (in orange).

TABLE 3

Table 3. Solutions to the Atomki anomaly, with best fit mass value (16.7 MeV) from Krasznahorkay et al. [1] and subsequent alternative masses (17.3 and 17.6 MeV) from Feng et al. [7] along with the corresponding ratio of BRs, ${B}$, as defined in Equation (1).

10. Conclusions

While there remains the possibility that the Atomki anomaly can be explained as a statistical fluctuation combined with yet unknown nuclear physics properties and/or unforeseen experimental conditions, the fact that presently such an effect has been determined with a 6.8σ significance, including a near-perfect fit of both the mass and angular excesses to the possibility of a new particle with a mass of about 17 MeV been produced, calls for a thorough investigation of plausible theoretical explanations.

With this in mind, in this review, we have presented particle physics scenarios that extend the SM to include the presence of either a spin-0 (pseudoscalar, A) boson or a spin-1 (axial-vector, Z′) boson, both of which can be made compliant with a variety of experimental data. Assuming the standard Lagrangian structures describing A and Z′ interactions with SM fermionic currents in both the lepton and quark sectors, we have determined the required couplings of such bosons to explain the Beryllium data.

As for the theoretically embeddings of these solutions, we can conclude the following. A light pseudoscalar state can appear in models with extended Higgs sectors in which an approximate ungauged global symmetry is spontaneously broken, examples of which include (type-II) 2HDMs with a SM-singlet near the Peccei-Quinn or R-symmetric limit, although in this case isospin breaking effects and non-universality in the Yukawa couplings of the new state to electrons and d-quarks must be allowed for. As for light gauge bosons with significant axial-vector couplings, two possible theoretical frameworks have been proven to be viable. Both require an additional U(1)′ group mixing with the SM one, U(1)_Y. In one case, which retains the SM Higgs sector, a family non-universal set of Z′ couplings to the known fermions must be invoked. In the other case, Z′ couplings to quarks and fermions of the SM can be retained in their universal form, yet this requires an enlarged Higgs sector, which we have identified as possibly being a type-I 2HDM. Needless to say, these two theoretical frameworks were constructed in presence of gauge invariance and anomaly cancelations plus they do not require isospin breaking.

While the above list of possible theoretical setups is clearly not exhaustive, it at least provides somewhat minimal frameworks (only containing enlarged Higgs and gauge sectors, possibly including heavy neutrinos but no exotic particles) within which further data upcoming from the Atomki experiment can be interpreted to pave the way for more dedicated phenomenological studies, which may in turn lead to refinements on the theoretical side.

Author Contributions

All authors worked on all parts of the manuscript. Listed below are which sections were first drafted by the different authors, but subsequently all authors contributed to all parts. LDR: Experimental constraints on the quark couplings and A U(1)′ extension of the SM with a light and weakly interacting Z′. SK: The Atomki experiment and 17 MeV beryllium anomaly, Candidates for the new boson, and Explanation of the beryllium anomaly with a pseudoscalar. SJDK: Experimental constraints on the spin-1 explanation, Experimental constraints on the lepton couplings, and Explanation of the beryllium anomaly with a family universal U(1)′. SM: Introduction, Experimental constraints on the pseudoscalar explanation, Explanation of the beryllium anomaly with a family non-universal U(1)′.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work of LD and SM is supported in part by the NExT Institute. SM also acknowledges partial financial contributions from the STFC Consolidated Grant ST/L000296/1. Furthermore, the work of LD has been supported by the STFC/COFUND Rutherford International Fellowship Programme (RIFP). SJDK and SK have received support under the H2020-MSCA grant agreements InvisiblesPlus (RISE) No. 690575 and Elusives (ITN) No. 674896. In addition SK was partially supported by the STDF project 13858. All authors acknowledge support under the H2020-MSCA grant agreement NonMinimalHiggs (RISE) No. 645722.

Footnotes

1. ^It should however be mentioned that this second anomaly was never documented in a published paper, only in proceedings contributions.

2. ^Lagrangians of this form have been used to motivate solutions to the flavor problem, so it may be of interest to investigate whether this U(1)′ may explain the allowed masses and mixings, but we perform no such careful investigation here.

References

1. Krasznahorkay AJ, Csatlós M, Csige L, Gácsi Z, Gulyás J, Hunyadi M, et al. Observation of anomalous internal pair creation in Be8 : a possible indication of a light, Neutral Boson. Phys Rev Lett. (2016) 116:042501. doi: 10.1103/PhysRevLett.116.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Krasznahorkay AJ, Csatlós M, Csige L, Gácsi Z, Ketel TJ, Krasznahorkay A, et al. On the creation of the 17 MeV X boson in the 17.6 MeV M1 transition of ⁸Be. EPJ Web Conf. (2017) 142:01019. doi: 10.1051/epjconf/201714201019

CrossRef Full Text | Google Scholar

3. Krasznahorkay AJ, Csatlós M, Csige L, Gulyás J, Hunyadi M, Ketel TJ, et al. New results on the Be-8 anomaly. In: 55th International Winter Meeting on Nuclear Physics. Bormio (2017).

Google Scholar

4. Krasznahorkay AJ, Csatlós M, Csige L, Gulyás J, Hunyadi M, Ketel TJ, et al. New experimental results for the 17 MeV particle created in ⁸Be. EPJ Web Conf. (2017) 137:08010. doi: 10.1051/epjconf/201713708010

CrossRef Full Text | Google Scholar

5. Krasznahorkay AJ, Csatlós M, Csige L, Gácsi Z, Gulyás J, Nagy Á, et al. New results on the ⁸Be anomaly. J Phys Conf Ser. (2018) 1056:012028. doi: 10.1088/1742-6596/1056/1/012028

CrossRef Full Text | Google Scholar

6. Gulyás J, Ketel TJ, Krasznahorkay AJ, Csatlós M, Csige L, Gácsi Z, et al. A pair spectrometer for measuring multipolarities of energetic nuclear transitions. Nucl Instrum Methods. (2016) A808:21–8. doi: 10.1016/j.nima.2015.11.009

CrossRef Full Text | Google Scholar

7. Feng JL, Fornal B, Galon I, Gardner S, Smolinsky J, Tait TMP, et al. Particle physics models for the 17 MeV anomaly in beryllium nuclear decays. Phys Rev. (2017) D95:035017. doi: 10.1103/PhysRevD.95.035017

CrossRef Full Text | Google Scholar

8. Ellwanger U, Moretti S. Possible explanation of the electron positron anomaly at 17 MeV in ⁸Be transitions through a light pseudoscalar. J High Energy Phys. (2016) 11:039. doi: 10.1007/JHEP11(2016)039

CrossRef Full Text | Google Scholar

9. Feng JL, Fornal B, Galon I, Gardner S, Smolinsky J, Tait TMP, et al. Protophobic fifth-force interpretation of the observed anomaly in ⁸Be nuclear transitions. Phys Rev Lett. (2016) 117:071803. doi: 10.1103/PhysRevLett.117.071803

CrossRef Full Text | Google Scholar

10. Gu PH, He XG. Realistic model for a fifth force explaining anomaly in ⁸Be* → ⁸Bee⁺e⁻ Decay. Nucl Phys. (2017) B919:209–17. doi: 10.1016/j.nuclphysb.2017.03.023

CrossRef Full Text | Google Scholar

11. Chen LB, Liang Y, Qiao CF. X(16.7) production in electron-position collision. arXiv:1607.03970. (2016).

Google Scholar

12. Liang Y, Chen LB, Qiao CF. X(16.7) as the solution of the NuTeV anomaly. Chin Phys. (2017) C41:063105. doi: 10.1088/1674-1137/41/6/063105

CrossRef Full Text | Google Scholar

13. Jia LB, Li XQ. The new interaction suggested by the anomalous ⁸Be transition sets a rigorous constraint on the mass range of dark matter. Eur Phys J. (2016) C76:706. doi: 10.1140/epjc/s10052-016-4561-3

CrossRef Full Text | Google Scholar

14. Kitahara T, Yamamoto Y. Protophobic light vector boson as a mediator to the dark sector. Phys Rev. (2017) D95:015008. doi: 10.1103/PhysRevD.95.015008

CrossRef Full Text | Google Scholar

15. Chen CS, Lin GL, Lin YH, Xu F. The 17 MeV anomaly in beryllium decays and U(1) portal to dark matter. Int J Mod Phys. (2017) A32:1750178. doi: 10.1142/S0217751X17501780

CrossRef Full Text | Google Scholar

16. Seto O, Shimomura T. Atomki anomaly and dark matter in a radiative seesaw model with gauged B − L symmetry. Phys Rev. (2017) D95:095032. doi: 10.1103/PhysRevD.95.095032

CrossRef Full Text | Google Scholar

17. Neves MJ, Helayël-Neto JA. A unified hidden-sector-electroweak model, paraphotons and the X-Boson. arXiv:1611.07974. (2016).

Google Scholar

18. Chiang CW, Tseng PY. Probing a dark photon using rare leptonic kaon and pion decays. Phys Lett. (2017) B767:289–94. doi: 10.1016/j.physletb.2017.02.022

CrossRef Full Text | Google Scholar

19. Kozaczuk J, Morrissey DE, Stroberg SR. Light axial vector bosons, nuclear transitions, and the ⁸Be anomaly. Phys Rev. (2017) D95:115024. doi: 10.1103/PhysRevD.95.115024

CrossRef Full Text | Google Scholar

20. Kahn Y, Krnjaic G, Mishra-Sharma S, Tait TMP. Light weakly coupled axial forces: models, constraints, and projections. J High Energy Phys. (2017) 05:002. doi: 10.1007/JHEP05(2017)002

CrossRef Full Text | Google Scholar

21. Dolan MJ, Kahlhoefer F, McCabe C, Schmidt-Hoberg K. A taste of dark matter: flavour constraints on pseudoscalar mediators. J High Energy Phys. (2015) 03:171. doi: 10.1007/JHEP07(2015)103,10.1007/JHEP03(2015)171

CrossRef Full Text | Google Scholar

22. Andreas S, Lebedev O, Ramos-Sanchez S, Ringwald A. Constraints on a very light CP-odd Higgs of the NMSSM and other axion-like particles. J High Energy Phys. (2010) 08:003. doi: 10.1007/JHEP08(2010)003

CrossRef Full Text | Google Scholar

23. Essig R, Harnik R, Kaplan J, Toro N. Discovering new light states at neutrino experiments. Phys Rev. (2010) D82:113008. doi: 10.1103/PhysRevD.82.113008

CrossRef Full Text | Google Scholar

24. Fundamental Physics at the Intensity Frontier (2012). Available online at: http://lss.fnal.gov/archive/preprint/fermilab-conf-12-879-ppd.shtml.

Google Scholar

25. Döbrich B, Jaeckel J, Kahlhoefer F, Ringwald A, Schmidt-Hoberg K. ALPtraum: ALP production in proton beam dump experiments. J High Energy Phys. (2016) 02:018. doi: 10.1007/JHEP02(2016)018

CrossRef Full Text | Google Scholar

26. Yamazaki T, Ishikawa T, Taniguchi T, Yamanaka T, Tanimori T, Enomoto R, et al. Search for a neutral boson in a two-body decay of K+ —> PI+ X0. Phys Rev Lett. (1984) 52:1089–91.

Google Scholar

27. Adler S, Aoki M, Ardebili M, Atiya MS, Bazarko AO, Bergbusch PC. Further search for the decay K+ —> π⁺ $\nu \bar{\nu }$ anti-nu in the momentum region P < 195-MeV/c. Phys Rev. (2004) D70:037102. doi: 10.1103/PhysRevD.70.037102

CrossRef Full Text | Google Scholar

28. Artamonov AV, Bassalleck B, Bhuyan B, Blackmore EW, Bryman DA, Chen S. Study of the decay $K^{+}\to {\pi }^{+}\nu \bar{\nu }$ in the momentum region 140 < P_π < 199 MeV/c. Phys Rev. (2009) D79:092004. doi: 10.1103/PhysRevD.79.092004

CrossRef Full Text | Google Scholar

29. Aaij R, Adeva B, Adinolfi M, Ajaltouni Z, Akar S, Albrecht J, et al. Measurement of the $B_s^0\to {\mu }^{+}{\mu }^{-}$ branching fraction and search for B⁰ → μ⁺μ⁻ decays at the LHCb experiment. Phys Rev Lett. (2013) 111:101805. doi: 10.1103/PhysRevLett.111.101805

CrossRef Full Text | Google Scholar

30. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T. Measurement of the $B_s^0\to {\mu }^{+}{\mu }^{-}$ Branching Fraction and Search for B⁰ → μ⁺μ⁻ with the CMS Experiment. Phys Rev Lett. (2013) 111:101804. doi: 10.1103/PhysRevLett.111.101804

CrossRef Full Text | Google Scholar

31. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. Observation of the rare $B_s^0\to {\mu }^{+}{\mu }^{-}$ decay from the combined analysis of CMS and LHCb data. Nature. (2015) 522:68–72. doi: 10.1038/nature14474

CrossRef Full Text | Google Scholar

32. Ammar R, Bean A, Besson D, Zhao X, Anderson S, Frolov VV, et al. Search for the familon via B+- —> pi+- X0, B+- —> K+- X0, and B0 —> K0(S)X0 decays. Phys Rev Lett. (2001) 87:271801. doi: 10.1103/PhysRevLett.87.271801

CrossRef Full Text | Google Scholar

33. Balest R, Cho K, Ford T, Johnson DR, Lingel K, Lohner M, et al. Upsilon (1s) —> gamma + noninteracting particles. Phys Rev. (1995) D51:2053–60.

Google Scholar

34. Aubert B, Bona M, Karyotakis Y, Lees JP, Poireau V, Prencipe E. Search for Invisible Decays of a Light Scalar in Radiative Transitions υ_3S → γ A0. In: Proceedings, 34th International Conference on High Energy Physics (ICHEP 2008). Philadelphia, PA (2008). Available online at: http://www-public.slac.stanford.edu/sciDoc/docMeta.aspx?slacPubNumber=slac-pub-13328.

Google Scholar

35. Davier M, Nguyen Ngoc H. An unambiguous search for a light higgs boson. Phys Lett. (1989) B229:150–5.

Google Scholar

36. Banerjee D, Burtsev VE, Chumakov AG, Cooke D, Crivelli P, Depero E, et al. Search for a hypothetical 16.7 MeV gauge Boson and dark photons in the NA64 experiment at CERN. Phys Rev Lett. (2018) 120:231802. doi: 10.1103/PhysRevLett.120.231802

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bergsma F, Dorenbosch J, Allaby JV, Amaldi U, Barbiellini G, Berger C. Search for axion like particle production in 400-GeV proton - copper interactions. Phys Lett. (1985) 157B:458–62. doi: 10.1016/0370-2693(85)90400-9

CrossRef Full Text | Google Scholar

38. Moretti S. Variations on a Higgs theme. Phys Rev. (2015) D91:014012. doi: 10.1103/PhysRevD.91.014012

CrossRef Full Text | Google Scholar

39. Anthony PL, Arnold RG, Arroyo C, Bega K, Biesiada J, Bosted PE, et al. Precision measurement of the weak mixing angle in Moller scattering. Phys Rev Lett. (2005) 95:081601. doi: 10.1103/PhysRevLett.95.081601

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Giudice GF, Paradisi P, Passera M. Testing new physics with the electron g-2. J High Energy Phys. (2012) 11:113. doi: 10.1007/JHEP11(2012)113

CrossRef Full Text | Google Scholar

41. Altmannshofer W, Chen CY, Bhupal Dev PS, Soni A. Lepton flavor violating Z' explanation of the muon anomalous magnetic moment. Phys Lett. (2016) B762:389–98. doi: 10.1016/j.physletb.2016.09.046

CrossRef Full Text | Google Scholar

42. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P. Final report of the muon E821 anomalous magnetic moment measurement at BNL. Phys Rev. (2006) D73:072003. doi: 10.1103/PhysRevD.73.072003

CrossRef Full Text | Google Scholar

43. Blum T, Denig A, Logashenko I, de Rafael E, Roberts BL, Teubner T, et al. The Muon (g-2) theory value: present and future. arXiv:1311.2198. (2013).

Google Scholar

44. Lindner M, Platscher M, Queiroz FS. A call for new physics : the Muon anomalous magnetic moment and lepton flavor violation. Phys Rept. (2018) 731:1–82. doi: 10.1016/j.physrep.2017.12.001

CrossRef Full Text | Google Scholar

45. Deniz M, Lin ST, Singh V, Li J, Wong HT, Bilmis S. Measurement of ${\bar{\nu }}_e$-electron scattering cross-section with a CsI(Tl) scintillating crystal array at the Kuo-Sheng nuclear power reactor. Phys Rev. (2010) D81:072001. doi: 10.1103/PhysRevD.81.072001

CrossRef Full Text | Google Scholar

46. Bilmis S, Turan I, Aliev TM, Deniz M, Singh L, Wong HT. Constraints on dark photon from neutrino-electron scattering experiments. Phys Rev. (2015) D92:033009. doi: 10.1103/PhysRevD.92.033009

CrossRef Full Text | Google Scholar

47. Raggi M. NA48/2 studies of rare decays. Nuovo Cim. (2016) C38:132. doi: 10.1393/ncc/i2015-15132-0

CrossRef Full Text | Google Scholar

48. Davoudiasl H, Lee HS, Marciano WJ. ‘Dark’ Z implications for parity violation, rare meson decays, and higgs physics. Phys Rev. (2012) D85:115019. doi: 10.1103/PhysRevD.85.115019

CrossRef Full Text | Google Scholar

49. Bouchiat C, Fayet P. Constraints on the parity-violating couplings of a new gauge boson. Phys Lett. (2005) B608:87–94. doi: 10.1016/j.physletb.2004.12.065

CrossRef Full Text | Google Scholar

50. Porsev SG, Beloy K, Derevianko A. Precision determination of electroweak coupling from atomic parity violation and implications for particle physics. Phys Rev Lett. (2009) 102:181601. doi: 10.1103/PhysRevLett.102.181601

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Fayet P. On the search for a new Spin 1 Boson. Nucl Phys. (1981) B187:184–204.

Google Scholar

52. Fayet P. Effects of the Spin 1 partner of the Goldstino (Gravitino) on neutral current phenomenology. Phys Lett. (1980) 95B:285–9.

Google Scholar

53. Fayet P. Extra U(1)'s and new forces. Nucl Phys. (1990) B347:743–68.

Google Scholar

54. Fayet P. U-boson production in e+ e- annihilations, psi and Upsilon decays, and Light Dark Matter. Phys Rev. (2007) D75:115017. doi: 10.1103/PhysRevD.75.115017

CrossRef Full Text | Google Scholar

55. Fayet P. U(1)(A) Symmetry in two-doublet models, U bosons or light pseudoscalars, and psi and Upsilon decays. Phys Lett. (2009) B675:267–71. doi: 10.1016/j.physletb.2009.03.078

CrossRef Full Text | Google Scholar

56. Fayet P. The light U boson as the mediator of a new force, coupled to a combination of Q, B, L and dark matter. Eur Phys J. (2017) C77:53. doi: 10.1140/epjc/s10052-016-4568-9

CrossRef Full Text | Google Scholar

57. Delle Rose L, Khalil S, Moretti S. Explanation of the 17 MeV Atomki anomaly in a U(1)' -extended two Higgs doublet model. Phys Rev. (2017) D96:115024. doi: 10.1103/PhysRevD.96.115024

CrossRef Full Text | Google Scholar

58. Accomando E, Coriano C, Delle Rose L, Fiaschi J, Marzo C, Moretti S. Z', Higgses and heavy neutrinos in U(1)' models: from the LHC to the GUT scale. J High Energy Phys. (2016) 07:086. doi: 10.1007/JHEP07(2016)086

CrossRef Full Text | Google Scholar

59. Bishara F, Brod J, Grinstein B, Zupan J. Chiral effective theory of dark matter direct detection. JCAP. (2017) 1702:009. doi: 10.1088/1475-7516/2017/02/009

CrossRef Full Text | Google Scholar

60. Vilain P, Wilquet G, Beyer R, Flegel W, Grote H, Mouthuy T, et al. Precision measurement of electroweak parameters from the scattering of muon-neutrinos on electrons. Phys Lett. (1994) B335:246–52. doi: 10.1016/0370-2693(94)91421-4

CrossRef Full Text | Google Scholar

61. Bellini G, Benziger J, Bick D, Bonetti S, Bonfini G, Buizza Avanzini M. Precision measurement of the ⁷Be solar neutrino interaction rate in Borexino. Phys Rev Lett. (2011) 107:141302. doi: 10.1103/PhysRevLett.107.141302

CrossRef Full Text | Google Scholar

62. Davoudiasl H, Lee HS, Marciano WJ. Muon g − 2, rare kaon decays, and parity violation from dark bosons. Phys Rev. (2014) D89:095006. doi: 10.1103/PhysRevD.89.095006

CrossRef Full Text | Google Scholar

63. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM. Review of particle physics. Chin Phys. (2016) C40:100001. doi: 10.1088/1674-1137/40/10/100001

CrossRef Full Text | Google Scholar

64. Delle Rose L, Khalil S, King SJD, Moretti S, Thabt AM. Atomki anomaly in family-dependent U(1)′ extension of the standard model. Phys Rev. (2019) D99:055022. doi: 10.1103/PhysRevD.99.055022

CrossRef Full Text | Google Scholar

65. Froggatt CD, Nielsen HB. Hierarchy of Quark Masses, Cabibbo Angles and CP Violation. Nucl Phys. (1979) B147:277–98. doi: 10.1016/0550-3213(79)90316-X

CrossRef Full Text | Google Scholar

66. Demir DA, Kane GL, Wang TT. The Minimal U(1)' extension of the MSSM. Phys Rev. (2005) D72:015012. doi: 10.1103/PhysRevD.72.015012

CrossRef Full Text | Google Scholar

67. Khan AN. Global analysis of the source and detector nonstandard interactions using the short baseline ν−e and $\bar{\nu }-e$ scattering data. Phys Rev. (2016) D93:093019. doi: 10.1103/PhysRevD.93.093019

CrossRef Full Text | Google Scholar

68. Aaij R, et al. Angular analysis of the B⁰ → K^*0e⁺e⁻ decay in the low-q² region. J High Energy Phys. (2015) 04:064. doi: 10.1007/JHEP04(2015)064

CrossRef Full Text | Google Scholar

69. Bečireviá D, Sumensari O, Zukanovich Funchal R. Lepton flavor violation in exclusive b → s decays. Eur Phys J. (2016) C76:134. doi: 10.1140/epjc/s10052-016-3985-0

CrossRef Full Text | Google Scholar