Anomalous Diffusion: A Basic Mechanism for the Evolution of Inhomogeneous Systems

In this article we review classical and recent results in anomalous diffusion and provide mechanisms useful for the study of the fundamentals of certain processes, mainly in condensed matter physics, chemistry and biology. Emphasis will be given to some methods applied in the analysis and characterization of diffusive regimes through the memory function, the mixing condition (or irreversibility), and ergodicity. Those methods can be used in the study of small-scale systems, ranging in size from single-molecule to particle clusters and including among others polymers, proteins, ion channels and biological cells, whose diffusive properties have received much attention lately.

“In water, this flowing matter, there is nothing permanent”
Jan Heweliusz

1. Introduction

1.1. General Concepts

Diffusion is a basic transport process involved in the evolution of many non-equilibrium systems toward equilibrium [1–13]. By diffusion, particles (or molecules) spread from regions of high concentration to those of low concentration leading, via a gradual mixing, to a situation in which they become evenly dispersed. Diffusion is of fundamental importance in many disciplines; for example, in growth phenomena, the Edwards-Wilkinson equation is given by a diffusion equation plus a noise [14]. In cell biology it constitutes a main form of transport for amino acids and other nutrients within cells [15].

For more than 200 years [1], diffusion has been a widely studied phenomena in natural science due to it's large number of applications. Initially, the experiments carried out by Robert Brown [16, 17] called the attention to the random trajectories of small particles of polen and also of inorganic matter. This irregular motion, later named Brownian motion, can be modeled by a random walk in which the mean square displacement is given by Einstein's relation [1]

$\begin{array}{ll}\langle {(\Delta r)}^2\rangle =2dDt,& (1)\end{array}$

where Δr is the displacement of the Brownian particle in a given time interval t, d is the spatial dimension, and D the diffusion coefficient. Whereas a single Brownian particle trajectory is chaotic, averaging over many trajectories reveals a regular behavior.

The purpose of this article is to review recent efforts aiming at formulating a theory for anomalous diffusion processes– i.e., those where the mean square displacement does not follow Equation (1) which can be applied to many different situations from theoretical physics to biology.

In the next section, we introduce the pioneering works on diffusion, and then call attention to the existence of anomalous diffusion. We discuss the main methods to treat anomalous diffusion and concentrate our efforts on the discussion of the generalized Langevin formalism.

1.2. The Tale of the Three Giants

At the birth of the gravitational theory Isaac Newton mentioned that he build up his theory based on the previous works of giants. Also, one cannot talk about diffusion without underscoring the works of Albert Einstein, Marian Smoluchowski, and Paul Langevin. At the dawn of the last century, the atomic theory was not widely accepted by the physical community. Einstein believed that the motion observed by Brown was due to the collisions of molecules such as proposed by Boltzmann in his famous equation. However, Boltzmann's equation was difficult to solve and therefore he proposed a simpler analysis combining the kinetic theory of molecules with the Fick's law, from which he obtained the diffusion equation

$\begin{array}{ll}\frac{\partial \rho (x,t)}{\partial t}=D{\nabla }^2\rho (x,t),& (2)\end{array}$

where ρ(x, t) is the density of particles at position x and time t. The solution of the above equation yields ρ(x, t) and

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}\langle x^2(t)\rangle ={\displaystyle \int x^2(t)\rho (x,t)dx=2Dt,}& (3)\end{array}$

where 〈x(t)〉 = 0, assuming the symmetry ρ(−x, t) = ρ(x, t). For simplicity, we have considered the motion one-dimensional and set all particles at the origin at time t = 0. Generalization to two and three dimensions is straightforward. He then considered the molecules as single non-interacting spherical particles with radius a and mass m, and subject to a friction γ when moving in the liquid [1, 18, 19].

Finally, he deduced the famous Einstein-Stokes relation [19] for the diffusion constant

$\begin{array}{ll}D=\frac{RT}{6\pi N_{a}a\eta }=\frac{RT}{m{N}_a\gamma }=\frac{RT\mu }{N_a},& (4)\end{array}$

where N_a is Avogadro's number, fundamental for atomic theory, but unknown at the time, R is the gas constant, μ the mobility, η the viscosity, and T the temperature.

The scientific community became very excited and, in the years following Einstein's papers, some dedicated experiments helped to verify Equation (3). Diffusion constants were measured and it became possible to estimate Avogadro's number from different experiments. Moreover, it was possible to estimate the radius of molecules with few hundreds of atoms. Einstein was successful in demonstrating that atoms and molecules were not mere illusions as critics used to suggest. Finally, the theory of Brownian motion started to set a firm ground. For instance, it became possible to associate diffusion with conductivity in the case of a gas of charged particles. Supposing each has the same charge e and is subjected to a time dependent electric field $\overrightarrow{E}=\overrightarrow{E}(\omega )\text{ exp}(-i\omega t)$, the conductivity $\tilde{\sigma }(\omega )$ can be defined by $\overrightarrow{J}(\omega )=\tilde{\sigma }(\omega )\overrightarrow{E}(\omega )$, where $\overrightarrow{J}(\omega )$ is the current. Now, it was possible to relate the diffusivity $\tilde{D}(w)$ with $\tilde{\sigma }(\omega )$ by the relation [1, 20, 21]

$\begin{array}{ll}\tilde{\sigma }(\omega )=\frac{n{e}^2}{k_{B}T}\tilde{D}(\omega ),& (5)\end{array}$

where is n the carrier density. From that it was obvious that connections between a diversity of response functions could be obtained.

Two major achievements in the theory of stochastic motion were due to Smoluchowski. As expressed by Novak et al. [22], “One was the Smoluchowski equation describing the motion of a diffusive particle in an external force field, known in the Western literature as the Fokker-Planck equation [23, 24]”

$\begin{array}{ll}\frac{\partial P(v,t,v_0)}{\partial t}=-\frac{\partial }{\partial v}\left[A(v)P(v,t,v_0)\right]+\frac{1}{2}\frac{{\partial }^2}{\partial v^2}\left[B(v)P(v,t,v_0)\right],& (6)\end{array}$

where

$\begin{array}{ll}A(v)=\frac{1}{\delta t}{\displaystyle {\int }_{-\infty }^{\infty }}(v^{\prime }-v)P(v^{\prime },\delta t,v)d{v}^{\prime }& (7)\end{array}$

and

$\begin{array}{ll}B(v)=\frac{1}{\delta t}{\displaystyle {\int }_{-\infty }^{\infty }}{(v^{\prime }-v)}^{2}P(v^{\prime },\delta t,v)d{v}^{\prime }.& (8)\end{array}$

Here P(v′, δt, v) is the transition probability between two states with different velocities. The second one, a fundamental cornerstone of molecular physical chemistry and of cellular biochemistry [22, 25] is “Smoluchowski's theory of diffusion limited coagulation of two colloidal particles.” Unfortunately, due to his premature death, the Nobel prize was not awarded to Smoluchowski. However, the scientific community pays tribute to him [26].

The last of the three giants was Langevin, who considered Newton's second law of motion for a particle as [27]

$\begin{array}{ll}m\frac{dv(t)}{dt}=-m\gamma v(t)+f(t),& (9)\end{array}$

dividing the environment's (thermal bath) influence into two parts: a slow dissipative force, −mγv, with time scale τ = γ⁻¹, and a fast random force f(t), which changes in a time scale Δt≪τ, subject to the conditions

$\begin{array}{ll}\langle f(t)\rangle =0,& (10)\end{array}$

$\begin{array}{ll}\langle f(t)v(0)\rangle =0,& (11)\end{array}$

and

$\begin{array}{ll}\langle f(t)f(t^{\prime })\rangle =\Lambda \delta (t-t^{\prime }).& (12)\end{array}$

If we solve Equation (9) and, using the equipartition theorem, impose $\langle v^2(t\to \infty )\rangle ={\langle v^2\rangle }_{eq}=k_{B}T/m$, where k_B = R/N_a is the Boltzmann constant, we obtain Λ = 2mγk_BT and write

$\begin{array}{ll}\langle f(t)f(t^{\prime })\rangle =2m\gamma k_{B}T\delta (t-t^{\prime }).& (13)\end{array}$

This last equation establishes a relation between the fluctuation and the dissipation in the system reconnecting the useful, although artificial, separation of the two forces. This relation has been named the fluctuation-dissipation theorem (FDT) and is one the most important theorems of statistical physics. Equations (10, 11, 13) yield the velocity-velocity correlation function that reads [28]

$\begin{array}{ll}{C}_v(t)=\langle v(t+t^{\prime })v(t^{\prime })\rangle =(k_{B}T/m)exp(-\gamma t),& (14)\end{array}$

the mean square displacement

$\begin{array}{ll}\langle x^2(t\gg \tau )\rangle ={\displaystyle {\int }_0^t}d{t}^{\prime }{\displaystyle {\int }_0^t}d{t}^{″}\langle v(t^{\prime })v(t^{″})\rangle =2Dt,& (15)\end{array}$

and

$\begin{array}{ll}D={\displaystyle {\int }_0^{\infty }}{C}_v(t)dt,& (16)\end{array}$

known as the Kubo formula. This bring us back to Einstein's results for diffusion, Equation (4).

The simplification introduced by the Langevin formalism makes it easy to carry out analytical calculations and computer simulations. Consequently, the Langevin equation, and its generalization (Section 3), has been applied successfully to the study of many different systems such as chain dynamics [29–34], liquids [35, 36], ratchets [37, 38], and synchronization [39, 40]. However, its major importance was to relate fluctuation with dissipation.

The Fokker-Planck Equation (6) with the Langevin choices becomes

$\begin{array}{ll}\frac{\partial P(v,t)}{\partial t}=\gamma \frac{\partial }{\partial v}\left[vP(v,t)\right]+\gamma \frac{k_{B}T}{m}\frac{{\partial }^2}{\partial v^2}\left[P(v,t)\right],& (17)\end{array}$

known as the Ornstein-Uhlenbeck equation. It obviously yields the same result as that of Einstein and Langevin. This completes the tale of the three giants. Their work established the bases of non-equilibrium statistical mechanics opening a new field in research for the next decades. For example, it was demonstrated that hydrodynamics could be obtained from the Boltzmann equation in particular situations [41], so that the physics community could appreciate the work of yet another giant.

2. Breakdown of the Normal Diffusive Regime

2.1. The Different Facets of the Anomaly: Subdiffusion and Superdiffusion

Inspection of different supposedly diffusive processes such as enhanced diffusion in the intracellular medium [42], cell migration in monolayers [43], Levy flight search on a polymeric DNA [44], or the Brownian motion in an inhomogeneous medium [45] reveals that the previous framework is not always fulfilled. Instead, in these and other similar examples the mean square displacement deviates from the linear temporal evolution. One of the most common anomalous behaviours is given by

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}\langle r^2(t)\rangle ~t^{\alpha },& (18)\end{array}$

where α ≠ 1 is a real positive number [4–6, 46].

The origin of this discrepancy is the tacit assumption made in the derivation of (1) that the Brownian particle moves in an infinite structureless medium acting as a heat bath. This assumption is generally incorrect when the Brownian motion takes place in a complex medium, as is the case of the previously mentioned examples. We illustrate in Figure 1 the mean square displacement 〈x²(t)〉 as a function of t for three distinct Brownian motions in one dimension. From the upper curve downwards, we have α = 1.5 (superdiffusion), α = 1 (normal diffusion), and α = 0.5 (subdiffusion).

FIGURE 1

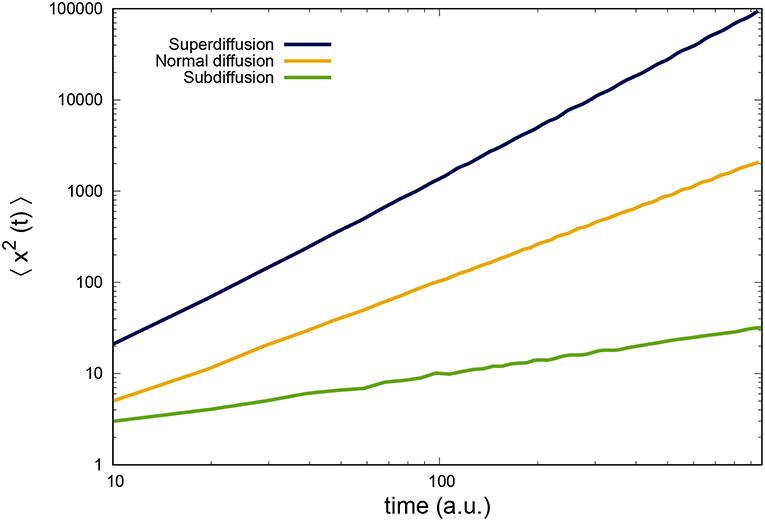
Figure 1. (Color) Time evolution of the mean square displacement (in arbitrary units) for normal and anomalous diffusion. For the upper curve α = 1.5 (superdiffusion), for the middle curve α = 1 (normal diffusion) and for the lower curve α = 0.5 (subdiffusion). From Lapas et al. [9], with permission from Physical Review Letters.

The recent interest in the study of complex systems has led to an increased focus on anomalous diffusion [4–7, 36, 42, 45], which has been described in biological systems [42–44], protostellar birth [47], complex fluids [48–53], electronic transportation [54–59], porous media and infiltration [60–62], drug delivery [63–66], fractal structures and networks [67–71], and in water's anomalous behavior [72–74], phase transitions in synchronizing oscillators [39, 40, 75–77], to name a few.

There are many formalisms that describe anomalous diffusion, ranging from thermodynamics [78–80], and fractional derivatives [4, 6] to generalized Langevin equations (GLE) [81–83]. The goal of this short review is to call attention to relevant research within the GLE framework and to some fundamental theorems in statistical mechanics.

3. The Generalized Langevin Equation Approach

3.1. Non-markovian Processes

The Langevin formalism within its classical description has some restrictions:

1. It has a relaxation time τ = γ⁻¹, and an unspecified Δt ≪ τ, while a diffusive process in a real system can present several time scales;

2. For short times t < Δt, predictions are unrealistic; for example, the derivative of C_v(t) is zero [84] at t = 0, while in Langevin's formalism C_v(t) = exp(−γ|t|), exhibiting a discontinuity.

3. If no external field is applied it cannot predict anomalous diffusion.

Up to now we have used time and ensemble averages without distinction, i.e. we implicitly used the Boltzmann Ergodic hypothesis (EH). The ensemble average for a variable B(t) is defined by

$\begin{array}{ll}\langle B(t)\rangle ={\displaystyle \int exp(-E/(k_{B}T))\Omega (E,B)B(t)dE,}& (19)\end{array}$

where Ω(E, B) is the number of states for a given energy E. For the time average we have

$\begin{array}{ll}\overline{B(t)}=\frac{1}{{\tau }_0}{\displaystyle {\int }_{-{\tau }_0/2}^{{\tau }_0/2}}B(t+t^{\prime })d{t}^{\prime }.& (20)\end{array}$

For times τ₀ ≫ τ, the Ergodic Hypothesis (EH) reads

$\begin{array}{ll}\overline{B(t)}=\langle B(t)\rangle ,& (21)\end{array}$

which means that the system should be able to reach every accessible state in configuration space given enough time. This is expected to be true for equilibrated macroscopic systems and also for systems that suffer small perturbations close to equilibrium.

In this section, we generalize Langevin‘s equation and study some of its consequence for diffusion. The first correction to the FDT was done by Nyquist [85] who formulated a quantum version of the FDT. Later on Mori [86, 87], and Kubo [88] used a projection operator method to obtain the equation of motion, the Generalized Langevin equation (GLE),

$\begin{array}{ll}\frac{dA(t)}{dt}=-{\displaystyle {\int }_0^t}\Pi (t-t^{\prime })A(t^{\prime })d{t}^{\prime }+F(t),& (22)\end{array}$

for a dynamical operator A(t), where Π(t) is a non-Markovian memory and F(t) is a random variable subject to

1. $\overline{F(t)}=0$,

2. $\overline{F(t)A(0)}=0$, and,

3. the Kubo fluctuation-dissipation theorem (FDT) [89, 90]

$\begin{array}{ll}{C}_F(t-t^{\prime })=\overline{F(t)F(t^{\prime })}={\langle A^2\rangle }_{eq}\Pi (t-t^{\prime }).& (23)\end{array}$

In this way, it is clear that time translational invariance holds in the Kubo formalism. An alternative to the projection operators, the recurrence relation method, was derived by Lee [84, 91, 92], and Lee and Hong [93].

It is easy to show that Equation (22) can give rise both to normal and to anomalous diffusion [1]. Let us consider two limiting case examples: first, when Π(t) = 2γδ(t), we recover the normal Langevin equation (9) with normal diffusion (α = 1); second, for a constant memory Π(t) = K, Equation (22) becomes

$\begin{array}{ll}\frac{d^{2}x}{d{t}^2}=-Kx+F(t),& (24)\end{array}$

where

$\begin{array}{ll}x(t)={\displaystyle {\int }_0^t}A(t^{\prime })d{t}^{\prime }.& (25)\end{array}$

Equation (24) is the equation of motion for a harmonic oscillator with zero diffusion constant (D = 0) and with exponent α = 0. Consequently, we may have different classes of diffusion for distinct memories.

Now, we can study the asymptotic behavior of Equation (25) or of its second moment, Equation (18), to characterize the type of diffusion presented by the system for any memory Π(t). Much information about the system's relaxation properties can be obtained by studying the correlation function

$\begin{array}{ll}{C}_A(t,t^{\prime })=\overline{A(t)A(t^{\prime })}=C_A(t-t^{\prime }).& (26)\end{array}$

The existence of stationary states warrants time-translation invariance so that the the two-time correlation function becomes a function only of the difference between two times, such as in the Kubo FDT above. We shall return to this point later. The main equation we are interested in is Equation (1), where for anomalous diffusion, D should be replaced by D(t) now defined by $D(t)={\int }_0^t{C}_A(t^{\prime })d{t}^{\prime }$ then

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}D(t)={\displaystyle \underset{t\to \infty }{lim}}{\displaystyle {\int }_0^t}{C}_A(t^{\prime })d{t}^{\prime }={\displaystyle \underset{z\to 0}{lim}}{\tilde{C}}_A(z).& (27)\end{array}$

From here onwards, the tilde over the function stands for the Laplace transform. For the last equality, we use the final-value theorem for Laplace transforms [94], which states that if f(t) is bounded on (0, ∞) and ${lim}_{t\to \infty }f(t)$ has a finite limit, then ${lim}_{t\to \infty }f(t)={lim}_{z\to 0}z\tilde{f}(z)$. Also note that the Laplace transform of the integral of a function is the Laplace transform of the function divided by z, then $\tilde{D}(z)={\tilde{C}}_A(z)/z$. Using z ∝ 1/t, we obtain the asymptotic behavior of D(t). In order to do that, we multiply Equation (22) by A(0), take the average and use the conditions (1) and (2) above for the noise to obtain the self-consistent equation

$\begin{array}{ll}\frac{dR(t)}{dt}=-{\displaystyle {\int }_0^t}\Pi (t-t^{\prime })R(t^{\prime })d{t}^{\prime },& (28)\end{array}$

where for simplicity we have defined

$\begin{array}{ll}R(t)=\frac{C_A(t)}{C_A(0)}.& (29)\end{array}$

Note that from Equation (22), we need to average from a large number of stochastic trajectories, while to obtain Equation (29), it is only necessary to solve a single equation, i.e., Equation (28). Further insight can be gained by analyzing the Laplace transformed version of Equation (28)

$\begin{array}{ll}\tilde{R}(z)=\frac{1}{z+\tilde{\Pi }(z)}.& (30)\end{array}$

From here, it is clear that the knowledge of $\tilde{\Pi }(z)$ in the limit z → 0 completely defines the asymptotic dynamics. For instance, if ${lim}_{z\to 0}\tilde{\Pi }(z)\propto z^{\mu }$ then Equation (27) becomes

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}D(t)\propto t^{\beta }& (31)\end{array}$

and consequently [5]

$\begin{array}{ll}\alpha =\beta +1,& (32)\end{array}$

where

$\begin{array}{ll}{\displaystyle \beta =\{\begin{array}{ll}\mu ,& \mathrm{\text{if }}-1<\mu <1\\ 1,& \mathrm{\text{if }}\mu \ge 1,\\ \end{array}}& (33)\end{array}$

We see that we have a cutoff limit for the exponent β and, therefore, also for α.

Due to the existence of correlations in the GLE that arise through hydrodynamical interactions [28], it has been proposed [5, 46, 95] to establish a connection between the random force F(t) and the noise density of states ρ(ω) of the surrounding media, modeled as a thermal bath of harmonic oscillators [5, 81] of the form

$\begin{array}{ll}F(t)={\displaystyle \int C(\omega )cos\left[\omega t+\varphi (\omega )\right]d\omega ,}& (34)\end{array}$

where 0 < ϕ < π are random phases. Now, using the Kubo FDT, Equation (23), and time averaging over the cosines, we obtain the memory as [5, 8]

$\begin{array}{ll}\Pi (t)={\displaystyle \int \rho (\omega )cos(\omega t)d\omega ,}& (35)\end{array}$

which is an even function independent of the noise distribution. Here, $\rho (\omega )=C^2(\omega ){\langle A^2\rangle }_{eq}/2$.

The consequences of considering a colored noise given by a generalization of the Debye spectrum

$\begin{array}{ll}\rho (\omega )={\displaystyle \{\begin{array}{ll}\frac{2\gamma }{\pi }{\left(\frac{\omega }{{\omega }_s}\right)}^{\nu },& \mathrm{\text{if }}\omega <{\omega }_s\\ 0,& \mathrm{\text{otherwise}},\end{array}}& (36)\end{array}$

with ω_s as a Debye cutoff frequency were analyzed in detail in Vainstein et al. [96]. The reason for the choice of this functional form for the noise density of states is that it was previously shown in Morgado et al. [5] and Costa et al. [8] that if $\tilde{\Pi }(z)\propto z^{\mu }$ as z → 0, then the same restriction as in Equation (33), with ν = μ, applies and the diffusion exponent [5] is given by Equation (32).

Later, this problem was revisited by Ferreira et al. [97] in which a generalized version of Equation (18) was considered, namely

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}\langle r^2(t)\rangle ~t^{\alpha }{(ln(t))}^{\pm n}.& (37)\end{array}$

Most authors [4–6, 46] have reported the cases of anomalous diffusion where, n = 0 and α ≠ 1. However, some authors such as for example, Srokowksi [98, 99] reports situations were for t → ∞, the dispersion behaves as

$\begin{array}{ll}\langle x^2(t)\rangle \propto t/ln(t),& (38)\end{array}$

i.e., a weak subdiffusive behavior for which we can say that α = 1⁻. In this way Ferreira et al. [97] generalizes the concept of α, to associate with Equation (37), the α^± exponents, which arise analogously to the critical exponents of a phase transition [100–102]. For example, in magnetic systems with temperatures T close to the transition temperature T_c, the specific heat at zero field, H = 0, exhibits the power law behavior $C_{H=0}\propto |T-T_c{|}^{-\alpha }$, where α is the critical exponent. However, for the two-dimensional Ising model [100] the critical exponent can be considered α = 0⁺, since the specific heat behaves logarithmically, C_{H = 0} ∝ ln |T − T_c|, instead. Logarithmic corrections [102] to scaling have also been applied to the diluted Ising model in two dimensions in Kenna and Ruiz-Lorenzo [103]. This generalized nomenclature is pertinent because there are many possible combinations of both logarithmic and power law behaviors. This result highlights the existence of different types of diffusion.

In this way, for the density of states (36), the generalized α becomes

$\begin{array}{ll}\alpha ={\displaystyle \{\begin{array}{ll}2,& \mathrm{\text{if }}\nu >1\\ 2^{-},& \mathrm{\text{if }}\nu =1\\ 1+\nu ,& \mathrm{\text{if }}-1<\nu <1.\end{array}}& (39)\end{array}$

In Equation (36), we choose the constant such that for normal diffusion $\tilde{\Gamma }(z=0)=\gamma$. The exponent for Ballistic diffusion (BD), α = 2, is the maximum for diffusion in the absence of an external field. The slow ballistic motion α = 2⁻ has properties that differ markedly from the ballistic case, see sections (3.3 and 3.4).

3.2. Non-exponential Relaxation

Besides the importance of the asymptotic behavior, the study of the correlation R(t) for finite times is also obviously significant, and there exists a vast literature describing non-exponential behavior of correlation functions in systems ranging from plasmas to hydrated proteins [104–112], since the pioneering works of Rudolph Kohlrausch [113] who described charge relaxation in Leyden jars using stretched exponentials, R(t) ≈ exp [−(t/τ)^β] with 0 < β < 1, and his son Friedrich Kohlrausch [114], who observed two universal behaviors: the stretched exponential and the power law. Since many features are shared among such systems and those that present anomalous diffusion [95, 115], it is natural that similar methods of analysis can be applied to both. For example, from Equation (28), $\frac{dR(t)}{dt}$ must be zero at t = 0, which is at odds with the result R(t) = exp(−γ|t|) of the memoryless Langevin equation. Nevertheless, we know that the exponential can be a reasonable approximation in some cases: Vainstein et al. [96] have presented a large diversity of correlation functions that can be obtained from Equation (28) once Π(t) is known. Since, from Equation (35), Π(t) is an even function then we can write

$\begin{array}{ll}\Pi (t)={\displaystyle \sum _{n=0}^{\infty }}{b}_n{t}^{2n}.& (40)\end{array}$

From Equation (28), they proved that R(t) must also be an even function, therefore

$\begin{array}{ll}R(t)={\displaystyle \sum _{n=0}^{\infty }}{a}_n{t}^{2n},& (41)\end{array}$

with a₀ = R(0) = 1. We insert Equations (40) and (41) into Equation (28) to obtain the recurrence relation [96]

$\begin{array}{ll}{a}_n=-\frac{2\gamma {\omega }_s}{\pi (2n)!}{\displaystyle \sum _{l=0}^{n-1}}\frac{{(-1)}^l\left[2(n-1-l)\right]!{\omega }_s^{2l}}{(2l+1+\nu )}{a}_{n-1-l},& (42)\end{array}$

which shows the richness and complexity of behavior that can arise from a non-Markovian model. The above defined convergent power series represents a large class of functions, including the Mittag-Leffler function [116] which behaves as a stretched exponential for short times and as an inverse power law in the long time scale. Note that even for the simplest case of normal diffusion, ν = 0, R(t) is not an exponential since at the origin its derivative is zero; however, for broad-band noise ω_s ≫ γ, i.e., in the limit of white noise it approaches the exponential R(t) = exp(−γt), for times larger than ${\tau }_s={\omega }_s^{-1}$.

In Figure 2, from Vainstein et al. [96], we display the rich behavior of the correlation function R(t) for the case of normal diffusion. Here, γ = 1 and ω_s = 2 and 20, for curves a and b, respectively. Curve c is the plot of exp(−γt). In the inset, we highlight that although curve b and the exponential approach one another for long times, for short times they differ appreciably. Also plotted is cos(ω₀t), with ${\omega }_0=\sqrt{\Pi (0)}$.

FIGURE 2

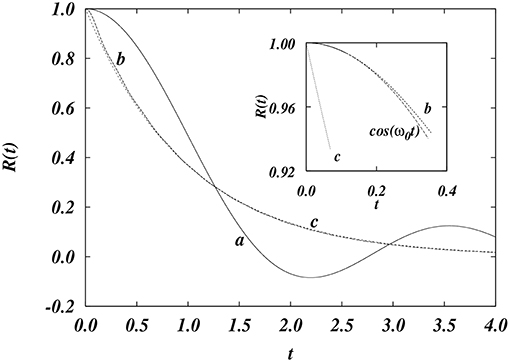
Figure 2. Plot of the correlation function R(t) for normal diffusion (ν = 0). Here, γ = 1 and ω_s = 2 and 20, for curves a and b, respectively. Curve c is the plot of exp(−γt). Note that curves b and c are indistinguishable, except near the origin (see inset). Inset: Plot of curves b, c and cos(ω₀t), near the origin. From Vainstein et al. [1], with permission from Europhysics Letters.

3.3. Basic Theorems of Statistical Mechanics

3.3.1. The Decay Toward an Equilibrium State

One of the most important aspects of dynamics is to observe the asymptotic behavior of a system or how it approaches equilibrium (or not). Observe that a direct solution for Equation (22) is

$\begin{array}{ll}A(t)=A(0)R(t)+{\displaystyle {\int }_0^t}R(t-t^{\prime })F(t)dt.& (43)\end{array}$

Given the initial states A(0), it is possible to average over many trajectories to obtain the temporal evolution of the moments $\overline{A^n(t)}$, with n = 1, 2, …. The first moment arises directly from an average of Equation (43),

$\begin{array}{ll}\overline{A(t)}=\overline{A(0)}R(t)\mathrm{\text{.}}& (44)\end{array}$

Taking the square of Equation (43) and averaging, we obtain

$\begin{array}{ll}\overline{A^2}=\overline{A^2}+R^2(t)\left[\overline{A^2(0)}-{\langle A^2\rangle }_{eq}\right]\mathrm{\text{.}}& (45)\end{array}$

The skewness is defined as a measure of the degree of asymmetry of the distribution of A(t), and is given by [83]

$\begin{array}{ll}\zeta (t)=\left[\frac{{\sigma }_A(0)}{{\sigma }_A(t)}\right]\zeta (0)R^3(t),& (46)\end{array}$

where ${\sigma }_A(t)=\overline{A^2(t)}-{\overline{A(t)}}^2$. We also obtain the non-Gaussian factor [83]

$\begin{array}{ll}\eta (t)=\left[\frac{\overline{A^2(0)}}{\overline{A^2(t)}}\right]\eta (0)R^4(t).& (47)\end{array}$

Consequently, we see that R(t) completely determines these averages. One can note that if the system is originally at equilibrium $\overline{A(0)}=0$ and $\overline{A^2(0)}={\langle A^2\rangle }_{eq}$, then the system remains in equilibrium. If the system is not in equilibrium, then

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}R(t)=0& (48)\end{array}$

drives the system toward equilibrium. The condition stated in Equation (48) is called the mixing condition (MC) and is a fundamental concept in statistical mechanics, which asserts that after a long time the system reaches equilibrium and forgets all initial conditions.

Note that parity is conserved as well: if the initial skewness is null, ζ(0) = 0 in Equation (46), it will remain null during the whole evolution; the same holds for the nongaussian factor.

3.3.2. The Kinchin Theorem and Ergodicity

The Khinchin theorem (KT) [9, 117] states that if the the MC holds, then ergodicity holds. As shown below, anomalous diffusion is a good field for testing ergodicity breaking [9, 10, 83]. For a situation where the MC is violated, we have

$\begin{array}{ll}\kappa ={\displaystyle \underset{t\to \infty }{lim}}R(t)={\displaystyle \underset{z\to 0}{lim}}z\tilde{R}(z)={\displaystyle \underset{z\to 0}{lim}}{\left[1+\frac{\tilde{\Pi }(z)}{z}\right]}^{-1}\ne 0,& (49)\end{array}$

where κ is the nonergodic factor [8, 9, 38, 118]. For example for $\tilde{\Pi }(z\to 0)\propto bz$, α = 2, and

$\begin{array}{ll}\kappa =\frac{1}{1+b}.& (50)\end{array}$

I.e., the MC is violated in the ballistic motion, and consequently ergodicity is violated, but not the KT. Note that for α = 2⁻, where R(t → ∞) → 1/ln(t) → 0, the MC is not violated. In this way the MC is satisfied for all diffusive processes in the range 0 < α < 2⁻ [97].

It is interesting to observe that Equation (49) for long time behavior is equivalent to the condition

$\begin{array}{ll}\Lambda ={\displaystyle \int U(\overrightarrow{r})d\overrightarrow{r}\to \infty ,}& (51)\end{array}$

for systems with long range interactions [119, 120], where $U(\overrightarrow{r})$ is the potential between the particles and the integration is performed over all space.

3.3.3. Gaussianization

As an illustration of the analytical results, we numerically integrated the GLE, Equation (22), to approximate the particle velocity distribution function, using Equations (35, 36) to generate the memory for ν = −0.5, 0, and 0.5, which by Equation (39) give α = 0.5, 1, and 1.5, respectively. The results are exhibited in Figure 3, from Lapas et al. [9], where we show the probability distribution functions as function of the momentum p. From left to right, we have subdiffusion (ν = −0.5), normal diffusion (ν = 0), and superdiffusion (ν = 0.5) for the values $a=\frac{2\gamma }{\pi }=0.25$. A value ω_s = 0.5 was used for normal and superdiffusion. In the case of subdiffusion, a broader noise ω_s = 2 is needed for it to arrive at the stationary state. It is expected that R(t → ∞) = 0 in all cases, and that the EH will be valid even for the subdiffusion (superdiffusion). It should be noted that despite large fluctuations in the time average, there is a good agreement between the ensemble and time distributions, in agreement with Equations (44–48), indicating the validity of the EH. In all cases, the distributions converge to the expected Maxwell-Boltzmann distribution, in accordance with analytical results [83].

FIGURE 3

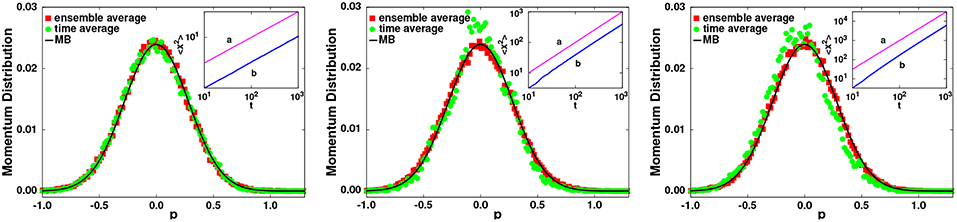
Figure 3. (Color online) Numerical results for the probability distribution function for subdiffusion (left, α = 0.5), normal diffusion (middle, α = 1) and superdiffusion (right, α = 1.5). The time averages (circles) are obtained by following one particle trajectory and calculating the histogram for times from t = 100 to t = 5000. For the ensemble averages (squares), we calculate the histogram using 5 · 10⁴ particles, at time t = 1000. The continuous line is the Maxwell-Boltzmann distribution. Insets: Curves a correspond to the functions t^α and curves b to the simulated mean square displacements. From Lapas et al. [9], with permission from Physical Review Letters.

In Figure 4 we show the evolution of the nongaussian factor. We see that for the Ballistic diffusion (BD), it does not reach a null value, but it evolves toward it. Note that even for a situation where κ ≠ 0, the nongaussian factor will be very small and the probability of it being non-zero in simulations after a long time is very small. For example for κ = 0.1, there will a factor of 10⁻⁴ in relation (47).

FIGURE 4

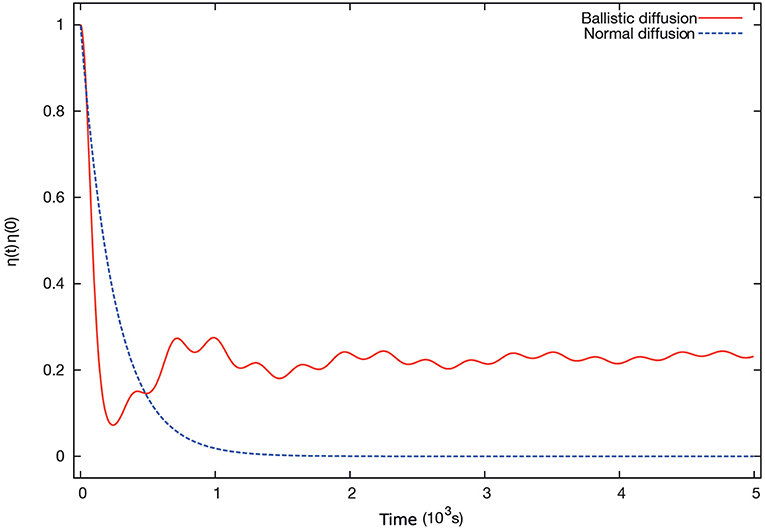
Figure 4. (Color online) Time evolution of the normalized non-Gaussian factor η(t)/η(0) for normal and ballistic diffusion. In both cases, we consider the initial PDF as a Laplace distribution with unit mean and unit variance. The functions R(t) are as in Figure 5. From Lapas et al. [83], with permission from Europhysics Letters.

In Figure 5, from Lapas et al. [83], we show the evolution of the kinetic temperature of the system by taking A²(t), with A = P, the momentum of the particles. In this case we should have ${\langle A^2\rangle }_{eq}-{\langle A\rangle }_{eq}^2\propto T$ [83] and the temperature evolution can be obtained from Equation (45). We consider both normal and ballistic diffusion (BD) in a reservoir characterized by T = 1.0 with initial high and low temperatures T₀ = 1.5 and T₀ = 0.5, respectively. For normal diffusion (dashed curve), we have R(t) = exp(−γt), with γ = 10⁻³. For BD, R(t) is calculated numerically in Lapas et al. [83] with γ = 1. Since BD's relaxation is slow, we take a “friction” γ a thousand times larger than that of normal diffusion for comparison. As expected, in the case of normal diffusion the system's temperature always relaxes to that of the reservoir, while for BD the temperature approaches that of the reservoir without reaching it Lapas et al. [83, 115]. Figure 4 displays the normalized non-Gaussian factor, Equation (47), as a function of time [83] for the cases in the previous figure, with the same convention for the labeling. For normal diffusion, the system's probability distribution evolves toward a Gaussian, which is not the case for BD. In the latter case, R(t) oscillates around the value predicted by Equation (50), even for long times, In both cases, the initial probability distribution function was the Laplace distribution, with 〈A²(0)〉 = 1 and 〈A(0)〉 = 0.

FIGURE 5

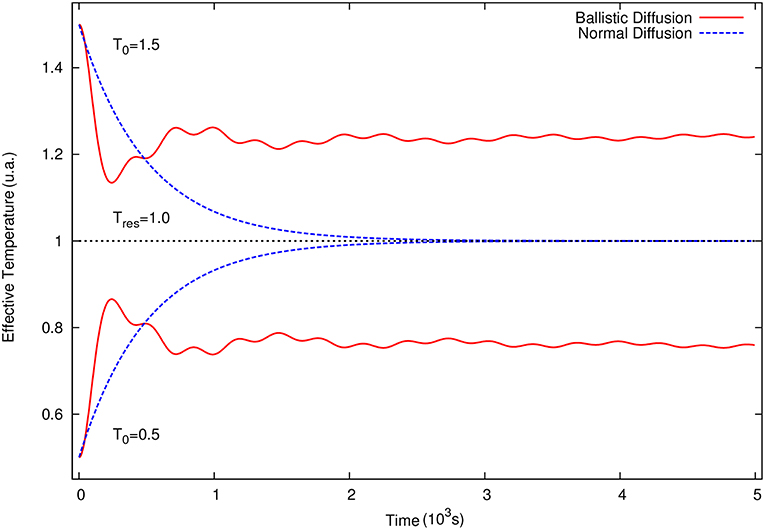
Figure 5. (Color) Time evolution of the effective kinetic temperature (in arbitrary units) for normal and ballistic diffusion. For BD we use the noise distribution ρ(ω) = 2γ/π for 1 < ω < 4 and ρ(ω) = 0, otherwise, and we found R(t) numerically (solid curve). Since BD converges very slowly, we use γ = 1 for BD and γ = 10⁻³ for normal diffusion with R(t) = exp(−γt), so we can compare both. We choose T₀ = 1.5 and T₀ = 0.5 for the initial temperatures. In both cases we used T = 1 for the reservoir temperature. From Lapas et al. [83], with permission from Europhysics Letters.

3.3.4. The Fluctuation-Dissipation Theorem

Figures 3, 4 are just illustrations of the results that can be obtained analytically from Equations (21–48). Lapas et al. [9, 83] have shown that the KT is valid for all forms of diffusion, and that the ballistic diffusion violates the EH, but not the KT.

Although it is expected that a system in contact with a heat reservoir will be driven to equilibrium by fluctuations, Figures 4, 5 show that it is not always the case and in some far from equilibrium situation it may not happen. The concept of “far from equilibrium” is itself sometimes misleading, since it depends not only on the initial conditions, but also on the possible trajectories the system may follow [8, 104, 105]. It was a known fact that the FDT can be violated in many slow relaxation processes [1, 121, 122], however, it was a surprise that it could occur in a GLE without disorder [123] or an external field [1, 8, 20]. Finally, Costa et al. [8] have called attention to the fact that if after a long time the fluctuations are not enough to drive the system to equilibrium then the fluctuation-dissipation theorem is violated. For the dissipation relation to be fulfilled, the MC condition, Equation (48), must be valid.

4. Beyond the Basics…and More Basic

In the last sections we have discussed some basic results for anomalous diffusion under the point of view of the formalism of the generalized Langevin equation which yield two main features: simplicity and exact results. Obviously, this approach does not exhaust the subject, since diffusion is a basic phenomenon in physics it is a starting point to many different formalisms which we shall briefly discuss.

4.1. Fractional Fokker-Planck Equation

We have seen that, in principle, all kinds of anomalous diffusion can be described by the GLE formalism, which is itself well established from the Mori method. Since normal diffusion can be studied both from Langevin equations and from Fokker-Planck equations, we would expect to obtain a generalized Fokker-Planck formalism for anomalous diffusion. Indeed, fractal formulations of the Fokker-Planck equation (FFPE) have been widely used in the literature in the last decades, in which the evolution of the probability distribution function P(x, t) reads [3, 4, 6]

$\begin{array}{ll}\frac{{\partial }^{\alpha }P(x,t)}{\partial t^{\alpha }}=\left[\frac{1}{m{\gamma }_{\alpha }}\frac{\partial U(x)}{\partial x}+D_{\alpha }\frac{{\partial }^2}{\partial x^2}\right]P(x,t),& (52)\end{array}$

where on the left-hand-side a fractional Rieman-Liouville time-derivative is defined as [124]

$\begin{array}{ll}\frac{{\partial }^{\alpha }P(x,t)}{\partial t^{\alpha }}=\frac{1}{\Gamma (1-\alpha )}\frac{\partial }{\partial t}{\displaystyle {\int }_0^t}\frac{P(x,s)}{{(t-s)}^{\alpha }}ds,& (53)\end{array}$

with 0 < α < 1. Note that the definition of fractional derivatives is not unique [124, 125], with a variety of possibilities, physically (almost) totally unexplored. We notice here that the nonlocal character of the fractional Fokker-Planck equation is similar to the memory kernel in the GLE. On the right hand side, γ_α is a generalized friction, U(x) is the potential, while D_α is generalized Einstein-Stokes relation

$\begin{array}{ll}{D}_{\alpha }=\frac{k_{B}T}{m{\gamma }_{\alpha }}.& (54)\end{array}$

The major result from Equation (52) for a force-free diffusion is the asymptotic solution

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}\langle x^2(t)\rangle =\frac{2D_{\alpha }}{\Gamma (1+\alpha )}{t}^{\alpha }.& (55)\end{array}$

Again, for α ≠ 1, we reach an anomalous diffusion regime [2, 4, 6, 126].

4.2. Interface Growth

Models for interface growth generally consider the random deposition of particles that diffuse to a surface and, as such, have been studied with Langevin equations and modified diffusion equations. Since diffusion with subsequent deposition is ubiquitous, rough surfaces at the interface of two media are very common in nature [14, 127–131] and the description of interface evolution is a very interesting problem in statistical physics. The major objective here is to describe the temporal evolution of the height $h(\overrightarrow{x},t)$ of the interface between two substrates [14, 127], where $\overrightarrow{x}$ is the d dimensional position vector and t is the time. We outline the evolution of h in Figure 6. In (a), we show a real forest fire propagation, a very complex situation. However, we can focus on the interface between the burnt and unburned regions. In (b), we provide a snapshot at a fixed time t of the height $h(\overrightarrow{x},t)$ for a microscopic growth process in which the green medium is penetrating the blue one with arbitrary units. These types of dynamics in d + 1 dimensional space are easy to understand, but not so simple to solve analytically. Experiments can be done for d = 1, 2, 3; however, they present hard theoretical problems for any d.

FIGURE 6

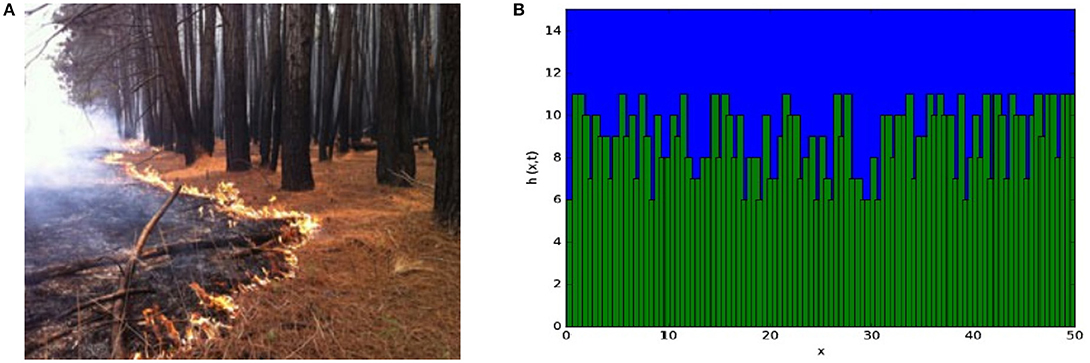
Figure 6. (Color online) (A) Fire propagation in the Amazon rainforest. Source: http://g1.globo.com/am/amazonas/noticia/2013/01/florestas-no-sul-do-am-estao-mais-vulneraveis-incendio-aponta-estudo.html; (B) Schematic representation on a microscopic scale of the height evolution $h(\overrightarrow{x},t)$, defining the interface between two media, as function of the position $\overrightarrow{x}$ for a given time t.

The two main quantities of interest are the average height

$\begin{array}{ll}\langle h(t)\rangle =\frac{1}{V}{\displaystyle \int h(\overrightarrow{x},t)d\overrightarrow{x},}& (56)\end{array}$

where V is the sample volume, and the standard deviation

$\begin{array}{ll}{w}^2(t)=\langle h^2(t)\rangle -{\langle h(t)\rangle }^2,& (57)\end{array}$

often called the surface width w(t), or roughness. Not surprisingly, this height fluctuation has a lot of information about the physical processes governing the system. The evolution of w(t) observed through experiments, computer simulations, and a few analytical results gives us some general features of growth dynamics.

Starting with a flat surface, w(0) = 0, the evolution exhibits four distinct regions: (a) for a very short period 0 < t < t₀, during which correlations are negligible, the process is a random deposition w(t) ~ t^1/2; (b) for t₀ < t < t_× we have w(t) ~ t^β. Here the t_× follows a power law of the form $t_{\times }~L^z$, where L is the size of the sample, z is the dynamic exponent, and β the growth exponent; (c) there is a transition region for t ~ t_×; (d) finally, for t ≫ t_×, the dynamic equilibrium leads to surface width saturation, w_s, which also follows a power law $w_s~L^{\alpha }$, where α is the roughness exponent. The crossing of the curves w(t) ~ t^β and w ~ w_s yields the universal relation

$\begin{array}{ll}z=\frac{\alpha }{\beta }.& (58)\end{array}$

It should be pointed out that these exponents are not related with those of the previous section.

To obtain w(t), we need to know $h(\overrightarrow{x},t)$ and there are two major theoretical ways to attack this problem: (1) Continuous growth equations; (2) Discrete growth models. Figure 6A is an example of the first, while Figure 6B is an example of the second.

4.2.1. Equation of Motion and Symmetries

The growth, in general, is due to the number of particles per unit of time $G(\overrightarrow{x},t)$ arriving on the surface at the position $\overrightarrow{x}$ and time t. The particle flux is not uniform since the particles are deposited at random positions [14]. Therefore, the evolution of $h(\overrightarrow{x},t)$ can be described by

$\begin{array}{ll}\frac{\partial h(\overrightarrow{x},t)}{\partial t}=G=F+\chi (\overrightarrow{x},t),& (59)\end{array}$

where the first term F is the average number of particles arriving at site $\overrightarrow{x}$. The second term, $\chi (\overrightarrow{x},t)$, reflects the random fluctuations and satisfies

$\begin{array}{ll}\langle \chi (\overrightarrow{x},t)\rangle =0,\mathrm{\text{ and}}& (60)\end{array}$

$\begin{array}{ll}\langle \chi (\overrightarrow{x},t)\chi ({\overrightarrow{x}}^{\prime },t^{\prime })\rangle =2D_g\delta (\overrightarrow{x}-{\overrightarrow{x}}^{\prime })\delta (t-t^{\prime }),& (61)\end{array}$

where, D_g measures the degree of growth randomness. The deterministic flux F must satisfy certain symmetry requirements, such as invariance under translation of position, $\overrightarrow{x}\to \overrightarrow{x}+\overrightarrow{x_0}$, height, h → h + h₀ and time t → t + t₀. To satisfy these conditions, it must depend only on derivatives, which, again by the symmetries $\overrightarrow{x}\to -\overrightarrow{x}$ and h → −h, must be of even order [14, 127]. Besides this, considering that symmetrically possible terms such as ${\nabla }^{2n}h(\overrightarrow{x},t)$, for n = 2, 3, …, are irrelevant in the long wavelength limit, since they go to zero faster than ${\nabla }^{2}h(\overrightarrow{x},t)$, we obtain, at the lowest-order in the derivatives, [127]

$\begin{array}{ll}\frac{\partial h(\overrightarrow{x},t)}{\partial t}=\nu {\nabla }^{2}h(\overrightarrow{x},t)+\chi (\overrightarrow{x},t),& (62)\end{array}$

known as Edwards-Wilkinson equation (EW). Note that it is basically a diffusion equation, as (2), plus a noise, where we have a surface tension ν associated with the Laplacian smoothening mechanism. The random deposition model with surface relaxation is in the same universality class as the EW model [132], i.e., they share the same exponents.

Because there are, however, a large class of growth phenomena which are not described by the EW equation, new formulations become necessary. The recently proposed Arcetri models [133] allow the study of more rigid interfaces than the EW model and still allow for exact solutions in any dimension d. Depending on the initial conditions, both growing interfaces and particle motion on the lattice can be modeled. Another classical model was proposed by Kardar et al. [128], inspired by the stochastic Burgers equation. They observed that lateral growth could be added to this equation via the nonlinear term of the Burgers equation so that Equation (62) becomes

$\begin{array}{ll}\frac{\partial h(\overrightarrow{x},t)}{\partial t}=\nu {\nabla }^{2}h(\overrightarrow{x},t)+\frac{\lambda }{2}{\left[\overrightarrow{\nabla }h(\overrightarrow{x},t)\right]}^2+\chi (\overrightarrow{x},t).& (63)\end{array}$

Since its formulation, the Kardar-Parisi-Zhang equation (KPZ) has been a prime model in the description of growth dynamics. The nonlinear term includes a new constant λ associated with the tilt mechanism and breaks down the symmetry h → −h. Consequently, the universality class of KPZ is different from that of EW.

Equation (63) is the simplest nonlinear equation that can describe a large number of growth processes [14, 128]. However, the apparent simplicity of this equation is misleading, since the nonlinear gradient term combined with the noise makes it one of the toughest problems in modern mathematical physics [134, 135]. On the other hand, its complexity is compensated for its generality. It is connected to a large number of stochastic processes, such as the direct polymer model [136], the weakly asymmetric simple exclusion process [137], the totally asymmetric exclusion process [138], direct d-mer diffusion [139], fire propagation [140–142], atomic deposition [143], evolution of bacterial colonies [144, 145], turbulent liquid-crystals [146–148], polymer deposition in semiconductors [149], and etching [150–161].

This problem in non-equilibrium statistical physics is analogous to the Ising model for equilibrium statistical physics, which is used as a basic model for understanding a large class of phenomena. The search for exact solutions to this equation in the d + 1 dimensional space has resulted in important contributions to mathematics; however, to date, they have been obtained only for specific situations and are limited to 1 + 1 dimensions [128, 135].

4.2.2. Scaling Invariance

In this small subsection we limit ourselves to scaling symmetries only. However, in interface growth, the shape of single-time and two-time responses and height correlation functions can be derived from the assumption of a local time-dependent scale-invariance [162]. For the KPZ equation, a systematic test of aging scaling was performed, showing the scaling relations for the two-time spatio-temporal autocorrelator and for the time-integrated response function [152, 163, 164].

The scaling invariance can be investigated through the transformation [14] $\overrightarrow{x}\to b\overrightarrow{x}$, h → b^α and t → t^z which yields, for the KPZ equation, (63)

$\begin{array}{ll}\nu \to b^{z-2}\nu ,& (64)\end{array}$

$\begin{array}{ll}{D}_g\to b^{z-d-2\alpha }{D}_g,& (65)\end{array}$

and

$\begin{array}{ll}\lambda \to b^{\alpha +z-2}\lambda & (66)\end{array}$

Scaling invariance demands that the exponents in Equations (64–66) must be zero. However, a simple inspection shows that they are inconsistent. The renormalization group approach of Kardar et al. [128], uses the nonlinear term as a perturbation, and their result shows that only Equation (66) remains invariant, yielding the famous Galilean invariance

$\begin{array}{ll}\alpha +z=2.& (67)\end{array}$

Equations (64, 65) are corrected by the renormalization, and the final result yields α = 1/2, β = 1/3, and z = 3/2, for 1 + 1 dimensions. Since the KPZ renormalization approach is valid only for 1 + 1 dimensions, questions about the validity of the Galilean invariance [165, 166] for d > 1 and the existence of an upper critical dimension for KPZ [167, 168] have been raised.

For d > 1, the numerical simulation of the KPZ equation is not an easy task [165, 166, 169–172], and the use of cellular automata models [150–161, 173–176] has become increasingly common for growth simulations. Polynuclear growth (PNG), is a typical example of a discrete model that has received a lot of attention, and the outstanding works of Prähofer and Spohn [177] and Johansson [178] drive the way to the exact solution of the distributions of the heights fluctuations f(h, t) in the KPZ equation for 1 + 1 dimensions [135]. By construction, h → h − 〈h〉, then f(h, t) has zero mean, so its skewness and kurtosis are the most important quantities to observe [148, 179–182]. In addition, Langevin equations for growth models have been discussed by some authors [183–185]. Several works have been done in the weakly asymmetric simple exclusion process [137], the totally asymmetric exclusion process [138, 186], and the direct d-mer diffusion model [139]: for a review see [171, 182, 187, 188]. More experimentally measured exponents for growing interfaces in four universality classes (KPZ, quenched KPZ, EW and Arcetri) can be found in Henkel and Durang [133] and references therein.

4.2.3. Cellular Automata Growth Models

Cellular automata are described by simple rules, which allow us to inquire about relevant properties of a complex dynamical system. For a given growth model, the first question to be answered is if the model belongs to the same universality class as KPZ. In this context, we expose here the etching model [150], which has attracted considerable attention in recent years [151–161]. These studies suggest a close relation between the etching model and KPZ. For example, for 1 + 1 dimensions Alves et al. [159] have proven that α = 1/2 exactly. Unfortunately, their method does not allow to obtain β or z.

The etching model describes the mechanism of an acid eroding a surface. The detailed description of the model can be found in Mello et al. [150]. For simplicity, let us consider a site i in a hypercube of side L and volume V = L^d in space Ψ of dimension d, and look at one of its nearest neighbors, j. If h_j > h_i, then it becomes equal to h_i. We then define the etching model following the steps:

1. At time t we randomly choose a site i ∈ V.

2. If h_j(t) > h_i(t), do h_j(t + Δt) = h_i(t).

3. Do h_i(t + Δt) = h_i(t) − 1.

In Figure 7, we show the mechanism of the etching model in one dimension: (a) step 1, we randomly select a site at time t, here i = 2 shown as green in the figure; step 2, the site i = 2 interacts with its neighbors j = 1, 3. Then in Figure 7 h₁(t + Δt) = h₂(t), meaning that it is strongly affected, and h₃(t + Δt) = h₃(t), meaning it is not affected; (c) step 3, h₂(t + Δt) = h₂(t) − 1. We describe here a process of strong interactions between the site and its neighbors.

FIGURE 7

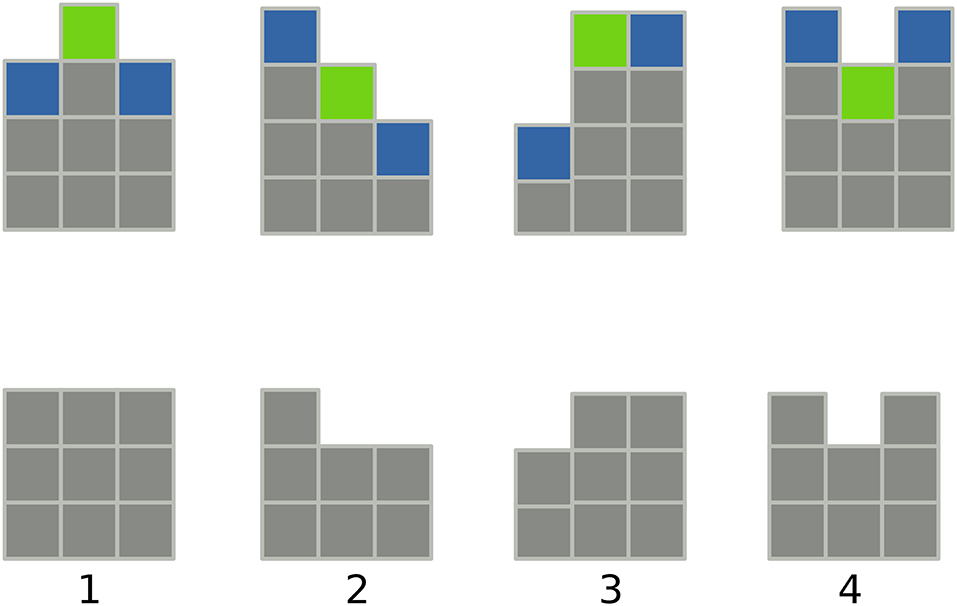
Figure 7. The etching mechanism in one dimension. The figures are the four situations in which the dynamics of the etching model can be divided. The initial configuration is at the top, where the selected site, in column 2, is green, and its first neighbors, in columns 1 and 3, are shown in dark blue. After the corrosion process the final situation is exhibited at the bottom. The steps are: step 1, site selection, green; step 2, interaction with nearest neighbors; step 3, decrease of height by one. From Alves et al. [159], with permission from Physics Review E.

Using these rules and averaging over N_e numerical experiments, it is possible to obtain the exponents α, β, and z [150–161]. Finally, the upper critical limit for the etching model (KPZ) was recently discussed by Rodrigues et al. [157], where it was shown numerically that there is no upper critical dimension for the etching model up to 6 + 1 dimensions. Thus, we have established a lower limit for the KPZ critical dimension, i.e., if it exists then d_c > 6, in agreement with other authors [139]. They have shown that the Galilean invariance (67) remains valid for d ≤ 6 as well. These problems, however, still lack an exact solution.

4.3. Reaction-Diffusion Processes

One could not complete a work on diffusion without a brief discussion of reaction-diffusion processes [186, 189–191]. Exactly solvable reaction-diffusion models consist largely of single species reactions in one dimension, e.g., variations of the coalescence process, A + A → A + S [192–194] and the annihilation process A + A → S + S [193, 194], where A and S denote occupied and empty sites, respectively. These simple reactions display a wide range of behavior characteristic of non-equilibrium kinetics, such as self organization, pattern formation, and kinetic phase transitions. Interval methods have provided many exact solutions for one-dimensional coalescence and annihilation models. The method of empty intervals, applicable to coalescence models, requires solution of an infinite hierarchy of differential difference equations for the probabilities E_n of finding n consecutive lattice sites simultaneously empty. For annihilation models, the method of parity intervals similarly requires determination of G_n, the probability of n consecutive lattice sites containing an even number of particles [190]. In the continuous limit, such models can be described exactly in terms of the probability E(t, x) of finding an empty interval of size x at time t. Under fairly weak conditions, the equation of motion for E(t, x) is a diffusion equation, albeit with the unusual boundary condition E(t, 0) = 1. In several cases, the exact and fluctuation-dominated behavior in d = 1 has been seen experimentally, since the 1990s. This is one of the rare cases where theoretical statistical mechanics can be compared with experiments and also shows that simple mean-field schemes are not enough. For an introduction see Ben-Avraham and Havlin [189], and for up to date references see Shapoval et al. [191]. Another important new development in diffusion concerns stochastic resets, as they were introduced by Evans and Majumdar (see [195–197] and references therein). This leads to important modifications of the stationary state and raises the question how to consider the status of the general theorem described in the present review.

5. Conclusions

In this short review we address diffusion, as a modern and important topic of statistical physics, with broad applications [4–6, 8, 9, 40, 42]. We emphasize the study of systems with memory, for which a generalized Langevin equation applies and describe how the diffusion exponent is obtained from the memory [5, 97]. We highlight the properties of response functions [1, 83] for the processes of anomalous relaxation [1, 115], Gaussianization and ergodicity [9, 83]. Moreover, we have established a hierarchy: the mixing condition is stronger than the ergodic hypothesis, which is itself stronger than the fluctuation-dissipation theorem. It is important to call attention again to Costa et al. [8], where it was observed that in the ballistic diffusion the fluctuation-dissipation theorem fails. Indeed, for the ballistic motion which, on average, behaves as a Newtonian particle with constant velocity, the fluctuations are not enough to bring the system to equilibrium, i.e., the dissipation, which for large times decays as 1/t, does not balance the fluctuations. This work points out that the violation of the mixing condition breaks down ergodicity, as required by the Khinchin theorem and the fluctuation dissipation theorem.

In conclusion, since the mechanism of diffusion is present in most nonequilibrium processes, diffusion is an exhaustive subject, and we have only called attention to some of its aspects. Consequently, we apologize to the authors of important works not mentioned here, such as aging [123, 152, 163, 164, 198] for example.

Author Contributions

FO suggested the work, and wrote some sections. RF was responsible for the section on non-Markovian processes and selected the figures. LL wrote the ergodicity and decay toward equilibrium sections. MV collaborated on the section on the generalized Langevin equation and reedited the text.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001, CNPq and FAPDF. MV was supported by a Senior fellowship (88881.119772/2016-01) from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) at MIT. MV would like to thank Prof. Jeff Gore for the hospitality at Physics of Living Systems, MIT.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Vainstein MH, Costa IVL, Oliveira FA. Mixing, ergodicity and the Fluctuation-dissipation Theorem in complex Systems. In: Miguel MC, Rubí M, editors. Jamming, Yielding, and Irreversible Deformation in Condensed Matter. Vol. 688 of Lecture Notes in Physics. Berlin;Heidelberg: Springer (2006). pp. 159–188.

Google Scholar

2. Shlesinger MF, Zaslavsky GM, Klafter J. Strange kinetics. Nature (1993) 363:31. doi: 10.1038/363031a0

CrossRef Full Text | Google Scholar

3. Metzler R, Barkai E, Klafter J. Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker-Planck equation approach. Phys Rev Lett. (1999) 82:3563. doi: 10.1103/PhysRevLett.82.3563

CrossRef Full Text | Google Scholar

4. Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1. doi: 10.1016/S0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

5. Morgado R, Oliveira FA, Batrouni GG, Hansen A. Relation between anomalous and normal diffusion in systems with memory. Phys Rev Lett (2002) 89:100601. doi: 10.1103/PhysRevLett.89.100601

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Metzler R, Klafter J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J Phys A. (2004) 37:161. doi: 10.1088/0305-4470/37/31/R01

CrossRef Full Text | Google Scholar

7. Sancho JM, Lacasta AM, Lindenberg K, Sokolov IM, Romero AH. Diffusion on a solid surface: anomalous is normal. Phys Rev Lett. (2004) 92:250601. doi: 10.1103/PhysRevLett.92.250601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Costa IVL, Morgado R, Lima MVBT, Oliveira FA. The Fluctuation-Dissipation Theorem fails for fast superdiffusion. Europhys Lett. (2003) 63:173. doi: 10.1209/epl/i2003-00514-3

CrossRef Full Text | Google Scholar

9. Lapas LC, Morgado R, Vainstein MH, Rubí JM, Oliveira FA. Khinchin Theorem and anomalous diffusion. Phys Rev Lett. (2008) 101:230602. doi: 10.1103/PhysRevLett.101.230602

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Weron A, Magdziarz M. Generalization of the Khinchin Theorem to Lévy flights. Phys Rev Lett. (2010) 105:260603. doi: 10.1103/PhysRevLett.105.260603

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Thiel F, Flegel F, Sokolov IM. Disentangling sources of anomalous diffusion. Phys Rev Lett. (2013) 111:010601. doi: 10.1103/PhysRevLett.111.010601

PubMed Abstract | CrossRef Full Text | Google Scholar

12. McKinley S, Nguyen H. Anomalous diffusion and the generalized Langevin equation. SIAM J. Math. Anal. (2018) 50, 5119–160. doi: 10.1137/17M115517X

CrossRef Full Text | Google Scholar

13. Flekkøy EG. Minimal model for anomalous diffusion. Phys Rev E. (2017) 95:012139. doi: 10.1103/PhysRevE.95.012139

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Barabási AL, Stanley HE. Fractal Concepts in Surface Growth. Cambridge: Cambridge University Press (1995).

Google Scholar

15. Murray JD. Mathematical Biology I. An Introduction. Vol. 17 of Interdisciplinary Applied Mathematics. 3rd edition. New York: Springer (2002).

16. Brown R. A brief account of microscopical observations made in the Months on June, July, and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in Organic and Inorganic Bodies. Phil Mag. (1828) 4:161. doi: 10.1080/14786442808674769

CrossRef Full Text | Google Scholar

17. Brown R. Mikroskopische Beobachtungen ber die im Pollen der Pflanzen enthaltenen Partikeln, und ber das allgemeine Vorkommen activer Molecle in organischen und unorganischen Kpern. Annalen der Physik (1828) 90:294–313. doi: 10.1002/andp.18280901016

CrossRef Full Text | Google Scholar

18. Einstein A. ber die von der molekularkinetischen Theorie der Wrme geforderte Bewegung von in ruhenden Flssigkeiten suspendierten Teilchen. Annalen der Physik. (1905) 322:549–60. doi: 10.1002/andp.19053220806

CrossRef Full Text | Google Scholar

19. Einstein A. Investigations on the Theory of the Brownian movement. New York, NY: Dover (1956).

Google Scholar

20. Dyre JC, Schrøder TB. Universality of AC conduction in disordered solids. Rev Mod Phys. (2000) 72:873–92. doi: 10.1103/RevModPhys.72.873

CrossRef Full Text | Google Scholar

21. Oliveira FA, Morgado R, Hansen A, Rubí JM. Superdiffusive conduction: AC conductivity with correlated noise. Physica A. (2005) 357:115–21. doi: 10.1016/j.physa.2005.05.056

CrossRef Full Text | Google Scholar

22. Gudowska-Nowak E, Lindenberg K, Metzler R. Preface: Marian Smoluchowski's 1916 paper a century of inspiration. J Phys A. (2017) 50:380301. doi: 10.1088/1751-8121/aa8529

CrossRef Full Text | Google Scholar

23. Risken H. The Fokker-Planck Equation. Berlin: Springer-Verlag (1989).

Google Scholar

24. Salinas S. Introduction to Statistical Physics. New York, NY: Springer (2001).

Google Scholar

25. Gadomski A, Kruszewska N, Bełdowski P, Lent B, Ausloos M. A tribute to Marian Smoluchowski's legacy on soft grains assembly and hydrogel formation. Acta Phys. Polon. B (2018) 49:993–1005. doi: 10.5506/APhysPolB.49.993

CrossRef Full Text | Google Scholar

26. On the Uniformity of Laws of Nature. XXX Marian Smoluchowski Symposium. 100^th Anniversary of Smoluchowski's Death. Krakow (2017). Available online at: http://www.smoluchowski.if.uj.edu.pl/smoluchowski-2017

27. Langevin P. Sur la thorie du mouvement Brownien. C R Acad Sci. (1908) 146:530.

Google Scholar

28. Reichl LE. A Modern Course in Statistical Physics. New York, NY: Wiley-Interscience (1998).

Google Scholar

29. Toussaint R, Helgesen G, Flekkøy EG. Dynamic roughening and fluctuations of dipolar chains. Phys Rev Lett (2004) 93:108304. doi: 10.1103/PhysRevLett.93.108304

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Oliveira FA, Taylor PL. Breaking in polymer chains. II. The Lennard Jones chain. J Chem Phys. (1994) 101:10118–125. doi: 10.1063/1.468000

CrossRef Full Text | Google Scholar

31. Oliveira FA, Gonzalez JA. Bond-stability criterion in chain dynamics. Phys Rev B. (1996) 54:3954–8. doi: 10.1103/PhysRevB.54.3954

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Oliveira FA. Transition-state analysis for fracture nucleation in polymers: the Lennard-Jones chain. Phys Rev B. (1998) 57:10576–82. doi: 10.1103/PhysRevB.57.10576

CrossRef Full Text | Google Scholar

33. Maroja AM, Oliveira FA, Cieśla M, Longa L. Polymer fragmentation in extensional flow. Phys Rev E. (2001) 63:061801. doi: 10.1103/PhysRevE.63.061801

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Dias CL, Dubé M, Oliveira FA, Grant M. Scaling in force spectroscopy of macromolecules. Phys Rev E. (2005) 72:011918. doi: 10.1103/PhysRevE.72.011918

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Rahman A, Singwi KS, Sjölander A. Stochastic Model of a Liquid and Cold Neutron Scattering. II. Phys Rev. (1962) 126:997–1004. doi: 10.1103/PhysRev.126.997

CrossRef Full Text | Google Scholar

36. Yulmetyev RM, Mokshin AV, Hänggi P. Diffusion time-scale invariance, randomization processes, and memory effects in Lennard-Jones liquids. Phys Rev E. (2003) 68:051201. doi: 10.1103/PhysRevE.68.051201

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bao JD. Transport in a flashing ratchet in the presence of anomalous diffusion. Phys Lett A. (2003) 314:203–8. doi: 10.1016/S0375-9601(03)00910-1

CrossRef Full Text | Google Scholar

38. Bao JD, Zhuo YZ, Oliveira FA, Hänggi P. Intermediate dynamics between Newton and Langevin. Phys Rev E. (2006) 74:061111. doi: 10.1103/PhysRevE.74.061111

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Longa L, Curado EMF, Oliveira FA. Roundoff-induced coalescence of chaotic trajectories. Phys Rev E. (1996) 54:R2201. doi: 10.1103/PhysRevE.54.R2201

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cieśla M, Dias SP, Longa L, Oliveira FA. Synchronization induced by Langevin dynamics. Phys Rev E. (2001) 63:065202. doi: 10.1103/PhysRevE.63.065202

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Huang K. Statistical Mechanics. New York, NY: John Wiley & Sons (1987).

Google Scholar

42. Santamar-a-Holek I, Vainstein MH, Rubí JM, Oliveira FA. Protein motors induced enhanced diffusion in intracellular transport. Physica A. (2009) 388:1515–20. doi: 10.1016/j.physa.2009.01.013

CrossRef Full Text | Google Scholar

43. Palmieri B, Bresler Y, Wirtz D, Grant M. Multiple scale model for cell migration in monolayers: elastic mismatch between cells enhances motility. Sci Rep. (2015) 5:11745. doi: 10.1038/srep11745

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Lomholt MA, Ambjörnsson T, Metzler R. Optimal target search on a fast-folding polymer chain with volume exchange. Phys Rev Lett. (2005) 95:260603. doi: 10.1103/PhysRevLett.95.260603

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Durang X, Kwon C, Park H. Overdamped limit and inverse-friction expansion for Brownian motion in an inhomogeneous medium. Phys Rev E. (2015) 91:062118. doi: 10.1103/PhysRevE.91.062118

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Morgado R, Costa IVL, Oliveira FA. Normal and anomalous diffusion: ergodicity and fluctuation-dissipation theorem. Acta Phys Polon B. (2004) 35:1359. Available online at: http://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=35&page=1365

Google Scholar

47. Vaytet N, Commerçon B, Masson J, González M, Chabrier G. Protostellar birth with ambipolar and ohmic diffusion. A A. (2018) 615:A5.

Google Scholar

48. Mason TG, Weitz D. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys Rev Lett. (1995) 74:1250. doi: 10.1103/PhysRevLett.74.1250

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Grmela M, Öttinger HC. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys Rev E. (1997) 56:6620. doi: 10.1103/PhysRevE.56.6620

CrossRef Full Text | Google Scholar

50. Bakk A, Fossum JO, da Silva GJ, Adland HM, Mikkelsen A, Elgsaeter A. Viscosity and transient electric birefringence study of clay colloidal aggregation. Phys Rev E. (2002) 65:021407. doi: 10.1103/PhysRevE.65.021407

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Sehnem AL, Aquino R, Campos AFC, Tourinho FA, Depeyrot J, Neto AMF. Thermodiffusion in positively charged magnetic colloids: influence of the particle diameter. Phys Rev E. (2014) 89:032308. doi: 10.1103/PhysRevE.89.032308

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Sehnem AL, Neto AMF, Aquino R, Campos AFC, Tourinho FA, Depeyrot J. Temperature dependence of the Soret coefficient of ionic colloids. Phys Rev E. (2015) 92:042311. doi: 10.1103/PhysRevE.92.042311

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Cabreira Gomes R, Ferreira da Silva A, Kouyat M, Demouchy G, Mriguet G, Aquino R, et al. Thermodiffusion of repulsive charged nanoparticles–the interplay between single-particle and thermoelectric contributions. Phys Chem Chem Phys. (2018) 20:16402–13. doi: 10.1039/C8CP02558D

PubMed Abstract | CrossRef Full Text | Google Scholar

54. de Brito PE, da Silva CAA, Nazareno HN. Field-induced localization in Fibonacci and Thue-Morse lattices. Phys Rev B. (1995) 51:6096–9. doi: 10.1103/PhysRevB.51.6096

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Monte AFG, da Silva SW, Cruz JMR, Morais PC, Chaves AS, Cox HM. Symmetric and asymmetric fractal diffusion of electron-hole plasmas in semiconductor quantum wells. Phys Lett A. (2000) 268:430–5. doi: 10.1016/S0375-9601(00)00193-6

CrossRef Full Text | Google Scholar

56. Monte AFG, da Silva SW, Cruz JMR, Morais PC, Chaves AS. Experimental evidence of asymmetric carrier transport in InGaAs quantum wells and wires grown on tilted InP substrates. Appl Phys Lett. (2002) 81:2460–2. doi: 10.1063/1.1507619

CrossRef Full Text | Google Scholar

57. Kumakura K, Makimoto T, Kobayashi N, Hashizume T, Fukui T, Hasegawa H. Minority carrier diffusion length in GaN: dislocation density and doping concentration dependence. Appl Phys Lett. (2005) 86:052105. doi: 10.1063/1.1861116

CrossRef Full Text | Google Scholar

58. Borges JB, da Silva SW, Morais PC, Monte AFG. Optical signatures of asymmetric fractal diffusion of electron-hole plasma in semiconductor quantum wells. Appl Phys Lett. (2006) 89:142103. doi: 10.1063/1.2358842

CrossRef Full Text | Google Scholar

59. Gudowska-Nowak E, Bochenek K, Jurlewicz A, Weron K. Hopping models of charge transfer in a complex environment: coupled memory continuous-time random walk approach. Phys Rev E. (2005) 72:061101. doi: 10.1103/PhysRevE.72.061101

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Filipovitch N, Hill K, Longjas A, Voller V. Infiltration experiments demonstrate an explicit connection between heterogeneity and anomalous diffusion behavior. Water Resour Res. (2016) 52:5167–78. doi: 10.1002/2016WR018667

CrossRef Full Text | Google Scholar

61. Aarão Reis FDA. Scaling relations in the diffusive infiltration in fractals. Phys Rev E. (2016) 94:052124. doi: 10.1103/PhysRevE.94.052124

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Aarão Reis FDA, Bolster D, Voller VR. Anomalous behaviors during infiltration into heterogeneous porous media. Adv Water Resour. (2018) 113:180–8. doi: 10.1016/j.advwatres.2018.01.010

CrossRef Full Text | Google Scholar

63. Gomes Filho MS, Oliveira FA, Barbosa MAA. A statistical mechanical model for drug release: investigations on size and porosity dependence. Physica A. (2016) 460:29–37. doi: 10.1016/j.physa.2016.04.040

CrossRef Full Text | Google Scholar

64. Ignacio M, Chubynsky MV, Slater GW. Interpreting the Weibull fitting parameters for diffusion-controlled release data. Physica A. (2017) 486:486–96. doi: 10.1016/j.physa.2017.05.033

CrossRef Full Text | Google Scholar

65. Gun L, Kaikai Z, Rui G. Simulation on Drug Molecules Permeability of the Blood-Brain-Barrier. Am J Biol Life Sci. (2017) 5:30.

Google Scholar

66. Soares JMD, Almeida JRGS, de Oliveira HP. Controlled release of extract of Morus nigra from Eudragit L-100 electrospun fibers: toxicity and in vitro release evaluation. Curr Trad Med. (2017) 3:146–54. doi: 10.2174/2215083803666170309123836

CrossRef Full Text | Google Scholar

67. Mandelbrot BB. The Fractal Geometry of Nature. Vol. 1. New York, NY: WH Freeman (1982).

68. Stauffer D, Stanley HE. From Newton to Mandelbrot. New York, NY: Springer-Verlag (1995).

Google Scholar

69. Cristea LL, Steinsky B. On totally disconnected generalised Sierpiński carpets. B Math Soc Sci Math. (2014) 57:27–34.

Google Scholar

70. Balankin AS. The topological Hausdorff dimension and transport properties of Sierpiński carpets. Phys Lett A. (2017) 381:2801–8. doi: 10.1016/j.physleta.2017.06.049

CrossRef Full Text | Google Scholar

71. Balankin AS. Mapping physical problems on fractals onto boundary value problems within continuum framework. Phys Lett A. (2018) 382:141–6. doi: 10.1016/j.physleta.2017.11.005

CrossRef Full Text | Google Scholar

72. Barbosa MAA, Barbosa FV, Oliveira FA. Thermodynamic and dynamic anomalies in a one-dimensional lattice model of liquid water. J Chem Phys. (2011) 134:024511. doi: 10.1063/1.3522772

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Bertolazzo AA, Kumar A, Chakravarty C, Molinero V. Water-like anomalies and phase behavior of a pair potential that stabilizes diamond. J Phys Chem B. (2015) 120:1649–59. doi: 10.1021/acs.jpcb.5b08432

PubMed Abstract | CrossRef Full Text | Google Scholar

74. da Silva FBV, Oliveira FA, Barbosa MAA. Residual entropy and waterlike anomalies in the repulsive one dimensional lattice gas. J Chem Phys. (2015) 142:144506. doi: 10.1063/1.4916905

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Bier M, Lisowski B, Gudowska-Nowak E. Phase transitions and entropies for synchronizing oscillators. Phys Rev E. (2016) 93:012143. doi: 10.1103/PhysRevE.93.012143

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Pinto PD, Oliveira FA, Penna ALA. Thermodynamics aspects of noise-induced phase synchronization. Phys Rev E. (2016) 93:052220. doi: 10.1103/PhysRevE.93.052220

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Pinto PD, Penna AL, Oliveira FA. Critical behavior of noise-induced phase synchronization. Europhys Lett. (2017) 117:50009. doi: 10.1209/0295-5075/117/50009

CrossRef Full Text | Google Scholar

78. Pérez-Madrid A. Gibbs entropy and irreversibility. Physica A. (2004) 339:339. doi: 10.1016/j.physa.2004.04.106

CrossRef Full Text | Google Scholar

79. Rubí JM, Bedeaux D. Brownian motion in a fluid in elongational flow. J Stat Phys. (1988) 53:125. doi: 10.1007/BF01011549

CrossRef Full Text | Google Scholar

80. Kuśmierz Ł, Dybiec B, Gudowska-Nowak E. Thermodynamics of superdiffusion generated by lévy–wiener fluctuating forces. Entropy (2018) 20:658. doi: 10.3390/e20090658

CrossRef Full Text | Google Scholar

81. Hänggi P, Talkner P, Borkovec M. Reaction-rate theory: fifty years after kramers. Rev Mod Phys. (1990) 62:251–341. doi: 10.1103/RevModPhys.62.251

CrossRef Full Text | Google Scholar

82. Morgado R, Cieśla M, Longa L, Oliveira FA. Synchronization in the presence of memory. Europhys Lett. (2007) 79:10002. doi: 10.1209/0295-5075/79/10002

CrossRef Full Text | Google Scholar

83. Lapas LC, Costa IVL, Vainstein MH, Oliveira FA. Entropy, non-ergodicity and non-Gaussian behaviour in ballistic transport. Europhys Lett. (2007) 77:37004. doi: 10.1209/0295-5075/77/37004

CrossRef Full Text | Google Scholar

84. Lee MH. Can the velocity autocorrelation function decay exponentially? Phys Rev Lett. (1983) 51:1227–30. doi: 10.1103/PhysRevLett.51.1227

CrossRef Full Text | Google Scholar

85. Nyquist H. Thermal agitation of electric charge in conductors. Phys Rev. (1928) 32:110–13. doi: 10.1103/PhysRev.32.110

CrossRef Full Text | Google Scholar

86. Mori H. Transport, collective motion, and Brownian motion. Prog Theor Phys. (1965) 33:423. doi: 10.1143/PTP.33.423

CrossRef Full Text | Google Scholar

87. Mori H. A continued-fraction representation of the time-correlation function. Prog Theor Phys. (1965) 34:399. doi: 10.1143/PTP.34.399

CrossRef Full Text | Google Scholar

88. Kubo R. Response, relaxation and fluctuation. In: Kirczenow G, Marro J, editors. Transport Phenomena. Lecture Notes in Physics. Vol. 31. Berlin; Heidelberg: Springer-Verlag (1974). p. 74-124.

Google Scholar

89. Kubo R, Toda M, Hashitsume N. Statistical Physics II. Berlin: Springer (1991).

Google Scholar

90. Kubo R. Fluctuation-dissipation theorem. Prog Phys. (1966) 29:255. doi: 10.1088/0034-4885/29/1/306

CrossRef Full Text | Google Scholar

91. Lee MH. Solutions of the generalized Langevin equation by a method of recurrence relations. Phys Rev B. (1982) 26:2547. doi: 10.1103/PhysRevB.26.2547

CrossRef Full Text | Google Scholar

92. Lee MH. Derivation of the generalized Langevin equation by a method of recurrence relations. J Math Phys. (1983) 24:512. doi: 10.1063/1.525628

CrossRef Full Text | Google Scholar

93. Lee MH, Hong J. Transport behavior of dense protons in a slab. Phys Rev B. (1984) 30:6756. doi: 10.1103/PhysRevB.30.6756

CrossRef Full Text | Google Scholar

94. Gluskin E. Let us teach this generalization of the final-value theorem. Eur J Phys. (2003) 24:591. doi: 10.1088/0143-0807/24/6/005

CrossRef Full Text | Google Scholar

95. Vainstein MH, Morgado R, Oliveira FA, de Moura FABF, Coutinho-Filho MD. Stochastic description of the dynamics of the random-exchange Heisenberg chain. Phys Lett A. (2005) 339:33–8. doi: 10.1016/j.physleta.2005.02.059

CrossRef Full Text | Google Scholar

96. Vainstein MH, Costa IVL, Morgado R, Oliveira FA. Non-exponential relaxation for anomalous diffusion. Europhys Lett. (2006) 73:726–732. doi: 10.1209/epl/i2005-10455-9

CrossRef Full Text | Google Scholar

97. Ferreira RMS, Santos MVS, Donato CC, Andrade JS, Oliveira FA. Analytical results for long-time behavior in anomalous diffusion. Phys Rev E. (2012) 86:021121. doi: 10.1103/PhysRevE.86.021121

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Srokowski T. Nonstationarity induced by long-time noise correlations in the Langevin Equation. Phys Rev Lett. (2000) 85:2232. doi: 10.1103/PhysRevLett.85.2232

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Srokowski T. Fluctuations in multiplicative systems with jumps. Phys Rev E. (2013) 87:032104. doi: 10.1103/PhysRevE.87.032104

CrossRef Full Text | Google Scholar

100. Kadanoff LP, Götze W, Hamblen D, Hecht R, Lewis E, Palciauskas VV, et al. Static phenomena near critical points: theory and experiment. Rev Mod Phys. (1967) 39:395. doi: 10.1103/RevModPhys.39.395

CrossRef Full Text | Google Scholar

101. Kadanoff LP. Statistical Physics: Statics, Dynamics and Renormalization. Singapore: World Scientific Publishing Company (2000).

Google Scholar

102. Kenna R, Johnston DA, Janke W. Self-consistent scaling theory for logarithmic-correction exponents. Phys Rev Lett. (2006) 97:155702. doi: 10.1103/PhysRevLett.97.155702

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Kenna R, Ruiz-Lorenzo JJ. Scaling analysis of the site-diluted Ising model in two dimensions. Phys Rev E. (2008) 78:031134. doi: 10.1103/PhysRevE.78.031134

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Rubí JM, Santamaría-Holek I, Pérez-Madrid A. Slow dynamics and local quasi-equilibrium—relaxation in supercooled colloidal systems. J Phys. (2004) 16:S2047. doi: 10.1088/0953-8984/16/22/002

CrossRef Full Text

105. Santamaría-Holek I, Pérez-Madrid A, Rubí JM. Local quasi-equilibrium description of slow relaxation systems. J Chem Phys. (2004) 120:2818. doi: 10.1063/1.1640346

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Vainstein MH, Stariolo DA, Arenzon JJ. Heterogeneities in systems with quenched disorder. J Phys A. (2003) 36:10907–19. doi: 10.1088/0305-4470/36/43/016

CrossRef Full Text | Google Scholar

107. Santos MBL, Oliveira EA, Neto AMF. Rayleigh scattering of a new lyotropic nematic liquid crystal system: crossover of propagative and diffusive behavior. Liq Cryst. (2000) 27:1485. doi: 10.1080/026782900750018654

CrossRef Full Text | Google Scholar

108. Benmouna F, Peng B, Gapinski J, Patkowski A, Ruhe J, Johannsmann D. Dynamic light scattering from liquid crystal polymer brushes swollen in a nematic solvent. Liq Cryst. (2001) 28:1353. doi: 10.1080/02678290110061395

CrossRef Full Text | Google Scholar

109. Peyrard M. Glass transition in protein hydration water. Phys Rev E. (2001) 64:011109. doi: 10.1103/PhysRevE.64.011109

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Colaiori F, Moore MA. Stretched exponential relaxation in the mode-coupling theory for the Kardar-Parisi-Zhang equation. Phys Rev E. (2001) 63:057103. doi: 10.1103/PhysRevE.63.057103

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Ferreira JL, Ludwig GO, Montes A. Experimental investigations of ion-acoustic double-layers in the electron flow across multidipole magnetic fields. Plasma Phys Control Fusion. (1991) 33:297–311. doi: 10.1088/0741-3335/33/4/003

CrossRef Full Text | Google Scholar

112. Bouchaud JP, Mézard M, Yedidia JS. Variational theory for disordered vortex lattices. Phys Rev Lett. (1991) 67:3840. doi: 10.1103/PhysRevLett.67.3840

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Kohlrausch R. Theorie des elektrischen Rckstandes in der Leidener Flasche. Annalen der Physik. (1854) 167:56–82. doi: 10.1002/andp.18541670103

CrossRef Full Text | Google Scholar

114. Kohlrausch F. ber die elastische Nachwirkung bei der Torsion. Annalen der Physik. (1863) 195:337. doi: 10.1002/andp.18631950702

CrossRef Full Text | Google Scholar

115. Lapas LC, Ferreira RM, Rubí JM, Oliveira FA. Anomalous law of cooling. J Chem Phys. (2015) 142:104106. doi: 10.1063/1.4914872

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Mittag-Leffler GM. Sur la reprsentation analytique d'une branche uniforme d'une fonction monogne. Acta Math. (1905) 29:101. doi: 10.1007/BF02403200

CrossRef Full Text | Google Scholar

117. Khinchin AI. Mathematical Foundations of Statistical Mechanics. New York, NY: Dover (1949).

118. Bao JD, Hänggi P, Zhuo YZ. Non-Markovian Brownian dynamics and nonergodicity. Phys Rev E. (2005) 72:061107. doi: 10.1103/PhysRevE.72.061107

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Silvestre C, Rocha Filho T. Ergodicity in a two-dimensional self-gravitating many-body system. Phys Lett A. (2016) 380:337–48. doi: 10.1016/j.physleta.2015.10.042

CrossRef Full Text | Google Scholar

120. Campa A, Dauxois T, Ruffo S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys Rep. (2009) 480:57–159. doi: 10.1016/j.physrep.2009.07.001

CrossRef Full Text | Google Scholar

121. Parisi G. Off-equilibrium fluctuation-dissipation relation in fragile glasses. Phys Rev Lett. (1997) 79:3660–3. doi: 10.1103/PhysRevLett.79.3660

CrossRef Full Text | Google Scholar

122. Dybiec B, Parrondo JMR, Gudowska-Nowak E. Fluctuation-dissipation relations under Lvy noises. EPL (2012) 98:50006. doi: 10.1209/0295-5075/98/50006

CrossRef Full Text | Google Scholar

123. Cugliandolo L, Kurchan J, Parisi G. Off equilibrium dynamics and aging in unfrustrated systems. J de Physique I. (1994) 4:1641–56. doi: 10.1051/jp1:1994212

CrossRef Full Text | Google Scholar

124. Oldham K, Spanier J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order. Vol. 111. San Diego, CA: Elsevier (1974).

Google Scholar

125. Kilbas AAA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Vol. 204. Amsterdam: Elsevier Science Limited (2006).

Google Scholar

126. Klafter J, Shlesinger MF, Zumofen G. Beyond Brownian Motion. Phys Today (1996) 49:33. doi: 10.1063/1.881487

CrossRef Full Text | Google Scholar

127. Edwards SF, Wilkinson DR. The surface statistics of a granular aggregate. Proc R Soc Lond A. (1982) 381:17–31. doi: 10.1098/rspa.1982.0056

CrossRef Full Text | Google Scholar

128. Kardar M, Parisi G, Zhang YC. Dynamic Scaling of Growing Interfaces. Phys Rev Lett. (1986) 56:889–92. doi: 10.1103/PhysRevLett.56.889

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Hansen A, Schmittbuhl J, Batrouni GG, de Oliveira FA. Normal stress distribution of rough surfaces in contact. Geophys Res Lett. (2000) 27:3639–42. doi: 10.1029/2000GL011757

CrossRef Full Text | Google Scholar

130. Cordeiro JA, Lima MVBT, Dias RM, Oliveira FA. Morphology of growth by random walk deposition. Phys A. (2001) 295:209. doi: 10.1016/S0378-4371(01)00075-9

CrossRef Full Text | Google Scholar

131. Schmittbuhl J, Chambon G, Hansen A, Bouchon M. Are stress distributions along faults the signature of asperity squeeze? Geophys Res Lett. (2006) 33:L13307. doi: 10.1029/2006GL025952

CrossRef Full Text | Google Scholar

132. Horowitz CM, Monetti RA, Albano EV. Competitive growth model involving random deposition and random deposition with surface relaxation. Phys Rev E. (2001) 63:066132. doi: 10.1103/PhysRevE.63.066132

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Henkel M, Durang X. Spherical model of growing interfaces. J Stat Mech Theory Exp. (2015) 2015:P05022. doi: 10.1088/1742-5468/2015/05/p05022

CrossRef Full Text | Google Scholar

134. Hairer M. Solving the KPZ equation. Ann Math. (2013) 178:559–664. doi: 10.4007/annals.2013.178.2.4

CrossRef Full Text | Google Scholar

135. Sasamoto T, Spohn H. One-dimensional kardar-parisi-zhang Equation: an exact solution and its Universality. Phys Rev Lett. (2010) 104:230602. doi: 10.1103/PhysRevLett.104.230602

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Kardar M. (1985). Roughening by impurities at finite temperatures. Phys. Rev. Lett. 55:2923. doi: 10.1103/PhysRevLett.55.2923

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Bertini L, Giacomin G. Stochastic Burgers and KPZ equations from particle systems. Commun Math Phys. (1997) 183:571–607. doi: 10.1007/s002200050044

CrossRef Full Text | Google Scholar

138. Spitzer F. Interaction of Markov processes. Adv Math. (1970) 5:246–90. doi: 10.1016/0001-8708(70)90034-4

CrossRef Full Text

139. Ódor G, Liedke B, Heinig KH. Directed d-mer diffusion describing the Kardar-Parisi-Zhang-type surface growth. Phys Rev E. (2010) 81:031112. doi: 10.1103/PhysRevE.81.031112

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Myllys M, Maunuksela J, Alava M, Ala-Nissila T, Merikoski J, Timonen J. Kinetic roughening in slow combustion of paper. Phys Rev E. (2001) 64:036101. doi: 10.1103/PhysRevE.64.036101

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Myllys M, Maunuksela J, Merikoski J, Timonen J, Horvath V, Ha M, et al. Effect of a columnar defect on the shape of slow-combustion fronts. Phys Rev E. (2003) 68:051103. doi: 10.1103/PhysRevE.68.051103

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Merikoski J, Maunuksela J, Myllys M, Timonen J, Alava MJ. Temporal and spatial persistence of combustion fronts in paper. Phys Rev Lett. (2003) 90:24501. doi: 10.1103/PhysRevLett.90.024501

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Csahók Z, Vicsek T. Kinetic roughening in a model of sedimentation of granular materials. Phys Rev A. (1992) 46:4577–81. doi: 10.1103/PhysRevA.46.4577

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Ben-Jacob E, Schochet O, Tenenbaum A, Cohen I, Czirk A, Vicsek T. Generic modelling of cooperative growth patterns in bacterial colonies. Nature (1994) 368:46–9. doi: 10.1038/368046a0

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Matsushita M, Fujikawa H. Diffusion-limited growth in bacterial colony formation. Physica A. (1990) 168:498–506. doi: 10.1016/0378-4371(90)90402-E

CrossRef Full Text | Google Scholar

146. Takeuchi KA, Sano M, Sasamoto T, Spohn H. Growing interfaces uncover universal fluctuations behind scale invariance. Sci Rep. (2011) 1:34. doi: 10.1038/srep00034

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Takeuchi KA, Sano M. Evidence for geometry-dependent universal fluctuations of the Kardar-Parisi-Zhang interfaces in liquid-crystal turbulence. J Stat Phys. (2012) 147:853–90. doi: 10.1007/s10955-012-0503-0

CrossRef Full Text | Google Scholar

148. Takeuchi KA. Crossover from growing to stationary interfaces in the Kardar-Parisi-Zhang class. Phys Rev Lett. (2013) 110:210604. doi: 10.1103/PhysRevLett.110.210604

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Almeida RAL, Ferreira SO, Ferraz I, Oliveira TJ. Initial pseudo-steady state & asymptotic KPZ universality in semiconductor on polymer deposition. Sci Rep. (2017) 7:3773. doi: 10.1038/s41598-017-03843-1

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Mello BA, Chaves AS, Oliveira FA. Discrete atomistic model to simulate etching of a crystalline solid. Phys Rev E. (2001) 63:041113. doi: 10.1103/PhysRevE.63.041113

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Aarão Reis F. Dynamic transition in etching with poisoning. Phys Rev E. (2003) 68:041602. doi: 10.1103/PhysRevE.68.041602

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Aarão Reis F. Universality in two-dimensional Kardar-Parisi-Zhang growth. Phys Rev E. (2004) 69:021610. doi: 10.1103/PhysRevE.69.021610

CrossRef Full Text | Google Scholar

153. Aarão Reis FDA. Numerical study of roughness distributions in nonlinear models of interface growth. Phys Rev E. (2005) 72:032601. doi: 10.1103/PhysRevE.72.032601

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Oliveira TJ, Aarão Reis FDA. Maximal- and minimal-height distributions of fluctuating interfaces. Phys Rev E. (2008) 77:041605. doi: 10.1103/PhysRevE.77.041605

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Tang G, Xun Z, Wen R, Han K, Xia H, Hao D, et al. Discrete growth models on deterministic fractal substrate. Phys A. (2010) 389:4552–7. doi: 10.1016/j.physa.2010.06.041

CrossRef Full Text | Google Scholar

156. Xun Z, Zhang Y, Li Y, Xia H, Hao D, Tang G. Dynamic scaling behaviors of the discrete growth models on fractal substrates. J Stat Mech Theory Exp. (2012) 2012:P10014. doi: 10.1088/1742-5468/2012/10/P10014

CrossRef Full Text | Google Scholar

157. Rodrigues EA, Mello BA, Oliveira FA. Growth exponents of the etching model in high dimensions. J Phys A. (2015) 48:35001–12. doi: 10.1088/1751-8113/48/3/035001

CrossRef Full Text | Google Scholar

158. Mello BA. A random rule model of surface growth. Physica A. (2015) 419:762–7. doi: 10.1016/j.physa.2014.10.064

CrossRef Full Text | Google Scholar

159. Alves WS, Rodrigues EA, Fernandes HA, Mello BA, Oliveira FA, Costa IVL. Analysis of etching at a solid-solid interface. Phys Rev E. (2016) 94:042119. doi: 10.1103/PhysRevE.94.042119

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Carrasco ISS, Oliveira TJ. Universality and dependence on initial conditions in the class of the nonlinear molecular beam epitaxy equation. Phys Rev E. (2016) 94:050801. doi: 10.1103/PhysRevE.94.050801

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Carrasco ISS, Oliveira TJ. Kardar-Parisi-Zhang growth on one-dimensional decreasing substrates. Phys Rev E. (2018) 98:010102. doi: 10.1103/PhysRevE.98.010102

PubMed Abstract | CrossRef Full Text | Google Scholar

162. Henkel M. From dynamical scaling to local scale-invariance: a tutorial. Eur Phys J Spec Top. (2017) 226:605–25. doi: 10.1140/epjst/e2016-60336-5

CrossRef Full Text | Google Scholar

163. Henkel M, Noh JD, Pleimling M. Phenomenology of aging in the Kardar-Parisi-Zhang equation. Phys Rev E. (2012) 85:030102. doi: 10.1103/PhysRevE.85.030102

PubMed Abstract | CrossRef Full Text | Google Scholar

164. Kelling J, Ódor G, Gemming S. Local scale-invariance of the 2+1 dimensional Kardar–Parisi–Zhang model. J Phys A. (2017) 50:12LT01. doi: 10.1088/1751-8121/aa5d87

CrossRef Full Text | Google Scholar

165. Wio HS, Revelli JA, Deza RR, Escudero C, de La Lama MS. Discretization-related issues in the Kardar-Parisi-Zhang equation: consistency, Galilean-invariance violation, and fluctuation-dissipation relation. Phys Rev E. (2010) 81:066706. doi: 10.1103/PhysRevE.81.066706

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Wio HS, Rodríguez MA, Gallego R, Revelli JA, Alés A, Deza RR. d-Dimensional KPZ equation as a stochastic gradient flow in an evolving landscape: interpretation and time evolution of its generating functional. Front Phys. (2017) 4:52. doi: 10.3389/fphy.2016.00052

CrossRef Full Text | Google Scholar

167. Colaiori F, Moore M. Upper critical dimension, dynamic exponent, and scaling functions in the mode-coupling theory for the Kardar-Parisi-Zhang equation. Phys Rev Lett. (2001) 86:3946. doi: 10.1103/PhysRevLett.86.3946

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Schwartz M, Perlsman E. Upper critical dimension of the Kardar-Parisi-Zhang equation. Phys Rev E. (2012) 85:050103. doi: 10.1103/PhysRevE.85.050103

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Lam CH, Shin FG. Improved discretization of the Kardar-Parisi-Zhang equation. Phys Rev E. (1998) 58:5592. doi: 10.1103/PhysRevE.58.5592

CrossRef Full Text | Google Scholar

170. Xu Z, Han H, Wu X. Numerical method for the deterministic Kardar-Parisi-Zhang equation in unbounded domains. Commun Comput Phys. (2006) 1:479–93.

Google Scholar

171. Halpin-Healy T, Takeuchi KA. A KPZ cocktail-shaken, not stirred… J Stat Phys. (2015) 160:794–814. doi: 10.1007/s10955-015-1282-1

CrossRef Full Text | Google Scholar

172. Torres MF, Buceta RC. Numerical integration of KPZ equation with restrictions. JStat Mech Theory Exp. (2018) 2018:033208. doi: 10.1088/1742-5468/aab1b3

CrossRef Full Text | Google Scholar

173. Kelling J, Ódor G, Gemming S. Dynamical universality classes of simple growth and lattice gas models. J Phys A. (2017) 51:035003. doi: 10.1088/1751-8121/aa97f3

CrossRef Full Text | Google Scholar

174. Předota M, Kotrla M. Stochastic equations for simple discrete models of epitaxial growth. Phys Rev E. (1996) 54:3933–42. doi: 10.1103/PhysRevE.54.3933

PubMed Abstract | CrossRef Full Text | Google Scholar

175. Chua ALS, Haselwandter CA, Baggio C, Vvedensky DD. Langevin equations for fluctuating surfaces. Phys Rev E. (2005) 72:051103. doi: 10.1103/PhysRevE.72.051103

PubMed Abstract | CrossRef Full Text | Google Scholar

176. Buceta RC, Hansmann D, von Haeften B. Revisiting random deposition with surface relaxation: approaches from growth rules to the Edwards-Wilkinson equation. J Stat Mech Theory Exp. (2014) 2014:p12028. doi: 10.1088/1742-5468/2014/12/P12028

CrossRef Full Text | Google Scholar

177. Prähofer M, Spohn H. Universal distributions for growth processes in 1 + 1 dimensions and random matrices. Phys Rev Lett. (2000) 84:4882–5. doi: 10.1103/PhysRevLett.84.4882

PubMed Abstract | CrossRef Full Text | Google Scholar

178. Johansson K. Shape fluctuations and random matrices. Commun Math Phys. (2000) 209:437–76. doi: 10.1007/s002200050027

CrossRef Full Text | Google Scholar

179. Oliveira TJ, Alves SG, Ferreira SC. Kardar-Parisi-Zhang universality class in (2+1) dimensions: universal geometry-dependent distributions and finite-time corrections. Phys Rev E. (2013) 87:040102. doi: 10.1103/PhysRevE.87.040102

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Alves SG, Oliveira TJ, Ferreira SC. Non-universal parameters, corrections and universality in Kardar–Parisi–Zhang growth. J Stat Mech Theory Exp. (2013) 2013:P05007. doi: 10.1088/1742-5468/2013/05/P05007

CrossRef Full Text | Google Scholar

181. Almeida RAL, Ferreira SO, Oliveira TJ, Aarão Reis FDA. Universal fluctuations in the growth of semiconductor thin films. Phys Rev B. (2014) 89:045309. doi: 10.1103/PhysRevB.89.045309

CrossRef Full Text | Google Scholar

182. Halpin-Healy T, Zhang YC. Kinetic roughening phenomena, stochastic growth, directed polymers and all that. Aspects of multidisciplinary statistical mechanics. Phys Rep. (1995) 254:215–414. doi: 10.1016/0370-1573(94)00087-J

CrossRef Full Text | Google Scholar

183. Haselwandter CA, Vvedensky DD. Scaling of ballistic deposition from a Langevin equation. Phys Rev E. (2006) 73:040101. doi: 10.1103/PhysRevE.73.040101

PubMed Abstract | CrossRef Full Text | Google Scholar

184. Haselwandter CA, Vvedensky DD. Renormalization of stochastic lattice models: Epitaxial surfaces. Phys Rev E. (2008) 77:061129. doi: 10.1103/PhysRevE.77.061129

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Silveira FA, Aarão Reis FDA. Langevin equations for competitive growth models. Phys Rev E. (2012) 85:011601. doi: 10.1103/PhysRevE.85.011601

PubMed Abstract | CrossRef Full Text | Google Scholar

186. Alcaraz FC, Bariev RZ. Exact solution of the asymmetric exclusion model with particles of arbitrary size. Phys Rev E. (1999) 60:79. doi: 10.1103/PhysRevE.60.79

PubMed Abstract | CrossRef Full Text | Google Scholar

187. Meakin P. The growth of rough surfaces and interfaces. Phys Rep. (1993) 235:189–289. doi: 10.1016/0370-1573(93)90047-H

CrossRef Full Text | Google Scholar

188. Krug J. Origins of scale invariance in growth processes. Adv Phys. (1997) 46:139–282. doi: 10.1080/00018739700101498

CrossRef Full Text | Google Scholar

189. Ben-Avraham D, Havlin S. Diffusion and Reactions in Fractals and Disordered Systems. Cambridge, MA: Cambridge University Press (2000).

Google Scholar

190. Abad E, Masser T, Ben-Avraham D. Lattice kinetics of diffusion-limited coalescence and annihilation with sources. J Phys A Math Gen. (2002) 35:1483. doi: 10.1088/0305-4470/35/7/301

CrossRef Full Text | Google Scholar

191. Shapoval D, Dudka M, Durang X, Henkel M. Cross-over between diffusion-limited and reaction-limited regimes in the coagulation-diffusion process. J Phys A Math Theor. (2018) 51:425002. doi: 10.1088/1751-8121/aadd53

CrossRef Full Text | Google Scholar

192. Doering CR, Ben-Avraham D. Diffusion-limited coagulation in the presence of particle input: exact results in one dimension. Phys Rev Lett. (1989) 62:2563. doi: 10.1103/PhysRevLett.62.2563

PubMed Abstract | CrossRef Full Text | Google Scholar

193. Krebs K, Pfannmüller MP, Wehefritz B, Hinrichsen H. Finite-size scaling studies of one-dimensional reaction-diffusion systems. Part I. Analytical results. J Stat Phys. (1995) 78:1429–70. doi: 10.1007/BF02180138

CrossRef Full Text | Google Scholar

194. Simon H. Concentration for one and two-species one-dimensional reaction-diffusion systems. J Phys A Math Gen. (1995) 28:6585. doi: 10.1088/0305-4470/28/23/013

CrossRef Full Text | Google Scholar

195. Evans MR, Majumdar SN. Diffusion with stochastic resetting. Phys Rev Lett. (2011) 106:160601. doi: 10.1103/PhysRevLett.106.160601

PubMed Abstract | CrossRef Full Text | Google Scholar

196. Evans MR, Majumdar SN. Diffusion with resetting in arbitrary spatial dimension. J Phys A Math Theor. (2014) 47:285001. doi: 10.1088/1751-8113/47/28/285001

CrossRef Full Text | Google Scholar

197. Durang X, Henkel M, Park H. The statistical mechanics of the coagulation–diffusion process with a stochastic reset. J Phys A Math Theor. (2014) 47:045002. doi: 10.1088/1751-8113/47/4/045002

CrossRef Full Text | Google Scholar

198. Hodge IM. Physical aging in polymer glasses. Science (1995) 267:1945–7. doi: 10.1126/science.267.5206.1945

PubMed Abstract | CrossRef Full Text | Google Scholar