Skyrmions and Antiskyrmions in Quasi-Two-Dimensional Magnets

A stable skyrmion, representing the smallest realizable magnetic texture, could be an ideal element for ultra-dense magnetic memories. Here, we review recent progress in the field of skyrmionics, which is concerned with studies of tiny whirls of magnetic configurations for novel memory and logic applications, with a particular emphasis on antiskyrmions. Magnetic antiskyrmions represent analogs of skyrmions with opposite topological charge. Just like skyrmions, antiskyrmions can be stabilized by the Dzyaloshinskii-Moriya interaction, as has been demonstrated in a recent experiment. Here, we emphasize differences between skyrmions and antiskyrmions, e.g., in the context of the topological Hall effect, skyrmion Hall effect, as well as nucleation and stability. Recent progress suggests that antiskyrmions can be potentially useful for many device applications. Antiskyrmions offer advantages over skyrmions as they can be driven without the Hall-like motion, offer increased stability due to dipolar interactions, and can be realized above room temperature.

1. Introduction

A magnetic skyrmion is a non-collinear configuration of magnetic moments with a whirling magnetic structure (see Figure 1). Magnetic skyrmions represent a (2+1)-dimensional analog of the Skyrme model [1], which is a (3+1)-dimensional theory. Thus, magnetic skyrmions are often referred to as baby-skyrmions. From a topological point of view, a magnetic skyrmion is described by an integer invariant, referred to as topological charge, that arises in the map from the physical two-dimensional space to the target space S₂. The formula for topological charge is:

$\begin{array}{ll}Q=\frac{1}{4\pi }\int d^{2}r({\partial }_x\text{m}\times {\partial }_y\text{m})·\text{m},& (1)\end{array}$

where m is a unit vector pointing in the direction of the magnetization. The topological charge describes how many times magnetic moments wrap around a unit sphere in the mapping (see Figure 1). Erasing a skyrmion requires globally modifying the system and, as a result, skyrmions possess topological protection. Initially, magnetic skyrmions of Bloch type (see Figure 1) [2–5] were discovered in chiral B20 compounds such as MnSi, FeGe, and Fe_1−xCo_xSi in which spin-orbit interactions and the absence of the center of inversion lead to appearance of the Dzyaloshinskii-Moriya interaction (DMI) [6, 7]. Sufficiently strong DMI can then lead to the formation of isolated skyrmions or even skyrmion lattices.

FIGURE 1

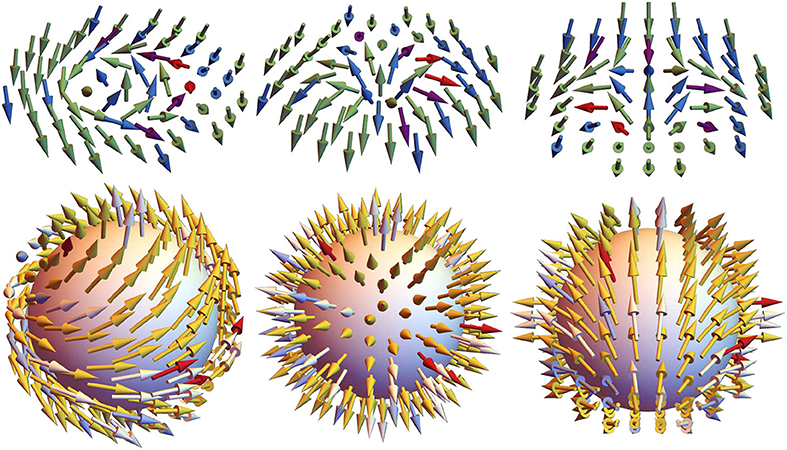
Figure 1. (Top) Bloch (left) and Néel (middle) skyrmions with topological charge Q = 1 and polarity p = 1. Antiskyrmion (right) with topological charge Q = −1 and p = 1. (Bottom) For Néel skyrmion (left), Bloch skyrmion (middle), and antiskyrmion (right) the moments wrap around a unit sphere upon application of stereographic projection.

Skyrmions stabilized by DMI are commonly referred to as Bloch- and Néel-type skyrmions (see Figure 1). Helicity and polarity are also used to describe skyrmions. Helicity can be defined as the angle of the global rotation around the z-axis that relates various skyrmions to the Néel skyrmion. For the Néel skyrmion, helicity is zero. Polarity describes whether the magnetization points in the positive (p = 1) or negative (p = −1) z-direction at the center of the skyrmion [8]. For Bloch and Néel skyrmions, the topological charge and polarity are equal (Q = p). The difference in helicity distinguishes Bloch and Néel skyrmions from one another. On the other hand, magnetic textures stabilized by DMI can also have opposite topological charge and polarity (Q = −p). Such magnetic textures are referred to as antiskyrmions. Antiskyrmions (see Figure 1) can be stabilized by bulk DMI with lower symmetry as was first predicted [9, 10] and later realized experimentally at room temperatures in Heusler compounds with D_2d symmetry [11]. It has also been predicted that interfacial DMI with C_2v symmetry can lead to formation of antiskyrmions in ultrathin magnetic films [12, 13]. In general, various types of skyrmions and antiskyrmions, as shown in Figure 3, can be stabilized by changing the form of DMI tensor [12]. Anisotropic interfacial DMI with C_2v symmetry has recently been realized in epitaxial Au/Co/W magnetic films [14].

Microscopically, DMI arises when the interaction of two magnetic atoms is mediated by a non-magnetic atom via the superexchange or double-exchange mechanisms (see Figure 2). In the absence of an inversion center, a non-collinear configuration of magnetic moments is preferred by DMI energy:

$\begin{array}{ll}{H}_{DMI}={{D}}_{12}·({\text{S}}_1\times {\text{S}}_2),& (2)\end{array}$

where S₁ and S₂ describe the spins and the DMI vector ${{D}}_{12}\propto {\text{r}}_1\times {\text{r}}_2$ (see Figure 2). The strength of DMI is proportional to the strength of the spin-orbit interaction, which is expected to scale with the fourth power of the atomic number. However, in some cases the particular form of the band structure and/or effects related to charge transfer can influence the strength of the spin-orbit interaction. Particularly strong spin-orbit interaction and DMI can arise at interfaces between magnetic films and non-magnetic metals where the 3d orbitals of magnetic atoms interact with 5d orbitals of the heavy metal [15]. Néel type-skyrmions stabilized by interfacial DMI have been obtained at low temperatures in epitaxially grown Fe and PdFe magnetic layers on Ir [16, 17]. Another approach is to stack magnetic and non-magnetic layers in such a way that additive interfacial DMI leads to the formation of Néel skyrmions. Such an approach leads to the formation of room temperature skyrmions in magnetic layers (e.g., Co) sandwiched between two different non-magnetic layers (e.g., Ir and Pt) [18–21].

FIGURE 2

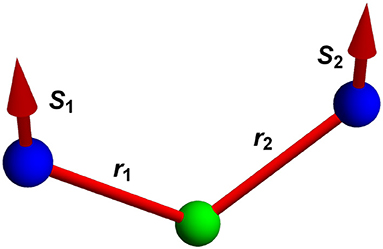
Figure 2. Interaction between two neighboring spins is mediated by the non-magnetic atom. The direction of DMI vector resulting from such interaction is defined by the bond vectors, i.e., ${{D}}_{12}\propto {\text{r}}_1\times {\text{r}}_2$.

Non-collinear magnetic textures can also arise due to dipolar interactions in the form of magnetic bubbles. Compared to skyrmions, magnetic bubbles have larger size and no definite chirality. Thus, antiskyrmions can be realized in systems with dipolar interactions [22]. Magnetic skyrmion bubbles are similar to magnetic bubbles but have definite chirality induced by DMI [23–25]. Skyrmion-like structures can be also realized in systems without DMI [26–28], e.g., it has been predicted that skyrmions of both chiralities can be stabilized in lattices with frustrated exchange interactions [29–31].

2. Description of Skyrmions and Antiskyrmions

Magnetic skyrmions in thin magnetic films can be well-understood by considering a continuous model with the free energy density written for a two-dimensional ferromagnet well below the Curie temperature:

$\begin{array}{ll}{F}=A{({\partial }_i\text{m})}^2-K{m}_z^2-H{m}_z+{\text{D}}_j·({\partial }_j\text{m}\times \text{m}),& (3)\end{array}$

where the free energy is $F=\int d^{2}r{F}$, we assume summation over repeated index i, j = x, y, and m is a unit vector along the magnetization direction. The first term in Equation (3) describes isotropic exchange with exchange stiffness A, the second term describes uniaxial anisotropy with strength K, the third term describes the Zeeman energy due to the external magnetic field H_e, H ≡ μ₀H_eM where M is the magnetization, and the last term corresponds to DMI described by a general tensor D_ij = (D_j)_i [12], where for a two-dimensional magnet j is limited to x and y. DMI is the most important term in Equation (3) for the formation of magnetic skyrmions. Modest DMI strength favors isolated metastable skyrmions [32], while strong DMI leads to condensation into a skyrmion lattice [33] (see discussion around Equation 5).

The form of the DMI tensor D_ij is determined by the crystallographic symmetry of the system [12]. In particular, non-zero elements of the DMI tensor are determined by relations:

$\begin{array}{ll}{D}_{ij}=(det{\text{R}}^{(\alpha )})R_{il}^{(\alpha )}{R}_{jm}^{(\alpha )}{D}_{lm},& (4)\end{array}$

where R^(α) are generators of the point group corresponding to the crystallographic symmetry, α = 1, 2, …, and the summation over repeated indices l and m is assumed. Note that the constraints on the DMI tensor in Equation (4) can be equivalently expressed via Lifshitz invariants [9, 34, 35].

A system invariant under SO(3) rotations then results in D_ij = Dδ_ij, where δ_ij is the Kronecker delta. Such DMI stabilizes Bloch-type skyrmions (see Figure 1). A system with C_∞v symmetry is invariant under proper and improper rotations around the z axis and allows only two non-zero tensor coefficients D₁₂ = −D₂₁ = D. Such DMI stabilizes Néel-type skyrmions (see Figure 1). Another important example arises for a system invariant under D_2d symmetry, for which again only two non-zero tensor coefficients are allowed, i.e., D₁₂ = D₂₁ = D. The latter case realizes a system with antiskyrmions (see Figure 1). Within a simple model given by Equation (3), all three examples given above are mathematically equivalent as they can be mapped to each other by a global spin rotation/reflection accompanied by an appropriate transformation of the DMI tensor [12]. Since the free energy does not change in such a mapping, one can expect that the same stability diagram will describe the above skyrmions and antiskyrmions (other examples of equivalent skyrmions and antiskyrmions are shown in Figure 3) [12]. This equivalence is no longer valid in the presence of dipolar interactions [36] or more complicated magnetocrystalline anisotropy. In fact, antiskyrmions offer increased stability due to the presence of dipolar interactions [36].

FIGURE 3

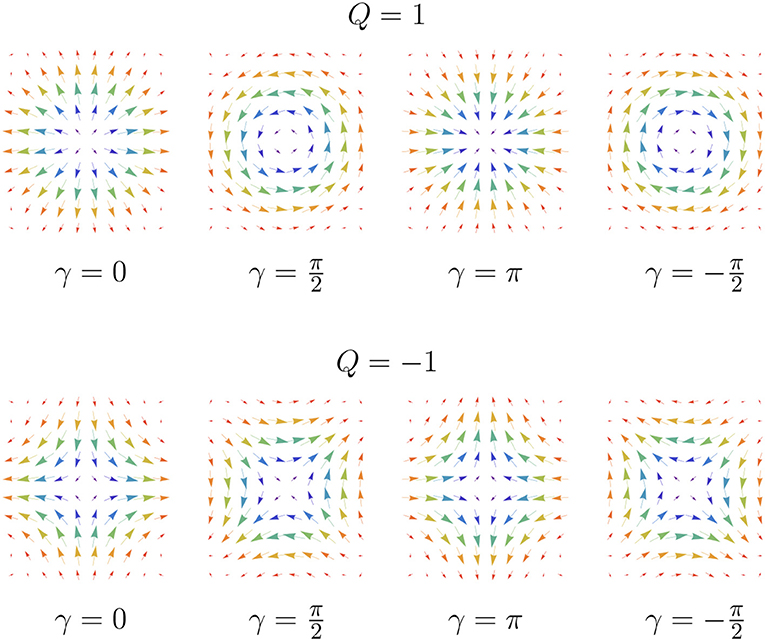
Figure 3. Magnetization configuration of skyrmions (Q = 1) and antiskyrmions (Q = −1) with fixed polarity (p = 1) and varying helicity. The length and direction of the arrows represent the in-plane component of m, and the color indicates m_z. A Néel skyrmion with Q = 1 and helicity γ = 0 corresponds to DMI with C_∞v symmetry. A Bloch skyrmion with Q = 1 and helicity γ = π/2 corresponds to DMI with SO(3) symmetry. Antiskyrmion with Q = −1 and helicity γ = 0 corresponds to DMI with D_2d symmetry. An arbitrary helicity γ can be obtained via the global rotation arounds the z-axis by an angle γ. Antiskyrmions can be obtained from skyrmions by a reflection with respect to a plane perpendicular to the plane of the magnet. Figure is adapted with permission from Güngördu et al. [12].

The parameters A, K, H, and D in the above examples enter the free energy density (3), and they determine whether magnetic skyrmions or antiskyrmions can be present in a system. Minimization of the free energy corresponding to Equation (3) leads to the phase diagram shown in Figure 4, where the phase boundaries separate the cycloid or spiral phase (SP), the hexagonal skyrmion lattice (SkX), the square cell skyrmion lattice (SC), and the ferromagnetic phase (FM) [12]. It is convenient to introduce a critical DMI:

$\begin{array}{ll}{D}_c=4{(AK)}^{1/2}/\pi ,& (5)\end{array}$

corresponding to the strength of DMI at which the formation of Dzyaloshinskii domain walls becomes energetically favorable [37]. In an infinite sample, the transition from isolated skyrmions to a skyrmion lattice or cycloid phase happens in the vicinity of this critical DMI strength [12, 33, 38] (see Figure 4). The magnetic skyrmion size changes substantially as one varies the strength of DMI. At D < D_c, the skyrmion size has been calculated analytically, $R_s\approx \Delta /\sqrt{2(1-D/D_c)}$, where $\Delta =\sqrt{A/K}$ [37]. The effects related to finite temperature and dipolar interactions modify this behavior, especially close to the divergence when R_s → ∞ at D = D_c [20]. At D > D_c, inside the skyrmion lattice phase the skyrmion lattice period can be estimated by the period of the equilibrium helix, L_D = 4πA/D [12, 33, 39]. Note that the ballpark value for the critical DMI is D_c~4 mJ/m² (we use parameters for Co/Pt multilayer [40]). Comparable DMI can be realized in magnetic layers sandwiched between non-magnetic layers. The skyrmion size can range from 8 nm at low temperatures (<30K) [41] to 50 nm at room temperature [18–20].

FIGURE 4

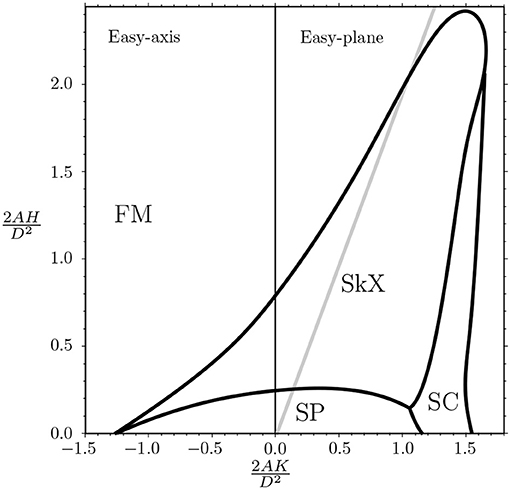
Figure 4. Zero temperature phase diagram for the three cases corresponding to SO(3), C_∞v, and D_2d symmetries is obtained by numerically solving the LLG equation. The axes correspond to the dimensionless magnetic field and dimensionless uniaxial anisotropy parameter (see Equation 3). The gray line separates the aligned and the tilted regions of the FM phase. This phase is taken over by the hexagonal skyrmion lattcie (SkX), spiral (SP), and the square cell skyrmion lattice (SC) phases in the regions defined by the bold lines. Figure is adapted with permission from Güngördu et al. [12].

In principle, the stability of a skyrmion can be hindered by finite temperature. In studies of magnetic memories, this question is usually answered by studying the Arrhenius law of escape from a particular state [42]. Recent studies based on harmonic transition state theory confirm that the life-time of isolated skyrmions is sufficient for realizations of magnetic memories [43].

3. Dynamics of Skyrmions and Antiskyrmions

A design of skyrmion-based memory device [15] closely resembles the race-track memory [44]. One of the challenges is to achieve efficient control of the skyrmion dynamics. Skyrmion dynamics can be induced by spin transfer torques (STT) [45–48], spin-orbit torques (SOT) (often referred to as spin Hall effect torques) [47, 49], voltage-controlled magnetic anisotropy [50], surface acoustic waves [51], temperature gradients [52–55], and other mechanisms.

Here, we discuss (anti)skyrmion dynamics due to STT and SOT induced by in-plane charge currents [31, 56]. These two mechanisms differ as the former vanishes in the absence of magnetic textures while the latter does not. Both mechanisms can be included in the Landau-Lifshitz-Gilbert equation:

$\begin{array}{ll}s(1-\alpha \text{m}\times )\dot{\text{m}}={\text{H}}_{\mathrm{\text{eff}}}\times \text{m}-(1-\beta \text{m}\times )({\text{j}}_s·\nabla )\text{m}+{\tau }_{so},& (6)\end{array}$

where s = M_s/γ is the spin density, M_s is the saturation magnetization, γ is (minus) the gyromagnetic ratio (γ > 0 for electrons), α is the Gilbert damping, H_eff = −δF/δm is the effective field, β is the factor describing non-adiabaticity, j_s is the in-plane spin current proportional to the charge current j, and τ_so is the spin-orbit torque [57]. For the spin Hall contribution, τ_so = (ℏθ_SH/2et_f)m × [m × (ẑ × j)], where θ_SH is the spin Hall angle, e is the electron charge, and t_f is the thickness of the ferromagnetic layer. The Thiele approach [58] applied to Equation (6) leads to equations of motion describing (anti)skyrmion dynamics:

$\begin{array}{ll}(Qẑ\times +\alpha \widehat{\eta })\text{v}=\text{F},& (7)\end{array}$

where $\widehat{\eta }$ is the damping dyadic tensor and F = F_so+F_st is the total force acting on the (anti)skyrmion due to SOT and STT. The SOT contribution is ${\text{F}}_{so}=\widehat{{B}}·\text{j}$ where the tensor $\widehat{{B}}$ is proportional to the spin Hall angle and is determined by the configuration of the (anti)skyrmion [56, 59]. The STT contribution is ${\text{F}}_{st}=(Qẑ\times +\beta \widehat{\eta }){\text{j}}_s$ [48]. We obtain the (anti)skyrmion velocity in an infinite sample:

$\begin{array}{ll}{v}_x=\frac{F_{y}Q+F_x\alpha \eta }{Q^2+{\alpha }^2{\eta }^2},v_y=\frac{-F_{x}Q+F_y\alpha \eta }{Q^2+{\alpha }^2{\eta }^2},& (8)\end{array}$

where for typical (anti)skyrmions η is of the order of 1. The velocity in Equation (8) scales as 1/Q. An interesting situation happens in a nanotrack geometry close to the edge. Due to the edge repulsion, an additional force term appears in Equation (8), v_y = 0, and the (anti)skyrmion velocity becomes v_x = F_x/(αη). As a result, a large (anti)skyrmion velocity is possible close to the edge due to SOT in systems with low Gilbert damping [47, 60].

From Equation (8), it is clear that (anti)skyrmions will move along a current with an additional side motion, resulting in the (anti)skyrmion Hall effect with the Hall angle ${\theta }_H={tan}^{-1}(v_y/v_x)$. Antiskyrmions exhibit an anisotropic Hall angle dependent on the current direction due to SOT, as the tensor $\widehat{{B}}$ becomes anisotropic for an antiskyrmion profile. This is in contrast to the isotropic behavior of skyrmions (the principal values are given by ${{B}}_{xx}=-{{B}}_{yy}$ for antiskyrmions with γ = 0 in Figure 3, and ${{B}}_{xx}={{B}}_{yy}$ for Néel skyrmions) [56]. It is also possible to completely suppress the antiskyrmion Hall effect by properly choosing the direction of the charge current or by coupling skyrmions and antiskyrmions in a multilayer stack [56]. Note that antiferromagnetic skyrmions [61] or synthetic antiferromagnetic skyrmions in antiferromagnetically coupled layers [62, 63] also exhibit a vanishing Hall angle. This behavior can be useful for realizations of magnetic memories.

Skyrmion dynamics consistent with Equation (8) have been observed in magnetic multilayers, e.g., in Pt/Co/Ta [19], Ta/CoFeB/TaO_x [23, 24], (Pt/CoFeB/MgO)₁₅ [64], and (Pt/Co/Ir)₁₀ [65]. SOT and STT contribute to Equation (7) differently. The major component of SOT force pushes skyrmion in the direction of the current flow while the major component of STT pushes skyrmion in the transverse direction. It follows from Equation (8) that in the presence of the edge repulsion the velocity due to SOT, v_x∝F_SOT/α, is expected to be larger than the velocity due to STT, v_x∝F_STT. Theoretical modeling [47] predicts that the velocity due to SOT is 60 m/s for the current 2 × 10¹¹Am⁻². Similar modeling of the motion induced by STT results in much smaller velocity of 8 m/s for the same current. It has also been confirmed experimentally that in a sufficiently large sample the sign of the transverse response is determined by the sign of the spin Hall angle and the topological charge. Some aspects of skyrmion dynamics are still puzzling, i.e., the dependence of the skyrmion Hall angle on the velocity and the dependence of the velocity on the skyrmion size. Variations in the skyrmion Hall angle have been attributed to the presence of pinning sites [66]. In principle, the presence of pinning sites could be problematic for realizations of magnetic memories [67]. Nevertheless, the presence of the skyrmion Magnus force induced by pinning sites results in significant reduction of the depinning threshold current density [68, 66], e.g., by several orders of magnitude if compared to domain wall dynamics. Experimentally, the depinning threshold current density can be as low as 10⁶Am⁻² [46].

4. Writing, Erasing, and Detecting

Interfacial skyrmions in Fe on Ir have been controllably written and erased by STT induced by an STM tip at 4.2 K in the presence of high magnetic fields [17]. For practical applications it is necessary to write and erase skyrmions at room temperature in the presence of weak or, preferably, no magnetic fields. STT has been demonstrated to generate skyrmions in a confined geometry of a Pt/Co nanodot [47]. A SOT mechanism in which a pair of domain walls is converted into a skyrmion has been demonstrated numerically to require relatively large current densities [69]. At room temperature, SOT has been used to create elongated chiral domains that, under application of inhomogeneous current, break into skyrmion bubbles [23]. In this experiment, the inhomogeneous current of relatively low magnitude, 5 × 10⁸ Am⁻², blows chiral domains into bubbles in analogy with how the Rayleigh-Plateau instabilities lead to formation of bubbles in fluid flows. This process has been reproduced by micromagnetic simulations [70]. Detailed analysis of topological charge density revealed that in the process of creating a skyrmion by SOT an unstable antiskyrmion can also be created for a period of time comparable to 0.5 ns [71]. As an antiskyrmion is not stable in the presence of interfacial DMI (C_∞v case), it eventually annihilates due to the presence of the Gilbert damping [72]. Thus, detailed studies of antiskyrmions can help in realizing new ways of writing and erasing skyrmions. Generation of skyrmions by charge currents has also been demonstrated for magnetic multilayer stacks [65], as well as for symmetric bilayers hosting pairs of skyrmions with opposite chirality [60]. Other approaches include laser-induced generation of topological defects [73, 74]. The feasibility of such an approach has been confirmed theoretically [75–78].

For device application, it is preferable to detect the presence of a skyrmion electrically. Several transport techniques have been suggested. Non-collinear magnetoresistance can be used to detect a skyrmion where changes in the band structure induced by non-collinear moments are detected by STM [79]. However, only non-collinearity is being detected and no information about the topological structure of a skyrmion is obtained. Measuring the z-component of magnetization is possible by employing the anomalous Hall effect [80]. This technique has been used to detect a single skyrmion [81]. Measurement of the topological Hall effect can directly reveal the topological nature of a skyrmion as the effect originates in the fictitious magnetic field proportional to the topological charge. The presence of skyrmions has been detected by measurements of the topological Hall effect in non-centrosymmetric bulk materials in the B20 group [82, 83]. In principle, antiskyrmions [11] should also exhibit the topological Hall effect but with the reversed sign due to the opposite topological charge. On the other hand, in magnetic multilayers the topological Hall effect is expected to be much smaller than the anomalous Hall contribution [81].

5. Conclusions and Outlook

In this article, we review recent progress in the field of skyrmionics—a field concerned with studies of tiny whirls of magnetic configurations for novel memory and logic applications. A particular emphasis has been given to antiskyrmions. These, similar to skyrmions, are particle-like structures with topological protection. Compared to skyrmions, antiskyrmions have opposite topological charge and are anisotropic. Recent experimental observation of antiskyrmions at room temperature [11] encourages further studies of transport and dynamical properties such as the topological Hall effect, antiskyrmion Hall effect, antiskyrmion nucleation and stability, and others. On the other hand, realization of antiskyrmions requires careful material engineering which should also be addressed in future studies. All in all, antiskyrmions offer some advantages over skyrmions as they can be driven without the Hall-like motion, offer increased stability due to dipolar interactions, and can be realized above room temperature. A possibility to annihilate a skyrmion-antiskyrmion pair can lead to new concepts of logic devices [84]. Reservoir computing is another application in which skyrmions could prove highly useful. The anisotropic magnetoresistance (AMR) and the motion and deformation of magnetic texture caused by the interaction of a voltage-induced electric current and a single skyrmion can provide a non-linear relationship between voltage and current, which is a key ingredient for reservoir computing [85]. Skyrmion fabrics, which may include skyrmions, antiskyrmions, skyrmion crystal structure, and domain walls, represent a potential way to implement skyrmion-based reservoir computing since they fulfill the requirements of an Echo State Network (ESN) [86]. It is expected that, similar to skyrmions, antiskyrmions can potentially result in new device concepts for memory and neuromorphic computing applications [85].

Author Contributions

AK conceived the project presented in this mini review article. AK and SS prepared the manuscript.

Funding

This work was supported by the DOE Early Career Award DE-SC0014189.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The topic editors are acknowledged for supporting this open-access publication.

References

1. Skyrme THR. A non-linear field theory. Proc R Soc Lond. (1961) 260:127–38.

Google Scholar

2. Bogdanov A, Hubert A. Thermodynamically stable magnetic vortex states in magnetic crystals. J Magn Magn Mater. (1994) 138:255–69.

Google Scholar

3. Rößler UK, Bogdanov AN, Pfleiderer C. Spontaneous skyrmion ground states in magnetic metals. Nature (2006) 442:797–801. doi: 10.1038/nature05056

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion Lattice in a Chiral Magnet. Science (2009) 323:915. doi: 10.1126/science.1166767

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yu XZ, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y, et al. Real-space observation of a two-dimensional skyrmion crystal. Nature (2010) 465:901–4. doi: 10.1038/nature09124

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dzyaloshinsky I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J Phys Chem Solids (1958) 4:241–55.

Google Scholar

7. Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev. (1960) 120:91–8.

Google Scholar

8. Zheng F, Li H, Wang S, Song D, Jin C, Wei W, et al. Direct imaging of a zero-field target skyrmion and its polarity switch in a chiral magnetic nanodisk. Phys Rev Lett. (2017) 119:197205. doi: 10.1103/PhysRevLett.119.197205

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bogdanov AN, Yablonskii D. Thermodynamically stable “vortices” in magnetically ordered crystals. the mixed state of magnets. J Exp Theor Phys. (1989) 95:178.

Google Scholar

10. Bogdanov AN, Rößler UK, Wolf M, Müller KH. Magnetic structures and reorientation transitions in noncentrosymmetric uniaxial antiferromagnets. Phys Rev B (2002) 66:214410. doi: 10.1103/PhysRevB.66.214410

CrossRef Full Text | Google Scholar

11. Nayak AK, Kumar V, Ma T, Werner P, Pippel E, Sahoo R, et al. Magnetic antiskyrmions above room temperature in tetragonal Heusler materials. Nature (2017) 548:561–6. doi: 10.1038/nature23466

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Güngördü U, Nepal R, Tretiakov OA, Belashchenko K, Kovalev AA. Stability of skyrmion lattices and symmetries of quasi-two-dimensional chiral magnets. Phys Rev B (2016) 93:064428. doi: 10.1103/PhysRevB.93.064428

CrossRef Full Text | Google Scholar

13. Hoffmann M, Zimmermann B, Müller GP, Schürhoff D, Kiselev NS, Melcher C, et al. Antiskyrmions stabilized at interfaces by anisotropic Dzyaloshinskii-Moriya interactions. Nat Commun. (2017) 8:308. doi: 10.1038/s41467-017-00313-0

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Camosi L, Rohart S, Fruchart O, Pizzini S, Belmeguenai M, Roussigné Y, et al. Anisotropic Dzyaloshinskii-Moriya interaction in ultrathin epitaxial Au/Co/W(110). Phys Rev B (2017) 95:214422. doi: 10.1103/PhysRevB.95.214422

CrossRef Full Text | Google Scholar

15. Fert A, Cros V, Sampaio J. Skyrmions on the track. Nat Nanotechnol. (2013) 8:152–6. doi: 10.1038/nnano.2013.29

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat Phys. (2011) 7:713–8. doi: 10.1038/nphys2045

CrossRef Full Text | Google Scholar

17. Romming N, Hanneken C, Menzel M, Bickel JE, Wolter B, von Bergmann K, et al. Writing and deleting single magnetic Skyrmions. Science (2013) 341:636–9. doi: 10.1126/science.1240573

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Moreau-Luchaire C, Moutafis C, Reyren N, Sampaio J, Vaz CAF, van Horne N, et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat Nanotechnol. (2016) 11:444–8. doi: 10.1038/nnano.2015.313

CrossRef Full Text | Google Scholar

19. Woo S, Litzius K, Krüger B, Im MY, Caretta L, Richter K, et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat Mater. (2016) 15:501–6. doi: 10.1038/nmat4593

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Boulle O, Vogel J, Yang H, Pizzini S, de Souza Chaves D, Locatelli A, et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat Nanotechnol. (2016) 11:449–54. doi: 10.1038/nnano.2015.315

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Soumyanarayanan A, Raju M, Gonzalez Oyarce AL, Tan AKC, Im MY, Petrović AP, et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat Mater. (2017) 16:898–904. doi: 10.1038/nmat4934

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Koshibae W, Nagaosa N. Theory of antiskyrmions in magnets. Nat Commun. (2016) 7:10542. doi: 10.1038/ncomms10542

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Jiang W, Upadhyaya P, Zhang W, Yu G, Jungfleisch MB, Fradin FY, et al. Blowing magnetic skyrmion bubbles. Science (2015) 349:283–286. doi: 10.1126/science.aaa1442

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jiang W, Zhang X, Yu G, Zhang W, Wang X, Benjamin Jungfleisch M, et al. Direct observation of the skyrmion Hall effect. Nat Phys. (2017) 13:162–9. doi: 10.1038/nphys3883

CrossRef Full Text | Google Scholar

25. Yu G, Upadhyaya P, Shao Q, Wu H, Yin G, Li X, et al. Room-temperature skyrmion shift device for memory application. Nano Lett. (2017) 17:261–8. doi: 10.1021/acs.nanolett.6b04010

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Polyakov AM, Belavin AA. Metastable states of two-dimensional isotropic ferromagnets. JETP Lett. (1975) 22:245–8.

Google Scholar

27. Volovik G, Mineev V. Particle-like solitons in superfluid ³He phases. Sov Phys JETP (1977) 45:1186.

Google Scholar

28. Dzyloshinskii I, Ivanov B. Localized topological solitons in a ferromagnet. JETP Lett. (1979) 29:540.

Google Scholar

29. Okubo T, Chung S, Kawamura H. Multiple-q states and the skyrmion lattice of the triangular-lattice heisenberg antiferromagnet under magnetic fields. Phys Rev Lett. (2012) 108:017206. doi: 10.1103/PhysRevLett.108.017206

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Leonov AO, Mostovoy M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat Commun. (2015) 6:8275. doi: 10.1038/ncomms9275

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhang X, Xia J, Zhou Y, Liu X, Zhang H, Ezawa M. Skyrmion dynamics in a frustrated ferromagnetic film and current-induced helicity locking-unlocking transition. Nat Commun. (2017) 8:1717. doi: 10.1038/s41467-017-01785-w

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Leonov AO, Monchesky TL, Romming N, Kubetzka A, Bogdanov AN, Wiesendanger R. The properties of isolated chiral skyrmions in thin magnetic films. New J Phys. (2016) 18:065003. doi: 10.1088/1367-2630/18/6/065003

CrossRef Full Text | Google Scholar

33. Banerjee S, Rowland J, Erten O, Randeria M. Enhanced stability of skyrmions in two-dimensional chiral magnets with Rashba spin-orbit coupling. Phys Rev X (2014) 4:031045. doi: 10.1103/PhysRevX.4.031045

CrossRef Full Text | Google Scholar

34. Dzyaloshinskii I. Theory of helicoidal structures in antiferromagnets. 1. Nonmetals. Sov Phys JETP (1964) 19:17.

Google Scholar

35. Bak P, Jensen MH. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J Phys C Solid State Phys. (1980) 13:L881–5.

Google Scholar

36. Camosi L, Rougemaille N, Fruchart O, Vogel J, Rohart S. Micromagnetics of antiskyrmions in ultrathin films. Phys Rev B (2018) 97:134404. doi: 10.1103/PhysRevB.97.134404

CrossRef Full Text | Google Scholar

37. Rohart S, Thiaville A. Skyrmion confinement in ultrathin film nanostructures in the presence of Dzyaloshinskii-Moriya interaction. Phys Rev B (2013) 88:184422. doi: 10.1103/PhysRevB.88.184422

CrossRef Full Text | Google Scholar

38. Siemens A, Zhang Y, Hagemeister J, Vedmedenko EY, Wiesendanger R. Minimal radius of magnetic skyrmions: statics and dynamics. New J Phys. (2016) 18:045021. doi: 10.1088/1367-2630/18/4/045021

CrossRef Full Text | Google Scholar

39. McGrouther D, Lamb RJ, Krajnak M, McFadzean S, McVitie S, Stamps RL, et al. Internal structure of hexagonal skyrmion lattices in cubic helimagnets. New J Phys. (2016) 18:095004. doi: 10.1088/1367-2630/18/9/095004

CrossRef Full Text | Google Scholar

40. Miron IM, Moore T, Szambolics H, Buda-Prejbeanu LD, Auffret S, Rodmacq B, et al. Fast current-induced domain-wall motion controlled by the Rashba effect. Nat Mater. (2011) 10:419–23. doi: 10.1038/nmat3020

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Bode M, Heide M, von Bergmann K, Ferriani P, Heinze S, Bihlmayer G, et al. Chiral magnetic order at surfaces driven by inversion asymmetry. Nature (2007) 447:190–3. doi: 10.1038/nature05802

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Langer JS. Statistical theory of the decay of metastable states. Ann Phys. (1969) 54:258–75.

Google Scholar

43. Bessarab PF, Müller GP, Lobanov IS, Rybakov FN, Kiselev NS, Jónsson H, et al. Lifetime of racetrack skyrmions. Sci Rep. (2018) 8:3433. doi: 10.1038/s41598-018-21623-3

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Hayashi M, Thomas L, Moriya R, Rettner C, Parkin SSP. Current-controlled magnetic domain-wall nanowire shift register. Science (2008) 320:209. doi: 10.1126/science.1154587

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Jonietz F, Mühlbauer S, Pfleiderer C, Neubauer A, Münzer W, Bauer A, et al. Spin transfer torques in MnSi at ultralow current densities. Science (2010) 330:1648. doi: 10.1126/science.1195709

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yu XZ, Kanazawa N, Zhang WZ, Nagai T, Hara T, Kimoto K, et al. Skyrmion flow near room temperature in an ultralow current density. Nat Commun. (2012) 3:988. doi: 10.1038/ncomms1990

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Sampaio J, Cros V, Rohart S, Thiaville A, Fert A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat Nanotechnol. (2013) 8:839–44. doi: 10.1038/nnano.2013.210

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Iwasaki J, Mochizuki M, Nagaosa N. Current-induced skyrmion dynamics in constricted geometries. Nat Nanotechnol. (2013) 8:742–7. doi: 10.1038/nnano.2013.176

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Woo S, Song KM, Han HS, Jung MS, Im MY, Lee KS, et al. Spin-orbit torque-driven skyrmion dynamics revealed by time-resolved X-ray microscopy. Nat Commun. (2017) 8:15573. doi: 10.1038/ncomms15573

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kang W, Huang Y, Zheng C, Lv W, Lei N, Zhang Y, et al. Voltage controlled magnetic skyrmion motion for racetrack memory. Sci Rep. (2016) 6:23164. doi: 10.1038/srep23164

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Nepal R, Güngördü U, Kovalev AA. Magnetic skyrmion bubble motion driven by surface acoustic waves. Appl Phys Lett. (2018) 112:112404. doi: 10.1063/1.5013620

CrossRef Full Text | Google Scholar

52. Kong L, Zang J. Dynamics of an insulating skyrmion under a temperature gradient. Phys Rev Lett. (2013) 111:067203. doi: 10.1103/PhysRevLett.111.067203

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Lin SZ, Batista CD, Reichhardt C, Saxena A. ac current generation in chiral magnetic insulators and skyrmion motion induced by the spin seebeck effect. Phys Rev Lett. (2014) 112:187203. doi: 10.1103/PhysRevLett.112.187203

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Kovalev AA. Skyrmionic spin Seebeck effect via dissipative thermomagnonic torques. Phys Rev B (2014) 89:241101. doi: 10.1103/PhysRevB.89.241101

CrossRef Full Text | Google Scholar

55. Mochizuki M, Yu XZ, Seki S, Kanazawa N, Koshibae W, Zang J, et al. Thermally driven ratchet motion of a skyrmion microcrystal and topological magnon Hall effect. Nat Mater. (2014) 13:241–6. doi: 10.1038/nmat3862

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Huang S, Zhou C, Chen G, Shen H, Schmid AK, Liu K, et al. Stabilization and current-induced motion of antiskyrmion in the presence of anisotropic Dzyaloshinskii-Moriya interaction. Phys Rev B (2017) 96:144412. doi: 10.1103/PhysRevB.96.144412

CrossRef Full Text | Google Scholar

57. Brataas A, Kent AD, Ohno H. Current-induced torques in magnetic materials. Nat Mater. (2012) 11:372–81. doi: 10.1038/nmat3311

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Thiele AA. Steady-state motion of magnetic domains. Phys Rev Lett. (1973) 30:230–3. doi: 10.1103/PhysRevLett.30.230

CrossRef Full Text | Google Scholar

59. Tomasello R, Martinez E, Zivieri R, Torres L, Carpentieri M, Finocchio G. A strategy for the design of skyrmion racetrack memories. Sci Rep. (2014) 4:6784. doi: 10.1038/srep06784

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Hrabec A, Sampaio J, Belmeguenai M, Gross I, Weil R, Chérif SM, et al. Current-induced skyrmion generation and dynamics in symmetric bilayers. Nat Commun. (2017) 8:15765. doi: 10.1038/ncomms15765

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Barker J, Tretiakov OA. Static and dynamical properties of antiferromagnetic Skyrmions in the presence of applied current and temperature. Phys Rev Lett. (2016) 116:147203. doi: 10.1103/PhysRevLett.116.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Zhang X, Ezawa M, Zhou Y. Thermally stable magnetic skyrmions in multilayer synthetic antiferromagnetic racetracks. Phys Rev B (2016) 94:064406. doi: 10.1103/PhysRevB.94.064406

CrossRef Full Text | Google Scholar

63. Woo S, Song KM, Zhang X, Zhou Y, Ezawa M, Liu X, et al. Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films. Nat Commun. (2018) 9:959. doi: 10.1038/s41467-018-03378-7

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Litzius K, Lemesh I, Krüger B, Bassirian P, Caretta L, Richter K, et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat Phys. (2017) 13:170–5. doi: 10.1038/nphys4000

CrossRef Full Text | Google Scholar

65. Legrand W, Maccariello D, Reyren N, Garcia K, Moutafis C, Moreau-Luchaire C, et al. Room-temperature current-induced generation and motion of sub-100 nm skyrmions. Nano Lett. (2017) 17:2703–12. doi: 10.1021/acs.nanolett.7b00649

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Reichhardt C, Ray D, Reichhardt CJO. Collective transport properties of driven skyrmions with random disorder. Phys Rev Lett. (2015) 114:217202. doi: 10.1103/PhysRevLett.114.217202

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Gross I, Akhtar W, Hrabec A, Sampaio J, Martínez LJ, Chouaieb S, et al. Skyrmion morphology in ultrathin magnetic films. Phys Rev Mater. 2018 2:024406. doi: 10.1103/PhysRevMaterials.2.024406

CrossRef Full Text

68. Lin SZ, Reichhardt C, Batista CD, Saxena A. Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep. Phys Rev B (2013) 87:214419. doi: 10.1103/PhysRevB.87.214419

CrossRef Full Text | Google Scholar

69. Zhou Y, Ezawa M. A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry. Nat Commun. (2014) 5:4652. doi: 10.1038/ncomms5652

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Lin SZ. Edge instability in a chiral stripe domain under an electric current and skyrmion generation. Phys Rev B (2016) 94:020402. doi: 10.1103/PhysRevB.94.020402

CrossRef Full Text | Google Scholar

71. Liu Y, Yan H, Jia M, Du H, Du A. Topological analysis of spin-torque driven magnetic skyrmion formation. Appl Phys Lett. (2016) 109:102402. doi: 10.1063/1.4962452

CrossRef Full Text | Google Scholar

72. Stier M, Häusler W, Posske T, Gurski G, Thorwart M. Skyrmion-anti-skyrmion pair creation by in-plane currents. Phys Rev Lett. (2017) 118:267203. doi: 10.1103/PhysRevLett.118.267203

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Finazzi M, Savoini M, Khorsand AR, Tsukamoto A, Itoh A, Duò L, et al. Laser-induced magnetic nanostructures with tunable topological properties. Phys Rev Lett. (2013) 110:177205. doi: 10.1103/PhysRevLett.110.177205

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Berruto G, Madan I, Murooka Y, Vanacore GM, Pomarico E, Rajeswari J, et al. Laser-induced skyrmion writing and erasing in an ultrafast cryo-lorentz transmission electron microscope. Phys Rev Lett. (2018) 120:117201. doi: 10.1103/PhysRevLett.120.117201

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Koshibae W, Nagaosa N. Creation of skyrmions and antiskyrmions by local heating. Nat Commun. (2014) 5:5148. doi: 10.1038/ncomms6148

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Fujita H, Sato M. Ultrafast generation of skyrmionic defects with vortex beams: Printing laser profiles on magnets. Phys Rev B (2017) 95:054421. doi: 10.1103/PhysRevB.95.054421

CrossRef Full Text | Google Scholar

77. Fujita H, Sato M. Encoding orbital angular momentum of light in magnets. Phys Rev B (2017) 96:060407. doi: 10.1103/PhysRevB.96.060407

CrossRef Full Text | Google Scholar

78. Yudin D, Gulevich DR, Titov M. Light-induced anisotropic skyrmion and stripe phases in a rashba ferromagnet. Phys Rev Lett. (2017) 119:147202. doi: 10.1103/PhysRevLett.119.147202

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Hanneken C, Otte F, Kubetzka A, Dupé B, Romming N, von Bergmann K, et al. Electrical detection of magnetic skyrmions by tunnelling non-collinear magnetoresistance. Nat Nanotechnol. (2015) 10:1039–42. doi: 10.1038/nnano.2015.218

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Nagaosa N, Sinova J, Onoda S, MacDonald AH, Ong NP. Anomalous hall effect. Rev Mod Phys. (2010) 82:1539–92. doi: 10.1103/RevModPhys.82.1539

CrossRef Full Text | Google Scholar

81. Maccariello D, Legrand W, Reyren N, Garcia K, Bouzehouane K, Collin S, et al. Electrical detection of single magnetic skyrmions in metallic multilayers at room temperature. Nat Nanotechnol. (2018) 13:233–7. doi: 10.1038/s41565-017-0044-4

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Lee M, Kang W, Onose Y, Tokura Y, Ong NP. Unusual hall effect anomaly in MnSi under pressure. Phys Rev Lett. (2009) 102:186601. doi: 10.1103/PhysRevLett.102.186601

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Neubauer A, Pfleiderer C, Binz B, Rosch A, Ritz R, Niklowitz PG, et al. Topological hall effect in the A phase of MnSi. Phys Rev Lett. (2009) 102:186602. doi: 10.1103/PhysRevLett.102.186602

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Zhang X, Ezawa M, Zhou Y. Magnetic skyrmion logic gates: conversion, duplication and merging of skyrmions. Sci Rep. (2015) 5:9400. doi: 10.1038/srep09400

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Prychynenko D, Sitte M, Litzius K, Krüger B, Bourianoff G, Kläui M, et al. Magnetic skyrmion as a nonlinear resistive element: a potential building block for reservoir computing. Phys Rev Appl. (2018) 9:014034. doi: 10.1103/PhysRevApplied.9.014034

CrossRef Full Text | Google Scholar

86. Bourianoff G, Pinna D, Sitte M, Everschor-Sitte K. Potential implementation of reservoir computing models based on magnetic skyrmions. AIP Adv. (2018) 8:055602. doi: 10.1063/1.5006918

CrossRef Full Text | Google Scholar