GTPack: A Mathematica Group Theory Package for Application in Solid-State Physics and Photonics

We present the Mathematica group theory package GTPack providing about 200 additional modules to the standard Mathematica language. The content ranges from basic group theory and representation theory to more applied methods like crystal field theory, tight-binding and plane-wave approaches capable for symmetry based studies in the fields of solid-state physics and photonics. GTPack is freely available via http://GTPack.org. The package is designed to be easily accessible by providing a complete Mathematica-style documentation, an optional input validation and an error strategy. We illustrate the basic framework of the package and show basic examples to present the functionality. Furthermore, we give a complete list of the implemented commands including references for algorithms within the Supplementary Material.

Introduction

Symmetry and symmetry breaking are basic concepts of nature. Thus, arguments based on the symmetry of the considered system play a significant role within almost all branches of physics. Group theory represents the mathematical language to deal with symmetry, since all transformations that leave a physical system invariant (usually described in terms of transformations of algebraic or differential equations) naturally form a group. The application of group theory in physics has a long tradition ranging back to the beginning of the twentieth century [1, 2]. Concentrating on solid-state and condensed matter physics, examples for the application of group theory can be found in the theory of the degeneracy of energy bands [3], color centers, d⁰ magnetism and impurity states [4–6], optical transitions [7], phase transitions, atoms and molecules on surfaces [8], x-ray diffraction and crystallography in Fourier space [9], construction of effective low-energy excitation Hamiltonians [10], the classification of the superconducting states of matter [11–15], and, more recently, topological band theory [16–20] and topological quantum computation [21]. Due to the similarity of the underlying formalism, several concepts can be transferred to the field of photonics, for example, the band theory of photonic crystals [22–24], impurities and defect modes [25], and selection rules and uncoupled modes [26, 27].

In many cases, non-trivial results can be obtained from basic group theoretical information like the characters of the irreducible representations or the Clebsch-Gordan coefficients. In the past decades these information were tabulated in various books (e.g., [28, 29]). A comprehensive and widely used online group theory tool is provided by the Bilbao crystallographic server [30]. The work with printed group theory tables is not suitable for automation and the probability of copying and pasting misprints is high. However, modern computer algebra systems are capable to provide the same information, assumed that the necessary algorithms are implemented. Especially, the computer algebra system GAP (groups, algorithms and programming) [31] represents a powerful program to deal with computationally demanding questions in abstract algebra. Similarly, the computer algebra system Mathematica is well established within the research community. However, a stable group theory package designed for applications in solid-state physics and photonics is not included in the standard version.

The development of the Mathematica group theory package GTPack was designed to fill this gap. The functionality was planned to cover both, an application in active research and an application in university teaching. Therefore a main focus is the development of a user-friendly application, via self-explanatory names for new commands, a comprehensive documentation system and an optional input validation.

The aim of the paper is to report on the initial version of the Mathematica group theory package GTPack which is freely available for academic usage via http://GTPack.org. In the first part of the paper we introduce the main functionality and structure of the package. Afterwards we give general information about the implementation of the commands. In the last part we provide simple examples to illustrate the package. The Supplementary Material contains a full reference of all implemented modules. A more comprehensive guide about applied group theory in connection to GTPack can be found in Hergert and Geilhufe [32].

Functionality and Structure

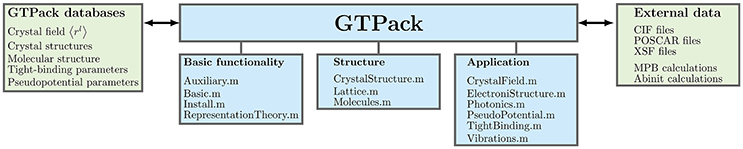
According to the functionality of the modules, GTPack is divided into various subpackages as illustrated in Figure 1. In general, the subpackages can be assembled in three groups, “basic functionality,” “structure,” and “applications.” Subpackages belonging to the class of “basic functionality” are Auxiliary.m, Basic.m, Install.m and RepresentationTheory.m. The package Auxiliary.m contains modules which are needed by GTPack or extend the general Mathematica language. Among others tesseral harmonics (real spherical harmonics) were added and also the Cartesian form of tesseral and spherical harmonics was implemented. Furthermore, the package contains modules for the handling with quaternions, the calculation of Gaunt coefficients, Dirac matrices or SU(2)-rotation matrices, to name but a few. The package Basic.m concentrates on general abstract group theory and, for example, provides modules for the calculation of classes, multiplication tables, left and right cosets and several logical commands to check for groups, Abelian groups, subgroups or invariant subgroups. Modules needed for basic representation theory are contained in the package RepresentationTheory.m. This package comprises the calculation of character tables, handling of irreducible representations, the calculation of Clebsch-Gordan coefficients, etc. Modules for the installation of point and space groups or symmetry elements can be found in Install.m.

FIGURE 1

Figure 1. Subpackage structure of GTPack and interaction with external data.

The second class “structure” comprises of the packages CrystalStructure.m, Lattice.m and Molecules.m. Within CrystalStructure.m, modules for loading, saving and handling of crystal structures can be found. Modules with similar functionality but specialized on molecules are contained within Molecules.m. The construction and manipulation of atomic clusters as well as several commands for dealing with the reciprocal space are summarized in the package Lattice.m.

Next to basic group theory GTPack also contains subpackages for particular applications in solid state physics and photonics. The third class “Applications” contains the subpackages CrystalField.m, ElectronicStructure.m, Photonics.m, PseudoPotential.m, TightBinding.m and Vibrations.m. The crystal field package CrystalField.m is capable of automatically generating crystal field Hamiltonians. Furthermore, it contains the generation of standard operator equivalents like Stevens [33] and Buckmaster-Smith-Thornley [34] operators. GTPack also allows for electronic structure calculations for periodic systems, i.e., crystals, in the framework of the tight-binding and the pseudopotential approximation. Modules to construct tight-binding Hamiltonians are summarized in TightBinding.m and modules for the pseudopotential approximation in PseudoPotential.m. The calculation of band structures, density of states as well as the calculation of a Fermi surface is practically independent of the underlying model Hamiltonian. Therefore such commands are contained within the package ElectronicStructure.m. In the framework of plane-waves it is also possible to calculate the band structure of photonic crystals. The necessary modules for the construction of the master equation for various geometrical objects can be found in the package Photonics.m. Commands for the investigation of phonons or molecular vibrational modes are contained in Vibrations.m.

For various applications it is necessary to incorporate data, for example, tight-binding parameters, crystal field parameters and crystal structures. Therefore, GTPack contains several modules for the creation and handling of databases (cf. Figure 1). Here, special file endings are used, such as *.parm and *.struc. Databases can be easily created, extended and modified by the user. Furthermore, GTPack includes commands for the interaction with external data formats and ab initio software. This concerns the import and export of structural data files *.cif [35] and *.xsf [36] and the output of the programs MIT Photonic Bands - MPB [37]¹. For the future it is intended to implement similar modules for VASP [38] and abinit [39].

Implementation

To distinguish new commands provided by GTPack from the standard Mathematica language and to prevent conflicts with new versions of Mathematica, all GTPack commands are starting with the characters GT (e.g., GTInstallGroup, GTCharacterTable, …). Options are denoted with a suffix GO (e.g., GOVerbose, GOIrepNotation, …). One of the main features of GTPack is the symbolic representation of symmetry elements. Symmetry elements for various standard axes (see Figure 2) are predefined and the respective symbols, such as C3z for a 3-fold rotation about the z-axis are protected. As a standard form they are displayed with subscripts, i.e., C_3z. Internally all symmetry elements are represented using matrices. The conversion between symbols and matrices can be done using GTGetMatrix and GTGetSymbol, respectively. Every module is implemented such that it is capable to handle lists of matrices in arbitrary representations. Depending on the application, GTPack uses a certain standard representation to provide a faithful matrix representation of point groups. Elements of ordinary point groups are represented by 3D rotation matrices of the group O(3). In the special case of planar groups, the standard representation can be chosen to be O(2). Symmetry elements within double groups are represented according to Damhus [41], where elements of groups not containing the inversion are represented by SU(2) matrices and elements of groups containing the inversion are represented by matrices of the direct product group SU(2)⊗S with S = {1, −1}. Additionally, users can also define a group by providing a multiplication table. In this case GTPack automatically installs the provided elements within the multiplication table as new symmetry elements using permutation matrices as faithful representations.

FIGURE 2

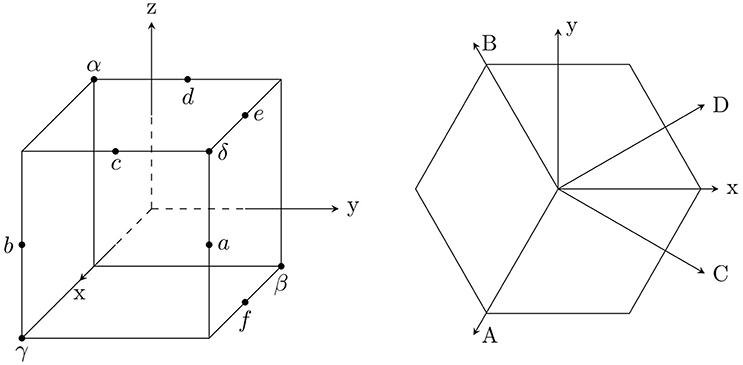
Figure 2. Rotation axes for symmetry elements in Schönflies notation (according to Cornwell [40]).

Character tables are frequently needed and can be calculated using GTCharacterTable. The module uses the Burnside algorithm [42], which is a reasonable choice for relatively small groups, such as point groups. Representation matrices can be generated using GTGetIrep, where the algorithm of Flodmark and Blokker is implemented [43]. Clebsch-Gordan coefficients, which are necessary to generate the basis of a direct product representation, can be calculated using GTClebschGordanCoefficients. Here, the algorithm of van Den Broek and Cornwell is implemented [44]. To calculate band structures of solids, GTPack supports a plane-wave basis [45, 46] and a tight-binding method in the two- and three-center form [47, 48]. The Master equation for photonic crystals is constructed by GTPhMaster as described in Sakoda [24].

Installation of GTPack

GTPack is installed similarly to all other Mathematica packages. After downloading and decompressing GTPack, the content of the package has to be copied to the application folder of Mathematica within the respective base directory. Here, the user can choose between making the package available for all users of the computer or only for her- or himself. If the package should be available for all users of the computer, the corresponding folder to copy to can be found by opening a Mathematica notebook and typing $BaseDirectory. If the package should be available exclusively for the current user of the computer the respective base directory can be found by typing $UserBaseDirectory. According to the path of the base or user base directory (called $dir in the following), the folder containing GTPack needs to be copied to the directory $dir\Applications. Afterwards, the package and the documentation are available. The package itself can be loaded within a Mathematica notebook by typing Needs[”GroupTheory‘”].

Examples

Installation of Groups and Character Table

In the first example, the installation of point groups and the calculation of character tables is shown. Within the example, the point group T is considered. Using GTPack, the point group is installed with the command GTInstallGroup as shown in Figure 3. The output is a list of symmetry elements, where each element is given in symbolic form. In total T contains 12 elements, where the symmetry elements are denoted using the Schönflies notation [32], where C_na denotes a rotation about the angle 2π/n about the rotation axis $\overrightarrow{a}$. The implemented standard axes are shown in Figure 2. Additional rotation axes can be installed using GTInstallAxis. Each symbol can be transformed into a rotation matrix using GTGetMatrix. A character table for a point group is installed using GTCharacterTable.

FIGURE 3

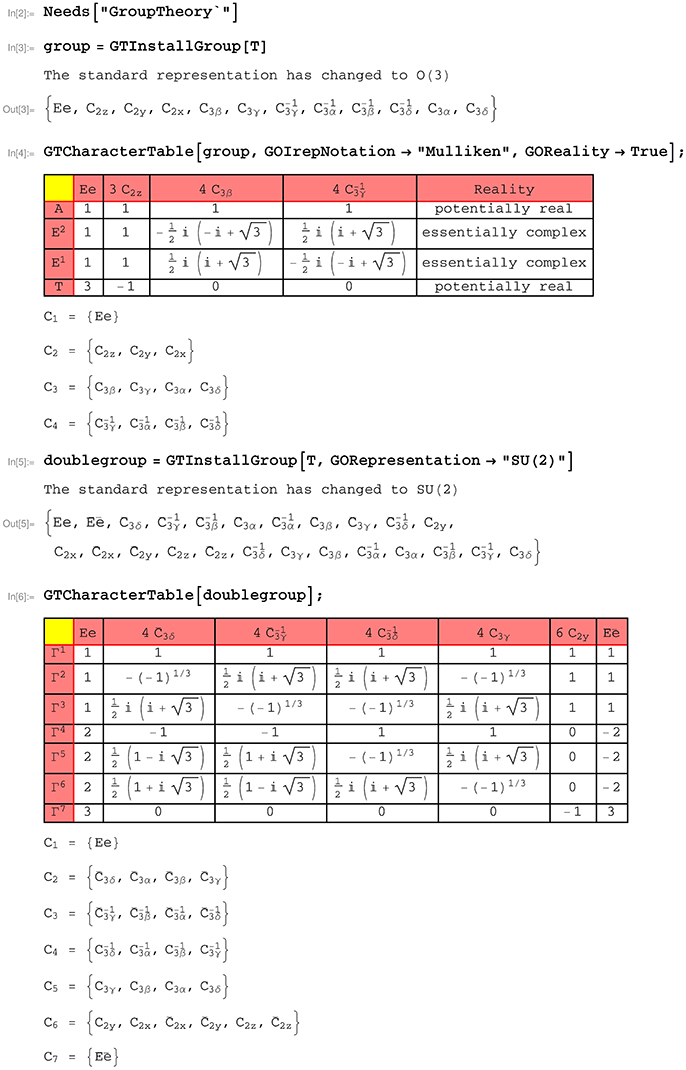
Figure 3. Installation of groups and double groups and calculation of the character tables using the commands GTInstallGroup and GTCharacterTable.

The command applies the Burnside algorithm for the calculation of the character table [42]. Within the command several options can be specified, such as an input validation (GOFast), a control of the printed output (GOVerbose), or the choice of notation for the irreducible representations (GOIrepNotation). For example, possible options for the names of irreducible representations are: the Mulliken notation [49, 50], which is widely used in chemistry and spectroscopy; the notation according to Bouckaert et al. [3], which is usually used in connection to band structure calculations; and a simple index notation, which is denoted by Bethe notation. To determine additional degeneracies of energy levels due to time-reversal symmetry, the reality of irreducible representations plays a central role [40]. Given a point group ${G}$, a representation Γ of ${G}$ is called: potentially real, if Γ is equivalent to a real representation and Γ ~ Γ*; pseudo-real, if Γ is not equivalent to a real representation, but Γ ~ Γ*; and essentially complex, if Γ ≁ Γ*. This property can be determined by means of the equation of Frobenius and Schur [40], given by

$\begin{array}{cc}\frac{1}{g}{\displaystyle \sum _{T\in G}\chi }(T^2)=\{\begin{array}{ll}1\hfill & \text{if }\Gamma \text{ is potentiallyreal}\hfill \\ 0\hfill & \text{if }\Gamma \text{ is essentially complex}\hfill \\ -1\hfill & \text{if }\Gamma \text{ is pseudo-real}\hfill \end{array}& (1)\end{array}$

Equation (1) can be evaluated using GTReality, or during the calculation of the character table by specifying the option GOReality. In the second part of the example in Figure 3 the character table is calculated for the double group of T. The double group is installed by specifying the option GORepresentation within the command GTInstallGroup and choosing SU(2) as standard representation. The additional symbols of the double group elements are denoted with an overline. Instead of four, the double group of T has seven classes and irreducible representations. The additional classes are classified by the theorem of Opechowski [51, 52]. The respective extra representations of the double group can be determined using GTExtraRepresentations.

Crystal-Field Splitting

Crystal field theory represents a semi-empirical approach to describe localized states in an atomic or crystallographic surrounding. The crystallographic surrounding or crystal field is described in terms of a small perturbation $V_{\mathrm{\text{cr}}}(\overrightarrow{r})$ leading to the total Hamiltonian

$\begin{array}{cc}\begin{array}{r}\left[-\frac{{\hslash }^2}{2m}{\nabla }^2+V(\overrightarrow{r})+V_{\mathrm{\text{cr}}}(\overrightarrow{r})\right]\psi (\overrightarrow{r})=E\psi (\overrightarrow{r}).\end{array}& (2)\end{array}$

The crystal field itself can be expanded in terms of spherical harmonics $Y_m^l$ [32],

$\begin{array}{cc}\begin{array}{r}{V}_{\mathrm{\text{cr}}}(\overrightarrow{r})={\displaystyle \sum _l}{\displaystyle \sum _{m=-l}^l}{r}^l{A}_{l,m}{Y}_m^l(\theta ,\varphi ),\end{array}& (3)\end{array}$

or more generally in terms of crystal field operators ${Ô}_m^l$,

$\begin{array}{cc}\begin{array}{r}{\widehat{V}}_{\mathrm{\text{cr}}}={\displaystyle \sum _l}{\displaystyle \sum _{m=-l}^l}{B}_{l,m}{Ô}_m^l.\end{array}& (4)\end{array}$

GTPack contains various modules to calculate matrix elements $⟨j{m}_1\left|{Ô}_m^l\right|j{m}_2⟩$ for operator equivalents, such as spherical harmonics, Buckmaster-Smith-Thornley operators [34], and Stevens operators [33]. The respective GTPack commands are GTGauntCoefficients, GTBSTOperator, and GTStevensOperator.

Depending on the underlying symmetry of the system some of the expansion coefficients A_{l, m} or B_{l, m} are zero. Given a symmetry group ${G}$, the Hamiltonian of the system and with that the crystal field expansion as to be invariant under the application of the projection operator of the identity representation,

$\begin{array}{cc}\begin{array}{r}{\widehat{{P}}}^1{V}_{\mathrm{\text{cr}}}(r,\theta ,\varphi )=V_{\mathrm{\text{cr}}}(r,\theta ,\varphi ).\end{array}& (5)\end{array}$

However, for any proper coordinate transformation $\widehat{P}(T)$ corresponding to an element $T\in {G}$ the spherical harmonics (and similarly crystal field operators ${Ô}_m^l$) transform as

$\begin{array}{cc}\begin{array}{r}\widehat{P}(T)Y_l^m={\displaystyle \sum _{m^{\prime }=-l}^l}{D}_{m^{\prime }m}^l(T)Y_l^{m^{\prime }},\end{array}& (6)\end{array}$

where $D_{m^{\prime }m}^l$ denotes the Wigner-D function. For improper coordinate transformations (inversion, reflections, etc.) a factor of (−1)^l has to be taken into account. Evaluating Equation (5) by using the expansion (3) and transformation behavior (6) leads to the under determined equation system

$\begin{array}{cc}\begin{array}{r}{A}_l^m=\frac{1}{g}{\displaystyle \sum _{T\in {G}}}{\displaystyle \sum _{m^{\prime }=-l}^l}{D}_{m{m}^{\prime }}^l(T)A_l^{m^{\prime }}.\end{array}& (7)\end{array}$

From Equation (7) it can be concluded which coefficients depend on each other and which coefficients vanish. The final symmetry adapted crystal field expansion can be calculated using GTPack by means of GTCrystalField. Figure 4 illustrates an example for the level splitting for a single d-electron in an octahedral, a cubic and a tetrahedral crystal field. The underlying point groups are O_h for the cubic and the octahedral case as well as T_d for the tetrahedral case. However, it turns out that both groups lead to the same crystal field expansion. First, the point group O_h is installed using GTInstallGroup. Afterwards the crystal field expansion is calculated using GTCrystalField up to a cutoff value of 2l. As we discuss d-electrons, the expansion is truncated after l = 4. Next, we define the surrounding field in terms of the nearest neighbors and create lists containing their positions and ionic charges. The splitting is calculated from the eigenvalues of the matrix elements over radial wave functions ${\psi }_m^l(\overrightarrow{r})=R^l(r)Y_m^l(\theta ,\varphi )$, as

$\begin{array}{cc}\begin{array}{r}{V}_{\mathrm{\text{cr}}}={\displaystyle \sum _{l^{\prime }=0}^{2l}}{\displaystyle \sum _{m=-l^{\prime }}^{l^{\prime }}}⟨r^{l^{\prime }}⟩A_{l^{\prime },m}⟨l{m}_1\left|l^{\prime }m\right|l{m}_2⟩,\end{array}& (8)\end{array}$

where

$\begin{array}{cc}\begin{array}{r}⟨r^l⟩=\int \text{d}r{r}^2{r}^l{R}^l{(r)}^2,\end{array}& (9)\end{array}$

and

$\begin{array}{cc}\begin{array}{r}⟨l{m}_1\left|l^{\prime }m\right|l{m}_2⟩=\int \text{d}\Omega Y_{m_1}^{l*}(\Omega )Y_m^{l^{\prime }}(\Omega )Y_{m_2}^l(\Omega ).\end{array}& (10)\end{array}$

The latter integral is called Gaunt coefficient and can be calculated by means of GTPack using GTGauntCoefficient. The values for ⟨ r^l′⟩ are materials specific and can be calculated, e.g., in the framework of the density functional theory [53]. GTPack provides commands to store and load explicit values from a database. However, in this example we introduce the generic parameters

$\begin{array}{cc}\begin{array}{r}ϵ\mathrm{\text{[oct]}}=\frac{3q<r^2>}{2\pi },\end{array}& (11)\end{array}$

and

$\begin{array}{cc}\begin{array}{r}\mathrm{\text{Dq[oct]}}=\frac{q⟨r^4⟩}{24\pi }.\end{array}& (12)\end{array}$

As can be verified from the Mathematica example in Figure 4, in all three cases a two-fold and a three-fold degenerate level can be found. In the cubic and octahedral case the two-fold degenerate state corresponds to the irreducible representation E_g and the three-fold degenerate level corresponds to the irreducible representation T_2g. For the tetrahedron the inversion symmetry is broken and the states are denoted by E and T₂, respectively. The final result is plotted in Figure 5.

FIGURE 4

Figure 4. Crystal field expansion and level splitting for a localized d-electron in an octahedral, a cubic and a tetrahedral crystal field.

FIGURE 5

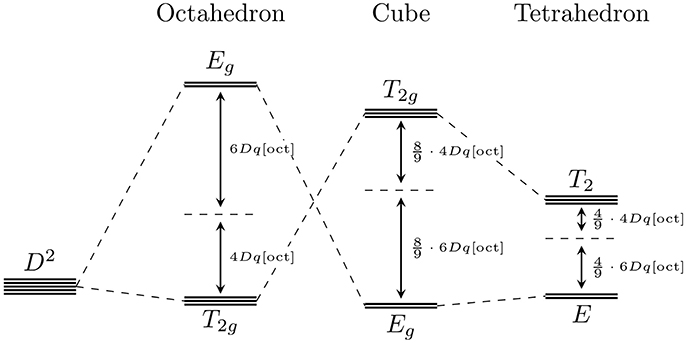
Figure 5. The level splitting for a localized d-electron into E_g (E) and T_2g (T₂) levels in an octahedral, a cubic and a tetrahedral crystal field.

Tight-Binding Bandstructure of Graphene

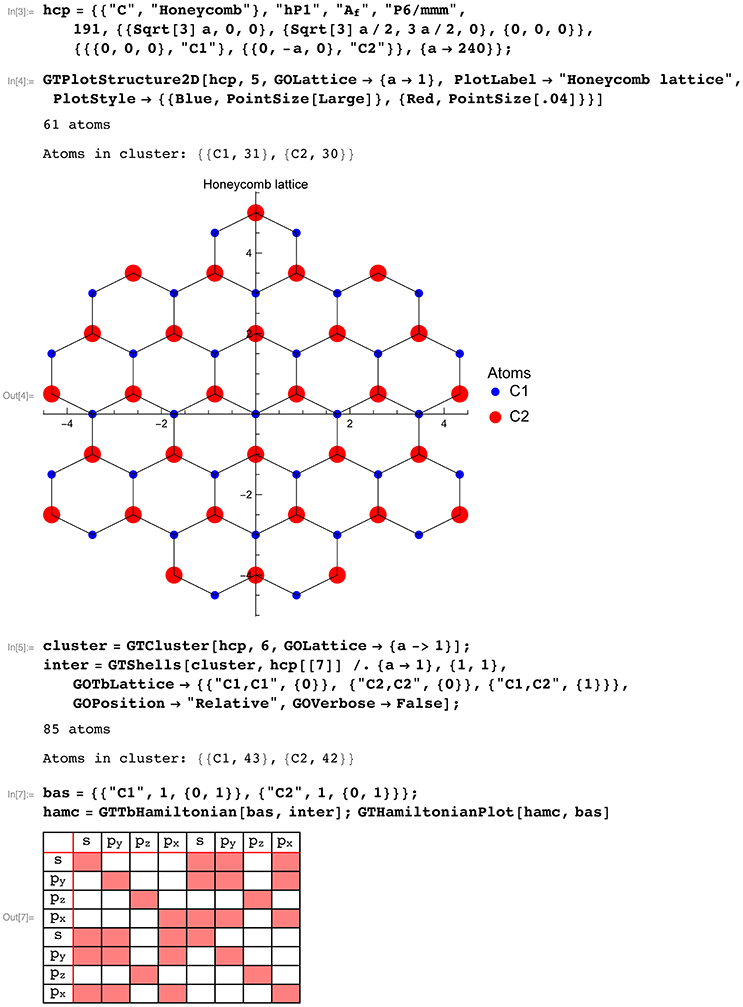
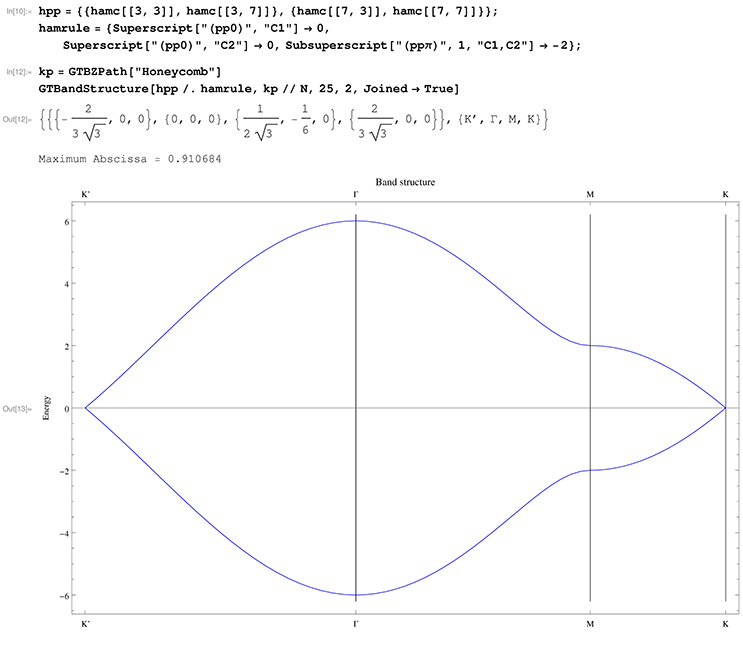
Due to the occurrence of Dirac nodes within the band structure and the resulting properties, graphene counts as one of the most studied materials to date [54, 55]. Within the following example the calculation of the band structure using the tight-binding approximation will be illustrated in the framework of GTPack. In Figure 6 the structure and the construction of the tight-binding Hamiltonian is shown. At first, the structure is given as a list in the standard GTPack format. The list contains the name of the structure and a prototype, four different names for the space group (Pearson symbol, Strukturbericht designation, international notation, and space group number), the lattice, and the sites containing the atom name and the atom position. Note that the first five information are optional and not important for the generation of the tight-binding model. GTPack provides modules to import structures, e.g., in the cif-format using GTImportCIF. The structural information can be plotted using the command GTPlotStructure2D. For the construction of the tight-binding model it is necessary to construct a real space cluster. This cluster is reordered into different shells corresponding to nearest neighbor, next nearest neighbor, next next nearest neighbor interactions, etc. The respective commands to do so are GTCluster and GTShells. From the information of the shells, the tight-binding Hamiltonian is constructed for s- and p-electrons. The zero and non-zero entries within the tight-binding Hamiltonian are illustrated using GTHamiltonianPlot. As can be seen within the plot, the p_z-orbitals do not hybridize with all the other orbitals. Hence, those can be considered to form a smaller tight-binding Hamiltonian of dimension 2 × 2. Setting up and solving the reduced 2 × 2 tight-binding Hamiltonian is shown in Figure 7. The high-symmetry path within the Brillouin zone (K′, Γ, M, K) is generated using the command GTBZPath. The points K and K′ denote the corners of the hexagonal Brillouin zone, M points to the middle of an edge and Γ is the Brillouin zone center. The band structure itself is calculated and plotted using GTBandStructure.

FIGURE 6

Figure 6. Structural information and construction of the tight-binding Hamiltonian for graphene.

FIGURE 7

Figure 7. Band structure calculation for graphene.

Analyzing Photonic Band Structures

Photonic crystals represent the optical analogs of ordinary crystals, where light is traveling through a periodic dielectric. Potential optical band gaps, i.e., forbidden frequencies where photons are not allowed to travel through the medium have motivated research for various applications replacing ordinary electronics and information technology [56]. Recently, photonic crystals have been discussed with respect to nodal points [57] and topological states in periodic and quasi periodic arrangements [58–60]. A group theory classification of the allowed modes yields additional information, e.g., with respect to uncoupled bands [27]. For two-dimensional photonic crystals, the vectorial Maxwell's equations can be transformed into two sets of independent equations for two modes [24], which are referred to as transversal magnetic (TM) and transversal electric (TE) modes. The resulting master equations are given by

$\begin{array}{cc}\begin{array}{rc}-\frac{1}{\epsilon ({\overrightarrow{r}}_{\parallel })}\left\{\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right\}{\text{E}}_z({\overrightarrow{r}}_{\parallel })& =\frac{{\omega }^2}{c^2}{\text{E}}_z({\overrightarrow{r}}_{\parallel }),\end{array}& (13)\end{array}$

$\begin{array}{cc}\begin{array}{rc}-\left\{\frac{\partial }{\partial x}\frac{1}{\epsilon ({\overrightarrow{r}}_{\parallel })}\frac{\partial }{\partial x}+\frac{\partial }{\partial y}\frac{1}{\epsilon ({\overrightarrow{r}}_{\parallel })}\frac{\partial }{\partial y}\right\}{\text{H}}_z({\overrightarrow{r}}_{\parallel })& =\frac{{\omega }^2}{c^2}{\text{H}}_z({\overrightarrow{r}}_{\parallel }).\end{array}& (14)\end{array}$

Here, the vector ${\overrightarrow{r}}_{\parallel }$ denotes a vector in the xy plane. For the solution of the masters equation, a plane-wave approach can be applied which transforms the Masters equations into an eigenvalue problem. Such an approach is implemented in GTPack, but also within the code MPB¹. GTPack can be applied to analyze photonic band structure calculations performed with MPB, as will be shown in the following. We consider a two-dimensional photonic crystal with a square lattice made of circular alumina rods (ε = 8.9) in air. The radius of the rods is given by R = 0.2a (a-lattice constant). This corresponds to a filling factor of γ = 0.126. The photonic band structure was calculated using MPB incorporating a tolerance of 10⁻⁷. The calculated band structure can be loaded, plotted and analyzed automatically using the command GTPhSymmetryBands as shown in Figure 8 for the transversal magnetic mode. The underlying point group is C_4v, which has four one-dimensional irreducible representation (A₁, A₂, B₁, B₂) and one two-dimensional irreducible representation (E). As can be seen in Figure 8, there is a spectral gap between the first and the second band. Degeneracies in the band structure correspond to the dimensions of the corresponding irreducible representation. Therefore, all single bands are associated to the one-dimensional irreducible representations. However, for example, for the second and the third band, a two-fold degeneracy can be found at the M point which corresponds to the two-dimensional irreducible representation E. To revise this point more clearly, the specific fields corresponding to the modes can be imported into the Mathematica notebook using GTPhMPBFields. Afterwards, the field is analyzed by applying the character projection operator for each irreducible representation. As expected, only the application of the operator corresponding to E shows non-zero results, as can be seen in Figure 9.

FIGURE 8

Figure 8. Photonic band structure for a two-dimensional square lattice of alumina rods in air calculated using MPB and analyzed with GTPack.

FIGURE 9

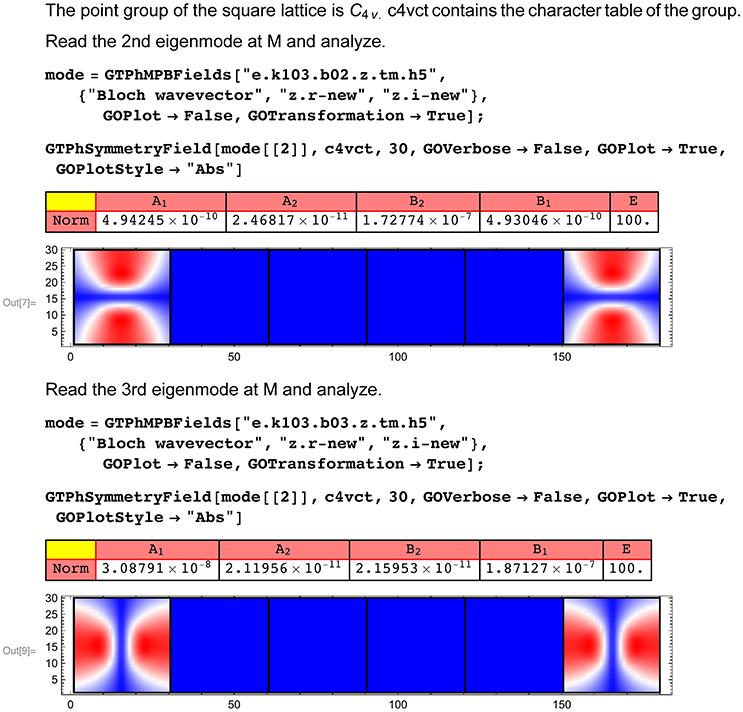
Figure 9. Application of the character projection operator to the field corresponding to the degeneracy between the second and third band of the transversal magnetic mode at M.

Advantages and Limitations

As an additional package to the standard Mathematica framework, GTPack is embedded into the Mathematica framework. The new modules provided within GTPack are designed for application in solid state physics and photonics and use notations which are common in these research communities. Having a programming framework at hand comes with the advantage of easy automation which is in contrast to recently published group theory tables. Most of the provided modules are kept general and can be applied in connection to any set of matrices forming a group. This allows for applications way beyond the provided point and space group setup. As usual, the package is constructed in a modular form and can be extended easily.

GTPack is under ongoing development and therefore comes with limitations in the first version. Among others, these comprise of the calculation of character tables for space groups and groups containing anti-unitary symmetry elements. The implemented modules for the calculation of photonic band structures currently do not reach the same performance as specialized numeric implementations such as MPB. Thus, export and import modules connect MPB with GTPack. Additionally, modules to export analytically generated tight-binding Hamiltonians to Fortran help to generate more efficient numeric codes. An extension to a parallel implementation for the usage of the cluster version of Mathematica is currently not planned. Concerning the symmetry analysis, irreducible representations can currently only be associated to the calculated bands if symmorphic space groups are taken into account. An extension for non-symmorphic groups is under development.

Conclusion

We presented the Mathematica group theory package GTPack together with four basic examples. The package contains about 200 additional commands dealing with basic group theory and representation theory and providing tools for applications in solid state physics and photonics. The package itself is structured into several subpackages. In connection to external databases it is possible to load, change and save data, like structural information or parameters for electronic and photonic band structure calculations. The package works externally with a symbolic representation of symmetry elements. Internally, matrices are used. GTPack can be obtained online via the web page http://GTPack.org.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge the support of Sebastian Schenk, especially with respect to his help in building up a documentation within the Mathematica framework. Furthermore, we are grateful for discussions and contributions from Markus Däne, Christian Matyssek, Stefan Thomas, Martin Hoffmann, and Arthur Ernst. This publication was funded by the German Research Foundation within the Collaborative Research Centre 762 (projects A4 and B1). Additionally, RG acknowledges funding from the European Research Council under the European Union's Seventh Framework Program (FP/2207-2013)/ERC Grant Agreement No. DM-321031.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00086/full#supplementary-material

Footnotes

1. ^ Available online at: http://ab-initio.mit.edu/mpb

References

1. Wigner E. Fifty years of symmetry operators. In: Zichichi A, editor Understanding the Fundamental Constituents of Matter. New York, NY: Plenum Press (1978). p. 879–92.

Google Scholar

2. Ahmad S, International Centre for Theoretical Physics TI. Group Theory, the New Language of Modern Physics. Trieste: International Centre for Theoretical Physics (1990).

Google Scholar

3. Bouckaert LP, Smoluchowski R, Wigner E. Theory of brillouin zones and symmetry properties of wave functions in crystals. Phys Rev. (1936) 50:58–67. doi: 10.1103/PhysRev.50.58

CrossRef Full Text | Google Scholar

4. Bethe HA. Splitting of terms in crystals. Ann Phys. (1929) 3:133.

Google Scholar

5. Inui T, Uemura Y. Theory of color centers in ionic crystals I electronic states of F-centers in Alkali Halides. Prog Theor Phys. (1950) 5:252–65. doi: 10.1143/ptp/5.2.252

CrossRef Full Text | Google Scholar

6. Chanier T, Opahle I, Sargolzaei M, Hayn R, Lannoo M. Magnetic state around cation vacancies in II–VI semiconductors. Phys Rev Lett. (2008) 100:026405. doi: 10.1103/PhysRevLett.100.02640518232895

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bassani F, Parravicini GP. Electronic States ans Optical Transitions in Solids. Oxford: Pergamon Press (1975).

Google Scholar

8. Miyamachi T, Schuh T, Märkl T, Bresch C, Balashov T, Stöhr A. Stabilizing the magnetic moment of single holmium atoms by symmetry. Nature (2013) 503:242–6. doi: 10.1038/nature12759

PubMed Abstract | CrossRef Full Text | Google Scholar

9. König A, Mermin ND. Screw rotations and glide mirrors: crystallography in Fourier space. Proc Natl Acad Sci USA (1999) 96:3502–6. doi: 10.1073/pnas.96.7.3502

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Liu CX, Qi XL, Zhang H, Dai X, Fang Z, Zhang SC. Model Hamiltonian for topological insulators. Phys Rev B (2010) 82:045122. doi: 10.1103/PhysRevB.82.045122

CrossRef Full Text | Google Scholar

11. Volovik GE, Gor'kov LP. Superconducting classes in heavy-fermion systems. J Exp Theor Phys. (1985) 61:843.

Google Scholar

12. Blount EI. Symmetry properties of triplet superconductors. Phys Rev B (1985) 32:2935. doi: 10.1103/PhysRevB.32.2935

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sigrist M, Ueda K. Phenomenological theory of unconventional superconductivity. Rev Mod Phys. (1991) 63:239. doi: 10.1103/RevModPhys.63.239

CrossRef Full Text | Google Scholar

14. Geilhufe RM, Balatsky AV. Symmetry analysis of odd-and even-frequency superconducting gap symmetries for time-reversal symmetric interactions. Phys Rev B (2018) 97:024507. doi: 10.1103/PhysRevB.97.024507

CrossRef Full Text | Google Scholar

15. Fernandes RM, Orth PP, Schmalian J. Intertwined vestigial order in quantum materials: nematicity and beyond. arXiv[Preprint]:180400818 (2018).

Google Scholar

16. Bradlyn B, Elcoro L, Cano J, Vergniory MG, Wang Z, Felser C. Topological quantum chemistry. Nature (2017) 547:298. doi: 10.1038/nature23268

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Geilhufe RM, Bouhon A, Borysov SS, Balatsky AV. Three-dimensional organic Dirac-line materials due to nonsymmorphic symmetry: a data mining approach. Phys Rev B (2017) 95:041103. doi: 10.1103/PhysRevB.95.041103

CrossRef Full Text | Google Scholar

18. Geilhufe RM, Borysov SS, Bouhon A, Balatsky AV. Data mining for three-dimensional organic dirac materials: focus on space group 19. Sci Rep. (2017) 7:7298. doi: 10.1038/s41598-017-07374-7

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wieder BJ, Kane CL. Spin-orbit semimetals in the layer groups. Phys Rev B (2016) 94:155108. doi: 10.1103/PhysRevB.94.155108

CrossRef Full Text | Google Scholar

20. Bouhon A, Black-Schaffer AM. Global band topology of simple and double Dirac-point semimetals. Phys Rev B (2017) 95:241101. doi: 10.1103/PhysRevB.95.241101

CrossRef Full Text | Google Scholar

21. Nayak C, Simon SH, Stern A, Freedman M, Sarma SD. Non-Abelian anyons and topological quantum computation. Rev Mod Phys. (2008) 80:1083. doi: 10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

22. López-Tejeira F, Ochiai T, Sakoda K, Sánchez-Dehesa J. Symmetry characterization of eigenstates in opal-based photonic crystals. Phys Rev B (2002) 65:195110. doi: 10.1103/PhysRevB.65.195110

CrossRef Full Text | Google Scholar

23. Hergert W, Däne M. Group theoretical investigations of photonic band structures. Phys Status Solid. (2003) 197:620–34. doi: 10.1002/pssa.200303110

CrossRef Full Text | Google Scholar

24. Sakoda K. Optical Properties of Photonic Crystals, Vol. 80. Berlin; Heidelberg: Springer Science & Business Media (2004).

Google Scholar

25. Sakoda K, Shiroma H. Numerical method for localized defect modes in photonic lattices. Phys Rev B (1997) 56:4830. doi: 10.1103/PhysRevB.56.4830

CrossRef Full Text | Google Scholar

26. Stefanou N, Karathanos V, Modinos A. Scattering of electromagnetic waves by periodic structures. J Phys. (1992) 4:7389. doi: 10.1088/0953-8984/4/36/013

CrossRef Full Text | Google Scholar

27. Sakoda K. Symmetry, degeneracy, and uncoupled modes in two-dimensional photonic lattices. Phys Rev B (1995) 52:7982. doi: 10.1103/PhysRevB.52.7982

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Altmann S, Herzig P. Point-Group Theory Tables. Oxford; New York, NY: Oxford University Press (1994).

Google Scholar

29. Bradley C, Cracknell A. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups. Oxford; New York, NY: Oxford University Press (2010).

Google Scholar

30. Aroyo MI, Perez-Mato J, Orobengoa D, Tasci E, De La Flor G, Kirov A. Crystallography online: bilbao crystallographic server. Bulg Chem Commun. (2011) 43:183–97.

Google Scholar

31. GAP. Groups, Algorithms, and Programming, Version 4.8.5 (2016).

32. Hergert W, Geilhufe M. Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica. Weinheim: Wiley-VCH (2018).

Google Scholar

33. Stevens KWH. Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions. Proc Phys Soc Sect A (1952) 65:209. doi: 10.1088/0370-1298/65/3/308

CrossRef Full Text | Google Scholar

34. Smith D, Thornley JHM. The use of ‘operator equivalents'. Proc Phys Soc. (1966) 89:779.

Google Scholar

35. Hall SR, Allen FH, Brown ID. The crystallographic information file (CIF): a new standard archive file for crystallography. Acta Crystallogr Sect A (1991) 47:655–85. doi: 10.1107/S010876739101067X

CrossRef Full Text | Google Scholar

36. Kokalj A. XCrySDena new program for displaying crystalline structures and electron densities. J Mol Graph Model. (1999) 17:176–9. doi: 10.1016/S1093-3263(99)00028-5

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Johnson SG, Joannopoulos JD. Block-iterative frequency-domain methods for Maxwells equations in a planewave basis. Opt Exp. (2001) 8:173–90. doi: 10.1364/OE.8.000173

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Kresse G, Furthmüller J. Software VASP, vienna (1999). Phys Rev B (1996) 54:169.

Google Scholar

39. Gonze X, Amadon B, Anglade PM, Beuken JM, Bottin F, Boulanger P. ABINIT: first-principles approach to material and nanosystem properties. Comput Phys Commun. (2009) 180:2582–615. doi: 10.1016/j.cpc.2009.07.007

CrossRef Full Text | Google Scholar

40. Cornwell JF. Group Theory in Physics. London; San Diego, CA; New York, NY; Boston, MA; Sydney, NSW; Tokyo; Toronto, ON: Academic Press (1984).

Google Scholar

41. Damhus T. Double groups as symmetry groups for spin-orbit coupling Hamiltonians. Match (1984) 16:21–82.

Google Scholar

42. Holt DF, Eick B, O'Brien EA. Handbook of Computational Group Theory. Boca Raton, FL; London; New York, NY; Washington, DC: CRC Press (2005).

Google Scholar

43. Flodmark S, Blokker E. A computer program for calculation of irreducible representations of finite groups. Int J Quant Chem. (1967) 1:703–11. doi: 10.1002/qua.560010676

CrossRef Full Text | Google Scholar

44. van Den Broek P, Cornwell J. Clebsch-Gordan coefficients of symmetry groups. Phys Stat Solid. (1978) 90:211–24. doi: 10.1002/pssb.2220900123

CrossRef Full Text | Google Scholar

45. Yu PY, Cardona M. Fundamentals of semiconductors, Physics and Materials Properties. Berlin; Heidelberg: Springer (2010).

Google Scholar

46. Dresselhaus MS, Dresselhaus G, Jorio A. Group Theory - Application to the Physics of Condensed Matter. Berlin; Heidelberg: Springer-Verlag (2008).

Google Scholar

47. Slater JC, Koster GF. Simplified LCAO method for the periodic potential problem. Phys Rev. (1954) 94:1498–524.

Google Scholar

48. Egorov RF, Reser BI, Shirokovskii VP. Consistent treatment of symmetry in the tight binding approximation. Phys Status Solid. (1968) 26:391–408. doi: 10.1002/pssb.19680260202

CrossRef Full Text | Google Scholar

49. Mulliken RS. Report on notation for the spectra of polyatomic molecules. J Chem Phys. (1955) 23:1997–2011.

Google Scholar

50. Mulliken RS. Erratum: report on notation for the spectra of polyatomic molecules. J Chem Phys. (1956) 24:1118.

Google Scholar

51. Altmann SL. Rotations, Quaternions and Double Groups. Mineola, NY: Dover Publications, Inc. (2005).

Google Scholar

52. Opechowski W. Sur les groupes cristallographiques doubles. Physica (1940) 7:552–62. doi: 10.1016/S0031-8914(40)90045-3

CrossRef Full Text | Google Scholar

53. Forstreuter J, Steinbeck L, Richter M, Eschrig H. Density-functional calculations for rare-earth atoms and ions. Phys Rev B (1997) 55:9415. doi: 10.1103/PhysRevB.55.9415

CrossRef Full Text | Google Scholar

54. Abergel D, Apalkov V, Berashevich J, Ziegler K, Chakraborty T. Properties of graphene: a theoretical perspective. Adv Phys. (2010) 59:261–482. doi: 10.1080/00018732.2010.487978

CrossRef Full Text | Google Scholar

55. Novoselov K, Geim AK, Morozov S, Jiang D, Katsnelson M, Grigorieva I. Two-dimensional gas of massless Dirac fermions in graphene. Nature (2005) 438:197–200. doi: 10.1038/nature04233

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Joannopoulos JD, Villeneuve PR, Fan S. Photonic crystals: putting a new twist on light. Nature (1997) 386:143. doi: 10.1038/386143a0

CrossRef Full Text | Google Scholar

57. Lu L, Fu L, Joannopoulos JD, Soljačić M. Weyl points and line nodes in gyroid photonic crystals. Nat Photon. (2013) 7:294. doi: 10.1038/nphoton.2013.42

CrossRef Full Text | Google Scholar

58. Wu LH, Hu X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys Rev Lett. (2015) 114:223901. doi: 10.1103/PhysRevLett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Lu L, Joannopoulos JD, Soljačić M. Topological photonics. Nat Photon. (2014) 8:821. doi: 10.1038/nphoton.2014.248

CrossRef Full Text | Google Scholar

60. Verbin M, Zilberberg O, Kraus YE, Lahini Y, Silberberg Y. Observation of topological phase transitions in photonic quasicrystals. Phys Rev Lett. (2013) 110:076403. doi: 10.1103/PhysRevLett.110.076403

PubMed Abstract | CrossRef Full Text | Google Scholar