Emergence of Cooperation as a Non-equilibrium Transition in Noisy Spatial Games

The emergence of cooperation among selfish agents that have no incentive to cooperate is a non-trivial phenomenon that has long intrigued biologists, social scientists and physicists. The iterated Prisoner's Dilemma (IPD) game provides a natural framework for investigating this phenomenon. Here, agents repeatedly interact with their opponents, and their choice to either cooperate or defect is determined at each round by knowledge of the previous outcomes. The spatial version of IPD, where each agent interacts only with their nearest neighbors on a specified connection topology, has been used to study the evolution of cooperation under conditions of bounded rationality. In this paper we study how the collective behavior that arises from the simultaneous actions of the agents (implemented by synchronous update) is affected by (i) uncertainty, measured as noise intensity K, (ii) the payoff b, quantifying the temptation to defect, and (iii) the nature of the underlying connection topology. In particular, we study the phase transitions between states characterized by distinct collective dynamics as the connection topology is gradually altered from a two-dimensional lattice to a random network. This is achieved by rewiring links between agents with a probability p following the small-world network construction paradigm. On crossing a specified threshold value of b, the game switches from being Prisoner's Dilemma, characterized by a unique equilibrium, to Stag Hunt, a well-known coordination game having multiple equilibria. We observe that the system can exhibit three collective states corresponding to a pair of absorbing states (viz., all agents cooperating or defecting) and a fluctuating state characterized by agents switching intermittently between cooperation and defection. As noise and temptation can be interpreted as temperature and an external field respectively, a strong analogy can be drawn between the phase diagrams of such games with that of interacting spin systems. Considering the 3-dimensional p − K − b parameter space allows us to investigate the different phase transitions that occur between these collective states and characterize them using finite-size scaling. We find that the values of the critical exponents depend on the connection topology and are different from the Directed Percolation (DP) universality class.

1. Introduction

The only thing that will redeem mankind is cooperation

Bertrand Russell

Consider a simple thought experiment: two autonomous agents are required to expend equal effort in order to achieve a mutually beneficial outcome. Each agent however realizes that they would be better off as “free riders”—they could reap the benefits of the other's work without any contribution on their part. If both agents think alike, no effort would be spent by either, leading to an undesirable outcome for both. This hypothetical scenario highlights one of the most puzzling and profound questions that has long intrigued biologists, sociologists and mathematicians alike, namely whether there is a simple mechanism that can explain the emergence and maintenance of cooperation. Indeed, the implications of the free rider problem in the context of human societies has long troubled many, as actions guided through self-interest invariably leads to an unsustainable burden on shared resources (often referred to as the tragedy of the commons [1]). However, far from being an unobtainable outcome, cooperation is in fact widely seen in nature and is a fundamental mechanism underlying the organization of systems as diverse as genomes, multicellular organisms and human societies [2]. It is the nature of this interaction-driven self-organized emergence of cooperative behavior in populations of individuals that only consider their self-interest, then, that poses a conundrum. In the words of Robert Axelrod: “Under what conditions will cooperation emerge in a world of egoists without central authority?” [3]. The theoretical framework of game theory has been employed to investigate the dynamical evolution of cooperation in social dilemmas [4], as well as in microbial populations [5] and, more generally, on networks of interactions [6].

Perhaps the best-known paradigm for the study of cooperative behavior is the Prisoner's Dilemma game [7]—a model that examines the possible outcomes of strategic interactions between players, and which does not favor unilateral cooperation. Over the last half century there have been numerous studies on various facets of this game [8]. While the classical two-player Prisoner's Dilemma game involving rational players is well-understood, bounded rationality can arise from the introduction of physical constraints. For instance, if the players are located on the vertices of a network, they will interact only with their nearest neighbors. In this situation, each player has incomplete information, as she will only be aware of the actions of her neighbors in the network. This is of particular significance in iterated games, wherein players can choose a new action at each subsequent time step. Here, complex dynamical behavior can arise depending on the decision-making mechanism and aspects of the underlying topology. Elucidating the role of spatial effects is hence a complex and long-standing challenge [9]. Following the surge of interest in network science over the last couple of decades, there have been several investigations into the collective dynamics of a large number of players that interact through games with their neighbors on an underlying network. While such studies have typically attempted to uncover aspects of network topology that would favor cooperation [10, 11], systems of this nature also yield a number of interesting questions from a statistical physics perspective [12, 13]. For instance, if the collective dynamical patterns are interpreted as “phases” of the system, then one may examine the nature of the resulting phase transitions, as well as the properties of inherent critical points.

In this work, we examine the emergent collective dynamics in a system of agents that interact through games with their neighbors on an underlying topology whose structure we systematically vary from that of a lattice to a random network. Unlike the majority of studies of such spatial games, the states of the agents are updated synchronously. In addition to the network structure, we consider the effect of stochasticity in decision-making, i.e., the degree of uncertainty associated with an agent's choice of action. Furthermore, we examine in detail the nature of the phase transitions between the different regimes of collective activity that this system exhibits. In the next section, we describe the canonical Prisoner's Dilemma model, explain its relationship with other cooperative games, and discuss the significance of “temptation.” We also briefly mention previous attempts at investigating various aspects of iterated games. We discuss the role played by spatial structure, and detail the mechanism through which one can interpolate between a square lattice and a random network. This is followed by a description of the results obtained from our simulations in which we examine the joint effects of noise and network structure on the resulting collective dynamics. In particular, we report critical exponents obtained through finite-size scaling for transitions between different collective states. In contrast to previous studies on the critical nature of such transitions, which have focused on the behavior as the game payoff value corresponding to “temptation” is varied, here we investigate the phase transitions with respect to the degree of uncertainty (analogous to “temperature” or thermal noise in physical systems that undergo transitions). We conclude with a discussion of the potential significance of these results, and suggest avenues for future exploration.

2. Two-Person Symmetric Games

The archetypal Prisoner's Dilemma (PD) game [15], a mathematical model used to study non-cooperative interactions between agents, belongs to the family of symmetric two-player games where each agent independently and simultaneously chooses between two possible actions, viz., cooperation (C) and defection (D). Such 2 × 2 games hence have four possible outcomes which are not equally favorable to both players [16, 17]. Agents are assumed to be “rational,” or purely self-interested, i.e., their sole criteria in making a decision is whether or not a particular action would lead to an outcome that benefits them. Depending on the outcome, each of the players receive payoffs P, R, S or T in accordance with the matrix shown in Figure 1 (left). If both players choose C, each receives the payoff R, which is the reward for mutual cooperation. On the other hand, if both choose D, they receive the payoff P, the penalty for mutual defection. However, if one player chooses C while the other chooses D, the defector receives T (the “temptation” to unilaterally defect) while the other receives S (the “sucker's payoff” for unreciprocated cooperation).

FIGURE 1

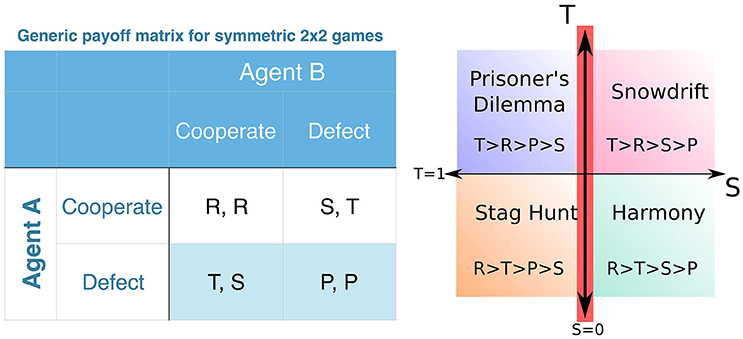
Figure 1. (Left) Generic payoff matrix for symmetric two-player games. The first and second entries of each payoff pair for each of the four possible outcomes refer to the payoffs assigned to agents A and B, respectively. (Right) Schematic illustrating the different types of symmetric 2 × 2 games that arise within the parameter range that we consider (adapted from [14]). Depending on the relative ordering of the payoffs the nature of the game changes between Prisoner's Dilemma (PD: T > R > P > S), Snowdrift (SD: T > R > S > P), Stag Hunt (SH: R > T > P > S) and Harmony (HA: R > T > S > P). Note that as R > P for all of these games, we can set R = 1 and P = 0 which fixes the scale and origin, respectively, of the units in which payoff values are measured. Thus, without any loss of generality, we visualize the games on the S − T plane in the figure. For the results presented here, we focus on the case S = 0, and vary the temptation T, i.e., we move along the T-axis, highlighted in red.

Different types of games can be defined in terms of the relative ordering of the payoff values P, R, S and T (Figure 1, right). For a PD game in the strict sense, T > R > P > S and 2R > T+S in the classical context. Often (following [18, 19]) the values of P are S are chosen identically to be zero, but in principle this represents a situation that lies on the border between PD and the Snowdrift (or Chicken) game for which T > R > S > P. The latter is an anti-coordination game which has been used to study brinkmanship [20] (e.g., in the scenario of mutual assured destruction in nuclear warfare) in which agents receive the least payoff if they both choose the same action D. Experiments where human players repeatedly play the Snowdrift game have consistently yielded higher levels of cooperation than situations in which they repeatedly play PD [21]. Another distinct game that can be defined using the same payoff matrix in Figure 1 (left) is the Stag Hunt (SH) game, which is often used to study situations of social coordination [22]. The main distinction between this game and PD is that unilateral defection is not as favorable as mutual cooperation, and the payoff structure is thus R > T ≥ P > S. Hence, by simply varying the temptation T, one can smoothly interpolate between a PD and an SH game. Note that, as R > P for all of these games, there is no loss of generality if we fix R = 1 and P = 0 which fixes the scale and origin, respectively, of the units in which payoff values are measured. Thus, in Figure 1 (right) we show only the S − T plane of the parameter space. For the simulations reported in this paper, following the convention introduced by Nowak and May [18], we restrict ourselves to the case S = 0 and vary the temptation T (whose value is denoted by b as per [18]), i.e., we move along the T-axis, highlighted in red in Figure 1 (right). Thus for T > 1, strictly speaking, we are on the borderline between PD and SD, while for T < 1, we are on the borderline between SH and the Harmony game (HA, for which R > T > S > P). However, for simplicity, we refer to the T > 1 and T < 1 regimes as PD and SH, respectively.

It is assumed that both players understand the consequence of each collective outcome resulting from their actions. In particular, in the case of PD, an agent is aware that if she chooses to defect she will at worst obtain a payoff of P (and at best T). Conversely, if she chooses to cooperate, she will at worst receive a payoff S (and at best R). As S < P and R < T, cooperation always appears to be less lucrative than defection to each player. Hence, the dominant strategy for each player in PD is to always defect. Note that mutual defection is also the Nash equilibrium in PD, as no player can do better by unilaterally deviating from it [23]. However, when both players choose to defect, they each receive the payoff P which leaves them worse off than if they had chosen to cooperate with each other (as R > P). Thus, the “dilemma” inherent in PD is that even though defection would be the rational choice for each agent, they would have done better had they both chosen to cooperate instead [24]. Note that in the SD and SH games, the players do not have a strictly dominant strategy and these games are in fact characterized by multiple Nash equilibria.

3. Iterated Games and Network Reciprocity

Although mutual defection appears to be the only possible outcome for rational agents in the one-shot PD game discussed above (but see [25, 26] for an alternative paradigm), other outcomes including mutual cooperation become possible when agents repeatedly play the game with each other. Such Iterated Prisoner's Dilemma (IPD) games can incorporate varying degrees of memory, i.e., information regarding the outcomes over several previous rounds. In order to observe outcomes other than mutual defection in IPD it is important that the players do not know the total number of rounds beforehand [27]. This is because when the agents are aware of this number, it can be proved by backward induction that the rational choice would be to always defect. In the absence of this knowledge, cooperative strategies can emerge [28]. Indeed, the IPD game has proven to be a robust tool for studying a wide range of scenarios involving the emergence of cooperative behavior [3, 29].

When populations of agents, whose interactions are constrained by an underlying connection topology, iteratively play PD with each of their nearest neighbors, additional non-trivial dynamical phenomena can emerge [30]. Specifically, the population can sustain a non-zero level of cooperation through a mechanism known as network reciprocity [2]. This concept is a generalization of “spatial reciprocity” that was first demonstrated by Nowak and May [18]. They considered a spatial IPD game wherein a system of agents are placed on the vertices of a square lattice. Each agent repeatedly engages in PD with those in the neighboring sites. Players are each initially assigned randomly selected actions (C or D) that are used in all of their interactions in that round. At the end of a round, each agent independently decides on the action to be employed in the next round by comparing her total payoff (received as a result of all interactions in that round) with that of her neighbors. Nowak and May demonstrated that even simple strategies for updating an agent's action, such as imitate the best, can elicit a non-trivial collective behavior. In particular, it was observed that cooperators and defectors coexist in the system for arbitrarily long times.

The inherent symmetries of a lattice impose certain constraints on the nature of the collective dynamics that can be observed in the spatial IPD. Moreover, the assumption that the connection topology of a regular lattice governs the interactions between agents in any biological or social setting is somewhat unrealistic. To this end, the more generalized structure of networks have been employed to define the neighborhood organization of agents playing IPD [9, 31–39]. An important question in this context relates to the effect of degree heterogeneity, i.e., variability in the number of neighbors of each agent. For this purpose, the IPD has been investigated with different classes of networks that are distinct in terms of the nature of the associated degree distribution. For example, it was observed that a greater level of cooperation can be obtained in both scale-free (SF) [40] and Erdös-Rényi (ER) networks [11], as compared to degree homogeneous networks. This outcome was seen to hold even for other games such as Snowdrift and Stag Hunt [41].

Another approach for investigating the role of network topology on system dynamics is provided by the small-world network construction paradigm introduced by Watts and Strogatz [42]. Here, beginning with a system of nodes connected to their neighbors in a regular lattice, long-range connections are introduced by allowing links to be randomly rewired with a probability p (Figure 2A). In the extreme case p = 1, one obtains a random network that, if sufficiently dense, has the properties of an ER network. For intermediate values, i.e. 0 < p < 1, the resulting network exhibits so-called “small-world” characteristics, corresponding to the coexistence of low average path length and high clustering. Note that the networks obtained all have the same average degree k_avg as the original lattice. Although there have been a number of studies on how small-world connection topology can affect the resulting collective dynamics in the context of the spatially extended IPD [43–46], there is scope for a detailed investigation of the joint effects of noise and topology on the emergence of cooperation.

FIGURE 2

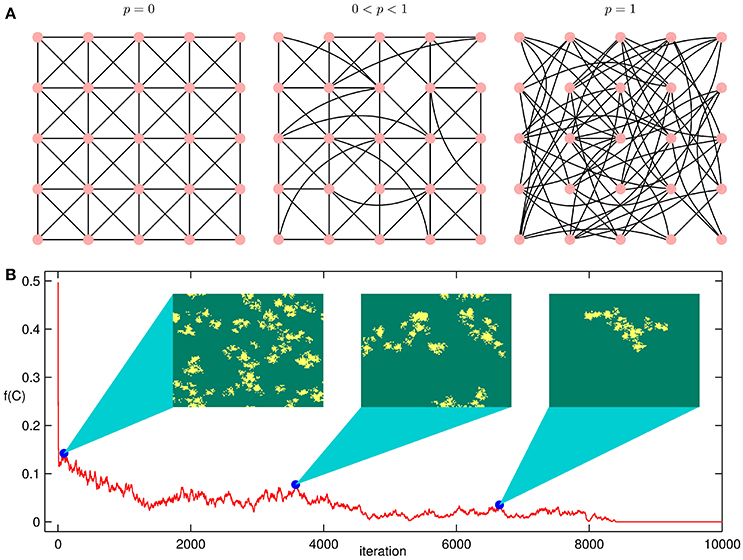
Figure 2. (A) Schematic illustrating the rewiring procedure for generating networks using the small-world construction paradigm [42]. Beginning with a system of nodes connected in a lattice topology [left], the decision to randomly rewire each link is specified by a probability p. For the extreme case p = 1, one obtains a random network that, if sufficiently dense, has the properties of an Erdös-Rényi network [right], while for intermediate values of p the resulting network [center] exhibits so-called “small-world” characteristics, viz., a high clustering coefficient and a small average path length. These networks are used here to investigate the role of connection topology on the collective dynamics in spatially extended versions of IPD. (B) A characteristic time-series of the fraction f(C) of cooperators in a lattice of N = 128 × 128 agents. Each agent plays IPD with their 8 nearest neighbors. The result shown is obtained using a temptation b = 1.1 and inverse noise K = 0.45. Initially, 50% of the agents are randomly selected to be cooperators. Snapshots of the lattice are displayed at three instants denoted by the filled circles on the time series. In each snapshot, cooperators are marked as yellow and defectors as green. Periodic boundary conditions have been assumed.

Introducing noise in the dynamics allows one to explore uncertainty on the part of the agent in deciding whether to switch between actions. Such uncertainty can arise from imperfect or incomplete information about the system that agents have access to. An action update rule that explicitly incorporates a tunable degree of stochasticity in the decision-making process is the Fermi rule [47]. Here, each agent i randomly picks one of her neighbors j and copies its action with a probability given by the Fermi distribution function:

$\begin{array}{ll}{\mathrm{\Pi }}_{i\to j}=\frac{1}{1+exp(-({\pi }_j-{\pi }_i)/K)},& (1)\end{array}$

where K can be thought of as the temperature, which is a measure of the “noise” in the decision-making process. In the noise-free case, i.e., in the limit K → 0, agent i must copy the action of j if π_j > π_i (as Π_i→j = 1), and will not copy j if π_j < π_i (as Π_i→j = 0). Conversely, in the limit K → ∞ this decision (whether i should copy the action of j) is made completely at random (as Π_i→j = 0.5). Note that, in the presence of noise, the Fermi rule allows agents to copy the action of neighbors that have a lower total payoff than them.

In this paper we investigate in detail how the emergent collective dynamics of a population of strategic agents is jointly affected by uncertainty in individual behavior and the topology of the network governing their interactions. We focus on systems of N = L × L agents (with L ranging between 48 and 128) that iteratively play a symmetric two-person game (PD or SH) against their neighbors (no self-interactions are considered) on a specified connection topology. The nature of the game is varied by using different values b for the temptation payoff. Agents synchronously update their actions (similar to Nowak and May [18], and Kuperman and Risau-Gusman [48]) using the aforementioned Fermi rule. By altering the intensity of noise (K), we also explore the role of uncertainty in the decision-making process. Finally, we observe how interpolating between a regular lattice (with periodic boundary conditions) and a random network by changing the rewiring probability p from 0 to 1 in the small-world network construction paradigm changes the nature of the collective states observed in the K − b parameter space. While there have been earlier studies of the phase diagrams of PD and SH games in spatially extended systems (see [9] for a review) as well as the effect of noise on their collective dynamics [49–58], there have been only a limited number of investigations into the nature of the phase transitions between the different regimes of collective behavior (see, for example, [47, 59–62]). Previous studies that have quantitatively analyzed the phase transition by measuring the critical exponents have focused on the transition obtained by changing the temptation payoff value b and have only considered asynchronous update schemes. In contrast, we investigate the “thermally-driven” transitions, i.e., those which arise upon varying the level of noise with synchronous (or parallel) updating of the states of the agents. Furthermore, we characterize the exponents using the method of finite-size scaling.

4. Results

When agents play IPD (i.e., b > 1) with neighbors on a lattice using the Fermi rule to update their actions, the system converges to one of two possible collective dynamical states depending on the choice of b and K. These correspond to (i) all agents defecting (all D), i.e., the fraction of cooperators f(C) = 0, and (ii) a fluctuating regime (0 < f(C) < 1) where each agent intermittently switches between cooperation and defection. At the interface of the all D and fluctuating regimes, we observe a long transient time in f(C) prior to the system converging to the final state, as is expected for critical slowing down in the neighborhood of a transition [63]. This is shown in Figure 2B for the case where the initial configuration is an equal mixture (50%) of cooperators and defectors, randomly distributed on a lattice (using a Moore neighborhood, i.e., each node has degree k = 8). We note that during this extended transient period cooperators tend to aggregate into a number of clusters of varying sizes. The formation of these clusters is driven by the fact that a cooperator receives a much higher aggregate payoff when its neighborhood has more cooperators [19]. On the other hand, defectors tend to benefit only if they are relatively isolated from other defectors. The boundaries of these clusters are unstable and evolve over time, as cooperators at the edge of a cluster find defection to be more lucrative and hence switch. For the case b < 1 (i.e., in the SH regime), a third collective state corresponding to all agents cooperating (all C: f(C) = 1) can be observed. We note that as agents can only adopt the actions of their neighbors the collective dynamical states corresponding to all C and all D are both absorbing states.

We next examine the collective dynamics over a range of values of b and K by varying the connection topology from a square lattice to a random network. This is done by choosing a range of different values of the rewiring parameter p. As seen in Figure 3, all three distinct regimes of collective dynamics can be observed in the generated networks. The three regimes, viz., all D, all C and fluctuating, interface at a single point in the resulting phase diagram. This is reminiscent of a “triple point” observed in the study of phase transitions in fluid systems. For the case of a lattice (p = 0) the all C regime is only observed for b < 1, i.e., in the SH regime, while fluctuation is observed for b > 1 for an intermediate range of values of K. In the limit of K → 0, where an agent deterministically chooses to copy the action of a randomly chosen neighbor if the latter's payoff is relatively higher, one may expect that the system will converge to an all D state for any b > 1. Indeed this is what we observe when the average degree is either very small or very large. Thus, increasing K can give rise to a reentrant phase behavior where the asymptotic state of the system in the PD regime can, for an optimal range of b, exhibit successive noise-driven order-to-disorder and disorder-to-order transitions. Specifically, the collective dynamical state of the system changes from the homogeneous all D (ordered) to the fluctuating (disordered) state and then back again to the all D state. However, for an intermediate range of average degree (including for k_avg = 8, used for all results shown here), we observe only the disorder-to-order transition. This is because the fluctuating regime exists even for K → 0 over a limited range of b(≥1). We note that, despite differences in the details of the models, this result is similar to the observation of non-zero fraction of cooperators reported for a range of b > 1 by Nowak and May [18] for their deterministic system.

FIGURE 3

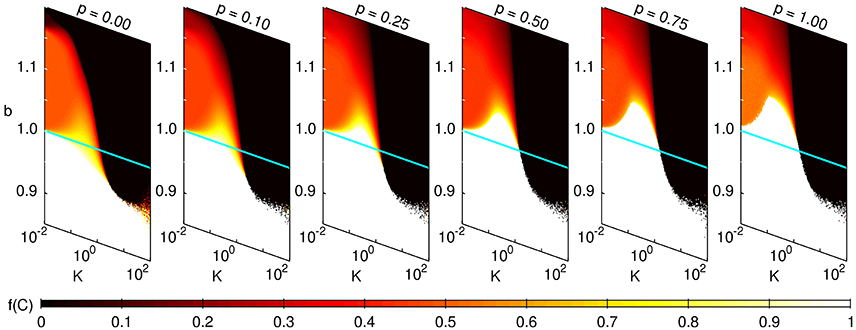
Figure 3. Phase diagrams for the fraction of cooperators on a network of size N = 128² and average degree k_avg = 8, displayed over a range of values of the temptation payoff b and noise K, for different values of the rewiring parameter p. The initial fraction of cooperators is 0.5. The color indicates the fraction of cooperators (f(C), whose value is indicated in the colorbar) in the system after 10⁴ iterations, with white corresponding to the case of all C (f(C) = 1) and black to all D (f(C) = 0). The blue horizontal line in each panel indicates b = 1, and demarcates the SH (b < 1) and PD (b > 1) regimes. For the case of a lattice (p = 0), we observe that a dynamical state corresponding to all C can only be achieved if b < 1, i.e., in the SH regime, while in the PD regime, this scenario will only emerge for larger p. The phase diagrams are constructed from single realizations of the dynamics for a given set of parameter values.

While increasing the temperature (or noise) is expected to drive a system from order to disorder, the reverse transition from the disordered or fluctuating state to the ordered all D state may appear surprising. A possible mechanism for the appearance of complete defection at higher values of K might be the noise-induced breakup of cooperator clusters. Similarly, an increase in the noise in the SH regime (b < 1) results in a transition from an all C to an all D state. As both all C and all D states are Nash-equilibria of the two-player SH, the appearance of only one of these states in the spatially extended system is presumably a symmetry-breaking effect of the implicit bounded rationality. The latter arises because interactions are restricted by the contact structure of the underlying network. Noise can then be seen as providing a mechanism for selecting between the two broken-symmetry absorbing states. For larger values of p, the all C state can be observed in the PD regime (b > 1) provided K is in an intermediate range. Thus, noise permits the appearance of an all C state in the PD regime as well as an all D state in the SH regime. We note that in earlier studies (e.g., [9]) which have investigated the state transitions in spatial games by varying b and K, the all D region is not observed in the SH regime (b < 1). This difference from our results can be explained as arising from the different updating schemes used, viz., asynchronous update, in contrast to the synchronous update scheme used here. We have explicitly verified that qualitatively similar results to those reported in the earlier studies are obtained by using an asynchronous update scheme. As p is increased further, the location of the triple point shifts from the b < 1 (SH) region to the b > 1 (PD) region.

For higher values of K, there appears to be a small region at the boundary between the all D and all C regimes characterized by 0 < f(C) < 1 (see Figure 3). We would like to emphasize that the dynamics in this region is qualitatively distinct from that in the fluctuating regime seen for small K. It is easy to see that in the limit of K → ∞ the system would either converge to an all C or all D state asymptotically regardless of b. However, convergence to these states can take extremely long times, much longer than the usual duration of simulations. Conversely, the fluctuating regime (which also has a mean value of f(C) between 0 and 1) is characterized by the fact that the asymptotic state is not one of the absorbing states. The time taken to converge to an absorbing state, τ_c, is displayed over a range of b and K in Figures 4A,B for the extreme cases p = 0 and p = 1, respectively. We observe that the all D and all C states in Figure 3 are characterized by small values of τ_c. The interface between these two absorbing states, examined in detail in Figures 4C,D, corresponding to an abrupt transition between f(C) = 0 and f(C) = 1, exhibits a divergence in the mean time 〈τ_c〉 required for the system to converge (shown for several system sizes). The fluctuating state, which by definition corresponds to a state distinct from any of the absorbing states, is characterized by τ_c having the maximum possible value, corresponding to the entire duration of simulation. Thus, as the divergence of τ_c cannot be used to characterize the order-disorder transition at the interface of the fluctuating and absorbing states, we have to identify the critical interface between them using a response function. For this purpose we consider the susceptibility of the order parameter [64]:

$\begin{array}{ll}\chi =N(\langle f^2(C)\rangle -{\langle f(C)\rangle }^2).& (2)\end{array}$

We next examine in detail the nature of the phase transitions between the three regimes of collective behavior for the extreme cases p = 0 and p = 1. For each of the transitions, we employ the following procedure. We first estimate the critical noise K_c(N) for each system size by obtaining the value of K at which the corresponding χ attains its peak χ_c(N). In order to determine how the critical noise scales with system size, we consider the expression [65]

$\begin{array}{ll}{K}_c(N)=K_c(\infty )+c{N}^{-1/\nu },& (3)\end{array}$

where K_c(∞) is the estimated critical noise for an infinitely large system, c is a constant and ν is a scaling exponent. As Equation (3) has three free parameters, we first estimate the parameter ν by considering the scaling of the width Δ(N) of the transition region of the order parameter with system size, viz., Δ(N) ~ N^−1/ν. To do this, we obtain the value of the order parameter at equidistant points around f_c(N), viz., $f_{1,2}(N)=f_c(N)\pm \frac{1}{2}df$ (we have chosen df = min[f_c(N), 1 − f_c(N)]). We then determine the noise strengths K_{1, 2}(N) at which the order parameter assumes the values f_{1, 2}(N). The width Δ(N) is calculated as the difference between K₁(N) and K₂(N), and least square fitting of log(Δ(N)) to log(N) provides an estimate of ν. The values of K_c(∞) and c in Equation (3) can then be obtained through a least square fit. Finally, we note that the value of the order parameter f_c(N) at the critical noise scales with system size as $f_c(N)~N^{-\beta /\nu }$, while the value of the susceptibility χ_c(N) at the critical noise scales with system size as ${\chi }_c(N)~N^{\gamma /\nu }$. Thus, least square fitting of log(f_c(N)) to log(N) provides the estimated value of β, while least square fitting of log(χ_c(N)) to log(N) provides the estimated value of γ. Note that for the case p = 0, the scaling is done with respect to $L(=\sqrt{N})$ rather than N.

FIGURE 4

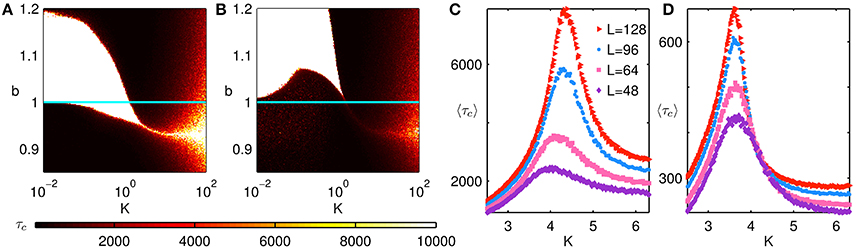
Figure 4. (A,B) Convergence time τ_c for agents on a network of size N = 128² and average degree k_avg = 8, for rewiring parameters (A) p = 0 and (B) p = 1. The blue horizontal line corresponds to b = 1, and demarcates the SH (b < 1) and PD (b > 1) regimes. Darker colors indicate a more rapid convergence to any one of the absorbing states (viz., all C or all D). We note that when K ≫ 1, larger values of τ_c are obtained. This is because at high noise intensity (high K), the system takes a long time to converge to an absorbing state. The regions marked as white in the high K regime correspond to the system not converging to the steady state within the duration of the simulation (10⁴ time steps). On the other hand, the white regions seen for lower K(≲1) correspond to the system persisting in a steady state, viz., the fluctuating regime. These two qualitatively different white regions can be differentiated by the sharpness of their boundaries. (C,D) The average convergence time 〈τ_c〉 as a function of K for the case (C) p = 0, b = 0.94 and (D) p = 1, b = 0.98. The results are averaged over 10³ trials, and shown for different system sizes. The situations displayed correspond to the transition between the all D and all C regimes. We observe that the convergence time at the interface of the two regimes diverges as the system size is increased.

We first consider the interface between the all D and fluctuating regimes. In Figures 5A,C we display the variation of average fraction of cooperators 〈f(C)〉 with noise noise K for the cases of p = 0 at b = 0.96 (a) and p = 1 at b = 1.05 (b), calculated over 10³ trials, for different system sizes N. We display the deviation of the order parameter 〈f(C)〉 from its value f_c(N) at the critical point K_c(N), scaled by N^β/ν. In Figures 5B,D we show the corresponding susceptibilities χ scaled by N^−γ/ν. We collapse the individual curves using finite size scaling. Thus, in Figures 5A,B the quantities are displayed as functions of the scaled abscissae $L^{1/\nu }(K-K_c(L))$, while in Figures 5C,D they are displayed as functions of the scaled abscissae $N^{1/\nu }(K-K_c(N))$. The two insets in Figure 5A show the obtained fit of Equation (3) to the critical noise K_c(L), with the estimated value of K_c(∞) displayed within (indicated by a black filled circle), as well as the least-square fit of log(f_c(L)) to log(L), with the estimated value of β/ν displayed. The two insets in Figure 5B show the least-square fit of log(Δ(L)) to log(L), with the estimated value of ν displayed within, as well as the least-square fit of log(χ_c(L)) to log(L), with the estimated value of γ/ν displayed. Similar insets are displayed in Figures 5C,D, which were obtained using N rather than L.

FIGURE 5

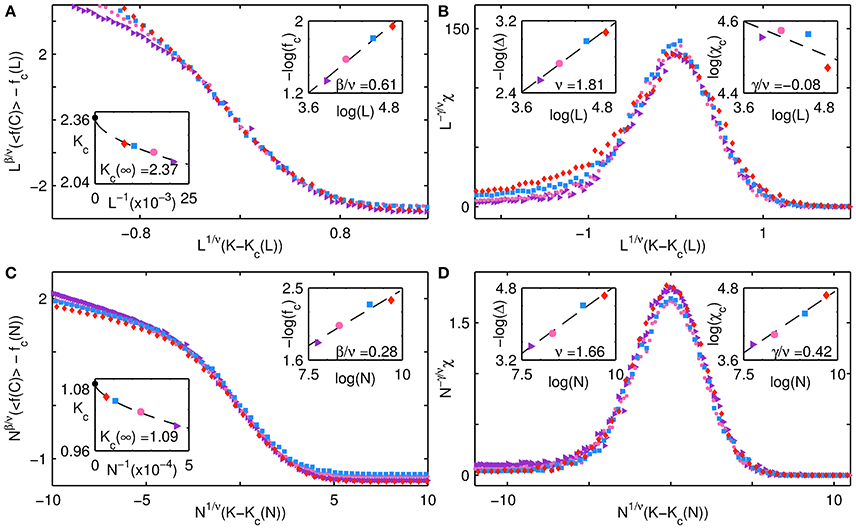
Figure 5. Collective behavior of a network of agents at the interface of all D and fluctuating regimes for different system sizes. Finite-size scaling results are shown for the cases (A,B) p = 0, b = 0.96, and (C,D) p = 1, b = 1.05. (A,C) show the order parameter, viz., mean fraction of cooperators 〈f(C)〉 (averaged over 10³ trials), while (B,D) show the corresponding dependence of the susceptibility χ [obtained from Equation (2) using values of f(C) obtained over 10³ trials] on K. The abscissae of each of the panels represents the deviation of the noise K from the critical noise value K_c(N), scaled by N^1/ν. The ordinate for (A,C) shows the deviation of the order parameter from its value f_c(N) at the critical point K_c(N), scaled by N^β/ν, while the ordinate for (B,D) shows the susceptibility scaled by N^γ/ν. The curves are seen to collapse upon using exponent values obtained from finite-size scaling, viz., (A,B) ν = 1.81 ± 0.14, β/ν = 0.61 ± 0.05, γ/ν = −0.08 ± 0.06 and (C,D) ν = 1.66 ± 0.14, β/ν = 0.28 ± 0.04, γ/ν = 0.42 ± 0.03. The insets in (A,C) show the least-square fits of Equation (3) to K_c and log(f_c) to log(N), while the insets in (B,D) show the least-square fits of log(Δ_c) to log(N) and log(χ_c) to log(N). Different symbols are used to indicate the different system sizes N for which the simulations were carried out, namely, a purple triangle (N = 48²), a pink circle (N = 64²), a blue square (N = 96²) and a red diamond (N = 128²). Note that for the case p = 0, i.e., (A,B), the scaling is in terms of L rather than N.

The collective behavior of the system at the interface between the fluctuating and all C regimes is examined in Figure 6. The panels show finite size scaling for the order parameter 〈f(C)〉 and response function χ for the extreme cases of p = 0 at b = 0.96 (a,b) and p = 1 at b = 1.05 (c,d). The critical exponents ν, β and γ are determined using methods that are discussed in the previous paragraph in the context of Figure 5. In Figure 7, we display corresponding results for the interface between the all C and all D regimes. Figures 7A,B show the behavior for the case of p = 0 at b = 0.94, while (Figures 7C,D) are for the case p = 1 at b = 0.98. We observe that the estimated values of the critical exponents β for the transition between all C and all D are effectively zero, independent of p, while ν ~ 1 for p = 0 and ν ~ 2 for p = 1. For the case of the regular lattice (p = 0) this implies that the width of the transition region simply scales as the length L of the lattice. Such a trivial scaling behavior is expected as this particular transition will be discontinuous in the thermodynamic limit, with the order parameter switching from a value equal to 0 in the all D state to a value equal to 1 in the all C state. For finite systems, the transition is less abrupt as the change in the value of the order parameter from 0 to 1 occurs over a transition region having finite width. In contrast, the other transitions, namely from all D to fluctuating, and from all C to fluctuating, are of a continuous nature, characterized by non-trivial values for the exponents ν, β, and γ.

FIGURE 6

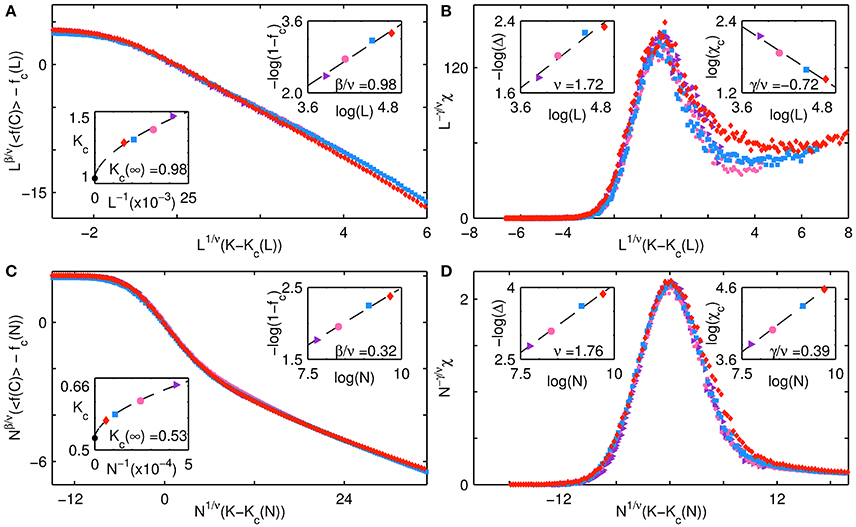
Figure 6. Collective behavior of a network of agents at the interface of the fluctuating and all C regimes for different system sizes. Finite-size scaling results are shown for the cases (A,B) p = 0, b = 0.96, and (C,D) p = 1, b = 1.05. (A,C) show the order parameter, viz., mean fraction of cooperators 〈f(C)〉 (averaged over 10³ trials), while (B,D) show the corresponding dependence of the susceptibility χ (obtained from Equation (2) using values of f(C) obtained over 10³ trials) on K. The abscissae of each of the panels represents the deviation of the noise K from the critical noise value K_c(N), scaled by N^1/ν. The ordinate for (A,C) shows the deviation of the order parameter from its value f_c(N) at the critical point K_c(N), scaled by N^β/ν, while the ordinate for (B,D) shows the susceptibility scaled by N^γ/ν. The curves are seen to collapse upon using exponent values obtained from finite-size scaling, viz., (A,B) ν = 1.72 ± 0.25, β/ν = 0.98 ± 0.10, γ/ν = −0.72 ± 0.06 and (C,D) ν = 1.76 ± 0.09, β/ν = 0.32 ± 0.02, γ/ν = 0.39 ± 0.01. The insets in (A,C) show the least-square fits of Equation (3) to K_c and log(1−f_c) to log(N), while the insets in (B,D) show the least-square fits of log(Δ_c) to log(N) and log(χ_c) to log(N). Different symbols are used to indicate the different system sizes N for which the simulations were carried out, namely, a purple triangle (N = 48²), a pink circle (N = 64²), a blue square (N = 96²) and a red diamond (N = 128²). Note that for the case p = 0, i.e., (A,B), the scaling is in terms of L rather than N.

FIGURE 7

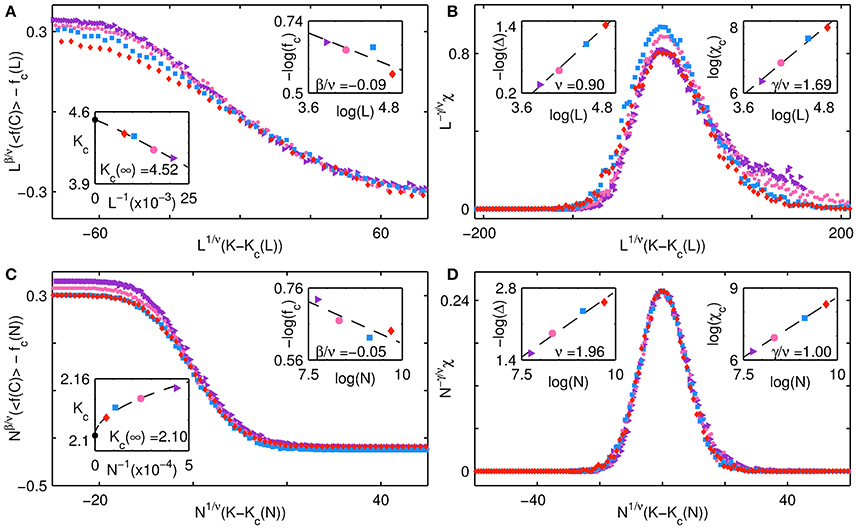
Figure 7. Collective behavior of a network of agents at the interface of the all D and all C regimes for different system sizes. Finite-size scaling results are shown for the cases (A,B) p = 0, b = 0.94, and (C,D) p = 1, b = 0.98. (A,C) Show the order parameter, viz., mean fraction of cooperators 〈f(C)〉 (averaged over 10³ trials), while (B,D) show the corresponding dependence of the susceptibility χ (obtained from Equation (2) using values of f(C) obtained over 10³ trials) on K. The abscissae of each of the panels represents the deviation of the noise K from the critical noise value K_c(N), scaled by N^1/ν. The ordinate for (A,C) shows the deviation of the order parameter from its value f_c(N) at the critical point K_c(N), scaled by N^β/ν, while the ordinate for (B,D) shows the susceptibility scaled by N^γ/ν. The curves are seen to collapse upon using exponent values obtained from finite-size scaling, viz., (A,B) ν = 0.90 ± 0.04, β/ν = −0.09 ± 0.04, γ/ν = 1.69 ± 0.12 and (C,D) ν = 1.96 ± 0.20, β/ν = −0.05 ± 0.02, γ/ν = 1.00 ± 10⁻⁴. The insets in (A,C) show the least-square fits of Equation (3) to K_c and log(f_c) to log(N), while the insets in (B,D) show the least-square fits of log(Δ_c) to log(N) and log(χ_c) to log(N). Different symbols are used to indicate the different system sizes N for which the simulations were carried out, namely, a purple triangle (N = 48²), a pink circle (N = 64²), a blue square (N = 96²) and a red diamond (N = 128²). Note that for the case p = 0, i.e., (A,B), the scaling is in terms of L rather than N.

5. Discussion

When played in a spatially extended setting the iterated PD game provides a framework for the investigation of the process of collective decision-making under conditions of bounded rationality. This is because agents are denied complete information about the entire system which would have allowed them to compute the optimal strategy. Specifically, while the payoff matrices are known and are identical for all agents, individuals only have knowledge of the choice of actions of that subset of agents with whom they had previously interacted (i.e., their topological neighbors). At each round, agents take into account the success of the actions adopted by their neighbors in the previous round and use this information to selectively copy an action to employ in the current round. Often this copying is done in a stochastic setting in order to capture the uncertainty associated with the incompleteness of an agent's knowledge about their environment. The copying process and stochasticity in the decision-making are additional factors that contribute to the deviation from perfect rationality. Here we have used a specific stochastic update (Fermi rule) that governs the probability with which an agent adopts the action of a randomly chosen neighbor. The uncertainty or noise associated with this process is quantified by the temperature K, which is one of the key parameters in our study. Another parameter that plays a crucial role in determining the collective dynamics is associated with the payoff matrix of the game, viz., the temptation T(= b) which is the payoff received by an agent upon unilateral defection. The value of b relative to R(= 1), i.e., the reward payoff for mutual cooperation, governs the nature of the game. As T decreases below R, the game changes from the Prisoner's Dilemma (characterized by an unique equilibrium that is given by the dominant strategy of mutual defection) to the Stag Hunt (characterized by multiple equilibria). The K − b parameter plane will hence exhibit different regimes of collective dynamics arising from the interplay between the distinct equilibria and the noise-driven fluctuations. Thus, on moving across the parameter plane one can expect to observe phase transitions between these regimes.

The principal collective dynamical regimes are a pair of absorbing states corresponding to homogeneous outcomes, viz., all agents cooperating (all C) and all agents defecting (all D), as well as a fluctuating regime where each agent switches intermittently between cooperation and defection. The existence of absorbing states implies that the observed transitions are necessarily non-equilibrium in nature. We observe that a regular lattice (p = 0) is unable to support an all C state in the PD regime (b > 1), regardless of the number of neighbors of each agent. We note that a novel aspect of our observation of all C in the PD regime for the case p = 1 is that we do not consider self-interactions, which was permitted in previous studies that reported this behavior [47, 62]. Also, while the two-player setting allows two coexisting equilibria in the SH regime (b < 1), we observe only a single asymptotic state for any specific choice of parameters for finite noise. Specifically, the all C state is the only regime that can observed at low noise, while at higher noise the all D state may also appear.

We have investigated in detail the transition between the different regimes and characterized them through measurement of the critical exponents using finite-size scaling. The transition between all D and all C is discontinuous, as it involves an abrupt change in the order parameter f(C), viz., the asymptotic fraction of cooperating agents. On the other hand, the transition from these absorbing states to the fluctuating regime is a continuous one, the latter collective state being characterized by persistent coexistence of cooperation and defection. This is reflected in the order parameter lying in the range 0<f(C)<1 in the fluctuating regime. It suggests that the junction of the interfaces of the three regimes of collective dynamics (all C, all D and fluctuating) is a bicritical point. The meeting of two critical (continuous) transition curves with a first-order (discontinuous) transition line is reminiscent of the situation seen in the anisotropic anti-ferromagnetic Heisenberg model (see Figure 4.6.11(A) of Chaikin and Lubensky [66]). An important feature of our simulation approach is the choice of synchronous (parallel) updating of the actions of the agents. We note that the synchronous update scheme has been cited earlier as the reason for certain non-equilibrium systems not exhibiting universality in their critical behavior [67, 68]. Thus, this could explain difference between the values of the critical exponents obtained by us that do not belong to the Directed Percolation (DP) universality class, unlike what has been reported in some previous studies [47, 62].

In addition to investigating the phase transitions for a specific nature of connection topology, we have studied how the collective dynamics changes as we interpolate between a lattice and a random network by rewiring links with probability p through the use of the small-world network construction paradigm. Upon considering the entire 3-dimensional p − K − b parameter space we find that the regime in which all agents are cooperating moves up in the K − b plane as p is increased. This helps explain the seemingly sudden emergence of complete cooperation in the PD regime when one changes the connection topology from a lattice to a random network while keeping the average number of neighbors fixed. We also show the existence of a triple point at which the different phases corresponding to the three collective states meet, similar to that seen in fluid systems. The location of this point in the parameter space depends on the coordination number (average degree) of the lattice (network), as well as p, and is thus related to the dimensionality of the space in which the system is embedded.

An important extension for the future will be a comparison of the nature of these transitions to other models of non-equilibrium phenomena (such as the Voter model [69]) and to see whether the exponents map to a well-known universality class. We note that the noise-induced uncertainty and the temptation payoff have an intuitive interpretation in terms of the parameters of interacting spin models, viz., temperature and external field, respectively. Thus, a strong analogy can be drawn between the phase diagrams of these two types of systems. Other open questions include the nature of the coarsening dynamics and the size distribution of the clusters of cooperating agents close to the order-disorder transition [11, 48, 70].

Author Contributions

SM, VS, and SS conceived and designed the experiment(s), SM performed the experiments, SM, VS, and SS analyzed the data, SM and SS wrote the paper. All authors reviewed the manuscript.

Funding

This research was supported in part by the IMSc Complex Systems (XII Plan) Project funded by the Department of Atomic Energy, Government of India.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Mustansir Barma, Chandrashekar Kuyyamudi, and Sidney Redner for helpful discussions. The simulations and computations required for this work were carried out using the Nandadevi and Satpura clusters at the IMSc High Performance Computing facility. The Satpura cluster is partly funded by the Department of Science and Technology, Government of India (Grant No. SR/NM/NS-44/2009) and the Nandadevi cluster is partly funded by the IT Research Academy (ITRA) under the Ministry of Electronics and Information Technology (MeitY), Government of India (ITRA-Mobile Grant No. ITRA/15(60)/DITNMD/01).

References

1. Hardin G. The tragedy of the commons. Science (1968) 162:1243–8. doi: 10.1126/science.162.3859.1243

CrossRef Full Text

2. Nowak MA. Five rules for the evolution of cooperation. Science (2006) 314:1560–3. doi: 10.1126/science.1133755

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Axelrod R. The Evolution of Cooperation. New York, NY: Basic Books (1984).

Google Scholar

4. Glance NS, Huberman BA. The dynamics of social dilemmas. Sci. Am. (1994) 270:76–81. doi: 10.1038/scientificamerican0394-76

CrossRef Full Text | Google Scholar

5. Gore J, Youk H, Van Oudenaarden A. Snowdrift game dynamics and facultative cheating in yeast. Nature (2009) 459:253–6. doi: 10.1038/nature07921

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature (2006) 441:502–5. doi: 10.1038/nature04605

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Axelrod R, Hamilton WD. The evolution of cooperation. Science (1981) 211:1390–6. doi: 10.1126/science.7466396

CrossRef Full Text | Google Scholar

8. Myerson RB. Game Theory. Cambridge, MA: Harvard University Press (2013).

Google Scholar

9. Szabó G, Fath G. Evolutionary games on graphs. Phys Rep. (2007) 446:97–216. doi: 10.1016/j.physrep.2007.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Santos FC, Rodrigues JF, Pacheco JM. Graph topology plays a determinant role in the evolution of cooperation. Proc R Soc B (2006) 273:51–5. doi: 10.1098/rspb.2005.3272

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Gòmez-Gardeñes J, Campillo M, Floría LM, Moreno Y. Dynamical organization of cooperation in complex topologies. Phys Rev Lett. (2007) 98:108103. doi: 10.1103/PhysRevLett.98.108103

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hauert C, Szabó G. Game theory and physics. Am J Phys. (2005) 73:405–14. doi: 10.1119/1.1848514

CrossRef Full Text | Google Scholar

13. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

14. Hauert C. Fundamental clusters in spatial 2 × 2 games. Proc R Soc B (2001) 268:761–9. doi: 10.1098/rspb.2000.1424

CrossRef Full Text | Google Scholar

15. Kuhn S. Prisoner's Dilemma. In: EN Zalta editor. Stanford Encyclopedia of Philosophy. Fall ed. (2014) Available online at: http://plato.stanford.edu/archives/fall2014/entries/prisoner-dilemma/

Google Scholar

16. Rapoport A, Guyer M. A taxonomy of 2x2 games. Gen Syst. (1966) 11:203–14.

17. Rapoport A. Two-Person Game Theory: The Essential Ideas. Ann Arbor, MI: University of Michigan Press (1966).

Google Scholar

18. Nowak MA, May RM. Evolutionary games and spatial chaos. Nature (1992) 359:826–9. doi: 10.1038/359826a0

CrossRef Full Text | Google Scholar

19. Nowak MA, May RM. The spatial dilemmas of evolution. Int J Bif Chaos (1993) 3:35–78. doi: 10.1142/S0218127493000040

CrossRef Full Text | Google Scholar

20. Rapoport A, Chammah AM. The game of Chicken. Am Behav Sci. (1966) 10:10–28. doi: 10.1177/000276426601000303

CrossRef Full Text | Google Scholar

21. Kümmerli R, Colliard C, Fiechter N, Petitpierre B, Russier F, Keller L. Human cooperation in social dilemmas: comparing the Snowdrift game with the Prisoners Dilemma. Proc R Soc B (2007) 274:2965–70. doi: 10.1098/rspb.2007.0793

CrossRef Full Text | Google Scholar

22. Skyrms B. The Stag Hunt and the Evolution of Social Structure. Cambridge: Cambridge University Press (2004).

Google Scholar

23. Osborne MJ, Rubenstein A A Course in Game Theory. Cambridge, MA: MIT Press (1994).

Google Scholar

24. Davis LH. Prisoners, Paradox, and Rationality. Am Philos Q. (1977) 14:319–27

Google Scholar

25. Sasidevan V, Sinha S. Symmetry warrants rational cooperation by co-action in social dilemmas. Sci Rep. (2015) 5:13071. doi: 10.1038/srep13071

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sasidevan V, Sinha S. Co-action provides rational basis for the evolutionary success of Pavlovian strategies. Sci Rep. (2016) 6:30831. doi: 10.1038/srep30831

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Neyman A. Cooperation in repeated games when the number of stages is not commonly known. Econometrica (1999) 67:45–64. doi: 10.1111/1468-0262.00003

CrossRef Full Text | Google Scholar

28. Aumann R. Acceptable points in general cooperative n-person games. In: Luce RD, Tucker AW, editors. Contributions to the Theory of Games IV. Princeton, NJ: Princeton University Press (1959). p. 287–324.

29. Nowak M. Evolutionary Dynamics: Exploring the Equations of Life. Cambridge, MA: Harvard University Press (2006).

30. Perc M, Gómez-Gardeñes J, Szolnoki A, Floría LM, Moreno Y. Evolutionary dynamics of group interactions on structured populations: a review. J R Soc Interface (2013) 10:1–17. doi: 10.1098/rsif.2012.0997

PubMed Abstract | CrossRef Full Text

31. Wu Z-X, Xu X-J, Chen Y, Wang Y-H. Spatial prisoner's dilemma game with volunteering in Newman-Watts small-world networks. Phys Rev E (2005) 71:037103. doi: 10.1103/PhysRevE.71.037103

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Perc M. Double resonance in cooperation induced by noise and network variation for an evolutionary prisoner's dilemma. New J Phys. (2006) 8:183. doi: 10.1088/1367-2630/8/9/183

CrossRef Full Text | Google Scholar

33. Masuda N. Participation costs dismiss the advantage of heterogeneous networks in evolution of cooperation. Proc R Soc B (2007) 274:1815–21. doi: 10.1098/rspb.2007.0294

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Szolnoki A, Perc M, Danku Z. Making new connections towards cooperation in the prisoner's dilemma game. EPL (2008) 84:50007. doi: 10.1209/0295-5075/84/50007

CrossRef Full Text | Google Scholar

35. Floría LM, Gracia-Lázaro C, Gómez-Gardeñes J, Moreno Y. Social network reciprocity as a phase transition in evolutionary cooperation. Phys Rev E (2009) 79:026106. doi: 10.1103/PhysRevE.79.026106

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Szolnoki A, Perc M, Szabó G. Phase diagrams for three-strategy evolutionary prisoner's dilemma games on regular graphs. Phys Rev E (2009) 80:056104. doi: 10.1103/PhysRevE.80.056104

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Perc M, Szolnoki A. Coevolutionary games - a minireview. Biosystems (2010) 99:109–25. doi: 10.1016/j.biosystems.2009.10.003

CrossRef Full Text | Google Scholar

38. Wang Z, Kokubo S, Tanimoto J, Fukuda E, Shigaki K. Insight into the so-called spatial reciprocity. Phys Rev E (2013) 88:042145. doi: 10.1103/PhysRevE.88.042145

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Gianetto DA, Heydari B. Network modularity is essential for evolution of cooperation under uncertainty. Sci Rep. (2015) 5:9340. doi: 10.1038/srep09340

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett. (2005) 95:098104. doi: 10.1103/PhysRevLett.95.098104

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Santos FC, Pacheco JM, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl Acad Sci USA. (2006) 103:3490–4. doi: 10.1073/pnas.0508201103

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Watts D, Strogatz S. Collective dynamics of ‘small-world' networks. Nature (1998) 393:440–2. doi: 10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Abramson G, Kuperman M. Social games in a social network. Phys Rev E (2001) 63:030901. doi: 10.1103/PhysRevE.63.030901

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kim BJ, Trusina A, Holme P, Minnhagen P, Chung JS, Choi MY. Dynamic instabilities induced by asymmetric influence: Prisoners dilemma game in small-world networks. Phys Rev E (2002) 66:021907. doi: 10.1103/PhysRevE.66.021907

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Masuda N, Aihara K. Spatial Prisoner's dilemma optimally played in small-world networks. Phys Lett A (2003) 313:55–61. doi: 10.1016/S0375-9601(03)00693-5

CrossRef Full Text | Google Scholar

46. Tomochi M. Defectors' niches: Prisoner's dilemma game on disordered networks. Soc Netw. (2004) 26:309–21. doi: 10.1016/j.socnet.2004.08.003

CrossRef Full Text | Google Scholar

47. Szabó G, Tőke C. Evolutionary Prisoner's dilemma game on a square lattice. Phys Rev E (1998) 58:69–73. doi: 10.1103/PhysRevE.58.69

CrossRef Full Text | Google Scholar

48. Kuperman M, Risau-Gusman S. Relationship between clustering coefficient and the success of cooperation in networks. Phys Rev E (2012) 86:016104. doi: 10.1103/PhysRevE.86.016104

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Szabó G, Vukov J, Szolnoki A. Phase diagrams for an evolutionary Prisoner's dilemma game on two-dimensional lattices. Phys Rev E (2005) 72:047107. doi: 10.1103/PhysRevE.72.047107

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Vukov J, Szabó G, Szolnoki A. Cooperation in the noisy case: Prisoner's dilemma game on two types of regular random graphs. Phys Rev E (2006) 73:067103. doi: 10.1103/PhysRevE.73.067103

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Perc M. Coherence resonance in a spatial prisoner's dilemma game. New J Phys. (2006) 8:22. doi: 10.1088/1367-2630/8/2/022

CrossRef Full Text | Google Scholar

52. Perc M, Marhl M. Evolutionary and dynamical coherence resonances in the pair approximated Prisoner's dilemma game. New J Phys. (2006) 8:142. doi: 10.1088/1367-2630/8/8/142

CrossRef Full Text | Google Scholar

53. Ren J, Wang W-X, Qi F. Randomness enhances cooperation: a resonance-type phenomenon in evolutionary games. Phys Rev E (2007) 75:045101. doi: 10.1103/PhysRevE.75.045101

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Perc M. Transition from gaussian to levy distributions of stochastic payoff variations in the spatial Prisoner's dilemma game. Phys Rev E (2007) 75:022101. doi: 10.1103/PhysRevE.75.022101

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Vukov J, Szabó G, Szolnoki A. Evolutionary Prisoner's dilemma game on Newman-Watts networks. Phys Rev E (2008) 77:026109. doi: 10.1103/PhysRevE.77.026109

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Szolnoki A, Vukov J, Szabó G. Selection of noise level in strategy adoption for spatial social dilemmas. Phys Rev E (2009) 80:056112. doi: 10.1103/PhysRevE.80.056112

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Szabó G, Szolnoki A, Vukov J. Selection of dynamical rules in spatial Prisoner's Dilemma games EPL (2009) 87:18007. doi: 10.1209/0295-5075/87/18007

CrossRef Full Text | Google Scholar

58. Helbing D, Yu W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc Natl Acad Sci USA. (2009) 106:3680–5. doi: 10.1073/pnas.0811503106

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Szabó G, Hauert C. Phase transitions and volunteering in spatial public goods games. Phys Rev Lett. (2002) 89:118101. doi: 10.1103/PhysRevLett.89.118101

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Wang W-X, Lü J, Chen G, Hui PM. Phase transition and hysteresis loop in structured games with global updating. Phys Rev E (2008) 77:046109. doi: 10.1103/PhysRevE.77.046109

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Helbing D, Lozano S. Phase transitions to cooperation in the Prisoner's dilemma. Phys Rev E (2010) 81:057102. doi: 10.1103/PhysRevE.81.057102

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Santos M, Ferreira AL, Figueiredo W. Phase diagram and criticality of the two-dimensional Prisoner's dilemma model. Phys Rev E (2017) 96:012120. doi: 10.1103/PhysRevE.96.012120

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Landau DP, Binder K. A Guide to Monte Carlo Simulations in Statistical Physics. Cambridge: Cambridge University Press (2015).

64. Marro J, Dickman R. Nonequilibrium Phase Transitions in Lattice Models. Cambridge: Cambridge University Press (1999).

Google Scholar

65. Stauffer D. Introduction to Percolation Theory. Taylor & Francis (1994).

Google Scholar

66. Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. Cambridge: Cambridge University Press (1995).

Google Scholar

67. Rolf J, Bohr T, Jensen MH. Directed percolation universality in asynchronous evolution of spatiotemporal intermittency. Phys Rev E (1998) 57:R2503–6. doi: 10.1103/PhysRevE.57.R2503

CrossRef Full Text | Google Scholar

68. Bohr T, van Hecke M, Mikkelsen R, Ipsen M. Breakdown of universality in transitions to spatiotemporal chaos. Phys Rev E (2001) 86:5482–5. doi: 10.1103/PhysRevLett.86.5482

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Dornic I, Chaté H, Chave J, Hinrichsen H. Critical coarsening without surface tension: the universality class of the voter model. Phys Rev Lett. (2001) 87:045701. doi: 10.1103/PhysRevLett.87.045701

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Assenza S, Gómez-Gardeñes J, Latora V. Enhancement of cooperation in highly clustered scale-free networks. Phys Rev E (2008) 78:017101. doi: 10.1103/PhysRevE.78.017101

PubMed Abstract | CrossRef Full Text | Google Scholar