
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
HYPOTHESIS AND THEORY article
Front. Phys. , 16 November 2017
Sec. High-Energy and Astroparticle Physics
Volume 5 - 2017 | https://doi.org/10.3389/fphy.2017.00057
This article is part of the Research Topic The Physics Associated with Neutrino Masses View all 9 articles
The λ mechanism (WL − WR exchange) of the neutrinoless double beta decay (0νββ-decay), which has origin in left-right symmetric model with right-handed gauge boson at TeV scale, is investigated. The revisited formalism of the 0νββ-decay, which includes higher order terms of nucleon current, is exploited. The corresponding nuclear matrix elements are calculated within quasiparticle random phase approximation with partial restoration of the isospin symmetry for nuclei of experimental interest. A possibility to distinguish between the conventional light neutrino mass (WL − WL exchange) and λ mechanisms by observation of the 0νββ-decay in several nuclei is discussed. A qualitative comparison of effective lepton number violating couplings associated with these two mechanisms is performed. By making viable assumption about the seesaw type mixing of light and heavy neutrinos with the value of Dirac mass mD within the range 1 MeV < mD < 1 GeV, it is concluded that there is a dominance of the conventional light neutrino mass mechanism in the decay rate.
The Majorana nature of neutrinos, as favored by many theoretical models, is a key for understanding of tiny neutrino masses observed in neutrino oscillation experiments. A golden process for answering this open question of particle physics is the neutrinoless double beta decay (0νββ-decay) [1–3],
in which an atomic nucleus with Z protons decays to another one with two more protons and the same mass number A, by emitting two electrons and nothing else. The observation of this process, which violates total lepton number conservation and is forbidden in the Standard Model, guaranties that neutrinos are Majorana particles, i.e., their own antiparticles [4].
The searches for the 0νββ-decay have not yielded any evidence for Majorana neutrinos yet. This could be because neutrinos are Dirac particles, i.e., not their own antiparticles. In this case we will never observe the decay. However, it is assumed that the reason for it is not sufficient sensitivity of previous and current 0νββ-decay experiments to the occurrence of this rare process.
Due to the evidence for neutrino oscillations and therefore for 3 neutrino mixing and masses the 0νββ-decay mechanism of primary interest is the exchange of 3 light Majorana neutrinos interacting through the left-handed V-A weak currents (mββ mechanism). In this case, the inverse 0νββ-decay half-life is given by Vergados et al. [1], DellOro et al. [2] and Vergados et al. [3]
where G01, gA and Mν represent an exactly calculable phase space factor, the axial-vector coupling constant and the nuclear matrix element (whose calculation represents a severe challenge for nuclear theorists), respectively. me is the mass of an electron. The effective neutrino mass,
is a linear combination of the three neutrino masses mi, weighted with the square of the elements Uei of the first row of the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) neutrino mixing matrix. The measured value of mββ would be a source of important information about the neutrino mass spectrum (normal or inverted spectrum), absolute neutrino mass scale and the CP violation in the neutrino sector. However, that is not the only possibility.
There are several different theoretical frameworks that provide various 0νββ-decay mechanisms, which generate masses of light Majorana neutrinos and violate the total lepton number conservation. One of those theories is the left-right symmetric model (LRSM) [5–9], in which corresponding to the left-handed neutrino, there is a parity symmetric right-handed neutrino. The parity between left and right is restored at high energies and neutrinos acquire mass through the see-saw mechanism, what requires presence of additional heavy neutrinos. In general one cannot predict the scale where the left-right symmetry is realized, which might be as low as a few TeV—accessible at Large Hadron Collider, or as large as GUT scale of 1015 GeV.
The LRSM, one of the most elegant theories beyond the Standard Model, offers a number of new physics contributions to 0νββ-decay, either from right-handed neutrinos or Higgs triplets. The main question is whether these additional 0νββ-mechanisms can compete with the mββ mechanism and affect the 0νββ-decay rate significantly. This issue is a subject of intense theoretical investigation within the TeV-scale left-right symmetry theories [10–14]. In analysis of heavy neutrino mass mechanisms of the 0νββ-decay an important role plays a study of related lepton number and lepton flavor violation processes in experiments at Large Hadron Collider [2, 15–19].
The goal of this article is to discuss in details the WL − WR exchange mechanism of the 0νββ-decay mediated by light neutrinos (λ mechanism) and its coexistence with the standard mββ mechanism. For that purpose the corresponding nuclear matrix elements (NMEs) will be calculated within the quasiparticle random phase approximation with a partial restoration of the isospin symmetry [20] by taking the advantage of improved formalism for this mechanism of the 0νββ-decay of Štefánik [21]. A possibility to distinguish mββ and λ mechanisms in the case of observation of the 0νββ-decay on several isotopes will be analyzed. Further, the dominance of any of these two mechanisms in the 0νββ-decay rate will be studied within seesaw model with right-handed gauge boson at TeV scale. We note that a similar analysis was performed by exploiting a simplified 0νββ-decay rate formula and different viable particle physics scenarios in Tello et al. [10], Barry and Reodejohann [11], Bhupal Dev et al. [12], Deppisch et al. [13] and Borah et al. [14].
Recently, the 0νββ-decay with the inclusion of right-handed leptonic and hadronic currents has been revisited by considering exact Dirac wave function with finite nuclear size and electron screening of emitted electrons and the induced pseudoscalar term of hadron current, resulting in additional nuclear matrix elements [21]. In this section we present the main elements of the revisited formalism of the λ mechanism of the 0νββ-decay briefly. Unlike in Štefánik et al. [21] the effect the weak-magnetism term of the hadron current on leading NMEs is taken into account.
If the mixing between left and right vector bosons is neglected, for the effective weak interaction hamiltonian density generated within the LRSM we obtain
Here, Gβ = GF cos θC, where GF and θC are Fermi constant and Cabbibo angle, respectively. The coupling constant λ is defined as
Here, MWL and MWR are masses of the Standard Model left-handed WL and right-handed WR gauge bosons, respectively. The left- and right-handed leptonic currents are given by
The weak eigenstate electron neutrinos νeL and νeR are superpositions of the light and heavy mass eigenstate Majorana neutrinos νj and Nj, respectively. We have
Here, U, S, T, and V are the 3 × 3 block matrices in flavor space, which constitute a generalization of the Pontecorvo-Maki-Nakagawa-Sakata matrix, namely the 6 × 6 unitary neutrino mixing matrix [22]
The nuclear currents are, in the non-relativistic approximation, [23]
Here, mN is the nucleon mass. , , and are, respectively, the vector, axial-vector, weak-magnetism and induced pseudoscalar form-factors. The nucleon recoil terms are given by
where qn = pn − is the momentum transfer between the nucleons. The initial neutron (final proton) possesses energy (En) and momentum (pn). rn, and , which act on the n-th nucleon, are the position operator, the isospin raising operator and the Pauli matrix, respectively.
By assuming standard approximations [21] for the 0νββ-decay half-life we get
The effective lepton number violating parameters ην (WL − WL exchange), ηλ (WL − WR exchange) and their relative phase Ψ are given by
The coefficients CI (I = mm, mλ and λλ) are linear combinations of products of nuclear matrix elements and phase-space factors:
The explicit form and calculated values of phase-space factors G0i (i = 1, 2, 3, 4, 10 and 11) of the 0νββ-decaying nuclei of experimental interest are given in Štefánik et al. [21]. The NMES, which constitute the coefficients CI in Equation (13), are defined as follows:
The partial nuclear matrix elements MI, where I = GT, F, T, ωF, ωGT, ωT, qF, qGT, and qT are given by
Here, OF,GT,T are the Fermi, Gamow-Teller and tensor operators and . The two-nucleon exchange potentials hI(r) with I = F, GT, T, ωF, ωGT, ωT, qF, qGT, and qT can be written as
where
and
Here, Ei, Ef and Ēn are energies of the initial and final nucleus and averaged energy of intermediate nuclear states, respectively. r = (rr − rs), rr, s is the coordinate of decaying nucleon and ji(qr) (i = 1, 2, 3) denote the spherical Bessel functions. , and , where q is the momentum exchange. The form factors , , and are defined in Simkovic et al. [24]. We note that factor 4 in definition of the two-nucleon exchange potentials hI(r) with I = ωF, ωGT, and ωT in Equation (48) of Štefánik et al. [21] needs to be replaced by factor 2.
The nuclear matrix elements are calculated in proton-neutron quasiparticle random phase approximation with partial restoration of the isospin symmetry for 48Ca, 76Ge, 82Se, 96Zr, 100Mo, 110Pd, 116Cd, 124Sn, 130Te and 136Xe, which are of experimental interest. In the calculation the same set of nuclear structure parameters is used as in Simkovic et al. [20]. The pairing and residual interactions as well as the two-nucleon short-range correlations derived from the realistic nucleon-nucleon Argonne V18 potential are considered [26]. The closure approximation for intermediate nuclear states is assumed with (Ēn − (Ei + Ef)/2) = 8 MeV. The free nucleon value of axial-vector coupling constant (gA = 1.25 − 1.27) is considered.
In Table 1 the calculated NMEs are presented. The values of MF,GT,T and Mν differ slightly (within 10%) with those given in Simkovic et al. [20], which were obtained without consideration of the closure approximation. By glancing Table 1 we see that MFω, GTω, Tω ≃ MF,GT,T and Mνω ≃ Mν as for the average neutrino momentum q = 100 MeV and used average energy of intermediate nuclear states we have q/(q + Ēn − (Ei + Ef)/2) ≃ 1. The absolute value of MFq, GTq, Tq is smaller in comparison with MF,GT,T by about 50% for Fermi NMEs and by about factor two in the case of Gamow-Teller and tensor NMEs. From Table 1 it follows that there is a significant difference between results of this work and the QRPA NMEs of Muto et al. [25], especially in the case of 100Mo. This difference can be attributed to the progress achieved in the 0νββ-decay formalism due to inclusion of higher order terms of nucleon currents [21, 24], the way of adjusting the parameters of nuclear Hamiltonian [27], description of short-range correlations [26] and restoration of the isospin symmetry [20].
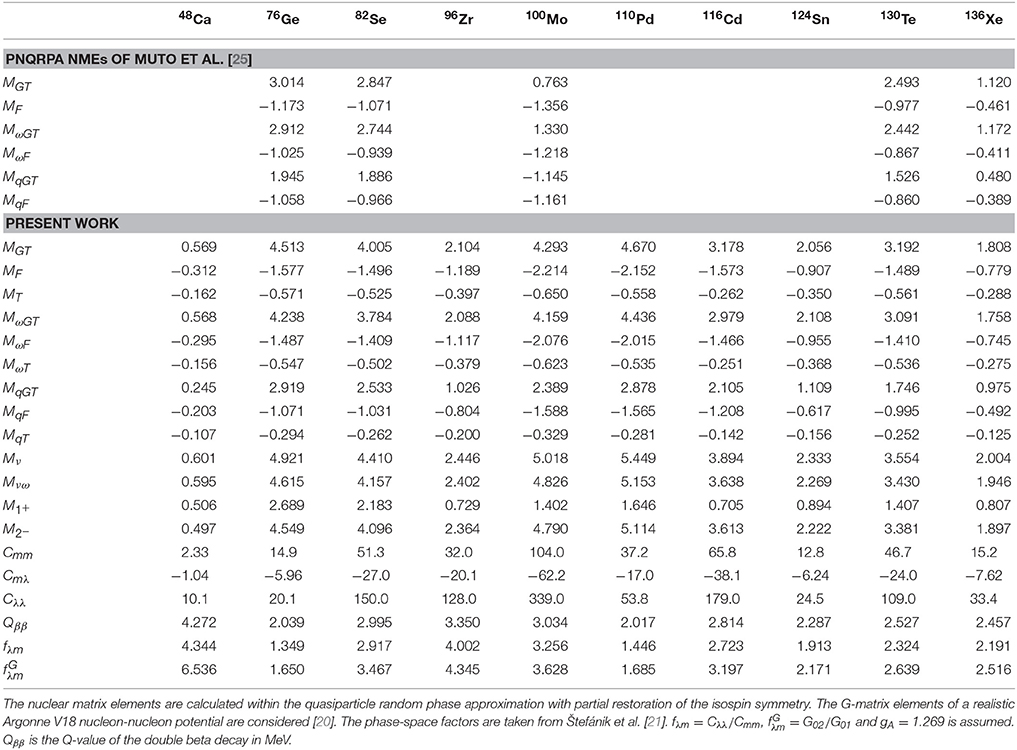
Table 1. The nuclear matrix elements of the 0νββ-decay associated with mββ and λ mechanisms and the coefficients Cmm, Cmλ and Cλλ (in 10−14 years−1) of the decay rate formula (see Equation 11).
Nuclear matrix elements , (λ mechanism) and Mν (mββ mechanism) for 10 nuclei under consideration are given in Table 1 and displayed in Figure 1. We note a rather good agreement between and Mν for all calculated nuclear systems. It is because the contribution of M1+ to M2− is suppressed by factor 9 and as a result M2− is governed by the Mνω contribution (see Equation 14). Values of exhibit similar systematic behavior in respect to considered nuclei as values of Mν and , but they are suppressed by about factor 2–3 (with exception of 48Ca).
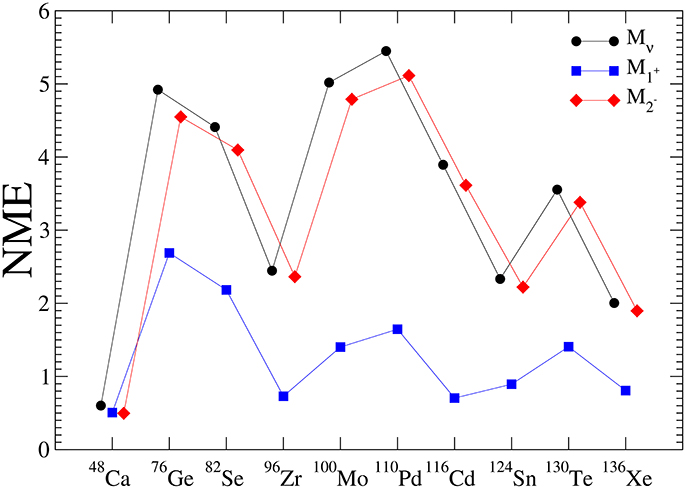
Figure 1. A comparison of the nuclear matrix elements M1+, M2− (λ mechanism) and Mν (mββ mechanism) of the 0νββ-decay.
The importance of the mββ and λ mechanisms depends, respectively, not only on values of ην and ηλ parameters, which are unknown, but also on values of coefficients CI (I = mm, mλ, λλ), which are listed for all studied nuclei in Table 1. They have been obtained by using improved values of phase-space factors G0k (k = 1, 2, 10 and 11) from Štefánik et al. [21]. We note that the squared value of MGT and fourth power of axial-vector coupling constant gA are included in the definition of coefficient CI unlike in Štefánik et al. [21]. We see that Cλλ is always larger when compared with Cmm. The absolute value of Cmλ is significantly smaller than Cmm and Cλλ. This fact points out on less important contribution to the 0νββ-decay rate from the interference of mββ and λ mechanisms.
For 10 nuclei of experimental interest the decomposition of coefficient Cλλ (see Equation 11) on partial contributions associated with phase-space factors G0k (k = 2, 10, and 11) is shown in Figure 2. By glancing the plotted ratio we see that Cλλ is dominated by a single contribution associated with the phase-space factor G02. From this and above analysis it follows that 0νββ-decay half-life to a good accuracy can be written as
with
For a given isotope the factor fλm reflects relative sensitivity to the mββ and λ mechanisms and is its approximation, which does not depend on NMEs. The values fλm and are tabulated in Table 1 and plotted as function of Qββ in Figure 3. We see that fλm depends only weakly on involved nuclear matrix elements (apart for the case of 48Ca) what follows from a comparison of fλm with . The value of fλm is mainly determined by the Q-value of double beta decay process. From 10 analyzed nuclei the largest value of fmλ is found for 48Ca and the smallest value for 76Ge. A larger value of fλm means increased sensitivity to mββ mechanism in comparison to λ mechanism and vice versa.
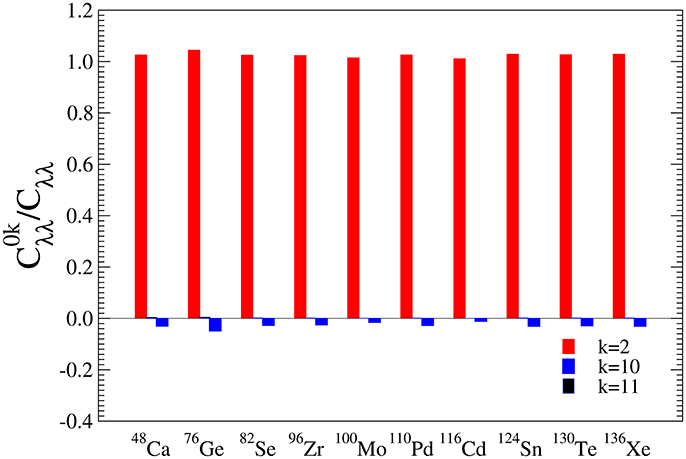
Figure 2. The decomposition of coefficient Cλλ (see Equation 11) on partial contributions associated with phase-space factors G0k (k = 2, 10 and 11) for nuclei of experimental interest. The partial contributions are identified by index k. The contributions from largest to the smallest are displayed in red, blue and black colors, respectively.
Figure 3. The factor fλm (see Equation 19) as function of Q-value of the double beta decay process (Qββ) plotted from the numbers of Table 1.
Upper bounds on the effective neutrino mass mββ and right-handed current coupling strength ηλ are deduced from experimental half-lives of the 0νββ-decay by using the coefficients Cmm, Cmλ and Cλλ of Table 1. The maximum and the value on axis (mββ = 0 or ηλ = 0) are listed in Table 2. The decays of 136Xe and 76Ge set the sharpest limit mββ ≤ 0.13 eV and 0.18 eV, and and 3.1 10−7, respectively. These are more stringent than those deduced from other experimental sources.
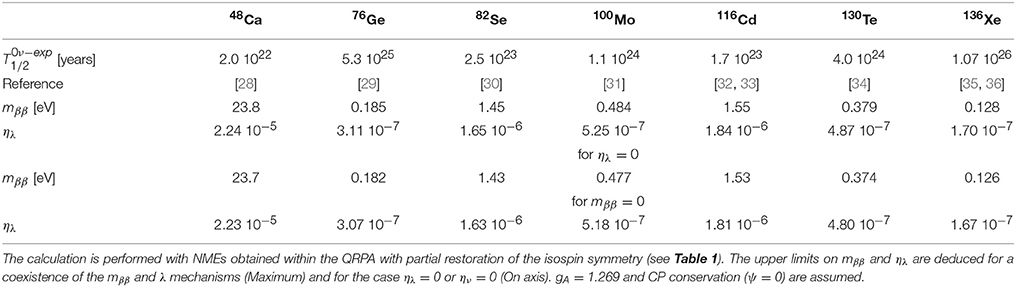
Table 2. Upper bounds on the effective Majorana neutrino mass mββ and parameter ηλ associated with right-handed currents mechanism imposed by current constraints on the 0νββ-decay half-life for nuclei of experimental interest.
It is well known that by measuring different characteristics, namely energy and angular distributions of two emitted electrons, it is possible to identify which of mββ and λ mechanisms is responsible for 0νββ-decay [21, 23]. It might be achieved only by some of future 0νββ-decay experiments, e.g., the SuperNEMO [37] or NEXT [38]. A relevant question is whether the underlying mββ or λ mechanism can be revealed by observation of the 0νββ-decay in a series of different isotopes. In Figure 4 this issue is addressed by an illustrative case of observation of the 0νββ-decay of 136Xe with half-life years, which can be associated with mββ = 50 meV or ηλ = 9.8 10−8. The 0νββ-decay half-life predictions associated with a dominance of mββ and λ mechanisms exhibit significant difference for some nuclear systems. We see that by observing, e.g., the 0νββ-decay of 100Ge and 100Mo with sufficient accuracy and having calculated relevant NMEs with uncertainty below 30%, it might be possible to conclude, whether the 0νββ-decay is due to mββ or λ mechanism.
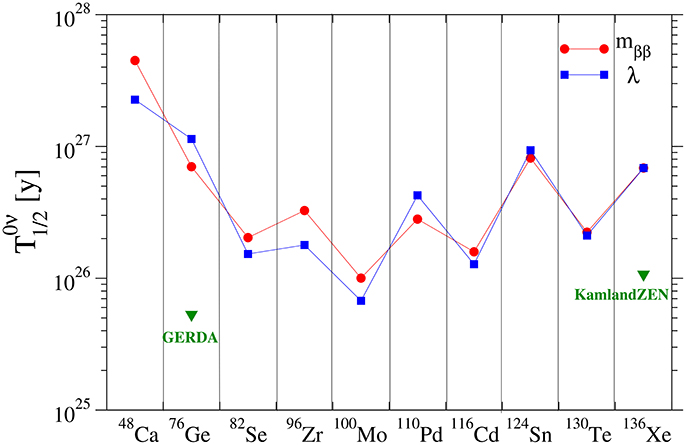
Figure 4. The 0νββ-decay half-lives of nuclei of experimental interest calculated for mββ (red circle) and λ (blue square) mechanisms by assuming an illustrative case of observation 0νββ-decay of 136Xe with half-life years (mββ = 50 meV or ηλ = 9.8 10−8). The current experimental limits on 0νββ-decay half-life of 76Ge (the GERDA experiment) and 136Xe (the Kamland-Zen experiment) are displayed with green triangles.
Currently, the uncertainty in calculated 0νββ-decay NMEs can be estimated up to factor of 2 or 3 depending on the considered isotope as it follows from a comparison of results of different nuclear structure approaches [3]. The improvement of the calculation of double beta decay NMEs is a very important and challenging problem. There is a hope that due to a recent progress in nuclear structure theory (e.g., ab initio methods) and increasing computing power the calculation of the 0νββ-decay NMEs with uncertainty of about 30 % might be achieved in future.
The 6 × 6 unitary neutrino mixing matrix (see Equation 8) can be parametrized with 15 rotational angles and 10 Dirac and 5 Majorana CP violating phases. For the purpose of study different LRSM contributions to the 0νββ-decay the mixing matrix is usually decomposed as follows [22]
Here, 0 and 1 are the 3 × 3 zero and identity matrices, respectively. The parametrization of matrices A, B, R and S and corresponding orthogonality relations are given in Xing [22].
If A = 1, B = 1, R = 0 and S = 0, there would be a separate mixing of light and heavy neutrinos, which would participate only in left and right-handed currents, respectively. In this case we get ηλ = 0, i.e., the λ mechanism is forbidden.
If masses of heavy neutrinos are above the TeV scale, the mixing angles responsible for mixing of light and heavy neutrinos are small. By neglecting the mixing between different generations of light and heavy neutrinos, the unitary mixing matrix takes the form
Here, mD represents energy scale of charged leptons and mLNV is the total lepton number violating scale, which corresponds to masses of heavy neutrinos. We see that U = U0 can be identified to a good approximation with the PMNS matrix and V0 is its analogue for heavy neutrino sector. Due to unitarity condition we find . Within this scenario of neutrino mixing the effective lepton number violating parameters ην (mββ mechanism) and ηλ (λ mechanism) are given by
with
The importance of mββ or λ-mechanism can be judged from the ratio
It is naturally to assume that ζm ≈ 1 and to consider the upper bound for the factor ζλ, i.e., there is no anomaly cancellation among terms, which constitute these factors. Within this approximation ηλ/ην does not depend on scale of the lepton number violation mLNV and is plotted in Figure 5. The Dirac mass mD is assumed to be within the range 1 MeV < mD < 1 GeV. The flavor and CP-violating processes of kaons and B-mesons make it possible to deduce lower bound on the mass of the heavy vector boson MW2>2.9 TeV [12]. From Figure 5 it follows that within accepted assumptions the λ mechanism is practically excluded as the dominant mechanism of the 0νββ-decay.
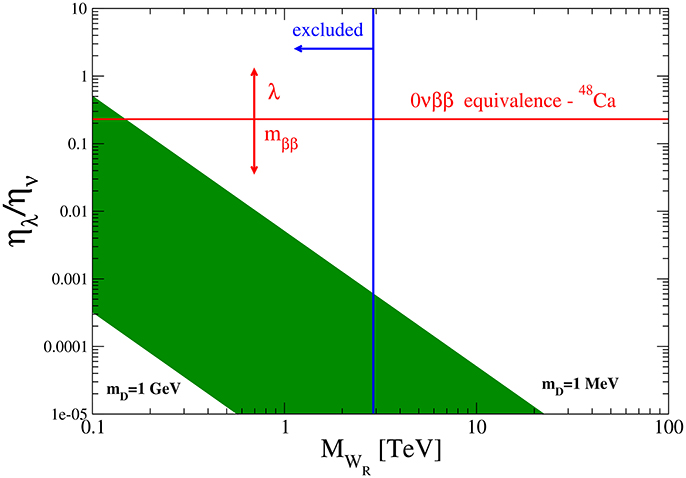
Figure 5. The allowed range of values for the ratio ηλ/ην (in green) as a function of the mass of the heavy vector boson MWR. The line of the 0νββ equivalence corresponds to the case of equal importance of both mββ and λ mechanisms in the 0νββ-decay rate.
In this section the light-heavy neutrino mixing of the strength mD/mLNV is considered. However, we note that there are models with heavy neutrinos mixings where strength of the mixing decouples from neutrino masses [39–44]. This subject goes beyond the scope of this paper.
The left-right symmetric model of weak interaction is an attractive extension of the Standard Model, which may manifest itself in the TeV scale. In such case the Large Hadron Collider can determine the right-handed neutrino mixings and heavy neutrino masses of the seesaw model. The LRSM predicts new physics contributions to the 0νββ half-life due to exchange of light and heavy neutrinos, which can be sizable.
In this work the attention was paid to the λ mechanism of the 0νββ-decay, which involves left-right neutrino mixing through mediation of light neutrinos. The recently improved formalism of the 0νββ-decay concerning this mechanism was considered. For 10 nuclei of experimental interest NMEs were calculated within the QRPA with a partial restoration of the isospin symmetry. It was found that matrix elements governing the conventional mββ and λ mechanisms are comparable and that the λ contribution to the decay rate can be associated with a single phase-space factor. A simplified formula for the 0νββ-decay half-life is presented (see Equation 19), which neglects the suppressed contribution from the interference of both mechanisms. In this expression the λ contribution to decay rate is weighted by the factor fλm, which reflects relative sensitivity to the mββ and λ mechanisms for a given isotope and depends only weakly on nuclear physics input. It is manifested that measurements of 0νββ-decay half-life on multiple isotopes with largest deviation in the factor fλm might allow to distinguish both considered mechanisms, if involved NMEs are known with sufficient accuracy.
Further, upper bounds on effective lepton number violating parameters mββ (ην) and ηλ were deduced from current lower limits on experimental half-lives of the 0νββ-decay. The ratio ηλ/ην was studied as function of the mass of heavy vector boson MWR assuming that there is no mixing among different generations of light and heavy neutrinos. It was found that if the value of Dirac mass mD is within the range 1 MeV < mD < 1 GeV, the current constraint on MWR excludes the dominance of the λ mechanism in the 0νββ-decay rate for the assumed neutrino mixing scenario.
FŠ: calculation of nuclear matrix elements and preparation of manuscript; RD: analysis of lepton number violating parameters and preparation of manuscript; DŠ: derivation of the formalism of neutrinoless double beta decay, and analysis of obtained results.
This work is supported by the VEGA Grant Agency of the Slovak Republic un- der Contract No. 1/0922/16, by Slovak Research and Development Agency under Contract No. APVV-14-0524, RFBR Grant No. 16-02-01104, Underground laboratory LSM—Czech participation to European-level research infrastructue CZ.02.1.01/0.0/0.0/16 013/0001733.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Vergados JD, Ejiri H, Šimkovic F. Theory of neutrinoless double beta decay. Rep Prog Phys. (2012) 71:106301. doi: 10.1088/0034-4885/75/10/106301
2. Dell'Oro S, Marcocci S, Viel M, Vissani F. Neutrinoless double beta decay: 2015 review. Adv High Energy Phys. (2016) 2016:2162659. doi: 10.1155/2016/2162659
3. Vergados JD, Ejiri H, Šimkovic F. Neutrinoless double beta decay and neutrino mass. Int J Mod Phys E (2016) 25:1630007. doi: 10.1142/S0218301316300071
4. Schechter J, Valle JWF. Neutrinoless Double beta Decay in SU(2) × U(1) Theories. Phys Rev D (1982) 25:2951–4. doi: 10.1103/PhysRevD.25.2951
5. Pati JC, Salam A. Lepton number as the fourth “color”. Phys Rev D (1974) 10:275–89. doi: 10.1103/PhysRevD.10.275
6. Mohapatra R, Pati JC. “Natural” left-right symmetry. Phys Rev D (1975) 11:2558–61. doi: 10.1103/PhysRevD.11.2558
7. Senjanović G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D (1975) 12:1502–4. doi: 10.1103/PhysRevD.12.1502
8. Mohapatra RN, Senjanović G. Neutrino mass and spontaneous parity nonconservation. Phys Rev Lett. (1980) 44:912–5. doi: 10.1103/PhysRevLett.44.912
9. Mohapatra RN, Senjanović G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev D (1981) 23:165–80. doi: 10.1103/PhysRevD.23.165
10. Tello V, Nemevšek M, Nesti F, Senjanović G, Vissani F. Left-right symmetry: from the LHC to neutrinoless double beta decay. Phys Rev Lett. (2011) 106:151801. doi: 10.1103/PhysRevLett.106.151801
11. Barry J, Reodejohann W. Lepton number and flavour violation in TeV-scale left-right symmetric theories with large left-right mixing. JHEP (2013) 1309:153. doi: 10.1007/JHEP09(2013)153
12. Bhupal Dev PS, Goswami S, Mitra M. TeV-scale left-right symmetry and large mixing effects in neutrinoless double beta decay. Phys Rev D (2015) 91:113004. doi: 10.1103/PhysRevD.91.113004
13. Deppisch F, Harz J, Hirsch M, Huang W, Päs H. Falsifying high-scale baryogenesis with neutrinoless double beta decay and lepton flavor violation. Phys Rev D (2015) 92:036005. doi: 10.1103/PhysRevD.92.036005
14. Borah D, Dasgupta A, Patra S. Dominant light-heavy neutrino mixing contribution to 0νββ in minimal left-right symmetric model with universal seesaw. arXiv: 1706.02456.
15. Nemevšek M, Nesti F, Senjanović G, Zhang Y. First limits on left-right symmetry scale from LHC data. Phys Rev D (2011) 83:115014. doi: 10.1103/PhysRevD.83.115014
16. Helo JC, Hirsch M, Päs H, Kovalenko SG. Short-range mechanisms of neutrinoless double beta decay at the LHC. Phys Rev D (2013) 88:073011. doi: 10.1103/PhysRevD.88.073011
17. Gluza J, Jelinski T. Heavy neutrinos and the pp → lljj CMS data. Phys Lett B (2015) 748:125–31. doi: 10.1016/j.physletb.2015.06.077
18. Gonzales L, Helo JC, Hirsch M, Kovalenko SG. Scalar-mediated double beta decay and LHC. JHEP (2016) 1612:130. doi: 10.1007/JHEP12(2016)130
19. Gluza J, Jelinski T, Szafron R. Lepton number violation and ‘Diracness' of massive neutrinos composed of Majorana states. Phys Rev D (2016) 93:113017. doi: 10.1103/PhysRevD.93.113017
20. Šimkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys Rev C (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501
21. Štefánik D, Dvornický R, Šimkovic F, Vogel P. Reexamining the light neutrino exchange mechanism of the 0νββ decay with left- and right-handed leptonic and hadronic currents. Phys Rev C (2015) 92:055502. doi: 10.1103/PhysRevC.92.055502
22. Xing Z. Full parametrization of the 6 × 6 flavor mixing matrix in the presence of three light or heavy sterile neutrinos. Phys Rev D (2012) 85:013008. doi: 10.1103/PhysRevD.85.013008
23. Doi M, Kotani T, Takasugi E. Double beta decay and majorana neutrino. Prog Theor Phys Suppl. (1985) 83:1–175. doi: 10.1143/PTPS.83.1
24. Šimkovic F, Pantis G, Vergados JD, Faessler A. Additional nucleon current contributions to neutrinoless double β decay. Phys Rev C (1999) 60:055502. doi: 10.1103/PhysRevC.60.055502
25. Muto K, Bender E, Klapdor HV. Nuclear structure effects on the neutrinoless double beta decay. Z Phys A (1989) 334:187–94. doi: 10.1007/BF01294219
26. Šimkovic F, Faessler A, Muether H, Rodin V, Stauf M. 0νββ-decay nuclear matrix elements with self-consistent short-range correlations. Phys Rev C (2009) 79:055501. doi: 10.1103/PhysRevC.79.055501
27. Rodin VA, Faessler A, Šimkovic F, Vogel P. Uncertainty in the 0νββ decay nuclear matrix elements Phys Rev C (2003) 68:044302. doi: 10.1103/PhysRevC.68.044302
28. Arnold R, Augier C, Bakalyarov AM, Baker JD, Barabash AS, Basharina-Freshville A, et al. Measurement of the double-beta decay half-life and search for the neutrinoless double-beta decay of 48Ca with the NEMO-3 detector. Phys Rev D (2016) 93:112008. doi: 10.1103/PhysRevD.93.112008
29. Agostini M, Allardt M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, et al. Background free search for neutrinoless double beta decay with GERDA Phase II. Nature (2017) 544:47–52. doi: 10.1038/nature21717
30. Arnold R, Augier C, Baker J, Barabash A, Broudin G, Brudanin V, et al. First results of the search for neutrinoless double-beta decay with the NEMO 3 detector. Phys Rev Lett. (2005) 95:182302. doi: 10.1103/PhysRevLett.95.182302
31. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Results of the search for neutrinoless double-β decay in 100Mo with the NEMO-3 experiment. Phys Rev D (2015) 92:072011. doi: 10.1103/PhysRevD.92.072011
32. Danevich FA, Bizzeti PG, Fazzini TF, Georgadze AS, Kobychev VV, Kropivyansky BN, et al. Double β decay of 116Cd. Final results of the Solotvina experiment and CAMEO project. Nucl Phys Proc Suppl. (2005) 138:230–2. doi: 10.1016/j.nuclphysbps.2004.11.056
33. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the 2νββ decay half-life and search for the 0νββ decay of 116Cd with the NEMO-3 detector. Phys Rev D (2017) 95:012007. doi: 10.1103/PhysRevD.95.012007
34. Alfonso K, Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, et al. Search for neutrinoless double-beta decay of 130Te with CUORE-0. Phys Rev Lett. (2015) 115:102502. doi: 10.1103/PhysRevLett.115.102502
35. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503
36. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the 2νββ decay half-life of 150Nd and a search for 0νββ decay processes with the full exposure from the NEMO-3 detector. Phys Rev D (2016) 94:072003. doi: 10.1103/PhysRevD.94.072003
37. Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, Bongrand M, et al. Probing new physics models of neutrinoless double beta decay with SuperNEMO. Eur Phys J C (2010) 70:927–43. doi: 10.1140/epjc/s10052-010-1481-5
38. Álvarez V, Ball M, Batallé M, Bayarri J, Borges FIG, Cárcel S, et al. The NEXT-100 experiment for neutrinoless double beta decay searches (Conceptual Design Report). arXiv: 1106.3630 (2011).
39. Pilaftsis A. Radiatively induced neutrino masses and large higgs-neutrino couplings in the standard model with majorana fields. Z Phys C (1992) 55:275–82. doi: 10.1007/BF01482590
41. Kersten J, Smirnov AY. Right-handed neutrinos at LHC and the mechanism of neutrino mass generation. Phys Rev D (2007) 76:073005. doi: 10.1103/PhysRevD.76.073005
42. Deppisch FF, Pilaftsis A. Lepton flavour violation and theta(13) in minimal resonant leptogenesis. Phys Rev D (2012) 83:076007. doi: 10.1103/PhysRevD.83.076007
43. Mitra M, Senjanović G, Vissani F. Neutrinoless double beta decay and heavy sterile neutrinos. Nucl Phys B (2012) 856:26–73. doi: 10.1016/j.nuclphysb.2011.10.035
Keywords: majorana neutrinos, neutrinoless double beta decay, right-handed current, left-right symmetric models, nuclear matrix elements, quasiparticle random phase approximation
Citation: Šimkovic F, Štefánik D and Dvornický R (2017) The λ Mechanism of the 0νββ-Decay. Front. Phys. 5:57. doi: 10.3389/fphy.2017.00057
Received: 01 August 2017; Accepted: 27 October 2017;
Published: 16 November 2017.
Edited by:
Diego Aristizabal Sierra, Federico Santa María Technical University, ChileReviewed by:
Janusz Gluza, University of Silesia of Katowice, PolandCopyright © 2017 Šimkovic, Štefánik and Dvornický. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fedor Šimkovic, c2lta292aWNAZm1waC51bmliYS5zaw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.