Stochastic Model of Acidification, Activation of Hemagglutinin and Escape of Influenza Viruses from an Endosome

1. Introduction

For most viruses, the initial step of infection starts when the viral particles bind to specific receptors and enter the cell through the membrane, inside an endosomal compartment (Figure 1). Viral particles are then transported inside the endosome, from the cell periphery towards the nucleus. Several modeling approaches, including kinetics rate equations [1], stochastic modeling [2, 3] and mechanics of molecular binding [4] have been developed to describe how membrane receptors are activated and engaged into endosomal pathways. However, little attention has been devoted to study viral trafficking inside an endosome, which is a critical and limiting step in replication and more generally to gene delivery [5–8].

FIGURE 1

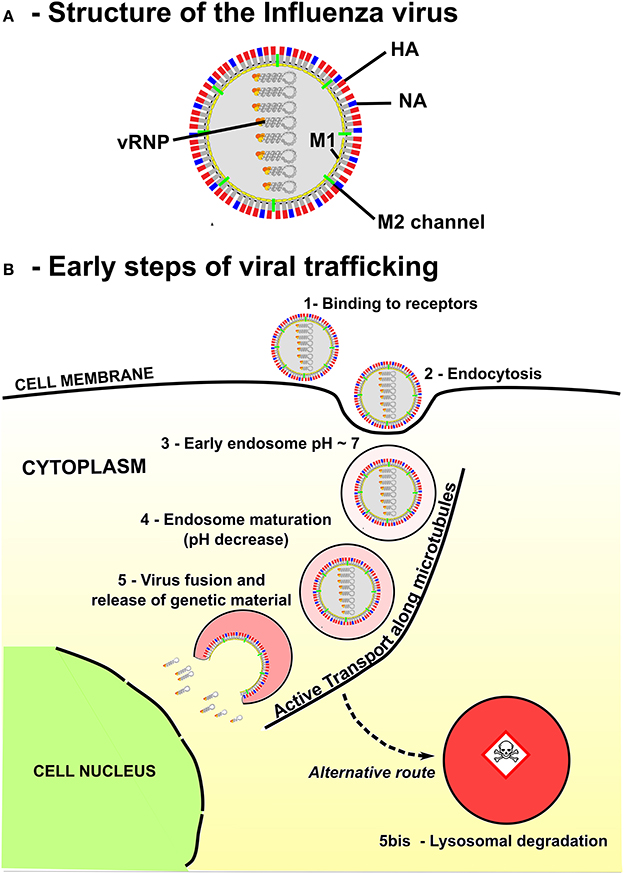
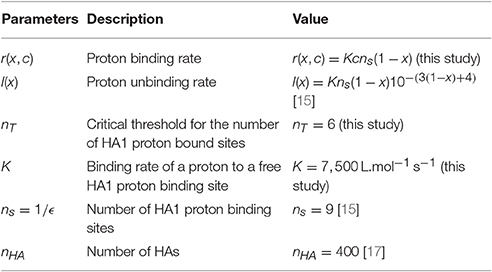
Figure 1. Structure and endosomal trafficking of the Influenza virus. (A) Influenza is an enveloped virus. Main spike proteins anchored in the envelope are the neuraminidase (NA) and the Hemagglutinin (HA). Protons can access the core of the virus through M2 channels. Main matrix protein is M1 protein. Viral genome of the virus is composed by eight viral ribonucleoproteins (vRNPs). (B) Influenza virus enters the cell via receptor-mediated endocytosis and progress rapidly toward an early endosome. Then, maturation is associated with an acidification of the endosome lumen and a retrograde transport of the endosome along the microtubules toward the nucleus, the destination of vRNPS for virus replication. The final destination of many endosomes is the degradative lysosomes. Thus, the timing of Influenza virus escape has to be tightly regulated to avoid degradation in lysosomes while delivering the genetic material close to the nucleus.

Cytoskeleton retrograde flow plays a key role for the Influenza virus transport inside the endosome toward the cell nucleus and to ensure a safe delivery of its genome near the nucleus, before replication [9, 10]. During this transport, the endosome can fuse with lysosomes, leading in that case to viral degradation. Thus, escaping the endosome at the right time must be tightly regulated to ensure that genes are released as close as possible from the nucleus, while avoiding degradation. Our goal here is to develop a first-principles model and the associated stochastic analysis to study this optimal escape time, and how it is controlled by acidification and conformational changes of viral proteins. The stochastic model developed in Lagache et al. [11] is inappropriate to compute the viral escape time based on the activation of a single molecule, and we develop here a different approach based on the mass-action equation for acidification.

The genome of Influenza virus is encoded by viral ribonucleoproteins (vRNPs) enveloped in a membrane. These vRNPs must translocate into the nucleus [12] (Figure 1) for reproduction. Endosomal escape is ensured by fusion between the endosomal and Influenza virus membrane. This fusion is mediated by a low pH conformational change of the viral glycoprotein hemagglutinin (HA) (Figure 1A). We account here for the detailed properties of the glycoprotein HA, composed of two linked subunits HA1 and HA2, the latter anchoring HA to the viral envelope. At neutral pH, HA is not active (in a non-fusogenic state), but as the pH decreases due to acidification (proton entry into the endosome), a partial dissociation of the HA1 subunit results in a spring-loaded conformational change of HA2 into an active (fusogenic) state [13]. Consequently, the residence time of the Influenza virus genome within an endosome before fusion depends on the kinetics of endosome acidification. Yet, the absence of direct in vivo measurements of these parameters makes the endosomal step of virus infection difficult to analyze both theoretically and experimentally. To estimate the timing of the pH-driven fusion of Influenza viruses, the model we develop here accounts for the main kinetic parameters of the fusion process: endosomal acidification, binding of protons to HAs and independent activation of multiple HA neighbors, leading to membrane fusion and release of the genome into the cytoplasm.

The manuscript is organized as follow: Section 2.1 presents the kinetic model for endosomal acidification, calibrated to experimental data (Figures in the SI). The model depends on the buffering capacity of the endosome, membrane leakage and proton pumping rate that controls proton fluxes inside the endosome. In Section 2.2, we model the discrete and cumulative binding of protons to HAs using a Markov jump process [14]. We find an analytical expression for the kinetics of HA conformational change at a fixed proton concentration, by analyzing the mean first passage time (MFPT) equation for the number of bound protons to a given threshold. In our previous work [11], we developed a jump model for the conformational change of active proteins for the escape of non-enveloped Adeno-Associated Viruses (AAV) from a vesicle. Contrary to the assumptions of [11], the binding rates of protons to HAs are non-linear [15] and thus we obtain here a different analytical expressions for the MFPT of bound protons to the critical threshold. Finally, in Section 2.3, we combine the kinetic models of acidification and HA conformational change and estimate the rate of HAs' activation inside the endosome. While the conformational change of a single protein for AAV is sufficient to lyse the endosome and release genes in cytoplasm, the Influenza virus is covered by 400 HAs and several adjacent HAs seems required for fusion.

We predict here the mean number of fusogenic HAs in the endosome and use Monte-Carlo simulations to compute the time needed for neighboring HAs to change conformation in the contact zone between the viral and endosomal membrane: we find that at least three adjacent activated HAs are necessary to trigger membrane fusion [16, 17], a cooperativity process that should prevent premature fusion. Some predictions are tested experimentally using co-labeling viruses and endosomal markers, confirming that intracellular fusion of viruses mainly occur in maturing endosomes (ME).

2. Results

2.1. Kinetic Model of Endosomal Acidification

The present model of endosomal acidification is based on computing the free number of protons P_e(t) at time t in the endosomal compartment. The protons enter with an entry rate λ(t)S through the V-ATPase proton pumps (S is the endosomal surface area and the rate λ(t) is associated with the proton pumps activity) and can escape with a leakage rate L_ext(t), but can also bind to endosomal buffers.

The proton pump rate λ(t) is mainly determined by the membrane potential Ψ(t) (Figure 11 in Grabe et al. [18]), which depends on the endosomal concentrations of several cations (H⁺, K⁺, Na⁺ …) and (Cl⁻ …). The ionic concentrations inside endosome are tightly regulated by channels, exchangers and leak and in particular, by raising the interior-positive membrane potential, Na-K ATPase exchangers have been proposed to limit the acidification of early compared to late endosomes [19].

2.1.1. Mass Action Law for Free Protons

To derive the time-dependent equations for the free protons, we use the balance of fluxes: the fast equilibrium between fluxes determines the number of protons ΔP_e(t) entering the endosome during the time step Δt

$\begin{array}{ll}\Delta P_e=\left(\lambda (t)S-L_{ext}(t)\right)\Delta t.& (1)\end{array}$

Entering protons are rapidly bound to endosomal buffers that we model using an ensemble of acid-base reactions [20]:

$\begin{array}{ll}{P}_e+B_1\stackrel{k_1}{\underset{k_1^{(-1)}}{\rightleftharpoons }}{P}_e\text{-}{B}_1,P_e+B_2\stackrel{k_2}{\underset{k_2^{(-1)}}{\rightleftharpoons }}{P}_e\text{-}{B}_2\dots ,P_e+B_n\stackrel{k_n}{\underset{k_n^{(-1)}}{\rightleftharpoons }}{P}_e\text{-}{B}_n,& (2)\end{array}$

where k_i (resp. $k_i^{(-1)}$) are binding (resp. unbinding) rate constants of protons to weak bases B_i, for 1 ≤ i ≤ n. The binding rates of entering protons to the endosomal basis can be reduced to a single constant that we call the effective buffering capacity ${\beta }_e^0$ of the endosome. The kinetics equation for the number of free protons P_e(t) inside an endosome is (Section 4)

$\begin{array}{ll}\frac{d{P}_e(t)}{dt}=\left(\lambda -L\frac{P_e(t)}{N_A{V}_e}\right)\frac{S\log (10)P_e(t)}{N_A{V}_e{\beta }_e^0}.& (3)\end{array}$

When the proton leakage is counterbalanced by the pump activity, after a time long enough, the pH reaches an asymptotic value pH_∞, where the endosome cannot be further acidified. This value is given by

$\begin{array}{ll}{P}_e(\infty )=N_A{V}_e{10}^{-{\text{pH}}_{\infty }},& (4)\end{array}$

Consequently, the rate λ depends on pH_∞ with

$\begin{array}{ll}\lambda =L{10}^{-{\text{pH}}_{\infty }},& (5)\end{array}$

and Equation (3) can be rewritten as

$\begin{array}{ll}\frac{d{P}_e(t)}{dt}=\left({10}^{-{\text{pH}}_{\infty }}-\frac{P_e(t)}{N_A{V}_e}\right)\frac{LS\log (10)P_e(t)}{N_A{V}_e{\beta }_e^0}.& (6)\end{array}$

To conclude, we derived here a first order kinetic model (Equation 32) for the endosome acidification, based on the rapid equilibration of protons with buffer (see Equation 36). However, Equation (6) alone is not sufficient to account for endosomal maturation, because the final pH_∞ [12] and the permeability L decreases with the endosomal maturation [19] as they depend on time, as we analyse below.

2.1.2. Modeling pH Change and Acidification of an Endosome

Acidification in live cell imaging and the transition from an early endosome (EE) to a late endosome (LE) is monitored by a gradual exchange of Rab5/Rab7 proteins [21]. We approximate here the kinetics of the ratio Rab5/Rab7 (Figure 4C in Rink et al. [21]) by a sigmoidal function

$\begin{array}{ll}\frac{\text{Rab7(t)}}{\text{Rab5(t)}+\text{Rab7(t)}}=\frac{1}{1+e^{-(t-t_{1/2})/{\tau }_c}},& (7)\end{array}$

with the two free parameters: the half-maturation t_1/2 and Rab conversion τ_c times. The steady-state pH_∞(t) relative to the amount of Rab7 is given by

$\begin{array}{ll}{\text{pH}}_{\infty }(t)={\text{pH}}_{\infty }^{\text{early}}+\left({\text{pH}}_{\infty }^{\text{late}}-{\text{pH}}_{\infty }^{\text{early}}\right)\frac{\text{Rab7(t)}}{\text{Rab5(t)}+\text{Rab7(t)}}.& (8)\end{array}$

Thus we propose that the permeability rate follows the Equation

$\begin{array}{ll}\text{L}(t)=L^{\text{early}}+\left(L^{\text{late}}-L^{\text{early}}\right)\frac{\text{Rab7(t)}}{\text{Rab5(t)}+\text{Rab7(t)}}.& (9)\end{array}$

2.1.3. Acidification Model Calibrated from Live Cell Imaging Kinetics

We now explain the calibration of the acidification model to experimental data: First, we fitted Equation (7) to the experimental data (Figure 4C of Rink et al. [21]) where the lag time between initiation and termination of the Rab5/Rab7 permutation is estimated to 10 min., leading to a time constant for τ_c = 100s.

We use data from endosomal acidification in MDCK cells where the pH inside endosomes decreases very quickly within the first 10–15 min (Figure 2) to reach a steady-state pH around 5.5 after 20 min, in agreement with [22]. The steady-state pH is ${\text{pH}}_{\infty }^{\text{early}}=6.0$ and ${\text{pH}}_{\infty }^{\text{late}}=5.5$ for early and late endosomes respectively [23]. Thus, we calibrated the permeability constant L and Rab conversion kinetics by solving numerically Equation 6 and fitting the experimental acidification curve (Figure 2). We found that the permeabilities of early and late endosomes are $L^{\text{early}}=3.510^{-3}{N}_A{\text{cm s}}^{-1}$ and $L^{\text{late}}=0.1N_A{\text{cm s}}^{-1}$, respectively, and the half-maturation time is t_1/2 = 10 min.

FIGURE 2

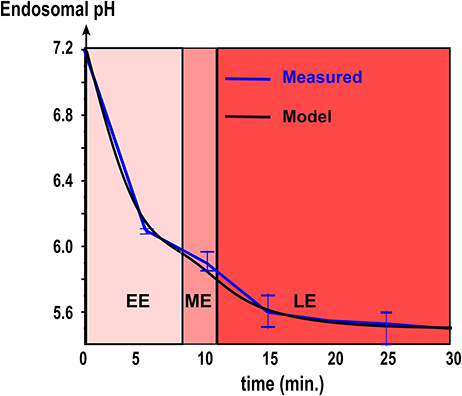
Figure 2. Endosomal acidification. The kinetics of acidification obtained with intracellular fluorescence microscopy (red line. Mean ± SEM) is compared with coarse-grained modeling (Equation 6, black line. Model parameters are summarized in Table 1).

2.1.4. Proton Influx Inside the Viral Core and Buffering

The last step of the kinetic model includes the buffering of protons to viral core components, defining the buffer capacity. Indeed, protein buffering capacity, influx of protons through M2-channels inside the viral core (Figure 1A) and the presence of viruses inside endosomes influences the overall buffering capacity of the endosome and acidification. To compute the influx through each viral M2 channel, we use a first order kinetics [24], summarized in the chemical equation

$\begin{array}{ll}{P}_e+M2\stackrel{k_e}{\underset{k_e^{-1}}{\rightleftharpoons }}M2\text{-}P\stackrel{k_v^{-1}}{\underset{k_v}{\rightleftharpoons }}{P}_v+M2.& (10)\end{array}$

When a proton P_e binds a free M2 protein channel with rates k_e(binding) and $k_e^{-1}$ (unbinding), it is transported inside the virus core with a rate $k_v^{-1}$, while exit occurs with a rate k_v. At steady state, the inward flux in a single virus is computed from Equation (10) (see [24])

$\begin{array}{ll}{j}_{M2}(P_e,P_v)=\frac{n_{M2}}{1+\alpha (P_e,P_v)}\left(k_e^{-1}-\frac{k_e{P}_e\alpha (P_e,P_v)}{N_A{V}_e}\right),& (11)\end{array}$

where n_M2 is the number of M2 channels per viral particle, P_v is the number of free protons inside the viral core and

$\begin{array}{ll}\alpha (P_e,P_v)=\frac{k_e^{-1}+k_v^{-1}}{k_e\left(\frac{P_e}{N_A{V}_e}+\frac{k_v^{-1}{P}_v}{k_e^{-1}{N}_A{V}_v}\right)},& (12)\end{array}$

To extract the buffer capacity of a virus, we accounted for the viral genome, the internal viral proteins and unspecific buffers that can be reached through the M2 channels [24]. The most abundant internal proteins are M1 (3, 000 copies per virus) and the nucleoproteins (NP, 330 copies per virus) [25] (Figure 1A). Proton binding sites of viral proteins are the ionogenic groups in their amino acid side chains [26], and the main ionogenic buffers in the endosome pH range are the aspartic acid (Asp, pKa = 3.9), the glutamic acid (Glu, pKa = 4.32) and the histidine (His, pKa = 6.04) [26]. Closely related binding sites can have strong influences on each other due to electrostatic interactions. In addition, the three-dimensional protein folding can hinder the accessibility of some residues to the solvent and protons.

Consequently, calculations based on the three-dimensional structure of the protein are necessary to determine the buffering capacity to pH. Using the spatial organization (crystal structure) of viral proteins, the overall buffering capacity β_i of the viral core is given by

$\begin{array}{ll}{\beta }_i={\beta }_v^0+{\beta }_v^{M1}+{\beta }_v^{NP}+{\beta }_v^{RNA},& (13)\end{array}$

where ${\beta }_v^0$ is the buffering capacity of the lumen inside the virus, and ${\beta }_v^{M1}$, ${\beta }_v^{NP}$ and ${\beta }_v^{RNA}$ are the buffering capacity of M1 and NP proteins, and viral RNA (see Section 4).

Similar to the flux Equation (6), the number of free protons P_v(t) contained in viral core at time t determines the influx of protons through M2 channels (Equation 11) and satisfies equation

$\begin{array}{ll}\frac{d{P}_v(t)}{dt}=\frac{\log (10)}{N_A{V}_v\left({\beta }_v^0+\text{}{\beta }_v^{M1}\text{}+\text{}{\beta }_v^{NP}+\text{}{\beta }_v^{RNA}\right)}{P}_v(t)j_{M2}\left(P_e(t),P_v(t)\right).& (14)\end{array}$

By solving numerically Equation (14) with the initial conditions $P_e(t=0)=10^{-7.2}{N}_A{V}_e$ and $P_v(t=0)=10^{-7.2}{N}_A{V}_v$, we estimate that = 60, 000 protons enter the viral core during endosomal maturation. Using Equation (6) for the endosomal acidification kinetic, we find that more than 20, 000, 000 protons bind to the endosomal buffers during acidification of an endosome with a radius r_e = 500 nm (Table 1). Thus, the buffering capacity of a single virus should not influence the endosomal acidification. However, the number of protons that bind to endosomal buffers drastically decreases to 175, 000 buffered protons when the endosomal radius is reduced r_e = 100 nm. In addition viral particles may accumulate during the endosomal journey [27]. Thus, for multiplicity of infection (MOI) and viral accumulation in endosomes, the viral buffering capacity may significantly affect the acidification kinetics of small and intermediate size endosomes.

TABLE 1

Table 1. Parameters of the endosome acidification model.

2.2. Markov Jump Model of HA Conformational Change

Although the number of protons entering in the endosome is quite huge, as discussed in the previous section, the actual number of free protons defining endosomal pH is surprisingly low (~300 at pH 6 in an endosome with a radius of r_e = 500 nm). In addition, there are few proton binding sites on a single HA that trigger a conformational change [15], which is the event of interest. This change of scale between many entering protons and few free protons and HA binding sites requires a different description than the previous continuous model.

To compute the mean time for HA conformation to change as the pH drops, we first extracted the forward and backward proton binding rates by converting the HA conformational change kinetics, obtained from experimental data at various pH [28] into rate constants.

At temperature T = 300K, when the pH decreases from 7 to 4, the number of protons bound to HA1 increases approximatively from 123 to 132 (Figure 3 in Huang et al. [15]), suggesting that the number of available number of binding site is n_s = 9 at acidic pH. The Influenza virus carries n_HA = 400 HA trimers [17] (Figure 3A) and thus there are exactly n_HAn_s sites that can competitively bind protons. In this section, we compute the mean time that a threshold n_T of bound protons to HA1 is reached, which is a model of fusogenic state, where proteins engage into the generation of a fusion pore with the endosomal membrane.

FIGURE 3

Figure 3. Free protons in the endosome triggers HA conformational change. (A) The right-hand side shows a scheme of an isolated HA trimer. Free protons in the endosome can bind to HA trimers. The protons binding rates r(X, c) and l(X) depend on the number of occupied sites X and on the concentration c of free protons in the endosome. When the number of bound protons reaches a given threshold, the HA trimer changes conformation into a fusogenic state. (B) MFPT of a discrete Markov jump process with transition rates r(X, c) and l(X) to a critical threshold n_T = 6 is estimated with Monte-Carlo simulations (N = 1000) (solid red line), and compared with WKB approximation (solid black line) and experimental data points [28].

2.2.1. Modeling HA Conformational Change

To analyse the conformational change of a single HA trimer, we follow the occupied proton sites X(t, c) at time t, for a fix proton concentration c. During time t and t + Δt, the number of specific bound sites can either increase with a probability r(X, c)Δt, when a proton arrives to a free site or decreases with probability l(X, c)Δt when a proton unbinds or remains unchanged with probability 1 − l(X, c)Δt − r(X, c)Δt (Figure 3A).

We estimate hereafter the rates l(X, c) and r(X, c) and the critical threshold n_T, by approximating the number of bound protons ${\tilde{X}}_0(c)$ with the proton concentration c variable, by a linear function (Figure 3 in Huang et al. [15])

$\begin{array}{ll}\begin{array}{l}{\tilde{X}}_0(c)={\tilde{X}}_0\left({10}^{-7}mol.L^{-1}\right)+X_0(c)={\tilde{X}}_0\left({10}^{-7}mol.L^{-1}\right)\\ +\left(\frac{7}{3}+\frac{\log (c)}{3\log 10}\right)n_s,\end{array}& (15)\end{array}$

where ${\tilde{X}}_0(10^{-7}mol.L^{-1})$ is the mean number of bound protons at pH = 7 and

$\begin{array}{ll}{X}_0(c)=\left(\frac{7}{3}+\frac{\log (c)}{3\log 10}\right)n_s& (16)\end{array}$

is the mean number of HA1 sites that are additionally protonated for a proton concentration c > 10⁻⁷mol. L⁻¹. Recently, we also used a similar jump model [11] to study the conformational change of active proteins for the escape of non-enveloped viruses, based on the assumption that proton binding and unbinding rates were linear functions of the proton concentration. Here however, the mean number of bound sites depends linearly on the endosomal pH (log of the proton concentration) (Equation 16), confirming the non-linear binding and unbinding rates of protons to HA.

To account for the non-linearity of the mean number of bound protons (Equation 16), we derived the expressions of the binding r and unbinding l rates of protons to HA binding sites. First, we assume that the binding rate r(X, c) depends on both the proton concentration c and the number of free binding sites X, whereas the unbinding rate l(X) depends only on X. Indeed, an increased concentration of protons inside the endosome favors the encounter and binding between protons and HA sites, but do not influence the unbinding rate of bound protons. Moreover, we assume that the binding rate r(X, c) depends linearly on the proton concentration c and the number of free sites n_s − X of the HA trimer leading to

$\begin{array}{ll}r(X,c)=Kc(n_s-X),& (17)\end{array}$

where K is the forward binding rate of a proton to a binding site.

To determine the non-linear proton unbinding rate l(X, c), we use the mean number of protons bound to HA at different pHs (Equation 16). Using at equilibrium the concentration $c(X)=10^{\frac{3X}{n_s}-7}$ for which X₀(c(X)) = X, the mass-action law leads to $\frac{l(X_0(c),c)}{r(X_0(c),c)}=1$ or equivalently $\frac{l(X)}{Kc(X)(n_s-X)}=1$, and we get

$\begin{array}{ll}l(X)=K(n_s-X){10}^{\frac{3X}{n_s}-7}.& (18)\end{array}$

In summary, the binding and unbinding rates r and l are given by

$\begin{array}{ll}r(X,c)=Kc(n_s-X),\text{ and }l(X,c)=l(X)=K(n_s-X){10}^{\frac{3X}{n_s}-7}.& (19)\end{array}$

2.2.2. Rate of HA Conformational Change

To compute the mean time that exactly n_T protons are bound to a single HA, we use a Markov jump process for the number of protonated sites X(t, c) among the n_s = 9 HA1 proton binding sites available. Following a similar approach as used in Lagache et al. [11] for non-enveloped viruses, we scale the variable

$\begin{array}{ll}x(t,c)=ϵX(t,c),& (20)\end{array}$

where ϵ = 1/n_s and we use the Wentzel-Kramers-Brillouin (WKB) expansion of the mean first passage time (MFPT) τ(c) of the scaled number of protonated sites x(t, c) to the (unknown) critical threshold 0 < x_T = ϵn_T < ϵn_s [11, 14, 29–31 ]

$\begin{array}{ll}\tau (c)\approx \frac{1}{r\left(x_0(c),c\right)}\frac{\sqrt{\frac{2\pi }{ϵ\frac{d}{dx}\left(\frac{l}{r}\right)\left(x_0(c),c\right)}}}{\varphi (x_T,c)},& (21)\end{array}$

where x₀(c) is the mean number of HA1 sites that are additionally protonated for a concentration c > 10⁻⁷mol.L⁻¹ (Equation 16). The function ϕ(x, c) is given by

$\begin{array}{ll}\varphi (x,c)=\frac{\exp \left(-\frac{1}{ϵ}{\displaystyle {\int }_{x_0(c)}^x\log }\left(\frac{l(s,c)}{r(s,c)}\right)ds\right)}{\sqrt{\frac{l(x,c)}{r(x,c)}}}\left(\frac{l(x,c)}{r(x,c)}-1\right).& (22)\end{array}$

Replacing the transition rates r(x, c) and l(x) by their expressions (19) in Equation (22), we obtain that (see Section 4)

$\begin{array}{ll}\begin{array}{l}\tau (c)=\\ \frac{\sqrt{6\pi }\exp \left(n_s\left(F\left(n_T/n_s\right)-F\left(7/3\text{}+\text{}\frac{\log (c)}{3\log (10)}\right)\right)\right)}{K\sqrt{c{n}_s\log (10)}\left(4+\text{}\frac{\log (c)}{\log (10)}\right)\left(c{10}^{7/2-3n_T/(2n_s)}-{10}^{3n_T/(2n_s)-7/2}\right)},\end{array}& (23)\end{array}$

where $F(x)=\frac{3}{2}log(10)x^2-log(10^{7}c)x$.

To conclude, the expression for the MFPT (23) differs from the one computed in Lagache et al. [11] (Equation 5) derived for a linear unbinding rate l(x, c) = k₋₁xn_s. Equation (23) links the affinities between the ligand (concentration c) and the binding sites of a trimer to the conformational change mean time τ(c) of the trimer. The two unknown parameters of the conformational MFPT (Equation 23) are the binding rate K of protons to HA sites and the number n_T of sites that have to be protonated (among the n_s = 9 total sites) to trigger the HA change of conformation.

The reciprocal of the mean time $\frac{1}{\tau (c)}$ has been measured for various pH values [28]: (τ(pH = 4.9))⁻¹ = 5.78s⁻¹, (τ(pH = 5.1))⁻¹ = 0.12s⁻¹,…, (τ(pH = 5.6))⁻¹ = 0.017s⁻¹. To estimate the unknown K and n_T, we thus use formula (23) to fit these data by a least square optimization procedure, and obtain that

$\begin{array}{ll}{n}_T\approx 6& (24)\end{array}$

and the forward rate

$\begin{array}{ll}K\approx {7.510}^{3}L.mo{l}^{-1}{s}^{-1}.& (25)\end{array}$

These two estimations are the predictions of the present model.

We reported here a good agreement between the WKB approximation (Equation 23) with the Monte-Carlo simulations of the Markov jump process, with the transition rates r(X, c) and l(X) given by Equation (19), and the experimental values of [28] (Figure 3B, model parameters are summarized in Table 2). The WKB solution is very close to the Markov jump simulations, especially for pH values ≥ 5.8, where the fusion takes place (Section 2.3 below). For lower values of the pH, the MFPT to threshold that triggers the conformational change of HA decreases drastically and a small discrepancy between discrete Monte-Carlo simulations and continuum WKB approximation can be seen. For these lower pH values, we observe that the WKB and the Monte-Carlo simulations agrees with the conformational change rates of HA, measured experimentally [28]. We highlight that the fitting of only two parameters K and n_T of the Markov model lead to a very good fit to all experimental data points, which indicates that the Markov jump approach with the WKB approximation is suitable to model the HA conformational changes.

TABLE 2

Table 2. Parameters of the HA's change of conformation model.

2.2.3. A High Potential Barrier of HA Binding Sites Ensures HA Stability at Neutral pH

We have seen in Section 2.1 that during endosomal acidification, a huge number of protons enter the endosome (more than 20*10⁶ that bind mostly to endosome buffers, leaving very few free protons (around 300 at pH 6)). To test whether HAs buffer entering protons or interact with the remaining few free protons, we estimate the potential barrier generated at each HA binding site. For this purpose, we compare the reciprocal of the forward rate constant K (Equation 25), which is the mean time for a proton to bind a HA protein, with the free Brownian diffusion time scale. For a fixed proton concentration at a value c, the proton binding time is ${\tau }_{bind}=\frac{1}{Kc}$, while the mean time for a proton to diffuse to the same binding site is [32–35]

$\begin{array}{ll}{\tau }_{diff}=\frac{V}{4\pi D_p\eta n(c)}.& (26)\end{array}$

The number of endosomal protons at concentration c is n(c) = N_AcV, while η is the interacting radius between a proton and a binding site and D_p the diffusion constant of a free proton (D_p = 100μm² s⁻¹ measured in the cytoplasm [36]). For η = 1 nm, we find a small ratio

$\begin{array}{ll}\frac{{\tau }_{diff}}{{\tau }_{bind}}=\frac{K}{4\pi D_p\eta N_A}={10}^{-4}.& (27)\end{array}$

This result indicates that, on average, only 1 out of 10⁴ encounters between a proton and a HA binding site lead to a binding event. Thus, the binding of protons to HA is strongly reaction-limited, dominated by a very high activation energy barrier at the HA binding sites. This high barrier prevents rapid proton binding and consequently, the buffering capacity of HAs can be neglected compared to the high capacity of other endosomal buffers. In addition, the activation energy barrier of HA binding sites ensures a high stability of the protein at pH above 6, as previously characterized in Table 2 of Krumbiegel et al. [28] and confirmed in Figure S1.

To conclude, we found that the threshold for HA1 conformational change occurs when there are n_T = 6 bound proton in a total of n_s = 9 binding sites. The binding is characterized by a very high potential barrier. Thus, when protons enter an endosome, they will first be captured by endosomal buffers. The remaining free protons can bind to HA1 sites after passing across the high potential barrier to trigger HA conformational change.

2.3. A Closed Model of Virus-Endosome Fusion

Combining the kinetic model of endosome acidification with the Markov jump model of HA conformational change, we now derive a kinetic model of HAs conformational change inside an endosome. We account for the n_T = 6 protons activating a HA1 trigger leading to HA conformational change. We now estimate the numbers HA₀(t), HA₁(t)…HA₆(t) of viral HAs that have 0, 1…6 bound protons at time t, and compute the number of fusogenic (active) HA₆(t), responsible for membrane fusion. From relation (17), the forward rate of a proton to a free HA1 binding site is

$\begin{array}{ll}\tilde{r}\left(X\right)=r\left(X,P_e(t)\right)/P_e(t)=\frac{K(n_s-X)}{N_A{V}_e}.& (28)\end{array}$

and the backward rate l(X) is given by relation 19, thus the chemical Equations for protons P_e and HA proteins are summarized by

$\begin{array}{ll}\begin{array}{l}H{A}_0+P_e\stackrel{\tilde{r}(0/n_s)}{\underset{l(1/n_s)}{\rightleftharpoons }}H{A}_1,\\ H{A}_1+P_e\stackrel{\tilde{r}(1/n_s)}{\underset{l(2/n_s)}{\rightleftharpoons }}H{A}_2,\\ \dots \\ H{A}_5+P_e\stackrel{\tilde{r}(5/n_s)}{\to }H{A}_6,\end{array}& (29)\end{array}$

where the rate constant depends on each stage as given by relation 28. The stage HA₆ is irreversible and the kinetic rate equations are

$\begin{array}{ll}\begin{array}{l}\frac{dH{A}_0(t)}{dt}=-\tilde{r}\left(\frac{0}{n_s}\right)P_e(t)H{A}_0(t)+l\left(\frac{1}{n_s}\right)H{A}_1(t),\\ \frac{dH{A}_1(t)}{dt}=\left(\tilde{r}\left(\frac{0}{n_s}\right)H{A}_0(t)-\tilde{r}\left(\frac{1}{n_s}\right)H{A}_1(t)\right)P_e(t)\\ +l\left(\frac{2}{n_s}\right)H{A}_2(t)-l\left(\frac{1}{n_s}\right)H{A}_1(t),\\ \dots \end{array}& (30)\end{array}$

$\begin{array}{ll}\frac{dH{A}_6(t)}{dt}=\tilde{r}\left(\frac{5}{n_s}\right)H{A}_5(t)P_e(t).& (31)\end{array}$

Once the proton entry rate (Equation 6) is known, these equations can be solved numerically.

2.3.1. Modeling the Onset of Fusion between Virus and Endosome Membranes

Membrane fusion is triggered by the conformational change of multiple adjacent trimers located in the contact zone between the viral and endosomal membranes [16, 17]. However, the exact number of fusogenic HAs involved in formation and fusion pore enlargement is still unclear. To estimate this number, we model the contact zone between the virus and endosome membranes by 120 HAs among 400 covering the viral particle [17] (Figure 4A). Thus, each trimer in the contact zone possesses 6 adjacent neighbors.

FIGURE 4

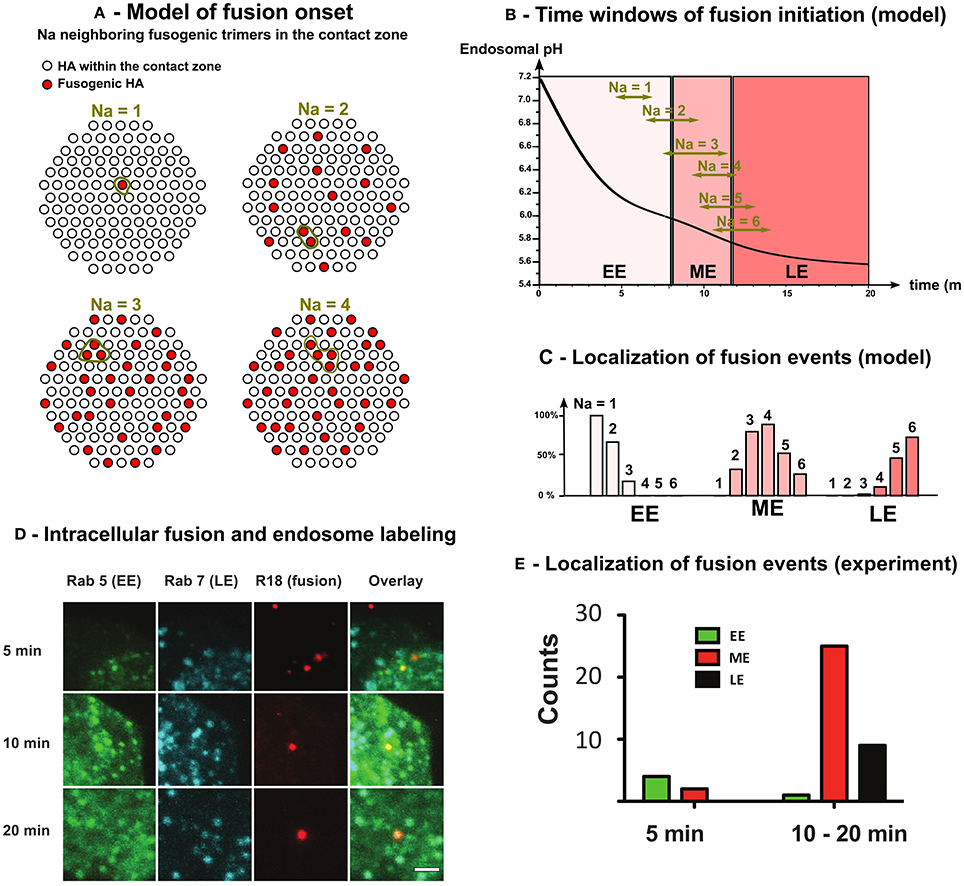
Figure 4. Model and fluorescence experiments of the intracellular onset of virus-endosome fusion. (A) The fusion between virus and endosome membranes is triggered by the conformational change of Na adjacent HAs in the contact zone between virus and endosome (= 120 among the 400 HAs covering the virus envelope [17]). (B) Solving Equation (31) we estimated the time window (95% confidence interval) of intracellular fusion for 1 ≤ Na ≤ 6. (C) Using time windows of fusion onset and endosome maturation kinetics (Equation 7), we estimated the localization (EE, ME, or LE) of fusion onset as function of the number Na of adjacent fusogenic HAs needed for the fusion onset.(D) MDCK cells expressing Rab5-CFP and Rab7-GFP were incubated with R18-labeled Influenza A viruses. Fusion was observed as a strong increase of R18 signal due to de-quenching after dilution. Scale bar = 1 μm (E) In vivo localization of fusion events. Fusion events were counted and categorized regarding their localization in early endosome (EE) (Rab5), ME (Rab5 + Rab7) or LE (Rab7).

We solved numerically Equation (31) and we chose the position of each new fusogenic HA (with n_T = 6 bound sites) randomly among the 400 HAs covering the virus envelope. For each simulation, we defined the onset of virus endosome fusion by the activation of Na adjacent HAs in the contact zone (Figure 4A). Using 1, 000 Monte-Carlo simulations, we estimated the mean and confidence interval at 95% of the fusion onset time for different Na. We found that for Na = 1 − 2, most viruses fuse in EE, whereas for Na = 3−4, they fuse in ME. Finally, for Na = 5 or 6, viruses mostly fuse in LE (Figures 4B,C). To conclude, viruses shall fuse in ME [16, 17] and thus Na = 3 − 4.

2.3.2. Intracellular Localization of Fused Viral Particle with Live Cell Imaging

To experimentally determine the localization of virus fusion, we used the fluorescent endosomal markers Rab5 (EE) and Rab7 (LE) in combination with an intracellular fusion assay to detect virus-endosome fusion so that the localization to a specific compartment can be assigned. Single virus spots were analyzed, where fusion was indicated by a pronounced increase of spot signal (Figure S2). To determine the cellular localization of virus fusion, we analyse infected Rab5- and Rab7-expressing cells with R18-labeled viruses (Figure 4D). We classified single endosomes based on the presence of the two Rab proteins into three classes (Figure S3). Early endosomes (EE) do not show Rab7 association, such as late endosomes (LE) do not posses Rab5 signal. When endosomes possess both signals, they were counted as maturing endosomes (ME).

We observe a gradual increase of Rab7 along with a decrease of Rab5 (Figure 4D). After 5 min, we rarely observe fusion events in Rab5-only endosomes. The majority of fusion events (61%) are detected in maturing endosomes between 10 and 20 min post infection (Figure 4E). At later time points, the localization of fusion events shifted toward late endosomes. However, de-quenching kinetics show that fusion mostly occurs between 10 and 20 min (Figure S2).

We conclude that virual fusion was essentially associated with maturing endosomes confirming that the number of adjacent fusogenic HA required to mediate fusion are Na = 3 or 4.

3. Discussion and Conclusion

Influenza viruses are internalized into endosomes via receptor-mediated endocytosis. During their transport along microtubules, endosomes accumulate protons, which eventually enable virus-endosome fusion mediated by the influenza HA. This fusion mediates the release of the viral genome in the cell cytoplasm. The duration of endosomal transport as well as the localization of fusion critically depend on endosomal acidification and HA conformational change at low pH. Here we presented a new model to investigate the role of key parameters that shape the endosomal residence time of influenza viruses.

The Markov-jump process model of HA conformational change that we have developed here shows that 6 bound protons are enough to trigger conformational change for a total of 9 binding sites. The model also reveals that the HA activation is characterized by a high potential barrier with a forward rate constant K = 7, 500L.mol⁻¹s⁻¹. Interestingly the unbinding rate depends on the number of binding sites, suggesting a modification that depends on history. This is in contrast with the large number of protons of the order of millions that enters and contributes to acidification. This confirms that buffers play a critical role to reduce this enormous quantity of protons into a countable number that will trigger HA activation. The multiscale process involved here is very different from the previous analysis and results [11] we found for the Adeno-associated virus.

Finally, associating the kinetic model of endosomal acidification with a Markov-jump process model of HA conformational change, we estimated how the number of fusogenic HAs evolved in time inside endosomes, and we modeled the onset of fusion with the stochastic activation of Na adjacent HAs. Using the model, we predict a high HA thermal stability at neutral pH due to a high activation barrier of proton binding sites. For Na ≥ 3, we show that fusion should occur in ME, preventing a premature fusion in EE. Because endosomal maturation is associated with retrograde transport of endosomes along MTs, we conclude that mature virus should accumulate near the nuclear surface. Moreover, when an endosome contains multiple copies of Influenza viruses, we found that the cumulative buffering capacity of viruses might delay the acidification kinetics and viral escape into ME and LE.

4. Materials and Methods

We describe here the experimental methods for extracting parameters used to validate the modeling approach. In the last section, we present the computation for the WKB computation for formula Equation (23).

4.1. Materials, Cell and Virus Culture

Madine Darby Canine Kidney (MDCK) cells were cultured in Dulbeccos Modified Eagles Medium (DMEM) without phenol red, supplemented with 1% penicillin/streptomycin and 10% fetal calf serum (FCS). The cells were passaged every 3–4 days. One day prior to the experiment, the cells were detached from the cell culture flask using 0.5 % Trypsin/EDTA for about 10 min. The cells were diluted in DMEM and 10–50 * 10⁵ cells were seeded in 35 mm poly-L-lysine coated glass bottom petri dishes (MatTek Corp.). Influenza A (H3N2) X-31 was propagated in chicken eggs and A/Panama/2007/99 on MDCK cells. Prior to the experiment the virus was diluted to 1 mg/ml protein concentration. Octadecylrhodamine B (R18) was purchased from Molecular Probes (Life Technologies, USA). Phosphate buffered saline (PBS) was used for all dilutions during the experiments. Double labeled FITC/Rhodamine dextran was purchased from Life Technologies (USA). FITC-dextran was purchased from Sigma-Aldrich, Germany. Rab5-GFP (in pCDNA3) and Rab7-GFP (pEGFP-C1) were kindly provided by Volker Haucke (FMP, Berlin). Rab7 was then cloned into pECFP. MDCK cells were transfected using Turbofect (Fermentas, USA) according to the manufacturers manual. To disrupt microtubules, the cells were incubated with medium containing 50 μM nocodazole (Sigma Aldrich, Germany) for 30 min before experiments.

4.2. Immunostaining

MDCK were washed in PBS buffer and fixed in PBS containing 2% paraformaldehyde and 0.2 % glutaraldehyde for 20 min. The cells were permeabilized with PBS containing 0.2% Triton X-100 and 0.2 % BSA for 20 min, washed in PBS and incubated in anti-Nucleoprotein (Millipore, USA) antibody for 1 h. The cells were washed in PBS and incubated with the secondary anti-mouse Cy2 conjugate antibody for 1 h (Amersham, GE, USA). Finally, the cells were counterstained using PBS containing 0.2 μ g/ml DAPI for 10 min.

4.3. Fluorescence Microscopy

For fluorescence microscopy, we used an Olympus FV1000-MPE confocal microscope (Olympus, Japan) equipped with 405 nm (DAPI), 440 nm (CFP), 488 nm (GFP), 559 nm (R18) and 635 nm (A647) laser lines, an Olympus 60x/1.2 water UPlanSApo objective and 405-458/515/559/635 405/488/559/635 dichroic mirror filter sets.

4.4. Endosomal pH Determination

One day prior to the experiment, MDCK cells were seeded into 35 mm poly-L-lysine coated glass bottom petri dishes (MatTek Corp.). For dextran labeling, the cells were washed with PBS and incubated in serum free medium for 30 min at 37° C, followed by 5 min with 10 mg/ml dextran at 37° C (pulse). After the pulse, the cells were immediately washed and image acquisition was started. For plotting the pH evolution (experiments and model), we considered a time delay of 5 min due to technical limitations and set the starting point to pH 7.2.

4.5. Determination of a pH Standard Curve

The pH standard curve for intracellular pH measurements was done as previously described by others ([23]). In short, MDCK cells were detached from the culture dish, washed and pelleted with 2,000 g for 5 min. The cells were divided into eight fractions, pelleted again and resuspended pH standard buffer (obtained by mixing 50 mM HEPES buffer with 50 mM MES buffer (both containing 50 mM NaCl, 30 mM ammonium acetate, 40 mM sodium azide and 10 μM nigerizin). The samples were left on ice for 5 min and analyzed by flow cytometry.

4.6. Calculation of the Proton Binding Capacity of Viral Proteins

Proton binding and the total charge of the proteins was calculated as follows. First, the pKa values of all titrable residues in the proteins were determined with electrostatic energy calculations using the software Karlsberg+ [37]. The calculations are based on the crystal structures with PDB IDs 1hgg, 1hgd, 2bat and 2q06. All non-protein molecules were removed from the structures and therefore not considered in the calculations. Except for hydrogen atoms, all atomic coordinates were kept as found in the crystal structure in the Karlsberg+ calculations. If a titratable residue was missing in the structure, it was assumed that its pKa value equals the model pKa of this residue. The model pKa is the experimental pKa value of a residue in aqueous solution. The protonation state and therefore the charge of a residue at a certain pH value are determined by its pKa value. Here a residue is considered to be protonated if its pKa value is larger than the corresponding pH value. The number of bound protons at a given pH value was then obtained by counting the protonated titratable residues in a protein, the total charge by summing up all individual residue charges.

4.7. Influenza Virus—Ghost Membrane Fusion Assay

To check that Influenza virus are fusion competent and calibrate intracellular fusion experiment we first performed an in vitro ghost-membrane assay [28]. We labeled Influenza viruses with lipophilic dye R18 and measured virus-membrane fusion by monitoring the fluorescence de-quenching (FDQ) of the lipid-like fluorophore R18 upon fusion of R18-labeled viruses with membranes. To this end, 10 μl of labeled virus suspension (1 mg/ml) were mixed with 40 μl ghost suspension (≈ 2*10⁵ cells) and incubated for 20 min at RT. Unbound virus was removed by centrifugation (5 min, 1,200 g). The virus-ghost suspension was transferred to a glass cuvette containing pre-warmed fusion buffer (pH 7.4), and the fluorescence was detected (λ_ex = 560 nm; λ_em = 590 nm) by using a Horiba Yobin Yvon FluoroMax spectrofluorometer. Fusion was triggered by the addition of citric acid (0.2 M). The suspension was stirred continuously with a 2 by 8 mm Teflon-coated magnetic stirring bar. After 600 s the fusion was stopped by adding Triton X-100 (50 μl, final concentration 0.5%) to obtain maximum R18 de-quenching. The final pH in the cuvette was measured using a standard pH meter. The percentage of FDQ was calculated as:

$FDQ(\%)=\frac{F(t)-F(0)}{(F_{max}-F(0))}*100$

where F(0) and F(t) are the fluorescence intensity before starting fusion and at a given time (t), respectively. We observed that fusion starts around pH 6 as predicted by our model and already shown experimentally [38] (Figure S1).

4.8. Intracellular Fusion Assay

Influenza virus was diluted to a final concentration of 1 mg/ml in PBS and incubated with 20 mM R18 for 30 min at room temperature. Unbound R18 was removed by centrifugation at 25.000 g for 5 min or gel filtration (G25 sephadex in PBS). The virus was resuspended/eluted in PBS. Immediately before the experiment, the virus was diluted to 40 μg/ml and viral aggregates were removed with a 0.2 μm sterile filter. The virus was applied to the cells and allowed to bind for 10 min at 4°C. The temperature was elevated to 37°C and the R18 fluorescence was monitored by confocal microscopy. 40 min after start of acquisition, the cells were fixed with PBS containing 2% paraformaldehyde and 0.2 % glutaraldehyde and the DNA was stained with Hoechst 33342 (Invitrogen, USA). The boundaries between cells were determined from the bright field image. Summed z-stacks were analyzed using an IDL-based particle identification software [39].

4.9. Derivation of the Acidification Kinetics Equation (3)

Protons that enter inside the endosome interact with endosomal buffers, and the number of free protons P_e(t) inside an endosome is given by the mass-action law

$\begin{array}{ll}\begin{array}{l}\frac{d{P}_e(t)}{dt}=\Delta P_e(t)+{\displaystyle \sum _{i=1}^n\left(k_i^{(-1)}{P}_e\text{-}{B}_i(t)-\frac{k_i}{N_A{V}_e}{P}_e(t)B_i(t)\right)}\\ =\left(\lambda (t)S-L_{ext}(t)\right)\\ +{\displaystyle \sum _{i=1}^n\left(k_i^{(-1)}{P}_e\text{-}{B}_i(t)-\frac{k_i}{N_A{V}_e}{P}_e(t)B_i(t)\right)},\end{array}& (32)\end{array}$

where P_e-B_i(t) and B_i(t) are the number of weak acids and bases inside the endosome at time t, N_A is the Avogadro constant and V_e is the volume of the endosome. Assuming that the membrane potential Ψ(t) reaches rapidly its steady state value Ψ(∞) compared to the acidification kinetics [18], we approximate the pumping rate λ(t)S with its steady state value λ

$\begin{array}{ll}\lambda (t)S=\lambda S.& (33)\end{array}$

where the parameter λ is related to the membrane potential Ψ(∞). In addition, the protons leak L_ext(t) is proportional to the endosomal concentration and the endosomal surface [20]

$\begin{array}{ll}{L}_{ext}(t)=LS\frac{P_e(t)}{N_A{V}_e},& (34)\end{array}$

where L is a permeability constant. Consequently, using approximations 33 and 34 in Equation (32), we obtain the general dynamics of free protons:

$\begin{array}{ll}\begin{array}{l}\frac{d{P}_e(t)}{dt}=\left(\lambda -L\frac{P_e(t)}{N_A{V}_e}\right)S\\ +{\displaystyle \sum _{i=1}^n\left(k_i^{(-1)}{P}_e\text{-}{B}_i(t)-\frac{k_i}{N_A{V}_e}{P}_e(t)B_i(t),\right)}.\end{array}& (35)\end{array}$

When the protons enter the endosome they can interact with buffers which is much faster than acidification. Thus, we assume that ΔP_e(t) protons entering the endosome during dt bind instantaneously to bases, which leads to step decrease −ΔB_i(t) of the number of proton binding sites of each base B_i(t):

$\begin{array}{ll}\Delta P_e(t)=-{\displaystyle \sum _{i=1}^n\Delta }{B}_i(t).& (36)\end{array}$

To estimate the pH change ΔpH(t) associated with the entry ΔP_e(t) of protons and the corresponding decrease −ΔB_i(t) of each base, we use Equation (2) at equilibrium

$\begin{array}{ll}{k}_i^{(-1)}{P}_e\text{-}{B}_i(t)=k_i\frac{P_e(t)B_i(t)}{N_A{V}_e}\text{, for all }1\le i\le n.& (37)\end{array}$

Thus,

$\begin{array}{ll}\frac{P_e(t)}{N_A{V}_e}=K_i\frac{C_i-B_i(t)}{B_i(t)}\text{, for all }1\le i\le n,& (38)\end{array}$

where $K_i=\frac{k_i^{(-1)}}{k_i}$ and C_i = P_e-B_i(0) + B_i(0) are constant. Consequently,

$\begin{array}{ll}\text{pH}(t)=p{K}_i+\frac{1}{\log (10)}\log \left(\frac{B_i(t)}{\left(C_i-B_i(t)\right)}\right)& (39)\end{array}$

where pK_i = −log(K_i)/log(10). By differentiating Equation (39) with respect to each B_i(t), we obtain the infinitesimal variation ΔpH(t) of the endosomal pH at time t

$\begin{array}{ll}\Delta \text{pH}(t)=\left(\frac{1}{\log (10)}\frac{C_i}{B_i(t)\left(C_i-B_i(t)\right)}\right)\Delta B_i(t).& (40)\end{array}$

Using Equation (38), we get

$\begin{array}{ll}\Delta \text{pH}(t)=\left(\frac{1}{\log (10)}\frac{{\left(N_A{V}_e{K}_i+P_e(t)\right)}^2}{P_e(t)C_i{N}_A{V}_e{K}_i}\right)\Delta B_i(t),& (41)\end{array}$

leading to

$\begin{array}{ll}\Delta B_i(t)=N_A{V}_e{\beta }_i\left(P_e(t)\right)\Delta \text{pH}(t),& (42)\end{array}$

where

$\begin{array}{ll}{\beta }_i\left(P_e(t)\right)=\log (10)C_i\frac{P_e(t)K_i}{{\left(P_e(t)+K_i{N}_A{V}_e\right)}^2}& (43)\end{array}$

is the buffering capacity of the weak acid-base couple (P_e-B_i, B_i). Finally, using Equations (36) and (42), the infinitesimal change ΔpH(t) of the endosomal pH associated with the entry of ΔP_e(t) protons is

$\begin{array}{ll}\Delta P_e(t)=-{\displaystyle \sum _{i=1}^n\Delta }{B}_i(t)=-N_A{V}_e\left({\displaystyle \sum _{i=1}^n{\beta }_i}\left(P_e(t)\right)\right)\Delta \text{pH}(t),& (44)\end{array}$

that is

$\begin{array}{ll}\Delta P_e(t)=-N_A{V}_e{\beta }_e^0\left(P_e(t)\right)\Delta \text{pH},& (45)\end{array}$

where ${\beta }_e^0(P_e(t))=\sum _{i=1}^n{\beta }_i(P_e(t))$ is the total buffering capacity of the endosome, which is approximately constant ${\beta }_e^0(P_e(t))={\beta }_e^0=40mM/pH$ [40]. Finally, using the proton extrusion and pumping rates (Equations 33 and 34), we obtain the kinetic Equation

$\begin{array}{ll}\frac{d\text{pH}(t)}{dt}=\left(L\frac{P_e(t)}{N_A{V}_e}-\lambda \right)\frac{S}{N_A{V}_e{\beta }_e^0}.& (46)\end{array}$

The endosomal pH is related to the number of free protons P_e(t) by

$\begin{array}{ll}\text{pH(t)}=-\frac{1}{\log (10)}\log \left(\frac{P_e(t)}{N_{A}V}\right).& (47)\end{array}$

Thus

$\begin{array}{ll}\frac{d\text{pH}(t)}{dt}=-\frac{1}{\log (10)P_e(t)}\frac{d{P}_e(t)}{dt},& (48)\end{array}$

and replacing the pH derivative in Equation (46), we obtain that the accumulation of free protons P_e(t) inside the ensosome during acidification is given by the kinetics Equation

$\begin{array}{ll}\frac{d{P}_e(t)}{dt}=\left(\lambda -L\frac{P_e(t)}{N_A{V}_e}\right)\frac{S\log (10)P_e(t)}{N_A{V}_e{\beta }_e^0}.& (49)\end{array}$

4.10. Estimation of the Viral Buffering Capacity (Equation 13)

First, we estimated the buffering capacity of NP proteins [41] by computing the pKa values of all titratable residues in the proteins with electrostatic energy calculations using the software Karlsberg+ [37]. We then determined the mean number of protonated residues $n_P^{NP}(pH)$ of NP proteins and we found that $n_P^{NP}(pH)$ increases almost linearly with pH:

$\begin{array}{ll}{n}_P^{NP}(pH)=n_P^{NP}(pH=7)+9\left(7-pH\right),& (50)\end{array}$

indicating that the buffering capacity of NPs is approximatively constant between pH 7 and 5 (Equation 42)

$\begin{array}{ll}{\beta }_v^{NP}=9\frac{330}{N_A{V}_v}=\frac{3000}{N_A{V}_v}& (51)\end{array}$

where $V_v=\frac{4}{3}\pi r_v^3$ is the volume of the viral internal lumen, for a spherical viral particle with radius r_v = 60 nm [42]. The structure of the matrix M1 protein is unknown and consequently, we use the cumulative contributions of Asp, Glu and His residues to estimate the number of M1 proton binding sites. We thus estimate the fraction P_i(pH) of occupied residues for a fixed pH using the equilibrium constant pKa_i for any residue i (Asp, Glu or His) to be

$\begin{array}{ll}{P}_i(pH)={\left({10}^{pH-pK{a}_i}+1\right)}^{-1}.& (52)\end{array}$

The mean number $n_P^{M1}(pH)$ of protonated site is then given by

$\begin{array}{ll}\begin{array}{l}{n}_P^{M1}(pH)=n_{Asp}^{M1}{\left({10}^{pH-3.9}+1\right)}^{-1}+n_{Glu}^{M1}{\left({10}^{pH-4.32}+1\right)}^{-1}\\ +n_{His}^{M1}{\left({10}^{pH-6.04}+1\right)}^{-1}.\end{array}& (53)\end{array}$

where the number of residue for each group is $n_{Asp}^{M1}=12$, $n_{Glu}^{M1}=12$ and $n_{His}^{M1}=5$. Using Equation (53), we plotted $n_P^{M1}(pH)$as function of the pH and observed that $n_P^{M1}(pH)$ is almost a linear function

$\begin{array}{ll}{n}_P^{M1}(pH)=n_P^{NP}(pH=7)+3.5\left(7-pH\right),& (54)\end{array}$

and obtain that

$\begin{array}{ll}{\beta }_v^{M1}=3.5\frac{3,000}{N_A{V}_v}=\frac{10,500}{N_A{V}_v}.& (55)\end{array}$

Additionally to internal M1s and NPs proteins, protons entering the viral core through M2 channels can also bind to viral nucleic acids and in particular to basic groups in the guanine, adenine and cytosine nucleotides [26]. In particular, the buffering capacity β^RNA of oligonucleotides in solution, for a concentration c_monomers of monomers, has been estimated to be ${\beta }^{RNA}=0.1c_{monomers}$ in the pH range 5–7 (Figure 3D in Stoyanov and Righetti, [26]). Consequently the buffering capacity ${\beta }_v^{RNA}$ of the = 12, 000 viral nucleotides [43] is approximatively equal to

$\begin{array}{ll}{\beta }_v^{RNA}=0.1\frac{12,000}{N_A{V}_v}=\frac{1,200}{N_A{V}_v}.& (56)\end{array}$

Finally, the viral core lumen should also contain other unspecific buffers such as cytoplasmic buffers enclosed during the viral assembly, leading to an unspecific buffering capacity ${\beta }_v^0(pH)$ inside the viral lumen that has to be added to the buffering capacities ${\beta }_v^{NP}$ and ${\beta }_v^{M1}$ of internal proteins. Due to possible ionic exchange between viral and endosomal lumens, we approximate ${\beta }_v^0(pH)$ with the endosomal buffering capacity ${\beta }_e^0$, which is independent of the pH and has been estimated to be [40]

$\begin{array}{ll}{\beta }_e^0=40mM/\text{pH}.& (57)\end{array}$

4.11. Derivation of Equation 23

Using the WKB approach [14], we obtain that the mean first passage time (MFPT) τ(c) of the scaled number of protonated sites x(t, c) to the (unknown) critical threshold 0 < x_T = ϵn_T < ϵn_s is given by [11, 29–31]

$\tau (c)\approx \frac{1}{r\left(x_0(c),c\right)}\frac{\sqrt{\frac{2\pi }{ϵ\frac{d}{dx}\left(\frac{l}{r}\right)\left(x_0(c),c\right)}}}{\varphi (x_T,c)},$

where x₀(c) is the mean number of HA1 sites that are additionally protonated for a concentration c > 10⁻⁷mol.L⁻¹ (Equation 16) and ϕ(x, c) is given by

$\varphi (x,c)=\frac{\exp \left(-\frac{1}{ϵ}{\displaystyle {\int }_{x_0(c)}^x\log }\left(\frac{l(s,c)}{r(s,c)}\right)ds\right)}{\sqrt{\frac{l(x,c)}{r(x,c)}}}\left(\frac{l(x,c)}{r(x,c)}-1\right).$

We first compute

$\begin{array}{l}{\displaystyle {\int }_{x_0(c)}^{x_T}\log }\left(\frac{l(s,c)}{r(s,c)}\right)ds={\displaystyle {\int }_{x_0(c)}^{x_T}\left(\log \left({10}^{3s-7}\right)-\log (c)\right)}ds\\ ={\displaystyle {\int }_{x_0(c)}^{x_T}(3\log (10)s-(7\log (10)}\\ +\log (c)))ds,\end{array}$

that is

$\begin{array}{l}{\displaystyle {\int }_{x_0(c)}^{x_T}\log }\left(\frac{l(s,c)}{r(s,c)}\right)ds={\displaystyle {\int }_{x_0(c)}^{x_T}(3\log (10)s}-\log ({10}^{7}c))ds\\ =F\left(x_T\right)-F\left(x_0(c)\right),\end{array}$

where

$F(x)=\frac{3}{2}\log (10)x^2-\log ({10}^{7}c)x.$

leading to

$\varphi (x_T,c)=\exp \left(-\frac{1}{ϵ}\left(F\left(x_T\right)-F\left(x_0(c)\right)\right)\right)\frac{\frac{{10}^{3x_T-7}}{c}-1}{\sqrt{\frac{{10}^{3x_T-7}}{c}}},$

that is,

$\begin{array}{l}\varphi (x_T,c)=\exp \left(-\frac{1}{ϵ}\left(F\left(x_T\right)-F\left(x_0(c)\right)\right)\right)\\ \left(\frac{{10}^{3x_T/2-7/2}}{\sqrt{c}}-\sqrt{c}{10}^{7/2-3x_T/2}\right).\end{array}$

Using expressions for the binding and unbinding rates 19, we get

$\begin{array}{l}\frac{d}{dx}\left(\frac{l}{r}\right)\left(x_0(c),c\right)=\frac{d}{dx}\left(\frac{{10}^{3x-7}}{c}\right)\left(x_0(c),c\right)\\ =\frac{3\log (10)}{c}{10}^{3x_0(c)-7},\end{array}$

which reduces to

$\frac{d}{dx}\left(\frac{l}{r}\right)\left(x_0(c),c\right)=3\log (10).$

Finally, re-injecting expression of potential ϕ(x_T, c) in the MFPT τ(c), we obtain that

$\begin{array}{l}\tau (c)=\frac{ϵ}{-Kc\left(\frac{4}{3}+\frac{\log (c)}{3\log (10)}\right)}\\ \frac{\sqrt{\frac{2\pi }{ϵ3\log (10)}}\exp \left(\frac{1}{ϵ}\left(F\left(x_T\right)-F\left(7/3+\frac{\log (c)}{3\log (10)}\right)\right)\right)}{\frac{{10}^{3x_T/2-7/2}}{\sqrt{c}}-\sqrt{c}{10}^{7/2-3x_T/2}}.\end{array}$

Using ϵ = 1/n_s and x_T = n_T/n_s, we get

$\begin{array}{l}\tau (c)=\\ \frac{\sqrt{6\pi }\exp \left(n_s\left(F\left(n_T/n_s\right)-F\left(7/3+\frac{\log (c)}{3\log (10)}\right)\right)\right)}{K\sqrt{c{n}_s\log (10)}\left(4\text{}+\text{}\frac{\log (c)}{\log (10)}\right)\left(c{10}^{7/2-3n_T/(2n_s)}-{10}^{3n_T/(2n_s)\text{}-\text{}7/2}\right)}.\end{array}$

Author Contributions

TL, AH, and DH: Designed research. TL and CS: Performed experimental and simulations works. TM: Contributed analytic tools. TL, CS, and DH Analyzed data. TL, CS, AH, and DH: Wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by a Marie Curie grant (DH), by the Deutsche Forschungsgemeinschaft (HE 3763/15-1) (AH) and the Bundesministerium fur Bildung und Forschung (eBio: ViroSign) (CS and AH). TL is partially funded by a fellowship from the Fondation pour la Recherche Medicale and a grant from the Philippe Foundation.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fphy.2017.00025/full#supplementary-material

References

1. D'Orsogna MR, Chou T. Optimal cytoplasmic transport in viral infections. PLoS ONE (2009) 4:e8165. doi: 10.1371/journal.pone.0008165

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gibbons MM, Chou T, D'orsogna MR. Diffusion-dependent mechanisms of receptor engagement and viral entry. J Phys Chem B (2010) 114:15403–12. doi: 10.1021/jp1080725

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Mistry B, D'Orsogna MR, Webb NE, Lee B, Chou T. Quantifying the Sensitivity of HIV-1 Viral Entry to Receptor and Coreceptor Expression. J Phys Chem B (2016) 120:6189–99. doi: 10.1021/acs.jpcb.6b02102

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Allard JF, Dushek O, Coombs D, Van Der Merwe PA. Mechanical modulation of receptor-ligand interactions at cell-cell interfaces. Biophys J. (2012) 102:1265–73. doi: 10.1016/j.bpj.2012.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sodeik B. Mechanisms of viral transport in the cytoplasm. Trends Microbiol. (2000) 8:465–72. doi: 10.1016/S0966-842X(00)01824-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Imelli N, Meier O, Boucke K, Hemmi S, Greber UF. Cholesterol is required for endocytosis and endosomal escape of adenovirus type 2. J Virol. (2004) 78:3089–98. doi: 10.1128/JVI.78.6.3089-3098.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Dauty E, Verkman AS. Actin cytoskeleton as the principal determinant of size-dependent DNA mobility in cytoplasm: a new barrier for non-viral gene delivery. J Biol Chem. (2005) 280:7823–8. doi: 10.1074/jbc.M412374200

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Xiao PJ, Samulski RJ. Cytoplasmic trafficking, endosomal escape, and perinuclear accumulation of adeno-associated virus type 2 particles are facilitated by microtubule network. J Virol. (2012) 86:10462–73. doi: 10.1128/JVI.00935-12

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Amoruso C, Lagache T, Holcman D. Modeling the early steps of cytoplasmic trafficking in viral infection and gene delivery. Siam J Appl Math. (2011) 71:2334–58. doi: 10.1137/100816572

CrossRef Full Text | Google Scholar

10. Schelker M, Mair CM, Jolmes F, Welke RW, Klipp E, Herrmann A, et al. Viral RNA Degradation and Diffusion Act as a Bottleneck for the Influenza A Virus Infection Efficiency. PLoS Comput Biol. (2016) 12:e1005075. doi: 10.1371/journal.pcbi.1005075

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lagache T, Danos O, Holcman D. Modeling the step of endosomal escape during cell infection by a nonenveloped virus. Biophys J. (2012) 102:980–9. doi: 10.1016/j.bpj.2011.12.037

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mercer J, Schelhaas M, Helenius A. Virus entry by endocytosis. Annu Rev Biochem. (2010) 79:803–33. doi: 10.1146/annurev-biochem-060208-104626

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Huang Q, Sivaramakrishna RP, Ludwig K, Korte T, Böttcher C, Herrmann A. Early steps of the conformational change of influenza virus hemagglutinin to a fusion active state: stability and energetics of the hemagglutinin. Biochim Biophys Acta (2003) 1614:3–13. doi: 10.1016/S0005-2736(03)00158-5

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Schuss Z. Theory and Applications of Stochastic Processes. New-York, NY: Springer (2010).

Google Scholar

15. Huang Q, Opitz R, Knapp EW, Herrmann A. Protonation and stability of the globular domain of influenza virus hemagglutinin. Biophys J. (2002) 82:1050–8. doi: 10.1016/S0006-3495(02)75464-7

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Danieli T, Pelletier SL, Henis YI, White JM. Membrane fusion mediated by the influenza virus hemagglutinin requires the concerted action of at least three hemagglutinin trimers. J Cell Biol. (1996) 133:559–69. doi: 10.1083/jcb.133.3.559

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ivanovic T, Choi JL, Whelan SP, van Oijen AM, Harrison SC. Influenza-virus membrane fusion by cooperative fold-back of stochastically induced hemagglutinin intermediates. Elife (2013) 2:e00333. doi: 10.7554/eLife.00333

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Grabe M, Wang H, Oster G. The mechanochemistry of V-ATPase proton pumps. Biophys J. (2000) 78:2798–813. doi: 10.1016/S0006-3495(00)76823-8

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Fuchs R, Schmid S, Mellman I. A possible role for Na⁺,K⁺-ATPase in regulating ATP-dependent endosome acidification. Proc Natl Acad Sci USA. (1989) 86:539–43. doi: 10.1073/pnas.86.2.539

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Grabe M, Oster G. Regulation of organelle acidity. J Gen Physiol. (2001) 117:329–44. doi: 10.1085/jgp.117.4.329

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rink J, Ghigo E, Kalaidzidis Y, Zerial M. Rab conversion as a mechanism of progression from early to late endosomes. Cell (2005) 122:735–49. doi: 10.1016/j.cell.2005.06.043

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zaraket H, Bridges OA, Duan S, Baranovich T, Yoon SW, Reed ML, et al. Increased acid stability of the hemagglutinin protein enhances H5N1 influenza virus growth in the upper respiratory tract but is insufficient for transmission in ferrets. J Virol. (2013) 87:9911–22. doi: 10.1128/JVI.01175-13

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Bayer N, Schober D, Prchla E, Murphy RF, Blaas D, Fuchs R. Effect of bafilomycin A1 and nocodazole on endocytic transport in HeLa cells: implications for viral uncoating and infection. J Virol. (1998) 72:9645–55.

PubMed Abstract | Google Scholar

24. Leiding T, Wang J, Martinsson J, DeGrado WF, Arsköld SP. Proton and cation transport activity of the M2 proton channel from influenza A virus. Proc Natl Acad Sci USA. (2010) 107:15409–14. doi: 10.1073/pnas.1009997107

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lamb R, Krug R. Orthomyxoviridae: The viruses and replication. In: Knipe D, Howley P, Griffin D, editors. Fields Virology. 4th Edn. Philadelphia, PA: Lippincott Wiliams and Wilkins (1996) 1487–1531.

26. Stoyanov AV, Righetti PG. Buffer properties of biopolymer solutions, as related to their behaviour in electrokinetic methodologies. J Chromatogr A. (1999) 838:11–8. doi: 10.1016/S0021-9673(99)00090-4

CrossRef Full Text | Google Scholar

27. Matlin KS, Reggio H, Helenius A, Simons K. Pathway of vesicular stomatitis virus entry leading to infection. J Mol Biol. (1982) 156:609–31. doi: 10.1016/0022-2836(82)90269-8

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Krumbiegel M, Herrmann A, Blumenthal R. Kinetics of the low pH-induced conformational changes and fusogenic activity of influenza hemagglutinin. Biophys J. (1994) 67:2355–60. doi: 10.1016/S0006-3495(94)80721-0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Knessl C, Matkowsky B, Schuss Z, Tier C. An asymptotic theory of large deviations for Markov jump-processes. Siam J Appl Math. (1985) 45:1006–28. doi: 10.1137/0145062

CrossRef Full Text | Google Scholar

30. Matkowsky B, Schuss Z, Knessl C, Tier C, Mangel M. Asymptotic solution of the Kramers-Moyal equation and first-passage times for Markov jump processes. Phys Rev A. (1984) 29:3359–69. doi: 10.1103/PhysRevA.29.3359

CrossRef Full Text | Google Scholar

31. Knessl C, Mangel M, Matkowsky B, Schuss Z, Tier C. Solution of Kramers-Moyal equations for problems in chemical physics. J Chem Phys. (1984) 81:1285–93. doi: 10.1063/1.447815

CrossRef Full Text | Google Scholar

32. Ward M, Keller J. Strong localized perturbations of eigenvalue problems. Siam J Appl Math. (1993) 53:770–98. doi: 10.1137/0153038

CrossRef Full Text | Google Scholar

33. Singer A, Schuss Z, Holcman D. Narrow Escape, part III: Non-smooth domains and Riemann surfaces. J Stat Phys. (2006) 122:491–509. doi: 10.1007/s10955-005-8028-4

CrossRef Full Text | Google Scholar

34. Schuss Z, Singer A, Holcman D. The narrow escape problem for diffusion in cellular microdomains. Proc Natl Acad Sci USA. (2007) 104:16098–103. doi: 10.1073/pnas.0706599104

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Holcman D, Schuss Z. Stochastic Narrow Escape in Molecular and Cellular Biology: Analysis and Applications. New-York, NY: Springer (2015).

Google Scholar

36. al Baldawi NF, Abercrombie RF. Cytoplasmic hydrogen ion diffusion coefficient. Biophys J. (1992) 61:1470–9.

PubMed Abstract | Google Scholar

37. Kieseritzky G, Knapp EW. Optimizing pKA computation in proteins with pH adapted conformations. Prot Struct Funct Bioinf. (2008) 71:1335–48. doi: 10.1002/prot.21820

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Korte T, Ludwig K, Booy FP, Blumenthal R, Herrmann A. Conformational intermediates and fusion activity of influenza virus hemagglutinin. J Virol. (1999) 73:4567–74.

PubMed Abstract | Google Scholar

39. Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. (2002) 82:2775–83. doi: 10.1016/S0006-3495(02)75618-X

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Van Dyke RW, Belcher JD. Acidification of three types of liver endocytic vesicles: similarities and differences. Am J Physiol. (1994) 266(1 Pt 1):C81–94.

PubMed Abstract | Google Scholar

41. Ng AKL, Zhang H, Tan K, Li Z, Liu Jh, Chan PKS, et al. Structure of the influenza virus A H5N1 nucleoprotein: implications for RNA binding, oligomerization, and vaccine design. FASEB J. (2008) 22:3638–47. doi: 10.1096/fj.08-112110

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Lamb RA, Choppin PW. The gene structure and replication of influenza virus. Annu Rev Biochem. (1983) 52:467–506. doi: 10.1146/annurev.bi.52.070183.002343

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Hutchinson EC, von Kirchbach JC, Gog JR, Digard P. Genome packaging in influenza A virus. J Gen Virol. (2010) 91(Pt 2):313–28. doi: 10.1099/vir.0.017608-0

PubMed Abstract | CrossRef Full Text | Google Scholar