Nucleotide-Induced Conformational Dynamics in ABC Transporters from Structure-Based Coarse Grained Modeling

ATP-binding cassette (ABC) transporters are integral membrane proteins which mediate the exchange of diverse substrates across membranes powered by ATP molecules. Our understanding of their activity is still hampered since the conformational dynamics underlying the operation of such proteins cannot yet be resolved in detailed molecular dynamics studies. Here a coarse grained model which allows to mimic binding of nucleotides and follow subsequent conformational motions of full-length transporter structures in computer simulations is proposed and implemented. To justify its explanatory quality, the model is first applied to the maltose transporter system for which multiple conformations are known and we find that the model predictions agree remarkably well with the experimental data. For the MalK subunit the switching from open to the closed dimer configuration upon ATP binding is reproduced and, moreover, for the full-length maltose transporter, progression from inward-facing to the outward-facing state is correctly obtained. For the heme transporter HmuUV, for which only the free structure could yet be determined, the model was then applied to predict nucleotide-induced conformational motions. Upon binding of ATP-mimicking ligands the structure changed from a conformation in which the nucleotide-binding domains formed an open shape, to a conformation in which they were found in tight contact, while, at the same time, a pronounced rotation of the transmembrane domains was observed. This finding is supported by normal mode analysis, and, comparison with structural data of the homologous vitamin B₁₂ transporter BtuCD suggests that the observed rotation mechanism may contribute a common functional aspect for this class of ABC transporters. Although in HmuuV noticeable rearrangement of essential transmembrane helices was detected, there are no indications from our simulations that ATP binding alone may facilitate propagation of substrate molecules in this transporter. Possible explanations are discussed in the light of currently debated transport scenarios of ABC transporters.

1. Introduction

ATP-binding cassette (ABC) transporters are molecular machines which are located in cell membranes and involved in the active transport of chemical substances [1, 2], thus representing key players for the maintenance of cellular homeostatis. Owing to their enzymatic activity of binding ATP molecules and catalyzing their hydrolysis reaction, they are capable of converting chemical energy into internal mechanical motions which are used to implement the transmembrane exchange of substrates. ABC transporters can function either as importers which organize the efficient uptake of molecules, e.g., nutrients critical for intracellular processes [3, 4], or as exporters, pumping lipids, metabolic products, toxins or drugs out of cells [5, 6]. ABC transporters have also been evidenced to be clinically relevant since they can contribute to the resistance of cancer cells to drugs, to antibiotic tolerance, or cause diseases such as cystic fibrosis [7, 8].

The common architecture of ABC transporters reveals two cytosolic nucleotide-binding domains (NBDs), the ABCs, and a pair of domains which are integrated into the membrane (the transmembrane domains, TMDs). Binding of intracellular ATP molecules and their hydrolysis inside the cassettes controls the conformation of the transmembrane domains which contain the substrate-specific translocation pathway, thus implementing the respective function of the transporter [9–11].

The structures of several ABC transporters have become available in the past and it has been shown that the NBDs are similar and constitute the engine core of the transporter, containing conserved sequence motifs which are involved in interactions with ATP molecules [12–16]. The TMDs, however, can considerably differ in their sequence and architecture despite all of them having a central pathway for the translocation of substrates. Moreover, since a few structures of transporters in the presence of nucleotides exist, valuable insights into possible conformational changes were gained and the basis for an understanding of their ATP-dependent activity could be established [17–21]. In addition to static structural data, molecular dynamics (MD) simulations have been performed for the NBD components of various ABC transporters [22–31]. It is well established that binding of ATP causes closing of the NBDs and opening of them is obtained after ATP hydrolysis. Although MD simulations are capable of describing ATP-induced structural changes in the isolated NBD core of ABC transporters, the entire conformational dynamics underlying the transport cycle involves global motions on timescales which, due to their heavy demand on computational resources, are still beyond the reach of such methods [32, 33].

Therefore, despite extensive experimental and modeling studies, important functional aspects of the operation of ABC transporters are still lacking to date. This particularly refers to the coupling of ATP-induced activity of the NBDs to the transport activity inside the TMDs. Resolving the conformational motions underlying these processes is essential to understand the mechanism of ABC transporters. In this situation, modeling studies that are based on present structures of transporter proteins and provide approximate descriptions of their dynamics may play an important role.

To overcome the apparent difficulties associated with MD methods, coarse-grained descriptions of protein dynamics have become more and more popular within the last decades [34, 35]. A widespread approach to analyze conformational motions in proteins with feasible computational burden is the elastic network model (ENM) [36, 37]. In this approximate description, entire amino acids are typically modeled as single point-like particles and the complex intramolecular interactions are replaced by empiric harmonical potentials which mediate effective interactions between them. Thus, within the framework of this mechanical model, a protein is viewed as a network of beads connected via deformable elastic springs. It has been shown that ENMs are able to reproduce well the pattern of residue displacement in protein structures due to thermal fluctuations and describe ligand-induced collective dynamics in molecular machines [38–40]. In most former studies predictions of functional conformational motions in proteins were based on the computation of normal modes of elastic networks, an approximation which allows for an efficient numerical implementation, but nonetheless may also be prone to fail as reported earlier [41, 42]. Elastic network normal mode analysis has been previously applied to study nucleotide-dependent conformational dynamics of the vitamin B₁₂ ABC transporter BtuCD [43]. More recently, relaxational elastic network models which take into account the full non-linear network dynamics have been applied to study mechanochemical motions in protein machines [44–46]. In a recent study we have used such models to follow, for the first time, entire operation cycles of an important motor protein in a structurally resolved manner [47, 48].

Here we propose and apply an approach which, based on the relaxational elastic network model, intends to investigate nucleotide-dependent dynamics of ABC transporters at the coarse-grained level. Based on the crystal structure of the nucleotide-free state of the transporter we have constructed a ligand-elastic-network model that implements interactions with ATP molecules in a simplified fashion. The focus in the performed computer experiments was on the study of conformational motions induced by binding of ATP ligands and the subsequent response generated in the transmembrane domains. By tracing the formation of an approximate in silico version of the nucleotide-complexed state of an ABC transporter the proposed approach allows to follow conformational changes of the full protein structure and thus explore the coupling of nucleotide-induced dynamics in the NBDs to motions inside the TMDs and relate it to possible gating mechanisms. As a proof of concept the model was first applied to transporter structures for which multiple structures are known and the quality of its predictions was evaluated by comparing the ligand-complexed conformations obtained from the simulations with the crystal structures in the presence of ATP-analogs. In the next step we have performed simulations for the ABC protein HmuUV, a transporter involved in conducting the import of heme substrates, which is essential in bacteria [49], but for which yet only the nucleotide-free structure could experimentally be determined [50].

Particularly our findings summarize as follows: (i) generally, binding of nucleotide-mimicking ligands induced large-amplitude global and ordered conformational motions that were robust, i.e., they were not sensitive to the specific interaction pattern applied between ligands and the protein within our description, (ii) model predictions agree remarkably well with structural data; for the MalK ABC dimer the switching from open to closed conformation is reproduced and for the full-length maltose transporter the progression from inward-facing to outward facing state of the transmembrane domains is correctly obtained, (iii) in HmuUV a coupling of tweezer-like motion of the NBDs and rotational motions of the TMDs was observed upon binding of ligands; this mechanism of coupled domain dynamics is supported by normal mode analysis and comparison with available structures of the homologous vitamin B₁₂ transporter BtuCD, (iv) in HmuuV noticeable rearrangement of essential transmembrane helices was detected but there are no clear indications from our modeling of how conformational motions induced by ATP binding alone may relate to mechanical aspects of gating in this transporter.

2. Materials and Methods

2.1. Network Construction and Dynamics

The performed investigations of ABC transporters were based on the crystal structure of the respective nucleotide-free conformation. We describe here the construction of their corresponding elastic networks and refer to Table 1 for more detailed information. The coarse-grained elastic network of a protein was obtained by first replacing each amino acid residue in the crystal structure by a single bead which was placed at the position of the alpha-carbon atom of the respective residue. These equilibrium positions were denoted by ${\overrightarrow{R}}_i^{(0)}$ for bead i. Then, to determine the pattern of network connections, the distance $d_{ij}^{(0)}=|{\overrightarrow{R}}_i^{(0)}-{\overrightarrow{R}}_j^{(0)}|$ between equilibrium positions of any two beads i and j was compared with a prescribed interaction radius r_int. If this distance was below r_int, the two beads were connected by a deformable elastic spring. The network connectivity was stored in matrix A with entries A_ij = 1, if beads i and j are connected, and A_ij = 0, else. For all ABC protein networks we have used an interaction radius of 9Å. The choice of the interaction radius in elastic network simulations has been widely debated on in the field. If the value is too small, the network would decompose into lose or even disconnected substructures, which would lead to unreliable results. On the other side, a too large interaction radius would render the network very stiff, thus preventing functional motions to occur. In this work, the interaction radius has be chosen based on observations from a previous study, where values between 8Å and 9.5Å have been found to be optimal to describe domain motions in many proteins [51].

TABLE 1

Table 1. Investigated ABC transporters.

The total elastic energy of the network is the sum of all spring contributions, i.e., $U=\sum _{i<j}^N\kappa \frac{A_{ij}}{2}{(d_{ij}-d_{ij}^{(0)})}^2$. Here, N is the number of beads in the protein network, $d_{ij}=|{\overrightarrow{R}}_i-{\overrightarrow{R}}_j|$ is the actual length of a spring connecting beads i and j in some deformed network conformation, with ${\overrightarrow{R}}_i$ being the actual position vector of bead i, and $d_{ij}^{(0)}$ is the corresponding natural length (as extracted from the PDB file). The spring stiffness constant κ is assumed to be the same for all network springs.

When thermal fluctuations and hydrodynamical interactions are neglected, the dynamics of the network can be described by a set of over-damped Newton equations. For bead i the equation of motion is

$\begin{array}{ll}\gamma \frac{d}{dt}{\overrightarrow{R}}_i=-\frac{\partial }{\partial {\overrightarrow{R}}_i}U+{\sigma }_i·{\overrightarrow{F}}_{i,lig}.& (1)\end{array}$

On the left hand side of Equation (1), γ is the friction coefficient assumed to be equal for all network beads. The first part on the right hand side are the elastic forces exerted by network springs which are connected to bead i and the second term ${\overrightarrow{F}}_{i,lig}$ is the force exerted by an ATP ligand. The parameter σ_i equals 1 if a ligand is connected to bead i, and is 0 otherwise. Interactions between the protein elastic network and ligands are described in the following section. Explicitly, Equation (1) reads

$\begin{array}{ll}\gamma \frac{d}{dt}{\overrightarrow{R}}_i=-{\displaystyle \sum _j^N}\kappa A_{ij}\frac{d_{ij}-d_{ij}^{(0)}}{d_{ij}}({\overrightarrow{R}}_i-{\overrightarrow{R}}_j)+{\sigma }_i·{\overrightarrow{F}}_{i,lig}.& (2)\end{array}$

2.2. Modeling of Nucleotide Binding

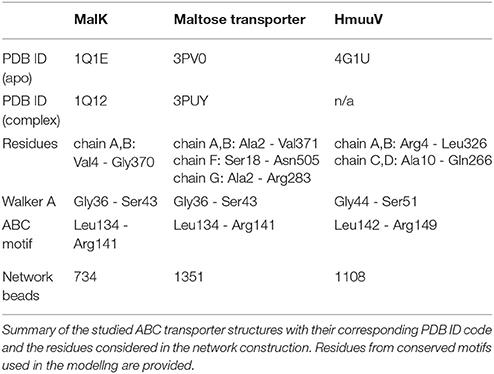
Based on the constructed elastic network of a nucleotide-free state of the ABC transporter we have established a ligand-elastic-network model in which each of the two ATP molecules was described by a single ligand bead and its binding process was modeled by placing it into the center of the nucleotide binding pocket and connecting it to pocket beads via elastic springs. The binding configuration is schematically displayed in Figure 1. In the simulations, ligand bead 1 was connected to the Walker A motif beads (Gly-Pro-X-Gly-X-Gly-Lys-Ser) from one NBD and the ABC motif beads (Leu-Ser-Gly-Gly-X-X-Gln-Arg) from the other domain. Accordingly, ligand bead 2 was connected to the corresponding motif beads from the second pocket. The natural lengths of the additional ligand-springs were chosen smaller than their corresponding initial lengths, implying that initially they were stretched and upon binding the generated forces between each ligand and the selected pocket beads were attractive.

FIGURE 1

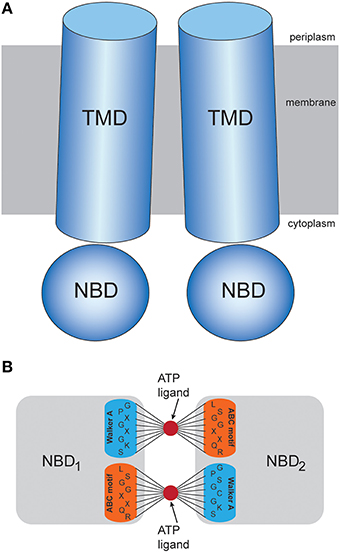
Figure 1. Transporter structure and modeling scheme. (A) Schematic representation of the domain organization in ABC transporters. (B) Illustration of the proposed coarse-grained ligand interaction scheme. An ATP-mimicking ligand bead is placed in the center of each nucleotide binding pocket, where it is bound to beads of the Walker A and ABC residue motifs via stretched elastic springs.

To check the robustness of our ligand-model, we have followed for each investigated ABC transporter, the formation of the ligand-complexed structure for different initial ligand-binding conditions. Starting always from the native conformation of the ABC protein network, the two ligand beads were simultaneously placed in their pockets but the natural lengths of ligand springs have been randomly varied in each realization (i.e., the strengths of initial deformations of ligand springs have been altered). More precisely, the following scheme was implemented in the simulations. The natural lengths of the ligand springs have been chosen as $d_{li{g}_1,p_k^1}^{(0)}=d_{li{g}_1,p_k^1}^{ini}∕{\alpha }_{p_k^1}$ for ligand 1 and $d_{li{g}_2,p_k^2}^{(0)}=d_{li{g}_2,p_k^2}^{ini}∕{\alpha }_{p_k^2}$ for ligand 2. Here, indices $p_k^1$ and $p_k^2$ (with k = 1, …, 16) denote the motif beads from pocket 1, pocket 2 respectively. Furthermore, $d_{li{g}_1,p_k^1}^{ini}(d_{li{g}_2,p_k^2}^{ini})$ was the initial length of the spring that connected ligand 1 (ligand 2) to the motif bead with index $p_k^1(p_k^2)$ upon its placement. The parameters ${\alpha }_{p_k^1}$ and ${\alpha }_{p_k^2}$ were random numbers chosen from an interval between 2.0 and 5.0, ensuring that natural spring lengths were shorter than their initial lengths. To impose symmetric ligand interactions, these parameters were the same for both ligands (i.e., ${\alpha }_{p_k^1}={\alpha }_{p_k^2}$), meaning that the spring connecting ligand 1 to a particular motif bead and the corresponding spring connection for ligand 2 had roughly the same prescribed natural length. Then, as a normalization condition for all realizations, the natural spring lengths were rescaled, such that the amplitude of the total force ${\overrightarrow{F}}_{lig}^{ini}$ exerted by each ligand upon binding takes a fixed common value, i.e., $\left|{\overrightarrow{F}}_{li{g}_1}^{ini}\right|∕\kappa =\sum _k(d_{li{g}_1,p_k^1}^{ini}-{\tilde{d}}_{li{g}_1,p_k^1}^{(0)})=F_1$, $\left|{\overrightarrow{F}}_{li{g}_2}^{ini}\right|∕\kappa =\sum _k(d_{li{g}_2,p_k^2}^{ini}-{\tilde{d}}_{li{g}_2,p_k^2}^{(0)})=F_2$, respectively. Here, ${\tilde{d}}_{li{g}_1,p_k^1}^{(0)}$ and ${\tilde{d}}_{li{g}_2,p_k^2}^{(0)}$ are the rescaled natural lengths of ligand springs. In the simulations of MalK and HmuUV values $F_1=0.5·\sum _k{d}_{li{g}_1,p_k^1}^{ini}$ and $F_2=0.5·\sum _k{d}_{li{g}_2,p_k^2}^{ini}$ were used for the forces. These values correspond to a force that would be generated if each ligand spring in a pocket would be initially stretched by half the average value of initial spring lengths. In the simulations of MalFGK₂ the factor 0.35 was used.

The equation of motion for ligand 1 was

$\begin{array}{ll}\gamma \frac{d}{dt}{\overrightarrow{R}}_{li{g}_1}={\displaystyle \sum _{k=1}^{16}}{\overrightarrow{F}}_{li{g}_1,p_k^1}& (3)\end{array}$

with the elastic forces

$\begin{array}{l}{\overrightarrow{F}}_{li{g}_1,p_k^1}=-\kappa \frac{d_{li{g}_1,p_k^1}-{\tilde{d}}_{li{g}_1,p_k^1}^{(0)}}{d_{li{g}_1,p_k^1}}({\overrightarrow{R}}_{li{g}_1}-{\overrightarrow{R}}_{p_k^1}).\end{array}$

The equation for ligand 2 was the same with index 2 instead of 1. Here, ${\overrightarrow{R}}_{li{g}_1}$ is the actual position of ligand 1 and $d_{li{g}_1,p_k^1}=|{\overrightarrow{R}}_{li{g}_1}-{\overrightarrow{R}}_{p_k^1}|$ are the actual lengths of ligand springs. For the ligand beads the same friction coefficient γ as for other network beads was assumed. The additional springs also had the same stiffness constant κ as all other elastic springs. According to Newton's actio and reactio principle the forces exerted by the ligand in Equation (2) are related to the forces in Equation (3) by ${\overrightarrow{F}}_{i,lig}=-{\overrightarrow{F}}_{lig,i}$. Note that in Equations (2) and (3) the dependencies on the friction coefficient γ and the spring stiffness constant κ can be removed using an appropriate rescaling of time.

Subsequent to binding of the two ligand beads, we have followed the formation of the in silico ligand-bound complex of the ABC transporter by integrating the set of Equations (2) and (3) until a stationary structure of the network-ligand complex was reached (time moment 2500 in the simulations). This procedure was carried out 50 times (for MalK and MalFGK₂ proof of concept simulations 20 times, respectively), each time with a different set of coefficients ${\alpha }_{p_k^1}$. In the simulations the equations of motion were numerically solved by employing an first-order integration scheme with a time-step of 0.1.

To visualize conformational changes resulting from ligand-binding, one ligand-bound complex obtained from a single simulation in each investigated ABC transporter was selected and its structure shown in the ribbon representation. To ensure reproducibility of these results, the parameters of ligand interactions used in the specific simulations are provided in Supplementary Table 1.

2.3. Characterization of Conformational Motions

In the simulations conformational motions have been characterized by tracing distance changes between network beads (or groups of beads). To determine the size of a nucleotide binding pocket, its gyration radius was computed as the RMSD of network beads which corresponded to the Walker A and ABC signature residues of a pocket (see Table 1) with respect to its geometrical center. The separation between the two NBDs was measured as the distance between their geometric centers. In the MalFGK₂ maltose transporter the width of the cytosolic gate was determined as the distance between the two network beads which corresponded to residues Thr176 from chain G and Leu429 from chain F, respectively. For HmuUV several variables have been monitored during the simulations. Beside the NBD separation we have also measured the separation between the TMD coupling helices as the distance between the Asp222 network bead of each TMD. The rotational shift of the TMDs with respect to the NBDs has been quantified by the angle between the vector which connects the geometric centers of the NBDs and that which connects the two centers of the TMDs. To further describe global motions of the TMDs, we have calculated during the simulations the principal axes of each TMD as the eigenvectors of its inertia matrix. To detect motions localized at the central interface of the TMDs, the distance between the Ala146 residue beads which belong to the TM5 helices and are located in the vicinity of the putative cytoplasmic substrate gate has been monitored. Near the periplasm side the distance between the Thr167 residue beads (from the TM5 helices) and that between the Arg176 beads (from the H5a helices) was traced. To depict conformations obtained from the simulations in the ribbon representation, a structural reconstruction from the alpha-carbon trace was performed [52]. For the visualization the VMD software was used [53].

2.4. Normal Mode Analysis and Modified ENM

The normal mode analysis for the HmuUV structure was performed using the AD-ENM server. There, the same interaction radius as in our simulations was used for the elastic network and the amplitude of displacement was set to 3.0. The structural displacement of the lowest non-zero mode was compared with the findings obtained from our simulations.

For the HmuUV ABC transporter, in addition to the usual elastic network model, a modified setup was considered. In the conventional elastic network description the bead connectivity is determined by applying the interaction radius for a specific static conformation of the protein and, once fixed, it is assumed not to change under structural changes of the network, i.e., existing links between beads cannot be broken and new links cannot be established either. Hence, the separation of two network beads which are initially connected by a spring is bound by the harmonic potential coupling them and can never be too large. In the elastic network of the HmuUV apo structure several links connecting the two TM5 helices at the central TMD interface close to the putative cytoplasmic gate were present. Since such links could artificially stiffen the network in that region and, hence, possibly prevent relative motions of the transmembrane helices, a modified elastic network description in which the interface between the two TMDs was softened was considered. In this model, for simplicity, the few links which connect the TM5 helix from one TMD with that of the other TMD have been cut after the original construction of the elastic network. More precisely, the 15 links which initially connected residue beads Asn144 to Ile153 of one TMD to the corresponding residue beads in the other TMD were removed. Then, in an independent set of simulations, the analysis for HmuUV was repeated using the modified description.

3. Results

Figure 1 shows the common architecture of ABC transporters consisting of two nucleotide-binding domains (NBDs) located in the cytosol and a pair of transmembrane domains (TMDs). In each NBD the conserved Walker A and ABC signature residue motifs, which are critical for the binding of ATP molecules and their hydrolysis reaction can be found. In the absence of nucleotides the motifs are spatially separated and the two binding pockets formed by them are in an open conformation, each ready to bind an ATP molecule. The TMDs typically consist of several alpha helices. At the central domain interface some of them constitute a confined channel structure through which the substrate is transported across the membrane.

We have considered the elastic network description to investigate conformational dynamics of ABC transporters in computer experiments. The network consisted of identical beads which represented entire amino acid residues and elastic springs connecting any two beads if their spatial distance was below a prescribed interaction radius. Details of the network construction can be found in the Materials and Methods section. The elastic network model is an approximative mechanical description of protein dynamics, capable of computationally handling large proteins with several hundreds (or even thousands) of amino acids and following slow conformational motions inside them in a structurally resolved way. The internal motions of proteins in solution are characterized by low Reynolds numbers and therefore dominated by friction. In fact, it has been shown that inertial effects are negligible on time scales of tens of picoseconds and slower conformational motions become relaxational [54]. Therefore, the slow conformational motions with characteristic timescales of milliseconds taking place in protein machines should be purely damped. Neglecting hydrodynamical effects and thermal fluctuations, the dynamics of the protein network can therefore be described by mechanical Newton's equations of motion considered in the over-damped limit. Thus, within the approximate nature of the model, internal motions in proteins are described as processes of conformational relaxation of its corresponding elastic network.

The aim of this study was to investigate nucleotide-induced conformational dynamics of ABC transporters, analyse the coupling of domain motions and discuss how structural changes inside the transmembrane part may contribute to the mechanism of substrate transport. For that purpose, we have constructed a ligand-elastic-network model of ABC transporters which incorporated binding of two ATP mimicking ligands to the pockets inside the NBDs. This approach will be described in the following section.

3.1. ATP-ligand Binding and Related Conformational Motions

Due to, in part, the lack of experimental data, interactions with ATP and the effect of binding and its hydrolysis is hitherto unknown in many ABC transporters. However, the two nucleotide-binding pockets are well-defined by the presence of the conserved Walker A and ABC signature motifs located in each NBD. Moreover, it has been shown previously, that most ABC transporters bind two ATP molecules in each single catalytic cycle [55]. On the other side, the coarse-grained nature of the elastic network model does not allow to resolve the complicated interactions between the protein and ATP molecules in full detail. To investigate conformational motions induced by binding of ATP molecules, we have constructed a dynamical ligand-elastic-network model of ABC transporters which incorporated binding of two ATP nucleotides to the NBDs in a simplified fashion. Details of the modeling and the network dynamics are provided in the Materials and Methods section and the limitations of our approach are mentioned in the Discussion section.

Similar to our previous publication, where entire operation cycles of the hepatitis C virus helicase motor protein were investigated using ENM modeling [47], binding of ATP was phenomenologically accounted for in the present study. Consistent with the coarse-grained character of the elastic network model, we have described an ATP-ligand by a single bead and modeled its binding process to the nucleotide pocket by allowing it to physically interact with network beads present there. We have selected those beads as interaction spots that corresponded to residues from the conserved sequence motifs mentioned above. More precisely, a ligand could interact with beads of the Walker A motif from one NBD and beads of the ABC motif from the other NBD. Binding of the two ATP-ligands was implemented by simultaneously placing each ligand bead into its binding pocket and creating spring connections to the motif beads. These additional elastic springs were initially stretched so that upon binding, attractive forces between each ligand and the selected pocket beads were generated. Therefore, as a result of the binding process, network deformations were initiated. First localized in the two binding pockets, they gradually spread and conformational relaxation motions of the entire protein network took place until a stationary structure of the elastic network complexed with the two ligands was reached.

To follow the formation of an approximate in silico version of the ligand-complexed transporter structure upon binding of the two ligand beads was the focus of our computer experiments. We have numerically integrated the set of equations of motion to obtain the position of all network beads at every instant of time. Since in our approach interactions between ATP ligands and the pocket were modeled only roughly, we have tested the robustness of the ligand network description and its predicted conformational changes by following the formation of the ligand-bound complex many times, each time starting from the nucleotide-free network. In each realization different ligand-binding patterns were applied by randomly varying initial deformations of the ligand springs (see Materials and Methods). To characterize conformational motions subsequent to binding of the two ligand-beads we have traced several geometric variables during the simulations, which reflect both global domain rearrangements as well as structural changes localized in the substrate translocation cavity of the TMDs (see Materials and Methods). A single process of conformational relaxation in the transporter elastic network, which was induced by binding of the two ligand beads and corresponded to the formation of a transporter-ligand complex, could therefore be visualized by a single trajectory in the space of these variables.

3.2. Proof of Concept Simulations

Predictions of the proposed ligand-elastic-network model were benchmarked by applying it to ABC transporters for which several crystal structures are known. Conformational motions subsequent to ligand binding were analyzed and the structure of the ligand-bound complex obtained from the simulations was compared with that of the corresponding crystal structure determined with ATP-analogs. First, for a general test of the suggested method, the isolated ATPase subunit of an ABC transporter was considered. After that, the full-length maltose transporter MalFGK₂ was investigated. A summary of the studied structures and details of the simulations are given in Table 1.

3.2.1. MalK ATPase Subunit

The MalK homodimer represents the ATPase engine which powers substrate translocation in the maltose transporter system of Escherichia coli. Each MalK monomer consists of a nucleotide binding domain which harbors the Walker A and ABC signature motifs and a regulatory domain (RG) which interacts with other enzymes [13]. Crystal structures of MalK in the absence of ATP and complexed with nucleotides are shown in Figure 2. Without ATP the monomers are separated and the MalK dimer structure is in the open shape conformation (Figures 2A,B). When binding of two ligands in the elastic network which corresponded to that open structure was modeled, we observed for all different realizations of ligand-binding conditions similar conformational dynamics along the formation of the ligand-complexed structures, as evidenced by the low dispersion in the trajectories which monitor changes of the protein structure (shown in Figure 3). Subsequent to binding of the ligands, deformations of the elastic networks which were localized in the nucleotide binding pockets became generated and the pockets closed. We detected a decrease in the gyration radii of the pockets of about 6Å (see Figure 3A). When such initial deformations eventually spread over the entire MalK network they induced global large-amplitude relative motions of the two NBDs with the separation between them decreasing about 9Å (see Figure 3B). Therefore, in all final ligand-complexed networks the MalK dimer was in a closed conformation with the two NBDs found to be in tight contact. All predicted ligand-bound structures obtained from the simulations compared with the ATP-bound form of the MalK crystal structure by a RMSD value less than 4Å; in comparison, the initial ATP-free MalK and ATP-bound MalK differ by an RMSD of 7.2Å. In Figures 2a,b we show one selected in silico ligand-bound structure together with the ATP-complexed crystal structure. The two conformations agree remarkably well. They align with an RMSD of 2.7Å. In the in silico structure the nucleotide binding pocket have gyration radii of 6.4Å and 6.3Å, respectively, and the NBDs are separated by 20.4Å. For comparison, the corresponding values in the ATP-bound crystal structure are 6.7Å and 6.8Å for the gyration radii of the pockets and 22.4Å for the NBD distance.

FIGURE 2

Figure 2. Nucleotide-induced conformational changes in the MalK dimer. (A,B) The apo crystal structure in ribbon representation is shown in top and side view perspective. Chain A is colored blue and chain B is shown in red. The alpha-carbon atoms from residues belonging to the Walker A motif in each chain are shown as orange beads. Those corresponding to the ABC signature motifs are colored in yellow. In the side view the subdomain organization of nucleotide-binding domain (NBD) and regulatory domain (RD) in each chain becomes apparent. (a,b) Comparison of modeling results and the ATP-bound crystal structure. A single ligand-complexed conformation obtained after modeling of nucleotide binding (in solid coloring) is superimposed with the ATP-bound experimental structure (in transparent gray). The two bound ligands are shown as black beads.

FIGURE 3

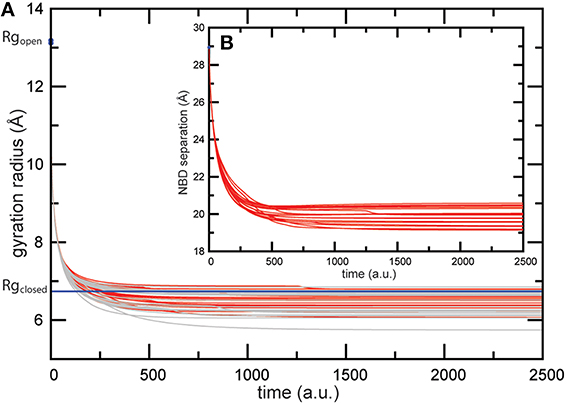
Figure 3. Trajectories of conformational changes in the MalK dimer. Trajectories characterizing conformational motions along the formation of the ligand-bound MalK structures are shown for 20 different ligand-binding realizations. The main panel (A) displays changes in the gyration radius of both pockets (red and gray curves). Corresponding values computed for the ATP-bound crystal structure are shown as blue lines. The inlet (B) displays changes in the separation of the two NBDs.

3.2.2. Maltose ABC Transporter

In the next step of benchmark simulations we have checked how well the coupling of ATP-induced motions and transmembrane dynamics is reproduced in our model by applying it to a full-length ABC protein. We have chosen the transporter MalFGK₂ from Escherichia coli which is involved in the import of maltose/maltodextrin substrates and represents the probably best studied ABC systems, for which multiple structures are available [20]. Its overall structure comprises the two ATPase forming cytoplasmic MalK subunits and two transmembrane domains, MalF and MalG. The structures we used have been co-determined with the periplasmic maltose binding protein MalE. Since here we are not interested in a detailed explanation of the transport cycle we have omitted the periplasmic parts in the simulation. Maltose importer structures are shown in Figure 4. Without nucleotides the MalK dimer is in the expected open conformation (Figure 4A). At the same time the TMDs are arranged in an inward-facing conformation with a closed periplasmic gate and the gate to the cytoplasm being wide open (Figure 4B).

FIGURE 4

Figure 4. Nucleotide-induced conformational changes in the MalFGK₂ maltose transporter. (A) The apo crystal structure shown in ribbon representation with chains colored differently. Conserved motifs inside the NBDs are colored as in Figure 2. (a) Comparison of modeling results and the AMP-PNP bound crystal structure. A single ligand-complexed conformation obtained after modeling of nucleotide binding (in solid coloring) is superimposed with the AMP-PNP complexed experimental structure (in transparent gray). The two bound ligands are shown as black beads. (B,b) Structure of the transmembrane maltose binding site and the coupling helices in the apo state and the ligand-complexed in silico conformation. Only two helices from each TMD are displayed as ribbons together with the surface representation (chain F: Asp364-Asn449 and chainG: Thr158-Arg238). Black lines have been aligned to the central helices to emphasize the correctly obtained progression from the inward-facing to the outward-facing TMD conformation.

When the nucleotide binding process was modeled in this transporter, we found similar conformational dynamics upon binding of the two ligands as for the previous simulations of the isolated MalK dimer; the nucleotide binding pockets were shrinking in its size and the large scale global motions which bring the NBDs in tight contact set in. In Figures 5A,B the radii of the pockets and the distance between the NBDs are plotted as they change along the formation of the ligand-bound complex. Again, as in the previous simulation, the conformational changes were robust and not sensitive to variations in the ligand binding interactions in our model. The gyration radii of the pockets changed about 2.5Å and in ligand-complexed conformations the pocket sizes compared well with those found in the ATP-complexed crystal structure (see Figure 5A). The separation of the NBDs decreased by approximately 2.5Å to a value around 22Å in the ligand-complexed conformations (see Figure 5B), which is in well agreement with the NBD distance computed for the ATP-complexed crystal structure (22.3Å). Regarding the coupling of nucleotide-induced motions in the NBDs to motions inside the TMDs, we found that all predicted ligand-bound structures obtained from the simulations compared with the ATP-bound form of the maltose transporter by a RMSD value of less than 3Å, indicating that the model reproduced well the nucleotide-activated conformational rearrangements of the full transporter structure. To check details of the transmembrane gating we have monitored in our simulations the size of the cytoplasmic gate along the formation of the ligand-bound transporter structures and found that it decreased by approximately 1.5Å (see Figure 5C) and is centred around a value of 8Å in the ligand-complexed states. For comparison, the gate size in the ATP-complexed crystal structure is 7.6Å.

FIGURE 5

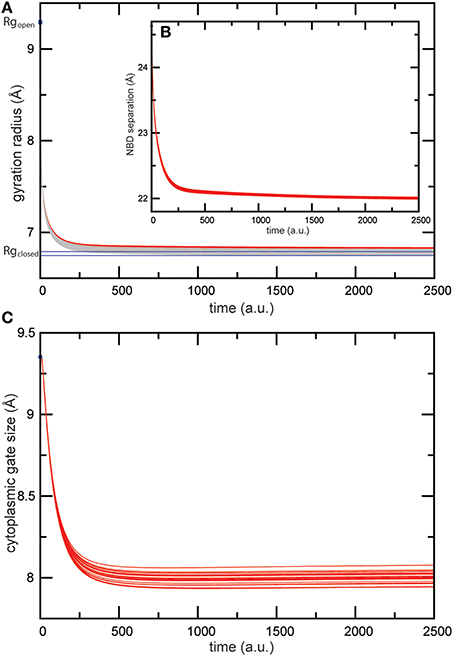
Figure 5. Trajectories of conformational changes in the maltose transporter. Trajectories characterizing conformational motions along the formation of the ligand-bound MalFGK₂ structures are shown for 20 different ligand-binding realizations. (A) Changes in the gyration radius of each nucleotide-binding pocket are shown as red and gray curves. Values of pocket radii computed for the AMP-PNP-bound crystal structure are indicated as blue lines. (B) Trajectories monitoring the separation of the two NBDs as it changed during the simulations. (C) Trajectories monitoring shrinking in the size of the cytoplasmic gate.

The obtained results evidence that our model is able to reproduce the ATP-induced structural changes in the maltose transporter system remarkably well. To visualize the structural agreement we have selected a single in silico ligand-bound complex of the transporter and compared its conformation with that of the ATP-complex crystal structure (see Figure 4a). Overall the conformations align with an RMSD value of 2.6Å. Figure 4a illustrates the high degree of conformational similarity of the transporter structures. This applies to the NBDs where the ligand binding events take place as well as to the remote TMDs, where the model does correctly reproduce the progression from the inward-facing to the outward-facing channel shape (compare Figure 4B and Figure 4b). As for the quantitative agreement we found that in the in silico structure the nucleotide binding pocket have gyration radii of 6.8Å and 6.7Å, respectively, and the NBDs are separated by 22.0Å. For comparison, the corresponding values in the ATP-bound crystal structure are 6.7Å and 6.8Å for the gyration radii of the pockets and 22.3Å for the NBD distance. The size of the cytoplasmic gate was 7.9Å (in silico) and 7.6Å (crystal).

3.3. HmuUV Heme Transporter

The performed benchmark simulations have evidenced the quality of the model to predict functional conformational dynamics of ABC transporters remarkably well. Next, the model is applied to the HmuUV transporter for which only a single structure, that of the nucleotide-free state, has yet been determined [50]. HmuUV is an ABC importer which is expressed in bacteria as part of their survival strategy since it presents an efficient agent for the acquisition of iron, which typically has a low intracellular concentration but is needed for various chemical processes [49]. Figure 6A shows the domain architecture of the HmuUV heme transporter in its nucleotide-free conformation. In the NBDs (chains C and D) the conserved ATP binding motifs (Walker A and ABC signature motif) are spatially separated and form two open binding pockets for ATP ligands at the domain interface (see Figure 6C). At the interface of the two TMDs (chains A and B), transmembrane helices 5 (TM5) and helices 5a (H5a) form a cone-shaped cavity which has been assigned the putative heme translocation pathway [50]. Their outward-facing arrangement indicates that in the nucleotide-free state of the transporter the pathway is open to the periplasm, whereas it is sealed to the cytoplasm by a narrow gate and heme passage would thus be sterically hindered in this region (Figure 6B).

FIGURE 6

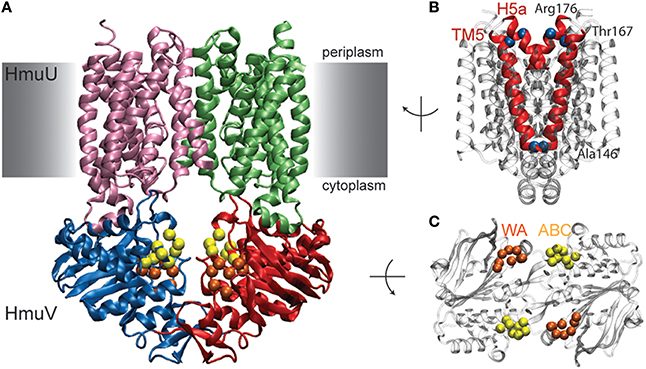
Figure 6. Nucleotide-free conformation of HmuUV heme transporter. (A) Structure of the heme transporter in ribbon representation. The domain coloring is similar to that of the maltose transporter and the conserved Walker A and ABC signature motifs from the NBDs are also highlighted similar to previous figures. They form two open nucleotide-binding pockets as shown in the top view of the isolated NBDs (shown in C). (B) Transmembrane helix 5 (TM5) and helix 5a (H5a) of both TMD chains are highlighted in red. In the chosen side view perspective they constitute a cone-shaped cavity which is sealed at the cytoplasmic side. Residues near the periplasmic and cytoplasmic side, whose positions have been followed during the simulations, are depicted as blue alpha-carbon beads.

Like in the previous simulations, following the construction of the HmuUV elastic network, ligand binding to the NBDs was modeled and the subsequent conformational changes followed by monitoring relaxation trajectories. The results are shown in Figure 7 and again, like in the previous cases, they were not sensitive to variations in the ligand binding conditions.

FIGURE 7

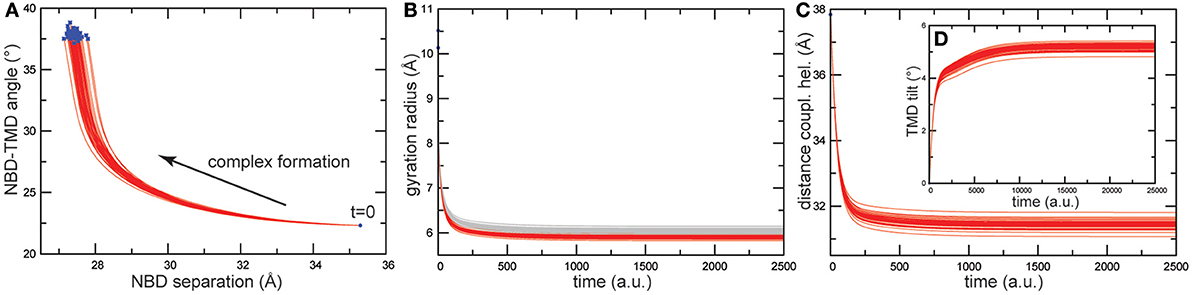
Figure 7. Trajectories of conformational changes in HmuUV. Trajectories characterizing conformational motions along the formation of ligand-complexed structures are shown for 50 different ligand-binding realizations. (A) Trajectories showing changes in the distance between the NBDs and in the orientation of the TMDs relative to the NBDs, subsequent to binding of the two ligand beads. They evidence the coupling between closing motions of the NBDs and relative global rotation of the TMDs. (B) Changes in the gyration radius of each nucleotide-binding pocket are shown as red and gray curves. Changes in the distance between the coupling helices (C), and in the tilt of one TMD (D) are displayed (see Materials and Methods).

3.3.1. Coupled Domain Motions

As for the motions generated inside the NBDs, they resemble those found for the MalK and the maltose transporter. The size of both nucleotide binding pockets decreased about 4Å (see Figure 7B) and large-amplitude relative motions of the NBDs bringing them into tight contact, with the distance between them decreasing about 8Å, were observed (see Figure 7A). Considering the coupling of domain dynamics in HmuUV, we find that ligand-induced structural changes in the NBDs cause drastic consequences in the conformation of the remote TMDs. First, the distance between two coupling helices which each connect a TMD with its NBD was significantly decreased about 6Å (see Figure 7C). Second, at the same time as the NBDs approached one another, the angle between the NBDs and the TMDs changed by about 20°, indicating global rotational motions of the TMDs relative to the NBDs (see Figure 7A). Rotational motions are first small after ligand binding but become pronounced when the steady conformations of the ligand-bound complexes are approached. In addition to the rotational dynamics, tilting motions of each individual TMD were observed as evidenced by a change in the orientation of the long principal axes of ~5° (see Figure 7D). To visualize global conformational changes, the structure of one selected ligand-bound complex was superimposed with that of the apo crystal structure of the HmuUV transporter (shown in Figure 8A). In the in silico obtained ligand-bound conformation the NBDs are separated by 27.3Å and the coupling helices are 31.3Å apart. The corresponding distances in the apo structure are 35.3Å and 37.8Å, respectively. Further on, the structural comparison clearly evidences the coupling of linear tweezer-like motions of the NBDs and a rotational displacement of the TMDs (see Figure 8a). This mode of coupling is confirmed by the normal mode analysis (see Materials and Methods). Indeed, the conformational motions corresponding to the first normal mode of the HmuUV elastic network (visualized in Supporting Video S1) resemble the collective domain motions identified by our model. Moreover, for the vitamin B₁₂ ABC transporter BtuCD, which is structurally similar to HmuUV, a similar scheme of domain coupling can be observed, as revealed through comparison of apo and nucleotide-complexed conformations [56, 57] (presented in Figures 8B,b). Such aspects will be further commented on in the Discussion section.

FIGURE 8

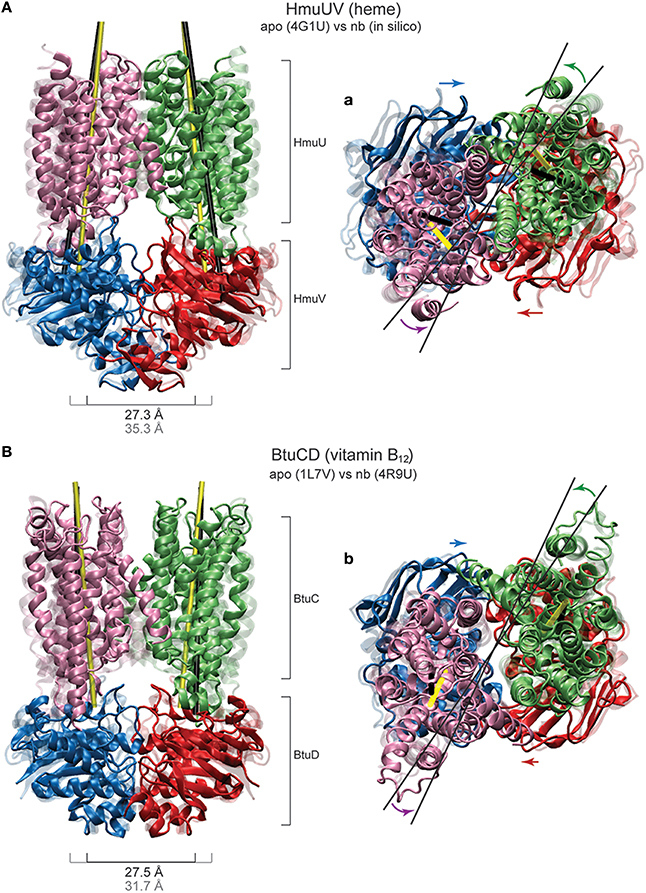
Figure 8. Coupled domain dynamics in HmuUV and BtuCD. Comparison of nucleotide-induced domain motions in the heme and the vitamin B₁₂ ABC transporter. (A,a) The HmuUV apo conformation (transparent ribbons) and a single ligand-complexed structure from the simulations (solid ribbons) are superimposed (with the two NBDs being aligned). In the front view perspective (A), the switching of the NBD dimer from the open to the closed shape is apparent. Corresponding values of the NBD separation are given. The tilting of each TMD is visualized by the change in the orientation of the long principle axes, depicted as thick black/yellow lines for the apo/complexed structure. In the top view perspective (a), the coupling of linear motions of the NBDs and rotational motions of the TMDs is indicated by colored arrows. The rotational shift of the TMDs is highlighted by thin black lines. (B,b) The apo and AMP-PNP bound crystal structure of BtuCD (transparent and solid ribbons, respectively) are superimposed with the two NBDs being aligned. Similar perspectives as in (A,a) are employed to best illustrate the similarity to HmuUV in the coupling of domain motions.

3.3.2. Rearrangement of TM Helices

In order to detect possibly functional motions localized in the putative heme translocation cavity, distances between residues near the periplasmic and cytoplasmic gate were traced as they changed along the formation of the ligand-complexed HmuUV structures. No significant change could be detected in the distance between the Ala146 residues of the TMDs, which are in proximity of the cytoplasmic gate (see Supplementary Figure 1A). Similarly, variations in the distance between residues Arg176 and Thr167, both located near the exit to the periplasm, were small (about 1Å see Supplementary Figure 1B). In all ligand-complexed structures latter distances were decreased as compared to the apo structure, indicating that relative motions of the TM5 and H5a helices may tend to cause slight closing near the periplasm side. The structural rearrangement of TM helices is shown in Figure 9, where the TMDs of the HmuUV apo structure was superimposed with those of the single ligand-bound structure obtained from the simulation (the same ligand-complexed structure as shown in Figure 8). Coupled to ligand-induced conformational dynamics of the NBDs, the internal organization of all TM helices and their relative orientations was changed. As shown in Figure 9, for TM helices 1–4 and 6–9 the changes were pronounced, whereas at the central domain interface helices 5, 5a, and 10 underwent only marginal tilting and no significant rearrangements inside the putative heme translocation cavity could be detected. These observations are confirmed by the normal mode analysis (see Materials and Methods). The structural displacements inside the TMDs, as predicted by the lowest normal mode, is found to agree remarkably well with results from our ligand-elastic-network simulations (compare Figure 9 left and middle panel).

FIGURE 9

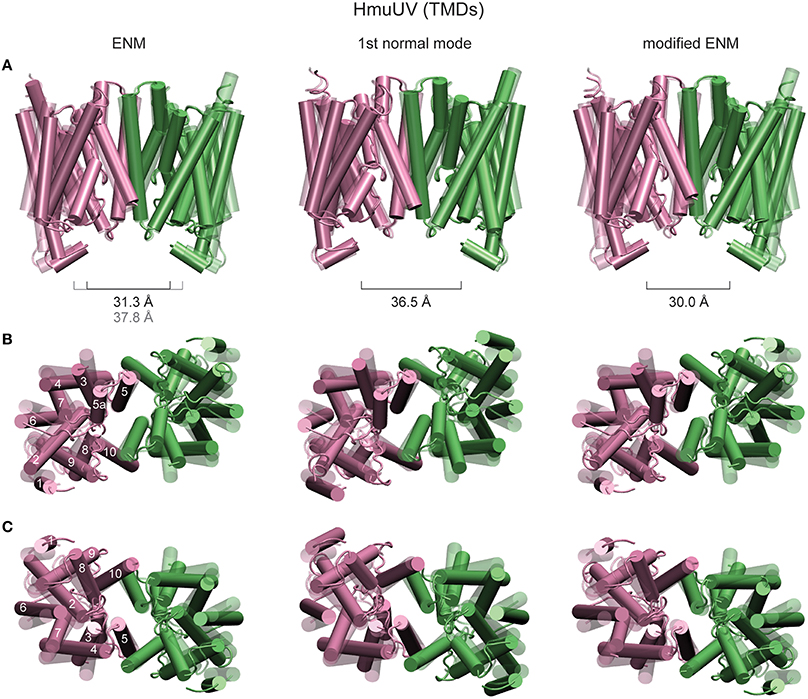
Figure 9. Structural rearrangements of TM helices in HmuUV. The TMDs of the HmuUV apo structure (transparent) are superimposed with those of ligand-bound structures obtained from the simulations and the structural displacements predicted by the normal mode analysis (all solid). TM helices are shown as tubes. The left column shows the same ligand-bound conformation as in Figure 8, obtained from the usual ENM. Structure changes predicted by the first normal mode are shown in the middle column. Right column: A single ligand-bound conformation as obtained from the modified ENM. Three different perspectives are provided. In row (A), the front view is chosen and the distance between the coupling helices is given. The view from the periplasm and that from the cytoplasmic side are provided in rows (B,C), respectively (for clarity the coupling helices have been omitted in these representation). For one TMD the TM helices are assigned their numeric labels.

In the original elastic network description, which the performed ligand-binding model was based on, the two TM5 helices were connected by several elastic springs in the region close to the putative cytoplasmic heme gate. Since such links could possibly prevent functional relative motions of TM helices, a modified elastic network description in which the interface between the TMDs was softened was considered. Details of the modified model are given in the Materials and Methods section. In an independent set of simulations, the formation of ligand-complexed HmuUV structures was followed using the modified description. Trajectories displaying changes in the widths of the cytoplasmic and periplasmic gate during the new simulations are provided in Supplementary Figures 1C,D. Despite the softened TMD interface they are still small (around 1Å) and their significance in functional gating cannot be evidenced. Structural changes inside the TMDs, which correspond to a single ligand-bound conformation obtained from the modified ENM, are shown in Figure 9 (right panel).

In conclusion, rearrangements of TM helices as obtained from the undertaken modeling do not give clear evidence for either gate opening or closing at the cytoplasm and periplasm side and hence, results from the current analysis may not be able to provide an explanation of how nucleotide-dependent conformational motions are coupled to the transmembrane gating dynamics in the HmuUV ABC transporter (see Discussion).

4. Discussion

In this paper a coarse grained model which allows to investigate nucleotide-induced conformational dynamics in ABC transporters is presented. Based on the elastic network description of the apo structure of the transporter, binding of nucleotide ligands to the ATP binding domains was mimicked in an approximate fashion. In this way the formation of the ligand-bound transporter complex could be followed and the underlying conformational motions analysed in computer simulations. The explanatory quality of the proposed model was first confirmed in a set of simulations where nucleotide-induced conformational changes predicted by the experimentally obtained crystal structures of the MalK NBD dimer and the full-length maltose ABC transporter were reproduced extremely well in silico. The model was then applied to explore functional dynamics of the heme-specific ABC transporter HmuUV, for which yet only the apo structure could been determined. It is remarkable that despite the gross simplifications present in the elastic network model, i.e., a protein is viewed as a meshwork of beads connected by deformable springs, it can still well describe the ATP-induced functional conformational changes in ABC transporters. For the MalK subunit the switching from open to the closed dimer configuration upon ATP binding is reproduced. Moreover, for the full-length maltose transporter MalFGK₂ progression from inward-facing to the outward-facing state is correctly obtained. Hence, the model is apparently also capable of covering functionally important aspects of intramolecular domain communication and coupling of nucleotide-induced conformational motions in the NBDs to gating dynamics in the remote TMDs in ABC transporters. As a common aspect of the conformational dynamics we found that in all ABC simulations binding of nucleotide ligands induced large-amplitude conformational changes inside the transporter structure which corresponded to ordered domain motions. These motions were robust and not sensitive to the specific interaction pattern that was applied between ligands and the transporter within our description. This indicates that interactions with nucleotides generate a generic response, a property which may assure that similar well-organized domain motions are repeated in each ATP-induced operation cycle and substrate transport is robustly maintained, despite the presence of possible perturbations. The most significant response was identified inside the two NBDs which, subsequent to ligand binding, underwent substantial motions bringing them from an open-shape conformation in which they were well separated, to a closed-shape form where they were found in tight contact. This structural transition is essential for the function; only in the compacted dimer formation with the nucleotides being tightly sandwiched between the Walker A and the ABC signature motifs, their hydrolysis reaction can be performed. Closing/opening of the NBD dimer related to ATP binding/hydrolysis represents a well-established mechanism underlying the cyclic operation of ABC transporters. However, the coupling to conformational dynamics in the transmembrane domains and their role in substrate gating is generally explored far less.

For the maltose transporter MalFGK₂ which represents the probably best studied ABC system with multiple structures being available, our model correctly reproduced major aspects of the conformational coupling: in the absence of ATP ligands the NBDs are in the open state and the TMDs are in the inward-facing conformation where the substrate may leave the transporter through the opened cytoplasmic gate, and, at the same time, the gate to the periplasm is closed and substrate entrance from the extracellular space is permitted. In contrast, in the nucleotide-complexed transporter the NBDs are found in close proximity, but the TMDs underwent a transition upon which the gate to the cytoplasm became closed and essential transmembrane helices were tilted toward an outward-facing conformation, possibly opening the gate to the periplasm.

For the heme ABC transporter HmuUV the situation is quite different since experimental data is basically lacking and only the crystal structure in absence of ATP analogs is known yet. In this structure the NBD dimer is opened and the TMDs adopt an outward facing conformation where the putative substrate translocation cavity is accessible from the periplasm but closed to the cytoplasm. Our simulations reveal an interesting coupling mechanism of domain dynamics in which the linear tweezer-like closing motions of the two NBDs, induced by nucleotide binding, are translated into pronounced global rotation motions of the TMDs. By comparing available structural data we deduced a similar coupling scheme for the vitamin B₁₂ transporter BtuCD, indicating a possible communality of domain communication in this class of ABC transporters. Rotation of the TMDs with respect to the NBDs should generally generate twisting at their interface and possibly alter the orientation of transmembrane helices. In the HmuUV simulations tilting of the TMDs was found, the coupling helices underwent significant motions, and structural rearrangements of TM helices were observed. Nonetheless, the conformation of the putative translocation cavity was not much affected by these motions. Hence, the current analysis is not able to provide indications that may link nucleotide binding to substrate gating activity in HmuUV.

4.1. Transport Mechanism in ABC Importers

Although a complete model of ABC transporters has not yet been fully elucidated, the transmembrane exchange of substrates can be described on a general level in terms of the alternating access model. It assumes the conformation of the substrate translocation cavity to exist in two states: In the outward-facing state, substrate molecules may enter the TMDs through the accessible periplasmic side, whereas the gate to the cytoplasm is sealed. In the inward-facing state instead, the gate to the perisplasm is closed but the cavity to the cytoplasm is opened, allowing the substrate to leave into the intracellular space. Substrate translocation is controlled by the switching between both states, a process which is driven by the nucleotide-dependent conformational dynamics of the NBDs, and hence couples to the open/closed state of the NBD dimer. For the transport cycle of ATP importers two opposing coupling mechanisms have been established based on structural and biochemical data for the maltose and the vitamin B₁₂ transporter. Type I importers (e.g., the maltose transporter MalFGK₂) adopt the inward-facing conformation in the absence of nucleotides but are found switched to the outward-facing conformation in the ATP-bound state [13, 58]. A distinct mechanism is debated for type II importers such as BtuCD [21, 56]. In BtuCD the outward-facing conformation is revealed in the apo state, in which the substrate cavity at the cytoplasmic side is sealed by gate I, but a second gate (gate II) is open [57]. In the AMP-PNP-bound state, the outward-facing conformation is obtained likewise but this time the space to the cytoplasm is closed by gate II whereas gate I became opened. Therefore, in the framework of the BtuCD model the process of nucleotide binding is neither coupled to gating activity near the cytoplasm, nor does it correlate with significant changes near the periplasmic region. As a matter of fact, for BtuCD there is currently no data available which evidences the release step of the vitamin B₁₂ substrate through the cytoplasmic gate of the transporter.

Similar to BtuCD, in the heme transporter HmuUV the outward-facing conformation is found coupled to the apo open-dimer state of the NBDs. With respect to the substrate gating activity our results for HmuUV are consistent with the BtuCD model, i.e., nucleotide-binding does not significantly affect the conformation of TMDs near the periplasm and changes near the cytoplasm cannot be directly related to substrate gating. It should be noted that for the conformational dynamics in HmuUV, the role of the substrate binding protein HmuT, which delivers the heme molecules from the extracellular space by docking at the periplasmic site of the TMDs, is unknown at present [50]. In the transport cycle of the BtuCD model the corresponding substrate binding protein BtuF is assumed to trigger rearrangements of the TMD translocation cavity [56, 57].

Results obtained here for the HmuUV ABC transporter have predictive character and experimental verification is required. Certainly it would be important to determine the structure complexed with ATP-analogs and in the presence of HmuT. Furthermore, predictions of domain interplay, in particular the rotational dynamics, can possibly be checked in site-directed spin labeling electron paramagnetic resonance (EPR) experiments.

4.2. Model Limitations and Concluding Remarks

Any coarse-grained model is obtained through approximations and therefore underlies limitations. The elastic-network model provides a mechanical description of nucleotide-induced dynamics in protein machines whereas, as the price paid for of the applied simplifications, the involved chemical processes cannot be resolved. In this study the elastic-network model could not resolve the chemical details that are important to correctly model interactions of ABC transporters with ATP molecules. Therefore, similar to our previous elastic-network study where full operation cycles of the hepatitis C virus helicase protein motor could be modeled [47], the process of ATP-binding was emulated only roughly and physical interactions were accounted for by empiric effective potentials. On the other hand the obtained results suggest that details of the ligand-protein interactions are not particularly important when considering nucleotide-induced global conformational dynamics; the same robust and generic motions were generated and they were not sensitive to variations in the interaction pattern. This observation agrees with our elastic-network studies of mechano-chemical dynamics of other molecular machines [45, 47]. It is indeed remarkable that a purely mechanical description can still capture essential properties of the functional dynamics in proteins. Generally, the current study demonstrates the feasibility of coarse-grained mechanical models in computer experiments of molecular machines. Apparently they cannot replace all-atom simulations. However, given the situation that detailed molecular dynamics methods are not yet capable of describing the entire conformational motions which underlie the transport cycle in ABC transporters, coarser models are potentially useful to explore important aspects of their operation. To study dynamical properties of membrane machines more realistically in computer experiments, it can be attempted in the future to combine elastic-network models with coarse-grained descriptions of the membrane, which would additionally allow to investigate their interplay.

Author Contributions

HF designed and performed research, analyzed data and prepared the manuscript.

Funding

This work was supported by a Grant-in-Aid for Scientific Research on Innovative Areas 'spying minority in biological phenomena' (23115007) and Platform for Dynamic Approaches to Living System of the Ministry of Education, Culture, Sports, Science and Technology, Japan. http://www.mext.go.jp/english/. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer and handling Editor declared their shared affiliation, and the handling Editor states that the process nevertheless met the standards of a fair and objective review.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2016.00003

Video S1. Coupled domain dynamics in HmuUV. Conformational motions as predicted by the lowest normal mode (see Materials and Methods). The structure is shown in ribbon representation in front (left) and top view perspective (right).

References

1. Higgins CF. ABC transporters: from microorganisms to man. Annu Rev Cell Biol. (1992) 8:67–113. doi: 10.1146/annurev.cb.08.110192.000435

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rees DC, Johnson E, Lewinson O. ABC transporters: the power to change. Nat Rev Mol Cell Biol. (2009) 10:218–27. doi: 10.1038/nrm2646

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Davidson AL, Chen J. ATP-Binding cassette transporters in bacteria. Annu Rev Biochem. (2004) 73:241–68. doi: 10.1146/annurev.biochem.73.011303.073626

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Moussatova A, Kandt C, O'Mara ML, Tieleman DP. ATP-binding cassette transporters in Escherichia coli. Biochim Biophys Acta (2008) 1778:1757–71. doi: 10.1016/j.bbamem.2008.06.009

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fath MJ, Kolter R. ABC transporters: bacterial exporters. Microbiol Rev. (1993) 75:995–1017.

Google Scholar

6. Chang G. Multidrug resistance ABC transporters. FEBS Lett. (2003) 555:102–105. doi: 10.1016/S0014-5793(03)01085-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gottesman MM, Ambudkar SV. Overview: ABC transporters and human disease. J Bioenerg Biomembr. (2001) 33:453–45. doi: 10.1023/A:1012866803188

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Borst P, Elferink O. Mammalian ABC transporters in health and disease. Annu Rev Biochem. (2002) 71:537–92. doi: 10.1146/annurev.biochem.71.102301.093055

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Schneider E, Hunke S. ATP-binding cassette (ABC) transport systems: functional and structural aspects of the ATP-hydrolyzing subunits/domains. FEMS Microbiol Rev. (1998) 22:1–20. doi: 10.1111/j.1574-6976.1998.tb00358.x

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hollenstein K, Dawson RJP, Locher KP. Structure and mechanism of ABC transporter proteins. Curr Opin Struct Biol. (2007) 17:412–8. doi: 10.1016/j.sbi.2007.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wen PC, Tajkhorshid E. Conformational coupling of the nucleotide-binding and the transmembrane domains in ABC transporters. Biophys J. (2011) 101:680–90. doi: 10.1016/j.bpj.2011.06.031

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Smith PC, Karpowich N, Millen L, Moody JE, Rosen J, Thomas PJ, et al. ATP binding to the motor domain from an ABC transporter drives formation of a nucleotide sandwiched dimer. Mol Cell (2002) 10:139–49. doi: 10.1016/S1097-2765(02)00576-2

CrossRef Full Text | Google Scholar

13. Chen J, Lu G, Lin J, Davidson AL, Quiocho FA. A tweezers-like motion of the ATP-binding cassette dimer in an ABC transport cycle. Mol Cell (2003) 12:651–61. doi: 10.1016/j.molcel.2003.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zaitseva J, Jenewein S, Jumpertz T, Holland B, Schmitt L. H662 is the linchpin of ATP hydrolysis in the nucleotide-binding domain of the ABC transporter HlyB. EMBO J. (2005) 24:1901–10. doi: 10.1038/sj.emboj.7600657

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Dawson RJP, Locher KP. Structure of a bacterial multidrug ABC transporter. Nature (2006) 443:180–5. doi: 10.1038/nature05155

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Procko E, Ferrin-O'Connell I, Ng, SL, Gaudet R. Distinct structural and functional properties of the ATPase sites in an asymmetric ABC transporter. Mol Cell (2006) 24:51–62. doi: 10.1016/j.molcel.2006.07.034

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dawson RJP, Locher KP. Structure of the multidrug ABC transporter Sav1866 from Staphylococcus aureus in complex with AMP-PNP. FEBS Lett. (2007) 581:935–8. doi: 10.1016/j.febslet.2007.01.073

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Oldham ML, Khare D, Quiocho FA, Davidson AL, Chen J. Crystal structure of a catalytic intermediate of the maltose transporter. Nature (2007) 450:515–21. doi: 10.1038/nature06264

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ward A, Reyes CL, Yu J, Roth CB, Chang G. Flexibility in the ABC transporter MsbA: alternating access with a twist. Proc Natl Acad Sci USA. (2007) 104:19005–10. doi: 10.1073/pnas.0709388104

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Oldham ML, Chen J. Crystal structure of the maltose transporter in a pretranslocation intermediate state. Science (2011) 332:1202–5. doi: 10.1126/science.1200767

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Korkhov VM, Mireku SA, Locher KP. Structure of AMP-PNP-bound vitamin B₁₂ transporter BtuCD-F. Nature (2012) 490:367–72. doi: 10.1038/nature11442

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jones PM, George AM. Mechanism of ABC transporters: a molecular dynamics simulation of a well characterized nucleotide-binding subunit. Proc Natl Acad Sci USA. (2002) 99:12639–44. doi: 10.1073/pnas.152439599

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Oloo EO, Tieleman DP. Conformational transitions induced by the binding of MgATP to the vitamin B12 ABC-transporter BtuCD. J Biol Chem. (2004) 279:45013–9. doi: 10.1074/jbc.M405084200

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Campbell JD, Sansom MS. Nucleotide binding to the homodimeric MJ0796 protein: a computational study of a prokaryotic ABC transporter NBD dimer. FEBS Lett. (2005) 579:4193–9. doi: 10.1016/j.febslet.2005.06.027

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Oloo EO, Fung EY, Tieleman DP. The dynamics of the MgATP-driven closure of MalK, the energy-transducing subunit of the maltose ABC transporter. J Biol Chem. (2006) 281:28397–407. doi: 10.1074/jbc.M513614200

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jones PM, George AM. Nucleotide-dependent allostery within the ABC transporter ATP-binding cassette: a computational study of the MJ0796 dimer. J Biol Chem. (2007) 282:22793–803. doi: 10.1074/jbc.M700809200

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ivetac A, Campbell JD, Sansom MSP. Dynamics and function in a bacterial ABC transporter: simulation studies of the BtuCDF system and its components. Biochemistry (2007) 46:2767–78. doi: 10.1021/bi0622571

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Wen PC, Tajkhorshid E. Dimer opening of the nucleotide binding domains of ABC transporters after ATP hydrolysis. Biophys J. (2008) 95:5100–10. doi: 10.1529/biophysj.108.139444

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Jones PM, George AM. Opening of the ADP-bound active site in the ABC transporter ATPase dimer: evidence for a constant contact, alternating sites model for the catalytic cycle. Proteins (2009) 75:387–96. doi: 10.1002/prot.22250

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Newstead S, Fowler PW, Bilton P, Carpenter EP, Sadler PJ, Campopiano DJ, et al. Insights into how nucleotide-binding domains power ABC transport. Structure (2009) 17:1213–22. doi: 10.1016/j.str.2009.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Damas JM, Oliveira ASF, Baptista AM, Soares CM. Structural consequences of ATP hydrolysis on the ABC transporter NBD dimer: molecular dynamics studies of HlyB. Protein Sci. (2011) 20:1220–30. doi: 10.1002/pro.650

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Oloo EO, Kandt C, O'Mara ML, Tieleman DP. Computer simulations of ABC transporter components. Biochem Cell Biol. (2006) 84:900–11. doi: 10.1139/o06-182

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Shaikh SA, Li J, Enkavi G, Wen PC, Huang Z, Tajkhorshid E. Visualizing functional motions of membrane transporters with molecular dynamics simulations. Biochemistry (2013) 52:569–87. doi: 10.1021/bi301086x

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Tozzini V. Coarse-grained models for proteins. Curr Opin Struct Biol. (2005) 15:144–50. doi: 10.1016/j.sbi.2005.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Tozzini V. Multiscale modeling of proteins. Acc Chem Res. (2009) 43:220–30. doi: 10.1021/ar9001476

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tirion MM. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys Rev Lett. (1996) 77:1905–8. doi: 10.1103/PhysRevLett.77.1905

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bahar I, Atilgan AR, Erman B. Direct evaluation of thermal fluctuations in protein using a single-parameter harmonic potential. Fold Des. (1997) 2:173–81. doi: 10.1016/S1359-0278(97)00024-2

CrossRef Full Text | Google Scholar

38. Haliloglu T, Bahar I, Erman B. Gaussian dynamics of folded proteins. Phys Rev Lett. (1997) 79:3090–3. doi: 10.1103/PhysRevLett.79.3090

CrossRef Full Text | Google Scholar

39. Tama F, Sanejouand YH. Conformational change of proteins arising from normal mode calculations. Prot Eng. (2001) 14:1–6. doi: 10.1093/protein/14.1.1

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zheng W, Doniach S. A comparative study of motor-protein motions by using a simple elastic-network model. Proc Natl Acad Sci USA. (2003) 100:13253–8. doi: 10.1073/pnas.2235686100

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Yang L, Song G, Jernigan RL. How well can we understand large-scale protein motions using normal modes of elastic networks. Biophys J. (2007) 93:920–9. doi: 10.1529/biophysj.106.095927

CrossRef Full Text | Google Scholar

42. Togashi Y, Yanagida T, Mikhailov AS. Nonlinearity of mechanochemical motions in motor proteins. PLoS Comput Biol. (2010) 6:e1000814. doi: 10.1371/journal.pcbi.1000814

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Sonne J, Kandt C, Peters GH, Hansen FY, Jensen MO, Tieleman DP. Simulation of the coupling between nucleotide binding and transmembrane domains in the ATP binding cassette transporter BtuCD. Biophys J. (2007) 92:2727–34. doi: 10.1529/biophysj.106.097972

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Togashi Y, Mikhailov AS. Nonlinear relaxation dynamics in elastic networks and design principles of molecular machines. Proc Natl Acad Sci USA. (2007) 104:8697–702. doi: 10.1073/pnas.0702950104

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Flechsig H, Popp D, Mikhailov AS. In silico investigation of conformational motions in superfamily 2 helicase proteins. PLoS ONE (2011) 6:e21809. doi: 10.1371/journal.pone.0021809

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Düttmann M, Togashi Y, Yanagida T, Mikhailov AS. Myosin-V as a mechanical sensor: an elastic network study. Biophys J. (2012) 102:542–51. doi: 10.1016/j.bpj.2011.12.013

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Flechsig H, Mikhailov AS. Tracing entire operation cycles of hepatitis C virus helicase in structurally resolved dynamical simulations. Proc Natl Acad Sci USA. (2010) 107:20875–80. doi: 10.1073/pnas.1014631107

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Flechsig H. Computational biology approach to uncover hepatitis C virus helicase operation. World J Gastroenterol. (2014) 20:3401–9. doi: 10.3748/wjg.v20.i13.3401

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Braun V, Hantke K. Recent insights into iron import by bacteria. Curr Opin Chem Biol. (2011) 15:328–34. doi: 10.1016/j.cbpa.2011.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Woo JS, Zeltina A, Goetz BA, Locher KP. X-ray structure of the Yersinia pestis heme transporter HmuUV. Nat Struct Mol Biol. (2012) 19:1310–5. doi: 10.1038/nsmb.2417

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Atilgan C, Gerek ZN, Ozkan SB, Atilgan AR. Manipulation of conformational change in proteins by single-residue perturbations. Biophys J. (2010) 99:933–43. doi: 10.1016/j.bpj.2010.05.020

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Maupetit J, Gautier R, Tuffery P. SABBAC: online Structural Alphabet-based protein BackBone reconstruction from Alpha-Carbon trace. Nucleic Acids Res. (2006) 34:147–51. doi: 10.1093/nar/gkl289

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Humphrey W, Dalke A, Schulten K. VMD - Visual Molecular Dynamics. J Molec Graphics (1996) 14:33–8. doi: 10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Kitao A, Hirata F, Go N. The effects of solvent on the conformation and the collective motions of proteins: normal mode analysis and molecular dynamics simulations of mellitin in water and vacuum. Chem Phys. (1991) 158:447–72. doi: 10.1016/0301-0104(91)87082-7

CrossRef Full Text | Google Scholar

55. Patzlaff JS, van der Heide T, Poolman B. The ATP/substrate stoichiometry of the ATP-binding cassette (ABC) transporter OpuA. J Biol Chem. (2003) 278:29546–51. doi: 10.1074/jbc.M304796200

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Locher KP, Lee AT, Rees DC. The E. coli BtuCD structure: a framework for ABC transporter architecture and mechanism. Science (2002) 296:1091–8. doi: 10.1126/science.1071142

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Korkhov VM, Mireku SA, Veprintsev DB, Locher KP. Structure of AMP-PNP-bound BtuCD and mechanism of ATP-powered vitamin B12 transport by BtuCD-F. Nat Struct Mol Biol. (2014) 21:1097–9. doi: 10.1038/nsmb.2918

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Chen J, Sharma S, Quiocho FA, Davidson AL. Trapping the transition state of an ATP-binding cassette transporter: evidence for a concerted mechanism of maltose transport. Proc Natl Acad Sci USA. (2001) 98:1525–30. doi: 10.1073/pnas.98.4.1525

PubMed Abstract | CrossRef Full Text | Google Scholar