Fully atomistic modeling of plasmonic bimetallic nanoparticles: nanoalloys and core-shell systems

1 Introduction

Metal nanoparticles (NPs) exhibit unique optical properties, which are mainly due to the formation of surface plasmons, i.e., collective excitations of conductive electrons. (Moskovits, 1985; Nie and Emory, 1997; Maier, 2007; Anker et al., 2008; Atwater and Polman, 2010; Santhosh et al., 2016). At the plasmon resonance frequency (PRF) such surface plasmons exhibit a resonant behavior, which gives rise to a huge enhancement of the electric field in the proximity of the NP surface. This phenomenon is exploited to increase the detection limit of common analytical techniques. (Kneipp et al., 1997; Maier et al., 2003; Muehlschlegel et al., 2005; Lim et al., 2010; Giannini et al., 2011; Neuman et al., 2018). PRF can be tuned by varying the NP shape, dimension, and chemical composition (Ag, Au, Al, …). As an alternative, bimetallic nanoalloys or core-shell NPs can be used. Such systems are constituted by two different metal elements, e.g., Ag-Au, Au-Cu, Cu-Ag (Xiang et al., 2008; Wang et al., 2009; Huang et al., 2015; Gong and Leite, 2016; Cao et al., 2018; Ma et al., 2020; Awada et al., 2021). In this case, the PRF can be tuned not only by modifying the aforementioned variables (size, shape, …) but also the relative concentration of the two metals.

Many theoretical approaches have been developed to describe the plasmonic properties of single metal NPs(Corni and Tomasi, 2001; 2002a; Aizpurua et al., 2003; Myroshnychenko et al., 2008; Hohenester and Trügler, 2012; Ciraci et al., 2013; Ciraci and Della Sala, 2016; Giovannini et al., 2019b; Bonatti et al., 2020; Coccia et al., 2020; Baghramyan et al., 2021; Giannone et al., 2021; Della Sala, 2022; Della Sala et al., 2022), among which is worth mentioning quantum hydrodynamic models, which are able to describe both nonlocal and electron spill-out effects (Ciraci et al., 2013; Raza et al., 2015; Ciraci and Della Sala, 2016). However, the most widely exploited methods are based on classical physics, (Corni and Tomasi, 2002b; Hao et al., 2007; Jensen and Jensen, 2008; Jensen and Jensen, 2009; Pérez-González et al., 2010; Halas et al., 2011; Ciracì et al., 2012; Chen et al., 2015), such as the Mie Theory (Mie, 1908), the finite difference time domain (FDTD) (Shuford et al., 2006), the Discrete Dipole Approximation (DDA) (Draine and Flatau, 1994) or exploit a continuum representation of the NP by means of the Boundary Element Method (BEM) (Corni and Tomasi, 2001; García de Abajo and Howie, 2002; Hohenester and Trügler, 2012; Hohenester, 2015). All the classical approaches mentioned above rely on defining a suitable permittivity function ɛ. Clearly, in the case of bimetallic systems, ɛ-dependent methods are not flexible enough to treat a priori any chemical composition and need to resort to experimentally measured ɛ values for specific alloy concentrations or to approximations, which may not be physically justified (such as a linear combination of the ɛ values of the two metals) (Peña-Rodríguez and Pal, 2011a; Verbruggen et al., 2013; Ma et al., 2015; Putra et al., 2017; Kuddah et al., 2020; Newmai et al., 2022).

Atomistic approaches appear as the most natural choice to overcome this problem. Full ab initio methods can be exploited, however, their prohibitive computational cost limits their application to relatively small systems (Barcaro et al., 2011; López Lozano et al., 2013; Barcaro et al., 2014; Barcaro et al., 2015; Olobardi et al., 2019; Asadi-Aghbolaghi et al., 2020; Danielis et al., 2021). For this reason, classical atomistic approaches have been developed, (Jensen and Jensen, 2008; Jensen and Jensen, 2009; Chen et al., 2015; Zakomirnyi et al., 2019; Zakomirnyi et al., 2020), however they have only marginally been applied to the description of bimetallic NPs (Sørensen et al., 2021).

In this work, we extend ωFQFμ (Giovannini et al., 2022) to simulate the optical properties of bimetallic NPs, with special emphasis on Ag-Au nanoalloys and core-shell systems. ωFQFμ is a fully atomistic, classical, approach, which assigns each atom of the metal nanoalloy with an electric charge and an electric dipole moment, which vary as a response to an externally applied electric field. The theoretical foundations of ωFQFμ lay in Drude’s theory of conduction, classical electrodynamics, interband transitions, and quantum tunneling. In fact, the Drude mechanism of charge exchange is modeled through the equation of motion of the electric charges (Giovannini et al., 2019b; Bonatti et al., 2020; Giovannini et al., 2020; Lafiosca et al., 2021; Bonatti et al., 2022), while interband contributions are taken into account by means of effective interband polarizability (Giovannini et al., 2022) introduced to mimic d-shell polarizability (Liebsch, 1993). Also, quantum tunneling effects, which play a crucial role in nanojunctions and nanoaggregates (Esteban et al., 2012; Giovannini et al., 2019b), are described by tuning charge exchange through a phenomenological function. Therefore, ωFQFμ conceptually differs from other approaches which are based on classical physics only.

The manuscript is organized as follows. In the next section, the formulation of ωFQFμ for bimetallic systems is presented. After a brief section presenting the computational details, the method is tested against the reproduction of the plasmonic properties of alloyed spherical NPs, alloyed nanorods, and spherical core-shell systems. Conclusions and a sketch of the future perspectives of the approach end the manuscript.

2 Materials and methods

2.1 Theoretical model

In this section, we extend ωFQFμ (Giovannini et al., 2022) to describe the optical properties of bimetallic systems. To this end, we follow the derivation reported in (Giovannini et al., 2019b) and (Giovannini et al., 2022). In ωFQFμ, the fluctuations of the electronic density of a plasmonic substrate composed of N atoms emerging as a response to the external electric field are represented by a set of N discrete fluctuating complex-valued charges q_i and N fluctuating complex-valued dipoles μ_i, which are located at atomic positions. The equation of motion of charges q originates from the continuity equation (Giovannini et al., 2019b) (atomic units are used throughout the paper):

$\frac{\mathrm{d}{q}_i}{\mathrm{d}t}={\displaystyle \sum _{ij}}{A}_{ij}\left(n_j\langle {\mathbf{p}}_j{\rangle }_i\cdot {\widehat{\mathbf{l}}}_{ji}-n_i\langle {\mathbf{p}}_i{\rangle }_j\cdot {\widehat{\mathbf{l}}}_{ij}\right)={\displaystyle \sum _{ij}}\left(A_j{n}_j\langle {\mathbf{p}}_j{\rangle }_i\cdot {\widehat{\mathbf{l}}}_{ji}-A_i{n}_i\langle {\mathbf{p}}_i{\rangle }_j\cdot {\widehat{\mathbf{l}}}_{ij}\right)(1)$

where n_i is the electron density on atom i, ${⟨{\mathbf{p}}_i⟩}_j$ is the momentum of the electron associated with atom i averaged over all the trajectories towards atom j. ${\widehat{\mathbf{l}}}_{ij}=-{\widehat{\mathbf{l}}}_{ji}$ is the unit vector connecting i and j. A_ij is the effective area dividing ith and jth atoms, and its value modulates the charge exchange between each atom pair. By following (Giovannini et al., 2019b; Giovannini et al., 2020; Giovannini et al., 2022), A_ij is approximated as an atomic parameter (A_i).The electron momentum p_i can be estimated by means of the Drude model of conductance (Bade, 1957) as follows:

$\frac{\mathrm{d}{\mathbf{p}}_i}{\mathrm{d}t}={\mathbf{E}}_i\left(t\right)-\frac{{\mathbf{p}}_i}{{\tau }_i}(2)$

where E_i(t) is the electric field acting on the ith atom and τ_i is the relaxation time associated with scattering events. Assuming the external uniform monochromatic electric field E^ext(t) = E^ext(ω) exp (−iωt) oscillates at frequency ω, we can reformulate Eqs 1, 2 in the frequency domain, i.e.:

$-\mathrm{i}\omega q_i={\displaystyle \sum _j}\left(A_j{n}_j\frac{\langle {\mathbf{E}}_j\left(\omega \right){\rangle }_i\cdot {\widehat{\mathbf{l}}}_{ji}}{1/{\tau }_j-\mathrm{i}\omega }-A_i{n}_i\frac{\langle {\mathbf{E}}_i\left(\omega \right){\rangle }_j\cdot {\widehat{\mathbf{l}}}_{ij}}{1/{\tau }_i-\mathrm{i}\omega }\right)(3)$

Following the original derivation reported in (Giovannini et al., 2019b), we can write:

${⟨{\mathbf{E}}_i\left(\omega \right)⟩}_j\cdot {\widehat{\mathbf{l}}}_{ij}\approx \frac{{\varphi }_j-{\varphi }_i}{l_{ij}}(4)$

where ϕ_i is the chemical potential of atom i and l_ij = l_ji is the distance between ith and jth atoms. By this, Eq. 3 becomes:

$-\mathrm{i}\omega q_i={\displaystyle \sum _j}\left(\frac{A_j{n}_j\left(1-f_{ji}\left(l_{ij}\right)\right)}{1/{\tau }_j-\mathrm{i}\omega }+\frac{A_i{n}_i\left(1-f_{ij}\left(l_{ij}\right)\right)}{1/{\tau }_i-\mathrm{i}\omega }\right)\frac{{\varphi }_i-{\varphi }_j}{l_{ij}}(5)$

where quantum tunneling effects are expressed in terms of a Fermi-like function f_ij (l_ij), which reads:

$f_{ij}\left(l_{ij}\right)=\frac{1}{1+\exp \left[-d_{ij}\left(\frac{l_{ij}}{s_{ij}\cdot l_{ij}^0}-1\right)\right]}(6)$

where $l_{ij}^0$ is the equilibrium distance between atoms i and j, and the parameters d_ij and s_ij determine the shape of the damping function. Notice that the inclusion of a phenomenological description of quantum tunneling is needed to correctly describe the optical response of plasmonic subnanometer junctions and hot-spots (Esteban et al., 2012; Esteban et al., 2015; Scholl et al., 2013; Giovannini et al., 2019b; Bonatti et al., 2022; Giovannini et al., 2022). Indeed, in the case of plasmonic nanoaggregates, charge transfer plasmons (CT) may occur. In ωFQFμ, the charge exchange among different NPs is governed by Drude and tunneling mechanisms, and the total system charge is conserved (see Eq. 5), allowing for a physically consistent description of such plasmonic modes. To make the notation more compact, the following terms are introduced (Lafiosca et al., 2021):

$w_i\left(\omega \right)=\frac{2n_i}{1/{\tau }_i-\mathrm{i}\omega }(7)$

$K_{ij}=A_i\frac{1-f_{ij}\left(l_{ij}\right)}{l_{ij}}(8)$

$z_i\left(\omega \right)=-\frac{\mathrm{i}\omega }{w_i\left(\omega \right)}(9)$

Dividing Eq. 5 by w_i(ω), we obtain:

$z_i\left(\omega \right)q_i=\frac{1}{2}{\displaystyle \sum _j}\left(K_{ij}+\frac{w_j\left(\omega \right)}{w_i\left(\omega \right)}{K}_{ji}\right)\left({\varphi }_i-{\varphi }_j\right)(10)$

where the chemical potential ϕ_i can be written as:

${\varphi }_i={\displaystyle \sum _k}{T}_{ik}^{\mathrm{q}\mathrm{q}}{q}_k+{\displaystyle \sum _k}{T}_{ik}^{\mathrm{q}\mathrm{\mu }}{\mathit{\mu }}_k+V_i^{\text{ext}}(11)$

The first and the second terms in Eq. 11 are the electric potential generated by the charges and the dipoles of the system, mediated by the interaction tensors T^qq and T^qμ (see (Giovannini et al., 2019a) for their definitions). $V_i^{\text{ext}}$ is the electric potential associated with the external electric field. By plugging Eq. 11 into Eq. 10, the linear equations ruling charge evolution are obtained, i.e.:

$\mathbf{Z}\left(\omega \right)\mathbf{q}=\frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right){\mathbf{T}}^{\mathrm{q}\mathrm{q}}\mathbf{q}+\frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right){\mathbf{T}}^{\mathrm{q}\mathrm{\mu }}\mathit{\mu }+\frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right)\mathbf{V}(12)$

where the following matrices are introduced:

$H_{ij}\left(\omega \right)=\frac{w_j\left(\omega \right)}{w_i\left(\omega \right)}{K}_{ji}(13)$

${\bar{K}}_{ij}=K_{ij}-{\displaystyle \sum _k}{K}_{ik}{\delta }_{ij}(14)$

$Z_{ij}=z_i{\delta }_{ij}(15)$

${\bar{H}}_{ij}=H_{ij}-{\displaystyle \sum _k}{H}_{ik}{\delta }_{ij}(16)$

The electric dipoles μ_i, which are introduced to properly model interband contributions, are obtained by solving the following set of linear equations:

${\mathit{\mu }}_i={\alpha }_i\left(\omega \right)\left[{\mathbf{E}}_i^{\text{ext}}\left(\omega \right)+{\mathbf{E}}_i^q\left(\omega \right)+{\mathbf{E}}_i^{\mu }\left(\omega \right)\right](17)$

where α_i(ω) is the frequency-dependent polarizability of the ith atom, related to interband terms, which multiplies the total electric field acting on the ith dipole, composed by the external field ${\mathbf{E}}_i^{\text{ext}}$, the field generated by the fluctuating charges, ${\mathbf{E}}_i^q$, and the field generated by the fluctuating dipoles, ${\mathbf{E}}_i^{\mu }$. If the system is homogeneous, α_i is calculated as reported in (Giovannini et al., 2022):

${\alpha }_i\left(\omega \right)\equiv {\alpha }_A^{\text{IB}}\left(\omega \right)=\frac{{\epsilon }_A^{\text{IB}}\left(\omega \right)}{4\pi n_A}(18)$

where ${\epsilon }_A^{\text{IB}}$ is the interband contribution to the frequency-dependent permittivity function and n_A is the number density of atoms of the chemical element A. ɛ^IB is calculated by subtracting the Drude term from the frequency-dependent permittivity.

If the system is heterogeneous, the link between the macroscopic, bulk dynamical permittivity ɛ^IB(ω) and the microscopic, atomistic frequency-dependent interband polarizability α_i(ω) is not straightforward. Let us focus on bimetallic systems, composed of two chemical elements A and B. We assume the interband polarizability of the ith atom belonging to the A moiety to be a function of the local composition of the system, i.e., ${\alpha }_{A,i}^{\text{IB,alloy}}(N_{A,i},N_{B,i})$, where N_A,i and N_B,i are the number of nearest neighbors of A and B type, respectively. The simplest approach is to model ${\alpha }_{A,i}^{\text{IB,\hspace{0.17em}alloy}}$ as the weighted average of ${\alpha }_A^{\text{IB}}$ and ${\alpha }_B^{\text{IB}}$. Therefore, the interband frequency-dependent polarizability of the ith atom of species A in the alloy composed by materials A and B is defined as follows:

${\alpha }_i\left(\omega \right)\equiv {\alpha }_{A,i}^{\text{IB,alloy}}\left(\omega \right)={\left(\frac{\frac{N_{A,i}+1}{{\alpha }_A^{\text{IB}}\left(\omega \right)}+\frac{N_{B,i}}{{\alpha }_B^{\text{IB}}\left(\omega \right)}}{N_{A,i}+N_{B,i}+1}\right)}^{-1}(19)$

Notice that, possible alternative approaches, e.g., to resort to arithmetic averages have been investigated. However, the weighted harmonic mean indeed gives the best numerical results (see Supplementary Figure S1 and Sec. S1 in the Supplementary Materials – SM).

Starting from Eq. 17, the final expression for the electric dipoles becomes (Giovannini et al., 2022):

${\mathit{\mu }}_i={\alpha }_i\left(\omega \right)\left[{\mathbf{E}}_i^{\text{ext}}+{\displaystyle \sum _k}{\mathbf{T}}_{ik}^{\mathrm{\mu }\mathrm{q}}{q}_k+{\displaystyle \sum _k}{\mathbf{T}}_{ik}^{\mathrm{\mu }\mathrm{\mu }}{\mathit{\mu }}_k\right](20)$

where the field generated by the multipoles is mediated by the interaction tensors T^μq and T^μμ, defined according to (Giovannini et al., 2019a).

The coupled charge-dipole equations can finally be written in a compact notation as follows:

$\left[\begin{array}{cc}\hfill \frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right){\mathbf{T}}^{\mathrm{q}\mathrm{q}}-\mathbf{Z}\left(\omega \right)\hfill & \hfill \frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right){\mathbf{T}}^{\mathrm{q}\mathrm{\mu }}\hfill \\ \hfill {\mathbf{T}}^{\mathrm{\mu }\mathrm{q}}\hfill & \hfill {\mathbf{T}}^{\mathrm{\mu }\mathrm{\mu }}-{\mathbf{Z}}^{\text{IB}}\left(\omega \right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{q}\hfill \\ \hfill \mathit{\mu }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{1}{2}\left(\bar{\mathbf{K}}+\bar{\mathbf{H}}\left(\omega \right)\right){\mathbf{V}}^{\text{ext}}\hfill \\ \hfill -{\mathbf{E}}^{\text{ext}}\hfill \end{array}\right](21)$

where Z^IB is a diagonal matrix, of which the elements $Z_i^{\text{IB}}(\omega )=-1/{\alpha }_i(\omega )$ are defined according to Eq. 19. Notice that in the case of homogenous systems, i.e., A = B, the standard ωFQFμ equations presented by Giovannini et al. (2022) are recovered. From the values of charges and dipoles, the complex polarizability $\bar{\alpha }$ can be computed, from which the absorption cross section σ^abs can be calculated:

$\bar{\alpha }{\left(\omega \right)}_{kl}=\frac{\partial {\bar{d}}_k\left(\omega \right)}{\partial E_l\left(\omega \right)}={\displaystyle \sum _i}{q}_{i,k}\left(\omega \right)\cdot \frac{k_i}{E_l\left(\omega \right)}-{\displaystyle \sum _i}{\mu }_{i,k}\left(\omega \right)(22)$

${\sigma }^{\text{abs}}=\frac{4\pi }{3c}\omega \mathrm{t}\mathrm{r}\left(\mathrm{I}\mathrm{m}\left(\bar{\alpha }\left(\omega \right)\right)\right)(23)$

In the previous equations d is the total complex dipole moment, i runs over NP atoms, k represents x, y, z positions of the ith atom, and l runs over x, y, z directions of the external electric field. c is the speed of light and $\text{Im}(\bar{\alpha })$ is the imaginary part of the complex polarizability $\bar{\alpha }$.

2.2 Computational details

The developed ωFQFμ approach is challenged to reproduce the optical response of several Ag-Au nanostructures. In particular, we first consider Ag-Au spherical nanoalloys with diameter D = 5.2 nm (4,347 atoms) and Ag-Au nanorods with D = 2.5 nm and length L = 10 nm (2,560 atoms), which are generated by using Atomic Simulation Environment (ASE) Python module v. 3.17 (Larsen et al., 2017). A lattice constant of 4.08 Å (Haynes, 2014) and a Face-Centered Cubic (FCC) packing are exploited. For both spheres and nanorods, ten alloy compositions are considered by starting from pure Ag structures and increasing the percentage of Au atoms, which randomly replace Ag atoms (from 0% to 100%, with a constant step of 10%). To gain statistical significance, for each Au percentage, ten nanoalloy structures are generated by randomly replacing the proper fraction of Ag with Au, similarly to the strategy followed in previous studies (Sørensen et al., 2021). As a further example, core-shell spherical systems, which are constituted by an inner Au sphere (D = 5.0 nm, 3,851 atoms) surrounded by an outer Ag shell (D = 6.25 nm, 3,698 atoms), are investigated.

ωFQFμ equations are solved by using a stand-alone Fortran 95 package. ωFQFμ parameters (see Eqs 5, 6, 18) for Ag and Au atoms are taken from (Giovannini et al., 2022). In particular, Drude and interband parameters are recovered from Ag and Au experimental permittivity functions (Etchegoin et al., 2006). The parameters d_ij = 12.0 and s_ij = 0.95 entering Eq. 6 are obtained by fitting ωFQFμ results for i = Ag and j = Au (and vice versa) on reference time-dependent density functional theory + tight binding (TD-DFT + TB) (Asadi-Aghbolaghi et al., 2020) absorption spectra of Ag-Au clusters (see Sec. S2 in the SM).

3 Results and discussion

3.1 Spherical nanoparticles and nanorods

The modeling of the dependence of the absorption cross-section σ^abs of a spherical NP on the Au concentration has received much attention in the literature (Papavassiliou, 1976; Link et al., 1999; Rioux et al., 2014; Ristig et al., 2015). In particular, a simple linear combination of Ag and Au permittivity functions combined with the Mie theory cannot reproduce the linear behavior of the plasmon red-shift upon increasing Au concentration which is experimentally observed (Link et al., 1999). This issue can be solved by following the strategy proposed by Rioux et al. (2014), who have developed an analytical and rigorous model to predict a composition-dependent complex dielectric function of Ag-Au alloys, based on critical point analysis of the band-structure of Ag and Au. By coupling such modeling to the Mie theory, the correct trend is followed for spherical nanoalloys. It is worth noting that such a strategy might be exploited within the more refined, yet continuum, BEM method, thus overcoming the limitations of this approach in describing the plasmonic properties of nanoalloys. However, while the methodology proposed by Rioux et al. (2014) is rigorous from the theoretical point of view, its extension to different alloy compositions, and to alloys of different chemical nature rather than Au and Ag is far from trivial, due to the high (about 30) number of parameters that would need to be fitted to obtain the composition dependent dielectric function.

Computed ωFQFμ values for σ^abs of a spherical NP with different Au concentrations are reported in (see Figure 1). In all cases, spectra are characterized by a main peak (associated with the dipolar mode, see Supplementary Figure S2 in the SM), which redshifts and lowers in intensity as the Au concentration increases. By plotting the PRF (in nm) as a function of the percentage of Au (see Figure 1C), a linear trend is observed (R² ∼ 1.00). This behavior perfectly follows Vegard’s law, which reads:

${\lambda }^{\mathit{V\; egard}}\left(x\right)=\left(1-x\right){\lambda }_{Ag}+x{\lambda }_{Au}(24)$

FIGURE 1

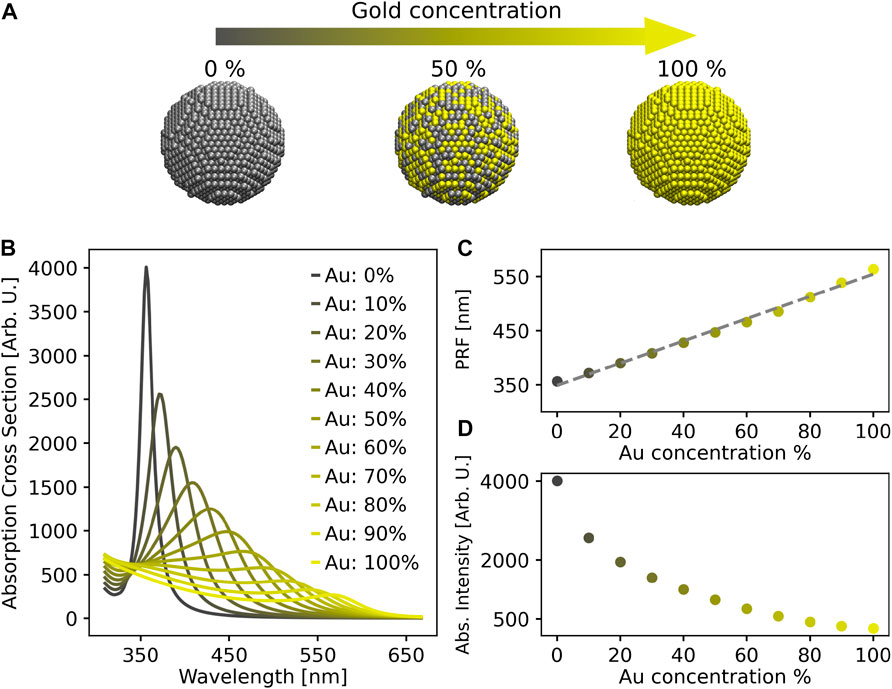
FIGURE 1. (A) Graphical depiction of spherical NP structures. ωFQFμ absorption cross-section (B), Plasmon Resonance Frequency (PRF) (C), and absorption intensity (D) as a function of Au concentration.

where x is the percentage of Au atoms. Such a linear dependence of the absorption wavelength on Au percentage is reported by many experimental works (Papavassiliou, 1976; Link et al., 1999; Rioux et al., 2014; Ristig et al., 2015). The slope (2.06 nm/% Au) of the line fitted on ωFQFμ results is in good agreement with experimental data (Link et al., 1999) (∼ 1.35 nm/% Au). Furthermore, by moving from pure Ag to pure Au NPs, the intensity of the plasmon band exponentially decreases (R² = 0.99, see Figure 1D), thus perfectly reproducing experimental findings (Link et al., 1999).

We note that, remarkably, other classical atomistic approaches may fail at reproducing the experimentally reported linear trend in wavelength and the exponentially decreasing intensity (Sørensen et al., 2021). Differently, ωFQFμ can correctly reproduce all the plasmonic properties of these structures, which is a key result of this paper.

We now move to discuss the plasmonic properties of Ag-Au alloy nanorods. Also in this case, we study the dependence of the absorption frequency on the Au concentration, which varies from 0% (pure Ag nanorod) to 100% (pure Au nanorod), with a constant step of 10%. ωFQFμ absorption cross sections, which are reported in Figure 2B, are clearly dominated by an intense peak which redshifts and decreases in intensity as the gold concentration increases. This peak is associated with the longitudinal dipolar mode (see also Supplementary Figure S3 in the SM). From a comparison with spherical NPs (see Figure 1B), we note that the dipolar peak moves to lower energies, independently of the chemical composition of the alloy nanorod. Also, in this case, additional bands can be appreciated in the region between 350 and 500 nm. There, octupolar plasmons arise (Bonatti et al., 2020), together with transversal dipolar modes. The associated bands associated are graphically depicted as an inset in Figure 2B, and redshift and lower in intensity as the Au concentration increases.

FIGURE 2

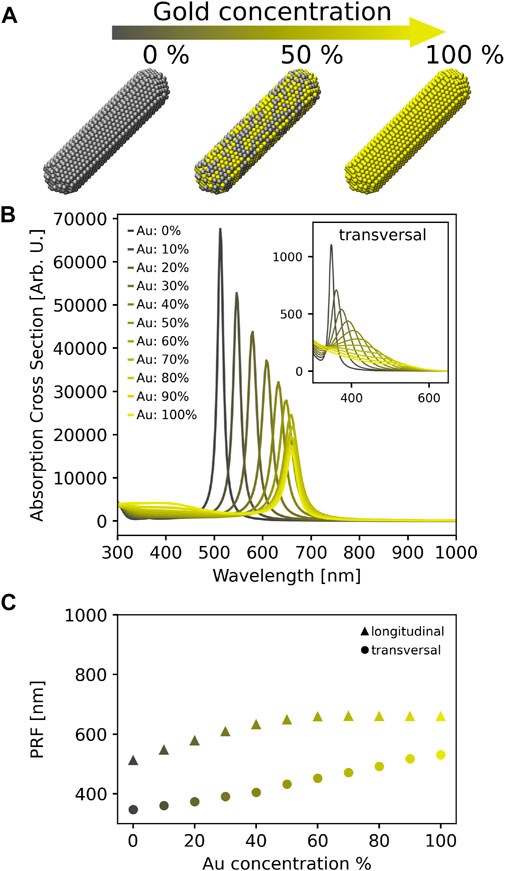
FIGURE 2. (A) Graphical depiction of nanorod structures. L = 10 nm and AR = 4. ωFQFμ absorption cross section (B) and Plasmon Resonance Frequency (PRF) (C) as a function of Au concentration. Both transversal (see inset in (B)) and longitudinal modes are considered.

The PRFs (in nm) of both the longitudinal and transversal dipolar modes as a function of the Au percentage are graphically depicted in Figure 2C. The transversal mode follows the linear trend (circles, R² = 0.99) predicted by Vegard’s law (see Eq. 24), while for the longitudinal plasmon, an evident deviation from the linear regime is observed, especially for Au concentrations larger than 40%. Our findings are in agreement with the experimental measurements reported by Bok et al. (2009), where for the transversal peak a linear trend is measured. Also, the experimental slope (1.47 nm/%Au) correlates significantly well with our calculations (1.92 nm/%Au). Differently, the longitudinal absorption wavelength is reported to be rather independent of the chemical composition for Au percentages $>$ 40%, while a slight blueshift is expected by increasing the Ag concentration Bok et al. (2009). Note that a DDA description is able to reproduce the composition dependence of the longitudinal mode but fails at describing the linear trend of the transversal peak (Bok et al., 2009). This is probably related to the exploited linear combination of Ag and Au permittivity functions. Remarkably, ωFQFμ correctly models both behaviors.

These findings can be explained by considering that the longitudinal dipolar mode falls at energies that are reasonably far from interband transition regions of both Ag and Au. In this regime, Drude free electrons play a dominant role (Link et al., 1999; Bok et al., 2009) and the good agreement with experiments reported by both DDA (Bok et al., 2009) and ωFQFμ show that the permittivity function in this region can be reasonably approximated as a linear combination of Ag and Au Drude contributions. Differently, the transversal plasmon mode absorbs at much higher energies, where interband effects cannot be neglected (Kreibig et al., 1995). This proves the reliability of ωFQFμ, which, differently from other models (Draine and Flatau, 1994), describes the plasmonic resonance by means of both electric charges and dipoles, modeling the intraband and interband mechanisms, respectively.

3.2 Au@Ag core-shell NPs

ωFQFμ is not limited to the description of nanoalloys, but can generally describe bimetallic nanostructures. To showcase its applicability, we consider pure core-shell (Au@Ag-0%) spherical NPs with a diameter D of 6.25 nm (3,698 atoms, see Figure 3A), constituted by a Au core (D_Au = 5 nm), and an external Ag shell (external D_Ag = 6.25 nm, D_Au/D_Ag = 0.8). In addition, to show the flexibility of ωFQFμ, the effect of alloying such structures, which has been experimentally realized (Ristig et al., 2015; Blommaerts et al., 2019), is also taken into account, by randomly replacing 18% of the core Au atoms with Ag, and viceversa for the Ag shell (Au@Ag-18%, see Figure 3A).

FIGURE 3

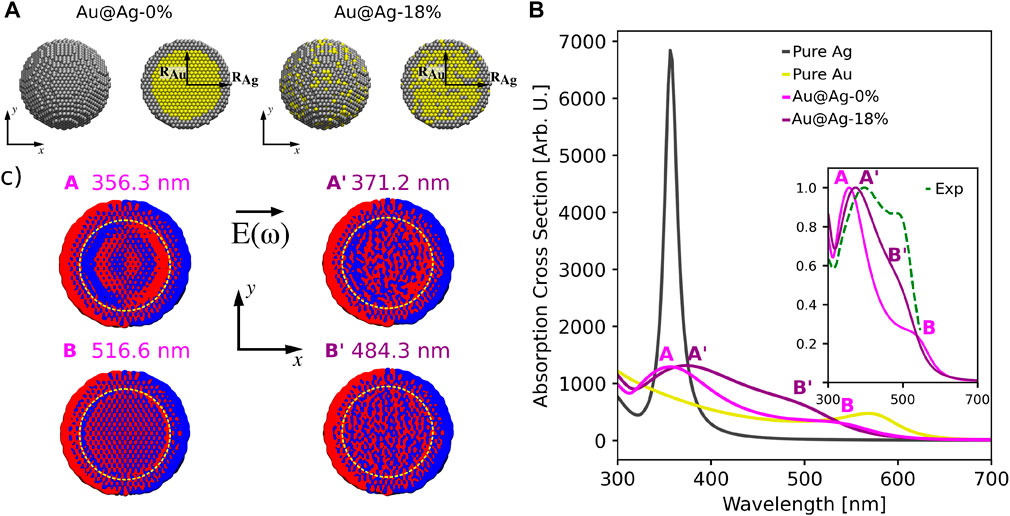
FIGURE 3. (A) Graphical depiction of Au@Ag-0% and Au@Ag-18% core-shell nanospheres (D = 6.25 nm). (B) Computed Au@Ag-0% and Au@Ag-18% absorption cross sections (data for pure Ag and Au structures are also reported, D = 6.25 nm). The normalized experimental spectrum reproduced from Peña-Rodríguez and Pal (2011b) is depicted in the inset, together with the normalized ωFQFμ Au@Ag-0% and Au@Ag-18% absorption cross sections. (C) Plasmon density computed at A, B (Au@Ag-0%) and A′, B′ (Au@Ag-18%) frequencies (isovalue = 0.0001 a. u.). The yellow dotted circle highlights the interface between the gold core and the silver shell.

Computed ωFQFμ absorption cross sections in the visible range for both core-shell systems are reported in Figure 3B, together with reference spectra for Ag and Au spherical NPs with D = 6.25 nm. Similarly to Figure 1B, Ag and Au reference absorption spectra are characterized by a main peak, located at about 360 nm and 570 nm for Ag and Au, respectively. The spectrum of the pure Au@Ag-0% core-shell is instead dominated by two peaks A and B, in agreement with (Peña-Rodríguez and Pal, 2011a; Chen et al., 2012; Gao et al., 2014), which fall at about 356 nm (A) and 517 nm (B). To deeply investigate the nature of the plasmons associated with these two bands, we graphically report in Figure 3C, left panel, the electron densities at the excitation energies for pure Au@Ag-0% core-shell (on a slice in the xy plane). As it can be appreciated, both peaks are associated with a global dipolar plasmon. However, they differ for the electron distribution in both the Au core and the interface between the two regions (see yellow dashed line in Figure 3C). Indeed, for peak A a huge charge accumulation at the interface is reported, while for peak B, the boundary between the Ag shell and the Au core is only partially marked. This is due to the fact that our model allows for charge exchange between the two layers, which is for instance not accounted for by other classical descriptions (Szántó et al., 2021). However, such a charge transfer is limited by the different tunneling barriers between the two metals, as introduced in Eq. 6, and by the different chemical nature (chemical hardness, polarizability, Drude parameters, …). As a consequence, charge accumulation at the Ag-Au interface is expected.

Similarly, the Au@Ag-18% absorption cross section (see Figure 3B) is characterized by two main peaks A′ and B′, which are blue- and red-shifted as compared to their counterparts in Au@Ag-0% system. Such a behavior can be justified by considering that by increasing the alloying degree up to 50%, a fully alloyed Ag-Au spherical NP is obtained. Therefore, in this situation, a single band is expected at about 450 nm (see also Figure 1B). The plasmonic nature of the electron densities computed at the A′ and B′ frequencies is graphically reported in Figure 3C, right panel. A global dipolar plasmon is observed. However, by also comparing with Au@Ag-0%, charge accumulation at the core-shell boundary is still present, but less pronounced, in particular for B′. This confirms the above speculation: indeed, by increasing the alloying degree, a decrease in the potential barrier at the interface is obtained.

To conclude the discussion on Au@Ag core-shell systems, we compare our results with experimental absorption cross sections reported by Peña-Rodríguez and Pal (2011b) (see inset in Figure 3B), who studied the plasmonic response of Au@Ag core-shell spherical NPs with D = 44.2 nm and characterized by D_Au/D_Ag = 0.81 (comparable with our simulations). As it can be noticed, the experimental spectrum is characterized by two main peaks at about 400 nm and 497 nm. This is in very good agreement with our calculations, thus further demonstrating the reliability of our model. In fact, only a slight discrepancy in relative intensities, probably due to different experimental conditions (size of the NP, solvent, …), is observed.

4 Conclusion

ωFQFμ has been extended to the description of bimetallic metal nanoalloys and core-shell NPs, and has been applied to spherical alloyed NPs and nanorods, for which alternative methods proposed in the literature fail, due to incorrect modeling of interband contributions. Remarkably, ωFQFμ correctly reproduces experimental trends, also in the case of core-shell systems; this is a direct consequence of the atomistic nature of the approach, which permits a physically consistent picture of the local environment of each specific atom.

ωFQFμ is general enough to describe any kind of bimetallic system; for instance, it can be applied to complex geometrical arrangements, such as subnanometer junctions, which form when two NPs approach each other. Such complex nanostructures require appropriate treatment of interband transitions and reliable modeling of quantum tunneling effects. The effect of alloying in subnanometer junctions has been only marginally investigated, due to the lack of theoretical approaches to correctly describe the plasmonic properties of alloys and generic bimetallic systems. ωFQFμ can indeed be applied to these systems and this investigation will be the topic of future studies. Also, ωFQFμ can be extended to generic multi-metallic nanostructures, through the generalization of Eq. 19 followed by a specification of the quantities entering Eq. 6.

As a final technological perspective, relevant for instance in sensing applications, the approach can be potentially applied to compute spectral properties of molecules adsorbed on bimetallic systems, by generalizing previous studies on homogenous substrates (Payton et al., 2013; Lafiosca et al., 2023). In this way, Surface-Enhanced spectroscopic signals can be simulated by retaining an atomistic description of the plasmonic substrate, which plays a crucial role in bimetallic systems, as it is demonstrated in this work.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LN, PL, and TG developed the theoretical methodology. LN, PL, and PG ran ωFQFμ calculations. TG, LN, and PL implemented the method into the stand-alone Fortran95 code for ωFQFμ calculations. LN, PL, PG, LB, and TG analyzed data and wrote the original draft manuscript. TG and CC discussed and supervised the whole project. CC acquired the funding and finalized the manuscript (final version). All authors contributed to the article and approved the submitted version.

Funding

This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement N. 818064). CC acknowledges funding from PNRR MUR project PE0000023-NQSTI.

Acknowledgments

We gratefully acknowledge the Center for High-Performance Computing (CHPC) at SNS for providing the computational infrastructure.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphot.2023.1199598/full#supplementary-material

References

Aizpurua, J., Hanarp, P., Sutherland, D., Käll, M., Bryant, G. W., and García de Abajo, F. J. (2003). Optical properties of gold nanorings. Phys. Rev. Lett. 90, 057401. doi:10.1103/physrevlett.90.057401

PubMed Abstract | CrossRef Full Text | Google Scholar

Anker, J. N., Hall, W. P., Lyandres, O., Shah, N. C., Zhao, J., and Van Duyne, R. P. (2008). Biosensing with plasmonic nanosensors. Nat. Mater. 7, 442–453. doi:10.1038/nmat2162

PubMed Abstract | CrossRef Full Text | Google Scholar

Asadi-Aghbolaghi, N., Ruger, R., Jamshidi, Z., and Visscher, L. (2020). Td-dft+ tb: An efficient and fast approach for quantum plasmonic excitations. J. Phys. Chem. C 124, 7946–7955. doi:10.1021/acs.jpcc.0c00979

CrossRef Full Text | Google Scholar

Atwater, H. A., and Polman, A. (2010). Plasmonics for improved photovoltaic devices. Nat. Mater. 9, 205–213. doi:10.1038/nmat2629

PubMed Abstract | CrossRef Full Text | Google Scholar

Awada, C., Dab, C., Grimaldi, M. G., Alshoaibi, A., and Ruffino, F. (2021). High optical enhancement in au/ag alloys and porous au using surface-enhanced Raman spectroscopy technique. Sci. Rep. 11, 4714. doi:10.1038/s41598-021-84093-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bade, W. (1957). Drude-model calculation of dispersion forces. i. general theory. J. Chem. Phys. 27, 1280–1284. doi:10.1063/1.1743991

CrossRef Full Text | Google Scholar

Baghramyan, H. M., Della Sala, F., and Ciracì, C. (2021). Laplacian-level quantum hydrodynamic theory for plasmonics. Phys. Rev. X 11, 011049. doi:10.1103/physrevx.11.011049

CrossRef Full Text | Google Scholar

Barcaro, G., Broyer, M., Durante, N., Fortunelli, A., and Stener, M. (2011). Alloying effects on the optical properties of ag–au nanoclusters from tddft calculations. J. Phys. Chem. C 115, 24085–24091. doi:10.1021/jp2087219

CrossRef Full Text | Google Scholar

Barcaro, G., Sementa, L., Fortunelli, A., and Stener, M. (2014). Optical properties of pt and ag–pt nanoclusters from tddft calculations: Plasmon suppression by pt poisoning. J. Phys. Chem. C 118, 28101–28108. doi:10.1021/jp508824w

CrossRef Full Text | Google Scholar

Barcaro, G., Sementa, L., Fortunelli, A., and Stener, M. (2015). Optical properties of nanoalloys. Phys. Chem. Chem. Phys. 17, 27952–27967. doi:10.1039/c5cp00498e

PubMed Abstract | CrossRef Full Text | Google Scholar

Blommaerts, N., Vanrompay, H., Nuti, S., Lenaerts, S., Bals, S., and Verbruggen, S. W. (2019). Unraveling structural information of turkevich synthesized plasmonic gold–silver bimetallic nanoparticles. Small 15, 1902791. doi:10.1002/smll.201902791

CrossRef Full Text | Google Scholar

Bok, H.-M., Shuford, K. L., Kim, S., Kim, S. K., and Park, S. (2009). Multiple surface plasmon modes for gold/silver alloy nanorods. Langmuir 25, 5266–5270. doi:10.1021/la803900w

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonatti, L., Gil, G., Giovannini, T., Corni, S., and Cappelli, C. (2020). Plasmonic resonances of metal nanoparticles: Atomistic vs. continuum approaches. Front. Chem. 8, 340. doi:10.3389/fchem.2020.00340

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonatti, L., Nicoli, L., Giovannini, T., and Cappelli, C. (2022). In silico design of graphene plasmonic hot-spots. Nanoscale Adv. 4, 2294–2302. doi:10.1039/d2na00088a

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, M., Liu, Q., Chen, M., Chen, L., Yang, D., Hu, H., et al. (2018). Fully alloying auag nanorods in a photothermal nano-oven: Superior plasmonic property and enhanced chemical stability. ACS Omega 3, 18623–18629. doi:10.1021/acsomega.8b03020

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Wu, H., Li, Z., Wang, P., Yang, L., and Fang, Y. (2012). The study of surface plasmon in au/ag core/shell compound nanoparticles. Plasmonics 7, 509–513. doi:10.1007/s11468-012-9336-6

CrossRef Full Text | Google Scholar

Chen, X., Moore, J. E., Zekarias, M., and Jensen, L. (2015). Atomistic electrodynamics simulations of bare and ligand-coated nanoparticles in the quantum size regime. Nat. Commun. 6, 8921. doi:10.1038/ncomms9921

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciraci, C., and Della Sala, F. (2016). Quantum hydrodynamic theory for plasmonics: Impact of the electron density tail. Phys. Rev. B 93, 205405. doi:10.1103/physrevb.93.205405

CrossRef Full Text | Google Scholar

Ciracì, C., Hill, R., Mock, J., Urzhumov, Y., Fernández-Domínguez, A., Maier, S., et al. (2012). Probing the ultimate limits of plasmonic enhancement. Science 337, 1072–1074. doi:10.1126/science.1224823

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciraci, C., Pendry, J. B., and Smith, D. R. (2013). Hydrodynamic model for plasmonics: A macroscopic approach to a microscopic problem. ChemPhysChem 14, 1109–1116. doi:10.1002/cphc.201200992

PubMed Abstract | CrossRef Full Text | Google Scholar

Coccia, E., Fregoni, J., Guido, C., Marsili, M., Pipolo, S., and Corni, S. (2020). Hybrid theoretical models for molecular nanoplasmonics. J. Chem. Phys. 153, 200901. doi:10.1063/5.0027935

PubMed Abstract | CrossRef Full Text | Google Scholar

Corni, S., and Tomasi, J. (2001). Enhanced response properties of a chromophore physisorbed on a metal particle. J. Chem. Phys. 114, 3739–3751. doi:10.1063/1.1342241

CrossRef Full Text | Google Scholar

Corni, S., and Tomasi, J. (2002a). Excitation energies of a molecule close to a metal surface. J. Chem. Phys. 117, 7266–7278. doi:10.1063/1.1507579

CrossRef Full Text | Google Scholar

Corni, S., and Tomasi, J. (2002b). Surface enhanced Raman scattering from a single molecule adsorbed on a metal particle aggregate: A theoretical study. J. Chem. Phys. 116, 1156–1164. doi:10.1063/1.1428349

CrossRef Full Text | Google Scholar

Danielis, N., Vega, L., Fronzoni, G., Stener, M., Bruix, A., and Neyman, K. M. (2021). Agpd, aupd, and aupt nanoalloys with ag-or au-rich compositions: Modeling chemical ordering and optical properties. J. Phys. Chem. C 125, 17372–17384. doi:10.1021/acs.jpcc.1c04222

CrossRef Full Text | Google Scholar

Della Sala, F., Pachter, R., and Sukharev, M. (2022). Advances in modeling plasmonic systems. J. Chem. Phys. 157, 190401. doi:10.1063/5.0130790

PubMed Abstract | CrossRef Full Text | Google Scholar

Della Sala, F. (2022). Orbital-free methods for plasmonics: Linear response. J. Chem. Phys. 157, 104101. doi:10.1063/5.0100797

PubMed Abstract | CrossRef Full Text | Google Scholar

Draine, B. T., and Flatau, P. J. (1994). Discrete-dipole approximation for scattering calculations. J. Opt. Soc. Am. A 11, 1491–1499. doi:10.1364/josaa.11.001491

CrossRef Full Text | Google Scholar

Esteban, R., Borisov, A. G., Nordlander, P., and Aizpurua, J. (2012). Bridging quantum and classical plasmonics with a quantum-corrected model. Nat. Commun. 3, 825. doi:10.1038/ncomms1806

PubMed Abstract | CrossRef Full Text | Google Scholar

Esteban, R., Zugarramurdi, A., Zhang, P., Nordlander, P., García-Vidal, F. J., Borisov, A. G., et al. (2015). A classical treatment of optical tunneling in plasmonic gaps: Extending the quantum corrected model to practical situations. Faraday Discuss. 178, 151–183. doi:10.1039/c4fd00196f

PubMed Abstract | CrossRef Full Text | Google Scholar

Etchegoin, P. G., Le Ru, E., and Meyer, M. (2006). An analytic model for the optical properties of gold. J. Chem. Phys. 125, 164705. doi:10.1063/1.2360270

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, C., Hu, Y., Wang, M., Chi, M., and Yin, Y. (2014). Fully alloyed ag/au nanospheres: Combining the plasmonic property of ag with the stability of au. J. Am. Chem. Soc. 136, 7474–7479. doi:10.1021/ja502890c

PubMed Abstract | CrossRef Full Text | Google Scholar

García de Abajo, F. J., and Howie, A. (2002). Retarded field calculation of electron energy loss in inhomogeneous dielectrics. Phys. Rev. B 65, 115418. doi:10.1103/physrevb.65.115418

CrossRef Full Text | Google Scholar

Giannini, V., Fernández-Domínguez, A. I., Heck, S. C., and Maier, S. A. (2011). Plasmonic nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 111, 3888–3912. doi:10.1021/cr1002672

PubMed Abstract | CrossRef Full Text | Google Scholar

Giannone, G., Smiga, S., D’Agostino, S., Fabiano, E., and Della Sala, F. (2021). Plasmon couplings from subsystem time-dependent density functional theory. J. Phys. Chem. A 125, 7246–7259. doi:10.1021/acs.jpca.1c05384

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovannini, T., Puglisi, A., Ambrosetti, M., and Cappelli, C. (2019a). Polarizable qm/mm approach with fluctuating charges and fluctuating dipoles: The qm/fqfμ model. J. Chem. Theory Comput. 15, 2233–2245. doi:10.1021/acs.jctc.8b01149

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovannini, T., Rosa, M., Corni, S., and Cappelli, C. (2019b). A classical picture of subnanometer junctions: An atomistic drude approach to nanoplasmonics. Nanoscale 11, 6004–6015. doi:10.1039/c8nr09134j

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovannini, T., Bonatti, L., Polini, M., and Cappelli, C. (2020). Graphene plasmonics: Fully atomistic approach for realistic structures. J. Phys. Chem. Lett. 11, 7595–7602. doi:10.1021/acs.jpclett.0c02051

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovannini, T., Bonatti, L., Lafiosca, P., Nicoli, L., Castagnola, M., Illobre, P. G., et al. (2022). Do we really need quantum mechanics to describe plasmonic properties of metal nanostructures? ACS Photonics 9, 3025–3034. doi:10.1021/acsphotonics.2c00761

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, C., and Leite, M. S. (2016). Noble metal alloys for plasmonics. ACS Photonics 3, 507–513. doi:10.1021/acsphotonics.5b00586

CrossRef Full Text | Google Scholar

Halas, N. J., Lal, S., Chang, W.-S., Link, S., and Nordlander, P. (2011). Plasmons in strongly coupled metallic nanostructures. Chem. Rev. 111, 3913–3961. doi:10.1021/cr200061k

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, F., Nehl, C. L., Hafner, J. H., and Nordlander, P. (2007). Plasmon resonances of a gold nanostar. Nano Lett. 7, 729–732. doi:10.1021/nl062969c

PubMed Abstract | CrossRef Full Text | Google Scholar

Haynes, W. (2014). CRC handbook of chemistry and physics. Boca Raton: CRC Press.

Google Scholar

Hohenester, U., and Trügler, A. (2012). MNPBEM – a Matlab toolbox for the simulation of plasmonic nanoparticles. Comput. Phys. Commun. 183, 370–381. doi:10.1016/j.cpc.2011.09.009

CrossRef Full Text | Google Scholar

Hohenester, U. (2015). Quantum corrected model for plasmonic nanoparticles: A boundary element method implementation. Phys. Rev. B 91, 205436. doi:10.1103/physrevb.91.205436

CrossRef Full Text | Google Scholar

Huang, J., Zhu, Y., Liu, C., Zhao, Y., Liu, Z., Hedhili, M. N., et al. (2015). Fabricating a homogeneously alloyed auag shell on au nanorods to achieve strong, stable, and tunable surface plasmon resonances. Small 11, 5214–5221. doi:10.1002/smll.201501220

PubMed Abstract | CrossRef Full Text | Google Scholar

Jensen, L. L., and Jensen, L. (2008). Electrostatic interaction model for the calculation of the polarizability of large noble metal nanoclusters. J. Phys. Chem. C 112, 15697–15703. doi:10.1021/jp804116z

CrossRef Full Text | Google Scholar

Jensen, L. L., and Jensen, L. (2009). Atomistic electrodynamics model for optical properties of silver nanoclusters. J. Phys. Chem. C 113, 15182–15190. doi:10.1021/jp904956f

CrossRef Full Text | Google Scholar

Kneipp, K., Wang, Y., Kneipp, H., Perelman, L. T., Itzkan, I., Dasari, R. R., et al. (1997). Single molecule detection using surface-enhanced Raman scattering (sers). Phys. Rev. Lett. 78, 1667–1670. doi:10.1103/physrevlett.78.1667

CrossRef Full Text | Google Scholar

Kreibig, U., Vollmer, M., Kreibig, U., and Vollmer, M. (1995). “Theoretical considerations,” in Optical properties of metal clusters, 13–201.

CrossRef Full Text | Google Scholar

Kuddah, M., Putra, M., and Djuhana, D. (2020). “The incident electrical field angle effect in localized surface plasmon resonance (lspr) of bimetallic ag-au nanorod using mnpbem simulation,” in IOP Conference Series: Materials Science and Engineering (IOP Publishing), 012058.

CrossRef Full Text | Google Scholar

Lafiosca, P., Giovannini, T., Benzi, M., and Cappelli, C. (2021). Going beyond the limits of classical atomistic modeling of plasmonic nanostructures. J. Phys. Chem. C 125, 23848–23863. doi:10.1021/acs.jpcc.1c04716

CrossRef Full Text | Google Scholar

Lafiosca, P., Nicoli, L., Bonatti, L., Giovannini, T., Corni, S., and Cappelli, C. (2023). Qm/classical modeling of surface enhanced Raman scattering based on atomistic electromagnetic models. J. Chem. Theory Comput. doi:10.1021/acs.jctc.3c00177

CrossRef Full Text | Google Scholar

Larsen, A. H., Mortensen, J. J., Blomqvist, J., Castelli, I. E., Christensen, R., Dułak, M., et al. (2017). The atomic simulation environment—A python library for working with atoms. J. Phys. Condens. Matter 29, 273002. doi:10.1088/1361-648x/aa680e

PubMed Abstract | CrossRef Full Text | Google Scholar

Liebsch, A. (1993). Surface-plasmon dispersion and size dependence of mie resonance: Silver versus simple metals. Phys. Rev. B 48, 11317–11328. doi:10.1103/physrevb.48.11317

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, D.-K., Jeon, K.-S., Kim, H. M., Nam, J.-M., and Suh, Y. D. (2010). Nanogap-engineerable Raman-active nanodumbbells for single-molecule detection. Nat. Mater. 9, 60–67. doi:10.1038/nmat2596

PubMed Abstract | CrossRef Full Text | Google Scholar

Link, S., Wang, Z. L., and El-Sayed, M. (1999). Alloy formation of gold-silver nanoparticles and the dependence of the plasmon absorption on their composition. J. Phys. Chem. B 103, 3529–3533. doi:10.1021/jp990387w

CrossRef Full Text | Google Scholar

López Lozano, X., Mottet, C., and Weissker, H.-C. (2013). Effect of alloying on the optical properties of ag–au nanoparticles. J. Phys. Chem. C 117, 3062–3068. doi:10.1021/jp309957y

CrossRef Full Text | Google Scholar

Ma, Y.-W., Zhang, L.-H., Wu, Z.-W., Yi, M.-F., Zhang, J., and Jian, G.-S. (2015). The study of tunable local surface plasmon resonances on au-ag and ag-au core-shell alloy nanostructure particles with dda method. Plasmonics 10, 1791–1800. doi:10.1007/s11468-015-9997-z

CrossRef Full Text | Google Scholar

Ma, J., Liu, X., Wang, R., Zhang, J., Jiang, P., Wang, Y., et al. (2020). Bimetallic core–shell nanostars with tunable surface plasmon resonance for surface-enhanced Raman scattering. ACS Appl. Nano Mater. 3, 10885–10894. doi:10.1021/acsanm.0c02144

CrossRef Full Text | Google Scholar

Maier, S. A., Kik, P. G., Atwater, H. A., Meltzer, S., Harel, E., Koel, B. E., et al. (2003). Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat. Mater. 2, 229–232. doi:10.1038/nmat852

PubMed Abstract | CrossRef Full Text | Google Scholar

Maier, S. A. (2007). Plasmonics: Fundamentals and applications. Springer Science & Business Media.

Google Scholar

Mie, G. (1908). Beiträge zur optik trüber medien, speziell kolloidaler metallösungen. Ann. Phys.-Berlin 330, 377–445. doi:10.1002/andp.19083300302

CrossRef Full Text | Google Scholar

Moskovits, M. (1985). Surface-enhanced spectroscopy. Rev. Mod. Phys. 57, 783–826. doi:10.1103/revmodphys.57.783

CrossRef Full Text | Google Scholar

Muehlschlegel, P., Eisler, H.-J., Martin, O. J., Hecht, B., and Pohl, D. (2005). Resonant optical antennas. Science 308, 1607–1609. doi:10.1126/science.1111886

PubMed Abstract | CrossRef Full Text | Google Scholar

Myroshnychenko, V., Rodríguez-Fernández, J., Pastoriza-Santos, I., Funston, A. M., Novo, C., Mulvaney, P., et al. (2008). Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 37, 1792–1805. doi:10.1039/b711486a

PubMed Abstract | CrossRef Full Text | Google Scholar

Neuman, T., Esteban, R., Casanova, D., García-Vidal, F. J., and Aizpurua, J. (2018). Coupling of molecular emitters and plasmonic cavities beyond the point-dipole approximation. Nano Lett. 18, 2358–2364. doi:10.1021/acs.nanolett.7b05297

PubMed Abstract | CrossRef Full Text | Google Scholar

Newmai, M. B., Verma, M., Dahiya, A., and Kumar, P. S. (2022). Monomer driven growth of catalytically active agau plasmonic nanoalloys. J. Phys. Chem. Solids161, 110371. doi:10.1016/j.jpcs.2021.110371

CrossRef Full Text | Google Scholar

Nie, S., and Emory, S. R. (1997). Probing single molecules and single nanoparticles by surface-enhanced Raman scattering. Science 275, 1102–1106. doi:10.1126/science.275.5303.1102

PubMed Abstract | CrossRef Full Text | Google Scholar

Olobardi, S., Vega, L., Fortunelli, A., Stener, M., Vines, F., and Neyman, K. M. (2019). Optical properties and chemical ordering of ag–pt nanoalloys: A computational study. J. Phys. Chem. C 123, 25482–25491. doi:10.1021/acs.jpcc.9b07382

CrossRef Full Text | Google Scholar

Papavassiliou, G. C. (1976). Surface plasmons in small au-ag alloy particles. J. Phys. F. Met. Phys. 6, L103–L105. doi:10.1088/0305-4608/6/4/004

CrossRef Full Text | Google Scholar

Payton, J. L., Morton, S. M., Moore, J. E., and Jensen, L. (2013). A hybrid atomistic electrodynamics–quantum mechanical approach for simulating surface-enhanced Raman scattering. Acc. Chem. Res. 47, 88–99. doi:10.1021/ar400075r

PubMed Abstract | CrossRef Full Text | Google Scholar

Peña-Rodríguez, O., and Pal, U. (2011a). Au@ ag core–shell nanoparticles: Efficient all-plasmonic fano-resonance generators. Nanoscale 3, 3609–3612. doi:10.1039/c1nr10625b

PubMed Abstract | CrossRef Full Text | Google Scholar

Peña-Rodríguez, O., and Pal, U. (2011b). Enhanced plasmonic behavior of bimetallic (ag-au) multilayered spheres. Nanoscale Res. Lett. 6, 279. doi:10.1186/1556-276X-6-279

PubMed Abstract | CrossRef Full Text | Google Scholar

Pérez-González, O., Zabala, N., Borisov, A., Halas, N., Nordlander, P., and Aizpurua, J. (2010). Optical spectroscopy of conductive junctions in plasmonic cavities. Nano Lett. 10, 3090–3095. doi:10.1021/nl1017173

PubMed Abstract | CrossRef Full Text | Google Scholar

Putra, M., Djuhana, D., Fauzia, V., Harmoko, A., and Imawan, C. (2017). “A numerical study of the sensitivity of surface plasmon resonance bimetallic silver-gold alloys using boundary element method,” in IOP Conference Series: Materials Science and Engineering (IOP Publishing), 012016.

CrossRef Full Text | Google Scholar

Raza, S., Bozhevolnyi, S. I., Wubs, M., and Mortensen, N. A. (2015). Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 27, 183204. doi:10.1088/0953-8984/27/18/183204

PubMed Abstract | CrossRef Full Text | Google Scholar

Rioux, D., Vallières, S., Besner, S., Muñoz, P., Mazur, E., and Meunier, M. (2014). An analytic model for the dielectric function of au, ag, and their alloys. Adv. Opt. Mater. 2, 176–182. doi:10.1002/adom.201300457

CrossRef Full Text | Google Scholar

Ristig, S., Prymak, O., Loza, K., Gocyla, M., Meyer-Zaika, W., Heggen, M., et al. (2015). Nanostructure of wet-chemically prepared, polymer-stabilized silver–gold nanoalloys (6 nm) over the entire composition range. J. Mater. Chem. B 3, 4654–4662. doi:10.1039/c5tb00644a

PubMed Abstract | CrossRef Full Text | Google Scholar

Santhosh, K., Bitton, O., Chuntonov, L., and Haran, G. (2016). Vacuum rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 7, 11823. doi:10.1038/ncomms11823

PubMed Abstract | CrossRef Full Text | Google Scholar

Scholl, J. A., García-Etxarri, A., Koh, A. L., and Dionne, J. A. (2013). Observation of quantum tunneling between two plasmonic nanoparticles. Nano Lett. 13, 564–569. doi:10.1021/nl304078v

PubMed Abstract | CrossRef Full Text | Google Scholar

Shuford, K. L., Ratner, M. A., Gray, S. K., and Schatz, G. C. (2006). Finite-difference time-domain studies of light transmission through nanohole structures. Appl. Phys. B 84, 11–18. doi:10.1007/s00340-006-2218-x

CrossRef Full Text | Google Scholar

Sørensen, L. K., Utyushev, A. D., Zakomirnyi, V. I., and Ågren, H. (2021). Atomistic description of plasmonic generation in alloys and core shell nanoparticles. Phys. Chem. Chem. Phys. 23, 173–185. doi:10.1039/d0cp04854b

PubMed Abstract | CrossRef Full Text | Google Scholar

Szántó, G., Csarnovics, I., and Bonyár, A. (2021). Numerical investigation of the refractive index sensitivity of au/ag core-shell nanostructures for sensing applications. Sens. Bio-Sens. 32, 100414. doi:10.1016/j.sbsr.2021.100414

CrossRef Full Text | Google Scholar

Verbruggen, S. W., Keulemans, M., Martens, J. A., and Lenaerts, S. (2013). Predicting the surface plasmon resonance wavelength of gold–silver alloy nanoparticles. J. Phys. Chem. C 117, 19142–19145. doi:10.1021/jp4070856

CrossRef Full Text | Google Scholar

Wang, C., Peng, S., Chan, R., and Sun, S. (2009). Synthesis of auag alloy nanoparticles from core/shell-structured ag/au. Small 5, 567–570. doi:10.1002/smll.200801169

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, Y., Wu, X., Liu, D., Li, Z., Chu, W., Feng, L., et al. (2008). Gold nanorod-seeded growth of silver nanostructures: From homogeneous coating to anisotropic coating. Langmuir 24, 3465–3470. doi:10.1021/la702999c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakomirnyi, V. I., Rinkevicius, Z., Baryshnikov, G. V., Sørensen, L. K., and Ågren, H. (2019). Extended discrete interaction model: Plasmonic excitations of silver nanoparticles. J. Phys. Chem. C 123, 28867–28880. doi:10.1021/acs.jpcc.9b07410

CrossRef Full Text | Google Scholar

Zakomirnyi, V. I., Rasskazov, I. L., Sørensen, L. K., Carney, P. S., Rinkevicius, Z., and Ågren, H. (2020). Plasmonic nano-shells: Atomistic discrete interaction versus classic electrodynamics models. Phys. Chem. Chem. Phys. 22, 13467–13473. doi:10.1039/d0cp02248a

PubMed Abstract | CrossRef Full Text | Google Scholar