- 1Institut für Theoretische Physik, Technische Universität Berlin, Berlin, Germany
- 2Institut für Physik, Technische Universität Ilmenau, Ilmenau, Germany
We investigate the spontaneous emission noise resilience of the phase-locked operation of two delay-coupled nanolasers. The system is modeled by semi-classical Maxwell–Bloch rate equations with stochastic Langevin-type noise sources. Our results reveal that a polarization dephasing time of two to three times the cavity photon lifetime maximizes the system’s ability to remain phase-locked in the presence of noise-induced perturbations. The Langevin noise term is caused by spontaneous emission processes which change both the intensity auto-correlation properties of the solitary lasers and the coupled system. In an experimental setup, these quantities are measurable and can be directly compared to our numerical data. The strong parameter dependence of the noise tolerance that we find may show possible routes for the design of robust on-chip integrated networks of nanolasers.
1 Introduction
Over the recent years, coupled nanophotonic laser networks have found a variety of applications, e.g., in photonic integrated circuits, on-chip optical computing, and optical communication (Heil et al., 2001; Zapf et al., 2017; Ma and Oulton, 2019; Ning, 2019; Lingnau et al., 2020; Robertson et al., 2020). A wide bandwidth of new and strongly varying implementations has led to great advantages, such as a small footprint, high speed, and room temperature compatibility (Zhang et al., 2014; Deka et al., 2020). However, new challenges to the theoretical treatment of such systems have arisen from these developments. The small size of nanolasers pushes their dynamical timescales into regimes for which a description via conventional semiconductor laser models [class-B laser models (Arecchi et al., 1984; Erneux and Glorieux, 2010)] is no longer sufficient (van Tartwijk and Agrawal, 1998; Lingnau et al., 2019). Due to device miniaturization, the cavity photon lifetime becomes comparable to the microscopic polarization lifetime. In particular, nanolasers made of metal nanocavities (Ning, 2010), metal-coated semiconductor nanolasers (Koulas-Simos et al., 2022), or 2D materials (Du et al., 2020) exhibit high photon losses and, therefore, have shortened cavity photon lifetime (Neogi et al., 2002; Li and Ning, 2012; Zhang et al., 2014). As a consequence, the dynamic degree of freedom of microscopic polarization is important for the theoretical description in addition to the electric field and charge carrier dynamics (Lorke et al., 2013; Aust et al., 2016).
We use a Maxwell–Bloch-type laser model to describe the three aforementioned dynamical quantities in the coupled setup of two nanolasers [two delay-coupled class-C laser models (Haken, 1975; Haken, 1985; van Tartwijk and Agrawal, 1998; Ohtsubo, 2008)]. The dynamical behavior of such lasers has been investigated previously in various setups, e.g., in feedback and coupling settings (Lingnau et al., 2019; Roos et al., 2021; Wang et al., 2021), and in direct comparison with class-B lasers (Hohl et al., 1997; Javaloyes et al., 2003; Erzgräber et al., 2006; Bonatto et al., 2012; Junges and Gallas, 2015; Seifikar et al., 2018). Here, we focus on the effect of spontaneous emission noise and derive insights about optimal conditions for the noise-resilient phase-locked operation of the two delay-coupled lasers. For our purpose, the exact noise distribution, e.g., as can be obtained via a stochastic simulator approach (Puccioni and Lippi, 2015; Wang et al., 2021), is less important. Hence, we use a simplified Langevin stochastic noise source. To quantify whether the lasers are phase-locked, we compute the phase correlation. By performing multiple parameter studies, we aim to unravel how the polarization timescale influences the noise resilience of synchronized laser emission. On that account, we limit our investigation to parameter settings that permit deterministic (i.e., without the stochastic noise source) phase locking among the two lasers. We quantify the tolerance to noise in parameter space by defining a critical noise strength which we can directly translate into the experimentally accessible intensity auto-correlation (g(2) function) of one laser.
2 Materials and methods
2.1 Coupled nanolaser model
The delay-coupled nanolasers are shown in Figure 1 and are described by the following set of macroscopic Maxwell–Bloch equations [class-C laser model, also used in (Roos et al., 2021)]:

FIGURE 1. Sketch of the two coupled nanolasers described by the Maxwell–Bloch class-C equations given in Eq. 1. The solitary frequencies of the lasers are detuned by 2δω = ω2 − ω1.
Here, the indices j, k ∈ {1, 2} enumerate the two lasers. The equations describe three dynamical quantities for each laser: The inversion N of a two-level system, the complex electric field amplitude E, and the microscopic polarization P. Each of these dynamical quantities is subject to internal loss processes and thus connected to a characteristic timescale on which the corresponding dynamics evolve: T is the inversion lifetime, T2 is the polarization lifetime, and Tph is the photon lifetime. The latter has been used for transforming Eq. 1 into a non-dimensionless form, e.g., all times and frequencies are given in units of Tph and
The coupling setup of the lasers is characterized by three parameters: the coupling strength K [we use a value of K = 0.1 corresponding to an intensity reflectivity of
2.2 Locked emission states
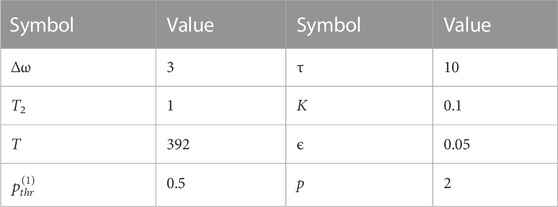
A solitary class-C laser operated below its second laser threshold has a stable emission state and will show only damped relaxation oscillations toward a steady-state solution after a perturbation. Above the second threshold, periodic oscillations or deterministic chaotic behavior occurs (Lingnau et al., 2019). We will operate our laser below the onset of instabilities at four times the first threshold; however, the coupling of two class-C lasers introduces additional emission states with complex dynamics even below the second threshold. Recently, the polarization lifetime T2 was found to fundamentally influence the locking structure of two coupled class-C lasers (Roos et al., 2021). A scan of the dynamics found in the parameter plane of the coupling phase and the detuning is shown in Figure 2A for a dephasing time of T2 = 1. The steady-state solutions, commonly referred to as compound laser modes (CLMs) (Erzgräber et al., 2006; Roos et al., 2021), can be followed in parameter space and are plotted in yellow/pink colors, as shown in Figure 2A. The color encodes the constant phase shift Δϕ between the emission of the two lasers,
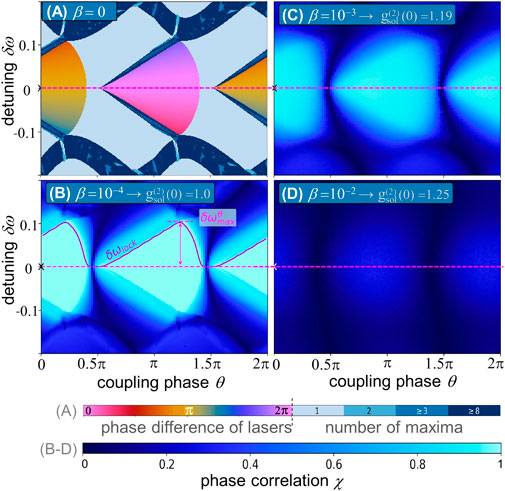
FIGURE 2. Deterministic dynamics (A) and phase correlation χ (B–D) of the two lasers in (θ, δω)-parameter space; (B–D) are obtained for noise strengths β (β and the corresponding
The electric fields for laser emission on a CLM are given by a constant intensity emission of each laser with an optical frequency Ω and a constant phase shift
In order to quantify the range for which locking is observed, the locking range δωlock has been introduced by Roos et al. (2021). It denotes the maximum possible detuning for which a stable CLM exists. In the deterministic case without noise (Figure 2A), the locking range is given by the extent of the yellow/pink areas in the y-direction. As can be seen in Figure 2A, the coupling phase is an important parameter for the dynamics of the system, and not every phase permits locking (there are phases where no CLM solutions exist). For our analysis, we are interested in the maximum locking range reached for the case of an optimally adjusted phase. We, therefore, define
which then allows us to study its dependence on system timescales as, e.g., the polarization lifetime T2. The maximum locking range is indicated in Figure 2B by the pink-dashed horizontal line.
For the stochastic case, where the Langevin noise source is applied, another measure needs to be defined to determine the transition to unlocked emission. For that, we define several tools. One quantity to identify whether the lasers remain on a CLM for a given noise strength is to look for the phase correlation of the electric fields and determine the noise strength where it overcomes a threshold (see the pink line in Figure 2B). The phase correlation χ is defined via the time average ⟨⋅⟩,
The phase correlation resembles the electric field correlation
The intensity auto-correlation function
It is also a good measure for describing the stochastic emission and will be used later on. It provides a value of 2 for noise-dominated emission and a value of 1 for coherent laser emission (Redlich et al., 2016).
To complete the picture and better understand the nature of the unlocking transition, we additionally consider the ensemble variance of the phase difference in order to define a diffusion coefficient D of the random walk-like dynamics of the phase (Otto et al., 2012; Redlich et al., 2017). D then also measures the state of synchronization as it is 0 for locked operation (i.e., no random walk) and larger than 0 otherwise.
The expectation value ⟨⋅⟩ens is with respect to an ensemble of time series with different stochastic realizations. We find that the variance evolves linearly with time for sufficiently large times. The last equality implies that the time evolution of the variance can be modeled as an uncorrelated random walk. This only holds true for times t larger than the characteristic system timescales such that all correlations have decayed.
3 Results
Figures 2B–D show the phase correlation, as defined in Eq. 5, plotted color-coded in the two-dimensional (θ, δω) parameter space for three different noise strengths. For a noise strength of β = 10–4 [see (b)], the dynamical locking structure of the deterministic system can still be seen [compare to (a)]. Here, it can be confirmed that the locked modes exhibit a phase correlation of χ = 1 (light blue colors). However, if the applied noise strength β is further increased [see (c) and (d)], the phase correlation strongly decreases for each parameter set. In addition to this unlocking transition that we quantify further in the following section, the noise does not induce any new features in the investigated parameter space.
To elaborate on the physical context of the unlocking process induced by the noise, we plot the phase correlation χ as a function of the noise strength β in Figure 3 (blue line) for zero detuning and zero phase (δω = 0, θ = 0). As expected, the phase correlation transitions from 1 to 0 as β increases. The noise strengths for which the scans of Figures 2B–D are performed can be seen as vertical dashed lines. The transition of the phase correlation gives rise to a practical possibility to quantify the unlocking of the lasers. We define the critical noise strength βlock in Eq. 8 as the maximum noise strength for which the phase correlation does not exceed a certain threshold of 1 − ϵ (we set ϵ = 0.05).
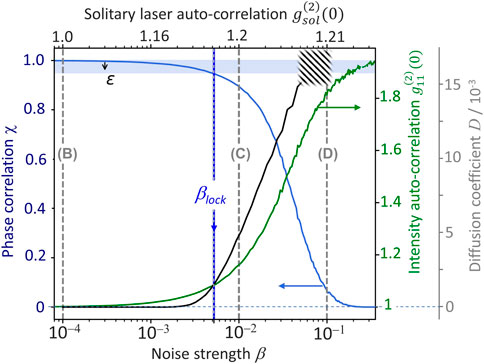
FIGURE 3. Statistical measures of the laser emission as functions of the noise strength β. The phase correlation χ is shown as a solid blue line (blue shading indicates ϵ defining the critical noise strength βlock). The green and black lines show the intensity auto-correlation (Eq. 6) and the diffusion coefficient (Eq. 7). Dashed vertical lines reference panels (B–D) of Figure 2. The top x-axis indicates the auto-correlation of a solitary laser (Eq. 9). Parameters as in Table 1, δω = 0 and θ = 0.
Figure 3 also shows the intensity auto-correlation
The critical noise strength βlock that we use to define the unlocking of the lasers cannot be measured and also changes with the set of equations that is used. In order to overcome this issue, we determine the intensity auto-correlation of a single laser without coupling.
which can directly be measured (Koulas-Simos et al., 2022) and is thus better suited for quantifying the amount of noise in the system. Thus, we always plot both quantities, β and
The last quantity that we evaluate to characterize the transition to unlocking is the diffusion coefficient D (black line in Figure 3). It increases from a value of 0 for low noise strengths to a maximum of D = 15 × 10−3 for β = 0.05. It should be noted that we excluded the region of high noise strength due to convergence problems (hashed area in Figure 3). As can be seen in Figure 3, the unlocking transition seen in quantity D is closely related to the change observed in the phase correlation χ with increasing noise strength. A diffusion coefficient of zero is found when eiΔϕ is entirely locked to a certain point on the unit circle, thus leading to χ = 1. Once the lasers unlock, the diffusion coefficient D increases linearly with the noise strength. This resembles a characteristic feature of a random walk.
To understand how the noise resilience of the synchronized state changes with the coupling phase θ, we plot the phase correlation (Eq. 5) as a function of θ and β in Figure 4 (blue color code). The critical noise strength βlock is printed as a blue line. As defined previously, it is the contour line that satisfies χ = 1 − ϵ and separates regions corresponding to unlocked and locked emission states. We see that the critical noise strength strongly depends on the coupling phase θ. Within the white areas, the deterministic system does not have a stable CLM solution that can be unlocked by noise (see Figure 2A). To exclude the details of the phase effects and to be able to study the maximum possible noise resilience of our laser system, we introduce the maximum critical noise strength.
This quantity is used to study the impact of the internal laser timescales on noise resilience as it describes the maximum noise that can be tolerated within one laser for the case where the phase is adjusted to its optimal value. As mentioned previously, the value of the noise strength is strongly model-dependent, and we rather determine the experimentally accessible intensity auto-correlation of a solitary laser at this maximum noise strength
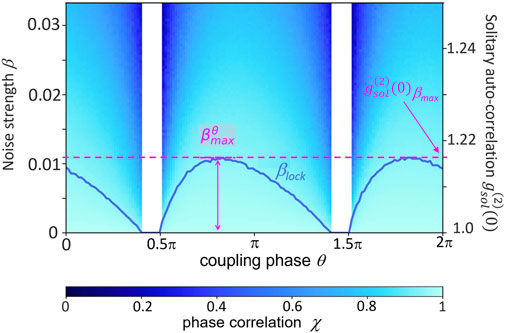
FIGURE 4. Phase correlation χ as a function of noise strength and coupling phase θ. The critical noise strength βlock, as determined from Eq. 8, is shown as a blue line, and the maximum noise strength is indicated by the horizontal pink-dashed line. The right y-axis gives the intensity auto-correlation of one solitary laser. Parameters as in Table 1, δω = 0.
One internal timescale that is specifically important for the dynamics of the nanolasers described with our class-C laser equations is the polarization lifetime T2. We aim to determine if there is an optimal value
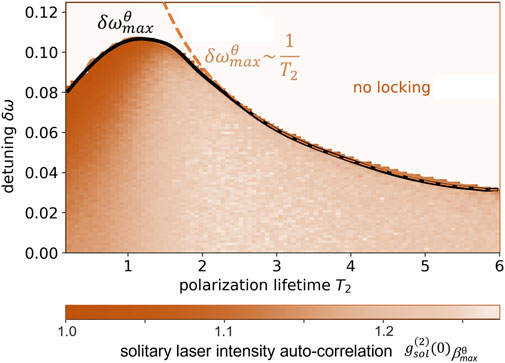
FIGURE 5. Maximum tolerated noise as a function of T2 and detuning δω color coded via the intensity auto-correlation
4 Conclusion
We investigated the impact of spontaneous emission noise on delay-coupled prototypical micro/nanolasers, which we describe using a Maxwell–Bloch type class-C laser model. This approach, despite its simplifications regarding the gain medium, provides valuable qualitative insights. In particular, it unravels the interplay among the different dynamical quantities and thereby highlights relevant trends. In order to quantify the noise-induced unlocking of the lasers, we have discussed the maximum tolerated noise strength in parameter space. The results for the noise strength are converted to the intensity auto-correlation of a single laser on the verge of unlocking. This enables easy comparison with experiments and other laser models. Our results revealed that the noise resilience of coupled lasers is, for small detunings, optimized by a polarization lifetime of two to three times the photon lifetime. Comparing the results for spontaneous emission noise with the behavior of the system under frequency detunings reveals an interesting trend: the lasers show a fundamentally different response to the two perturbations. The detuning locking range is maximized by a polarization lifetime of the order of the photon lifetime, which, however, leads to a drastic decrease in the noise resilience of the lasers.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
The project was initiated and lead by SM and KL. Numerical simulations were performed by AR. All authors discussed the results and wrote the manuscript.
Funding
The work was funded by the German Research Foundation within SFB910 project B9.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arecchi, F. T., Lippi, G. L., Puccioni, G. P., and Tredicce, J. R. (1984). Deterministic chaos in laser with injected signal. Opt. Commun. 51, 308–314. doi:10.1016/0030-4018(84)90016-6
Aust, R., Kaul, T., Ning, C. Z., Lingnau, B., and Lüdge, K. (2016). Modulation response of nanolasers: What rate equation approaches miss. Opt. Quantum Electron. 48, 109. doi:10.1007/s11082-016-0378-4
Bonatto, C., Kelleher, B., Huyet, G., and Hegarty, S. P. (2012). Transition from unidirectional to delayed bidirectional coupling in optically coupled semiconductor lasers. Phys. Rev. E 85, 026205. doi:10.1103/physreve.85.026205
Deka, S. S., Jiang, S., Pan, S. H., and Fainman, Y. (2020). Nanolaser arrays: Toward application-driven dense integration. Nanophotonics 10, 149–169. doi:10.1515/nanoph-2020-0372
Ding, K., and Ning, C. Z. (2013). Fabrication challenges of electrical injection metallic cavity semiconductor nanolasers. Semicond. Sci. Technol. 28, 124002. doi:10.1088/0268-1242/28/12/124002
Du, W., Li, C., Sun, J., Xu, H., Yu, P., Ren, A., et al. (2020). Nanolasers based on 2d materials. Laser Photonics Rev. 14, 2000271. doi:10.1002/lpor.202000271
Erneux, T., and Glorieux, P. (2010). Laser dynamics. (UK: Cambridge University Press. doi:10.1017/cbo9780511776908
Erzgräber, H., Krauskopf, B., and Lenstra, D. (2006). Compound laser modes of mutually delay-coupled lasers. SIAM J. Appl. Dyn. Syst. 5, 30–65. doi:10.1137/040619958
Haken, H. (1975). Analogy between higher instabilities in fluids and lasers. Phys. Lett. 53A, 77–78. doi:10.1016/0375-9601(75)90353-9
Heil, T., Fischer, I., Elsäßer, W., Mulet, J., and Mirasso, C. R. (2001). Chaos synchronization and spontaneous symmetry-breaking in symmetrically delay-coupled semiconductor lasers. Phys. Rev. Lett. 86, 795–798. doi:10.1103/physrevlett.86.795
Hohl, A., Gavrielides, A., Erneux, T., and Kovanis, V. (1997). Localized synchronization in two coupled nonidentical semiconductor lasers. Phys. Rev. Lett. 78, 4745–4748. doi:10.1103/physrevlett.78.4745
Javaloyes, J., Mandel, P., and Pieroux, D. (2003). Dynamical properties of lasers coupled face to face. Phys. Rev. E 67, 036201. doi:10.1103/physreve.67.036201
Junges, L., and Gallas, J. A. C. (2015). Stability diagrams for continuous wide-range control of two mutually delay-coupled semiconductor lasers. New J. Phys. 17, 053038. doi:10.1088/1367-2630/17/5/053038
Koulas-Simos, A., Buchgeister, J., Drechsler, M. L., Zhang, T., Laiho, K., Sinatkas, G., et al. (2022). Quantum fluctuations and lineshape anomaly in a high-beta silver-coated inp-based metallic nanolaser. Laser Photonics Rev. 2022, 2200086. doi:10.1002/lpor.202200086
Li, D. B., and Ning, C. Z. (2012). Interplay of various loss mechanisms and ultimate size limit of a surface plasmon polariton semiconductor nanolaser. Opt. Express 20, 16348. doi:10.1364/oe.20.016348
Lingnau, B., Lüdge, K., Schöll, E., and Chow, W. W. (2013). Microscopic versus α-factor descriptions of dynamics in quantum-dot lasers. Photonics Conf. (IPC) IEEE 22, 81–82. doi:10.1109/ipcon.2013.6656379
Lingnau, B., Perrott, A. H., Dernaika, M., Caro, L., Peters, F. H., and Kelleher, B. (2020). Dynamics of on-chip asymmetrically coupled semiconductor lasers. Opt. Lett. 45, 2223–2226. doi:10.1364/ol.390401
Lingnau, B., Turnwald, J., and Lüdge, K. (2019). Class-C semiconductor lasers with time-delayed optical feedback. Phil. Trans. R. Soc. A 377, 20180124. doi:10.1098/rsta.2018.0124
Lorke, M., Suhr, T., Gregersen, N., and Mørk, J. (2013). Theory of nanolaser devices: Rate equation analysis versus microscopic theory. Phys. Rev. B 87, 205310. doi:10.1103/physrevb.87.205310
Ma, R. M., and Oulton, R. (2019). Applications of nanolasers. Nat. Nanotechnol. 14, 12–22. doi:10.1038/s41565-018-0320-y
Neogi, A., Lee, C. W., Everitt, H. O., Kuroda, T., Tackeuchi, A., and Yablonovitch, E. (2002). Enhancement of spontaneous recombination rate in a quantum well by resonant surface plasmon coupling. Phys. Rev. B 66, 153305. doi:10.1103/physrevb.66.153305
Ning, C. Z. (2010). Semiconductor nanolasers. Phys. Status Solidi B 247, 774–788. doi:10.1002/pssb.200945436
Ning, C. Z. (2019). Semiconductor nanolasers and the size-energyefficiency challenge: A review. Adv. Phot. 1, 1. doi:10.1117/1.ap.1.1.014002
Ohtsubo, J. (2008). Semiconductor lasers: Stability, instability and chaos. 2 edn. Berlin Heidelberg: Springer-Verlag.
Otto, C., Lüdge, K., Vladimirov, A. G., Wolfrum, M., and Schöll, E. (2012). Delay-induced dynamics and jitter reduction of passively mode-locked semiconductor lasers subject to optical feedback. New J. Phys. 14, 113033. doi:10.1088/1367-2630/14/11/113033
Puccioni, G. P., and Lippi, G. L. (2015). Stochastic simulator for modeling the transition to lasing. Opt. Express 23, 2369–2374. doi:10.1364/oe.23.002369
Redlich, C., Lingnau, B., Holzinger, S., Schlottmann, E., Kreinberg, S., Schneider, C., et al. (2016). Mode-switching induced super-thermal bunching in quantum-dot microlasers. New J. Phys. 18, 063011. doi:10.1088/1367-2630/18/6/063011
Redlich, C., Lingnau, B., Huang, H., Raghunathan, R., Schires, K., Poole, P. J., et al. (2017). Linewidth rebroadening in quantum dot semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 23, 1–10. doi:10.1109/jstqe.2017.2701555
Robertson, J., Hejda, M., Bueno, J., and Hurtado, A. (2020). Ultrafast optical integration and pattern classification for neuromorphic photonics based on spiking vcsel neurons. Sci. Rep. 10, 6098. doi:10.1038/s41598-020-62945-5
Roos, A., Meinecke, S., and Lüdge, K. (2021). Stabilizing nanolasers via polarization lifetime tuning. Sci. Rep. 11, 18558. doi:10.1038/s41598-021-97757-8
Schelte, C., Camelin, P., Marconi, M., Garnache, A., Huyet, G., Beaudoin, G., et al. (2019). Third order dispersion in time-delayed systems. Phys. Rev. Lett. 123, 043902. doi:10.1103/physrevlett.123.043902
Schunk, N., and Petermann, K. (1986). Noise analysis of injection-locked semiconductor injection lasers. IEEE J. Quantum Electron. 22, 642–650. doi:10.1109/jqe.1986.1073018
Seifikar, M., Amann, A., and Peters, F. H. (2018). Dynamics of two identical mutually delay-coupled semiconductor lasers in photonic integrated circuits. Appl. Opt. 57, E37–E44. doi:10.1364/ao.57.000e37
van Tartwijk, G. H. M., and Agrawal, G. P. (1998). Laser instabilities: A modern perspective. Prog. Quantum Electron. 22, 43–122. doi:10.1016/s0079-6727(98)00008-1
Wang, T., Jiang, C., Zou, J., Yang, J., Xu, K., Jin, C., et al. (2021). Nanolasers with feedback as low-coherence illumination sources for speckle-free imaging: A numerical analysis of the superthermal emission regime. Nanomaterials 11, 3325. doi:10.3390/nano11123325
Zapf, M., Röder, R., Winkler, K., Kaden, L., Greil, J., Wille, M., et al. (2017). Dynamical tuning of nanowire lasing spectra. Nano Lett. 17, 6637–6643. doi:10.1021/acs.nanolett.7b02589
Keywords: laser dynamics, coupled lasers, class-C lasers, noise resilience, unlocking transition, non-linear dynamics
Citation: Roos A, Meinecke S and Lüdge K (2023) Spontaneous emission noise resilience of coupled nanolasers. Front. Photonics 4:1169988. doi: 10.3389/fphot.2023.1169988
Received: 20 February 2023; Accepted: 22 March 2023;
Published: 12 April 2023.
Edited by:
Cheng Wang, ShanghaiTech University, ChinaReviewed by:
Jianan Duan, Harbin Institute of Technology, Shenzhen, ChinaSong-Sui Li, Southwest Jiaotong University, China
Copyright © 2023 Roos, Meinecke and Lüdge. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kathy Lüdge, a2F0aHkubHVlZGdlQHR1LWlsbWVuYXUuZGU=
 Aycke Roos1
Aycke Roos1 Kathy Lüdge
Kathy Lüdge