Parametric amplification in coupled nonlinear waveguides: The role of coupling dispersion

We present the theory of parametric amplification in coupled nonlinear waveguides considering the frequency dependency of the coupling strength. We show that coupling dispersion can indeed compensate for the uncoupled individual waveguides dispersion enabling a substantial tailoring of the gain spectrum. Our theory describes both phase-sensitive and phase-insensitive operational modes, it can be straightforwardly generalized to include arbitrary higher-order waveguide and coupling dispersion and its predictions agree very well with numerical simulations both in the presence and in the absence of waveguide losses. It provides a tool for the design of novel versatile parametric amplifiers based both on coupled integrated waveguides and dual-core fibers too.

1 Introduction

Optical parametric amplifiers are devices with great technological potential for signal amplification in optical communications. This is due to their broad bandwidth, low noise figure and exploitation of waveguides intrinsic Kerr nonlinearity, not requiring any particular rare-earth based material doping. Parametric amplification is based on the four-wave mixing process where two photons from a powerful pump wave are annihilated and two photons are created at different frequencies called signal and idler respectively, provided that certain phase-matching conditions are satisfied (Stolen and Bjorkholm, 1982; Mahric, 2007). Parametric amplification has been demonstrated in a variety of configurations in nonlinear optical fibers (Hansryd et al., 2002; Takasaka et al., 2012; Gordienko et al., 2017; Olsson et al., 2018; Andrekson and Karlsson, 2020; Gordienko et al., 2023). However it can be achieved also in silicon and silicon nitride waveguides which are promising for optical amplification in integrated devices (Ye et al., 2021a; Ye et al., 2021b).

Parametric amplification in two coupled nonlinear waveguides has been suggested very generally in the past in the context of nonlinear optical couplers (Mecozzi, 1988; Trillo et al., 1989). It has been recently proposed as a promising practical solution for optical communications featuring: flat gain profile, phase-matching in the normal dispersion regime thanks to the coupling contribution, and 0-dB noise figure in the phase-sensitive operational mode (Ribeiro et al., 2017; 2018). Preliminary experimental results in a dual-core highly nonlinear fiber have been obtained too (Szabo et al., 2021; Ribeiro et al., 2022). Some of the authors of the present paper have furthermore shown that if the coupling is chosen with a proper spatial dependence, it can compensate for the mismatch dynamically arising due to the pump attenuation (Ribeiro and Perego, 2022a; Ribeiro and Perego, 2022b), which could solve a substantial problem in integrated amplifiers where the attenuation is of the order of 1 dB/m (Karlsson et al., 2021). The latter coupled waveguides geometry can lead, for specific parameters choice, to superior performances in terms of bandwidth and bandwidth-gain product, compared both to the standard and to the tapered single waveguide silicon nitride parametric amplifiers (Zhao et al., 2020).

In the present work, we show that the frequency dependency of the coupling, and in particular the coupling dispersion—the second derivative of the coupling strength with respect to frequency evaluated at the pump frequency—can play an important role in compensating for the chromatic dispersion of the individual waveguides. This is due to the collective behavior of the interacting waves propagating along coupled waveguides. The justification of the relevance of this particular effect is grounded on the fact that coupled nonlinear waveguides can be fabricated in such a way that the contribution of the coupling dispersion is strong enough to compensate for the individual waveguide dispersion. Indeed, the role of the frequency dependent coupling strength has been explored in the past especially in the study of coupled silicon waveguides. In that context it enables the existence of solitons and modulation instability in conditions where these phenomena would not be possible in the single uncoupled waveguide (Benton and Skryabin, 2009; de Nobriga et al., 2010; Ding et al., 2012). However, the role of coupling dispersion in parametric amplification has not yet been investigated analytically to the best of our knowledge. The impact on the modulation instability spectrum of the first coefficient in the Taylor expansion of the coupling around the pump frequency has been theoretically studied in the past for two evanescently coupled core fibers (Li et al., 2011; 2012) and also in generalized forms of the two coupled nonlinear Schrödinger equations (Nithyanandan et al., 2013; Nair et al., 2018; Li et al., 2020a; Li et al., 2020b). It has been shown that this term can lead to the generation of additional spectral sidebands both in the normal and in the anomalous dispersion regime, provided that the pump power distribution is asymmetric in the two waveguides. In this work we show a different phenomenon and, namely, that the second-order term in the expansion can enable complete compensation of the group velocity dispersion of the single waveguide in the case when the pump power distribution is symmetric in the two waveguides. We provide analytical formulas for the parametric gain in the phase-sensitive (PS) and phase-insensitive (PI) regime too, considering characteristic parameters for both lossless coupled core fibers and lossy integrated silicon nitride waveguides amplifiers. This provides a novel tool for dispersion engineering to be exploited in the design of broadband, flat gain, low noise figure, and energy efficient parametric amplifiers.

2 Materials and methods

The starting point of our theory consists of the two nonlinear Schrödinger equations which rule the propagation of the electric field amplitudes A_1,2 along two identical coupled waveguides:

$\frac{\partial A_1}{\partial z}=i\sum _{n=0}^{\infty }\frac{{\beta }_n}{n!}{\left(i{\partial }_t\right)}^n{A}_1+i\gamma |A_1{|}^2{A}_1-\frac{\alpha }{2}{A}_1+i\sum _{n=0}^{\infty }\frac{C_n}{n!}{\left(i{\partial }_t\right)}^n{A}_2,(\mathrm{1a})$

$\frac{\partial A_2}{\partial z}=i\sum _{n=0}^{\infty }\frac{{\beta }_n}{n!}{\left(i{\partial }_t\right)}^n{A}_2+i\gamma |A_2{|}^2{A}_2-\frac{\alpha }{2}{A}_2+i\sum _{n=0}^{\infty }\frac{C_n}{n!}{\left(i{\partial }_t\right)}^n{A}_1.(\mathrm{1b})$

β_n and C_n are the n-th coefficient of the Taylor expansion of the frequency-dependent propagation constant β(ω) and coupling C(ω) respectively, γ and α are the nonlinearity and attenuation coefficients, t is the temporal coordinate and z is the spatial evolution coordinate along the longitudinal waveguides dimension. In the context of degenerate four-wave mixing, the electric field amplitudes A_1,2 can be expressed as combinations of pump, signal, and idler waves oscillating with angular frequency ω₀, ω_s = ω₀ + Ω and ω_i = ω₀ − Ω, and with amplitudes u_p1,p2, u_s1,s2 and u_i1,i2 respectively, reading

$A_{\mathrm{1,2}}\left(z,t\right)=u_{p1,p2}\left(z\right)+u_{s1,s2}\left(z,\mathrm{\Omega }\right)e^{-i\mathrm{\Omega }t}+u_{i1,i2}\left(z,\mathrm{\Omega }\right)e^{i\mathrm{\Omega }t}.(2)$

The substitution of Eq. 2 into the coupled NLSEs (Eq. 1a and 1b) yields six coupled equations governing the propagation of the six waves. The equations for waveguide 1 read

$\frac{\partial u_{p1}}{\partial z}=\left(i{\beta }_0-\frac{\alpha }{2}+i\gamma |u_{p1}{|}^2\right)u_{p1}+i{C}_0{u}_{p2},(\mathrm{3a})$

$\frac{\partial u_{s1}}{\partial z}=\left[i\beta \left({\omega }_s\right)-\frac{\alpha }{2}+2i\gamma |u_{p1}{|}^2\right]u_{s1}+iC\left({\omega }_s\right)u_{s2}+i\gamma u_{p1}^2{u}_{i1}^{\ast },(\mathrm{3b})$

$\frac{\partial u_{i1}}{\partial z}=\left[i\beta \left({\omega }_i\right)-\frac{\alpha }{2}+2i\gamma |u_{p1}{|}^2\right]u_{i1}+iC\left({\omega }_i\right)u_{i2}+i\gamma u_{p1}^2{u}_{s1}^{\ast },(\mathrm{3c})$

where the small sidebands approximation |u_p|² ≫|u_s,i|² has been considered. Swapping indexes 1 and 2 gives other three equations for waveguide 2.

We focus on the case where the pump waves are identical in the two waveguides with common initial phase ϕ₀, i.e.,

$u_{p1}=u_{p2}=\sqrt{\frac{P_p}{2}}{e}^{-\frac{\alpha }{2}z}{e}^{i{\varphi }_p},(\mathrm{4a})$

${\varphi }_p={\varphi }_0+\left({\beta }_0+C_0\right)z+\frac{\gamma }{2}{P}_p{z}_{\text{eff}},(\mathrm{4b})$

where P_p is the total input pump power and $z_{\text{eff}}={\int }_0^z{e}^{-\alpha z^{\prime }}\mathrm{d}{z}^{\prime }$ (in the lossless case, z_eff → z). A continuous wave solution with equal power but π relative phase between the two pump waves exists too, however we will focus here on the symmetric phase solution as it enables the flat gain profile for one of the system supermodes. By introducing e_s1,s2,i1,i2 defined by

$u_{s1,s2}=e_{s1,s2}{e}^{i{\beta }_{\text{odd}}z}{e}^{-\frac{\alpha }{2}z+i{\varphi }_p},(\mathrm{5a})$

$u_{i1,i2}=e_{i1,i2}{e}^{-i{\beta }_{\text{odd}}z}{e}^{-\frac{\alpha }{2}z+i{\varphi }_p},(\mathrm{5b})$

where ${\beta }_{\text{odd}}=\frac{\beta ({\omega }_s)-\beta ({\omega }_i)}{2}$, signal and idler equations can be separated into two sets of uncoupled equations which in matrix form read

${\partial }_z{E}_{\pm }=i{M}_{\pm }{E}_{\pm }=i\left(\begin{array}{cc}\hfill K_{\pm }\pm C_{\text{odd}}\hfill & \hfill \gamma \frac{P_p}{2}{e}^{-\alpha z}\hfill \\ \hfill -\gamma \frac{P_p}{2}{e}^{-\alpha z}\hfill & \hfill -K_{\pm }\pm C_{\text{odd}}\hfill \end{array}\right)E_{\pm }(6)$

with $E_{\pm }={(e_{s\pm },e_{i\pm }^{\ast })}^T={(e_{s1}\pm e_{s2},e_{i1}^{\ast }\pm e_{i2}^{\ast })}^T$ being the sidebands of supermodes $A_{\pm }=(A_1\pm A_2)/\sqrt{2}$, $K_{\pm }=(\frac{\mathrm{\Delta }\beta }{2}\pm \frac{\mathrm{\Delta }C}{2}\pm C_0-C_0)+\gamma \frac{P_p}{2}{e}^{-\alpha z}$, Δβ(Ω) = β(ω_s) + β(ω_i) − 2β₀, ΔC(Ω) = C (ω_s) + C (ω_i) − 2C₀ and $C_{\text{odd}}=\frac{C({\omega }_s)-C({\omega }_i)}{2}$. Eq. 6 admits an exact solution in the lossless case and an approximate one in the lossy scenario resulting in the appearance of the effective length z_eff (see (Alem et al., 2015; Ribeiro and Perego, 2022a; Zhao et al., 2022) for various applications of this approximation in the context of parametric amplification and modulation instability). The solution is formally $E_{\pm }(z,\mathrm{\Omega })=e^{i{\int }_0^z{M}_{\pm }(z^{\prime })\mathrm{d}{z}^{\prime }}{E}_{\pm }(0,\mathrm{\Omega })$, where the exponential expressions read as follows

$e^{i{\int }_0^z{M}_{\pm }\left(z^{\prime }\right)\mathrm{d}{z}^{\prime }}=e^{\pm i{C}_{\text{odd}}z}{N}^{\pm }=(7)$

$\left(\begin{array}{cc}\hfill \cosh \left({\rho }_{\pm }\right)+i{\theta }_{\pm }\frac{\sinh \left({\rho }_{\pm }\right)}{{\rho }_{\pm }}\hfill & \hfill i\gamma \frac{P_p}{2}{z}_{\text{eff}}\frac{\sinh \left({\rho }_{\pm }\right)}{{\rho }_{\pm }}\hfill \\ \hfill -i\gamma \frac{P_p}{2}{z}_{\text{eff}}\frac{\sinh \left({\rho }_{\pm }\right)}{{\rho }_{\pm }}\hfill & \hfill \cosh \left({\rho }_{\pm }\right)-i{\theta }_{\pm }\frac{\sinh \left({\rho }_{\pm }\right)}{{\rho }_{\pm }}\hfill \end{array}\right)e^{\pm i{C}_{\text{odd}}z}$

with ${\theta }_{\pm }=\gamma \frac{P_p}{2}{z}_{\text{eff}}+\frac{\mathrm{\Delta }\beta \pm \mathrm{\Delta }C}{2}z-C_{0}z\pm C_{0}z$ and ${\rho }_{\pm }=\sqrt{{(\gamma \frac{P_p}{2}{z}_{\text{eff}})}^2-{\theta }_{\pm }^2}$.

3 Results

To highlight the role of coupling dispersion in the parametric amplification process we calculated analytically the z-dependent gain for u_s− = u_s1 − u_s2 — the signal of supermode A₋ —, defined as the ratio between the value of u_s− square modulus at coordinate z to its value at the input of the amplifier: $G(z)=\frac{|u_{s-}(z){|}^2}{|u_{s-}(0){|}^2}$. Considering the solution $E_{\pm }(z,\mathrm{\Omega })=e^{\pm i{C}_{\text{odd}}z}{N}^{\pm }{E}_{\pm }(0,\mathrm{\Omega })$, one has an expression that depends on the N⁻ matrix elements and on the initial conditions for the supermode signal and idler amplitudes as

$G\left(z\right)=e^{-\alpha z}\frac{|N_{11}^{-}{e}_{s-}\left(0\right)+N_{12}^{-}{e}_{i-}^{\ast }\left(0\right){|}^2}{|e_{s-}\left(0\right){|}^2},(8)$

where $N_{11}^{-}$ and $N_{12}^{-}$ are elements of the matrix defined in Eq. 7, while the factor e^−αz comes from the definition of amplitudes u_s1,s2 as a function of e_s1,s2 as described by Eq. 5a. In our study we focus on the “−” supermode as, unlike the “+” one, it can exhibit a flat gain spectrum which is appealing for applications (Ribeiro et al., 2017). We have compared these analytical predictions with numerical simulations of the coupled NLSEs (Eq. 1a and 1b) performed using a split-step Fourier algorithm. In simulations the gain has been computed as $G(z)=\frac{|{\widehat{A}}_{-}(z){|}^2}{|{\widehat{A}}_{-}(0){|}^2}$, where ${\widehat{A}}_{-}$ is the Fourier transform of A₋. In simulations we have considered a time window defined by [−41.7, 41.7] ps with 1,024 grid points, resulting in a time separation Δt = 0.0814 ps. This corresponds to a frequency window of [−6.144, 6.132] THz ⋅ 2π with a frequency separation dΩ = 0.012 THz ⋅ 2π. The integration step size dz is specified in each figure caption for the various scenarios considered. The initial conditions for the simulations correspond to combinations of pump waves with vanishing initial phase (ϕ_p = 0) and signal waves, that is $A_{\mathrm{1,2}}(0,t)=\sqrt{P_p/2}+{\sum }_n{u}_{s1,s2}(0)e^{-in\text{d}\mathrm{\Omega }t}+{\sum }_n{u}_{i1,i2}(0)e^{in\text{d}\mathrm{\Omega }t}$, where the input signal and idler amplitudes u_s1,s2,i1,i2 (0) will be specified case by case later and n is an integer. The gain has been calculated for signals having higher/lower frequency compared to the pump by considering positive/negative n in the sums only. Despite our theory being valid for an arbitrary order of waveguide and coupling dispersion, in the following particular examples we have considered the expansions up to the second order only. We also notice that the odd terms in the coupling Taylor expansion, described by C_odd, do not enter the gain expression for the supermodes when the two waveguides are pumped with equal power. A small pump power imbalance between the two waveguides can result in modifications and degradation of the amplifier gain as it has been analyzed in detail in (Shi et al., 2023a). Alternatively the amplifier can be intentionally pumped with different power in the two waveguides, as asymmetric continuous wave solutions exist too (Li et al., 2011; Shi et al., 2023b). In the latter case the interplay between power asymmetry and odd terms of the frequency dependent coupling causes supermodes interaction leading to intermodal four-wave mixing and to the separation of signal and idler waves between the two different supermodes too (Shi et al., 2023b). Firstly, we focus on the PI regime, selecting as initial conditions u_i1 (0) = u_i2 (0) = 0, and u_s2 (0) = −u_s1 (0) corresponding to the excitation of “−” supermode only. This configuration provides the best performance in terms of noise figure (Ribeiro et al., 2018), flat gain profile for identical pump power and phase in the two waveguides, and the compensation of second-order group velocity dispersion by second-order coupling dispersion parameter as will be further shown in this paper. The PI gain is therefore given by

$G^{\text{PI}}\left(z\right)=e^{-\alpha z}|N_{11}^{-}{|}^2=e^{-\alpha z}\left(1+S^2\right),(9)$

where $S=\gamma \frac{P_p}{2}{z}_{\text{eff}}\frac{\sinh ({\rho }_{-})}{{\rho }_{-}}$. The C₂ dependent gain for lossless (using parameters typical of coupled core fibers) and lossy (using parameters typical of silicon nitride waveguides) PI parametric amplifiers are shown in Figures 1A, B and in Figures 2A, B respectively considering both anomalous and normal dispersion waveguides. The agreement between theory and simulations is excellent as the examples shown in Figures 1C, D and in Figures 2C, D clearly demonstrate. We observe that coupling dispersion, if properly chosen, is able to compensate for individual waveguides dispersion hence substantially improving the amplifier gain bandwidth. The largest bandwidth is achieved when C₂ = β₂ as it can be clearly seen from Figures 1A, B, and from Figures 2A, B. PS operation in coupled waveguides parametric amplifiers can be implemented in a large number of different scenarios (Ribeiro et al., 2017; 2018). Here, without loss of generality, we focus on one particular case to illustrate the predictive power of our theory and the role of C₂ in this regime too. After fixing u_s1 (0) we choose the initial condition as follows, u_i1 (0) = u_s1 (0), u_s2 (0) = u_i2 (0) = −u_s1 (0). If we assume that the initial phase of e_s1 is ϕ_s, the analytical gain expression reads

$G^{\text{PS}}\left(z\right)=e^{-\alpha z}|N_{11}^{-}{e}^{i{\varphi }_s}+N_{12}^{-}{e}^{-i{\varphi }_s}{|}^2.(10)$

The dependency of the gain on the initial phase ϕ_s is shown in Figures 3A, B for the lossy amplifier. We then fixed ϕ_s to maximize the gain, and calculated the gain spectrum both analytically and numerically, which is shown in Figures 3C, D, where the PI gain is also reported as a reference. An excellent agreement between theory and simulations is achieved in this case too. We note that in this work we have considered the signal of “−” supermode as the amplifier output. If the signal of “+” supermode u_s+ = u_s1 + u_s2 is chosen instead, then analogous dispersion compensation effects arise but requiring C₂ with the opposite sign.

FIGURE 1

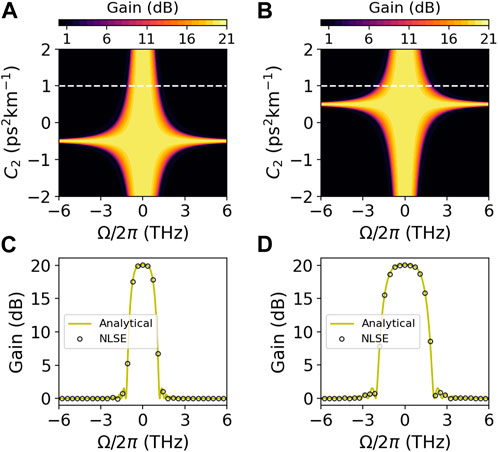
FIGURE 1. Phase insensitive lossless amplifier Map of parametric analytical gain versus frequency and C₂ in anomalous (A) and normal (B) dispersion regime; and gain spectrum versus frequency comparison between numerics and theory for anomalous (C) and normal (D) dispersion regime with C₂ = 1 ps²km⁻¹ (corresponding to dashed lines in (A,B). Other parameters used are β₂ =±0.5 ps²km⁻¹, γ = 10 W⁻¹km⁻¹, P_p = 6 W, C₀ = 15 km⁻¹ and z = 0.1 km. The input signal wave into waveguide 1 used in simulations is $u_{s1}(0)=10^{-4}\sqrt{\text{W}}$ and the integration step is dz =10^–3 km.

FIGURE 2

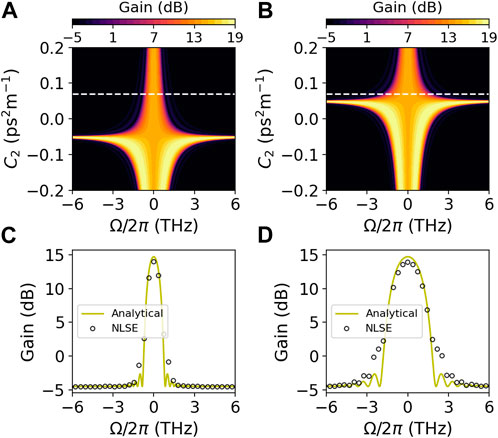
FIGURE 2. Phase insensitive lossy amplifier Map of parametric analytical gain versus frequency and C₂ in anomalous (A) and normal (B) dispersion regime; and gain spectrum versus frequency comparison between numerics (circles) and theory (solid lines) for anomalous (C) and normal (D) dispersion regime with C₂ = 0.07 ps²m⁻¹ (corresponding to dashed lines in (A,B). Other parameters used are β₂ = ±0.05 ps²m⁻¹, γ = 1.2 W⁻¹m⁻¹, P_p = 6 W, C₀ = 1.8 m⁻¹, z = 1.5 m and α = 0.69 m⁻¹ corresponding to 3 dBm⁻¹. The input signal wave into waveguide 1 used in simulations is $u_{s1}(0)=10^{-4}\sqrt{\text{W}}$ and the integration step is dz = 10^–3 m.

FIGURE 3

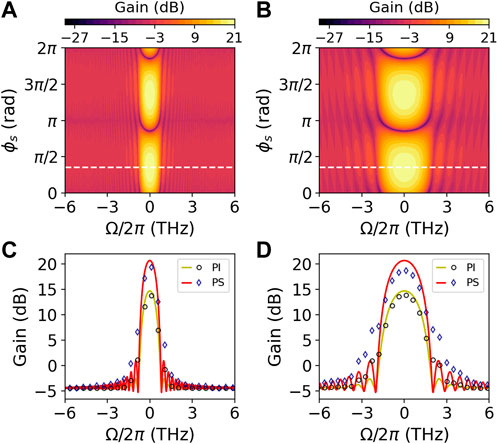
FIGURE 3. Phase sensitive lossy amplifier Map of parametric gain calculated analytically versus frequency and ϕ_s in anomalous (A) and normal (B) dispersion regime; gain spectrum versus frequency for anomalous (C) and normal (D) dispersion regime with ϕ_s = 0.35π (corresponding to dashed lines in (A,B) comparing numerics (diamonds) with analytics (red solid lines). The phase insensitive gain spectrum from Figure 2 is also shown as a reference. Other parameters used are β₂ = ±0.05 ps²m⁻¹, γ = 1.2 W⁻¹m⁻¹, P_p = 6 W, C₀ = 1.8 m⁻¹, z = 1.5 m, C₂ = 0.07 ps²m⁻¹ and α = 0.69 m⁻¹ corresponding to 3 dBm⁻¹. The input signal wave into waveguide 1 used in simulations is $u_{s1}(0)=10^{-4}{e}^{i{\varphi }_s}\sqrt{\text{W}}$ and the integration step is dz = 10^–3 m.

It is furthermore important to mention that the performances of the lossy parametric amplifier with frequency dependent coupling could be improved in terms of gain-bandwidth product by exploiting the benefits of spatially dependent coupling to compensate for pump attenuation induced phase-matching degradation. This has been demonstrated in (Ribeiro and Perego, 2022a; Ribeiro and Perego, 2022b) for coupling having a constant frequency profile. A detailed analysis of the coupled waveguides parametric amplifier with both spatially and frequency dependent coupling will be presented in a future work.

4 Discussion

Compared to a recent numerical study of parametric amplification in coupled waveguides, also considering wavelength dependency of the coupling strength (Su and Biaggio, 2022), our work provides elegant, practical and easy-to-use analytical expressions for the design of an effective dual-waveguide parametric amplifier, accounting for coupling dispersion of an arbitrary order. Considering terms of order greater than 2, both in the single waveguide and in the coupling dispersion, is particularly relevant when the net combined contribution of both single waveguide group velocity and second-order coupling dispersion is close to zero, and there is a need to describe parametric amplifiers operating over a larger bandwidth. In that case, higher-order waveguide dispersion and coupling dispersion terms in the expansion must be taken into account and constitute the limiting factors for the gain spectrum. These terms can be straightforwardly included in the theoretical framework presented in this work and their magnitude would depend on the particular fabrication geometry and materials, which should be evaluated on an individual basis. Furthermore our theory can be also generalized to include the effects of free carrier dispersion (Chaturvedi et al., 2017) and two-photon absorption (Tsoy et al., 2001) which are relevant in silicon waveguides.

In conclusion, we have shown that coupling dispersion is a fundamental physical effect that enables dispersion engineering in dual-waveguide parametric amplifiers, determining substantial tailoring of the gain spectrum and offering the possibility of broadband parametric amplification also when the individual waveguides have normal dispersion. This powerful tool adds a substantial degree of versatility to the already promising features of dual-waveguide parametric amplifiers such as flat gain spectrum, 0-dB noise figure, and compensation of loss induced mismatch. Further developments in the study of frequency dependent coupling for dispersion compensation can be relevant for fiber amplifiers with a large number of cores and for arrays of integrated waveguides with different coupling topologies, as well as for other photonic devices that involve multiple coupled modes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, upon reasonable request.

Author contributions

AMP and VR initiated the study, MS performed the analytical calculations and the numerical simulations, all the authors analyzed the data, AMP wrote the manuscript with inputs from VR and MS

Funding

All the authors acknowledge support from EPSRC project EP/W002868/1. AMP acknowledges support from the Royal Academy of Engineering through the Research Fellowship scheme.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alem, M., Soto, M. A., and Thévenaz, L. (2015). Analytical model and experimental verification of the critical power for modulation instability in optical fibers. Opt. Express 23, 29514–29532. doi:10.1364/oe.23.029514

PubMed Abstract | CrossRef Full Text | Google Scholar

Andrekson, P. A., and Karlsson, M. (2020). Fiber-based phase-sensitive optical amplifiers and their applications. Adv. Opt. Phot. 12, 367–428. doi:10.1364/aop.382548

CrossRef Full Text | Google Scholar

Benton, C. J., and Skryabin, D. V. (2009). Coupling induced anomalous group velocity dispersion in nonlinear arrays of silicon photonic wires. Opt. Express 17, 5879–5884. doi:10.1364/oe.17.005879

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaturvedi, D., Mishra, A. K., and Kumar, A. (2017). Analysis of free carrier effects on modulational instability in silicon-on-insulator nano-waveguides. J. Opt. Soc. Am. B 34, 1060–1069. doi:10.1364/josab.34.001060

CrossRef Full Text | Google Scholar

de Nobriga, C. E., Hobbs, G. D., Wadsworth, W. J., Knight, J. C., Skryabin, D. V., Samarelli, A., et al. (2010). Supermode dispersion and waveguide-to-slot mode transition in arrays of silicon-on-insulator waveguides. Opt. Lett. 35, 3925–3927. doi:10.1364/ol.35.003925

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, W., Staines, O. K., Hobbs, G. D., Gorbach, A. V., de Nobriga, C., Wadsworth, W. J., et al. (2012). Modulational instability in a silicon-on-insulator directional coupler: Role of the coupling-induced group velocity dispersion. Opt. Lett. 37, 668–670. doi:10.1364/ol.37.000668

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordienko, V., Ferreira, F. M., Ribeiro, V., and Doran, N. (2023). Design of an interferometric fiber optic parametric amplifier for the rejection of unwanted four-wave mixing products. Opt. Express 31, 8226–8239. doi:10.1364/oe.476884

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordienko, V., Stephens, M. F. C., El-Taher, A. E., and Doran, N. J. (2017). Ultra-flat wideband single-pump Raman-enhanced parametric amplification. Opt. Express 25, 4810–4818. doi:10.1364/oe.25.004810

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansryd, J., Andrekson, P. A., Westlund, M., Li, J., and Hedekvist, P. O. (2002). Fiber-based optical parametric amplifiers and their applications. IEEE J. Sel. Top. Quantum Electron. 8, 506–520. doi:10.1109/JSTQE.2002.1016354

CrossRef Full Text | Google Scholar

Karlsson, M., Schröder, J., Zhao, P., and Andrekson, P. A. (2021). “Analytic theory for parametric gain in lossy integrated waveguides,” in Conference on lasers and electro-optics (D.C., United States: Optical Society of America). JTh3A.5.

CrossRef Full Text | Google Scholar

Li, J. H., Chiang, K. S., and Chow, K. W. (2011). Modulation instabilities in two-core optical fibers. J. Opt. Soc. Am. B 28, 1693–1701. doi:10.1364/josab.28.001693

CrossRef Full Text | Google Scholar

Li, J. H., Chiang, K. S., Malomed, B. A., and Chow, K. W. (2012). Modulation instabilities in birefringent two-core optical fibres. J. Phys. B Atomic, Mol. Opt. Phys. 45, 165404. doi:10.1088/0953-4075/45/16/165404

CrossRef Full Text | Google Scholar

Li, J. H., Sun, T. T., Ma, Y. Q., Chen, Y., Cao, Z. L., Xian, F. L., et al. (2020a). Modulation instabilities in nonlinear two-core optical fibers with fourth order dispersion. Optik 208, 164134. doi:10.1016/j.ijleo.2019.164134

CrossRef Full Text | Google Scholar

Li, J. H., Sun, T. T., Ma, Y. Q., Chen, Y. Y., Cao, Z. L., and Xian, F. L. (2020b). The effects of fourth-order dispersion on modulation instabilities in two-core optical fibers with asymmetric CW state. Phys. Scr. 95, 115502. doi:10.1088/1402-4896/abba4c

CrossRef Full Text | Google Scholar

Mahric, M. E. (2007). Fiber optical parametric amplifiers, oscillators and related devices: Theory, applications, and related devices. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Mecozzi, A. (1988). Parametric amplification and squeezed-light generation in a nonlinear directional coupler. Opt. Lett. 13, 925–927. doi:10.1364/ol.13.000925

PubMed Abstract | CrossRef Full Text | Google Scholar

Nair, A. A., Porsezian, K., and Jayaraju, M. (2018). Impact of higher order dispersion and nonlinearities on modulational instability in a dual-core optical fiber. Eur. Phys. J. D. 72, 6. doi:10.1140/epjd/e2017-80437-6

CrossRef Full Text | Google Scholar

Nithyanandan, K., Raja, R. V. J., and Porsezian, K. (2013). Modulational instability in a twin-core fiber with the effect of saturable nonlinear response and coupling coefficient dispersion. Phys. Rev. A 87, 043805. doi:10.1103/physreva.87.043805

CrossRef Full Text | Google Scholar

Olsson, S. L. I., Eliasson, H., Astra, E., Karlsson, M., and Andrekson, P. A. (2018). Long-haul optical transmission link using low-noise phase-sensitive amplifiers. Nat. Commun. 9, 2513. doi:10.1038/s41467-018-04956-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ribeiro, V., Karlsson, M., and Andrekson, P. (2017). Parametric amplification with a dual-core fiber. Opt. Express 25, 6234–6243. doi:10.1364/oe.25.006234

PubMed Abstract | CrossRef Full Text | Google Scholar

Ribeiro, V., Lorences-Riesgo, A., Andrekson, P., and Karlsson, M. (2018). Noise in phase-(in)sensitive dual-core fiber parametric amplification. Opt. Express 26, 4050–4059. doi:10.1364/oe.26.004050

PubMed Abstract | CrossRef Full Text | Google Scholar

Ribeiro, V., and Perego, A. M. (2022a). Parametric amplification in lossy nonlinear waveguides with spatially dependent coupling. Opt. Express 30, 17614–17624. doi:10.1364/oe.457583

PubMed Abstract | CrossRef Full Text | Google Scholar

Ribeiro, V., and Perego, A. M. (2022b). “Theory of parametric amplification in coupled lossy waveguides,” in Conference on lasers and electro-optics (D.C., United States: Optical Society of America).

CrossRef Full Text | Google Scholar

Ribeiro, V., Szabó, A. D., Rocha, A. M., Gaur, C. B., Ali, A. A. I., Quiquempois, Y., et al. (2022). Parametric amplification and wavelength conversion in dual-core highly nonlinear fibers. J. Light. Technol. 1, 6013–6020. doi:10.1109/JLT.2022.3186809

CrossRef Full Text | Google Scholar

Shi, M., Ribeiro, V., and Perego, A. M. (2023a). On the resilience of dual-waveguide parametric amplifiers to pump power and phase fluctuations. Appl. Phys. Lett. 122, 101102. doi:10.1063/5.0136729

CrossRef Full Text | Google Scholar

Shi, M., Ribeiro, V., and Perego, A. M. (2023b). Parametric amplification based on intermodal four-wave mixing between different supermodes in coupled-core fibers. Opt. Express 31, 9760. doi:10.1364/oe.480480

CrossRef Full Text | Google Scholar

Stolen, R., and Bjorkholm, J. (1982). Parametric amplification and frequency conversion in optical fibers. IEEE J. Quantum Electron. 18, 1062–1072. doi:10.1109/JQE.1982.1071660

CrossRef Full Text | Google Scholar

Su, J., and Biaggio, I. (2022). Dual-core optical fibers for efficient mid-infrared generation via third-order frequency mixing and coupling-length phase matching. J. Opt. Soc. Am. B 39, 729–741. doi:10.1364/josab.449934

CrossRef Full Text | Google Scholar

Szabo, A. D., Ribeiro, V., Gaur, C. B., Ali, A. A. I., Mussot, A., Quiquempois, Y., et al. (2021). Dual-polarization c+l-band wavelength conversion in a twin-core highly nonlinear fibre. Proceedings of the OFC 2021 Virtual conference, 06-10 June 2021, San Francisco, CA, USA, Paper MB5.4

CrossRef Full Text | Google Scholar

Takasaka, S., Mimura, Y., Takahashi, M., Sugizaki, R., and Ogoshi, H. (2012). “Flat and broad amplification by quasi-phase-matched fiber optical parametric amplifier,” in Optical fiber communication conference (D.C., United States: Optical Society of America). OTh1C.4.

CrossRef Full Text | Google Scholar

Trillo, S., Wabnitz, S., Stegeman, G. I., and Wright, E. M. (1989). Parametric amplification and modulational instabilities in dispersive nonlinear directional couplers with relaxing nonlinearity. J. Opt. Soc. Am. B 6, 889–900. doi:10.1364/josab.6.000889

CrossRef Full Text | Google Scholar

Tsoy, E. N., de Sterke, C. M., and Abdullaev, F. K. (2001). Influence of two-photon absorption on modulational instability. J. Opt. Soc. Am. B 18, 1144–1149. doi:10.1364/JOSAB.18.001144

CrossRef Full Text | Google Scholar

Ye, Z., Zhao, P., Twayana, K., Karlsson, M., Andrekson, P. A., and Torres-Company, V. (2021a). “Ultralow-loss meter-long dispersion-engineered silicon nitride waveguides,” in Conference on lasers and electro-optics (D.C., United States: Optical Society of America). SF1C.5. doi:10.1364/CLEO_SI.2021.SF1C.5

CrossRef Full Text | Google Scholar

Ye, Z., Zhao, P., Twayana, K., Karlsson, M., Torres-Company, V., and Andrekson, P. A. (2021b). Overcoming the quantum limit of optical amplification in monolithic waveguides. Sci. Adv. 7, eabi8150. eabi8150. doi:10.1126/sciadv.abi8150

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, P., Karlsson, M., and Andrekson, P. A. (2022). Low-noise integrated phase-sensitive waveguide parametric amplifiers. J. Light. Technol. 40, 128–135. doi:10.1109/JLT.2021.3119423

CrossRef Full Text | Google Scholar

Zhao, P., Ye, Z., Vijayan, K., Naveau, C., Schröder, J., Karlsson, M., et al. (2020). Waveguide tapering for improved parametric amplification in integrated nonlinear si3n4 waveguides. Opt. Express 28, 23467–23477. doi:10.1364/oe.389159

PubMed Abstract | CrossRef Full Text | Google Scholar