A Multi-Wavelength Phase Retrieval With Multi-Strategy for Lensfree On-Chip Holography

Due to convenient operation and robust imaging, multi-wavelength phase retrieval has been widely applied in lensfree on-chip digital holographic microscope (LFOCDHM). Nevertheless, the insufficient diffraction variation and small number of measurements on the LFOCDHM make it difficult to eliminate the twin image by multi-wavelength phase retrieval. We propose a multi-wavelength phase retrieval for LFOCDHM based on energy constraint, global update strategy, and vector extrapolation acceleration. Simulations and experiments on the LFOCDHM show that our proposed method realizes efficient elimination effect and robust reconstruction with three wavelengths for illumination while maintaining fast convergence. More importantly, the proposed method is simple and non-parametric. It is believed that the proposed method could provide a promising solution for LFOCDHM.

1 Introduction

Lensfree on-chip digital holographic microscope (LFOCDHM) is a new computational imaging technology. Due to its large field of view, high resolution, cost-effectiveness, perfect portability, and easy operation (Ozcan and McLeod 2016; Zhang et al., 2020), LFOCDHM plays an important role in analysis applications requiring large statistics, such as the Papanicolaou smear test for cervical cancer (Greenbaum and Ozcan 2012; Greenbaum et al., 2014) and blood smear inspection for malaria diagnosis (Bishara et al., 2011). LFOCDHM is essentially in-line holography that has the twin image in the direct reconstruction result and the twin image reduces the imaging quality. Iterative phase retrieval (IPR) method provides a feasible and simple computational method to eliminate the twin image (Gerchberg 1972; Fienup 1982; Latychevskaia 2019). To avoid the need for prior knowledge of samples, different multi-intensity IPRs have been proposed, including lateral translation of image sensors (Wu et al., 2016), axial scanning of sample-to-sensor distances (Zhang et al., 2017), etc.

In contrast to the IPR algorithm described above, wavelength-scanning (Bao et al., 2012; Noom et al., 2014; Sanz et al., 2015; Zuo et al., 2015) is a common practice on LFOCDHM, which avoids complex and time-consuming mechanical operations and steadily eliminates the twin image through multi-wavelength phase retrieval (MWPR). Due to the close sample-to-sensor distance and the small number of measurements required to ensure imaging resolution and convenient operation, LFOCDHM cannot produce sufficient diffraction diversity. This limitation leads to a series of problems such as low convergence accuracy, susceptibility to noise interference, and slow convergence speed of MWPR, making it difficult to eliminate the twin image. Therefore, a MWPR with effective elimination, stable reconstruction, and fast convergence is essential for LFOCDHM.

The performance of MWPR is mainly improved from three aspects. First, when appropriate constraints are imposed on the object plane, efficient elimination effect will be realized with a small number of wavelengths. For example, the weighted feedback constraint (Cheng et al., 2018) and the energy constraint (Latychevskaia and Fink, 2007; Li et al., 2016) realized efficient elimination effect without prior knowledge about the sample. Second, an appropriate updating strategy will improve the stability and robustness against the interference of noise. For example, the adaptive step-size strategy (Zuo et al., 2016; Wu et al., 2021) and the global update strategy (Liu et al., 2015; Gao and Cao, 2021) reinforced the true signal while reducing the influence of noise without prior knowledge about the noise statistics. Last but not least, the technique for the acceleration of iterative image restoration algorithms ensures great convergence accuracy while improving the convergence speed significantly. For instance, the vector extrapolation acceleration method (Biggs and Mark 1997) achieved favorable convergence performance without complex parameter calibration. Nevertheless, none of the existing research was carried out from all three aspects simultaneously. The potential of MWPR has not been fully explored. It is desirable that a new MWPR can be proposed for LFOCDHM to realize simple, clear, stable, and fast imaging.

In this work, we propose a MWPR based on energy constraint, global update strategy and vector extrapolation acceleration named MWPREGV for fast and robust elimination of the twin image on LFOCDHM. MWPREGV realizes more efficient elimination effect and more stable reconstruction by energy constraint and global update strategy, and meanwhile it improves the convergence speed by vector acceleration method. At the same time, the MWPREGV is simple and non-parametric. By numerical simulation and experimental verification, LFOCDHM with MWPREGV is able to provide simple, clear, stable, and fast imaging under three wavelength illumination.

2 Principles

2.1 Multi-Wavelength Lensfree On-Chip Digital Holographic Microscope

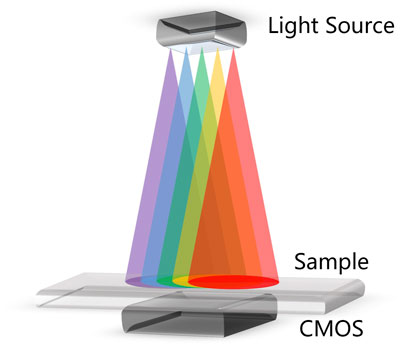
The LFOCDHM is a cost-effective and compact system without any lenses or other optical elements between the object and the sensor plane, and it places the sample as close as possible to the imaging sensor to obtain a wide-field hologram. Multi-wavelength LFOCDHM uses different wavelengths of light sources to irradiate the sample to record different holograms shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of multi-wavelength LFOCDHM.

The hologram recorded by LFOCDHM under the assumption of a thin sample is given by

$\begin{array}{c}{I}_n={\left|H_n\left(u_n\right)\right|}^2+{\epsilon }_n, n=\mathrm{1,2},\dots ,N,\end{array}(1)$

where $N$ denotes the number of measurements, $I_n$ denotes the intensity image recorded by the sensor, $H_n$ denotes the transmission mode of diffraction, ${\epsilon }_n$ denotes the noise in the imaging, and $u_n$ denotes the complex amplitude distribution function of the sample under ${\lambda }_n$ illumination, which is given by

$\begin{array}{c}{u}_n=A_n{\text{e}}^{i{\phi }_n}\end{array}(2)$

where $A_n$ denotes the amplitude and ${\phi }_n$ represents the phase. The absorption of the sample is assumed to be independent of the illumination wavelength, which is a reasonable assumption for most weakly scattering samples. Under different wavelength illumination, the amplitude is the same and the phase varies proportionally, which can be expressed as

$\begin{array}{c}{A}_1=A_2=\cdots =A_N\end{array}(3)$

$\begin{array}{c}{\phi }_{n+1}=\frac{{\lambda }_n}{{\lambda }_{n+1}}{\phi }_n\end{array}(4)$

This assumption implies that $u_1$, $u_2$, $\cdots$, $u_N$ can be uniformly represented by $u$. We consider the $u_1$ as $u$, then $u_n$ can be expressed as:

$\begin{array}{c}{u}_1=u=A{\text{e}}^{i\phi }\end{array}(5)$

$\begin{array}{c}{u}_n=A{\text{e}}^{i\frac{{\lambda }_1}{{\lambda }_n}\phi }\end{array}(6)$

Due to the inherent ill-posedness of the phase retrieval problem, finding the desired $u$ is the efficient way to eliminate the twin image. To avoid tedious parameter calibration, we choose the alternating projection method as the iterative model for MWPR, which finds desired $u$ by iterating back and forth between the object and image planes and adding intensity constraints on the image plane. Compared to the reconstruction from a single-intensity image $\left(N=1\right)$ that finds desired $u$ in a single known constraint set $C_1$ shown in Figure 2A, the reconstruction from some different intensity images $\left(N>1\right)$ is easier to find desired $u$ in the intersection of some known constraint sets $C_1$, $C_2$, $\cdots$, $C_N$ shown in Figure 2B, which is formulated as a feasibility problem:

$\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d}u\in C_1\cap C_2\cap \cdot \cdot \cdot \cap C_N(7)$

FIGURE 2

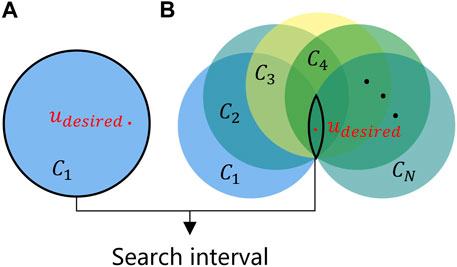
FIGURE 2. Two-dimensional illustration of the IPR reconstruction from (A) a single-intensity image ($N=1$) and (B) some different intensity images $\left(N>1\right)$.

The size of the intersection set is related to the diffraction diversity determined by the difference and number of holograms. When there is sufficient diffraction diversity, the size of the intersection will be small and the MWPR will find the desired $u$ quickly and accurately. Small source-to-sample distances and a small number of measurements make it difficult to produce a sufficient number of holograms with significant differences, resulting in poor elimination effect on LFOCDHM. Therefore, additional constraints are required to be imposed on the object plane to realize clear imaging for LFOCDHM.

2.2 Energy Constraint

The intensity of the hologram is mainly influenced by the intensity of the reference light. Dividing the measured hologram $I_{measure}$ by the background image $I_{background}$ measured after removing the sample results in the normalized hologram $I_{norm}$, which will avoid non-uniform illumination of the light source:

$\begin{array}{c}{I}_{norm}=I_{measure}/I_{background}\end{array}(8)$

The basic physical notion of energy conservation requires that absorption will not lead to an increased amplitude following a scattering process. Since the normalized hologram eliminates the effect of the reference light intensity which is equivalent to irradiating the sample with a unit light wave, the amplitude $A$ on the object plane should not exceed 1. Therefore, during the iterative process, the amplitude part of regions with amplitude exceeding 1 are considered as interference from the twin image and should be replaced by 1 while the phase part remains, and the other regions are retained. This process can be expressed as:

$\begin{array}{c}u\prime \left(x,y\right)=\{\begin{array}{c}u(x,y), A\left(x,y\right)<1\\ e^{i\phi \left(x,y\right)}, A\left(x,y\right)\ge 1\end{array}\end{array}(9)$

where $u\prime$ denotes the updated complex amplitude distribution function and $\left(x,y\right)$ is the Cartesian coordinate system on the object plane.

2.3 Global Update Strategy

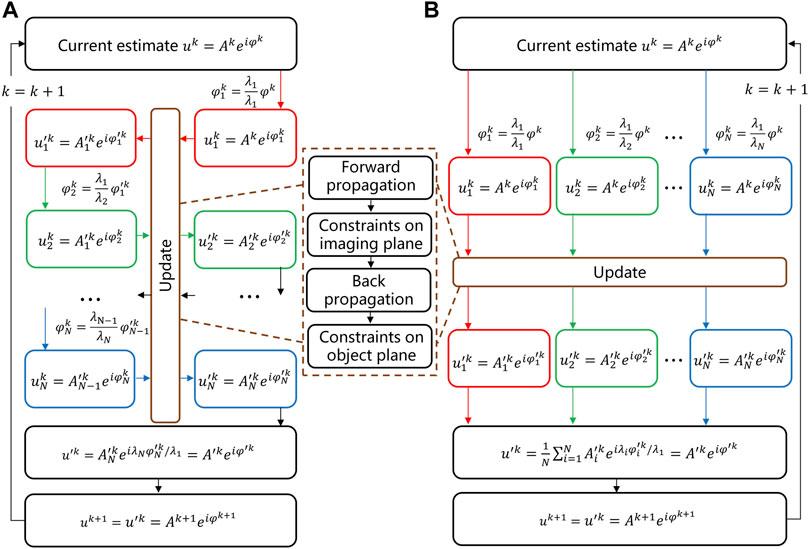
Figure 3 shows the computational flowchart of two common update strategies for MWPR in the $k^{\text{th}}$ iteration, where $u^{\prime k}$, $u_1^{\prime k,}{u}_2^{\prime k,}\cdots u_N^{\prime k}$ denotes the updated complex amplitude distribution, $A^{\prime k,}$ $A_1^{\prime k,}{A}_2^{\prime k,}\cdots A_N^{\prime k}$ denotes the updated amplitude distribution, and ${\phi }^{\prime k,}$ ${\phi }_1^{\prime k,}{\phi }_2^{\prime k,}\cdots {\phi }_N^{\prime k}$ denotes the updated phase distribution. The incremental update strategy shown in Figure 3A updates the $u_n^k$ at the ${\lambda }_n$ wavelength based on the $u_{n-1}^{\prime k}$ that has updated at the ${\lambda }_{n-1}$ wavelength. The global update strategy shown in Figure 3B updates the $u_n^k$ at the ${\lambda }_n$ wavelength based on the $u^k$ and takes the average of the updated $u_n^{\prime k}$ as a result of the $k^{\text{th}}$ iteration.

FIGURE 3

FIGURE 3. Flowchart of the (A) incremental update strategy and (B) global update strategy.

The incremental update strategy converges quickly. However, it is an error accumulation process, resulting in iterative computation being sensitive to noise in the case of a small number of measurements. As a result, the incremental update strategy leads to unstable convergence and imaging artifacts under noise interference. Inexpensive imaging sensors are prone to introduce a series of disturbances such as scattering noise, dark noise, and readout noise during image acquisition, which is especially challenging for low-cost LFOCDHM. Compared with the incremental update strategy, the averaging operation in the global update strategy can effectively suppress the effect of noise and improves the convergence stability. Therefore, the global update strategy is more suitable for LFOCDHM. However, it converges slowly.

2.4 Vector Extrapolation Acceleration Method

The use of acceleration methods can compensate for the disadvantage of slow convergence of global update strategy. Compared with other acceleration methods, the vector extrapolation acceleration method requires only a small amount of information about the iterative algorithm to improve the convergence speed and convergence accuracy, which is nonparametric. This acceleration method is a form of vector extrapolation, which gains a correction step and information for adjusting the step length based on previous iteration. Since IPR is to recover the missing phase, we chose the vector extrapolation acceleration method to update the phase. This process in the $k^{\text{th}}$ iteration can be expressed as:

$\begin{array}{c}{\phi }^{k+1}={\phi }^k+{\alpha }^k{h}^k\end{array}(10)$

where

$\begin{array}{c}{h}^k={\phi }^k-{\phi }^{k-1}\end{array}(11)$

$\begin{array}{c}{\alpha }^k=\frac{{\displaystyle \sum g^k{g}^{k-1}}}{{\displaystyle \sum g^{k-1}{g}^{k-1}}}\end{array}(12)$

$\begin{array}{c}{g}^k=\phi {\prime }^k-{\phi }^k\end{array}(13)$

3 Performance Analysis of Multi-Wavelength Phase Retrieval

3.1 Numerical Results

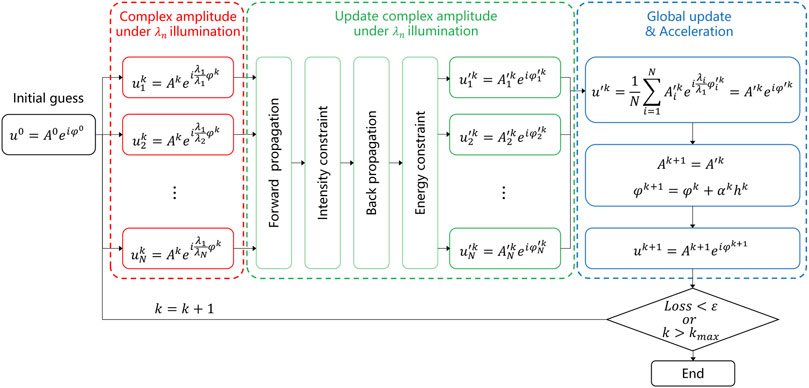
Algorithmic details about the MWPREGV are shown in Figure 4 as follows: (1) initializing the first estimation of $u^0$ with the average of all holograms back-propagated to the object plane with the angular spectrum method; (2) forward-propagating $k^{\text{th}}$ estimation of $u_n^k$ to recording plane with the angular spectrum method and replacing the computed amplitude distribution of recording plane with the modulus of recorded holograms yet retaining the computed phase; (3) back-propagating this synthesized complex amplitude distribution to the object plane with the angular spectrum method and updating the computed amplitude distribution of object plane based on energy constraint to obtain the updated complex amplitude distribution $u_n^{\prime k}$; (4) averaging the $u_n^{\prime k}$ to obtain a globally updated complex amplitude distribution $u^{\prime k}$; (5) updating the phase distribution ${\phi }^k$ based on the globally updated phase distribution $\phi {\prime }^k$ by the vector extrapolation acceleration method yet retaining the globally updated amplitude distribution $A{\prime }^k$ and thus the result $u^{k+1}$ of the $k^{\text{th}}$ iteration is obtained; and (6) iteratively running steps (2) to (5) so that the reconstructed accuracy $Loss$ meets the given requirement $\epsilon$ or the number of iterations $k$ reaches the maximum number $k_{max}$.

FIGURE 4

FIGURE 4. Flowchart of the MWPREGV for LFOCDHM.

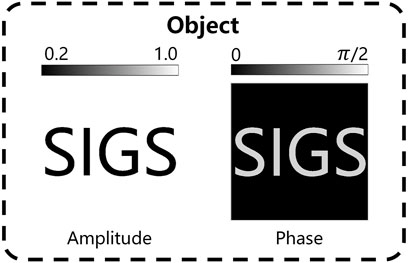
To produce sufficient diffraction variations, a virtual object is illuminated by ${\lambda }_{\mathrm{1,2,3}}=623\mathrm{nm,}\mathrm{523}\mathrm{nm,}460\mathrm{nm}$, and its amplitude and phase under ${\lambda }_1$ illumination are shown in Figure 5. The other parameters are listed as follows: (1) the imaging size is 1.1 × 1.1 mm² (512 × 512 pixels); (2) the distance from light source to sample is 100 mm, and the distance from sample to sensor is 1 mm. To quantify the reconstruction quality, we use the relative error (RE) as reconstructed accuracy $Loss$, which is defined as

$\begin{array}{c}\mathrm{R}\mathrm{E}=\frac{{\Vert u_{est}-u_{true}\Vert }^2}{{\Vert u_{true}\Vert }^2}\end{array}(14)$

where ${\Vert ·\Vert }^2$ denotes the Euclidean norm, $u_{est}$ denotes the estimated value of $u$, and $u_{true}$ denotes the ground truth value of $u$.

FIGURE 5

FIGURE 5. Simulated virtual objects with complex amplitude.

We first compared the performance of MWPR and MWPR based on energy constraint (MWPRE). When the distance from the virtual object to sensor is 30 mm, MWPR eliminates most of the twin image after 50 iterations, as shown in Figure 6A. When the distance from the virtual object to sensor is 1 mm, MWPR only partially eliminates the twin image after 50 iterations due to insufficient diffraction variation, resulting in a large deviation between $u_{est}$ and $u_{true}$, as shown in Figure 6B. In contrast, MWPRE after the same number of iterations almost completely eliminates the twin image for the same diffraction variation shown in Figure 6C. And it achieves better convergence accuracy and faster convergence speed, as shown in Figure 6D.

FIGURE 6

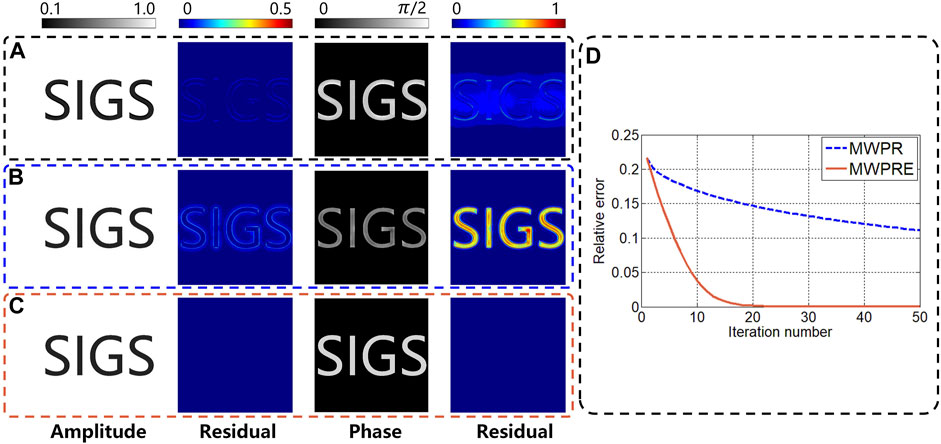
FIGURE 6. Reconstruction by (A) MWPR when the distance from the virtual object to sensor is 30 mm. Reconstruction by (B) MWPR and (C) MWPRE when the distance from the virtual object to sensor is 1 mm. (D) Convergence performance of MWPR and MWPRE.

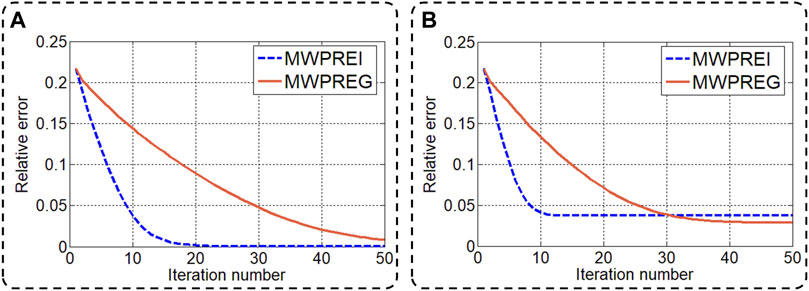
Next, we compared the convergence behavior of the incremental update strategy and global update strategy on the MWPRE (MWPREI and MWPREG). The MWPREI converges much faster than the global update strategy and has a better convergence accuracy when the ideal holograms and background images without noise are used, as shown in Figure 7A. Nevertheless, when adding white Gaussian noise to obtain holograms and background images with a signal-to-noise ratio of 30 dB, we find that the MWPREG achieves better convergence accuracy as expected, as shown in Figure 7B. Therefore, the global update strategy is more suitable for LFOCDHM with a lot of noisy interferences.

FIGURE 7

FIGURE 7. Convergence behavior of MWPREI and MWPREG with (A) noiseless and (B) noisy data.

Finally, we tested the impact of the acceleration algorithm on the MWPREG, as shown in Figure 8. Compared with the MWPREG, the MWPREGV achieves more efficient elimination and faster convergence, which compensates for the disadvantage of slow convergence due to the global update strategy without tedious parameter calibration.

FIGURE 8

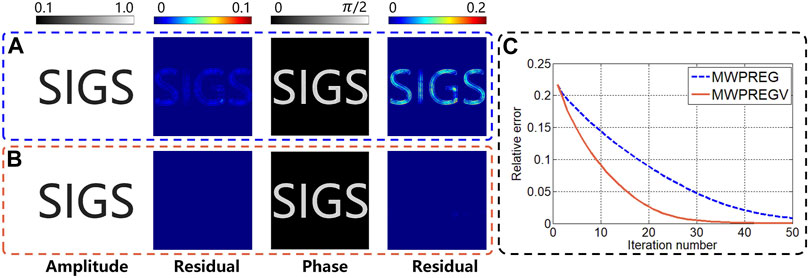
FIGURE 8. Reconstruction by (A) MWPREG and (B) MWPREGV. (C) Convergence performance of MWPREG and MWPREGV.

3.2 Validation on Experimental Data

We tested the proposed method on ant mounts, housefly leg mounts, and bee wing mounts. The experimental setup is shown in Figure 1. An RGB LED (LZ4-04DCA, ${\lambda }_{\mathrm{1,2,3}}=623\mathrm{nm},523\mathrm{nm,}460\mathrm{nm}$) is utilized as the illumination source to avoid scattering noise, and a CMOS sensor with a pixel size of 2.2 μm (2592 × 1944, MT9P031) is utilized to record the hologram. The distance from the light source to the sample is 100 mm, and the distance from the sample to the sensor is 1.2 mm. Since the ground truth value of $u$ is unknown in the experiment, the $Loss$ is used to evaluate the speed of convergence rather than the quality of the reconstruction, which is given by:

$\begin{array}{c}Loss=\Vert \left|H_1\left(u\right)\right|-\sqrt{I_1}{\Vert }^2\end{array}(15)$

Figure 9B shows full FOV(∼27.78 mm²) holograms of the LFOCDHM captured at the 523 nm wavelength, which has a larger field of view than microscopic images taken with a 4 × times objective lens shown in the Figure 9A and Figure 9C show the reconstructed amplitude distribution by using MWPR after 15 iterations, indicating that only partial elimination of the twin image can be achieved. In contrast, MWPRE eliminates most of the twin image after 15 iterations, as shown in Figure 9D. However, the reconstruction by MWPRE is not satisfactory due to the interference of noise, which is far from the microscopic images taken with a ×4 objective lens. Under the same conditions, MWPREGV realizes more efficient elimination effect after the same number of iterations, making the reconstruction similar to the microscopic images taken with a ×4 objective lens, as shown in Figure 9E. And as shown in Figure 9F, MWPREGV converges to a stable value with a faster rate compared to MWPREG.

FIGURE 9

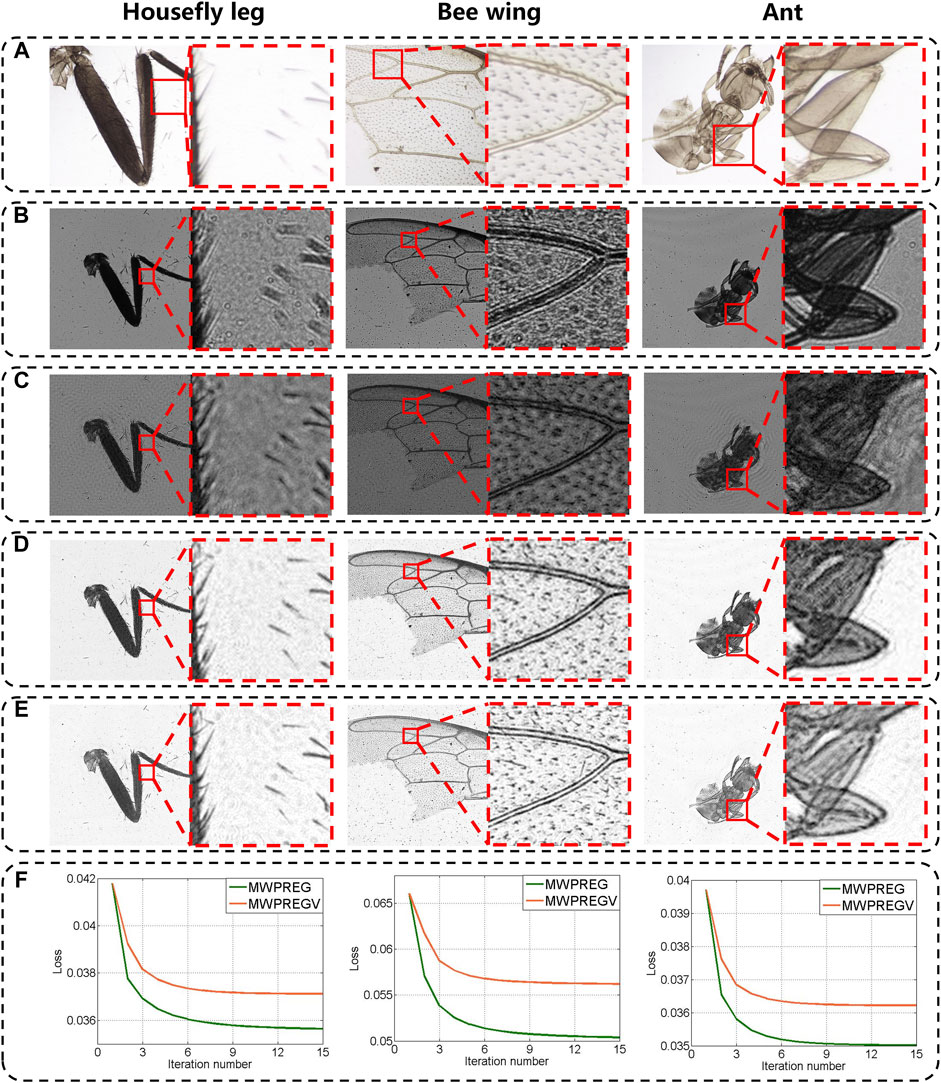
FIGURE 9. (A) Microscope images taken with a ×4 objective lens. (B) Full-FOV raw hologram captured at the 523 nm wavelength. The reconstructed amplitude by (C) MWPR, (D) MWPRE, and (E) MWPREGV. (F) Convergence performance of MWPREG and MWPREGV.

4 Conclusion

In this study, we propose a MWPR based on energy constraint, global update strategy, and vector extrapolation acceleration for LFOCDHM, termed MWPREGV. MWPREGV realizes efficient elimination effect by imposing energy constraint on the object plane, and meanwhile it combines the global update strategy and the vector extrapolation acceleration to improve the stability and robustness of the reconstruction towards noise yet retains the fast convergence speed. More importantly, MWPREGV avoids the need for complex parameter calibrations, which is attractive for simplifying the operation of LFOCDHM. Simulation and experimental results show that LFOCDHM with MWPREGV is feasible to realize clear, stable, and fast imaging under three-wavelength illumination. Compared to the microscope with a ×4 objective lens, LFOCDHM with MWPREGV realizes almost the same imaging effect with a larger field of view at a lower cost, which is believed to have more potential application directions in the future.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

QW, JM, and PS performed the research and wrote the manuscript. All authors have read and approved the content of the manuscript.

Funding

This work was supported by Shenzhen general research fund (JCYJ20190813172405231 and JCYJ20200109143031287).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, P., Situ, G., Pedrini, G., and Osten, W. (2012). Lensless Phase Microscopy Using Phase Retrieval with Multiple Illumination Wavelengths. Appl. Opt. 51 (22), 5486. doi:10.1364/ao.51.005486

PubMed Abstract | CrossRef Full Text | Google Scholar

Biggs, D., and Mark, A. (1997). Acceleration of Iterative Image Restoration Algorithms. Appl. Opt. 36 (8), 1766. doi:10.1364/ao.36.001766

PubMed Abstract | CrossRef Full Text | Google Scholar

Bishara, W., Sikora, U., Mudanyali, O., Su, T.-W., Yaglidere, O., Luckhart, S., et al. (2011). Holographic Pixel Super-resolution in Portable Lensless On-Chip Microscopy Using a Fiber-Optic Array. Lab. Chip 11 (7), 1276–1279. doi:10.1039/c0lc00684j

PubMed Abstract | CrossRef Full Text | Google Scholar

Fienup, J. R. (1982). Phase Retrieval Algorithms: A Comparison. Applied optics 21 (15), 2758–2769.

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Y., and Cao, L. (2021). Generalized Optimization Framework for Pixel Super-resolution Imaging in Digital Holography. Opt. Express 29 (18), 28805–28823. doi:10.1364/OE.434449

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerchberg, R. W. (1972). A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik 35, 237–250.

Google Scholar

Greenbaum, A., Zhang, Y., Feizi, A., Chung, P. L., Luo, W., Kandukuri, S. R., et al. (2014). Wide-field Computational Imaging of Pathology Slides Using Lens-free On-Chip Microscopy. Sci. Transl Med. 6 (267), 267ra175. doi:10.1126/scitranslmed.3009850

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenbaum, A., and Ozcan, A. (2012). Maskless Imaging of Dense Samples Using Pixel Super-resolution Based Multi-Height Lensfree On-Chip Microscopy. Opt. Express 20 (3), 3129–3143. doi:10.1364/oe.20.003129

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, C., Li, Q., Zhang, X., Tan, J., Liu, S., and Liu, Z. (2018). Enhancing Imaging Contrast via Weighted Feedback for Iterative Multi-Image Phase Retrieval. J. Biomed. Opt. 23 (1), 1–10. doi:10.1117/1.JBO.23.1.016015

CrossRef Full Text | Google Scholar

Latychevskaia, T., and Fink, H.-W. (2007). Solution to the Twin Image Problem in Holography. Phys. Rev. Lett. 98 (23), 233901. doi:10.1103/PhysRevLett.98.233901

PubMed Abstract | CrossRef Full Text | Google Scholar

Latychevskaia, T. (2019). Iterative Phase Retrieval for Digital Holography: Tutorial. J. Opt. Soc. Am. A. 36 (12), D31–D40. doi:10.1364/JOSAA.36.000D31

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Xiao, W., and Pan, F. (2016). Phase Retrieval Method from Multiple-Wavelength Holograms for In-Line Holography. Optik 127 (1), 90–95. doi:10.1016/j.ijleo.2015.10.017

CrossRef Full Text | Google Scholar

Liu, Z., Guo, C., Tan, J., Wu, Q., Pan, L., and Liu, S. (2015). Iterative Phase-Amplitude Retrieval with Multiple Intensity Images at Output Plane of Gyrator Transforms. J. Opt. 17 (2), 025701. doi:10.1088/2040-8978/17/2/025701

CrossRef Full Text | Google Scholar

Noom, D. W. E., Boonzajer Flaes, D. E., Labordus, E., Eikema, K. S. E., and Witte, S. (2014). High-speed Multi-Wavelength Fresnel Diffraction Imaging. Opt. Express 22 (25), 30504–30511. doi:10.1364/OE.22.030504

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozcan, A., and McLeod, E. (2016). Lensless Imaging and Sensing. Annu. Rev. Biomed. Eng. 18, 77–102. doi:10.1146/annurev-bioeng-092515-010849

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanz, M., Picazo-Bueno, J. A., García, J., and Micó, V. (2015). Improved Quantitative Phase Imaging in Lensless Microscopy by Single-Shot Multi-Wavelength Illumination Using a Fast Convergence Algorithm. Opt. Express 23 (16), 21352–21365. doi:10.1364/OE.23.021352

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Sun, J., Zhang, J., Lu, L., Chen, R., Chen, Q., et al. (2021). Wavelength-scanning Lensfree On-Chip Microscopy for Wide-Field Pixel-Super-Resolved Quantitative Phase Imaging. Opt. Lett. 46 (9), 2023–2026. doi:10.1364/OL.421869

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Zhang, Y., Luo, W., and Ozcan, A. (2016). Demosaiced Pixel Super-resolution for Multiplexed Holographic Color Imaging. Sci. Rep. 6, 28601. doi:10.1038/srep28601

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Sun, J., Chen, Q., Li, J., and Zuo, C. (2017). Adaptive Pixel-Super-Resolved Lensfree In-Line Digital Holography for Wide-Field On-Chip Microscopy. Sci. Rep. 7 (1), 11777. doi:10.1038/s41598-017-11715-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Sun, J., Chen, Q., and Zuo, C. (2020). Resolution Analysis in a Lens-free On-Chip Digital Holographic Microscope. IEEE Trans. Comput. Imaging 6, 697–710. doi:10.1109/tci.2020.2964247

CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., and Chen, Q. (2016). Adaptive Step-Size Strategy for Noise-Robust Fourier Ptychographic Microscopy. Opt. Express 24 (18), 20724–20744. doi:10.1364/OE.24.020724

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., Zhang, J., Hu, Y., and Chen, Q. (2015). Lensless Phase Microscopy and Diffraction Tomography with Multi-Angle and Multi-Wavelength Illuminations Using a LED Matrix. Opt. Express 23 (11), 14314–14328. doi:10.1364/OE.23.014314

PubMed Abstract | CrossRef Full Text | Google Scholar