
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Photonics , 04 March 2022
Sec. Optical Information Processing and Holography
Volume 3 - 2022 | https://doi.org/10.3389/fphot.2022.846731
This article is part of the Research Topic Digital Holography: Applications and Emerging Technologies View all 14 articles
Interferenceless coded aperture correlation holography (I-COACH) provides an alternative way for the 3D imaging of spatial incoherent illuminated or fluorescent sample. However, the low imaging signal-to-noise ratio (SNR) is one of the bottlenecks that restrict the application of I-COACH. The limitation is mainly originated from the strong bias level that presents in the recorded holograms. Phase shifting methods were implemented in I-COACH to eliminate the background noise while the multiple-exposures recording mechanism significantly reduces the temporal resolution of the system. In this paper, we proposed a compressive I-COACH imaging method with high reconstruction quality and without the sacrifice of the imaging speed. The 3D holographic image reconstruction was implemented under compressive sensing framework while only one single-exposure object hologram and one point spread hologram are necessary. High quality reconstructions were obtained using the proposed method, even for the down-sampled holograms. The imaging SNR of the I-COACH system was improved by a factor of more than 16.5% when comparing with the imaging SNR obtained by the conventional cross-correlation reconstruction method. The proposed method provides a fast and high-fidelity imaging method that can potentially benefit the imaging through scattering medium, partial aperture imaging, and other fields.
Holography based on two-beam mutual-coherent and interference has unique advantages in the field of quantitative phase contrast imaging and 3D imaging because it can record and reconstruct not only the amplitude but also the phase of the light that emitted or reflected from the object. However, coherent sources are not always practically available, especially in some important applications such as astronomical imaging and fluorescence microscopy. In addition, the coherent speckle noise in the reconstructed images has significantly affected the imaging performance of the holographic system (Men et al., 2017). On the other hand, incoherent holography that first was proposed by Mertz and Young in 1961 has extended the application of holography to the field of spatial incoherent imaging (Rogers, 1950; Mertz et al., 1961). The basic idea of original incoherent holography is that the spatial incoherent objects can be 3D reconstructed from their Fresnel zone plate projection patterns (hologram). The incoherent holographic techniques were then further developed and improved by Lohmann, Stroke, and Cochran (Lohmann, 1965; Stroke and Restrick, 1965; Cochran, 1966). One significant difference between incoherent holography and conventional holography is that the mutual coherence between any two different points on the sample is no longer necessary for holographic recording. Instead, the holographic recording scheme was based on the characteristics of spatial self-coherence by splitting the light that emitted from each point on the object into two beams and then recording the resulting interference patterns. However, incoherent holographic methods are normally failed in providing images with sufficient SNR. The problems are mainly arising from the strong bias in the recorded holograms as the results of the incoherent superposition of all the point holograms.
A new type of incoherent digital holography, coined as coded aperture correlation holography (COACH), was proposed in 2016 (Vijayakumar et al., 2016), which originated from Fresnel incoherent correlation holography (FINCH) (Men et al., 2017). COACH possesses the advantages of higher axial-resolution and higher spectral-resolution when comparing with FINCH. In COACH, the pseudorandom coded phase mask (CPM) generated using Gerchberg-Saxton (GS) algorithm is loaded onto the spatial light modulator (SLM), and the self-interference holographic recording is realized based on the beam splitting using the polarization sensitive characteristics of the SLM (Vijayakumar et al., 2016). The 3D reconstruction of the object is realized by cross-correlating the object hologram (OH) with the point spread holograms (PSHs) that have been recorded at all possible axial planes. That the 3D information of an object can be encoded and decoded even without the use of self-interference recording was found by later research. The interferenceless coded aperture correlation holography (I-COACH) was proposed for 3D imaging without any two-wave interference (Vijayakumar and Rosen, 2017). Comparing with COACH, I-COACH has a much simpler optical setup and improved photon-energy efficiency. However, the temporal resolution of the system is sacrificed because multi-exposure phase shifting technique and image averaging method were used to suppress the background noise that dominates the reconstructed images. Different techniques such as phase filtering (PF) (RatnamRai et al., 2017), non-linear reconstruction (NLR) (Rai and Rosen, 2019; Liu et al., 2020), and adaptive reconstruction (Wan et al., 2021) were used to suppress the background noise and improve the temporal resolution of the I-COACH system. However, the increases of temporal resolution normally come with the decreases of reconstruction quality. On the other hand, compressive sensing (CS) theory has demonstrated that signals, assumed to be sparse in some basis and sampled by multiplex encoding systems, may be accurately inferred with high probability from much fewer measurements than suggested by Nyquist’s sampling theorem. In digital holography, the CS technique provides a high-efficiency way for 3D object reconstruction from single real-valued (intensity) hologram. Specifically, the 3D sample is modulated by the optical system to form a 2D hologram, and the reconstruction process is implemented under the CS framework to achieve 3D tomographic imaging of the sample (Zhang et al., 2018). In compressive digital holography, the theoretical model of the holographic recording procedure of a 3D object was first established based on vector diffraction theorem. The forward and backward propagation models, with sparsity regularization imposed on the object, were then used to solve the so-called under-determined inverse problem that will be met when trying to reconstruct 3D objects from their single-exposure digital hologram. As a result, the bias and twin-images can be suppressed (Brady et al., 2009; Lim et al., 2011; Brady et al., 2015; Zhang et al., 2018).
In this paper, inspired by the basic idea of compressive holography, we propose a compressive I-COACH 3D imaging method with high imaging quality and most importantly without the sacrifice of the system temporal resolution. In CS-I-COACH, only single-exposure PSH and OH are necessary for the 3D reconstruction of the object. The imaging model under the CS frame of the I-COACH was first discussed, followed by the preliminary experimental results on 2D and 3D objects that demonstrate the validity of the proposed method. The dependence of the CS reconstruction accuracy in I-COACH on the scattering degree of the CPM was analyzed. The implementation of CS high fidelity reconstruction for under-sampled holograms was also discussed. We believe the proposed method provides a powerful research tool and benefits the optical research fields such as 3D tracking, imaging through scattering medium, and partial aperture imaging.
Nyquist sampling frequency is a sufficient but not necessary condition for the high-fidelity retrieval of a discrete signal. CS theory demonstrates that if the signal is sparse itself or can be represented sparse in a certain domain (i.e., Fourier domain or wavelet domain), the original signal can be reconstructed with high probability using numerical optimization approaches, even when the sampling rate is much lower than the value required by the Nyquist criterion. CS can be used for image reconstruction in imaging systems because most natural images are sparse or have sparsity in some transform domains. Assume the image f can be expressed on the orthogonal base φ = {φ1,φ2…,φn } as:
where the coefficient
where
An I-COACH optical setup is shown in Figure 1. The object or pinhole is critically illuminated with spatial incoherent light, the diffracted light is collected and collimated by the lens L, and then modulated by the phase mask which comprises pseudorandom CPM and a quadratic phase mask (QPM) with focal length fs. The light scattered by the phase mask is then projected to the sensor plane by the QPM. The hologram of the object is recorded by the image sensor.
In the system as show in Figure 1, for a point object at the position of (xs,ys,zs), the intensity distribution Ipsh on the CCD plane can be calculated and given as (Wan et al., 2021):
where the sign
The system of I-COACH is treated as a linear space-invariant imaging system (Wan et al., 2021). Assume that the intensity response of the K-th axial position plane of the 3D object at zs =zk to the CCD plane is the convolution of the system point spread function and the 2D object plane. Therefore, the intensity pattern of the object at a certain depth level on the CCD and the hologram reconstruction with pure phase filtering can be given as Eqs. 5, 6, respectively, which show the sensing model under the CS frame of I-COACH.
where
The matrix
As described above, the CS model of I-COACH and the optimized solution algorithm are established, combined with the sensing matrix to suppress the influence of the bias term on the reconstructed image, which is expected to obtain a high quality reconstructed image quickly by single exposure of PSH and OH.
Preliminary experiments were carried out to demonstrate the validity and imaging performance of the proposed CS-I-COACH system. In the first experiment, the transmitted object was imaged, and the imaging performances of the CS-I-COACH were quantitatively evaluated and compared with conventional I-COACH methods. The next experiment verified the high SNR imaging capabilities of CS-I-COACH for under-sampled holograms.
As shown in Figure 2, the pinhole or object was illuminated by the incoherent light emitting diode (LED) (Thorlabs LED 625L4, 700 mW, center wavelength of λ = 625 nm, Δλ = 17 nm) placed at the front focal plane of the lens L0 with focal length f0 = 150 mm. The light from the beam splitter BS1 was collimated by the lens L0 and passed through a polarizer P. The polarizer P polarizes the light along the orientation of the active axis of the spatial light modulator (SLM, Holoeye PLUTO, 1,080 × 1920 pixels, 8 μm pixel pitch, phase-only modulation) located at a distance of 55 mm from the L0. On the SLM, a phase mask is displayed whereas its phase is the combination of a CPM and a QPM with a focal length of fs = 150 mm. The light modulated by the SLM was collected by a Charge Coupled Device (CCD, Thorlabs CS235MU,1,200 × 1920 pixels, 5.86 μm pixel pitch, and monochrome) located at a distance of zh = 171 mm from the SLM.
In the first experiment, the ability of CS-I-COACH to image two-dimensional transmissive objects was demonstrated. Similar with our work before (Wan et al., 2021; Liu et al., 2022), the scattering degree σ = 0.167 and the annular width ω = 1 pixel were chosen as the optimization parameters of the CPM in the modified GS algorithm. The PSH was recorded by placing in Channel-1 a 20 μm diameter pinhole at the front focal plane of the input lens L0. Channel-2 was blocked during the recording of PSH. Then with Channel-1 blocked, the object hologram OH was recorded with a United States Air Force resolution chart (USAF 1951 RES-1, Newport, placed at the front focal plane of the L0, line-groups of 4 and 5 have been illuminated) as the 2D object. The synthesized coded phase mask (SCPM), the hologram of a 20 μm diameter pinhole (PSH), and the hologram of a USAF target chart (OH) are shown in Figure 3, respectively.

FIGURE 3. The SCPM used in hologram recording and experimentally recorded holograms.(A) Phase of the SCPM; (B) the Point spread hologram; (C) the object hologram.
The reconstructed images of the single-exposure PSH and OH were obtained using different traditional reconstruction methods and the CS-I-COACH reconstruction method, respectively, and the results are shown in Figure 4. The reconstructed images from the single-exposure PSH and OH as shown in Figures 3B,C were obtained using different methods of cross-correlation (CC), pure phase filtering (PF), non-linear reconstruction (NLR), and CS-I-COACH, respectively. The results are shown in Figure 4. For the CS-I-COACH, Eq. 8 was solved using the TwIST algorithm with λTwIST = 0.001 (iteration = 50). Regularization parameter of τTV = 0.01 was used. For comparison, the direct imaging result obtained in the same system (by using the SLM as a lens) is shown in Figure 4A. The strong background noise that presents in the CC results (Figure 4B) was suppressed partially by the PF (Figure 4C) and more effectively by the NLR (Figure 4D) reconstruction method. However, the imaging performances of the I-COACH system, especially the background noise level, were still much worse than the direct imaging (Figure 4A). The CS-based methods, on the other hand, provide results with much better quality (Figure 4E) than their conventional reconstruction counterparts. The improvements on the imaging quality can be seen more clearly from the inserted line profiles and the peak-signal-to-noise-ratio (PSNR) (Bioucas-Dias and Figueiredo, 2007) data of the reconstructions (Figure 4F). Among those, one can notice that the CS-I-COACH reconstruction has better SNR than all the conventional I-COACH reconstruction methods and direct imaging results. It turned out to be that for all the different methods, CS-based I-COACH reconstructions can always have an improved PSNR by a factor of 45.8% (CC), 42% (PF), and 16.5% (NLR). Since additional processing is required in NLR methods to find the optimal modulation parameters (o and p in Eq. 7) (Liu et al., 2020), the more time-efficient phase-filtering-based methods (PF and CS-I-COACH) that provide similar imaging performance were used in the following experiments on 3D objects.
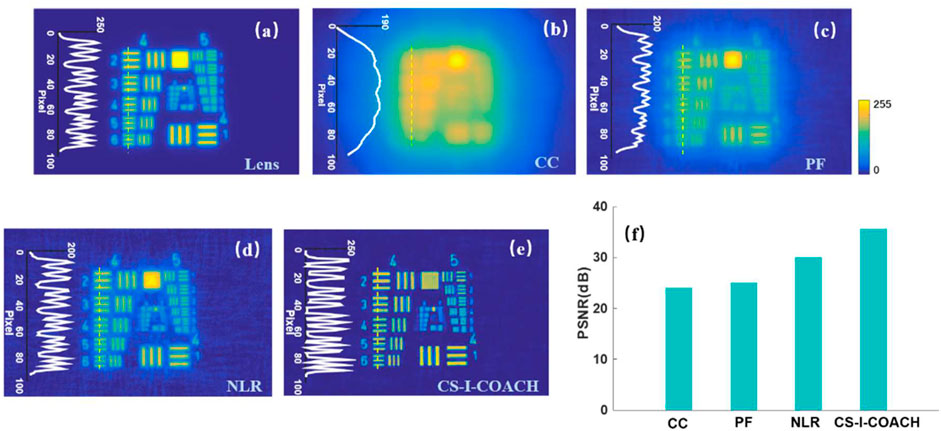
FIGURE 4. Comparison of the results of different reconstruction methods of PSH and OH for single exposure. (A) Lens imaging; (B) cross-correlation; (C) phase filtered cross-correlation; (D) non-linear reconstruction with parameters o = 0.8 and p = −0.2; (E) our proposed CS-I-COACH compression reconstruction method; (F) the PSNR of the reconstructed images from different methods.
The CS reconstruction accuracy is highly correlated with the incoherence between the sparse operator (i.e., the sparsity transform matrix that has been applied on the object) and the imaging modal of the system (i.e., the matrix that describes the transform relationship between the object and the measurement). The incoherence can be described theoretically by the number of the non-zero off-diagonal elements in the autocorrelation of the sensing matrix. In the I-COACH system, the incoherence can be controlled by using different scattering degrees σ of the CPM. To obtain the optimal scattering degree σ in the modified GS algorithm (Liu et al., 2020) corresponding to the best imaging quality of the CS-I-COACH system, the entropy merit was used to quantitatively evaluate the quality of the reconstructed images in this paper (Men et al., 2017). Entropy is a measure of the disorder in a system, which in this case is maximized when the magnitude of the reconstructed image is distributed over the entire image plane and minimized when the entire image points are accumulated in the smallest area as possible. Therefore, for the relatively simple objects that have been used in the following experiments, a minimum entropy is expected to yield the reconstruction with the optimal SNR. From the intensity distribution function of the reconstructed image
where m and n are the pixel coordinates of the image and

FIGURE 5. The dependence of CS-I-COACH reconstruction accuracy on the scattering degrees σ of the CPM. Inserted blue-colored numbers indicate the entropy of the corresponding image.
We further demonstrated in our system one of the most interesting applications of CS in holography, i.e., the high-fidelity image retrieval from under-sampled holograms. The recorded holograms of the PSH and OH were down-sampled randomly in the spatial frequency domain, and then used to reconstruct the object image. The dependence of the reconstruction accuracy (again evaluated by the entropy of the image, inserted blue-colored values) on the sampling rate S is shown in Figure 6. That the CS reconstructed images still preserve a reasonable quality until S = 10% was found in the results. Meanwhile, under the sample condition, the reconstructions obtained using conventional reconstruction methods were dominated by the strong background noise.

FIGURE 6. Reconstructed images from under-sampled holograms using different methods. (a1-a7) Cross-correlation (CC), (b1-b7) phase filtering (PF), (c1-c7) non-linear reconstruction (NLR) with parameters o = 0.8 and p = −0.2, and (d1-d7) CS-I-COACH reconstructions.
In the next experiment the proposed method was used for 3D imaging. The 20 μm diameter pinhole was moved within a range of 12 mm (6 mm above and 6 mm below) around the front focal plane of L0, with 1 mm step interval. The PSHs library at 13 different axial positions were then recorded. To simulate a 3D object, two transmission resolution targets (NBS, 1963A 1X R2L2S1N, and USAF 1951 1X, USAF GO Edmund optics), with an axial distance of 6 mm, were placed at the front focal plane of L0, in Channel-1 and Channel-2, respectively. The line-groups of 4, 5 of the USAF targets, and the line-groups of 36 and 40 of the NBS target, were illuminated by the LED source. Initially, two targets were placed in the front focal plane of the lens L0. Then, the two targets in Channels 1 and 2 are moved simultaneously in reverse directions at 1 mm step, and the corresponding 7 object holograms are recorded to simulate 13 different depth planes of the 3D objects. The reconstructed images obtained using different reconstruction methods are shown in Figure 7. It can be seen from the results that 3D imaging performances of I-COACH can be improved by the proposed method since the defocus images attenuate more quickly with the increase of the axial space in the CS reconstructions when comparing it with PF and NLR results.
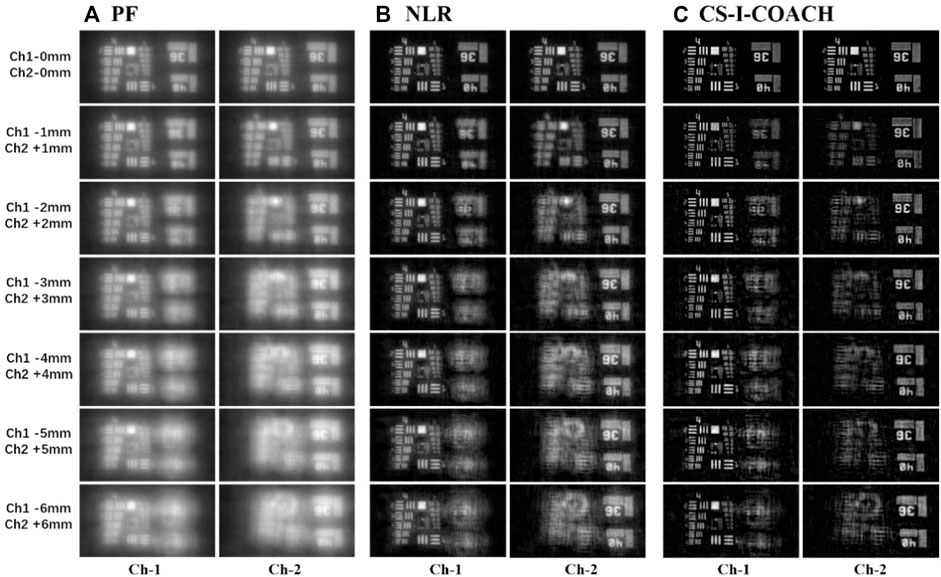
FIGURE 7. Reconstructions of the 3D objects with different axial spaces in between using (A) PF, (B) NLR, and (C) CS methods.
In this paper, we have successfully suppressed the background noise and improved the reconstruction quality of the conventional I-COACH methods without sacrificing the imaging speed. This was achieved by establishing the compressive sensing model and then by numerically reconstructing the holograms under the CS framework. Our experimental results have demonstrated that the PSNR of the reconstructed images can be improved by a factor of 16.5% via the proposed method. Meanwhile, CS reconstructions can still preserve reasonable quality for a 10% under-sampled hologram. In our method, the 3D imaging performance of I-COACH was improved by suppressing the effects of out-of-focus images that are present in the reconstructions. With those improved system imaging performances, we believe the proposed CS-I-COACH method will benefit the research areas such as imaging through scattering medium and partial aperture imaging.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
YW: Conceptualization, Methodology, Supervision, Writing-Reviewing and Editing, Project administration, Funding acquisition. CL: Software, Writing-Original draft preparation, Methodology, Investigation. TM: Conceptualization, Methodology, Software, Investigation.
National Natural Science Foundation of China (61575009); Natural Science Foundation of Beijing Municipality (4182016).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bioucas-Dias, J. M., and Figueiredo, M. A. T. (2007). A New TwIST: Two-step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 16 (12), 2992–3004. doi:10.1109/tip.2007.909319
Brady, D. J., Choi, K., Marks, D. L., Horisaki, R., and Lim, S. (2009). Compressive Holography. Opt. Express 17 (15), 13040–13049. doi:10.1364/oe.17.013040
Brady, D. J., Mrozack, A., MacCabe, K., and Llull, P. (2015). Compressive Tomography. Adv. Opt. Photon. 7, 756–813. doi:10.1364/aop.7.000756
Cochran, G. (1966). New Method of Making Fresnel Transforms with Incoherent Light*. J. Opt. Soc. Am. 56 (11), 1513–1517. doi:10.1364/josa.56.001513
Lim, S. D., Marks, D. L., and Brady, D. J. (2011). Sampling and Processing for Compressive Holography [Invited]Sampling and Processing for Compressive Holography. Appl. Opt. 50 (34), H75–H86. doi:10.1364/ao.50.000h75
Liu, C., Man, T. L., and Wan, Y. H. (2020). Optimized Reconstruction with Noise Suppression for Interferenceless Coded Aperture Correlation Holography. Appl. Opt. 59 (6), 1769–1774.
Liu, C., Man, T. L., and Wan, Y. H. (2022). High-quality Interferenceless Coded Aperture Correlation Holography with Optimized High SNR Holograms. Appl. Opt. 61 (3), 661–668. doi:10.1364/ao.444783
Lohmann, A. W. (1965). Wavefront Reconstruction for Incoherent Objects. J. Opt. Soc. Am. 55 (11), 1555–1556. doi:10.1364/josa.55.1555_1
Men, G. F., Pascal, P., and Wang, H. Y. (2017). .Research Progress of Fresnel Incoherent Correlation Digital Holography. Imaging Sci. Photochem. 35 (2), 199–207.
Mertz, L., and Young, N. O. (1961). “Fresnel Transform of Images,”. Editor K. J. Habell.Proceedings of the International Conference on Optical Instruments and Techniques.London: Chapman Hall, 305.
Rai, M. R., and Rosen, J. (2019). Noise Suppression by Controlling the Sparsity of the point Spread Function in Interferenceless Coded Aperture Correlation Holography (I-COACH). Opt. Express 27 (17), 24311–24323. doi:10.1364/oe.27.024311
Ratnam Rai, M., Vijayakumar, A., and Rosen, J. (2017). Single Camera Shot Interferenceless Coded Aperture Correlation Holography. Opt. Lett. 42 (19), 3992–3995. doi:10.1364/ol.42.003992
Rogers, G. L. (1950). .Gabor Diffraction Microscopy: the Hologram as a Generalized Zone-Plate. Nature, 166,237. doi:10.1038/166237a0
Stroke, G. W., and Restrick, R. C. (1965). Holography with Spatially Noncoherent Light. Appl. Phys. Lett. 7 (9), 229–231. doi:10.1063/1.1754392
Vijayakumar, A., Kashter, Y., Kelner, R., and Rosen, J. (2016). Coded Aperture Correlation Holography-A New Type of Incoherent Digital Holograms. Opt. Express 24 (11), 12430–12441. doi:10.1364/oe.24.012430
Vijayakumar, A., and Rosen, J. (2017). Interferenceless Coded Aperture Correlation Holography-A New Technique for Recording Incoherent Digital Holograms without Two-Wave Interference. Opt. Express 25 (12), 13883–13896. doi:10.1364/oe.25.013883
Wan, Y., Liu, C., Ma, T., Qin, Y., and Lv, S. (2021). Incoherent Coded Aperture Correlation Holographic Imaging with Fast Adaptive and Noise-Suppressed Reconstruction. Opt. Express 29, 8064–8075. doi:10.1364/oe.418918
Keywords: incoherent holography, coded aperture imaging, 3D imaging, compressive sensing, high quality reconstruction
Citation: Liu C, Man T and Wan Y (2022) Compressive Interferenceless Coded Aperture Correlation Holography With High Imaging Quality. Front. Photonics 3:846731. doi: 10.3389/fphot.2022.846731
Received: 31 December 2021; Accepted: 25 January 2022;
Published: 04 March 2022.
Edited by:
Yaping Zhang, Kunming University of Science and Technology, ChinaReviewed by:
Jianglei Di, Guangdong University of Technology, ChinaCopyright © 2022 Liu, Man and Wan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuhong Wan, eWhvbmd3QGJqdXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.