- 1Institute of Photonics, Leibniz University Hannover, Hannover, Germany
- 2Hannover Center for Optical Technologies, Leibniz University Hannover, Hannover, Germany
- 3Cluster of Excellence PhoenixD (Photonics, Optics, and Engineering—Innovation Across Disciplines), Leibniz University Hannover, Hannover, Germany
- 4Xlim Research Institute, CNRS UMR 7252, Université de Limoges, Limoges, France
The well-established frequency-to-time mapping technique is employed as a convenient and time-efficient method to directly characterize the spectral correlations of biphoton states from a pulsed-excited spontaneous parametric down-conversion process. We were enabled by this technique to implement for the first time, the spectral Hanbury-Brown and Twiss measurement, revealing directly the single frequency-mode bandwidth of the biphoton state.
Introduction
The characterization of spectral and temporal properties of biphoton states generated in spontaneous parametric down-conversion (SPDC) or spontaneous four-wave mixing (SFWM) is essential to assess their utility towards different applications in quantum information processing and metrology. For example, the joint spectral intensity (JSI) of biphoton states should often be tailor-made in order to achieve quantum interference of high visibility (Metcalf et al., 2013; Joshi et al., 2020; Khodadad Kashi et al., 2021). To date the characterization techniques have been primarily based on successive and time-consuming frequency scans over the biphoton state spectrum. Spectral filtering of photonpairs yields inefficient detection rates, which degrades the signal-to-noise ratio (SNR) and in turn restricts the accessible spectral resolution. In addition, the limited frequency-bandwidth of the filtering devices further constraints the spectral resolution of the scheme. In alternative characterization techniques, such as the one based on position-to-frequency mapping, a low spectral resolution per pixel/detector as well as a low frequency sampling rate are the main limitations (Johnsen et al., 2014). In another approach, which relies on Fourier spectroscopy, a very low spectral resolution paired with measurement instability and long integration time to reconstruct the JSI can be identified (Wasilewski et al., 2006; Eckstein et al., 2014). In methods based on stimulated SPDC or SFWM, despite the contribution of seed light in providing high generation rates and hence enabling a fast implementation, the stimulated emission itself appears as a source of noise due to the spatial and spectral overlap with photonpairs originating from the parametric process (Eckstein et al., 2014; Jizan et al., 2015; Kaneda et al., 2020).
In this paper, we demonstrate the first-time experimental implementation of spectral Hanbury Brown and Twiss (HBT) interferometry via the well-established frequency-to-time mapping (FTM) technique (Leaird et al., 2011; Goda, K. and Jalali, B. 2013; Goda et al., 2009; Mahjoubfar et al., 2017), also commonly referred to as dispersive Fourier transform (DFT) (Wetzel et al., 2012; Godin et al., 2013; Nguyen et al., 2013), which relies on chromatic dispersion to translate the frequency components of an optical spectrum onto a time-stretched temporal waveform (Lu et al., 2018; Goda, K. and Jalali, B., 2013). The FTM had been previously demonstrated (Valencia et al., 2002; Brida et al., 2006; Baek et al., 2008) and employed as a technique to characterize the JSI of parametric processes (Avenhaus et al., 2009; Eckstein et al., 2014). However, in these implementations the spectral resolution was limited due to the employment of avalanche photo detectors with large timing jitters, which to be compensated for, required additional lengths of the dispersion compensating fiber (DCF) at the cost of large amounts of loss imposed on the measurement. In our present work, the FTM technique enabled us to directly (through only a single coincidence measurement) characterize the single frequency-mode bandwidth and the spectral correlations of a biphoton state generated in a pulsed-driven SPDC process within a periodically-poled lithium niobate (PPLN) waveguide.
The frequency components of the biphoton state are temporally resolved post-propagation through a DCF. The fine timing resolution of our singlephoton detection system allows for the spectrally-resolved detection and thus the direct frequency-mapping of the biphoton state in time. In particular, this technique enables the spectral characterization of biphoton states without the need to perform time-consuming successive frequency scans with expensive filtering devices. Specifically, this is achieved through only a single coincidence measurement over the SPDC biphoton spectrum: contrary to the hitherto commonly-adopted schemes composed of successive scans over the frequency distribution of the biphoton state, in our approach the time-resolved coincident detections are exploited to directly reconstruct the signal-idler JSI, to gain access to the coincidence to accidental ratio (CAR), and to directly implement the spectral HBT interferometry (Silva et al., 2016). Importantly, for the first time we directly measure and demonstrate the dependency of the second-order auto-correlation function
Experimental Setup
The experimental setup (see Figure 1A) consisted of a PPLN waveguide excited by a 10
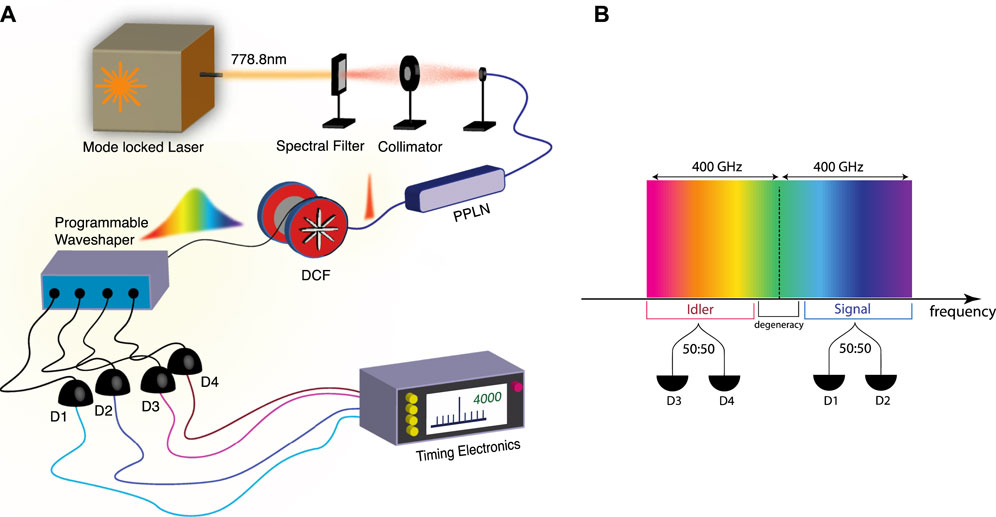
FIGURE 1. (A) Experimental setup which employs the FTM technique to characterize the SPDC biphoton spectrum (see main text for more details). (B) Spectral configuration defined with the use of a programmable waveshaper for characterization of the SPDC biphoton spectrum. The signal (idler) spectral intensity with
Frequency-to-Time Mapping
The frequency-to-time mapped replica of the signal and idler spectra are shown in Figure 2. The frequency components within the signal and idler spectrum (
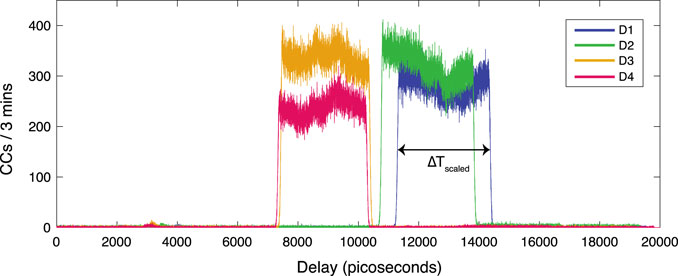
FIGURE 2. Time-stretched replica of the signal and idler spectra. The
By relating the time-scaled replica of
It is important to note that the frequency resolving capability achievable with our spectrometer is 29 and 10 times higher than those reported in the articles by Avenhaus et al. (2009) and Eckstein et al. (2014), respectively. In these experiments the detectors' timing jitter of 180 and 250 ps have restricted the achievable spectral resolutions to
By comparison, the presented system here allows a more efficient demonstration of FTM-assisted spectral characterization of parametric processes, mitigating in a more efficient way the effects of loss by having incorporated an infrastructure of better specifications.
Second-Order Auto-Correlation Function
Propagation of the SPDC biphoton state spectrum through the DCF led to time-resolved detection of its frequency components. As a result, by probing the collected two-fold coincident events on detectors D1 and D2, we were able to directly measure the spectral second-order auto-correlation function (Silva et al., 2016)
associated with the signal field. Figure 3A illustrates the dependency of
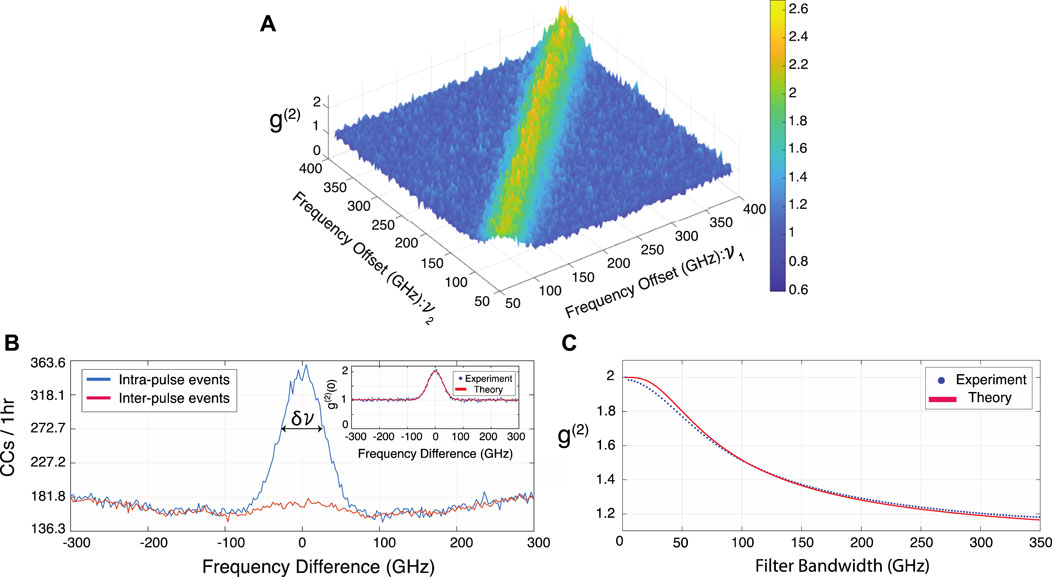
FIGURE 3. (A) Spectral second-order auto-correlation
In Figure 3B, the total intra- and inter-pulse coincidence counts as function of spectral difference
Assuming an undispersed SPDC biphoton spectrum with a total signal bandwidth of
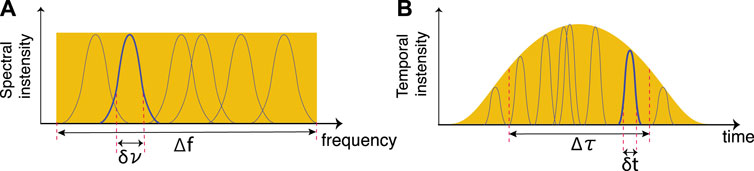
FIGURE 4. Schematic illustration of the signal (A) spectral and its reciprocal (B) temporal intensity profiles under the assumption of propagation through a non-dispersive medium. The undispersed signal spectrum (
With this demonstration, we lay particular stress on the necessity of system calibration prior to spectral characterization of biphoton states. For single photon detectors with timing resolution that exceeds the reciprocal of the biphoton state spectrum, the accuracy of the measured single frequency-mode bandwidth is undermined if gauged via observing the dependency of the
Joint Spectral Intensity and Coincidence to Accidental Ratio
The FTM technique allows for a direct measurement of the JSI and the CAR. The time-resolved coincidence events corresponding to the high-purity signal-idler photon pairs were collected to reconstruct the JSI and to obtain the CAR of our photon-pair source.
In Figure 5A, the JSI of the signal and idler photons is illustrated as function of their symmetric positive and negative frequency offset from the degeneracy point,
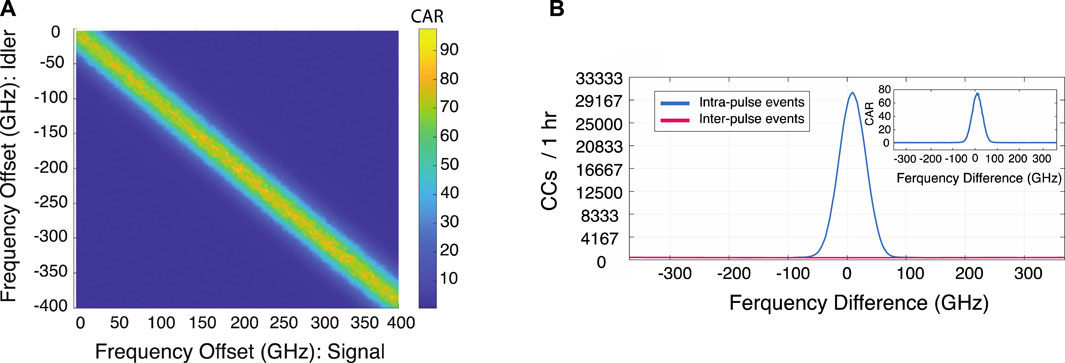
FIGURE 5. (A) Joint Spectral Intensity coincidence to accidental ratio (CAR) versus signal and idler frequency offset from the SPDC degeneracy point
It is important to note that the FTM technique is merely considered for spectral characterization of broad spectra such as biphoton state spectra of ultra-short pulsed-excited parametric processes and for sources where the temporal width of the photons’ wave packets fall below the temporal resolution of the detection system. In particular, spectral characterization of photon pairs generated in high Q-factor (Q > 1000000) resonators (Puckett et al., 2021) as well as from continuous wave-driven parametric processes are practicable neither with FTM technique nor via the state-of-the-art programmable filters, owing to the ultra-narrow line-widths of the modes that fall in the order of kHz. These systems are better characterized directly in the time-domain.
Conclusion
To date the HBT interferometry had been entirely performed by probing temporal correlations, together with variable spectral filtering. In this research we were enabled by the FTM technique to show for the first time the direct measurement of the spectral second-order autocorrelation function. Via a single coincidence measurement, we performed direct spectral characterization of a biphoton state from pulsed-excited SPDC process. To this end, time-resolved intra- and inter-pulse coincidence detections were collected on-the-fly in synchronization with the pulsed-laser repetition rate, and by relying on the fine timing resolution of our SNSPDs,
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
AK performed the conception and design of the study with contributions of MK. AK performed the experiment, the data analysis and wrote the manuscript. LS, RH, and BW provided input and contributed to discussion. MK supervised and coordinated the project. All authors contributed to the revision of the manuscript.
Funding
AK and MK acknowledge funding from the German Federal Ministry of Education and Research, Quantum Futur Program (PQuMAL). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 950618 (STREAMLINE project) and No. 947603 (QFreC project). BW further acknowledges the support of the French ANR through the OPTIMAL project (ANR-20-CE30-0004) and the Région Nouvelle-Aquitaine (SCIR & SPINAL projects).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, A., and Wang, L.-G. (2021). Hanbury Brown and Twiss Effect in the Spatiotemporal Domain II: The Effect of Spatiotemporal Coupling. OSA Continuum 4 (8), 2221. doi:10.1364/osac.434377
Avenhaus, M., Eckstein, A., Mosley, P. J., and Silberhorn, C. (2009). Fiber-assisted Single-Photon Spectrograph. Opt. Lett. 34 (18), 2873–2875. doi:10.1364/ol.34.002873
Baek, S.-Y., Kwon, O., and Kim, Y.-H. (2008). Nonlocal Dispersion Control of a Single-Photon Waveform. Phys. Rev. A. 78 (1), 1–4. doi:10.1103/PhysRevA.78.013816
Brida, G., Chekhova, M. V., Genovese, M., Gramegna, M., and Krivitsky, L. A. (2006). Dispersion Spreading of Biphotons in Optical Fibers and Two-Photon Interference. Phys. Rev. Lett. 96 (14), 1–4. doi:10.1103/PhysRevLett.96.143601
Bromberg, Y., Lahini, Y., Small, E., and Silberberg, Y. (2010). Hanbury Brown and Twiss Interferometry with Interacting Photons. Nat. Photon 4 (10), 721–726. doi:10.1038/nphoton.2010.195
Bruno, N., Martin, A., Guerreiro, T., Sanguinetti, B., and Thew, R. T. (2014). Pulsed Source of Spectrally Uncorrelated and Indistinguishable Photons at Telecom Wavelengths. Opt. Express 22 (14), 17246. doi:10.1364/oe.22.017246
Eckstein, A., Boucher, G., Lemaître, A., Filloux, P., Favero, I., Leo, G., et al. (2014). High-Resolution Spectral Characterization of Two Photon States via Classical Measurements. Laser Photon. Rev. 8 (5), L76–L80. doi:10.1002/lpor.201400057
Goda, K., and Jalali, B. (2013). Dispersive Fourier Transformation for Fast Continuous Single-Shot Measurements. Nat. Photon 7 (2), 102–112. doi:10.1038/nphoton.2012.359
Goda, K., Solli, D. R., Tsia, K. K., and Jalali, B. (2009). Theory of Amplified Dispersive Fourier Transformation. Phys. Rev. A. 80 (4). doi:10.1103/PhysRevA.80.043821
Godin, T., Wetzel, B., Sylvestre, T., Larger, L., Kudlinski, A., Mussot, A., et al. (2013). Real Time Noise and Wavelength Correlations in Octave-Spanning Supercontinuum Generation. Opt. Express 21 (15), 18452. doi:10.1364/oe.21.018452
Jeltes, T., McNamara, J. M., Hogervorst, W., Vassen, W., Krachmalnicoff, V., Schellekens, M., et al. (2007). Comparison of the Hanbury Brown-Twiss Effect for Bosons and Fermions. Nature 445 (7126), 402–405. doi:10.1038/nature05513
Jizan, I., Helt, L. G., Xiong, C., Collins, M. J., Choi, D.-Y., Joon Chae, C., et al. (2015). Bi-Photon Spectral Correlation Measurements from a Silicon Nanowire in the Quantum and Classical Regimes. Sci. Rep. 5 (July), 1–9. doi:10.1038/srep12557
Johnsen, K. D., Kolenderski, P., Scarcella, C., Thibault, M., Tosi, A., and Jennewein, T. (2014). Time and Spectrum-Resolving Multiphoton Correlator for 300-900 Nm. J. Appl. Phys. 116 (14), 143101. doi:10.1063/1.4897296
Joshi, C., Farsi, A., Dutt, A., Kim, B. Y., Ji, X., Zhao, Y., et al. (2020). Frequency-Domain Quantum Interference with Correlated Photons from an Integrated Microresonator. Phys. Rev. Lett. 124 (14), 143601. doi:10.1103/PhysRevLett.124.143601
Kaneda, F., Oikawa, J., Yabuno, M., China, F., Miki, S., Terai, H., et al. (2020). Spectral Characterization of Photon-Pair Sources via Classical Sum-Frequency Generation. Opt. Express 28 (26), 38993. doi:10.1364/oe.412448
Khodadad Kashi, A., and Kues, M. (2021). Spectral Hong-Ou-Mandel Interference between Independently Generated Single Photons for Scalable Frequency‐Domain Quantum Processing. Laser Photon. Rev. 15 (5), 2000464–2000466. doi:10.1002/lpor.202000464
Torres-Company, V., Leaird, D. E., and Weiner, A. M. (2011). Dispersion Requirements in Coherent Frequency-To-Time Mapping. Opt. Express 19 (24), 24718. doi:10.1364/oe.19.024718
Lu, H.-H., Odele, O. D., Leaird, D. E., and Weiner, A. M. (2018). Arbitrary Shaping of Biphoton Correlations Using Near-Field Frequency-To-Time Mapping. Opt. Lett. 43 (4), 743. doi:10.1364/ol.43.000743
Mahjoubfar, A., Churkin, D. V., Barland, S., Broderick, N., Turitsyn, S. K., and Jalali, B. (2017). Time Stretch and its Applications. Nat. Photon 11 (6), 341–351. doi:10.1038/nphoton.2017.76
Metcalf, B. J., Thomas-Peter, N., Spring, J. B., Kundys, D., Broome, M. A., Humphreys, P. C., et al. (2013). Multiphoton Quantum Interference in a Multiport Integrated Photonic Device. Nat. Commun. 4. doi:10.1038/ncomms2349
Meyer-Scott, E., Montaut, N., Tiedau, J., Sansoni, L., Herrmann, H., Bartley, T. J., and Silberhorn, C. (2017). Limits on the Heralding Efficiencies and Spectral Purities of Spectrally Filtered Single Photons from Photon-Pair Sources. Phys. Rev. A. 95 (6), 1–8. doi:10.1103/PhysRevA.95.061803
Nguyen, D. M., Godin, T., Toenger, S., Combes, Y., Wetzel, B., Sylvestre, T., et al. (2013). Incoherent Resonant Seeding of Modulation Instability in Optical Fiber. Opt. Lett. 38 (24), 5338. doi:10.1364/ol.38.005338
Puckett, M. W., Liu, K., Chauhan, N., Zhao, Q., Jin, N., Cheng, H., et al. (2021). 422 Million Intrinsic Quality Factor Planar Integrated All-Waveguide Resonator with Sub-MHz Linewidth. Nat. Commun. 12 (1), 1–8. doi:10.1038/s41467-021-21205-4
Schwartz, M., Schmidt, E., Rengstl, U., Hornung, F., Hepp, S., Portalupi, S. L., et al. (2018). Fully On-Chip Single-Photon Hanbury-Brown and Twiss Experiment on a Monolithic Semiconductor-Superconductor Platform. Nano Lett. 18 (11), 6892–6897. doi:10.1021/acs.nanolett.8b02794
Silva, B., Sánchez Muñoz, C., Ballarini, D., González-Tudela, A., De Giorgi, M., Gigli, G., et al. (2016). The Colored Hanbury Brown-Twiss Effect. Sci. Rep. 6, 1–9. doi:10.1038/srep37980
Valencia, A., Chekhova, M. V., Trifonov, A., and Shih, Y. (2002). Entangled Two-Photon Wave Packet in a Dispersive Medium. Phys. Rev. Lett. 88 (18), 1836011–1836014. doi:10.1103/PhysRevLett.88.183601
Wasilewski, W., Wasylczyk, P., Kolenderski, P., Banaszek, K., and Radzewicz, C. (2006). Joint Spectrum of Photon Pairs Measured by Coincidence Fourier Spectroscopy. Opt. Lett. 31 (8), 1130. doi:10.1364/ol.31.001130
Wetzel, B., Stefani, A., Larger, L., Lacourt, P. A., Merolla, J. M., Sylvestre, T., et al. (2012). Real-Time Full Bandwidth Measurement of Spectral Noise in Supercontinuum Generation. Sci. Rep. 2, 1–7. doi:10.1038/srep00882
Keywords: frequency-to-time mapping, dispersive fourier transform, spontaneous parametric processes, joint spectral intensity, coincidence to accidental ratio, Hanbury Brown and Twiss measurement
Citation: Khodadad Kashi A, Sader L, Haldar R, Wetzel B and Kues M (2022) Frequency-to-Time Mapping Technique for Direct Spectral Characterization of Biphoton States From Pulsed Spontaneous Parametric Processes. Front. Photonics 3:834065. doi: 10.3389/fphot.2022.834065
Received: 12 December 2021; Accepted: 10 February 2022;
Published: 02 March 2022.
Edited by:
Frank Setzpfandt, Friedrich Schiller University Jena, GermanyReviewed by:
Kasturi Saha, Indian Institute of Technology Bombay, IndiaDaniele Bajoni, University of Pavia, Italy
Copyright © 2022 Khodadad Kashi, Sader, Haldar, Wetzel and Kues. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael Kues, michael.kues@iop.uni-hannover.de
 Anahita Khodadad Kashi
Anahita Khodadad Kashi Lynn Sader
Lynn Sader Raktim Haldar
Raktim Haldar Benjamin Wetzel
Benjamin Wetzel Michael Kues
Michael Kues