- 1Department of Information Engineering, University of Brescia, Brescia, Italy
- 2CNR-INO (National Institute of Optics), Brescia, Italy
Introduction
Nonlinear science, i.e., the study of systems capable of generating new frequencies, is ubiquitous and fascinating; as opposed to linear science, where we often have well known tools to tackle a specific problem, when nonlinearity comes into play, and the whole can be more than the sum of its parts, we can seldom resort to standard techniques. Even in the non stochastic framework, the field is often unpredictable: the emergence of qualitatively new phenomena is anticipated and made welcome, offering incredible outcomes for basic and applied sciences.
Nonlinear optics is a particular and rich subset of nonlinear science. Although nonlinear effects in optics are known since a very long time, modern nonlinear optics was born with the invention of the optical maser, today known as the laser. In a seminal paper by Franken and co-workers in 1961, second harmonic generation was demonstrated by tightly focusing a pulsed ruby optical maser into crystalline quartz (Franken et al., 1961). In the following years a plethora of nonlinear effects in light-matter interaction were experimentally demonstrated and often rapidly found their way to market applications in several different fields, ranging from telecommunications to imaging for health care and characterization.
Due to the short interaction lengths between light and matter, in the early stage, nonlinear optical effects were often associated with very low efficiencies; for this reason, a very important milestone has been set moving from bulk nonlinear optics to guided wave nonlinear optics. The flourishing field of nonlinear guided wave optics started shortly after the optical fiber became a popular transmission medium (Stolen et al., 1974). This gave an incredible boost to the efficiency of nonlinear optical effects, because light-matter interaction lengths could be increased by several orders of magnitude (from few centimeters to tens of kilometers). The richness of new physics, which since then has appeared, has deeply fed this research area and, in turn, the field has given back incredible success to the researchers. For all these reasons, nonlinear optics could quickly move into the field of extreme events; just to mention only a few of the remarkable outcomes of this part of the history of nonlinear optics: the field of solitons is strongly indebted to nonlinear optics and viceversa, since optical fibers gave an ideal playground where to observe and test the properties of these fascinating waves, which were first predicted in water waves and then became, in the sixties, one incredible chapter of modern mathematical physics (Zakharov and Shabat, 1970). This is, still today, a rich and flourishing research field with important, and sometimes surprising, outcomes for optical communications and optical sensing with new fascinating phenomena like rogue waves (Dudley, 2019).
In line with what Richard Feynman said at the annual American Physical Society meeting in 1959, there is still plenty of room at the bottom, nonlinear optics, in the last 20 years, deeply dived into nanotechnologies and nanophotonics (Kauranen and Zayats, 2012; Shcherbakov et al., 2014; Carletti et al., 2015). Anelastic scattering from metallic and non metallic nanoparticles (Figure 1) is now a very hot research topic for both basic and applied science (Koshelev and Kivshar, 2020). In this framework, the interplay between periodicity and nonlinearity is a huge and still largely unexplored research field where possible applications ranges, for example, from telecommunications to healthcare and energy harvesting.
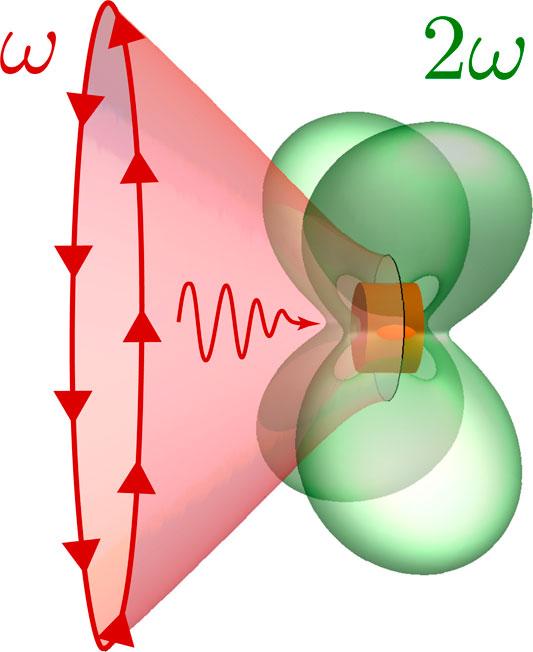
FIGURE 1. Artistic view of the second-harmonic field generated from a subwavelength dielectric nanoparticle pumped by an azimuthally polarized beam at the Bound State in the Continuum (BIC) conditions (Carletti et al., 2018).
Some keywords of today Grand Challenges in nonlinear optics are: Nonlinear guided-wave optics; Nonlinear scattering from nanoparticles; Nonlinear optics in metamaterials and metasurfaces; Nonlinear optics in dissipative systems; Nonlinear optics in time dependent media; Nonlinear topological phenomena and PT-symmetric photonic structures; Nonlinear optomechanical and optothermal coupling; Nonlinear optical circuits for machine learning and artificial intelligence; Dielectric and hybrid nanophotonics for nonlinear devices and systems: Statistical behavior, coherence, and turbulence in nonlinear optics; Quantum optics including the generation, manipulation and detection of nonclassical light via nonlinear optical interactions; Non-perturbative nonlinear optics; Ultrafast phenomena and high harmonics generation; Extreme events in nonlinear optics, including solitons, modulational instability and rogue waves; Theoretical and computational methods in nonlinear optics.
This fascinating research area is at the hearth of many key enabling devices for a plethora of applications driven by societal challenges and needs; here we aim at a holistic approach to address the theoretical, computational, physical, and engineering aspects of modern nonlinear optics.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Carletti, L., Koshelev, K., De Angelis, C., and Kivshar, Y. (2018). Giant nonlinear response at the nanoscale driven by Bound States in the Continuum. Phys. Rev. Lett. 121 (3), 033903. doi:10.1103/PhysRevLett.121.033903
Carletti, L., Locatelli, A., Stepanenko, O., Leo, G., and De Angelis, C. (2015). Enhanced second-harmonic generation from magnetic resonance in AlGaAs nanoantennas. Optic Express 23 (20), 26544–26550. doi:10.1364/OE.23.026544
Dudley, M., Genty, G., Mussot, A., Chabchoub, A., and Dias, F. (2019). Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 1 (11), 675–689. doi:10.1038/s42254-019-0100-0
Franken, P. A., Hill, A. E., Peters, C. W., and Weinreich, G. (1961). Generation of optical harmonics. Phys. Rev. Lett. 7 (4), 118–119. doi:10.1103/PhysRevLett.7.118
Kauranen, M., and Zayats, A. V. (2012). Nonlinear plasmonics. Nat. Photonics 6 (11), 737–748. doi:10.1038/nphoton.2012.244
Koshelev, K., and Kivshar, Y. (2020). Dielectric resonant metaphotonics. ACS Photonics doi:10.1021/acsphotonics.0c01315
Shcherbakov, M. R., Neshev, D. N., Hopkins, B., Shorokhov, A. S., Staude, I., Melik-Gaykazyan, E. V., et al. (2014). Enhanced third-harmonic generation in silicon nanoparticles driven by magnetic response. Nano Lett. 14 (11), 6488–6492. doi:10.1021/nl503029j
Stolen, R. H., Bjorkholm, J. E., and Ashkin, A. (1974). Phase-matched three-wave mixing in silica fiber optical waveguides. Appl. Phys. Lett. 24 (7), 308–310. doi:10.1063/1.1655195
Keywords: nonlinear optics, metamaterials and metasurfaces, high harmonic generation, nonclassical light, nonlinear devices
Citation: De Angelis C (2021) Nonlinear Optics. Front. Photon. 1:628215. doi: 10.3389/fphot.2020.628215
Received: 11 November 2020; Accepted: 17 November 2020;
Published: 26 January 2021.
Edited and reviewed by:
Vincenzo Giannini, Instituto de Estructura de la Materia (IEM), SpainCopyright © 2021 De Angelis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Costantino De Angelis, Y29zdGFudGluby5kZWFuZ2VsaXNAdW5pYnMuaXQ=
 Costantino De Angelis
Costantino De Angelis