Alexander Dejaco
Christoph Dorn
Michael Paal
Michael Gruber1- 1Department of Anesthesia, University Hospital Regensburg, Regensburg, Germany
- 2Institute of Pharmacy, University of Regensburg, Regensburg, Germany
- 3Institute for Laboratory Medicine, Hospital of the University of Munich (LMU), Munich, Germany
Accurate assessment of renal function is of great clinical and scientific importance, as it is an important pharmacokinetic covariate of pivotal drugs. The iohexol clearance is nearly identical to the glomerular filtration rate, but its determination usually requires an intravenous injection and therefore bears intrinsic risks. This motivates to showcase an “en passant” approach to quantification of renal function without additional risk or blood sampling beyond routine care using real-world data. We enrolled 37 intensive care patients who received high doses of iohexol for computed tomography imaging, and quantified series of iohexol plasma concentrations by high-performance liquid chromatography (HPLC-UV). Iohexol clearance was derived by both log-linear regression and nonlinear least squares fitting and compared to glomerular filtration rate estimated by the CKD-EPI-2021 formulas. Nonlinear fitting not only turned out to be more accurate but also more robust in handling the irregularly timed data points. Concordance of iohexol clearance against estimations based on both creatinine and cystatin C showed a slightly higher bias (−3.44 mL/min/1.73 m2) compared to estimations based on creatinine alone (−0.76 mL/min/1.73 m2), but considerably narrower limits of agreement (±42.8 vs. 56 mL/min/1.73 m2) and higher Lin’s correlation (0.84 vs. 0.72). In summary, we have demonstrated the feasibility and performance of the “en passant” variant of the iohexol method in intensive care medicine and described a working protocol for its application in clinical practice and pharmacologic studies.
1 Introduction
Correct assessment of renal function is of great importance in intensive care medicine, given that critically ill patients frequently suffer from pre-existing chronic kidney disease (CKD) and undergo acute changes in kidney function due to their current critical condition, e.g., cardiogenic shock, sepsis, or hemorrhage. The glomerular filtration rate (GFR) is the most important pharmacokinetic covariate of pivotal drugs in intensive care, including antiinfectives, anticonvulsives, or anticoagulants (Udy et al., 2017). Dose adjustments based on imprecise markers can impair efficacy and safety of such drugs and even increase mortality (Camargo et al., 2019). Beyond being beneficial for patient care, a more accurate assessment of GFR could be worthwhile to enhance the data quality of pharmacometric research in intensive care medicine.
Routine estimation of glomerular filtration (eGFR) is typically based on endogenous markers such as creatinine and cystatin C. The quantification of serum creatinine is inexpensive, but endogenous creatinine production in the critically ill is highly variable (e.g., due to loss of muscle mass), rendering estimation of GFR on its basis inaccurate and slow to respond to fluctuations. While cystatin C is a more precise marker at the population level (Inker et al., 2021), it also provides only an approximation of the true GFR (Kirwan et al., 2013), being influenced by co-morbidities such as thyroid disease, inflammation, or diabetes (Stevens et al., 2009). Also, it is more costly and therefore less commonly used.
Using a defined dose of an exogenous marker eliminates most of the imprecision inherent to endogenous markers. The iohexol method is currently one of the preferred procedures for accurate measurement of GFR (mGFR) (Delanaye et al., 2016). Iohexol is a non-ionized contrast agent with ideal characteristics for GFR determination, with low protein binding (Mützel et al., 1980) and elimination only by glomerular filtration, without tubular secretion or reabsorption (Olsson et al., 1983). Protocols for iohexol-based measurements of GFR have previously been described and thoroughly investigated (Jacobsson, 1983; Brown and O’Reilly, 1991; Erley et al., 2001; Schwartz et al., 2006; Delanaye et al., 2018). Such protocols typically use a very low dose iohexol (e.g. 5 g) and apply multiple-, four-, two-, and even one-time sampling. While iohexol is considered rather safe with a very low incidence of complications (Gaspari et al., 2018), there is a residual potential for nephrotoxicity and allergic reactions. It is, however, frequently applied in critically ill patients for radiographic studies, where the diagnostic benefit clearly outweighs the small risk.
In the present study, we investigated the feasibility of a pragmatic “en passant” application of the iohexol mGFR method to residual blood specimens from intensive care patients who received high dose iohexol contrast-enhanced computed tomography (CT) imaging as part of regular treatment. The aim was to establish a standardized protocol that can be used in clinical and pharmacological studies.
2 Materials and methods
2.1 Study design
This prospective observational feasibility study was performed at the surgical intensive care unit (ICU) of the University Hospital Regensburg, Germany, between February and June 2023. The study was registered at the German Clinical Trials Register (DRKS00031449) and was approved by the Institutional Review Board of the University of Regensburg (23-3202_1-101). Adult patients who received iohexol (Accupaque™ 755 mg/mL) for contrast-enhanced CT imaging during their intensive care treatment and had no extrarenal elimination of iohexol (e.g., by dialysis) were eligible for inclusion. In case of repeated iohexol administrations, patients were allowed to participate more than once. Patient characteristics as well as timing and dosing of iohexol injections 3 days before and after the day of inclusion were identified from the patients’ medical records. Residual samples after arterial or venous blood gas analyses in heparinized test tubes for up to 96 h after iohexol administration were collected. These whole blood samples were centrifuged at 3,000 g for 10 min and approximately 300 µL plasma specimens were obtained. Samples were stored at −20°C, and subjected to quantitative analysis within 3 months.
2.2 Bioanalytical method
Plasma iohexol was quantified using a Prominence LC20 modular HPLC system equipped with an SPD-M30A PDA detector (set to 245 nm) and LabSolution software (Shimadzu, Duisburg, Germany). The autosampler was kept at 6°C, the column oven at 40°C. Separation was performed using a CORTECS T3 2.7 µ 100 mm × 3 mm analytical column (Waters, Eschborn, Germany) preceded by a guard column protection system (Nucleoshell RP18 2.7 µ 4 mm × 3 mm, Macherey-Nagel, Düren, Germany). The mobile phase consisted of 0.1 M sodium phosphate buffer/acetonitrile 96:4 (v/v), final pH 3.0. Plasma sample treatment included deproteinization of 50 µL plasma with 200 µL 7% perchloric acid, incubation for 15 min at 4°C and centrifugation (3 min/10,500 g) to separate the precipitated proteins. An aliquot of 1 µL was injected into the HPLC. The retention time for iohexol was 3.3 min with a flow rate of 0.4 mL/min. Linearity in spiked plasma of healthy volunteers was given from 5 to 5,600 mg/L (R
2.3 Calculation of GFR
After single intravenous injection, iohexol distributes in the extracellular space within the first 2 h, after which the concentration-time curve in plasma can be described as negative mono-exponential function (Bröchner-Mortensen, 1972; Schwartz et al., 2006): C = C0e−kt. The parameters of this simple one-compartment model can be estimated by a fitting procedure. Both the slope-intercept (SI) and the nonlinear least squares (NLLS) optimization methods were applied in the present study.
SI method: After log-transformation of the concentration data, the intercept ln(C0) and slope k of a linear fit are determined by simple unweighted linear regression (Sapirstein et al., 1955). The volume of distribution is then given by
NLLS method: Estimates of the model parameters (C0 and κ) are derived by solving the unweighted least squares optimization problem iteratively using the Levenberg-Marquardt algorithm (Marquardt, 1963) on the original (non-transformed) concentration data.
Whenever multiple injections of iohexol occurred, the predicted residual concentration-time curve from the previous injection was subtracted from the subsequent data points. To correct for the neglection of the distribution phase of iohexol (the first 2 h after injection), the formula by Jødal and Brøchner-Mortensen was applied as
where Scr is serum creatinine, κ is 0.7 for females and 0.9 males, α is −0.241 for females and −0.302 for males.
where κ is 0.7 for females and 0.9 males, α is −0.219 for females and −0.144 for males (Inker et al., 2021). Creatinine and cystatin C were measured on the day of iohexol administration.
2.4 Statistics
Patient data were recorded in LibreOffice Calc 7.3, then processed and analyzed in Python 3 with JupyterLab 4.0. The simple linear regression model was programmed using the scikit-learn 1.3 library. The nonlinear model and statistics were programmed using the scipy 1.11 library, and matplotlib 3.7 was used for visualizations. The bootstrap analysis was also coded in Python 3. Descriptive data are presented as number with percentage or median with min-max range. All statistics were calculated on an untransformed original scale, unless otherwise specified. The coefficient of determination and the root mean square error (RMSE) are used to describe the model fits. Lin’s concordance correlation coefficient and Bland-Altman analysis are used to describe the agreement of the different methods to determine GFR, where bias is defined as mean difference between two variables, and the limits of agreement (LOA) as 1.96 standard deviations.
3 Results
Data from 37 intensive care patients who underwent contrast-enhanced CT scans were collected in the present study. All 37 subjects were Caucasian. Ten out of these 37 subjects had received iohexol on multiple occasions and were therefore included more than once, resulting in a total of 48 concentration-time curves with 488 plasma specimens subjected to iohexol quantification. Due to the exclusive use of residual blood samples from routine patient care, the timing of the data points was variable.
3.1 Eligible data points for the calculation of iohexol clearance
The onset of the mono-exponential elimination phase (i.e., the time at which the distribution phase of iohexol is completed) was determined by visual inspection on a semi-logarithmic scale. In several cases, distribution took place up to 2 h after iohexol injection. Inspection also showed that the concentration-time curves often began to exhibit fluctuations in slope after about 24–36 h. Therefore, to be consistent in the context of this proof of concept, only measurements between two and 24 h after the time of injection were used (140 out of the 488 plasma specimens) to estimate the model parameters. A full overview of all attained samples and their timings can be seen in Supplementary Figure S1. The initial fits revealed that the residual error variability considerably increases with increasing delay between injection of iohexol and the first concentration measurement (Supplementary Figures S2, S3). On that basis, 12 h after injection was used as the upper limit for the first time point. The delay of the first measurement was longer than that in four cases, which were therefore excluded from further analysis. This led to a final number of 27 investigated subjects and a total of n = 32 eligible concentration-time curves for calculation of the GFR, based on a total of 140 samples (median 5 (range 2–13) concentrations per curve). Table 1 shows the characteristics of the final patient cohort. Iohexol doses ranged from 52.8 to 181.2 g (median 75.5 g). The concentration-time curves of all recruited subjects are given in Figure 1A, while Figure 1B depicts the curves used as basis for calculation of the mGFR after application of the above mentioned criteria.
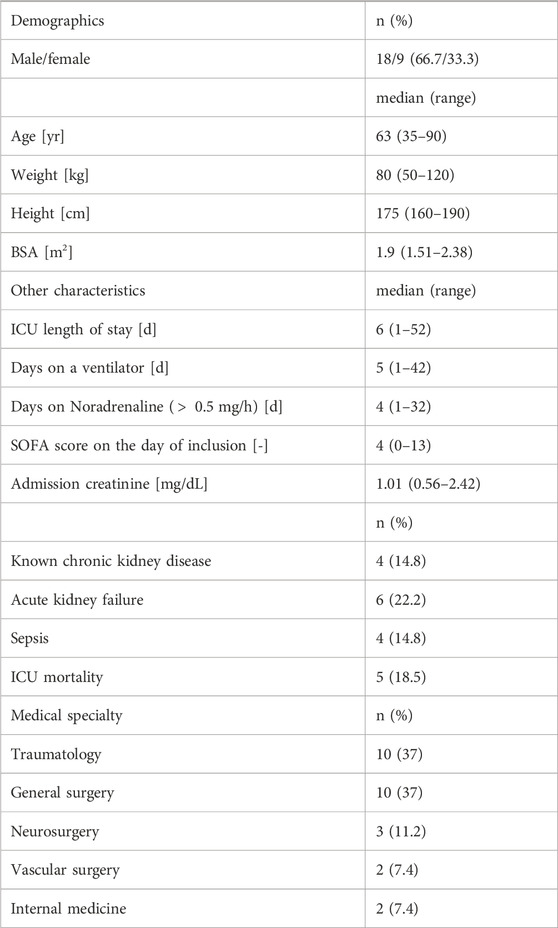
TABLE 1. Demographic and other characteristics of the subjects included in the final analysis (n = 27). Primary medical specialty is based on the main reason for ICU admission.
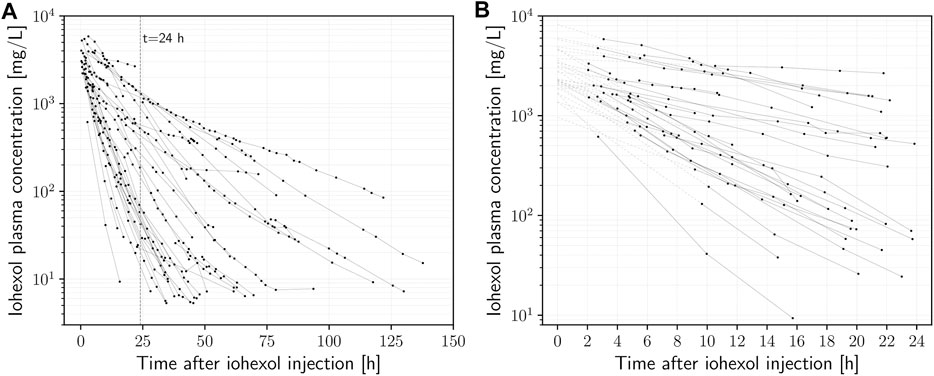
FIGURE 1. (A) Plasma iohexol semi-logarithmic concentration-time curves (n = 27) of intensive care patients receiving iohexol contrast-enhanced CT imaging. (B) Data points used for calculation of mGFR (
3.2 Fitting metrics
All n = 32 curves included in the final analysis displayed adequate fits by visual inspection on the original and semi-logarithmic scales. The pooled standardized residuals for both NLLS and SI method fits can be seen in Supplementary Figures S4, S5. NLLS fits for curves with more than two plasma concentrations yielded a median R2 of 0.995 (range 0.956–0.999) with a median RMSE of 27.48 mg/L (range 2.32–304.1 mg/L), and the SI method resulted in a median R2 of 0.991 (range 0.944–0.999) with a median RMSE of 38.72 mg/L (range 3.85–416.27 mg/L). In two instances only two plasma specimens were available (R2 = 1 and RMSE = 0). Based on the metrics and visual inspection, NLLS was deemed the more adequate and reliable method in the extrapolation of the curves backwards to t = 0 and thus more robust to determine the PK parameters, particularly C0. Figure 2 shows examples of concentration-time curves from the dataset, highlighting the superiority of NLLS in determining C0, as the SI method implicitly puts more weight on the late values. To illustrate this effect even more clearly, we resampled the data points in a bootstrapping simulation with 1,000 iterations including an additional normally distributed random error term with mean zero and a standard deviation of 50 mg/L, and plotted the variability of the predictions as a color band (Figure 2B). The superiority of NLLS can be clearly seen, with much larger uncertainty in the extrapolation of the data back to t = 0, when the SI method is used. Analyses given in the following sections are based on fits that apply the NLLS method.
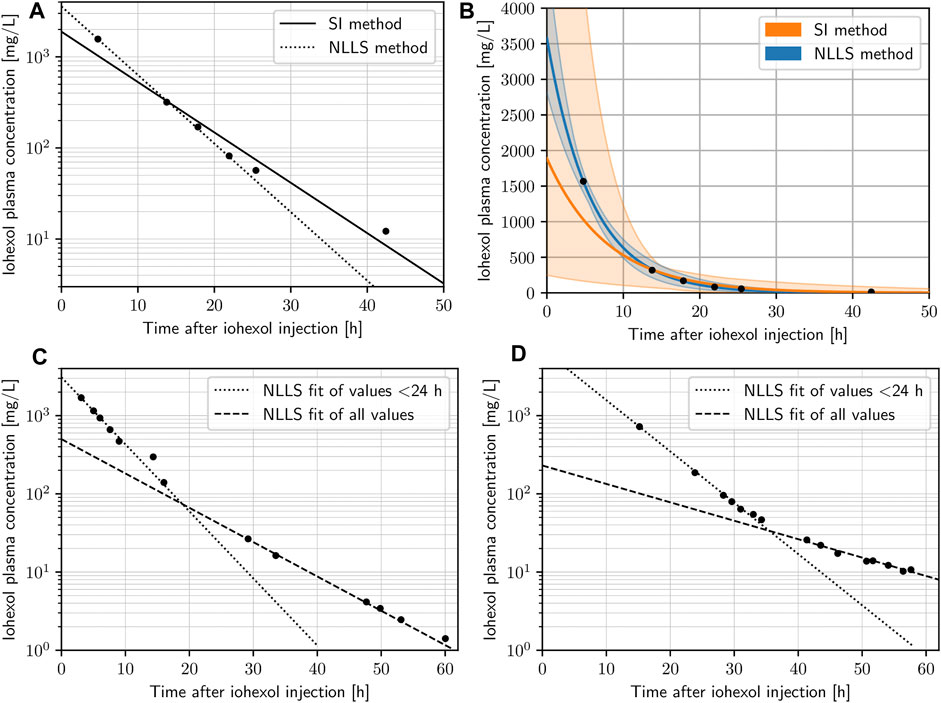
FIGURE 2. (A) Concentration-time data points of a given subject with both nonlinear least squares (NLLS) method (dotted) and the slope-intercept (SI) method (dashed) fits on a semi-logarithmic scale. (B) Concentration-time data points of a given subject with both NLLS method (blue) and SI method (orange) fits on the original scale, highlighting the level of uncertainty of predictions (color bands) based on a bootstrapping simulation of 1,000 iterations for each data point adding a normally distributed random error. (C,D) Concentration-time data points of two subjects on the semi-logarithmic scale highlighting changes in the subjects physiology with an NLLS fit using the values < 24 only (dotted) and an NLLS fit using all values (dashed).
3.3 Estimated and measured GFR
Estimations of the GFR with the CKD-EPI-2021 formulas resulted in: median 66.7 mL/min/1.73 m2 (range 20.2–123.6 mL/min/1.73 m2) for eGFRcr, and median 70.3 mL/min/1.73 m2 (range 18.9–131.6 mL/min/1.73 m2) for eGFRcr,cys. Measured GFR by means of the iohexol clearance using NLLS fitting resulted in a median of 62.6 mL/min/1.73 m2 (range 4.7–203.9 mL/min/1.73 m2), and median volume of distribution of 32.9 L (range 14.6–67 L). The distributions of the GFR and Vd are shown in Supplementary Figures S6, S7. Bland-Altman analysis yielded a bias (±LOA) of −0.76 ± 56 mL/min/1.73 m2 for mGFR against eGFRcr (Figure 3A), and of −3.44 ± 42.8 mL/min/1.73 m2 for mGFR against eGFRcr,cys (Figure 3B), with a Lin’s concordance correlation coefficient of 0.72 and 0.83, respectively.
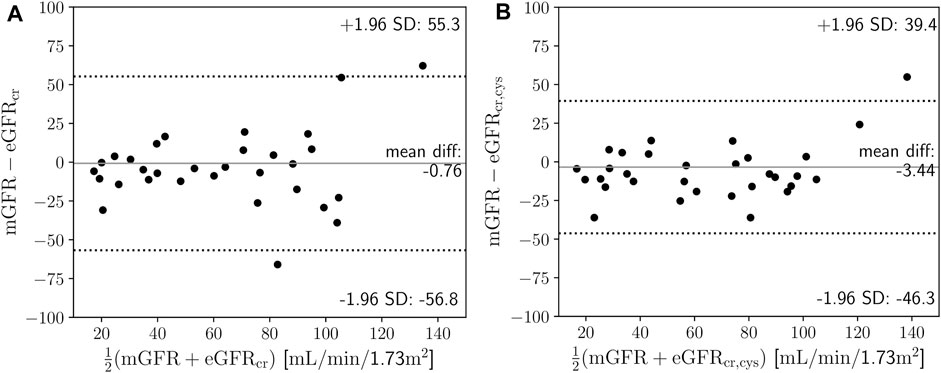
FIGURE 3. (A) Mean difference plot of measured glomerular filtration rate (mGFR) based on iohexol clearance against creatinine-based estimated glomerular filtration rate (eGFRcr) (Eq. 1). (B) Mean difference plot of mGFR based on iohexol clearance against creatinine- and cystatin C-based eGFRcr,cys (Eq. 2). SD is standard deviation.
3.4 Examples of clinically relevant findings
On inspection of the concentration-time curves (Figure 1A) and the resulting GFRs, we were able to easily identify multiple cases in which considerable deviations of the eGFR from the mGFR occurred to an extent that could also be clinically relevant. For example, one subject showed an acute deterioration in renal function, reflected by a decrease in mGFR between multiple measurements of 88% within 48 h (from 31.46 to 3.77 mL/min/1.73m2), while creatinine-based eGFR showed only a drop of 33.9% (from 54.38 to 35.92 mL/min/1.73m2). The eGFR revealed the severity of the acute renal impairment only after an additional delay of approximately 2 days, dropping by 60% from 35.92 on day two to 14.31 mL/min/1.73m2 on day four (Supplementary Table S8). As another example, a given subject showed signs of augmented renal clearance with very rapid elimination of iohexol on visual inspection of the data. The mGFR was 175.2 mL/min/1.73m2 while creatinine-based estimation with 114 mL/min/1.73m2 seemed to considerably underestimate the GFR.
4 Discussion
To our knowledge, this study is the first to demonstrate the feasibility of “en passant” quantification of the glomerular filtration rate based on the exploitation of coincidental administration of high-dose iohexol for computed tomography imaging. We detail the procedural requirements for the implementation of additive mGFR monitoring in intensive care, that could be particularly useful for clinical and pharmacometric studies. Estimated from retrospective data in our surgical ICU, a patient receives a contrast-enhanced CT scan on average every 7 days. It therefore seems quite realistic that our technique can be applied regularly to this cohort - at least once during a patient’s course of treatment in intensive care. The key advantages of our “en passant” iohexol method are twofold: Firstly, it allows the quantification of renal function utilizing exclusively residual blood samples obtained during routine clinical care, and secondly, unlike alternative methods, it does not require urine collection (e.g., creatinine urine clearance) and spares patients from the additional risks associated with intravenous injection of exogenous markers. Interestingly, opportunistic CT urography-based approaches to measure the GFR have also recently been described, showing good agreement with iohexol clearance-based mGFR (Stehlé et al., 2023), again highlighting the value of maximizing the use of data from routine patient care. CT-based protocols typically involve CT-urography exams using iopromide or iomeprol as the contrast agent, and may have advantages over other techniques. E.g., the ability to identify asymmetric renal disease (Hackstein et al., 2001; Hackstein et al., 2004; Yuan et al., 2016; You et al., 2018; Jeong et al., 2021; Stehlé et al., 2023). The widely used creatinine-based method for estimating GFR, however, is known to be quite inaccurate. It has recently been shown that it tends to overestimate GFR in intensive care patients (Sangla et al., 2020), particularly with longer length of stay in the ICU which is related to continuous loss of muscle mass (Haines et al., 2023). Also, the eGFR has been shown to underestimate GFR in the presence of augmented renal clearance (Bilbao-Meseguer et al., 2018; Collet et al., 2021), which aligns well with our findings presented in Section 3.4, while creatinine clearance can lead to significant underestimation when compared to the iohexol clearance as a gold standard. (Collet et al., 2021). On the other hand, it is known that iohexol clearance aligns closely with the actual GFR and is therefore a more reliable marker. The resulting mGFR values from our “en passant” approach showed agreement with eGFRcy,cys comparable to recent data for intensive care patients under ideal conditions, which described a bias of −11 ± 51.5 mL/min/1.73 m2 (Sangla et al., 2020), while our data showed −3.44 ± 42.8 mL/min/1.73 m2.
The classic iohexol method has long been established and validated (Erley et al., 2001; Schwartz et al., 2006; Delanaye et al., 2016; Carrara and Gaspari, 2018; Sangla et al., 2020; Dhont et al., 2022). In conventional protocols, a very low dose of iohexol (e.g. 5 g) is used and sampling is carried out according to a strict schedule. In contrast, we demonstrated the feasibility of calculating GFR by iohexol clearance after high doses and effectively randomly timed concentration measurements. The impact of the timing of concentration measurements on the accuracy of mGFR calculation is a topic of intense discussion (Stolz et al., 2010; Delanaye et al., 2016; Baklouti et al., 2021) and both extensive and limited sampling approaches have been described (Sarem et al., 2015). A crucial step is hereby the extrapolation of the concentration-time curve back to the time of iohexol injection t = 0 in order to get C0 for subsequent calculation of
It is also important to recognize that the described models of renal elimination work under the assumption of constant physiology during the investigated time-frame. This assumption needs to be considered carefully, particularly in intensive care patients where acute changes frequently occur. When reconstructing a concentration-time curve by a limited number of data points, such fluctuations will create difficulties in fitting the model to the data, and the likelihood to encounter fluctuations in patient physiology (most importantly renal function) increases with the length of the data acquisition. In our dataset, the slopes of the concentration-time curves are relatively constant during the first 24 h after injection, but then a considerable number start to experience fluctuations (Figure 1). This is best illustrated by the examples in Figures 2C, D, which show almost perfect log-linear behavior up to a point between 24 and 36 h, where their slope changes (e.g. deterioration of renal function). Notably, this also demonstrates for early detection of acute renal failure, when our method is applied.
Some limitations of the presented study should be mentioned. As a proof-of-concept, in line with the opportunistic “en passant” character of the method, sampling followed clinical requirements only, and not an optimized schedule. Particularly in the early phase (two to 12 h), data points were scarce or completely lacking in some patients (Supplementary Figure S1). The coefficient of determination and the root mean square error were used as goodness of fits metrics. While they are useful measures to identify very inappropriate fits, they are not able to reliably determine goodness of fit of nonlinear models. However, our goal was not to research and validate different fitting methods, but rather determine an adequate strategy for an “en passant” protocol. Also, as the only direct validation of our mGFR values, we compared to the eGFR and not a reference standard. However, mGFR with iohexol itself is accepted as the current gold standard when strict sampling schemes are followed. Still, larger studies involving a different, more reliable method of cross-checking renal function than the CKD-EPI-2021 for comparison are needed. In particular, the urinary clearance of iohexol seems to be an excellent candidate, with, e.g., inulin or 51Cr-EDTA clearance being reasonable alternatives. Moreover, the purpose of this study was to demonstrate the feasibility of the “en passant” approach using pragmatic real-world data, and not to validate (or invalidate) estimates of GFR. The pitfalls and imprecision of eGFR based on creatinine and also cystatin C in critically ill patients are well known (Stevens et al., 2009; Kirwan et al., 2013; Haines et al., 2023).
In conclusion, the “en passant” iohexol method is a versatile tool that could in the future be used to improve targeted therapies as well as pharmacokinetic research. E.g., to reduce unexplained variability in pharmacokinetic models, to assess protein binding of drugs (as renal drug clearance divided by iohexol clearance), or to determine the volume of distribution of iohexol within a PK study as a reference to improve our understanding the distribution of other drugs.
Based on our findings and previous guidelines for the iohexol method (Carrara and Gaspari, 2018), the following recommendations to the “en passant” approach seem reasonable: 1) The first measurement should be close to the beginning of the elimination phase at 2 h but no earlier, 2) limit the length of the interval for which the GFR is to be calculated to minimize the risk of physiologic changes occurring during the investigation, 3) NLLS should be used for curve fitting rather than the SI method, and 4) data should be visually inspected to identify acute changes in renal function. Only the first section of the concentration-time curve, i.e., before any significant fluctuations occur, should then be used for calculation of mGFR. The calculated GFR will be valid for that interval.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics statement
The study involving humans was approved by the Institutional Review Board (IRB) of the University Regensburg, Landshuterstr. 3, 93040, Regensburg, Germany, ZXRoaWtrb21taXNzaW9uQHVyLmRl. The study was conducted in accordance with the local legislation and institutional requirements. Informed consent from participants was not required in accordance with the IRB as well as legal and data protection regulations, given the strictly observational nature of the study using leftover biomaterials from routine clinical care, only.
Author contributions
AD: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Visualization, Writing–original draft, Writing–review and editing. CD: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Supervision, Writing–review and editing. MP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–review and editing. MG: Data curation, Formal Analysis, Investigation, Methodology, Resources, Supervision, Visualization, Writing–review and editing. BMG: Data curation, Methodology, Project administration, Resources, Supervision, Writing–review and editing. MGK: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Supervision, Visualization, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors declare that financial support was received for this research by the clinical scientist program of the Faculty of Medicine, University of Regensburg, and for publication of this article by the University Library of the University of Regensburg.
Acknowledgments
The authors thank the medical and nursing staff of the surgical ICU of the University Hospital Regensburg for their reliable help.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphar.2024.1346343/full#supplementary-material
References
Baklouti, S., Concordet, D., Borromeo, V., Pocar, P., Scarpa, P., and Cagnardi, P. (2021). Population pharmacokinetic model of iohexol in dogs to estimate glomerular filtration rate and optimize sampling time. Front. Pharmacol. 12, 634404. doi:10.3389/fphar.2021.634404
Bilbao-Meseguer, I., Rodríguez-Gascón, A., Barrasa, H., Isla, A., and Solinís, M. Á. (2018). Augmented renal clearance in critically ill patients: a systematic review. Clin. Pharmacokinet. 57, 1107–1121. doi:10.1007/s40262-018-0636-7
Bröchner-Mortensen, J. (1972). A simple method for the determination of glomerular filtration rate. Scand. J. Clin. Laboratory Investigation 30, 271–274. doi:10.3109/00365517209084290
Brown, S. C., and O’Reilly, P. H. (1991). Iohexol clearance for the determination of glomerular filtration rate in clinical practice: evidence for a new gold standard. J. Urology 146, 675–679. doi:10.1016/s0022-5347(17)37891-6
Camargo, M. S., Mistro, S., Oliveira, M. G., and Passos, L. C. S. (2019). Association between increased mortality rate and antibiotic dose adjustment in intensive care unit patients with renal impairment. Eur. J. Clin. Pharmacol. 75, 119–126. doi:10.1007/s00228-018-2565-7
Carrara, F., and Gaspari, F. (2018). GFR measured by iohexol: the best choice from a laboratory perspective. J. Laboratory Precis. Med. 3, 77. doi:10.21037/jlpm.2018.09.07
Collet, M., Hijazi, D., Sevrain, P., Barthélémy, R., Labeyrie, M.-A., Prié, D., et al. (2021). Evaluation of glomerular filtration rate using iohexol plasma clearance in critically ill patients with augmented renal creatinine clearance: a single-centre retrospective study. Eur. J. Anaesthesiol. 38, 652–658. doi:10.1097/EJA.0000000000001501
Delanaye, P., Ebert, N., Melsom, T., Gaspari, F., Mariat, C., Cavalier, E., et al. (2016). Iohexol plasma clearance for measuring glomerular filtration rate in clinical practice and research: a review. Part 1: how to measure glomerular filtration rate with iohexol? Clin. Kidney J. 9, 682–699. doi:10.1093/ckj/sfw070
Delanaye, P., Flamant, M., Dubourg, L., Vidal-Petiot, E., Lemoine, S., Cavalier, E., et al. (2018). Single-versus multiple-sample method to measure glomerular filtration rate. Nephrol. Dial. Transplant. 33, 1778–1785. doi:10.1093/ndt/gfx345
Dhont, E., Windels, C., Snauwaert, E., Van Der Heggen, T., de Jaeger, A., Dhondt, L., et al. (2022). Reliability of glomerular filtration rate estimating formulas compared to iohexol plasma clearance in critically ill children. Eur. J. Pediatr. 181, 3851–3866. doi:10.1007/s00431-022-04570-0
Du Bois, D., and Du Bois, E. F. (1916). Clinical calorimetry: tenth paper a formula for estimating approximate surface area when size and weight are known. Archives Intern. Med. XVII, 863–871. doi:10.1001/archinte.1916.00080130010002
Erley, C. M., Bader, B. D., Berger, E. D., Vochazer, A., Jorzik, J. J., Dietz, K., et al. (2001). Plasma clearance of iodine contrast media as a measure of glomerular filtration rate in critically ill patients. Crit. Care Med. 29, 1544–1550. doi:10.1097/00003246-200108000-00008
Gaspari, F., Thakar, S., Carrara, F., Perna, A., Trillini, M., Aparicio, M. C., et al. (2018). Safety of iohexol administration to measure glomerular filtration rate in different patient populations: a 25-year experience. Nephron 140, 1–8. doi:10.1159/000489898
Hackstein, N., Puille, M. F., Bak, B. H., Scharwat, O., and Rau, W. S. (2001). Measurement of single kidney contrast media clearance by multiphasic spiral computed tomography: preliminary results. Eur. J. Radiology 39, 201–208. doi:10.1016/s0720-048x(01)00323-0
Hackstein, N., Wiegand, C., Rau, W. S., and Langheinrich, A. C. (2004). Glomerular filtration rate measured by using triphasic helical CT with a two-point Patlak plot technique. Radiology 230, 221–226. doi:10.1148/radiol.2301021266
Haines, R. W., Fowler, A. J., Liang, K., Pearse, R. M., Larsson, A. O., Puthucheary, Z., et al. (2023). Comparison of cystatin C and creatinine in the assessment of measured kidney function during critical illness. Clin. J. Am. Soc. Nephrol. CJASN 18, 997–1005. doi:10.2215/CJN.0000000000000203
Inker, L. A., Eneanya, N. D., Coresh, J., Tighiouart, H., Wang, D., Sang, Y., et al. (2021). New creatinine- and cystatin C-based equations to estimate GFR without race. N. Engl. J. Med. 385, 1737–1749. doi:10.1056/NEJMoa2102953
Jacobsson, L. (1983). A method for the calculation of renal clearance based on a single plasma sample. Clin. Physiol. Oxf. Engl. 3, 297–305. doi:10.1111/j.1475-097x.1983.tb00712.x
Jeong, S., Park, S. B., Chang, I. H., Shin, J., Chi, B. H., Park, H. J., et al. (2021). Estimation of renal function using kidney dynamic contrast material-enhanced CT perfusion: accuracy and feasibility. Abdom. Radiol. 46, 2045–2051. doi:10.1007/s00261-020-02826-7
Jødal, L., and Brøchner-Mortensen, J. (2009). Reassessment of a classical single injection 51Cr-EDTA clearance method for determination of renal function in children and adults. Part I: analytically correct relationship between total and one-pool clearance. Scand. J. Clin. Laboratory Investigation 69, 305–313. doi:10.1080/00365510802566882
Kirwan, C. J., Philips, B. J., and Macphee, I. A. M. (2013). Estimated glomerular filtration rate correlates poorly with four-hour creatinine clearance in critically ill patients with acute kidney injury. Crit. Care Res. Pract. 2013, 406075. doi:10.1155/2013/406075
Marquardt, D. W. (1963). An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Industrial Appl. Math. 11, 431–441. doi:10.1137/0111030
Mützel, W., Siefert, H. M., and Speck, U. (1980). Biochemical-pharmacologic properties of iohexol. Acta Radiol. Suppl. 362, 111–115. doi:10.1177/0284185180021362s20
Olsson, B., Aulie, A., Sveen, K., and Andrew, E. (1983). Human pharmacokinetics of iohexol. A new nonionic contrast medium. Investig. Radiol. 18, 177–182. doi:10.1097/00004424-198303000-00015
Pottel, H., Schaeffner, E., Ebert, N., van der Giet, M., and Delanaye, P. (2021). Iohexol plasma clearance for measuring glomerular filtration rate: effect of different ways to calculate the area under the curve. BMC Nephrol. 22, 166. doi:10.1186/s12882-021-02376-0
Sangla, F., Marti, P. E., Verissimo, T., Pugin, J., de Seigneux, S., and Legouis, D. (2020). Measured and estimated glomerular filtration rate in the ICU: a prospective study. Crit. Care Med. 48, e1232–e1241. doi:10.1097/CCM.0000000000004650
Sapirstein, L. A., Vidt, D. G., Mandel, M. J., and Hanusek, G. (1955). Volumes of distribution and clearances of intravenously injected creatinine in the dog. Am. J. Physiology 181, 330–336. doi:10.1152/ajplegacy.1955.181.2.330
Sarem, S., Nekka, F., Ahmed, I. S., Litalien, C., and Li, J. (2015). Impact of sampling time deviations on the prediction of the area under the curve using regression limited sampling strategies. Biopharm. Drug Dispos. 36, 417–428. doi:10.1002/bdd.1951
Schwartz, G. J., Furth, S., Cole, S. R., Warady, B., and Muñoz, A. (2006). Glomerular filtration rate via plasma iohexol disappearance: pilot study for chronic kidney disease in children. Kidney Int. 69, 2070–2077. doi:10.1038/sj.ki.5000385
Stehlé, T., Wei, F., Brabant, S., Luciani, A., Grimbert, P., Prié, D., et al. (2023). Glomerular filtration rate measured based on iomeprol clearance assessed at CT urography in living kidney donor candidates. Radiology 309, e230567. doi:10.1148/radiol.230567
Stevens, L. A., Schmid, C. H., Greene, T., Li, L., Beck, G. J., Joffe, M., et al. (2009). Factors other than glomerular filtration rate affect serum cystatin C levels. Kidney Int. 75, 652–660. doi:10.1038/ki.2008.638
Stolz, A., Hoizey, G., Toupance, O., Lavaud, S., Vitry, F., Chanard, J., et al. (2010). Evaluation of sample bias for measuring plasma iohexol clearance in kidney transplantation. Transplantation 89, 440–445. doi:10.1097/TP.0b013e3181ca7d1b
Udy, A. A., Dulhunty, J. M., Roberts, J. A., Davis, J. S., Webb, S. A. R., Bellomo, R., et al. (2017). Association between augmented renal clearance and clinical outcomes in patients receiving β-lactam antibiotic therapy by continuous or intermittent infusion: a nested cohort study of the BLING-II randomised, placebo-controlled, clinical trial. Int. J. Antimicrob. Agents 49, 624–630. doi:10.1016/j.ijantimicag.2016.12.022
You, S., Ma, X., Zhang, C., Li, Q., Shi, W., Zhang, J., et al. (2018). Determination of single-kidney glomerular filtration rate (GFR) with CT urography versus renal dynamic imaging Gates method. Eur. Radiol. 28, 1077–1084. doi:10.1007/s00330-017-5061-z
Yuan, X., Zhang, J., Tang, K., Quan, C., Tian, Y., Li, H., et al. (2016). Determination of glomerular filtration rate with CT measurement of renal clearance of iodinated contrast material versus 99mTc-DTPA dynamic imaging “gates” method: a validation study in asymmetrical renal disease. Radiology 282, 552–560. doi:10.1148/radiol.2016160425
Keywords: measured glomerular filtration rate (mGFR), estimated glomerular filtration rate (eGFR), intensive care medicine (ICM), contrast-enhanced computed tomography imaging, “en passant” iohexol clearance, pharmacokinetic studies
Citation: Dejaco A, Dorn C, Paal M, Gruber M, Graf BM and Kees MG (2024) Determination of glomerular filtration rate “en passant” after high doses of iohexol for computed tomography in intensive care medicine—a proof of concept. Front. Pharmacol. 15:1346343. doi: 10.3389/fphar.2024.1346343
Received: 29 November 2023; Accepted: 16 January 2024;
Published: 01 February 2024.
Edited by:
Edgar Jaimes, Memorial Sloan Kettering Cancer Center, United StatesReviewed by:
Nahid Tabibzadeh, Assistance Publique Hopitaux De Paris, FranceKaty Sanchez-Pozos, Hospital Juárez de México, Mexico
Copyright © 2024 Dejaco, Dorn, Paal, Gruber, Graf and Kees. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander Dejaco, YWxleGFuZGVyLmRlamFjb0BrbGluaWsudW5pLXJlZ2Vuc2J1cmcuZGU=