- 1Department of Health Statistics, School of Public Health, Shanxi Medical University, Taiyuan, Shanxi, China
- 2School of Pharmacy, Shanxi Medical University, Taiyuan, China
Background: Topical lidocaine microemulsion preparations with low toxicity, low irritation, strong transdermal capability and convenient administration are urgently needed.
Methods: Box-Behnken design was performed for three preparation conditions of 5% lidocaine microemulsions: mass ratio of the mass ratio of surfactant/(oil phase + surfactant) (X1), the mass ratio of olive oil/(α-linolenic acid + linoleic acid) (X2) and the water content W% (X3). Then, five multi-objective genetic algorithms were used to optimize the three evaluation indices to optimize the effects of lidocaine microemulsion preparations. Finally, the ideal optimization scheme was experimentally verified.
Results: Non-dominated Sorting Genetic Algorithm-II was used for 30 random searches. Among these, Scheme 2: X1 = 0.75, X2 = 0.35, X3 = 75%, which resulted in Y1 = 0.17 μg/(cm2·s) and Y2 = 0.74 mg/cm2; and the Scheme 19: X1 = 0.68, X2 = 1.42, X3 = 75% which resulted in Y1 = 0.14 μg/(cm2·s) and Y2 = 0.80 mg/cm2, provided the best matches for the objective function requirements. The maximum and average fitness of the method have reached stability after 3 generations of evolution. Experimental verification of the above two schemes showed that there were no statistically significant differences between the measured values of Y1 and Y2 and the predicted values obtained by optimization (p > 0.05) and are close to the target value.
Conclusion: Two lidocaine microemulsion preparation protocols were proposed in this study. These preparations resulted in good transdermal performance or long anesthesia duration, respectively.
1 Introduction
Lidocaine is widely used in clinical local anesthetic drugs (Jiamin et al., 2013). Preparation as a surface anesthetic with strong penetrating ability can promote rapid pain relief, overcome the first-pass effect of the liver, and reduce pain following laser cosmetic surgery, dermatological surgery, and puncture examination, resulting in better outcomes. Microemulsion is a novel transdermal drug delivery preparation. Microemulsions are simple to prepare and promote transdermal drug absorption, improve drug solubility and stability, and reduce skin irritation (Tian et al., 2012). Microemulsions are the preferred type of preparation for local anesthetic drugs. Microemulsions are transparent or translucent, thermodynamically stable colloidal systems formulated with an oil phase, water, surfactant, and cosurfactant (Callender et al., 2017). Preparation of microemulsions generally requires a chemically stable oil phase, in which the drug is soluble. In addition, microemulsions must support penetration and association of the drug with the surfactant molecules (Heuschkel et al., 2008). Long chain triglycerides of vegetable origin such as hemp oil, cottonseed oil, and soybean oil are commonly used oil phases. Surfactants, also known as emulsifiers or amphoteric compounds, play an important role in formation of microemulsions through their ability to solubilize and reduce interfacial tension between the oil and water phases (Brosig et al., 2023). Surfactants can be classified as nonionic and ionic. Commonly used surfactants are lecithin (phosphatidylcholine), sodium deoxycholate (bile salt), polyoxyethlene sorbitan monolaurate (Tween 20, 40, 60, 80) and sorbitan monolaurate (Span 20, 40, 60, 80) (Bonferoni et al., 2019). Cosurfactant further reduce interfacial tension, and increase the fluidity of the interface, thereby increasing the entropy of the system. Cosurfactants may also adjust the curvature of the interfacial film by partitioning between the tails of the surfactant chains, allowing greater penetration of the oil between the surfactant tails (Flanagan and Singh, 2006; Golwala et al., 2020). Medium- or short-chain alcohols such as ethanol, ethylene glycol, propylene glycol and polyethylene glycol are commonly used as cosurfactants (Zhang et al., 2014).
Selecting the right surfactant and cosurfactant is a major step in designing a microemulsion system. However, surfactants and cosurfactant have potential to irritate or corrode tissues (Lawrence and Rees, 2000). Many surfactants irritate the skin through their relative ability to dissolve lipid membranes (Effendy and Maibach, 1995). A study by Fitsum F. Sahle showed that increased surfactant content resulted in increased epidermal irritation (Sahle et al., 2014). Therefore, reduction of surfactant content is important in topical lidocaine microemulsions to promote low toxicity, low irritation, strong transdermal properties, and convenient administration. The following key findings have driven microemulsion development: (1) Use of mixed oil as the oil phase can significantly increase the microemulsion area, thereby reducing the amount of surfactant used in the preparation process (You et al., 2014); (2) The method of mixing surfactant can effectively improve the solubility of surfactant, thus increasing the area of microemulsion, allowing for use of less surfactant (Sun et al., 2014); (3) The microemulsion area of olive oil (OL) is larger in the absence of cosurfactant than in the presence of cosurfactant under the action of mixed surfactant, and vitamin E succinate (VES) can further increase the area of microemulsion of OL (Jing et al., 2019). Based on the above research basis, the group, Prof. Tian, conducted a research on the preparation process of low surfactant, co-surfactant free lidocaine microemulsion with vitamin E succinate assisted mixed oil phase.
During the development process, we evaluated the effectiveness of lidocaine microemulsion preparation using the following three indicators: steady-state penetration rate, skin retention and microemulsion particle size. Steady-state permeation rate and skin retention are two important parameters related to transdermal drug delivery, which are commonly used to study and evaluate drug penetration and absorption in the skin. Among them, steady state permeation rate is the rate at which a drug passes through the membrane or interface of an organism or drug delivery system to reach a steady state. This parameter is important for determining efficiency and control of drug transdermal delivery because it can be used to estimate the rate of drug absorption in the skin. Skin retention refers to the amount of drug that remains in skin tissue after a certain period of time. This parameter is used to evaluate the residence time of drugs on the skin. The amount of skin retention is crucial for evaluation of local treatment and skin irritation. Therefore, this study required multi-objective optimization (Bansal et al., 2021) to optimize microemulsion preparation conditions for the three objectives simultaneously. However, traditional multi-objective optimization methods such as contour plots (Li et al., 2011; Patel et al., 2014), multi-objective weighting (Horn et al., 1994; Augusto et al., 2006), goal programming (Horn et al., 1994; Tamiz et al., 1998; Corne et al., 2000), the constraint method (Haimes et al., 1971) and the minimax method (Li and Li, 1996) can only provide an unique optimal solution. However, these approaches violate the principle of multi-objective optimization and is highly subjective in assigning target weights. Therefore, we need to coordinate and compromise among the sub-objectives to optimize each sub-objective (Xunxue, 2006).The genetic algorithm approach (Holland, 1975; Farhang-Mehr et al., 2002) is suitable for optimizing complex multi-objective, nonlinear systems with good global search performance. Genetic algorithms can obtain a set of solutions in each run such that each target is optimal, and no other solution in the search space is superior. This result is called the Pareto non-inferior solution set (De Jong, 1975; Konak et al., 2006; Xunxue, 2006; Bansal et al., 2021). As a result, researchers can be provided with a variety of alternative, uncontrolled optimal solutions.
In this study, five multi-objective genetic algorithms were used to optimize the preparation conditions for a lidocaine microemulsion. The optimization effects of the five genetic algorithms were compared to select the relatively optimal preparation scheme, and the most ideal scheme was experimentally verified to determine the optimal preparation conditions of a lidocaine microemulsion formulation.
2 Materials and methods
2.1 Materials
The test materials and chemical sources are detailed in the paper “Design, optimization and evaluation of cosurfactant free microemulsion-based hydrogel with low surfactant for enhanced transdermal delivery of lidocaine” published in International Journal of Pharmaceutics by our group in August 2020 (Zhang et al., 2020).
2.2 Preparation of lidocaine microemulsions
The lidocaine microemulsion is comprised of lidocaine 5% (w/w), Alpha-linolenic acid (ALA), linoleic acid (LA), OL, VES, Cremophor RH40, sorbitan monooleate 80 (Span 80), and water.
Preparation of mixed oil phase (O) was performed as follows: ALA and LA were mixed at a 1:4 ratio. This mixture was then mixed with OL at 1:4, 1:1, and 4:1 to obtain mixed oils O1, O2 and O3, respectively. Vitamin E succinate was used as the auxiliary oil, and complexes of O1-VES, O2-VES and O3-VES (6:1 w/w) were used as the oil phase, which significantly increased the microemulsion area, allowing for reduced amount of surfactant.
Preparation of mixed surfactant (S) was performed as follows: RH40 and Span 80 were mixed at a 5:1 (w/w) ratio. This allowed for improved the solubility of the surfactant, increased microemulsion area, and reduced the amount of surfactant.
Microemulsions containing lidocaine were prepared by dissolving lidocaine 5% (w/w) in a mixture of different proportions of O and S at room temperature, then slowly adding the appropriate amount of water with magnetic stirring.The mass ratio of mixed oil phase to mixed surfactant, the weight ratio of oil phase mixing, and the water content as lidocaine microemulsion drug delivery system were determined based on our previous study. These factors were expressed as the mass ratio of S/(O + S) (X1), the weight ratio of OL/(ALA + LA) (X2), and the water content W% (X3), respectively.
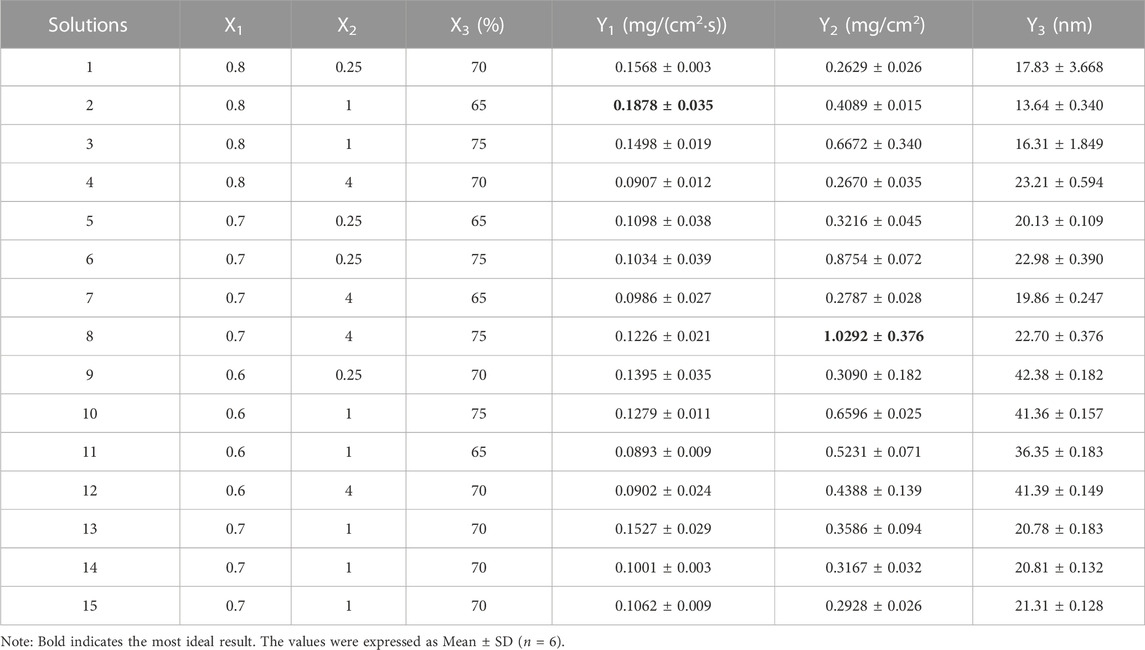
A 3-factor, 3-level Box-Behnken design was used for the above factors, with a total of 15 test protocols, each replicated six times. The levels of X1, X2, and X3 were 0.6–0.8, 0.25–4, and 65%–75%, respectively. Steady-state permeation rate (Y1), skin retention (Y2), and microemulsion particle size (Y3) were used as evaluation indices to evaluate the effects of the preparation process. A larger Y1 value results in better microemulsion transdermal properties, and a larger Y2 value results in longer duration of anesthetic effects. The Y3 must be less than 100 nm to guarantee the transdermal properties of the microemulsion. The steady-state permeability, skin retention, and particle size of the lidocaine microemulsions are shown in Table 1. Although the microemulsion particle size (Y3) met the requirement of less than 100 nm in all 15 protocols, the steady-state permeation rate (Y1) and skin retention (Y2) were not simultaneously optimal in the test results. Therefore, the preparation process conditions must be optimized using mathematical modeling combined with a multi-objective optimization approach to optimize Y1 and Y2 simultaneously.
2.3 Methods of model building
Since the microemulsion particle sizes were all less than 100 nm, Y3 was no longer modeled. Steady-state permeation rate (Y1) and skin retention (Y2) were used as dependent variables, and the mass ratio of S/(O + S) (X1), weight ratio of OL/(ALA + LA) (X2), and W% (X3) were used as independent variables. Quadratic polynomial models were developed for Y1 and Y2 as the objective functions for the multi-objective optimization of process conditions.
The fit of the model is determined by the coefficient of determination (R2). R2 is an indicator for evaluating the effectiveness of model fitting, which estimates how well the fitted model fits the observed values. An R2 of 1 indicates that the predicted values of the model exactly match the actual values, and values closer to 1 indicate high accuracy.
The model expressions are as follows:
(i < j, m is the number of factors)
2.4 Multi-objective genetic algorithms
A quadratic polynomial full model established by Y1 and Y2 are set as the objective functions of multi-objective optimization, and the two objective functions are set to be maximized. The ranges of the three factors were set as X1: 0.6–0.8, X2: 0.25–4.0 and X3: 65%–75%. Five multi-objective genetic algorithms, detailed in Sections 2.4.1–2.4.5, were used to optimize the drug delivery system.
2.4.1 Vector evaluated genetic algorithm
Vector Evaluated Genetic Algorithm (VEGA) (Schaffer, 1985; Xunxue and Chuang, 2005; Dias and De Vasconcelos, 2002) is a population-based non-Pareto method (Dan and Rui, 2004). This method uses a proportional selection mechanism, which is superior to a single-objective algorithm. The principle of VEGA is to generate a corresponding subpopulation for each sub-objective function. If the number of sub-objectives of a multi-objective problem is k, the population needs to be randomly and equally divided into k subpopulations of equal size, where the size of each subpopulation is N/k (N is the size of entire population). Each sub-objective function completes selection, evaluation, and operation in its corresponding subpopulation independently, then forms a new group for crossover and variation operation. Therefore, the process of “splitting, juxtaposition, evaluation, selection, and merging”is executed in a cycle, resulting in a non-inferior solution to the problem.
2.4.2 Multiple objective genetic algorithm
Multiple Objective Genetic Algorithm (MOGA) (Fonseca and Fleming, 1993) ranks each individual in the population using the concept of “Pareto Optimal Individuals”, so that the best individuals values in the population have a greater chances to be inherited by the next-generation population. Following a specified number of generations of cycles, the optimal solution of the multi-objective optimization problem can finally be searched. The algorithm flow of MOGA is as follows: an initial population p with sample number N is randomly generated. After the non-dominated sorting, the first generation population Q is generated by cross-variance and other operations. Then, the parent population p is merged with the child population Q to generate the second generation population, and the non-dominated set is constructed by non-dominated sorting and calculating the distance between individuals. A new population is generated by crossover and mutation, and the cycle is repeated until the termination condition is satisfied. Finally, the distance between individuals is calculated, and the optimal alternative is obtained by reordering the fitness according to the base.
2.4.3 Niched pareto genetic algorithm
Niched Pareto Genetic Algorithm (NPGA) (Fonseca and Fleming, 1993; Horn et al., 1994) uses a tournament selection mechanism to select the best individuals for subsequent evolutionary reproduction, while incorporating niche technique to maintain the diversity and homogeneity of the distribution of individuals in the candidate solution set. The selection mechanism of NPGA is a combination of tournament selection and external auxiliary selection. After obtaining the initial population, 10 individuals are randomly selected to form the external comparison set CS. In addition, two individuals, pi and pj, are randomly selected to make a two-by-two comparison with the above 10 individuals. If one of these is superior to the comparison set and the other is inferior to the comparison set, the former is selected and copied. If both randomly selected individuals are superior or inferior to the external comparison set, the better of the two is selected using the sharing mechanism. That is, according to the number of niches, focus on selecting individuals with the smallest number of niche for replication to obtain the optimal solution with uniform distribution on the front end.
2.4.4 Non-dominated sorting genetic algorithm
Non-dominated Sorting Genetic Algorithm (NSGA) (Srinivas and Deb, 1994) uses non-dominated sorting as the solution sorting criterion, and the fitness is reasonably assigned to a diverse search space (Heris et al., 2011). In this approach, all individuals are graded at different levels, and before performing the selection operator, the population is graded and sorted according to dominance and non-dominance relationships. To maintain population diversity, all individuals in the population are assigned a virtual fitness value (generally proportional to the population size), and individuals at the same level have the same virtual fitness value, thus ensuring that individuals at the same level have the same probability of replication. This group of graded individuals is then ignored, and the other individuals in the population are graded again according to the dominance non-dominance relationship and given new virtual fitness values that are less than the values in the previous level. This operation is repeated for the remaining individuals until all individuals in the population are graded.
2.4.5 Non-dominated sorting genetic algorithm-II
Non-dominated Sorting Genetic Algorithm-II (NSGA-II) (Deb et al., 2000) greatly reduces computational complexity by introducing a fast non-dominated sorting algorithm, using an elite strategy design to increase the sample space, and using individual crowding and crowding comparison operators as grading criteria. This can provide a multi-objective optimized Pareto non-inferiority solution set and ensure the diversity of the population. The algorithm process of NSGA-II is as follows. First, the parent population Pn is used to generate the child population Qn, and the two populations are combined to form a population Rn of size 2n. A non-inferiority classification operation is performed on this population. Then, the crowding degree of all individuals in each non-inferior class is calculated. The next-generation population Pn+1 is generated according to the principle of crowding selection operator, and the number of evolutionary generations is n+1. Then, whether the number of evolutionary generations of this population is greater than the maximum number of evolutionary generations is determined. If yes, then the algorithm ends, otherwise it continues to evolve. The algorithm continues to evolve until it reaches the maximum number of evolutionary generations specified.
2.5 Optimization parameters
The parameters of the five multi-objective genetic algorithms were set as follows: the initial population was 30, the probability crossover was 0.8, the probability of mutation was 0.05, the maximum evolutionary generation was 100, and 30 random searches were performed to give the Pareto non-inferiority solution set.
2.6 Measurement of steady-state permeation rate, skin retention, and particle size
The abdominal skin (free of subcutaneous fat and adherent tissue) of guinea pigs was rinsed with saline and fixed with the horned layer facing upward between the supply and receiving cell. We added 1.0 g of each formulation was placed on the skin surface of the supply cells, and 15 mL of the receiving solution consisting of phosphate buffered saline and ethanol was placed under a magnetic rotor (set to 350 rpm) in the receiving cells. The temperature was maintained at 37°C ± 0.1°C. Samples (2.0 mL) were taken at predetermined time points (0.5, 1.0, 2.0, 4.0, 6.0, 8.0, 10.0, and 12.0 h), and filtered through 0.45-µm microporous filtration membrane. The cells were then replenished with an equal amount of fresh receiving solution. The filtrates were analyzed using high performance liquid chromatography (HPLC), the peak areas were determined, and the corresponding drug concentrations were calculated. The cumulative permeation of the drug was then calculated based on the transdermal diffusion area, the drug concentration at different time points, and the volumes of the receiving pool and the sampling volume. The slope of the linear regression curve of the cumulative permeation of the drug against t (h) represents the steady-state permeation rate.
After the skin permeability measurement was completed, the skin was rinsed with fresh receiving solution. The skin was dried on filter paper, then cut and soaked in methanol (4 mL) for 24 h to fully extract the drug remaining in the skin. The concentration of lidocaine in the supernatant was then analyzed using HPLC to determine skin retention.
The microemulsion was diluted 50-fold with distilled water and particle size was determined using a Nano Zetasizer (ZS90, Malvern Instruments, Worcestershire, UK).
2.7 Statistical software
Model establishment and statistical analysis of optimization results were performed using SPSS 22.0. Multi-objective genetic algorithm optimization was performed using a Matlab 2009a plug-in SGALAB toolbox bete5008 written by a member of the group, Chen, a software engineer at the University of Glasgow, United Kingdom. The average level of Pareto non-inferiority solutions and objective function values were expressed as the median and interquartile range.
3 Results
3.1 Quadratic polynomial model and model fitting results
The quadratic polynomial full model and model fit results for steady-state infiltration rate (Y1) and skin retention (Y2) are shown below. The R2 value of the two models were 0.6537 and 0.7264, respectively, which indicated that the respective variables could explain 65.4% and 72.6% of the variation in Y1 and Y2, respectively. The explanations of the respective variables of the models are high, and the models are well fitted.
3.2 Multi-objective genetic algorithm optimization results
The random search results, fitness evolution algebra, and optimal non-inferiority solution schemes of VEGA, MOGA, and NSGA were inferior to those obtained using NPGA and NSGA-Ⅱ. To remain concise, only the random search results and maximum fitness and average fitness evolution curves from NPGA and NSGA-Ⅱ, which have relatively better optimization effects, are listed in this manuscript. The optimization results of the remaining three methods are summarized in the appendix.
Our primary criterion for determining the most desirable regimen is that the regimen results in a relatively maximum steady-state penetration rate, and skin retention. On the basis of the above we would like to use less surfactant. Additionally, based on these two criteria, the amount of material in the formulation would be relatively small.
3.2.1 NPGA optimization results
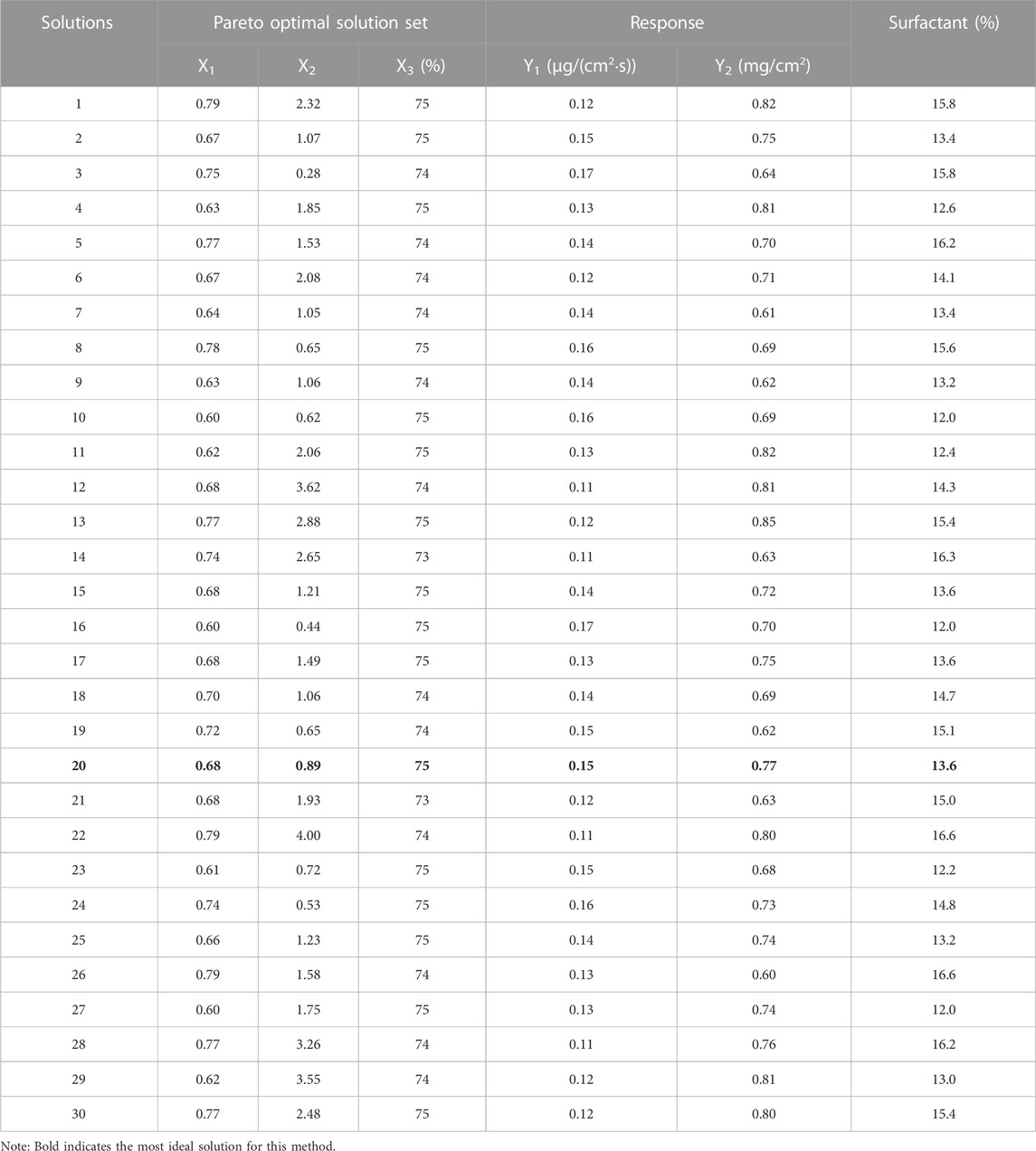
The non-inferior solution schemes obtained from the NPGA random search (30 iterations) are shown in Table 2. According to the requirements for the objective function, the optimal process conditions were selected in the Pareto solution set with X1 = 0.68, X2 = 0.89, and X3 = 75% for Scheme 20. The steady-state permeation rate and skin retention of lidocaine microemulsion were Y1 = 0.15 mg/(cm2·s) and Y2 = 0.77 mg/cm2.
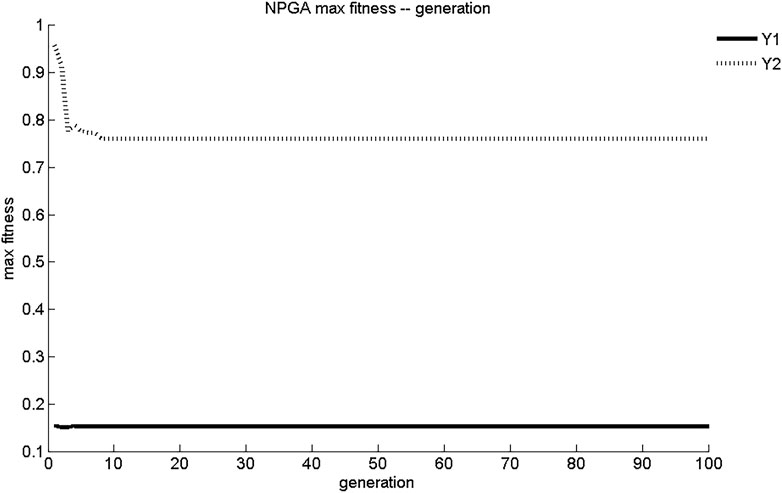
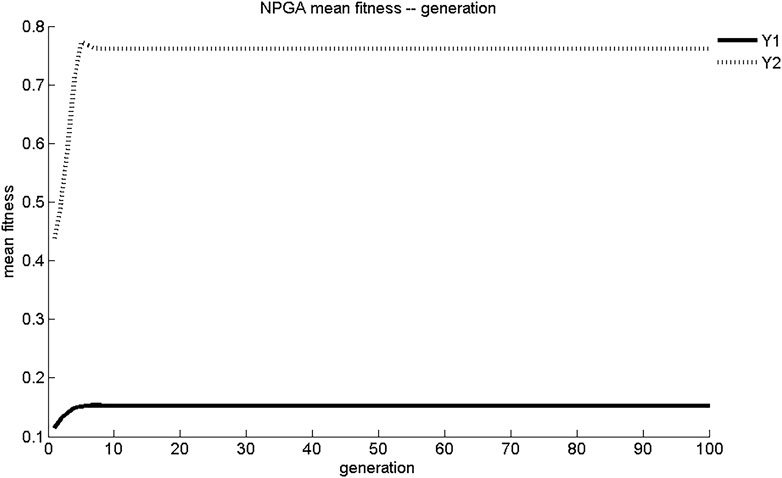
The maximum fitness and average fitness evolution curves of the two sub-objective functions obtained using NPGA optimization are shown in Figures 1, 2. The maximum fitness evolution curve is used to evaluate the convergence performance of the algorithm, reflecting the change in the solution. This is a measure of whether the algorithm can find the global optimal solution to the problem with infinite iterations. As shown in Figure 1, NPGA found the maximum fitness for Y1 and Y2 only after 7 generations of evolution. These values were 0.153 mg/(cm2·s) and 0.761 mg/cm2, respectively. The convergence of NPGA was general. The average fitness evolution curve was used to evaluate the dynamic performance of the algorithm, reflecting the change of the objective function with the best fitness and the largest value in each generation with the number of evolutionary generations. As shown in Figure 2, the objective function in the initial generations had lower adaptation and smaller objective function values. As the number of evolutionary generations increased, the fitness of the objective function increased rapidly and the objective function value increased. There was a slight degradation around five generations of evolution. After about seven generations of evolution, the values of Y1 and Y2 were stable at 0.15 mg/(cm2·s) and 0.76 mg/cm2, respectively. The dynamic performance of NPGA was average.
3.2.2 NSGA-Ⅱ optimization results
The non-inferior solution schemes obtained from 30 random searches using NSGA-II are shown in Table 3. According to the requirements for the objective function, the optimal process conditions were Scheme 2 with X1 = 0.75, X2 = 0.35, and X3 = 75% in the Pareto solution set. The corresponding steady-state permeation rate and skin retention of lidocaine microemulsion were Y1 = 0.17 mg/(cm2·s) and Y2 = 0.74 mg/cm2, respectively. Scheme 19, with X1 = 0.68, X2 = 1.42, and X3 = 75% also presented optimal process conditions to obtain Y1 = 0.14 mg/(cm2·s) and Y2 = 0.80 mg/cm2.
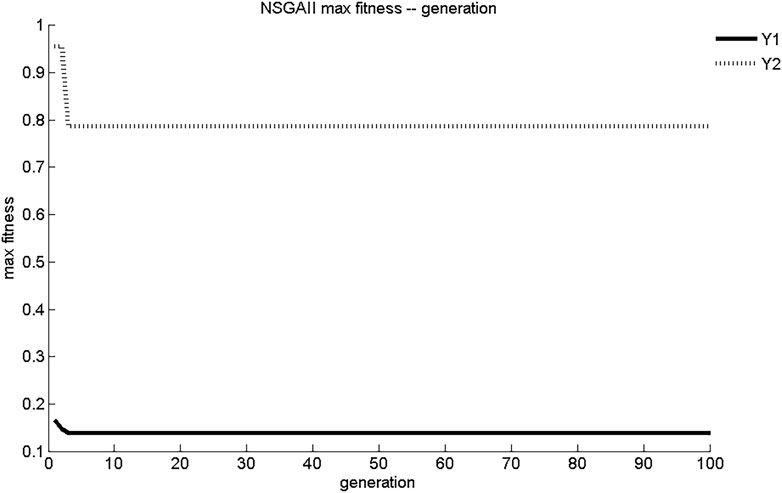
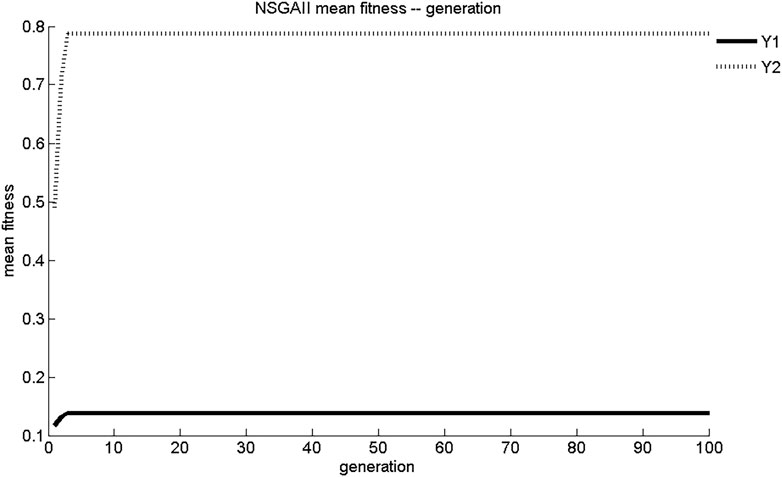
The evolution curves of maximum fitness and average fitness of the two sub-objective functions obtained by NSGA-II search are shown in Figures 3, 4. As shown in Figure 3, NSGA-II found the maximum fitness of Y1 and Y2 at the third generation of evolution, with results of 0.139 mg/(cm2·s) and 0.788 mg/cm2, respectively. The convergence of NSGA-II was better. As shown in Figure 4, the initial generations of objective function had lower adaptation and smaller objective function values. As the number of generations of evolution increased, the fitness of the objective function increases rapidly and the value of objective function increased. After three generations of evolution, the values of Y1 and Y2 stabilized at 0.14 mg/(cm2·s) and 0.79 mg/cm2, respectively. The dynamic performance of NSGA-II was better.
3.3 Comparison of five multi-objective genetic algorithms for ideal non-inferior solution schemes
According to the objective requirements of Y1 and Y2, the objective function values, maximum fitness, and average fitness evolutionary generations corresponding to the most ideal Pareto non-inferiority solution schemes in the set of five multi-objective genetic algorithms Pareto non-inferiority solutions were determined as shown in Table 4. Scheme 2 of NSGA-II: X1 = 0.75, X2 = 0.35, X3 = 75%; Scheme 19 of NSGA-II: X1 = 0.68, X2 = 1.42, X3 = 75%; and NPGA Scheme 20: X1 = 0.68, X2 = 0.89, X3 = 75% were better fits than optimal schemes determined using VEGA, MOGA, and NSGA. However, compared with NPGA, which evolved for seven generations to reach stability in maximum and average fitness, NSGA-II only required three generations, and the convergence and dynamics of the algorithm were better. The ideal Pareto solution schemes of MOGA, VEGA, and NSGA did not match the preparation process requirements and were prone to early convergence, with poor local search capability and dynamics.
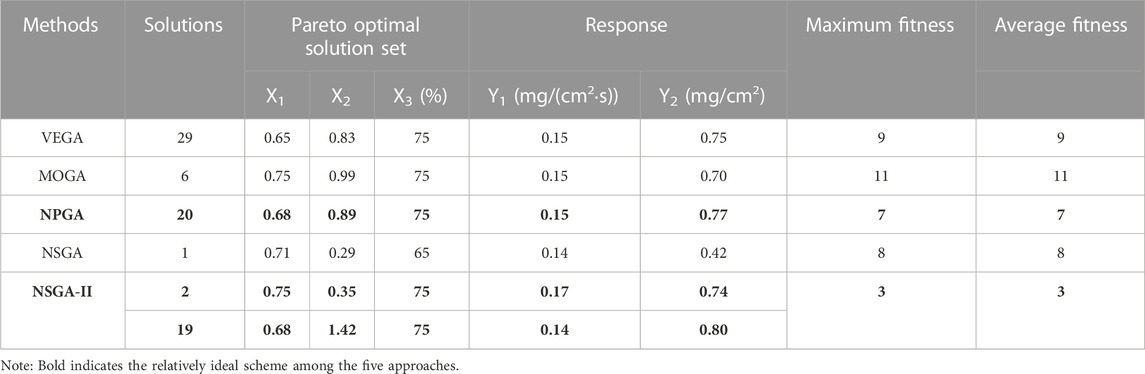
TABLE 4. Comparison of five multi-objective genetic algorithms for ideal non-inferior solution schemes.
3.4 Comparison of the search performance of five multi-objective genetic algorithms
Most of the Pareto non-inferior solutions and objective function values of the five multi-objective genetic algorithms did not have normal distributions. Therefore, the median (M) and interquartile range (IQR) were used to describe the center and variance of the solutions and objective values (Table 5). The median levels of the sub-objective function values obtained by NSGA-II optimization were
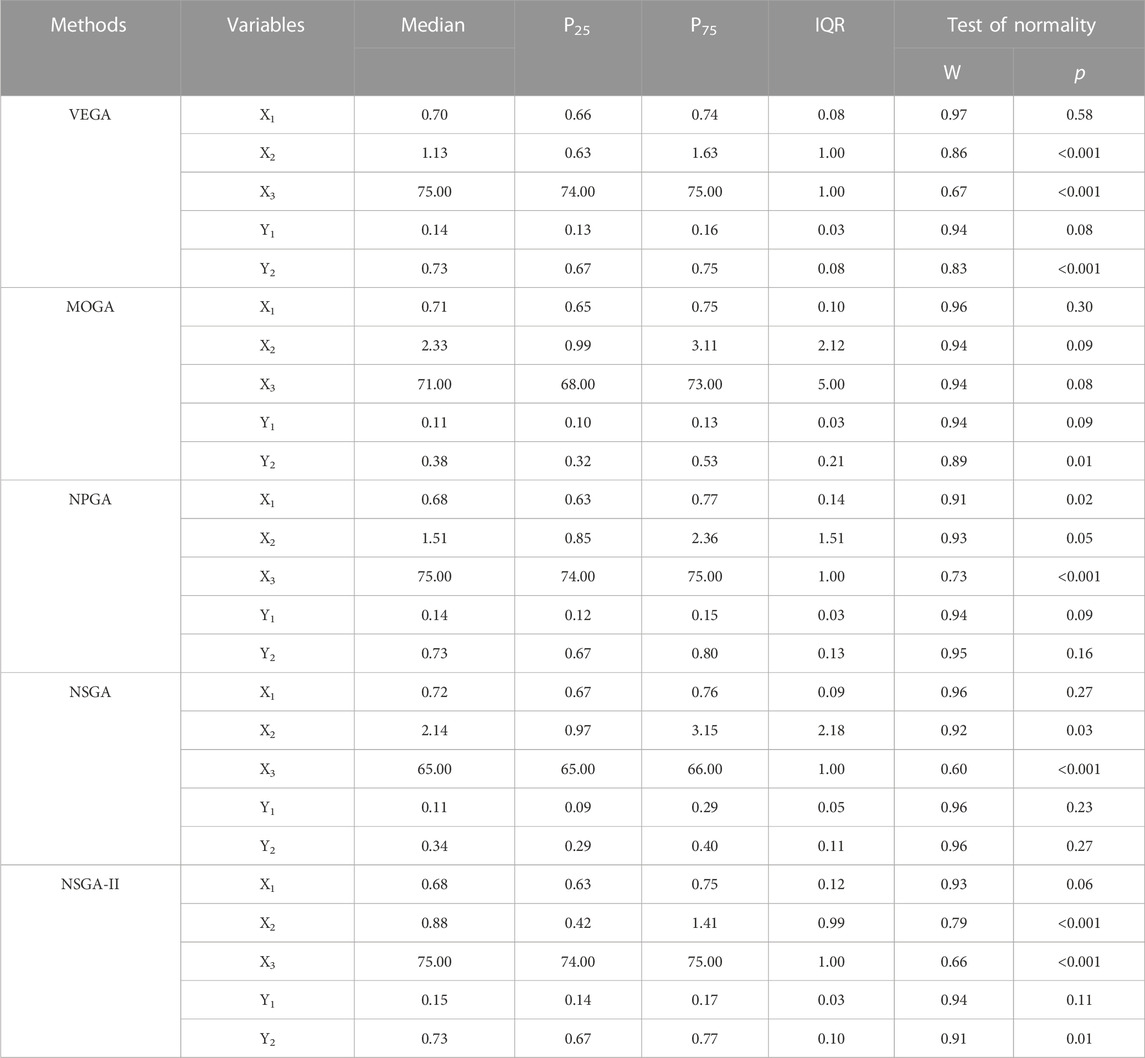
TABLE 5. The average level of objective function values and the Pareto non-inferiority solutions of five multi-objective genetic algorithm.
3.5 Experimental validation results
The Pareto non-inferior solution Scheme 2: X1 = 0.75, X2 = 0.35, X3 = 75% and Scheme 19: X1 = 0.68, X2 = 1.42, X3 = 75% obtained from NSGA-II search were selected and validated in three trials, the median and interquartile range values are shown in Table 6. The median levels of both Y1 and Y2 obtained by experimental validation were not statistically different from the target values obtained by NSGA-II search (p > 0.05). These results confirmed that the modeling and multi-objective optimization of this study were satisfactory. Therefore, both of these schemes can be used for lidocaine microemulsion preparation, and the preparation scheme according to desired preparation effects.
4 Discussion
In this study, five multi-objective genetic algorithms, VEGA, MOGA, NPGA, NSGA, and NSGA-II, were used for multi-objective optimization of steady-state penetration rate and skin retention in lidocaine microemulsion preparations. We compared the optimization results of the five multi-objective genetic algorithms in terms of the most desirable optimization scheme and the search performance of the algorithms. Then, we experimentally validated that the modeling and optimization schemes proposed in this study work matched performance. A formulator focused on better transdermal properties may choose preparation conditions with a mass ratio of S/(O + S) of 0.75, a weight ratio of OL/(ALA + LA) of 0.35, and a water content of 75%. The resulting microemulsion shows a steady-state permeation rate of 0.17μg/(cm2·s) and skin retention of 0.74 mg/cm2. The corresponding optimal microemulsion formulation determined by this scheme was 1.11% OL, 0.64% ALA, 2.54% LA, 0.71% VES, 15.00% surfactant, 5.00% lidocaine, and 75.00% water. A formulator focused on preparing microemulsions with durations of action could choose a mass ratio of S/(O + S) of 0.68, a weight ratio of OL/(ALA + LA) of 1.42, and a water content of 75%. This results in a microemulsion with a steady-state permeation rate of 0.14μg/(cm2·s) and a skin retention of 0.80 mg/cm2. The corresponding optimal microemulsion formulation determined by this scheme was 3.23% OL, 0.45% ALA, 1.81% LA, 0.91% VES, 13.60% surfactant, 5.00% lidocaine, and 75.00% water.
Many studies have aimed to optimize formulations for microemulsions in the pharmaceutical and food industries. However, the transdermal permeation rates reported in the in vitro permeability experiments of these microemulsion formulations are not satisfactory compared to the permeation rates of Scheme 2 provided in this study. For example, Patel et al. conducted a study on the effect of different mixing ratios of excipients on the in vitro permeation of ketoconazole in a microemulsion, and found that the highest permeation rate of the optimal formula was 54.65 ± 1.72 μg/cm2/h (Patel et al., 2011). In an in vitro permeation study of a topical dosage form of hesperidin, Tsai et al. determined that the optimal microemulsion formulation had a permeation rate of 46.56 μg/cm2/h (Tsai et al., 2010). Wang et al. (2019) evaluated use of microemulsions for transdermal administration of high doses of lidocaine and prepared microemulsions for experimental evaluation. The permeability flux of the microemulsion formulation was determined 500.40 ± 23.34 μg/cm2/h. In contrast, our formulations showed a higher steady-state penetration rate of lidocaine microemulsion (0.17 μg/(cm2·s)), which was significantly higher than the penetration effect of the microemulsion formulations studied above. In our preparation targeted for longer duration of action, the penetration rate of lidocaine microemulsion reached 0.14 μg/(cm2·s)
Similarly, a few studies evaluating microemulsion preparation have explored the effect of microemulsion on skin retention. Maulvi et al. prepared a lidocaine tripotassium phosphate complex microemulsion. Skin retention studies showed that the microemulsion reached a maximum retention of 350 μg/g at 2 h (Maulvi et al., 2020). Boonme et al. evaluated the properties, stability, and skin permeability and retention of microemulsions containing nicotinamide. The 24 h nicotinamide infiltration into receptor fluids was 777.46 ± 60.11 μg/cm2 (Boonme et al., 2016). Niu et al. conducted a study on microemulsion-based keratin-chitosan gel to improve skin penetration/retention and activity of curcumin. The maximum skin drug retention was 3.75 ± 0.24 μg/cm2 for this microemulsion formulation (Niu et al., 2023). Scheme 19 in our study resulted in a longer duration of action of 0.80 mg/cm2. Which was higher than the skin retention in the above study. The skin retention in Scheme 2 reached 0.74 mg/cm2. Therefore, the regimens for preparation of lidocaine microemulsions proposed in this study performed well in terms of both penetration rate and skin retention.
Most microemulsion formulations contain more than 20% of surfactant. For example, Zhao, Jiang et al. studied a microemulsion preparation of Antarctic krill oil with 24% surfactant and 8% cosurfactant (Zhao et al., 2020). Wang et al. (2019) studied the feasibility of using microemulsions containing of 28% surfactants and cosurfactants for transdermal delivery of high-dose lidocaine. Ngawhirunpat et al. (2013) studied the preparation of ketoprofen microemulsions for transdermal delivery. Among the formulations that achieved the highest skin permeation flux, the dosage of surfactant (Cremophor RH40) was 22.5%, and the dosage of cosurfactant (PEG 400) was 22.5%. Xu et al. (2016) prepared microalgae oil microemulsions without co-surfactants, but but with more than 20% surfactant. These studies show that many microemulsion formulations rely on higher amounts of surfactant and cosurfactant. In our study, Scheme 2 and Scheme 19 had surfactant content below 15% and as low as 13.6%. This result demonstrates our progress in reducing the amount of surfactant and cosurfactant in microemulsion formulations, which should reduce toxicity and skin irritation.
In conclusion, the preparation schemes proposed in this study were practical and improved upon previously developed formulations using an optimization algorithm. In addition, NSGA-II greatly reduced the number of pre-experiments necessary to optimize preparation conditions, resulted in reduced use of materials and significant cost savings. Furthermore, our study demonstrated the value of using a multi-objective optimization strategy in the pharmaceutical field.
5 Conclusion
This study proposed two sets of lidocaine microemulsion preparation. The first included a mass ratio of surfactant/(oil phase + surfactant) (X1) = 0.75, a mass ratio of olive oil/(α-linolenic acid + linoleic acid) (X2) = 0.35, and water content W% (X3) = 75%, which resulted in better transdermal performance. When X1 = 0.68, X2 = 1.42, and X3 = 75%, the microemulsion resulted in longer anesthesia duration.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics statement
The animal study was approved by the Research Medical Ethics Committee of Shanxi Medical University, China. The study was conducted in accordance with the local legislation and institutional requirements.
Author contributions
YQ: Writing–original draft. XW: Writing–review and editing. HR: Writing–review and editing. YC: Writing–review and editing. JR: Writing–review and editing. CH: Writing–review and editing. ZZ: Writing–review and editing. JL: Writing–review and editing. RZ: Writing–review and editing. YL: Writing–review and editing. QT: Writing–review and editing. LQ: Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. This research is supported by the National Natural Science Foundation of China under grant 81973155.
Acknowledgments
We thank all teachers in the statistical research office of Shanxi Medical University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphar.2023.1272454/full#supplementary-material
Abbreviations
ALA, α-linolenic acid; IQR, Interquartile-quartile range; LA, Linoleic acid; MOGA, Multiple Objective Genetic Algorithm; NPGA, Niched Pareto Genetic Algorithm; NSGA, Non-dominated Sorting Genetic Algorithm; NSGA-Ⅱ, Non-dominated Sorting Genetic Algorithm-II; OL, Olive oil; VES, Vitamin E succinate; VEGA, Vector Evaluated Genetic Algorithm.
References
Augusto, O. B., Rabeau, S., Depince, P., and Bennis, F. (2006). Multi-objective genetic algorithms: A way to improve the convergence rate. Eng. Appl. Artif. Intell. 19 (5), 501–510. doi:10.1016/j.engappai.2006.01.010
Bansal, S., Singh, M., Dubey, R. K., and Panigrahi, B. K. (2021). Multi-objective genetic algorithm based deep learning model for automated COVID-19 detection using medical image data. J. Med. Biol. Eng. 41 (5), 678–689. doi:10.1007/s40846-021-00653-9
Bonferoni, M. C., Rossi, S., Sandri, G., Ferrari, F., Gavini, E., Rassu, G., et al. (2019). Nanoemulsions for "Nose-to-Brain" drug delivery. Pharmaceutics 11 (2), 84. doi:10.3390/pharmaceutics11020084
Boonme, P., Boonthongchuay, C., Wongpoowarak, W., and Amnuaikit, T. (2016). Evaluation of nicotinamide microemulsion on the skin penetration enhancement. Pharm. Dev. Technol. 21 (1), 116–120. doi:10.3109/10837450.2014.971378
Brosig, S., Cucuzza, S., Serno, T., Bechtold-Peters, K., Buecheler, J., Zivec, M., et al. (2023). Not the usual suspects: Alternative surfactants for biopharmaceuticals. ACS Appl. Mater Interfaces 15 (29), 34540–34553. doi:10.1021/acsami.3c05610
Callender, S. P., Mathews, J. A., Kobernyk, K., and Wettig, S. D. (2017). Microemulsion utility in pharmaceuticals: Implications for multi-drug delivery. Int. J. Pharm. 526 (1-2), 425–442. doi:10.1016/j.ijpharm.2017.05.005
Corne, D. W., Knowles, J. D., and Oates, M. J. (2000). “The Pareto envelope-based selection algorithm for multiobjective optimization,” in International conference on parallel problem solving from nature (Berlin, Heidelberg: Springer-Verlag).
Dan, L., and Rui, Z. (2004). A multi-objective genetic algorithm for optimal portfolio problems. Trans. Tianjin Univ. 10 (4), 310–314.
De Jong, D. A. J. D. D. (1975). An analysis of the behavior of a class of genetic adaptive systems. Report.
Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. J. I. C. O. P. P. S. F. N. (2000). “A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II,” in Parallel problem solving from nature PPSN VI (Berlin, Heidelberg: Springer-Verlag).
Dias, A. H. F., and De Vasconcelos, J. A. J. I. T. O. M. (2002). Multiobjective genetic algorithms applied to solve optimization problems. IEEE Trans. Magnetics 38 (2), 1133–1136. doi:10.1109/20.996290
Effendy, I., and Maibach, H. I. (1995). Surfactants and experimental irritant contact dermatitis. Contact Dermat. 33 (4), 217–225. doi:10.1111/j.1600-0536.1995.tb00470.x
Farhang-Mehr, A., Azarm, S. J. S., and Optimization, M. (2002). Entropy-based multi-objective genetic algorithm for design optimization. Struct. Multidiscip. Optim. 24 (5), 351–361. doi:10.1007/s00158-002-0247-6
Flanagan, J., and Singh, H. (2006). Microemulsions: A potential delivery system for bioactives in food. Crit. Rev. Food Sci. Nutr. 46 (3), 221–237. doi:10.1080/10408690590956710
Fonseca, C. M., and Fleming, P. J. (1993). “Genetic algorithms for multiobjective optimization: Formulation, discussion and genralization,” in Proceedings of the 5th international conference on genetic algorithms (Urbana-Champaign, IL, USA: Spinger).
Golwala, P., Rathod, S., Patil, R., Joshi, A., Ray, D., Aswal, V. K., et al. (2020). Effect of cosurfactant addition on phase behavior and microstructure of a water dilutable microemulsion. Colloids Surf. B Biointerfaces 186, 110736. doi:10.1016/j.colsurfb.2019.110736
Haimes, Y. Y., Lasdon, L. S., and Wismer, D. A. J. I. T. O. S. (1971). On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Trans. Syst. Man, Cybern. 1 (3), 296–297. doi:10.1109/TSMC.1971.4308298
Heris, S., Mostapha, K., and Khaloozadeh and, H. (2011). Open- and closed-loop multiobjective optimal strategies for HIV therapy using NSGA-II. IEEE Trans. Biomed. Eng. 58, 1678–1685. doi:10.1109/TBME.2011.2110651
Heuschkel, S., Goebel, A., and Neubert, R. H. (2008). Microemulsions--modern colloidal carrier for dermal and transdermal drug delivery. J. Pharm. Sci. 97 (2), 603–631. doi:10.1002/jps.20995
Horn, J., Nafpliotis, N., and Goldberg, D. E. (1994). “A niched Pareto genetic algorithm for multi-objective optimization. Evolutionary computation,” in 1994 IEEE World Congress on Computational Intelligence., Proceedings of the First IEEE Conference on, Orlando, FL, USA, 27-29 June 1994 (IEEE).
Jiamin, L., Nan, L., Hairong, X., and Xiaoyan, D. (2013). Pharmacokinetics, release and permeate in vitro on transdermal drug delivery system. J. Logist. Univ. CAPF(Medical Sci. 22 (12), 1137–1140. doi:10.3969/j.issn.2095-3720.2013.12.033
Jing, P., Tan, X., Zhang, D., and Tian, Q. (2019). Causes of the olive oil microemulsion area increase and its application evaluation as a moisturizing antibacterial body lotion carrier. Chin. Pharm. J. 54 (11), 900–907. doi:10.11669/cpj.2019.11.009
Konak, A., Coit, D. W., Smith, A. E. J. R. E., and Safety, S. (2006). Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 91 (9), 992–1007. doi:10.1016/j.ress.2005.11.018
Lawrence, M. J., and Rees, G. D. (2000). Microemulsion-based media as novel drug delivery systems. Adv. Drug Deliv. Rev. 45 (1), 89–121. doi:10.1016/s0169-409x(00)00103-4
Li, R., and Li, Y. J. J. O. H. E. (1996). A real time control for multi-objective optimization of mix proportion of concrete. Constr. Build. Mater. 366, 129928. doi:10.1016/j.conbuildmat.2022.129928
Li, W., Yi, S., Wang, Z., Chen, S., Xin, S., Xie, J., et al. (2011). Self-nanoemulsifying drug delivery system of persimmon leaf extract: Optimization and bioavailability studies. Int. J. Pharm. 420 (1), 161–171. doi:10.1016/j.ijpharm.2011.08.024
Maulvi, F. A., Pillai, L. V., Patel, K. P., Desai, A. R., Shukla, M. R., Desai, D. T., et al. (2020). Lidocaine tripotassium phosphate complex laden microemulsion for prolonged local anaesthesia: In vitro and in vivo studies. Colloids Surf. B Biointerfaces 185, 110632. doi:10.1016/j.colsurfb.2019.110632
Ngawhirunpat, T., Worachun, N., Opanasopit, P., Rojanarata, T., and Panomsuk, S. (2013). Cremophor RH40-PEG 400 microemulsions as transdermal drug delivery carrier for ketoprofen. Pharm. Dev. Technol. 18 (4), 798–803. doi:10.3109/10837450.2011.627871
Niu, J., Yuan, M., Gao, P., Wang, L., Qi, Y., Chen, J., et al. (2023). Microemulsion-based keratin-chitosan gel for improvement of skin permeation/retention and activity of curcumin. Gels 9 (7), 587. doi:10.3390/gels9070587
Patel, A., Shelat, P., and Lalwani, A. (2014). Development and optimization of solid self-nanoemulsifying drug delivery system (S-SNEDDS) using Scheffe's design for improvement of oral bioavailability of nelfinavir mesylate. Drug Deliv. Transl. Res. 4 (2), 171–186. doi:10.1007/s13346-014-0191-1
Patel, M. R., Patel, R. B., Parikh, J. R., Solanki, A. B., and Patel, B. G. (2011). Investigating effect of microemulsion components: In vitro permeation of ketoconazole. Pharm. Dev. Technol. 16 (3), 250–258. doi:10.3109/10837451003610845
Sahle, F. F., Wohlrab, J., and Neubert, R. H. (2014). Controlled penetration of ceramides into and across the stratum corneum using various types of microemulsions and formulation associated toxicity studies. Eur. J. Pharm. Biopharm. 86 (2), 244–250. doi:10.1016/j.ejpb.2013.07.011
Schaffer, J. D. (1985). “Multiple objective optimization with vector evaluated genetic algorithms,” in Proceedings of the 1st international conference on genetic algorithms (Pittsburgh, PA, USA: Spinger).
Srinivas, N., and Deb, K. J. E. C. (1994). Multiobjective function optimization using nondominated sorting genetic algorithms. Journal 2 (3), 1301–1308. doi:10.1162/evco.1994.2.3.221
Sun, Y., Yan, K., and Huang, X. (2014). Formation, characterization and enzyme activity in water-in-hydrophobic ionic liquid microemulsion stabilized by mixed cationic/nonionic surfactants. Colloids Surf. B Biointerfaces 122, 66–71. doi:10.1016/j.colsurfb.2014.06.040
Tamiz, M., Jones, D., and Romero, C. J. E. J. O. R. (1998). Goal programming for decision making: An overview of the current state-of-the-art. Eur. J. Operational Res. 111 (3), 569–581. doi:10.1016/s0377-2217(97)00317-2
Tian, Q., Ren, F., Xu, Z., Xie, Y., and Zhang, S. (2012). Preparation of high solubilizable microemulsion of naproxen and its solubilization mechanism. Int. J. Pharm. 426 (1-2), 202–210. doi:10.1016/j.ijpharm.2012.01.019
Tsai, Y. H., Lee, K. F., Huang, Y. B., Huang, C. T., and Wu, P. C. (2010). In vitro permeation and in vivo whitening effect of topical hesperetin microemulsion delivery system. Int. J. Pharm. 388 (1-2), 257–262. doi:10.1016/j.ijpharm.2009.12.051
Wang, Y., Wang, X., Wang, X., Song, Y., Wang, X., and Hao, J. (2019). Design and development of lidocaine microemulsions for transdermal delivery. AAPS PharmSciTech 20 (2), 63. doi:10.1208/s12249-018-1263-1
Xu, Z., Jin, J., Zheng, M., Zheng, Y., Xu, X., Liu, Y., et al. (2016). Co-surfactant free microemulsions: Preparation, characterization and stability evaluation for food application. Food Chem. 204, 194–200. doi:10.1016/j.foodchem.2016.01.073
Xunxue, C., and Chuang, L. (2005). A preference-based multi-objective concordance genetic algorithm. J. Softw. 16, 2761–2770. doi:10.1360/jos0761
Xunxue, C. (2006). Multiobjective evolutionary algorithms and their applications. Beijing, China: National Defense Industry Press.
You, X., Xing, Q., Tuo, J., Song, W., Zeng, Y., and Hu, H. (2014). Optimizing surfactant content to improve oral bioavailability of ibuprofen in microemulsions: Just enough or more than enough? Int. J. Pharm. 471 (1-2), 276–284. doi:10.1016/j.ijpharm.2014.05.031
Zhang, D., Ye, D., Jing, P., Tan, X., Qiu, L., Li, T., et al. (2020). Design, optimization and evaluation of co-surfactant free microemulsion-based hydrogel with low surfactant for enhanced transdermal delivery of lidocaine. Int. J. Pharm. 586, 119415. doi:10.1016/j.ijpharm.2020.119415
Zhang, Y., Shang, Z., Gao, C., Du, M., Xu, S., Song, H., et al. (2014). Nanoemulsion for solubilization, stabilization, and in vitro release of pterostilbene for oral delivery. AAPS PharmSciTech 15 (4), 1000–1008. doi:10.1208/s12249-014-0129-4
Keywords: lidocaine microemulsion, multi-objective optimization, genetic algorithm, Pareto non-inferior solution, non-dominated sorting genetic algorithm-II
Citation: Qiao Y, Wang X, Ren H, Cui Y, Ren J, Hao C, Zhao Z, Liu J, Zhao R, Li Y, Tian Q and Qiu L (2023) A study on the preparation conditions of lidocaine microemulsion based on multi-objective genetic algorithm. Front. Pharmacol. 14:1272454. doi: 10.3389/fphar.2023.1272454
Received: 04 August 2023; Accepted: 19 September 2023;
Published: 29 September 2023.
Edited by:
Hong Shen, Bristol Myers Squibb, United StatesReviewed by:
Dongyue Yu, Bristol Myers Squibb, United StatesNian Tong, Bristol Myers Squibb, United States
Shuo Wang, University of Washington, United States
Copyright © 2023 Qiao, Wang, Ren, Cui, Ren, Hao, Zhao, Liu, Zhao, Li, Tian and Qiu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lixia Qiu, cWx4XzExMjZAMTYzLmNvbQ==
 Yuchao Qiao1
Yuchao Qiao1 Chongqi Hao
Chongqi Hao Lixia Qiu
Lixia Qiu