A novel method to estimate the absorption rate constant for two-compartment model fitted drugs without intravenous pharmacokinetic data

The in vivo performances of most drugs after extravascular administration are fitted well with the two-compartment pharmacokinetic (PK) model, but the estimation of absorption rate constant (k_a) for these drugs becomes difficult during unavailability of intravenous PK data. Herein, we developed a novel method, called the direct method, for estimating the k_a values of drugs without using intravenous PK data, by proposing a new PK parameter, namely, maximum apparent rate constant of disposition (k_max). The accuracy of the direct method in k_a estimation was determined using the setting parameters (k₁₂, k₂₁, and k₁₀ values at high, medium, and low levels, respectively) and clinical data. The results showed that the absolute relative error of k_a estimated using the direct method was significantly lower than that obtained using both the Loo-Riegelman method and the statistical moment method for the setting parameters. Human PK studies of telmisartan, candesartan cilexetil, and tenofovir disoproxil fumarate indicated that the k_a values of these drugs were accurately estimated using the direct method based on good correlations between the k_a values and other PK parameters that reflected the absorption properties of drugs in vivo (T_max, C_max, and C_max/AUC_0-t). This novel method can be applied in situations where intravenous PK data cannot be obtained and is expected to provide valuable support for PK evaluation and in vitro-in vivo correlation establishment.

1 Introduction

The absorption rate of drugs refers to the rate at which the drug enters systemic circulation after passing through the mucosal lining since extravascular administration (i.e., orally, perorally, rectally, etc.), and this rate consequently affects the peak time (T_max) and peak concentration (C_max) of drugs in vivo (Tozer et al., 1996). Quantitative assessment of the drug absorption rate constant (k_a) plays a vital role in the pharmaceutical industry. For instance, the correlation between the in vivo absorption rate and the in vitro dissolution rate (IVIVC) of a dosage form can predict the bioavailability of a drug and help avoid excessive number of clinical trials (Zhang et al., 2021). According to the U.S. Food and Drug Administration (FDA), proprietary preparations with identical active pharmaceutical ingredients are regarded as bioequivalents if the rate and extent of drug absorption between the test and reference formulations do not show any significant differences (FDA, 2003). To date, several methods have been widely employed for k_a estimation, and can be classified into two different categories: i) methods based on the compartmental pharmacokinetic (PK) model, including the Wagner-Nelson method (suitable for the one-compartment PK model) and the Loo-Riegelman method (suitable for the two-compartment PK model); ii) methods based on the non-compartmental PK model, including the numerical deconvolution method and the statistical moment method.

In addition to the absorption and elimination phases, the two-compartment model for a drug includes a distribution phase, where the drug is distributed from a central compartment to a peripheral compartment; this model differs from the one-compartment model that treats the body as one uniform component (Figures 1A, D). In this case, the Loo-Riegelman method is the classic method, as it considers the distribution phase for estimating the k_a values of drugs with the two-compartment model. This method requires the data of PK parameters including k₁₀ (first-order elimination rate constant), k₁₂ (first-order rate constant of the drugs transfer from the central compartment to the peripheral compartment), and k₂₁ (first-order rate constant of the drugs transfer from the peripheral compartment to the central compartment); these data need to be obtained from the intravenous administration of the corresponding drugs to estimate their k_a (Wagner, 1975). The numerical deconvolution method calculates the k_a of drugs and does not involve the limitations of the compartmental model, but it requires the same sampling time and intervals for both intravenous and extravascular administrations (Yu et al., 1996). Thus, intravenous PK data are necessary for estimating the k_a when using either the Loo-Riegelman method or the numerical deconvolution method. However, determining the intravenous PK parameters of drugs is challenging if they can be administered only through the extravascular route because of safety concerns in human volunteers.

FIGURE 1

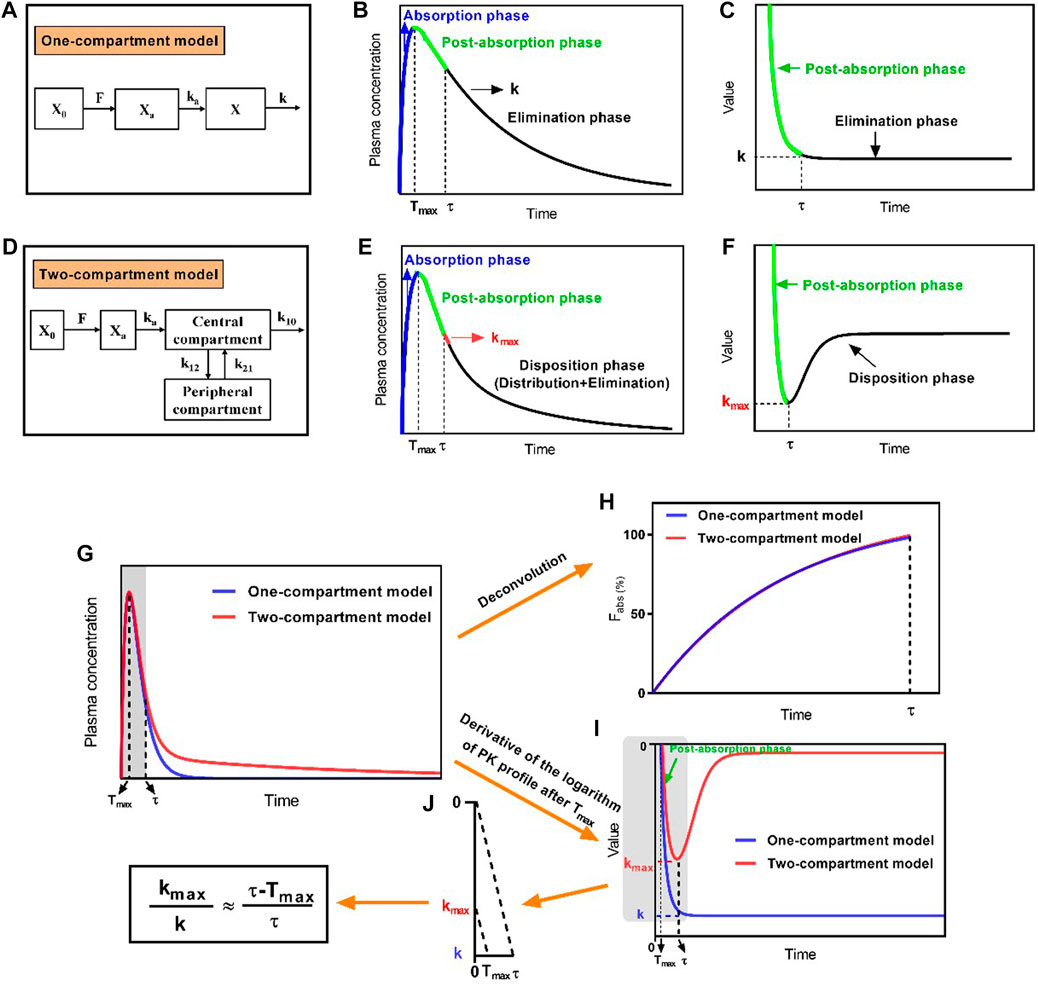
FIGURE 1. Schematic diagram of the development of the direct method by proposing the maximum apparent rate constant of disposition (k_max) and its corresponding time point (τ) in the two-compartment model. (A) Schematic diagram of the extravascular administration for the one-compartment model, (B) characteristic profile of the one-compartment model, and (C) derivative of the logarithmic plasma drug concentration–time profile after T_max, which shows an invariable elimination rate constant (k); (D) schematic diagram of the extravascular administration for the two-compartment model, (E) characteristic profile of the two-compartment model, and (F) derivative of the logarithmic plasma drug concentration–time profile after T_max, for which the k_max and its corresponding time point of τ were available; (G) plasma drug concentration–time profile of drugs fitting the one-compartment model or two-compartment model; (H) absorption profiles of drugs after deconvolution; (I) derivative of the logarithmic plasma drug concentration–time profiles; (J) The relationship of $\frac{{\mathrm{k}}_{\max }}{\mathrm{k}}\approx \frac{\mathrm{\tau }-{\mathrm{T}}_{\max }}{\mathrm{\tau }}$.

The statistical moment method can also be applied to the non-compartmental PK model by applying overall random variables obtained from the in vivo process of drugs. k_a is estimated by calculating the difference in mean residence time (MRT) between various types of administrations to avoid the use of intravenous PK data. However, many factors affect the accuracy of k_a estimated using the statistical moment method, such as the precision of detecting low plasma drug concentration and the lack of appropriate data for determining the logarithmic linearity in the terminal phase that yields the accurate elimination rate constant (k_T) (Riegelman and Collier, 1980). Therefore, the deficiency in intravenous PK data or poor accuracy of the method hinders k_a estimation for drugs with the two-compartment model.

Generally, the plasma concentration (C) and k_a of drugs for extravascular administration in the one-compartment model had the following relationship (Eq. 1):

$\mathrm{C}=\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{F}{\mathrm{X}}_0}{\mathrm{V}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{k}\right)}\exp \left(-\mathrm{k}\mathrm{t}\right)-\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{F}{\mathrm{X}}_0}{\mathrm{V}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{k}\right)}\exp \left(-{\mathrm{k}}_{\mathrm{a}}\mathrm{t}\right)(1)$

where F is the drug bioavailability, X₀ is the dose, V is the apparent volume of distribution, and k is the elimination rate constant. When differentiating with respect to time t, it gets the following equation:

$\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=\frac{{\mathrm{k}}_{\mathrm{a}}^2\mathrm{F}{\mathrm{X}}_0}{\mathrm{V}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{k}\right)}\exp \left(-{\mathrm{k}}_{\mathrm{a}}\mathrm{t}\right)-\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{k}\mathrm{F}{\mathrm{X}}_0}{\mathrm{V}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{k}\right)}\exp \left(-\mathrm{k}\mathrm{t}\right)(2)$

As the plasma drug concentration reached the C_max (i.e., $\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=0$), Eq. 2 was simplified to Eq. 3, which was a classical equation to quickly calculate k_a for the one-compartment model (Zhi, 1990).

${\mathrm{T}}_{\max }=\frac{\ln {\mathrm{k}}_{\mathrm{a}}-\mathrm{l}\mathrm{n}\mathrm{k}}{{\mathrm{k}}_{\mathrm{a}}-\mathrm{k}}(3)$

When the PK model was not considered, the concentration–time curve consisted of two sections: the first-order rate increase curve and the first-order rate decrease curve. The basic formula satisfied $\mathrm{C}=\mathrm{A}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{k}\mathrm{t})-\mathrm{B}\mathrm{e}\mathrm{x}\mathrm{p}(-{\mathrm{k}}_{\mathrm{a}}\mathrm{t})$, where k is the elimination rate constant in the one-compartment model or the total removal rate constant of the drugs removed from the central compartment because of their distribution (k₁₂) and elimination (k₁₀) in the two-compartment model. Thus, k_a was estimated for drugs that fitted with the two-compartment model after the k in Eq. 3 was replaced with “k₁₂ + k₁₀,” referred to as the alternative method (Zeng et al., 2020). This method has excellent accuracy and convenience compared with both the Loo-Riegelman method and the statistical moment method. However, the alternative method also requires intravenous PK data to calculate k₁₀ and k₁₂. Thus, identifying a novel PK parameter in the two-compartment model to replace the k (in Eq. 3) may be one of the effective ways for estimating k_a without the need for intravenous PK data.

In the present study, a new parameter, namely, maximum apparent rate constant of disposition (k_max), was defined to develop a novel method (named as “the direct method”) for k_a estimation. The accuracy of k_a estimated using the direct method was investigated by setting the k₁₂, k₂₁, and k₁₀ values at high, medium, and low levels, respectively, after the relationship and range of these parameters were determined from previously published reports. Additionally, the accuracy of the k_a value estimated using the direct method was compared with the accuracies determined using the Loo-Riegelman method and the statistical moment method. Three model drugs (telmisartan (TMS), candesartan cilexetil (CSC), and tenofovir disoproxil fumarate (TDF)) with different formulations were selected, and their PK parameters were assessed in humans. The direct method was used to estimate the k_a values of three model drugs, and from the results, correlations were established between their estimated k_a values and the other PK parameters that reflected the absorption properties of the drugs in vivo. These correlations were analyzed to verify the accuracy of the direct method in estimating the k_a value of drugs.

2 Materials and methods

2.1 Materials

Tablet dosage forms with different immediate-release (IR) formulations, including TMS (F_M1 and F_M2, specifications: 80 mg), CSC (F_C1 and F_C2, specifications: 4 mg), and TDF (F_D1 and F_D2, specifications: 300 mg), were kindly supplied by three different pharmaceutical companies.

2.2 Development of the direct method for k_a estimation

2.2.1 Definition of k_max

Unlike the one-compartment model, which has an invariable value of k (Figure 1B), the plasma drug concentration–time curve that fixed well with the two-compartment model was divided into three phases: the absorption phase, post-absorption phase, and disposition phase (i.e., sum of the distribution and elimination phase; Figure 1E). The portion of the curve before T_max represented the absorption phase, during which the rate of increasing plasma drug concentration was significantly higher than the rate of its disposition, and the portion of the curve after T_max represented the post-absorption phase, during which the disposition rates of the drugs were higher than the absorption rates. Thereafter, the disposition rate gradually decreased until it reached an invariable terminal elimination process. At the end time of the post-absorption phase (τ), the absorption phase had completed; thus, only the disposition phase remained. This phase presented the highest apparent rate of drug disposition (k_max) at the first time interval after τ (Figure 1E). Moreover, the derivative of the logarithm of the plasma drug concentration–time profile reflected the real-time rate of decreasing drug concentration (i.e., the slope of the logarithmic PK curve after T_max), which gradually increased and then remained at a constant rate (k) for the one-compartment model because of the presence of the post-absorption phase after T_max (Figure 1C). By contrast, the rate of declining drug concentration continuously showed changes in the order of increase, decrease, and constant that presented the k_max at τ for the two-compartment model (Figure 1F).

2.2.2 Development of the direct method

The k_a, X₀, F, and V in the one-compartment model and two-compartment model were set as the same values, as well as k = k₁₂ + k₁₀. The absorption phase, post-absorption phase, and disposition phase satisfied first-order kinetics. The absorption phases of two simulated drug concentration–time curves had almost overlapped (Figure 1G). The absorption profiles had also overlapped after deconvolution (Figure 1H). The absorption was complete at time point τ, which corresponded to k_max. After the derivative of the logarithmic plasma drug concentration–time profile, k_max and k showed unequal values, and the value of k_max was always less than that of k, but the value of τ was always greater than that of T_max. When the values of k_max, k, T_max, and τ were extracted from Figure 1I, the four parameters had the following relationship after proportional scaling of triangles (Eq. 4; Figure 1J).

$\frac{{\mathrm{k}}_{\max }}{\mathrm{k}}\approx \frac{\mathrm{\tau }-{\mathrm{T}}_{\max }}{\mathrm{\tau }}(4)$

Equation 4 was transformed into Eq. 5:

$\mathrm{k}\approx \frac{{\mathrm{\tau }\ast \mathrm{k}}_{\max }}{\mathrm{\tau }-{\mathrm{T}}_{\max }}(5)$

Thus, Eq. 3 was approximately transformed into Eq. 6 using the relationship established in Eq. 5.

${\mathrm{T}}_{\max }=\frac{\ln {\mathrm{k}}_{\mathrm{a}}-\ln \frac{{\mathrm{\tau }\ast \mathrm{k}}_{\max }}{\mathrm{\tau }-{\mathrm{T}}_{\max }}}{{\mathrm{k}}_{\mathrm{a}}-\frac{{\mathrm{\tau }\ast \mathrm{k}}_{\max }}{\mathrm{\tau }-{\mathrm{T}}_{\max }}}(6)$

In this case, the values of T_max were obtained from the plasma drug concentration–time curves, and the values of k_max and τ were obtained from the logarithm of the plasma drug concentration–time curves for the two-compartment model after extravascular administration. Subsequently, k_a was estimated using Newton’s iteration method with the Python software package (version 3.6.7). Therefore, the direct method did not require measurement of the intravenous concentration of drugs.

2.3 Validation of the direct method by setting parameters

2.3.1 Parameter setting and model judgment

To ensure that the setting parameters satisfied the two-compartment model, the human plasma drug concentration–time curves of 36 drugs fitting the two-compartment model in the fasted or fed states were obtained from previously published reports, and the corresponding data were extracted using GetData Graph Digitizer software (version 2.25, https://www.getdata-graph-digitizer.com/). The preliminary k_a, k₁₂, k₂₁, and k₁₀ values of these drugs were calculated using WinNonlin software (version 8.2, Certara Co., United States), which were attributed to the inability to obtain these parameters from the literature.

The k_a, k₁₂, k₂₁, and k₁₀ values were sorted in the descending order. The average values of the top one-third, middle one-third, and bottom one-third of these data (n = 12) were set as high, medium, and low levels, respectively. Then, the different levels of each parameter were combined randomly. Plasma drug concentration was calculated at different time points (intervals of 0.1 h) after factoring the setting parameters (k_a, k₁₂, k₂₁, and k₁₀) into the following Eqs 7–9:

$\mathrm{C}=\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{F}{\mathrm{X}}_0\left({\mathrm{k}}_{21}-{\mathrm{k}}_{\mathrm{a}}\right)}{{\mathrm{V}}_{\mathrm{c}}\left(\mathrm{\alpha }-{\mathrm{k}}_{\mathrm{a}}\right)\left(\mathrm{\beta }-{\mathrm{k}}_{\mathrm{a}}\right)}\bullet \exp \left(-{\mathrm{k}}_{\mathrm{a}}\mathrm{t}\right)+\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{F}{\mathrm{X}}_0\left({\mathrm{k}}_{21}-\mathrm{\alpha }\right)}{{\mathrm{V}}_{\mathrm{c}}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{\alpha }\right)\left(\mathrm{\beta }-\mathrm{\alpha }\right)}\bullet \exp \left(-\mathrm{\alpha }\mathrm{t}\right)+\frac{{\mathrm{k}}_{\mathrm{a}}\mathrm{F}{\mathrm{X}}_0\left({\mathrm{k}}_{21}-\mathrm{\beta }\right)}{{\mathrm{V}}_{\mathrm{c}}\left({\mathrm{k}}_{\mathrm{a}}-\mathrm{\beta }\right)\left(\mathrm{\alpha }-\mathrm{\beta }\right)}\bullet \exp \left(-\mathrm{\beta }\mathrm{t}\right)(7)$

where X₀, F, and V_c were randomly set as fixed values (e.g., X₀ = 2,200 μg, F = 1, V_c = 10 L). The α and β variables in Eq. 7, which represent the distribution phase mixed first-order rate constant and the elimination phase mixed first-order rate constant, respectively, were determined using Eqs 8, 9:

$\mathrm{\alpha }=\frac{\left({\mathrm{k}}_{12}{+\mathrm{k}}_{21}{+\mathrm{k}}_{10}\right)+\sqrt{{\left({\mathrm{k}}_{12}{+\mathrm{k}}_{21}{+\mathrm{k}}_{10}\right)}^2-4{\mathrm{k}}_{21}{\mathrm{k}}_{10}}}{2}(8)$

$\mathrm{\beta }=\frac{\left({\mathrm{k}}_{12}{+\mathrm{k}}_{21}{+\mathrm{k}}_{10}\right)-\sqrt{{\left({\mathrm{k}}_{12}{+\mathrm{k}}_{21}{+\mathrm{k}}_{10}\right)}^2-4{\mathrm{k}}_{21}{\mathrm{k}}_{10}}}{2}(9)$

Furthermore, the Akaike information criteria (AIC) values were calculated using Eqs 10, 11 to evaluate the compartmental model of the drug concentration–time curves.

$\mathrm{A}\mathrm{I}\mathrm{C}=\mathrm{N}\bullet \ln {\mathrm{R}}_{\mathrm{e}}+2\mathrm{p}(10)$

${\mathrm{R}}_{\mathrm{e}}={\displaystyle \sum _{\mathrm{i}-1}^{\mathrm{n}}}{\mathrm{W}}_{\mathrm{i}}{\left({\mathrm{C}}_{\mathrm{i}}-{\widehat{\mathrm{C}}}_{\mathrm{i}}\right)}^2(11)$

where N is the number of experimental groups, R_e is the sum of squares of the weighted residuals, p is the number of model parameters, W_i is the weight coefficient, C_i is the experimental plasma drug concentration, and Ĉ_i is the estimated plasma drug concentration. The AIC values of drugs in the one-compartment model and two-compartment model were calculated; the smaller the AIC value, the better the fitting (Kadam et al., 2013).

2.3.2 Estimation of k_a using the direct method

T_max was determined from the data of the plasma drug concentration–time curves of the setting parameters. The k_max was fitted from the slope of the logarithm of plasma drug concentration–time curve at the first time interval after the time point τ. The k_a value was then estimated using the direct method (Eq. 6). The accuracy of k_a estimation was calculated by comparing the estimated k_a from Eq. 6 to the setting value of k_a (i.e., the true k_a value) using Eq. 12:

$\mathrm{R}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(\mathrm{R}\mathrm{E}\right)\%=\frac{{{\mathrm{k}}_{\mathrm{a}\left(\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)}-\mathrm{k}}_{\mathrm{a}\left(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\right)}}{{\mathrm{k}}_{\mathrm{a}\left(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\right)}}\times 100\%(12)$

2.3.3 Estimation of k_a using the Loo-Riegelman method

The setting k₁₂, k₂₁, and k₁₀ values were used to estimate the k_a value using the Loo-Riegelman method. Briefly, k_a was calculated using the following equation (Eq. 13):

$\ln \left(1-{\mathrm{F}}_{\mathrm{a}\mathrm{b}\mathrm{s}}\right)=-{\mathrm{k}}_{\mathrm{a}}\mathrm{t}+\mathrm{b}(13)$

and the in vivo absorption fraction (F_abs) was obtained using Eq. 14:

${\mathrm{F}}_{\mathrm{a}\mathrm{b}\mathrm{s}}=\frac{{\left({\mathrm{X}}_{\mathrm{A}}\right)}_{\mathrm{t}}}{{\left({\mathrm{X}}_{\mathrm{A}}\right)}_{\infty }}=\frac{{\mathrm{C}}_{\mathrm{t}}+{\mathrm{k}}_{10}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}}\mathrm{C}{\mathrm{d}}_{\mathrm{t}}+\frac{{\left({\mathrm{X}}_{\mathrm{p}}\right)}_{\mathrm{t}}}{{\mathrm{V}}_{\mathrm{c}}}}{{\mathrm{k}}_{10}{\displaystyle \underset{0}{\overset{\infty }{\int }}}\mathrm{C}{\mathrm{d}}_{\mathrm{t}}}(14)$

The $\frac{{\left({\mathbf{X}}_{\mathbf{p}}\right)}_{\mathbf{t}}}{{\mathbf{V}}_{\mathbf{c}}}$ value in Eq. 14 was calculated using Eq. 15:

$\frac{{\left({\mathrm{X}}_{\mathrm{p}}\right)}_{\mathrm{t}}}{{\mathrm{V}}_{\mathbf{c}}}=\frac{{\left({\mathrm{X}}_{\mathrm{p}}\right)}_{\mathrm{t}-1}}{{\mathrm{V}}_{\mathrm{C}}}\exp \left(-{\mathrm{k}}_{21}∆\mathrm{t}\right)+\frac{{\mathrm{k}}_{12}{\mathrm{C}}_0}{{\mathrm{k}}_{21}}\left[1-\exp \left(-{\mathrm{k}}_{21}∆\mathrm{t}\right)\right]+\frac{{\mathrm{k}}_{12}\left(\frac{∆\mathrm{c}}{∆\mathrm{t}}\right){∆\mathrm{t}}^2}{2}(15)$

where ${\left({\mathrm{X}}_{\mathrm{A}}\right)}_{\mathrm{t}}$ and ${\left({\mathrm{X}}_{\mathrm{A}}\right)}_{\infty }$ are the amount of drug entering systemic circulation at time t and infinite time, respectively. ${\left({\mathrm{X}}_{\mathrm{p}}\right)}_{\mathrm{t}}$ is the amount of drug entering the peripheral compartment at time t. Moreover, ∆c and ∆t represent the differences in the plasma drug concentration and time between two consecutive samples, respectively.

2.3.4 Estimation of k_a using the statistical moment method

The k_a value determined upon fitting the plasma drug concentration–time data of the setting parameters with the statistical moment method was compared with that determined upon fitting plasma drug concentration–time data with the direct method. The calculation of the statistical moment method performed to make this comparison is shown in Eq. 16:

$\frac{1}{{\mathrm{k}}_{\mathrm{a}}}=\mathrm{M}\mathrm{A}\mathrm{T}=\mathrm{M}\mathrm{R}\mathrm{T}-\frac{1}{{\mathrm{k}}_{\mathrm{T}}}=\frac{\mathrm{A}\mathrm{U}\mathrm{M}\mathrm{C}}{\mathrm{A}\mathrm{U}\mathrm{C}}-\frac{1}{{\mathrm{k}}_{\mathrm{T}}}(16)$

where MAT is the average absorption time, MRT is the average residence time after extravascular administration, and k_T is the elimination rate constant at the terminal phase. The area under the plasma drug concentration–time curve (AUC) was calculated using the trapezoidal method. AUMC, which represented the area under the moment curve, was calculated using Eq. 17:

$\mathrm{A}\mathrm{U}\mathrm{M}\mathrm{C}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{n}-1}}\frac{{\mathrm{c}}_{\mathrm{i}}{\mathrm{t}}_{\mathrm{i}}+{\mathrm{c}}_{\mathrm{i}+1}{\mathrm{t}}_{\mathrm{i}+1}}{2}\left({\mathrm{t}}_{\mathrm{i}+1}-{\mathrm{t}}_{\mathrm{i}}\right)+\frac{{\mathrm{c}}_{\mathrm{n}}{\mathrm{t}}_{\mathrm{n}}}{{\mathrm{k}}_{\mathrm{T}}}+\frac{{\mathrm{c}}_{\mathrm{n}}}{{{\mathrm{k}}_{\mathrm{T}}}^2}(17)$

where C_i, C_i+1, and C_n are the drug concentrations at time points t_i, t_i+1, and t_n, respectively.

2.4 Validation of the direct method using clinical data

2.4.1 Clinical data of the model drugs

The plasma concentrations of three model drugs, namely, TMS, CSC, and TDF, were obtained from PK studies involving healthy human volunteers. The clinical studies were conducted in accordance with the Declaration of Helsinki, and the experimental protocols were approved by the Chinese Food and Drug Administration (CFDA) and the Institutional Research Ethics Committee of Xiangya School of Pharmacy, Central South University (project code: 2020006). All enrolled volunteers were fully informed of the protocol of the clinical studies, and their consents to participate were approved. PK studies had randomized, open-label, and single-dose designs, wherein the PK parameters were compared after the oral administration of different formulations containing TMS, CSC, or TDF.

Briefly, PK studies of TMS tablets were conducted with a two-way crossover design on 26 healthy volunteers in the fasted state, which included a 7-day washout period between treatments. Blood samples were collected in heparin-containing vacutainers before administration (0 h) and 0.17, 0.33, 0.5, 0.75, 1, 1.25, 1.5, 2, 2.5, 3, 4, 6, 8, 10, 12, 24, 48, 72, and 96 h after the administration of the F_M1 or F_M2 tablets.

PK studies of CSC tablets were conducted with a two-way crossover design on 24 volunteers in the fasted state, which included a 7-day washout period between treatments. Blood samples were collected in heparin-containing vacutainers before administration (0 h) and 0.33, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, 3, 4, 6, 8, 12, 24, and 48 h after the administration of the F_C1 or F_C2 tablets.

PK studies of TDF tablets were conducted with a two-way crossover design on 24 volunteers in the fasted state and the fed state (the fed state consisted of a high-fat meal with a nutritional composition of 522-kcal fat, 288-kcal carbohydrates, 149-kcal protein, and 959-kcal total calories). Studies of TDF tablets featured the 7-day washout period between treatments. Blood samples were collected in heparin-containing vacutainers before administration (0 h) and 0.25, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 5, 6, 8, 10, 12, 24, 36, and 48 h after the administration of the F_D1 or F_D2 tablets.

All blood samples were centrifuged at 3,500 rpm for 10 min. The plasma samples were separated and then stored at −70°C until analysis by high-performance liquid chromatography-tandem mass spectrometry (Agilent, United States).

2.4.2 Determination of PK parameters

CSC and TDF were rapidly and completely hydrolyzed to candesartan and tenofovir in the plasma, respectively, after absorption from the gastrointestinal tract (Gleiter and Morike, 2002; Kearney et al., 2004). The U.S. FDA recommended the detection of plasma concentrations of candesartan and tenofovir in human PK studies of CSC tablet (FDA, 2008) and TDF tablet (FDA, 2012), respectively. PK parameters, namely, C_max, T_max, AUC_0-t, AUC_0-∞, and elimination half-life (t_1/2), of TMS, candesartan, and tenofovir were calculated using the WinNonlin software package. All data were expressed as mean ± standard deviation.

2.4.3 Validation of the direct method

The values of k_max and τ for TMS, CSC, and TDF were obtained by calculating the logarithm of the plasma drug concentration–time curves. The k_a values for TMS, CSC, and TDF were estimated using the direct method (Eq. 6), statistical moment method (Eq. 16), and Loo-Riegelman method (Eq. 13), respectively. Pearson’s correlation analysis (SPSS 25.0; SPSS Inc., United States) was performed to evaluate the relationship between the k_a values and other PK parameters that reflected the absorption properties of the drugs in vivo (T_max, C_max, and C_max/AUC_0-t). Furthermore, the absorption rate versus time profiles were fitted using Eq. 18:

${\mathrm{F}}_{\mathrm{a}\mathrm{b}\mathrm{s}}=\left[1-\exp \left(-{\mathrm{k}}_{\mathrm{a}}\mathrm{t}\right)\right]\ast 100\%(18)$

2.5 Statistical analysis

All statistical analyses were performed using SPSS software package (version 25.0; SPSS Inc., United States) and assessed using Student’s t-test. Data with p < 0.05 were considered to have a statistically significant difference.

3 Results

3.1 Characteristics of k_a, k₁₀, k₁₂, and k₂₁ for drugs with the two-compartment model

The AIC values of 36 IR formulations were determined. All the drugs were more suitable for the two-compartment model because the AIC₂ values (for the two-compartment model) were smaller than the AIC₁ values (for the one-compartment model; Table 1). The ranges of k_a (0.210–1.726 h⁻¹), k₁₂ (0.044–0.847 h⁻¹), k₂₁ (0.010–0.451 h⁻¹), and k₁₀ (0.012–1.003 h⁻¹) were estimated. Interestingly, the sum of k₁₂ and k₁₀ was less than the value of k_a for all drugs ((k_a > k₁₂ + k₁₀; Table 1). Additionally, the values of k_a and k₁₂ were both higher than the values of k₂₁ for all drugs (k_a > k₁₂ > k₂₁; Table 1). The mean values of k₁₀ were significantly higher than that of k₂₁ (^*p < 0.05), excepted for a few drugs (e.g., acyclovir, daclatasvir, and levonorgestrel), whose k₁₀ values were less than their k₂₁ values. These results provided the rationale for setting the available values of k_a, k₁₀, k₁₂, and k₂₁ for the drugs satisfying the two-compartment model.

TABLE 1

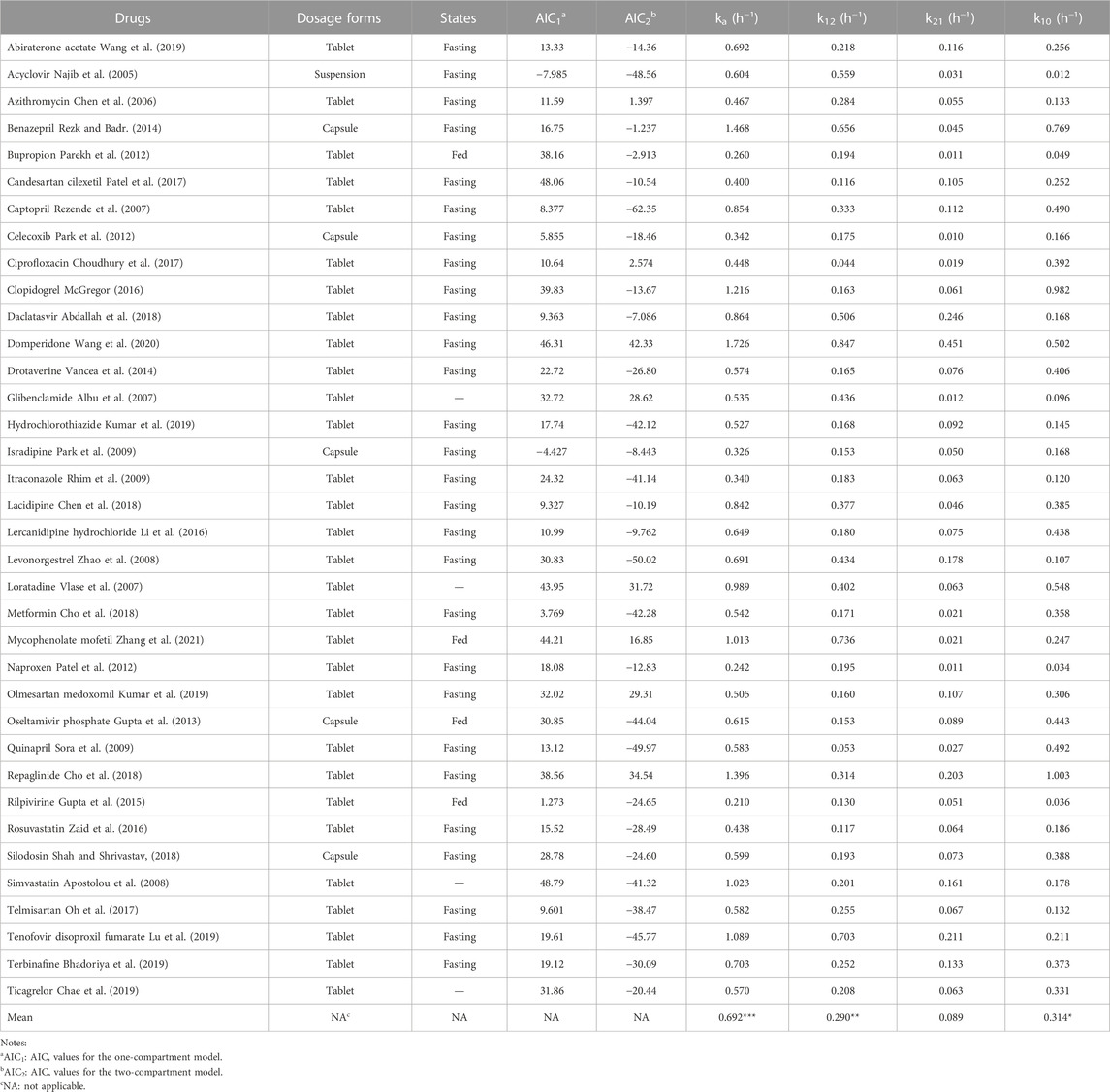
TABLE 1. The values of k_a, k₁₀, k₁₂, and k₂₁ of 36 drugs with IR dosage forms estimated using the WinNonlin software in the two-compartment model after oral administrations in human (^***p < 0.001 vs k₁₂, k₂₁, k₁₀, respectively; ^**p < 0.01 vs. k₂₁; ^*p < 0.05 vs k₂₁ by Student’s t-test).

3.2 Assessing the accuracy of k_a estimated using the direct method with the setting parameters

To investigate the accuracy and sensitivity of the direct method, the high, medium, and low values of k_a, k₁₂, k₂₁, and k₁₀ were set according to previous reports (Table 1). The setting values of k_a were 1.098, 0.603, and 0.375 h⁻¹; the setting values of k₁₂ were 0.525, 0.211, and 0.133 h⁻¹; the setting values of k₂₁ were 0.176, 0.067, and 0.025 h⁻¹; the setting values of k₁₀ were 0.571, 0.271, and 0.100 h⁻¹, respectively (Table 2). Thirty-nine groups were finally obtained with the combination of the values of k_a, k₁₂, k₂₁, and k₁₀ based on the relationships among them (k_a > k₁₂ + k₁₀, k_a > k₁₂ > k₂₁). All groups satisfied the two-compartment model (AIC₁ > AIC₂; Table 2). The values of T_max, k_max, and τ were obtained from the drug concentration−time curves of the corresponding group (Figure 2A), which showed that the T_max increased following a decrease in k_a. The values of k_a were then estimated using the direct method, Loo-Riegelman method, and statistical moment method. The RE of the k_a estimated using the direct method had both positive and negative values when compared with the setting k_a (i.e., the true k_a value), the values of which were less than 20% in most groups. However, all RE values obtained using the Loo-Riegelman method were positive, wherein estimated k_a > true k_a. On the contrary, most of the RE values obtained using the statistical moment method were negative, wherein estimated k_a < true k_a.

TABLE 2

TABLE 2. The k_a values estimated using the different methods with the setting data (39 groups).

FIGURE 2

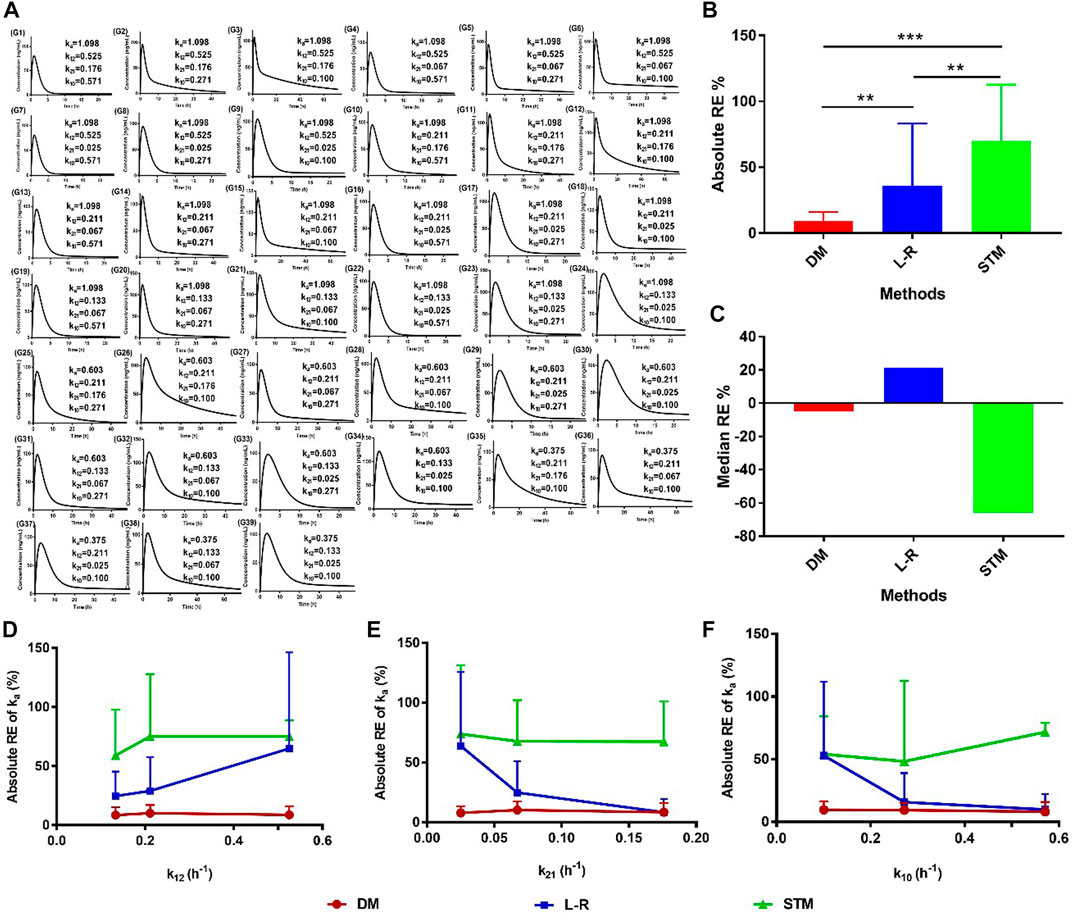
FIGURE 2. Accuracy of the k_a estimated using the direct method with the setting parameters. (A) Plasma drug concentration–time profiles of the setting groups; (B) absolute values and (C) median values of RE for the k_a values estimated using different methods. Absolute RE of k_a with changes in (D) k₁₂, (E) k₂₁, and (F) k₁₀ estimated using different methods. Data are presented as mean ± standard deviation, ^**p < 0.01 and ^***p < 0.001. DM: direct method; L-R: Loo-Riegelman method; RE: relative error; STM: statistical moment method.

The absolute values of RE were calculated, and the data are shown in Figure 2B. The absolute RE of k_a estimated using the direct method was significantly less than that estimated using either the statistical moment method (^**p < 0.01) or the Loo-Riegelman method (^***p < 0.001). The absolute RE of k_a estimated using the Loo-Riegelman method was significantly less than that estimated using the statistical moment method (^**p < 0.01). The median RE of k_a estimated using the direct method (−4.98%) was better than that estimated using the Loo-Riegelman method (21.5%) and the statistical moment method (−65.9%; Figure 2C). The accuracy of k_a estimated using the direct method was not affected by changes in k₁₂, k₂₁, and k₁₀, which also demonstrated excellent accuracy when compared with that estimated using the Loo-Riegelman method and the statistical moment method (Figures 2D–F). Therefore, the direct method yielded a more accurate value and did not require the determination of k₁₂, k₂₁, and k₁₀ from intravenous PK measurements.

3.3 Validation of the direct method in human PK studies

The mean plasma drug concentration–time curves of TMS, candesartan, and tenofovir were obtained from PK evaluation in human (Figure 3). The PK parameters are listed in Table 3.

FIGURE 3

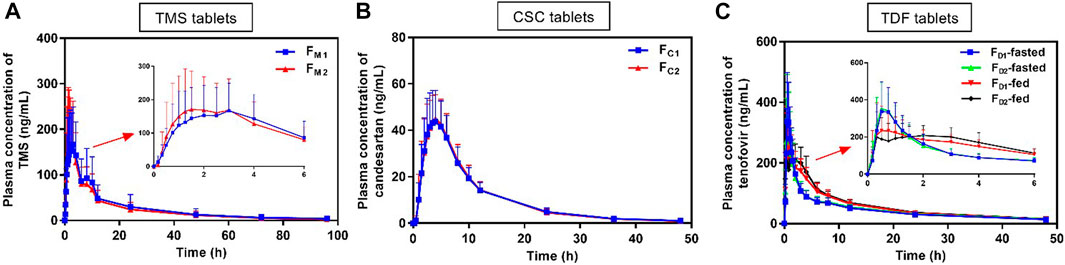
FIGURE 3. Mean plasma concentration versus time profiles of (A) TMS, (B) candesartan (metabolite of CSC), and (C) tenofovir (metabolite of TDF) obtained after the oral administration of TMS (n = 26), CSC (n = 24), and TDF tablets (n = 24) in humans. Data are presented as mean ± standard deviation. CSC: candesartan cilexetil; TDF: tenofovir disoproxil fumarate; TMS: telmisartan.

TABLE 3

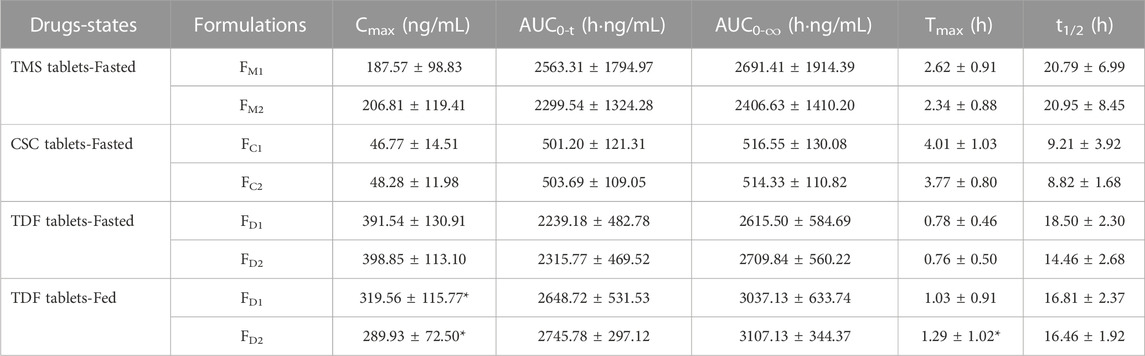
TABLE 3. PK parameters of TMS, candesartan (metabolite of CSC), tenofovir (metabolite of TDF) following administration of single dose of TMS (n = 26), CSC (n = 24) and TDF tablets (n = 24) in the fasted or/and fed state, respectively. Data are presented as mean ± standard deviation, ^*p < 0.05 vs. the same formulation in the fasted state.

The mean plasma concentrations of F_M2 were higher than those of F_M1 over a period of 0.5–3.0 h after oral administration (Figure 3A), and the C_max of F_M2 was higher than that of F_M1 (Table 3). Overall, the plasma drug concentration–time profiles (Figure 3B) and the PK parameters (Table 3) of F_C1 and F_C2 were similar. The C_max of tenofovir in the fed state was significantly lower than that of tenofovir in the fasted state for both F_D1 and F_D2 (^*p < 0.05; Figure 3C; Table 3), and the T_max of tenofovir in the fed state was also larger than that of tenofovir in the fasted state (^*p < 0.05 for F_D2). The three model drugs with different T_max values (0.5–4.0 h) represented low, medium, and high absorption rates of the IR dosage forms.

The k_a values of the TMS, CSC, and TDF tablets were estimated using different methods. Data of intravenous PK parameters of TMS were obtained from a previously published report (Stangier et al., 2000) and were used to estimate k_a using the Loo-Riegelman method. However, it was difficult to acquire the in vivo data of CSC, TDF, and their respective metabolites (candesartan, tenofovir) after intravenous administration. The k_a value for F_M2 estimated using the direct method was higher than that of F_M1 estimated using the same method. These values had a consistent trend with the estimation of k_a using the Loo-Riegelman method, but it had a contrary trend to the estimation of k_a using the statistical moment method (Table 4). k_a estimated using the direct method for F_C1 was similar to that of F_C2, whereas k_a estimated using the statistical moment method of F_C1 was higher than that of F_C2. The estimated k_a of both F_D1 and F_D2 in the fasted state was higher than those of F_D1 and F_D2 in the fed state (^*p < 0.05 for F_D2). The k_max values of both F_D1 and F_D2 in the fasted state were also higher than that of F_D1 and F_D2 in the fed state (^*p < 0.05). Moreover, the k_a value of F_D1 was consistent with that of F_D2 estimated using the direct method in the same state. This finding was contrary to that obtained using the statistical moment method, which yielded the k_a value of F_D1 that was higher than that of F_D2.

TABLE 4

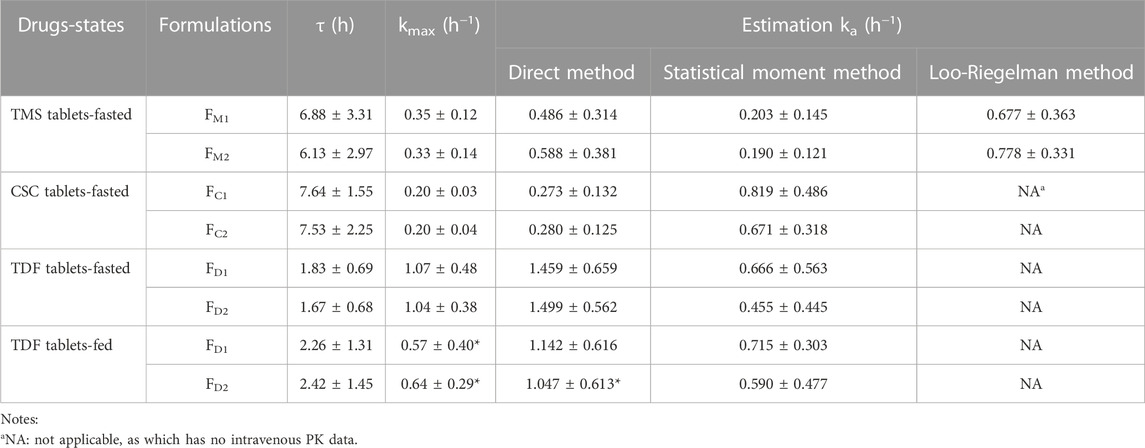
TABLE 4. The k_a values estimated using the different method for the TMS, CSC, TDF tablets in the fasted or/and fed state. Data are presented as mean ± standard deviation, ^*p < 0.05 vs. k_a value of the same formulation estimated using the direct method in the fasted state.

The mean absorbed fraction-time profiles of TMS tablets showed that the absorbed fraction of F_M2 was faster than those of F_M1 using the direct method and the Loo-Riegelman method within the first 4 h (Figures 4A1, B1), which was consistent with the mean plasma drug concentration-time profiles (Figure 3A) and C_max value of TMS (Table 3). However, the absorption profiles of F_M1 and F_M2 had nearly overlapped when estimated using the statistical moment method (Figure 4C1), which was inconsistent with their in vivo experimental data. The values of k_a estimated using the direct method were positively correlated with both C_max and C_max/AUC_0-t (correlation coefficient (R) > 0.4, p < 0.01; Figures 4A2, A3) and negatively correlated with T_max (R = −0.858, p < 0.001; Figure 4A4) as observed in Pearson’s correlation analysis. However, the k_a estimated using the Loo-Riegelman method (Figures 4B2–B4) and the statistical moment method (Figures 4C2–C4) demonstrated only slight correlation with these parameters (p > 0.1).

FIGURE 4

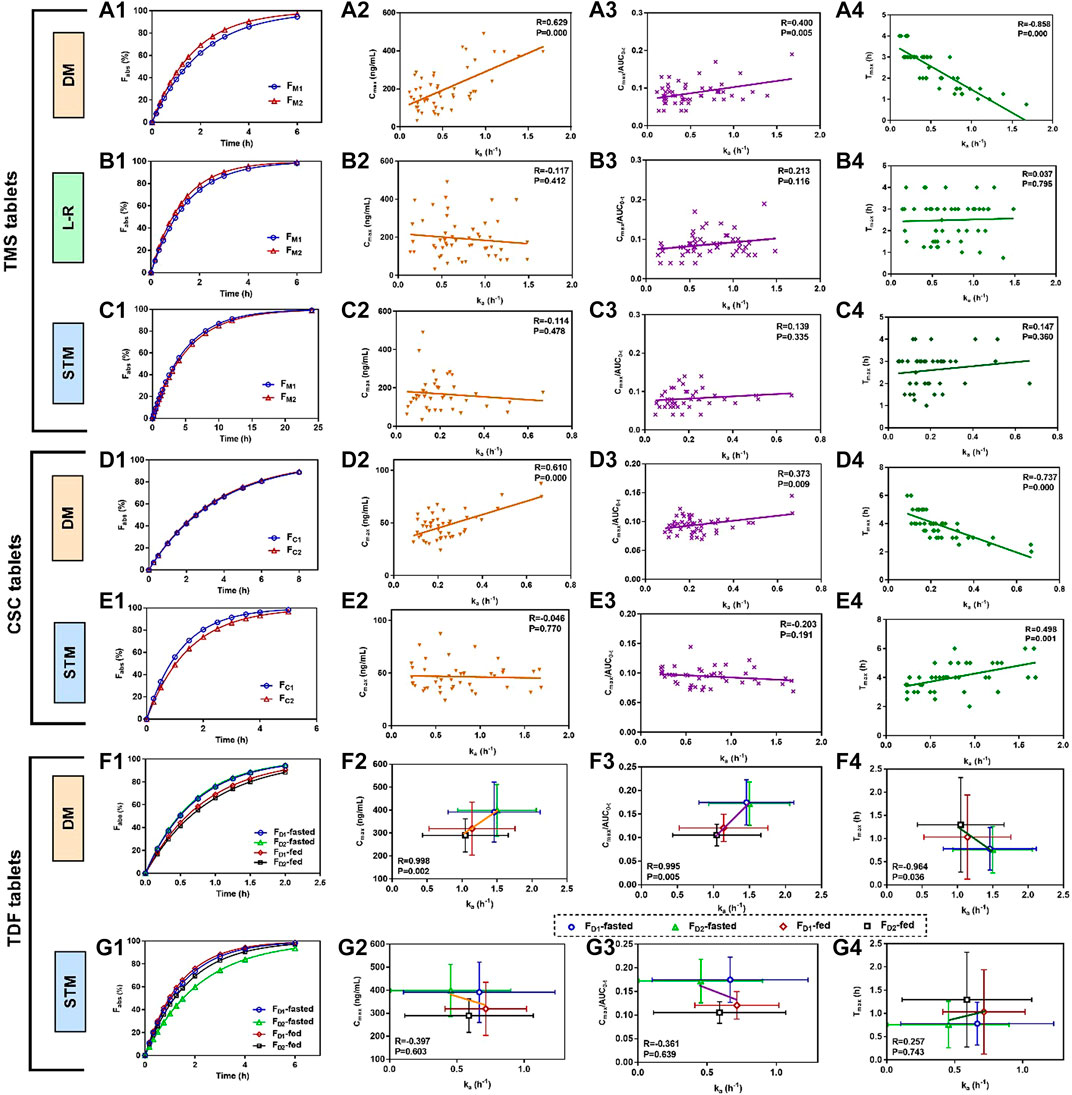
FIGURE 4. Mean absorbed fraction versus time profiles of TMS tablets, CSC tablets, and TDF tablets and correlations between estimated k_a values and the other PK parameters that reflected the absorption properties of the drugs in vivo (T_max, C_max and C_max/AUC_0-t). (A1) Mean absorbed profiles of TMS tablets estimated using the DM, and the correlations between the values of k_a and (A2) C_max, (A3) C_max/AUC_0-t, (A4) T_max; (B1) mean absorbed profiles estimated using the L-R method, and the correlations between the values of k_a and (B2) C_max, (B3) C_max/AUC_0-t, (B4) T_max; (C1) mean absorbed profiles estimated using the STM, and the correlations between the values of k_a and (C2) C_max, (C3) C_max/AUC_0-t, (C4) T_max; (D1) mean absorbed profiles of CSC tablets estimated using the DM, and the correlations between the values of k_a and (D2) C_max, (D3) C_max/AUC_0-t, (D4) T_max; (E1) mean absorbed profiles estimated using the STM, and the correlations between the values of k_a and (E2) C_max, (E3) C_max/AUC_0-t and (E4) T_max. (F1) Mean absorbed profiles of TDF tablets obtained using the DM, and the correlations between the values of k_a and (F2) C_max, (F3) C_max/AUC_0-t, (F4) T_max; (G1) mean absorbed fraction versus time profiles of TDF tablets obtained using the STM, and the correlations between the values of k_a and (G2) C_max, (G3) C_max/AUC_0-t, and (G4) T_max. Data of the correlations for TDF tablets are presented as mean ± standard deviation. All correlations were investigated using Pearson’s correlation analysis (p < 0.05 indicates good correlation). CSC: candesartan cilexetil; DM: direct method; L-R method: Loo-Riegelman method; PK: pharmacokinetic; STM: statistical moment data; TDF: tenofovir disoproxil fumarate; TMS: telmisartan.

The similarity in the estimated k_a between F_C1 and F_C2 led to nearly overlapped absorbed fraction-time profiles using the direct method (Figure 4D1). The estimated k_a values were positively correlated with both C_max and C_max/AUC_0-t (p < 0.01; Figures 4D2, D3) and negatively correlated with T_max (p < 0.001; Figure 4D4). However, these two profiles were not similar when estimated using the statistical moment method (Figure 4E1), which were inconsistent with their in vivo performance (Figure 3B). The k_a estimated using the statistical moment method also showed only slight correlation with both C_max and C_max/AUC_0-t (Figures 4E2, E3), while it was positively correlated with T_max (Figure 4E4).

The mean absorbed fraction-time profiles of the TDF tablets were obtained after the k_a values were estimated using both the direct method (Figure 4F1) and the statistical moment method (Figure 4G1). The absorptions of TDF in both formulations (F_D1 and F_D2) in the fasted state were higher than that in the fed state when assessed using the direct method. The estimated k_a values for F_D1 and F_D2 were strongly correlated with the corresponding average values of C_max, C_max/AUC_0-t, and T_max in both the fed and fasted states (R > 0.96, p < 0.05; Figures 4F2–F4). However, data from the absorption curves were inconsistent with the in vivo concentration data (Figure 3C) when assessed using the statistical moment method (Figure 4G1). Furthermore, the k_a estimated using the statistical moment method had only slight correlations with C_max, C_max/AUC_0-t, and T_max (p > 0.6; Figures 4G2–G4).

4 Discussion

The k_a, k₁₂, k₂₁, and k₁₀ values of drugs with the two-compartment model have shown variation owing to their physicochemical properties and dosage form (Byron and Notari, 1976), but the relationships between these parameters have not been reported. The accuracies of the estimated k_a, k₁₂, k₂₁, and k₁₀ values for the IR formulations of drugs are higher than those for the extended-release formulations because the former is affected at a lesser rate by the rate of dissolution in vivo (Franek et al., 2015). In this case, 36 IR dosage forms with different T_max (0.75–4.0 h) and t_1/2 (1.2–52.8 h) values, as well as satisfying the two-compartment model, were used to estimate the k_a, k₁₂, k₂₁, and k₁₀ values (Table 1), mainly for investigating the relationships between these parameters. In theory, the value of k₁₂ should be higher than that of k₂₁ (k₁₂ > k₂₁) because of the dynamics of drug distribution from the central compartment to the peripheral compartment. Meanwhile, the absorption rate of a drug needs to be greater than the sum of the distribution and elimination rates (k_a > k₁₂ + k₁₀), so that the concentration of a drug can be determined in the plasma after extravascular administration. Elucidating the relationships between these parameters could circumvent any void in setting data for investigations using the direct method. However, the k_a, k₁₂, k₂₁, and k₁₀ values of 36 IR dosage forms were assessed only by preliminary quantification to observe their relationships using WinNonlin software (built-in residual method). As expected, the k_a values of TMS, CSC, and TDF estimated using WinNonlin software were different from the values of k_a calculated using the direct method (Tables 1, 4).

The range of T_max for all setting groups was 0.5–4.0 h (Table 2), which was representative of the in vivo performance of most of the IR dosage forms in practice. The k_a estimated using the direct method was evidently affected by k_max, T_max, and τ values (Eq. 6), and the negative correlation between k_max and T_max (or τ) could ensure that the estimated k_a was accurate and independent of the changes in k₁₂, k₂₁, and k₁₀ (Figures 2D–F). The statistical moment method, as a non-compartmental method, should be non-sensitive to the changes in compartmental parameters (i.e., k₁₂, k₂₁, and k₁₀). However, the most values of k_a estimated using the statistical moment method had low levels (Table 2) because small values of k_T were obtained from the terminal sampling point (Riegelman and Collier, 1980). The estimated values of k_a were undoubtedly and sensitively affected by k₁₂, k₂₁, and k₁₀ values when applying the Loo-Riegelman method (Figures 2D–F), according to Eqs 14, 15 (Byron and Notari, 1976; Zeng et al., 2020). However, all the estimated values of k_a were higher than the true values of k_a, which might have been attributed to the difference in the number of time points in the unabsorbed fraction (1–F_abs%) that were fitted in the linear regression analysis. Moreover, the mean absolute RE of the k_a estimated using the Loo-Riegelman method had a relatively large value because of a few outliers (RE > 100%) that negatively affected the fitting precision, but it also had a better estimating accuracy than that of the statistical moment method (Figures 2B, C).

The three model drugs, whose T_max (0.5–4.0 h) values were different, were selected to explore the accuracy and scopes of the direct method in practice (Oh et al., 2017; Patel et al., 2017; Lu et al., 2019). The empirical k_a values of these drugs could not be obtained from previously reported studies. Therefore, the relationships between the absorption rate and the PK data were investigated to indirectly verify the accuracy of the direct method. Generally, the high absorption rate of the drugs showed a large C_max and a short T_max (Han et al., 2018). The values of C_max and C_max/AUC_0-t represented the in vivo exposure of the drugs, which were also related to the k_a values (Tozer et al., 1996). The k_a values of the three model drugs estimated using the direct method were positively correlated with the in vivo exposure of TMS (Figures 4A2, A3), CSC (Figures 4D2, D3), and TDF (Figures 4F2, F3), which might be advantageous in predicting the in vivo exposure of the different formulations. Negative correlations were observed between k_a and T_max (Figures 4A4, 4D4, 4F4), which were consistent with previous literature results (Han et al., 2018). However, both the Loo-Riegelman method (used only for TMS) and the statistical moment method failed to establish the correlation between the estimated k_a and their C_max, C_max/AUC_0-t, and T_max values. The k_a of CSC estimated using the statistical moment method was positively correlated with T_max, which was contrary to the literature precedent (Han et al., 2018).

The PK parameters of drugs, including C_max, AUC_0-t, T_max, and k_a, are generally affected by the intake of high-fat foods (Winter et al., 2013). In this study, the decreased k_a and C_max values and prolonged T_max values of TDF in the fed states were compared to those in the fasted state. The similar in vivo results of TDF between the fed and fasted states were consistent with that reported in a previous study (Lu et al., 2013). A difference in the estimated k_a of TDF was observed between the fed and fasted states when assessed using the direct method (Table 4), and linear correlations with C_max, C_max/AUC_0-t, and T_max values were observed (Figures 4F2–F4). On the contrary, the statistical moment method failed to produce a difference in the estimated k_a between the fed and fasted states, and no correlations were observed between the estimated k_a and their C_max, C_max/AUC_0-t, and T_max values (Figures 4G2–G4). Therefore, these results corroborated that the direct method was sensitive and accurate when estimating k_a for applications related to PK evaluations.

Although the absorption of a drug after oral administration was terminated at a finite time point after T_max in a previous study (Macheras, 2019), the exact endpoint was unclear. In this study, τ represented the endpoint of the post-absorption phase in the PK profiles, at which the absorption process had finished. The values of τ for TMS, CSC, and TDF tablets were obtained in the fed and/or fasted states (Table 4). The average values of F_abs for these drugs exceeded 90% at the mean value of τ (Figures 4A1, 4D1, 4F1), which verified the inference of the direct method.

As the accuracies of k_max, τ, and T_max greatly affected the estimation of k_a, sufficient sampling points in PK studies might be needed to obtain accurate values of k_max, τ, and T_max. In the present study, the sampling points for PK studies of the three model drugs in humans were designed as conventional sampling points (such as 0.17 h, 0.33 h, 0.5 h, 1 h, … ), rather than sampling points with intervals of 0.1 h for the setting data. The conventional points did not significantly affect the calculation of k_a, demonstrating that the direct method was highly feasible for estimating the absorption rate of drugs in practical applications. However, more drugs fitting with the two-compartment PK model should be evaluated in further studies to verify the accuracy and applicability of the direct method.

5 Conclusion

In this study, the direct method was developed and used for estimating the k_a value of a drug with the two-compartment model using the equation ${\mathrm{T}}_{\max }=\frac{\ln {\mathrm{k}}_{\mathrm{a}}-\ln \frac{{\mathrm{\tau }*\mathrm{k}}_{\max }}{\mathrm{\tau }-{\mathrm{T}}_{\max }}}{{\mathrm{k}}_{\mathrm{a}}-\frac{{\mathrm{\tau }*\mathrm{k}}_{\max }}{\mathrm{\tau }-{\mathrm{T}}_{\max }}}$, wherein the values of T_max, k_max, and τ were readily obtained from the plasma drug concentration–time curves after extravascular administration. The k_a estimated using the direct method with the setting data had satisfactory accuracy compared with that obtained using both the Loo-Riegelman method and the statistical moment method. The k_a values of three model drugs (TMS, CSC, and TDF) were estimated by the direct method, which was consistent with the corresponding PK profiles. From these calculations, good correlations were established between the k_a values and other PK parameters that reflected the in vivo absorption of the drugs. These results substantiated the accuracy of the direct method in estimating the absorption rate of a drug, which is beneficial in practical applications where intravenous PK data cannot be obtained. The direct method is expected to provide valuable support for PK evaluation and IVIVC establishment.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by Chinese Food and Drug Administration (CFDA) and the Institutional Research Ethics Committee of Xiangya School of Pharmaceutical Sciences, Central South University. The patients/participants provided their written informed consent to participate in this study.

Author contributions

FL, HY, GZ, and LW participated the research design; FL, HY, and GZ conducted the research; FL, GZ, LW, and ZC performed data analysis; FL and GZ contributed to the writing of the manuscript.

Funding

The financial supported from the National Nature Science Foundation of China (Grant No. 82073932).

Acknowledgments

The authors are grateful for the technical supported from Hunan Huize Bio-pharmaceutical Co., Ltd.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdallah, O. M., Abdel-Megied, A. M., and Gouda, A. S. (2018). Development and validation of LC-MS/MS method for simultaneous determination of sofosbuvir and daclatasvir in human Plasma: Application to pharmacokinetic study. Biomed. Chromatogr. 32, e4186. doi:10.1002/bmc.4186

PubMed Abstract | CrossRef Full Text | Google Scholar

Albu, F., Georgita, C., David, V., and Medvedovici, A. (2007). Determination of glibenclamide in human plasma by liquid chromatography and atmospheric pressure chemical ionization/MS-MS detection. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 846, 222–229. doi:10.1016/j.jchromb.2006.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Apostolou, C., Kousoulos, C., Dotsikas, Y., Soumelas, G. S., Kolocouri, F., Ziaka, A., et al. (2008). An improved and fully validated LC-MS/MS method for the simultaneous quantification of simvastatin and simvastatin acid in human plasma. J. Pharm. Biomed. Anal. 46, 771–779. doi:10.1016/j.jpba.2007.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhadoriya, A., Shah, P. A., Shrivastav, P. S., Bharwad, K. D., and Singhal, P. (2019). Determination of terbinafine in human plasma using UPLC-MS/MS: Application to a bioequivalence study in healthy subjects. Biomed. Chromatogr. 33, e4543. doi:10.1002/bmc.4543

PubMed Abstract | CrossRef Full Text | Google Scholar

Byron, P. R., and Notari, R. E. (1976). Critical analysis of "flip-flop" phenomenon in two-compartment pharmacokinetic model. J. Pharm. Sci. 65, 1140–1144. doi:10.1002/jps.2600650804

PubMed Abstract | CrossRef Full Text | Google Scholar

Chae, S. I., Yoo, H. J., Lee, S. Y., Chung, E. K., Shim, W. S., and Lee, K. T. (2019). Development and validation of simple LC-MS-MS assay for the quantitative determination of ticagrelor in human plasma: Its application to a bioequivalence study. J. Chromatogr. Sci. 57, 331–338. doi:10.1093/chromsci/bmz001

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, B. M., Liang, Y. Z., Chen, X., Liu, S. G., Deng, F. L., and Zhou, P. (2006). Quantitative determination of azithromycin in human plasma by liquid chromatography-mass spectrometry and its application in a bioequivalence study. J. Pharm. Biomed. Anal. 42, 480–487. doi:10.1016/j.jpba.2006.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Li, L., Song, S., Du, Y., Jin, X., Ding, P., et al. (2018). Determination of lacidipine in human plasma by LC-MS/MS: Application in a bioequivalence study. Int. J. Clin. Pharmacol. Ther. 56, 493–500. doi:10.5414/CP203250

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, H. Y., Ngo, L., Kim, S. K., Choi, Y., and Lee, Y. B. (2018). Bioequivalence of a fixed-dose repaglinide/metformin combination tablet and equivalent doses of repaglinide and metformin tablets. Int. J. Clin. Pharmacol. Ther. 56, 292–300. doi:10.5414/CP203199

PubMed Abstract | CrossRef Full Text | Google Scholar

Choudhury, H., Gorain, B., Paul, A., Sarkar, P., Dan, S., Chakraborty, P., et al. (2017). Development and validation of an LC-MS/MS-ESI method for comparative pharmacokinetic study of ciprofloxacin in healthy male subjects. Drug Res. (Stuttg) 67, 94–102. doi:10.1055/s-0042-116593

PubMed Abstract | CrossRef Full Text | Google Scholar

FDA (2008). Candesartan cilexetil. Available at: https://www.accessdata.fda.gov/drugsatfda_docs/psg/Candesartan_Cilexetil_tab_20838_RC8-04.pdf.

Google Scholar

FDA (2012). Tenofovir disoproxil fumarate. Available at: https://www.accessdata.fda.gov/drugsatfda_docs/psg/Tenofovir%20Disoproxil%20Fumarate%20022577%20RC09-12.pdf.

Google Scholar

FDA (2003). U.S. Department of health and human services, food and drug administration. Center for drug evaluation and research. Guidance for industry. Bioavailability and bioequivalence studies for orally administered drug products-general considerations.

Google Scholar

Franek, F., Jarlfors, A., Larsen, F., Holm, P., and Steffansen, B. (2015). In vitro solubility, dissolution and permeability studies combined with semi-mechanistic modeling to investigate the intestinal absorption of desvenlafaxine from an immediate- and extended release formulation. Eur. J. Pharm. Sci. 77, 303–313. doi:10.1016/j.ejps.2015.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleiter, C. H., and Morike, K. E. (2002). Clinical pharmacokinetics of candesartan. Clin. Pharmacokinet. 41, 7–17. doi:10.2165/00003088-200241010-00002

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, A., Guttikar, S., Patel, Y., Shrivastav, P. S., and Sanyal, M. (2015). Reliable LC-MS/MS assay for the estimation of rilpivirine in human plasma: Application to a bioequivalence study and incurred sample reanalysis. Drug Test. Anal. 7, 290–299. doi:10.1002/dta.1665

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, A., Guttikar, S., Shrivastav, P. S., and Sanyal, M. (2013). Simultaneous quantification of prodrug oseltamivir and its metabolite oseltamivir carboxylate in human plasma by LC-MS/MS to support a bioequivalence study. J. Pharm. Anal. 3, 149–160. doi:10.1016/j.jpha.2012.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Y. R., Lee, P. I., and Pang, K. S. (2018). Finding T_max and C_max in multicompartmental models. Drug Metab. Dispos. 46, 1796–1804. doi:10.1124/dmd.118.082636

PubMed Abstract | CrossRef Full Text | Google Scholar

Kadam, R., Bourne, D., Kompella, U., and Aquilante, C. (2013). Effect of cytochrome P450 2C8*3 on the population pharmacokinetics of pioglitazone in healthy Caucasian volunteers. Biol. Pharm. Bull. 36, 245–251. doi:10.1248/bpb.b12-00657

PubMed Abstract | CrossRef Full Text | Google Scholar

Kearney, B. P., Flaherty, J. F., and Shah, J. (2004). Tenofovir disoproxil fumarate: Clinical pharmacology and pharmacokinetics. Clin. Pharmacokinet. 43, 595–612. doi:10.2165/00003088-200443090-00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, A., Dwivedi, S. P., and Prasad, T. (2019). Method validation for simultaneous quantification of olmesartan and hydrochlorothiazide in human plasma using LC-MS/MS and its application through bioequivalence study in healthy volunteers. Front. Pharmacol. 10, 810. doi:10.3389/fphar.2019.00810

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Shi, F., He, X., Jian, L., and Ding, L. (2016). A rapid and sensitive LC-MS/MS method for determination of lercanidipine in human plasma and its application in a bioequivalence study in Chinese healthy volunteers. J. Pharm. Biomed. Anal. 128, 67–72. doi:10.1016/j.jpba.2016.05.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Jia, Y., Chen, L., Ding, Y., Yang, J., Chen, M., et al. (2013). Pharmacokinetics and food interaction of a novel prodrug of tenofovir, tenofovir dipivoxil fumarate, in healthy volunteers. J. Clin. Pharm. Ther. 38, 136–140. doi:10.1111/jcpt.12023

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Yang, Y., Zhang, Q., Zhou, R., Liu, Z., and Hu, W. (2019). Pharmacokinetic and bioequivalence study of emtricitabine/tenofovir disoproxil fumarate tablets in healthy Chinese subjects. Int. J. Clin. Pharmacol. Ther. 57, 623–632. doi:10.5414/CP203533

PubMed Abstract | CrossRef Full Text | Google Scholar

Macheras, P. (2019). On an unphysical hypothesis of Bateman equation and its implications for pharmacokinetics. Pharm. Res. 36, 94. doi:10.1007/s11095-019-2633-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mcgregor, G. P. (2016). Pivotal bioequivalence study of Clopacin®, a generic formulation of clopidogrel 75 mg film-coated tablets. Adv. Ther. 33, 186–198. doi:10.1007/s12325-016-0290-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Najib, N. M., Idkaidek, N., Beshtawi, M., Mohammed, B., Admour, I., Alam, S. M., et al. (2005). Bioequivalence assessment of lovrak (julphar, UAE) compared with zovirax (glaxo wellcome, UK)--Two brands of acyclovir--in healthy human volunteers. Biopharm. Drug Dispos. 26, 7–12. doi:10.1002/bdd.426

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, M., Park, S. E., Ghim, J. L., Choi, Y. K., Shim, E. J., Shin, J. G., et al. (2017). Comparative pharmacokinetics of a fixed-dose combination vs concomitant administration of telmisartan and S-amlodipine in healthy adult volunteers. Drug Des. Devel Ther. 11, 3543–3550. doi:10.2147/DDDT.S148534

PubMed Abstract | CrossRef Full Text | Google Scholar

Parekh, J. M., Sutariya, D. K., Vaghela, R. N., Sanyal, M., Yadav, M., and Shrivastav, P. S. (2012). Sensitive, selective and rapid determination of bupropion and its major active metabolite, hydroxybupropion, in human plasma by LC-MS/MS: Application to a bioequivalence study in healthy Indian subjects. Biomed. Chromatogr. 26, 314–326. doi:10.1002/bmc.1660

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J. H., Park, Y. S., Rhim, S. Y., Jhee, O. H., Kim, S. H., Yang, S. C., et al. (2009). Quantification of isradipine in human plasma using LC-MS/MS for pharmacokinetic and bioequivalence study. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 877, 59–64. doi:10.1016/j.jchromb.2008.11.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, M. S., Shim, W. S., Yim, S. V., and Lee, K. T. (2012). Development of simple and rapid LC-MS/MS method for determination of celecoxib in human plasma and its application to bioequivalence study. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 902, 137–141. doi:10.1016/j.jchromb.2012.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, D. P., Sharma, P., Sanyal, M., Singhal, P., and Shrivastav, P. S. (2012). Challenges in the simultaneous quantitation of sumatriptan and naproxen in human plasma: Application to a bioequivalence study. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 902, 122–131. doi:10.1016/j.jchromb.2012.06.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, R., Palmer, J. L., Joshi, S., Di Cio Gimena, A., and Esquivel, F. (2017). Pharmacokinetic and bioequivalence studies of a newly developed branded generic of candesartan cilexetil tablets in healthy volunteers. Clin. Pharmacol. Drug Dev. 6, 492–498. doi:10.1002/cpdd.321

PubMed Abstract | CrossRef Full Text | Google Scholar

Rezende, K. R., Mundim, I. M., Teixeira, L. S., Souza, W. C., Ramos, D. R., Cardoso, C. R., et al. (2007). Determination of captopril in human plasma, using solid phase extraction and high-performance liquid chromatography, coupled to mass spectrometry: Application to bioequivalence study. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 850, 59–67. doi:10.1016/j.jchromb.2006.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Rezk, M. R., and Badr, K. A. (2014). Development, optimization and validation of a highly sensitive UPLC-ESI-MS/MS method for simultaneous quantification of amlodipine, benazeprile and benazeprilat in human plasma: Application to a bioequivalence study. J. Pharm. Biomed. Anal. 98, 1–8. doi:10.1016/j.jpba.2014.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Rhim, S. Y., Park, J. H., Park, Y. S., Kim, D. S., Lee, M. H., Shaw, L. M., et al. (2009). A sensitive validated LC-MS/MS method for quantification of itraconazole in human plasma for pharmacokinetic and bioequivalence study in 24 Korean volunteers. Pharmazie 64, 71–75.

PubMed Abstract | Google Scholar

Riegelman, S., and Collier, P. (1980). The application of statistical moment theory to the evaluation of in vivo dissolution time and absorption time. J. Pharmacokinet. Biopharm. 8, 509–534. doi:10.1007/BF01059549

PubMed Abstract | CrossRef Full Text | Google Scholar

Shah, P. A., and Shrivastav, P. S. (2018). Determination of silodosin and its active glucuronide metabolite KMD-3213G in human plasma by LC-MS/MS for a bioequivalence study. Biomed. Chromatogr. 32, e4041. doi:10.1002/bmc.4041

PubMed Abstract | CrossRef Full Text | Google Scholar

Sora, I., Cristea, E., Albu, F., Udrescu, S., David, V., and Medvedovici, A. (2009). LC-MS/MS assay of quinapril and its metabolite quinaprilat for drug bioequivalence evaluation: Prospective, concurrential and retrospective method validation. Bioanalysis 1, 71–86. doi:10.4155/bio.09.5

PubMed Abstract | CrossRef Full Text | Google Scholar

Stangier, J., Su, C. A., and Roth, W. (2000). Pharmacokinetics of orally and intravenously administered telmisartan in healthy young and elderly volunteers and in hypertensive patients. J. Int. Med. Res. 28, 149–167. doi:10.1177/147323000002800401

PubMed Abstract | CrossRef Full Text | Google Scholar

Tozer, T. N., Bois, F. Y., Hauck, W. W., Chen, M. L., and Williams, R. L. (1996). Absorption rate vs. exposure: Which is more useful for bioequivalence testing? Pharm. Res. 13, 453–456. doi:10.1023/a:1016061013606

PubMed Abstract | CrossRef Full Text | Google Scholar

Vancea, S., Gall, Z., Donath-Nagy, G., and Borka-Balas, R. (2014). Rapid LC-MS/MS method for determination of drotaverine in a bioequivalence study. J. Pharm. Biomed. Anal. 98, 417–423. doi:10.1016/j.jpba.2014.06.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Vlase, L., Imre, S., Muntean, D., and Leucuta, S. E. (2007). Determination of loratadine and its active metabolite in human plasma by high-performance liquid chromatography with mass spectrometry detection. J. Pharm. Biomed. Anal. 44, 652–657. doi:10.1016/j.jpba.2006.08.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner, J. G. (1975). Application of the Loo-Riegelman absorption method. J. Pharmacokinet. Biopharm. 3, 51–67. doi:10.1007/BF01066595

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Hu, C., Gao, D., Zhao, Z., Chen, X., Hu, X., et al. (2019). Pharmacokinetics and bioequivalence of generic and branded abiraterone acetate tablet: A single-dose, open-label, and replicate designed study in healthy Chinese male volunteers. Cancer Chemother. Pharmacol. 83, 509–517. doi:10.1007/s00280-018-3754-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Qin, Z., Ren, G., Zhai, Y., Fu, K., Lu, C., et al. (2020). Development of a sensitive UPLC-MS/MS assay for domperidone and pharmacokinetics of domperidone tablet formulations in fasting and fed Chinese healthy subjects. Int. J. Clin. Pharmacol. Ther. 58, 177–182. doi:10.5414/CP203529

PubMed Abstract | CrossRef Full Text | Google Scholar

Winter, H., Ginsberg, A., Egizi, E., Erondu, N., Whitney, K., Pauli, E., et al. (2013). Effect of a high-calorie, high-fat meal on the bioavailability and pharmacokinetics of PA-824 in healthy adult subjects. Antimicrob. Agents Chemother. 57, 5516–5520. doi:10.1128/AAC.00798-13

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Z., Schwartz, J. B., Sugita, E. T., and Foehl, H. C. (1996). Five modified numerical deconvolution methods for biopharmaceutics and pharmacokinetics studies. Biopharm. Drug Dispos. 17, 521–540. doi:10.1002/(SICI)1099-081X(199608)17:6<521::AID-BDD974>3.0.CO;2-A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaid, A. N., Al Ramahi, R., Cortesi, R., Mousa, A., Jaradat, N., Ghazal, N., et al. (2016). Investigation of the bioequivalence of rosuvastatin 20 mg tablets after a single oral administration in Mediterranean Arabs using a validated LC-MS/MS method. Sci. Pharm. 84, 536–546. doi:10.3390/scipharm84030536

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, Y., Liu, J., Liu, W., Jiang, S., Wang, S., and Cheng, Z. (2020). A new method for the estimation of absorption rate constant in two-compartment model by extravascular administration. J. Pharm. Sci. 109, 1802–1810. doi:10.1016/j.xphs.2020.01.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, G., Sun, M., Jiang, S., Wang, L., Tan, Y., Wang, L., et al. (2021). Investigating a modified apparatus to discriminate the dissolution capacity in vitro and establish an IVIVC of mycophenolate mofetil tablets in the fed state. J. Pharm. Sci. 110, 1240–1247. doi:10.1016/j.xphs.2020.10.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L. Z., Zhong, G. P., Bi, H. C., Ding, L., Deng, Y., Guan, S., et al. (2008). Determination of levonorgestrel in human plasma by liquid chromatography-tandem mass spectrometry method: Application to a bioequivalence study of two formulations in healthy volunteers. Biomed. Chromatogr. 22, 519–526. doi:10.1002/bmc.963

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhi, J. G. (1990). Unique pharmacokinetic characteristics of the one-compartment first-order absorption model with equal absorption and elimination rate constants. J. Pharm. Sci. 79, 652–654. doi:10.1002/jps.2600790725

PubMed Abstract | CrossRef Full Text | Google Scholar