DACPGTN: Drug ATC Code Prediction Method Based on Graph Transformer Network for Drug Discovery

The Anatomical Therapeutic Chemical (ATC) classification system is a drug classification scheme proposed by the World Health Organization, which is widely used for drug screening, repositioning, and similarity research. The ATC system assigns different ATC codes to drugs based on their anatomy, pharmacological, therapeutics and chemical properties. Predicting the ATC code of a given drug helps to understand the indication and potential toxicity of the drug, thus promoting its use in the therapeutic phase and accelerating its development. In this article, we propose an end-to-end model DACPGTN to predict the ATC code for the given drug. DACPGTN constructs composite features of drugs, diseases and targets by applying diverse biomedical information. Inspired by the application of Graph Transformer Network, we learn potential novel interactions among drugs diseases and targets from the known interactions to construct drug-target-disease heterogeneous networks containing comprehensive interaction information. Based on the constructed composite features and learned heterogeneous networks, we employ graph convolution network to generate the embedding of drug nodes, which are further used for the multi-label learning tasks in drug discovery. Experiments on the benchmark datasets demonstrate that the proposed DACPGTN model can achieve better prediction performance than the existing methods. The source codes of our method are available at https://github.com/Szhgege/DACPGTN.

1 Introduction

Drug research and development is time-consuming and costly. A new drug, from development to launch, takes decades of research and hundreds of millions of dollars. How to find new indications from existing approved drugs and reduce the cost of research discovery is a hot field in bioinformatics (Pushpakom et al., 2019; Jarada et al., 2020). The World Health Organization has established a complete drug classification system, Anatomical Therapeutic Chemical (ATC) (MacDonald and Potvin, 2004). Specifically, the standard ATC code in the ATC system can be used to represent drug class information, which facilitates the use of drugs during the treatment phase. When the ATC code of a drug compound is known, can be inferred its active ingredient, therapeutic, pharmacological, and chemical properties. Therefore, predicting the ATC code of a drug helps to use the drug correctly or identify novel potential indications, and speed up the drug development process, which is a common idea for drug repositioning research. (Hutchinson et al., 2004). The ATC code system divides drugs into five levels, based on the first-level of ATC codes, drugs are classified into 14 anatomical classes including Alimentary tract and metabolism, Blood and blood forming organs, Cardiovascular system, Dermatologicals, Genitourinary system and sex hormones, Systemic hormonal preparations, excluding sex hormones and insulins, Anti-infectives for systemic use, Antineoplastic and immunomodulating agents, Musculoskeletal system, Nervous system, Antiparasitic products, insecticides and repellents, Respiratory system, Sensory organs, Various. For a drug, it may belong to more than one class in first-level at the same time.

There are a large number of drugs without ATC codes in widely used drug information databases. ATC code prediction of new or existing drugs using traditional experimental methods is cumbersome and time-consuming. The development and application of machine learning provide the possibility to realize the rapid classification of drugs ATC code (Dunkel et al., 2008; Wu et al., 2013). In recent years, some multi-label classification methods have been proposed for drug ATC Code prediction. Chen et al. (2012), firstly proposed a method to classify drug ATC code by integrating drug chemistry-chemistry interaction information and chemistry-chemistry similarity information, and constructed benchmark dataset for the first-level code prediction of drug ATC code. Based on this benchmark dataset, some classification methods integrating multiple drug information to predict drug ATC codes are proposed. Cheng et al. (2017b) proposed a multi-label Gaussian kernel regression classifier named iATC-mISF. Based on medicinal chemical–chemical interaction, structure, and fingerprint similarity, assign the first-level ATC code to drugs. After that, Cheng et al. (2017a) improved the classifier’s performance by further integrating the predictor iATC-mDO based on the drug ontology information (Degtyarenko et al., 2007). Based on this, iATC-mISF has been upgraded to iATC-mHyb. Nanni and Brahnam (2017) developed a multi-label classifier EnsLIF based on gradient histogram algorithm, which constructs the one-dimensional feature vector of drug compounds into a two-dimensional matrix. Zhou et al. (2020a) constructed multiple drug interaction networks, extracted the drug features in the network through the network embedding algorithm Mashup (Cho et al., 2016), and transformed the original multi-label classification problem into multiple binary classification problems by using Random k-labelsets (RAKEL) algorithm (Tsoumakas and Vlahavas, 2007). In the classification stage, the classical machine learning algorithm support vector machine (SVM) (Cortes and Vapnik, 1995) is used to construct the classifier iATC-NRAKEL, which has achieved good results. Based on the iATC-NRAKEL classifier, Zhou et al. (2020b) proposed a multi-label classifier iATC-FRAKEL only used the fingerprints of drugs as feature. In addition, web services are provided. By integrating drug-drug interaction information, structural similarity, and fingerprint similarity, and using the NLSP method (Szymański et al., 2016) to explore the correlation between labels. Wang et al. (2019b) proposed a method ATC-NLSP, to predict the first-level ATC code of drugs, which uses a machine learning framework to provide better prediction results.

With the successful application of deep learning technology in many fields, Nanni et al. (2020) proposed a first-level ATC code multi-label classifier system (FUS3) by integrating multiple deep learning methods. The model used convolutional neural network (CNN) and Long-Short-Term Memory network (LSTM) (Hochreiter and Schmidhuber, 1997) to extract implicit features, then train two calssifiers to identify the ATC codes of drugs using extracted features. In the latest study, Zhao et al. (2021) proposed a new drug ATC code end-to-end prediction model CGATCPred, which utilized a multi-layer Convolutional Neural Network (CNN) to extract composite features from multiple types of drug features. The association graph structure of ATC code labels is established and combined with the word embedding information, the GCN (Kipf and Welling, 2016) network is applied to extract the label information. New features were obtained based on composite features and the generated label information. The generated features were spliced with the composite features extracted from the CNN layer, and then were input to the fully connected neural network layer to predict the ATC code of the drugs.

For the ATC code prediction problem, most of the existing classification methods generally consider the information of the drug itself or the relationships between the ATC code and drugs. These approaches ignore the potential importance of other relevant information in drug ATC code prediction, such as target protein and disease information associated with drugs. Several studies have demonstrated that similar drugs have similar in chemical properties, indications, etc (Chiang and Butte, 2009; Li and Lu, 2012). Based on this property, the general hypothesis is that when two drugs act on the same target protein or disease, or they have multiple interactions between two drugs and target protein or disease, they may have the same ATC code labels.

In this article, to improve the performance of drug ATC code identification, we proposed a novel drug ATC code prediction method based on the Graph Transformer Network (Yun et al., 2019). Traditional deep learning frameworks have some limitations (Zhang et al., 2018; Wang et al., 2019a). For example, it cannot effectively exploit the interaction information in heterogeneous networks or requires predefined fixed interactions between nodes. GTN model is a self-learning method for heterogeneous graphs. It uses graph transformer layer to learn potential interactions information between different nodes from multiple heterogeneous graphs (Shi et al., 2016) and apply learned information to node classification tasks. The crucial idea of GTN is heterogeneous network representation learning, which is suitable for exploring the interaction between different types of nodes is helpful for the performance improvement of classification tasks. For drug ATC code prediction, we integrate drugs and drug-related biomedical entities including targets and diseases. Then, we use the known interactions information to construct a set of heterogeneous networks, which contains information about different nodes. GTN model can be used to find potential interactions between different entities from these constructed heterogeneous networks, and these potential interactions can help to predict the ATC code of drugs. Therefore, a new first-level drug ATC code prediction model DACPGTN is proposed based on GTN.

DACPGTN predicts the first-level ATC code for a given drug by applying biomedial features and interactions of drugs, diseases and targets. In the study, drug-drug similarity information was obtained by integrating different types of compound interactions. Meanwhile, the similarity information of drug-related target proteins and diseases is calculated based on the known interactions between biomedical entities. The similarity information was used to construct a composite feature matrix. Next, we consider the introduction of drug-target protein, drug-disease and target protein-disease interactions information. Based on the known interactions information, a set of interaction heterogeneous networks between different biomedical entities are constructed. Then, the graph structure of the potential interactions information between drug-target protein-disease can be obtained by using the graph transformer layer. Finally, the composite feature matrix and the learned potential interactions information networks are fed into the prediction module for learning. According to the above steps, we can obtain the final prediction of the drug ATC code. Experiments on the benchmark datasets demonstrate that the DACPGTN model can achieve better prediction performance than the existing methods.

The main contributions of this article are as follows:

1) For the drug ATC code prediction task, the DACPGTN model considers the impact of integration drug-related biomedical entity information including target proteins and diseases on drug ATC code prediction performance.

2) By utilizing graph transformer network and multiple heterogeneous networks, DACPGTN learns potential valuable interactions information for identifying ATC code for drugs.

3) In this study, the GTN model is improved to address the problem of drug ATC code prediction. The previous research transformed the drug ATC code prediction problem into multiple independent binary classification problems (Kumari and Srivastava, 2017). By using cross-entropy loss function and softmax function, we improved the GTN model and solved the class-imbalance and complex parameter settings for model training. Moreover, prediction performance can be improved by using linear layers and adding Dropout layers between layers.

2 Materials

2.1 Dataset

2.1.1 Drugs and Anatomical Therapeutic Chemical Codes

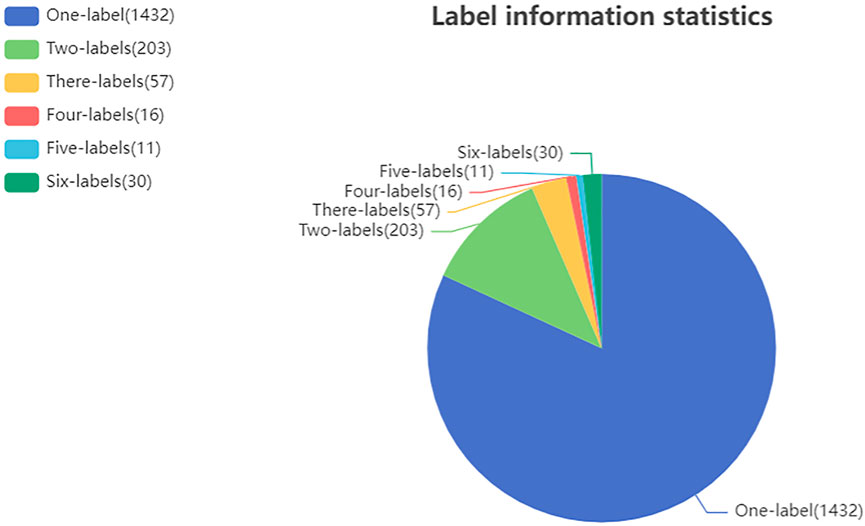
For the ATC Code prediction problem, Chen et al. (2012) constructed benchmark dataset to facilitate comparison of models at the first-level of the ATC code. The benchmark dataset contains 3,883 drugs with one or more first-level classes of the ATC code. Moreover, we have collected drug related target proteins and diseases from the KEGG (Kanehisa and Goto, 2000) and Drugbank (Wishart et al., 2008), which are publicly available databases involving substantial data describing drugs, diseases, target proteins and interactions among them. Filtering the collected data revealed that 1,749 out of 3,883 drugs have target or disease information. Then, these 1,749 drugs were used as the benchmark dataset in our experiments. In this study, the prediction of a drug’s first-level ATC code is formulated as a multi-label problem (Tsoumakas and Katakis, 2007). For each given drug, it may have two or more labels to annotate its classification. The statistics for ATC code label information of all drugs in our dataset is shown in Figure 1.

FIGURE 1

FIGURE 1. Benchmark dataset label information analysis.

Meanwhile, the dataset can be represented as a set of elements as: S = S₁ ∪ S₂ ∪ S₃⋯ ∪ S₁₃ ∪ S₁₄, where S_i represents drugs in the ith class. Let D_i represents the ith drug, and $j\in \left\{1,2,\cdots ,14\right\}$ represents the label of drug-class. The 1,749 drug compounds in the dataset can be classified into 14 ATC classes, as shown in Table 1. The ATC code labels for each given drug can be represented by a 14-bit binary vector defined as $Lable\left(D_i\right)=\left[L_{i1},L_{i2},L_{i3},\cdots ,L_{\mathit{i13}},L_{\mathit{i14}}\right]\left(i=\mathrm{1,2,3},\dots ,1749\right)$. Where L_ij represents the relationship between drug D_i and first-level ATC code class j. The value of L_ij is defined as follows:

$L_{ij}=\left\{\begin{array}{c}\begin{array}{cc}1\hfill & ifDrugibelongstoclassj\hfill \end{array}\hfill \\ \begin{array}{cc}0\hfill & else\hfill \end{array}\hfill \end{array}\right.$

TABLE 1

TABLE 1. The 1749 drug compounds in the benchmark dataset are broken down into 14 ATC classes.

2.1.2 Drug Targets and Indications

As mentioned above, the target proteins and diseases associated with 1749 drugs in the experiment were extracted from KEGG (Kanehisa and Goto, 2000) and Drugbank (Wishart et al., 2008), the two most widely used drug information databases. Specifically, the drug-related target proteins in the experiment were obtained from Drugbank, and we pre-processed the available information using the conversion tool provided on the Uniprot website to obtain 982 targets associated with the 1,749 drugs. Then, the drug-related diseases in the experiment were obtained from the KEGG database, and based on the known interactions information, a total of 355 related diseases were obtained. Table 2 summarizes the dataset in terms of numbers of drugs, target proteins, and diseases, as well as the interactions among them.

TABLE 2

TABLE 2. Statistics of the Benchmark standard dataset used in this study.

2.2 Construction of Similarity Matrix and Heterogeneous Networks

2.2.1 Drug, Target, and Disease Similarity Matrix

In this study, seven types of drug-drug similarity information for 1749 drugs extracted from the previous literature (Zhao et al., 2021). SM_Sim, SM_Exp, SM_Dat, SM_Tex, SM_Com were obtained from the interaction information of “similarity”, “experimental”, “database”, “text mining” and “Combined score” between drug pairs. SM_cp and SM_sub were obtained using the compound similarity calculation tools SIMCOMP and SUBCOMP provided by the KEGG dataset. A single data source may be incomplete or limited, and it is extremely important to integrate various biomedical data from multiple sources in practice (Luo et al., 2021). Data integration helps to improve the accuracy of the data and the performance of drug repositioning, and we used averaging operations on the seven similarity matrices to obtain the final drug-drug similarity score matrix M_RR.

For the 982 target proteins used in the experiments, combined score between proteins were obtained from the String library (Szklarczyk et al., 2019) to construct a protein-protein interaction score matrix. The combined score represents interaction strength between the two proteins. The larger the combined score, the stronger the interaction between the two proteins. After processing with the min-max normalization method, protein-protein similarity scores matrix M_TT is obtained.

Based on the hypothesis that similar drugs may treat similar diseases, we integrated disease similarity information for identifying the key features of drugs to assist the ATC code prediction in our study. Disease similarity is calculated by utilizing known interaction information between diseases and drugs (Luo et al., 2016). Specifically, for the 355 diseases in our experiments, we construct a drug-disease interactions matrix by using all drugs in the Chen et al. (2012) benchmark dataset. As for this drug-disease interactions matrix, if there exists an interaction between drug R_i and disease D_j, the edge weight of R_i and D_j is initially assigned as 1 and otherwise 0. Finally, the Pearson correlation coefficient (Benesty et al., 2009) of the matrix is calculated to obtain the disease-disease similarity matrix M_DD.

2.2.2 Drug-Target-Disease Heterogeneous Networks

We collected the known interactions information of the three biomedical entity nodes of drugs, target proteins, and diseases in the KEGG and Drugbank databases. The known interactions information is used to construct the corresponding heterogeneous network.

More specifically, we let $R=\left\{R_1,R_2,\cdots ,R_m\right\}$ denotes m drugs, $T=\left\{T_1,T_2,\cdots ,T_q\right\}$ denotes the q targets and $D=\left\{D_1,D_2,\cdots ,D_n\right\}$ denotes the n disease. The drug-target network contains m drugs and q targets, if there exists an interaction between drug R_i and target T_j, the edge weight of R_i and T_j is initially assigned as 1 and otherwise 0. Likewise, the drug-disease network includes m drugs and n diseases, if there exists an interaction between drug R_i and disease D_j, the edge weight of R_i and D_j is initially assigned as 1 and otherwise 0. Meanwhile, the target-disease network consists of q targets and n diseases, if there exists an interaction between target T_i and disease D_j, the edge weight of T_i and D_j is initially assigned as 1 and otherwise 0. H_RT, H_DD and H_TD are defined as the interaction matrices of drug-target network, drug-disease network and target-disease network, respectively.

3 Drug Anatomical Therapeutic Chemical Code Prediction Model Based on GTN

In this study, we have proposed a DACPGTN model for multi-label prediction of drug ATC code based on the GTN model. We first integrate the drugs and their associated target proteins and diseases, and construct a composite feature matrix by using the similarity information of the three biomedical entities as features. Meanwhile, a set of heterogeneous networks are constructed based on the known interactions information between different biomedical entities. Based on the Graph Transformer Network (Yun et al., 2019), the potential interactions information between drug-target-disease is obtained from these heterogeneous networks, which has an impact on the prediction of drug ATC code. Then, the constructed composite feature matrix and the learned potential interactions information between biomedical entities are fed into the end-to-end prediction module to obtain the ATC code prediction results for a given drug. The overall framework of the DACPGTN model is shown in Figure 2.

FIGURE 2

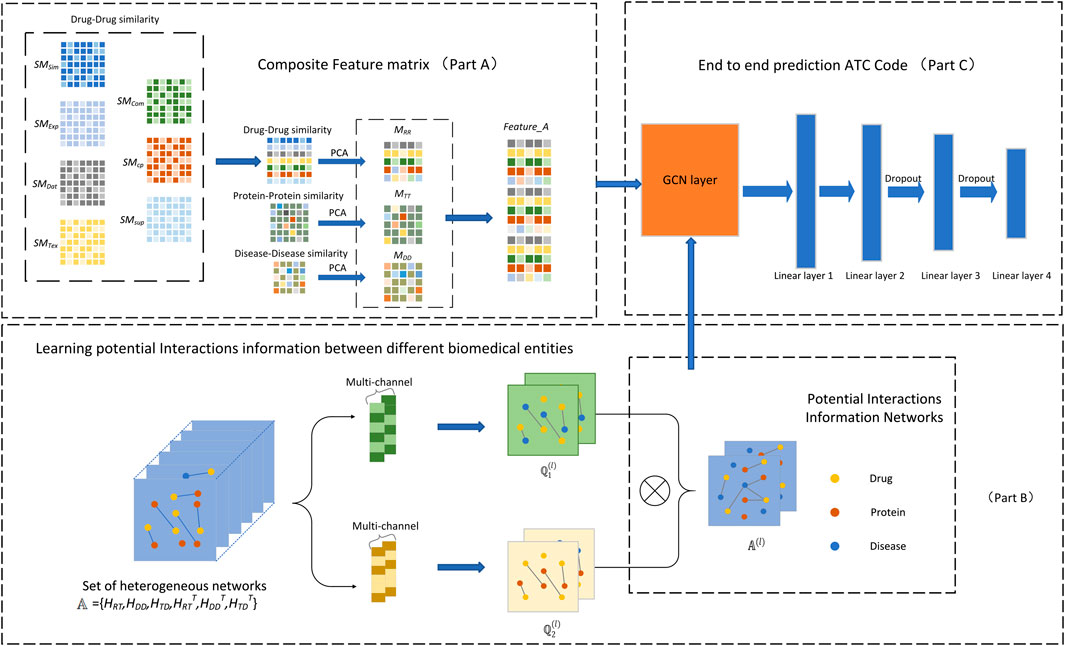
FIGURE 2. Overall framework of DACPGTN. The feature information of different biomedical entities is integrated to construct a composite feature matrix as the node feature input of the prediction module (Part A). The graph transformer layer is used to obtain the potential interactions information between different biomedical entities from heterogeneous networks set (Part B). The prediction stage uses the composite feature matrix and the learned Potential Interactions Information Networks to obtain prediction results (Part C).

3.1 Construction of Composite Feature Matrix

The similarity information of the three biomedical entities including drugs, targets and diseases is used to construct similarity matrix representing their features. Principal component analysis (PCA) (Abdi and Williams, 2010), commonly used technique for dimension reduction, is used to project drugs, targets and diseases into a low-dimensional space. Then, these low-dimensional matrices are unified to obtain the corresponding feature matrix. Using PCA can remove the noise data to a certain extent, maximize the retention features at the same time, provide valuable information for drug ATC code prediction. It is verified experimentally that the model has the best training effect when the dimension is 300. After unifying the feature dimensions, the feature matrices of the three biomedical entities are spliced to obtain the final node composite feature matrix $Feature\text{\_}A=\left[M_{RR};M_{TT};M_{DD}\right]$ (Part A of Figure 2).

3.2 Learning Potential Interactions Between Entities Based on Graph Transformer Layer

In this study, the graph transformer model is applied to learn valuable interactions information between drugs, targets and diseases from the heterogeneous networks constructed above. The constructed drug-target heterogeneous network, drug-disease heterogeneous network, and target-disease heterogeneous network are sequentially transposed and the dimensions are unified. Then, the set of heterogeneous networks $\mathbb{A}=\left\{H_{RT},H_{DD},H_{TD},{H_{RT}}^T,{H_{DD}}^T,{H_{TD}}^T\right\}$is obtained. The graph transformer layer is used for set $\mathbb{A}$ to obtain networks of potential interactions information between three biomedical entities: drugs, target proteins and diseases. The transfer of interaction information between nodes is achieved by multiplication operations between different associated heterogeneous networks (Wang et al., 2019a) (Part B of Figure 2).

Specifically, the graph transformer layer is used to perform a soft selection of different edge types and composite relations (Chen et al., 2018) to find new graph structures from multiple candidate heterogeneous networks. The graph transformer layer is implemented as formula (1):

$Q=F\left(\mathbb{A};W_{\varphi }\right)=\varphi \left(\mathbb{A};softmax\left(W_{\varphi }\right)\right)(1)$

Where ϕ is the convolution layer and W_ϕ ∈ R^1×1×K is the parameter of the convolution layer ϕ.

The graph transformer layer selects different types of interaction matrices from the set $\mathbb{A}$. Then, a new graph structure is learned by matrix multiplication of the selected interaction matrices Q₁ and Q₂. The soft selection of the interaction matrix refers to obtaining non-negative weights from $softmax\left(W_{\phi }\right)$, and perform 1 × 1 convolution weighted summation over the candidate matrices in the heterogeneous network set $\mathbb{A}$. In the implementation process, the constructed interaction matrix is operated on graph transformer layer by Eq. 2–4, each Q₁ can be expressed as $Q_i=\sum _{t\in {\mathcal{T}}^e}{\alpha }_t^{(l)}{A}_t$, ${\mathcal{T}}^e$ represents the set of networks, l represents the l-th graph transformer layer, and ${\alpha }_t^{(l)}$ represents the weight of the current network matrix in the lth layer. The connection between different nodes is obtained by multiplication of different types of interaction matrices. For $\mathbb{A}$, the graph transformer layer is used to learn potential interactions information between the three biomedical entities to obtain a new graph information matrix.

When the weight-based graph structure is obtained, the multiplication operation between the new graph structures is performed. To improve numerical stability, the interaction matrix obtained for each layer is normalized by its degree matrix D⁻¹.

$Q_1=F\left(\mathbb{A};W_{\varphi }\right)=\varphi \left(\mathbb{A};softmax\left(W_{\phi }^1\right)\right)(2)$

$Q_2=F\left(\mathbb{A};W_{\varphi }\right)=\varphi \left(\mathbb{A};softmax\left(W_{\phi }^2\right)\right)(3)$

$A^{\left(l\right)}=D^{-1}{Q}_1{Q}_2(4)$

The graph transformer layer can also learn a variety of connection relationships between different node types. To learn multiple potential interaction information networks between biomedical entities simultaneously, we use C channels in parallel to accomplish this operation and add the identity matrix I to $\mathbb{A}$ for learning variable-length interaction information. By setting the output channels of the 1 × 1 convolution in the graph transformer layer to multi-channel C, the adjacency matrices Q₁, Q₂ become adjacency tensor ${\mathbb{Q}}_1^{(l)},{\mathbb{Q}}_2^{(l)}\in {\mathbf{R}}^{N\times N\times C}$. After stacking l graph transformer layers, the tensor ${\mathbb{A}}^{(l)}\in {\mathbf{R}}^{N\times N\times C}$ is obtained.

In order to discover potential interactions between different nodes to inform the label prediction of drug nodes, the graph transformation layer is applied to the heterogeneous network sets $\mathbb{A}$ to learn the node interactions information in each associated heterogeneous network. For example, according to the relationship of drug-target protein, target protein-disease, etc., we can learn the interactions between the drug and potential disease, such as $\left(Drug\stackrel{D\text{\_}T}{\to }Target\stackrel{T\text{\_}D}{\to }Disease\right)$, etc.

3.3 Realization of End-To-End Prediction of DACPGTN Model

For the prediction module of the DACPGTN model, we use GCN as the feature extractor of the end-to-end module, and then take the node composite feature matrix and the learned potential interactions information as the input of the end-to-end prediction module. Embeddings of drug nodes are extracted through GCN, multiple linear layers and Dropout (Srivastava et al., 2014) layers are combined to predict the final drug ATC code. A novel loss function is introduced to complete the training of the model in this experiment. The detailed implementation process of the end-to-end prediction module is shown in Part C of Figure 2.

3.3.1 Graph Convolutional Neural Network Learning on Composite Feature Matrix and New Graph Structure

Graph Convolutional Neural Network (GCN) (Kipf and Welling, 2016) is a semi-supervised learning algorithm, which is used for the convolutional operation of the associated information graph structure and the composite feature matrix. For the GCN network, layer-to-layer propagation is performed according to formula (5):

$H^{\left(l+1\right)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)(5)$

Where $\tilde{A}$ is a new graph matrix generated by graph transformer layer, $\tilde{D}$ is the degree matrix of $\tilde{A}$, H is the input feature of the current GCN network layer, that is, the constructed node feature matrix, W^(l) ∈ R^d×d is a trainable weight matrix, H^(l+1) is the output of the feature matrix of the GCN network layer, and σ represents the activation function Relu. When the output channel of the graph transformer layer 1 × 1 convolution is set to multi-channel C, the GCN layer is applied to each channel of the tensor, and the multi-channel operation is performed through formula (6).

$Z={\parallel }_{i=1}^C\sigma \left({\tilde{D}}_i^{-1}{\tilde{A}}_i^{\left(l\right)}XW\right)(6)$

Where ∥ represents the connection operator, C represents the number of output channels, ${\tilde{A}}_i^{(l)}=A_i^{(l)}+I$ represents the ith adjacency matrix of the tensor ${\mathbb{A}}^{(l)}$ add the identity matrix I, ${\tilde{D}}_i$ represents the degree matrix of $A_i^{(l)}$, W ∈ R^d×d represents the trainable cross-channel shared weight matrix, X ∈ R^N×d represents the feature matrix Feature_A, N and d represent the number of biomedical entity nodes and the node features dimension in Feature_A, respectively.

The GCN network obtain dimension-specific drug node embeddings after a convolution operation on the node feature matrix Feature_A and the adjacency tensors ${\mathbb{A}}^{(l)}$. For the case of networks with few nodes, it has been shown in the literature that if a GCN network is stacked with multiple layers, the output features may be over-smoothed and vertices from different clusters may become indistinguishable (Li et al., 2018; Li et al., 2019). In this study, limited by few nodes, the GCN network used in the feature extraction module has only one layer. The drug nodes embedding extracted by the GCN network is used as the input information for the next part of the linear layers.

3.3.2 Transformation of Multi-Label Problem

As a multi-label classification problem, drug ATC code prediction differs from the traditional single-label multi-classification task. It requires that the prediction output of the model is not a fixed value. For a given drug, it may have one or more labels representing its classification information at the same time, which further increases the requirements of the classifier. For this problem, the common idea of previous research is to transform the multi-label classification problem into multiple independent binary classification problems. Each binary classification problem corresponds to a label in the label vector and determines the drug’s ATC code. For multiple independent binary classification problems, the sigmoid activation function with binary classification cross-entropy loss (BCEloss) is used to average the loss of all binary classifications, which is applied to model training to obtain the final prediction result. When the real class of the sample is far less than the number of all classes of the problem, there will be a class-imbalance problem, and some balance strategies are generally used to solve this problem. For example, setting a threshold for each binary classification problem or manually adjusting the weights of positive and negative samples, etc. To simplify the complex series of operations after transforming a multi-label problem into multiple independent binary classification problems, we refer to Su’s use of Circle loss (Su, 2020; Sun et al., 2020). The softmax activation function is combined with the Cross-Entropy Loss function for multi-label classification problems. The implementation is as follows:

In a single-label classification problem, assuming that the scores of each class are $\left\{S_1,S_2,\dots ,S_{n-1},S_n\right\}$, and the target class is t ∈ {1, 2, … , n}, its cross-entropy loss function is defined as formula (7):

$-\log \frac{e^{S_t}}{{\sum }_{i=1}^n{e}^{S_i}}=-\log \frac{1}{{\sum }_{i=1}^n{e}^{S_i-S_t}}=\log \sum _{i=1}^n{e}^{S_i-S_t}=\log \left(1+\sum _{i=1,i\ne t}^n{e}^{S_i-S_t}\right)(7)$

It can be derived as an approximation of the max function as shown in formula (8):

$\log \left(1+\sum _{i=1,i\ne t}^n{e}^{S_i-S_t}\right)\approx \max \left\{\begin{array}{c}\hfill 0\hfill \\ \hfill s_1-s_t\hfill \\ \hfill ⋮\hfill \\ \hfill s_{t-1}-s_t\hfill \\ \hfill s_{t+1}-s_t\hfill \\ \hfill ⋮\hfill \\ \hfill s_n-s_t\hfill \end{array}\right\}(8)$

In this loss, all non-target class scores $\left\{S_1,\cdots ,S_{t-1},S_{t+1},\cdots ,S_n\right\}$ are compared with target class scores S_t and their maximum difference should be less than zero, thus ensuring that target class score is greater than each non-target class score. In the multi-label classification problem, we also want each target class score to be no less than the score of each non-target class, and the generalization of Loss is obtained according to the same principle (Sun et al., 2020), as formula (9):

$\log \left(1+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}},j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{s_i-s_j}\right)=\log \left(1+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}}}{e}^{s_i}\sum _{j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{-s_j}\right)(9)$

Where Ω_pos and Ω_neg are the set of target and non-target classes for a given sample in the multi-label problem, respectively.

When the samples have a fixed number of labels k in a multi-label classification problem, the above formula can be used directly to output the k classes with the top score in the prediction stage. In the actual multi-label prediction problem, the number of labels k owned by the sample is a constant with non-fixed value, and a threshold is needed to determine all classes of the sample. To this end, an additional class of S₀ is introduced, and it is desired that all scores of the target class are greater than S₀ and all scores of the non-target class are less than S₀, which is obtained as formula (10):

$\log \left(1+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}},j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{s_i-s_j}+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}}}{e}^{s_i-s_0}+\sum _{j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{s_0-s_j}\right)=\log \left(e^{S_0}+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}}}{e}^{s_i}\right)+\log \left(e^{-s_0}+\sum _{j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{-s_j}\right)(10)$

Setting the threshold S₀ to the default value of 0, we can get the simplified formula (10) of formula (11):

$\log \left(1+\sum _{i\in {\mathrm{\Omega }}_{\mathit{neg}}}{e}^{s_i}\right)+\log \left(1+\sum _{j\in {\mathrm{\Omega }}_{\mathit{pos}}}{e}^{-s_j}\right)(11)$

The final Loss is obtained as a generalization of the softmax activation function with the cross-entropy loss function on the multi-label classification problem, as formula (12):

$loss\left(y_{\mathit{true}},y_{\mathit{pred}}\right)=logsumexp\left(y_{\mathit{pred-neg}},0\right)+logsumexp\left(y_{\mathit{pred-pos}},0\right)(12)$

In this experiment, formula(12) is used to calculate the loss. Once the loss is obtained, backpropagation is performed to train the model. In the prediction stage of the model, classes with target scores greater than 0 are output. Compared with the methods in previous ATC code prediction studies, the multi-label problem is no longer transformed into multiple binary classifications, but into the comparison of target class scores and non-target class scores. In the optimization process, the logsumexp function (Blanchard et al., 2019) automatically takes part with the largest loss for learning. The logsumexp function will reduce the weight of the items that have been optimized well, and highlight the items with larger errors, and the class-imbalance problem is solved to some extent.

3.3.3 Predicting Drug Anatomical Therapeutic Chemical Code

After extracting the feature embedding of nodes through the GCN(Kipf and Welling, 2016) network, we further process the embedding of drug nodes using linear layers and Dropout (Srivastava et al., 2014) layers to obtain better drug ATC code prediction performance. Specifically, the drug nodes embedding extracted by the GCN module is used as the input of the first linear layer. The output dimension of the last linear layer is the same as the dimension of the drug ATC label vector, which is used as the prediction result of the drug ATC code, and the model is optimized using the loss function introduced above. To solve the problem of multi-layer network stacking, a Relu activation function (Agarap, 2018) is used after the first linear layer, and Dropout layers are added between subsequent linear layers. The Dropout layer removes the neuron nodes from the network with a certain probability. In random gradient descent, the randomly removed neurons can make each iteration train a different network and increase the diversification of the network, thus improving the generalization ability of the model.

4 Experiments and Results

In this section, our experiments are performed on the benchmark dataset. First, the evaluation metrics used in this study are introduced. Then, the performance of DACPGTN is evaluated in comparison with several state-of-the-art drug ATC code prediction methods. Next, the effects of parameters and multiple sources of information on the DACPGTN model are analyzed through experiments.

4.1 Evaluation Metrics

For multi-label classification problems, since the samples have one or more labels at the same time, traditional single-label evaluation metrics are not applicable here. Compared with the traditional single-label evaluation metrics, the evaluation metrics for multi-label problems are more complex and complete. Five evaluation metrics for evaluating the performance of multi-label classifiers are defined in the literature published by Chou (Chou, 2013), and previous studies of the drug ATC label classification problem have used this evaluation criterion for comparison. To ensure the fairness of the experiments, we also use this evaluation criterion in our experiments. The definitions of the evaluation metrics are given in Equation (13–17):

$Aiming=\frac{1}{N}\sum _{i=1}^N\left(\frac{Y_i\cap Y_i^{*}}{\left|Y_i^{\ast }\right|}\right)(13)$

$Coverage=\frac{1}{N}\sum _{i=1}^N\left(\frac{Y_i\cap Y_i^{\ast }}{\left|Y_i\right|}\right)(14)$

$Accuracy=\frac{1}{N}\sum _{i=1}^N\left(\frac{\left|Y_i\cap Y_i^{\ast }\right|}{\left|{Y_i\cup Y}_i^{\ast }\right|}\right)(15)$

$Absolute-True=\frac{1}{N}\sum _{i=1}^{N}K\left(Y_i,Y_i^{\ast }\right)(16)$

$Absolute-False=\frac{1}{N}\sum _{i=1}^N\left(\frac{\left|{Y_i\cup Y}_i^{\ast }\right|-\left|Y_i\cap Y_i^{\ast }\right|}{M}\right)(17)$

where N is the total number of samples, M is the number of labels, the operator $\left|\cdot \right|$ is used to calculate the number of elements in the set, ∪/∩ represents the merge/intersection operation of the set, Y_i represents the true label vector of the current sample i, $Y_i^{*}$ represents the predicted label vector of the current sample i after the model, and K represents the function to determine whether the two vectors are identical, through formula (18):

$K\left(Y_i,Y_i^{\ast }\right)=\left\{\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right.\left(\genfrac{}{}{0.0pt}{}{{ifY}_i^{\ast }exactlythesameas{Y}_i}{else}\right)(18)$

For our experiments, we used the 10-fold cross-validation (Refaeilzadeh et al., 2009) to evaluate the model’s performance. K-fold cross-validation is a rigorous evaluation method. In each fold, the dataset is divided into (training set: validation set): test set = (9:1):1. The performance of the model is evaluated by taking the average of 10 times repeated 10-fold cross-validations to ensure that the error in the experimental results is as small as possible.

4.2 DACPGTN Model Settings

This section lists the parameter settings of the experiment in Table 3. The learning rate is adapted by Adam optimizer (Zhang, 2018). This algorithm has an excellent performance in deep learning and has significant advantages compared with other types of random optimization algorithms. The model selection is based on the performance of the validation sets. We set the model training iterations for 250 epochs. Before each training, the performance of the current model on the validation set is compared with the performance of the previous epoch. Finally, select the model that achieves the best performance on the validation set to save. Setting of model parameters, based on the GTN model. The GCN network output dimensions that affect prediction performance are discussed in detail in Section 4.4. The overall DACPGTN model was implemented using the Python-based Pytorch 1.5.1 framework. These experiments were implemented on Windows 10 using python 3.6 and executed on a PC with a 2.90 GHz Intel Core i7-10700 processor and 32.0 GB RAM.

TABLE 3

TABLE 3. DACPGTN model parameter settings.

4.3 Comparison With Other Anatomical Therapeutic Chemical Code Multi-Label Classifiers

In this section, the DACPGTN model was compared with some of the state-of-the-art methods in drug ATC code prediction. We compared three state-of-the-art methods, 1) CGATCPred (Zhao et al., 2021), it uses a multi-layer convolutional neural network (CNN) to extract composite features from multiple types of drug-drug similarities, and uses a GCN network to learn the information between ATC Code labels. All the information learned is integrated and a neural network is used to make the final prediction. 2) iATC-NRAKEL (Zhou et al., 2020a), have constructed multiple drug-drug interaction networks, extracted the drug features by the network embedding algorithm Mashup. In the classification stage, the classic machine learning algorithm support vector machine was used. 3) iATC-mISF(Cheng et al., 2017b), a multi-label Gaussian kernel regression classifier. The first-level ATC Code for a given drug is predicted based on drug chemistry-chemistry interactions, drug structure similarity and drug fingerprint similarity. At the same time, in order to verify that deep learning method can provide better prediction performance than traditional multi-label classifiers, we also compare two basic multi-label classification methods ML-KNN(Szymanski and Kajdanowicz, 2017) and ML-RandomForest (Szymanski and Kajdanowicz, 2017). The parameter settings of all comparison models are the same as the optimal parameters in the original article, and the traditional classifier parameters are set as default. The comparative experiments are carried out on the dataset we constructed, and the results are shown in Table 4.

TABLE 4

TABLE 4. Comparison with other ATC Code multi-label classifiers (10 × 10-fold CV).

As shown in Table 4, our proposed DACPGTN model has the best performance on the Benchmark dataset. Compared with the optimal model CGATCPred in drug ATC Code prediction problem, the improvement is 6.8% in Aiming,5% in Coverage,6% in Accuracy, and 6.1% in Absolute true. Accuracy and Absolute true are the most important among the five evaluation metrics (Qiu et al., 2016), and our model achieves a certain degree of improvement in these two metrics. To clearly show the performance of DACPGTN with 10 times repeated10-fold cross-validation, we illustrated a boxplot of accuracy and absolute true in Figure 3. The two measurements did not vary considerably, representing the stability of DACPGTN under different divisions of drugs. These results suggest that the DACPGTN model, which can learn potential interactions information between different biomedical entities from multiple heterogeneous graphs by using graph transformer layer. DACPGTN integrated potential interactions information and composite features between these nodes, which can achieve better performance in drug ATC code prediction.

FIGURE 3

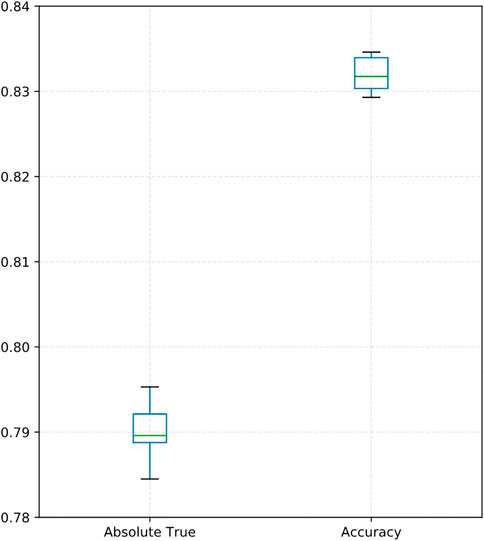
FIGURE 3. Boxplot showing the absolute trues and accuracies of DACPGTN with 10-fold cross-validation for 10 times.

4.4 The Effect of GCN Network Output Dimension

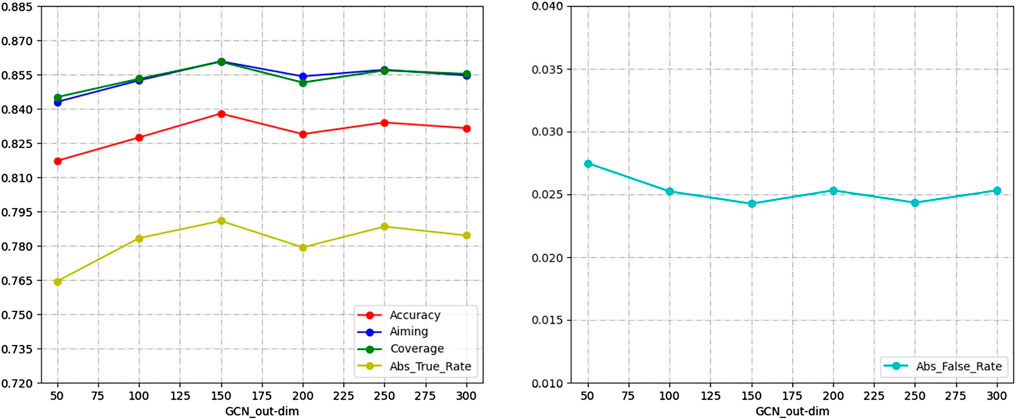
In this experiment, the GCN network as a feature extractor provides classification information for the end-to-end prediction stage by learning the composite feature matrix and the potential interactions information matrix obtained from the graph transformer layer. In order to verify the effect of the GCN network node feature output size on the experimental results, the following experiments were conducted. The results are shown in Figure 4.

FIGURE 4

FIGURE 4. GCN network Output dimension selection.

For the results of the experiments, we compare the performance of the GCN network in different output dimensions on five evaluation metrics. As shown in Figure 4, the model achieves the best prediction performance when the output dimension of the GCN network is 150. Therefore, the GCN network output dimension was set to 150, and all experiments were performed on this parameter.

4.5 The Effect of Multi-Source Interaction Information

To obtain drug-target protein interaction information and drug-disease interaction information on the impact of the drug ATC prediction problem. We used the drug-target protein interaction information and drug-disease interaction information as the input of the heterogeneous network, respectively, and reconstructed the feature matrix. The parameters of the experiments are the same as those in Section 4.2, and the results are shown in Table 5.

TABLE 5

TABLE 5. Experimental results of single-source interaction information.

As shown in Table 5, the performance of the model degrades when only drug-target protein interaction information or only drug-disease interaction information is used as candidate adjacency matrix for heterogeneous networks. Meanwhile, only drug-target protein interaction information was used better than only drug-disease interaction information, and the experiment results were consistent with our expectation. Compared with single interaction information, the DACPGTN model obtained better prediction performance by considering multiple sources of interactions information. It is fully demonstrated that the DACPGTN model can extract useful information from multi-source interaction information for prediction. That is, new graph structures obtained by learning different heterogeneous graphs can contribute to the drug ATC code prediction problem.

4.6 Predicting Anatomical Therapeutic Chemical Code for New Drugs

To evaluate the capability of the DACPGTN model in predicting ATC Code for new drugs, we have conducted the following series of experiments. For a given new drug, it may not be possible to obtain information on its known targets or disease interactions. We consider three potential cases: 1) Drugs have interactions with targets. 2) Drugs have only interactions with diseases. 3) Drugs have no interactions with targets and diseases. For each potential case, we sequentially masked the interactions information for all drugs in the test set. The known interaction information of drugs in the heterogeneous network is removed, and the heterogeneous network set is reconstructed. Specifically, we set all elements of the row in the drug correspondence heterogeneous network to 0. When the known interactions information is removed, the given drug thus becomes a new drug with only drug-target interaction information or drug-disease interaction information or without any known interaction information. We performed the ten times repeated 10-fold cross-validation experiments for each case and took the average value to ensure that the error was sufficiently small. The experimental results are shown in Table 6. The experimental results show that the performance of the DACPGTN model decreases when the new drugs have different degrees of missing interaction information, but the performance of the model remains at a high level. This good performance may be related to the principle of the GCN network. When the test node learns fewer potential interactions by graph transformer layer or only self-interaction information, the GCN network can still transform the node features on the whole graph space. New drugs prediction experiments have demonstrated that the DACPGTN model has practical application. When a new drug is given, its target or disease interaction information is missing, or the interaction information between the new drug and these two types of biomedical nodes is unknown. We can still integrate existing heterogeneous networks to make well-performing ATC code predictions for new drugs using only drug-drug similarity information or partially known interactions information.

TABLE 6

TABLE 6. New drugs prediction experiment results.

4.7 Case Studies

To further validate the reliability capability of DACPGTN, we selected some representative drugs for detailed case studies. Due to the early construction of the benchmark dataset and the limited information on drugs ATC code included, the DACPGTN model will give false positives of ATC code for some drugs in the prediction phase. As drug discovery research progresses, the pharmacological properties and ATC code of some drugs in the experimental dataset will be newly validated and supplemented. We have analyzed and validated some representative drugs predicted by our model with false positive ATC code through authoritative public databases, such as DrugBank (Wishart et al., 2008), CTD (Davis et al., 2021) and KEGG (Kanehisa and Goto, 2000). The predicted results and the supporting evidences are summarized in Table 7. For example, Brinzolamide (D00652) is a highly specific, non-competitive, reversible carbonic anhydrase inhibitor. It is indicated in the treatment of elevated intraocular pressure in patients with ocular hypertension or open-angle glaucoma. This drug was originally classified under the Sensory Organs, and new studies suggest it has been added to the cardiovascular class of the KEGG database. Carisoprodol (D00768) is a centrally acting skeletal muscle relaxant that does not act directly on skeletal muscle but acts directly on the central nervous system (CNS). Overdose of carisoprodol can depress the CNS and in severe cases induce coma. In the Drugbank database, based on studies in animal models, carisoprodol-induced muscle relaxation is associated with changes in the activity of interneurons in the spinal cord and descending reticulum located in the brain. Homatropine methylbromide (D02070) is a quaternary ammonium muscarinic acetylcholine receptor antagonist belonging to the group of medicines called anti-muscarinics. Research in the DrugBank database shows that it is used to treat duodenal or gastric ulcers or intestinal problems and prevent nausea, vomiting, and motion sickness. Meanwhile, Homatropine methylbromide is classed explicitly as Alimentary tract and metabolism in the KEGG database. These successful prediction result show that our model can provide valuable information for drug discovery and predict the potential pharmacological properties of drugs.

TABLE 7

TABLE 7. Eight inferred drugs ATC class based on the DACPGTN model.

5 Conclusion

Considering drug ATC code identification can play an important role in drug discovery and development, we proposed an end-to-end model DACPGTN based on graph transformer network to predict the ATC code for drugs effectively in this study. DACPGTN formulated the ATC code prediction of drugs as a multi-label classification problem. By applying transformer network, DACPGTN learned comprehensive interactions among drugs, diseases and targets to construct drug-target-disease heterogeneous networks. Moreover, DACPGTN integrated various biomedical information to obtain more representative features of drugs, diseases and targets. Based on the learned heterogeneous network and features, graph convolution network was used to obtain network embedding of drugs for drug ATC code multi-label classification task. For the drug ATC code multi-label prediction problem, we transformed it into the calculation of the difference between the score of the target class and the score of the non-target class, which solves the class-imbalance problem to a certain extent. The results of cross-validation experiments have demonstrated that DACPGTN is an effective approach to identify the ATC code of drugs, which can help the pharmacological discovery of drugs. In the future work, more high-quality data and biomedical entities can be incorporated to obtain more effective features of drugs. In addition, the performance and usefulness of the DACPGTN model can be further improved by utilizing attention-based mechanisms.

Data Availability Statement

The datasets for this study can be found in the https://github.com/Szhgege/DACPGTN/tree/main/data.

Author Contributions

CY and ZS conceived and designed the approach. ZS performed the experiments. GZ and HL analyzed the data. CY and ZS wrote the manuscript. HL and JW supervised the whole study process and revised the manuscript. All authors have read and approved the final version of manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant number (No. 61802113 and No. 61802114); Education Department of Henan Province (No. 222102210238).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdi, H., and Williams, L. J. (2010). Principal Component Analysis. WIREs Comp. Stat. 2, 433–459. doi:10.1002/wics.101

CrossRef Full Text | Google Scholar

Agarap, A. F. (2018). Deep Learning Using Rectified Linear Units (Relu). CoRR abs/1803.08375.

Google Scholar

Benesty, J., Chen, J., Huang, Y., and Cohen, I. (2009). “Pearson Correlation Coefficient,” in Noise Reduction in Speech Processing (Berlin, Heidelberg: Springer), 1–4. doi:10.1007/978-3-642-00296-0_5

CrossRef Full Text | Google Scholar

Blanchard, P., Higham, D. J., and Higham, N. J. (2019). Accurate Computation of the Log-Sum-Exp and Softmax Functions. arXiv preprint arXiv:1909.03469.

Google Scholar

Chen, L., Zeng, W. M., Cai, Y. D., Feng, K. Y., and Chou, K. C. (2012). Predicting Anatomical Therapeutic Chemical (Atc) Classification of Drugs by Integrating Chemical-Chemical Interactions and Similarities. PLoS One 7, e35254. doi:10.1371/journal.pone.0035254

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Kalantidis, Y., Li, J., Yan, S., and Feng, J. (2018). “Aˆ-Nets: Double Attention Networks,” in Advances in Neural Information Processing Systems. Editors S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Montréal Canada: Curran Associates, Inc.), 31.

Google Scholar

Cheng, X., Zhao, S. G., Xiao, X., and Chou, K. C. (2017a). Iatc-Mhyb: A Hybrid Multi-Label Classifier for Predicting the Classification of Anatomical Therapeutic Chemicals. Oncotarget 8, 58494–58503. doi:10.18632/oncotarget.17028

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, X., Zhao, S. G., Xiao, X., and Chou, K. C. (2017b). Iatc-Misf: A Multi-Label Classifier for Predicting the Classes of Anatomical Therapeutic Chemicals. Bioinformatics 33, 341–346. doi:10.1093/bioinformatics/btw644

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiang, A. P., and Butte, A. J. (2009). Systematic Evaluation of Drug-Disease Relationships to Identify Leads for Novel Drug Uses. Clin. Pharmacol. Ther. 86, 507–510. doi:10.1038/clpt.2009.103

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, H., Berger, B., and Peng, J. (2016). Compact Integration of Multi-Network Topology for Functional Analysis of Genes. Cell Syst. 3, 540–548. doi:10.1016/j.cels.2016.10.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Chou, K. C. (2013). Some Remarks on Predicting Multi-Label Attributes in Molecular Biosystems. Mol. Biosyst. 9, 1092–1100. doi:10.1039/C3MB25555G

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortes, C., and Vapnik, V. (1995). Support-Vector Networks. Mach. Learn 20, 273–297. doi:10.1007/BF00994018

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis, A. P., Grondin, C. J., Johnson, R. J., Sciaky, D., Wiegers, J., Wiegers, T. C., et al. (2021). Comparative Toxicogenomics Database (Ctd): Update 2021. Nucleic Acids Res. 49, D1138–D1143. doi:10.1093/nar/gkaa891

PubMed Abstract | CrossRef Full Text | Google Scholar

Degtyarenko, K., De Matos, P., Ennis, M., Hastings, J., Zbinden, M., McNaught, A., et al. (2007). Chebi: A Database and Ontology for Chemical Entities of Biological Interest. Nucleic Acids Res. 36, D344–D350. doi:10.1093/nar/gkm791

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunkel, M., Günther, S., Ahmed, J., Wittig, B., and Preissner, R. (2008). Superpred: Drug Classification and Target Prediction. Nucleic Acids Res. 36, W55–W59. doi:10.1093/nar/gkn307

PubMed Abstract | CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchinson, J. M., Patrick, D. M., Marra, F., Ng, H., Bowie, W. R., Heule, L., et al. (2004). Measurement of Antibiotic Consumption: A Practical Guide to the Use of the Anatomical Thgerapeutic Chemical Classification and Definied Daily Dose System Methodology in Canada. Can. J. Infect. Dis. 15, 29–35. doi:10.1155/2004/389092

PubMed Abstract | CrossRef Full Text | Google Scholar

Jarada, T. N., Rokne, J. G., and Alhajj, R. (2020). A Review of Computational Drug Repositioning: Strategies, Approaches, Opportunities, Challenges, and Directions. J. Cheminform 12, 46. doi:10.1186/s13321-020-00450-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanehisa, M., and Goto, S. (2000). Kegg: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 28, 27–30. doi:10.1093/nar/28.1.27

PubMed Abstract | CrossRef Full Text | Google Scholar

Kipf, T. N., and Welling, M. (2016). Semi-Supervised Classification with Graph Convolutional Networks. arXiv preprint arXiv:1609.02907.

Google Scholar

Kumari, R., and Srivastava, S. K. (2017). Machine Learning: A Review on Binary Classification. Int. J. Comput. Appl. 160, 11–15. doi:10.5120/ijca2017913083

CrossRef Full Text | Google Scholar

Li, G., Muller, M., Thabet, A., and Ghanem, B. (2019). “Deepgcns: Can Gcns Go as Deep as Cnns?,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 27 October-02 November, 2019.

Google Scholar

Li, J., and Lu, Z. (2012). “A New Method for Computational Drug Repositioning Using Drug Pairwise Similarity,” in 2012 IEEE International Conference on Bioinformatics and Biomedicine, Philadelphia, USA, October 4-7, 2012 (IEEE), 1–4. doi:10.1109/BIBM.2012.6392722

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Han, Z., and Wu, X.-M. (2018). “Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning,” in Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, Louisiana, USA, February 2‐7, 2018.

Google Scholar

Luo, H., Li, M., Yang, M., Wu, F. X., Li, Y., and Wang, J. (2021). Biomedical Data and Computational Models for Drug Repositioning: A Comprehensive Review. Brief. Bioinform 22, 1604–1619. doi:10.1093/bib/bbz176

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, H., Wang, J., Li, M., Luo, J., Peng, X., Wu, F. X., et al. (2016). Drug Repositioning Based on Comprehensive Similarity Measures and Bi-Random Walk Algorithm. Bioinformatics 32, 2664–2671. doi:10.1093/bioinformatics/btw228

PubMed Abstract | CrossRef Full Text | Google Scholar

MacDonald, K., and Potvin, K. (2004). Interprovincial Variation in Access to Publicly Funded Pharmaceuticals: A Review Based on the Who Anatomical Therapeutic Chemical Classification System. Can. Pharm. J. 137, 29–34. doi:10.1177/171516350413700703

CrossRef Full Text | Google Scholar

Nanni, L., and Brahnam, S. (2017). Multi-Label Classifier Based on Histogram of Gradients for Predicting the Anatomical Therapeutic Chemical Class/Classes of a Given Compound. Bioinformatics 33, 2837–2841. doi:10.1093/bioinformatics/btx278

PubMed Abstract | CrossRef Full Text | Google Scholar

Nanni, L., Brahnam, S., and Lumini, A. (2020). “Ensemble of Deep Learning Approaches for Atc Classification,” in Smart Intelligent Computing and Applications. Editors S. Satapathy, V. Bhateja, J. Mohanty, and S. Udgata (Singapore: Springer), 117–125. doi:10.1007/978-981-13-9282-5_12

CrossRef Full Text | Google Scholar

Pushpakom, S., Iorio, F., Eyers, P. A., Escott, K. J., Hopper, S., Wells, A., et al. (2019). Drug Repurposing: Progress, Challenges and Recommendations. Nat. Rev. Drug Discov. 18, 41–58. doi:10.1038/nrd.2018.168

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, W. R., Sun, B. Q., Xiao, X., Xu, Z. C., and Chou, K. C. (2016). Iptm-Mlys: Identifying Multiple Lysine Ptm Sites and Their Different Types. Bioinformatics 32, 3116–3123. doi:10.1093/bioinformatics/btw380

PubMed Abstract | CrossRef Full Text | Google Scholar

Refaeilzadeh, P., Tang, L., and Liu, H. (2009). “Cross-Validation,” in Encyclopedia of Database Systems. Editors L. Liu, and M. T. Özsu (Boston, MA: Springer), 5, 532–538. doi:10.1007/978-0-387-39940-9_565

CrossRef Full Text | Google Scholar

Shi, C., Li, Y., Zhang, J., Sun, Y., and Philip, S. Y. (2016). A Survey of Heterogeneous Information Network Analysis. IEEE Trans. Knowl. Data Eng. 29, 17–37. doi:10.1109/TKDE.2016.2598561

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

[Dataset] Su, J. (2020). Extending ”softmax+cross Entropy” to Multi-Label Classification Problems. https://github.com/bojone/bert4keras.

Google Scholar

Sun, Y., Cheng, C., Zhang, Y., Zhang, C., Zheng, L., Wang, Z., et al. (2020). “Circle Loss: A Unified Perspective of Pair Similarity Optimization,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, June 16 - 19, 2020. doi:10.1109/cvpr42600.2020.00643

CrossRef Full Text | Google Scholar

Szklarczyk, D., Gable, A. L., Lyon, D., Junge, A., Wyder, S., Huerta-Cepas, J., et al. (2019). STRING V11: Protein-Protein Association Networks with Increased Coverage, Supporting Functional Discovery in Genome-wide Experimental Datasets. Nucleic Acids Res. 47, D607–D613. doi:10.1093/nar/gky1131

PubMed Abstract | CrossRef Full Text | Google Scholar

Szymanski, P., and Kajdanowicz, T. (2017). A Scikit-Based Python Environment for Performing Multi-Label Classification. J. Mach. Learn. Res. 20 (6), 01460.

Google Scholar

Szymański, P., Kajdanowicz, T., and Kersting, K. (2016). How is a Data-Driven Approach Better Than Random Choice in Label Space Division for Multi-Label Classification? Entropy 18, 282. doi:10.3390/e18080282

CrossRef Full Text | Google Scholar

Tsoumakas, G., and Katakis, I. (2007). Multi-Label Classification: An Overview. Int. J. Data Warehous. Min. (IJDWM) 3, 1–13. doi:10.4018/jdwm.2007070101

CrossRef Full Text | Google Scholar

Tsoumakas, G., and Vlahavas, I. (2007). “Random K-Labelsets: An Ensemble Method for Multilabel Classification,” in European Conference on Machine Learning, Warsaw, Poland, September 17-21, 2007 (Springer), 406–417. doi:10.1007/978-3-540-74958-5_38

CrossRef Full Text | Google Scholar

Wang, X., Wang, Y., Xu, Z., Xiong, Y., and Wei, D. Q. (2019b). Atc-nlsp: Prediction of the Classes of Anatomical Therapeutic Chemicals Using a Network-Based Label Space Partition Method. Front. Pharmacol. 10, 971. doi:10.3389/fphar.2019.00971

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Ji, H., Shi, C., Wang, B., Ye, Y., Cui, P., et al. (2019a). “Heterogeneous Graph Attention Network,” in The World Wide Web Conference, San Francisco CA USA, May 13 - 17, 2019, 2022–2032. doi:10.1145/3308558.3313562

CrossRef Full Text | Google Scholar

Wishart, D. S., Knox, C., Guo, A. C., Cheng, D., Shrivastava, S., Tzur, D., et al. (2008). Drugbank: A Knowledgebase for Drugs, Drug Actions and Drug Targets. Nucleic Acids Res. 36, D901–D906. doi:10.1093/nar/gkm958

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L., Ai, N., Liu, Y., Wang, Y., and Fan, X. (2013). Relating Anatomical Therapeutic Indications by the Ensemble Similarity of Drug Sets. J. Chem. Inf. Model 53, 2154–2160. doi:10.1021/ci400155x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, S., Jeong, M., Kim, R., Kang, J., and Kim, H. J. (2019). “Graph Transformer Networks,” in Advances in Neural Information Processing Systems. Editors H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Vancouver Canada: Curran Associates, Inc.), 32.

Google Scholar

Zhang, Y., Xiong, Y., Kong, X., Li, S., Mi, J., and Zhu, Y. (2018). “Deep Collective Classification in Heterogeneous Information Networks,” in Proceedings of the 2018 World Wide Web Conference, Lyon, France, April 23 - 27, 2018, 399–408. doi:10.1145/3178876.3186106

CrossRef Full Text | Google Scholar

Zhang, Z. (2018). “Improved Adam Optimizer for Deep Neural Networks,” in 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, Canada, June 4-6, 2018 (IEEE), 1–2. doi:10.1109/IWQoS.2018.8624183

CrossRef Full Text | Google Scholar

Zhao, H., Li, Y., and Wang, J. (2021). A Convolutional Neural Network and Graph Convolutional Network-Based Method for Predicting the Classification of Anatomical Therapeutic Chemicals. Bioinformatics 37, 2841–2847. doi:10.1093/bioinformatics/btab204

CrossRef Full Text | Google Scholar

Zhou, J. P., Chen, L., and Guo, Z. H. (2020a). Iatc-Nrakel: An Efficient Multi-Label Classifier for Recognizing Anatomical Therapeutic Chemical Classes of Drugs. Bioinformatics 36, 1391–1396. doi:10.1093/bioinformatics/btz757

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J. P., Chen, L., Wang, T., and Liu, M. (2020b). Iatc-Frakel: A Simple Multi-Label Web Server for Recognizing Anatomical Therapeutic Chemical Classes of Drugs with Their Fingerprints Only. Bioinformatics 36, 3568–3569. doi:10.1093/bioinformatics/btaa166

PubMed Abstract | CrossRef Full Text | Google Scholar