- 1College of Computer Science and Technology, Jilin University, Changchun, China
- 2Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun, China
- 3Sichuan University Library, Sichuan University, Chengdu, China
- 4Department of Respiratory Medicine, The First Hospital of Jilin University, Changchun, China
- 5The First Hospital of Jilin University, Changchun, China
Antibiotic resistance is a major public health concern. Antibiotic combinations, offering better efficacy at lower doses, are a useful way to handle this problem. However, it is difficult for us to find effective antibiotic combinations in the vast chemical space. Herein, we propose a graph learning framework to predict synergistic antibiotic combinations. In this model, a network proximity method combined with network propagation was used to quantify the relationships of drug pairs, and we found that synergistic antibiotic combinations tend to have smaller network proximity. Therefore, network proximity can be used for building an affinity matrix. Subsequently, the affinity matrix was fed into a graph regularization model to predict potential synergistic antibiotic combinations. Compared with existing methods, our model shows a better performance in the prediction of synergistic antibiotic combinations and interpretability.
Introduction
Antibiotic resistance is a growing health crisis, and it is emerging globally (Author Anonymous, 2013; Zhabiz et al., 2014; Murray et al., 2022). This crisis has been ascribed to the wide use and even abuse of antibiotics in the clinic, as well as a lack of economic incentives and market regulation of new antibiotic development (Ventola, 2015; Farha et al., 2021). An increasing number of Big Pharma have stopped developing new antibiotics, and the number of new FDA-approved antibiotics has gradually decreased since the 1980s (Ventola, 2015). Therefore, we have to find an alternative way to address this pressing public health problem.
Antibiotic combinations offer an effective strategy to combat antibiotic resistance (Tyers and Wright, 2019; Lv et al., 2021). Generally, antibiotic combinations can be divided into three groups: synergy, additive, and antagonism (Cokol et al., 2011). Synergistic antibiotic combinations are often used in clinics because they can offer better efficacy at lower doses (Mathers, 2015). In the microbiology laboratory, synergy or antagonism is usually identified through the fractional inhibitory concentration index (FICI) (Odds, 2003). However, this approach is expensive and time-consuming. To date, more than 300 antibiotics have been discovered (Wright, 2014), generating at least 44, 850 drug pairs. In addition, the efficacies of antibiotic combinations were also affected by doses (Maan et al., 2021), metabolic conditions (Cokol et al., 2018), and bacterial strains (Chandrasekaran et al., 2016). Consequently, millions of drug pairs need to be tested. As a result, it is impossible to screen synergistic antibiotic combinations by experimental approaches. Recently, with the development of artificial intelligence, many researchers have started to use computational approaches to identify synergistic drug combinations (Sheng et al., 2017; Weinstein et al., 2017). They used drug structures (Mason et al., 2017; Mason et al., 2018) and chemo-genomics data (Chandrasekaran et al., 2016) as input to the “black-box” machine learning model to predict potential synergistic drug combinations. Although these models have shown good performance (Chandrasekaran et al., 2016; Mason et al., 2017; Mason et al., 2018), some limitations still exist. First and foremost, the curse of dimensionality is a serious problem. Specifically, the number of features (chemogenomic data: 3,979 and Morgan fingerprint: 2048) is much greater than the number of training sets (approximately 100). Furthermore, some features [e.g., chemo-genomics (Nichols et al., 2011)] are not only difficult to obtain but also hard to use to explain the mechanisms of the synergy effect. Therefore, more effective and interpretable features are needed.
Network pharmacology is a new paradigm for drug discovery (Hopkins, 2008) that can help us better understand intricate relationships between drugs, targets, pathways, and diseases (Menche et al., 2015; Cheng et al., 2019; Wang J. et al., 2021; Wang Y. et al., 2021; Li et al., 2021). In network pharmacology, the actions of drugs are regarded as perturbations to the network (Csermely et al., 2013). When a node is perturbed, neighboring nodes will also be affected (Saraswathi et al., 2009). However, perturbation experiments are expensive and time-consuming (Nichols et al., 2011). In this study, we introduced a network propagation method to simulate perturbation patterns of drug pairs (Figure 1B). Intuitively, variations in the medication regimen (synergy or antagonism) cause them to have a slight difference in the network structure and dynamics. Subsequently, we used the network proximity method (Figure 1C) to quantify the relationships between the interactomes between targets of different drugs. We found that synergistic antibiotic combinations tend to have smaller network proximity. In other words, network proximity is a good parameter to classify drug pairs and to avoid the curse of dimensionality. Finally, we introduced a mechanism-driven graph regularization model to predict synergistic antibiotic combinations based on this finding (Figure 1D). The results demonstrated that our method outperformed other existing methods in the prediction of synergistic antibiotic combinations and interpretability.
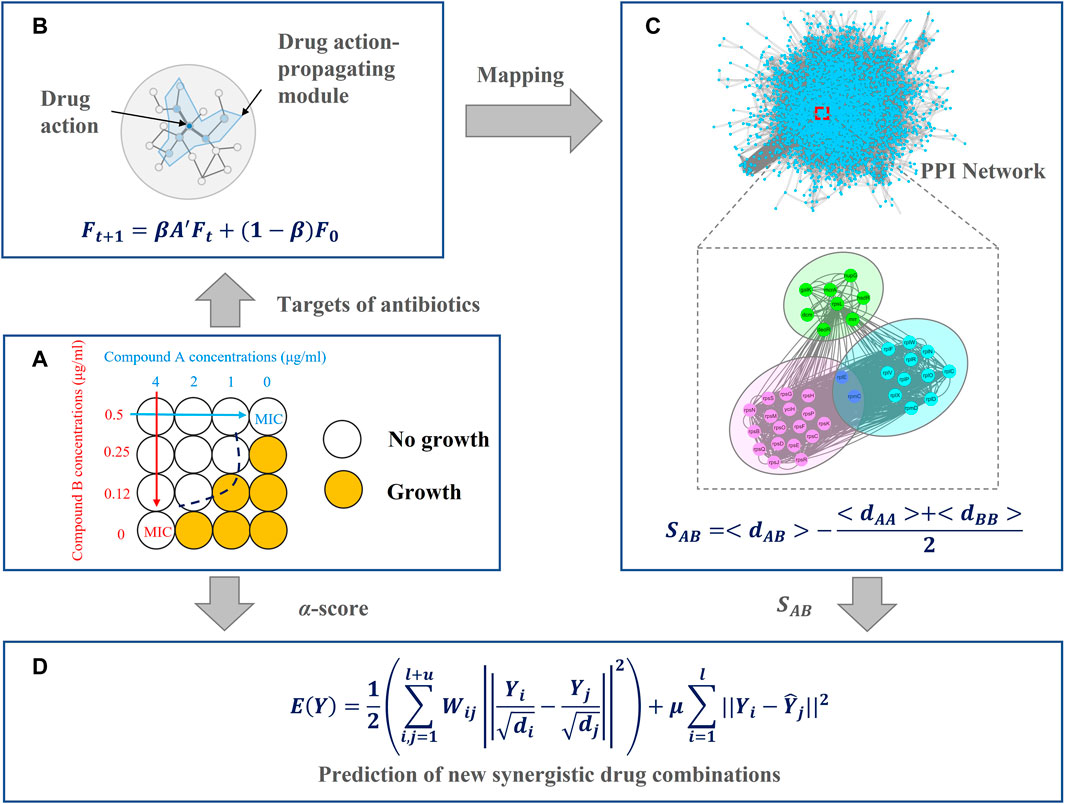
FIGURE 1. Overview of the network-based method for antibiotic combinations, including four main parts (A) collect antibiotic combinations and target information from the literature (B) describe drug actions by network propagation (C) evaluate relationships between each drug pair by network proximity, and (D) predict new synergistic antibiotic combinations.
Materials and Methods
In this section, we introduced the architecture of our model, as shown in Figure 1. In Figure 1A, we collected antibiotic combinations and their targets from the literature. In Figure 1B, the targets of these antibiotics were fed into the network propagation model. When a node is perturbed, neighboring nodes will also be affected, resulting in a subnetwork. We named this subnetwork as a drug action-propagating module (DAPM). In Figure 1C, we used a network proximity model to quantify the relationships between drug pairs. In Figure 1D, the network proximity of each drug pair was converted to an affinity matrix. This affinity matrix and the known antibiotic combinations were employed to build a graph regularization model, thereby predicting new synergistic antibiotic combinations.
Constructing the Protein–Protein Network and Drug–Target Network
We constructed the PPI network of Escherichia coli based on the STRING database version 11.5 (Szklarczyk et al., 2020). The interactions with a score less than 0.7 were ignored. The ultimate network included 59, 496 interactions involving 4, 020 proteins.
We collected drug–target interactions from previous literature reports or the DrugBank database (Wishart et al., 2017). Since we used the data from the in vitro antimicrobial test, proteins from bacteria were considered and proteins of Homo sapiens were ignored in this study.
Collecting Pairwise Antibiotic Combinations
In this study, we focused on pairwise antibiotic combinations by recent experimental data of the Escherichia coli strain MG1655 (Chandrasekaran et al., 2016). Interactions were quantified based on the α-score, and the following three types were used: synergy (α-score ≤ −0.25), additive (−0.25< α-score < 1), and antagonism (α-score ≥ 1) (Cokol et al., 2011). In this study, we only considered antibiotics with known targets (protein or RNA). In total, 91 pairwise antibiotic combinations involving 14 antibiotics were retained.
Network Propagation of Drug Action
Targets of the aforementioned antibiotics were fed into a network propagation model (Vanunu et al., 2010) to simulate the propagation of drug-action effects on the PPI network:
where
Since
Hence,
Quantification of Relationships Between Each Drug Pair
Subsequently, the Jaccard index (Eq. 5) and network proximity model (Eq. 6) (Menche et al., 2015; Cheng et al., 2019) were used to quantify the relationships of each DAPM:
where SA and SB are the nodes of drug A and drug B in their DAPMs, respectively.
where
where A and B are the DAPMs of drug A and drug B, respectively.
Prediction of Synergistic Antibiotic Combinations Based on Graph Regularization
Given three drugs (drug A, drug B, and drug C), if drug A–drug B is a synergistic antibiotic combination and drug A and drug C are pharmacologically similar, then drug C–drug B will likely be a synergistic antibiotic combination. Therefore, we can define a loss function:
where Y and
where Sij is the network proximity (Eq. 6) between drug i and drug j. The classifying model is as follows.
We then take the derivation of
where
where I is the identity matrix,
Performance Evaluation Metrics
The performance of the graph regularization model was estimated using the precision (Eq. 13), recall (Eq. 14), accuracy (Eq. 15), and F1 (Eq. 16), and these evaluation metrics can be defended as follows:
where TP, FP, FN, and TN are true positive, false positive, false negative, and true negative, respectively.
Results
The Data Set of Antibiotic Combinations
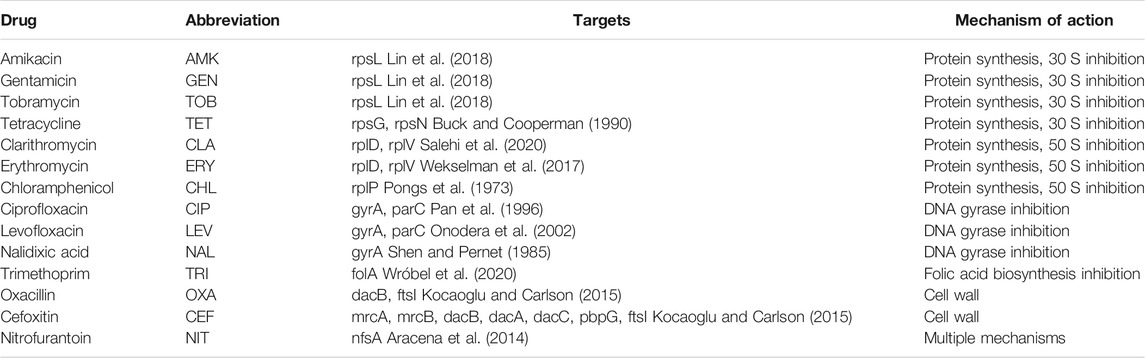
We used previously reported antibiotic combinations involving 14 antibiotics (Chandrasekaran et al., 2016) listed in Table 1. These antibiotics range over various mechanisms of action, including protein biosynthesis, DNA and RNA replication, folate metabolism, and cell wall biosynthesis. Since we concentrated on the subtle differences among synergy, additive, and antagonism, all 91 pairwise combinations fall into three categories, according to the α-score (Supplementary Table S1). Targets of these antibiotics were collected from previous literature studies (Pongs et al., 1973; Shen and Pernet, 1985; Buck and Cooperman, 1990; Pan et al., 1996; Onodera et al., 2002; Aracena et al., 2014; Kocaoglu and Carlson, 2015; Wekselman et al., 2017; Lin et al., 2018; Salehi et al., 2020; Wróbel et al., 2020). Because some antibiotics are RNA-targeted small molecules, ribosomal proteins that affect antibiotic binding are considered targets of antibiotics. For example, 30S ribosomal proteins S7 (rpsG) and S14 (rpsN) were shown to be the most important for tetracycline binding (Buck and Cooperman, 1990). Mutations of 50S ribosomal proteins L22 (rplV) and L4 (rplD) will lead to macrolide (erythromycin, etc.) resistance (Wekselman et al., 2017).
Network analysis showed that the shortest distance between targets of antibiotic combinations ranged from 0 to 5 (Supplementary Figure S1). Most antibiotic combinations (92.3%) did not share the same targets. Approximately thirty percent of antibiotic combinations were adjacent, and almost half of synergistic antibiotic combinations (57.1%) were included (Supplementary Figure S1). However, a considerable portion of antagonistic or additive antibiotic combinations have adjacent targets, but they are not synergistic (Supplementary Figure S1). Therefore, mere knowledge of the network structure may not be sufficient to explain the intricate interactions among antibiotic combinations and their targets. To investigate the network-based relationship between antibiotic combinations and their targets, we introduced network propagation (Vanunu et al., 2010) to predict the effect of antibiotics and antibiotic combinations on the PPI network.
Network Propagation of Drug Actions
Network propagation has been used to quantify the influence of mutations in colorectal tumorigenesis (Shin et al., 2017). When a mutation arises in a node, perturbation spreads out along the protein–protein interaction (PPI) network and eventually forms a mutation-propagating module. Similar to mutation, if a drug acts on a node, neighboring nodes are also affected (Figure 1B) (Saraswathi et al., 2009). Predictably, the impact is greatest in its neighbors, whereas nodes far away from targets receive attenuated influences. Therefore, we can generate a subnetwork with drug targets as hubs, and the nodes (
Based on the network propagation method (Eq. 1), these antibiotics and antibiotic combinations were mapped to the PPI network to investigate the potential relationships of these subnetworks (Figure 1). On average, DAPMs include approximately 13 nodes, although almost all drugs only have 1 to 2 targets. Because of the high threshold, each DAPM consisted almost exclusively of nearest neighbors. Interestingly, we found that there are areas of overlap for some antibiotic combinations and that antibiotic combinations are associated with the synergy effect (Figure 1C). Hence, we inferred that the structure of DAPKs can be used to quantify interactions between drug pairs and thereby predict synergetic antibiotic combinations.
Network-Based Relationship Between DAMPs
Network proximity was used to investigate FDA-approved drug combinations (Cheng et al., 2019) and herb combinations in traditional Chinese medicine (Wang Y. et al., 2021; Zhang et al., 2021). Compared with random herd pairs, herd pairs in traditional Chinese medicine formulas tend to have smaller network proximity (Wang Y. et al., 2021). To probe whether it could also be used to distinguish synergy, additive, and antagonism, we used the Jaccard index (Eq. 5) and network proximity (Eq. 6) to quantify DAMP–DAMP interactions. We found that all possible antibiotic combinations can be divided into three topologically distinct categories: a) overlap: two DAMPs overlap but do not equate (Figure 2A); b) separation: two DAMPs are topologically separated (Figure 2B); and c) identical: two DAMPs are completely consistent (Figure 2C).
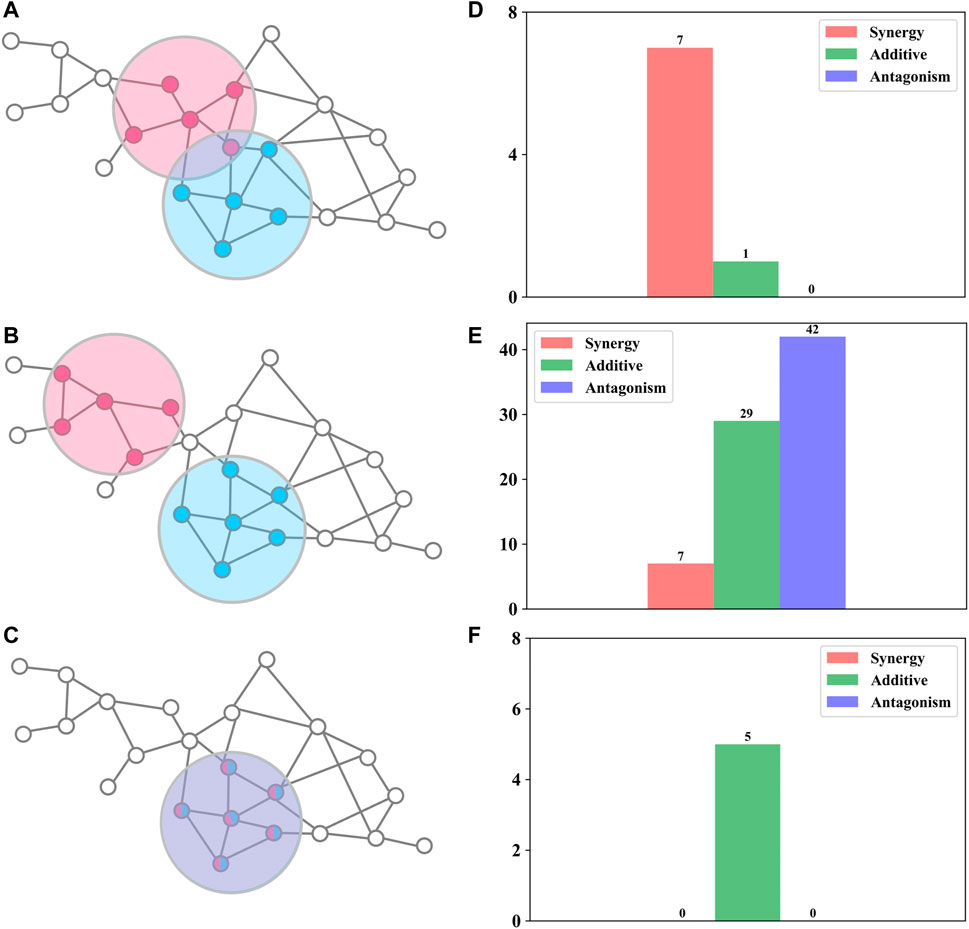
FIGURE 2. Relationships between drug interactions and network structures (A–C) Sketch map of the three topologically distinct classes (D–F) The number of synergistic, additive, and antagonistic drug combinations for the corresponding network structure.
For overlap (Figures 2A,D), these antibiotic combinations are probably synergetic (87.5%,
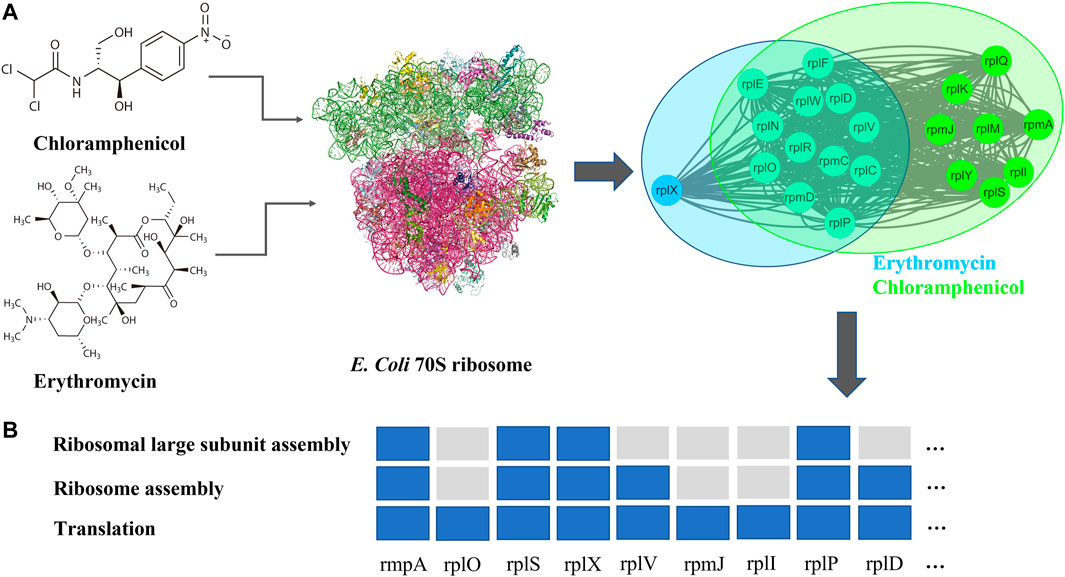
FIGURE 3. (A) Chemistry structural formula, targets (PDB ID: 4V48), and DAPMs of chloramphenicol and erythromycin (B) gene enrichment analysis (Mi et al., 2018) for DAPMs of chloramphenicol and erythromycin.
For separation (Figures 2B,E), these antibiotic combinations were almost not synergetic (90.1%,
For identical (Figures 2C,F), these antibiotic combinations showed a definite additive effect (100%). For example, clarithromycin and erythromycin not only act on the same targets (Table 1) but also have similar chemical structures (98.1%, Tanimoto similarity; more details can be found in SI). Hence, we consider the two drugs to be pharmacologically identical, which leads to an additive effect.
To demonstrate the usefulness of the PPI network, an ablation test was performed where the PPI network was randomized. Supplementary Figure S3 shows that the randomized PPI network produces worse results, so an accurate PPI network is crucial for our model.
Prediction of Synergistic Antibiotic Combinations by Graph Regularization
Graph regularization is a useful model to predict different relationships between various types of biological entities (Luo et al., 2018; Ding et al., 2020). Through the aforementioned analysis, we found that if two drugs are pharmacologically similar, then the drug pair is probably a synergistic antibiotic combination (Figure 2D). Therefore, we can define a loss function of Y (Eq. 8). However, if two drugs are pharmacologically identical (SAB = −1), then the drug pair shows an additive effect (Figure 2C). Therefore, we set Wij of these drug pairs to 0 (Eq. 9). Next, we used the aforementioned 14 antibiotics (Table 1) for the training set to predict interactions with the following three antibiotics (Table 2) by Eq. 12. The entire predicted scores are listed in Table 3. A larger predicted score of drug pairs suggests that they would probably be the synergistic antibiotic combinations. In Supplementary Tables S2–S6, we confirmed that the algorithm is not sensitive to the choice of
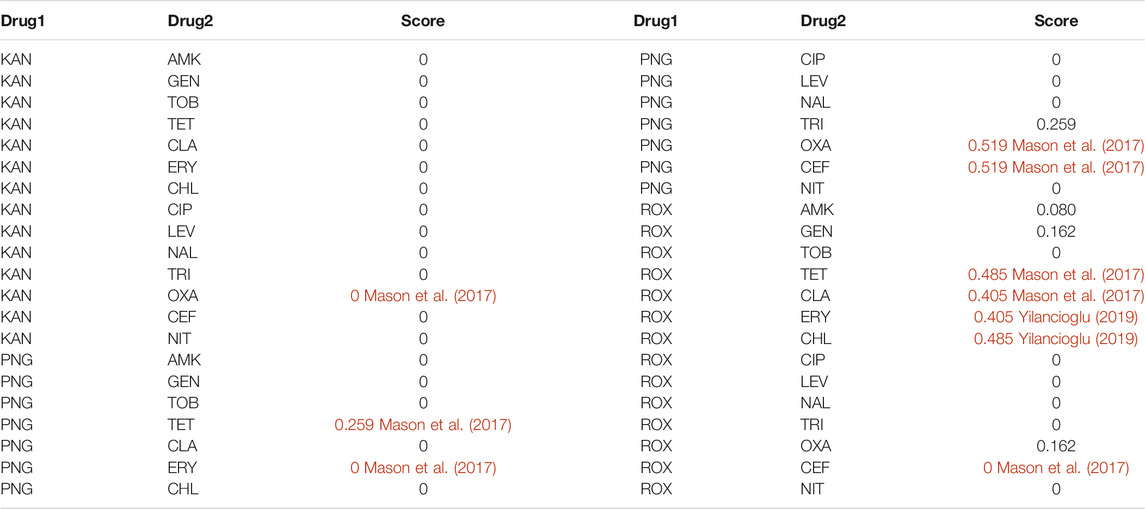
TABLE 3. The entire predicted scores were calculated by a graph regularization model and synergistic antibiotic combinations are colored red.
Comparison With Other Methods
Previously, there have been studies to predict synergistic antibiotic combinations through computational methods. In this section, we compared the performance of our model (Eqs 13–16) with other methods, such as CosynE (Mason et al., 2017) and INDIGO (Chandrasekaran et al., 2016) on the benchmark dataset. As shown in Table 4, our model achieved better performance in terms of various metrics.
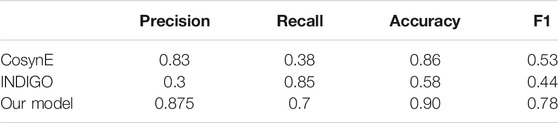
TABLE 4. Performance comparison of CosynE (Mason et al., 2017), INDIGO (Chandrasekaran et al., 2016), and our model.
Discussion
To reduce the cost and time of high-throughput drug combination experiments, we proposed a graph learning framework (Figure 1) to predict potential synergistic antibiotic combinations. First, we collected antibiotic combinations (Supplementary Table S1) and their corresponding targets (Table 1) from the literature. Network analysis revealed that the shortest distance between targets of antibiotic combinations was not sufficient to classify synergistic antibiotic combinations (Supplementary Figure S1). Therefore, we proposed a network proximity method combined with network propagation to quantify the relationships of antibiotic combinations (Figures 1B,C). An important finding is that synergistic antibiotic combinations have a specific network topological relationship, that is, the overlap pattern (Figure 2). This suggests that synergistic antibiotic combinations tend to act on the same biological pathways. Using the antibiotic combination erythromycin and chloramphenicol as a case study, we confirmed that the network proximity of their DAMPs is negative (Supplementary Table S1), and they can inhibit protein synthesis in a synergistic way (Figure 3B). In addition, the network proximity of each drug pair can be fed into the graph regularization model (Eq. 8) to predict new synergistic antibiotic combinations. Most of the predicted synergistic antibiotic combinations have been proven by a series of experiments (Table 3).
Previously, chemo-genomics data (Chandrasekaran et al., 2016) or structural compound fingerprints (Mason et al., 2017) have been used to build machine learning models and thereby predict antibiotic interactions between drug pairs. Based on the concepts proposed by these models, many potential synergistic antibiotic combinations were predicted and validated. However, the performance of these two methods is moderate (Table 4) because of the curse of dimensionality. Compared to these two approaches, our model is based on a feature at deeper molecular levels, the network proximity of DAMPs, which provides a more elegant and efficient way to describe the relationship of drug pairs. This not only makes our model have better predictability (Table 4) but also allows our model to achieve better interpretability. Even so, there are some limitations in our model. First, we focused on the paired antibiotic combinations. In the future, we will also investigate high-order drug combinations. Second, the PPI network is crucial for our model (Supplementary Figure S3). In the current model, an undirected network was used, and next, we will adopt a directed and signed network, which may be useful for improving the performance of our model.
Conclusion
Antibiotic combinations provide a useful way to combat antibiotic resistance. In this study, we proposed a graph learning framework to understand the mechanisms of drug pairs and to predict synergistic antibiotic combinations. By quantifying the relationship between drug pairs based on the network proximity of DAMPs, a graph regularization model can identify potential synergistic antibiotic combinations. This allows us to explore the need for antibiotic combinations more effectively.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
JL, YJ, and YS designed the experiments and wrote the manuscript. GL and WG supervised and provided instructive advice. GL obtained funding.
Funding
This work was supported by the National Nature Science Foundation of China (grant numbers 61772226 and 61862056), the Science and Technology Development Program of Jilin Province (grant number 20210204133YY), and The Natural Science Foundation of Jilin Province (Grant number No. 20200201159JC).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors also particularly appreciate Yakun Chen (College of Chemistry, Jilin University) for his instructive discussion and careful proofreading.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphar.2022.849006/full#supplementary-material
References
Aracena, P., Lazo-Hernández, C., Molina-Berríos, A., Sepúlveda, D. R., Reinoso, C., Larraín, J. I., et al. (2014). Microsomal Oxidative Stress Induced by NADPH Is Inhibited by Nitrofurantoin Redox Biotranformation. Free Radic. Res. 48 (2), 129–136. doi:10.3109/10715762.2013.836695
Buck, M. A., and Cooperman, B. S. (1990). Single Protein Omission Reconstitution Studies of Tetracycline Binding to the 30S Subunit of Escherichia coli Ribosomes. Biochemistry 29 (22), 5374–5379. doi:10.1021/bi00474a024
Chandrasekaran, S., Cokol-Cakmak, M., Sahin, N., Yilancioglu, K., Kazan, H., Collins, J. J., et al. (2016). Chemogenomics and Orthology-Based Design of Antibiotic Combination Therapies. Mol. Syst. Biol. 12 (5), 872. doi:10.15252/msb.20156777
Cheng, F., Kovács, I. A., and Barabási, A. L. (2019). Network-based Prediction of Drug Combinations. Nat. Commun. 10, 1197. doi:10.1038/s41467-019-09186-x
Cokol, M., Chua, H. N., Tasan, M., Mutlu, B., Weinstein, Z. B., Suzuki, Y., et al. (2011). Systematic Exploration of Synergistic Drug Pairs. Mol. Syst. Bio 7 (1), 544. doi:10.1038/msb.2011.71
Cokol, M., Li, C., and Chandrasekaran, S. (2018). Chemogenomic Model Identifies Synergistic Drug Combinations Robust to the Pathogen Microenvironment. PLOS COMPUTATIONAL BIOLOGY 14 (12), e1006677. doi:10.1371/journal.pcbi.1006677
Csermely, P., Korcsmáros, T., Kiss, H. J., London, G., and Nussinov, R. (2013). Structure and Dynamics of Molecular Networks: A Novel Paradigm of Drug Discovery: A Comprehensive Review. Pharmacol. Ther. 138 (3), 333–408. doi:10.1016/j.pharmthera.2013.01.016
Ding, P., Shen, C., Lai, Z., Liang, C., Li, G., and Luo, J. (2020). Incorporating Multisource Knowledge to Predict Drug Synergy Based on Graph Co-regularization. J. Chem. Inf. Model. 60 (1), 37–46. doi:10.1021/acs.jcim.9b00793
Farha, M. A., French, S., and Brown, E. D. (2021). Systems-Level Chemical Biology to Accelerate Antibiotic Drug Discovery. Acc. Chem. Res. 54 (8), 1909–1920. doi:10.1021/acs.accounts.1c00011
Hopkins, A. L. (2008). Network Pharmacology: the Next Paradigm in Drug Discovery. Nat. Chem. Biol. 4 (11), 682–690. doi:10.1038/nchembio.118
Kocaoglu, O., and Carlson, E. E. (2015). Profiling of β-lactam Selectivity for Penicillin-Binding Proteins in Escherichia coli Strain DC2. Antimicrob. Agents Chemother. 59 (5), 2785–2790. doi:10.1128/AAC.04552-14
Li, S., Zhang, F., Xiao, X., Guo, Y., Wen, Z., Li, M., et al. (2021). Prediction of Synergistic Drug Combinations for Prostate Cancer by Transcriptomic and Network Characteristics. Front. Pharmacol. 12 (315), 634097. doi:10.3389/fphar.2021.634097
Lin, J., Zhou, D., Steitz, T. A., Polikanov, Y. S., and Gagnon, M. G. (2018). Ribosome-Targeting Antibiotics: Modes of Action, Mechanisms of Resistance, and Implications for Drug Design. Annu. Rev. Biochem. 87 (1), 451–478. doi:10.1146/annurev-biochem-062917-011942
Luo, J., Ding, P., Liang, C., and Chen, X. (2018). Semi-supervised Prediction of Human miRNA-Disease Association Based on Graph Regularization Framework in Heterogeneous Networks. Neurocomputing 294, 29–38. doi:10.1016/j.neucom.2018.03.003
Lv, J., Deng, S., and Zhang, L. (2021). A Review of Artificial Intelligence Applications for Antimicrobial Resistance. Biosafety and Health 3 (1), 22–31. doi:10.1016/j.bsheal.2020.08.003
Maan, M. K., Chaudhry, T. H., Sattar, A., Shabbir, M. A. B., Ahmed, S., Mi, K., et al. (2021). Dose Optimization of Aditoprim-Sulfamethoxazole Combinations against Trueperella Pyogenes from Patients with Clinical Endometritis by Using Semi-mechanistic PK/PD Model. Front. Pharmacol. 12 (3099), 753359. doi:10.3389/fphar.2021.753359
Mason, D. J., Stott, I., Ashenden, S., Weinstein, Z. B., Karakoc, I., Meral, S., et al. (2017). Prediction of Antibiotic Interactions Using Descriptors Derived from Molecular Structure. J. Med. Chem. 60 (9), 3902–3912. doi:10.1021/acs.jmedchem.7b00204
Mason, D. J., Eastman, R. T., Lewis, R. P. I., Stott, I. P., Guha, R., and Bender, A. (2018). Using Machine Learning to Predict Synergistic Antimalarial Compound Combinations with Novel Structures. Front. Pharmacol. 9, 1096. doi:10.3389/fphar.2018.01096
Mathers, A. J. (2015). Antibiotics in Laboratory Medicine, 6th Edition. Clin. Infect. Dis. 60 (9), 1446–1447. doi:10.1093/cid/civ078
Menche, J., Sharma, A., Kitsak, M., Ghiassian, S. D., Vidal, M., Loscalzo, J., et al. (2015). Disease Networks. Uncovering Disease-Disease Relationships through the Incomplete Interactome. Science 347 (6224), 1257601. doi:10.1126/science.1257601
Mi, H., Muruganujan, A., Ebert, D., Huang, X., and Thomas, P. D. (2018). PANTHER Version 14: More Genomes, a New PANTHER GO-Slim and Improvements in Enrichment Analysis Tools. Nucleic Acids Res. 47 (D1), D419–D426. doi:10.1093/nar/gky1038
Murray, C. J. L., Ikuta, K. S., Sharara, F., Swetschinski, L., Robles Aguilar, G., Gray, A., et al. (2022). Global burden of Bacterial Antimicrobial Resistance in 2019: a Systematic Analysis. The Lancet 399, 629–655. doi:10.1016/S0140-6736(21)02724-0
Nichols, R. J., Sen, S., Choo, Y. J., Beltrao, P., Zietek, M., Chaba, R., et al. (2011). Phenotypic Landscape of a Bacterial Cell. Cell 144 (1), 143–156. doi:10.1016/j.cell.2010.11.052
Odds, F. C. (2003). Synergy, Antagonism, and what the Chequerboard Puts between Them. J. Antimicrob. Chemother. 52 (1), 1. doi:10.1093/jac/dkg301
Onodera, Y., Okuda, J., Tanaka, M., and Sato, K. (2002). Inhibitory Activities of Quinolones against DNA Gyrase and Topoisomerase IV of Enterococcus faecalis. Antimicrob. Agents Chemother. 46 (6), 1800–1804. doi:10.1128/AAC.46.6.1800-1804.2002
Pan, X. S., Ambler, J., Mehtar, S., and Fisher, L. M. (1996). Involvement of Topoisomerase IV and DNA Gyrase as Ciprofloxacin Targets in Streptococcus Pneumoniae. Antimicrob. Agents Chemother. 40 (10), 2321–2326. doi:10.1128/AAC.40.10.2321
Pappas, G., Athanasoulia, A. P., Matthaiou, D. K., and Falagas, M. E. (2009). Trimethoprim-sulfamethoxazole for Methicillin-Resistant Staphylococcus aureus: a Forgotten Alternative? J. Chemother. 21 (2), 115–126. doi:10.1179/joc.2009.21.2.115
Pongs, O., Bald, R., and Erdmann, V. A. (1973). Identification of Chloramphenicol-Binding Protein in Escherichia coli Ribosomes by Affinity Labeling. Proc. Natl. Acad. Sci. U S A. 70 (8), 2229–2233. doi:10.1073/pnas.70.8.2229
Salehi, N., Attaran, B., Zare-Mirakabad, F., Ghadiri, B., Esmaeili, M., Shakaram, M., et al. (2020). The Outward Shift of Clarithromycin Binding to the Ribosome in Mutant Helicobacter pylori Strains. Helicobacter 25 (6), e12731. doi:10.1111/hel.12731
Saraswathi, V., Amit, G., and Priti, H. (2009). Intra and Inter-molecular Communications through Protein Structure Network. Curr. Protein Pept. Sci. 10 (2), 146–160. doi:10.2174/138920309787847590
Serio, A. W., Keepers, T., Andrews, L., Krause, K. M., and Bush, K. (2018). Aminoglycoside Revival: Review of a Historically Important Class of Antimicrobials Undergoing Rejuvenation. EcoSal Plus 8 (1). doi:10.1128/ecosalplus.ESP-0002-2018
Shen, L. L., and Pernet, A. G. (1985). Mechanism of Inhibition of DNA Gyrase by Analogues of Nalidixic Acid: the Target of the Drugs Is DNA. Proc. Natl. Acad. Sci. U S A. 82 (2), 307–311. doi:10.1073/pnas.82.2.307
Sheng, Z., Sun, Y., Yin, Z., Tang, K., and Cao, Z. (2017). Advances in Computational Approaches in Identifying Synergistic Drug Combinations. Brief Bioinform 19 (6), 1172–1182. doi:10.1093/bib/bbx047
Shin, D., Lee, J., Gong, J. R., and Cho, K. H. (2017). Percolation Transition of Cooperative Mutational Effects in Colorectal Tumorigenesis. Nat. Commun. 8 (1), 1270. doi:10.1038/s41467-017-01171-6
Szklarczyk, D., Gable, A. L., Nastou, K. C., Lyon, D., Kirsch, R., Pyysalo, S., et al. (2020). The STRING Database in 2021: Customizable Protein-Protein Networks, and Functional Characterization of User-Uploaded Gene/measurement Sets. Nucleic Acids Res. 49 (D1), D605–D612. doi:10.1093/nar/gkaa1074
Tyers, M., and Wright, G. D. (2019). Drug Combinations: a Strategy to Extend the Life of Antibiotics in the 21st century. Nat. Rev. Microbiol. 17 (3), 141–155. doi:10.1038/s41579-018-0141-x
Vanunu, O., Magger, O., Ruppin, E., Shlomi, T., and Sharan, R. (2010). Associating Genes and Protein Complexes with Disease via Network Propagation. Plos Comput. Biol. 6 (1), e1000641. doi:10.1371/journal.pcbi.1000641
Ventola, C. L. (2015). The Antibiotic Resistance Crisis: Part 1: Causes and Threats. P T 40 (4), 277–283. doi:10.1016/S0194-5998(97)80284-7
Wang, J., Luo, L., Ding, Q., Wu, Z., Peng, Y., Li, J., et al. (2021a). Development of a Multi-Target Strategy for the Treatment of Vitiligo via Machine Learning and Network Analysis Methods. Front. Pharmacol. 12 (2524), 754175. doi:10.3389/fphar.2021.754175
Wang, Y., Yang, H., Chen, L., Jafari, M., and Tang, J. (2021b). Network-based Modeling of Herb Combinations in Traditional Chinese Medicine. Brief. Bioinf. 22 (5), bbab106. doi:10.1093/bib/bbab106
Weinstein, Z. B., Bender, A., and Cokol, M. (2017). Prediction of Synergistic Drug Combinations. Curr. Opin. Syst. Biol. 4, 24–28. doi:10.1016/j.coisb.2017.05.005
Wekselman, I., Zimmerman, E., Davidovich, C., Belousoff, M., Matzov, D., Krupkin, M., et al. (2017). The Ribosomal Protein uL22 Modulates the Shape of the Protein Exit Tunnel. Structure 25 (8), 1233–e3. doi:10.1016/j.str.2017.06.004
Wishart, D. S., Feunang, Y. D., Guo, A. C., Lo, E. J., Marcu, A., Grant, J. R., et al. (2017). DrugBank 5.0: a Major Update to the DrugBank Database for 2018. Nucleic Acids Res. 46 (D1), D1074–D1082. doi:10.1093/nar/gkx1037
Wright, G. D. (2014). Something Old, Something New: Revisiting Natural Products in Antibiotic Drug Discovery. Can. J. Microbiol. 60 (3), 147–154. doi:10.1139/cjm-2014-0063
Wróbel, A., Arciszewska, K., Maliszewski, D., and Drozdowska, D. (2020). Trimethoprim and Other Nonclassical Antifolates an Excellent Template for Searching Modifications of Dihydrofolate Reductase Enzyme Inhibitors. J. Antibiot. (Tokyo) 73 (1), 5–27. doi:10.1038/s41429-019-0240-6
Yeh, P., Tschumi, A. I., and Kishony, R. (2006). Functional Classification of Drugs by Properties of Their Pairwise Interactions. Nat. Genet. 38 (4), 489–494. doi:10.1038/ng1755
Yilancioglu, K. (2019). Antimicrobial Drug Interactions: Systematic Evaluation of Protein and Nucleic Acid Synthesis Inhibitors. Antibiotics (Basel) 8 (3), 114. doi:10.3390/antibiotics8030114
Zhabiz, G., Omar, B., and Donald Gene, P. (2014). Bacteriophage Therapy: a Potential Solution for the Antibiotic Resistance Crisis. The J. Infect. Developing Countries 8 (02), 129–136. doi:10.3855/jidc.3573
Keywords: antibiotic combination, antimicrobial resistance, graph learning, bacterial infection, synergy effect
Citation: Lv J, Liu G, Ju Y, Sun Y and Guo W (2022) Prediction of Synergistic Antibiotic Combinations by Graph Learning. Front. Pharmacol. 13:849006. doi: 10.3389/fphar.2022.849006
Received: 05 January 2022; Accepted: 14 February 2022;
Published: 08 March 2022.
Edited by:
Xiujuan Lei, Shaanxi Normal University, ChinaReviewed by:
Dong Xu, University of Missouri, United StatesFabricio Alves Barbosa da Silva, Oswaldo Cruz Foundation, Brazil
Copyright © 2022 Lv, Liu, Ju, Sun and Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guixia Liu, bGl1Z3hAamx1LmVkdS5jbg==; Weiying Guo, Z3Vvd3lAamx1LmVkdS5jbg==
 Ji Lv
Ji Lv Guixia Liu1,2*
Guixia Liu1,2* Yuan Ju
Yuan Ju Ying Sun
Ying Sun Weiying Guo
Weiying Guo