Comparison of initial learning algorithms for long short-term memory method on real-time respiratory signal prediction

Aim: This study aimed to examine the effect of the weight initializers on the respiratory signal prediction performance using the long short-term memory (LSTM) model.

Methods: Respiratory signals collected with the CyberKnife Synchrony device during 304 breathing motion traces were used in this study. The effectiveness of four weight initializers (Glorot, He, Orthogonal, and Narrow-normal) on the prediction performance of the LSTM model was investigated. The prediction performance was evaluated by the normalized root mean square error (NRMSE) between the ground truth and predicted respiratory signal.

Results: Among the four initializers, the He initializer showed the best performance. The mean NRMSE with 385-ms ahead time using the He initializer was superior by 7.5%, 8.3%, and 11.3% as compared to that using the Glorot, Orthogonal, and Narrow-normal initializer, respectively. The confidence interval of NRMSE using Glorot, He, Orthogonal, and Narrow-normal initializer were [0.099, 0.175], [0.097, 0.147], [0.101, 0.176], and [0.107, 0.178], respectively.

Conclusions: The experiment results in this study indicated that He could be a valuable initializer in the LSTM model for the respiratory signal prediction.

1. Introduction

During radiation therapy treatment delivery process, tumor in certain organs, such as the lung, would be subject to substantial motion due to patient respiration (1–5). This motion may lead to the leakage of radiation dose from the tumor target to nearby normal tissues, which would sharply degrade the accuracy and quality of the radiation therapy treatment. Respiratory motion could be measured and monitored by several mature techniques. However, the real-time adaptation to motion during radiotherapy treatment is challenging, and latencies in hundreds of milliseconds may still exist (6–10). Hence, prediction of the tumor motion in advance could help reduce these latencies and improve the quality of radiotherapy treatment in mobile cancers.

Many machine learning models have been proposed to predict the respiratory motion. Putra et al. investigated the prediction performance of the Kalman filter (KF) for a short latency (11). Recent studies have demonstrated the merit of artificial neural network (ANN) models on respiratory signal prediction, especially for the nonlinear signals (3, 12, 13). Sharp et al. indicated that the ANN models could have better prediction performance as compared to the KF method (6). Sun et al. proposed a revamped multilayer perceptron neural network (MLP-NN) called Adaboost MLP-NN (ADMLP-NN), which showed more accurate predictions than the MLP-NN (3). One of the main limitations of the ANN models was that they generally ignore the temporal dependence of the previous inputs. The recurrent neural network (RNN) was introduced to include the consideration of temporal information. However, the gradient disappearance and explosion problems restricted the application of RNN on long-term memory prediction. A special RNN model known as long short-term memory (LSTM) (14) had been proposed to overcome the above weakness of RNN (gradient disappearance and explosion problems). Various studies have demonstrated the superior performance of the LSTM model in different time-series prediction tasks (15–20), including the respiratory signal prediction. Wang et al. showed that the prediction performance of a suitable LSTM model could be three-fold higher than that of the ADMLP-NN model (18). Another two studies also showed the potential of the LSTM model in the respiratory signal prediction (19, 20).

Neural network models are sensitive to their initial weights (21, 22). When the neural network was successfully proposed initially, the Narrow-normal initializer was usually used to generate the initial value of weight from a predefined normal sampling distribution. The weights between layers are initialized using a fixed variance distribution, which may cause the problem of gradient disappearance or gradient explosion (21, 22). This defect hampered the extensive use of the Narrow-normal initializer. The Glorot initializer (23) provided a normalized initialization, which could maintain the activation and the back-propagated gradient variances during training based on the linear activation. Then, He et al. took the rectifier nonlinearity into account and proposed the He initializer (24). Sachs et al. illustrated that if the initial weight obeyed an orthogonal matrix, the initial conditions could keep the error vector norm through the deep neural network during back propagation process while generating depth independent learning times. Based on this finding, the orthogonal initializer (25) was proposed.

While the critical importance of the proper weight initializers on time-series prediction performance has often been noted in previous works (21–26), researchers often focused on improving the model architecture. Therefore, there is a lack of knowledge on the effect of initializer on respiratory signal prediction using the LSTM model. The aim of this study was to examine the effect of different initializer on the performance of LSTM model in the patient respiratory signal prediction. The primary contributions of this study were concluded as follows:

1. To the best of our knowledge, this is the first study to investigate the effectiveness of the weight initializers on the respiratory prediction problem using the LSTM model. In this study, we investigated the influence of the four common weight initializers discussed in the literature (22, 27) on the prediction performance of LSTM model using 304 breathing motion cases from an open-access database collected by the CyberKnife Synchrony tracking system (Accuray, Sunnyvale, CA) with a 26-Hz sampling rate.

2. We further investigated the effect of the irregular breathing patterns on the prediction performance for each initializer and demonstrated the advantage of using the He initializer on irregular respiratory pattern patients.

The results illustrated that the initial weight algorithms in the LSTM model would exert substantial effect on the respiratory signal prediction performance. The He initializer could be an optimal choice for the respiratory signal prediction, especially for the irregular respiratory pattern patients.

2. Methods

2.1. Prediction process

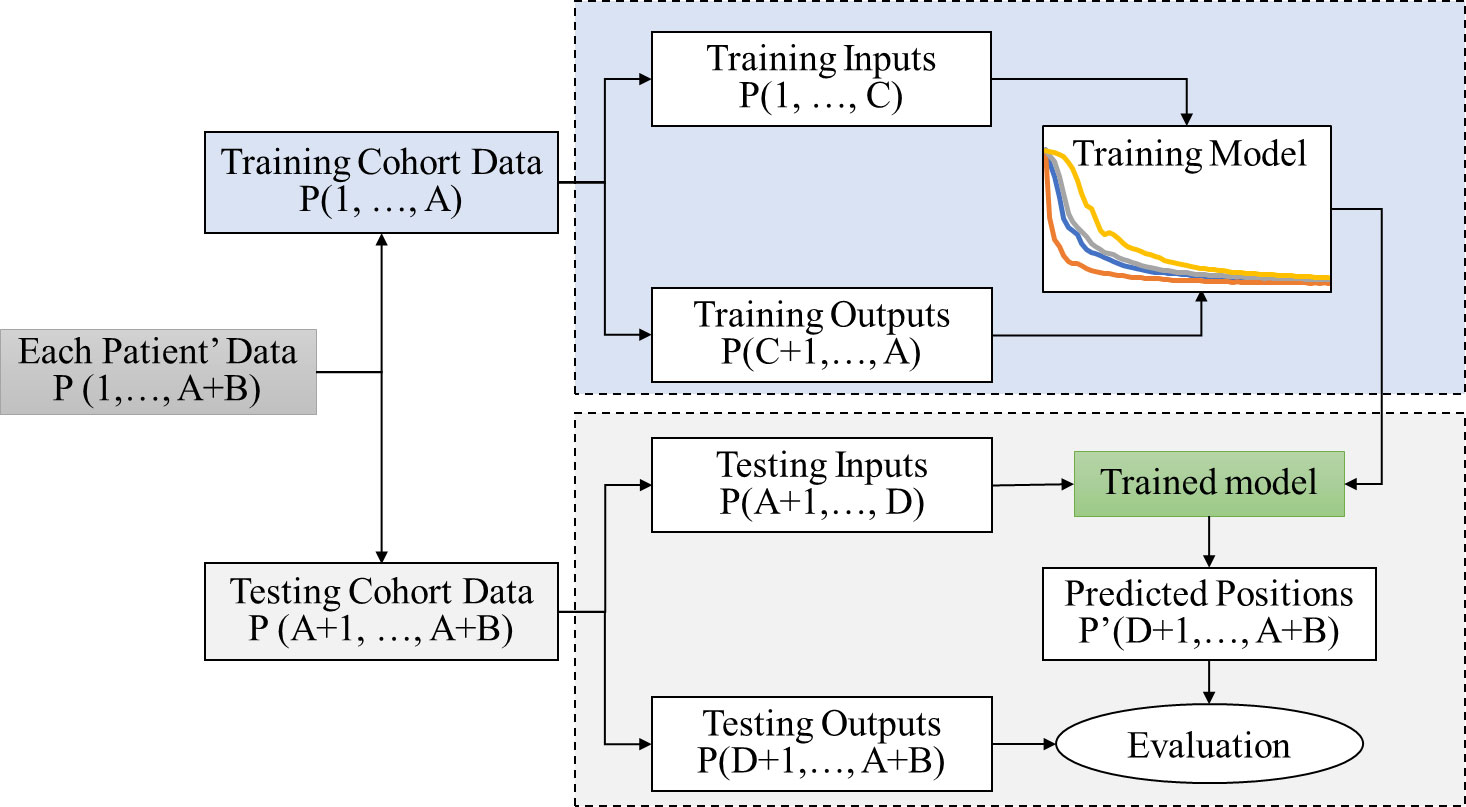
The general workflow for the prediction process used in this study is outlined in Figure 1. Each respiratory signal was divided into two segments separated by time A. Respiratory signals prior to time A were used as training data, and those after time A were used for testing. Among the training data, the signals before and after time C were used as the input and prediction outputs, respectively. LSTM neural network was implemented as the prediction model. The testing data (positions after the time A) were used to evaluate the developed LSTM prediction model. The testing data were divided into two segments separated by time D. The signals before time D were defined as the testing input, and those after time D were defined as the testing outputs or ground truth. The trained LSTM prediction model was applied to the testing inputs to generate the prediction signal P’, which was compared to the testing outputs or ground truth P for evaluation.

FIGURE 1

Figure 1 Flow chart of the prediction algorithm.

2.2. Long short-term memory neural network

A bidirectional architecture LSTM layer was developed to test the performance of all the four initializers in this study (17, 18). The formulas of the LSTM layer are illustrated in the Equations 1–8.

$\begin{array}{ll}{i}_t=\sigma \left(W_{xi}{x}_t+W_{hi}{h}_{t-1}+W_{ci}{c}_{t-1}+b_i\right)& (1)\end{array}$

$\begin{array}{ll}{f}_t=\sigma \left(W_{xf}{x}_t+W_{hf}{h}_{t-1}+W_{cf}{c}_{t-1}+b_f\right)& (2)\end{array}$

$\begin{array}{ll}{c}_t=f_t{c}_{t-1}+i_{t}tanh\left(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c\right)& (3)\end{array}$

$\begin{array}{ll}{o}_t=\sigma \left(W_{xo}{x}_t+W_{ho}{h}_{t-1}+W_{co}{c}_t+b_o\right)& (4)\end{array}$

$\begin{array}{ll}{h}_t=o_{t}tanh(c_t)& (5)\end{array}$

$\begin{array}{ll}{h}_t^f=tanh\left(W_{xh}^f{x}_t+W_{xh}^f{h}_{t-1}^f+b_h^f\right)& (6)\end{array}$

$\begin{array}{ll}{h}_t^b=tanh\left(W_{xh}^b{x}_t+W_{hh}^b{h}_{t+1}^b+b_h^b\right)& (7)\end{array}$

$\begin{array}{ll}{y}_t=W_{hy}^f{h}_t^f+W_{hy}^b{h}_t^b+b_y& (8)\end{array}$

Here, i_t, f_t, c_t, o_t, h_t, $h_t^f$, $h_t^b$, and y_t refer to the input gate, forget gate, memory cell vectors, output gate, hidden vector sequence, forward hidden vector sequence, backward hidden vector sequence, and output, respectively. The tanh and σ stand for the two activation functions as given by the Equations 9 and 10.

$\begin{array}{ll}\sigma (x)=\frac{1}{1+e^{-x}}& (9)\end{array}$

$\begin{array}{ll}\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}& (10)\end{array}$

W_xi, W_hi, W_ci, W_xf, W_hf, W_cf, W_xc, W_hc, W_xo, W_ho, and W_co denote the weighted parameters, while the b_i, b_f, b_c, and b_o represent the intercepts. A plurality of LSTM layers can be stacked into a deeper neural network, which can fit the complicated functions between the inputs and targets.

2.3. Initializers

For the Glorot initializers (also called the Xavier initializer), the weights W_ij of each layer were initialized with the heuristic as follows (23):

$\begin{array}{ll}{W}_{ij}~\mathcal{U}\left[-\sqrt{\frac{6}{{\mathcal{N}}_{ℐ}+{\mathcal{N}}_{\mathcal{O}}}},\sqrt{\frac{6}{{\mathcal{N}}_{ℐ}+{\mathcal{N}}_{\mathcal{O}}}}\right]& (11)\end{array}$

Here, U[ −δ, δ ] was sampled independently from a zero-mean uniform distribution in the bounds [ −δ, δ ] . N₀ was four times of the hidden unit number, and N_J was the input channel number.

For the He initializer (24), the weights W_ij were sampled according to a zero-mean normal (Gaussian) distribution with the following standard deviation (SD):

$\begin{array}{ll}{W}_{ij}~\mathcal{G}\left[-\sqrt{\frac{2}{{\mathcal{N}}_{ℐ}}},\sqrt{\frac{2}{{\mathcal{N}}_{ℐ}}}\right]& (12)\end{array}$

Here, the size of N_J was the input channel number for the input weight and the hidden unit number for the recurrent weight.

For the Orthogonal initializer (25), the orthogonal matrix Q was first established by producing the Gaussian matrices randomly and then computed by the QR decomposition using the formula Z = QR, where Z obeyed unit normal distribution.

For the Narrow-normal initializer, the weights were obtained by sampling from a normal distribution with 0 mean and 0.01 SD independently.

2.4. Prediction performance evaluation

A total of 304 breathing motion traces collected by the CyberKnife Synchrony (Accuray, Sunnyvale, CA) tracking system and procured from an open dataset (18, 28) were used in this study. The detail information of the dataset is illustrated in Table 1. The first 1-min signal was used to train the LSTM model with different initial methods, while the following 30 s was applied to evaluate the effectiveness of each initial method. The ahead time was about 385 ms (10 samples). All the evaluation metrics were based on the following default hyper-parameters in this study: three LSTM layers, 0.001 initial learning rate, 50 time lags, and 300 hidden units.

TABLE 1

Table 1 Detail information of the dataset used in this study.

RMSE is one of the main metrics used for respiratory signal prediction evaluation (2–4, 8–11, 19, 20). However, the root mean square error (RMSE) was not a dimensionless and normalized metric (29), and it would not be suitable for comparing the performance of respiratory signal prediction across different patients before normalization (12, 18). Hence, in order to minimize the effect of signal amplitude on different cases, the NRMSE instead of the RMSE between the real and predicted signal were used to evaluate the predication performance for all initializers (29). The NRMSEs used in this study are illustrated by Equations 13 and 14.

$\begin{array}{ll}NRMSE=\frac{\sqrt{\frac{1}{t_{A+B}-t_{\text{D}+1}+1}{\sum }_{t=t_{\text{D}+1}}^{A+B}{\left(P^{\prime }\left(t\right)-P\left(t\right)\right)}^2}}{Range\left(P\left(t\right)\right)}& (13)\end{array}$

$\begin{array}{ll}\begin{array}{c}Range\left(P\left(t\right)\right)=Max\left(P\left(t\right)\right)-Min\left(P\left(t\right)\right) tϵ\left(D+1,A+B\right) \end{array}& (14)\end{array}$

Here, P(t) and P'(t) were the ground truth and predicted signal at the time fame t, respectively.

Breathing irregularity was examined to test prediction performance of the LSTM model using the four initializers on different breathing patterns. As illustrated in the Equation 15, the breathing irregularity was defined as the average of the standard deviation (SD) of the maximum (i.e., peak) and minimum (i.e., valley) amplitudes. Patients were split into two groups by the median value of the irregularity (r= 0.22).

$\begin{array}{ll}r=\frac{S{D}_{peaks}+S{D}_{valleys}}{2}& (15)\end{array}$

3. Results

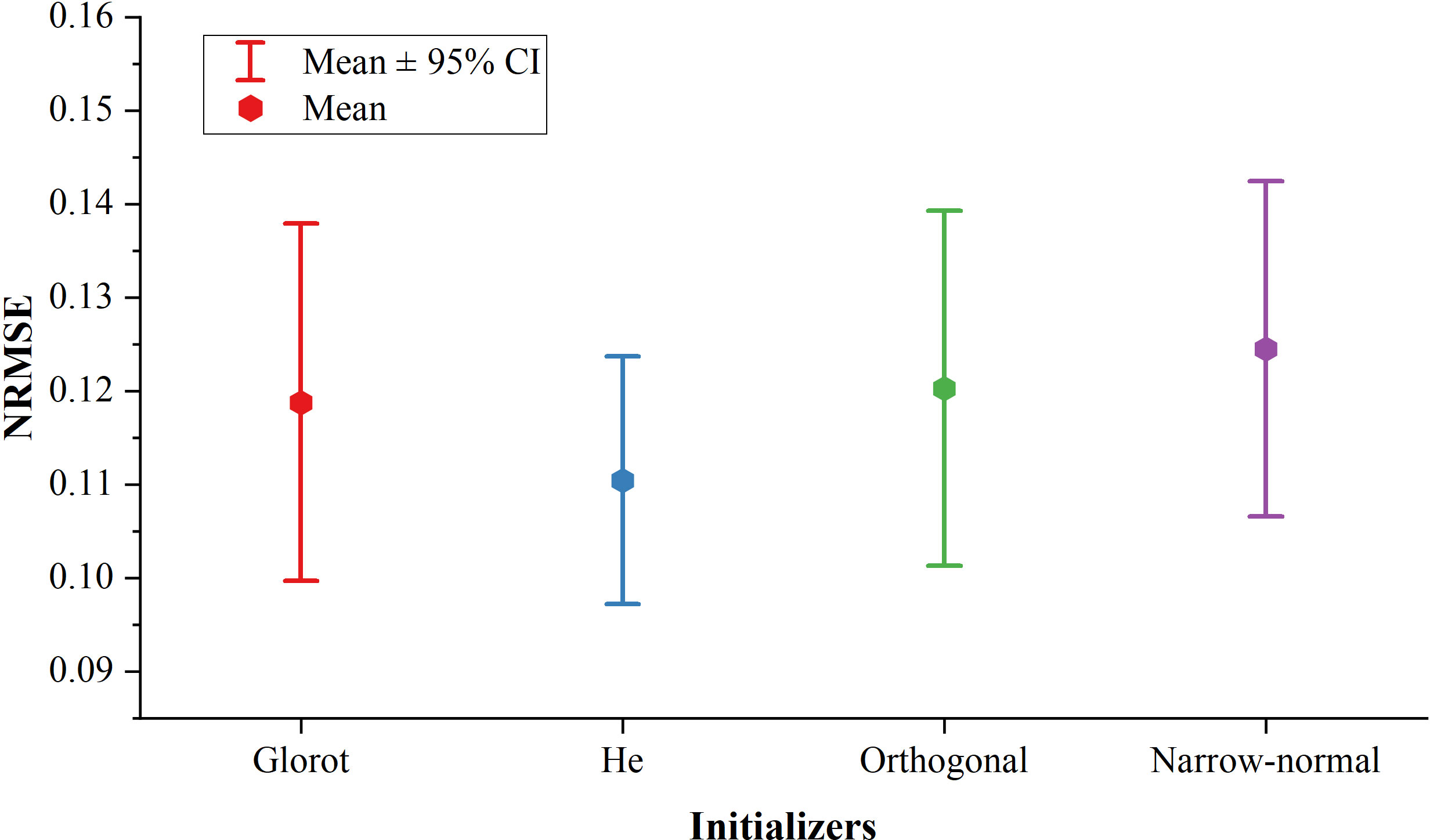
Figure 2 shows the NRMSEs using four initializers (Glorot, He, Orthogonal, and Narrow-normal) with a 385-ms ahead time. The He initializer showed the best prediction performance. The mean of NRMSE using the He initializer was lower by 7.5%, 8.3%, and 11.3% compared to the Glorot, Orthogonal, and Narrow-normal initializer, respectively. The He initializer was more robust than the other three initializers, as it achieved the narrowest confidence interval (CI) among all the four initializers.

FIGURE 2

Figure 2 Prediction performance of the four initializers.

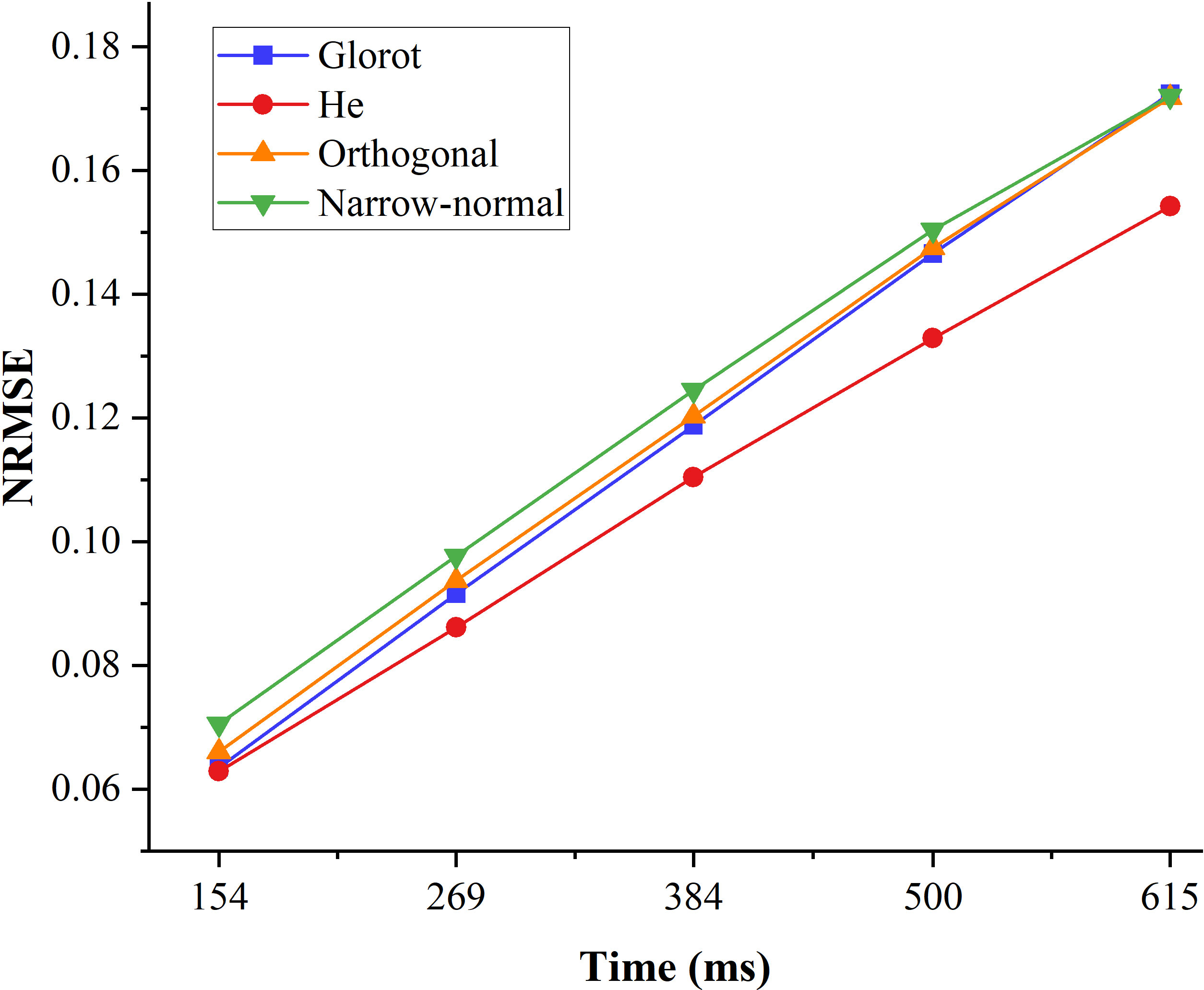
The prediction performance of the four initializers with different ahead time is shown in Figure 3. The prediction performance using all of the four initializers decreased when the ahead time increases. The prediction performance using the He initializer for all the ahead time examined in this study were higher than the other three initializers. The average prediction performance gap between the He initializer and other three initializers increased when the ahead time increases.

FIGURE 3

Figure 3 Prediction performance of the four initializers with different ahead times.

The prediction performance of the regular and irregular breathing groups, which are divided by the median irregularity is shown in Figure 4. For all the four initializers, the performance of the irregular group was inferior to the regular group. The prediction performances of Glorot, He, and Orthogonal were similar in the regular group. However, the mean of NRMSE in the irregular group using the He initializer was superior by 11.0% (Glorot), 11.6% (Orthogonal), and 14.1% (Narrow-normal), respectively. The upper limits of the 95% confidence interval (CI) of the NRMSE for the irregular group patients were lowest for He (0.147) and were 0.175, 0.176, and 0.178 for Glorot, Orthogonal, and Narrow-normal, respectively.

FIGURE 4

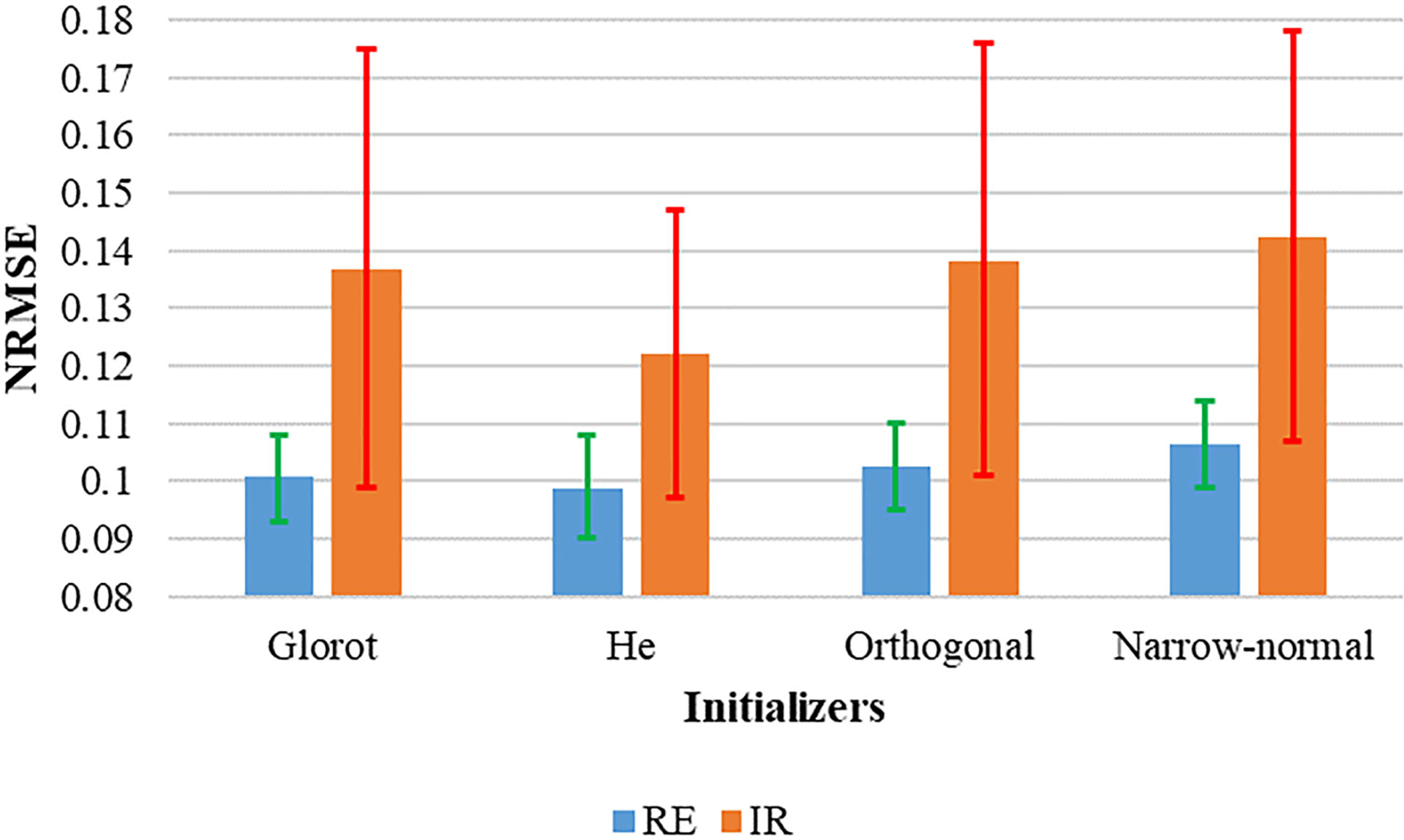
Figure 4 Prediction performance of the two groups divided by the median irregularity. The green and red bars represented 95% CI of the NRMSE for the RE and IR groups, respectively.

The effect of the four important hyper-parameters on the prediction performance was explored and shown in Figure 5. Four different values (1, 2, 3, and 4) were selected to evaluate the effect of the N_l on the prediction performance (Figure 5A). The LSTM model showed the similar prediction performance with one to three LSTM layers for the Glorot and Orthogonal initializers. For He and Narrow-normal initializers, the LSTM model with two or three LSTM layers showed similar prediction performance. The effect of T_l on the prediction performance was examined by five selected values (1, 5, 10, 25 and 50) (Figure 5B). Time lag of 10 showed the best performance for the He and Narrow-normal initializers, while 5 showed the best performance for the other two initializers. The influence of H_u was explored on five values (30, 50, 100, 300, and 500) (Figure 5C). The prediction performance kept improving as the H_u increased from 30 to 500 for all the four initializers. Four L_r values (0.0001, 0.001, 0.01, and 0.1) were investigated. The NRMSE using the first three initializers (Glorot, He, and Orthogonal) was lowest when L_r was 0.001. Narrow-normal initializer showed the best prediction performance when L_r was 0.01.

FIGURE 5

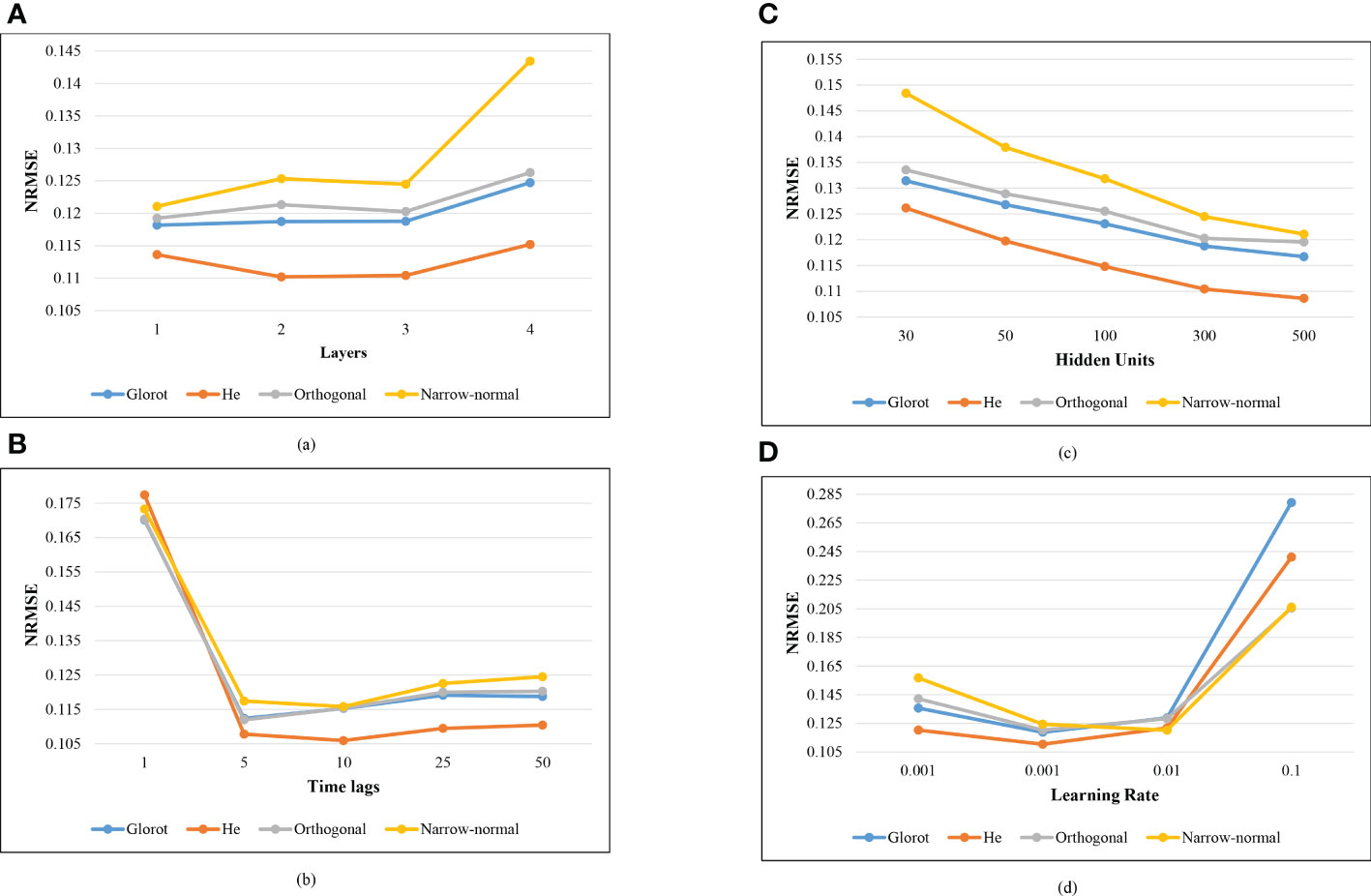
Figure 5 Effect of the hyper-parameters on the prediction performance. (A) Number of the LSTM layers (N_l). (B) Time lags (T_l). (C) Hidden units (H_u). (D) Learning rate (L_r).

4. Discussion

The effect of four common initializers on the performance of respiratory signal prediction using the LSTM model was examined in this study. The results illustrated that the He initializer outperformed the other three initializers for its higher respiratory prediction performance. A suitable initializer would substantially improve the prediction performance.

The prediction performance using all the four initializers became lower when the ahead time increases. This was probably because the relationship between the training and predicted respiratory signals would diminish when the ahead time increases. However, the prediction performance deterioration using the He initializer was slower than the other three methods. This may suggest that the He initializer could enhance LSTM’s ability to capture longer ahead time information.

The prediction performance of the irregular breathing group was lower than the regular breathing group for all the four initializers. This may be contributed by the factor that the relationship between the prior and future signals in the irregular group was more difficult to capture than that in the regular group. The prediction performance of Glorot, He, and Orthogonal was similar in the regular group. However, the mean of NRMSE using the He initializer in the irregular group was lower compared to other three initializers. This suggested the superior ability of He initializer in capturing connection between prior and future signals. The upper limit of the 95% CI of the NRMSE using the He initializer was lower than that using other three initializers, suggesting that the He initializer might improve the general performance of the LSTM model in breathing signal prediction.

We also investigated the influence of hyper-parameters setting on the prediction performance for each initializer. A total of four important hyper-parameters was examined in this study. A large numerical value of the first three hyper-parameters (N_l, T_l, and H_u) represented a complex network, which would fit a more complicated function but easy to overfit. The prediction performance became better as the first three hyper-parameters increased initially. However, as these three hyper-parameters continue to increase, the prediction performance improved only slightly and even could deteriorate. This may be because when these three hyper-parameters were too small, the LSTM model would not fit the respiratory curve well. Hence, the increase in these three hyper-parameters could improve the prediction performance initially. However, too large N_l, T_l, and H_u would raise the risk of overfitting for the LSTM model and potentially degrade the prediction accuracy. The L_r scales and updates the magnitude of the LSTM model weights to minimize the loss function. If L_r was too small, the converge time would be long, and the risk of trapping in undesirable local minimum increases. On the other hand, if L_r was too large, a suboptimal result may be obtained. Finally, 0.001 and 0.01 achieved the best performance for Narrow-normal and the other three initializers, respectively.

One of the limitations of this study was that all the respiratory signals from this database were originally detected by the fiducial marker placed on patient’s chest. These external signals may be different from the real internal tumor motion. Besides, the dataset was collected from a single center. In the future, we would further evaluate the effect of the initializers on actual tumor motion signals or internal respiratory signals ideally from multi-centers.

5. Conclusion

The influence of the four weight initializers on the performance of respiratory signal prediction using the LSTM model was investigated in this study. The results suggested that the weight initialization methods would exert substantial effect on the respiratory signal prediction performance. The He initializer could be an optimal initializer for the respiratory signal prediction using the LSTM model, especially for the irregular respiratory pattern patients.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

WS and QW designed the methodology. WS and JD wrote the program. WS performed data analysis, interpretation and drafted the manuscript. LZ, JD, and QW revised this manuscript critically for important intellectual content and contributed to the interpretation of data. All authors reviewed the manuscript. All authors read and approved the final manuscript.

Funding

This work was partially supported by the National Natural Science Foundation of China (62103366), the General Project of Chongqing Natural Science Foundation (grant cstc2020jcyj-msxm2928), and Duke Kunshan University Education Development Foundation (22KDKUF032).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Verma P, Wu H, Langer M, Das I, Sandison G. Survey: Real-time tumor motion prediction for image-guided radiation treatment. Computing Sci Eng (2011) 13(5):24–35.

Google Scholar

2. Chang PC, Dang J, Dai JR, Sun WZ. Real-time respiratory tumor motion prediction based on a temporal convolutional neural network: Prediction model development study. J Med Internet Res (2021) 23(8):0–e27235.

Google Scholar

3. Sun WZ, Jiang MY, Ren L, Dang J, You T, Yin FF, et al. Respiratory signal prediction based on adaptive boosting and multi-layer perceptron neural network. Phys Med Biol (2017) 62(17):6822–35.

PubMed Abstract | Google Scholar

4. Bukhari W, Hong SM. Real-time prediction and gating of respiratory motion using an extended kalman filter and Gaussian process regression. Phys Med Biol (2015) 60(1):233–52.

PubMed Abstract | Google Scholar

5. Vergalasova I, Cai J, Yin F-F. A novel technique for markerless, self-sorted 4d-cbct: Feasibility study. Med Phys (2012) 39(3):1442–51.

PubMed Abstract | Google Scholar

6. Sharp GC, Jiang SB, Shimizu S, Shirato H. Prediction of respiratory tumour motion for real-time image guided radiotherapy. Phys Med Biol (2004) 49:425–40.

PubMed Abstract | Google Scholar

7. Ernst F, Schlaefer A, Schweikard A. Predicting the outcome of respiratory motion prediction. Med Phys (2011) 38(10):5569–81.

PubMed Abstract | Google Scholar

8. Sun WZ, Chun QW, Ren L, Dang J, Yin FF. Adaptive respiratory signal prediction using dual multi-layer perceptron neural networks (MLP-NNs). Phys Med Biol (2020) 65(18):185005.

PubMed Abstract | Google Scholar

9. Torshabi AE, Riboldi M, Fooladi AAI, Mosalla M, Borani G, et al. An adaptive fuzzy prediction model for real time tumor tracking in radiotherapy via external surrogates. J Appl Clin Med Phys (2013) 14(1):102–14.

Google Scholar

10. Ren Q, Nishioka S, Shirato H, Berbeco RI. Adaptive prediction of respiratory motion for motion compensation radiotherapy. Phys Med Biol (2007) 52(22):6651–61.

PubMed Abstract | Google Scholar

11. Putra D, Haas OCL, Mills JA, Bumham KJ. Prediction of tumour motion using interacting multiple model filter. In: 2006 IET 3rd international conference on advances in medical, signal and information processing - MEDSIP 2006. Glasgow, UK (2016) pp. 1–4, doi: 10.1049/cp:20060350

CrossRef Full Text | Google Scholar

12. Isaksson M, Jalden J, Murphy MJ. On using an adaptive neural network to predict lung tumor motion during respiration for radiotherapy applications. Med Phys (2005) 32:3801–9.

PubMed Abstract | Google Scholar

13. Tsai TI, Li DC. Approximate modeling for high order non-linear functions using small sample sets. Expert Syst Appl (2008) 34(1):564–9.

Google Scholar

14. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput (1997) 9:1735–80.

PubMed Abstract | Google Scholar

15. Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. Adv Neural Inf Process Syst (2014) 2:3104–3112.

Google Scholar

16. Cho K, Van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation, in: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Doha, Qatar (2014) pp. 1724–34.

Google Scholar

17. Rahman MM, Watanobe Y, Nakamura K. A bidirectional lstm language model for code evaluation and repair. Symmetry (2021) 13(2):247.

Google Scholar

18. Wang R, Liang X, Zhu X, Xie Y. A feasibility of respiration prediction based on deep bi-LSTM for real-time tumor tracking, in: IEEE Access. (2018) Vol. 6. pp. 51262–8.

Google Scholar

19. Lin H, Shi CY, Wang B, Chan MF, Tang X, Ji W. Towards real-time respiratory motion prediction based on long short-term memory neural networks. Phys Med Biol (2019) 64(8):085010.

PubMed Abstract | Google Scholar

20. Wang G, Li Z, Li G, Dai G, Xiao Q, Bai L, et al. Real-time liver tracking algorithm based on LSTM and SVR networks for use in surface-guided radiation therapy. Radiat Oncol (2021) 16(1):13.

PubMed Abstract | Google Scholar

21. Peng AY, Koh YS, Riddle P, Pfahringer B. Using supervised pretraining to improve generalization of neural networks on binary classification problems. Joint Eur Conf Mach Learn Knowledge Discovery Database (2018) 11051, 410-425.

Google Scholar

22. Li H, Krek M, Perin G. A comparison of weight initializers in deep learning-based side-channel analysis. In: Applied cryptography and network security workshops. Cham: Springer (2020) 11051:410–425.

Google Scholar

23. Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. JMLR Workshop Conf Proc (2010) 9:249–256.

Google Scholar

24. He K, Zhang X, Ren S, Sun J. Developing deep into rectifiers: Surpassing human-level performance on ImageNet classification, in: 2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile (2015) pp. 1026-34, doi: 10.1109/ICCV.2015.123

CrossRef Full Text | Google Scholar

25. Saxe AM, Mcclelland JL, Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. Int Conf Learn Representations (2014).

Google Scholar

26. Kim HC, Kang MJ. Comparison of weight initialization techniques for deep neural networks. Int J Advanced Culture Technol (2019) 7(4):283–8.

Google Scholar

27. Qi ZA, Ro B. Performance of neural network for indoor airflow prediction: Sensitivity towards weight initialization. Energy Buildings (2021) 246:111106.

Google Scholar

28. Floris E. Compensating for quasi-periodic motion in robotic radiosurgery. New York: Springer (2012). doi: 10.1007/978-1-4614-1912-9

CrossRef Full Text | Google Scholar

29. Debaditya C, Hazem E. Performance testing of energy models: Are we using the right statistical metrics? J Building Perform Simulation (2018) 11(4):433–48.

Google Scholar