Development and Validation of Prognostic Model for Lung Adenocarcinoma Patients Based on m6A Methylation Related Transcriptomics

Existing studies suggest that m⁶A methylation is closely related to the prognosis of cancer. We developed three prognostic models based on m⁶A-related transcriptomics in lung adenocarcinoma patients and performed external validations. The TCGA-LUAD cohort served as the derivation cohort and six GEO data sets as external validation cohorts. The first model (mRNA model) was developed based on m⁶A-related mRNA. LASSO and stepwise regression were used to screen genes and the prognostic model was developed from multivariate Cox regression model. The second model (lncRNA model) was constructed based on m⁶A related lncRNAs. The four steps of random survival forest, LASSO, best subset selection and stepwise regression were used to screen genes and develop a Cox regression prognostic model. The third model combined the risk scores of the first two models with clinical variable. Variables were screened by stepwise regression. The mRNA model included 11 predictors. The internal validation C index was 0.736. The lncRNA model has 15 predictors. The internal validation C index was 0.707. The third model combined the risk scores of the first two models with tumor stage. The internal validation C index was 0.794. In validation sets, all C-indexes of models were about 0.6, and three models had good calibration accuracy. Freely online calculator on the web at https://lhj0520.shinyapps.io/LUAD_prediction_model/.

Introduction

Lung cancer ranks as the major cause of cancer death, accounting for almost a quarter of cancer deaths (1). Lung adenocarcinoma (LUAD) is the most common subtype of lung cancer, accounting for more than 40% of lung cancer incidence (2).N⁶-methyladenosine (m⁶A), the most abundant form of posttranscriptional RNA modification in eukaryotes, plays an important role in a variety of biological processes by regulating the translation, processing, splicing, stabilization, and degradation of target RNA (3). The abundance and effects of m⁶A methylation modification on RNA are maintained by its methyltransferases (‘writers’), binding proteins (‘readers’), and demethylases (‘erasers’) (4).

Existing studies suggest that m⁶A methylation is closely related to the prognosis of cancer. An increasing number of m⁶A-related genes have been developed as molecular markers of cancer prognosis. In lung adenocarcinoma, several biomarkers have also been developed. Some of the biomarkers are based on single gene model, such as YTHDC2 (5), NPM1 (6) and LCAT3 (7). Some others are multigene-based, including Wang (5 genes) (8), Sun (10 genes) (9), and Zhu (6 genes) (10). Such molecular biomarkers have been shown to enhance the accuracy of overall survival (OS) prediction in LUAD.

However, the predictive power of these markers is often limited. First, most models were constructed based only on mRNAs or lncRNAs. Second, most of the models lack some key parameters, prognostic index or baseline survival function, which make it difficult for others to validate or use them. Further on, even if complete parameters related to model validation are provided (unfortunately, none is found in prediction model related to lung adenocarcinoma at present), few convenient online interaction tools are available.

Based on the above fact, we attempted to develop models to fill in the gaps in prognostic model of lung adenocarcinoma using m⁶A-related transcriptomics to predict OS. First, we developed a mRNA prognostic model and a lncRNA prognostic model for lung adenocarcinoma on TCGA cohort and evaluated the two models on several GEO data sets. And then we used the two models and some clinical variables as alternative predictors to construct a multi-omics clinical prediction model. All prediction models developed have two to six independent external validation sets. To further facilitate the practical application of the constructed prediction model in clinical practice, we developed a free online calculator: https://lhj0520.shinyapps.io/LUAD_prediction_model/.

Methods

Data Acquisition and Processing

For model derivation, we downloaded RNA-seq data (counts values) of 585 LUAD patients (version: 07-20-2019) and corresponding clinical information (version: 08-07-2019) in GDC TCGA from the UCSC Xena public data hub (http://xena.ucsc.edu/). A total of 486 samples with primary tumors and overall survival greater than 30 days were retained. The expression data from the TCGA data portal were quantile normalized and log2-transformed (11). In addition, the somatic mutation data of LUAD patients were also downloaded as a mutation annotation format (MAF) file from GDC Data Portal (https://portal.gdc.cancer.gov/).

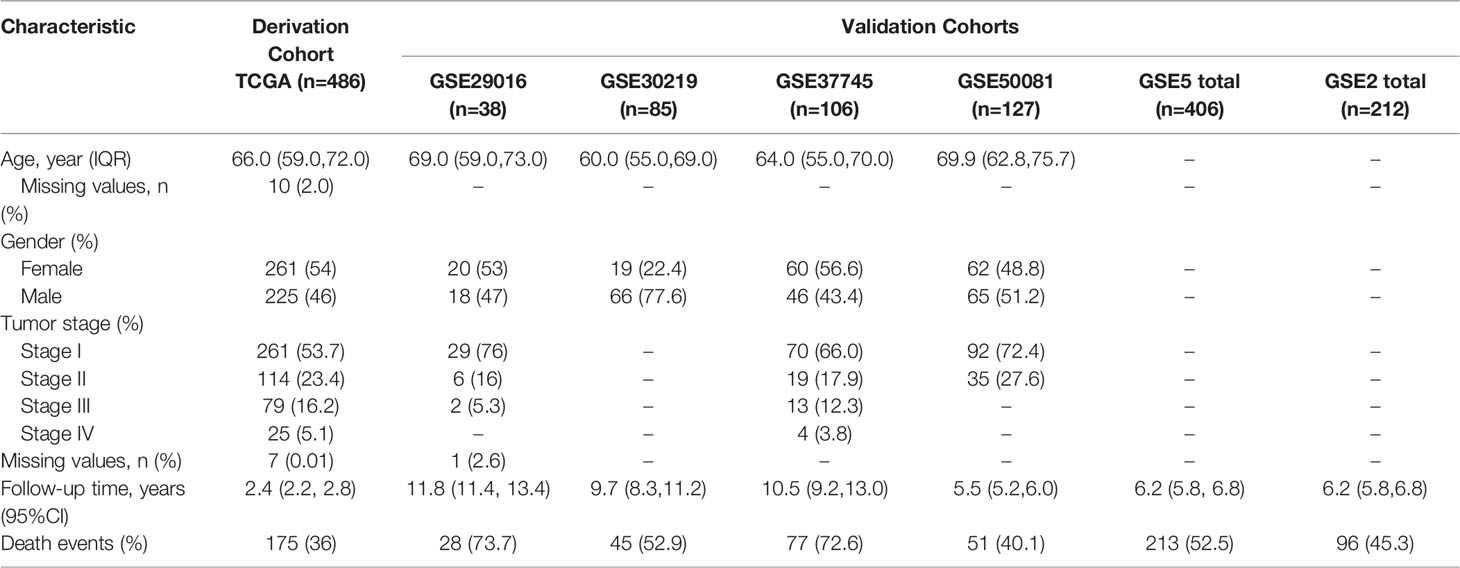
For model validation study, 6 datasets from GEO (https://www.ncbi.nlm.nih.gov/geo/) database were considered, including GSE29016 (GPL6947, n=38), GSE29013 (GPL570, n=30) GSE3141 (GPL570, n=58), GSE30219 (GPL570, n=85), GSE37745 (GPL570, n=106), and GSE50081 (GPL570, n=127). We downloaded the series matrix files and their platform annotation information. All the microarray data were quantile normalized and the Robust Multichip Average (RMA) method was used for background adjusted (12).

Annotation of LncRNA Expression

The lncRNAs were extracted according to file downloaded from GENCODE project (https://www.gencodegenes.org/, release 37).

Selection of m⁶A Methylation Regulators and m⁶A-Related mRNAs

We obtained m⁶A methylation regulators from the literature (13). For m⁶A-related genes in LUAD, genes annotated as ‘protein coding’ were retained from the m6AVar database (http://rmvar.renlab.org/) (14), which is a comprehensive database of m⁶A-associated variants.

Selection of m⁶A-Related LncRNAs

Spearman rank correlation analysis was conducted between m⁶A methylation regulatory factors and lncRNAs. Rank correlation coefficient | R_s | >0.3 and P <0.05 were used as the selection criteria.

Development and Validation of Model Based on mRNAs

Using the mRNA dataset of TCGA LUAD patients as a derivation cohort, we developed a prognostic model to predict OS. As the first step of variable selection, the least absolute shrinkage and selection operator (LASSO) method (15) of R package ‘glmnet’ was used to reduce the dimension of genes. The optimal value of λ was selected by tenfold cross-validation, and corresponding variables with nonzero coefficients were retained. Next, the “stepAIC” function with “both” in the R package “MASS” was applied to perform stepwise Cox regression (16) for the retained genes, and the optimal gene combination was obtained according to the lowest Akaike information criterion (AIC) value.

Based on the obtained Cox model, the risk score, i.e., prognostic index (PI), could be calculated directly using the “predict” function in R package “rms” with the parameter “type= lp” (17). The calculation formula is as follows:

$\begin{array}{ll}RiskScore\left(PI\right)=\left({\displaystyle {\sum }_{i=1}^n{\beta }_i\ast Ex{p}_i}\right)-\overline{x},& (1)\end{array}$

where n refers to the total number of genes in the model; β_i refers to the coefficient of each gene; and Exp_i refers to the expression level of each gene; $\overline{x}$ refers to the mean of PI.

There are two fundamental aspects, discrimination and calibration, to evaluate the performance of the model. Discrimination refers to the ability of a model to differentiate between high-risk patients and low-risk patients (18). It is represented by Harrell’s c-index of concordance (C-index) (19). Internal validation adopted bootstrapping (1000 resamples). The C-index was calculated by the “validate” function in the R package “rms” (17). Time-dependent ROC curves at 1-, 3- and 5-year were created by the “survivalROC” R package (20). Through the “cindex” function of the “pec” R package (21), the dynamic time-dependent C-index curve of each dataset was plotted. Calibration refers to the agreement between the predicted and observed survival probabilities (18). The calibration plot was applied to assess the calibration of our model at 1, 3 and 5 years respectively by the “rms” R package (17).

In addition, we estimated the baseline survival function, S₀(t) which is an essential indicator for prediction model (22) and presented it by Kaplan–Meier curves. For the Cox proportional hazards model, the survival probability at different time points are calculated by the following formula (23):

$\begin{array}{ll}S\left(t|X\right)=S_0{\left(t\right)}^{exp\left(PI\right)},& (2)\end{array}$

where S(t|X) denotes the predicted survival at time t for a patient with predictors X; S₀(t) denotes the baseline survival function; and PI denotes the linear predictors. The baseline survival is estimated as , S₀(t) = exp[-H₀(t)] where H₀(t) is the baseline cumulative hazard (22). It can be computed by the “basehaz” function in the “survival” R package (24).

The baseline survival function is crucial, which loads the information needed to evaluate the calibration of survival probabilities in the derivation dataset and more than that calibration in validation datasets (22). Therefore, if we want to validate the Cox model, it is necessary to know the baseline survival function and regression coefficient of the model.

The “surv_cutpoint” function in the R package “survminer” was used to determine the appropriate cutoff value of PI based on the maximum rank statistics (25), and patients in each data set were divided into two risk groups. The predicted survival curve of each person could be calculated by the baseline survival probability. Then, the calibration accuracy of the model can also be evaluated by comparing the average predicted survival probability curve with the observed survival probability curve in the two risk groups (18).

The mRNA model has four GEO external validation sets. Three single data sets included: GSE37745 (n=106), GSE29016 (n=38), and GSE50081 (n=127). Another dataset was pooled by five datasets (GSE3141, GSE29013, GSE30219, GSE37745 and GSE50081). The combined dataset was adjusted for batch effect through the “ComBat” function of the “sva” R package (26). We referred to this combined dataset as the “GSE5total” dataset.

Development and Validation of Model Based on LncRNAs

For lncRNA model, we used four steps to obtain appropriate lncRNAs. First, the random survival forest (RSF) (27), a machine learning method for regression, was used to conduct preliminary feature screening for m⁶A-related lncRNAs through “rfsrc” function of “randomForestSRC” R package (28). This algorithm was used to rank prognostic lncRNAs (ntree =1000), and we selected the top 100 lncRNAs for the next step of selection. Second, we applied LASSO to shrink variables. Then, the prognostic factors retained by the LASSO algorithm were analyzed by best subset selection. To realize this method in the Cox proportional hazards model, we used the R package “BeSS” (29). Finally, stepwise Cox regression was used to select the optimal model from the factors obtained in the previous step.

The performance evaluation and PI calculation methods of lncRNA model were the same as mRNA model.

Two datasets, GSE30219 (n=85) and GSE50081 (n=127), were used to validate the lncRNA model. For expanding the sample size of the validation set, we combined the above two data sets into one data set and named it “GSE2total” to validate.

Development and Validation of Comprehensive Prediction Model

To further expand the clinical prediction capacity of m⁶A-related model, we decided to develop a more comprehensive clinical prediction model (we called it the “comprehensive prediction model”) by combining two risk scores obtained from the above models with clinical variables.

We used multiple imputation by chained equations of the R package “mice” to impute the missing values of clinical variables (5 times) (30). The number of iterations in each imputation was five by default. The variables used in the multiple imputation model included the two risk scores(mRNA risk score and lncRNA risk score), three clinical factors that were common in the derivation and validation datasets (age, sex and tumor stage) and the outcome (the Nelson–Aalen estimator of the baseline cumulative hazard and the outcome indicator) (31, 32). For 5 imputed data sets, we put each imputed set below each other into a stacked data with a weight of 1/5 per patient (5 means number of imputation) (33).

The predictive factors in the multivariate Cox regression model were screened by stepwise regression. The performance evaluation and PI calculation methods of this model were still the same as mRNA model. Two datasets from GEO database, GSE37745 (n=106) and GSE50081 (n=127), were used to validate.

Somatic Mutation Analysis

The “maftools “R package was used to analyze TCGA somatic mutation data (34).

Immunotherapy Exploration of the Model

Immune checkpoints, negative regulators of immune activation, can downregulate the immune state of the body and limit antitumor responses (35, 36). Tumor Immune Dysfunction and Rejection (TIDE) is a computational framework developed to assess the potential of tumor immune escape from gene-expressed cancer samples and to measure the responsiveness of immune checkpoint inhibitors (37, 38). TIDE scores were calculated for each of 486 LUAD patients by the TIDE website (http://tide.dfci.harvard.edu/).

Drug Prediction

By using the “calcPhenotype” function of the R package “oncoPredict” (39) and the database resources of Genomics of Drug Sensitivity in Cancer (GDSC) V2 as development data, six commonly used chemotherapy drugs (paclitaxel, fluorouracil, cisplatin, vinorelbine, gemcitabine, and docetaxel) were used for analysis, and the half-maximum inhibitory concentration (IC50) of each drug was estimated in every sample.

Statistical Analysis

All statistical analyses were performed using R (version 4.1.0). A bivariate normal distribution test was performed on the data requiring correlation analysis. The Shapiro-Wilk test and Bartlett’s test of homogeneity of variances were performed on the data requiring comparison between groups. Student’s t test was used if the continuous variable was normally distributed, and the Wilcoxon rank sum test was used if the continuous variable was not normally distributed. P < 0.05 was considered statistically significant. Median follow-up time was calculated by reverse Kaplan-Meier method (40). The survival curves were analyzed using log-rank test.

Results

Patient Cohorts

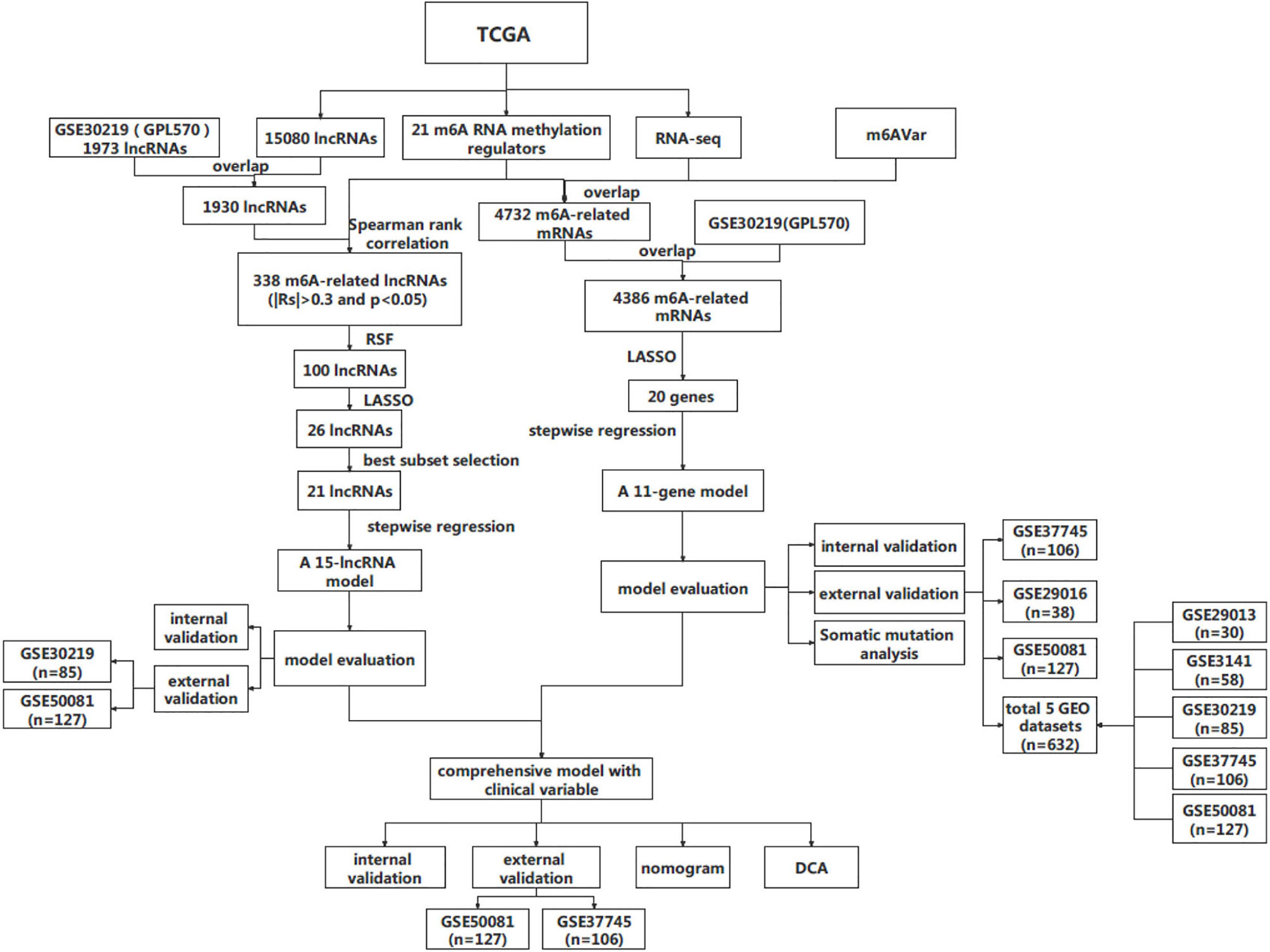
The design and workflow of the models constructed in this study are shown in Figure 1. The patient characteristics are summarized in Table 1. For the derivation cohort, a total of 486 patients had 175 deaths and an event rate of 36%, with a median overall survival of 2.4 years (95%CI: 2.2-2.8).

FIGURE 1

Figure 1 The workflow of this study. RSF, random survival forest; DCA, decision curve analysis.

TABLE 1

Table 1 Patient characteristics.

In the comprehensive prediction model, the number of events per variable in derivation model was 35 (175/5), indicating a reasonable number of events compared to the number of candidate predictors. This quantity meets the EPV principle required by the sample size of the prediction model, that is, there should be at least ten events per variable (23). We observed only a slight percentage of missing values for age and tumor stage in the TCGA cohort, 2.1% and 1.4%, respectively (Figure S1A). Figure S1B shows that the missing values of the data variables correspond to random missing values (41). All 486 patients who met the requirements for the development data were included in the model after imputation.

Figure 2 shows the survival curves (Figures 2A–C) and baseline survival probability curves (Figures 2D–F) of each data set in the three models.

FIGURE 2

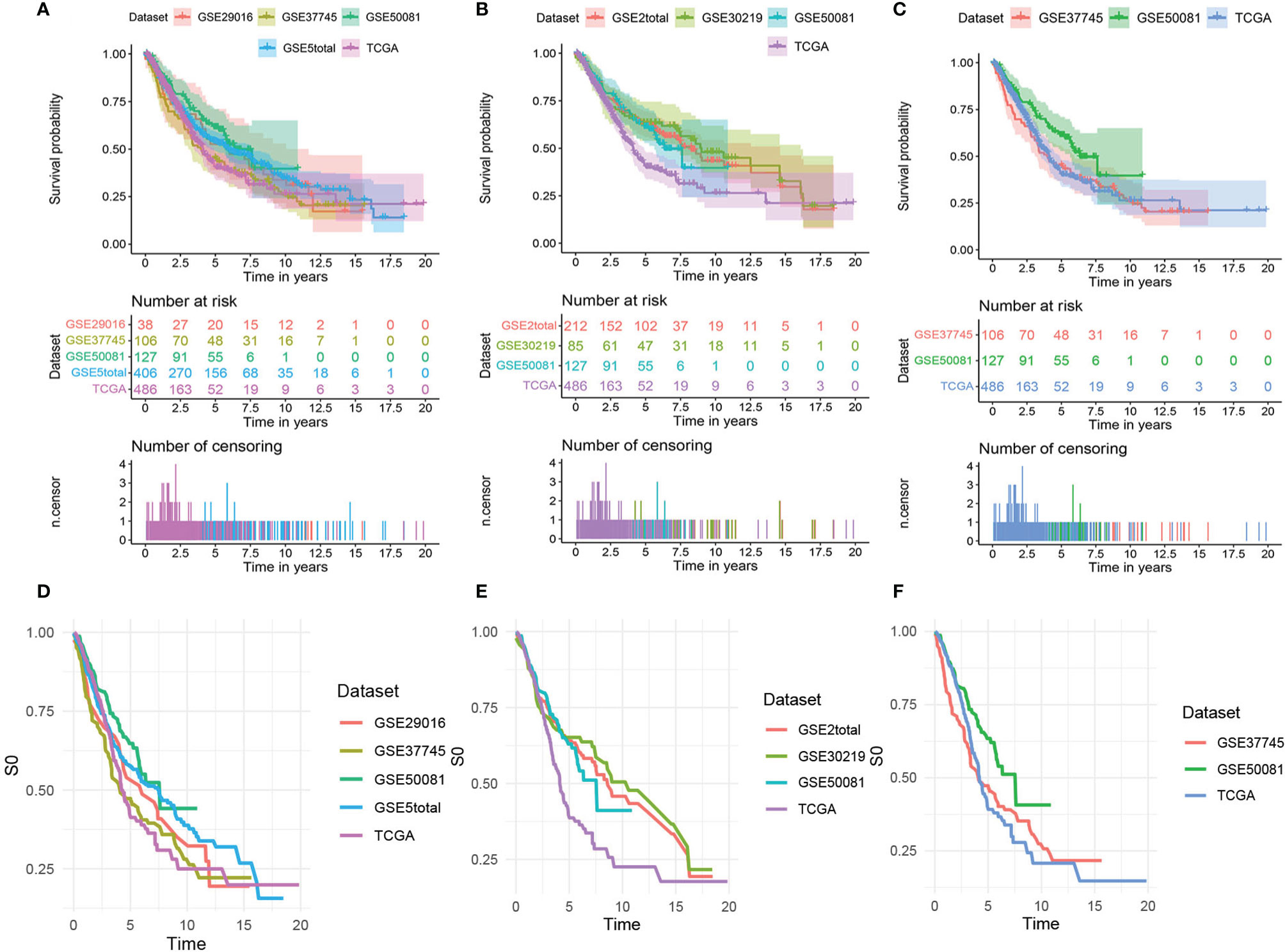
Figure 2 The survival curves and baseline survival probability curves of each data set in the three models. The survival curves of each data set in (A) the mRNA model, (B) the lncRNA model, and (C) the comprehensive clinical model. The baseline survival probability curves of each data set in (D) the mRNA model, (E) the lncRNA model, and (F) the comprehensive clinical model.

Development and Validation of the mRNA Model

The 21 m⁶A regulatory factors extracted from the literature are listed in Table S1. Common genes obtained from the three data sets m6AVar, TCGA and GSE30219 and 21 regulatory factors were included; finally, we obtained 4386 mRNAs related to m⁶A (Figure 3A).

FIGURE 3

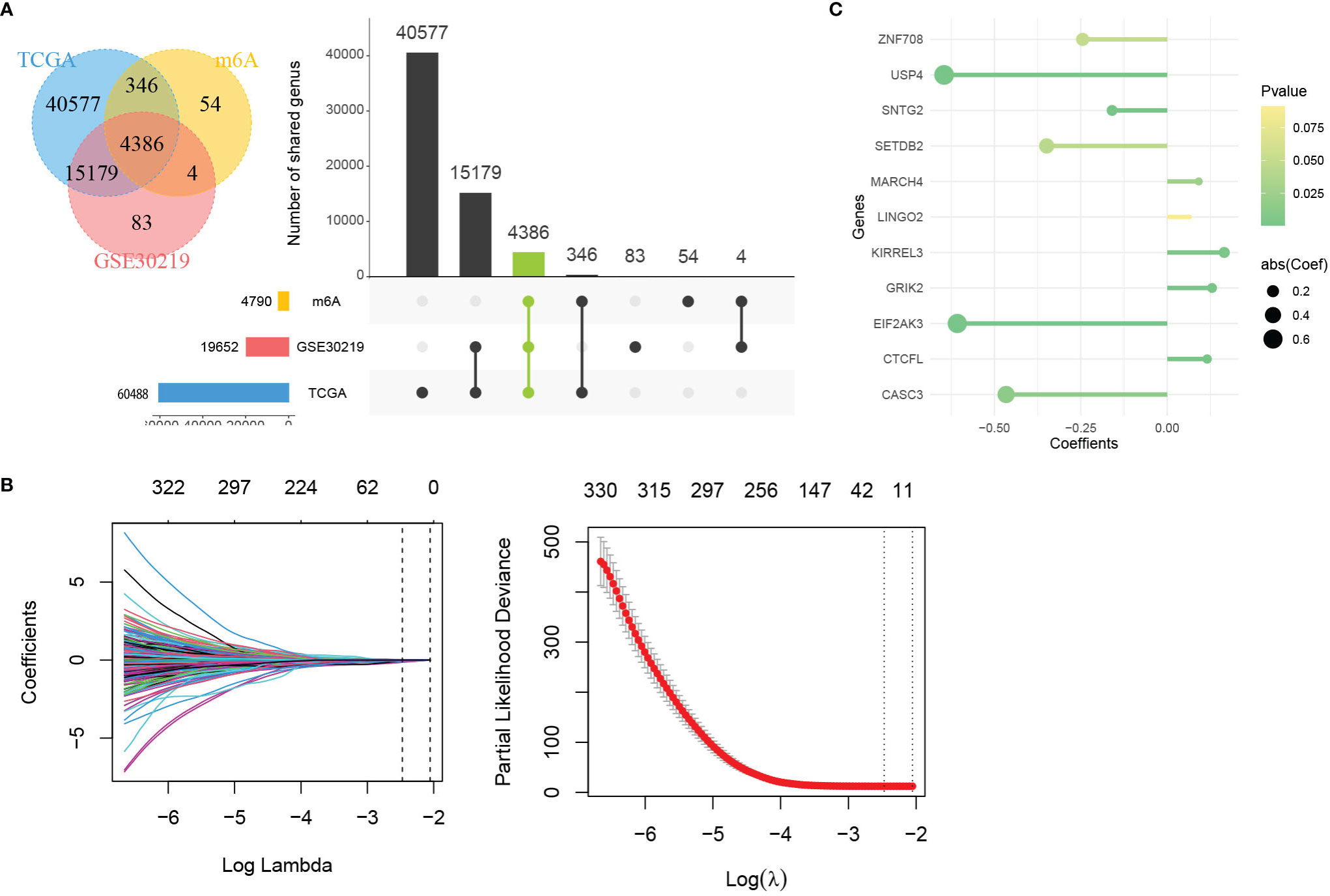
Figure 3 Identification of genes in mRNA model. (A) Venn plot of 4386 mRNAs related to m⁶A. (B) LASSO shrinking path diagram. (C) The coefficients of 11 genes in the model.

These genes were screened by LASSO (Figure 3B) and stepwise regression successively, and a prediction model containing 11 mRNAs associated with OS was obtained (CASC3, USP4, CTCFL, SETDB2, MARCH4, KIRREL3, GRIK2, EIF2AK3, SNTG2, LINGO2 and ZNF708). Figure 3C shows the coefficients of the model visually. Based on the genes and coefficients in the development data set, PI was constructed as follows:

$$\begin{array}{ccccc}PI=-0.46605\times CASC3-0.64556\times USP4+0.11549\times CTCFL& -0.34872\times SETDB2+0.09105\times MARCH4& +0.16502\times KIRREL3+0.12956\times GRIK2-0.60740\times EIF2AK3& -0.15933\times SNTG2+0.06450\times LINGO2-0.24452\times ZNF708& +23.20828\end{array}$$

The distribution of PI in the derivation and validation data sets were shown in Figure S2A. The base survival probability of the mRNA model from 1 to 10 years was given in Table S2. By substituting the calculated PI and the basic survival probability at different time points into formula (2), the prognostic survival probability of individual at corresponding time points can be obtained

In internal validation, the apparent C-index of the model was 0.751(95%CI:0.711-0.791), and the optimism-corrected C-index with 1000 bootstrap resamples was 0.736. The 1-year, 3-year and 5-year AUCs of the model were 0.768, 0.788, and 0.756, respectively (Figure 4A). The calibration plot shows that the model has good agreement between predicted and observed survival probabilities at 1, 3 and 5 years (Figure 4B). In addition, patients were divided into two risk groups based on the optimal cutoff value of PI (Figure 4C). In Figure 4D, the observed Kaplan–Meier survival curves (the solid line) were close to the average predicted survival curves (the dotted line) in the two risk groups, which also proved that our prediction model had good calibration accuracy. Figure S3 shows the Kaplan–Meier survival curves (Figure S3A) and risk factor association diagrams (Figure S3B) for the two risk groups.

FIGURE 4

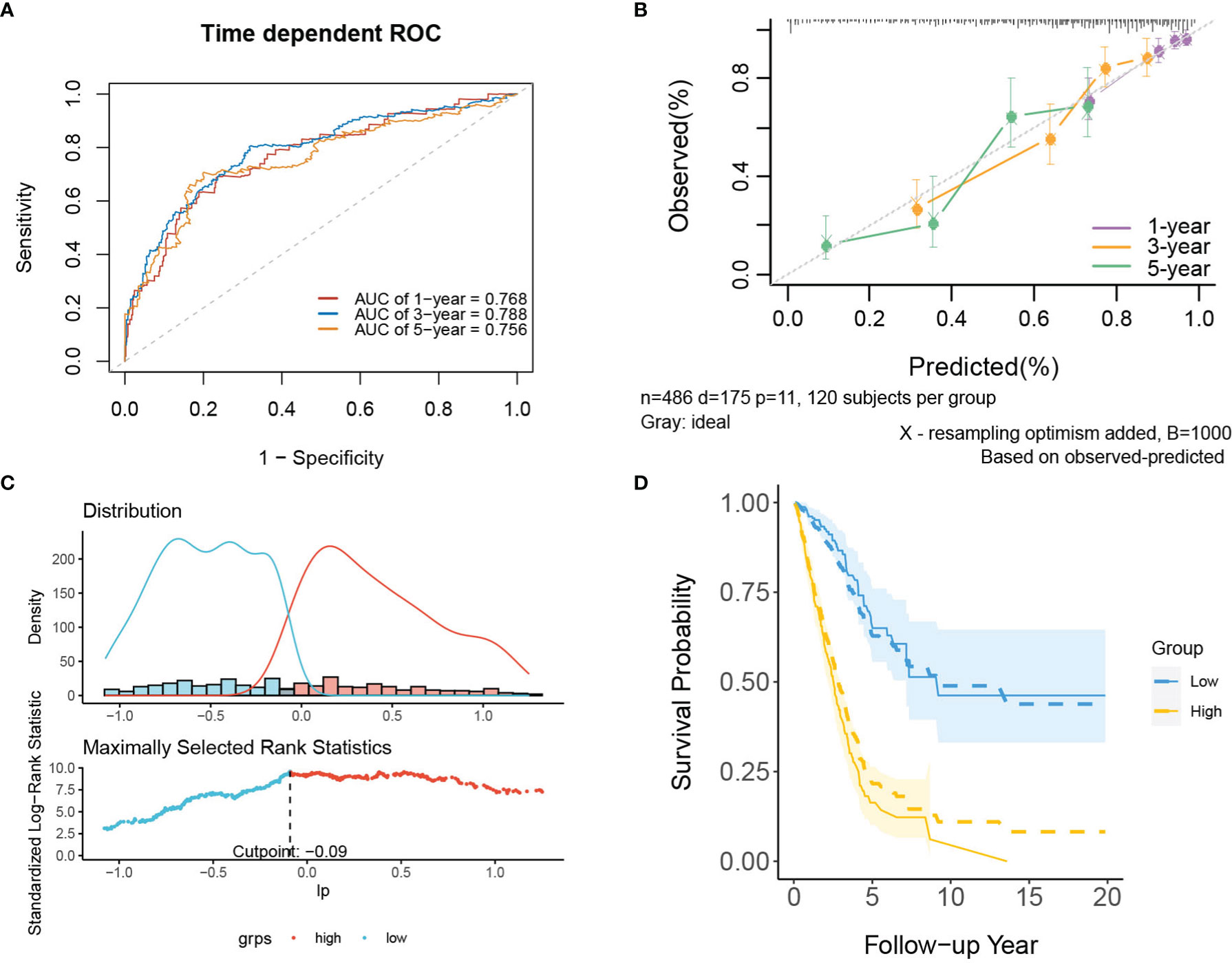
Figure 4 The performance of the mRNA model in the derivation dataset. (A) 1-,3-,5-year ROC curves and (B) calibration plot of the mRNA model. (C) The optimal cutoff value of PI. (D) Predicted versus observed survival probability in per risk group. Solid line: observed Kaplan-Meier curve; dotted line: average predicted survival curve; shaded area: 95% confidence interval of observed survival probability.

In the external validation cohorts, C indexes of the model were acceptable, which were 0.598(95%CI:0.511-0.685) (GSE50081), 0.608(95%CI:0.510-0.707)(GSE29016), 0.634(95%CI:0.571-0.697)(GSE37745) and 0.608(95%CI:0.567-0.649)(GSE5total). In addition, Figure S4A shows C-indexes of the model over 1-10 years in all datasets. According to the time-dependent ROC curves (Figure 5), the area under the curves of the model in the four validation sets of 1, 3 and 5 years were all above 0.6, which also indicated that its discriminative ability is satisfactory. The calibration diagrams from the four validation sets show the good calibration accuracy of the model in external validation (Figure 6). Patients in the validation sets were divided into two risk groups based on the maximum rank statistics (Figures S5A–D), and the average predicted survival curves (the dotted line) and observed survival curves (the solid line) of the two groups were compared to further verify the calibration accuracy of the model (Figures S5E–H). The long-term prediction ability of the model in the GSE50081 (Figure S5E) and GSE29016 (Figure S5F) datasets was not as good as that in the other two datasets (Figures S5G–H). However, within 5 years, the calibration accuracy of the model is acceptable. Subsequently, the Kaplan–Meier survival curves of the two risk groups and the risk factor association diagrams of the model in each validation set are shown in Figures S6, S7 respectively.

FIGURE 5

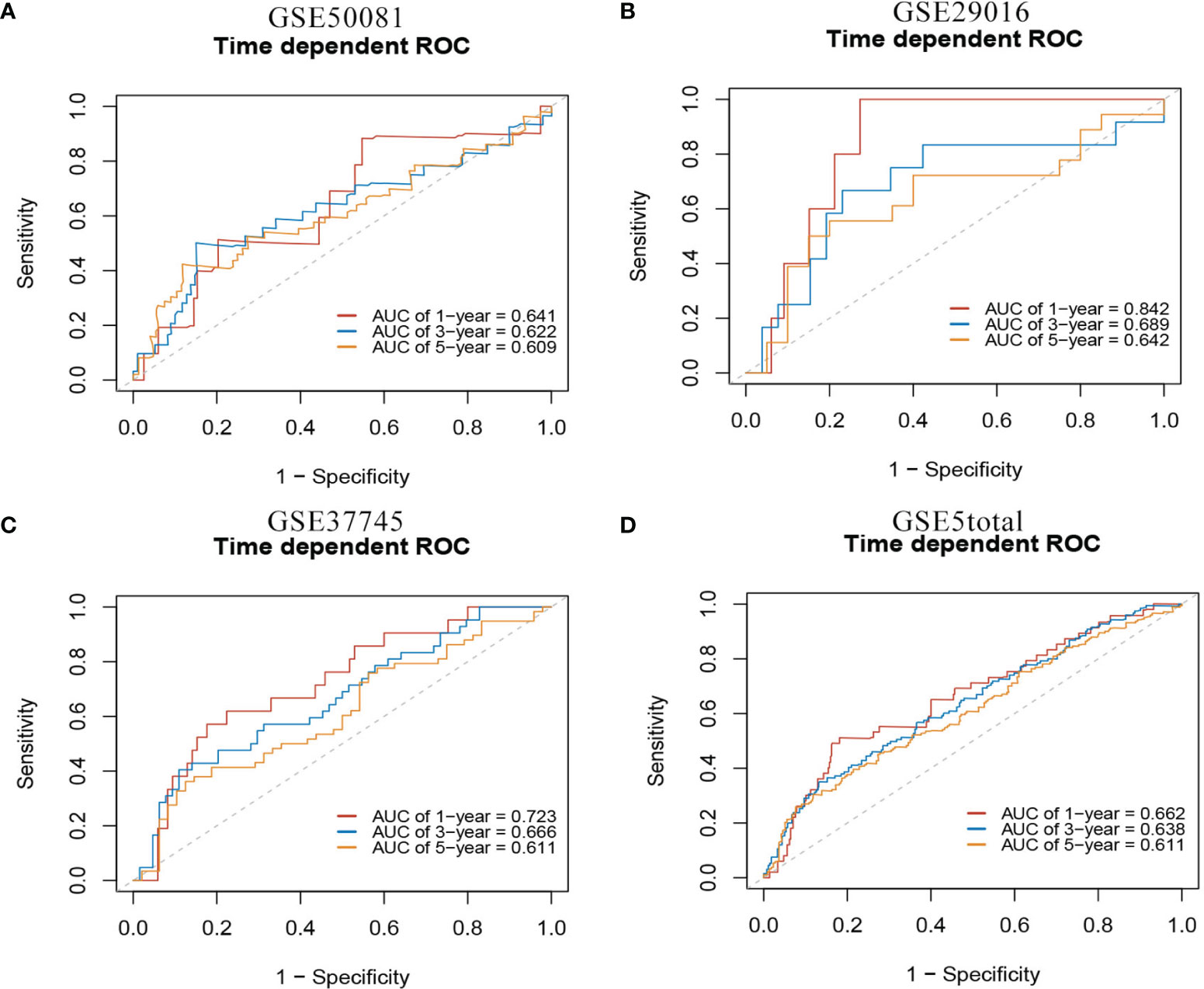
Figure 5 1-,3-,5-year ROC curves of mRNA model in external validation data sets. (A) GSE50081 dataset. (B) GSE29016 dataset. (C) GSE37745 dataset. (D) GSE5total dataset.

FIGURE 6

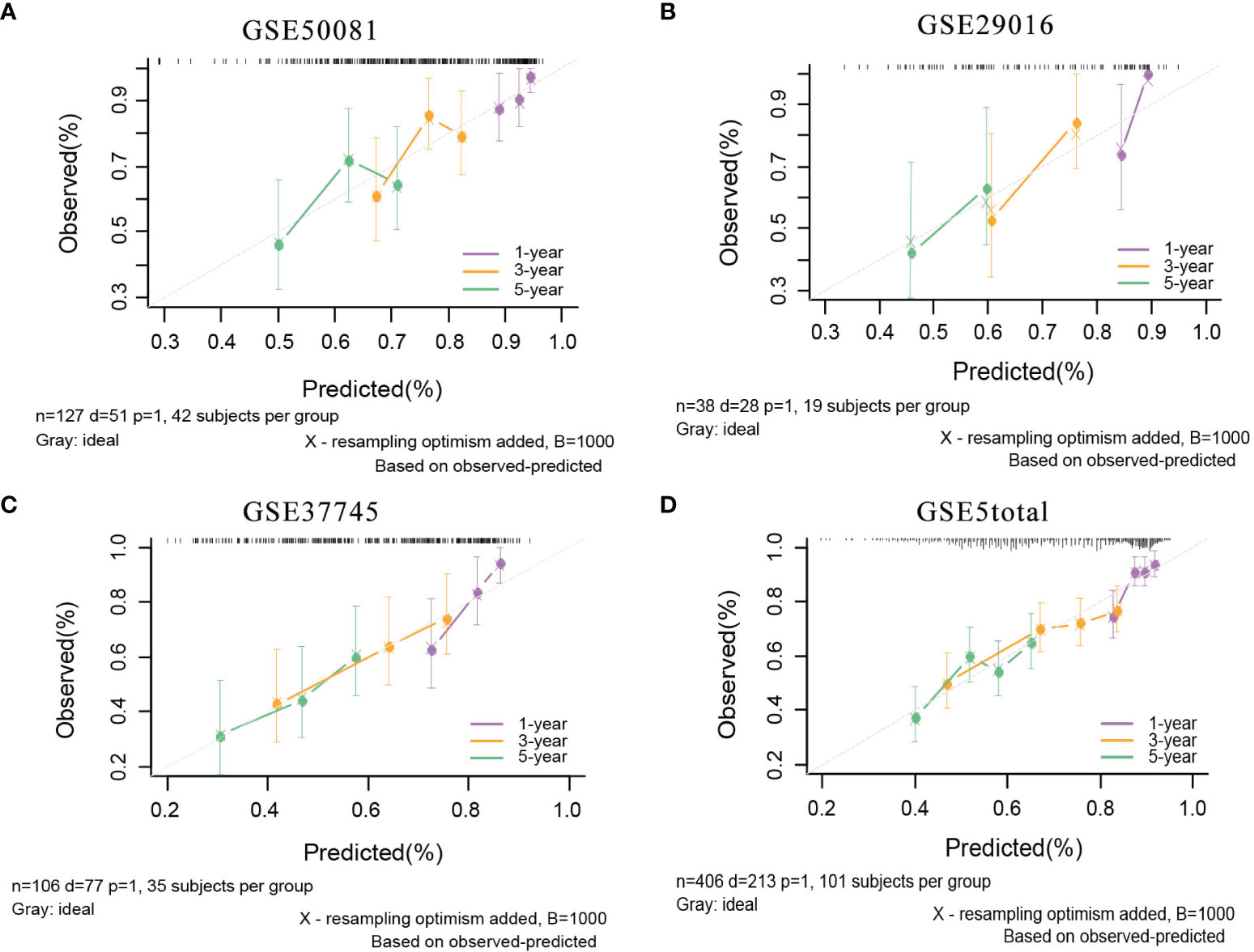
Figure 6 The calibration plots of mRNA model in external validation data sets. (A) GSE50081 dataset. (B) GSE29016 dataset. (C) GSE37745 dataset. (D) GSE5total dataset.

Development and Validation of the lncRNA Model

First, 1930 common lncRNAs of TCGA and GSE30219 data sets were obtained (Figure 7A). Then, genes were screened by the importance score of random survival forest (Figure 7B), and the top 100 genes were reserved for the next step. Twenty-six genes were obtained by LASSO screening of 100 reserved genes (Figure 7C). Next, we selected the best subset selection method for further screening of genes and obtained 21 genes (Figure 7D). Finally, 15 lncRNAs of the prediction model associated with OS were obtained by stepwise regression (SNHG12, RPARP-AS1, CRNDE, LMO7DN, AC008467.1, LINC00639, AC107464.1, AL445931.1, FLG-AS1, C5orf66, AC026250.1, AC245595.1, LINC01933, LINC01137, RUSC1-AS1). Furthermore, the co-expression networks of 21 m⁶A and 1930 lncRNAs were visualized by a Sankey diagram, as shown in Figure 8A. In addition, the heatmap of the correlation between 21 m⁶A genes and 15 lncRNAs in the model is shown in Figure 8B.

FIGURE 7

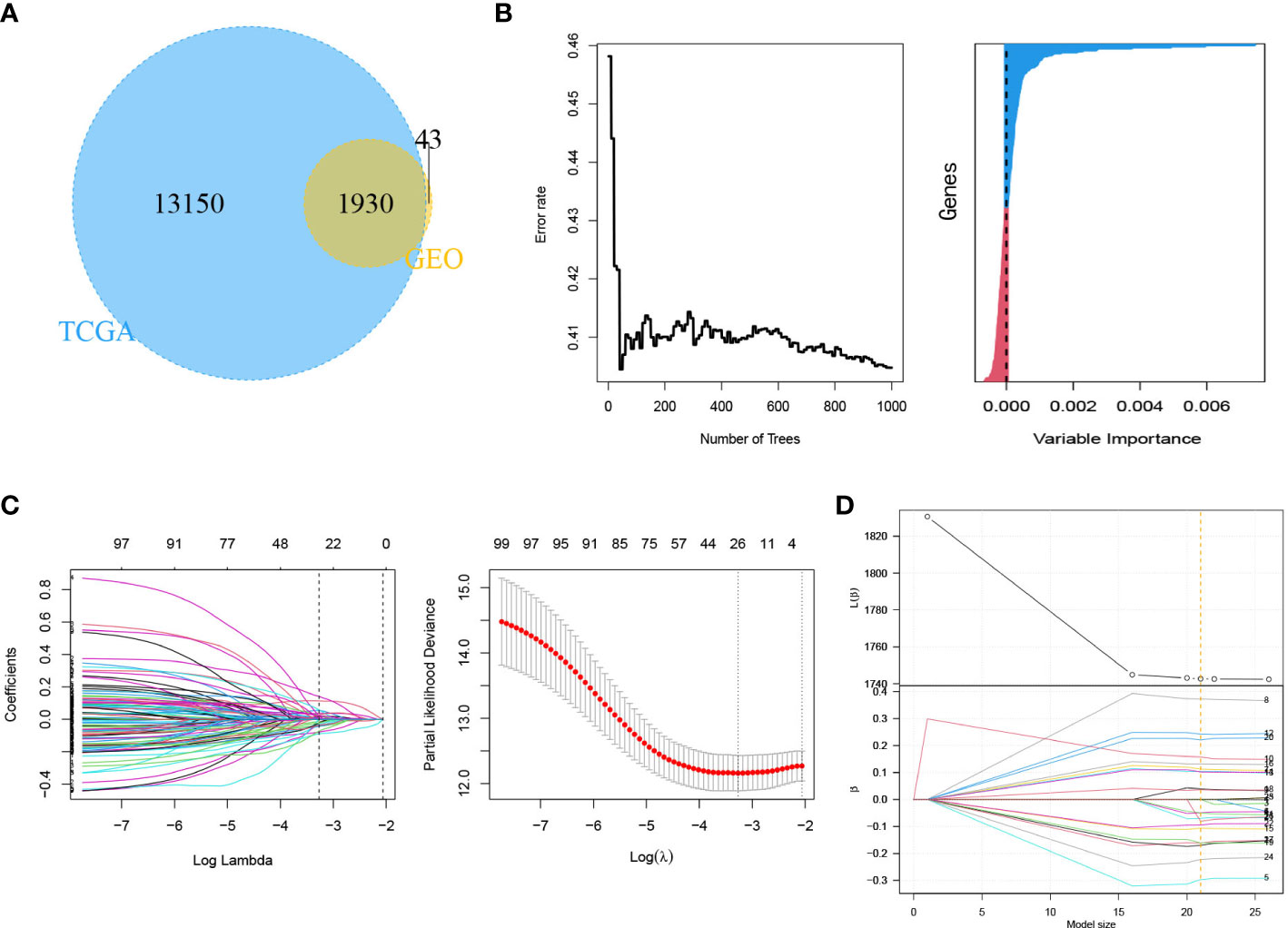
Figure 7 Identification of genes in lncRNA model. (A) Venn plot of 1930 lncRNAs related to m⁶A. (B) Random survival forest analysis. (C) LASSO shrinking path diagram. (D) The coefficient profile plot of the coefficient and loss paths for best subset selection.

FIGURE 8

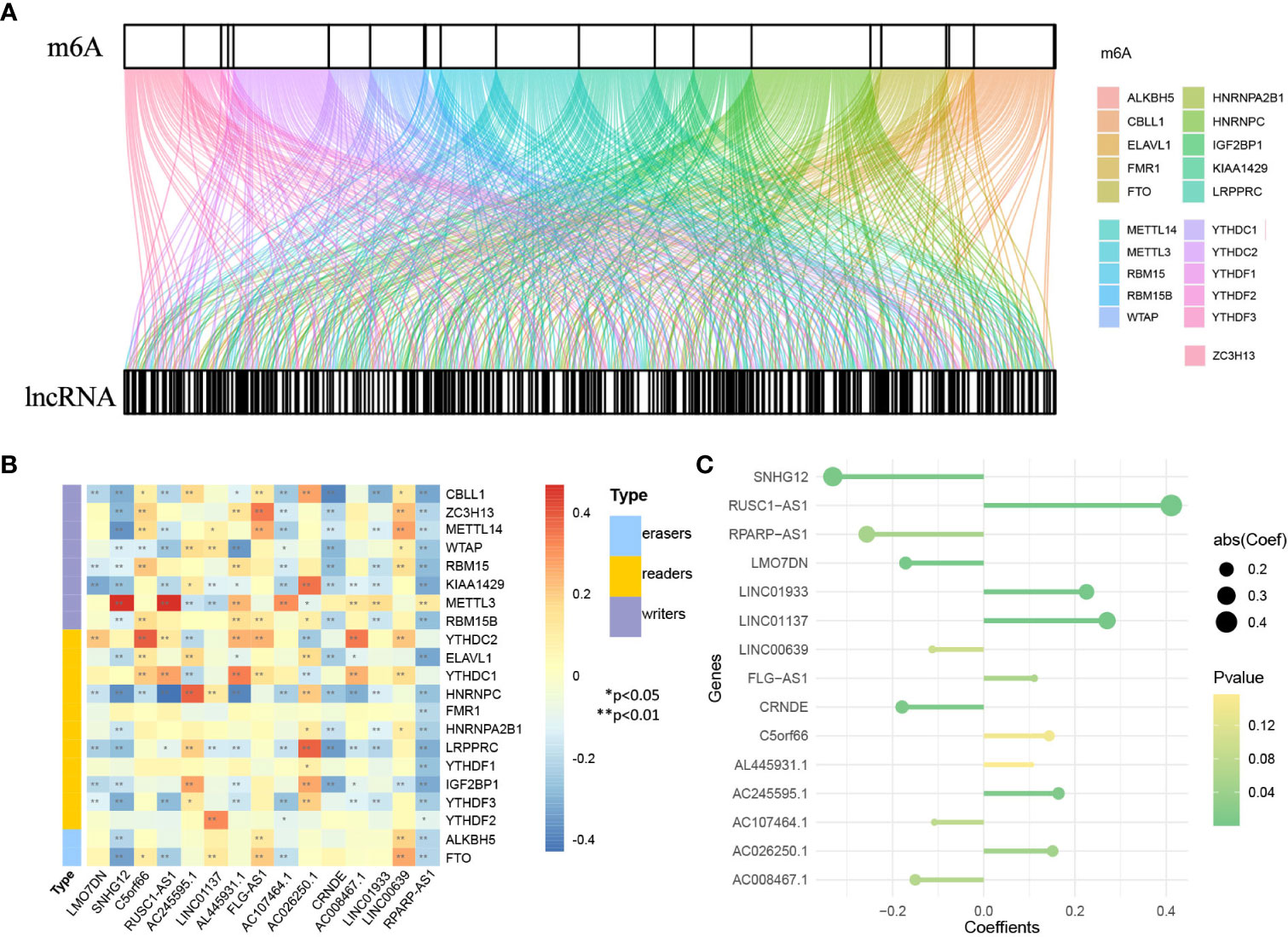
Figure 8 Identification of genes in lncRNA model. (A) Sankey diagram of 21 m⁶A regulators and 1930 m⁶A-related lncRNAs. (B) The heatmap for the correlation between 21 m⁶A genes and 15 prognostic m⁶A-related lncRNAs. (C) The coefficients of 15 lncRNAs in the model.

Based on the genes and coefficients in the development data set, PI was constructed as follows:

$$\begin{array}{lllllll}PI=-0.17135\times LM07DN-0.33117\times SNHG12+0.14349\times C5orf66& +0.41125\times \left(RUSC1-AS1\right)+0.16394\times AC245595.1& +0.27029\times LINC01137+0.10490\times AL445931.1& +0.11064\times \left(FLG-AS1\right)-0.10828\times AC107464.1& +0.15101\times AC026250.1-0.17919\times CRNDE& -0.15018\times AC008467.1+0.22517\times LINCO1933& -0.11297\times LINC00639-0.25657\times \left(PRARP-AS1\right)-0.07307\end{array}$$

Figure 8C shows the coefficients of the model visually. The distribution of PI in the development data set and validation set is shown in Figure S2B. The base survival probability of the lncRNA model from 1 to 10 years is given in Table S2

In internal validation, the apparent C-index was 0.730(95%CI:0.688-0.772), and the optimism-corrected C-index with 1000 bootstrap replications was 0.707. The AUCs of the model at 1, 3 and 5 years were 0.754, 0.796, and 0.751, respectively (Figure 9A). The calibration plot shows that the model has good agreement between predicted and observed survival probabilities at 1, 3 and 5 years (Figure 9B). Furthermore, patients were divided into two risk groups based on the optimal truncation value of PI (Figure 9C). It was further found that the observed Kaplan–Meier survival curves in the two risk groups were close to the average predicted survival curves (Figure 9D), which also proved that our prediction model had good calibration accuracy. Figure S8 shows the Kaplan–Meier survival curves (Figure S8A) and risk factor association diagrams (Figure S8B) for the two risk groups.

FIGURE 9

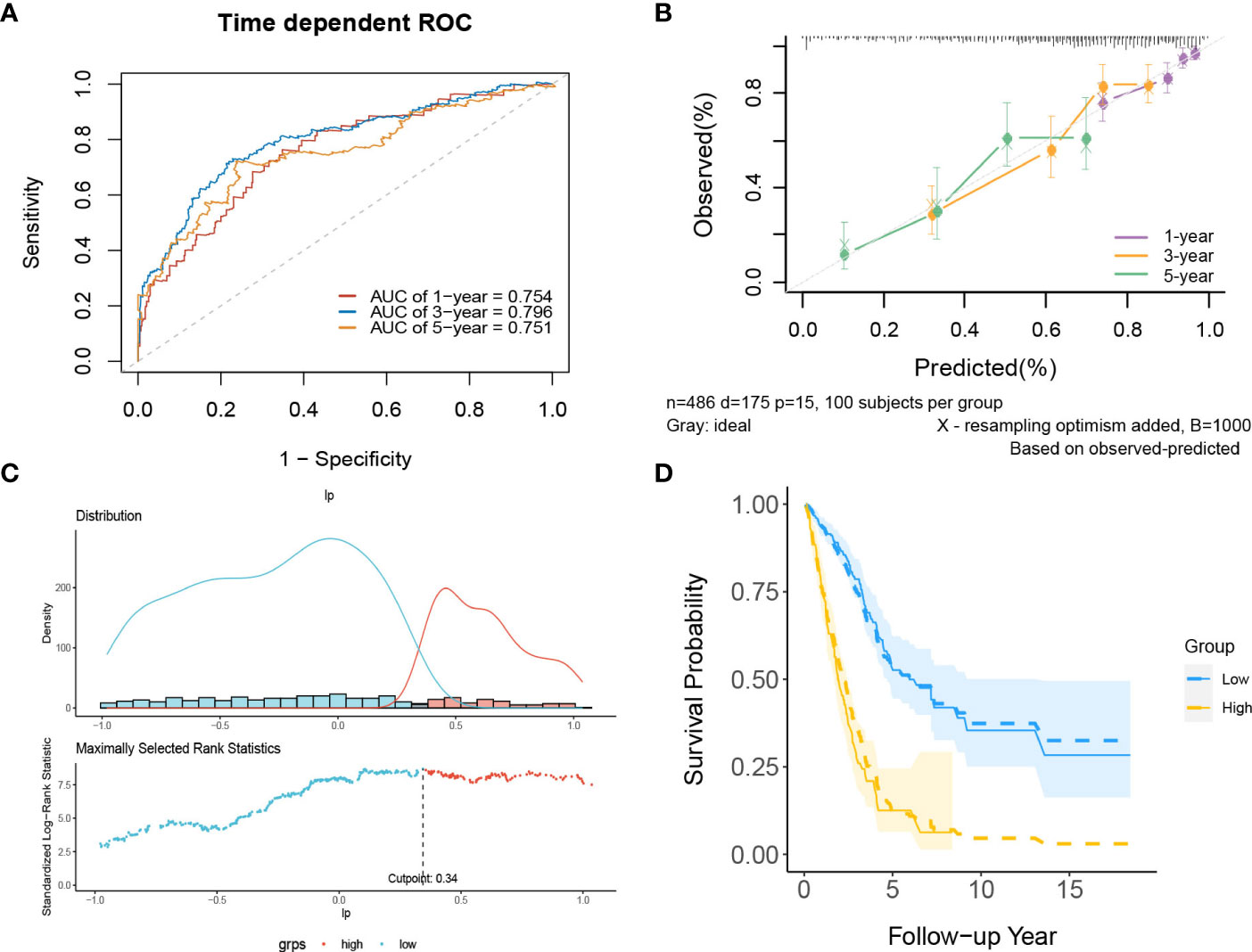
Figure 9 The performance of the lncRNA model in the derivation dataset. (A) 1-,3-,5-year ROC curves and (B) calibration plot of the lncRNA model. (C) The optimal cutoff value of PI. (D) Predicted versus observed survival probability in each risk group. Solid line: observed Kaplan-Meier curve; dotted line: average predicted survival curve; shaded area: 95% confidence interval of observed survival probability.

In the external validation cohorts, three C indexes of the model were 0.596(95%CI:0.506-0.685)(GSE50081), 0.602(95%CI:0.525-0.682)(GSE30219) and 0.596(95%CI:0.534-0.658)(GSE2total). In addition, Figure S4B shows C-indexes of the model over 1-10 years in four datasets. Although C-indexes of the model in the validation set is lower than derivation set, they remained at 0.6 during the decade. According to the time-dependent ROC curves (Figures 10A–C), the area under the curves of the model in the three validation sets of 1, 3 and 5 years were all above 0.6. Figures 10D–F shows the calibration accuracy of the model in three external verification sets. Patients in the validation sets were divided into two risk groups based on the maximum rank statistics (Figures S9A–C), and the average predicted survival curves and observed survival curves in the two groups were compared to further validate the calibration accuracy of the model (Figures S9D–F). Unfortunately, the external validation calibration accuracy of the lncRNA model was not as ideal as that of mRNA model, but the prediction results within three years were close to the observations and did not deviate too far from reality within five years. Subsequently, the Kaplan–Meier survival curves of the two risk groups and the risk factor association diagrams of the model in each validation set are shown in Figures S10, S11 respectively.

FIGURE 10

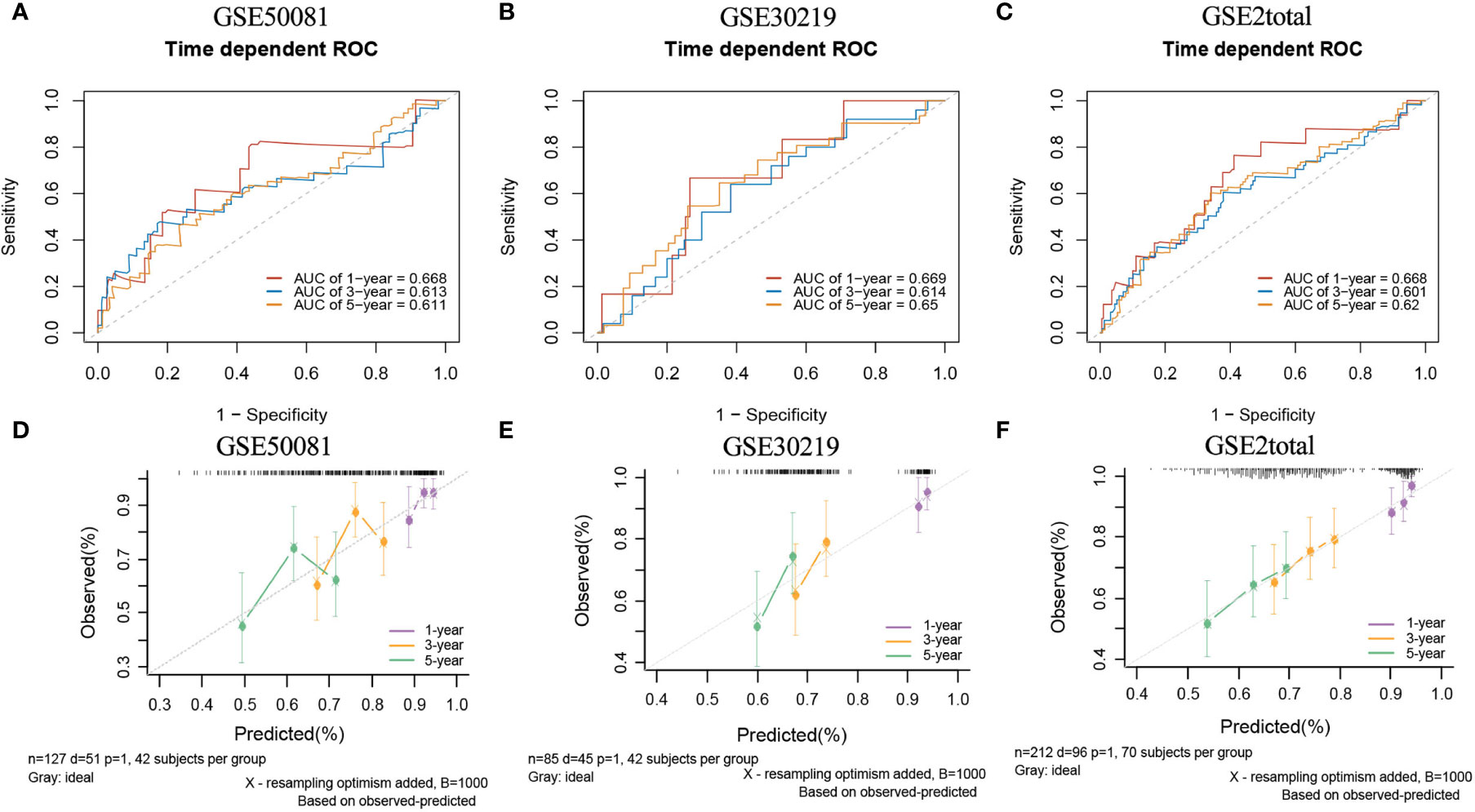
Figure 10 The ROC curves and calibration plots of lncRNA model in external validation data sets. ROC curves at 1-,3-,5-year: (A) GSE50081 dataset, (B) GSE30219 dataset, and (C) GSE2total dataset. The calibration plots at 1-,3-,5-year: (D) GSE50081 dataset, (E) GSE30219 dataset, and (F) GSE2total dataset.

Development and Validation of the Comprehensive Prediction Model

The prognostic indexes of the two gene models were used as candidate predictors, and the comprehensive prediction model was constructed by stepwise regression combined with three clinical variables (age, sex and tumor stage) to predict OS. The final model included three predictors: mRNA risk score, lncRNA risk score, and tumor stage. Based on the coefficients and predictors obtained from all imputed datasets, the final PI is structured as:

$$\begin{array}{l}\text{PI}=-0.3295+0.6015\times \text{mRNA Risk Score}+0.4540\times \text{IncRNA Risk Score }+\\ \text{tumor stage}\end{array}$$

in which:

Tumor stage: stage I=0, stage II= 0.6567, stage III= 0.7510, stage IV= 0.9675

The distribution of PI in the development data set and validation set is shown in Figure S2C. The base survival probability of the comprehensive prediction model from 1 to 10 years is also given in Table S2.

In internal validation, the apparent C-index was 0.795(95%CI:0.780-0.810) the optimism-corrected C-index with 1000 bootstrap replications was 0.794. The 1-year, 3-year and 5-year AUCs of this model were 0.824, 0.847, and 0.809, respectively (Figure 11A). The calibration plot shows that the model has good agreement between predicted and observed survival probabilities at 1, 3 and 5 years (Figure 11B). Again, patients were divided into two risk groups based on the optimal truncation value of PI (Figure 11C). The observed Kaplan–Meier survival curves for the two risk groups almost overlap with the average predicted survival curves shown in Figure 11D, further confirming that the prediction model has good calibration accuracy in the derivation set.

FIGURE 11

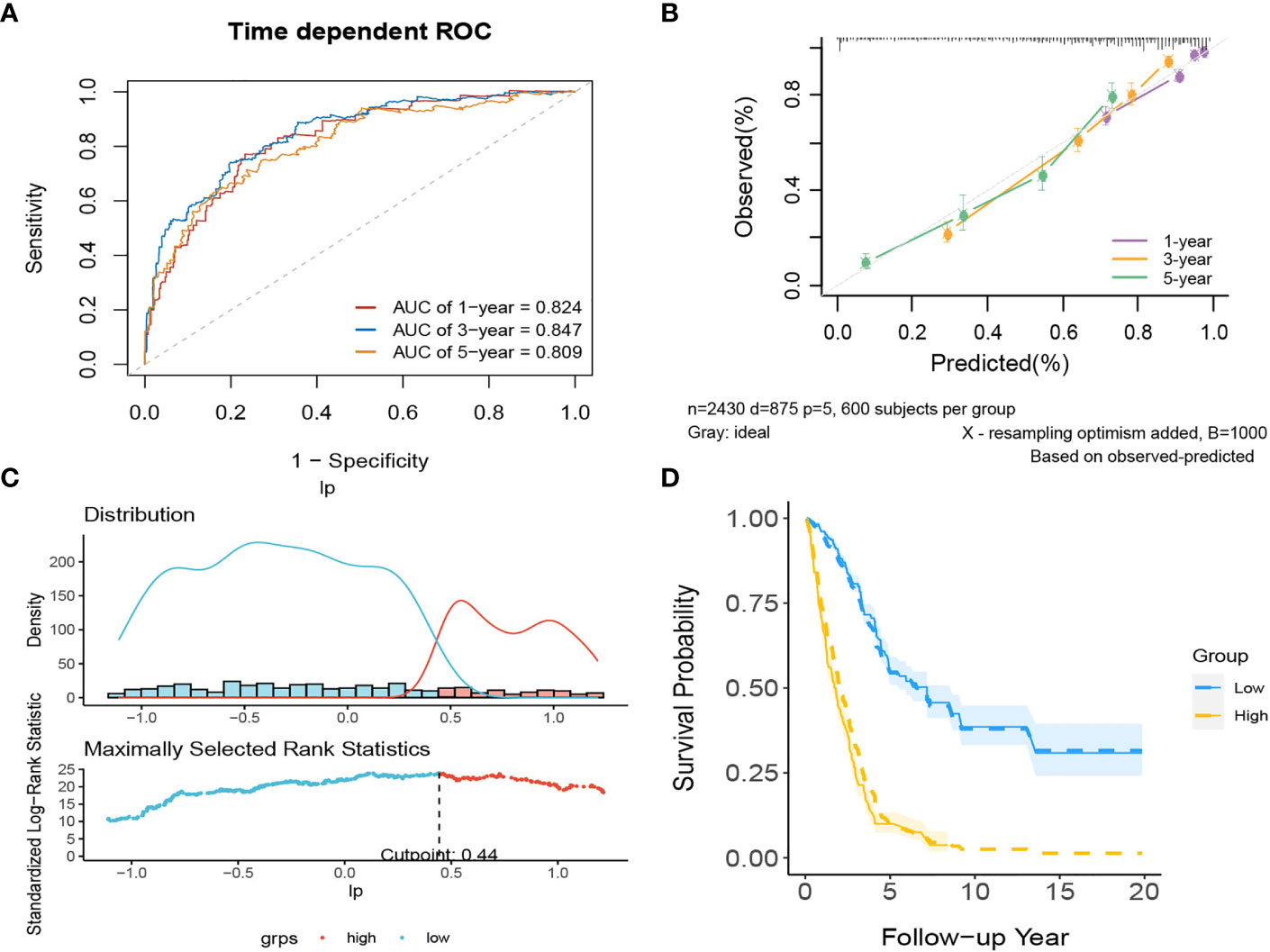
Figure 11 The performance of the comprehensive model in the derivation dataset. (A) 1-,3-,5-year ROC curves and (B) calibration plot of the comprehensive model. (C) The optimal cutoff value of PI. (D) Predicted versus observed survival probability per risk group.

There are two data sets used as external validation sets for this model. In the external validation cohorts, the two C indexes of the model were 0.649(95%CI:0.564-0.733)(GSE50081) and 0.606(95%CI:0.536-0.677) (GSE37745). Figure S4C shows the C-index of the model over 1-10 years in the three datasets. Figures 12A–B shows the ROC curve of the model in the two validation sets, and Figures 12C–D shows the calibration plots. Again, we divided samples into two risk groups (Figures S12A, B) and then compared the observed survival curves in the two risk groups with the average predicted survival curves (Figures S12C, D). In GSE50081, the model still has the risk of underestimating the survival probability (Figure S12C). However, in GSE37745, the predicted average survival probability curves were quite close to the actual curve, showing very good consistency (Figure S12D).

FIGURE 12

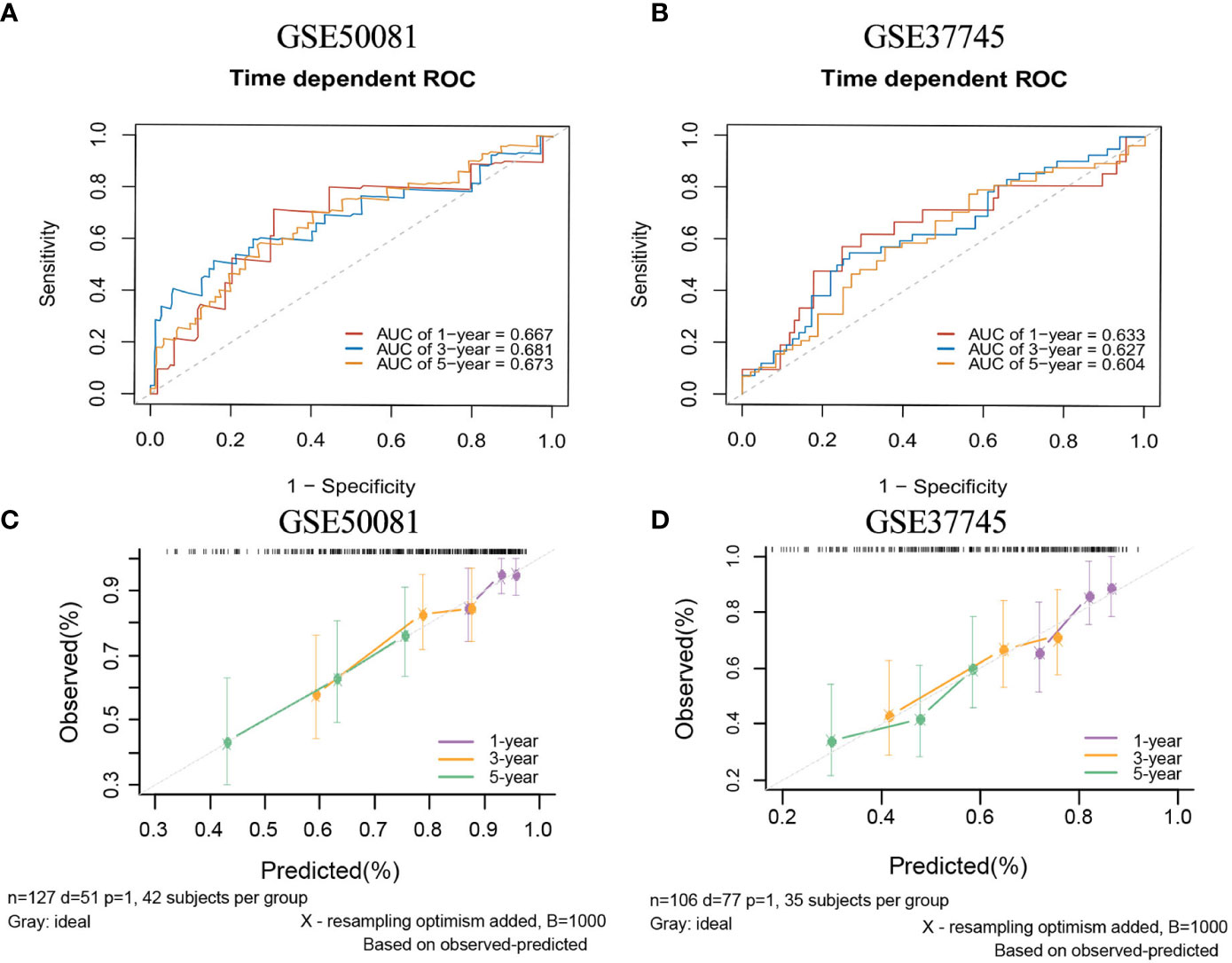
Figure 12 The ROC curves and calibration plots of comprehensive model in external validation data sets.1-,3-,5-year ROC curves: (A) GSE50081 dataset and (B) GSE37745 dataset. The calibration plots: (C) GSE50081 dataset and (D) GSE37745 dataset.

From this model, we created a nomogram to predict the prognostic survival probability of patients with lung adenocarcinoma at 1, 3 and 5 years (Figure S13). Subsequently, we used decision curve analysis (DCA) to compare and demonstrate the net benefits of the clinical utility of the three models at 1, 3 and 5 years (Figure S14). With increasing time, the net benefits of the three models continued to increase, and the net benefits of the mRNA model and lncRNA model at the three time points showed little difference. As a matter of course, the net benefit of the comprehensive model is always the greatest.

Online Calculators for Models

To facilitate the clinical application of the model, the three model calculations mentioned in this paper can be completed by this website: https://lhj0520.shinyapps.io/LUAD_prediction_model/. Enter or select the value of the variable and the time you want to predict in the gray box on the left side of the page and then click the “forecast” button at the bottom to obtain the corresponding point estimate or survival curve on the right side (Figure S15).

Drug Prediction and TIDE Immunotherapy Prediction Analyses

Chemotherapy plays a critical role in curing or controlling lung adenocarcinoma. The IC50 estimates of 6 common chemotherapeutic drugs were calculated from the GDSC database. The difference of IC50 between the high and low risk groups in the mRNA model was compared. The results (Figure 13A) showed that the IC50 values of all 6 drugs were significantly different between the high-risk group and the low-risk group, and patients in the low-risk group were more sensitive than the high-risk group.

FIGURE 13

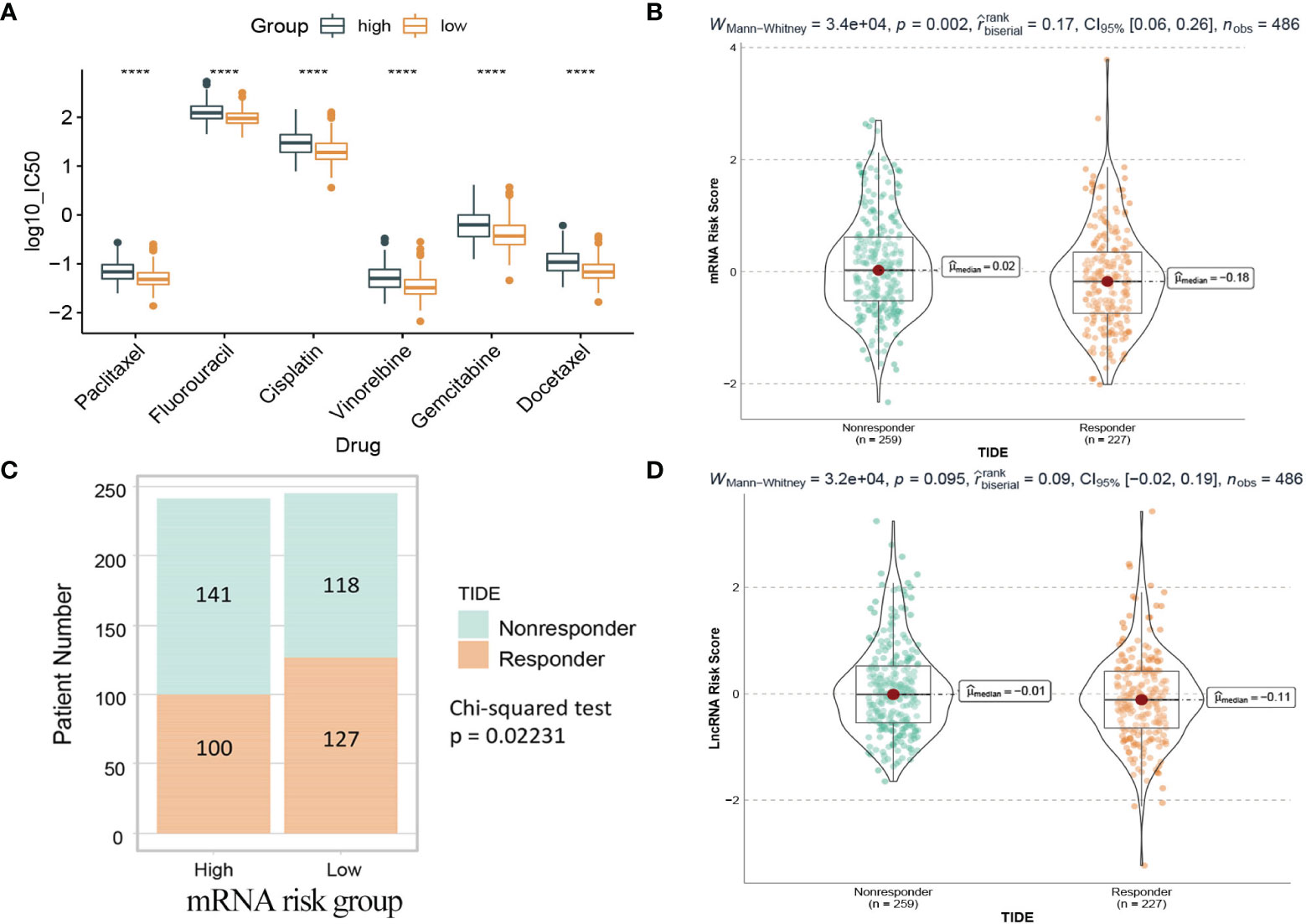
Figure 13 Drug prediction and TIDE immunotherapy prediction analyses. (A) Box plot of IC50 values of six chemotherapy drugs between the two risk groups in the mRNA model. (B) The mRNA risk score between TIDE predicted responders and non-responders. (C) Distribution of TIDE responders and non-responders in the mRNA risk groups. (D) The lncRNA risk score between TIDE predicted responders and non-responders. Responder: the patient who responds to the immune checkpoint inhibitors. Nonresponder: the patient who does not respond to the immune checkpoint inhibitors. ****: <0.0001.

Immunotherapy using immune checkpoint inhibitors has brought hope to LUAD patients. The response of 486 patients in the TCGA dataset to immune checkpoint inhibitors was calculated based on the gene expression matrix through the TIDE website. As shown in Figure 13B, for the mRNA model, the risk score of patients in the nonresponse group (n=259) was higher than that in the response group (n=227), and the difference was statistically significant (Wilcoxon test, p=0.002). Further analysis (Figure 13C) showed that patients in the low-risk group (127/245) were more sensitive to immunotherapy than those in the high-risk group (100/241). In contrast, in the lncRNA model, the difference was not statistically significant (Wilcoxon test, p=0.095), so it could not be considered that there was a difference in risk scores between the two groups (Figure 13D).

Study of Somatic Variation in the mRNA Model

We obtained single nucleotide mutations data for 476 LUAD patients (ten samples were not available) from the GDC Data Portal. Figure 14A is a summary of the mutation data. More detailed mutation information is shown in Figure 14B. Different colors represent different types of mutations. In addition, we compared the mutations in genes in the mRNA model between the two risk groups (Figure 14C). GRIK2 was found to be the mutated gene with the most common frequency in both groups, which mutated more in the high-risk group (Figure 14D). More intriguingly, we calculated co-occurrence and mutually exclusive mutations between 11 genes and found only two group co-occurrence mutations, including GRIK2(Figure S16A). Subsequently, we plotted the mutation frequency of genes into gene word clouds, as shown in Figure S16B. Further, we calculated the tumor mutation burden (TMB) in 476 samples (Figure S16C). We compared the TMB of the responder and non-responder groups in TIDE. The TMB of the responder group was higher than that of the non-responder group (Wilcoxon test, p=0.028, Figure S16D), indicating that patients with higher TMB may have a better effect on immunotherapy.

FIGURE 14

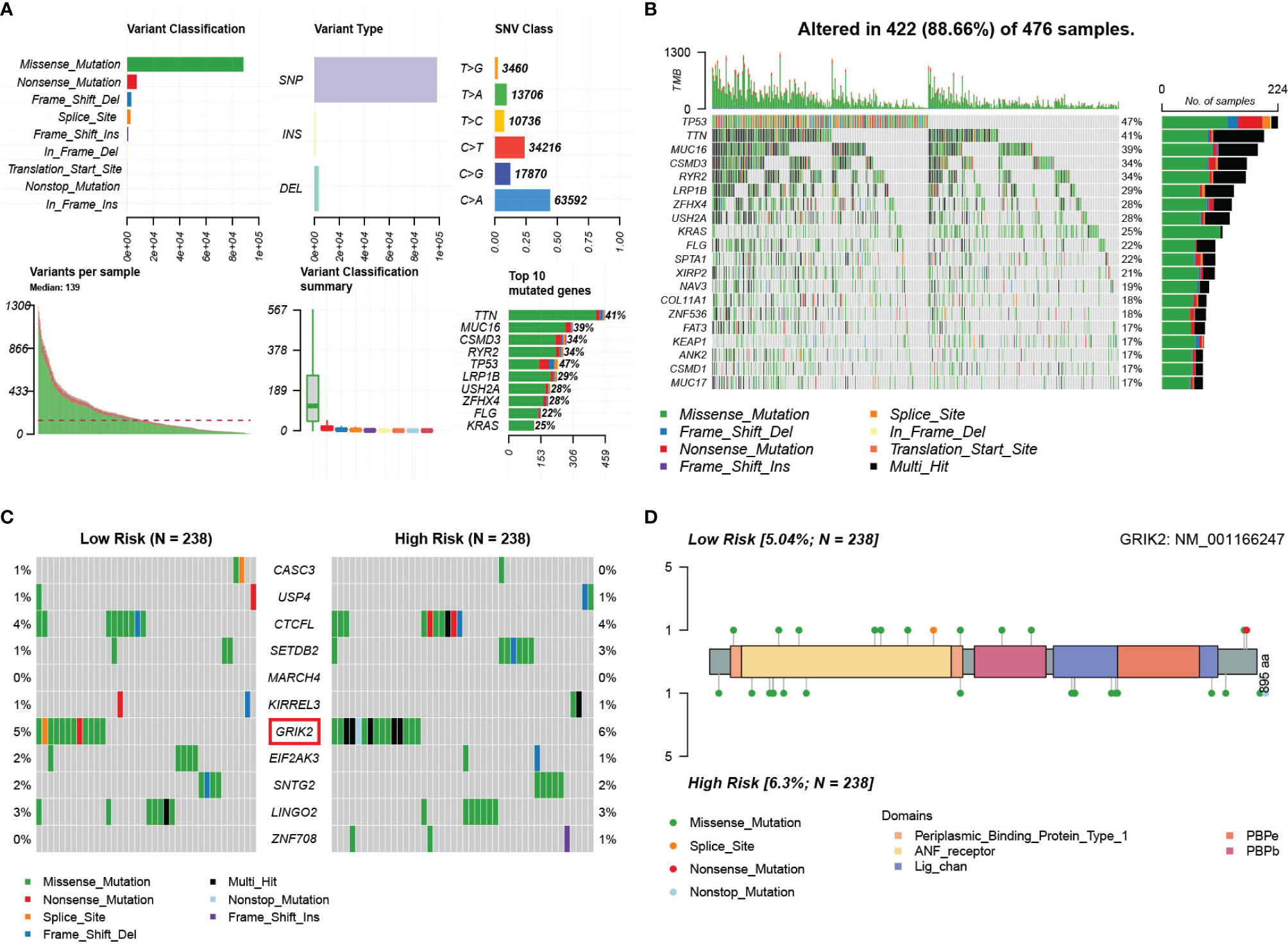
Figure 14 Landscape of somatic mutations in lung adenocarcinoma patients in TCGA. (A) the summary of the mutation data. (B) The waterfall plot of the mutation distribution of the top 20 most frequently mutated genes. (C) The waterfall plot of the mutation distribution of 11 predictors between two risk groups in the mRNA model. (D) The lollipop pot of the differential distribution of variants of GRIK2 between two risk groups in mRNA model.

Discussion

Commonly used predictive models for lung adenocarcinoma based on m⁶A methylated relevant genes have been developed, but these models are not yet complete in terms of application. This study constructed clinical prediction models at three different levels based on m⁶A-related mRNAs, lncRNAs and clinical information data, and collected multiple external validation sets for validation. We reported this study according to the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis Statement (TRIPOD). The complete checklist is shown in Table S3.

The first model was developed based on m⁶A-related mRNA and contained 11 genes in total (Table S4). Compared with other models, our model contains more genes. However, in several independent external validation sets, the model shows relatively stable and good discrimination and calibration. At present, studies have shown that USP4, EIF2AK3 and CTCFL genes are related to the prognosis of lung adenocarcinoma (42–44).

The 11 genes are all obtained from m6Avar database (now updated to “RMVar”). Variants of these genes were hypothesized to affect RNA modifications (e.g., m⁶A) and thus disease (14). The m⁶A-associated variants of 11 genes came from three different confidence levels of sources and two aspects of modification function (Figure S17). Four of the mutations lead to lost m⁶A sites (USP4, CTCFL, GRIK2, SNTG2) and ten of the mutations lead to gain m⁶A sites (ZNF708, LINGO2, EIF2AK3, KIRREL3, MARCH4, SETDB2, USP4, CASC3). For m⁶A sites with high confidence level were derived from miCLIP or PA-m6A-seq experiments (3, 45, 46) and the three m⁶A-associated variants (SETDB2, MARCH4, EIF2AK3) were retained because of locating nearby the m⁶A sites or disrupting DRACH motif around the m⁶A sites (47–49). For m⁶A sites having a medium confidence level which were predicted from the previously published MeRIP-seq data (50–52), the four m⁶A-associated variants (KIRREL3, EIF2AK3, ZNF708, LINGO2) were derived from the intersection between the variants and the m⁶A sites generated from MeRIP-Seq experiments. For m⁶A sites with a low confidence level predicted by transcriptome-wide prediction, the seven m⁶A-associated variants (CTCFL, GRIK2, SNTG2, CASC3, KIRREL3 and USP4 have two variants) were predicted by the Random Forest prediction model (14). In addition, disease-related data from GWAS and ClinVar databases were collected to determine that the variants of 11 genes were pathogenic mutations leading to dysregulation of m⁶A modification in lung adenocarcinoma (14). Furthermore, we calculated the correlation coefficients between 11 genes and 21 m⁶A regulatory factors (Figure S18). It turns out that there are varying degrees of correlation between each predictor and regulator.

For mRNA risk score, we also explored their relationship with common chemotherapy drugs and immunotherapy. The study found that patients in the low-risk group were less resistant to commonly used chemotherapy drugs than those in the high-risk group. Furthermore, 11 mRNAs and risk score were calculated for their association with each chemotherapy drug (Figure S19). Risk scores were positively correlated with IC50 of all drugs (i.e., patients with higher scores had higher resistance to chemotherapy drugs), indicating that patients with higher scores were insensitive to chemotherapy. Five of the 11 mRNAs (CTCFL, MARCH4, KIRREL3, GRIK2, LINGO2) were also positively correlated with IC50 of all drugs. By analyzing the relationship between TIDE score and mRNA risk score, we found that patients with low TIDE scores were more likely to respond to immune checkpoint inhibitors. This may help predict the efficacy of immunotherapy for LUAD. In addition, it is currently believed that a higher value of tumor mutation load represents the higher immunogenicity of the tumor, which is more conducive to immunotherapy drugs, and our analysis also confirmed this view again.

The second model was constructed based on m⁶A related lncRNAs. There are 15 predictors in total (Table S5). The variables screening process of lncRNA model is relatively complex, and repeated exploration is to find a prediction model with relatively good discrimination. There are not enough studies on lncRNA in lung adenocarcinoma, but four at present: SNHG12, RPARP-AS1, CRNDE, LMO7DN. SNHG12 has been experimentally predicted as a potential biomarker for the diagnosis, treatment and prognosis of LUAD (53). RPARP-AS1 and CRNDE were included as two predictors in another literature (54). LMO7DN has also been suggested as a predictor of lung adenocarcinoma associated with ferroptosis (55).

The third model combined the risk scores of the first two models with clinical variable. There are 3 predictors in total: mRNA risk score, lncRNA risk score, tumor stage. We considered combination of prognostic indices of the two transcriptomic predictive models with clinical variables as a new approach to prognosis prediction and achieved good results.

This study has several advantages. First, all models are based on public cohort data from reliable sources that predict a long survival interval of up to 10 years. Each model was externally validated by multiple independent data sets and stable validation results were obtained. In addition, considering the usability of the model, a model-related web calculator has been developed for anyone to use.

There are several limitations to our study. First, when constructing the comprehensive model, we narrowed the candidate predictors in the development model to three (age, sex, and tumor stage), taking into account the fragmentary clinical variables in validation sets. But it also simplifies the final model somewhat. Secondly, the three models derived in this study are somewhat complicated. In order to reduce the difficulty of practical prediction caused by complex and diverse models, we developed a web calculator containing all models. Thirdly, the performance of our model in external verification will take into account the difference between verification set and derivation set. If the difference is too large, our model may not achieve good performance.

In conclusion, we developed and externally validated three models to predict survival probability of lung adenocarcinoma based on m⁶A-related transcriptomics. This may provide clues to new strategies or therapeutic targets for lung adenocarcinoma.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://xena.ucsc.edu/. https://www.ncbi.nlm.nih.gov/geo/.

Author Contributions

HL, S-BL, and JS contributed to conceptualization and project administration. HL, S-BL, JC, and NY downloaded and analyzed the data. HL, SB-L wrote the manuscript, with assistance from JS, LB, XZ, KL, and ZT. All authors reviewed the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China (81773541), funded from the Priority Academic Program Development of Jiangsu Higher Education Institutions at Soochow University, the State Key Laboratory of Radiation Medicine and Protection (GZK1201919) to ZT, National Natural Science Foundation of China (81872552, U1967220) to JC. Science and Technology Innovation team project of the Suzhou Vocational health college (SZWZYTD201804), Qing-Lan Project of Jiangsu Province in China (2021) to S-BL. National Natural Science Foundation of China (82172441), Suzhou Key Clinical Diagnosis and Treatment Technology Project (LCZX201925) to KL.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the contributions of TCGA and GEO databases.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fonc.2022.895148/full#supplementary-material

References

1. Siegel RL, Miller KD, Jemal A. Cancer Statistics, 2020. CA Cancer J Clin (2020) 70(1):7–30. doi: 10.3322/caac.21590

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhu M, Cui Y, Mo Q, Zhang J, Zhao T, Xu Y, et al. Characterization of M(6)A RNA Methylation Regulators Predicts Survival and Immunotherapy in Lung Adenocarcinoma. Front Immunol (2021) 12:782551. doi: 10.3389/fimmu.2021.782551

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dominissini D, Moshitch-Moshkovitz S, Schwartz S, Salmon-Divon M, Ungar L, Osenberg S, et al. Topology of the Human and Mouse M6a RNA Methylomes Revealed by M6a-Seq. Nature (2012) 485(7397):201–6. doi: 10.1038/nature11112

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yang Y, Hsu PJ, Chen YS, Yang YG. Dynamic Transcriptomic M(6)A Decoration: Writers, Erasers, Readers and Functions in RNA Metabolism. Cell Res (2018) 28(6):616–24. doi: 10.1038/s41422-018-0040-8

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ma L, Chen T, Zhang X, Miao Y, Tian X, Yu K, et al. The M(6)A Reader YTHDC2 Inhibits Lung Adenocarcinoma Tumorigenesis by Suppressing SLC7A11-Dependent Antioxidant Function. Redox Biol (2021) 38:101801. doi: 10.1016/j.redox.2020.101801

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Liu XS, Zhou LM, Yuan LL, Gao Y, Kui XY, Liu XY, et al. NPM1 Is a Prognostic Biomarker Involved in Immune Infiltration of Lung Adenocarcinoma and Associated With M6a Modification and Glycolysis. Front Immunol (2021) 12:724741. doi: 10.3389/fimmu.2021.724741

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Qian X, Yang J, Qiu Q, Li X, Jiang C, Li J, et al. LCAT3, a Novel M6a-Regulated Long non-Coding RNA, Plays an Oncogenic Role in Lung Cancer via Binding With FUBP1 to Activate C-MYC. J Hematol Oncol (2021) 14(1):112. doi: 10.1186/s13045-021-01123-0

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang H, Zhao X, Lu Z. M(6)A RNA Methylation Regulators Act as Potential Prognostic Biomarkers in Lung Adenocarcinoma. Front Genet (2021) 12:622233. doi: 10.3389/fgene.2021.622233

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sun J, Ping Y, Huang J, Zeng B, Ji P, Li D. N6-Methyladenosine-Regulated mRNAs: Potential Prognostic Biomarkers for Patients With Lung Adenocarcinoma. Front Cell Dev Biol (2021) 9:705962. doi: 10.3389/fcell.2021.705962

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhu J, Wang M, Hu D. Deciphering N(6)-Methyladenosine-Related Genes Signature to Predict Survival in Lung Adenocarcinoma. BioMed Res Int (2020) 2020:2514230. doi: 10.1155/2020/2514230

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Liu X, Li N, Liu S, Wang J, Zhang N, Zheng X, et al. Normalization Methods for the Analysis of Unbalanced Transcriptome Data: A Review. Front Bioeng Biotechnol (2019) 7:358. doi: 10.3389/fbioe.2019.00358

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Welsh EA, Eschrich SA, Berglund AE, Fenstermacher DA. Iterative Rank-Order Normalization of Gene Expression Microarray Data. BMC Bioinf (2013) 14:153. doi: 10.1186/1471-2105-14-153

CrossRef Full Text | Google Scholar

13. Guo B, Zhang H, Wang J, Wu R, Zhang J, Zhang Q, et al. Identification of the Signature Associated With M(6)A RNA Methylation Regulators and M(6)A-Related Genes and Construction of the Risk Score for Prognostication in Early-Stage Lung Adenocarcinoma. Front Genet (2021) 12:656114. doi: 10.3389/fgene.2021.656114

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zheng Y, Nie P, Peng D, He Z, Liu M, Xie Y, et al. M6avar: A Database of Functional Variants Involved in M6a Modification. Nucleic Acids Res (2018) 46(D1):D139–D45. doi: 10.1093/nar/gkx895

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Goeman JJ. L1 Penalized Estimation in the Cox Proportional Hazards Model. Comp Stud (2010) 52(1):70–84. doi: 10.1002/bimj.200900028

CrossRef Full Text | Google Scholar

16. Venables WN, Ripley BD. Modern Applied Statistics With S. In: Statistic and Computing. Springer (2002).

Google Scholar

17. Harrell FE. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis: Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. Cham: Springer (2010). XXV, 582 p. doi: 10.1007/978-3-319-19425-7

CrossRef Full Text | Google Scholar

18. Wang J, Yuan T, Ding H, Xu J, Keusters WR, Ling X, et al. Development and External Validation of a Prognostic Model for Survival of People Living With HIV/AIDS Initiating Antiretroviral Therapy. Lancet Reg Health West Pac (2021) 16:100269. doi: 10.1016/j.lanwpc.2021.100269

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Harrell F Jr., Califf RM. Evaluating the Yield of Medical Tests. JAMA (1982) 247(18):2543. doi: 10.1001/jama.1982.03320430047030

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Heagerty PJ, Lumley T, Pepe MSJB. Time-Dependent ROC Curves for Censored Survival Data and a Diagnostic Marker. Biometrics (2000) 56(2):337–44. doi: 10.1111/j.0006-341X.2000.00337.x

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gerds TA, Kattan MW, Schumacher M, Yu C. Estimating a Time-Dependent Concordance Index for Survival Prediction Models With Covariate Dependent Censoring. Stat Med (2013) 32(13):2173–84. doi: 10.1002/sim.5681

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Royston P, Altman DG. External Validation of a Cox Prognostic Model: Principles and Methods. BMC Med Res Methodol (2013) 13:15. doi: 10.1186/1471-2288-13-33

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Steyerberg EW. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. Springer (2019) 66(2):661–2. doi: 10.1007/978-3-030-16399-0

CrossRef Full Text | Google Scholar

24. Therneau T, Therneau T, Grambsch P. Modeling Survival Data: Extending the Cox Model (Statistics for Biology and Health). Springer (2000). doi: 10.1007/978-1-4757-3294-8

CrossRef Full Text | Google Scholar

25. Hothorn T. Maxstat: Maximally Selected Rank Statistics in R. Biometri J. (2015) 44. doi: 10.1002/1521-4036(200203)44:23.0.CO;2-Z

CrossRef Full Text | Google Scholar

26. Leek JT, Johnson WE, Parker HS, Jaffe ®, Storey JDJB. The SVA Package for Removing Batch Effects and Other Unwanted Variation in High-Throughput Experiments. Bioinformatics (2012) 28(6):882–3. doi: 10.1093/bioinformatics/bts034

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ishwaran H. Random Survival Forest. JAAS (2008) 2:25–31. doi: 10.1214/08-AOAS169

CrossRef Full Text | Google Scholar

28. Ishwaran H, Kogalur UB. Randomforestsrc: Random Forests for Survival, Regression and Classification (RF-SRC). (2021). Available at: https://cran.r-project.org/web/packages/randomForestSRC/citation.html.

Google Scholar

29. Wen C, Zhang A, Quan S, Wang X. BeSS: Best Subset Selection for Sparse Generalized Linear Model and Cox Model. J Stat Softw (2020) 94:1–24. doi: 10.18637/jss.v094.i04

CrossRef Full Text | Google Scholar

30. Murad H, Dankner R, Berlin A, Olmer L, Freedman LS. Imputing Missing Time-Dependent Covariate Values for the Discrete Time Cox Model. Stat Methods Med Res (2019) 29(8):962280219881168. doi: 10.1177/0962280219881168

CrossRef Full Text | Google Scholar

31. Moons K, Donders R, Stijnen T, Harrell FE. Using the Outcome for Imputation of Missing Predictor Values was Preferred. J Clin Epideminol (2006) 59(10):1092–101. doi: 10.1016/j.jclinepi.2006.01.009

CrossRef Full Text | Google Scholar

32. White IR, Royston P. Imputing Missing Covariate Values for the Cox Model. Stat Med (2010) 28(15):1982–98. doi: 10.1002/sim.3618

CrossRef Full Text | Google Scholar

33. Wood AM, White IR, Royston P. How Should Variable Selection be Performed With Multiply Imputed Data? Stat Med (2010) 27(17):3227–46. doi: 10.1002/sim.3177

CrossRef Full Text | Google Scholar

34. Mayakonda A, Koeffler HP. Maftools: Efficient Analysis, Visualization and Summarization of MAF Files From Large-Scale Cohort Based Cancer Studies. BioRxiv (2016) 2016:052662. doi: 10.1101/052662

CrossRef Full Text | Google Scholar

35. Ribas A, Wolchok JD. Cancer Immunotherapy Using Checkpoint Blockade. Science (2018) 359(6382):1350–5. doi: 10.1126/science.aar4060

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Chen X, Zhu Z, Li X, Yao X, Luo L. The Ferroptosis-Related Noncoding RNA Signature as a Novel Prognostic Biomarker in the Tumor Microenvironment, Immunotherapy, and Drug Screening of Gastric Adenocarcinoma. Front Oncol (2021) 11:778557. doi: 10.3389/fonc.2021.778557

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Fu J, Li K, Zhang W, Wan C, Zhang J, Jiang P, et al. Large-Scale Public Data Reuse to Model Immunotherapy Response and Resistance. (2020) 12:1–8. doi: 10.1186/s13073-020-0721-z

CrossRef Full Text | Google Scholar

38. Jiang P, Gu S, Deng P, Fu J, Sahu A, Hu X, et al. Signatures of T Cell Dysfunction and Exclusion Predict Cancer Immunotherapy Response. Nat Med (2018) 2018:1550–8. doi: 10.1158/2326-6074.CRICIMTEATIAACR18-B077

CrossRef Full Text | Google Scholar

39. Maeser D, Gruener RF, Huang RS. Predict: An R Package for Predicting In Vivo or Cancer Patient Drug Response and Biomarkers From Cell Line Screening Data. JBiB Onco (2021) 11:bbab260. doi: 10.1093/bib/bbab260

CrossRef Full Text | Google Scholar

40. Schemper M, Smith TL. A Note on Quantifying Follow-Up in Studies of Failure Time. Control Clin Trials (1996) 17(4):343–6. doi: 10.1016/0197-2456(96)00075-X

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Templ M, Alfons A, Filzmoser P. Exploring Incomplete Data Using Visualization Techniques. Adv Data Anal Classificat (2011) 6(1):29–47. doi: 10.1007/s11634-011-0102-y

CrossRef Full Text | Google Scholar

42. Das T, Lee EY, You HJ, Kim EE, Song EJ. USP15 and USP4 Facilitate Lung Cancer Cell Proliferation by Regulating the Alternative Splicing of SRSF1. Cell Death Discovery (2022) 8(1):24. doi: 10.1038/s41420-022-00820-0

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Li N, Qiu L, Zeng C, Fang Z, Chen S, Song X, et al. Bioinformatic Analysis of Differentially Expressed Genes and Pathways in Idiopathic Pulmonary Fibrosis. Ann Transl Med (2021) 9(18):1459. doi: 10.1183/13993003.congress-2021.OA4331

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tran AN, Dussaq AM, Kennell T Jr., Willey CD, Hjelmeland AB. HPAanalyze: An R Package That Facilitates the Retrieval and Analysis of the Human Protein Atlas Data. BMC Bioinf (2019) 20(1):463. doi: 10.1186/s12859-019-3059-z

CrossRef Full Text | Google Scholar

45. Meyer KD, Saletore Y, Zumbo P, Elemento O, Mason CE, Jaffrey SR. Comprehensive Analysis of mRNA Methylation Reveals Enrichment in 3' UTRs and Near Stop Codons. Cell (2012) 149(7):1635–46.

Google Scholar

46. Schwartz S, Mumbach M, Jovanovic M, Wang T, Maciag K, Bushkin GG, et al. Perturbation of M6a Writers Reveals Two Distinct Classes of mRNA Methylation at Internal and 5′ Sites. Cell Rep (2014) 8(1):284–96. doi: 10.1016/j.celrep.2014.05.048

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhang Z, Chen LQ, Zhao YL, Yang CG, Luo GZ. Single-Base Mapping of M6a by an Antibody-Independent Method. Sci Adv (2019) 2019:eaax0250. doi: 10.1101/575555

CrossRef Full Text | Google Scholar

48. Ke S, Alemu EA, Mertens C, Gantman EC, Fak JJ, Mele A, et al. A Majority of M6a Residues are in the Last Exons, Allowing the Potential for 3’ UTR Regulation. Genes Dev (2015) 29(19):2037–53. doi: 10.1101/gad.269415.115

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Sendinc E, Valle-Garcia D, Dhall A, Chen H, Henriques T, Navarrete-Perea J, et al. PCIF1 Catalyzes M6am mRNA Methylation to Regulate Gene Expression. Mol Cell (2019) 75(3):620–30.e9. doi: 10.1016/j.molcel.2019.05.030

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Liu J, Li K, Cai J, Zhang M, Zhang X, Xiong X, et al. Landscape and Regulation of M(6)A and M(6)Am Methylome Across Human and Mouse Tissues. Mol Cell (2020) 77(2):426–40 e6. doi: 10.1016/j.molcel.2019.09.032

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Hasan I, Mohsin K, Gokhale NS, Mcintyre A, Geon-Woo K, Young JJ, et al. N6 -Methyladenosine Modification of Hepatitis B Virus RNA Differentially Regulates the Viral Life Cycle. Proc Nat Acad Sci (2018) 115:201808319. doi: 10.1073/pnas.1808319115

CrossRef Full Text | Google Scholar

52. Li Z, Qian P, Shao W, Shi H, He XC, Madelaine G, et al. Suppression of m6A reader Ythdf2 promotes hematopoietic stem cell expansion. Cell Res (2018) 28(9):14. doi: 10.1038/s41422-018-0072-0

CrossRef Full Text | Google Scholar

53. Zhang H, Wang Y, Lu J. Identification of Lung-Adenocarcinoma-Related Long non-Coding RNAs by Random Walking on a Competing Endogenous RNA Network. Ann Transl Med (2019) 7(14):339. doi: 10.21037/atm.2019.06.69

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Zheng J, Zhao Z, Wan J, Guo M, Wang Y, Yang Z, et al. N-6 Methylation-Related lncRNA is Potential Signature in Lung Adenocarcinoma and Influences Tumor Microenvironment. J Clin Lab Anal (2021) 35(11):e23951. doi: 10.1002/jcla.23951

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Lu L, Liu LP, Zhao QQ, Gui R, Zhao QY. Identification of a Ferroptosis-Related LncRNA Signature as a Novel Prognosis Model for Lung Adenocarcinoma. Front Oncol (2021) 11:675545. doi: 10.3389/fonc.2021.675545

PubMed Abstract | CrossRef Full Text | Google Scholar