
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Oncol. , 24 November 2020
Sec. Radiation Oncology
Volume 10 - 2020 | https://doi.org/10.3389/fonc.2020.531344
This article is part of the Research Topic Modeling for Prediction of Radiation-Induced Toxicity to Improve Therapeutic Ratio in the Modern Radiation Therapy Era View all 35 articles
 Jon Espen Dale1,2
Jon Espen Dale1,2 Silvia Molinelli3
Silvia Molinelli3 Barbara Vischioni3*
Barbara Vischioni3* Viviana Vitolo3
Viviana Vitolo3 Maria Bonora3
Maria Bonora3 Giuseppe Magro3
Giuseppe Magro3 Andrea Mairani3,4
Andrea Mairani3,4 Azusa Hasegawa3,5
Azusa Hasegawa3,5 Tatsuya Ohno6
Tatsuya Ohno6 Olav Dahl1
Olav Dahl1 Francesca Valvo3
Francesca Valvo3 Piero Fossati3,7
Piero Fossati3,7Background and Purpose: The Italian National Center of Oncological Hadrontherapy (CNAO) has applied dose constraints for carbon ion RT (CIRT) as defined by Japan’s National Institute of Radiological Sciences (NIRS). However, these institutions use different models to predict the relative biological effectiveness (RBE). CNAO applies the Local Effect Model I (LEM I), which in most clinical situations predicts higher RBE than NIRS’s Microdosimetric Kinetic Model (MKM). Equal constraints therefore become more restrictive at CNAO. Tolerance doses for the brainstem have not been validated for LEM I-weighted dose (DLEM I). However, brainstem constraints and a Normal Tissue Complication Probability (NTCP) model were recently reported for MKM-weighted dose (DMKM), showing that a constraint relaxation to DMKM|0.7 cm3 <30 Gy (RBE) and DMKM|0.1 cm3 <40 Gy (RBE) was feasible. The aim of this work was to evaluate the brainstem NTCP associated with CNAO’s current clinical practice and to propose new brainstem constraints for LEM I-optimized CIRT at CNAO.
Material and Methods: We reproduced the absorbed dose of 30 representative patient treatment plans from CNAO. Subsequently, we calculated both DLEM I and DMKM, and the relationship between DMKM and DLEM I for various brainstem dose metrics was analyzed. Furthermore, the NTCP model developed for DMKM was applied to estimate the NTCPs of the delivered plans.
Results: The translation of CNAO treatment plans to DMKM confirmed that the former CNAO constraints were conservative compared with DMKM constraints. Estimated NTCPs were 0% for all but one case, in which the NTCP was 2%. The relationship DMKM/DLEM I could be described by a quadratic regression model which revealed that the validated DMKM constraints corresponded to DLEM I|0.7 cm3 <41 Gy (RBE) (95% CI, 38–44 Gy (RBE)) and DLEM I|0.1 cm3 <49 Gy (RBE) (95% CI, 46–52 Gy (RBE)).
Conclusion: Our study demonstrates that RBE-weighted dose translation is of crucial importance in order to exchange experience and thus harmonize CIRT treatments globally. To mitigate uncertainties involved, we propose to use the lower bound of the 95% CI of the translation estimates, i.e., DLEM I|0.7 cm3 <38 Gy (RBE) and DLEM I|0.1 cm3 <46 Gy (RBE) as brainstem dose constraints for 16 fraction CIRT treatments optimized with LEM I.
There is an increasing interest in using carbon ion radiotherapy (CIRT) for the treatment of advanced, radioresistant tumors. The physical properties of CIRT allow for delivering a high dose to the tumor, while the finite distal depth dose and sharp lateral penumbra can be utilized to spare nearby organs at risk (OARs) from excessive dose. Furthermore, carbon ions exhibit high linear energy transfer (LET) properties, which lead to more efficient cell killing (higher relative biological effectiveness (RBE)), compared with photon and proton RT. However, there are substantial uncertainties regarding the clinical RBE of carbon ions. Therefore, prescription doses, tolerance doses to OARs, and normal tissue complication probability (NTCP) models based on experience with photon or proton RT may not be applicable to CIRT and should preferably be derived from CIRT data.
Two major approaches have been used for the clinical implementation of CIRT. Spearheaded by the National Institute of Radiological Sciences (NIRS), Chiba, Japan, the Japanese centers are using hypofractionated treatment schedules (16 fractions of 3.6–4.6 Gy (RBE)) in which prescription doses and OAR tolerance doses initially were defined through carefully conducted dose-escalation trials. Originally, the mixed beam model (1) was developed to predict the RBE of the passively scattered carbon ion beams with tumor response as the relevant endpoint. Later, with the implementation of scanned beam delivery, the modified microdosimetric kinetic model (MKM) (2–5) was introduced. Since these two models have been validated for consistency, they are hereby collectively abbreviated as MKM.
In contrast, CIRT at the Gesellschaft für Schwerionenforschung (GSI), Darmstadt, Germany, was initiated with moderately hypofractionated schedules (20–22 fractions of 3.0–3.5 Gy (RBE)) in which the Local Effect Model Version I (LEM I) (6, 7) was used to predict the RBE of CIRT for late responding normal tissues (i.e., central nervous system tissue). Trusting the LEM I to be sufficiently accurate, dose constraints derived from photon RT could be applied for CIRT treatments. An additional assumption for this approach was that the linear quadratic (LQ) formalism was applicable also for CIRT.
When the National Center of Oncological Hadrontherapy (CNAO, Italy) (8) started treating patients with LEM I-optimized CIRT in 2012, the successful treatment approach developed at NIRS was adopted. However, comparative studies show that the LEM I predicts a 5–15% higher RBE in the spread out Bragg peak (SOBP) of a carbon ion beam, relative to the MKM (9, 10). In the entrance region, the RBE predicted by LEM I can be 60% higher (11). Consequently, dependent on the clinical indication, prescription doses at CNAO (reported in LEM I-weighted dose, DLEM I) were increased 5–15% relative to the prescription doses at NIRS (reported in MKM-weighted dose (DMKM)) (9, 10). In contrast, dose constraints to OARs were not adjusted. This was a cautious approach mitigating various uncertainties related to the adaptation of NIRS prescription doses (i.e., differences in RBE model, beam delivery method, dose optimization process, etc.).
For the brainstem, the dose constraint at CNAO was therefore set to be <30 Gy (RBE) to no more than 1% of the organ’s volume (DLEM I│1%), following the tradition of NIRS (12). Since this constraint becomes more restrictive in LEM I-optimized CIRT, CNAO has so far treated more than 1,000 patients with advanced tumors in the head and neck region (for example, skull base, nasopharynx, and sinonasal sites) without experiencing any grade of radiation-induced brainstem injury. Thus, the constraint needs to be updated to provide optimal treatments in cases where the target volume is located close to the brainstem. However, it is challenging to propose new and reasonable constraints since no toxic events have been reported from any institution applying LEM I-weighted doses for CIRT.
Recently, a dose-response analysis of brainstem toxicity following DMKM-optimized CIRT at Gunma University Heavy Ion Medical Center (GHMC) (13) was published by Shirai et al. (14). None of the 85 patients included in this analysis experienced symptomatic brainstem toxicity. However, four cases of focal brainstem contrast enhancement were detected on routine magnetic resonance imaging (MRI) during follow-up. This was defined as central nervous system (CNS) necrosis grade 1 events according to the Common Terminology Criteria for Adverse Events version 4.0 (CTCAE). Even these asymptomatic events did not occur before the maximum dose (DMKM|max) exceeded 48 Gy (RBE), showing that current constraint may be conservative even when applied for DMKM. The brainstem volume receiving more than 30 Gy (RBE) (V30 Gy (RBE)) and 40 Gy (RBE) (V40 Gy (RBE)) were independent risk factors for this endpoint. Brainstem toxicity of any grade did not occur before V30 Gy (RBE) exceeded 0.7 cm3 and V40 Gy (RBE) exceeded 0.1 cm3. Since these values relate to radiologically detectable, but asymptomatic alterations in the brainstem, they may serve as constraints to avoid symptomatic injury. Shirai et al. also fitted their data to the Lyman-Kutcher-Burman (LKB) NTCP model (15–17), resulting in the following model parameters: volume-effect parameter (n) = 0.08, biodiversity parameter (m) = 0.08, and the equivalent uniform dose (EUD) corresponding to 50% probability of toxicity (TD50) = 32.4 Gy (RBE).
The goal of this work is therefore to:
1. evaluate the brainstem NTCP associated with CNAOs current clinical practice by applying the NTCP model published by Shirai et al.
2. convert the DMKM validated constraints into DLEM I, providing guidance for the proposal of new dose constraints to be used at CNAO and other centers applying LEM I.
The dose distributions of 30 CIRT treatments with target volumes close to the brainstem were included in this study. Details on disease site, histology, and prescription dose are presented in Table 1. The treatments were given at CNAO in the period 2013–2014 as part of prospective protocols (CNAO S9/2012/C, CNAO S12/2012/C, and CNAO S15/2012/C) approved by the Regional Ethics Committee. Signed consent was required for participation. The plans were optimized for a prescribed DLEM I of 68.8–76.8 Gy (RBE) in 16 fractions (4 fractions/week) using the syngo® RT Planning (Siemens Healthcare, Erlangen, Germany) treatment planning system (TPS). Dose constraint for the brainstem was DLEM I│1% ≤30 Gy (RBE). Additionally, a constraint of DLEM I│1% ≤35 Gy (RBE) was applied to a 3-mm planning OAR volume (PRV) for plan optimization purposes.
In general, the strategy to obtain a robust treatment plan is similar at CNAO and GHMC: Multiple beam angles (3 to 4), dominantly originating from the horizontally fixed beam line, are achieved by couch rotation and/or by multiple immobilization positions where the patient’s head is positioned either straight or rotated. Due to particle range uncertainty, beam angles are chosen so that most of the dose to the brainstem originates from the beam’s sharp lateral penumbra, rather than the distal dose fall-off. Beams traversing through the brainstem are never used.
The patients’ computed tomography (CT) image files, structure set files, dose files, and plan files were exported from the syngo® TPS and imported to the matRad open source multimodality radiation TPS (https://e0404.github.io/matRad/) (18) in which the absorbed dose (DAbs) and DLEM I were reproduced. The input parameters used clinically for LEM I were applied, i.e., αγ = 0.1 Gy−1, βγ = 0.05 Gy−2, Dt = 30 Gy, smax = 3.1 Gy−1, Rn = 5 μm (7). The DVHs of targets and OARs were compared with the corresponding DVHs of the dose distribution from the syngo® TPS to ensure correct reproduction of both DAbs and DLEM I (results not reported). Secondly, MKM was implemented in the matRad TPS code using the input parameters used clinically (Rd = 0.32 µm, Rn = 3.9 µm, α0 = 0.172 Gy−1, β = 0.0615 Gy−2, αr = 0.764 Gy−1, FClin = 2.39) (2, 11) and DMKM was derived from the exact same absorbed dose and LET spectra. This enabled a direct comparison of each patient’s DLEM I and DMKM based exclusively on the differences in the RBE modeling.
Using the DMKM distributions, the brainstem NTCP for each treatment plan was calculated by the LKB method, using the model parameters suggested by Shirai et al. (14): n = 0.08, m = 0.08, and TD50 = 32.4 Gy (RBE).
For each brainstem, the DMKM|0.7 cm3 and DMKM|0.1 cm3 were plotted as a function of DLEM I|0.7 cm3 and DLEM I|0.1 cm3, respectively. A curve fitting procedure was performed with the software IBM SPSS Statistics for Windows, version 24.0 (IBM Corp., Armonk, NY, U.S.A.) in order to produce a dose translation model.
As a last step, we wanted to verify that the dose translation model correctly predicted the DLEM I/DMKM relationship also for higher brainstem doses than our original data. Therefore, five treatment plans, in which the original DLEM I constraint caused suboptimal dose coverage to the clinical target volume (CTV D95% <95% of prescription dose), were reoptimized applying a new set of DLEM I constraints as proposed by this work (see “RESULTS”). Subsequently, these new plans were recalculated to DMKM. These procedures, which were conducted exclusively to confirm the relationship of the RBE models, were performed with the RayStation® 6.99 TPS (RaySearch Laboratories AB, Stockholm, Sweden), where both the LEM I and MKM were implemented with the respective model input parameters as mentioned earlier.
Brainstem DVHs in relative and absolute volumes are presented in both DLEM I and DMKM in Figure 1, showing the substantial decrease in RBE-weighted doses when the MKM is applied as RBE model.
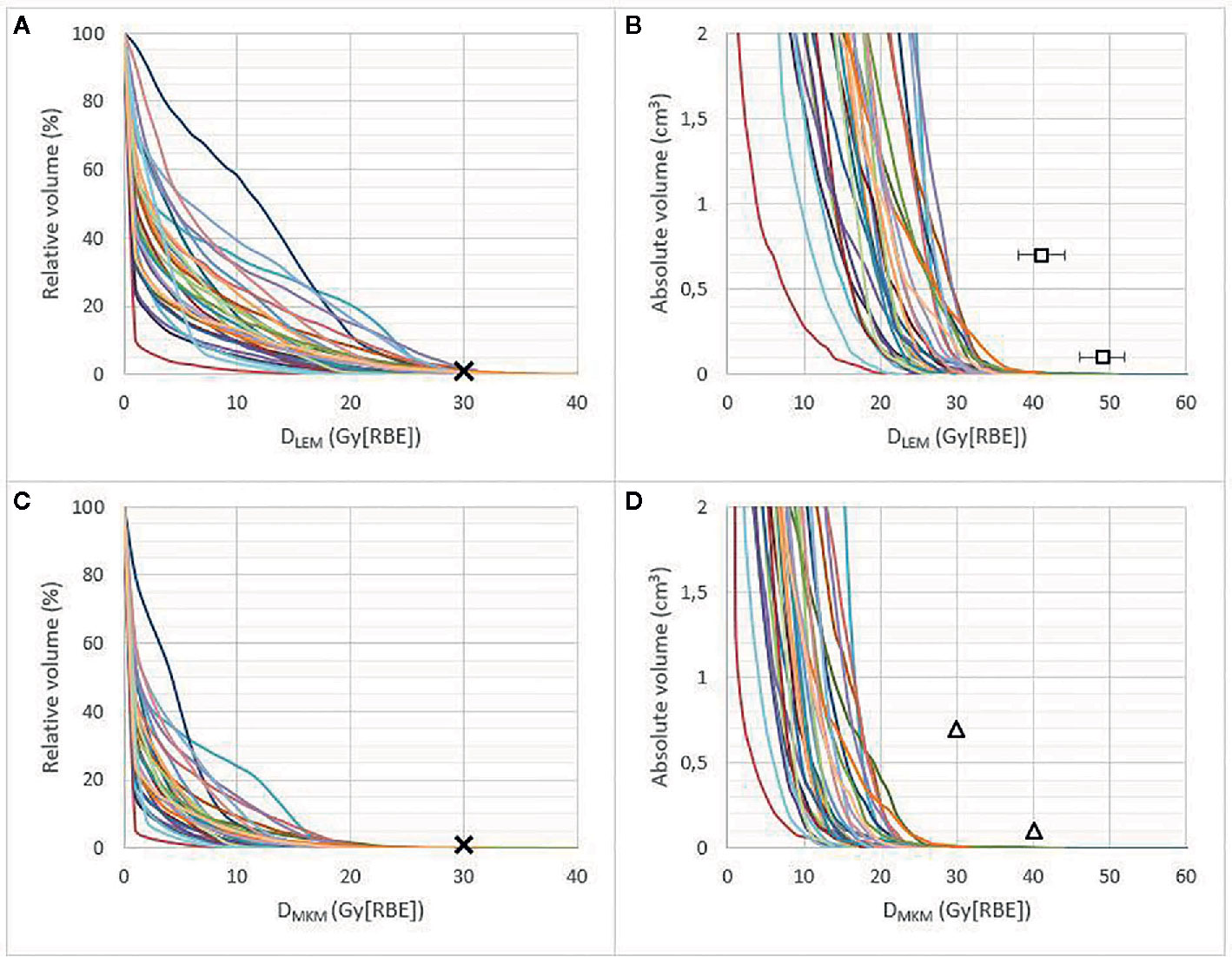
Figure 1 Brainstem DVHs in relative (A, C) and absolute volume (≤2 cm3) (B, D) of 30 patients treated at CNAO, presented in DLEM I (A, B) and DMKM (C, D). Crosses represent the former CNAO and NIRS dose constraint of D1% ≤30 Gy (RBE). Triangles represent the new DMKM constraints V40 Gy (RBE) <0.1 cm3 and V30 Gy (RBE) <0.7 cm3 as defined by Shirai et al. (14). Squares in (B) represent the possible new DLEM I constraints (error bars, 95% CI) resulting from the dose translation model presented in this work, see Figure 3.
The median brainstem DLEM I|1% was 23.7 Gy (range, 11.2–31.3 (RBE)), which corresponded to only 12.4 Gy (range, 5.5–21.8 (RBE)) in DMKM, highlighting the restraining effect of the original CNAO constraint in achieving optimal CIRT treatments.
Only four of the brainstems received DMKM >30 Gy (RBE), each of them to a volume smaller than 0.05 cm3. As seen in Figures 1B, D, the highest DLEM I to the brainstem volumes 0.7 and 0.1 cm3 were 29 Gy (RBE) and 35 Gy (RBE), respectively, corresponding to 17 Gy (RBE) and 25 Gy (RBE) in DMKM. These modest doses resulted in a very low probability of asymptomatic (grade 1) brainstem injury according to the NTCP model published by Shirai et al. (14): One patient had an NTCP of 2%, while the NTCPs of the remaining 29 patients were close to 0%, see Figure 2.
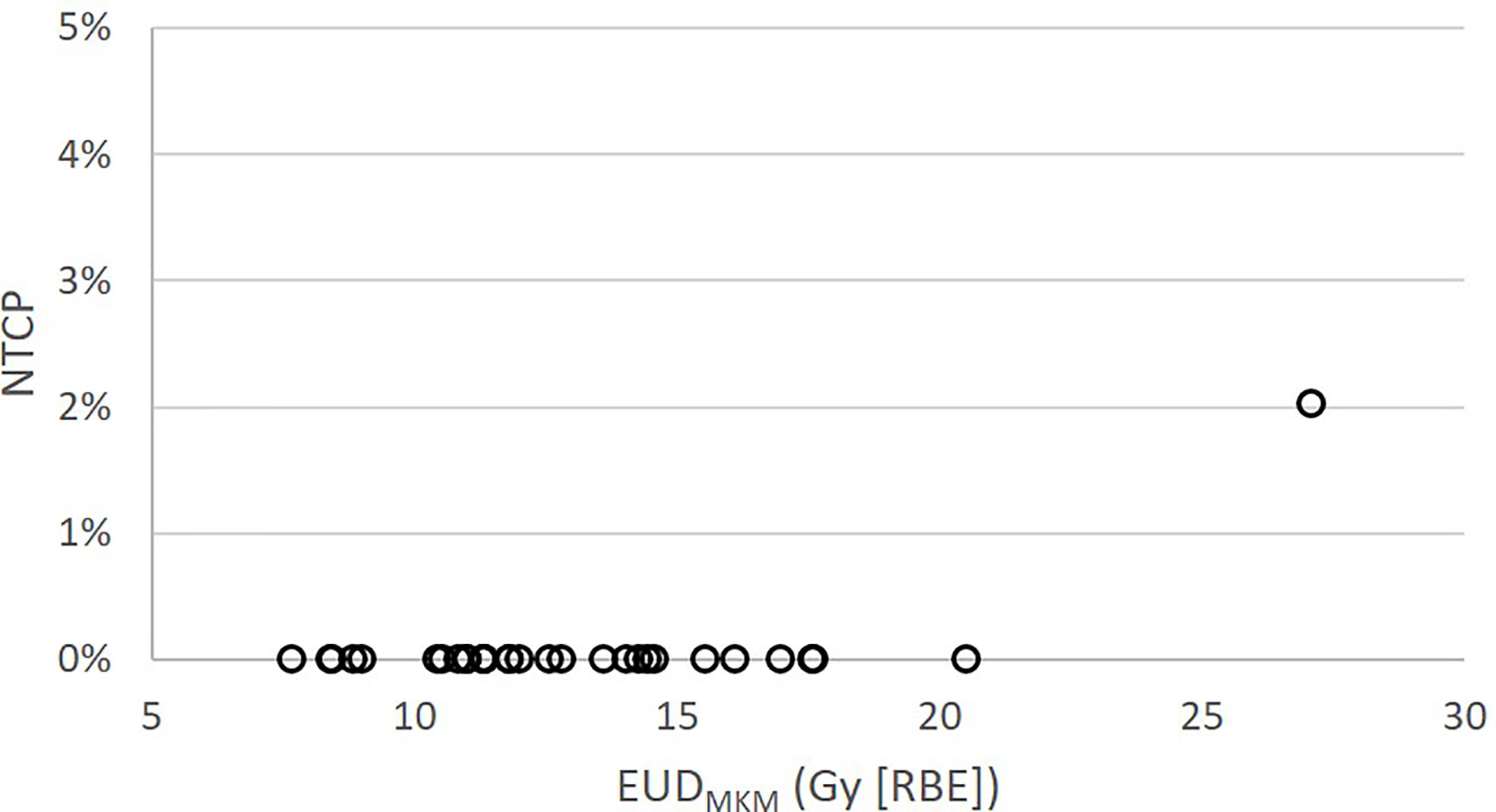
Figure 2 Brainstem NTCP for the 30 patients treated at CNAO as function of EUDMKM according to the NTCP model published by Shirai et al. (14).
For each patient, the brainstem dose metrics DLEM I|0.7 cm3 and DLEM I|0.1 cm3 were plotted against the corresponding dose metric in DMKM (Figure 3). With the assumption that the intercept should be at origin (DLEM = 0 Gy (RBE) when DMKM = 0 Gy (RBE)), we found that the quadratic regression model
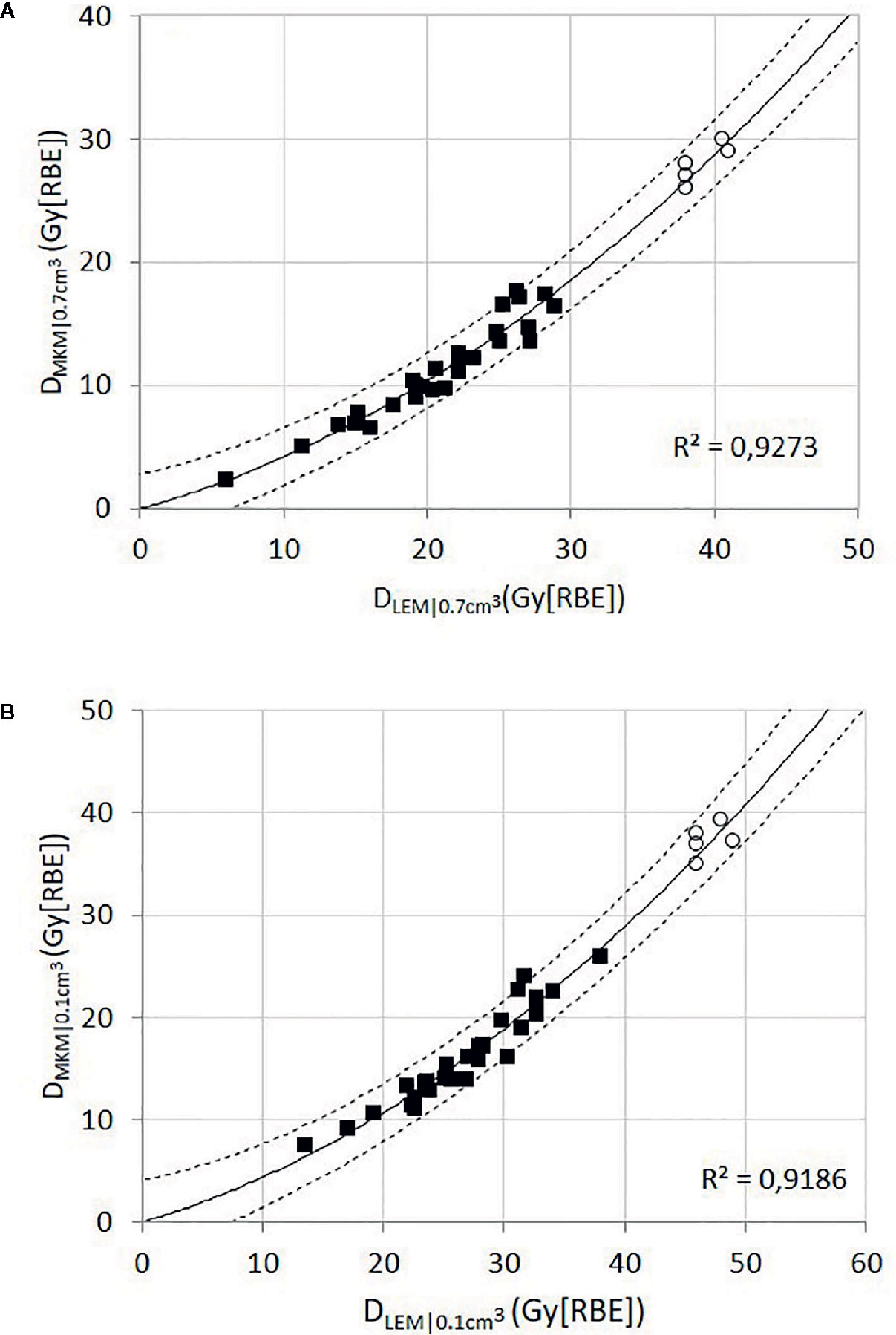
Figure 3 Black squares represent the relationship of DLEM I to DMKM for the dose metrics D0.7 cm3 (A) and D0.1 cm3 (B) for each individual brainstem. The solid line represents the quadratic function providing the best fit to the data points (black squares), assuming that the intercept should be in the origin. The dashed lines represent the 95% CI. The open circles represent the data collected from the reoptimized plans; these data points were not used for the curve fitting procedure.
adequately fit both sets of data (coefficients of determination, R2 ≥ 0.918). Extrapolation of the models to the relevant dose levels revealed that a DMKM|0.7 cm3 of 30 Gy (RBE) and a DMKM|0.1 cm3 of 40 Gy (RBE) translates into a DLEM I|0.7 cm3 of 41 Gy (RBE) (95% CI, 38–44 Gy (RBE)) and a DLEM I|0.1 cm3 of 49 Gy (RBE) (95% CI, 46–52 Gy (RBE)), respectively.
Subsequently, we reoptimized five of the treatment plans in which the old brainstem constraint (DLEM I|1% <30 Gy (RBE)) caused suboptimal CTV dose coverage. For the reoptimization, new brainstem constraints within the lower half of the 95% CI of the dose translation estimates were applied, i.e., DLEM I|0.7 cm3 <38–41 Gy (RBE) and DLEM I| cm3 <46–49 Gy (RBE). The relationship of DLEM I to DMKM for the dose metrics D0.7 cm3 and D0.1 cm3 from the reoptimized plans are plotted as open circles in the scatterplots of Figure 3. As can be seen, the values of these data pairs agree with the prediction of the dose translation model. To demonstrate the potential clinical impact of relaxing the constraints, a comparison of the original and reoptimized plans, displayed in both DLEM I and DMKM, is presented in Figure 4. For this patient, the proportion of the CTV receiving >95% of the prescription dose increased from 74 to 95%.
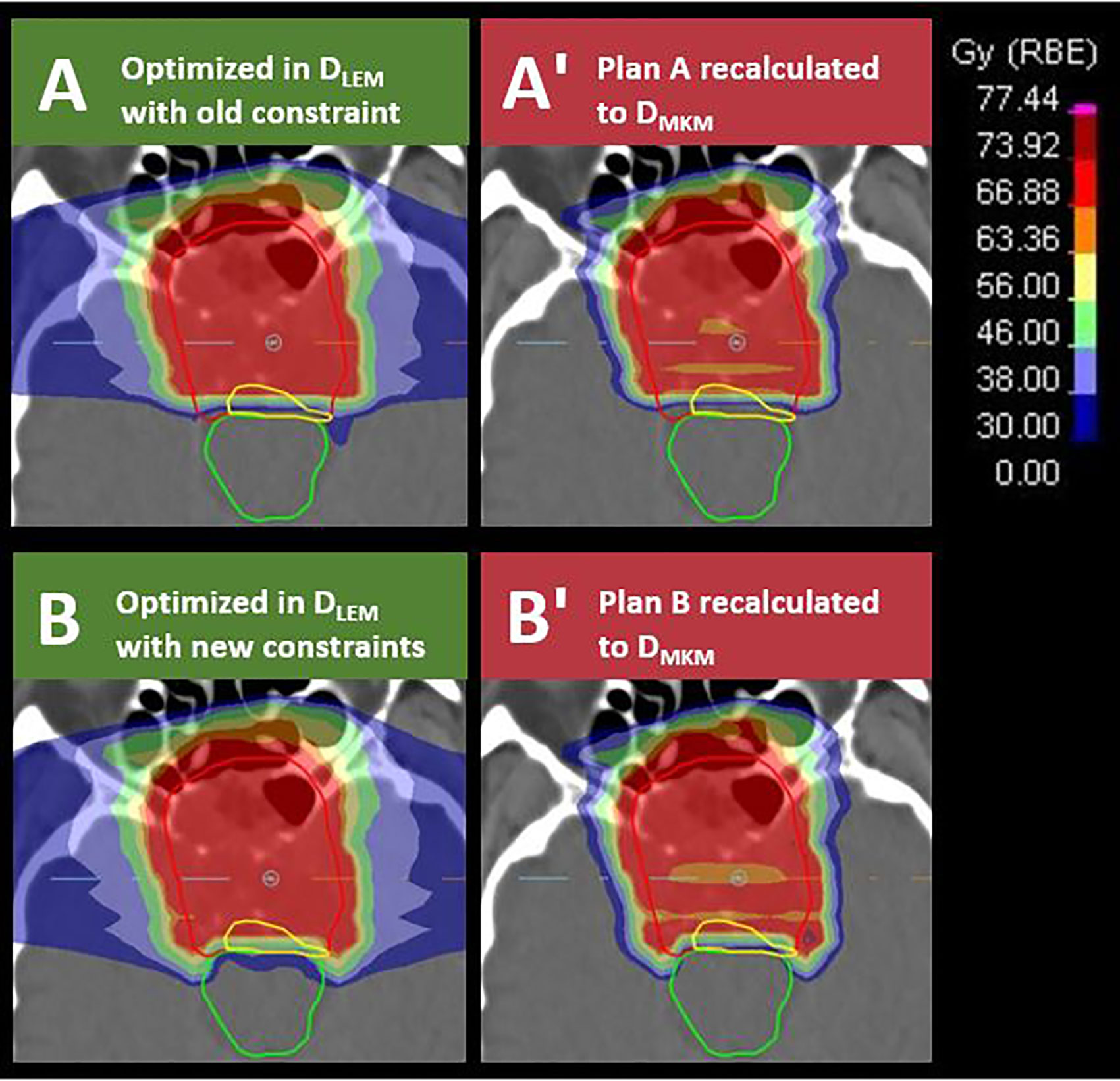
Figure 4 Transversal sections of DLEM I-optimized treatment plans applying brainstem (green contour) constraints of DLEM I|1% <30 Gy (RBE) in plan (A) or DLEM I|0.7 cm3 <38 Gy (RBE) and DLEM|0.1 cm3 <46 Gy (RBE) in plan B). The dose constraint levels are illustrated by dark blue, light blue, and light green isodose, respectively. Plans were subsequently recalculated to DMKM (A′, B′). Red isodose in plan (A, B) represents 95% of the target dose (70.4 Gy (RBE) in DLEM I). Note the improved dose coverage to the CTV (red contour) and to the part of the CTV in which the tumor recurred (yellow contour) in plan B compared with plan A. Dose to the brainstem remains compliant with the constraints defined by Shirai et al. when evaluated in DMKM (B′).
For the implementation of CIRT at CNAO, the goal has been to replicate the successful results achieved at Japanese CIRT centers, by translating NIRS prescription doses into equiefficient doses within the LEM I dose prescription system (9, 10). However, initially the OAR dose constraints were not adjusted correspondingly. This study clearly shows that the original brainstem dose constraint applied at CNAO is too conservative compared with the clinical practice in Japanese centers. In a recent publication on skull base chordomas treated at CNAO, Iannalfi et al. found that 92% of the local recurrences were attributable to suboptimal target dose in regions close to the brainstem or optic pathways (19). The estimated 5-year local control (LC) rate was 71%. This is inferior to the results reported by Japanese centers, where 5-year LC rates within the range 76–92% have been reported (20, 21).
Consequently, updated constraints for LEM I-optimized CIRT are urgently needed. In our opinion, due to the lack of publications addressing brainstem NTCP for LEM I-optimized CIRT, this aim was only achievable by making use of DMKM-validated dose constraints. Relating the CNAO DVHs to the new DMKM constraints defined by Shirai et al. (Figure 1D) suggests that doses to the brainstem volumes 0.7 and 0.1 cm3 potentially could be increased by 13 Gy (RBE) and 15 Gy (RBE) in DMKM, respectively, compared with the former practice at CNAO. According to our dose constraint translation, the corresponding increase in DLEM I would be approximately 12 Gy (RBE) (95% CI, 9–15 Gy (RBE)) and 14 Gy (RBE) (95% CI, 11–17 Gy (RBE)). This unveils an opportunity for improved target dose coverage, and thus improved treatment outcome, as demonstrated in Figure 4.
Recently, the European Particle Therapy Network (EPTN) released a consensus paper for dose constraints to various OARs (22), suggesting a general constraint of D0.03 cm3 ≤54 Gy (RBE) to the brainstem, with an option to allow for D0.03 cm3 ≤60 Gy (RBE) to the brainstem surface. Both constraints were expressed in equivalent dose in 2 Gy fractions (EQD2), with an assumed α/β ratio of 2 Gy. These guidelines are based on photon and proton RT toxicity data and are not necessarily applicable for CIRT due to the larger uncertainties involved in the prediction of the RBE. However, similar constraints are used for CIRT at the Heidelberg Ion Beam Therapy Center (HIT) in Germany (23), building on previous clinical experience of the GSI. Various publications from this institution explicitly report an absence of brainstem toxicity (24, 25). Consequently, these constraints are considered safe for CIRT under HIT’s current treatment paradigm, which consists of 20–22 fractions of 3.0–3.5 Gy (RBE) and 5–7 fractions per week. Although HIT also applies LEM I, these constraints may not be safely transferred to the 16 fraction/4 fractions per week treatment schedule of CNAO, as EQD2 conversion may not be sufficiently precise when fraction doses increase, due to uncertainties in the prediction of RBE.
That being said, it is interesting to observe that our translated constraints, when converted into EQD2, relate closely to the EQD2 constraints used in clinical practice at HIT (23), see Figure 5.
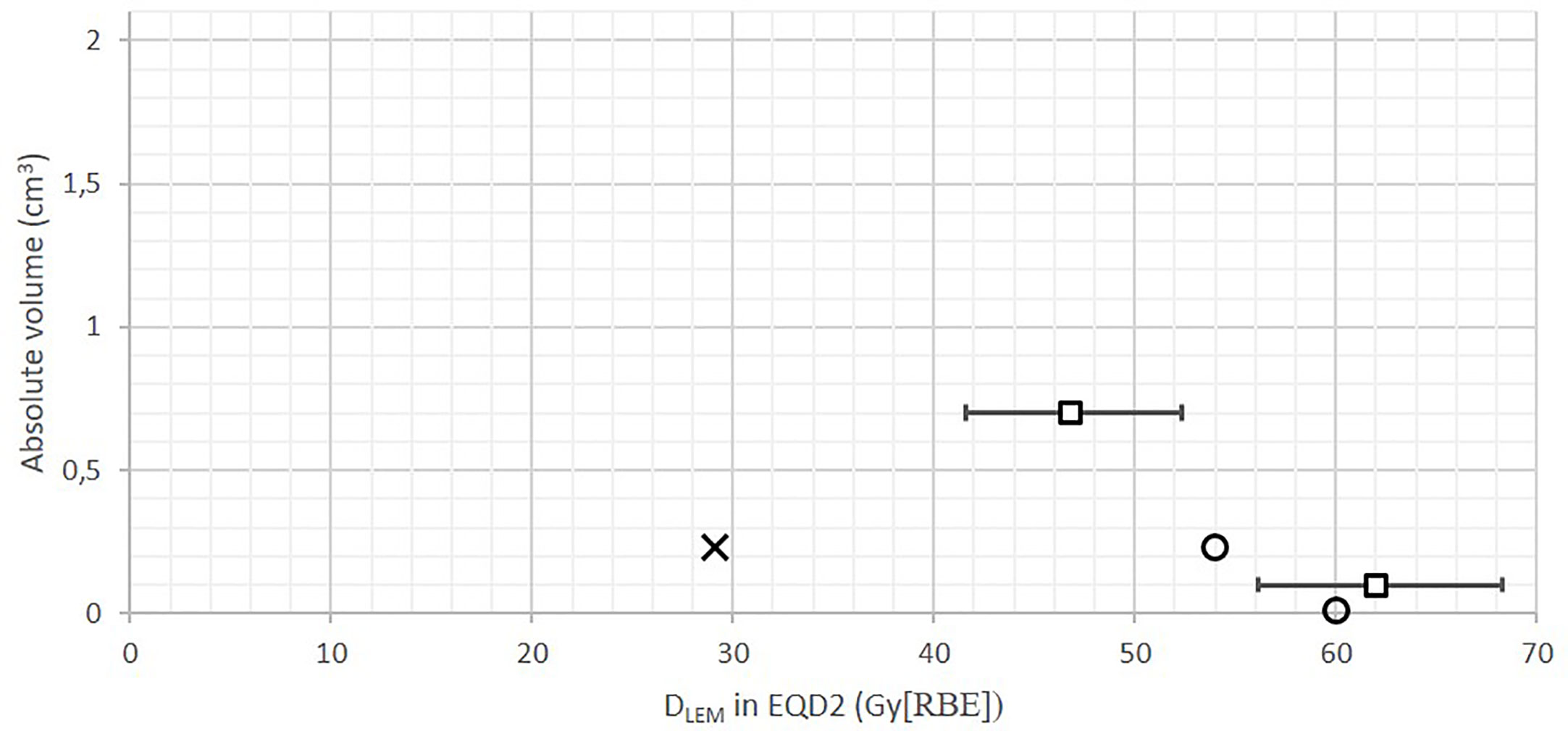
Figure 5 Absolute volume DVH showing old CNAO DLEM I|1% <30 Gy (RBE) constraint (cross) and the translated Shirai constraints DLEM I|0.7 cm3 <41 Gy (RBE) and DLEM I|0.1 cm3 <49 Gy (RBE) (squares, error bars = 95% CI), converted into EQD2 (assuming α/β ratio = 2 Gy) in comparison with the EQD2 constraints applied at HIT as reported by Nikoghosyan et al. (21): DLEM I|1% <54 Gy (RBE) and DLEM I|max <60 Gy (RBE) (circles). As an approximation to the absolute volume relating to the D1% constraints, the median brainstem volume in our data set (26 cm3) was used. The translated constraints are more closely related to the constraints used at HIT than the old CNAO constraint.
In 2010, as part of the Quantitative Analysis of Normal Tissue Effects in the Clinic (QUANTEC) effort, brainstem constraints and tolerance doses following photon and proton RT were summarized in Figure 1 in the organ-specific paper by Mayo et al. (26). Making use of the LQ model, tolerance doses from either normofractionated treatments or single fractionation stereotactic treatments were extrapolated to provide an approximation for the tolerance dose for hypofractionated treatments. The figure is reused in Figure 6 of this paper, in which the DLEM I|0.1 cm3 constraint we derived from this work has been superimposed as a red circle. Clearly, our constraint complies with the projections of the LQ model, supporting the capacity of the LEM I to predict the RBE of CIRT for this endpoint with sufficient accuracy.
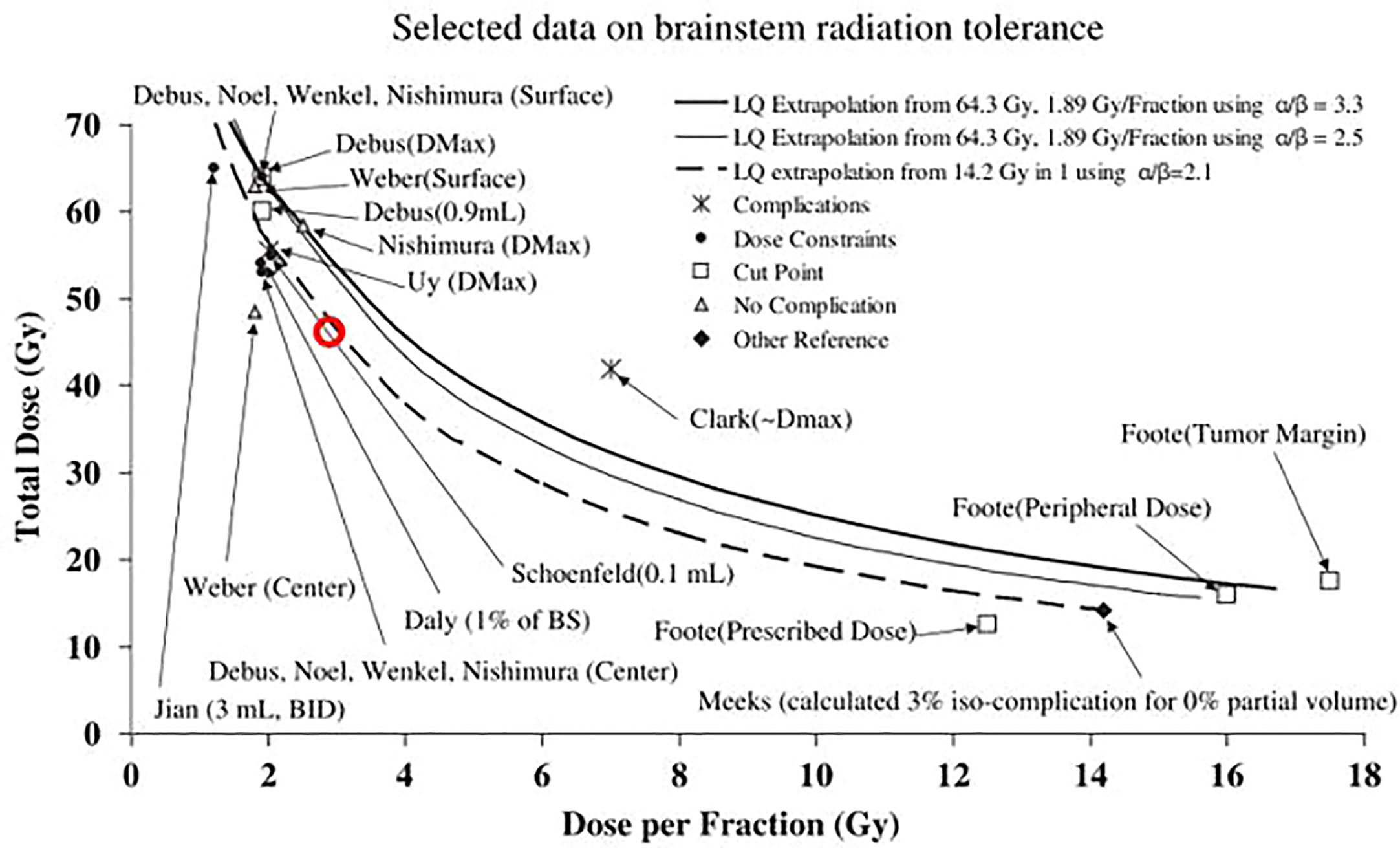
Figure 6 Figure 1 from Mayo et al. (23) reprinted with permission, comparing selected data on brainstem tolerance and dose constraints from stereotactic RT or normofractionated photon or proton RT, compared with the linear quadratic (LQ) model extrapolations. Data points are marked with the corresponding author and dose parameter considered in parenthesis. The DLEM I|0.1 cm3 <46 Gy (RBE) constraint for a 16-fraction LEM I-optimized CIRT, estimated by dose translation of the corresponding DMKM constraint is superimposed as a red circle on the original figure.
An advantage of our dose translation approach is that the fractionation regimen at GHMC is similar to that of CNAO, and therefore the uncertainty related to EQD2 conversion can be avoided. Furthermore, both GHMC and CNAO have adopted the traditions of NIRS, in regard to the choice of beam number, angles, and strategies to achieve a robust treatment plan. Lastly, both centers are restricted to the use of fixed beam lines, which inevitably restricts the freedom of beam angles and consequently favors harmonization of the treatments at the two centers additionally.
However, our method is affected by unavoidable uncertainties. Firstly, transferring dose constraints from a center with passive scattering beam delivery (PS) to a center with pencil beam scanning (PBS) may be controversial. The beam delivery techniques will inevitably cause differences in the radiation quality (mixture of primary and secondary particles and their corresponding LET values) of the beams, and the distribution and weighting of Bragg peaks may be very dissimilar. However, two studies have confirmed that the biological effect of the carbon ion beams of NIRS, HIT, and CNAO are identical (27, 28).
Secondly, the DAbs underlying the RBE-weighted dose is calculated by different beam models at the two institutions. It has been shown that the DAbs of a given RBE-weighted dose could on average vary about 2.5% in the target region of head and neck treatments, depending on the beam model (9). Differences related to beam modeling in the out-of-target areas have not been investigated, but one would expect to find more profound deviations in DAbs especially within the lateral penumbra dose fall-off. This region is certainly sensitive to how the lateral spread of the beam is modeled. This is of importance, since the sharp lateral penumbra of the carbon ion beam typically is utilized to avoid high doses to the brainstem when it is located close to the tumor.
To conclude, these latter issues infer that the DMKM that we reproduce in this work, based on the DAbs of CNAO DLEM I-optimized treatment plans, are not an exact replica of GHMC treatment plans. Nevertheless, our dose translation approach definitely provides guidance as to how much the DLEM I constraints at CNAO may be relaxed in order to match the Japanese constraints. As a measure of caution, we propose the lower bound of the 95% CI of the dose translation estimates, i.e., DLEM I|0.7 cm3 <38 Gy (RBE) and DLEM I|0.1 cm3 <46 Gy (RBE), as possible brainstem constraints for LEM I-optimized CIRT in a 16-fraction schedule. These proposed constraint values imply DLEM I/DMKM conversion factors of 1.27 and 1.15 for DMKM fraction doses of 1.88 Gy (RBE) and 2.5 Gy (RBE) respectively, which is quite modest compared with the target dose conversion factors found by Steinsträter et al. (29), where conversion factors for the respective fraction doses were found to be >1.44 and >1.21.
Finally, as our conclusions rely on the results of Shirai et al., the limitations described in their study also apply to our work (small number of events, single institution study, etc.). Another essential assumption for the application of these constraints is that asymptomatic MRI contrast enhancement does not necessarily evolve into necrosis and therefore constraints that safeguard against this event most certainly will prevent the more meaningful clinical endpoint. Mere contrast enhancement is regarded as evidence of increased permeability of the blood-brain barrier (BBB), which results from radiation-induced alterations in endothelial and glial cell function (30). However, increased permeability does not necessarily lead to parenchymal damage as demonstrated for the spinal cord in a rat model (31). This phenomenon has also been documented for radiation-induced injury of the brain following CIRT, and it is hypothesized that since smaller volumes of CNS tissue is irradiated by particle therapy in comparison with photon RT, the probability of recovery will be higher (32). The observation that the lesions reported by Shirai et al. were reversible or stable in the absence of therapeutic intervention further supports the argument that no real necrosis had occurred.
In this setting, applying the CTCAE term CNS necrosis grade 1 when only contrast enhancement is evident, as done by Shirai et al., may be confusing and potentially discourage physicians from referring patients to CIRT. However, the CTCAE lacks a proper predefined term to discriminate increased permeability in the BBB from a necrotic process. Moreover, neither the SOMA-LENT scale (subterm MRI in the Analytic scale) (33) nor the RTOG/EORTC Late Morbidity Scoring Schema (subterm Brain) (34) exhibit sufficient granularity to encompass this distinction. We therefore suggest to apply the CTCAE term Nervous system disorders—Other, and specifying it as Brainstem reaction as an analogy to the Temporal lobe reaction term coined by Gilman et al. (35), in which contrast enhancement would be a grade 1 “reaction,” thus avoiding the use of the misleading and more distressing term “necrosis.”
Based on this work, these new constraints, DLEM I|0.7 cm3 <38 Gy (RBE) and DLEM I|0.1 cm3 <46 Gy (RBE), have been implemented in the prospective treatment protocols of CNAO since October 2018. They can serve as constraints also for other centers applying LEM I within CIRT schedules of 16 fractions. Indeed, these constraints have also been selected as the most optimal constraints available and have therefore recently been implemented in clinical practice at the MedAustron Ion Therapy Center (Wiener-Neustadt, Austria) for 16 fractions of CIRT treatment of skull base tumors optimized with LEM I.
This paper highlights a challenge that is unique for CIRT compared with other external beam RT modalities: the exchange of experience between Japanese and European CIRT facilities is severely hampered by the use of disparate RBE models. Fortunately, we anticipate that the recalculation of treatment plans to the alternative RBE model will become substantially less time consuming due to the introduction of such functionality in commercial TPSs. We therefore hope to see future CIRT publications reporting OAR toxicity, NTCP, and related dose metrics in both DMKM and DLEM I, as our group recently has done for the optic nerve (36). This would accelerate the much needed validation of OAR constraints for both RBE models.
The datasets generated for this study are available on request to the corresponding author.
The patients analyzed in the study cannot be identified as all the research has been conducted with anonymized data. All patients enrolled in the clinical trials at CNAO gave their free informed consent to the treatment and the use of their anonymized data for research purposes. The anonymized patient data used for this study originated from the clinical trials “CNAO S9/2012/C”, “CNAO S12/2012/C” and “CNAO S15/2012/C” approved by the CNAO Ethics Committee.
The manuscript was mainly authored by JD with support from PF, SM, OD, TO, and BV. JD performed data analysis. Clinical treatment plans were optimized by medical physicists SM, GM, and AM with FV, MB, VV, BV, and PF as the responsible radiation oncologists. Clinical data were collected by VV, MB, BV, AH, and PF. JD, SM, and GM performed the recalculation of all treatment plans. FV, VV, and BV are responsible for the treatment protocols and analyzed patient follow-up together with MB and PF. JD, SM, OD, AM, TO, AH, and PF contributed to the development of the study methodology. All authors critically reviewed the manuscript. All authors contributed to the article and approved the submitted version.
This work was supported by grants (grant no: BFS2015PAR02) from the Trond Mohn Foundation, Ytrebygdsvegen 215, Kokstad, Postboks 7150, 5020 BERGEN, Norway, tlf: +47 479 00 111, org.nr: 988 029 327.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Kanai T, Endo M, Minohara S, Miyahara N, Koyama-ito H, Tomura H, et al. Biophysical characteristics of HIMAC clinical irradiation system for heavy-ion radiation therapy. Int J Radiat Oncol Biol Phys (1999) 44(1):201–10. doi: 10.1016/S0360-3016(98)00544-6
2. Inaniwa T, Kanematsu N, Matsufuji N, Kanai T, Shirai T, Noda K, et al. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the National Institute of Radiological Sciences, Japan. Phys Med Biol (2015) 60(8):3271–86. doi: 10.1088/0031-9155/60/8/3271
3. Hawkins RB. A Microdosimetric-Kinetic Model for the Effect of Non-Poisson Distribution of Lethal Lesions on the Variation of RBE with LET. J Radiat Res (2003) 160(1):61–69, 9. doi: 10.1667/RR3010
4. Hawkins RB. A microdosimetric-kinetic model of cell death from exposure to ionizing radiation of any LET, with experimental and clinical applications. Int J Radiat Biol (1996) 69(6):739–55. doi: 10.1080/095530096145481
5. Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res (1994) 140(3):366–74. doi: 10.2307/3579114
6. Scholz M, Kellerer MA, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy. Radiat Environ Biophys (1997) 36(1):59–66. doi: 10.1007/s004110050055
7. Kramer M, Scholz M. Treatment planning for heavy-ion radiotherapy: calculation and optimization of biologically effective dose. Phys Med Biol (2000) 45(11):3319–30. doi: 10.1088/0031-9155/45/11/314
8. Rossi S. The National Centre for Oncological Hadrontherapy (CNAO): Status and perspectives. Phys Med (2015) 31(4):333–51. doi: 10.1016/j.ejmp.2015.03.001
9. Molinelli S, Magro G, Mairani A, Matsufuji N, Kanematsu N, Inaniwa T, et al. Dose prescription in carbon ion radiotherapy: How to compare two different RBE-weighted dose calculation systems. Radiother Oncol (2016) 120(2):307–12. doi: 10.1016/j.radonc.2016.05.031
10. Fossati P, Molinelli S, Matsufuji N, Ciocca M, Mirandola A, Mairani A, et al. Dose prescription in carbon ion radiotherapy: a planning study to compare NIRS and LEM approaches with a clinically-oriented strategy. Phys Med Biol (2012) 57(22):7543–54. doi: 10.1088/0031-9155/57/22/7543
11. Magro G, Dahle T, Molinelli S, Ciocca M, Fossati P, Ferrari A, et al. The FLUKA Monte Carlo code coupled with the NIRS approach for clinical dose calculations in carbon ion therapy. Phys Med Biol (2017) 62(9):3814–27. doi: 10.1088/1361-6560/aa642b
12. Koto M, Hasegawa A, Takagi R, Sasahara G, Ikawa H, Mizoe JE, et al. Feasibility of carbon ion radiotherapy for locally advanced sinonasal adenocarcinoma. Radiother Oncol (2014) 113(1):60–5. doi: 10.1016/j.radonc.2014.09.009
13. Ohno T, Kanai T, Yamada S, Yusa K, Tashiro M, Shimada H, et al. Carbon Ion Radiotherapy at the Gunma University Heavy Ion Medical Center: New Facility Set-up. Cancers (2011) 3(4):4046–60. doi: 10.3390/cancers3044046
14. Shirai K, Fukata K, Adachi A, Saitoh JI, Musha A, Abe T, et al. Dose-volume histogram analysis of brainstem necrosis in head and neck tumors treated using carbon-ion radiotherapy. Radiother Oncol (2017) 125(1):36–40. doi: 10.1016/j.radonc.2017.08.014
15. Lyman JT. Complication probability as assessed from dose-volume histograms. Radiat Res Suppl (1985) 8:S13–9. doi: 10.2307/3583506
16. Burman C, Kutcher GJ, Emami B, Goitein M. Fitting of normal tissue tolerance data to an analytic function. Int J Radiat Oncol Biol Phys (1991) 21(1):123–35. doi: 10.1016/0360-3016(91)90172-Z
17. Niemierko A. Reporting and analyzing dose distributions: a concept of equivalent uniform dose. Med Phys (1997) 24(1):103–10. doi: 10.1118/1.598063
18. Wieser H-P, Cisternas E, Wahl N, Ulrich S, Stadler A, Mescher H, et al. Development of the open-source dose calculation and optimization toolkit matRad. Med Phys (2017) 44(6):2556–68. doi: 10.1002/mp.12251
19. Iannalfi A, D’Ippolito E, Riva G, Molinelli S, Gandini S, Viselner G, et al. Proton and carbon ions radiotherapy in skull base chordomas: a prospective study based on a dual particle and a patient-customized treatment strategy. Neuro Oncol (2020) 22(9):1348–58. doi: 10.1093/neuonc/noaa067
20. Takagi M, Demizu Y, Nagano F, Terashima K, Fujii O, Jin D, et al. Treatment outcomes of proton or carbon ion therapy for skull base chordoma: a retrospective study. Radiat Oncol (2018) 13(1):232. doi: 10.1186/s13014-018-1173-0
21. Koto M, Ikawa H, Kaneko T, Hagiwara Y, Hayashi K, Tsuji H, et al. Long-term outcomes of skull base chordoma treated with high-dose carbon-ion radiotherapy. Head Neck (2020) 42(9):2607–13. doi: 10.1002/hed.26307
22. Lambrecht M, Eekers DBP, Alapetite C, Burnet NG, Calugaru V, Coremans IEM, et al. Radiation dose constraints for organs at risk in neuro-oncology; the European Particle Therapy Network consensus. Radiother Oncol (2018) 128(1):26–36. doi: 10.1016/j.radonc.2018.05.001
23. Nikoghosyan AV, Karapanagiotou-Schenkel I, Munter MW, Jensen AD, Combs SE, Debus J, et al. Randomised trial of proton vs. carbon ion radiation therapy in patients with chordoma of the skull base, clinical phase III study HIT-1-Study. BMC Cancer (2010) 10:607. doi: 10.1186/1471-2407-10-606
24. Schulz-Ertner D, Karger CP, Feuerhake A, Nikoghosyan A, Combs SE, Jakel O, et al. Effectiveness of carbon ion radiotherapy in the treatment of skull-base chordomas. Int J Radiat Oncol Biol Phys (2007) 68(2):449–57. doi: 10.1016/j.ijrobp.2006.12.059
25. Uhl M, Mattke M, Welzel T, Oelmann J, Habl G, Jensen AD, et al. High control rate in patients with chondrosarcoma of the skull base after carbon ion therapy: first report of long-term results. Cancer (2014) 120(10):1579–85. doi: 10.1002/cncr.28606
26. Mayo C, Yorke E, Merchant TE. Radiation associated brainstem injury. Int J Radiat Oncol Biol Phys (2010) 76(3 Suppl):S36–41. doi: 10.1016/j.ijrobp.2009.08.078
27. Uzawa A, Ando K, Koike S, Furusawa Y, Matsumoto Y, Takai N, et al. Comparison of biological effectiveness of carbon-ion beams in Japan and Germany. Int J Radiat Oncol Biol Phys (2009) 73(5):1545–51. doi: 10.1016/j.ijrobp.2008.12.021
28. Facoetti A, Vischioni B, Ciocca M, Ferrarini M, Furusawa Y, Mairani A, et al. In vivo radiobiological assessment of the new clinical carbon ion beams at CNAO. Radiat Prot Dosimetry (2015) 166(1-4):379–82. doi: 10.1093/rpd/ncv145
29. Steinstrater O, Grun R, Scholz U, Friedrich T, Durante M, Scholz M, et al. Mapping of RBE-weighted doses between HIMAC- and LEM-Based treatment planning systems for carbon ion therapy. Int J Radiat Oncol Biol Phys (2012) 84(3):854–60. doi: 10.1016/j.ijrobp.2012.01.038
30. Yuan H, Gaber MW, Boyd K, Wilson CM, Kiani MF, Merchant TE, et al. Effects of fractionated radiation on the brain vasculature in a murine model: blood-brain barrier permeability, astrocyte proliferation, and ultrastructural changes. Int J Radiat Oncol Biol Phys (2006) 66(3):860–6. doi: 10.1016/j.ijrobp.2006.06.043
31. Siegal T, Pfeffer MR. Radiation-induced changes in the profile of spinal cord serotonin, prostaglandin synthesis, and vascular permeability. Int J Radiat Oncol Biol Phys (1995) 31(1):57–64. doi: 10.1016/0360-3016(94)E0305-4
32. Kishimoto R, Mizoe JE, Komatsu S, Kandatsu S, Obata T, Tsujii H, et al. MR imaging of brain injury induced by carbon ion radiotherapy for head and neck tumors. Magn Reson Med Sci (2005) 4(4):159–64. doi: 10.2463/mrms.4.159
34. Cox JD, Stetz J, Pajak TF. Toxicity criteria of the Radiation Therapy Oncology Group (RTOG) and the European Organization for Research and Treatment of Cancer (EORTC). Int J Radiat Oncol Biol Phys 1995 31(5):1341–6.
35. Gillmann C, Lomax AJ, Weber DC, Jakel O, Karger CP. Dose-response curves for MRI-detected radiation-induced temporal lobe reactions in patients after proton and carbon ion therapy: Does the same RBE-weighted dose lead to the same biological effect? Radiother Oncol (2018) 128(1):109–14. doi: 10.1016/j.radonc.2018.01.018
Keywords: carbon ion radiotherapy, normal tissue complication probability, dose constraints, local effect model, microdosimetric kinetic model, relative biological effectiveness (RBE), brainstem tolerance
Citation: Dale JE, Molinelli S, Vischioni B, Vitolo V, Bonora M, Magro G, Mairani A, Hasegawa A, Ohno T, Dahl O, Valvo F and Fossati P (2020) Brainstem NTCP and Dose Constraints for Carbon Ion RT—Application and Translation From Japanese to European RBE-Weighted Dose. Front. Oncol. 10:531344. doi: 10.3389/fonc.2020.531344
Received: 31 January 2020; Accepted: 04 September 2020;
Published: 24 November 2020.
Edited by:
Ester Orlandi, Instituto Nazionale dei Tumori (IRCSS), ItalyReviewed by:
Naruhiro Matsufuji, National Institutes for Quantum and Radiological Science and Technology, JapanCopyright © 2020 Dale, Molinelli, Vischioni, Vitolo, Bonora, Magro, Mairani, Hasegawa, Ohno, Dahl, Valvo and Fossati. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Barbara Vischioni, YmFyYmFyYS52aXNjaGlvbmlAY25hby5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.