
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Nucl. Eng., 26 July 2024
Sec. Nuclear Materials
Volume 3 - 2024 | https://doi.org/10.3389/fnuen.2024.1341754
This article is part of the Research TopicWomen in Nuclear Engineering ResearchView all 15 articles
 Emily De Stefanis1*
Emily De Stefanis1* Kemal Ramic2
Kemal Ramic2 Judith Vidal3
Judith Vidal3 Youyang Zhao3
Youyang Zhao3 Leighanne C. Gallington4
Leighanne C. Gallington4 Ryan Bedell1
Ryan Bedell1 Li (Emily) Liu1*
Li (Emily) Liu1*Ionic liquid materials are viable candidates as a heat transfer fluid (HTF) in a wide range of applications, notably within concentrated solar power (CSP) technology and molten salt reactors (MSRs). For next-generation CSP and MSR technologies that strive for higher power generation efficiency, a HTF with wide liquid phase range and energy storage capabilities is crucial. Studies have shown that eutectic chloride salts exhibit thermal stability at high temperatures, high heat storage capacity, and are less expensive than nitrate and carbonate salts. However, the experimental data needed to fully evaluate the potential of eutectic chloride salts as a HTF contender are scarce and entail large uncertainties. Considering the high cost and potential hazards associated with the experimental methods used to determine the properties of ionic liquids, molecular modeling can be used as a viable alternative resource. In this study, the eutectic ternary chloride salt MgCl2–NaCl–KCl is modeled using ab-initio molecular dynamics simulations (AIMDs) in the liquid phase. Using the simulated data, the thermophysical and transport properties of eutectic chloride salt can be calculated: density, viscosity, heat capacity, diffusion coefficient, and ionic conductivity. For an initial model validation, experimental pair-distribution function data were obtained from X-ray total scattering techniques and compared to the theoretical pair-distribution function. Additionally, theoretical viscosity values are compared to experimental viscosity values for a similar system. The results provide a starting foundation for a MgCl2–NaCl–KCl model that can be extended to predict other fundamental properties.
Next-generation technologies that require high operating temperatures to achieve a higher efficiency of power generation need a heat transfer fluid (HTF) that has high thermal stability, high heat storage capabilities, and is available in large quantities for the foreseeable future. The goal of a higher efficiency power generation method is needed due to the growing demand for energy. In order to decrease the reliance of power generation on the combustion of fossil fuels, the development of capable clean power technologies is crucial. Next-generation concentrated solar power (CSP) plants combined with thermal energy storage (TES) utilize a sCO2-Brayton power cycle instead of the traditional steam-Rankin power cycle (González-Roubaud et al., 2017). Due to the higher operating temperature of the sCO2-Brayton cycle, traditional nitrate salts, such as Hitec, used for the steam-Rankine cycle cannot be used due to the low temperature of the liquid phase of 130 °C–550 °C (Fernandez et al., 2015; Mehos, et al., 2017). Two candidate upgrades from nitrate salts are carbonate and chloride salts. Both these salts have reliable thermal stability at high temperatures and a wide liquid phase range, but carbonate salts are more expensive than chloride salts (Ding et al., 2019).
Myers Jr and Goswami (2016) analyzed 133 chloride salt systems, showing that NaCl and MgCl2 are the best choices for high-temperature heat transfer and storage applications. The melting points of the separate ionic compounds NaCl, MgCl2, and KCl are very high at 801°C, 714 °C, and 770 °C, respectively (Parker et al., 2022). Eutectic salt mixtures utilize the advantage of a lower melting point. MgCl2–NaCl–KCl is a potential candidate for generation-3 CSP technology due to its lower melting point (≈400°C), wide liquid range, and reliable thermal stability (Xu et al., 2018). However, the available thermophysical data on this eutectic chloride system is scarce and contains large uncertainties. An alternative route to studying the physical chemistry of molten salts is molecular dynamics simulations.
From fundamental studies on local structure to investigations into thermodynamic and kinetic properties, recent research on molten salts has demonstrated that molecular dynamics (MD) simulations are a valuable alternative. MD simulations, classical and ab-initio (or first principles), are used to study and calculate the properties of molten salt systems. Classical MD simulations (CMDs) are based on the principle of statistical mechanics, describing the forces on each atom with an interatomic potential/force field. From a quantum mechanical perspective, ab-initio MD simulations (AIMDs) solve the interatomic forces using the instantaneous positions of the atoms. Due to the complexity of molten salt systems, CMD has questionable accuracy because the existing interatomic potentials do not fully capture the complex nature of the ionic liquid. AIMDs enjoy higher accuracy than CMD because the interatomic forces are calculated to solve Newton’s equations of motion, which substitute the need for interatomic potentials/force fields (Marx and Hutter, 2000).
Before the research of Car and Parrinello (1985) on AIMDs, salt systems were simulated using CMDs based on interatomic potentials such as the Born–Mayer–Huggins–Tosi–Fumi (BMHTF) rigid ion interionic potential and the Buckingham pair potential. The development of the BMHTF potential approximation introduced new insights into the physical chemistry of alkali halides. The approximation estimates the potential energy of the system as a summation of all the interactions between all ion pairs. Early studies of simulated NaCl-type solid alkali halides used a variation of the BMHTF rigid-ion potential (Fumi and Tosi, 1964). However, this methodology cannot be accurately replicated for single salt ionic liquid systems due to the absence of many-body and long-range interactions that are essential for predicting the transport phenomena of ionic liquids, such as ionic conductivity (Salanne and Madden, 2011). Galamba and Costa Cabral (2007) confirmed this theory by comparing the results of a molten NaCl system that was simulated with both classical and first principles molecular dynamics. This study used the force-autocorrelation functions as a comparison to provide insight into the dependency of polarization effects. Using the basis of first-principles calculations with density functional theory (DFT), Ohtoriet al. (2015) parameterized a polarizable ion model (PIM) for single salt systems: NaCl and KCl. Their results show good agreement with the salt’s experimental values of transport properties. However, this contradicted DeFever et al. (2020), who found that the PIM potentials could not produce accurate melting points for different alkali chlorides, such as NaCl and KCl. Furthermore, Zhou et al. (2022) simulated the ternary chloride salt MgCl2–NaCl–KCl using a PIM and showed, in comparison with experimental results, the accuracy of the calculation for multi-component systems. The system they studied has the same components as our eutectic chloride salt but with different concentrations While Zhou et al. (2022) showed hope for the PIM, unresolved contradictions persist among the available studies that have yet to be reconciled.
The evident constraints of CMDs and PIM have prompted a shift towards the simulation of molten salt systems with AIMDs. The methodology of this study was influenced by the findings in studies using AIMDs to simulate similar chloride molten salt systems. Liang et al. (2020) simulated molten MgCl2 using first-principles molecular dynamics simulation (FPMDs) and showed agreement between the theoretical model and experimental data regarding the thermo-kinetic and structural properties. In another study, they used FPMDs to demonstrate the effect of the dispersion correction term and the concentration on the prediction of thermo-kinetic properties. Other candidates for the heat transfer fluid of a CSP plant, NaCl–CaCl2 and NaCl–CaCl2–MgCl2, were simulated by Rong et al. (2020; 2021), who investigated the thermophysical and structural properties using AMIDs. They concluded that thermophysical properties decrease with increasing temperature by observing the weakened bonding interactions. Rising temperature weakens the bonding interactions which increases the distance between the ion pairs as a result of volume expansion, thus revealing that the large ion clusters are divided into smaller dispersed clusters. It is worth noting that they used Car–Parrinello dynamics with CPMD computational software package. Furthermore, this research utilizing AIMDs to model similar chloride molten salt systems have lain the groundwork for the methodology explored in this study.
The present study utilizes the Vienna ab-initio simulation package (VASP). Previous work simulated eutectic salt systems similar to the present study to predict thermo-kinetic properties such as NaCl–MgCl2 (Xu et al., 2020; Duemmler et al., 2022), MgCl2–KCl (Xu, et al., 2021), and NaCl–KCl–MgCl2 (Li, 2020) at different compositions than ours. These studies have shown the applicability of AIMD simulations for molten salt systems. However, because the interactions between the ions are calculated at every step, AIMD is computationally expensive, resulting in limits to the simulation system size and total simulation time. Bengtson et al. (2014) showed in a convergence study with a simulated LiCl–KCl molten salt system that the properties of the system with 64 atoms were consistent with a 1,000 atom system. They also showed that a minimal simulation time of 6–12 picoseconds (ps) is enough for statistical physical analysis. Duemmler et al. (2023) disputed these claims, arguing that the minimum total simulation time needed to calculate thermo-kinetic or thermophysical properties is 300 ps. Their results underestimated the diffusion coefficient compared to experimental values reported by Janz and Bansal (1982), as did the results published by Bengtson et al. (2014), but were closer to the experimental values. Duemmler et al. (2023) claimed that the results of Bengtson et al. (2014) “…overpredicted […] the actual DFT-predicted diffusion coefficient, which led their results to be more accurate compared to experiment,” thus concluding that their methodology was more accurate, robust, and thorough than those of Janz and Bansal (1982). These studies have shown that AIMDs are a reliable alternative resource for studying chloride molten salt systems.
The aim of this research is to investigate the applicability of first principles AIMD simulations to predict the transport and thermophysical properties of eutectic chloride salt in the liquid phase range. Its data consists entirely of unpublished results and will be used to improve the future model. This research attempts to fill gaps in the fundamental understanding and vital literature needed to access the compatibility of an ionic liquid as a heat transfer fluid.
The implications of the findings of this study extend beyond the realm of fundamental research into the practical applications of next-generation CSP and MSR technologies. As highlighted previously, the demand for high-efficiency power generation methods necessitates HTFs with specific characteristics such as high thermal stability and heat storage capabilities. By leveraging AIMDs, this study contributes to ongoing efforts to accurately understand and predict the behavior of molten salt systems. The application of AIMDs in predicting these properties offers a cost-effective and less hazardous alternative to traditional experimental methods.
First-principles AIMD simulations were performed using the Vienna Ab-Initio Simulation Package (VASP) based on density functional theory (DFT) and the Born–Oppenheimer approximation with periodic boundary conditions (Vosko et al., 1980; Kresse and Hafner, 1993; Kresse and Hafner, 1994; Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). The interactions between electrons and nucleus are defined by the projector augmented wave (PAW) method, and the revised Perdew–Burke–Ernzerhof (rPBE) DFT of the generalized gradient approximation (GGA) is used for the electron exchange-correlation. The kinetic energy cutoff is 400 eV, and the system has a 1 × 1 × 1 k-point mesh. The timestep chosen is two femtoseconds (fs) to avoid energy drift. Fermi smearing with a smearing parameter of 0.2 eV was used for the partial occupancies of the wave function (Grimme, 2006a; Grimme et al., 2011; Hacene, et al., 2012; Hutchinson and Widom, 2012).
In this research, the molten salt system under investigation is a ternary chloride salt MgCl2–NaCl–KCl, 44.8 mol% MgCl2–29.4 mol% NaCl–25.8 mol% KCl, provided by NREL. Based on the experimental compositions, two systems were generated and used in this study: 142-atom (26 Mg2+, 17 Na+, 15 K+, 84 Cl-, 58 cations and 84 anions) (Grimme et al., 2010) and 83-atom (15 Mg2+, 10 Na+, 9 K+, 49 Cl-, 34 cations and 49 anions). The following were regarded as the valence electrons: Mg2+ 3s2, Na+ 2s22p63s1, K+ 3s23p64s1, and Cl 3s23p5. The 83-atom system was used for the initial evaluation of the dispersion forces. Both systems were used to predict the structure and properties of the ternary salt.
The starting configuration file of the two systems was generated using PACKMOL, which calculated the initial geometries of the system by randomly packing atoms into a given volume based on the experimental composition and density at a specified temperature (Martínez et al., 2009). The cell sizes for the 83-atom system ranged 13.75–14.20 Å; the cell sizes for the 142-atom system ranged 16–17 Å. Before these initial configuration files could be used for AIMD simulations, the system needed to be pre-equilibrated with classical interatomic potential molecular dynamic (IPMD) simulations. These were performed with a Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) and utilized the Born–Mayer–Huggins potentials for each component of our system (Mayer, 1933; Fumi and Tosi, 1964; Tosi and Fumi, 1964; Thompson, et al., 2022). Even though there were limitations with the force field potentials for complex ternary salts, the accuracy of the pre-equilibration stage was not essential. The pre-equilibration IPMD simulation used an NVT ensemble at the specified temperature for 5 ps to lose the memory of the initial configuration from PACKMOL (Martínez et al., 2009). This method of pre-equilibration using IPMD followed Bengtson et al. (2014) and Nam, et al. (2014) The final configuration of the IPMD simulation was used for the following AIMD simulations. With the final configuration of the system from the IPMD simulation, the configuration underwent another step of equilibration using an isobaric–isothermal (NPT) ensemble for total simulation time (Steinmann and Corminboeuf, 2011). A generalized-gradient approximation exchange hole model was used for dispersion coefficients of approximately 100 ps at the respective temperature with a timestep of 1 fs and pressure of 1 atm. The NPT ensemble used the Langevin thermostat with a temperature coefficient set to 10 ps−1. The goal of the NPT equilibration was to evaluate the density and energy of the system. The configuration used for the next simulation was selected from the trajectory of the NPT equilibration simulation. This configuration was selected from a timestep where the density of the system was approximately its average density from the overall simulation. With this selected configuration file, the system underwent an NVT ensemble using a Nosè thermostat for 100 ps with a timestep of 2fs, referred to as the “production run”. The production runs from each temperature were used to estimate the thermodynamic properties at that temperature. The first 5 ps from the production run were neglected from the analysis and served as further equilibration. The simulated temperatures for both the 83-atom and 142-atom systems are 723 K, 773 K, 823 K, 873 K, 923 K, and 973 K.
Properties were predicted using the trajectories from the production runs at the respective temperature. Each trajectory had a total simulation time of approximately 100 ps, used an NVT ensemble, and then was analyzed using MDANSE (Goret, 2017). The results given in Section 3.1 were simulated with an NPT ensemble while those in Section 3.2 were simulated with an NVT ensemble—the production runs.
The diffusion coefficient was calculated using Einstein’s equation, which states that the self-diffusion coefficient is evaluated from the slope of the mean-squared displacement (MSD) (Einstein, 1905). The MSD is a statistical analysis of the particle trajectory in the simulation and was calculated using MDANSE (Eq. 1). The diffusion coefficient was calculated from the MSD (Eq. 2).
Ionic conductivity was calculated for each ion with Nernst–Einstein approximation (Eq. 3). It is a scalar quantity of the diffusion coefficient (Bockris and Reddy, 1998).
where q is the charge of the ion, n is the unit volume concentration of carrier ions, D is the diffusion coefficient for the respective ion, kB is the Boltzmann constant, and T is the temperature.
Viscosity was calculated using the Einstein–Stokes approximation (Eq. 4) (Zwanzig, 1983; Alonso & March, 1999).
where λ is the effective atomic diameter, kB is the Boltzmann constant, T is the temperature, and D is the diffusion coefficient. The effective atomic diameter is determined by the radius at which the first peak appears—the radial distribution function (RDF) of the system, calculated using MDANSE.
Heat capacity was calculated at each temperature using Einstein’s model for heat capacity of an oscillator modulated by the phonon spectrum (Eq. 5 ).
This equation is solved using the vibrational density of states (VDOS) of the system, which are calculated from MDANSE. The equation used to calculate heat capacity is shown as Eq. 6:
The density of the salt in the molten phase was measured with a density meter employing Archimedes’ principle of buoyancy. This meter utilizes the weight of an object, such as high purity nickel cylinder, and a quartz container, which holds the molten salt. The measurement relies on measuring the object’s mass before and after submerging in the molten salt. The scale used had a full capacity of 50 g and an uncertainty of ±0.1%. Utilizing the disparity in the mass between the object in air and submerged in molten salt, the density of the molten salt across various temperatures is calculated using Eq. 7:
where
For comparison and validation of our AIMD simulation results, X-ray total scattering techniques are utilized to investigate the atomic structure of a material system by collecting Bragg, diffuse, and inelastic scattering. The diffraction pattern of a system is obtained from the scattering pattern. In total scattering studies, the pair distribution function (PDF) is obtained by performing a Fourier transformation on the system’s scattering pattern. The PDF illustrates the probability of finding interatomic distances between pairs of atoms in a system (Egami and Billinge, 2012). The experimental PDF will be compared to the PDF of the simulated system.
A scattering experiment measures the probability of X-rays scattered at a certain angle and with a certain energy. X-ray scattering experiments collect the static scattering function of a sample,
Here, n is the number density of particles in a sample. The inter-particle structure factor is extracted from the experimental static scattering function data after subtracting the background. This inter-particle structure factor,
Total X-ray scattering data were collected on the 11-ID-B beamline at the Advanced Photon Source at Argonne National Laboratory. (Borkiewicz et al., 2019). The sample container was a 1 mm diameter quartz tube 75% filled with our salt sample. The incident X-ray wavelength was 0.2115 Å. The X-ray scattering measurements were converted to X-ray diffraction patterns with GSAS-II (Toby and Von Dreele, 2013). The diffraction patterns were then converted into experimental PDFs with PDFgetx2 (Qiu, 2004).
The findings of this study help fill the fundamental gaps in the existing literature on molten salt systems, specifically regarding the application of AIMDs in predicting thermophysical and transport properties. By employing AIMDs, this research explores the atomistic behavior of eutectic ternary chloride salt in its liquid phase. The simulated data thus obtained can be used to calculate properties crucial for evaluating the capability of this salt as a HTF, including density, viscosity, heat capacity, diffusion coefficient, and ionic conductivity.
The first simulations were performed using generalized gradient approximation (GGA) exchange-correlation functionals (ecf), such as Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1996), revised PBE (rPBE) (Zhang & Yang, 1998), Becke’s ecf with Lee–Yang–Parr (BLYP) hybrid functional (Vosko et al., 1980; Stephens, Devlin, Chabalowski and Frisch, 1994), and revised PBE for solids (PBEsol) (Perdew et al., 2008). Additionally, a different type of functional was also tested for comparison: Van der Waals density functional (vdW-DF), which consists of a semi-local exchange-correlation functional that is improved with an added term that accounts for dispersion interactions (Dion, Rydberg, Schroder, Langreth and Lundqvist, 2004; Roman-Perez and Soler, 2009; Klimes et al., 2010; Klimes et al., 2011; Zhang & Yang, 1998). Dispersion forces that were tested with the above exchange-correlation functionals are DFT D2 (Grimme, 2006a), DFT D3-0D zero-damping function (Grimme et al., 2010), DFT D3-BJ with Becke–Johnson damping function (Grimme, Antony, Ehrlich, and Krieg, 2010; Grimme et al., 2011), and a density-dependent energy correction DFT dDsC (Steinmann and Corminboeuf, 2011). The different exchange-correlation functionals with and without dispersion correction terms combinations that were tested are listed in Table 1.
Each combination of exchange-correlation functional with or without a dispersion correction term listed in Table 1 was simulated with an 83-atom system using an NPT ensemble for 100 ps at 973 K with a timestep of one femtosecond. The trajectory files were analyzed using Molecular Dynamics Analysis for Neutron Scattering Experiments (MDANSE) software. The density values were calculated from analysis of the trajectory with MDANSE. Table 1 shows the calculated density of the system of each simulated system after the first 5 ps. The standard deviation is calculated from the calculated density after the first 5 ps. Included in Table 1 is the experimental density of the salt at that temperature. The experimental density of this salt system was provided by Dr. Vidal’s group from the National Renewable Energy Laboratory (NREL).
Of the 13 combinations of exchange-correlation functionals with or without dispersion forces, only three fell within 2% of the experimental density: GGA rPBE DFT-dDsC, revPBE-vdW, and PBEsol. However, PBEsol was not tested further because it was optimized for solid materials. When no dispersion correction term is included, the simulations that rely solely on the exchange-correlation functionals (GGA: PBE, rPBE, and BLYP) underestimate the density. Bengtson et al. (2014) concluded that GGA PBE with the semi-empirical DFT-D2 method dispersion correction term provided accurate results for ionic liquid systems, but it overestimated the density of our system. The simulated salt system is LiCl-KCl (Bengtson et al., 2014). The two cases that produced a density data within 1% and were tested further at the lower temperatures in the liquid phase are a) GGA rPBE DFT-dDsC and b) revPBE-vdW. The system was simulated with an NPT ensemble at temperatures of 723 K, 773 K, 823 K, 873 K, and 923 K with a and b exchange-correlation functionals and dispersion force terms. Figure 1 shows the calculated density from these simulated systems using functionals a and b. The data was calculated after the first 5 ps of the simulation. The standard deviation of the simulated density was calculated over 95 ps. The experimental data included in this figure was provided by Dr. Judith Vidal’s group at NREL. The method used to obtain this experimental data is described in Section 2.2.1.
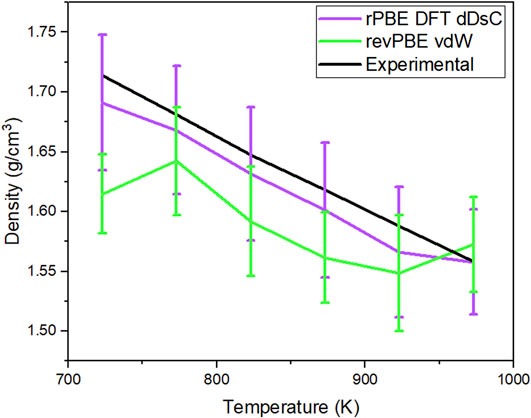
Figure 1. Density comparison of the 83-atom system simulated with GGA rPBE DFT dDsC and revPBE-vdW compared with the experimental density of the salt.
In Figure 1, the calculated density of the simulated system’s a and b are compared to the experimental density of the salt system. For Case A, GGA rPBE DFT dDsC, the timestep for the simulation was 1fs and ran for 100 ps. The error bars for the calculated density are wide enough to be comparable with the experimental density values. For Case B, revPBE-vdW, the timestep of the simulation was 3fs and ran for 40ps. The error bars for some of the temperatures are wide enough to barely be comparable with the experimental density. Cases A and B were run at different timesteps and total simulation times because the computational cost of Case B is much more expensive than A. For example, in the time taken for the calculations GGA rPBE dDsC for 600 timesteps, revPBE-vdW calculates 60 timesteps. Based on the calculated density of the simulated system and considering computational cost, the exchange-correlation functional and dispersion correction term that will be used for the remainder of this research is GGA rPBE DFT-dDsC.
The 83-atom system was used to observe the effect of the total simulation time of the production runs in the calculated properties. Figure 2 show the thermo-kinetic properties of the 83-atom system with a shorter and longer total simulation time of production run. The trajectory simulation time for the shorter simulation was approximately 25 ps, and the longer simulation was approximately 100 ps. For both simulations, the first 5 ps of the production run is neglected in the calculation as the original trajectory length was 5 ps longer. The methods for calculation of the properties are given in Section 2.1.2.
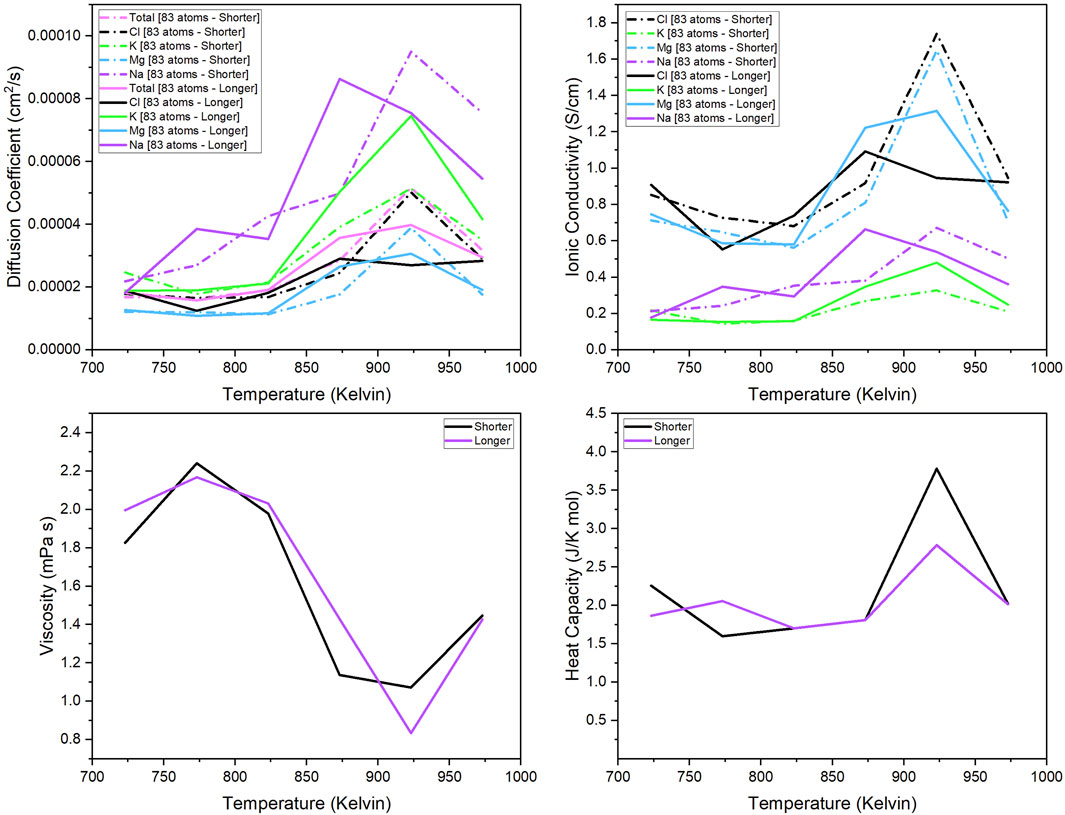
Figure 2. Diffusion coefficient of each component (total, Mg, Na, K, Cl); Ionic conductivity of each separate component (Mg, Na, K, Cl); Viscosity and heat capacity of the 83-atom system simulated at 723 K–973 K.
Figure 2 compare the shorter vs. longer simulation time for the 83-atom system. The properties calculated were the diffusion coefficient of each species (total, Cl, K, Mg, Na) (upper left quadrant), ionic conductivity of each species (Cl, K, Mg, Na) (upper right quadrant), and the viscosity and (4) heat capacity of the system. The results of the properties were predicted for the 83-atom system with a total simulation time of 25 ps (shorter) and 100 ps (longer). The experimental values of these properties for our salt system with the same composition are limited and are not available for comparison. In Figure 2, the calculated diffusion coefficient at each temperature for the 83-atom system with shorter and longer simulation times shows that the simulation time does not have a significant effect on the results. At temperatures below 825 K, there is very little difference between the diffusion coefficients from the shorter and longer simulations. This trend can also be seen in the comparison of the calculated ionic conductivity values for the 83-atom system shorter and longer simulation times (Figure 2). The accuracy of this calculation is questionable, considering that the ionic conductivity should theoretically increase with increasing temperature and there is little difference between values at the lowest and highest temperature. In Figure 2, the calculated viscosity values are shown for the 83-atom system with shorter and longer simulation times. This shows that there is very little difference between the values from the shorter and longer simulation times. This trend can also be seen in Figure 2 for the comparison of the calculated heat capacity values.
Figure show the thermo-dynamic properties for the 142- and 83-atom systems. The methods for calculation were discussed in section 2.1.2. The trajectory used for analysis had a simulation time of approximately 100 ps and a timestep of 1fs and 2fs for the 83-atom and 142-atom systems, respectively. In Figure, the properties calculated were (a) diffusion coefficient of each species (total, Cl, K, Mg, Na), (b) ionic conductivity of each species (Cl, K, Mg, Na), and the (c) viscosity and (d) heat capacity of the 83- and 142-atom systems simulated at 723 K–973 K, respectively. The experimental values of these properties for our salt system with the same composition are limited and are not available for comparison.
Figure 3 shows the comparison of the calculate diffusion coefficient from the 83- and 142-atoms systems. The calculated diffusion coefficient for the 142-atom system is almost consistent with theoretical predictions, with temperature increasing as the diffusion coefficient increases. Figure 3 shows the ionic conductivity of the 83- and 142-atom systems. Since the ionic conductivity is a scalar of the diffusion coefficient, it is a safe assumption that it also follows the same temperature dependency trend. Figure 3 shows the viscosity values for the 83- and 142-atom systems. Theoretically, viscosity should decrease as the temperature increases, and the viscosity values for the 142-atom system follow that trend. This is one example where it is evident that the 142-atom system is more accurate than the 83-atom system. The calculations for the 142-atom simulation shows near consistency with theoretical predictions— as temperature increases, viscosity decreases. Figure 3 shows the calculated heat capacity values for the 83- and 142-atom systems. In theory, the heat capacity of the molten salt should increase with increasing temperatures. It can be seen in this comparison how the unit cell size affects the predicted properties. The values for the 142-atom system are consistent with the theory that heat capacity increases with increasing temperature. The line for the 142-atom system is quite straight without much scatter, unlike the rest of the calculations; this is concerning but the calculations have been reviewed.
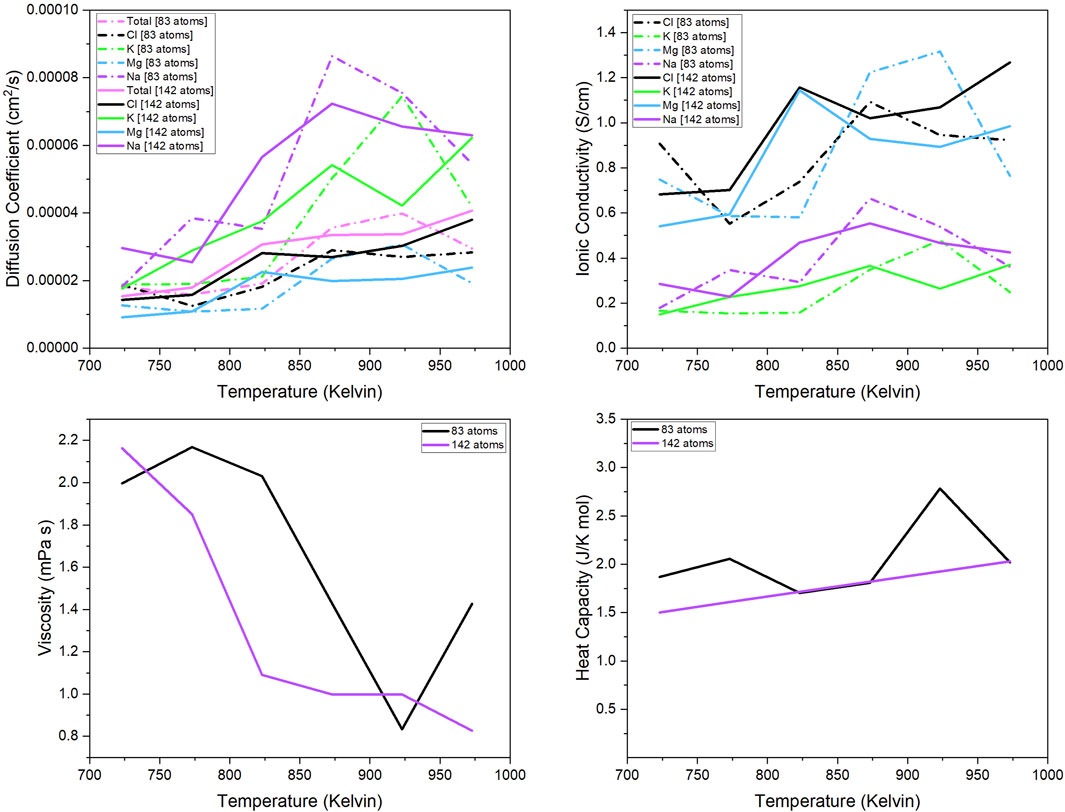
Figure 3. Diffusion coefficient of each component (total, Mg, Na, K, Cl); Ionic conductivity of each separate component (Mg, Na, K, Cl); Viscosity and heat capacity of the 83- and 142-atom systems simulated at 723 K–973 K.
This method of calculating viscosity and heat capacity has questionable accuracy because the Stokes–Einstein relationship assumes that the system has spherical particle random motion, which is not the case for fluids with intermediate range structures, such as ionic liquids. In future calculations, a more sophisticated method of statistical mechanics, such as green-kubo analysis, will be used for viscosity and heat capacity calculation. This requires the calculation of the autocorrelation function of the system’s stress tensor.
Total scattering measurements were taken for comparison against the AIMD simulation results. The x-ray PDF data for the MgCl2–NaCl–KCl salt in the liquid phase was obtained through the sine Fourier transform of the scattering pattern (Section 2.2.2). Figure 4 shows the PDF of the salt in the liquid phase. These measurements were taken for comparison against the PDF of our simulated salt system.
Comparisons between the theoretical and existing experimental data provide insights into the accuracy and reliability of AIMDs in modeling molten salt systems. Initial validation efforts include the comparison of the theoretical and experimental PDF of the eutectic system in the liquid phase to confirm the molten environment. Additionally, the theoretical viscosity values predicted from the AIMDs are compared to the experimental viscosity of a similar system. These comparisons serve to establish the credibility of predicting properties of molten salts systems with AMIDs.
In Figure 5, the experimental PDF of the liquid system was compared to the theoretical PDF from the simulated system at the specified temperature. The trajectory was from the 142-atom production run with a simulation time of approximately 100 ps. The theoretical PDF was obtained from MDANSE. It can be seen at both 723 K and 973 K that the positions of the first and second major peak in the PDF are at the same interatomic distance, approximately 2.4 and 3.6 Å, respectively. The literature values for the bond length between Mg–Cl, Na–Cl, and K–Cl in the solid phase are 2.8, 2.36, and 2.7 Å (Bickelhaupt, Sola and Fonesca Guerra, 2007). The slight difference between the first peak and the Na–Cl bond length is due to the system being in a liquid phase. The difference between them is the magnitude of the intensity, for which it can be assumed that the simulated system is in a fully diffusive regime. The discrepancy between the two systems is caused by the calculation of the simulated PDF not considering the periodicity of the simulation cell. Non-consideration of the periodicity also makes the theoretical PDF go to 0 instead of 1. These results show that the AIMD simulation estimates both the short- and medium-range atomic structure.
To contextualize our findings and attempt to fill the gaps in the fundamental knowledge of molten salts, the theoretical viscosity values of our system are compared to the experimental viscosity values of a similar system (Figure 6). Both systems have the same main components, but the difference is the concentration of each. Wang et al. (2021) measured MgCl2–NaCl–KCl at the concentration of (wt%) 45.98%–15.11%–38.91%. These experimental values were reported in centi-Poise, which is equal to our units of milli-pascal seconds.
The theoretical viscosity value was calculated using the Einstein–Stokes approximation. The viscosity values of this system can be calculated using this approximation because the eutectic salt exhibits Brownian motion in the molten phase. However, the disparity observed between the theoretical and experimental viscosity values may stem from the possibility that the calculation relies on the assumption of the minimal interactions between ions, a factor critical for this approximation. This results in an underestimation of viscosity values due to the interactions of ions not being negligible. It is also possible that the size of the 142-atom system is not sufficient to capture the atomic behavior. While theoretical viscosity values do not display the same magnitudes as the experimental values, they do exhibit the same trend: viscosity decreases with increasing temperature.
In this study, AIMD simulations are utilized to study the ternary chloride salt system in the liquid phase range: 723K–973 K. Through a comprehensive evaluation of various exchange-correlation functionals and dispersion forces, it was determined that the GGA rPBE exchange-correlation functional with the dDsC dispersion correction term provides the most accurate description of our system. The production run trajectories were then used to predict key properties such as diffusion coefficient, ionic conductivity, viscosity, and heat capacity.
The impact of simulation parameters, including total simulation time and unit cell size, was systematically examined. Results indicate that the predicted properties exhibit minimal sensitivity to changes in simulation time for an 83-atom system. Additionally, comparing properties between 83- and 142-atom systems reveal that the larger system aligns more closely with theoretical predictions. It is worth noting that the calculation of heat capacity yielded invalid values, considering the assumed units shown.
Further validation was conducted through comparison with experimental data, PDF, and viscosity measurements. For the PDF, the location of the peaks in the theoretical PDF differs slightly from the experimental PDF, affirming the assumption that the simulation captures short- and medium-range atomic interactions. The disparity found between the theoretical and experimental PDF is the difference in magnitudes of the G(r). The discrepancy between the magnitudes of intensity is due to not considering the periodicity of the simulation cell. This shows that our simulated liquid phase structure is similar to the real liquid phase structure. Additionally, a disparity was observed between the theoretical and experimental viscosity values, possibly due to assumptions made in the calculation process.
Overall, this research helps address fundamental gaps in the understanding of molten salt systems at an atomic level. The insights gained by leveraging AIMDs can inform the design and optimization process of HTFs for clean energy technologies, thus supporting advancements in sustainable energy generation. Future directions for research include investigating simulation parameters and how the properties are affected. In the context of existing literature, this research contributes to ongoing efforts to advance clean energy technologies. By providing insights into the thermo-kinetic properties of eutectic chloride salts, this study supports the optimization and design of HTFs for high-efficiency power generation, thus addressing the growing demand for clean and sustainable energy.
The data that support the findings of this study are available from the corresponding author upon reasonable request.
ES: Writing–original draft, Writing–review and editing, Investigation, Data curation, Formal Analysis, Visualization. KR: Investigation, Conceptualization, Methodology, Writing–review and editing. JV: Investigation, Writing–review and editing. YZ: Resources, Writing–review and editing. LG: Resources, Writing–review and editing. RB: Resources, Writing–review and editing. LL: Writing–review and editing, Conceptualization, Funding Acquisition, Project administration, Resources, Supervision.
This material is based upon work supported by the U.S. Department of Energy’s Office of Energy Efficiency and Renewable Energy (EERE) under the Generation 3 Concentrated Solar Power (CSP) Systems award number DE-EE0008380. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose. This research used resources at Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory (IPTS 23984). This research used the resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. AIMD simulations were performed on the supercomputer at RPI, CCI-AIMOS.
This manuscript has been authorized by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript or to allow others to do so for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan.
The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alonso, J. A., and March, N. H. (1999). Relation between transport and thermodynamic properties in liquid sp-electron metals near freezing. Phys. Rev. E 60 (4), 4125–4129. doi:10.1103/physreve.60.4125
Bengtson, A., Nam, H. O., Saha, S., Sakidja, R., and Morgan, D. (2014). First-principles molecular dynamics modeling of the LiCl–KCl molten salt system. Comput. Mater. Sci. 83, 362–370. doi:10.1016/j.commatsci.2013.10.043
Bickelhaupt, F., Sola, M., and Fonesca Guerra, C. (2007). Table salt and other alkali metal chloride oligomers: structure, stability, and bonding. Inorg. Chem. 46, 5411–5418. doi:10.1021/ic070328u
Bockris, J., and Reddy, A. K. (1998) Modern electrochemistry: an introduction to an interdisciplinary area, 1. USA: Plenum Press.
Borkiewicz, O. J., Ruett, U., Beyer, K., and Gallington, L. (2019). New capabilities at beamline 11-ID-B of the advanced Photon source. Found. Crystallogr. 75, a352. doi:10.1107/s0108767319096570
Car, R., and Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55 (22), 2471–2474. doi:10.1103/physrevlett.55.2471
DeFever, R. S., Wang, H., Zhang, Y., and Maginn, E. J. (2020). Melting points of alkali chlorides evaluated for a polarizable and non-polarizable model. J. Chem. Phys. 153 (1), 011101. doi:10.1063/5.0012253
Ding, W., Bonk, A., and Bauer, T. (2019). Molten chloride salts for next generation CSP plants: selection of promising chloride salts and study on corrosion of alloys in molten chloride salts. AIP Conf. Proc. 2126, 200014. doi:10.1063/1.5117729
Dion, M., Rydberg, H., Schroder, E., Langreth, D. C., and Lundqvist, B. I. (2004). Van der Waals density functional for general geometries. Phys. Rev. Lett. 92 (24), 246401. doi:10.1103/physrevlett.92.246401
Duemmler, K., Woods, M., Karlsson, T., Gakhar, R., and Beeler, B. (2022). An ab initio molecular dynamics investigation of the thermophysical properties of molten NaCl-MgCl 2. J. Nucl. Mater. 570, 153916. doi:10.1016/j.jnucmat.2022.153916
Duemmler, K., Woods, M., Karlsson, T., Gakhar, R., and Beeler, B. (2023). First-principles-derived transport properties of Molten chloride salts. Jounral Nucl. Mater. 585, 154601. doi:10.1016/j.jnucmat.2023.154601
Egami, T., and Billinge, S. (2012) Underneath the Bragg peaks: structural analysis of complex materials. Second Edition. Pergamon, Elmsford, NY: Elsevier.
Einstein, A. (1905). "On the movement of small particles suspended in stationary liquids required by the molecularkinetic theory of heat." . Ann.d. Phys. 17, 549–560. doi:10.1002/andp.19053220806
Fernandez, A. G., Galleguillos, L., Fuentealba, E. L., and Perez, F. J. (2015). Thermal characterization of HITEC molten salt for energy storage in solar linear concentrated technology. J. Therm. Analysis Calorim., 122, 3–9. doi:10.1007/s10973-015-4715-9
Fumi, F. G., and Tosi, M. P. (1964). Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—I: the Huggins-Mayer and Pauling forms. J. Phys. Chem. Solids 25: 31–43. doi:10.1016/0022-3697(64)90159-3
Galamba, N., and Costa Cabral, B. J. (2007). First principles molecular dynamics of molten NaCl. J. Chem. Phys. 126 (12), 124502. doi:10.1063/1.2711187
González-Roubaud, E., Pérez-Osorio, D., and Prieto, P. (2017). Review of commercial thermal energy storage in concentrated solar power plants: steam vs. molten salts. Renew. Sustain. Energy Rev. 80, 133–148. doi:10.1016/j.rser.2017.05.084
Goret, G. B., Aoun, B., and Pellegrini, E. (2017). MDANSE: an interactive analysis environment for molecular dynamics simulations. J. Chem. Inf. Model. 57 (1), 1–5. doi:10.1021/acs.jcim.6b00571
Grimme, S. (2006a). Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27 (15), 1787–1799. doi:10.1002/jcc.20495
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurateab initioparametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132 (15), 154104. doi:10.1063/1.3382344
Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32 (7), 1456–1465. doi:10.1002/jcc.21759
Hacene, M., Anciaux-Sedrakian, A., Rozanska, X., Klahr, D., Guignon, T., and Fleurat-Lessard, P. (2012). Accelerating VASP electronic structure calculations using graphic processing units. Jounral Comput. Chem. 33 (32), 2581–2589. doi:10.1002/jcc.23096
Hutchinson, M., and Widom, M. (2012). VASP on a GPU: application to exact-exchange calculations of the stability of elemental boron. Comput. Phys. Commun. 183 (7), 1422–1426. doi:10.1016/j.cpc.2012.02.017
Janz, G. J., and Bansal, N. P. (1982). Molten salts data: diffusion coefficients in single and multi-component salt systems. J. Phys. Chem. Reference Data 11 (3), 505–693. doi:10.1063/1.555665
Klimes, J., Bowler, D. R., and Michaelides, A. (2010). Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201. doi:10.1088/0953-8984/22/2/022201
Klimes, J., Bowler, D. R., and Michaelides, A. (2011). Van der Waals density functionals applied to solids. Phys. Rev. B 83 (19), 195131. doi:10.1103/physrevb.83.195131
Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6 (1), 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Hafner, J. (1993). Ab initiomolecular dynamics for open-shell transition metals. Condens. Matter 48, 13115–13118. doi:10.1103/physrevb.48.13115
Kresse, G., and Hafner, J. (1994). Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 6 (40), 8245–8257. doi:10.1088/0953-8984/6/40/015
Kresse, G. a., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. b 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758
Li, X. N., Liu, W., Tang, Z., and Wang, J. (2020). Unrevealing the thermophysical properties and microstructural evolution of MgCl2–NaCl–KCl eutectic: FPMD simulations and experimental measurements. Sol. Energy Mater. Sol. Cells 210, 110504. doi:10.1016/j.solmat.2020.110504
Liang, W., Wu, J., Ni, H., Lu, G., and Yu, J. (2020). First-principles molecular dynamics simulations on the local structure and thermo-kinetic properties of molten magnesium chloride. J. Mol. Liq. 298, 112063. doi:10.1016/j.molliq.2019.112063
Martínez, L., Andrade, R., Birgin, E. G., and Martínez, J. M. (2009). PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 30 (13), 2157–2164. doi:10.1002/jcc.21224
Marx, D., and Hutter, J. (2000). “Modern methods and algorithms of quantum chemistry,” in John von Neumann Institute for Computing, Jülich, Germany, 2000. Julich, Germany: John von Neumann Institute for Computing. Editor J. Grotendorst (Germany: IEEE).
Mayer, J. E. (1933). Dispersion and Polarizability and the van der Waals Potential in the Alkali Halides. J. Chem. Phys. 1 (4), 270–279. doi:10.1063/1.1749283
Mehos, M., Turchi, C., Vidal, J., Wagner, M., Ma, Z., Ho, C., et al. (2017) Concentrating solar power Gen3 demonstration roadmap. Golden, CO: NREL. No. NREL/TP-5500-67464. National Renewable Lab (NREL).
Myers Jr, P. D., and Goswami, D. Y. (2016). Thermal energy storage using chloride salts and their eutectics. Appl. Therm. Eng. 109 (2016): 889–900. doi:10.1016/j.applthermaleng.2016.07.046
Nam, H. O., Bengtson, A., Vörtler, K., Saha, S., Sakidja, R., and Morgan, D. (2014). First-principles molecular dynamics modeling of the molten fluoride salt with Cr solute. J. Nucl. Mater. 449 (1-3), 148–157. doi:10.1016/j.jnucmat.2014.03.014
Ohtori, N., Mathieu, S., and Madden, P. A. (2015). Calculations of thermal conductivities of ionic materials by simulation with polarizable interaction potentials. J. Chem. Phys. 113 (17-18), 2422–2450. doi:10.1063/1.3086856
Parker, S. S., Long, A. M., Lhermitte, C. R., Monreal, M., and Jackson, J. R. (2022). Thermophysical properties of liquid chlorides from 600 to 1600 K: Melt point, enthalpy of fusion, and volumetric expansion. J. Mol. Liq. 346, 118147. doi:10.1016/j.molliq.2021.118147
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100 (13), 136406. doi:10.1103/physrevlett.100.136406
Qiu, X. J., Thompson, J. W., and Billinge, S. J. L. (2004). PDFgetX2: a GUI-driven program to obtain the pair distribution function from X-ray powder diffraction data. J. Appl. Crystallogr. 37 (4), 678. doi:10.1107/s0021889804011744
Roman-Perez, G., and Soler, J. M. (2009). Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes. Phys. Rev. Lett. 103 (9), 096102. doi:10.1103/physrevlett.103.096102
Rong, Z., Ding, J., Wang, W., Pan, G., and Liu, S. (2020). Ab-initio molecular dynamics calculation on microstructures and thermophysical properties of NaCl–CaCl2–MgCl2 for concentrating solar power. Sol. Energy Mater. Sol. Cells 216, 110696. doi:10.1016/j.solmat.2020.110696
Rong, Z., Pan, G., Lu, J., Liu, S., Ding, J., Wang, W., et al. (2021). Ab-initio molecular dynamics study on thermal property of NaCl–CaCl2 molten salt for high-temperature heat transfer and storage. Renew. Energy 163, 579–588. doi:10.1016/j.renene.2020.08.152
Salanne, M., and Madden, P. A. (2011). Polarization effects in ionic solids and melts. Mol. Phys. 109 (19), 2299–2315. doi:10.1080/00268976.2011.617523
Steinmann, S. N., and Corminboeuf, C. (2011). A generalized-gradient approximation exchange hole model for dispersion coefficients. J. Chem. Phys. 134 (4), 044117. doi:10.1063/1.3545985
Stephens, P. J., Devlin, F. J., Chabalowski, C. F., and Frisch, M. J. (1994). Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98 (45), 11623–11627. doi:10.1021/j100096a001
Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171
Toby, B. H., and Von Dreele, R. B. (2013). GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 46 (2), 544–549. doi:10.1107/s0021889813003531
Tosi, M. P., and Fumi, F. G. (1964). Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—II: the generalized Huggins-Mayer form. J. Phys. Chem. Solids 25 (1), 45–52. doi:10.1016/0022-3697(64)90160-x
Vosko, S. H., Wilk, L., and Nusair, M. (1980). Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 58 (8), 1200–1211. doi:10.1139/p80-159
Xu, T., Li, X., Guo, L., Wang, F., and Tang, Z. (2020). Powerful predictability of FPMD simulations for the phase transition behavior of NaCl-MgCl2 eutectic salt. Sol. Energy 209, 568–575. doi:10.1016/j.solener.2020.09.038
Xu, T., Li, X., Li, N., Liu, M., Wang, F., and Tang, Z. (2021). In-depth explorations on the microstructural, thermodynamic and kinetic characteristics of MgCl2-KCl eutectic salt. J. Mol. Liq. 347, 118275. doi:10.1016/j.molliq.2021.118275
Xu, X., Dehghani, G., Ning, J., and Li, P. (2018). Basic properties of eutectic chloride salts NaCl-KCl-ZnCl2 and NaCl-KCl-MgCl2 as HTFs and thermal storage media measured using simultaneous DSC-TGA. Sol. Energy 162, 431–441. doi:10.1016/j.solener.2018.01.067
Zhou, W., Zhang, Y., and Salanne, M. (2022). Effects of fluoride salt addition to the physico-chemical properties of the MgCl2-NaCl-KCl heat transfer fluid: a molecular dynamics study. Sol. Energy Mater. Sol. Cells 239, 111649. doi:10.1016/j.solmat.2022.111649
Keywords: molten salts, chloride molten salts, Ab-initio molecular dynamics, simulations, VASP, MgCl2, NaCl
Citation: De Stefanis E, Ramic K, Vidal J, Zhao Y, Gallington LC, Bedell R and Liu L( (2024) Ab-initio molecular dynamics study of eutectic chloride salt: MgCl2–NaCl–KCl. Front. Nucl. Eng. 3:1341754. doi: 10.3389/fnuen.2024.1341754
Received: 20 November 2023; Accepted: 22 May 2024;
Published: 26 July 2024.
Edited by:
Charlotte Becquart, Laboratoire UMET, FranceReviewed by:
Benjamin Beeler, North Carolina State University, United StatesCopyright © 2024 De Stefanis, Ramic, Vidal, Zhao, Gallington, Bedell and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Emily De Stefanis, ZGVzdGVlQHJwaS5lZHU=; Li (Emily) Liu, bGl1ZUBycGkuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.