Quantifying neptunium oxidation states in nitric acid through spectroelectrochemistry and chemometrics

Controlled-potential in situ thin-layer spectropotentiometry was leveraged to generate visible/near-infrared (VIS/NIR) absorption spectral data sets for the development of chemometric models to quantify Np(III/IV/V/VI) oxidation states in HNO₃. This technology would be valuable in laboratory studies and when monitoring process solutions to guide feed adjustments for radiochemical separations—the performance of which depends on oxidation state. This approach successfully isolated and stabilized Np species in pure (∼99%) oxidation states without compromising solution optical properties. Multivariate curve resolution–alternating least squares models were evaluated to resolve spectral and component concentrations from a scan that sequentially produced Np(VI), Np(V), Np(IV), and Np(III) spectra with mixtures of two valences at a time. Although it provided a useful approximation, the method was not able to quantitively resolve each component likely because of rotational ambiguity. Additionally, partial least squares regression models were built from artificial and electrochemically generated VIS/NIR spectral training sets to study the effect of interionic interactions on spectral characteristics. Models built with true Bi-chemical mixtures of coexisting Np oxidation states and spectra generated from additive combinations of pure end points had similar prediction performance. This methodology can be used to directly quantify Np concentration and the ratio of Np oxidation states and other actinides in remote settings such as hot cells.

1 Introduction

Spectrophotometry, or ultraviolet–visible–near-infrared (UV-VIS-NIR) absorption spectroscopy, quantitatively measures the electronic spectra of molecular species and has been used for decades to characterize aqueous Np species in acidic solutions. (Sjoblom and Hindman, 1951; Ryan, 1960; Eisensterin and Pryce, 1966; Varga et al., 1970; Friedman and Toth, 1980; Ban et al., 2014; Edelstein, 2015). Determining the relative proportion of Np oxidation state(s) and total Np concentration by spectrophotometry is challenging because of its complex redox chemistry (adopting oxidation states from +3 to +6), coordination chemistry, interionic associations, and dependence of absorption bands on temperature and solution conditions. (Chatterjee et al., 2017; Sadergaski and Morgan, 2022). Quantifying multiple Np oxidation states is also particularly challenging owing to numerous overlapping peaks. This issue renders univariate methods like Beer’s law unusable in real-world online monitoring applications. (Sadergaski et al., 2022a; Sinkov et al., 2022). On the other hand, multivariate chemometric regression models can account for each variable to give accurate predictions. These methods can account for systems with overlapping and covarying spectral characteristics. (Lascola et al., 2017; Sadergaski et al., 2020; Tse et al., 2022).

Chemometric algorithms generally fall into two categories, referred to as unsupervised and supervised. Several helpful review articles on the topic can be found in the literature (Kirsanov et al., 2017; Lackey et al., 2023) One of the most common unsupervised methods is principal component analysis (PCA), and partial least squares regression (PLSR) is one of the most established supervised methods. PCA produces unique solutions by sequentially producing an orthogonal bilinear matrix decomposition to explain the maximum variance in the measured signal. The orthogonal (independent) solutions are helpful in identifying the number of different sources of variation in the data and helps identify underlying features causing the data variation. However, these solutions are abstract because they are orthogonal linear combinations of the underlying factors.

Multivariate curve resolution–alternating least squares (MCR-ALS), similar to PCA, assumes the fulfillment of a bilinear model and can be used to describe multicomponent mixture systems to resolve pure component concentration and spectral contributions. (Alcaráz et al., 2017; Pellegrino and Olivieri, 2020; Olivieri, 2021). The goal of MCR-ALS is to identify the true underlying sources of data variation directly using spectral components that can be easily interpreted by non-chemometricians. Even though MCR-ALS does not require previous information about the system, unique solutions are not usually obtained unless external information such as constraints are provided during matrix decomposition. MCR-ALS solutions are not unique, such as most bilinear decomposition methods, and the resolved components contain several ambiguities, including rotational, permutation, and intensity. (Pellegrino and Olivieri, 2020; Olivieri, 2021). Users often narrow the range of potential MCR solutions by including constraints that are often based on chemical or mathematical features of the data set. When implemented properly, constraints can provide a helpful driving force in the iterative process to arrive at the correct solution. In complex systems, MCR-ALS may not provide a quantitative solution to the mixture problem. For quantitative predictions, PLSR models can be trained to cover the range of anticipated conditions to successfully model complex spectral features in spectral systems. PLSR solves for orthogonal vectors in the latent space (latent variables [LVs]) that best explain the covariance between the measured signal (spectra) and response matrix (concentrations). PLSR depends on a training set, which is composed of calibration and validation samples. (Sadergaski et al., 2021a; Sadergaski and Andrews, 2022; Andrews et al., 2023).

Spectral training sets containing Np in +3, +4, +5, and +6 oxidation states can be obtained electrochemically while recording optical spectra in situ. However, in most process conditions that use various HNO₃ concentrations, Np will generally be in the +4, +5, and/or +6 oxidation states. A controlled spectropotentiometric approach has been leveraged previously to study the mechanisms for Np and Pu redox reactions in HNO₃ solutions but has not been applied to the development of regression models to measure their relative concentrations or applied to systems with Np concentrations >10 mM. (Edelstein, 2015; Lines et al., 2017; Chatterjee et al., 2020). In this work, thin-layer, in situ spectropotentiometry was used to isolate Np species in pure oxidation states without compromising solution optical properties from the additional redox reagents to generate spectral data for the development of supervised and unsupervised methods for quantifying Np in various oxidation states. (Elgrishi et al., 2018; Andrews and Sadergaski, 2023a).

In a simple system that follows Beer’s law, absorption is directly proportional to concentration. (Harris, 2007). To date, most spectral databases of Np in HNO₃ solutions have not been established at concentrations greater than 10 mM. (Chatterjee et al., 2017). This linear relationship may break down at elevated solute concentrations >0.01 M, where interionic associations between solute ions (e.g., NpO₂⁺ and NpO₂²⁺) become more significant. (Guillaume et al., 1982). Previous work presumes that these interactions and corresponding spectral features must be accounted for to develop accurate models. (Chatterjee et al., 2017). If this assumption is true, then electrochemically generated spectral data sets must not only be composed of pure oxidation states but must also be proportionate mixtures of Np(IV), Np(V), and Np(VI). If these effects are insignificant, then spectral data sets could be generated synthetically using pure end point spectra to generate mixtures of all relevant combinations of Np oxidation states. This approach would aid the generation of data sets with radiological samples and minimize the time, waste, and money associated with model development. These samples can be selected using design of experiments, which generate mixture designs within a statistical framework. (Zahran et al., 2003; Sadergaski et al., 2022b).

This work evaluates the use of MCR-ALS and PLSR models to quantify Np oxidation states generated during multiple electrochemical scans in which various proportions of Np(III/IV/V/VI) coexisted in solution. Three points of scientific advancement in this work include 1) combined PCA and Kennard–Stone (KS) sample selection to retrieve representative spectra from electrochemically generated data; 2) systematic comparisons of PLSR prediction performance between models built using additive combinations of pure end point spectra and electrochemically generated spectra with coexisting ions, revealing an inconsequential contribution from interionic associations at approximately 0.08 M Np in 2 M HNO₃; and 3) proposed a unique combination of techniques and an effective application strategy to develop robust regression models for the quantitative analysis of Np(III/IV/V/VI) in HNO₃. This capability will help the ²³⁸Pu Supply Program at Oak Ridge National Laboratory to monitor essential radiochemical processes needed to produce ²³⁸Pu, a power source for radioisotope thermoelectric generators (RTGs) needed for NASA space missions. (Sadergaski et al., 2021b; Andrews and Sadergaski, 2023b). Implementing optical spectroscopy, multivariate chemometrics, and online monitoring capabilities in radiochemical hot cells can support radiochemical processing and scale-up efforts. Additionally, a thorough understanding of Np is needed for reprocessing, waste storage, environmental applications, and additional systems within the nuclear fuel cycle.

2 Methods

All chemicals were commercially obtained (American Chemical Society–grade) and used as received unless otherwise stated. Concentrated HNO₃ (70%) was purchased from Sigma-Aldrich. Samples were prepared using deionized water with Millipore Sigma Milli-Q purity (18.2 MΩ∙cm at 25°C).

2.1 Sample preparation and electrochemistry

A²³⁷Np nitrate hydrate sample was prepared in house at Oak Ridge National Laboratory. The sample was weighed out into a 1 mL volumetric flask with a combination of deionized water and 70% HNO₃ to achieve 2 M HNO₃. Purity was confirmed by alpha-particle spectroscopy. The sample was prepared and analyzed in a negative pressure glove box.

The sample (700 µL) was placed in a 1.7 mm path length cuvette (PINE Research) for the spectroelectrochemical measurements. Electrochemical tests were controlled with an SP-300 potentiostat (Biologic). (Andrews and Sadergaski, 2023a). A screen-printed Pt honeycomb working/counter electrode (Pine Research) was used with a pseudo reference electrode. A cell potential above the standard redox couple of NpO₂²⁺/NpO₂⁺ was applied to adjust the oxidation state to nearly 100% Np(VI). Then, the cell potential was carefully reduced at 0.1 V increments until all of the Np was converted to Np(III). Finally, the cell potential was abruptly switched above the NpO₂²⁺/NpO₂⁺ redox couple to rapidly oxidize the sample back to Np(VI). The applied cell potential as a function of time is provided in the Supporting Information (Supplementary Figure S1). This approach does not compromise solution optical properties by avoiding the addition of redox reagents for isolating and stabilizing Np species in pure oxidation states. (Chatterjee et al., 2017).

2.2 Optical spectroscopy

Absorption spectra were collected using an Ocean Insight QEPro (316–1,104 nm at 0.71 nm increments) and NIRQuest (898–1,705 nm at 1.53 nm increments) spectrophotometer. The QEPro measurements were recorded as an average of 15 replicates at 40 ms intervals, and the NIRQuest measurements were an average of three replicates at 300 ms intervals. Absorption spectra were processed using OceanView software (Ocean Insight, Orlando, Florida, USA). A stabilized broadband (360–2,600 nm) light source (SLS201L, ThorLabs) was used for absorption measurements. The sample cuvette was placed in a StellarNet cuvette holder with SMA fiber adapters. A QBIF400-MIXED Ocean Insight fiber bundle enabled simultaneous QEPro and NIRQuest measurements. Spectra were collected at a room temperature of 20°C. Spectral regions from 325 to 400 nm and 1,380 to 1,700 nm were omitted from the analysis because of low signal intensity.

2.3 Design of experiments

Experimental designs were built using Design-Expert (v.11.0.5.0) by Stat-Ease Inc. (Minneapolis, MN, USA). D (determinant)-optimal designs utilize an algorithm to select sample concentrations by iteratively minimizing the determinant of the variance-covariance matrix X^TX. Relative analyte concentrations of Np(III/IV/V/VI) were generated from a mixture design, each as a fraction between zero and one. The fraction of design space was calculated by mean error type: δ = 2, σ = 1, and α = 0.05. (Zahran et al., 2003; Sadergaski et al., 2022b). Delta (d) describes the maximum acceptable half-width (i.e., margin of error), sigma (s) is an estimate of the standard deviation, and alpha (α) is the significance level used in the statistical analysis. This design required 10 model points using a quadratic model and 5 lack-of-fit (LOF) points (Supplementary Table S1). LOF points minimize the distance to other model points (i.e., runs) while conserving the optimality criterion. LOF points were included in the model to improve the fraction of design space (1.0) by including additional vertex, edge, plane, and interior points. Synthetic mixture spectra were not generated experimentally, but as an additive combination of weighted endpoint spectra.

2.4 Multivariate analysis and preprocessing

The Unscrambler X software (version 10.4) from the Camo Analytics AS software package (Camo Analytics AS, Oslo, Norway) was used for data preprocessing and chemometric analyses. Spectra were mean-centered prior to PCA and PLSR. A NIPALS (nonlinear iterative partial least squares) algorithm was used for PCA and partial least squares (PLS). A comprehensive overview of PCA can be found in the literature. MCR-ALS uses an iterative cycle to simultaneously optimize both concentration profile(s) and instrument response matrices. MCR decomposes the spectral data X (I × J) into a concentration matrix C and sources S^T based a bilinear model defined in Eq. 1:

$\mathbf{X}=\mathbf{C}{\mathbf{S}}^{\mathbf{T}}+\mathbf{E},(1)$

where C (I × N) and the sources S^T (N × J) consist of the concentration and spectral profiles of the N deconvoluted sources, and E (I × J) represents the residuals matrix. Where I represents the number of samples and J the number of spectral variables. It is possible to enter estimates, a C-type (i.e., concentration), or an S^T-type matrix (i.e., spectra) as an initial guess (i.e., nonrandom estimate) in The Unscrambler. Additional details for MCR-ALS constraints can be found in the Supporting Information.

PLSR correlates spectral features to analyte concentrations by modeling concentration and spectral information in the regression coefficient matrix. (Lackey et al., 2023). PLSR iteratively relates two data matrices: the independent X (i.e., spectra) and dependent Y (i.e., concentrations), using combinations of LVs. In PLSR, the measured value is often called the X-block or predictor block (i.e., spectra), and the response variable is called the Y-block or predicted block (i.e., concentration matrix). These scores and loadings (i.e., LVs) are used to derive regression coefficients in the modeling process. The best number of LVs is often chosen by the last LV to show a significant decrease in the explained variance or root mean square error (RMSE) of the cross validation (CV) data. CV statistics were calculated by leaving one sample out. PLSR models can be built with one Y variable (PLS-1) or multiple Y variables (PLS-2). In this work, PLS-2 models were built to help account for covariance or multicollinearity between species represented in the spectral data set.

The concentration profile estimates from MCR-ALS were compared with a PLSR prediction approach adapted from a previous work. (Sadergaski et al., 2022a). This method selects samples from data sets using PCA and KS, estimates the relative concentrations between zero and one for each species in this reduced training set by deconvolution, then builds a predictive PLSR model from those estimates. In a fourth step, the concentration matrix used for PLSR was scaled so the estimates match the real concentration values.

2.5 Statistics and limits of detection

Model performance was evaluated using calibration, CV, and validation (i.e., prediction) metrics. The primary statistics used to evaluate model performance was the RMSEs of the calibration (RMSEC), CV (RMSECV), and prediction (RMSEP). RMSE values have the same units as the measured values. The CV statistics using designed calibration sets may not accurately estimate model stability and prediction performance. (Sadergaski et al., 2021a). PLSR model prediction performance testing on samples not included in the training set is important because the RMSE of CV is only an estimate, especially when using a designed sample matrix. RMSEs for the calibration, CV, and validation were calculated using Eq. (2):

$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\left({\widehat{y}}_i-y_i\right)}^2}{n}},(2)$

where ${\widehat{y}}_i$ is the predicted concentration, y_i is the measured concentration, and n is the number of samples. PLSR models were optimized by minimizing the RMSEP. Percent RMSEP was calculated by dividing the RMSEP by the median model values using Eq. (3):

$RMSEP\%=\frac{RMSEP}{y_{\text{med}}}\times 100\%,(3)$

where y_med represents the median of each analyte concentration range. Each RMSE value is in units of analyte concentration. Lower RMSEP values indicate better model performance. Strong prediction performance is achieved when RMSEP is less than or equal to 5%, satisfactory performance when RMSEP is between 5% and 10%, and indicative performance when RMSEP is between 10% and 15%. (Sadergaski and Morgan, 2022) The deviation (i.e., uncertainty) in predicted Y-values (i.e., concentrations) for each individual sample was estimated as a function of the global model error, sample leverage, and residual X-variance. (Vries and Ter Braak, 1995) Standard error of prediction (SEP) and bias were also used to evaluate prediction performance. SEP is the RMSEP corrected for bias.

3 Results and discussion

3.1 Np VIS/NIR absorption spectra

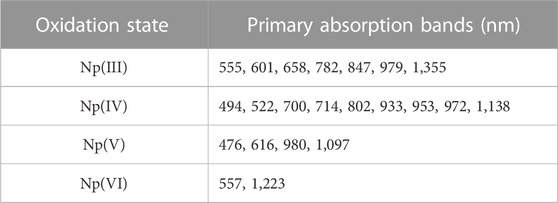
Several discrepancies exist in the literature regarding Np absorption spectra in HNO₃; conversely, numerous spectra have been reported and are generally consistent. Most studies aim to understand the behavior of Np at concentrations near 1 mM, and very few studies have examined Np VIS/NIR spectra at concentrations >0.01 M Np. (Chatterjee et al., 2017). Spectroelectrochemical experiments were conducted on solutions of approximately 0.08 M Np in 2 M HNO₃. A potentiometric setup in parallel with a three-electrode card coupled to UV-Vis and NIR spectrophotometers allowed for spectral data collection during controlled, stepwise changes in potential (Supplementary Figure S1). This method allows for changes in Np oxidation state as a function of potential and recording spectra as light passed through the diffusion layer along the holes in the working electrode.

Many studies have reported characteristic electronic spectra of Np oxidation states ranging from Np(III) to Np(VI). (Sjoblom and Hindman, 1951; Ryan, 1960; Friedman and Toth, 1980; Ban et al., 2014; Chatterjee et al., 2017; Sadergaski and Morgan, 2022). However, similar redox potentials, differing chemical and redox behavior, the ability to react with certain complexing ligands, and differing stabilities in acid of various concentrations all contribute to the complex redox chemistry of Np and the difficulty in acquiring electronic spectra of single oxidation states. (Chatterjee et al., 2017). A total of 1,300 spectra were generated during the sequential step-wise reduction from Np(VI) to Np(III), generating approximately 99% pure spectra for each oxidization state, as shown in Figure 1. Significant overlap of spectral peaks in both the UV-Vis and NIR regions is observed. For Np(III), high absorption is observed near the UV region (<460 nm), with several notable peaks given in Table 1 that span the entire Vis region. The only peak without significant overlap was the broad band near the 1,355 nm signal in the NIR region. The region above approximately 1,370 nm was omitted from the analysis owing to overlap with the strong NIR H₂O band region centered near 1,450 nm and detector saturation. (Sadergaski et al., 2021a; Sadergaski et al., 2023). Several peaks are observed in the UV-Vis region of the electronic spectrum of Np(IV). The most notable peak is a broad signal in the UV-Vis region, which observed from approximately 700 nm–730 nm. Previous studies indicate that this spectral region is highly sensitive to acid concentration. Another packet of broad signals occurs in the NIR region at approximately 930, 960, and 975 nm, as well as another weak peak near 1,140 nm.

FIGURE 1

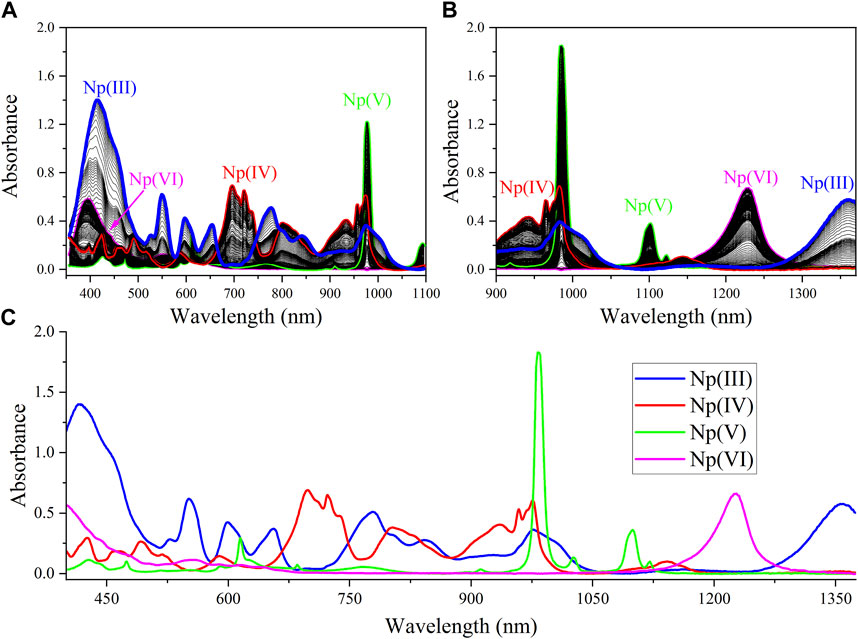
FIGURE 1. Np(III/IV/V/VI) absorption spectra generated from the sequential step from Np(VI) to Np(III): (A) Vis, (B) NIR, and (C) fused spectra.

TABLE 1

TABLE 1. Characteristic Np absorption bands by oxidation state.

For Np(V), the UV-Vis region contains several minor peaks listed in Table 1, but the primary absorption bands occur near 615 and 980 nm. Computational studies of the Np(V) neptunyl cation have attributed absorption bands in the region of approximately 433 nm and below to charge transfer transitions. At wavelengths above 433 nm, peaks are attributed primarily to the intense f → f transitions. (Edelstein, 2015). The intense peak in the NIR region at 980 nm dominates the spectrum and has a molar extinction coefficient that is nearly an order of magnitude larger than any peak in this scan. The 980 nm peak in Figure 1 is not distorted, but it is saturating the detector. The nonlinear instrument response for this peak has been described and accounted for in previous studies and is due to a higher molar absorptivity relative to other peaks in the spectrum. (Sadergaski and Morgan, 2022; Andrews and Sadergaski, 2023b). For Np(VI), high absorption in the low-wavelength range <420 nm was observed. A broad system of overlapping peaks occurred near 555 nm, and the most characteristic feature of the Np(VI) spectrum is an asymmetric peak that occurs in the NIR region near 1,223 nm. (Ban et al., 2014).

Numerous isosbestic points were identified between Np(III) and Np(IV) spectra. Isosbestic points were not identified between all four Np oxidation states. The most useful isosbestic points for the more process-relevant oxidation states [i.e., Np(VI), Np(V), Np(IV)] occurred near 608 and 646 nm. In general, less peak overlap occurred in the NIR region >900 nm (other than the 970–990 nm region), and the peak intensities are somewhat balanced. Therefore, this region was assessed by PCA analysis.

3.2 PCA analysis and KS sample selection

A 3D scores plot for the PCA model built using baseline-corrected NIR spectra, collected during the scan from Np(VI) to Np(III), is shown in Figure 2. The Np(III) will not typically be encountered in process solutions, but it was included here to make the modeling more challenging. Principal components (PCs) 1–3 describe a total of 99.94% of the explained X-variance. Despite spectral data corresponding to the presence of four Np oxidation states, only three PCs were needed to describe the structured variation in the data set. A 3D scatter plot revealed a systematic sample pattern (Figure 2). The closer samples are in the 3D scores plot, the more similar they are with respect to the three components. The periodicity (i.e., regular increase/decrease) is consistent with the electrochemical scan, which gradually converted Np from one oxidation state to the next. A separate PCA model was built using the entire NIR spectrum, and four PCs were needed to describe 99.97% of the data variance because of the saturation of the 980 nm peak, which required an additional loading to compensate for the peak broadening and so-called flat top. This behavior has been leveraged in a recent study to construct a hierarchical model to monitor a larger concentration range. (Andrews and Sadergaski, 2023b).

FIGURE 2

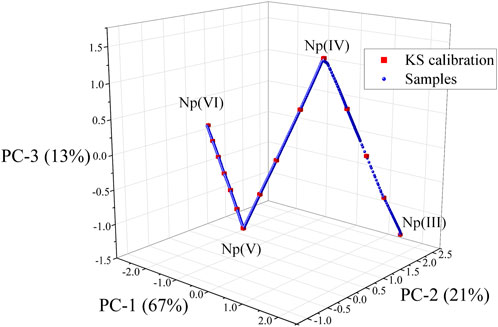
FIGURE 2. 3D scatter plot of the scores for principal component (PC)-1, PC-2, and PC-3. Sample selected by the KS algorithm are shown as the red squares. Location of pure Np oxidation states are noted as the end points and vertex points.

Pure Np(VI), Np(V), Np(IV), and Np(III) spectra corresponded to the end points or vertex points in the plot. The points connecting each end point or vertex point correspond to mixtures of two oxidation states at a time. This result confirms that no more than two Np oxidations coexisted in solution at a given time. Each PCA loading in the model gave importance (i.e., large positive or negative values) to spectral variables corresponding to the predominant peaks in the spectra for each Np oxidation state. However, each loading contained spectral features for two or more oxidation states (data not shown here).

The KS sample selection algorithm was used to select a subset of 15 calibration and 15 validation samples to evenly cover the multivariate space described by PCA. The locations of KS calibration samples are shown in Figure 2 (red squares), and the spectra corresponding to each sample are shown in Supplementary Figure S2. This method reduced the number of spectra from 1,300 to 15 for further evaluation. These samples were used to train supervised PLSR models to develop a method for isolating the relative concentration of each Np oxidation state in the mixed spectra.

3.3 PLSR regression models

PLSR models X and Y matrices to find the structure in X that best predicts the concentration matrix Y by maximizing the covariance between X and Y. The set of 15 KS-selected spectra comprised the matrix X, and a deconvolution method, also known as digital subtraction, was used to assign concentration values to each spectrum. (Chatterjee et al., 2017). It is common practice to trim spectral data because trimming typically improves model performance by removing noise so the model can focus on regions of high correlations to the response matrix. (Lackey et al., 2023). Because of the substantial overlap of peaks in the spectrum, the entire region was included in the model. However, the region corresponding to the 980 nm peak was removed from the regression model owing to peak saturation at high Np(V) concentrations. Future work could evaluate the development of PLS-1 regression models, which could be tailored to each species individually, and a hierarchical approach could account for a wide range of Np(V) concentrations. (Andrews and Sadergaski, 2023b).

PLS used three LVs to describe the variation in the data when the 980 nm band was removed from the analysis. Four factors were needed to describe >99% of the variance when the entire NIR spectrum was modeled. The number of LVs was comparable with the number of oxidation states modeled in the system, which suggests that spectral features related to interionic associations from coexisting ions are possibly negligible. If these features were significant, additional LVs would likely be included in the model.

The explained Y-variance using three factors for the calibration and cross validation (CV) were 99.94% and 99.9%, respectively. Therefore, additional latent variables (i.e., factors) were not included in the model to avoid introducing noise. Parity plots for the calibration and validation values are shown in Figure 3. Similar values between RMSEC and RMSECV values indicate a balanced model and enough samples in the calibration set. However, the difference between RMSEC and RMSECV for factors 1 and 2 suggests that the 15 spectra approach the minimum required in the calibration set (Supplementary Figure S3). The percent RMSECV values for Np(VI), Np(V), Np(IV), and Np(III) are 1.3%, 3.0%, 2.8%, and 1.4%, respectively. RMSECV values provide an estimate of the deviation associated with future predictions and suggest that the model has the desired level of accuracy for the intended purpose. A 3D scores plot for the PLS-2 model is shown in Supplementary Figure S4 and reveals similar systematic features to the PCA 3D scores plot in Figure 2.

FIGURE 3

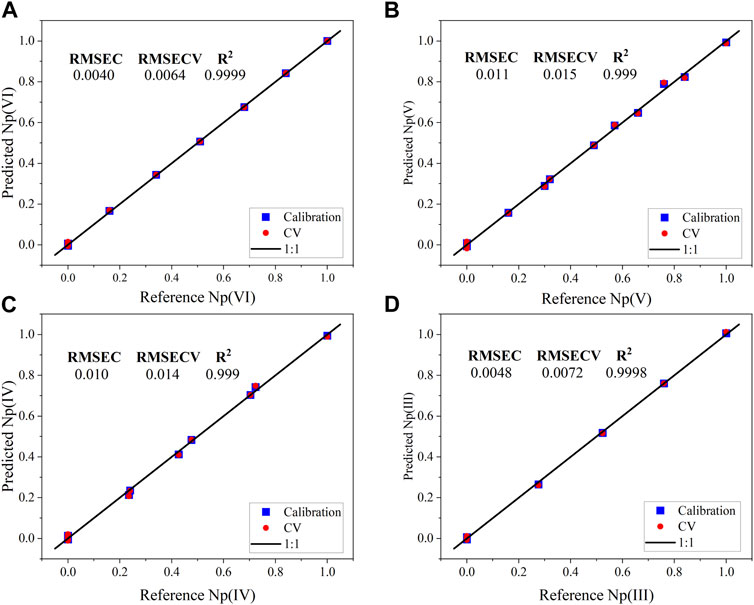
FIGURE 3. PLS-2 regression model parity plots (Factor-3) for the calibration and cross validation data from the KS-selected NIR spectra for the normalized concentrations of (A) Np(VI), (B) Np(V), (C) Np(IV), and (D) Np(III).

The scores relationship may be related to the spectra incorporated in the model. Even though pure spectra for each oxidation state are captured in the data set, only three unique steps from one oxidation state are represented in the model [i.e., Np(VI) to Np(V), Np(V) to Np(IV), and Np(IV) to Np(III)]. Only one or two Np oxidation states existed in solution at a given point during the scan. Therefore, synthetic spectra were generated using a mixture design applied to pure end point spectra. This process could be referred to as digital addition, which is the antithesis of digital subtraction. The synthetic NIR mixture spectra (Supplementary Figure S4) and the design parameters (Supplementary Table S1) are shown in the Supporting Information. The PLS-2 model generated from KS-selected NIR spectra (KS-PLS2) was used to predict the relative concentrations of Np oxidation states in these spectra. The synthetic spectra could be considered outliers in some sense because unique proportions of Np oxidation states are represented in the spectra that were not included in the PLS-2 calibration set. The prediction performance for each oxidation state was strong and comparable with the RMSECV statistics presented in Figure 3. The RMSEP values for Np(VI), Np(V), Np(IV), and Np(III) were 0.0043, 0.022, 0.0077, and 0.018, respectively.

3.4 Predicting KS validation set

To further evaluate the difference between models generated using true mixtures and synthetic mixtures, a mixture PLS-2 model (M-PLS-2) was developed using the mixture spectra and relative mixture concentrations. The RMSEC and RMSECV value rounded to zero, which suggests that the data were fit seamlessly. This result is an artifact of the so-called perfectly linear combinations of pure spectra. The M-PLS-2 model and the KS-PLS2 model were used to predict KS-selected validation spectra not included in either data set. The prediction statistics are shown in Table 2. The RMSEP, SEP, and bias values were all similar and represent strong prediction performance. Bias values close to zero are preferred and indicate a random distribution of points above and below the regression line. This result suggests that building synthetic models from pure reference spectra may be sufficient to model systems with true mixtures where spectral features related to interionic associations may not be completely absent but are, in effect, negligible and represent only a small portion of the variance in the model. This result is significant because it means that each combination of Np oxidation states may not need to be generated to build a useful predictive model.

TABLE 2

TABLE 2. Prediction statistics for the KS-PLS2 model and M-PLS-2 models.

PCA analysis and PLSR models were also evaluated using the Vis region from 450 to 900 nm. No clear advantages over the NIR region (900–1,370 nm) were observed, so the results were not included in this work. Under certain circumstances, it could be advantageous to use this region of the absorption spectrum because no NIR water absorption bands are present in this region. (Sadergaski et al., 2021a). NIR absorption water bands occur near 960, 1,200, and 1,450 nm and are highly dependent on temperature, ionic strength, and the presence of ions. The contribution from the NIR water band to the Np spectral features are considered negligible in this work because of the small path length (0.17 cm) and relatively low total Np concentration. Future work could explore a sensor fusion or stacked regression approach to account for the entire spectrum. (Lines et al., 2020; Sadergaski and Andrews, 2022).

3.5 MCR-ALS resolve the Np(VI) to Np(III) scan

MCR-ALS was also evaluated because it could be advantageous compared with the PLSR model approach because it would not require the researcher to deconvolute training set spectra. The 30 KS-selected calibration and validation spectra were analyzed by MCR-ALS to determine the optimal conditions. This method improved the speed of calculations. Solutions derived from the entire set (1,300 spectra) compared with the set of 30 KS spectra were similar (data not shown here). Constraints can minimize the ambiguity in the data decomposition and results but can also play a negative role in the resolution process. The application of constraints should always be grounded in sound reasoning and understanding of the system. Several of the most common constraints were evaluated in this work, including non-negativity, unimodality, and closure. The non-negativity constraint for concentrations and spectra applied in this situation. Additionally, the closure constraint was useful because the total Np concentration, the principle of mass balance, was constant across all samples in the model. Initial estimates from pure reference spectra were also tested but did not appear to improve the resolution process. Regions of the most overlap between oxidation states and the nonlinear 980 nm peak were also omitted from the model.

The MCR-ALS component concentrations and spectra are shown in Supplementary Figure S7. The model suffered from some rotational ambiguity owing to overlapping peaks but was useful for resolving the general features in the data set. It resolved Np(VI), Np(IV), and Np(III) concentrations well. However, the primary Np(V) peak near 1,097 nm was not resolved owing to overlap with both Np(IV) and Np(VI) peaks in this region. On the other hand, the model appeared to resolve Np(IV) concentrations even through they overlapped significantly with the Np(III) peak in the 900–950 nm region. MCR-ALS analysis of the visible region (450–900 nm) yielded similar results. Future iterations could evaluate nonlinear MCR-ALS to account for the nonlinearity of the Np(V) 980 nm peak and include local rank or physiochemical constraints. These constraints can help suppress the ambiguity linked to overlapping peaks.

3.6 PLSR predictions

The KS-PLS2 and M-PLS-2 models were used to predict the relative concentration of Np oxidation states in each sample generated during the scan from VI to III. The normalized concentration profiles are shown in Figure 4. The predicted concentrations of Np in each oxidation state are nearly identical. Slight fluctuation was observed above and below zero, but the estimated deviation (average of 0.01) was sufficient to cover this and not misinterpret the presence of oxidation states that were not coexisting in the sample. The estimated deviation in the M-PLS-2 prediction was comparable with the KS-PLS2 model. However, the error bars shrunk as the relative fraction of oxidation states approached 1. It was lowered by nearly an order of magnitude to ±0.001. This result is likely because of bias in the model toward the pure end points because the model was built using only these spectra. Future versions could investigate the addition of noise or other artifacts to the pure spectra that could help the model cope with pure end points and mixtures more consistently.

FIGURE 4

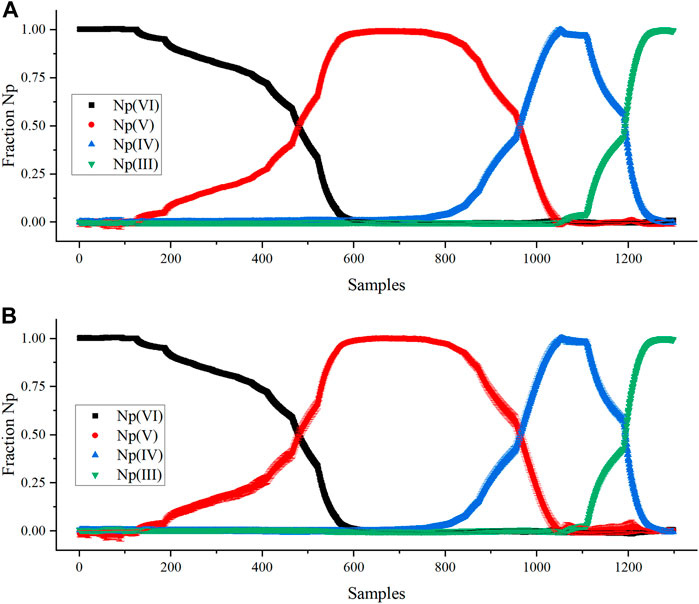
FIGURE 4. Comparing PLSR model Np(VI), Np(V), Np(IV), and Np(III) normalized concentration predictions by (A) KS-PLS2-NIR model and (B) M-PLS-2 model.

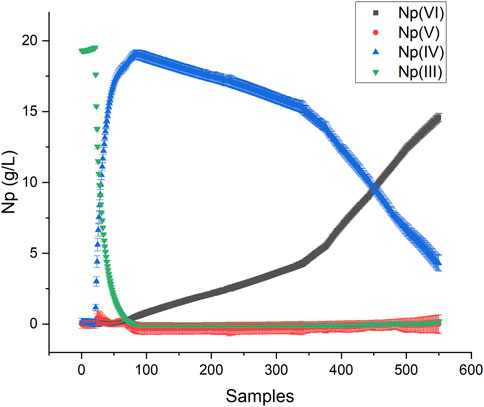
The Y matrix for PLS was scaled by the Np concentration (g/L) to achieve the desired units. Multiplying the Y matrix composed of fractions by the total Np concentration adjusted the magnitude of the vectors but not the direction. This method is a simple way to scale the regression model to the appropriate units. The scaled KS-PLS2-NIR model was used to predict the Np oxidation states in a rapid scan from Np(III) to Np(VI), where the potential was changed abruptly from reducing to oxidizing conditions (Figures S1). This oxidizing scan was more rapid (11 min) than the stepwise reducing scan described above (43 min). This process generated a unique combination of oxidation states, primarily Np(IV) and Np(VI) (Figure 5). This method tested the model’s prediction performance on samples not included in the training set to see if it could cope with spectra corresponding to a unique combination of Np oxidation states [i.e., Np(IV) and Np(VI)]. Very little Np(V) was produced in this scan because the conversion from NpO₂⁺ to NpO₂²⁺ is rapid and not hindered by the formation of the actinyl ion from free Np⁴⁺ ions. The scan stepped slightly outside the electrochemical window for HNO₃, which produced bubbles in the optical pathlength; thus, the scan was stopped prior to complete Np(VI) conversion.

FIGURE 5

FIGURE 5. PLSR predictions during the oxidizing scan from Np(III) to Np(VI).

A Hotelling’s T² statistic with a critical limit based on an F-test (p-value of 5%) was used to identify outliers or situations where spectra were outside the variation captured in the calibration set. It describes the distance to the model center based on the principal components. Each sample falls within the confidence interval, which suggests that the model viewed these samples as falling within the space described by the training set (Supplementary Figure S8). Thus, it is unlikely that significant interionic associations between Np(IV) and Np(VI) resulted in distinct spectral characteristics for this system. This result implies that useful models can still be developed and deployed even when models are not built using spectra representative of each coexisting ion.

The Np molar absorptivity values depend on solution composition, acidity, ionic strength, and temperature. Previous work identified temperature fluctuations in the Np(V) absorption spectrum. (Sadergaski and Morgan, 2022). These shifts can be accounted for using multivariate chemometric methods, but overall, temperature effects presented a small portion of the structured variation in the data set that could likely be neglected over minor temperature differences. In general, Beer’s law applies well for dilute solutions approximately ≤0.01 M for most solutes. (Harris, 2007). In concentrated solutions, solute molecules begin to influence one another owing to their proximity, which changes their properties. The absorbing molecule could also participate in concentration-dependent chemical equilibria. A conservative assumption was that digital subtraction ignores spectral features related to interionic associations. (Chatterjee et al., 2017). It likely depends on the medium, but accounting for interionic associations may not be necessary in certain conditions to develop models that are useful for the intended purpose. (Topin et al., 2010). This work reveals that interionic associations between Np ions of various oxidation states is likely insignificant in HNO₃. However, cation–cation (e.g., NpO₂⁺ to NpO₂²⁺) interactions are expected at concentrations near 0.2 M Np and greater and will likely need to be accounted for. (Guillaume et al., 1982). This work, along with previous work, suggests that accounting for differences owing to acidity, particularly Np(VI) nitrate complexes, may pose the greatest challenge and richest opportunity for online monitoring applications of Np and other actinides (e.g., Pu).. (Ryan, 1960; Lines et al., 2017).

4 Conclusion

A combined spectroelectrochemical and chemometric method was established for the quantification of Np(III/IV/V/VI) in HNO₃. PCA described the data within a multivariate space compatible with KS sample selection. This approach successfully chose a set of representative samples spanning the range of anticipated conditions in the data set. PLSR models built using synthetic mixtures and spectra corresponding to samples with coexisting neptunium oxidation states had similar prediction performance. This result suggests that interionic associations are negligible in this system (∼20 g/L Np) and minimizes the number of experiments necessary to train and validate chemometric models, which is particularly useful for harsh and restrictive radiological applications. Error statistics associated with the model derived from synthetic (i.e., digital addition) mixtures should be considered with caution because of the pristine nature of the data, which caused RMSEC and RMSECV values in the model to approach zero and questionable estimates of the deviation in predicting pure endpoint spectra. Overall, PLSR is a promising option to make accurate predictions in process solutions with multiple Np oxidation states without requiring post-analysis by subject matter experts. This technique and the overarching findings could be leveraged for building spectral data sets and predictive chemometric models to bolster online monitoring applications to support the ²³⁸Pu Supply Program at Oak Ridge National Laboratory and additional opportunities within the nuclear field.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LS: Conceptualization, Formal Analysis, Writing–original draft. HA: Data curation, Writing–review and editing, Methodology. SG: Investigation, Writing–review and editing. AP: Project administration, Resources, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Funding for this effort was provided by the Science Mission Directorate of NASA and administered by the US Department of Energy Office of Nuclear Energy under contract DEAC05-00OR22725. This work used resources at the Radiochemical Engineering Development Center operated by the US Department of Energy’s Oak Ridge National Laboratory.

Acknowledgments

The authors wish to thank Laetitia Delmau and Kristian Myhre for helpful discussions regarding Np spectrophotometry and electrochemistry. This work was supported by the ²³⁸Pu Supply Program at Oak Ridge National Laboratory.

Licenses and permissions

This manuscript has been authored by UT-Battelle LLC under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared parent affiliation with the authors at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1323372/full#supplementary-material

References

Alcaráz, M. R., Andreas Schwaighofer, A., Goicoechea, H., and Lendl, B. (2017). Application of MCR-ALS to reveal intermediate conformations in the thermally induced α-β transition of poly-l-lysine monitored by FT-IR spectroscopy. Acta Part A Mol. Bio. Spec. 185, 304–309. doi:10.1016/j.saa.2017.05.005

CrossRef Full Text | Google Scholar

Andrews, H. B., and Sadergaski, L. R. (2023a). Leveraging visible and near-infrared spectroelectrochemistry to calibrate a robust model for Vanadium(IV/V) in varying nitric acid and temperature levels. Talanta 259, 124554. doi:10.1016/j.talanta.2023.124554

PubMed Abstract | CrossRef Full Text | Google Scholar

Andrews, H. B., and Sadergaski, L. R. (2023b). Hierarchical modeling to enhance spectrophotometry measurements – overcoming dynamic range limitations for remote monitoring of neptunium. Chemosensors 11, 274. doi:10.3390/chemosensors11050274

CrossRef Full Text | Google Scholar

Andrews, H. B., Sadergaski, L. R., and Cary, S. K. (2023). Pursuit of the ultimate regression model for samarium(III), europium(III), and LiCl using laser-induced fluorescence, design of experiments, and a genetic algorithm for feature selection. ACS Omega 8, 2281–2290. doi:10.1021/acsomega.2c06610

PubMed Abstract | CrossRef Full Text | Google Scholar

Ban, Y., Hakamatsuka, Y., Tsutsui, N., Urage, S., Hagiya, H., and Matsumura, T. (2014). Spectroscopic study of Np(V) oxidation to Np(VI) in 3 mol/dm³ nitric acid at elevated temperatures. Radiochim. Acta 102, 775–780. doi:10.1515/ract-2013-2193

CrossRef Full Text | Google Scholar

Chatterjee, S., Bryan, S. A., Casella, A. J., Peterson, J. M., and Levitskaia, T. G. (2017). Mechanisms of neptunium redox reactions in nitric acid solutions. Inorg. Chem. Front. 4, 581–594. doi:10.1039/c6qi00550k

CrossRef Full Text | Google Scholar

Chatterjee, S., Peterson, J. M., Casella, A. J., Levitskaia, T. G., and Bryan, S. A. (2020). Mechanisms of plutonium redox reactions in nitric acid solutions. Inorg. Chem. 59, 6826–6838. doi:10.1021/acs.inorgchem.0c00199

PubMed Abstract | CrossRef Full Text | Google Scholar

Edelstein, N. M. (2015). Reanalysis of the aqueous spectrum of the neptunyl(V) [NpO₂⁺] ion. J. Phys. Chem. A 119, 11146–11153. doi:10.1021/acs.jpca.5b08576

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisensterin, J. C., and Pryce, M. H. L. (1966). Interpretation of the solution absorption spectra of the (PuO₂)⁺⁺ and (NpO₂)⁺ ions. J. Res. Natl. Bur. Stand. A 70, 765–173. doi:10.6028/jres.070A.013

CrossRef Full Text | Google Scholar

Elgrishi, N., Rountree, K. J., McCarthy, B. D., Rountree, E. S., Eisenhart, T. T., and Dempsey, J. L. (2018). A practical beginner’s guide to cyclic voltammetry. J. Chem. Educ. 95 (2), 197–206. doi:10.1021/acs.jchemed.7b00361

CrossRef Full Text | Google Scholar

Friedman, H. A., and Toth, L. M. (1980). Absorption spectra of Np(III), (IV), (V) and (VI) in nitric acid solution. J. Inorg. Nucl. Chem. 42, 1347–1349. doi:10.1016/0022-1902(80)80298-3

CrossRef Full Text | Google Scholar

Guillaume, B., Begun, G. M., and Hahn, R. L. (1982). Raman spectrometric studies of “cation-cation” complexes of pentavalent actinides in aqueous perchlorate solutions. Inorg. Chem. 21 (3), 1159–1166. doi:10.1021/ic00133a055

CrossRef Full Text | Google Scholar

Harris, D. C. (2007). Quantitative chemical analysis. 7th Edition. United States: W.H. Freeman and Company. Chapter 18.

Google Scholar

Kirsanov, D., Rudnitskaya, A., Legin, A., and Babain, V. (2017). UV-VIS spectroscopy with chemometric data treatment: an option for on-line control in nuclear industry. J. Radioanal. Nucl. Chem. 312, 461–470. doi:10.1007/s10967-017-5252-8

CrossRef Full Text | Google Scholar

Lackey, H. E., Sell, R. L., Nelson, G. L., Bryan, T. A., Lines, A. M., and Bryan, S. A. (2023). Practical guide to chemometric analysis of optical spectroscopic data. J. Chem. Educ. 100, 2608–2626. doi:10.1021/acs.jchemed.2c01112

CrossRef Full Text | Google Scholar

Lascola, R., O’Rourke, P. E., and Kyser, E. A. (2017). A piecewise local partial least squares (PLS) method for the quantitative analysis of plutonium nitrate solutions. Appl. Spectrosc. 7, 2579–2594. doi:10.1177/0003702817734000

CrossRef Full Text | Google Scholar

Lines, A. M., Adami, S. R., Sinkov, S. I., lumetta, G. J., and Bryan, S. A. (2017). Multivariate analysis for quantification of plutonium(IV) in nitric acid based on absorption spectra. Anal. Chem. 89 (17), 9354–9359. doi:10.1021/acs.analchem.7b02161

PubMed Abstract | CrossRef Full Text | Google Scholar

Lines, A. M., Hall, G. G., Asmussen, S., Allred, J., Sinkov, S., Heller, F., et al. (2020). Sensor fusion: comprehensive real-time, on-line monitoring for process control via visible, near-infrared, and Raman spectroscopy. ACS Sens. 5, 2467–2475. doi:10.1021/acssensors.0c00659

PubMed Abstract | CrossRef Full Text | Google Scholar

Olivieri, A. C. (2021). A down-to-earth analyst view of rotational ambiguity in second-order calibration with multivariate curve resolution – a tutorial. Anal. Chim. Acta. 1156, 338206. doi:10.1016/j.aca.2021.338206

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellegrino, R. B., and Olivieri, A. C. (2020). A new parameter for measuring the prediction uncertainty produced by rotational ambiguity in second-order calibration with multivariate curve resolution. Anal. Chem. 92, 9118–9123. doi:10.1021/acs.analchem.0c01395

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryan, J. L. (1960). Species involved in the anion-exchange absorption of quadrivalent actinide nitrates. J. Phys. Chem. 64, 1375–1385. doi:10.1021/j100839a007

CrossRef Full Text | Google Scholar

Sadergaski, L. R., and Andrews, H. B. (2022). Simultaneous quantification of uranium(VI), samarium, nitric acid, and temperature with combined ensemble learning, laser fluorescence, and Raman scattering for real-time monitoring. Analyst 147, 4014–4025. doi:10.1039/d2an00998f

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadergaski, L. R., DePaoli, D. W., and Myhre, K. G. (2020). Monitoring the caustic dissolution of aluminum alloy in a radiochemical hot cell using Raman spectroscopy. Appl. Spectrosc. 74 (10), 1252–1262. doi:10.1177/0003702820933616

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadergaski, L. R., Hagar, T. J., and Andrews, H. B. (2022b). Design of experiments, chemometrics, and Raman spectroscopy for the quantification of hydroxylammonium, nitrate, and nitric acid. ACS Omega 7, 7287–7296. doi:10.1021/acsomega.1c07111

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadergaski, L. R., Irvine, S. B., and Andrews, H. B. (2023). Partial least squares, experimental design, and near-infrared spectrophotometry for the remote quantification of nitric acid concentration and temperature. Molecules 28, 3224. doi:10.3390/molecules28073224

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadergaski, L. R., and Morgan, K. (2022). Applying two- dimensional correlation spectroscopy and principal component analysis to understand how temperature affects the neptunium(V) absorption spectrum. Chemosensors 10 (11), 475. doi:10.3390/chemosensors10110475

CrossRef Full Text | Google Scholar

Sadergaski, L. R., Myhre, K. G., and Delmau, L. H. (2022a). Multivariate chemometric methods and Vis-NIR spectrophotometry for monitoring plutonium-238 anion exchange column effluent in a radiochemical hot cell. Talanta Open 5, 100120. doi:10.1016/j.talo.2022.100120

CrossRef Full Text | Google Scholar

Sadergaski, L. R., Patton, K. K., Toney, G. K., DePaoli, D. W., and Delmau, L. H. (2021b). Measuring neptunium concentration using optical spectrometry for the plutonium-238 supply Program. Oak Ridge, TN: Oak Ridge National Laboratory. ORNL Report no. ORNL/TM-2021/2072.

Google Scholar

Sadergaski, L. R., Toney, G. K., Delmau, L. H., and Myhre, K. G. (2021a). Chemometrics and experimental design for the quantification of nitrate salts in nitric acid: near-infrared spectroscopy absorption analysis. Appl. Spectrosc. 75 (9), 1155–1167. doi:10.1177/0003702820987281

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinkov, S. I., Hall, G. B., Heller, F. D., and Lumetta, G. J. (2022). Neptunium redox speciation and determination of its total concentration in dissolved fuel simulant solutions by spectrophotometry. J. Radioanal. Nucl. Chem. 331, 5579–5595. doi:10.1007/s10967-022-08665-8

CrossRef Full Text | Google Scholar

Sjoblom, R., and Hindman, J. C. (1951). Spectrophotometry of neptunium in perchloric acid solutions. J. Am. Chem. Soc. 73, 1744–1751. doi:10.1021/ja01148a091

CrossRef Full Text | Google Scholar

Topin, B. S., Aupiais, J., and Baglan, N. (2010). Determination of the stability constants of nitrate complexes of Np(V) and Pu(V) using CE-ICP-MS. Radiochim. Acta 98, 71–75. doi:10.1524/ract.2010.1687

CrossRef Full Text | Google Scholar

Tse, P., Shafer, J., Bryan, S. A., Nelson, G. L., and Lines, A. M. (2022). Measuring Nd(III) solution concentration in the presence of interfering Er(III) and Cu(II) ions: a partial least squares analysis of ultraviolet–visible spectra. Appl. Spectrosc. 76, 173–183. doi:10.1177/00037028211053852

PubMed Abstract | CrossRef Full Text | Google Scholar

Varga, L. P., Reisfeld, M. J., and Asprey, L. B. (1970). Electronic spectra of the 5f³ actinides: U³⁺, Np⁴⁺, Pu⁵⁺ and AmO₂⁺⁺. The f³ intermediate coupling diagram. J. Chem. Phys. 53, 250–255. doi:10.1063/1.1673772

CrossRef Full Text | Google Scholar

Vries, S. D., and Ter Braak, C. J. F. (1995). Prediction error in partial least squares regression: a critique on the deviation used in the Unscrambler. Chemom. Intell. Lab. Syst. 30, 239–245. doi:10.1016/0169-7439(95)00030-5

CrossRef Full Text | Google Scholar

Zahran, A., Anderson-Cook, C. M., and Myers, R. H. (2003). Fraction of design space to assess prediction capability of response surface designs. J. Qual. Tech. 35 (4), 377–386. doi:10.1080/00224065.2003.11980235

CrossRef Full Text | Google Scholar