Real-time infrared spectroscopy coupled with blind source separation for nuclear waste process monitoring

On-line infrared absorbance spectroscopy enables rapid measurement of solution-phase molecular species. Many spectra-to-concentration models exist for spectral data, with some models able to handle overlapping spectral bands and nonlinearities. However, model accuracy is limited by the quality of training data used in model fitting. The process spectra of nuclear waste simulants at the Savannah River Site display incongruity between training and process spectra; the glycolate spectral signature in the training data does not match the glycolate signature in Savannah River National Laboratory process data. A novel blind source separation algorithm is proposed that preprocesses spectral data so that process spectra more closely resemble training spectra, thereby improving model quantification accuracy when unexpected sources of variation appear in process spectra. The novel blind source separation preprocessing algorithm is shown to improve nitrate quantification from an R² of 0.934 to 0.988 and from 0.267 to 0.978 in two instances analyzing nuclear waste simulants from the Slurry Receipt Adjustment Tank and Slurry Mix Evaporator cycle at the Savannah River Site.

1 Introduction

The Savannah River Site, located in Aiken, South Carolina, has been immobilizing nuclear waste since 1996. The site operates the Defense Waste Processing Facility (DWPF), which processes and vitrifies high-level radioactive waste into borosilicate glass (Lambert et al., 2016; 2021; Ray et al., 2018; Lambert and Howe, 2021; Woodham et al., 2021). Approximately 35 million gallons of high-level waste containing insoluble solids of long-lived radionuclides remain to be stabilized. As part of the DWPF, sludge waste from the tank farm and effluent from the Salt Waste Processing Facility undergo feed preparation in the Sludge Receipt and Adjustment Tank (SRAT). From the SRAT, the waste is added to the Slurry Mix Evaporator (SME). The SME represents the primary control point for DWPF processing for a variety of processing factors; it is the last processing point where chemical additions occur to alter batch composition and where batches can be evaluated without disrupting melter operation (Ray et al., 2018). Because of the feed preparation at the SRAT and the qualifying and regulatory measurements made at the SME, implementation of real-time sensors at these vessels could improve decision-making for waste processing.

During SRAT processing, nitric acid and glycolic acid are fed to the current waste batch in accordance with the nitric-glycolic acid flowsheet (Lambert et al., 2016; Woodham et al., 2021) to neutralize the alkaline sludge waste and reduce mercury (HgO → Hg⁰) for recovery. The system begins with a caustic solution phase (pH 13), which becomes acidic (pH 4) as nitric acid and glycolic acid are introduced. The next batch process occurs in the Slurry Mix Evaporator (SME), where water is evaporated to concentrate the waste, and frit (glass formers) is added to create the feed supplied to the melter. The species’ concentrations change during the process due to ongoing reactions, such as mercury reduction and nitrite conversion to nitrate (Woodham et al., 2021). The waste also has high solids content, which reaches 25 wt% in the SRAT and 50 wt% in the SME (reported as total solids at 110°C) (Woodham et al., 2021). Furthermore, during batch processing, the heels from previous batches are incorporated into successive batches, which results in deviations of batch compositions from feed streams.

In this work, chemical constituents are classified by whether they are quantified by the spectra-to-concentration model. Targets are quantified species, while non-targets are not quantified despite possibly existing in solution. Species may be labeled non-targets because they are: at insignificant concentrations, not relevant for processing, or difficult to quantify because of model and data mismatch. The presence of non-target species can disrupt the quantification of target species, particularly if non-target species are not considered during model fitting. To deal with overlapping non-target species, a blind source separation (BSS) algorithm is proposed. The first and second steps of the BSS algorithm use classical least squares (CLS) followed by principal component analysis (PCA) to identify spectral estimates from mixture spectra. The third and final step of the algorithm uses multivariate curve resolution—alternating least squares (MCR-ALS) to iterate the estimates from the first two steps and any available reference spectra into a bilinear mixture model that matches available process spectra. The proposed BSS algorithm improves the estimation of target species by removing non-target contributions from mixture spectra. In this work, the BSS algorithm removes non-targets given only reference spectra of the target species, nitrate and nitrite, and a poor reference spectrum (a reference spectrum that does not match the shape of the component’s spectrum at process conditions) of the most abundant non-target species, glycolate.

The proposed BSS algorithm improves upon similar algorithms by introducing the CLS and PCA steps to identify spectral estimates that are input into MCR-ALS. In the context of process monitoring, the proposed BSS algorithm may reduce the number and frequency of calibration experiments required for spectroscopic monitoring without compromising accuracy, since non-targets may be omitted from training data. In addition, BSS-preprocessing could facilitate real-time results in scenarios where decision-making is time-sensitive, but process spectra deviate from training data due to unforeseen process conditions, ordinarily requiring additional calibration experiments and corresponding process down-time.

In this paper, Attenuated total reflectance - Fourier transform infrared spectroscopy (ATR-FTIR) is used to analyze anions in the SRAT and SME processes. A novel BSS algorithm is developed to preprocess spectral data by removing the influence of non-target species. To test the proposed algorithm, partial least squares regression (PLSR) prediction accuracy is compared for BSS-preprocessed spectra and spectra with no BSS-preprocessing applied. Lastly, the utility of ATR-FTIR measurements for real-time monitoring is demonstrated in the context of nuclear waste slurries at the Savannah River Site by quantifying a continuous 65-h run of scaled-down SRAT and SME processes.

2 Materials and methods

2.1 Overview of the waste

A simplified process flowsheet for the DWPF is shown in Figure 1. The physical and chemical composition of a representative sludge simulant (i.e., the SRAT feed) is shown in Table 1, while the composition of the final processing points (i.e., the SRAT and SME product slurries) are shown in Table 2. The SRAT feed undergoes chemical preparation (acid addition) in the SRAT before receiving glass frit additions and dewatering at the SME. Nitrate (N${\mathrm{O}}_3^{-}$) and nitrite (N${\mathrm{O}}_2^{-}$) were chosen as target species for estimation because of their process relevance (see Tables 1, 2) and potential for in-line monitoring. Other infrared-active species that may be present during waste processing and labeled as non-targets are: glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$, carbonate $(\mathrm{C}{\mathrm{O}}_{\mathrm{3}}^{\mathrm{2}-})$, oxalate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{2}-})$, formate $(\mathrm{C}\mathrm{H}{\mathrm{O}}_{\mathrm{2}}^{-})$, phosphate $(\mathrm{P}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{3}-})$, and sulfate $(\mathrm{S}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{2}-})$. Glycolate is a non-target because its observed process spectra show deviations from available reference and training spectra, complicating its quantification. Species other than glycolate are labeled as non-targets because of their small expected process concentrations. Known anion reactions that may occur during the SRAT and SME processes include: nitrite destruction, nitrite-to-nitrate conversion, glycolate destruction, glycolate-to-formate conversion, and glycolate-to-oxalate conversion. Detailed information on the expected anion conversions is provided by Woodham and coworkers (Woodham et al., 2021). Typically, anion concentrations at the Savannah River Site are quantified with ion chromatography (IC), which is associated with approximately 10% uncertainty and waiting times on the order of days (White et al., 2015). In addition to ionic species, the simulant also contains the following solids as detected by inductively coupled plasma - atomic emission spectroscopy: Ag, Al, Ba, Ca, Cr, Cu, Fe, Hg, K, Mg, Mn, Na, Ni, Pd, Rh, Ru, S, Si, Zn, and Zr (Woodham et al., 2021).

FIGURE 1

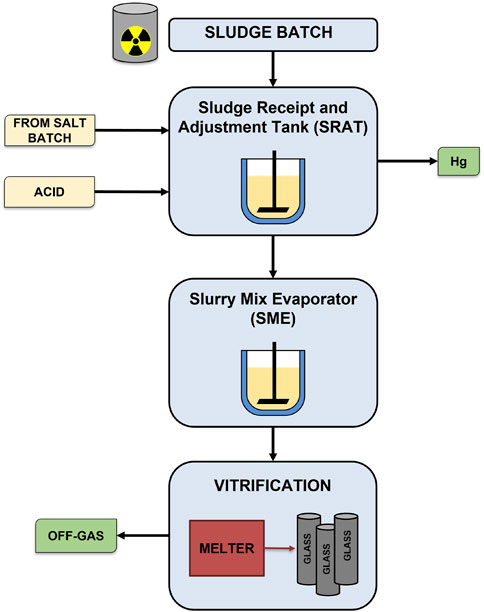
FIGURE 1. Simplified flowsheet for Defense Waste Processing Facility (DWPF) (Ray et al., 2018).

TABLE 1

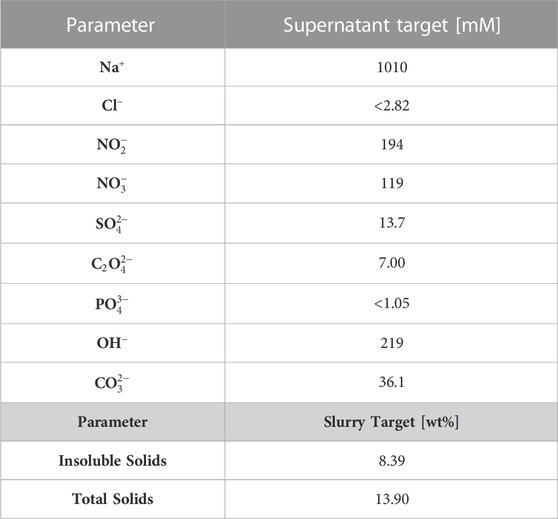
TABLE 1. Simulant SRAT feed composition (i.e., expected process input), corresponding to nonradioactive simulated Tank 40–8 measured by Woodham et al. (2021). The wt% total solids (TS) represents the solids that do not dissolve after heating to 110°C, while the wt% insoluble solids (IS) represents the difference between the measured total solids and dissolved solids.

TABLE 2

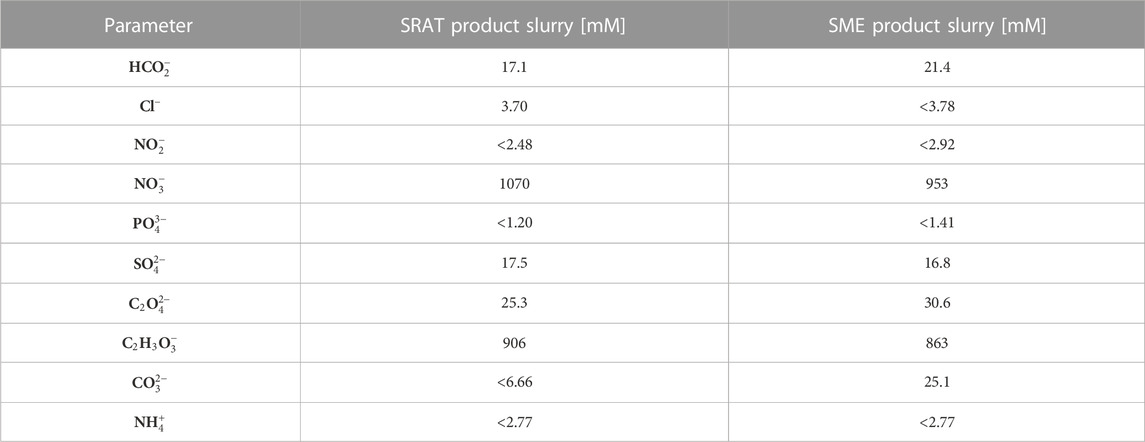
TABLE 2. Simulant SRAT product and SME product concentrations (i.e., expected midpoint and process output, respectively) corresponding to nonradiaoctive simulated Tank 40–8 SRAT/SME product slurries reported by Woodham et al. (2021).

2.2 Design of experiments

Nonradioactive experiments mimicking the DWPF SRAT and SME cycles were performed in a 2-L Mettler Toledo Reaction Calorimeter (RC1) vessel equipped with temperature, pH, and ATR-FTIR probes. Due to the high solids content, the sludge waste was probed with in-situ ATR-FTIR spectroscopy, which was able to measure infrared-active molecules in the solution phase without interference from solid particles because of a shallow laser penetration depth of 2–3 μm (Cornel et al., 2008). ATR-FTIR measured concentrations were compared to IC measured concentrations collected by the Savannah River National Laboratory Process Science Analytical Laboratory. Before IC measurement, samples were caustic quenched by addition of 50% NaOH, which has been reported to increase the accuracy of ion measurements via IC (White et al., 2015). Samples were taken from the SRAT/SME cycles at different processing points in two separate experiments, referred to as Run 1 and Run 2. Run 1 process data correspond to five IC measurements from a SRAT/SME experiment (Supplementary Table S1) with corresponding ATR-FTIR spectra. Run 2 process data correspond to three IC measurements from a SRAT/SME experiment (Supplementary Table S2), also with corresponding ATR-FTIR data. Run 2 has an additional 3899 spectra (collected every minute over the course of 65 h) that do not have associated IC measurements; the spectra will be used to show real-time changes in the SRAT and SME processes. The RC1 vessel was used to collect spectral data for model training (eight experiments shown in Supplementary Table S3), which were designed to match reported anion concentrations in the SRAT/SME sludge simulant (Table 1) and SRAT/SME product (Table 2) for the most abundant anions: nitrate, nitrite, and glycolate. Training data were collected using sodium salts without controlling pH, so training data pHs are basic.

2.3 Blind source separation

Blind source separation refers to techniques that infer original or source signals solely from measurements of signal mixtures (Naik and Wang, 2014). In the context of spectroscopy and this work, blind source separation can be used to estimate and remove the pure sources that make up a signal mixture, even when those sources are unknown. Blind source separation has been shown by Maggioni et al., 2019; Kocevska et al., 2021. to be effective in preprocessing spectra to remove non-target species from Raman and ATR-FTIR spectra in nuclear waste simulants. Kocevska’s BSS algorithm incorporated available process information by augmenting mixture data to include known reference spectra, thereby guiding the identification of sources by independent component analysis (ICA) and MCR-ALS. The proposed algorithm of this work, in contrast, does not require algorithmic identification of known sources; known species are constrained to match user-supplied references, while unknown species are found in a “blind” manner similar to Maggioni’s and Kocevska’s BSS algorithms. The new preprocessing structure allows for available reference spectra to be directly incorporated into a BSS algorithm without estimating them algorithmically. In Kocevska’s and Maggioni’s works, sources identified with ICA and MCR-ALS, even well-known species, are limited in quality by the accuracy of the BSS algorithm; found sources may not always match user-supplied references. A quantitative comparison of BSS methods can be found in Supplementary Figures S1, S2, and in Supplementary Table S4. The proposed algorithm gives the user control over which components are modified and subtracted by the blind source separation algorithm, while still identifying and subtracting unknown species that may arise in real-time due to changing process conditions. In the context of nuclear waste monitoring, such an algorithm could facilitate real-time spectral preprocessing that utilizes available references for target species, while allowing for continual removal of non-target species that may appear or change throughout processing.

The proposed algorithm uses a combined CLS and principal component analysis (PCA) step, rather than ICA as reported previously (Maggioni et al., 2019; Kocevska et al., 2021), to provide initial guesses for MCR-ALS with a nonnegativity constraint. Deviation from a linear combination of known sources (the error matrix from CLS fitting) is used to identify sources in the mixture spectra that do not correspond to known species. Applying PCA to the CLS error matrix to identify unknown sources from mixture spectra has been reported by Haaland and Melgaard, who referred to this technique as spectral residual augmented classical least squares (SRACLS) (Haaland and Melgaard, 2000; Haaland and Melgaard, 2002). Their method improved the prediction accuracy and robustness of CLS by identifying sources of variation not present in their training data. In this work, the residuals of the CLS model fit are analyzed by PCA and then supplied to MCR-ALS to provide a bilinear model for source subtraction. The methodological pipeline is shown in Figure 2.

FIGURE 2

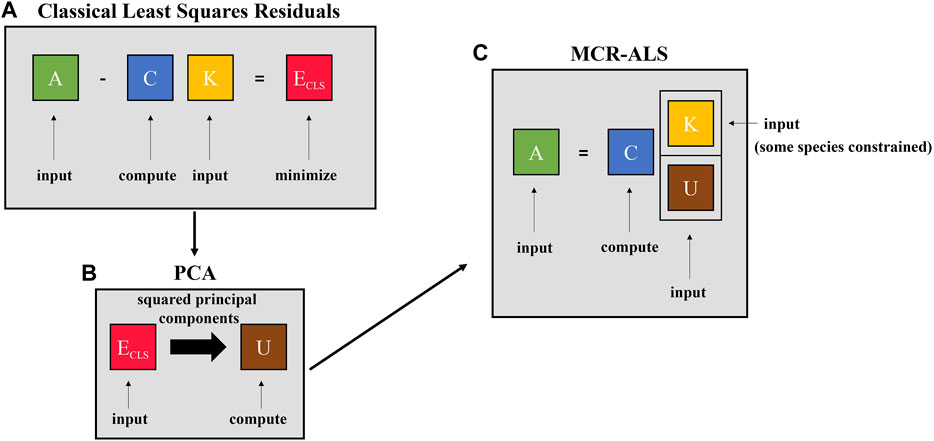
FIGURE 2. Methodological pipeline for the proposed BSS algorithm in three steps: (A) calculate residuals of classical least squares where mixture spectra (A) and reference spectra (K) are used to find the concentration matrix (C) that minimizes (in the least-squares sense) the residual matrix (E_CLS), which provides an estimate of species that do not have known reference spectra, (B) perform principal component analysis on the residual matrix (E_CLS) and extract the (elementwise) squared principal components (U), and (C) perform multivariate curve resolution - alternating least squares using known reference spectra (K) and estimates of unknown sources from principal component analysis (U) to identify a physically realistic mixture model that matches the mixture spectra. After the mixture model is identified, source subtraction can be done as is shown in Eq. 9.

As shown in Figure 2A, the first step of the BSS algorithm is the well-established CLS relationship (Eq. 1), which is used to model mixture spectra with all known reference spectra (targets and non-targets) so that any additional species present can be identified from CLS model error. Model error, in general, accounts for both measurement noise and model mis-match. In the application of spectroscopy, one cause of model mis-match is the presence of unknown species. Minimizing error, E_CLS, in the least squares sense and solving for concentrations, C, is shown in Eq. 2 (Melgaard et al., 2002). The least-squares solution can be found by setting E_CLS = 0 and solving for the concentration matrix, C. Model error can then be solved for in terms of target references, K, and process spectra, A, by rearranging Eq. 1 and inserting Eq. 2, yielding Eq. 3:

$\mathbf{A}=\mathbf{C}\mathbf{K}+{\mathbf{E}}_{\mathrm{C}\mathrm{L}\mathrm{S}}(1)$

$\mathbf{C}=\mathbf{A}{\mathbf{K}}^{\mathbf{T}}{\left(\mathbf{K}{\mathbf{K}}^{\mathbf{T}}\right)}^{-1}(2)$

${\mathbf{E}}_{\mathrm{C}\mathrm{L}\mathrm{S}}=\mathbf{C}\mathbf{K}-\mathbf{A}=\mathbf{A}{\mathbf{K}}^{\mathbf{T}}{\left(\mathbf{K}{\mathbf{K}}^{\mathbf{T}}\right)}^{-1}\mathbf{K}-\mathbf{A}(3)$

where A is an n × q matrix of mixture spectra, C is an n × p concentration matrix of pure components, K is an p × q matrix of pure component reference spectra of the target species, and E_CLS is an n × q matrix representing noise and error that is not modeled with linear combinations of the known reference spectra. In this work, there are n experimental observations, q is the dimension of the spectra (reported wavenumbers), and p is the number of sources for which references exist.

The second step of the proposed BSS algorithm, shown in Figure 2B, applies PCA to the residuals from the error matrix of CLS fitting, E_CLS. PCA reduces the dimensionality of data by projecting the data onto a space of reduced dimension while maximizing the variance in the projected data (Bishop, 2006; Brunton and Kutz, 2022). PCA assumes that the data have been mean-centered, meaning that the data have been mean-centered by subtracting the mean row, ${\bar{\mathbf{E}}}_{\mathrm{C}\mathrm{L}\mathrm{S}}$, from each row of the original matrix. The principal components of a matrix can be found as the eigenvectors of the matrix’s covariance matrix, Φ. Calculating the covariance matrix, shown in Eq. 4, and finding the associated eigenvectors, shown in Eq. 5, yield the principal components of PCA:

$\mathbf{\Phi }=\frac{1}{n-1}{\left({\mathbf{E}}_{\mathrm{C}\mathrm{L}\mathrm{S}}-{\bar{\mathbf{E}}}_{\mathrm{C}\mathrm{L}\mathrm{S}}\right)}^{\text{T}}\left({\mathbf{E}}_{\mathrm{C}\mathrm{L}\mathrm{S}}-{\bar{\mathbf{E}}}_{\mathrm{C}\mathrm{L}\mathrm{S}}\right)(4)$

${\mathbf{\Phi }\mathbf{v}}_i={\lambda }_i{\mathbf{v}}_i(5)$

where v_i is the i^th eigenvector (i^th principal component) corresponding to λ_i, the i^th eigenvalue. In the context of the present BSS algorithm, the largest r eigenvalues are retained in addition to the corresponding eigenvectors/principal components, where r is the number of expected sources beyond to the p known references. The principal components from PCA, rather than loadings as used by Haaland and Melgaard, are used in this work (Haaland and Melgaard, 2002). Principal components have unit scaling, whereas loadings do not, and so principal components were chosen as “standardized” initial guesses for the subsequent MCR-ALS algorithm. The principal components, once computed, are squared so that the spectra are nonnegative for MCR-ALS (step three). This process is shown in Eq. 6, where the elements of each principal component are squared (◦2 represents the elementwise square or Hadamard power of a matrix). This follows the methodology of Maggioni’s two-step BSS algorithm that squares independent components from ICA (which may also have negative components) before inputting into MCR-ALS, which has a nonnegativity constraint applied (Maggioni et al., 2019).

$\mathbf{U}={\mathbf{V}}^{◦2}=\left[\begin{array}{cccc}\hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \\ \hfill {\mathbf{v}}_1^{◦2}\hfill & \hfill {\mathbf{v}}_2^{◦2}\hfill & \hfill \dots \hfill & \hfill {\mathbf{v}}_r^{◦2}\hfill \\ \hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \end{array}\right](6)$

The third step of the BSS algorithm, shown in Figure 2C, uses the known references and estimated unknown sources from PCA as source estimates for MCR-ALS. MCR-ALS is a bilinear model that decomposes mixture spectra into a concentration matrix, C, and a reference spectra matrix, S^T, as is shown in Eq. 7 (Tauler et al., 1993; Tauler, 1995; Jaumot et al., 2015). In Figure 2C, the reference spectra are divided into known references (K) and estimated references (U) that are the squared principal components from the PCA step.

$\mathbf{D}={\mathbf{C}\mathbf{S}}^{\text{T}}+{\mathbf{E}}_{\text{MCR}-\text{ALS}}(7)$

For MCR-ALS, initial guesses can be supplied for either C or S^T. In this work, reference spectra (S^T) are supplied which MCR-ALS iterates to match the process spectra. MCR-ALS is calculated with a nonnegativity constraint in this work to eliminate negative or physically unrealistic spectra. The initial guess for spectra, ${\mathbf{S}}_{\text{Guess}}^{\text{T}}$ is given by a vector of concatenated columns of p known reference spectra and r spectral estimates provided by PCA. The number of spectral estimates, r, is determined by the MCR-ALS algorithm, which is described in Section S3. Eq. 8 shows the initial guess provided for S^T. In this work, the MCR-ALS algorithm applies a constraint that the target species remain identical to the user-supplied references; this is a default functionality of the MCR-ALS algorithm and denoted by the bar $(\stackrel{̄}{})$ over species held constant in Eq. 8 (Camp, 2019). The constraint on target species may be advantageous for a real-time monitoring scenario since the constraint gives the blind source separation algorithm predictable behavior for the target species, improving model interpretability and reliability. In this paper, references are provided for $\mathrm{N}{\mathrm{O}}_{\mathrm{3}}^{-}$, $\mathrm{N}{\mathrm{O}}_{\mathrm{2}}^{-}$, ${\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}^{-}$, and H₂O. The MCR-ALS algorithm constrains the calculated spectra to match the user-supplied reference spectra for $\mathrm{N}{\mathrm{O}}_{\mathrm{3}}^{-}$, $\mathrm{N}{\mathrm{O}}_{\mathrm{2}}^{-}$, and H₂O.

${\mathbf{S}}_{\text{Guess}}^{\text{T}}=\left[\begin{array}{cccccccc}\hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \\ \hfill {\bar{\mathbf{k}}}_{\mathrm{N}{\mathrm{O}}_{\mathrm{3}}^{-}}^{\text{T}}\hfill & \hfill {\bar{\mathbf{k}}}_{\mathrm{N}{\mathrm{O}}_{\mathrm{2}}^{-}}^{\text{T}}\hfill & \hfill {\mathbf{k}}_{{\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}^{-}}^{\text{T}}\hfill & \hfill {\bar{\mathbf{k}}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\text{T}}\hfill & \hfill {\mathbf{u}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}}1}^{\text{T}}\hfill & \hfill {\mathbf{u}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}}2}^{\text{T}}\hfill & \hfill \dots \hfill & \hfill {\mathbf{u}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}r}}^{\text{T}}\hfill \\ \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \end{array}\right](8)$

The MCR-ALS algorithm produces a model that is capable of decomposing the process spectra into estimated source spectra. Subsequently, the sources corresponding to non-targets are subtracted. In this work, glycolate is a non-target species and is subtracted, along with any other detected sources. Water, while not a target, is the solvent and not subtracted in this work since it does not contribute significant spectral variation between measurements. Eq. 9 shows the subtraction of non-target sources using the model produced by MCR-ALS.

${\mathbf{A}}_{\text{Preprocessed}}=\mathbf{A}-\left[\begin{array}{ccc}\hfill ------\hfill & \hfill {\mathbf{C}}_{{\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}^{-}}\hfill & \hfill ------\hfill \\ \hfill ------\hfill & \hfill {\mathbf{C}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}}1}\hfill & \hfill ------\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill \\ \hfill ------\hfill & \hfill {\mathbf{C}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}r}}\hfill & \hfill ------\hfill \end{array}\right]\left[\begin{array}{cccc}\hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \\ \hfill {\mathbf{S}}_{{\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}^{-}}^{\text{T}}\hfill & \hfill {\mathbf{S}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}}1}^{\text{T}}\hfill & \hfill \dots \hfill & \hfill {\mathbf{S}}_{\text{Guess\hspace{0.17em}\hspace{0.17em}r}}^{\text{T}}\hfill \\ \hfill |\hfill & \hfill |\hfill & \hfill \hfill & \hfill |\hfill \end{array}\right](9)$

After source subtraction, the resulting preprocessed data can be robust to infrared-active species outside of the training dataset and spectral changes that occur in complex mixtures. Process implementation of BSS preprocessing can enable more accurate quantification of target analytes. However, concurrently operating fault detection algorithms should, in general, utilize unaltered spectra, since the BSS preprocessing discussed in this work may mask equipment failures or significant spectral changes that may be valuable for detecting sensor or process faults.

2.4 Partial least squares regression

PLSR with four latent variables is used to quantify all of the spectra in this work, and is performed after BSS-preprocessing described in Section 2.3. PLSR has been well-reported in its ability to quantify complex mixture spectra with overlapping spectral bands, particularly when monitoring nuclear waste solutions with vibrational spectroscopy. Recent work in the nuclear field has applied PLSR to: locally linear regimes using piecewise PLSR with absorbance spectroscopy (Lascola et al., 2017), multiple species in real Hanford waste using Raman spectroscopy (Tse et al., 2021), and sodium salt solutions with a limited training set using ATR-FTIR and Raman spectroscopy (Kocevska et al., 2021). Since concentration is restricted to nonnegative values, a nonnegativity constraint is applied to all PLSR results for physical accuracy. Prior to being input into PLSR models but following BSS-preprocessing from Section 2.3, all spectra are filtered with the Savitzky-Golay method utilizing seven filter points, a second order polynomial, and a first order derivative. Spectra and concentrations are standard scaled by mean-subtraction and scaling to unit variance immediately prior to PLSR quantification.

2.5 Computation

Python 3.9 was used for all computation and data analysis in this work, with the code and experimental dataset from this work published on GitHub. The scikit-learn implementations of PLSR, PCA, and FastICA were used, while SciPy was used for Savitzky-Golay Filtering. The NIST package, pyMCR, was used to perform MCR-ALS (Camp, 2019).

3 Results and discussion

ATR-FTIR reference spectra of measurable solution analytes are shown in Section 3.1. The ATR-FTIR spectrum of glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$ is observed to display nonlinear peak-shifting as a result of variable process parameters in Section 3.2. In Section 3.3, the developed BSS algorithm is used to remove a glycolate source from spectra of Run 1 and is used to identify and remove two glycolate sources from Run 2. Lastly five spectra from Run 1 are quantified in Section 3.4 and 3902 spectra from Run 2 are quantified in Section 3.5.

3.1 Reference spectra

ATR-FTIR reference spectra were collected to determine spectral signatures of possible analytes in the SRAT and SME vessels. While nitrate and nitrite represent the target species for the slurry, the slurry may include additional anions at low concentrations (see Tables 1, 2). Reference data for all known IR-active species at approximate SRAT/SME concentrations are shown in Figure 3 with reference spectra concentrations listed in Table 3. The target species are highly IR-active, while some of the non-target species (such as oxalate and formate) have weak IR signals at process-relevant concentrations. Since the non-target species, excluding glycolate, are not present at high concentrations in the waste, it is possible that they do not significantly interfere with the signals of the targets. The peaks of non-target species (shown in Figure 3B) other than glycolate were not included as references in the BSS algorithm. Carbonate and sulfate are 2.58 and 2.70 times more concentrated in the references of Figure 3B than in the typical feed to the SRAT (Table 1). Carbonate, sulfate, and other non-targets were not reliably observed in the mixture spectra, and so the BSS algorithm is tasked with identifying these species if they are significantly present in the solution.

FIGURE 3

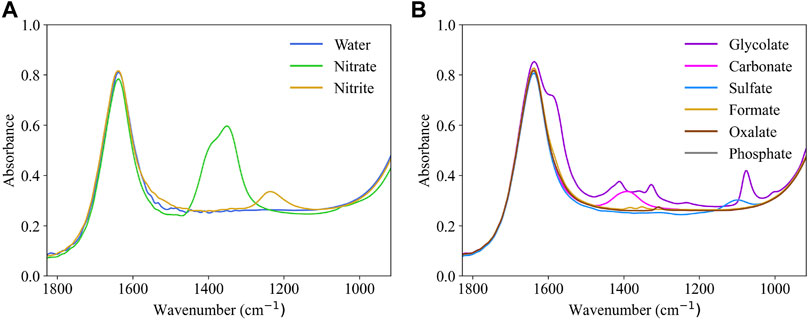
FIGURE 3. Reference spectra of aqueous (A) target anions (including water) and (B) non-target anions found in the DWPF waste during the SRAT and SME processes collected at 25°C. Corresponding concentrations are listed in Table 3.

TABLE 3

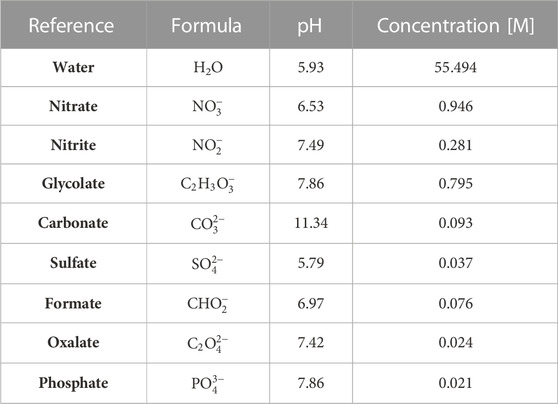
TABLE 3. Concentrations of reference spectra shown in Figure 3, representative of expected process concentrations from Tables 1, 2. Collected at 25°C and pH-calibrated at 22°C.

3.2 Processing variables: temperature and pH

Processing variables can affect ATR-FTIR signals, which affects both interpretation and reliability of signal-to-composition models. Processing variables of interest for the SRAT/SME process include temperature and pH. Temperature starts at room temperature (approximately 25°C) but is near-boiling (approximately 93°C) for much of the process. Likewise, pH begins at 13 and drops to 4 through acid addition. In this section, variations in spectra with processing parameters will be discussed to determine what nonlinearities, if any, are present in the ATR-FTIR spectra of the SRAT and SME processes.

Low-temperature (25°C) and high-temperature (80°C–93°C) 1 M reference spectra of nitrate (N${\mathrm{O}}_3^{-}$), nitrite (N${\mathrm{O}}_2^{-}$), glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$, and glycolic acid (C₂H₄O₃) are shown in Figure 4. Nitrate, shown in Figure 4A, has a temperature-dependent peak shift that can be seen on the lower-wavenumber side of the 25°C nitrate peak. The nitrate anion (N${\mathrm{O}}_3^{-}$) has previously been shown to display peak-shifting in the Raman spectrum resulting from ion association (Kocevska et al., 2022). In addition, temperature-dependent ion association has been demonstrated by Yu et al. (2012). At elevated temperatures (40°C → 80°C) and high concentrations of sodium nitrate, Yu et al. attribute shift in the Raman spectrum to complex aggregated contact ions, indicating that sodium (Na⁺) and nitrate (N${\mathrm{O}}_3^{-}$) tend to aggregate at higher temperatures. There is a decrease in the total peak area and a shift in location of the nitrate peak, indicating possible shifting between sub-peaks for the nitrate anion. The peak location for nitrite, glycolate, and glycolic acid all display subtle temperature variations with our instrument, shown in Figures 4B–D. However, pH has a greater impact than temperature on FTIR spectra at the Savannah River Site.

FIGURE 4

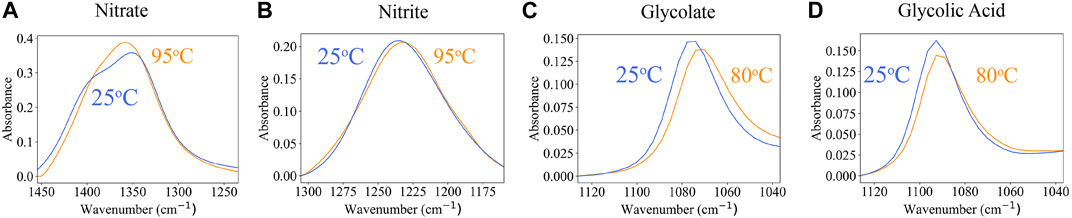
FIGURE 4. Comparison of 1 M ATR-FTIR absorbance spectra at low and high temperatures for (A) nitrate (N${\mathrm{O}}_3^{-}$), (B) nitrite (N${\mathrm{O}}_2^{-}$), (C) glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$, and (D) glycolic acid (C₂H₄O₃).

The feed stream to the SRAT typically has a pH of 13, which decreases to a pH around 4 after the addition of both nitric acid and glycolic acid. This pH shift affects the speciation of weak acids, such as glycolic acid, in the solution phase. Glycolate begins SRAT processing in a deprotonated form, due to the high solution pH, and shifts to a protonated form as the solution pH decreases. Glycolate speciation, shown in Figures 5A, is calculated by using the pKa of glycolic acid and Eq. 10. Based on values available in the literature, a pKa value of 3.83 for glycolic acid at 25°C is used (Serjeant and Dempsey, 1979).

$molefractionofprotonatedacid=\frac{10^{-pH}}{10^{-pH}+10^{-pKa}}(10)$

The ATR-FTIR spectra of glycolate, after the spectra of water have been subtracted, are shown as a function of pH in Figure 5B. As can be seen from the magnified region in Figure 5B, the glycolate peak matches the peak seen in the training data at high pH. As pH is lowered, another peak appears on the higher-wavenumber side of the high pH glycolate peak while the original peak decreases. The result is a 15 cm⁻¹ shift in the 1078 cm⁻¹ glycolate peak to 1093 cm⁻¹. The acidic form of nitrite (N${\mathrm{O}}_2^{-}$), nitrous acid (HNO₂), is a weak acid with a pKa of 2.3 (das Graças Gomes et al., 1993). However, nitrite-destruction reactions decrease nitrite below the limit of detection for ATR-FTIR before nitrous acid is expected to be detectable in solution.

FIGURE 5

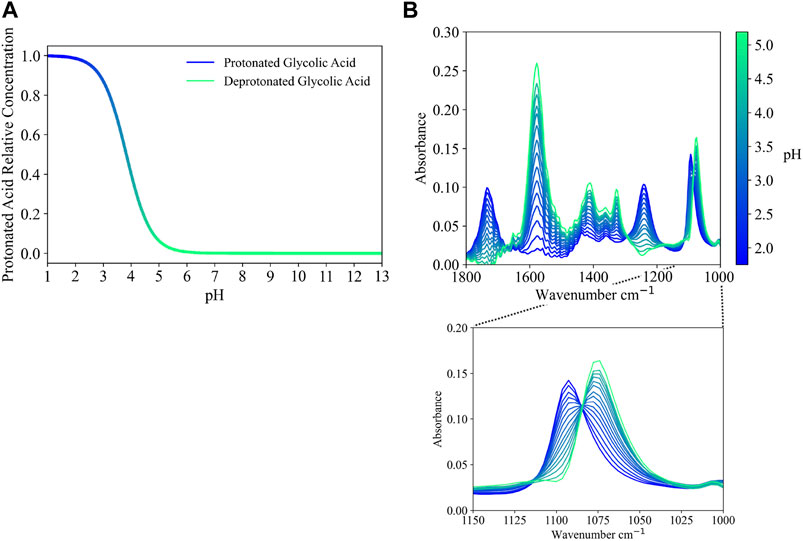
FIGURE 5. (A) Protonation of glycolic acid calculated as a function of pH using a pKa of 3.83 (Serjeant and Dempsey, 1979) and (B) reference spectra (water subtracted) for glycolate at 25°C as a function of pH.

Since the key measurements during DWPF processing occur at a constant temperature of 93°C, the training data for the system were collected at 93°C and are shown in Figure 6A. Approximate pH data are shown in Supplementary Tables S1–S3 in the Supplementary Information. The process data, shown in Figure 6B (Run 1) and 6c (Run 2), were sampled during runs of the SRAT/SME cycle. The spectra baseline and the shape of the glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$ peak differ between the training and process spectra shown in Figure 6. The effect of the variable baseline is minimized by taking the first derivative of the spectra using the Savitzky-Golay Filter (not shown). The glycolate peaks in both process runs deviate from that of the training data, as is shown by the magnified sections in Figure 6. Specifically, the glycolate peak from Run 1 (Figure 6B) has a shoulder on the higher-wavenumber side that is not present in the training data (Figure 6A). Run 2 (Figure 6C) has, by comparison to Run 1, a sharper glycolate peak that has a smaller shoulder on the higher-wavenumber side and shoulder on the lower-wavenumber side as well. The peak-shifting from Figure 5 may account for much of the difference observed between training data and process data in Figure 6. These changes in the glycolate peak location and shape may affect a spectra-to-concentration model fit using the training data from Figure 6A, where the glycolate peak is in a single location.

FIGURE 6

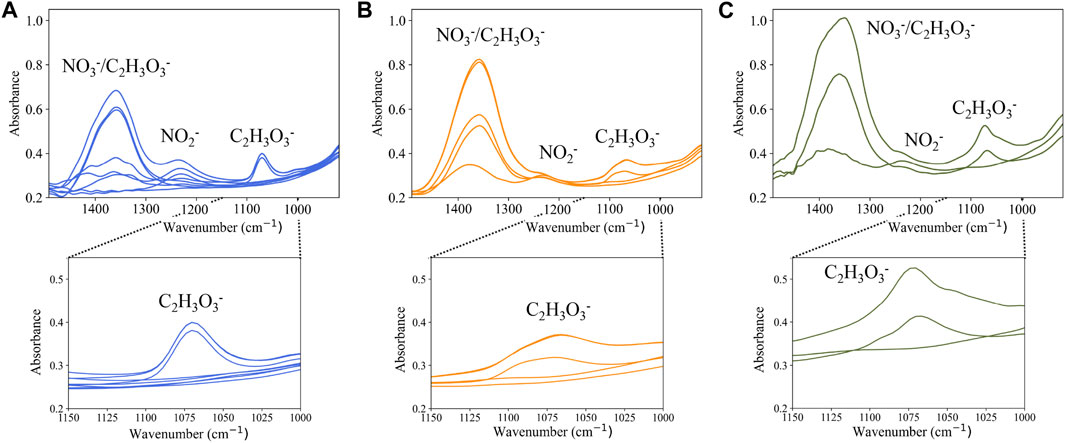
FIGURE 6. (A) PLSR model training data, (B) process data from Run 1 collected from five different conditions in the SRAT/SME process, and (C) process data from Run 2 from three different conditions in the SRAT/SME process. The magnified region (1000–1150 cm⁻¹) highlights the glycolate $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$ peak.

3.3 Blind source separation source matching

In this work, nitrate and nitrite are target species to be quantified. Therefore, it is the objective of the BSS algorithm to remove non-target species: known sources that deviate from training conditions (glycolate) and unknown sources with unknown spectra (potentially oxalate, carbonate, formate, phosphate, and sulfate). While the presence and approximate concentration ranges of non-target components may be known, much of their chemistry has not been fully elucidated in the complex mixtures present in the DWPF.

The BSS algorithm proposed in Section 2.3 was run separately on the process spectra from Run 1 (Figure 6B) and Run 2 (Figure 6C). The BSS algorithm was provided the target reference spectra (including water) from Figure 3A and an initial guess for glycolate from the high-pH reference in Figure 3B. The MCR-ALS step determined the number of additional sources, beyond glycolate, to be zero for Run 1 and one for Run 2.

Run 1 BSS source matching is shown in Figure 7A, where the BSS-determined glycolate source (pink) is compared to the high-pH glycolate reference (dashed black) and the mixture spectra (blue) of Run 1. BSS, particularly the MCR-ALS step, estimates the glycolate contribution to be broader than the supplied reference, as can be seen by the pink curve having greater peak width at the 1078 cm⁻¹ peak than the dashed black curve. The MCR-ALS algorithm produces this “widened” glycolate source by altering the provided reference spectra of non-targets to match the calculated bilinear model (Eq. 7) with the experimental mixture spectra from Figure 7A (shown in blue). From Figure 7A, the BSS-determined source (pink) better matches the qualitative shape of the measured (blue) peak at 1078 cm⁻¹ than the supplied high-pH glycolate reference (dashed black).

FIGURE 7

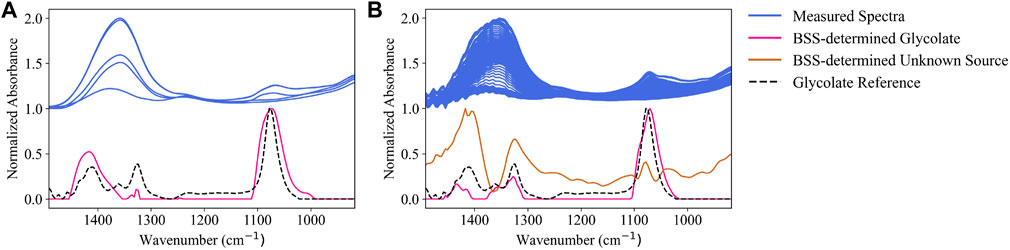
FIGURE 7. Comparisons between measured spectra (93°C), high-pH glycolate reference (25°C), BSS-estimated glycolate reference, and a calculated source from the BSS algorithm for (A) Run 1 and (B) Run 2.

Run 2 BSS source matching is shown in Figure 7B, where continuous run data (3902 spectra) of the SRAT and SME processes are analyzed. A source (brown) is identified in Figure 7B that does not match any user-input reference sources. The proposed source resembles a baseline shift, in addition to model mismatch in the region of glycolate (1078 cm⁻¹) and nitrate, carbonate, and glycolate (1410 cm⁻¹). The discovered peak centered on 1410 cm⁻¹ may correspond to glycolate or carbonate, both of which have associated peaks in that location. The combined baseline and model mismatch may demonstrate a limitation of using PCA (or other latent variable methods) to identify sources; principal components may not be have a single physical interpretation and may instead be a combination of sources. During Run 2 (Figure 7B), the glycolate peak (pink) is again “widened” to match the appearance of glycolate in the mixture spectra (blue).

3.4 Quantification of anions in SRAT/SME samples (Run 1)

Figure 8A shows BSS-preprocessing and its removal of estimated glycolate contributions from process spectra of Run 1. Peaks are subtracted in the vicinity of 1078 cm⁻¹ and 1450 cm⁻¹. The parity plots comparing the concentration predictions for PLSR models using either original spectra or BSS preprocessed spectra are shown in Figure 8B. Quantifiable improvements are achieved with BSS preprocessing applied and are shown in Table 4. Nitrate quantification is improved from an R² value of 0.934 to an R² value of 0.988 with BSS preprocessing applied to the spectra. Nitrite quantification is also improved, but the quantification at process concentrations is limited for both original and preprocessed spectra. This error is likely due to low concentration of the nitrite anion in solution and corresponding low intensity of the nitrite peak in the FTIR spectrum. In Table 4, mean percent error is not quantified for nitrite since it has IC-measured concentrations of zero, which causes a division-by-zero error.

FIGURE 8

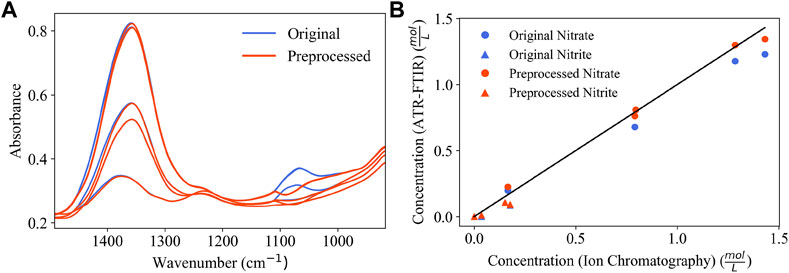
FIGURE 8. (A) Overlay of Run 1 spectra before and after BSS-preprocessing; (B) parity plot comparing Run 1 concentration predictions for a PLSR model (blue) and PLSR model with BSS-preprocessing applied (red).

TABLE 4

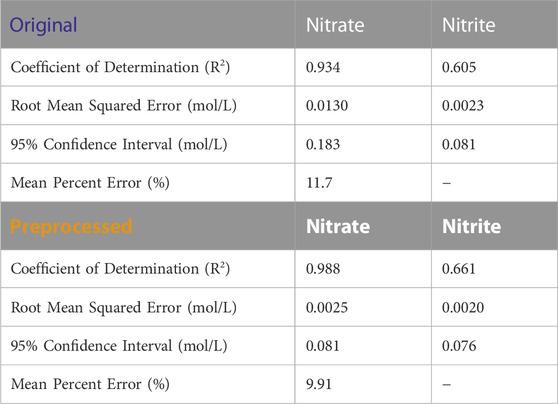
TABLE 4. Table of error metrics corresponding to Figure 8B.

Applying blind source separation to the process data improves the quantification of nitrate and possibly nitrite while also providing visually interpretable results through peak subtraction. The peak that is removed at 1078 cm⁻¹ corresponds to glycolate based on process knowledge and peak location. However, this glycolate peak has a different shape than the supplied glycolate reference and the spectra appearing in the training dataset. The BSS algorithm is able to improve the initial guess of the glycolate spectrum to better match the components observed in the mixture spectra, resulting in an accurate bilinear mixture model that allows glycolate contributions to be removed for improved model quantification.

3.5 Quantification of anions in continuous SRAT/SME samples (Run 2)

Figure 9A shows BSS-preprocessing and its removal of estimated glycolate contributions from 3902 process spectra. The parity plots comparing the concentration predictions for PLSR models using both original spectra and BSS preprocessing are shown in Figure 9B. Quantifiable improvements are achieved with BSS preprocessing for nitrate quantification. The model error is shown in Table 5. Nitrate quantification is improved from an R² value of 0.267 to an R² value of 0.978 with BSS preprocessing applied to the spectra. Nitrite quantification is less accurate with an initial R² of 0.722 which decreases to 0.703 with BSS-preprocessing. A limitation of nitrite quantification results for Run 2 are that only three timepoints have corresponding IC-reported concentration values, and two of the three timepoints report the nitrite IC concentration at zero (measured below 100 ppm). Therefore, there is a single measurement containing nitrite for quantification for Run 2. Nitrate, however, is present in significant amounts in all three timepoints in Figure 9B. Supplementary Table S5, Supplementary Figures S3, S4 in the Supplementary Information show a comparative study where the BSS algorithm is provided different combinations of low- and high-pH glycolate sources.

FIGURE 9

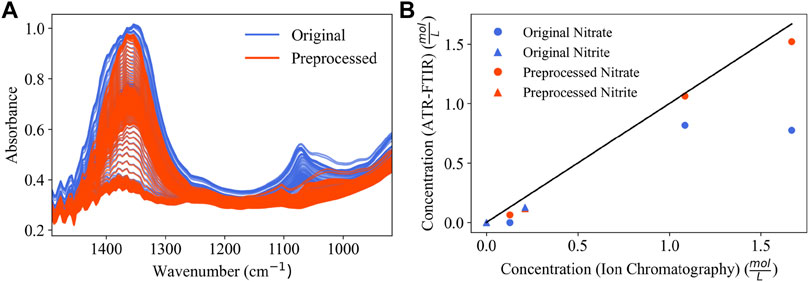
FIGURE 9. (A) Overlay of 3902 process spectra from Run 2 before and after BSS-preprocessing; (B) parity plot comparing Run 2 concentration predictions for a PLSR model (blue) and a PLSR model with BSS-preprocesssing applied (red).

TABLE 5

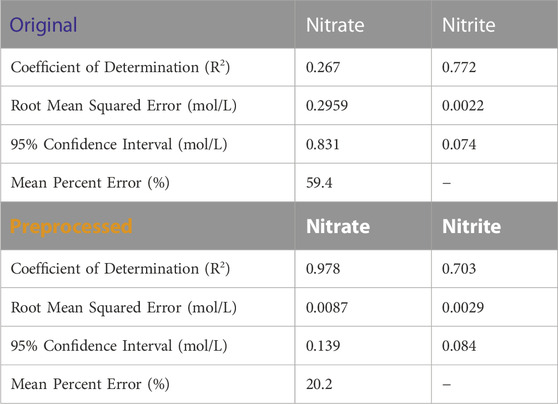
TABLE 5. Table of error metrics corresponding to Figure 9B.

ATR-FTIR has the capability for real-time measurements, whereas IC measurements often incur measurement delays. Figure 10, which reports concentrations at every timepoint for Run 2 along with the three timepoints with IC data, highlights the distinction between time resolution provided by ATR-FTIR and IC for a typical SRAT/SME cycle. Glycolate contributions have been removed using BSS preprocessing in Figure 10A, whereas no BSS preprocessing is applied in Figure 10B. In Figure 10A, only two species are quantified: nitrate and nitrite. However, these two species match the reported IC concentrations (denoted by the circles and triangles) more closely throughout processing than the equivalent quantification with no preprocessing in Figure 10B. Most notable is the difference in nitrate quantification, which is much improved when BSS-preprocessing is applied. The better agreement of BSS-preprocessed ATR-FTIR prediction with IC measurements in Figure 10A has the drawback of not quantifying glycolate, even if Figure 10B suggests that glycolate is quantified poorly given the available training data. In the case where it is desirable to improve quantification of nitrate and nitrite via BSS and additionally quantify glycolate, two separate models could be constructed for providing original glycolate estimates (still including any errors of the original spectra) while improving nitrate and nitrite estimates through source subtraction.

FIGURE 10

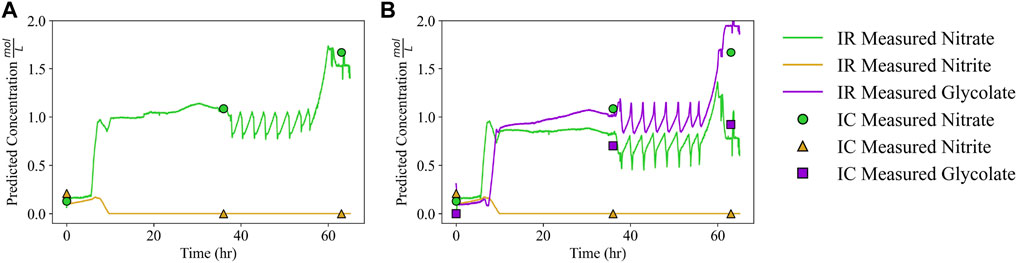
FIGURE 10. Continuous SRAT and SME data (Run 2) quantified using (A) BSS to remove glycolate contributions and a PLSR quantification model and (B) only a PLSR quantification model where glycolate is quantified and not removed.

Based on the results for quantifying nitrate and nitrite, ATR-FTIR is able to measure the concentration of target anions as they undergo additions and reactions in the SRAT/SME processes. Nitrate concentration, monitored via ATR-FTIR in Figure 10, sharply increases 8 h into Run 2. The measured nitrate increase corresponds to the addition of nitric acid in the SRAT, which indicates ATR-FTIR can verify nitric acid addition. Additionally the saw-tooth pattern appearing in Figure 10 around 40 h into the process corresponds to the repeated addition of water followed by a dewatering step. Dewatering is observed as an increase in concentration as the solvent evaporates, concentrating the remaining solution. In SRAT/SME processing, solution-phase concentration information during the dewatering step can be used to verify that the expected mass is evaporated. By measuring nitrate concentration, unexpected changes in heating efficiency, changes in specific heat of the feed stream, or clogs in the vapor outlet could be detected and undergo further troubleshooting. Similarly, the nitrite anion can be monitored to ensure that all nitrite is destroyed through acid addition, at least to the limit that is detectable with ATR-FTIR. In Figure 10B, qualitative information is provided for the glycolate anion despite quantitative inaccuracy. The glycolate concentration can be seen to sharply increase shortly after the nitrate concentration increases. This is from the glycolic acid addition, which follows the nitric acid addition and introduces glycolate to the SRAT. The acid additions also lower the solution pH to about 4, which will cause some glycolate to exist in its protonated form for the remaining duration of SRAT/SME processing.

The presence of nitrate, an abundant analyte that is active in the infrared spectrum, may allow for other nonvolatile and nonreactive solution species to be estimated with a mass-balance during the chemical additions, dewatering process, and up until the slurry is transported to the melter. As the final control point before the slurry is melted, close monitoring of the solution-phase in the SRAT and SME could accelerate and support decisions made by the DWPF Analytical Laboratory regarding waste batch approval (Ray et al., 2018).

4 Conclusion

This work serves as both a proof of concept on the use of ATR-FTIR spectroscopy for monitoring slurry samples at the Savannah River Site and an example of a novel blind source separation algorithm for improving quantification of complex mixture spectra. ATR-FTIR spectroscopy performs rapid process measurements compared to typical IC sample analysis, enabling real-time monitoring and decision-making. However, the complex chemistry and variable process parameters in vessels at the Savannah River Site necessitate ATR-FTIR spectra-to-composition models that are robust to changing chemical and process conditions. In this work, measured ATR-FTIR spectra were combined with a blind source separation algorithm to overcome limited training spectra that do not match process spectra. Specifically, the glycolate anion $({\mathrm{C}}_{\mathrm{2}}{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{3}}^{-})$ is observed to change spectroscopic behavior in slurries typical of the Savannah River Site, which is attributed to shifting pH from nitric and glycolic acid additions during processing. To address the behavior of the glycolate anion in future Savannah River Site monitoring tasks, a spectroscopic training set may be constructed that probes the full range of process-relevant pH’s so that acidic and basic forms of glycolate are included in spectroscopic training data.

The concentrations of target species, nitrate $(\mathrm{N}{\mathrm{O}}_{\mathrm{3}}^{-})$ and nitrite $(\mathrm{N}{\mathrm{O}}_{\mathrm{2}}^{-})$, were predicted by PLSR using both raw and BSS-preprocessed spectra. For two different runs of the SRAT/SME processes, nitrate quantification improved from an R² of 0.934 to 0.988 and from 0.267 to 0.978 when subtracting overlapping BSS-estimated glycolate peaks from measured spectra. BSS preprocessing may be useful even when reference spectra are available, since process conditions can stray from well-controlled bounds where quantification models are typically designed, impacting the spectral signatures of key species. Beyond nuclear waste processing, applications of the presently discussed blind source separation technique may be found in instances where spectral quantification of complex mixture spectra is necessary, but process information is limited a priori or process conditions vary.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

SC: Conceptualization, Formal Analysis, Writing–original draft. SK: Conceptualization, Investigation, Writing–review and editing. SN: Investigation, Writing–review and editing. RP: Writing–review and editing. AH: Writing–review and editing, Investigation. DL: Writing–review and editing, Project administration, Resources. RR: Project administration, Resources, Writing–review and editing. MG: Project administration, Resources, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Support by the U.S. Department of Energy under Cooperative Agreement DE-FC01-06EW07053, entitled “The Consortium for Risk Evaluation with Stakeholder Participation III,” is gratefully acknowledged. This work was produced by Battelle Savannah River Alliance, LLC under Contract No. 89303321CEM000080 with the U.S. Department of Energy. Publisher acknowledges the U.S. Government license to provide public access under the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan). This material is based upon work supported under an Integrated University Program Graduate Fellowship.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1295995/full#supplementary-material

References

Bishop, C. M. (2006). Pattern recognition and machine learning. Springer.

Google Scholar

Brunton, S. L., and Kutz, N. J. (2022). Data-driven science and engineering. 2nd edn. Cambridge: Cambridge University Press.

Google Scholar

Camp, C. H. (2019). PyMCR: a Python library for multivariate curve resolution analysis with alternating regression (MCR-AR). J. Res. Natl. Inst. Stand. Technol. 124 (124018), 1–10. doi:10.6028/jres.124.018

CrossRef Full Text | Google Scholar

Cornel, J., Lindenberg, C., and Mazzotti, M. (2008). Quantitative application of in situ ATR-FTIR and Raman Spectroscopy in crystallization processes. Anal. Chem. 47, 4870–4882. doi:10.1021/ie800236v

CrossRef Full Text | Google Scholar

das Graças Gomes, M., da, S. S., Borges, S., Lopes, L. G., and Franco, D. W. (1993). UV-visible spectrum of nitrous acid in solution: pKa determination and analytical applications. Anal. Chim. Acta 282, 81–85. doi:10.1016/0003-2670(93)80354-N

CrossRef Full Text | Google Scholar

Haaland, D. M., and Melgaard, D. K. (2000). New prediction-augmented classical least-squares (PACLS) methods: application to unmodeled interferents. Appl. Spectrosc. 54, 1303–1312. doi:10.1366/0003702001951228

CrossRef Full Text | Google Scholar

Haaland, D. M., and Melgaard, D. K. (2002). New augmented classical least squares methods for improved quantitative spectral analyses. Vib. Spectrosc. 29, 171–175. doi:10.1016/S0924-2031(01)00199-0

CrossRef Full Text | Google Scholar

Jaumot, J., de Juan, A., and Tauler, R. (2015). MCR-ALS GUI 2.0: new features and applications. Chemom. Intelligent Laboratory Syst. 140, 1–12. doi:10.1016/j.chemolab.2014.10.003

CrossRef Full Text | Google Scholar

Kocevska, S., Maggioni, G. M., Crouse, S. H., Prasad, R., Rousseau, R. W., and Grover, M. A. (2022). Effect of ion interactions on the Raman spectrum of NO3—: toward monitoring of low-activity nuclear waste at Hanford. Chem. Eng. Res. Des. 181, 173–194. doi:10.1016/j.cherd.2022.03.002

CrossRef Full Text | Google Scholar

Kocevska, S., Maggioni, G. M., Rousseau, R. W., and Grover, M. A. (2021). Spectroscopic quantification of target species in a complex mixture using blind source separation and partial least-squares regression: a case study on Hanford waste. Industrial Eng. Chem. Res. 60, 9885–9896. doi:10.1021/acs.iecr.1c01387

CrossRef Full Text | Google Scholar

Lambert, D. P., and Howe, A. M. (2021), May Aiken, SC, United States. Savannah River National Laboratory. Antifoam development for eliminating flammability hazards and decreasing cycle time in the Defense waste processing facility. Tech. Rep. doi:10.2172/1630277

CrossRef Full Text | Google Scholar

Lambert, D. P., Nikolov, A. D., Wasan, D. T., Williams, M. S., Howe, A. M., and Woodham, W. H. (2021). A novel defoamer for processing nuclear waste: testing and performance. Environ. Prog. Sustain. Energy 40, 1–13. doi:10.1002/ep.13607

CrossRef Full Text | Google Scholar

Lambert, D. P., Williams, M. S., Brandenburg, C. H., and Newell, J. D. (2016). Sludge batch 9 simulant runs using the nitric-glycolic acid flowsheet Technical Report. Aiken, SC, United States Savannah River National Laboratory. doi:10.2172/1335822

CrossRef Full Text | Google Scholar

Lascola, R., O’Rourke, P. E., and Kyser, E. A. (2017). A piecewise local partial least squares (PLS) method for the quantitative analysis of plutonium nitrate solutions. Appl. Spectrosc. 71, 2579–2594. doi:10.1177/0003702817734000

PubMed Abstract | CrossRef Full Text | Google Scholar

Maggioni, G. M., Kocevska, S., Grover, M. A., and Rousseau, R. W. (2019). Analysis of multicomponent ionic mixtures using blind source separation: a processing case study. Industrial Eng. Chem. Res. 58, 22640–22651. doi:10.1021/acs.iecr.9b03214

CrossRef Full Text | Google Scholar

Melgaard, D. K., Haaland, D. M., and Wehlburg, C. M. (2002). Concentration residual augmented classical least squares (CRACLS): a multivariate calibration method with advantages over partial least squares. Appl. Spectrosc. 56, 615–624. doi:10.1366/0003702021955178

CrossRef Full Text | Google Scholar

Naik, G. R., and Wang, W. (2014). Blind source separation: advances in theory, algorithms and applications. Springer. doi:10.1007/978-3-642-55016-4

CrossRef Full Text | Google Scholar

Ray, J., Culbertson, B., Marra, S., and Plodinec, M. (2018). DWPF glass product control Program. Technical Report.

Google Scholar

Serjeant, E., and Dempsey, B. (1979). Ionisation constants of organic acids in aqueous solution. Oxford: Pergamon Press.

Google Scholar

Tauler, R. (1995). Multivariate curve resolution applied to second order data. Chemom. Intelligent Laboratory Syst. 30, 133–146. doi:10.1016/0169-7439(95)00047-X

CrossRef Full Text | Google Scholar

Tauler, R., Izquierdo-Ridorsa, A., and Casassas, E. (1993). Simultaneous analysis of several spectroscopic titrations with self-modelling curve resolution. Chemom. Intelligent Laboratory Syst. 18, 293–300. doi:10.1016/0169-7439(93)85006-3

CrossRef Full Text | Google Scholar

Tse, P., Shafer, J., Bryan, S. A., and Lines, A. M. (2021). Quantification of Raman-interfering polyoxoanions for process analysis: comparison of different chemometric models and a demonstration on real Hanford waste. Environ. Sci. Technol. 55, 12943–12950. doi:10.1021/acs.est.1c02512

PubMed Abstract | CrossRef Full Text | Google Scholar

White, T. L., Lambert, D. P., Zamecnik, J. R., and Riley, W. T. (2015). Ion chromatography (IC) Analysis of Glycolate in simulated waste. Technical Report. Aiken: Savannah River National Laboratory.

Google Scholar

Woodham, W. H., Howe, A. M., and Siegfried, M. J. (2021). Tech. Rep. September Aiken, SC, United States. Savannah River National Laboratory. Sludge batch 10 flowsheet testing with non-radioactive simulants. doi:10.2172/1821142

CrossRef Full Text | Google Scholar

Yu, J. Y., Zhang, Y., Tan, S. H., Liu, Y., and Zhang, Y. H. (2012). Observation on the ion association equilibria in NaNO3 droplets using micro-Raman spectroscopy. J. Phys. Chem. B 116, 12581–12589. doi:10.1021/jp306367v

PubMed Abstract | CrossRef Full Text | Google Scholar