Validation of time-dependent shift using the pulsed sphere benchmarks

1 Introduction

As computing hardware has evolved through the digital age from serial CPU execution to distributed memory, massively parallel, heterogeneous architecture machines, software has often had to be refactored or completely rewritten with different algorithms to ensure that computation efficiency does not suffer. Most recently, the push toward exascale computing Evans et al. (2022) involving machines with millions of cores, mixing CPUs and graphical processing units (GPUs), and a hierarchy of memories with various access speeds, has created significant challenges for simulation across a wide variety of disciplines.

One particularly exacting example is Monte Carlo radiation transport. Simulation tools for the transport of radiation using the Monte Carlo method are ubiquitous in science and engineering fields, including nuclear reactor physics, radiation oncology, high energy density physics, and nuclear criticality safety. These algorithms involve the use of pseudo-random numbers to sample from probability distributions that describe the interaction of particles with matter, the tracking of these particles throughout the defined heterogeneous spatial domain, and the tallying of quantities of interest to the modeler. One attractive feature of Monte Carlo algorithms is that they often can operate without discretizations in the particle phase space—direction, energy, space, and time; this means that convergence of the Monte Carlo solution typically is a function of the number of particle histories (N) used, not any sort of grid imposed on the various independent variables in the simulation. One drawback, however, is that the convergence as a function of particle histories obeys the Central Limit Theorem, which states that mean quantities of interest approach the true mean at a rate that depends on N^1/2. Often, this means that Monte Carlo methods can be quite computationally expensive.

In the majority of applications, the time scale of the radiation motion is quite small compared to time scale of other processes, and steady-state transport simulations are sufficient. However, there are some specific use cases—ultra fast reactivity excursions in nuclear reactors or high energy density experiments involving nuclear fusion, for example,—where the detailed time dependence of the particle population is needed. Over the years, there have been time-dependent neutron transport codes developed (Buck and Hall, 1999, TART; Cullen, 2000, Mercury; Procassini et al., 2004; MCATK; Shim et al., 2012; Leppänen, 2013; Adams et al., 2015; McCARD), some were optimized for execution on older machines, and others employ approximate treatments of time-dependence to make larger problems solveable in reasonable wall clock times.

Recently, true time-dependence [via census particles and population control Reynolds and Palmer (2022); Reynolds et al. (2022)] has been incorporated in the Shift code originated at Oak Ridge National Laboratory (ORNL). Shift is a general-purpose massively-parallel Monte Carlo radiation transport code with a primary design objective to provide efficient parallel calculations on both CPUs and GPUs on computing scales from laptops to supercomputers. Due to limitations in the CUDA language used to run Shift’s code on GPUs, the GPU codebase has been maintained separately from the CPU codebase Hamilton and Evans (2019).

To ensure that Monte Carlo codes are ready for production use, they must undergo both verification and validation. Verification is the process of determining whether a piece of software is solving a specific set of equations correctly. Typically, verification involves defining a problem with an analytic or manufactured solution and testing the software to make sure it converges to the proper result at the predicted rate. Our verification work has been described in previous publications Reynolds and Palmer (2022); Reynolds et al. (2022). Validation is the process of determining whether a particular simulation tool is solving the correct equations. Comparison with data obtained from experiments is essential for validation. Robust suites of benchmarks exist for nuclear criticality Briggs et al. (2003), and nuclear reactor physics Briggs (2006) problems, but the vast majority of these experiments cannot be used to evaluate the algorithmic features of truly time-dependent Monte Carlo codes.

A number of validation problems have already been simulated with Shift, but none of them were time-dependent problems since Shift did not have time-dependent features Peplow et al. (2019). To validate the new time-dependent features of Shift, we have employed the pulsed sphere benchmarks as they are relatively simple problems that have been used for many validation studies in the past, and incorporate results of a time-dependent nature Miller et al. (2018); Whalen et al. (1992); Procassini and McKinley (2010). The novelty and significance of the work in this paper is two-fold. We present the first validation of the Shift Monte Carlo neutron transport code with the pulsed sphere benchmarks, and we provide comparisons of new, truly time-dependent simulations of the pulsed-sphere benchmarks with time-independent simulations that use a time-of-flight approximation to convert spectral detector responses to time bins. Comparisons of Shift results with those from the widely used MCNP Kulesza et al. (2022) code.

Producing time-dependent results from a time-independent version of Shift requires some approximations, but these results provide a useful baseline for the validation of time-dependent Shift since any discrepancies can be attributed to either existing issues in Shift or the new features.

2 Materials and methods

2.1 Pulsed spheres

The pulsed sphere benchmarks are a series of experiments performed at Lawrence Livermore National Laboratory (LLNL) in the 1960s–1990s. These benchmarks were specifically designed with the goal of validating neutron transport codes and assessing nuclear cross section data Wong et al. (1972). The pulsed-sphere benchmarks are valuable in evaluating time-dependent features and as they measure neutron time of arrival.

The pulsed spheres consist of four main sections: the target assembly, the sphere (of a given material), the experiment pit, and the detector. A simplified version of the setup is shown in Figure 1.

FIGURE 1

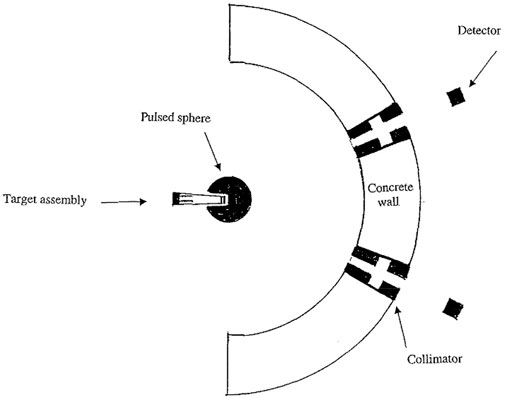
FIGURE 1. Simplified not-to-scale geometry of the setup Marchetti and Hedstrom (1998).

The target assembly is placed into a truncated conical insert in the sphere, and a beam of 400 keV deuterons is directed onto a small tritium-laced titanium target near the center. The result is a T(d,n)⁴He reaction that produces ∼14.1 MeV neutrons, with a slightly angularly-dependent energy distribution. The experiments measured the time of flight neutron flux at different angles from the incoming deuteron beam. The deuteron beam operated such that a short pulse of neutrons was generated, typically ranging from a full-width half maximum of 2–10 ns depending on the experiment.

Various materials and sphere sizes were measured over the course of the experimental campaigns. Certain fissile and liquid materials were housed in shells of steel or other metals. Other solid materials were assembled as shells with the goal of optimizing material while accommodating different-sized experiments. Scattering, absorption, and sometimes fission reactions in the spheres drive the time-of-flight results measured at the detector. A majority of the spherical setups ranged from 5 to 20 cm, although a couple larger systems were measured as well.

The experiment pit consists of an aluminum floor and concrete walls. The walls are a significant aspect of the simulations as collimators penetrate the walls at specific angles that lead to detectors in separate rooms. This arrangement isolates the detector from neutrons that do not originate directly from the sphere. The flight path from the center of the sphere to the detector ranged from about 750 to 1,000 cm depending on the beamline. The fact that the flight path is significantly larger than the radii of the spheres is important to resolve neutron energy from the time-of-flight measurements. While not explicitly stated if the flight path was measured to the front, middle, or end of the 5 cm detector, previous work indicates that uncertainty is negligible to the results Goricanec et al. (2017). Three different beamlines named 26°, 30°, and 120° were used. The actual angles of interest for the 30° and 120° beamlines were 38.89°, and 116.71° respectively since they were named after the angle with respect to the 26° beamline instead of the axis of symmetry around the incoming deuteron beam.

The detectors used in the experiments were NE213-A or Pilot-B scintillators and measured the neutron flux within each detector in 2 ns time bins. Each detector has its own efficiency curve as a function of the neutron energy, and those response curves can be easily implemented into Monte Carlo codes.

The result of interest is the time at which the neutrons reach the detector. This time-of-flight was experimentally measured in 2 ns time bins. As shown in Figure 2, there is an initial peak of uncollided neutrons that fly straight from the source to the detector, whereas neutrons that collide, slow down, and take longer to reach the detector. The absorption, scattering, and fission cross sections as well as the physical parameters of the sphere determine the behavior of the time-of-flight curve.

FIGURE 2

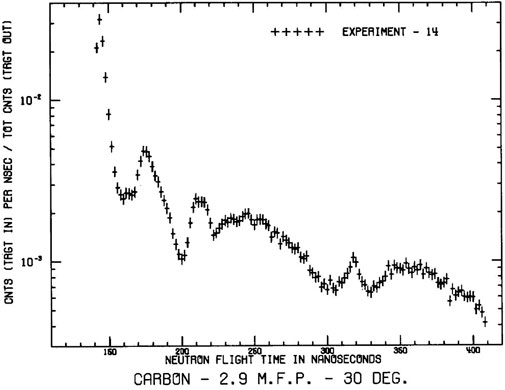
FIGURE 2. Example time-of-flight results for a 2.9 mfp carbon sphere Marchetti and Hedstrom (1998).

2.2 Modeling the pulsed spheres in Shift

An existing set of pulsed sphere models was simulated in the Monte Carlo code MCNP to provide additional comparisons for Shift. Even though MCNP does not have true time dependence, each neutron’s time-of-flight can be kept track of by tallying the distance between each collision divided by the speed between those collisions. The MCNP models did not include the entire pit and collimator assemblies. Instead, the beamlines to the detector were modeled as black absorbers with a thin layer of concrete which has been shown to negligibly affect the results Goricanec et al. (2017). This also allowed MCNP to implement a ring detector to take advantage of the symmetry of the problem around the axis of the deuteron beam. A ring detector is a variant of a point detector that can provide accurate results with far fewer histories for problems with axial symmetry.

To model the pulsed spheres in Shift, ORNL’s Lava library was used to translate a portion of the MCNP model into a form readable by the Shift solver. The Lava library ORNL (2022) was included as a package in Shift, and it can replicate the geometry, materials, and neutron source present in an MCNP input.

Tallies had to be manually defined in Shift, which led to several modeling issues that needed to be resolved. Shift does not possess next-event estimator detectors such as the point and ring detectors available in MCNP. A new cell was inserted into the Shift model to represent the detector, and a standard tracklength tally over the cell produced the estimation of the flux. At each collision in the simulation, point and ring detectors tally the probability that the next collision will occur on the point or ring which, in many cases, reduces the variance of the solution. Since Shift used a standard flux tally, it requires significantly more histories to reduce the statistical uncertainty to be on the same order as MCNP.

Neither the time-independent version of Shift nor MCNP possess features such as census particles for true time stepping. MCNP, however, does keep track of a time parameter for each neutron. Time-independent Shift does not have that capability, so the detector cannot collect the results into time bins. For steady-state Shift, the best substitute for time-binned tallies is energy-binned tallies taken at the detector, since the energy of the neutron is directly related to its velocity, and therefore the time the neutron takes to reach the detector. The energy-binned results can be compared directly to MCNP, and although an approximation is required to produced the time-binned spectrum, those results can provide a useful comparison for the time-dependent results. The relativistic first-flight approximation in can be used to convert the energy of the neutrons into the time-of-flight:

$E=rme\ast \left(\left(\frac{1}{\sqrt{\left(1-\left({\left(fp\right)}^2/\left(t^2{c}^2\right)\right)\right)}}\right)-1\right).(1)$

In equation 1, E is the energy of the neutron [MeV], rme is the rest mass energy of the neutron [MeV], fp is the length of the flight path to the detector [cm], t is the time of flight [ns], and c is the speed of light [cm/ns]. This approximation assumes that each neutron travels from the center of the sphere to the detector at its final energy. The assumption that all collisions happen at time 0 at the center of the sphere is only reasonable if the total flight path is significantly longer than the radius of the sphere. For the Monte Carlo codes, energy bin boundaries were defined such that the energy bins would translate to 2 ns wide time bins once converted to match the experiments and time-binned results. This approximation was used to report energy-binned results for the experiments even though the tallies themselves were only time-binned.

The time-dependent version of Shift does not require such approximation and can be directly compared with MCNP results. There are algorithmic differences in how the two codes treat a time-dependent problem, but as long as the time-of-flight of each neutron is tracked properly, both codes should yield similar results. Both MCNP and time-dependent Shift calculate a time parameter for each neutron, but Shift goes further by adding time steps to the simulation. Instead of transporting neutrons or batches of neutrons to the end of their life and then going back to the beginning and transporting more like MCNP, Shift transports all particles only to the end of the next time step. Shift stores particles and their information in census when they reach the end of the time step until it is ready to begin the next step. Time steps may be of great importance to problems where intermediate solutions are of interest such as transient reactor behavior. The pulsed spheres do not exercise the full extent of transient simulation capabilities that time steps can unlock, but they do test the basic features of the time-dependent build.

All simulations in this work were performed with the ENDF/B-VII.1 nuclear data library for consistency.

Table 1 describes the pulsed sphere models that were simulated in Shift. All these simulations were performed with detectors on the 30° degree beamline. The listed pulse width is the full width half maximum of the source pulse.

TABLE 1

TABLE 1. Description of the spheres simulated in this work.

3 Results

3.1 Direct comparison to MCNP

The best comparison of time-independent Shift to other codes is the energy-binned detector results, which are shown below in the top half of Figures 3–10. These results are directly comparable since no approximation of the results themselves needs to be made. The energy bin boundaries for both simulations were based on applying the first flight equation to the 2 ns time bins so that the energy-binned tallies could be converted neatly into 2 ns time bins for comparisons. Consequentially, there are limited numbers of wider energy bins at higher energies and denser bins at lower energies. Since Shift is running the exact same problem as MCNP besides the detector setup, the results should match fairly well.

FIGURE 3

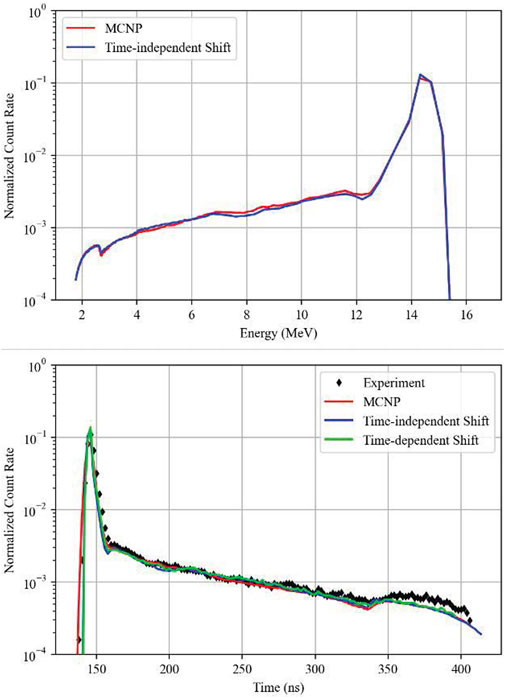
FIGURE 3. Beryllium, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 4

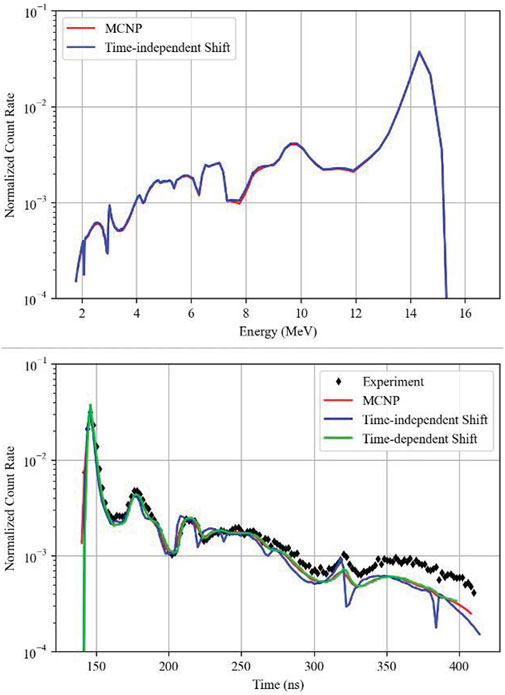
FIGURE 4. Carbon, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 5

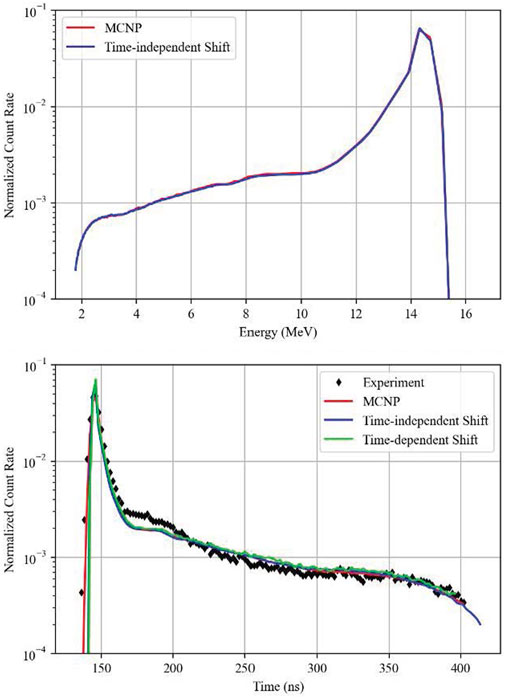
FIGURE 5. Lithium, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 6

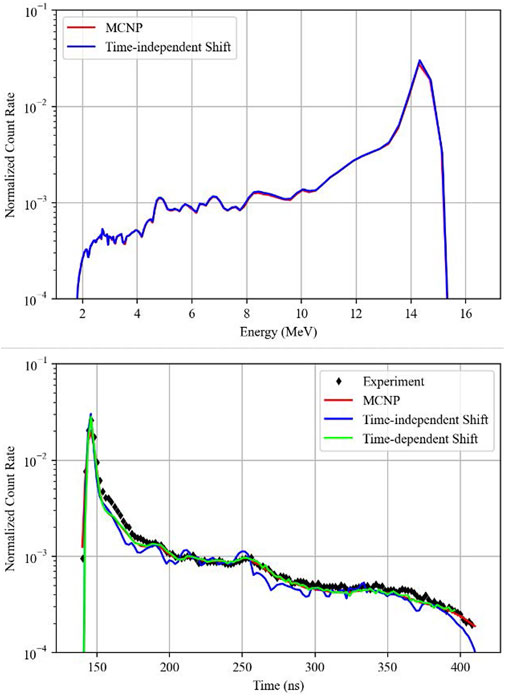
FIGURE 6. Nitrogen, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 7

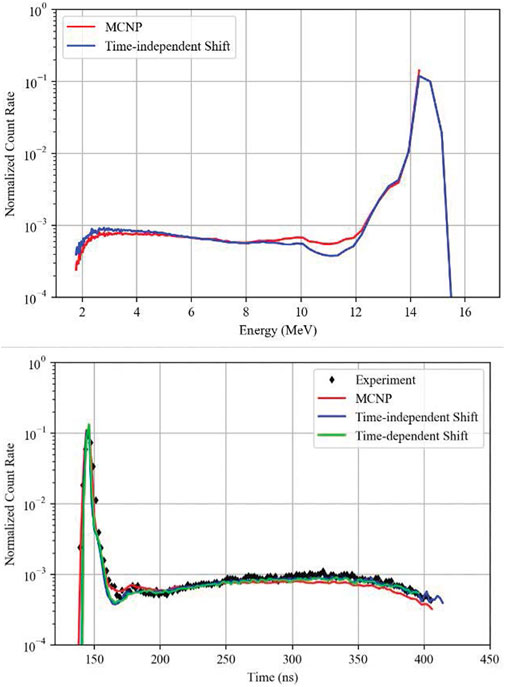
FIGURE 7. Iron, top: nergy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 8

FIGURE 8. Lead, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 9

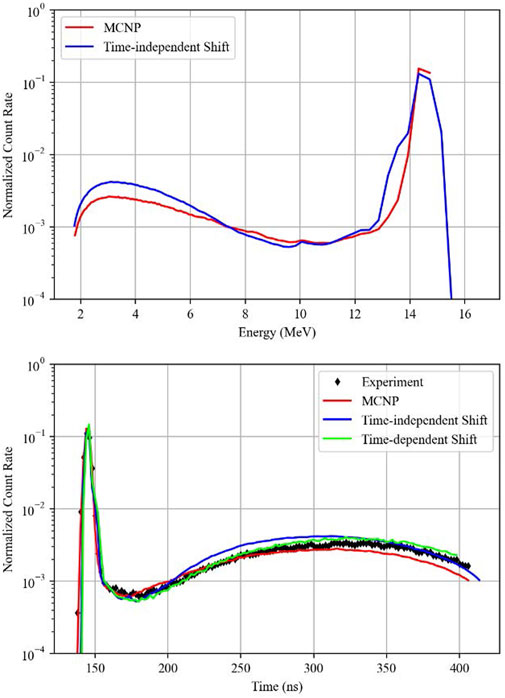
FIGURE 9. ²³⁵U, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

FIGURE 10

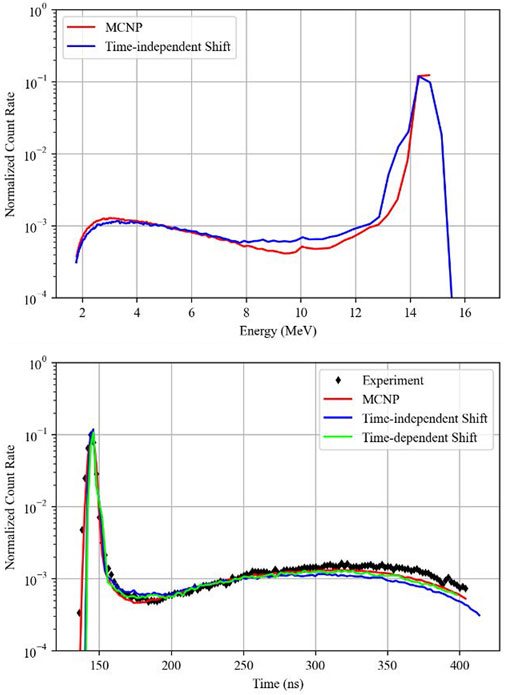
FIGURE 10. ²³⁸U, top: energy-binned MCNP (10⁷ histories) vs. Shift (10⁹ histories); bottom: comparison of time-dependent Shift (10⁹ histories) with time-independent Shift (10⁹ histories) and MCNP (10⁷ histories).

For several spheres including berylium, carbon, lead, lithium, and liquid nitrogen, Shift and MCNP produced nearly identical results.

There are some discrepancies between MCNP and Shift for iron, ²³⁵U, and ²³⁸U. Shift predicts a dip in the flux around 11 MeV that is not present in MCNP, and Shift predicts a higher flux than MCNP around 13–14 MeV for ²³⁵U and ²³⁸U. The iron used in the experiments was composed of about 1% ⁵⁵Mn, and in our modeling we observed that the ENDF/B-VII.1 data libraries had a cross section discrepancy for this isotope which produced errors in Shift. At high energies, the sum of the scattering and absorption cross sections was not equal to the total cross section. The effect was most likely too small to significantly impact the results shown for iron in Figure 7, since the difference between the total cross section and the scattering plus absorption cross sections was typically less than 10%.

3.2 First flight approximation

For the validation of Shift, the results need to be compared with experimental data which can be accomplished by using the relativistic first flight approximation in Eq. 1. This approximation will introduce some error which is dependent on the size and material composition of the sphere. The energy-binned results from Shift in Figures 3–10 were converted and compared with experiment data and MCNP results. The time-of-flight MCNP results were tallied from the same simulations as those energy-binned results using a separate time-binned tally. These converted results, and the comparisons with MCNP, are presented in the bottom graphs of Figures 3–10.

The bottom graphs in Figures 4, 6 show how the first flight approximation can lead to a degradation of results for large spheres with highly scattering media. The carbon and nitrogen spheres in these simulations were about 21 and 56 cm in radius respectively, and there are distinct differences due to scattering behavior over the spectrum. Given that the energy-binned spectrum in Shift was nearly identical to MCNP for both of these spheres, the difference in the time-of-flight results between the codes is most likely entirely due to the errors in the approximation. For the rest of the spheres, where results matched between MCNP and Shift in the energy-binned spectrum, they also matched the time-of-flight results. Small differences at the tail end of the spectrum between the codes and experimental values are expected due to D-D reactions not being modeled in the simulations. These reactions produce an additional 2.5 MeV neutrons Procassini and McKinley (2010); Goricanec et al. (2017). Neither MCNP nor Shift agree with the experimental data for the lithium sphere, with differences approaching 33% in the time period between 170 and 200 ns.

Due to the bins being evenly spaced, some of the more exaggerated differences from the energy-binned uranium results are less apparent, but the codes still produce results that are noticeably different for the fissile materials.

3.3 Time-dependent results

The time-dependent CPU code base version of Shift facilitates geometry specifications that correlate directly with MCNP, which means direct comparisons of time-of-flight results can be performed. The current implementation of Shift sets the time-bin boundaries equal to the time step, so the time steps were set to 2 ns to replicate the experimental bins. The bottom graphs in Figures 3–10 contain the results of the time-dependent Shift simulations and comparisons with MCNP.

Small discrepancies between Shift and MCNP still arise in the iron and uranium spheres, but errors are still generally on the same order of magnitude as the differences between the experimental values and the simulation results from either code. Other than the aforementioned carbon and nitrogen spheres, the two uranium spheres showed the greatest differences between time-independent and time-dependent Shift implementations.

Table 2 compares the percent difference of the point of maximum discrepancy for several comparisons. The range was limited to the area of interest between 160 and 300 ns for several reasons. Tally results for the uncollided peak at the start of the time spectrum tend to differ significantly between the codes and experimental data due to the limited number of bins for the rapidly changing behavior. Additionally, the code models do not include the impact of D-D neutrons and tend to drift away from the experimental data near the end of the time spectrum.

TABLE 2

TABLE 2. Maximum relative difference [%] in the 160–300 ns range.

To confirm what can be seen graphically, Shift produces results that are very close to MCNP for most spheres. Without the hindrance of the first flight approximation, time-dependent Shift consistently produces more accurate results than time-independent Shift and most of the results compare closely to experiment with both versions of the code. In most cases, where Shift does not align with experimental data, MCNP also experiences some discrepancies. In those cases, the differences most likely originate from the nuclear data.

4 Conclusion

LLNL’s pulsed-sphere benchmark experiments were simulated in Shift to validate both the time-independent as well as new time-dependent features. Time-of-flight results for both the time-independent and time-dependent builds of Shift result in errors that are of a similar order of magnitude as MCNP when compared to experimental data. This is the first validation attempt with the Shift code that employed the pulsed sphere benchmarks. Aside from a few minor discrepancies in iron and uranium that could warrant future investigation, Shift aligns with MCNP exceedingly well.

Time-dependent algorithms have been implemented in the GPU version of Shift, but geometry limitations have prevented the easy exploration of problems like the pulsed spheres to date. The pulsed spheres do not exercise the full time-dependent capabilities of Shift. Transient problems that cannot be simulated using time-independent methods such as reactor cores with moving control rods will be the focus of future work.

A study of the computational performance of the time-dependent version of Shift is ongoing, on massively-parallel CPU and GPU architectures, is the subject of a separate article currently in preparation.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CP: Conceptualization, Writing–original draft, Writing–review and editing. JN: Data curation, Formal Analysis, Writing–original draft. TP: Funding acquisition, Writing–review and editing. AR: Methodology, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Center for Exascale Monte-Carlo Neutron Transport (CEMeNT) a PSAAP-III project funded by the Department of Energy, grant number: DE-NA003967.

Conflict of interest

Author AR is employed by TerraPower LLC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adams, T., Nolen, S., Sweezy, J., Zukaitis, A., Campbell, J., Goorley, T., et al. (2015). Monte Carlo application toolkit (MCATK). Ann. Nucl. Energy 82, 41–47. doi:10.1016/j.anucene.2014.08.047

CrossRef Full Text | Google Scholar

Briggs, J. B. (2006). International handbook of evaluated reactor physics benchmark experiments. Tech. Rep. NEA/NSC/DOC Paris, Fr.

Google Scholar

Briggs, J. B., Scott, L., and Nouri, A. (2003). The international criticality safety benchmark evaluation project. Nucl. Sci. Eng. 145, 1–10. doi:10.13182/NSE03-14

CrossRef Full Text | Google Scholar

Buck, R. M., and Hall, J. M. (1999). Applications of the COG multiparticle Monte Carlo transport code to simulated imaging of complex objects. Radiat. Sources Radiat. Interact. (SPIE) 3771, 127–134. doi:10.1117/12.363699

CrossRef Full Text | Google Scholar

Cullen, D. E. (2000). Tart 2000: a coupled neutron-photon, 3-D, combinatorial geometry, time dependent, Monte Carlo transport code. UCRL-ID-126455-REV-3. Livermore, CA, United States: Lawrence Livermore National Lab.LLNL.

Google Scholar

Evans, T. M., Siegel, A., Draeger, E. W., Deslippe, J., Francois, M. M., Germann, T. C., et al. (2022). A survey of software implementations used by application codes in the Exascale Computing Project. Int. J. High Perform. Comput. Appl. 36, 5–12. doi:10.1177/10943420211028940

CrossRef Full Text | Google Scholar

Goricanec, T., Trkov, A., and Noy, R. C. (2017). Analysis of the U-238 Livermore pulsed sphere experiments benchmark evaluations. https://inis.iaea.org/collection/NCLCollectionStore/_Public/49/059/49059862.pdf?r=1.

Google Scholar

Hamilton, S. P., and Evans, T. M. (2019). Continuous-energy Monte Carlo neutron transport on GPUs in the Shift code. Ann. Nucl. Energy 128. doi:10.1016/j.anucene.2019.01.012

CrossRef Full Text | Google Scholar

Kulesza, J. A., Adams, T. R., Armstrong, J. C., Bolding, S. R., Brown, F. B., Bull, J. S., et al. (2022). MCNP® code version 6.3.0 theory & user manual. Tech. Rep. LA-UR-22-30006. Los Alamos, NM, USA: Los Alamos National Laboratory. doi:10.2172/1889957

CrossRef Full Text | Google Scholar

Leppänen, J. (2013). Development of a dynamic simulation mode in Serpent 2 Monte Carlo code. Proc. M&C, 5–9. https://api.semanticscholar.org/CorpusID:198925618.

Google Scholar

Marchetti, A. A., and Hedstrom, G. W. (1998), New Monte Carlo simulations of the LLNL pulsed-sphere experiments UCRL-ID-131461. Livermore, CA, United States: Lawrence Livermore National Lab.LLNL.

Google Scholar

Miller, T. M., Menedeu, E. L., Mancusi, D., and Zoia, A. (2018). Comparison of mavric/Monaco and tripoli-4® simulations of the llnl pulsed spheres benchmark experiments in 20th Topical Meeting of the Radiation Protection & Shielding Division of ANS, Santa Fe, New Mexico, United States, August 2018.

Google Scholar

ORNL (2022). SCALE 6.2 manual. https://scale-manual.ornl.gov/UtilOverview.html.

Google Scholar

Peplow, D. E., Banerjee, K., Davidson, G. G., Stewart, I. R., Swinney, M. W., and Wagner, J. N. (2019). Preliminary validation of the Shift Monte Carlo code for fixed-source radiation transport problems. Nucl. Technol. 206 (1), 107–125. doi:10.1080/00295450.2019.1625663

CrossRef Full Text | Google Scholar

Procassini, R., Cullen, D., Greenman, G., and Hagmann, C. (2004). Verification and validation of Mercury: a modern, Monte Carlo particle transport code. UCRL-CONF-208667. Livermore, CA, United States: Lawrence Livermore National Lab LLNL.

Google Scholar

Procassini, R. J., and McKinley, M. S. (2010).Modern calculations of pulsed-sphere time-of-flight experiments using the Mercury Monte Carlo transport code LLNL-PROC-453212. Livermore, CA, United States: Lawrence Livermore National Lab LLNL.

Google Scholar

Reynolds, A. J., and Palmer, T. S. (2022). Verification and scaling of time-dependent Shift using the AZURV1 benchmark. Transactions 126. doi:10.13182/T126-38060

CrossRef Full Text | Google Scholar

Reynolds, A. J., Variansyah, I., and Palmer, T. (2022). Implementation, verification, and scaling of history- and event-based time-dependent Shift.

Google Scholar

Shim, H.-J., Han, B.-S., Jung, J.-S., Park, H.-J., and Kim, C.-H. (2012). McCARD: Monte Carlo code for advanced reactor design and analysis. Nucl. Eng. Technol. 44, 161–176. doi:10.5516/NET.01.2012.503

CrossRef Full Text | Google Scholar

Whalen, D. J., Cardon, D. A., Uhle, J. L., and Hendricks, J. S. (1992). New Monte Carlo simulations of the LLNL pulsed-sphere experiments. UCRL-ID-131461. Livermore, CA, United States: Lawrence Livermore National Lab LLNL.

Google Scholar

Wong, C., Anderson, J. D., Brown, P., Hansen, L. F., Kammerdiener, J. L., Logan, C., et al. (1972). Livermore pulsed sphere program: program summary through July 1971. UCRL-51144. Livermore, CA, United States: Lawrence Livermore National Lab LLNL.

Google Scholar