- 1Institute of Resource Ecology, Helmholtz-Zentrum Dresden-Rossendorf, Dresden, Germany
- 2Technische Universität Dresden, Dresden, Germany
Post-irradiation annealing of neutron-irradiated reactor pressure vessel steels is a matter of both technical and scientific interest. Small-angle neutron scattering (SANS), while being sensitive to nm-sized irradiation-induced solute-atom clusters, provides macroscopically representative and statistically reliable measures of cluster volume fraction, number density and size. In the present study, SANS was applied to uncover the size distribution of clusters in as-irradiated samples of a VVER-1000 weld and their gradual dissolution as function of the post-irradiation annealing temperature. The same samples were used to measure Vickers hardness. The results are consistent with Mn-Ni-Si-rich clusters of less than 2 nm radius to be the dominant source of both scattering and hardening. Annealing gave rise to small but significant partial recovery at 350°C and almost complete recovery at 475°C. The dispersed-barrier hardening model was applied to bridge the gap between the characteristics of nano-features and macro-hardness.
1 Introduction
Neutron irradiation of the belt line region of the reactor pressure vessel (RPV) gives rise to a progressing shift of the brittle—ductile transition temperature (so-called neutron embrittlement) of the RPV material (Brumovsky, 2015; Soneda, 2015; Tomimatsu et al., 2015). For safety reasons, this effect limits the lifetime of the RPV and, as the RPV is practically irreplaceable, the operation of the whole reactor unit. Post-irradiation recovery annealing of the RPV material is a way to reverse or mitigate embrittlement. There is considerable interest in the post-irradiation annealing behavior of RPV steels and welds for several reasons. First, insight into the annealing behavior contributes to a better understanding of the irradiation-induced nanostructure, in particular with respect to the thermal stability of different populations of irradiation-induced nanofeatures. Such kind of studies may advantageously be accompanied by computer simulations (Chiapetto et al., 2015; Ke et al., 2017; Konstantinović et al., 2019). Second, large-scale annealing treatments of the RPV belt line region (Pelli and Törrönen, 1998; Brumovsky, 2015; Server and Nanstad, 2015) of operating nuclear power plants have been carried out to date or are envisaged in order to mitigate embrittlement and extend the duration of safe reactor operation. This kind of benefit is based on a partial or complete recovery of both the as-irradiated nanostructure and the mechanical properties of the RPV material. In this context, studies of the annealing behavior formed the basis to identify optimum post-irradiation annealing regimes in terms of temperature and time (Popp et al., 1989) (e.g., 475°C/152 h for VVER-440 reactors) or to demonstrate the success of realized high-temperature dry annealings (Pelli and Törrönen, 1998; Viehrig et al., 2009). Alternatively, less demanding and more cost-efficient procedures such as low-temperature (e.g., 343°C) wet annealing within the RPV design limits (Pelli and Törrönen, 1998; Krasikov, 2012) might give rise to partial recovery possibly allowing for some limited but worthwhile lifetime extension. The actual benefit of wet annealing in particular cases is under discussion.
Along with the characterization of the mechanical properties (Pachur, 1982; Kryukov et al., 1998; Laot et al., 2022), several methods with nm-scale sensitivity have been applied to uncover the post-irradiation annealing behavior of RPV steels and welds in terms of nanostructure. These include positron annihilation spectroscopy (PAS) (Brauer et al., 1991), transmission electron microscopy (TEM) (Gurovich et al., 2013), small-angle neutron scattering (SANS) (Ulbricht et al., 2006) including in situ SANS (Boothby et al., 2015), atom probe tomography (APT) (Pareige et al., 1997; Miller et al., 2009; Styman et al., 2015), Auger electron spectroscopy (AES) (Gurovich et al., 2013), Mössbauer spectroscopy (Slugeǹ et al., 1999) and electrical resistivity (Ilola et al., 2002). APT is distinguished by the capability to provide the local composition of both nm-scale solute atom clusters and the surrounding matrix as well as size and number density of clusters. Segregations on dislocations and grain boundaries can also be characterized. SANS allows the macroscopically representative (probed volume of the order of 50 mm3) and statistically reliable (number of recorded scattering events of the order of 106) determination of the size distribution of nm-scale clusters. For ferromagnetic materials, the separation of magnetic (interaction of neutrons with the magnetic moments of the atoms) and nuclear (interaction of the neutrons with the nuclei) scattering yields additional information on the dominant type of clusters. TEM provides information on irradiation-induced dislocation loops, which cannot be routinely detected by APT and SANS.
For RPV steels with a high level of impurity Cu, coherent body-centered cubic (bcc) Cu-rich clusters were found to be the dominant irradiation-induced nanofeatures (Odette, 1983). These clusters were demonstrated to partly dissolve and partly transform into thermodynamically stable precipitates upon post-irradiation annealing (Pareige et al., 2005; Ulbricht et al., 2007). The latter remove Cu from the matrix and, therefore, may give rise to slower hardening and embrittlement upon reirradiation as compared to the original irradiation. For low-Cu (<0.1 wt%) RPV steels, model alloys and welds, Mn-Ni-Si-rich clusters have been identified to be the irradiation-induced nanofeatures that dominate hardening (Auger et al., 1994; Miller et al., 2006; Styman et al., 2015). Controversial views about the Fe fraction (ranging from 6% to 80%) and the dominant mechanism of formation (radiation-induced segregation versus radiation-enhanced diffusion) of this kind of clusters have been reported (Meslin et al., 2010; Edmondson et al., 2017; Ke et al., 2017; Castin et al., 2020; Belkacemi et al., 2021). Mn-Ni-Si-rich clusters were also reported to either dissolve upon annealing (Miller et al., 2009) or, at least after irradiation to high fluences, to evolve into stable intermetallic phases (Sprouster et al., 2016; Edmondson et al., 2017). For both Cu-rich clusters in high-Cu RPV steels and Mn-Ni-Si-rich clusters in low-Cu RPV steels, the factors deciding over cluster dissolution or transformation into stable phases upon irradiation and post-irradiation annealing have not yet been clarified.
Irradiation-induced dislocation loops (Kočík et al., 2002; Gurovich et al., 2013), sub-nm vacancy clusters (Kočík et al., 2002), nanovoids (at least after irradiation to high fluences) (Bergner et al., 2015) and segregations of P, Ni, and Si to pre-existing line dislocations and grain boundaries (Miller et al., 2009) were reported to contribute to hardening and embrittlement independently of the impurity Cu level. Some of these nanofeatures are unspecifically classified as unstable matrix defects (UMD), that means, they dissolve at annealing temperatures corresponding to or slightly higher than the respective irradiation temperature (Odette and Lucas, 1998). Others may be stable at least up to essentially higher annealing temperatures. It is important to note that segregation of Mn, Ni and Si to dislocation loops plays a role in the mechanism of formation of Mn-Ni-Si-rich clusters (Messina et al., 2020; Belkacemi et al., 2021). Therefore, the distinction of loops and clusters may be subject to some ambiguity. Moreover, P was also reported to be enriched in Mn-Ni-Si-rich clusters (Miller et al., 2009). However, the effect is limited by the available amount of P and will be neglected below.
While numerous nanostructure studies of neutron-irradiated RPV steels and welds, occasionally including a single post-irradiation annealing treatment, were reported (see references above and references cited therein), nanostructure studies covering systematic variations of the post-irradiation annealing temperature over a wide range are relatively scarce and already represent an added value per se (Brauer and Popp, 1987; Brauer et al., 1991; Slugeǹ et al., 1999; Ilola et al., 2002; Ulbricht et al., 2006; Boothby et al., 2015; Toyama et al., 2020). In these studies, post-irradiation annealings of equal duration (isochronal annealing) are typically conducted at stepwise increasing temperatures from irradiation temperature or slightly above up to the highest temperature of interest (Pachur, 1982). Other temperature—time regimes are also possible, e.g., isothermal annealings with the annealing time varied (Pachur, 1982). Depending on both the availability of as-irradiated material and the type of experiment, either the same sample is exposed to all temperatures with experiments inserted after each individual annealing or a set of samples is exposed to different temperatures, one sample per temperature, with the set of experiments done afterwards in one block. These procedures make a difference with respect to both the temperature—time regime experienced by the samples and the sample volumes probed in the experiments, which has to be taken into account for the interpretation of the results.
The study reported here was focused on the post-irradiation annealing behavior of a low-Cu VVER-1000 weld material with the Russian designation SV10KhGNMAA (Kuleshova et al., 2002; Brumovsky, 2015). Samples of as-irradiated material were exposed to isochronal annealings of 10 h duration at temperatures between 350°C and 475°C, one sample per temperature. SANS experiments supplemented by Vickers hardness testing were carried out for each of these samples as well as the as-irradiated and unirradiated reference samples. The key objective was a deeper understanding of the thermal stability of the reported Mn-Ni-Si-rich clusters. SANS is distinguished from other methods with nanostructure sensitivity for revealing statistically reliable and macroscopically representative (probed volume of approximately 50 mm3) characteristics of the irradiation-induced solute atom clusters. The discussion will start from the as-irradiated nanostructure taking into account results reported for the same type of as-irradiated weld materials studied by complementary techniques such as TEM (Gurovich et al., 2013) and APT (Miller et al., 2009). A consistent discussion of the annealing kinetics revealed by SANS will then be given and compared with Vickers hardness measurements. Finally, the studied VVER-1000 weld material will be compared with other RPV materials with respect to their post-irradiation annealing behavior.
2 Experiments
2.1 Material
The material is a SV10KhGNMAA-type weld as utilized in VVER-1000 reactors. Unirradiated samples representative of unit 1 of the South-Ukrainian Nuclear Power Plant were provided in the 1980s by VNIIAES. The composition of the weld is specified in Table 1. The submerged-arc weld was post-weld heat treated at 610°C—620°C for 5 h, furnace cooled to 400°C and then air cooled (Kuleshova et al., 2002). Yield stress Rp0.2 and Vickers hardness HV10 are 595 MPa and 206 ± 7, respectively.
An inverse pole figure map (IPF-Z) obtained by electron backscatter diffraction (EBSD) is shown in Figure 1 to represent the microstructure of the weld. The color key is given as inset. The mean grain size (equivalent circle diameter from averaged grain area) was measured to be 2.5 µm. The grains are elongated with an average grain aspect ratio of 2.4.

FIGURE 1. Microstructure of the as-received weld in terms of an inverse pole figure map (IPF-Z) obtained by EBSD.
2.2 Irradiation and annealing
Specimens of size 10 × 10 × 55 mm3 were irradiated in the near-core high-flux channels of the VVER-2 prototype reactor at Rheinsberg. The irradiation temperature was (255 ± 5)°C. The neutron flux was in the range 2.8–5.4 × 1012 cm−2·s−1 (E > 0.5 MeV). The mean neutron fluence received by the studied samples was estimated to be 65.1 × 1018 cm−2 (E > 0.5 MeV), which corresponds to a neutron exposure of 0.065 dpa (displacements per atom). A number of small samples of size 10 × 10 × 1 mm3 were cut from unirradiated and as-irradiated bars, more exactly from broken halves of the Charpy-type samples tested before. Part of the small as-irradiated samples was exposed to annealing treatments in Argon atmosphere followed by furnace cooling. The annealing temperatures of the individual samples later characterized by means of SANS were chosen to be 350, 400, 425, 450°C, and 475°C, one sample per temperature. The annealing time was 10 h.
2.3 Methods
The SANS experiment was conducted at the beamline D11 of ILL Grenoble using a neutron wavelength of 0.5 nm (wavelength spread of 10%), a beam diameter of 7 mm and two sample—detector distances of 1.1 m and 5 m. During the measurements a saturation magnetic field of 1.4 T oriented perpendicular to the neutron beam was applied to the samples. Absolute calibration was done using a water standard. The ILL software routines were applied to separate magnetic and nuclear scattering cross sections
After completion of the SANS experiment, the Vickers hardness (load 98.1 N) was measured using the same samples. Average values and standard deviations were calculated from 10 hardness tests for each sample. It is important to note that the volumes probed by means of SANS and Vickers hardness testing are both macroscopic and roughly coincide.
3 Results
The scattering cross sections measured for the unirradiated reference sample and the as-irradiated sample are plotted in Figure 2 as functions of the scattering vector Q. The total scattering cross sections (upper plot) as well as the separated nuclear (center plot) and magnetic (lower plot) cross sections are covered. The cross sections measured for the post-irradiation annealed sample (475°C) are also included. It is worth noting that 475°C corresponds to the temperature of large-scale dry annealings performed for VVER-440 type reactors. Figure 2 shows that there is a pronounced irradiation-induced increase of the scattering cross sections in the Q-range 0.8—3 nm−1. At Q-values below 0.8 nm−1, the cross sections of the unirradiated and as-irradiated conditions coincide for both nuclear and magnetic scattering. The observed behavior indicates the formation of irradiation-induced nanofeatures giving rise to additional small angle scattering. We will come back to the characteristics of these nanofeatures later below. Figure 2 also shows that the post-irradiation annealing treatment at 475°C results in an almost complete recovery of the scattering cross sections of the unirradiated reference. This indicates that the nanofeatures responsible for the irradiation-induced increase of the measured scattering cross sections essentially disappeared as a result of the annealing.
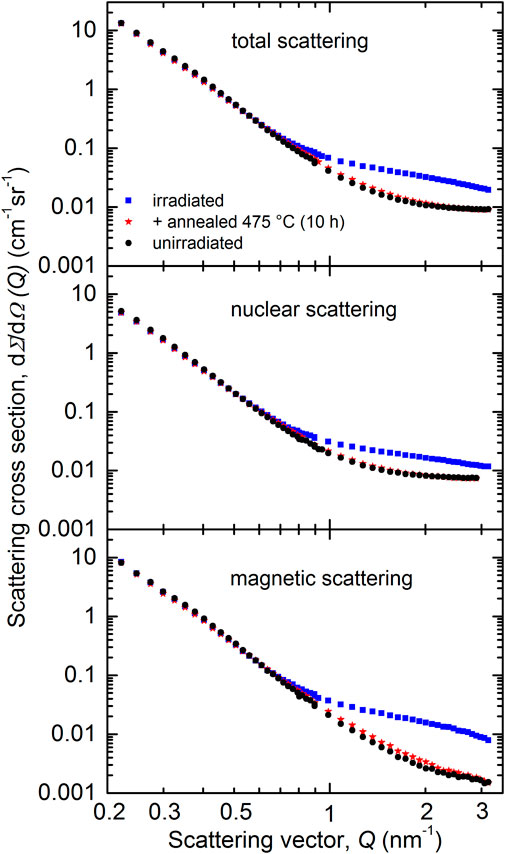
FIGURE 2. Measured total (upper plot), nuclear (center plot) and magnetic (lower plot) scattering cross sections for the unirradiated reference, the as-irradiated condition and the post-irradiation annealed condition (475°C) of the weld material.
The scattering curves measured for the isochronal (10 h) post-irradiation annealed samples, one sample for each temperature, are shown in Figure 3 in the same format as used for Figure 2 above. The unirradiated reference and the as-irradiated condition from Figure 2 are included as lines for comparison. Our major finding is a gradual recovery of the irradiation-induced increase of the scattering cross sections at increasing annealing temperature. Minor deviations of the scattering cross sections observed in the Q-range below 0.8 nm−1 are interpreted as the consequence of the typical heterogeneity of multi-layer welds and the resulting sample-to-sample scatter. This kind of scatter is neglected in the further analysis, but may contribute to the experimental error of the calculated percentage of recovery.
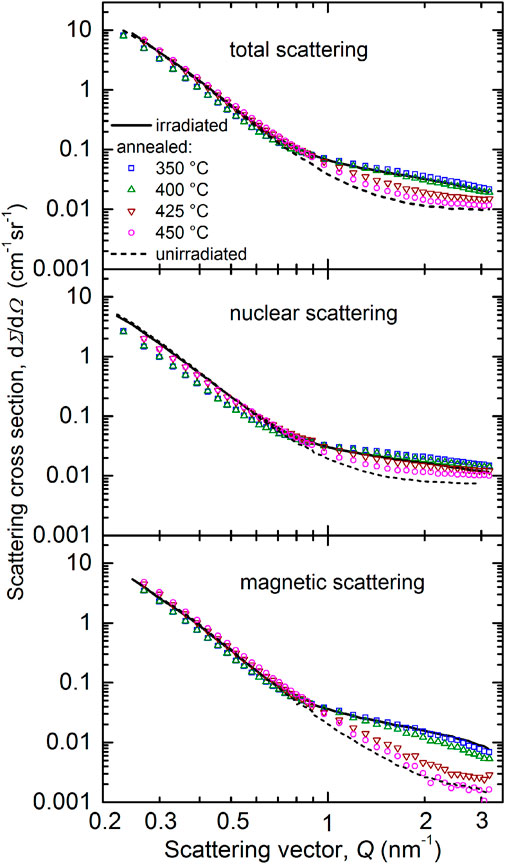
FIGURE 3. Measured total (upper plot), nuclear (center plot) and magnetic (lower plot) scattering cross sections for the post-irradiation annealed conditions (350°C–450°C) of the weld material. For comparison, the unirradiated and as-irradiated conditions are reproduced from Figure 2 as lines.
In order to derive the characteristics of irradiation-induced scatterers or scatterers remaining after the post-irradiation annealings, we have taken the difference between the respective magnetic scattering curves and the unirradiated reference. These magnetic difference scattering curves are summarized in Figure 4. Error bars obtained from the application of the standard software (Lindner et al., 1992) are given. The lines in Figure 4 represent the Fourier counterparts of the size distributions of scatterers approximated as cubic splines, the coefficients of which were determined by way of fitting according to (Glatter, 1980) as described in Section 2.3. The good fit between lines and symbols indicates the correctness of the calculated size distributions of irradiation-induced scatterers or those remaining after annealing.
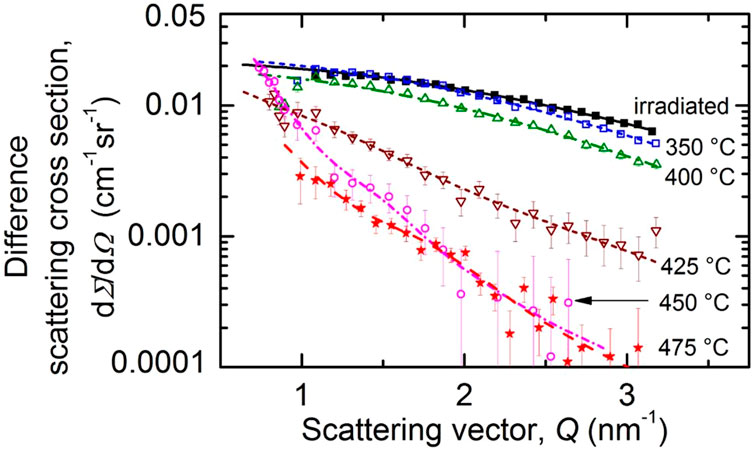
FIGURE 4. Measured magnetic difference scattering cross sections for the as-irradiated and post-irradiation annealed conditions of the weld material with the unirradiated condition subtracted. The lines are the fitted Fourier counterparts of the size distributions.
The size distributions of scatterers are summarized in Figure 5 in terms of volume fraction per size increment. It is important to repeat that these size distributions were calculated under the assumption of non-magnetic scatterers in a ferromagnetic matrix. In the case that the scatterers bear a non-zero magnetic moment, the magnetic scattering contrast between scatterer and matrix is correspondingly reduced and the reconstructed volume fractions would be higher than those given in Figure 5.
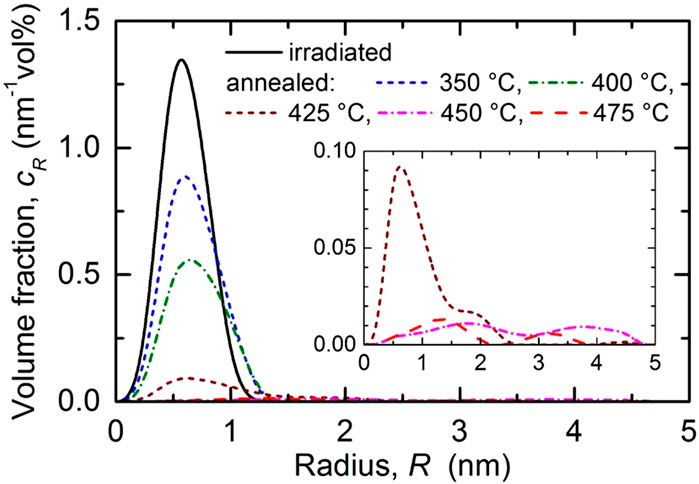
FIGURE 5. Size distribution of the irradiation-induced scatterers in terms of volume fraction per size increment for the as-irradiated condition of the weld and size distributions of the remaining scatterers after post-irradiation annealing. For the three highest annealing temperatures see inset.
We have found that the size distributions are essentially monomodal except for the three highest annealing temperatures, for which the size distribution extends to slightly larger sizes and a bimodality seems to emerge, though at very low volume fractions. A more quantitative description of the characteristics of the irradiation-induced scatterers is based on the total volume fraction of scatterers, the total number density, the mean size and the averaged A-ratio. These quantities are listed in Table 2 for the as-irradiated and post-irradiation annealed conditions. The error ranges represent the uncertainty of the fit procedure and the effect of the lower detection limit (0.5 nm in terms of radius) of SANS. The measured changes of Vickers hardness numbers (or equivalently Vickers hardness in units of kgf/mm2) as compared to the unirradiated condition are also included in Table 2. The results indicate that both the total volume fraction and the total number density of irradiation-induced scatterers remaining after annealing as well as the changes of Vickers hardness monotonically decrease as function of the annealing temperature. There is a weak tendency of the mean size of scatterers to increase. The A-ratio tends to decrease up to 425°C.
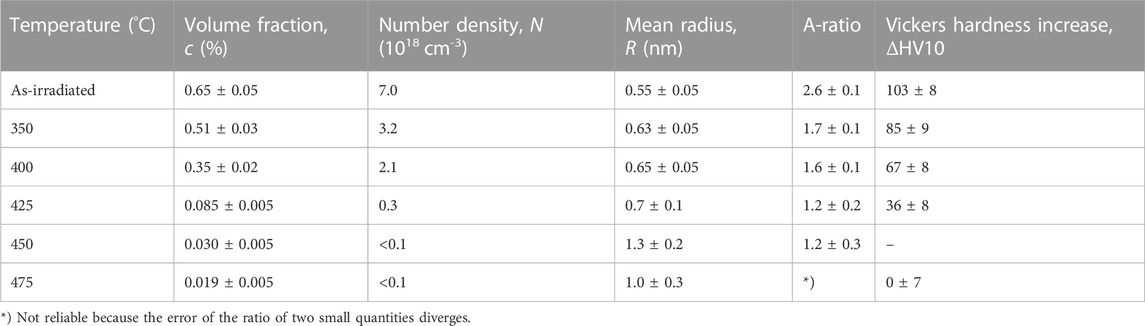
TABLE 2. Total volume fraction, total number density, mean radius and A-Ratio of the irradiation-induced scatterers as well as increase of the Vickers hardness ΔHV10 obtained for as-irradiated and post-irradiation annealed samples of VVER-1000 weld.
4 Discussion
The A-ratio is a one-parameter indicator of the dominant type of scatterers. However, it is not possible to identify the composition of scatterers in complex alloys, such as RPV steels, from the A-ratio alone. Therefore, we refer to published results obtained by complementary methods for the same kind of VVER-1000 type weld. An APT study (Miller et al., 2009) indicated irradiation-induced Mn-Ni-Si-rich clusters of radii below 1 nm for a weld irradiated at 290°C up to a similar neutron fluence (65 × 1018 cm-2). A TEM study (Gurovich et al., 2013), same temperature and fluence as above, revealed two types of nanofeatures, namely, dislocation loops of diameter 5—6 nm and spherical nanofeatures of diameter 3—4 nm. Taking into account method-related uncertainties of measures of size, there is no doubt that the spherical nanofeatures of the reported TEM study and the scatterers detected here by means of SANS can be identified as the Mn-Ni-Si-rich clusters observed in the reported APT study. Dislocation loops can also be assumed to be present but do not give rise to measurable SANS intensities (Bergner et al., 2008).
It is straightforward to cross-check the measured A-ratios against the reported composition of the Mn-Ni-Si-rich clusters. Assuming solute-atom clusters containing Mn, Ni, and Si (rest Fe) fully coherent with the bcc Fe matrix and using magnetic moments of Fe and Ni in the clusters consistent with the bulk magnetic moments of Fe and Ni, respectively, a theoretical A-ratio can be calculated according to (Mathon et al., 1997)
where nX is the concentration of element X in the clusters and the coefficients in the numerator and denominator are the nuclear and magnetic scattering lengths, respectively, both in units of fm. It is important to note that the A-ratio according to Eq. 1 is invariant against changes of the Fe fraction in the clusters at constant ratios of the contributing alloying elements. Moreover, Mn is the one and only element in the considered system that exhibits a negative nuclear scattering length. Therefore, Mn is capable of reducing the A-ratio to below the value for nanovoids, that is below A = 1 + (6.0/9.45)2 = 1.4. In order to further illustrate the effect of the cluster composition on the A-ratio, Eq. 1 is plotted in Figure 6 starting from the cluster composition reported for as-irradiated VVER-1000 weld, Mn:Ni:Si = 15:50:24 (Miller et al., 2009). In these plots, the fractions of either Mn or Ni or Si are varied, while the fractions of the other two elements are adjusted such that their reported ratios are kept constant. Figure 6 indicates that a high Mn fraction reduces the A-ratio and a high Ni fraction raises the A-ratio up to values > 10, while Si gives rise to minor variations. The indication line “A = 3.6” in Figure 6 corresponds to the reported cluster composition.
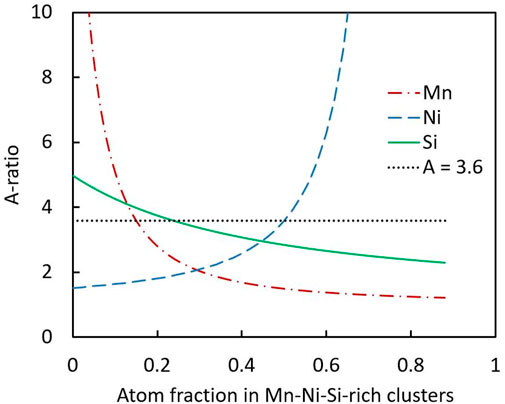
FIGURE 6. A-ratio as function of the composition of Mn-Ni-Si-rich clusters. Reference is the cluster composition reported for as-irradiated VVER-1000 weld obeying a ratio Mn:Ni:Si = 0.15:0.50:0.24 (Miller et al., 2009). The curves correspond to the individual variation of Mn, Ni, and Si as indicated. The reported Fe-fraction of 0.11 and the ratio of the remaining two elements were kept constant.
The calculated A-ratios are listed in Table 3 for selected cluster compositions. We have found that the reported mean composition (see lowest line in Table 3) for the as-irradiated VVER-1000 weld yields a higher A-ratio of 3.6 as compared to the measured value of 2.6. On the one hand, an assumed increase of the Mn content with a corresponding reduction of the Ni content (second line in Table 3), both within the reported experimental error bars (Miller et al., 2009), reproduces the measured A-ratio. On the other hand, the reported Mn content of the weld according to (Miller et al., 2009) (0.77 wt% as compared to 1.14 wt% in the present study) may be responsible for a lower Mn content in the clusters and a correspondingly higher A-ratio without the need to refer to error bars. It can be concluded that the A-ratio measured for the irradiation-induced scatterers is consistent with the reported cluster composition of Mn-Ni-Si-rich clusters. If not otherwise stated, we replace the unspecific term “scatterers” by the more specific term Mn-Ni-Si-rich clusters below.
Considering the evolution of the measured A-ratio resulting from the annealings, we have observed a decrease at increasing annealing temperature (Table 2). This may be due to the stepwise removal of Ni (and Si) atoms from the clusters while keeping the Mn atoms inside. The value A = 1.7 measured for the sample annealed at 350°C would be consistent with clusters composed of Mn, Ni and Si at the ratio 35:30:24 (third line in Table 3) or 35:35:0 (fourth line), for example. It is worth noting that there is a field of different Ni:Si-ratios yielding the same A-ratio, hence the Ni:Si-ratio cannot be derived from the A-ratio alone. Finally, the value A = 1.2 measured for annealing temperatures of 425°C and 450°C would be consistent with almost pure Mn clusters (fifth line). Indeed, there is no other option to reach such a small value. Taking into account that the coefficient of diffusion of Mn in Fe at 450°C is higher than the coefficients of Ni and Si (Messina et al., 2020), our observation indicates a deeper binding of Mn atoms in the clusters.
Post-irradiation annealed (450°C/2 h and 450°C/10 h) samples of VVER-1000 weld were also studied by means of APT (Miller et al., 2009). The reported APT maps indicate few Mn-Ni-Si-rich clusters after 2 h annealing (compositions were not reported), but almost no clusters after 10 h annealing. In one instance, there seems to be a Mn enrichment at a position without Ni- and Si-enrichments. Another reported piece of information of relevance here is related to the average radial concentration profiles of Mn, Ni, and Si in the clusters for the as-irradiated weld (Miller et al., 2009). These profiles indicate that Mn is most concentrated in the cluster cores, while Ni and Si concentrations are highest in the outer shell of the clusters. It is thus reasonable to assume that, upon annealing, Ni and Si leave the clusters first, while Mn remains bound in the clusters longest. This scenario would be consistent with the evolution of the A-ratio observed in the present study. It is interesting to note that APT results reported for a western-type weld (Ringhals unit 3) indicated that annealing at 450°C/30 min did not significantly alter the population of Mn-Ni-Si-rich clusters, while additional annealing at 500°C/10 min reduced the volume fraction of clusters by 50% (Styman et al., 2015). These authors also concluded that the dissolution was led by diffusion of Mn atoms away from the clusters. The reported observations partly differ from the present findings. Obviously, the annealing response depends on the material, irradiation conditions and annealing procedure.
One of the impactful properties of the observed nanoscale Mn-Ni-Si-rich clusters is their capability to act as obstacles for dislocation slip and, consequently, to efficiently harden the material. The dispersed-barrier hardening model (Seeger, 1958) is applied below to estimate the obstacle strength α of the clusters according to
where Δσy is the increase of the yield stress with respect to the unirradiated reference. M, G and b are the Taylor factor (here 3.06), shear modulus (here 82.2 GPa) and the magnitude of the Burgers vector (here 0.248 nm). N and d = 2R are the number density and the diameter of the clusters according to Table 2. It is important to note that a possible contribution of loops is ignored in Eq. 2, which exclusively takes into account Mn-Ni-Si-rich clusters. We will justify this assumption later in the discussion. As an approximation, a conversion from the change of the Vickers hardness number (which corresponds to the Vickers hardness in units of kgf/mm2) to the change of yield stress in units of MPa was applied in order to link Eq. 2 with the measured changes of Vickers hardness ΔHV10. The conversion factor β was reported to be 3.27 (Tabor, 1956). More recently Busby et al. (Busby et al., 2005) reported a theoretical value of 3.55 and an empirical estimate of 3.06 ± 0.15 for ferritic steels including RPV steels. In the present study, we have used an own, perhaps more representative estimate, namely, β = 3.29 ± 0.11, based on the own HZDR database covering measured values of Vickers hardness HV10 and yield stress for neutron-irradiated RPV steels (including the VVER-1000 weld of the present study), see inset in Figure 7.
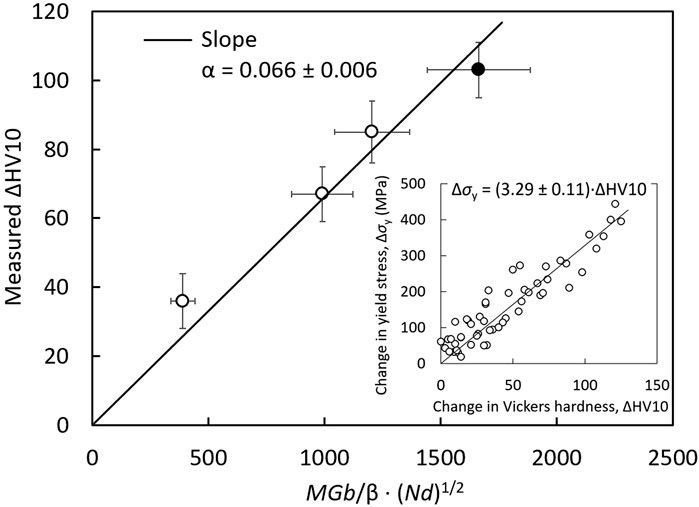
FIGURE 7. Increase of the Vickers hardness measured for the as-irradiated (full circle) and post-irradiation annealed (empty circles) conditions of VVER-1000 weld compared with the predictions based on Eq. 2. The inset indicates the conversion factor between changes of HV10 and yield stress.
A plot of the measured Vickers hardness increase versus the term
The statistical error of α does not include any bias due to possible non-zero average magnetic moments of the clusters and underestimations of the number densities resulting therefrom. It is worth noting that the changing composition of the clusters upon post-irradiation annealing, as indicated by the changing A-ratio of SANS, does not seem to substantially alter the obstacle strength. As indicated by the ranking of obstacle strengths obtained in the same framework of Eq. 2 for different families of irradiation-induced defects according to Table 4, this value corresponds to relatively weak shearable obstacles. It is interesting to note that the ranking of obstacle strengths is reasonable with respect to the type of obstacles. Indeed, Cr-rich α′-phase particles in Fe-Cr alloys are fully coherent with the matrix and exhibit a small α–α′ lattice mismatch (Korzavyi et al., 2009). They can be easily cut by dislocations. Cu-rich precipitates in RPV steels are known to be still coherent with the bcc matrix at small sizes but exhibit significant lattice distortion (Osetsky and Serra, 1996), which interacts with dislocations and gives rise to a higher obstacle strength. Mn-Ni-Si-rich clusters are obviously between these cases.
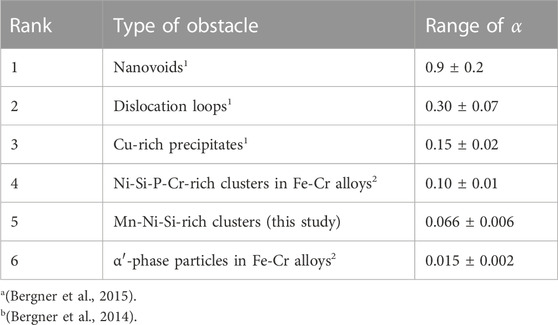
TABLE 4. Ranking of different families of irradiation-induced obstacles with respect to their obstacle strength empirically estimated in the framework of Eq. 2. Values refer to RPV steels and welds if not otherwise stated. The errors were derived from linear regressions.
Coming back to a possible hardening contribution of irradiation-induced dislocation loops, there are two substantial counter-arguments:
• First, the number densities of loops are reported to be much smaller than the number densities of clusters in RPV steels. For a VVER-1000 weld irradiated up to a similar neutron fluence, number density and diameter of loops were reported to be approximately 1.5 × 1016 cm−3 and 5.5 nm, respectively (Gurovich et al., 2013), that means, two to three orders of magnitude less in terms of number density as compared to the clusters in the as-irradiated weld of the present study. Taking into account the slightly larger size and larger obstacle strength of loops, the hardening contribution of loops is still only a small fraction of the contribution of clusters. This is even more pronounced for Pythagorean superposition of two contributions, the result of which is close to the larger one of the two contributions.
• Second, it is well accepted that loops in RPV steels are associated with clusters (Chiapetto et al., 2015; Castin et al., 2020). Undecorated loops can glide until getting bound to solute atoms or clusters (Castin et al., 2020). This process impedes further glide and loop growth. APT-based experimental evidence of a cluster linked with a loop (Wagner, 2017) is indicated in Figure 8. It is, therefore, unreasonable to consider loops as independent obstacles, as long as the clusters are already fully taken into account.
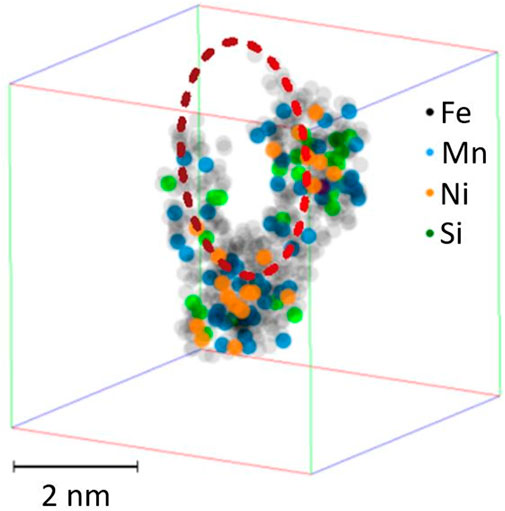
FIGURE 8. Loop decorated with solute atoms as revealed by an APT study of a neutron-irradiated RPV steel, reproduced with permission from (Wagner, 2017).
Another important property of the Mn-Ni-Si-rich clusters is their thermal stability. We have found that, depending on the temperature of annealing, the clusters progressively disappear, which may be the case by way of dilution or shrinkage. Table 2 indicates no decrease of the cluster size at increasing annealing temperature, meaning that a substantial contribution of shrinkage can be ruled out. The process of dissolution is certainly a complex multi-step process covering elementary steps such as vacancy migration, interstitial migration and solute—defect interactions. Some of these processes may be thermally activated. Figure 9 shows an Arrhenius plot of the fraction of dissolved clusters as function of the inverse absolute temperature of annealing. The results for the VVER-1000 weld of the present study (empty red circles) are compared with results reported for a western-type RPV steel (0.15 wt% Cu, 1.42 wt% Mn, 0.73 wt% Ni) irradiated and annealed under the same conditions (full black circles) (Ulbricht et al., 2006). A unique elementary process characterized by an activation energy of EA = (1.22 ± 0.05) eV can be attributed to the latter. This is consistent with the assumption of vacancy migration with a migration energy Em = 1.3 eV (Hardouin Duparc et al., 2002) controlling the rate of dissolution. The present data are not consistent with vacancy migration being the rate controlling step of cluster dissolution in the whole range of annealing temperatures. Either the activation energy is significantly smaller than 1.3 eV or there is a change of the rate-controlling step inside the considered temperature range. This view is consistent with vacancy-assisted migration being the dominant mechanism of Cu diffusion in Cu-rich RPV steels, while for Mn, Ni, and Si, interstitial-assisted migration is dominant (Mn) or at least contributes (Ni and Si) (Messina et al., 2020). The migration energy of interstitials was reported to be Em = 0.3 eV (Hardouin Duparc et al., 2002).
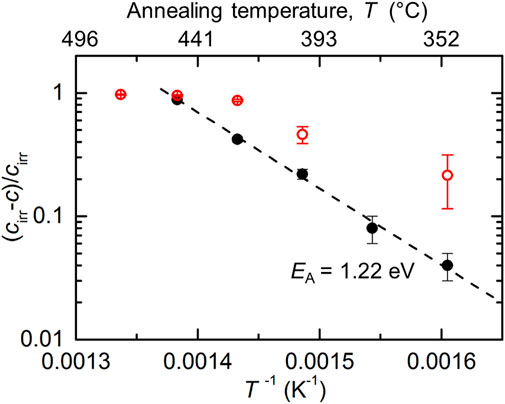
FIGURE 9. Arrhenius-plot of the normalized dissolved volume fraction of clusters (cirr-c)/cirr as function of the inverse absolute temperature for the present weld (empty red circles) and a western-type RPV steel (Ulbricht et al., 2006) (black dots).
It is also interesting to note that the clusters in the present weld exhibit the highest rate of dissolution at temperatures slightly slower than for the considered western-type weld, meaning that they are less stable or, in other words, recovery at a given temperature, say 450°C, is more efficient.
Finally, we shall briefly address the efficiency of annealing recovery from the technical point of view, see Figure 10. Annealing of the irradiated weld material at 350°C/10 h, which may be considered as representative for envisaged large-scale wet annealings at 343°C, gives rise to (22 ± 9)% recovery in terms of cluster volume fraction and (17 ± 12)% recovery in terms of Vickers hardness. These partial recoveries are small but significant. Corresponding data in terms of recovery of the transition temperature shift are currently not available for this material.
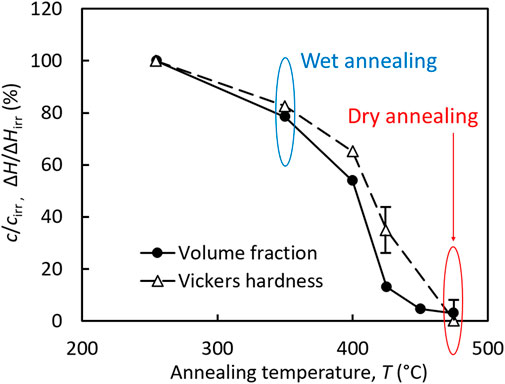
FIGURE 10. Percentage of recovery achieved by annealing as function of annealing temperature. Temperatures of interest for technical purposes related to wet and dry annealing are indicated.
Annealing at 475°C/10 h, which may be considered as approximately representative for realized large-scale dry annealings at 475°C/152 h performed for VVER-440 type reactors, gives rise to (97 ± 1)% recovery in terms of cluster volume fraction and (100 ± 7)% recovery in terms of Vickers hardness (Figure 10), that is complete or almost complete recovery toward the unirradiated condition. On the one hand, this can be compared with reported transition temperatures T48 obtained using a reference Charpy impact energy of 48 J (Viehrig et al., 2001). These authors reported T48 values of −16°C, +175°C, and −1°C for the unirradiated, as-irradiated, and post-irradiation annealed (475°C/10 h) condition of the same VVER-1000 weld (same irradiation conditions as in the present study). This corresponds to 92% recovery, that means, only slightly less than the 97% recovery in terms of cluster volume fraction. On the other hand, (Gurovich et al., 2013), suggested a higher post-irradiation annealing temperature of 565°C to avoid temper embrittlement that may occur at 475°C. Unfortunately, SANS is not adequate (or at least not the best choice) to study temper embrittlement and segregation of solute atoms at grain boundaries.
5 Conclusion
The post-irradiation annealing behavior of a VVER-1000 weld was investigated by means of SANS and Vickers hardness. Taking into account related reported studies, the following conclusions can be drawn from the results:
(1) The SANS results are consistent with irradiation-induced Mn-Ni-Si-rich clusters to be the dominant type of scatterers in the as-irradiated weld. The number density of these clusters decreases with increasing annealing temperature without any reduction of the mean size, while the A-ratio indicates increasing Mn:Ni and Mn:Si ratios in the clusters.
(2) An Arrhenius plot of the dissolved cluster volume fraction shows, contrary to a western-type RPV steel, a change of slope implying processes of different activation energies to compete in the overall process of cluster dissolution.
(3) The dispersed barrier hardening model allows microstructure-informed predictions of the hardness changes. Quantitative agreement between prediction and measurement is achieved for a comparably small obstacle strength of 0.066, which indicates shearable clusters. The obstacle strength does not noticeably change upon annealing up to 425°C.
(4) Annealing at 475°C/10 h gives rise to almost complete recovery in terms of cluster volume fraction and hardening. Annealing at 350°C/10 h, which is close to the maximum temperature accessible for wet annealing, results in a small but significant partial recovery.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AU: Conceptualization, methodology, investigation, data analysis, writing—review and editing. JD: Investigation, writing—review and editing. PC: Investigation, Writing—review and editing. EA: Conceptualization, funding acquisition, writing—review and editing. FB: Funding acquisition, methodology, data analysis, writing—original draft, Writing—review and editing.
Funding
This research contributes to the German project WetAnnealing funded by the Federal Ministry for the Environment, Nature Conservation, Nuclear Safety and Consumer Protection (BMUV) under contract No. 1501605 and to the European project STRUMAT-LTO, which has received funding from the Euratom research and training programme 2019–2020 under grant agreement No. 945272.
Acknowledgments
Technical assistance by Vanessa Reinke and Wolfgang Webersinke is gratefully acknowledged.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Auger, P., Pareige, P., Akamatsu, M., and Van Duysen, J.-C. (1994). Microstructural characterization of atom clusters in irradiated pressure vessel steels and model alloys. J. Nucl. Mater. 211 (3), 194–201. doi:10.1016/0022-3115(94)90347-6
Belkacemi, L. T., Meslin, E., CrocombetteRadiguetLeprêtre, J-P. B. F., and Décamps, B. (2021). Striking effect of solute elements (Mn, Ni) on radiation-induced segregation/precipitation in iron-based model alloys. J. Nucl. Mater. 548, 152807. doi:10.1016/j.jnucmat.2021.152807
Bergner, F., Gillemot, F., Hernandez-Mayoral, M., Serrano, M., Toeroek, G., Ulbricht, A., et al. (2015). Contributions of Cu-rich clusters, dislocation loops and nanovoids to the irradiation-induced hardening of Cu-bearing low-Ni reactor pressure vessel steels. J. Nucl. Mater. 461, 37–44. doi:10.1016/j.jnucmat.2015.02.031
Bergner, F., Pareige, C., Hernandez-Mayoral, M., Malerba, L., and Heintze, C. (2014). Application of a three-feature dispersed-barrier hardening model to neutron-irradiated Fe-Cr model alloys. J. Nucl. Mater. 448 (1–3), 96–102. doi:10.1016/j.jnucmat.2014.01.024
Bergner, F., Ulbricht, A., Hernandez-Mayoral, M., and Pranzas, P. K. (2008). Small-angle neutron scattering study of neutron-irradiated iron and an iron-nickel alloy. J. Nucl. Mater. 374 (1–2), 334–337. doi:10.1016/j.jnucmat.2007.07.008
Boothby, R. M., Hyde, J. M., Swan, H., Parfitt, D., Wilford, K., and Lindner, P. (2015). SANS examination of irradiated RPV steel welds during in-situ annealing. J. Nucl. Mater. 461, 45–50. doi:10.1016/j.jnucmat.2015.02.036
Brauer, G., Liszkay, L., Molnar, B., and Krause, R. (1991). Microstructural aspects of neutron embrittlement of reactor pressure vessel steels - a view from positron annihilation spectroscopy. Nucl. Eng. Des. 127 (1), 47–68. doi:10.1016/0029-5493(91)90039-K
Brauer, G., and Popp, K. (1987). Neutron embrittlement of reactor pressure vessel steels: A challenge to positron annihilation and other methods. Phys. Status Solidi (a) 102 (1), 79–90. doi:10.1002/pssa.2211020106
Brumovsky, M. (2015). Embrittlement of reactor pressure vessels (RPVs) in WWER-type reactors. Irradiat. Embrittlement React. Press. Vessels (RPVs) Nucl. Power Plants 107, 31. doi:10.1533/9780857096470.2.107
Busby, J. T., Hash, M. C., and Was, G. S. (2005). The relationship between hardness and yield stress in irradiated austenitic and ferritic steels. J. Nucl. Mater. 336 (2–3), 267–278. doi:10.1016/j.jnucmat.2004.09.024
Castin, N., Bonny, G., Bakaev, A., Bergner, F., Domain, C., Hyde, J. M., et al. (2020). The dominant mechanisms for the formation of solute-rich clusters in low-Cu steels under irradiation. Mater. Today Energy 17, 100472. doi:10.1016/j.mtener.2020.100472
Chiapetto, M., Becquart, C. S., Domain, C., and Malerba, L. (2015). Kinetic Monte Carlo simulation of nanostructural evolution under post-irradiation annealing in dilute FeMnNi. Phys. Status Solidi C. 12 (1–2), 20–24. doi:10.1002/pssc.201400143
Edmondson, P. D., Parish, C. M., and Nanstad, R. K. (2017). Using complimentary microscopy methods to examine Ni-Mn-Siprecipitates in highly-irradiated reactor pressure vessel steels. Acta Mater. 134, 31–39. doi:10.1016/j.actamat.2017.05.043
Frisius, F., and Buenemann, D. (1979). “The measurement of radiation defects in iron alloys by means of the small angle neutron scattering,” in Proceedings of the conference on irradiation behaviour of metallic materials for fast reactor core components (Marcoule: CEA).
Glatter, O. (1980). Determination of particle-size distribution functions from small-angle scattering data by means of the indirect transformation method. J. Appl. Crystallogr. 13 (1), 7–11. doi:10.1107/S0021889880011429
Gurovich, B., Kuleshova, E., Shtrombakh, Ya., Fedotova, S., Zabusov, O., Prikhodko, K., et al. (2013). Evolution of weld metals nanostructure and properties under irradiation and recovery annealing of VVER-type reactors. J. Nucl. Mater. 434 (1–3), 72–84. doi:10.1016/j.jnucmat.2012.11.026
Hardouin Duparc, A., Moingeon, C., Smetniansky-de-Grande, N., and Barbu, A. (2002). Microstructure modelling of ferritic alloys under high flux 1 MeV electron irradiations. J. Nucl. Mater. 302 (2–3), 143–155. doi:10.1016/S0022-3115(02)00776-6
Ilola, R., Nadutov, V., Valo, M., and Hänninen, H. (2002). On irradiation embrittlement and recovery annealing mechanisms of Cr–Mo–V type pressure vessel steels. J. Nucl. Mater. 302 (2–3), 185–192. doi:10.1016/S0022-3115(02)00780-8
Ke, H., Wells, P., Edmondson, P. D., Almirall, N., Barnard, L., Odette, G. R., et al. (2017). Thermodynamic and kinetic modeling of Mn-Ni-Si precipitates in low-Cu reactor pressure vessel steels. Acta Mater. 138, 10–26. doi:10.1016/j.actamat.2017.07.021
Kočík, J., Keilová, E., Čı́žek, J., and Procházka, I. (2002). “TEM and PAS study of neutron irradiated VVER-type RPV steels. J. Nucl. Mater. 303 (1), 52–64. doi:10.1016/S0022-3115(02)00800-0
Konstantinović, M. J., Uytdenhouwen, I., Bonny, G., Castin, N., Malerba, L., and Efsing, P. (2019). Radiation induced solute clustering in high-Ni reactor pressure vessel steel. Acta Mater. 179, 183–189. doi:10.1016/j.actamat.2019.08.028
Korzavyi, P. A., Ruban, A. V., Odqvist, J., Nilsson, J.-O., and Johansson, B. (2009). Electronic structure and effective chemical and magnetic exchange interactions in bcc Fe-Cr alloys. Phys. Rev. B 79, 054202. doi:10.1103/PhysRevB.79.054202
Krasikov, E. A. (2012). “Controlling RPV embrittlement through wet annealing in support of life attainment and life extension decisions,” in 3. International conference on nuclear power plant life management (PLiM) for long term operations (LTO) (Vienna: nternational Atomic Energy Agency). (IAEA).
Kryukov, A. M., Nikolaev, Yu.A., and V Nikolaeva, A. (1998). Behavior of mechanical properties of nickel-alloyed reactor pressure vessel steel under neutron irradiation and post-irradiation annealing. Nucl. Eng. Des. 186 (3), 353–359. doi:10.1016/S0029-5493(98)00247-7
Kuleshova, E. A., Gurovich, B. A., Shtrombakh, Ya.I., Erak, D. Yu., and Lavrenchuk, O. V. (2002). Comparison of microstructural features of radiation embrittlement of VVER-440 and VVER-1000 reactor pressure vessel steels. J. Nucl. Mater. 300 (2–3), 127–140. doi:10.1016/S0022-3115(01)00752-8
Laot, M., Naziris, K., Bakker, T., D’Agata, E., Martin, O., and Kolluri, M. (2022). Effectiveness of thermal annealing in recovery of tensile properties of compositionally tailored PWR model steels irradiated in LYRA-10. Metals 12 (6), 904. doi:10.3390/met12060904
Lindner, P., May, R. P., and Timmins, P. A. (1992). Upgrading of the SANS instrument D11 at the ILL. Phys. B Condens. Matter 180, 967–972. doi:10.1016/0921-4526(92)90524-V
Mathon, M. H., Barbu, A., Dunstetter, F., Maury, F., Lorenzelli, N., and de Novion, C. H. (1997). Experimental study and modelling of copper precipitation under electron irradiation in dilute FeCu binary alloys. J. Nucl. Mater. 245 (2–3), 224–237. doi:10.1016/S0022-3115(97)00010-X
Meslin, E., Radiguet, B., Pareige, P., and Barbu, A. (2010). Kinetic of solute clustering in neutron irradiated ferritic model alloys and a French pressure vessel steel investigated by atom probe tomography. J. Nucl. Mater. 399, 137–145. doi:10.1016/j.jnucmat.2009.11.012
Messina, L., Schuler, T., Nastar, M., Marinica, M.-C., and Olsson, P. (2020). Solute diffusion by self-interstitial defects and radiation-induced segregation in ferritic Fe–X (X=Cr, Cu, Mn, Ni, P, Si) dilute alloys. Acta Mater. 191, 166–185. doi:10.1016/j.actamat.2020.03.038
Miller, M. K., Chernobaeva, A. A., Shtrombakh, Y. I., Russell, K. F., Nanstad, R. K., Erak, D. Y., et al. (2009). Evolution of the nanostructure of VVER-1000 RPV materials under neutron irradiation and post irradiation annealing. J. Nucl. Mater. 385 (3), 615–622. doi:10.1016/j.jnucmat.2009.01.299
Miller, M. K., Sokolov, M. A., Nanstad, R. K., and Russell, K. F. (2006). APT characterization of high nickel RPV steels. J. Nucl. Mater. 351 (1–3), 187–196. doi:10.1016/j.jnucmat.2006.02.013
Odette, G. R., and Lucas, G. E. (1998). Recent progress in understanding reactor pressure vessel steel embrittlement. Radiat. Eff. Defects Solids 144 (1–4), 189–231. doi:10.1080/10420159808229676
Odette, G. R. (1983). On the dominant mechanism of irradiation embrittlement of reactor pressure vessel steels. Scr. Metall. 17 (10), 1183–1188. doi:10.1016/0036-9748(83)90280-6
Osetsky, Yu.N., and Serra, A. (1996). Study of copper precipitates in α-iron by computer simulation II. Interatomic potential for Fe[sbnd]Cu interactions and properties of coherent precipitates. Philos. Mag. A 73 (1), 249–263. doi:10.1080/01418619608242981
Pachur, D. (1982). Radiation annealing mechanisms of low-alloy reactor pressure vessel steels dependent on irradiation temperature and neutron fluence. Nucl. Technol. 59 (3), 463–475. doi:10.13182/NT82-A33004
Pareige, P., Radiguet, B., Krummeich-Brangier, R., Barbu, A., Zabusov, O., and Kozodaev, M. (2005). Atomic-level observation with three-dimensional atom probe of the solute behaviour in neutron-ion- or electron-irradiated ferritic alloys. Philos. Mag. 85 (4–7), 429–441. doi:10.1080/02678370412331320233
Pareige, P., Stoller, R. E., Russell, K. F., and Miller, M. K. (1997). Atom probe characterization of the microstructure of nuclear pressure vessel surveillance materials after neutron irradiation and after annealing treatments. J. Nucl. Mater. 249 (2–3), 165–174. doi:10.1016/S0022-3115(97)00215-8
Pelli, R., and Törrönen, K. (1998). On thermal annealing of irradiated PWR pressure vessels. Int. J. Press. Vessels Pip. 75 (15), 1075–1095. doi:10.1016/S0308-0161(97)00078-1
Popp, K., Brauer, G., Leonhardt, W. D., and Viehrig, H. -W. 1989. “Evaluation of thermal annealing behavior of neutron-irradiated reactor pressure vessel steels using nondestructive test methods Symposium on irradiation embrittlement and aging of reactor pressure vessels; Philadelphia, PA (USA L. E. Steele ASTM STP 1011. Philadelphia
Seeger, A. K. 1958. “On the theory of radiation damage and radiation hardening.Second united nations international conference on the peaceful uses of atomic energy, 6:250–273. Geneva, Switzerland: United Nations, New York.
Server, W. L., and Nanstad, R. K. (2015). Integrity and embrittlement management of reactor pressure vessels (RPVs) in light-water reactors. Irradiat. Embrittlement React. Press. Vessels (RPVs) Nucl. Power Plants 55, 132. doi:10.1533/9780857096470.2.132
Slugeǹ, V., Segers, D., De Bakker, P. M. A., De Grave, E., Magula, V., Van Hoecke, T., et al. (1999). Annealing behaviour of reactor pressure-vessel steels studied by positron-annihilation spectroscopy, mössbauer spectroscopy and transmission electron microscopy. J. Nucl. Mater. 274 (3), 273–286. doi:10.1016/S0022-3115(99)00073-2
Soneda, N. (2015). Irradiation embrittlement of reactor pressure vessels (RPVs) in nuclear power plants. Woodhead publishing series in energy. Cambridge, UK: Woodhead Publishing. number 26.
Sprouster, D. J., Sinsheimer, J., Dooryhee, E., Ghose, S. K., Wells, P., Stan, T., et al. (2016). Structural characterization of nanoscale intermetallic precipitates in highly neutron irradiated reactor pressure vessel steels. Scr. Mater. 113, 18–22. doi:10.1016/j.scriptamat.2015.10.019
Styman, P. D., Hyde, J. M., Parfitt, D., Wilford, K., Burke, M. G., English, C. A., et al. (2015). Post-irradiation annealing of Ni–Mn–Si-enriched clusters in a neutron-irradiated RPV steel weld using atom probe tomography. J. Nucl. Mater. 459, 127–134. doi:10.1016/j.jnucmat.2015.01.027
Tabor, D. (1956). The physical meaning of indentation and scratch hardness. Br. J. Appl. Phys. 7 (5), 159–166. doi:10.1088/0508-3443/7/5/301
Tomimatsu, M., Hirota, T., Hardin, T., and Todeschini, P. (2015). Embrittlement of reactor pressure vessels (RPVs) in pressurized water reactors (PWRs). Irradiat. Embrittlement React. Press. Vessels (RPVs) Nucl. Power Plants 57, 106. doi:10.1533/9780857096470.2.57
Toyama, T., Yamamoto, T., Ebisawa, N., Inoue, K., Nagai, Y., and Odette, G. R. (2020). Effects of neutron flux on irradiation-induced hardening and defects in RPV steels studied by positron annihilation spectroscopy. J. Nucl. Mater. 532, 152041. doi:10.1016/j.jnucmat.2020.152041
Ulbricht, A., Bergner, F., Boehmert, J., Valo, M., Mathon, M. -H., and Heinemann, A. (2007). SANS response of vver440-type weld material after neutron irradiation, post-irradiation annealing and reirradiation. Philos. Mag. 87 (12), 1855–1870. doi:10.1080/14786430601102999
Ulbricht, A., Bergner, F., Dewhurst, C. D., and Heinemann, A. (2006). Small-angle neutron scattering study of post-irradiation annealed neutron irradiated pressure vessel steels. J. Nucl. Mater. 353 (1–2), 27–34. doi:10.1016/j.jnucmat.2006.02.083
Viehrig, H. -W., Boehmert, J., Dzugan, J., and Richter, H. (2001). “Master curve evaluation of irradiated Russian VVER type reactor pressure vessel steels,” in Effects of radiation on materials: 20th international symposium. Astm stp 1405. Editors S. T. Rosinski, M. L. Grossbeck, T. R. Allen, and A. S. Kumar (West Conshohocken: American Society for Testing and Materials).
Viehrig, H.-W., Schuhknecht, J., Rindelhardt, U., Weiss, F.-P., Busby, J. T., Hanson, B., et al. (2009). Investigation of beltline welding seam of the greifswald WWER-440 Unit 1 reactor pressure vessel. J. ASTM Int. 6 (5), 101925. doi:10.1520/JAI101925
Keywords: reactor pressure vessel, weld, neutron irradiation, annealing, small-angle neutron scattering, vickers hardness, solute-rich clusters, recovery
Citation: Ulbricht A, Dykas J, Chekhonin P, Altstadt E and Bergner F (2023) Small-angle neutron scattering study of neutron-irradiated and post-irradiation annealed VVER-1000 reactor pressure vessel weld material. Front. Nucl. Eng. 2:1176288. doi: 10.3389/fnuen.2023.1176288
Received: 28 February 2023; Accepted: 13 April 2023;
Published: 24 April 2023.
Edited by:
Peng Wang, University of Michigan, United StatesReviewed by:
Mukesh Bachhav, Idaho National Laboratory (DOE), United StatesTianyi Chen, Oregon State University, United States
Jia-Hong Ke, Idaho National Laboratory (DOE), United States
Copyright © 2023 Ulbricht, Dykas, Chekhonin, Altstadt and Bergner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. Bergner, Zi5iZXJnbmVyQGh6ZHIuZGU=
 A. Ulbricht1
A. Ulbricht1 E. Altstadt
E. Altstadt F. Bergner
F. Bergner
