Investigating the effect of pore water composition and isosaccharinic acid (ISA) on sorption of Pu to a CEM III/C-based mortar

In the frame of the safe disposal of short-lived low and intermediate level nuclear waste (SL-ILW), ONDRAF/NIRAS (Belgium) has submitted a license application for the exploitation of a near surface facility in Dessel (Belgium). A significant part of the waste intended for the surface repository is Pu-contaminated and has been conditioned by means of CEM III/C based mortar, produced in the CILVA-installation at the Belgoprocess site in Dessel. To establish more accurate data on sorption of Pu to the CILVA mortar, an experimental test set-up was designed in order to screen which factors were likely to affect Pu sorption to the mortar. The different factors of the design were variables related to the pore water composition of the mortar on the one hand (concentrations of Ca²⁺, Cl⁻, SO₄²⁻, S²⁻, K⁺ and OH⁻ (pH)), and variables characteristic for batch sorption experiments on the other hand ([Pu], solid-to-liquid ratio and equilibration time). The results of this screening indicate that over the tested variables, only the concentration of Ca²⁺ in the synthetic pore water affects Pu sorption to the CILVA matrix to a significant extent. Additionally, from literature it is expected that the presence of isosaccharinic acid (ISA), a cellulose degradation product, would affect Pu sorption, with increasing concentrations of ISA frequently correlated with decreased sorption. To address the nature and extent of the impact of both [Ca²⁺] and [ISA] and their combined effect on sorption of Pu to the mortar, an experimental set-up for surface response measurement (SRM) was designed. A Central Composite Design (CCD) in two factors was selected for the SRM, with three test points and a four point repetition of the centre point. The execution of this experimental set-up and the resulting responses, allowed for the development of a polynomial model to predict the average response of Pu sorption (expressed as R_d) as a function of [ISA] and of [Ca²⁺]. In addition, the [Ca²⁺] in solution in equilibrium with the mortar could be assessed from the established dataset, which allowed to predict Pu sorption as a function of [ISA] at the intrinsic [Ca²⁺] in the mortar’s pore water.

Introduction

When processing different types of waste, including radioactive waste, cementitious materials have been widely used as solidification/stabilization agents (Atkins, 1992; Chen, 2009). One of the benefits of using cement is its high sorption capacity towards toxic elements and radionuclides (RN). In the frame of the safe disposal of nuclear waste, the Belgian national agency for radioactive waste and enriched fissile material, ONDRAF/NIRAS, has submitted a license application for the exploitation of a near surface facility for the disposal of short-lived low and intermediate level waste (category A (cat. A) waste). To assess the safety of such surface disposal facility, sorption values for various radionuclides on cementitious components are used in safety calculations (ONDRAF/NIRAS, 2019a; ONDRAF/NIRAS, 2019b).

A significant part of the waste intended to be disposed in the surface repository is Pu-contaminated waste, which has been conditioned in the CILVA-installation at the Belgoprocess site in Dessel, Belgium. Sorption data for Pu and other actinides to cementitious matrices were already reported in literature (Wang, 2009; Ochs, 2010; Wieland, 2014; Ochs, 2016; Wang, 2020), and values selected as reference are presently used in the safety case for near surface disposal. Nevertheless, the reported R_d values for Pu and similar actinides vary greatly, with for instance R_d values ranging from 5*10³ L/kg to 1*10⁵ L/kg for Pu on fresh cement (Wang, 2020). In addition, the CILVA matrix, a CEM III/C based mortar, differs from most of the reference cementitious materials studied in literature. The CILVA mortar is a mixture of a blast furnance cement (CEM III/C, 81 up to 95% slag), two types of sand, and a superplasticizer (Table 1). Hence, the composition of the cement phase and the conditions dominating the cement pore water differ from those of a CEM I matrix, which is the most studied cementitious matrix. For example, due to the presence of a high amount of blast furnance slag (BFS), the pore water of the CILVA mortar is strongly reducing, which is expected to affect the mobility of a redox-sensitive compound like Pu.

TABLE 1

TABLE 1. Composition of the CILVA immobilization matrix, for a volume of approximately 250 L.

In addition to conditions inherent to the CILVA mortar itself, the content of isosaccharinic acid (ISA), a cellulose degradation product associated with cat. A waste, was identified as potentially having an impact on Pu sorption, with a clear decrease in sorption with increasing [ISA] (Altmaier et al., 2013; Tasi et al., 2018b; Wang, 2020; Tasi et al., 2021). In order to decide to which extent cellulose containing waste would be eligible for the surface disposal facility, it was therefore deemed essential to define more accurate and representative sorption values for Pu, specifically for the CILVA mortar and its pore water, in the presence of a range of ISA concentrations. The primary aim of the presented study is therefore not to unravel phenomenological processes nor to increase comprehension of adsorption mechanisms, but essentially to quantify sorption properties.

Although the CILVA mortar is expected to evolve due to interactions of the repository with the environment, this work focusses on the unaltered mortar. Based on the CILVA pore water characteristics, an experimental matrix was defined to screen for variables affecting Pu sorption to the CILVA matrix. Following this screening, consisting of a Plackett-Burman (P.-B.) factorial design, a surface response measurement (SRM) according to a Central Composite Design (CCD) was planned and executed to investigate the extent of [Ca²⁺] and [ISA] on the response, the only two factors for which an effect could be either expected based on literature (ISA) or shown statistically via the screening study (Ca²⁺).

Materials and methods

Batch sorption experiments

Sorption of Pu to the CILVA matrix was studied through batch sorption tests, by bringing Pu and CILVA mortar in contact with each other inside a synthetic CILVA pore water (SCPW, see below). Care was taken to perform all experiments in their (randomized) run order and independently from each other, in order to limit experimental bias and interdependency.

An elaborate protocol on how to perform batch sorption experiments of RN to a cementitious matrix, and more specifically of Pu to the CILVA mortar, is provided in Wouters et al. (2022b). The sorption experiments were performed according to the following sequence: 1) preparation of different SCPW background solutions, 2) addition of CILVA to the solutions, followed by a 14 days pre-equilibration period, 3) addition of Pu and ISA to the CILVA-suspensions, followed by an equilibration period of 7–21 days, 4) sampling of the spiked suspensions for analysis of Pu. All the steps were performed under inert atmosphere in order to preserve the reduced state of the fresh CILVA mortar and to facilitate control of the experimental system. Each step is further described in details in the following paragraphs.

Preparation of SCPW background solutions

Synthetic CILVA pore water

To avoid alteration of the CILVA mortar through cement degradation and to assess Pu behaviour in representative conditions, the composition of the synthetic solution used for the batch sorption tests was close to that of the CILVA pore water, while still allowing sufficient variability to assess the impact of factors like pH, Eh, and ion concentrations on Pu sorption. In Wouters et al. (2022a), the composition of the natural CILVA pore water and a baseline recipe for synthetic CILVA pore water (SCPW) is discussed in detail.

Based on the experimental plan discussed below, different SCPW solutions were prepared under inert atmosphere. Salts used to prepare the solutions were NaCl, K₂SO₄, Ca(OH)₂, KOH, NaOH, Na₂S.9H₂O, KCl and Na₂SO₄ (all analytical grade).

pH

pH was measured when preparing the SCPW solutions, and corrected for by addition of small volumes (<100 µL) of high molarity solutions of NaOH or HNO₃. pH was not measured after addition of Pu and ISA, to avoid loss of Pu to the pH electrode. Instead, pH was measured before addition of Pu and ISA, and at equilibrium (see protocol in Wouters et al. (2022b)). To remediate for the alkali-error at high pH, the pH electrode was calibrated with a series of NaOH and/or KOH concentrations, using the protocol and readily available Excel file published by Traynor et al. (2020).

ORP/Eh

The Oxidation-Reduction Potential (ORP) of the suspensions was measured with a Ag/Pt electrode, with the ORP defined relative to a reference electrode (Argenthal Ag/AgCl). To allow comparison with other redox measurements, ORP readings were converted to the potential of the Standard Hydrogen Electrode (SHE) to obtain the Eh. Eh was measured only at the time of Ca-sampling (see below), so after 2 weeks of pre-equilibration of the CILVA mortar in the SCPW background solution with different [Ca²⁺].

Addition of CILVA to SCPW background solutions

Preparation of CILVA mortar

The CILVA immobilization matrix is a mortar consisting of CEM III/C, two types of sand and a superplasticizer, with a water to cement ratio of 0.38 (Table 1). CEM III/C is a highly reducing cement containing 81 to 95 w% of blast furnace slag (BFS). The composition of both the CILVA mortar and CEM III/C have been discussed previously in Wouters et al. (2022a).

The CILVA matrix was produced as 4 × 4 × 8 cm³ specimens at Belgoprocess (Dessel, Belgium), following the protocol by Vanherck (2017), where it was allowed to hydrate for 12 months, while being kept under water. At 12 months, the CILVA prisms were stored under inert atmosphere at 95%–98% RH. In order to address sorption in suspension, a 4 × 4 × 1 cm³ piece of the mortar was reduced completely to a powder with grain size <74 µm under inert atmosphere, after which the powder was thoroughly mixed to ensure homogeneity. The water content of powdered CILVA was determined to be 3.3 %w/w (Wouters et al., 2022a).

Solid-to-liquid ratio (S/L)

Given the narrow window of feasible Pu concentrations due to solubility and detection limits, the S/L was chosen between 0.1 and 0.5 g/L for the screening, taking into account an expected maximum R_d of 10⁵ L/kg. For the surface response measurement (SRM), a S/L of 0.22 g/L was selected.

Pre-equilibration of CILVA in SCPW

The cementitious phase was allowed to pre-equilibrate with the synthetic pore water for a period of 2 weeks prior to the start of the sorption experiments, at the targeted S/L (Tits and Wieland, 2018; Wouters et al., 2022b) inside the test tubes designated for the actual sorption experiments (Nalgene™ Oak Ridge high speed centrifuge tubes, PPCO, 38 mL). Pre-equilibration was performed in the test vials predestined for the sorption experiments, on a shaker inside a glovebox with N₂ atmosphere. During these 2 weeks, the samples were vortexed briefly every 2–3 days to keep the solid phase from developing pellets or adhering to the test vials.

Addition of Pu and ISA to CILVA suspensions

For detection purposes, ²³⁸Pu was selected as the most favourable isotope. It has a half-life of 87.76 years and decays mainly as an α-particle. A 3.7 MBq ²³⁸Pu source in 4 M HNO₃ was purchased from Eckert and Ziegler Nuclitec GmbH. The source was reported to yield >99.9% α-activity and had ²⁴¹Am removed prior to shipping (<0.0005% ²⁴¹Am). To correct the pH for the addition of HNO₃ when adding the Pu-spike to the CILVA suspension, a corresponding volume of high molarity NaOH was added.

Pure Na-α-ISA was produced based on the protocol provided by Van Loon and Glaus (1998) and is described in detail in Wouters et al. (2022c). ISA was added to the CILVA suspension at the time of Pu addition, in a broad range of concentrations (10^–1 to 10^–5 M) in the SRM, and at a fixed concentration of 10^–3 M in the screening. No pH correction was performed after addition of ISA.

After addition of Pu and ISA, the samples were returned to the shaker and left to equilibrate for 7–21 days in the screening, and 14 days in the SRM.

Sampling for Pu and Ca²⁺ analysis

After the equilibration time (7–21 days), the suspensions were centrifuged for 30 min at 21,000 *g. The size cut-off for Pu colloids at these centrifugation conditions would be 18 nm, given a particle density of 9 g/cm³ (Rundberg, 1987). Intrinsic spherical Pu-colloids of a reported diameter of 2 nm (Micheau, 2020) should however still be in solution after the centrifugation effort. Because there is no evidence of large Pu-colloids (>18 nm) in the given experimental conditions, the centrifugation effort is assumed to only target Pu sorbed to the cementitious phase. After centrifugation, duplicate samples of 5 mL of the supernatants were taken under inert atmosphere for Pu analysis by liquid scintillation counting (LSC). The centrifugation conditions were selected as sufficient to spin down the crushed CILVA mortar while leaving non-sorbed Pu in the liquid phase.

To determine the amount of Pu sorbed to the tubes, 0.1 M HCl was added to the emptied vials, after which Pu was allowed to desorb from the vials for 24 h, and a 2 mL sample was taken in duplicate and analysed by LSC.

Through HCl desorption, it can be calculated how much of the Pu was available for sorption at the time of sampling, and as such, how much was sorbed to the CILVA matrix. The distribution coefficient R_d can be calculated according to Eq. 1:

$\mathrm{R}\mathrm{d}=\frac{{\mathrm{A}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}-{\mathrm{A}}_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}}-{\mathrm{A}}_{\mathrm{e}\mathrm{q}}}{{\mathrm{A}}_{\mathrm{e}\mathrm{q}}}.\frac{\mathrm{V}}{\mathrm{m}}(1)$

with A_acid being the amount of RN (expressed as activity in Bq) desorbed from the test tube with a low pH (acid) solution, A_init being the initial activity of Pu in solution (Bq), A_eq the activity of Pu in solution at equilibrium (Bq), V the volume of the liquid phase (L) and m the dry weight of the added CILVA (kg).

The activity of Pu in solution was determined by liquid scintillation counting. A sample of 5 mL (SCPW solution) or 2 mL (HCl solution) was mixed with respectively 15 or 18 mL of dedicated LSC cocktail (Optiphase HiSafe 3, Perkin Elmer). Pu activity was detected in the 200—700 keV window on a TRI-CARB 2100TR LSC counter (Packard), with a maximum counting time of 90 min per sample and a 2sigma% of 0.5%. The efficiency of ²³⁸Pu detection in both background solutions was determined at 95%–96%.

In the SRM, duplicate samples (500 µL) were taken for analysis of [Ca²⁺] in the synthetic pore water, in equilibrium with the CILVA matrix, prior to the addition of Pu and ISA. Samples were taken after centrifugation of 30 min at 21,000*g. After sampling, CILVA was resuspended by vortexing. [Ca²⁺] analysis was performed by ICP-OES (Thermo Scientific iCAP 7,400 rad) after acidification of the samples with 2% HNO₃, by SCK CEN’s ISO 17025 certified Radiochemical Analysis Labs (RCA).

Design of the experiment

Screening for active factors

A factorial experimental screening design was adopted to address the effects of multiple factors. For this screening study, aimed to identify factors that have an important effect on the response under study when they are changed between their low and high value, the following a priori model is postulated for each response (Eq. 2):

$y=b_0+{\displaystyle \sum _{i=1}^p}{b}_i*x_i(2)$

with $b_i$ being the unknown coefficients of the model, $x_i$ the factor associated with the coefficient $b_i$, and $y$ being the response, i.e., log R_d in the present study.

Selection of factors and factor ranges

Nine factors were selected as possibly affecting Pu sorption (Table 2), of which six refer to the major chemical components of the CILVA pore water ([Cl⁻], [S²⁻], [Ca²⁺], [SO₄²⁻], [K⁺] and pH) and three are key to the design of a traditional sorption experiment (S/L, [Pu] and equilibration time).

TABLE 2

TABLE 2. Boundary values for nine factors identified for factorial design (screening).

Chlorides were varied between concentrations as low as 20 mM and as high as 1.25 M, to cover the concentration range expected in a CILVA matrix. The lower boundary is selected based on the [Cl⁻] measured in CILVA pore water (Wouters et al., 2022a), while the higher value is expected to cover the [Cl⁻] in a cementitious matrix in contact with chloride bearing waste (Coppens, 2020). The ranges of [S²⁻], [Ca²⁺], [SO₄²⁻], [K⁺] and pH cover the uncertainties on the pore water chemistry of this particular mortar. The addition of S^2- also enables preservation of reducing conditions. The ranges for S/L, [Pu] and equilibration time were selected based on preliminary tests and the detection limits for Pu.

In the screening study, all factors, except equilibration time and pH, were log-transformed before being normalized. The physical boundaries of the experimental domain are normalized over the n-dimensional vector space, with n being the number of factors.

In order to overcome practical issues associated with a design heavily relying on varying combinations of different ions, and thus to allow adjustments for electro neutrality, it was opted to keep [Na⁺] as free-floating, ranging between 3.08*10^–2 M and 1.40 M. Hence, [Na⁺] is not a factor in the design, even though the exact [Na⁺] in the CILVA pore water remains uncertain. The choice for [Na⁺] as free-floating element was driven by the fact that this element is the most abundant ion in the CILVA pore water (together with OH⁻). In addition, because the impact of ISA on Pu sorption is already established, [ISA] was not included as a factor in the screening step either. Instead, it was kept constant, at an intermediate level of 10^–3 M.

Plackett-Burman design

The resulting experimental screening design was set up according to a Plackett-Burman (P.-B.) design (Plackett and Burman, 1946) in seven factors: [Cl⁻], [S²], [Ca²⁺], pH, equilibrium time, [SO₄²⁻] and a group factor in which [Pu], S/L and [K⁺] were varied simultaneously since they were expected not to have an impact on the response. The design was composed of 11 independent sorption tests: the eight runs typical for a P.-B. design were complemented with three centre points. The resulting experimental plan (Table 3) was executed in randomised order and care was taken to assure independent runs.

TABLE 3

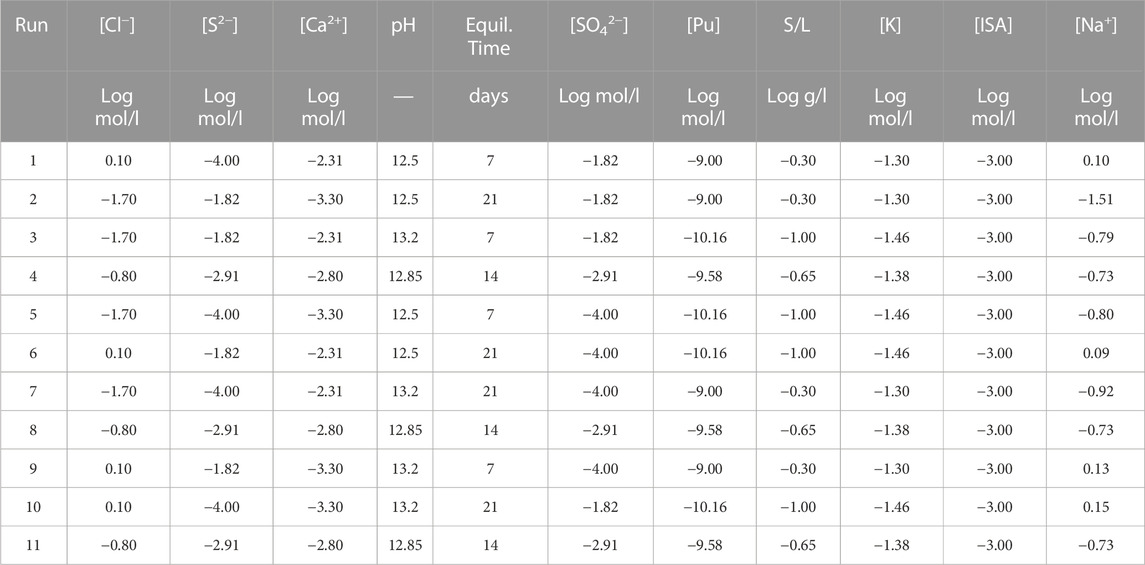
TABLE 3. Experimental plan for the screening design. All factors, except for pH and the equilibrium time, were log-transformed. [Pu], S/L and [K] were grouped and as such varied simultaneously. [ISA] was kept constant in the screening. [Na⁺] was considered as floating to allow balancing of the solutions.

The coefficients of the model associated with each of the factors are estimated through Ordinary Least Squares (OLS). Details are provided in the Supplementary Material. By means of ANOVA, the significance of each of these estimates is assessed. Power calculations revealed that this experimental plan, in combination with ANOVA and a significant threshold of 5%, allows to detect active factors in 80% of the cases as long as the effect of a change of one of the factors from one to the other extreme is at least 3 times the standard deviation of the experimental error.

Surface response measurement

The screening study, according to the P.-B. design, was followed by a surface response measurement (SRM) study on the previously identified factors ([ISA] and [Ca²⁺]). The aim of this study was to develop a model that predicts with sufficient precision the response (R_d) as a function of the factor levels.

In a SRM-study, a second order model with interactions is postulated a priori, as shown in Eq. 3:

$y=b_0+{\displaystyle \sum _{i=1}^m}{b}_i*x_i+{\displaystyle \sum _{i=1}^m}{b}_{ii}*x_i^2+{\displaystyle \sum _{i=1,i\ne j}^m}{b}_{ij}*x_i*x_j+\epsilon (3)$

with:

• $b_i$, $b_{ii}$, $b_{ij}$ the unknown coefficients of the model;

• $x_i$ the ith-coded factor level;

• $\epsilon$ the error normally distributed around 0; N (0,σ²);

• $y$ the response

• $m$ the amount of factors.

Model building and validation

The model building starts by adopting the a priori model; coefficients are estimated through ordinary least squares (OLS), and verification of the pertinence of a power-transformation (Myers and Montgomery, 1995). Possible erroneous experimental runs are identified by means of a normal-plot of the residuals, and if those would have a too important weight into the equation according to the D-cook’s distance (Myers and Montgomery, 1995), they can be excluded from the model building stage after careful consideration. Indeed, the model coefficients are estimated trough OLS adopting all runs, including potential erroneous runs. Since the model is fitted through OLS, the mean of residuals is zero while the central limit theorem states that the experimental errors are normally distributed. Hence if the residuals are equal to the errors, they are normal-distributed with a mean of zero. Plotting the residuals on a normal plot would make residuals to deviate from a straight line when their magnitude is greater than the experimental error, indicating an erroneous run. Additionally, it is verified whether the model could be simplified without reducing the predictive quality.

The validation of such a model consists of multiple steps. First, an examination is needed on whether the model actually explains the observations more than the constant average value - the so-called null-model - would. Secondly, it is checked whether the residuals (the differences between the observed values and the predicted ones) are normally distributed and whether they can be explained by the experimental error (which is assessed through repetitions), a so-called lack-of-fit test. In addition, the prediction of the model can be compared at dedicated test points, which are measured but not used to estimate the coefficients.

Central Composite Design

As [Ca²⁺] was the only factor for which an effect on Pu sorption was indicated by the screening, the effect of this factor was further looked into, in combination with the concentration of ISA. During the SRM, the [Ca²⁺] and the [ISA] were the only varied factors; the other variables are kept at a constant level throughout the entire SRM, except for the [Na⁺] (floating factor). Except for the pH, intermediate values were selected for all inactive variables within the range previously selected for the screening (Wouters et al., 2022a). As for the pH, it was decided to choose the lower value (pH 12.5), as this would lower the chance of Ca-saturation at the highest [Ca²⁺].

It was decided to adopt a spherical CCD (Central Composite Design) in two factors (Myers and Montgomery, 1995), an experimental plan with by default 9 treatments.

However, performing experiments with a high [Ca²⁺] of 8.1*10^–3 M, as defined by the star-point coordinates [1.4142; 0] of such a design, might lead to incorrect results due to the possible precipitation of Ca-phases. Therefore, failure of that particular point was anticipated, and the matrix was complemented with an extra experiment at coordinates [1; 0] (the so-called “reserve point”). This point would only be used for model building if indeed, the experiment at coordinates [1.4142; 0] would fail; if not, it would be used as an additional test point. The centre point was repeated five times. The predictive quality of the resulting model (if validated models could be developed) including this compensation, would still be more than acceptable. As can be deduced from the standardised-error-plot (Supplementary Figure S1), the precision is reduced a bit near the right-hand side of the domain, but the ratio between the prediction error and the experimental error remains below 1.

In addition, three test-points were added to challenge the predictive properties of the model. Test points were selected in an arbitrary way, taking into account equal spacing and sufficient distance from model points and the edge of the design space. For illustration purposes these test-points are visualized in Supplementary Figure S1, at a distance of ca. 0.71 ($\sqrt{0.5}$) coded units from the centre.

The experimental plan, a CCD complemented with test points and a reserve point, covers a relevant range of [Ca²⁺] and [ISA], and aims at defining the impact of [Ca²⁺] and [ISA] on sorption of Pu to the CILVA matrix, including their combined effect. The experimental plan of the SRM, expressed in physical units, is provided in Table 4. For experimental execution, the 17 runs were randomized and prepared one after the other.

TABLE 4

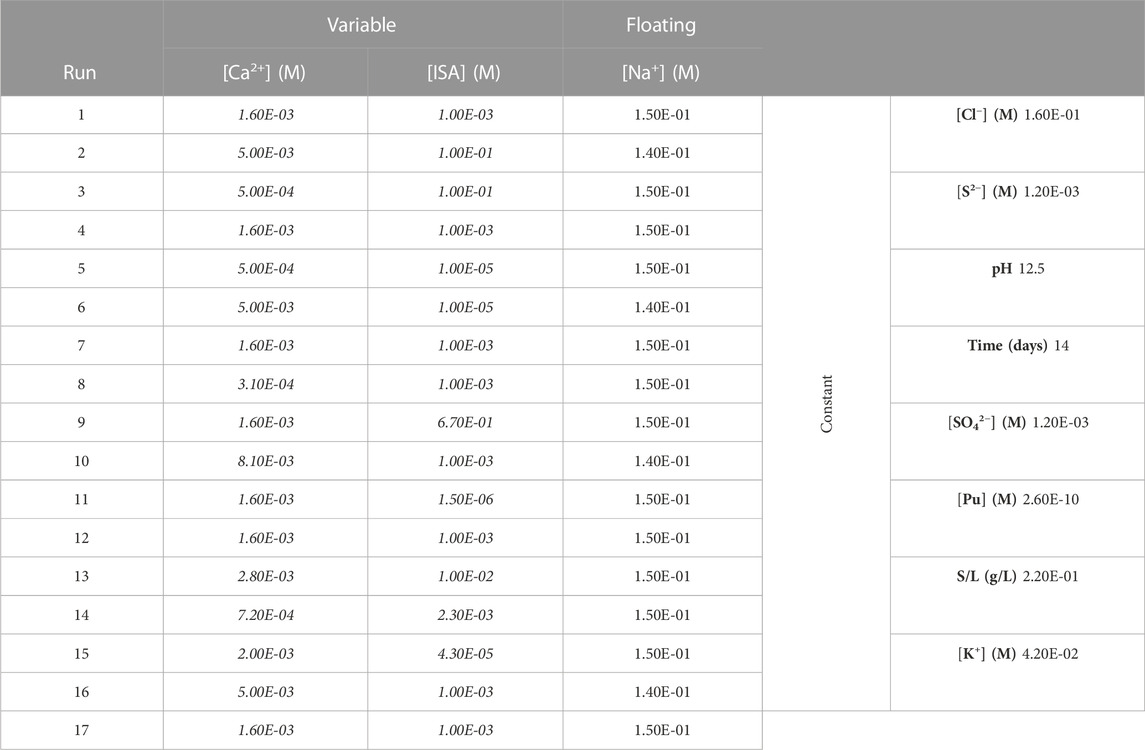
TABLE 4. Experimental plan for surface response measurement (SRM), based on Central Composite Design (CCD). Only the levels of [Ca²⁺] and [ISA] are varied according to the experimental design. [Na] is a floating variable of which the levels are allowed to vary to allow mass balancing of the solutions. The other factors are kept constant throughout the 17 experiments.

Responses

During the screening, only one response was measured, namely, the R_d of Pu on the CILVA mortar.

During the SRM four responses were measured.

1. The R_d of Pu on the CILVA mortar was the primary response of interest. This response was used in further model building, in order to predict the R_d in function of varying factors.

2. [Ca²⁺] was considered a response worth following up, since it was an active factor in the screening step and because [Ca²⁺] in equilibrium with the CILVA mortar could differ from the initial [Ca²⁺] added to the system. The difference between the [Ca²⁺] in the experimental plan and [Ca²⁺] after the pre-equilibration period was defined as a response to proceed with in further model building to estimate the intrinsic [Ca²⁺] in the CILVA pore water.

3. pH was included as a response, as it is known to possibly affect RN sorption, and because its stability in the different solutions and suspensions was unknown. This response was not used in further model building.

4. The redox potential Eh was selected as a response, because of the redox-sensitivity of Pu, and the unknown state and stability of the redox environment in the different suspensions. This response was not used in further model building.

Results and discussion

Screening response: R_d of Pu to CILVA mortar

The calculated R_d values for the 11 screening runs are presented in Table 5. ANOVA (Table 6) revealed statistical evidence for the contribution of [Ca²⁺] to the variation of log Rd, at the 5% significance threshold. This was confirmed by the normal plot shown in Supplementary Figure S2.

TABLE 5

TABLE 5. R_d values for the 11 experiments of the P.-B. design for screening of active factors.

TABLE 6

TABLE 6. ANOVA table of the screening experiments for log R_d.

Since the coefficient related to the [Ca²⁺] factor is estimated at −0.6 and the standard deviation on the log R_d value is estimated at 0.207, the effect size of this factor on the log transformed response in question was estimated at a Cohen’s d-value of 5.8 (Cohen, 1988). For the other factors, the ANOVA did not result in a p-value below 5%; hence no effect of these factors is shown. However, that does not mean these other factors do not influence the R_d value at all. With respect to the experimental error, their effect might be not sufficiently big to result, for the adopted experimental plan, in p-values lower than the adopted significance threshold. This is especially true for factors for which the p-value of the coefficients are only slightly above the significance threshold (e.g., S^2-).

The reduced linear model in [Ca²⁺] explains about 75% (R²) of the observed log R_d variation. However, the residuals of Run 7 seem to be deviating (Supplementary Figure S3), indicating an issue with this run. In addition, the lack-of-fit of this reduced linear model is not convincing (Supplementary Table S1). Indeed, the limited amount of degrees of freedom, especially for the pure error, limits the power of this test. Consequently, only in cases with a rather high deviation from the null-hypothesis (i.e., the pure error and the residuals have an identical variance) low p-values can be expected with high probability.

Hence, [Ca²⁺] is considered as the primary factor responsible for the variability observed in log R_d value, while due to the limited amount of degrees of freedom in the denominator of the lack-of-fit test, an important higher order term, i.e., a quadratic effect, can not be excluded. As such, out of the seven factors addressed in the screening, only [Ca²⁺] was considered as an active factor and therefore taken into account in the subsequent surface response measurement.

SRM response: pH

After pre-equilibration of CILVA during 2 weeks in presence of different concentrations of Ca²⁺ in SCPW, pH is relatively stable around pH 12.60 with a standard deviation of 0.05 pH units across all experiments. At the end of the sorption experiments, the pH seems to vary more (standard deviation of 0.11 pH units) but the average (pH 12.46) remains close to the initial value of 12.50.

SRM response: Eh

As expected, the Eh showed to be similar for all 17 experiments, with an average Eh of −298 mV and a standard deviation of 12 mV). Because all manipulations were performed in a glovebox with inert atmosphere and no significant amounts of oxidants were added, these reducing Eh values are considered to be representative for the redox environment during the subsequent sorption experiments.

SRM responses: R_d of Pu sorption to CILVA mortar, and [Ca²⁺]

The R_d values and [Ca²⁺] in equilibrium in the different CILVA suspensions are provided in Table 7 for the 17 runs. It should be noted that these values are the average of duplicate samples from each of the 17 experiments.

TABLE 7

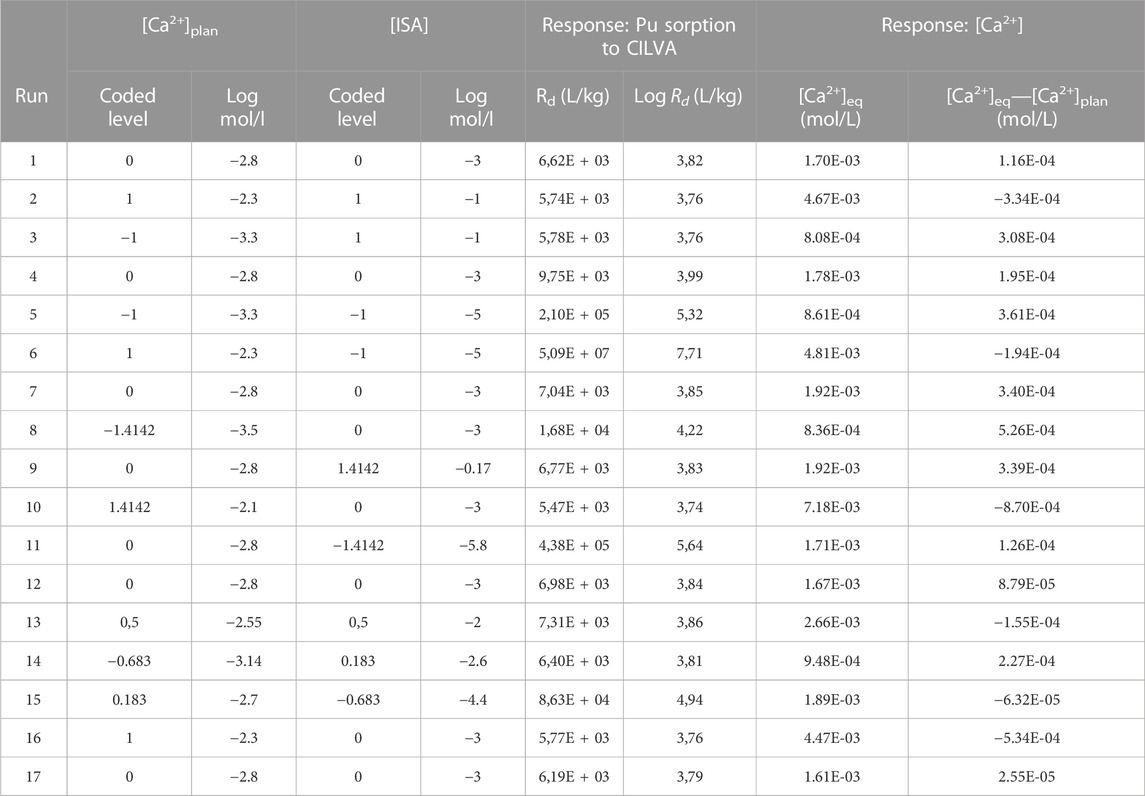
TABLE 7. Responses obtained for the 17 experiments, with [Ca²⁺] and [ISA] levels indicated both as coded factor levels in log(M) and as molar concentrations. Results on Pu to the CILVA mortar are provided as R_d and log R_d. As for Ca²⁺, the [Ca²⁺] after pre-equilibration is provided ([Ca²⁺]_eq), as well as its difference from the values foreseen in the experimental plan ([Ca²⁺]_eq—[Ca²⁺]_plan).

Modelling of Pu sorption in function of Ca²⁺ and ISA

A box-cox power transformation (Myers and Montgomery, 1995) revealed that the log transformation of the R_d response was the most adequate and allowed to significantly reduce the residuals. Additionally, after the log transformation and least-square estimation of the model coefficients, D-cook’s distances were calculated for each of the experimental runs, as well as the normal-plot for the residuals, as shown in Supplementary Figures S4, S5 respectively. The D-cook’s distance is a measure for the importance a certain run has on the model coefficients. In general, a D-cook’s distance below 1 indicates the run is not influencing the coefficients much. Hence, for runs that might be erroneous, it can be verified to what extent the model is affected by a possible error. In this respect, the half-normal plot clearly indicates a possible error for Run 6, and this run also has a considerable effect on the model coefficients. In addition, the ANOVA for this model indicates that the residuals cannot be explained solely by the experimental error as being assessed by the repetitions of the centre point; the p-value of this lack-of-fit test is less than 0.01% (not shown).

Because of the particularity of Run 6, it was decided to exclude it from the model building. This decision is supported by experimental-technical experience concerning this particular run, since it was flagged as questionable already before the start of the statistical analysis. The [Pu] in the supernatant of Run 6 was very close to the detection limit and the value would therefore be disputable or at least prone to relatively high deviations.

Ignoring Run 6 and by default excluding the test points and the reserve points in the model building, leads to the ANOVA presented in Table 8.

TABLE 8

TABLE 8. ANOVA of the model for the log Rd-value of Pu on CILVA excluding Run 6.

This ANOVA indicates that the model actually adds information (i.e., the model is significantly better than the null-model) and that the predictive properties are sufficient, despite ignoring 1 experiment (Run 6). Indeed, the lack-of-fit is not significant, meaning that the residuals can be solely explained by the experimental error as assessed by repetitions of the centre point. The pure error has a mean square value of 0.0058, as can be deduced from Table 8. There are two degrees of freedom for the lack-of-fit and four degrees of freedom for the pure error. Also note that the F-value of 0.16 is the ratio of the lack-of-fit to the pure error, not the other way around. In absence of a fit, it would be expected to have a lack-of-fit which is significantly higher than the pure error, which would turn the ratio to greater than one. The resulting model, expressed in coded variables, can be found in Supplementary Table S2. The properties of the model are provided in Supplementary Table S3 and show a. o an R² of 0.99 and a standard deviation of 0.0647. This standard deviation is based on the repetitions in the experimental design and the residuals of the polynomial model. Due to the non-significant lack of fit, it can be interpreted as the experimental error.

The star point did not lead to erroneous results and as such the reserve point added to the experimental matrix could be used as an extra test point. Comparing the three test points and the reserve point with the predictions of the model as described in Table 9, the predictions are in good agreement with the observations. However, for two out of four (indicated in red in Table 9) they differ more from the actual value than would be expected from the estimated experimental error, i.e., the predicted values at the test points are not included in the 95% prediction intervals. This indicates that albeit close to reality, a slight underestimation of reality can not be excluded, as indicated by the actual R_d values of two test points being higher than their predicted values, especially for the test point at low ISA concentration.

TABLE 9

TABLE 9. Actual (experimental) values versus predicted values for the test and reserve points.

Consequently, given i) good fit statistics, ii) no indications of a lack-of-fit and iii) good agreement between test points and predictions (with slight deviations), the model is considered valuable for the prediction of Pu sorption as a function of [Ca²⁺] and [ISA], taking into account a possible, minor underestimation of reality. The predictions for the average response of this model are given in the contour plot in Figure 1.

FIGURE 1

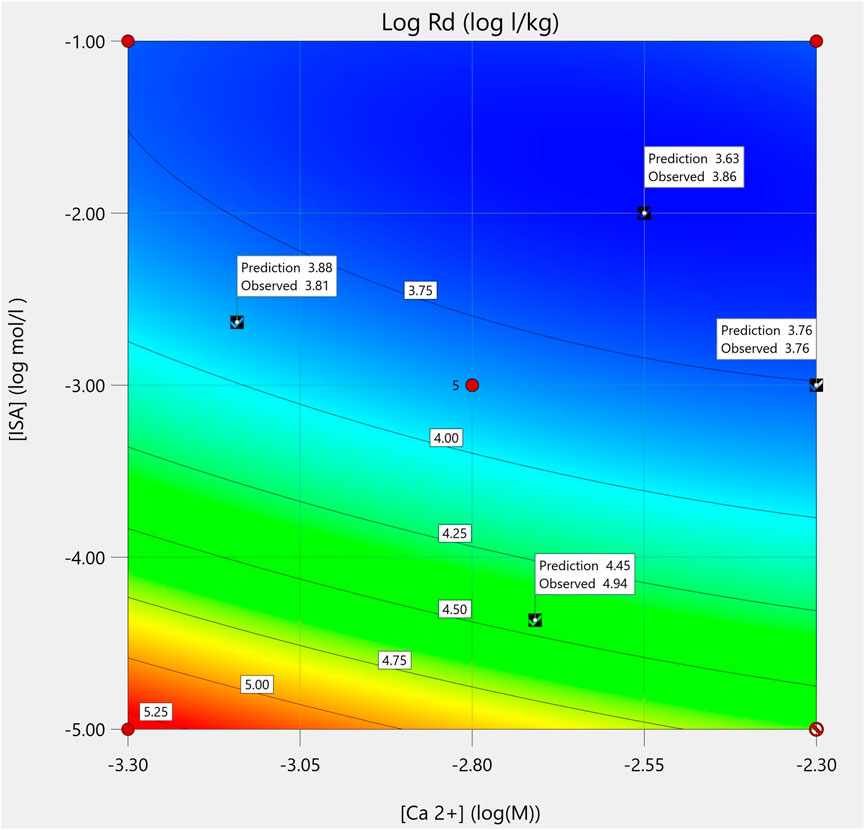
FIGURE 1. Contour plot of the model as a function of [Ca²⁺] and [ISA] (log M), with the test points indicated with check marks and their predicted and observed values.

The effect of [Ca²⁺], [ISA] and their interaction on Pu sorption

From the model coefficients (Supplementary Table S2) and the contour plot (Figure 1), it can be deduced that sorption of Pu to the CILVA matrix decreases with increasing concentrations of ISA and Ca²⁺. These observations are in agreement with recent literature, reporting decreased sorption of Pu and other RN (U, Th, Np, Am, Eu … ) to cementitious matrices with increasing concentrations of ISA (Wieland et al., 2002; Tits et al., 2005; Diesen et al., 2017; Tasi et al., 2021) and Ca²⁺ (Altmaier et al., 2009).

In the presence of ISA and in absence of Ca²⁺, RN-ISA complexes are expected to dominate the aqueous speciation of tetravalent actinides in the alkaline pH range (Gaona et al., 2008). Hence the prevailing hypothesis is that decreased RN sorption in the presence of ISA above a generally observed threshold of 0.1 mM (Wang, 2020), is caused by a shift in the equilibrium between sorbed RN and RN in solution, due to the formation of RN-ISA complexes. More specifically for Pu, it was shown that the solubility of PuO₂ (ncr, hyd) increases in the presence of ISA with up to 2.5 log units, and that ISA forms stable complexes with Pu under alkaline, reducing conditions (Gaona et al., 2008; Tasi et al., 2018a). In addition, or alternatively, sorption of ISA to the cementitious matrix, and as such occupying sorption sites, can also be hypothesized to have an impact on RN (Pu) sorption (Pointeau et al., 2008; Glaus and Van Loon, 2009; Tasi et al., 2021). In this respect, it could be argued that sorption of the ISA-RN complex to the cement phase would also contribute to the overall decrease of RN sorption, if the R_d of ISA is lower than the R_d of the RN, and assuming the complex behaves mainly as ISA. As such, the overall decrease of Pu sorption to the CILVA matrix would be the net effect of the equilibria between i) Pu and CILVA, ii) ISA and CILVA, iii) Pu and ISA and iv) the Pu-ISA complex and CILVA. In addition, the degradation of cementitious phases by ISA could play a role as well (Tasi et al., 2021) and would be yet another mechanism which could contribute to the decrease of RN sorption in the presence of ISA, especially at low S/L and high [ISA]. Indeed, Çevirim-Papaioannou et al. (2022) calculated that at a S/L of 1 g/L, up to 50% of CaO in HCP could dissolve in the presence of 10^–1 M ISA, due to the formation of Ca-ISA complexes.

The impact of [Ca²⁺] on sorption of RN has been scarcely documented. In general, it is found that a low concentration of Ca²⁺ would result in degradation of the cementitious phase, due to Ca-leaching (Berner, 1988). This would result in decreased RN sorption with decreasing [Ca²⁺] or decreasing Ca/Si ratio of the cementitious phase (Androniuk et al., 2017), which seems to contradict the experimental findings. In the experimental design however, care was taken to limit the range of [Ca²⁺] as such that Ca-leaching due to low [Ca²⁺] in solution should not occur to an important extent. In contrast, Ca²⁺ could sorb to the calcium silicate hydrate (CSH) phase of a cementitious matrix (Androniuk et al., 2017). As it has been described before that these sorption sites also sorb uranyl cations through surface complexation (Androniuk et al., 2017), it can be envisioned that a similar mechanism applies for the Pu cation. Hence, Ca²⁺ and Pu would compete for the same sorption sites, resulting in lower sorption of Pu at higher [Ca²⁺].

In addition, Altmaier et al. (2009) describes increased solubility of Pu in the presence of increased concentrations of CaCl₂. It was found that the increased Pu solubility was due to the formation of Ca-Pu-OH complexes and could therefore be attributed to the increased [Ca²⁺] (and not increased [Cl⁻]). This does seem to contrast with the findings of Smith et al. (2018), who describe decreased solubility of another actinide (Np) with increasing [Ca²⁺], due to the formation of a less soluble Ca-containing Np-hydroxide phase. In addition, it has been described previously that a higher [Ca²⁺] would have an enhancing effect on the solubility of PuO₂ in the presence of ISA, by forming a quaternary complex (Ca-Pu-OH-ISA) (Tasi et al., 2018b). Tits et al. (2005) also described the desorption of Th from calcite in the presence of ISA as being the result of the formation of Th-Ca-ISA complexes.

It is therefore hypothesized that the decreased sorption of Pu to the CILVA matrix in the presence of higher [Ca²⁺] is due to either of both i) competition of Pu and Ca²⁺ for sorption sites, and ii) complexation of Pu with Ca²⁺ and/or ISA, either by the associated steric hindrance impeding sorption to the CILVA surface, or by an altered equilibrium between Pu sorbed to the surface and Pu in solution.

The model coefficients provided in Supplementary Table S2 also show an interaction effect between both factors ([ISA] and [Ca²⁺]), meaning that a change in the value of one factor influences the impact of the other factor. Since the interaction effect has a positive sign, while the main effects of [Ca²⁺] and [ISA] both have a negative sign, the impact of [ISA] on Pu sorption is more pronounced at lower [Ca²⁺]. In other words, at higher [Ca²⁺], the above-described decrease of the R_d due to increased [ISA] is weaker. This interaction could also work the other way round: at higher [ISA], the decrease of R_d due to increased [Ca²⁺] is less pronounced. This observation slightly weakens the above-described hypothesis that the formation of Pu-ISA-Ca complexes causes decreased Pu sorption. It could be imagined however that cation bridging by Ca²⁺ would increase sorption of ISA to the CILVA surface. In this respect, the formation of surface complexes of cement-Ca-ISA-Pu through cation bridging could explain why increased [Ca²⁺] seems to mitigate the inverse effect of [ISA] on Pu sorption. In addition, a higher [Ca²⁺] already in solution could mitigate portlandite dissolution and decalcification of CSH phases by ISA, thereby causing less degradation of the cementitious phases, and as such less decrease of Pu sorption in the presence of high [ISA]. However, though our data cannot confirm it, the most plausible hypothesis to explain this interaction effect, is based on the above-mentioned occupation of sorption sites by Ca²⁺. It has been described before that sorption of Ca²⁺ to CSH surfaces is less pronounced in the presence of gluconate, caused by the formation of stable Ca-gluconate complexes (Androniuk and Kalinichev, 2020; Kutus et al., 2020). Since in alkaline solutions the stability constant of Ca-ISA is reported to be larger than that of Ca-gluconate complexes (Dudás et al., 2017), the formation of strong Ca-ISA complexes is expected to have a similar effect on the sorption of Ca²⁺ to the CSH phases of the CILVA matrix. As such, if less Ca²⁺ is sorbed to the CSH surface in the presence of ISA, more sorption sites are available for Pu or Pu-containing complexes. Hence, Ca²⁺ sorption to CSH phases could be a crucial mechanism when interpreting both the impact of [Ca²⁺], and the interaction between the impact of [Ca²⁺] and [ISA], on Pu sorption to the CILVA matrix, though further investigations would be needed to confirm it.

Determination of the intrinsic [Ca²⁺]

In addition to the sorption of Pu, the [Ca²⁺] at the assumed equilibrium with the sorbent has been measured. These analyses allow for the calculation of the difference between the added concentration of Ca²⁺ and its measured concentration: [Ca²⁺]_eq.—[Ca²⁺]_plan. If the difference is zero, the concentration added to the experiment is in equilibrium with the sorbent. We define that concentration as the intrinsic Ca²⁺ concentration. An effort was made to derive the intrinsic [Ca²⁺] by considering the [Ca²⁺]_eq.—[Ca²⁺]_plan as a response from the experimental design discussed above and subsequent model building. It should be noted that the [Ca²⁺]_eq is measured prior to addition of ISA. Therefore, the concentration of ISA cannot have an effect on this response.

The ANOVA table of the quadratic model for [Ca²⁺]eq—[Ca²⁺]plan is given in Table 10. It can be derived that the model is adding additional information and the residuals can be solely explained by the experimental error. The fit statistics can be consulted in Supplementary Table S4 and the model coefficients in Supplementary Table S5.

TABLE 10

TABLE 10. ANOVA of the model for [Ca²⁺]eq—[Ca²⁺]plan.

When comparing the test points and reserve point with the predictions of the model, the predictions are found to be in good agreement with the observations as is illustrated, in coded factor variables, in Figure 2.

FIGURE 2

FIGURE 2. Model predictions for [Ca²⁺]_eq—[Ca²⁺]_plan together with the 95% prediction interval.

Due to the validity of this model, the intrinsic [Ca²⁺] can be estimated. However, due to the uncertainty on the model coefficients, the intrinsic [Ca²⁺] is not simply the intercept between y = 0 and the model prediction, since the exact value of x for f(x) equal to 0 is unknown. Care must be taken not to emphasize a point estimate. Therefore, a 95% confidence region is calculated for the area of x for which f(x) equals zero, applying the approach as published by Box and Hunter (1954). The details on this calculation can be consulted in the Supplementary Material. The intrinsic [Ca²⁺] is estimated to be in the interval [1.95; 3.09] mM, which is in line with the reported [Ca²⁺] in the pore water of aged BFS-rich cements (Vollpracht et al., 2016).

Pu sorption in function of ISA at the upper level of the intrinsic [Ca²⁺]

Since the predicted sorption is higher for the lower level of the confidence region of the intrinsic [Ca²⁺], compared to the higher level, it is considered, in our research context, more prudent to fix the [Ca²⁺] at the high end of the confidence region (at 3.09 mM) when predicting Pu sorption at varying concentrations of ISA. The predictions of the model (R_d expressed in log l/kg) for a fixed [Ca²⁺] of 3.09 mM (or 0.586 in coded units) are illustrated in Figure 3.

FIGURE 3

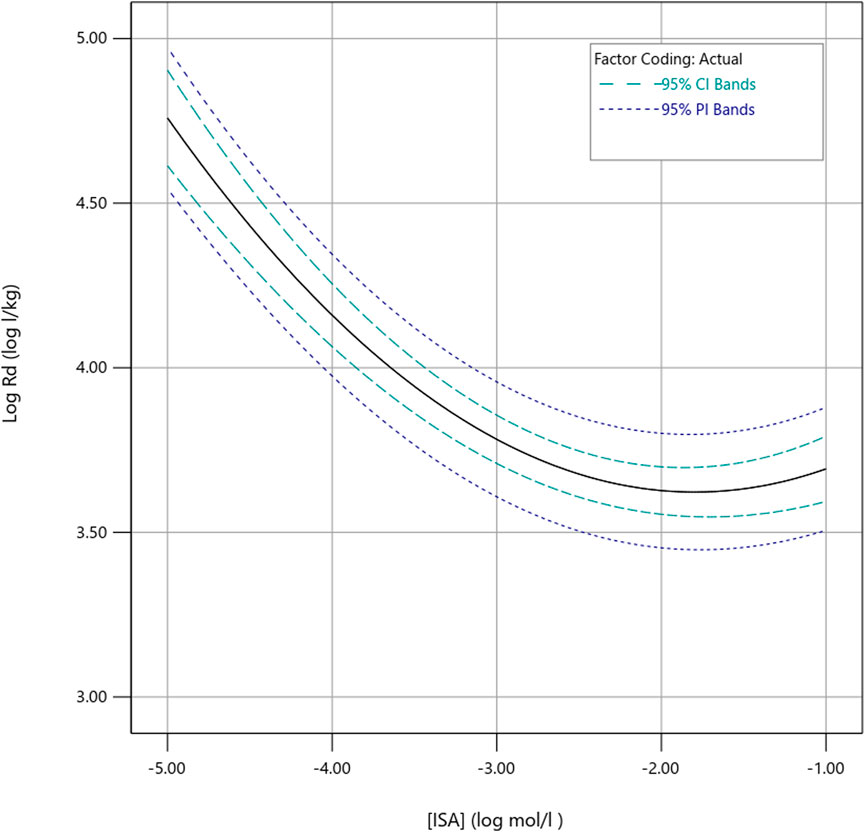
FIGURE 3. Model predictions for R_d as a function of the ISA concentration, for a fixed [Ca²⁺] of 3.09 mM. Both the best estimate and a 95% prediction interval and confidence interval are visualised.

As expected, Pu sorption is predicted to decrease with increasing concentrations of ISA, as discussed above. The factor of decrease in R_d is estimated to be approximately 2 log units (log l/kg), and is most pronounced between [ISA] 10^–5 M and 10^–2 M. These predictions are achieved for the upper estimate of the intrinsic [Ca²⁺]. Therefore, best estimates of log R_d values for Pu sorption to the CILVA matrix in the presence of ISA are expected to stay above 3.5, with the lower estimate of the 95% prediction interval slightly below this log R_d value of 3.5, in the vicinity of 3.45. Once a [ISA] of 10^–2 M is reached, no further decrease of R_d is apparent. A similar trend was observed before by Tasi et al. (2021) and was reported to correlate with decreasing zeta potential of cement particles at [ISA] > 10^–3 M. It is therefore hypothesized that sorption of ISA to the cement sorption sites decreases the zeta potential (Missana et al., 2022), and facilitates co-adsorption of Pu with ISA through Ca-Pu-OH-ISA surface complexes, thereby increasing the R_d again, despite the formation of Pu in a hypothetical (Ca-)Pu-ISA-complex in solution.

Conclusion

In the absence of ISA, strong sorption of Pu to cementitious materials in reduced conditions has been reported earlier (Wang (2020)). Overall, the CSH phases of the cementitious sorbent are considered the most important sink for actinides like Pu. Experimental studies on sorption of Pu to CSH or cement however are limited, and comparison of the existing experimental studies of the cement-Pu system are complicated because of a.o. different means of phase separation, different initial Pu concentrations, varying or unknown redox conditions, and different types and states of cement. As such, there were insufficient data to accurately predict sorption of Pu to the CILVA immobilization matrix in its natural (reducing) conditions.

In this respect, an experimental test set-up was designed in order to screen which factors were likely to affect Pu sorption to the mortar, followed by a surface response measurement (SRM) to assess the extent of these effects. Only for the concentration of Ca²⁺ in the synthetic pore water, statistical evidence of an effect was found during the screening. Following these findings and based on the effect of ISA on Pu sorption reported in the literature, the extent of the impact of both [ISA] and [Ca²⁺] was studied in the SRM, including their combined effect.

From the experimental results it could be deduced that an increase of [ISA] and of [Ca²⁺] results in a decrease of Pu sorption to the CILVA matrix. In addition, the results showed some interaction effect between these two factors: at higher [Ca²⁺], the decrease of the R_d due to increased [ISA] is weaker. Different mechanisms were discussed to possibly contribute to these separate and combined effects of [ISA] and [Ca²⁺] on Pu sorption, including competition with Ca²⁺ for sorption sites, and the formation of binary and ternary complexes between Pu, ISA and/or Ca²⁺.

In addition, the confidence region for the intrinsic [Ca²⁺], i.e., the concentration of Ca²⁺ which is in equilibrium with the sorbents, was estimated at [1.95; 3.09] mM. The [Ca²⁺] representative for the boundary of this 95% confidence region leading to the lowest predictions for R_d, was estimated to be at the higher end of the confidence region, being 3.09 mM. The effect of ISA on Pu sorption was calculated for the upper boundary of the [Ca²⁺] confidence region which was assumed to provide the most conservative R_d values. The subsequent prediction shows a clear decreasing trend of the R_d with approximately 2 log units (log l/kg), while increasing [ISA] from 10^–5 M to 10^–2 M, and a stabilisation of R_d at [ISA] above approximately 10^–2 M. At the lower estimate of the 95% prediction interval for the R_d, predictions fall slightly below a log R_d value of 3.5, in the vicinity of 3.45 while the lower estimate of the 95% confidence interval is above a log R_d value of 3.5.

Data availability statement

The datasets presented in this article are not readily available because authorisation is needed from both partners (SCK CEN and ONDRAF/NIRAS) to make data available. Requests to access the datasets should be directed to DD, ZGR1cmNlQHNja2Nlbi5iZQ==; CE, ZS5jb3BwZW5zQG5pcm9uZC5iZQ==.

Author contributions

DD and BdB: General conceptualization of the project. EC: Statistical conceptualization of the research plan. KW: Concretization of the research plan and execution of experiments. EC: Statistical data analysis. KW, EC, BdB, and DD: Data interpretation. KW, EC, BdB, and DD: Literature study. KW: Writing of the first draft of the manuscript. KW and EC: Writing of the manuscript. BdB and DD: Administration. All authors have read the manuscript and agree with its publication.

Funding

This work is performed in the framework of a public-public cooperation between ONDRAF/NIRAS and SCK CEN.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1151271/full#supplementary-material

References

Altmaier, M., Gaona, X., and Fanghänel, T. (2013). Recent advances in aqueous actinide chemistry and thermodynamics. Chem. Rev. 113, 901–943. doi:10.1021/cr300379w

PubMed Abstract | CrossRef Full Text | Google Scholar

Altmaier, M., Neck, V., Lützenkirchen, J., and Fanghänel, T. (2009). Solubility of plutonium in MgCl2 and CaCl2 solutions in contact with metallic iron. Radiochim. Acta 97, 187–192. doi:10.1524/ract.2009.1593

CrossRef Full Text | Google Scholar

Androniuk, I., and Kalinichev, A. G. (2020). Molecular dynamics simulation of the interaction of uranium (VI) with the C-S-H phase of cement in the presence of gluconate. Appl. Geochem. 113, 104496. doi:10.1016/j.apgeochem.2019.104496

CrossRef Full Text | Google Scholar

Androniuk, I., Landesman, C., Henocq, P., and Kalinichev, A. G. (2017)., 99. Parts A/B/C, 194–203.Adsorption of gluconate and uranyl on C-S-H phases: Combination of wet chemistry experiments and molecular dynamics simulations for the binary systems, Phys. Chem. Earth

CrossRef Full Text | Google Scholar

Atkins, M., and Glasser, F. P. (1992). Application of portland cement-based materials to radioactive waste immobilization. Waste Manag. 12, 105–131. doi:10.1016/0956-053x(92)90044-j

CrossRef Full Text | Google Scholar

Berner, U. R. (1988). Modelling the incongruent dissolution of hydrated cement minerals. Radiochim. Acta 44/45, 387–394. doi:10.1524/ract.1988.4445.2.387

CrossRef Full Text | Google Scholar

Box, G. E. P., and Hunter, W. G. (1954). A confidence region for the solution of a set of simultaneous equations with an application to experimental design. Biometrika 41, 190–199. doi:10.2307/2333016

CrossRef Full Text | Google Scholar

Çevirim-Papaioannou, N., Jo, Y., Franke, K., Fuss, M., De Blochouse, B., Altmaier, M., et al. (2022). Uptake of niobium by cement systems relevant for nuclear waste disposal: Impact of ISA and chloride. Cem. Concr. Res. 153, 106690. doi:10.1016/j.cemconres.2021.106690

CrossRef Full Text | Google Scholar

Chen, Q. Y., Tyrer, M., Hills, C. D., Yang, X. M., and Carey, P. (2009). Immobilisation of heavy metal in cement-based solidification/stabilisation: A review. Waste Manag. 29, 390–403. doi:10.1016/j.wasman.2008.01.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. (1988). Statistical power analysis for the behavioral sciences. New York, NY, USA: Lawrence Erlbaum Associates.

Google Scholar

Coppens, E. 2020. Fenomenologie van de interactie van chloriden met cement tot ca. 1 m%. ONDRAF/NIRAS, Brussels, Belgium. Available at: e.coppens@nirond.be.

Google Scholar

Diesen, V., Forsberg, K. M., and Jonsson, M. (2017). Effects of cellulose degradation products on the mobility of Eu (III) in repositories for low and intermediate level radioactive waste. J. Hazard. Mater. 340, 384–389. doi:10.1016/j.jhazmat.2017.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Dudás, C., Kutus, B., Böszörményi, É., Peintler, G., Kele, Z., Pálinkó, I., et al. (2017). Comparison of the Ca2+ complexing propertiesof isosaccharinate and gluconate – is gluconate a reliable structural and functional model ofisosaccharinate? Dalton Trans. 46, 13888–13896. doi:10.1039/c7dt03120c

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaona, X., Montoya, V., Colas, E., Grive, M., and Duro, L. (2008). Review of the complexation of tetravalent actinides by ISA and gluconate under alkaline to hyperalkaline conditions. J. Contam. Hydrol. 102, 217–227. doi:10.1016/j.jconhyd.2008.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Glaus, M. A., and Van Loon, L. R. (2009). PSI Bericht Nr, 08-01. Villigen: Paul Scherrer Institute. https://www.dora.lib4ri.ch/psi/islandora/object/psi%3A25722/datastream/PDF/Glaus-2009-Chemical_reactivity_of_%CE%B1-isosaccharinic_acid-%28published_version%29.pdf.Chemical Reactivity of α-Isosaccharinic acid in heterogeneous alkaline systems

Google Scholar

Kutus, B., Gaona, X., Pallagi, A., Pálinkó, I., Altmaier, M., and Sipos, P. (2020). Recent advances in the aqueous chemistry of the calcium(II)-gluconate system – equilibria, structure and composition of the complexes forming in neutral and in alkaline solutions. Coord. Chem. Rev. 417, 213337. doi:10.1016/j.ccr.2020.213337

CrossRef Full Text | Google Scholar

Micheau, C. V., Dourdain, S., Dumas, T., Denis Menut, D., Solari, P. L., et al. (2020). Relevance of formation conditions to the size, morphology and local structure of intrinsic plutonium colloids. R. Soc. Chem. 7, 2252–2266.

CrossRef Full Text | Google Scholar

Missana, T., García-Gutiérrez, M., Alonso, U., and Fernández, A. M. (2022). Effects of the presence of isosaccharinate on nickel adsorption by calcium silicate hydrate (CSH) gels: Experimental analysis and surface complexation modelling. J. Environ. Chem. Eng. 10, 108500. doi:10.1016/j.jece.2022.108500

CrossRef Full Text | Google Scholar

Myers, R. H., and Montgomery, D. C. (1995). Response surface methodology, process and product optimization using designed experiments. New York: John Wiley and Sons.

Google Scholar

Ochs, M., Vielle-Petit, L., Wang, L., Giffaut, E., Wieland, E., and Mallants, D. (2010). Additional sorption parameters for the cementitious barriers of a near surface repository. Cham: NIROND-TR 2010. -06X E. ONDRAF/NIRAS, Brussels. Available on request to b.dblochouse@nirond.be or e.coppens@nirond.be.

Google Scholar

Ochs, M., Wang, L., and Mallants, D. (2016). Radionuclide and metal sorption on cement and concrete. Switzerland: Springer International Publishing.

Google Scholar

Ondraf/Niras, (2019). Hoofdstuk 14. Veiligheidsevaluatie - langetermijnveiligheid. https://www.niras.be/sites/default/files/HS14_Veiligheidsevaluatie%20-%20langetermijnveiligheid.pdf.

Google Scholar

Ondraf/Niras, (2019). Hoofdstuk 5. Kennis van de fenomenologie van de kunstmatige barrières in hun omgeving. https://www.niras.be/sites/default/files/HS05_Kennis%20van%20de%20fenomenologie%20van%20de%20kunstmatige%20barri%C3%A8res%20in%20hun%20omgeving.pdf.

Google Scholar

Plackett, R. L., and Burman, J. P. (1946). The design of optimum multifactorial experiments. Biometrika 33, 305–325. doi:10.1093/biomet/33.4.305

CrossRef Full Text | Google Scholar

Pointeau, I., Coreau, N., and Reiller, P. E. (2008). Uptake of anionic radionuclides onto degraded cement pastes andcompeting effect of organic ligands. Radiochim. Acta 96, 367–374. doi:10.1524/ract.2008.1503

CrossRef Full Text | Google Scholar

Rundberg, R. S. M., Triay, I. R., and Torstenfelt, N. B. (1987). Size and density of a 242Pu colloid. MRS Online Proc. Libr. 112, 243–248. doi:10.1557/proc-112-243

CrossRef Full Text | Google Scholar

Smith, K. F., Bryan, N. D., Law, G. T. W., Hibberd, R., Shaw, S., Livens, F. R., et al. (2018). Np(V) sorption and solubility in high pH calcite systems. Chem. Geol. 493, 396–404. doi:10.1016/j.chemgeo.2018.06.016

CrossRef Full Text | Google Scholar

Tasi, A., Gaona, X., Fellhauer, D., Böttle, M., Rothe, J., Dardenne, K., et al. (2018a). Thermodynamic description of the plutonium – α-d-isosaccharinic acid system I: Solubility, complexation and redox behavior. Appl. Geochem. 98, 247–264. doi:10.1016/j.apgeochem.2018.04.014

CrossRef Full Text | Google Scholar

Tasi, A., Gaona, X., Rabung, T., Fellhauer, D., Rothe, J., Dardenne, K., et al. (2021). Plutonium retention in the isosaccharinate – cement system. Appl. Geochem. 126, 104862. doi:10.1016/j.apgeochem.2020.104862

CrossRef Full Text | Google Scholar

Tasi, A., Gaona, X., Rabung, T., Fellhauer, D., Rothe, J., Dardenne, K., et al. (2018b). Thermodynamic description of the plutonium - alpha-D-isosaccharinic acid system ii: Formation of quaternary Ca(II)-Pu(IV)-OH-ISA complexes. Appl. Geochem. 98, 351–366. doi:10.1016/j.apgeochem.2018.06.014

CrossRef Full Text | Google Scholar

Tits, J., and Wieland, E. (2018). Actinide sorption by cementitious materials. https://www.dora.lib4ri.ch/psi/islandora/object/psi%3A21061/datastream/PDF/Tits-2018-Actinide_sorption_by_cementitious_materials-%28published_version%29.pdf.

Google Scholar

Tits, J., Wieland, E., and Bradbury, M. H. (2005). The effect of isosaccharinic acid and gluconic acid on the retention of Eu(III), Am(III) and Th(IV) by calcite. Appl. Geochem. 20, 2082–2096. doi:10.1016/j.apgeochem.2005.07.004

CrossRef Full Text | Google Scholar

Traynor, B., Uvegi, H., Olivetti, E., Lothenbach, B., and Myers, R. J. (2020). Methodology for pH measurement in high alkali cementitious systems. Cem. Concr. Res. 135, 106122. doi:10.1016/j.cemconres.2020.106122

CrossRef Full Text | Google Scholar

Van Loon, L., and Glaus, M. A. (1998). Experimental and theoretical studies on alkaline degradation of cellulose and its impact on the sorption of radionuclides. https://inis.iaea.org/collection/NCLCollectionStore/_Public/30/045/30045577.pdf.

Google Scholar

Vanherck, D. (2017). Module matrix CILVA. UBT/2015-01697. Belgoprocess, Dessel. Available at: e.coppens@nirond.be.

Google Scholar

Vollpracht, A., Lothenbach, B., Snellings, R., and Haufe, J. (2016). The pore solution of blended cements: A review. Mater. Struct. 49, 3341–3367. doi:10.1617/s11527-015-0724-1

CrossRef Full Text | Google Scholar

Wang, L., Martens, E., Jacques, D., De Cannière, P., Berry, J. A., and Mallants, D. (2009). Review of sorption values for the cementitious near field of a near-surface radioactive waste disposal facility. https://inis.iaea.org/search/search.aspx?orig_q=RN:46133948.

Google Scholar

Wang, L. (2020). Recent literature on sorption values of Pu and other actinides on cementitious materials – support to the experimental program determining sorption value of Pu on CILVA mortar. T-0432. SCK CEN, Mol. Available on request to ddurce@sckcen.be or b.dblochouse@nirond.be.

Google Scholar

Wieland, E. (2014). Sorption data base for the cementitious near field of L/ILW and ILW repositories for provisional safety analyses for SGT-E2. Technical Report https://nagra.ch/wp-content/uploads/2022/08/e_ntb14-008.pdf.

Google Scholar

Wieland, E., Tits, J., Dobler, J.-P., and Spieler, P. (2002). The effect of α-isosaccharinic acid on the stability of and Th(IV) uptake by hardened cement paste. Radiochim. Acta 90, 683–688. doi:10.1524/ract.2002.90.9-11_2002.683

CrossRef Full Text | Google Scholar

Wouters, K., De Blochouse, B., Coppens, E., Durce, D., Wang, L., and Maes, N. (2022). Variables impacting sorption of Pu to the CILVA-immobilization matrix: Results of screening for active factors in experimental design. https://researchportal.sckcen.be/en/publications/variables-impacting-sorption-of-pu-to-the-cilva-immobilization-ma.

Google Scholar

Wouters, K., Durce, D., De Blochouse, B., and Maes, N. (2022). Recommendations for performing batch sorption experiments of radionuclides to a cementitious matrix. T-0733. SCK CEN, Mol. Available on request to ddurce@sckcen.be or b.dblochouse@nirond.be.

Google Scholar

Wouters, K., Verstrepen, G., Verpoucke, G., Mastroleo, F., Bleyen, N., and Durce, D. 2022. Synthesis of isosaccharanic acid (ISA).

Google Scholar