- Energy Geosciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
The charged mineral/electrolyte interfaces are ubiquitous in the surface and subsurface–including the surroundings of the geological disposal sites for radioactive waste. Therefore, understanding how ions interact with charged surfaces is critically important for predicting radionuclide mobility in the case of waste leakage. At present, the Surface Complexation Models (SCMs) are the most successful thermodynamic frameworks to describe ion retention by mineral surfaces. SCMs are interfacial speciation models that account for the effect of the electric field generated by charged surfaces on sorption equilibria. These models have been successfully used to analyze and interpret a broad range of experimental observations including potentiometric and electrokinetic titrations or spectroscopy. Unfortunately, many of the current procedures to solve and fit SCM to experimental data are not optimal, which leads to a non-transferable or non-unique description of interfacial electrostatics and consequently of the strength and extent of ion retention by mineral surfaces. Recent developments in Artificial Intelligence (AI) offer a new avenue to replace SCM solvers and fitting algorithms with trained AI surrogates. Unfortunately, there is a lack of a standardized dataset covering a wide range of SCM parameter values available for AI exploration and training–a gap filled by this study. Here, we described the computational pipeline to generate synthetic SCM data and discussed approaches to transform this dataset into AI-learnable input. First, we used this pipeline to generate a synthetic dataset of electrostatic properties for a broad range of the prototypical oxide/electrolyte interfaces. The next step is to extend this dataset to include complex radionuclide sorption and complexation, and finally, to provide trained AI architectures able to infer SCMs parameter values rapidly from experimental data. Here, we illustrated the AI-surrogate development using the ensemble learning algorithms, such as Random Forest and Gradient Boosting. These surrogate models allow a rapid prediction of the SCM model parameters, do not rely on an initial guess, and guarantee convergence in all cases.
1 Introduction
The charged mineral/electrolyte interfaces are ubiquitous in the surface and subsurface. Therefore, being able to estimate ion sorption by these interfaces is critically important in safety assessments of the geological disposal sites for the spent nuclear fuel. Surface Complexation Models (SCMs) are the most successful thermodynamic frameworks for describing ion retention by mineral surfaces (Dzombak and Morel, 1990; Lyklema, 1991; Lyklema, 1995; Lützenkirchen, 2006; Karamalidis and Dzombak, 2010). These models consist of the equilibrium reactions describing the surface and bulk ion speciation and account for the effect of the surface charge/field on the interfacial chemistry. The distribution of charges at the mineral/electrolyte interface is described using the electrical double layer (EDL) models that are based on the Poisson differential equation to connect the interfacial charge accumulation with the spatial distribution of the electrostatic field and potential (Lyklema, 1991; Lyklema, 1995).
Recent developments in Artificial Intelligence (AI) offer a new avenue to replace SCM solvers and fitting protocols with trained AI surrogates if only sufficient datasets are available. AI methods can identify and extract patterns in a large dataset and learn a mapping from a complex input to output if only they are exposed to a sufficiently large number of examples.
Unfortunately, existing datasets are limited because SCMs are typically used to interpret sparse experimental data. Moreover, there is a lack of consistent SCMs evaluation and fitting protocols and reported parameter values often vary among research teams even if the same experimental data were considered (Lützenkirchen, 2006). The experimental protocols are also not standardized, which leads to scattered values of the most basic quantitative descriptors of electrical double layer, such as Point of Zero Charge or Isoelectric Point for the same minerals (Kosmulski, 2001; Kosmulski, 2002; Kosmulski, 2009a; Kosmulski, 2009b; Kosmulski, 2011; Kosmulski, 2016; Kosmulski, 2018; Kosmulski, 2020).
Therefore, to use AI for data exploration and reveal hidden patterns, correlations, and features in the ion retention thermodynamics, we need an extensive SCM dataset covering a wide range of possible mineral surfaces and experimental conditions. This study fills that gap by describing a computational protocol to generate a SCM dataset and translating it to AI-learnable inputs. Here, using our protocol, we generated an extensive SCM dataset for the prototypical oxide/electrolyte interface (see Section Data Availability Statement).
We illustrated the AI surrogate development for the SCM of oxide/electrolyte interface using ensemble learning algorithms. In the following study, we will compare these surrogates with the Deep Neural Networks and discuss AI-models interpretability and possible protocols to incorporate physics and chemistry as constraints into the learning process. Our preliminary results presented in this study show that surrogate models allow a rapid prediction of the SCM model parameters, do not rely on an initial guess, and guarantee convergence in all cases.
In the following study, we will extend our dataset by including radionuclide sorption, speciation, and the effect of the radiation and heat on sorption equilibria.
The ultimate goal of our research is to generate AI-surrogates for many SCMs and reactive transport models that become standardized and computationally inexpensive alternatives to the analytical/numerical models. One of AI surrogates’ primary goals is to rapidly predict the physicochemical properties from the experimental data without involving a fitting of analytical models.
2 Theory and computation
2.1 Surface complexation model
All mineral surfaces in contact with aqueous solution acquire charged, but the charging mechanisms vary among minerals (Dzombak and Morel, 1990; Lyklema, 1991; Lyklema, 1995; Lützenkirchen, 2006; Karamalidis and Dzombak, 2010). In the case of oxides, the surface charge is due to H+/OH− uptake or release by the surface exposed oxygen atoms or dissociative water sorption on the surface exposed metal sites (Yates et al., 1974; Hohl and Stumm, 1976; Schindler et al., 1976; Davis et al., 1978). The surface oxygen atoms show amphoteric behavior, being able to accept H+ and act as a base or donate H+ and thus act as an acid. One or two proton binding reactions typically capture this acid-base behavior of oxide surface (Yates et al., 1974; Davis et al., 1978; Van Riemsdijk et al., 1991). One of the most popular protonation schemes, 2-pK (Yates et al., 1974; Davis et al., 1978), assumes the presence of a charge-neutral surface site, denoted as ≡SOH0, where S stands for surface metal/metalloid site, which can either accept or donate protons according to the following reactions:
where K1,K2 stand for two equilibrium constants (hence the name 2-pK, pK= − log10K). The brackets {} in the above reactions represent the surface concentration.
In reality, the charge assigned to the surface site is rarely an integer. The fractional values reflect the actual bonding environment of the surface exposed atoms and the specificity of a given mineral surface. These partial charges can be assigned using Pauling bond valence rules (Hiemstra et al., 1989a; Hiemstra et al., 1989b; Hiemstra et al., 1996; Hiemstra and Van Riemsdijk, 1996) or the first principle quantum-chemical calculations (Zarzycki, 2007a; Zarzycki, 2007b).
The charged surfaces attract electrolyte ions, which accumulate near the surface and form a spatial charge distribution known as the electrical double layer. In many cases, the co- and counter-ion adsorb non-specifically and remain fully hydrated. In these cases, they form the outer-sphere surface complexes, which are assumed to be located in the layer parallel to the surface, β-plane (see Figure 1). The β-plane is separated from the surface by at least one layer of interfacial water. The ions complexation reactions and corresponding equilibrium constants are given by:
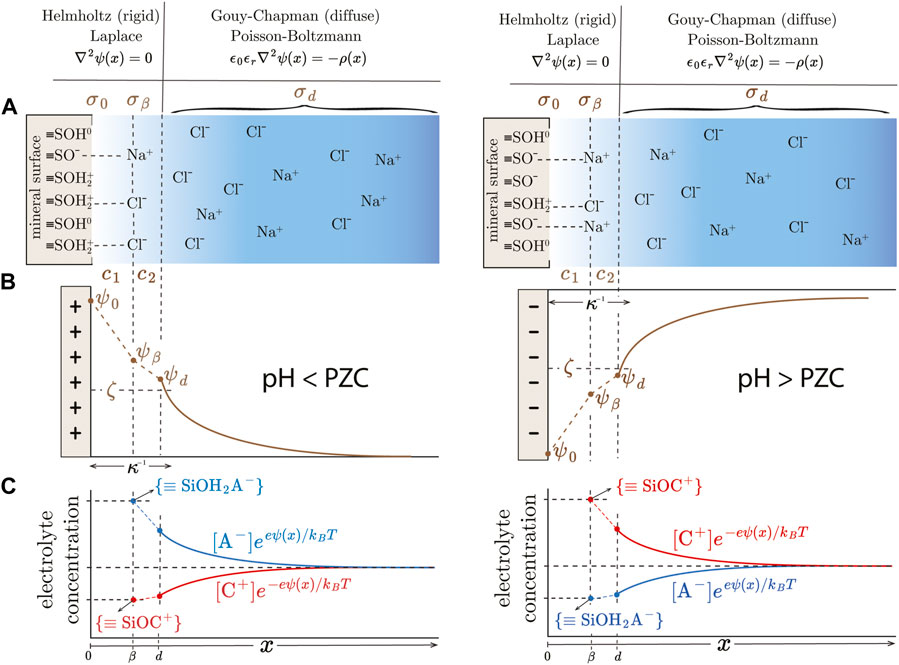
FIGURE 1. Schematic illustration of the electrical double layer developed at the oxide/electrolyte interface according to 2-pK Triple Layer Model (TLM) for pH
The concentration of protons at the surface and ions in the β-plane are not the same as in the bulk solution. The ion concentration in the EDL is affected by the presence of the electric field gradient, which is usually accounted by using the Boltzmann weight, that is (Yates et al., 1974; Davis et al., 1978):
where kB is the Boltzmann constant, T is the temperature, i stands for ion type, zi is its formal charge, and ψ(x) is the potential at the surface (x = 0, ψ0) in the case of proton sorption or potential in the β-plane (x = β, ψβ) in the case of electrolyte ions.
The electrostatic Boltzmann weights were introduced into SCM reactions to account for the variation in chemical potential caused by the variable surface charge (Yates et al., 1974; Hohl and Stumm, 1976; Schindler et al., 1976; Davis et al., 1978). Consequently, the surface reactions are expressed using the law of mass action subjected to the electric field (Brown et al., 1999). For example, eq. (Dzombak and Morel, 1990). can be rewritten as:
where
The activities should replace the bulk concentration. Here, the activity coefficients γi are calculated using the Davies equation (Davies, 1962):
where I is the ionic strength of the electrolyte solution and ϵr is the relative dielectric constant of the solution.
The surface complexation reactions, eqs. (Dzombak and Morel, 1990; Lyklema, 1991; Lützenkirchen, 2006; Karamalidis and Dzombak, 2010). have been frequently rephrased as multicomponent Langmuir-type isotherms to emphasize that surface charging and ions complexation are treated as localized (chemi)sorption of ions at the specified lattice sites in the presence of the mean-field type electric field (Dzombak and Morel, 1990; Lyklema, 1995). Consequently, the surface concentrations can be replaced by the fractional coverages, θi (Yates et al., 1974; Charmas et al., 1995; Rudzinski et al., 1999; Prélot et al., 2002; Zarzycki et al., 2004a; Zarzycki et al., 2004b; Zarzycki et al., 2005a; Zarzycki et al., 2005b; Piasecki, 2006; Zarzycki, 2006; Zarzycki, 2007a; Zarzycki, 2007c; Piasecki et al., 2007; Piasecki et al., 2010):
where i =SO−, SOH,
Note that the assumption that protons are located, or chemisorbed, in the 0-plane and electrolyte ions are localized in the β-plane are consistent with the requirement that the charge distribution in the rigid part of EDLs is governed by the Laplace equation (d2ψ/dx2 = 0, constant capacitor models).
By using θ-notation, the surface charge is defined as a sum of positive and negative charges at the surface:
where Bs = eNs. Similarly, the charge in the β-plane is defined as the average of the charges accumulated in β-plane (Yates et al., 1974; Davis et al., 1978):
The charge neutrality condition allows us to define the diffuse charge as:
The surface complexation reactions eqs. (Dzombak and Morel, 1990; Lyklema, 1991; Lützenkirchen, 2006; Karamalidis and Dzombak, 2010), along with the mass balance eq. (Kosmulski, 2002) and charge neutrality eq. (Kosmulski, 2018) form a set of six nonlinear equations with seven unknown variables: ψ0, ψβ and θi. In order to solve these equations, one needs to reduce the number of unknowns to become equal to the number of equations. The reduction is accomplished by assuming that
The first assumption allows us to connect surface, β-plane, and diffuse potentials using the integral capacitances c1 and c2 and surface and diffuse layer charge densities (Figure 1):
Now, the surface and β-layer potentials can be rewritten as functions of charges and ψd (Yates et al., 1974):
The second assumption provides a link between the diffuse layer potential and diffuse charge density, and is known as the Grahame relationship (Lyklema, 1991; Lyklema, 1995):
The proportionally coefficient fGC is given by:
where ϵ0 is the vacuum permittivity, and κ is a measure of the EDL thickness and is defined through the inverse of the Debye length (λd) as (Lyklema, 1991; Lyklema, 1995):
Note that eq. (Yates et al., 1974) is back-propagated to the surface and β-plane through capacitances via eq. (Kosmulski, 2001).
The diffuse charge can also be defined as the sum of all charges accumulated between the slip plane and the bulk solution phase (Verwey and Overbeek, 1948; Lyklema, 1991; Lyklema, 1995):
where ψ(x), ρ(x) are the electrostatic potential and charge density at a distance x from the surface, respectively. By integrating eq. (Davis et al., 1978) with assumptions that electric field E = −∇ψ and potential ψ disappear in the bulk electrolyte yields eq. (Yates et al., 1974).
Summing up, the SCM is a combination of the chemisorption models for the Helmholtz part of the EDL, and the physisorption model for the diffuse part. From the mathematical point of view, such division is consistent with applying the Laplace and Poisson differential equation for the charge distribution in the rigid and diffuse parts of the EDL, respectively. Note that the sorption model improves the Poisson-Boltzmann model of the EDL by imposing a limit on surface charge and β-layer charge because protonation occurs at specific coordination sites with known surface site density (Dzombak and Morel, 1990), see eqs. (Kosmulski, 2002; Kosmulski, 2011; Kosmulski, 2020).
2.2 Numerical methods
The governing equations in the SCMs are not only nonlinear due to the exponential dependence of ions activities on the surface potential, eq. (Lyklema, 1995), but they are also convoluted due to the assumption of the parallel-plate capacitor, eq. (Kosmulski, 2001). The complexity of the equations is not immediately apparent. Here, we rewrote the governing equations to show the convoluted character explicitly.
Let’s start by presenting the complexation reactions, eqs. (Dzombak and Morel, 1990; Lyklema, 1991; Lützenkirchen, 2006; Karamalidis and Dzombak, 2010). in terms of the fractional coverages:
where aC, aA stand for the activity of cations and anions (e.g.,
Solving equations (Hiemstra et al., 1989a; Hiemstra et al., 1989b; Van Riemsdijk et al., 1991; Hiemstra et al., 1996), supplemented with conservation of the surface site density, eq. (Kosmulski, 2002), gives:
where the denominator, Θ, is given by:
Finally, we can rewrite the eq. (Kosmulski, 2001). into two master equations that connect surface and β-layer potentials with the surface charge and diffuse layer potential:
and
The convolution is given through the surface charge dependence on the surface and diffuse layer potentials
where
Even in a simple 2-pK TLM model, the nonlinear and convoluted character of the governing equations makes the numerical solution challenging.
2.2.1 Newton-Raphson iterative procedure
There is a lack of a general method of solving a set of nonlinear equations directly (Press et al., 2007; Bethke, 2022). However, there are many indirect, iterative procedures that have been successfully applied (Bethke, 2022). The most common algorithm is the Newton-Raphson iterative procedure, which tries to improve the initial guess incrementally until the closest multidimensional minimum is found. If the numerical problem can be wrapped into a single master equation, here eq. (Brown et al., 1999), then nonlinear/multidimensional minimization procedures can also be used. In this study, we used a computational protocol that starts with the Newton-Raphson minimization and then validates the solution using the simplex optimization.
Any of the SCMs equations can be rewritten to a general form that attempts to minimize the residual Ri that is defined as a difference between the left- and right-hand side of the equation:
Specifically, for the 2-pK TLM model, one can write the residual difference for the master equation as follows:
The charge neutrality condition gives a complementary equation:
Note, that
Now, we are faced with the problem of finding a common minimum of two non-linear and convoluted functions (
with the incremental adjustments (δψ0 and δψd) that are obtained by solving the following equation:
Many nonlinear functions have more than one root, and the choice of the initial guess determines which local minima are localized. In many cases, the iterative procedure can diverge or cycle indefinitely if a poor initial guess is provided. We alleviate this problem by allowing automatic restart of the minimizer with a new random initial guess if convergence becomes stagnant or a maximum number of iterations is reached without a sufficient reduction of Ri.
The variations of the electrostatic potentials (ψ0, ψd) are expected not to exceed water oxidation and reduction potentials. Specifically, the electrostatic potentials remain within the millivolt range for most environmentally relevant conditions (Lützenkirchen, 2006; Kosmulski, 2009a). The sign of the potential varies with the pH, and changes on both sides of the point of zero charge (ψ0) or isoelectric point (ψd).
The thresholds for the variations in electrostatic potentials are set to 10–6 mV. If the optimization does not converge within 2000 iterations, the optimization is restarted with a new initial guess. If the convergence is not reached after 50 restarts, multidimensional minimization is used instead of Newton-Raphson.
2.2.2 Multidimensional minimization
As described above, the task of solving the SCMs equation can be cast as the task of minimizing residual differences Ri. The Newton-Raphson procedure is a fast and robust algorithm that can rapidly converge to a multidimensional root, providing the initial guess is sufficiently close to the root.
We implemented the simplex minimization procedure as an alternative route to the Newton-Raphson algorithm (from (Press et al., 2007)). Although the downhill simplex method, as described by Nelder and Mead (Nelder and Mead, 1965), is one of the slowest minimization algorithms, it has several advantages. First, it does not require derivative evaluation, a step that often poses a challenge for convoluted functions. Second, it is expected to always converge to an approximate solution, even in the cases when the Newton-Raphson procedure becomes stagnant (e.g., vanishing or diverging gradient) (Brandt, 2014). We have also used the simplex method to validate the Newton-Raphson numerical solution.
2.2.3 Local vs. global minima
The numerical solvers described above always converge to the local minima on the solution space. Many local minima are revealed as solution clusters if the parameter space is densely sampled. What is more, if the AI is exposed to the large dataset covering the parameter space, the topology of the multidimensional solution space can be inferred by AI methods, and the global minimum and local minima can be identified as divergence regions for the solvers (metastable regions). By identifying the metastable regions, we can learn which combinations of the parameter values are responsible for the solvers’ divergence and how these values translate to the chemistry/physics of the mineral/electrolyte interface.
2.3 Dataset preprocessing for AI/ML exploration
The performance of machine learning (ML) models relies on the quantity and representation quality of the data on which these models are trained. In the case of the mineral/electrolyte interface, the available experimental observations are limited, sparse, and often obtained in a non-consistent fashion (Kosmulski, 2001; Lützenkirchen, 2006; Kosmulski, 2009a). On the other hand, the existing analytical surface complexation models (SCMs) can be conveniently used to generate sufficient data to successfully train ML models. To allow ML-models to be applicable for a wide range of the oxide/electrolyte interfaces, the dataset needs to cover wide range of the possible values of the SCM model parameters and environmental conditions–in other words explore the SCMs parameter and conditions space. Figure 2 illustrates the workflow of constructing an AI surrogate for predicting the SCM model parameters values from the input (e.g., experimental datapoints).
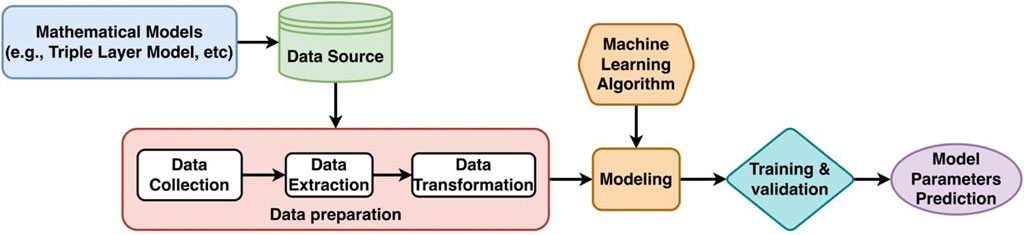
FIGURE 2. A general workflow for developing machine learning surrogate models for the Surface Complexation Models (SCM) can infer the analytical model parameter values.
Here, we used the 2-pK Triple Layer model of the oxide/electrolyte interface because it an archetypal and the most generic model among all SCMs. We used this analytical model to generate a large dataset of titration curves by randomly sampling the parameter space. We focused on the surface charge/electrokinetic potential as a function of pH, because they are the most commonly reported experimental observations (Figure 3A). We sampled the parameter space composed of the model parameters (ion affinities, capacitances) and environmental conditions (pH, electrolyte concentration, surface site density).
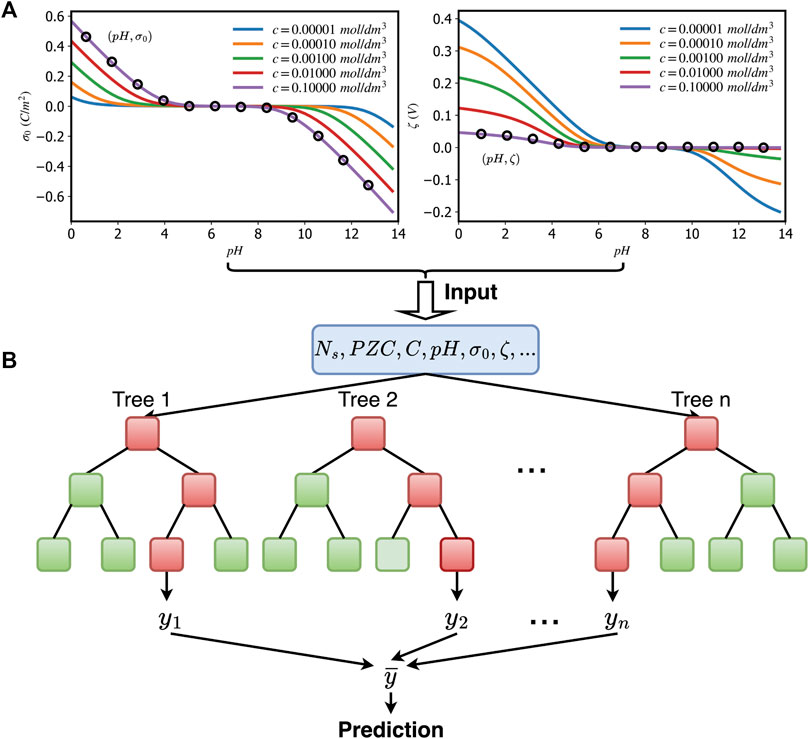
FIGURE 3. Data extraction and machine learning training process: an example of showing five unique surface charge/surface potential vs. pH curves generated by a 2-pK TLM (A) and an illustration of the application of feeding data extracted from (A) to the Random Forest algorithm (B). All decision trees take the same input. We obtain the final prediction by averaging n individual tree predictions.
Figure 3 illustrates our approach of data extraction from synthetic dataset to create the AI-learnable dataset. Next, this dataset is normalized and split into training, validation, and test subsets. The dataset generated in this study and preprocesses AI-learnable inputs are available in our GitHub repositories (see Section Data Availability Statement).
3 Developing radionuclide sorption dataset
Here, we presented the generic computational framework for generating synthetic titration datasets for the oxide mineral/electrolyte interfaces. The dataset accompanying this study covers the physicochemical range of the SCM model parameters expected for oxides (see (Kosmulski, 2001; Sverjensky, 2005; Kosmulski, 2009a)). The next step in our research is to extend our computational framework to include bulk and interfacial chemistries of radionuclides, along with more challenging interfaces.
To model the radionuclide sorption, we need to address several challenges related to the polydentate and multinuclear sorption of polyvalent ions. In addition, the complex electrolyte solution requires the general Gouy-Champan charge-potential relationship. Finally, to model the radionuclides migration in a geological repository scenario, we also include the mineral surfaces with ion-exchange sites (e.g., clays with permanent charge) or soluble/evolving surfaces (e.g., carbonates).
Below we discuss the recommended strategy to address some of these challenges. An extended synthetic dataset describing radionuclide sorption will be made available after finishing ongoing validation and testing.
3.1 Extension to radionuclide sorption
3.1.1 Multi-dentate and multi-nuclear surface complexes
The correct treatment of radionuclide speciation by mineral surfaces is challenging due to the many possible surfaces and aqueous complexation reactions. For example, the polyvalent/multinuclear species are expected to form multi-dentate surface species, but the equilibrium reactions and constants are differently defined by various research teams (Benjamin, 2002; LaViolette and Redden, 2002; Wang and Giammar, 2013; Lutzenkirchen et al., 2015). For example, the bidentate uranium
Alternatively, one can consider a binary-binding surface site that is composed of two primary surface hydroxyl groups as follows:
The mass balance equations are identical for both reactions, but the mass law action equations are different, with a quadratic dependence on the ≡ SOHz sites density in eq. (Zarzycki et al., 2004b) and linear dependence in eq. (Zarzycki et al., 2005b). Consequently, the value of the intrinsic equilibrium constant depends on the formulation of the surface reaction and, in general, is not transferable between these two treatments. In the case of significant ion retention by the mineral surfaces, the possible mix-states of surface complexes with varying denticity for the same ion are possible, and the analytical treatment of such sorption via the SCMs approach is deemed to fail. One could consider an average denticity as a weighted sum of formed polydentate surface complexes, but it will be impossible to introduce the fractional stoichiometric coefficient that varies with the electrolyte and radionuclide concentration and still use mass law action to describe sorption equilibrium. Here, we define all multidentate surface complexation reactions using the second approach, which is considering a more complex generic surface site in the case of the polydentate sorption of polyvalent/multinuclear radionuclide sorption. Our equilibrium constants are transferable to the models that are consistently using only single sorption sites via the correction factors as described by Lutzenkirchen et al. (Lutzenkirchen et al., 2015).
3.1.2 Gouy-Champan charge-potential relationship for non-symmetric electrolytes
In the case of polyvalent ions sorption modeling, the Gouy-Champan equation that relates the diffuse layer potential with the diffuse layer charge (eq. 2) is no longer valid. Eq. (Yates et al., 1974). is only applicable if the electrolyte is symmetric, that is 1:1 or 2:2. In the case of non-symmetric electrolytes (e.g., CaCl2, UCl4), and polyvalent ions (e.g., U4+,
In the case of dilute electrolyte solution, the magnitudes of the diffuse potential and charge are small, and the relative error caused by using a simplified Grahame equation, (Yates et al., 1974), instead of eq. (Zarzycki, 2006) is negligible. However, in the case of the larger electrolyte concentration, the double layer thickness decreases, and both the diffuse potential and charge need to be linked through the full equation. The correct relationship between the diffuse charge and potential is also needed in the case of the overlapping or confined electrical double layers due to increased ionic strength between the charged surfaces. We used eq. (Zarzycki, 2006) to generate a synthetic dataset of radionuclides sorption to mineral surfaces. This dataset will be used to generate new types of AI/ML surrogates that can handle multidentate/multinuclear radionuclide surface complexes.
4 Illustration of AI-surrogate development: Ensemble methods
This section presents two illustrative examples of training Machine Learning Ensemble Learning models on the synthetic dataset generated by the analytical 2-pK TLM model. Ensemble learning refers to a class of algorithms combining the predictions from simple (weak) models to obtain a better predictive performance than each of the constituent models. Here, we implemented the most successful ensemble learning models, namely the Random Forest (RF) and Extreme Gradient Boosting (XGBoost), to build a robust supervised regression model.
4.1 Random forest
The random forest (RF) algorithm consists of several decision tree regressors whose predictions are combined together in an averaging scheme to improve the overall predictive power of the weak learners–decision trees (Géron, 2019).
4.2 Gradient boosting
At the moment, the gradient boosting algorithms are one of the most successful classes of regression algorithms. Similar to the Random Forest, the gradient boosting relies on an ensemble of weak learners (decision trees), but here they are not independently trained on the subset of data with averaged predictions but build sequentially on top of each other to reduce progressively the errors of each weak learner (Géron, 2019).
4.3 Performance and analysis
The RF and XGBoost methods described above were trained using a set of vectors, each consisting of the seven titration points (pH,σ0 (pH), ζ) and the global system descriptors (Point of Zero Charge, surface site density, and electrolyte concentration)–see Figure 3B. We used the XGBoost and RF algorithms as implemented in the scikit-learn package (Pedregosa et al., 2011).
Figure 4 shows the model performance on the training set, using five model parameters as the output (target). Figure 5 shows the model performance on the test dataset. The overall accuracy of the both models is incredible with R2 score around 0.993.
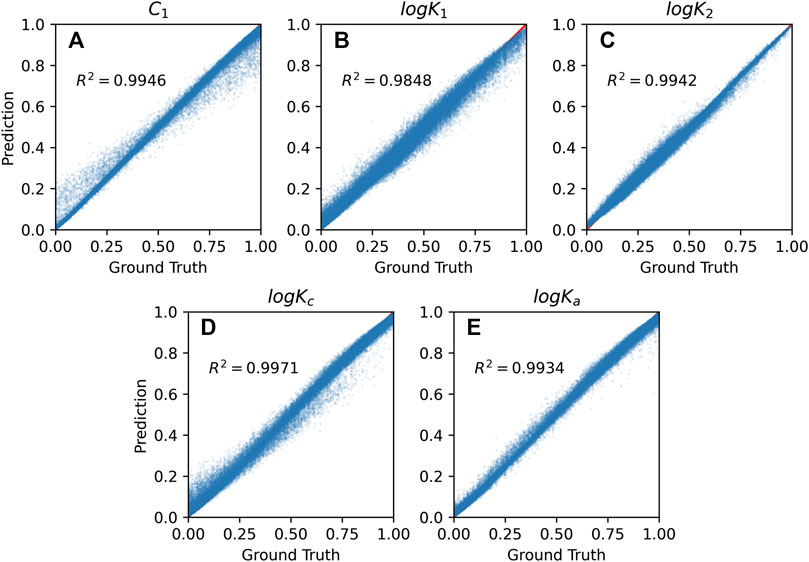
FIGURE 4. Random forest prediction vs. numerical method calculation on the training set for five SCM’s model parameter values: (A) capacitances C1, (B,C) equilibrium constants logK1 and logK2, (C,D) binding constants logKc and logKa.
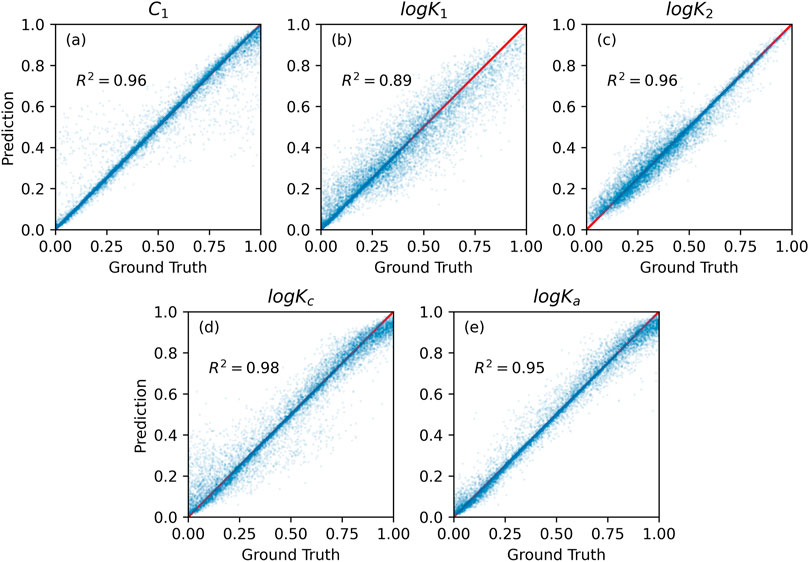
FIGURE 5. Random forest prediction vs. numerical method calculation on the test set for five SCM’s model parameter values: (A) capacitances C1, (B,C) equilibrium constants logK1 and logK2, (C,D) binding constants logKc and logKa.
The high value of the R2 score indicates that RF has successfully learned the underlying relationship between the input information and the corresponding SCM model parameters during the training. The correlation between RF prediction and the ground truth is about 0.95 on the test set (see Figure 5). Concluding, RF-based surrogate can predict accurately the SCM model parameters.
The comparison of the performance of XGBoost on training and test sets are shown in Figures 6, 7. Surprisingly, the XGBoost method was less accurate than RF, even though it is usually outperforming RF algorithms (Géron, 2019). Specifically, RF achieved higher prediction accuracy for all model parameters on training set. XGBoost was the least accurate in predicting logK1 parameter value (see Table 1). Although XGBoost-based SCM surrogate is inferior to RF-based surrogate in terms of the predictive power, it learn the mapping from input to output about 100 times faster than RF (Table 1).
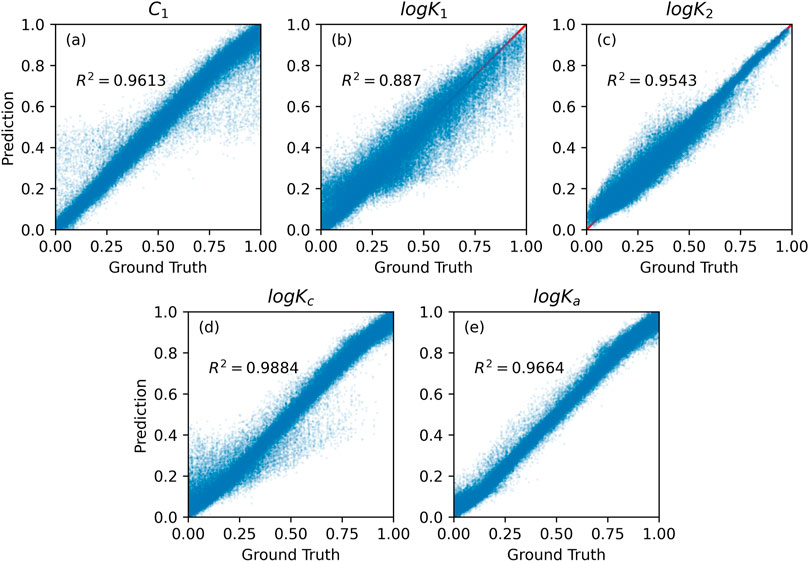
FIGURE 6. Gradient boosting prediction vs. numerical method calculation on the training set for five SCM’s model parameter values: (A) capacitances C1, (B,C) equilibrium constants logK1 and logK2, (C,D) binding constants logKc and logKa.
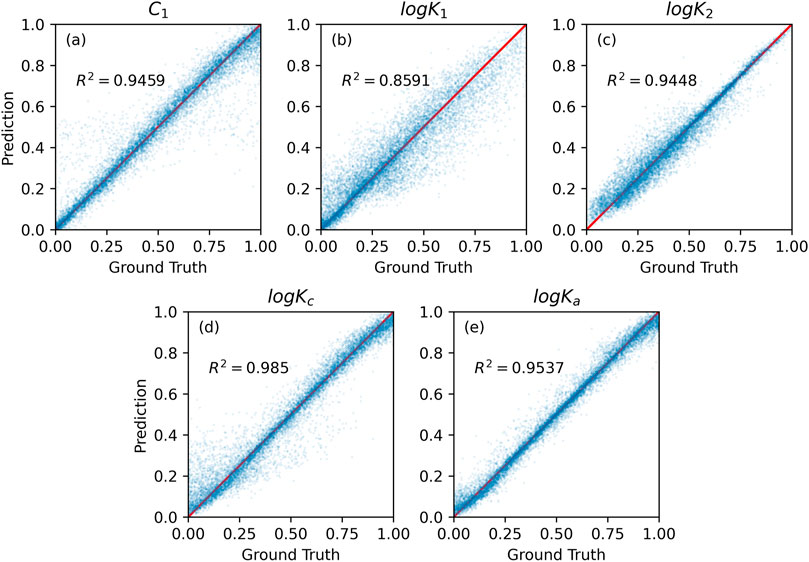
FIGURE 7. Gradient boosting prediction vs. numerical method calculation on the test set for five SCM’s model parameter values: (A) capacitances C1, (B,C) equilibrium constants logK1 and logK2, (C,D) binding constants logKc and logKa.
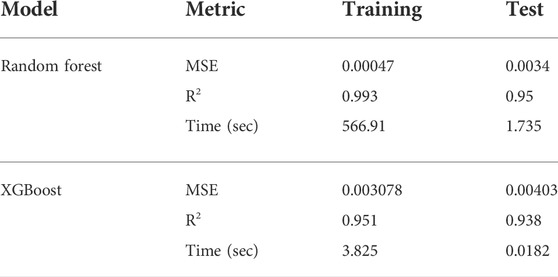
TABLE 1. Comparison of the ML-based SCM surrogate performance Random Forest (RF) and Extreme Gradient Boosting (XGBoost). MSE stands for the mean squared error between prediction and ground truth. R2 refers to the average score in the training or test set. Time refers to the computational time used for training or testing the model.
5 Conclusion and summary
Here, we presented the generic computational framework for generating synthetic titration datasets for oxide mineral/electrolyte interfaces using the 2-pK Triple Layer Model–one of the most frequently used Surface Complexation Models. We showed construction of the mathematical model, derivation of the nonlinear and convoluted master equations, and computational approaches to solve the governing equations.
Finally, we provided a dataset for the surface charge and ζ-potential titration curves covering a wide range of physicochemical parameters, such as acid-base oxide properties, electrolyte concentration, surface site density, capacitances, and ion binding constants. We also made available AI-readable datasets by preprocessing raw titration data (see repositories in Section Data Availability Statement).
The following steps in our research include the development of the synthetic radionuclide sorption dataset, synthetic titration curves for oxides in the presence of multivalent, multi-centered radionuclide surface complexes, and complex electrolyte solutions. Specifically, we are developing a synthetic dataset that incorporates radionuclide complexation reactions in the bulk solution and near the mineral surfaces in reducing and oxidizing conditions and varying temperatures to mimic the conditions expected in the nuclear waste geological repositories.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/nodameCL/synthetic-SCM-dataset.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
PZ was supported by the U.S. Department of Energy, Office of Nuclear Energy, Used Fuel Disposition Campaign, under Award Number DE-AC02-05CH11231. CL was supported by the U.S. Department of Energy (DOE) Chemical Sciences, Geosciences, and Biosciences Division under Contract DE-AC02-05CH11231.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Benjamin, M. M. (2002). Modeling the mass-action expression for bidentate adsorption. Environ. Sci. Technol. 36, 307–313. doi:10.1021/es010936n
Bethke, C. (2022). Geochemical and biogeochemical reaction modeling. Cambridge: Cambridge University Press.
Brandt, S. (2014). Data analysis. Statistical and computational methods for scientists and engineers. Cham: Springer.
Brown, G. E., Henrich, V. E., Casey, W. H., Clark, D. L., Eggleston, C., Felmy, A., et al. (1999). Metal oxide surfaces and their interactions with aqueous solutions and microbial organisms. Chem. Rev. 99, 77–174. doi:10.1021/cr980011z
Charmas, R., Piasecki, W., and Rudzinski, W. (1995). Four layer complexation model for ion adsorption at electrolyte/oxide interface: Theoretical foundations. Langmuir 11, 3199–3210. doi:10.1021/la00008a053
Davis, J. A., James, R. O., and Leckie, J. O. (1978). Surface ionization and complexation at the oxide/water interface: I. Computation of electrical double layer properties in simple electrolytes. J. Colloid Interface Sci. 63, 480–499. doi:10.1016/S0021-9797(78)80009-5
Dzombak, D. A., and Morel, F. M. M. (1990). Surface complexation modeling: Hydrous ferric oxide. New York: Wiley.
Géron, A. (2019). Hands-on machine learning with scikit-learn, keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems. Sebastopol: O’Reilly.
Hiemstra, T., De Wit, J., and Van Riemsdijk, W. (1989). Multisite proton adsorption modeling at the solid/solution interface of (hydr)oxides: A new approach. J. Colloid Interface Sci. 133, 105–117. doi:10.1016/0021-9797(89)90285-3
Hiemstra, T., and Van Riemsdijk, W. (1996). A surface structural approach to ion adsorption: The charge distribution (cd) model. J. Colloid Interface Sci. 179, 488–508. doi:10.1006/jcis.1996.0242
Hiemstra, T., Van Riemsdijk, W., and Bolt, G. (1989). Multisite proton adsorption modeling at the solid/solution interface of (hydr)oxides: A new approach. J. Colloid Interface Sci. 133, 91–104. doi:10.1016/0021-9797(89)90284-1
Hiemstra, T., Venema, P., and Riemsdijk, W. (1996). Intrinsic proton affinity of reactive surface groups of metal (hydr)oxides: The bond valence principle. J. Colloid Interface Sci. 184, 680–692. doi:10.1006/jcis.1996.0666
Hohl, H., and Stumm, W. (1976). Interaction of Pb2+ with hydrous γ-Al2O3. J. Colloid Interface Sci. 55, 281–288. doi:10.1016/0021-9797(76)90035-7
Karamalidis, A. K., and Dzombak, D. A. (2010). Surface complexation modeling: Gibbsite. Hoboken: Wiley.
Kosmulski, M. (2009). Compilation of PZC and IEP of sparingly soluble metal oxides and hydroxides from literature. Adv. Colloid Interface Sci. 152, 14–25. doi:10.1016/j.cis.2009.08.003
Kosmulski, M. (2016). Isoelectric points and points of zero charge of metal (hydr)oxides: 50 years after parks’ review. Adv. Colloid Interface Sci. 238, 1–61. doi:10.1016/j.cis.2016.10.005
Kosmulski, M. (2011). The pH-dependent surface charging and points of zero charge. J. Colloid Interface Sci. 353, 1–15. doi:10.1016/j.jcis.2010.08.023
Kosmulski, M. (2020). The pH-dependent surface charging and points of zero charge. VIII. Update. Adv. Colloid Interface Sci. 275, 102064. doi:10.1016/j.cis.2019.102064
Kosmulski, M. (2018). The pH-dependent surface charging and points of zero charge. VII. Update. Adv. Colloid Interface Sci. 251, 115–138. doi:10.1016/j.cis.2017.10.005
Kosmulski, M. (2002). The pH-dependent surface charging and the points of zero charge. J. Colloid Interface Sci. 253, 77–87. doi:10.1006/jcis.2002.8490
LaViolette, R. A., and Redden, G. D. (2002). Comment on ”modeling the mass-action expression for bidentate adsorption. Environ. Sci. Technol. 36, 2279–2280. doi:10.1021/es0206137
Lutzenkirchen, J., Marsac, R., Kulik, D. A., Payne, T. E., Xue, Z. R., Orsetti, S., et al. (2015). Treatment of multi-dentate surface complexes and diffuse layer implementation in various speciation codes. Appl. Geochem. 55, 128–137. doi:10.1016/j.apgeochem.2014.07.006
Nelder, J. A., and Mead, R. (1965). A simplex-method for function minimization. Comput. J. 7, 308–313. doi:10.1093/comjnl/7.4.308
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.
Piasecki, W. (2006). Determination of the parameters for the 1-pk triple-layer model of ion adsorption onto oxides from known parameter values for the 2-pk tlm. J. Colloid Interface Sci. 302, 389–395. doi:10.1016/j.jcis.2006.06.039
Piasecki, W., Zarzycki, P., and Charmas, R. (2010). Adsorption of alkali metal cations and halide anions on metal oxides: Prediction of hofmeister series using 1-pK triple layer model. Adsorption 16, 295–303. doi:10.1007/s10450-010-9245-y
Piasecki, W., Zarzycki, P., and Rudzinski, W. (2007). Relaxation time of proton adsorption from solution onto magnetite and anatase: Classical and new theoretical approach. Croat. Chem. Acta 80, 345–349.
Prélot, B., Charmas, R., Zarzycki, P., Thomas, F., Villiéras, F., Piasecki, W., et al. (2002). Application of the theoretical 1-pK approach to analyzing proton adsorption isotherm derivatives on heterogeneous oxide surfaces. J. Phys. Chem. B 106, 13280–13286. doi:10.1021/jp0200573
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (2007). Numerical recipes: The art of scientific computing. Cambridge: Cambridge University Press.
Rudzinski, W., Charmas, R., Piasecki, W., Prelot, B., Thomas, F., Villieras, F., et al. (1999). Calorimetric effects of simple ion adsorption at the silica/electrolyte interface: Quantitative analysis of surface energetic heterogeneity. Langmuir 15, 5977–5983. doi:10.1021/la981336d
Schindler, P., Fürst, B., Dick, R., and Wolf, P. (1976). Ligand properties of surface silanol groups. I. Surface complex formation with Fe3+, Cu2+, Cd2+, and Pb2+. J. Colloid Interface Sci. 55, 469–475. doi:10.1016/0021-9797(76)90057-6
Sverjensky, D. A. (2005). Prediction of surface charge on oxides in salt solutions: Revisions for 1:1 (M+L-) electrolytes. Geochim. Cosmochim. Acta 69, 225–257. doi:10.1016/j.gca.2004.05.040
Van Riemsdijk, W. H., Bolt, G. H., and Koopal, L. K. (1991). The electrified interface of the soil solid phase. Dordrecht: Springer, 81–113. chap. 2.
Verwey, E. J. W., and Overbeek, J. T. G. (1948). Theory of the stability of lyophobic colloids. The interaction of sol particles having an electric double layer. New York: Elsevier.
Wang, Z. M., and Giammar, D. E. (2013). Mass action expressions for bidentate adsorption in surface complexation modeling: Theory and practice. Environ. Sci. Technol. 47, 3982–3996. doi:10.1021/es305180e
Yates, D. E., Levine, S., and Healy, T. W. (1974). Site-binding model of the electrical double layer at the oxide/water interface. J. Chem. Soc. Faraday Trans. 1. 1 70, 1807–1818. doi:10.1039/F19747001807
Zarzycki, P., Charmas, R., and Piasecki, W. (2004). Formal mathematical analysis of the existence of the common intersection point in relation to determining the parameters describing ion adsorption at the oxide/electrolyte interface: Comparison of the triple and four-layer models. Adsorption 10, 139–149. doi:10.1023/b:adso.0000039869.47241.02
Zarzycki, P., Charmas, R., and Szabelski, P. (2004). Study of proton adsorption at heterogeneous oxide/electrolyte interface. Prediction of the surface potential using Monte Carlo simulations and 1-pK approach. J. Comput. Chem. 25, 704–711. doi:10.1002/jcc.10419
Zarzycki, P. (2007). Comparison of the Monte Carlo estimation of surface electrostatic potential at the hematite (0001)/electrolyte interface with the experiment. Appl. Surf. Sci. 253, 7604–7612. doi:10.1016/j.apsusc.2007.03.064
Zarzycki, P. (2007). Computational study of proton binding at the rutile/electrolyte solution interface. J. Phys. Chem. C 111, 7692–7703. doi:10.1021/jp066278g
Zarzycki, P. (2007). Monte Carlo modeling of ion adsorption at the energetically heterogeneous metal oxide/electrolyte interface: Micro- and macroscopic correlations between adsorption energies. J. Colloid Interface Sci. 306, 328–336. doi:10.1016/j.jcis.2006.10.059
Zarzycki, P. (2006). Monte Carlo study of the topographic effects on the proton binding at the energetically heterogeneous metal oxide/electrolyte interface. Langmuir 22, 11234–11240. doi:10.1021/la0625042
Zarzycki, P., Szabelski, P., and Charmas, R. (2005). A Monte Carlo simulation of the heterogeneous adsorption of hydrogen ions on metal oxides: Effect of inert electrolyte. Appl. Surf. Sci. 252, 752–758. doi:10.1016/j.apsusc.2005.02.058
Keywords: surface complexation modeling, machine learning, surrogate, sorption dataset, mineral surface, surface charge
Citation: Li C and Zarzycki P (2022) A computational pipeline to generate a synthetic dataset of metal ion sorption to oxides for AI/ML exploration. Front. Nucl. Eng. 1:977743. doi: 10.3389/fnuen.2022.977743
Received: 24 June 2022; Accepted: 22 August 2022;
Published: 15 September 2022.
Edited by:
Mavrik Zavarin, Lawrence Livermore National Laboratory (DOE), United StatesReviewed by:
Tiziana Missana, Centro de Investigaciones Energéticas, SpainAnna Romanchuk, Lomonosov Moscow State University, Russia
Copyright © 2022 Li and Zarzycki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chunhui Li, Y2h1bmh1aWxpQGxibC5nb3Y=; Piotr Zarzycki, cHB6YXJ6eWNraUBsYmwuZ292
 Chunhui Li
Chunhui Li Piotr Zarzycki
Piotr Zarzycki