- 1Department of Chemistry, Lomonosov Moscow State University, Moscow, Russia
- 2Nuclear Safety Institute of Russian Academy of Sciences, Moscow, Russia
Obtaining reliable thermodynamic sorption data is essential for establishing databases that can be used for the numerical safety evaluations of radioactive waste storage and disposal facilities. For this purpose, new experimental data on the sorption of U(VI), Np(V), and Eu(III) onto synthesized goethite in a wide range of experimental conditions were collected. Thermodynamic surface complexation models based on different approaches were developed and parametrized to fit a large dataset, including experimental data from the current work as well as available literature data. The proposed heuristic optimization procedure allowed identifying and comparing different parametrization variants and their uncertainties for considered models. The developed models pass the test on additional Cd(II) and Zn(II) data, simultaneously providing a reliable description of the sorption process for five cations and could probably be extended using the obtained linear free energy relationship.
1 Introduction
Various approaches to describe the sorption of radionuclides onto minerals have been discussed for a long time. The interest in this matter never ceased because sorption on environmental minerals is one of the main processes affecting radionuclides and heavy metals transport in the environment (Schindler and Stumm, 1987; Dzombak and Morel, 1990; Hochella and White, 1990; Appelo and Postma, 1993; OECD/NEA, 2012; Geckeis et al., 2013; Kersting, 2013; Payne et al., 2013; Romanchuk and Kalmykov, 2020). Therefore, understanding and numerical description of these processes are essential in the context of radioecology, remediation of contaminated areas, and safety assessment of radioactive waste storage and disposal facilities of different types. The predicted safety of a repository (or predicted risk from a contaminated site) will depend on the quality of the thermodynamic database used during calculations.
Descriptions of sorption reactions are highly relevant in the context of the current trends of reactive transport modeling, and computational tools for the analysis of fluid flow in the geological environment at kilometer scales coupled with chemical processes.
In the late 1970s, the surface complexation modeling (SCM) approach was introduced as a replacement for empirical methods to describe sorption reactions. SCM describes sorption in terms of chemical reactions between surface functional groups and dissolved chemical species (Stumm et al., 1970; Huang and Stumm, 1976; Davis and Kent, 1990). This powerful approach became widespread due to its high forecasting ability. Compared to the distribution coefficient (Kd) or empirical isotherm models (e.g., Langmuir and Freundlich), SCM can predict the impact of solution chemistry on sorption with various parameters over a broad range of pH values and other conditions.
However, SCM has several shortcomings. First, there is a problem with the determination of chemical reactions occurring at the surface during solute uptake and the resulting surface species. Various spectroscopic methods, such as extended X-ray absorption fine structure (EXAFS), time-resolved laser fluorescence spectroscopy (TRLFS), Raman or infrared spectroscopy, X-ray photoelectron spectroscopy (XPS), X-ray reflectivity techniques and others, can help to determine to some extent the species of radionuclide at the surface of a material (Geckeis et al., 2013; Rihs et al., 2014). However, these methods require a sufficiently high concentration of sorbate (usually more than 10−6 M) and are strongly limited by specific conditions. Since strong sorption sites dominate interaction at low radionuclide surface saturation and spectroscopic methods require high surface saturation, this it is hardly possible to confidently determine speciation during interaction with strong sorption centers. The only example is Cm TRLFS which is able to detect speciation of Cm at trace concentrations well below one monolayer on a surface (Geckeis et al., 2013).
It is even more challenging to establish the nature of sorption sites on the surface of minerals, in particular their chemical activity towards cations and their concentration. There are no direct methods that are simple to perform and easy to interpret for such characterization. Potentiometric titration is often used for surface site concentration determination previously. However, there are many artifacts including slow kinetics, surface contamination, dissolution or precipitation during the titration, carbonate influences, and others that make this method poorly reproducible from lab to lab and unreliable. Different microscopic techniques such as TEM, cryo-TEM, electron tomography, and so on have recently been used to determine surface site density, for example for goethite as well (Livi et al., 2017). However, these techniques are time-consuming and expensive and by design limited to the investigations on small amounts of particles. Therefore, such results may not be representative even for the sample as a whole, not to mention the reliability of the obtained parameters for the simulations of batch experiments or environments. This lack of a simple and direct technique makes model fitting of experimental data a primary tool for SCM parametrization.
All of the abovementioned factors have led to a variety of papers on the sorption of radionuclides and heavy metals on the surface of abundant minerals with very different ways to describe these sorption reactions. Even for the same chemical system, the approaches, constant values, site concentration, etc. are different. For example, RES3T thermodynamic sorption database contains more than 1700 sorption constants onto goethite from published literature sources (Brendler et al., 2003). And, unfortunately, the situation in 2022 has not significantly changed compared to that in 1990. Despite exhaustive guidelines (Payne et al., 2013), thermodynamic modeling of sorption is still challenging and controversial. Some of the most recent works offer applying different approaches to the modeling of large experimental datasets taken from literature for U(VI) sorption onto goethite (Satpathy et al., 2021) and quartz (Zavarin et al., 2022) correspondingly. The proposed approaches make it possible to obtain a more robust model. However, it is still the case of a single radionuclide. It is also worth adding that, for several reasons, there are much more data on U(VI) sorption compared to other radionuclides.
The focus of the current paper is an experimental and numerical study of the sorption of radionuclides that differ considerably in their chemical characteristics (U(VI), Np(V), and Eu(III)) onto synthesized goethite. Goethite is an abundant mineral in the environment. Because it is a product of oxidative iron corrosion it may be observed in nuclear waste disposal conditions. Goethite also demonstrates a high sorption affinity for most cations, including radionuclides. In this work, we aimed to develop a robust model that describes the sorption of several radionuclides under a wide range of experimental conditions. And particularly for this purpose new experimental dataset over a wide range of pH values and concentrations was obtained and combined with previously published data.
For the fitting SCM to the collected dataset and dealing with the corresponding parametrization uncertainties, the optimization workflow was built on the basis of a well-proven particle swarm optimization (PSO) algorithm (Shi and Eberhart, 1998) with multiple starts, and also subsequent filtering and clustering steps. By the use of this workflow, several models based on alternative conceptualizations (particularly, alternative hypotheses of surface speciation) were optimized and compared.
There were several overlapping goals of this exercise. Firstly, understandably, we wanted to acquire a robust set of SCM reaction constants for radionuclides onto goethite based on an extensive dataset. In the next place, there was an intention to refine and adjust a general approach to the model fitting to the specific needs of simultaneous modeling of sorption processes for different radionuclides based on the data from multiple sources. And last but not least we wanted to explicitly list the conceptual uncertainties and corresponding expert choices during the SCM development and parametrization process.
2 Materials and methods
2.1 Laboratory experiments
2.1.1 Synthesis and characterization of goethite
Two different goethite samples were studied in this work. The first goethite sample was synthesized by the method described in Cornell and Schwertmann, 2003. Briefly, ferrihydrite that was made by adding NaOH solution to concentrated Fe(NO3)3 was converted to goethite by thermal treatment at 70°C for 60 h. The crystalline structure and phase purity of the goethite was confirmed by X-ray diffraction (Supplementary Figure S1) using Rigaku D/Max-2500 diffractometer with a graphite monochromator using Cu Kα radiation (λ = 0.15418 nm). The specific surface area was determined by the Brunauer–Emmett–Teller (BET) technique and was equal to 105 m2/g. The morphology of the particles was defined using high-resolution transmission electron microscopy (HRTEM) (Supplementary Figure S2). The HRTEM images were obtained with an aberration-corrected JEOL 2100F instrument operated at 200 kV.
The acidity constants of the surface hydroxyl groups of goethite were determined by potentiometric titration. All titrations were performed under a nitrogen atmosphere at 25°C using an automatic potentiometric titrator (848 Titrino Plus) equipped with a 5-ml autoburette and Metrohm combined pH glass electrode (model 60262100). A constant temperature of 25.0 ± 0.1°C was maintained in the cell using a water-jacketed titration vessel with a circulating bath. The ionic strength was maintained by KCl in the range of 0.02–0.07 M. The titrations were performed in a pH range of 4–10. For the titrations, the following adding procedure was used: a new portion of titrant was added after constant pH (within 0.02 pH units) was established.
Another goethite sample was synthesized by a different method (Atkinson, 1967). For this sample, 200 ml of 2.5 M KOH was added to 50 g of Fe(NO3)3·9H20 in 825 ml of water in a Teflon vessel, which was then aged for 24 h in an oven at 60°C. The crystalline structure of the goethite was also confirmed by X-ray diffraction (Supplementary Figure S1). The specific surface area was determined by the BET technique and was equal to 35.5 m2/g. The corresponding HRTEM images are presented in Supplementary Figure S3.
2.1.2 Sorption experiments
For sorption experiments, 238,233,232U, 152Eu, and 237,239Np were used, and the radiochemical purity of the stock solutions was checked by γ-spectrometry and α-spectrometry (ORTEC DSPec50 radiometric complex with a coaxial gamma detector and semiconductor alpha detectors; Ametek, United States). The experiments were done at pH below 6 to eliminate the influence of carbonate on the experimental system. Sorption experiments were performed in plastic vials (HDPE) to avoid radionuclide sorption onto the vial walls. For the studied elements, sorption onto vial walls was negligible throughout the entire pH range. In all cases, 0.1 M NaClO4 (A.G.) was used as a background electrolyte. Experiments on Np(V) sorption were carried out under an N2 atmosphere to eliminate the influence of carbonate on the experimental system.
The initial total concentration of radionuclides in the experiments was kept below the solubility limit for hydroxides of these elements. The concentration of goethite used for the experiment ranged from 0.1 to 0.6 g/L. After adding radionuclides, the pH was measured and adjusted by the addition of small amounts of diluted HClO4 or NaOH. After equilibration, the solid phase was separated by centrifugation at 40000 g for 20 min. To ensure that steady-state conditions were reached, aliquots of solutions were taken periodically to determine the uptake. The radionuclide uptake was calculated from the difference between the initial radioactivity and that measured after equilibration. The radioactivity of the solutions was measured using liquid scintillation spectrometry using a Quantulus 1,220 liquid scintillation spectrometer (Perkin Elmer, United States).
2.2 Set of literature data
Goethite is one of the most widely researched minerals in the context of radionuclide or heavy metal sorption. Goethite is the end-point of transformations of various iron hydroxides and is widely present in the environment. The interactions of U(VI) with goethite are the most extensively studied interactions in the context of radionuclide sorption due to the following factors: first, the importance of research related to uranium behavior in the environment, and second, the relative simplicity of working with these materials in the laboratory. Experimental data on U(VI) sorption onto goethite are presented in quite a few works (Hsi and Langmuir, 1985; Jung et al., 1999; Villalobos et al., 2001; Missana et al., 2003; Sherman et al., 2008; Guo et al., 2009; Yusan and Erenturk, 2011; Coutelot et al., 2018). In most of these studies, thermodynamic modeling of uranium sorption is performed by applying different models and concepts, consequently resulting in quite different sorption constants. The most significant drawback of most of these works is a severely limited range of experimental conditions that does not allow the determination of universal constants. In the present work, we have made an effort to collect the bulk of the experimental data sets from different papers for model application purposes.
The comparison of different experimental data is sometimes nontrivial, and discrepancies between experimental data from different papers are likely to occur. The reason for these variations may lie in differences in experimental conditions. First, even fine differences in the origin of goethite samples and the characterization procedure used may affect the sorption process. Different solid-liquid separation techniques may be another important source of variation in sorption values. The filtration procedure may induce the underestimation of sorption values if particles with sorbed radionuclides pass through the filter, for example (Honeyman and Santschi, 1991). Furthermore, in some cases, filtration may lead to the overestimation of the sorption value if radionuclides are partly sorbed onto the filter material. Centrifugation with insufficient speed may also result in incomplete solid-liquid separation. The most challenging factor is that all these effects are highly dependent on the pH value.
Another issue of high concern in the case of uranium is that at a relatively high total concentration (more than 10−4 M), it may form poorly soluble intrinsic phases. The formation of these phases during sorption experiments mimics the main sorption process, which complicates the determination of the primary chemical process controlling the behavior.
Eu(III) sorption onto goethite is less studied than U(VI) sorption onto goethite. Only a few papers present experimental data of good quality (Ledin et al., 1994; Fujita and Tsukamoto, 1997; Fairhurst and Warwick, 1998; Naveau et al., 2005) and the examined experimental conditions are quite limited.
Np(V) sorption has been researched in several works (Fujita et al., 1995; Kohler et al., 1999; Khasanova et al., 2007; Kalmykov et al., 2008; Snow et al., 2013). Again, the experimental conditions in most of the works were not very diverse, in particular regarding the solid/liquid ratio range. The results from Fujita et al., 1995 were excluded from the dataset for the optimizations because naturally occurring goethite was used. The impurities that may be present in natural minerals may confuse sorption processes.
The sorption data from all of the papers discussed above were used in the parameter optimization procedure in addition to the experimental data obtained in the current work.
Data on cadmium and zinc (Balistrieri and Murray, 1982; Hoins et al., 1993; Spathariotis and Kallianou, 2007; Swedlund et al., 2009; Komárek et al., 2018) sorption onto goethite were added to verify the obtained models, as well as to expand the range of LFER.
2.3 Modeling approach
2.3.1 Surface complexation modeling
Surface complexation modeling is based on a mechanistic description of interfacial processes. It is assumed that the adsorption process is similar to aqueous complexation, where surface functional groups are defined as surface ligands that interact with cations to form surface complexes by the following general reaction:
where ≡SOH represents functional groups on the surface.
The usual mass law equation and mole balance formalism can be applied. Different approaches for taking account of cations’ or anions’ electrostatic interactions with the surface have been described comprehensively in (Goldberg et al., 2007; Geckeis et al., 2013). The most popular approaches are the use of a nonelectrostatic model (NEM) which does not account for electrostatic effects or the diffuse-double layer model (DDL) (Dzombak and Morel, 1990) which takes into consideration a “diffuse” layer where sorbate ions are attracted to the charged surface.
An important part of modeling is to determine the sorption reaction of particular surface species: mono- or polydentate (multidentate) species or ternary complexes containing ligands, such as hydroxyl and carbonate groups.
The most common and simple modeling approach is to represent sorption with the formation of monodentate complexes, such as in equation 1 (Mathur and Dzombak, 2006; Wang and Giammar, 2013). However, some of the data from spectroscopic studies or detailed atomistic (mechanistic) models give reasons to assume polydentate complexes as well. It is highly challenging to determine the exact species of radionuclides on a mineral surface. A common technique being used for this purpose is EXAFS. This method gives information on the local surroundings of the atoms, particularly those sorbed onto the mineral surface. The main disadvantage of this technique in the context of sorption studies is that it needs a relatively high concentration of the element of interest, which may affect the element’s speciation, and analyses of some elements may not be possible at all because of their low solubility. Another complication is that EXAFS spectra from sorbed species are usually relatively low in quality because surface species do not have a regular structure, in contrast to crystalline compounds. Moreover, if several surface species of the element of interest are present on the sample EXAFS spectra will give averages. These issues make the analysis of EXAFS spectra, which is already complex enough, difficult and controversial even more.
As in the case of batch sorption studies, uranium speciation on the surface of iron-containing minerals is relatively well studied by the EXAFS technique (Bargar et al., 1999, 2000; Moyes et al., 2000; Ulrich et al., 2006; Sherman et al., 2008). In most cases, the formation of bidentate uranium species on mineral surfaces was assumed. The EXAFS spectra of Eu(III) sorbed onto different minerals are even more complicated and do not provide clear evidence for the analysis of surface complexes’ structure (Tan et al., 2009; Bouby et al., 2010). There are several examples of EXAFS spectra of Am(III) sorbed onto magnetite that confirm the formation of tridentate complexes on the surface (Finck et al., 2016; Morelová et al., 2020). Similarly, it was assumed from EXAFS results that Pu(III) also formed tridentate complexes on magnetite (Kirsch et al., 2011). Studies of EXAFS spectra of Np(V) sorbed onto iron oxide gave controversial results. Bidentate complex formation was mentioned in some works (Amayri et al., 2007; Müller et al., 2015), while (Combes et al., 1992) provided another explanation.
Therefore, spectroscopic techniques provide a basis for describing sorption processes involving the formation of polydentate complexes on the surface. However, precise determination of the stoichiometry for all cases is complicated due to experimental limitations. Computer simulations of surface speciation may help address this issue, but there are still many open questions in this area. Importantly, accounting for polydentate complexes using geochemical codes requires careful treatment (Lützenkirchen et al., 2015).
The parameters for modeling aqueous speciation of the Eu(III), Np(V), U(VI) are presented in Supplementary Table S1. The parameters for the Cd(II) and Zn(II) was taken from (Puigdomenech, 2006).
2.3.2 Parameter optimization
A central part of the surface complexation modeling is the fitting of the model to the experimental sorption data by adjusting the model’s parameters (Payne et al., 2013). This model fitting process also could be referred to as model calibration, parameter optimization, or inverse modeling.
The model fitting process requires two computational tools: a geochemical speciation code for implementing the relevant model and software providing parameter optimization procedure. In this paper, we used PHREEQC (Parkhurst and Appelo, 1999) and MOUSE (Linge et al., 2020) codes correspondingly for these purposes. We have also written several scripts in Python language for data transformation and visualization.
In general, the parameter optimization procedure is pretty straightforward (Figure 1A). The key concepts of this process are the following:
• The numerical model itself. During the optimization it is treated as a “black box”: it means that we iteratively change inputs and analyze corresponding outputs of the model, but don’t use any information about what is going on inside it.
• Candidate parameter combination which could be also represented as a point in the multidimensional parametric space.
• The objective function which measures the fitness of the model by defining the distance between experimental data and modeled outputs.
• Optimization algorithm which is a strategy to search effectively through candidate parameter sets (to move through parametric space) based on the dynamic of the objective function in the previous steps
• Criteria for the optimization to stop.
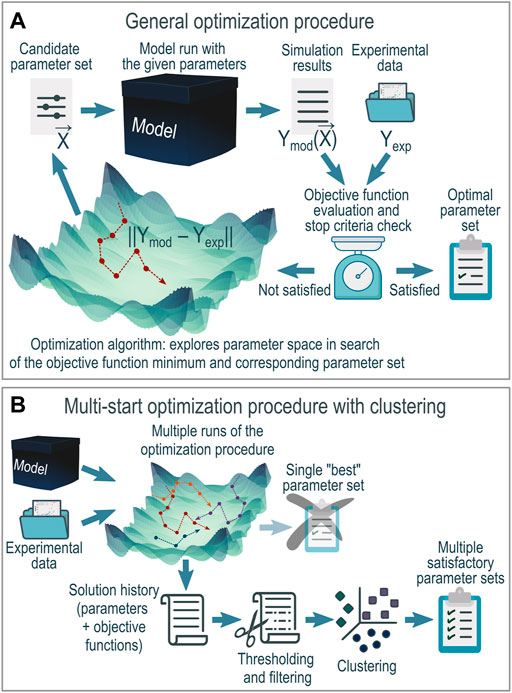
FIGURE 1. Parameter optimization procedure: (A) in general and (B)multi-start modification with clustering used in the current work.
In this paper, we use the well-proven Particle swarm optimization (PSO) algorithm that mimics the swarm behavior of flocking birds searching for food (Kennedy and Eberhart, 1995), in particular its inertia-weight modification (Shi and Eberhart, 1998), but we address method choice issues in the Discussion section.
As the objective function in the optimization, we used the squared differences of experimental and simulated values weighted by the number of points (sometimes referred to as the multivariate mean squared error, MMSE). Weights
where q is a data component (curve),
Unfortunately, several overlapping and interdependent factors complicate the practical application of the described optimization procedure as is. The first of them is the existence of multiple equally acceptable solutions. Particularly, for the SCM there are always at least several possible ways to fit the model output by varying the parameters to the experimental dataset (OECD/NEA, 2012).
Secondly, in the general case, there are no guarantees of convergence to the global minima for any optimization algorithm. But, finally, even if some optimization method could find the global minima, this solution would not be undoubtedly the best choice due to the possibility of overfitting. Overfitting in this context means that the best solution (model parameter combination) found by minimization of the distance between model outputs and a particular (even wide-ranging) dataset could be conditioned both by the data of interest itself and by the associated “noise” such as experimental uncertainty and outliers.
In this work in an attempt to overcome these issues, we configured (Figure 1B) a more elaborate parameter optimization procedure by:
• Employing multiple starts of the optimization algorithm to obtain more than one realization of the stochastic behavior of the algorithm and reduce the possibility that the particular realization used for further analysis was coincidentally inefficient.
• Analyzing not the single “best” optimization outcome but the whole history of parametric space exploration with posterior thresholding and filtering to cover the variety of satisfactory parameter combinations.
• Clustering remaining solutions to aggregate similar model parameter combinations and distinguish between different variants of parametrization and spread within the limits of one particular variant.
Specifically, the threshold for the objective function was set as 1.1∙MMSEibest for each start of the optimization procedure and 2∙MMSEbest for combining the solutions from all multiple starts, where MMSEibest is the best objective function for the ith optimization, and MMSEbest is the overall best obtained objective function value for the particular model and dataset. As an additional condition for filtering out unsatisfactory solutions were relations between the logarithms of sorption constants and the logarithm of the corresponding aqueous hydrolysis stability constants, so-called linear free energy relationships (LFER).
As a clustering method, we used the DBSCAN (Density-Based Spatial Clustering of Applications with Noise) method (Ester et al., 1996). It is an unsupervised method that given a set of points in multidimensional space, groups together the points in the dense regions (points with many nearby neighbors), marking points that lie alone in low-density regions (whose nearest neighbors are relatively far) as outliers.
3 Results and discussion
3.1 Experimental sorption data
To determine the acidity constants of the goethite sample with SSA = 105 m2/g, potentiometric titration was performed (Supplementary Figure S4). Using these experimental data, as a result of the optimization procedure, acidity constants were found to be logKa1 = 6.7 and logKa2 = −10.7. During the optimization total surface site concentration was fixed at 2.31 sites/nm2. The DDL model was used to account for electrostatic effects. The result is in agreement with the literature data (Cornell and Schwertmann, 2003).
In this work, sorption data for Eu(III), Np(V), and U(VI) in a wide range of cation/goethite ratios were obtained (Figure 2). The limits of the radionuclide concentration and pH for sorption were determined by considering competing reactions such as precipitation and complexation with carbonate. In the case of Np(V), experiments were performed under an N2 atmosphere, while for other radionuclides pH during the sorption experiments was kept below 6 to exclude CO2 dissolution. For all studied cations, partial surface saturation conditions were reached when sorption values decreased with increasing cation concentration in solution. Surface saturation is a prerequisite for determining the concentration of sorption sites. Notably, surface saturation was observed in the concentration range of approximately 10−6 mol/g (goethite). It is a common approach to fix the concentration of sorption sites onto oxide mineral surface to 2.31 sites/nm2 (Davis and Kent, 1990; Dzombak and Morel, 1990). For the studied goethite with a specific surface area of 105 m2/g, this value is equivalent to 4·10−4 mol (sorption site)/g (goethite). Thus, if all sorption sites on the goethite surface had the same strength towards the sorption reaction, saturation would not be reached in the entire studied concentration range. Therefore, the experimental data show the necessity of applying the model with two types of sorption sites which assumes the presence of a small amount of relatively “strong” sites on the goethite surface that have a higher affinity towards sorbed cations, while the remaining sites are “weak” sorption sites.
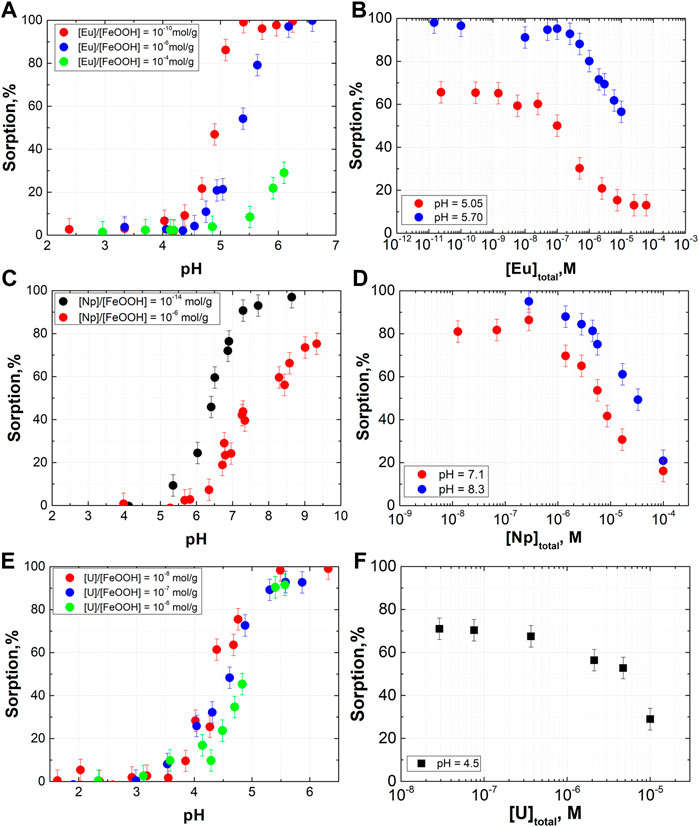
FIGURE 2. Data on (A,B) Eu(III), (C,D) Np(V) and (E,F) U(VI) sorption onto goethite (SSA = 105 m2/g) (I = 0.1 M, (A) [Eu]/[FeOOH] = 10−10 mol/g—[Eu] = 3·10−11 M, [α-FeOOH] = 0.3 g/L; [Eu]/[FeOOH] = 10−6 mol/g—[Eu] = 1·10−6 M, [α-FeOOH] = 0.3 g/L; [Eu]/[FeOOH] = 10−4 mol/g—[Eu] = 2·10−5 M, [α-FeOOH] = 0.1 g/L; (B) [α-FeOOH] = 0.3 g/L; (C) [Np]/[FeOOH] = 10−14 mol/g—[Np] = 1·10−14 M, [α-FeOOH] = 0.3 g/L; [Np]/[FeOOH] = 10−6 mol/g—[Np] = 8·10−7 M, [α-FeOOH] = 0.1 g/L; (D) [α-FeOOH] = 0.3 g/L; (E) [U]/[FeOOH] = 10−8 mol/g—[U] = 8·10−8 M, [α-FeOOH] = 0.3 g/L; [U]/[FeOOH] = 10−7 mol/g—[U] = 5·10−7 M, [α-FeOOH] = 0.3 g/L; [U]/[FeOOH] = 10−6 mol/g—[U] = 1·10−6 M, [α-FeOOH] = 0.1 g/L; (F) [α-FeOOH] = 0.6 g/L).
It is well known that differences in the sorption affinities of surface sites may be explained by the crystallographic structure. Different crystal facets contain different amounts of sorption sites with various chemical reactivities. For polycrystalline samples usually present in the environment, it is difficult to quantitatively account for sorption sites on the basis of structural considerations. Therefore, in most cases, sorption site concentrations are derived from sorption data. However, even for the same mineral, different samples may differ significantly in terms of not only SSA but also crystal facet relations and point defects that may influence sorption. Therefore, in this work, we also performed experiments with two different synthesized goethite samples with quite different SSAs: 105 and 35.5 m2/g. The sorption of Eu(III) was examined in this case (Figure 3). Surface saturation was clearly reached at a lower concentration of Eu(III) in the case of the sample with SSA 35.5 m2/g. The shape of the isotherms indicates that the concentration of both strong and weak sites is lower for the goethite sample with a lower SSA. The lower level of sorption at trace concentrations is the result of a lower strong site concentration, while a steeper decline in sorption on the isotherm is an indicator of a lower concentration of weak sites. These results were used in the modeling procedure.
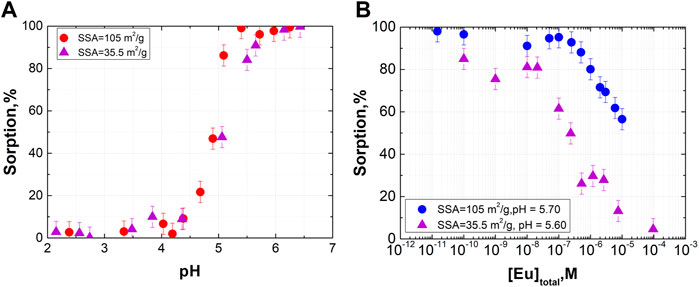
FIGURE 3. Eu(III) sorption onto different goethite samples with different SSAs (I = 0.1M, [α-FeOOH] = 0.3 g/L, (A): [Eu] = 3·10−11 M).
3.2 Different conceptual models and different modeling units
For the description of the obtained experimental data, we tested both monodentate and polydentate assumptions of complex formation during radionuclide sorption onto goethite. The DDL model was used for account electrostatic effects during sorption. We hypothesized the formation of polydentate complexes during sorption with the formation of uncharged surface species: Eu(III) is assumed to form tridentate, U(VI) bidentate, and Np(V) monodentate complexes correspondingly.
In addition to the monodentate and polydentate modeling conceptions, in this work, we proposed and tested a hybrid conceptual model. This model is based on the assumption that strong sites form monodentate complexes with radionuclides, while weak sites form polydentate. In fact, if the amount of strong sites is quite low it would be difficult to reach the polydentate interaction with them. At the same time, spectroscopic techniques in view of the requirement for relatively high sorbate concentrations which was explained above, probably give the possibility to see the interaction with the weak sites. The parameter optimization results were compared for all three alternative models.
Another essential step during model development is the choice of sorption units. In this work during the parameter optimization procedure, the sorption data were treated in sorption percentage (%) and concentration of cations in solution (mol/L) on the Y-axis. In the published guideline (Payne et al., 2013), it was recommended to make the fitting procedure of Kd data. The reason is that the Kd values are often used in performance assessment calculations. However, during the laboratory sorption experiments, the uncertainty of Kd determination in the case of close to 0 and 100% sorption is very high, significantly affecting the optimization in these units. Most of the optimization in the recent work has been done in percent (%) units. However, it should be noted that for reliable performance assessment, it is crucial to estimate the difference between the model values of Kd and the real data. Underestimation of Kd may be caused by different reasons, such as the complexation of radionuclides with anions or competition with cations that are present in the solution. This fact requires consideration in the conceptual model.
The general scheme of the evolution of the conceptual model in the present work is presented in Supplementary Figure S5.
3.3 Evolution of modeling of U(VI) sorption
As discussed above, experimental data on U(VI) sorption onto goethite are widely available in the literature. In the present work, firstly, we tested different approaches to modeling U(VI) sorption. Three datasets were used during the optimization: a new experimental dataset (Section 3.1), literature data, and their combination. During the first stage, we avoided addressing the effect of carbonate-ion complexation on sorption. The effect of carbonates is significant in the case of U(VI) sorption at pH values higher than 5 where CO2 may dissolve in water which makes the chemical system more complex. Therefore, only the results of sorption experiments that were performed in an inert atmosphere or at pH values lower than 5 were included in the dataset.
Various sorption reactions assuming that monodentate species are formed on the surface have been tested (Supplementary Table S2). First, simple reactions of U(VI) sorption onto strong (KmU1) and weak sites (KmU2) were used during modeling. The constant values for both reactions are quite similar for all studied datasets, while sorption site concentrations fluctuate slightly. Differences in the shape and size of goethite particles in different papers may be the source of the variety of sorption site concentrations in the modeling results. This variability confirms the difficulty of unambiguous determination of the concentration of sorption sites. The obtained parameters give an adequate description of the experimental data. Only sorption at pH values higher than 9 cannot be described given these parameters (see example in Figure 4A). To take into account sorption at higher pH values, reactions with the formation of ternary surface species should be included in the model (KmU3, KmU4). The addition of these reactions to the model improves the convergence, it can be seen by the decrease in the objective function value and on the plot in Figure 4B. In the case of the current experimental dataset, the reliable determination of KmU3, and KmU4 is not possible because of the absence of experimental data at high pH values where these reactions are significant.
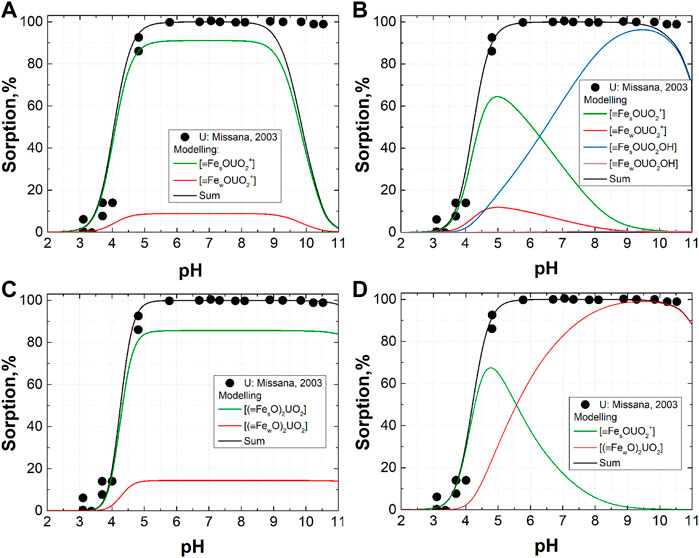
FIGURE 4. Application of the obtained parameters (see Supplementary Table S2) to the modeling of experimental data from the paper of Missana et al., 2003: (A)—logKmU1 = 4.6, logKmU2 = 1.7, [≡FesOH] = 0.033; (B)—logKmU1 = 4.0, logKmU2 = 1.6, logKmU3 = -3.4, logKmU4 = -7.3, [≡FesOH] = 0.052; (C)—logKpU1 = -1.9, logKpU2 = -4.4, [≡FesOH] = 0.079; (D)—logKhU1 = 4.3, logKhU2 = -4.2, [≡FesOH] = 0.034.
Sorption reactions without proton removal (KmU5, KmU6) were also added to the model. Such types of surface species have been reported in the literature (Girvin et al., 1991; Marmier et al., 1997; Cromieres et al., 1998; Naveau et al., 2005; Powell et al., 2018). At the same time, the formation of ≡FeOHCatn+ probably fails to account for the chemical properties of most cations. Actinides and lanthanides are cations that are highly charged and can therefore undergo hydrolysis and sorption with the formation of inner-sphere complexes. The pH dependence of sorption proves this mechanism. However, it is noteworthy that the test addition of these reactions improved the model fit to the experimental data; they were excluded only by chemical reasoning.
Parameter optimization for the model assuming the formation of polydentate complexes (in particular bidentate complexes) of U(VI) onto the goethite surface gives slightly better convergence, especially in the case of the literature dataset using lower numbers of parameters (Supplementary Table S3). Again, the values of the reaction constants (KpU1, KpU2) vary less than the concentration of sorption sites. In this case, the sorption of U(VI) at high pH values can be described using only two reactions: sorption on strong and weak sites (Figure 4C).
A similar outcome was observed for the hybrid approach: monodentate complexes with strong sites and polydentate with weak sites (Supplementary Table S4). A good convergence with experimental and literature data was observed for the model with 3 parameters (site concentration and two constants values KhU1, KhU2) (Figure 4D). We can see, as has been observed in many past modeling efforts, that batch sorption data modeling is inherently an underconstrained problem which leads to a non-unique solution to the SCM, and, consequently, additional considerations are required to justify the choice of the SCM parameters.
3.4 Evolution of modeling of the whole dataset
A similar approach was used to describe the sorption of Eu(III), Np(V), and U(VI) separately and all at once. The assumption of only one type of sorption site on the goethite surface with a concentration of 2.31 sites/nm2 did not give good simulation results because surface saturation for all the studied radionuclides manifests at much lower concentrations as discussed above. Assuming only one type of sorption site with varying concentrations may result in an adequate fit of the sorption of Eu(III), Np(V), and U(VI) separately; however, the resulting concentration of sorption sites is very different for each radionuclide. Fitting of the whole dataset using one type of sorption site did not give good convergence using either monodentate, polydentate, or hybrid approaches. Therefore, the assumption of two sorption site types on the goethite surface was further used. Using this assumption, three approaches (monodentate, polydentate, and hybrid) were applied to a wider dataset (experimental and literature data) and experimental data alone. The two units of sorption data (% and mol/L) were used as well.
At first, the optimization procedure for each model variant (i.e.combination of a conceptual model, sorption units, and dataset) was performed 10 times. The purpose of these repeated optimizations was mainly to test the stability of the obtained parameter set and ensure that we do not rely on the outcome of some accidentally inefficient optimization. However, we noticed that sometimes solutions with equally good (relatively low) objective functions could differ significantly (see example in Supplementary Figure S6A–S11A).
It brought us to the idea of the explicit exploration of the variety of possible solutions. To do this, 100 runs of the optimization procedure were made for each model variant and then obtained histories of parametric space exploration (sets of parameters and corresponding objective functions) were analyzed.
This analysis consisted of multiple stages. First, we had the whole optimization history, e.g., the progression of the parameter combinations from random ones to the best ones, and we needed to set a threshold for near-best solutions. This step is motivated by the possibility of overfitting and resulting from it chance to cast away solutions equally as acceptable as the technically best one just because of a slightly worse objective function. In this exercise, for simplicity and after confirming that these solutions were still satisfactory from the expert’s point of view we set the threshold as follows: at best solution increased by 10% for each optimization run, and at the doubled value of the best solution when merging the results of multiple runs. Further, it could be considered to set this threshold with consideration of the experimental data uncertainties.
As a result of the thresholding step, we obtained hundreds of near-best solutions instead of a single formally best one. Predictably, a lot of them were pretty similar, so we needed to extract from this vast amount the smaller list of distinctive parameter combinations, due to this we applied the clustering procedure as the next step. To be fair, the clustering step provided still a larger number of possible solutions than we expected but made it possible to visually analyze their variety (Figure 5A, Supplementary Figure S6B–S11B).
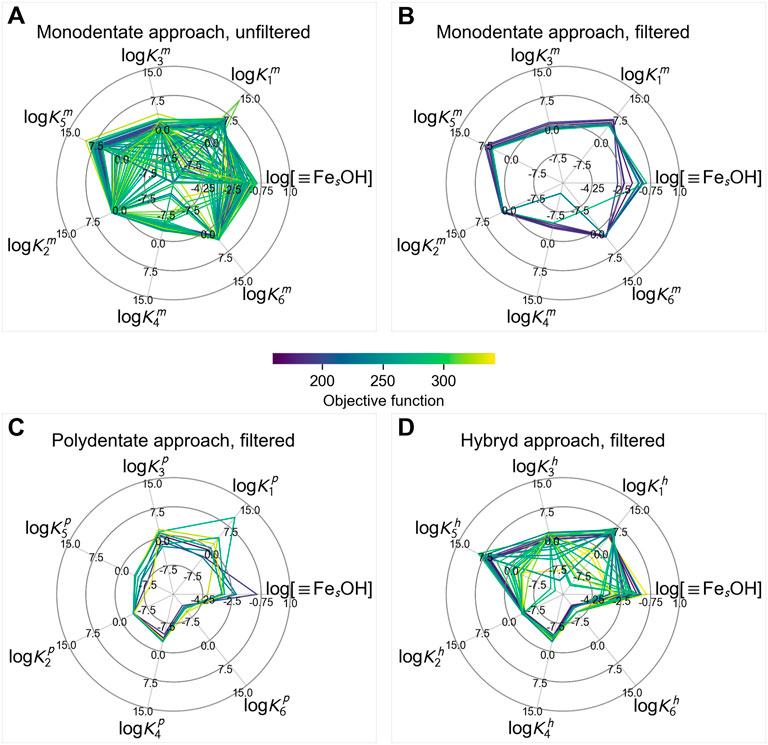
FIGURE 5. Clusters of the obtained solution in the: (A) monodentate approach, (B) monodentate approach after filtering, (C) polydentate approach after filtering, (D) hybrid approach after filtering. Sorption units are %, the dataset contains experimental and literature data.
No significant differences were scored when comparing the optimization performed in different sorption units (% or mol/L). From our experience, it is difficult to say which is better. Since in the case of % unit, there is a clear inflection in the sorption data, perhaps these units are a little more convenient for use and interpretation. However, there is still no unambiguous opinion.
The obtained clusters of possible sets of parameters mainly differ in the concentration of the strong sites (log [≡FesOH]), which in turn provides variation in the constants of sorption reaction where strong sites are involved (logK1, logK3, logK5). If there were a reliable way to determine the concentration of strong sorption sites, optimization of the whole sorption model would be much easier and more unambiguous.
In the absence of such a method, an alternative possibility is to filter the obtained solutions based on some valid chemical reasoning that could be formalized in numerical conditions on parameter values. In this case, two conditions were introduced for this purpose. First, the constant of the sorption reaction with the strong site should be higher than the constant of the similar reaction with the weak site (this assumption does not work in the case of the hybrid approach). The second condition was the Linear free energy relationship (LFER), the assumption of the linear correlation between the equilibrium constants of hydrolysis reaction in solution and sorption reaction based on their analogy. Previously it was successfully used for several minerals (Schindler et al., 1976; Balistrieri et al., 1981; Hachiya et al., 1984; Bradbury and Baeyens, 2005; Romanchuk and Kalmykov, 2014). Applying this filtering procedure has significantly reduced the number of candidate parameter combinations (Figures 5B–D, Supplementary Figure S6D–S11D).
And finally, the parameter sets with the lowest value of the objective function were selected from the thresholded and filtered list of candidate solutions. The corresponding values of parameters and objective function are given in Table 1. In the case of the hybrid approach, there were two solutions with nearly equal values of the objective function. The parameters are given through the slash. The uncertainties for the parameter values given in Table 1 are standard deviations for the values within selected clusters. We understand that it is not an ideal and quite rough description of the underlying uncertainties and discuss some avenues for corresponding further work in Section 2.4.6. To visualize the obtained solutions, the modeling results together with experimental data were plotted in Figure 6. The models derived by all three approaches give an adequate description of the experimental data in the wide range of conditions for the three radionuclides. To make the comparison of obtained models easier we also provided the values of adjusted determination coefficient R2adj (scaled from 0 to 1) as an additional measure of the goodness of fit calculated for each of the final models in Table 1. We discuss briefly goodness-of-fit measures in Section 2.4.6 and Section S8 of the supplementary material. Of course, it is worth noting that a numerical description of the behavior of a single radionuclide or even more so of a single experiment usually looks better, but the strength of this approach is the simultaneous description of several radionuclides. This is essential in the context of developing models for the safety assessment of radioactive waste storage and disposal facilities or areas contaminated with radionuclides.
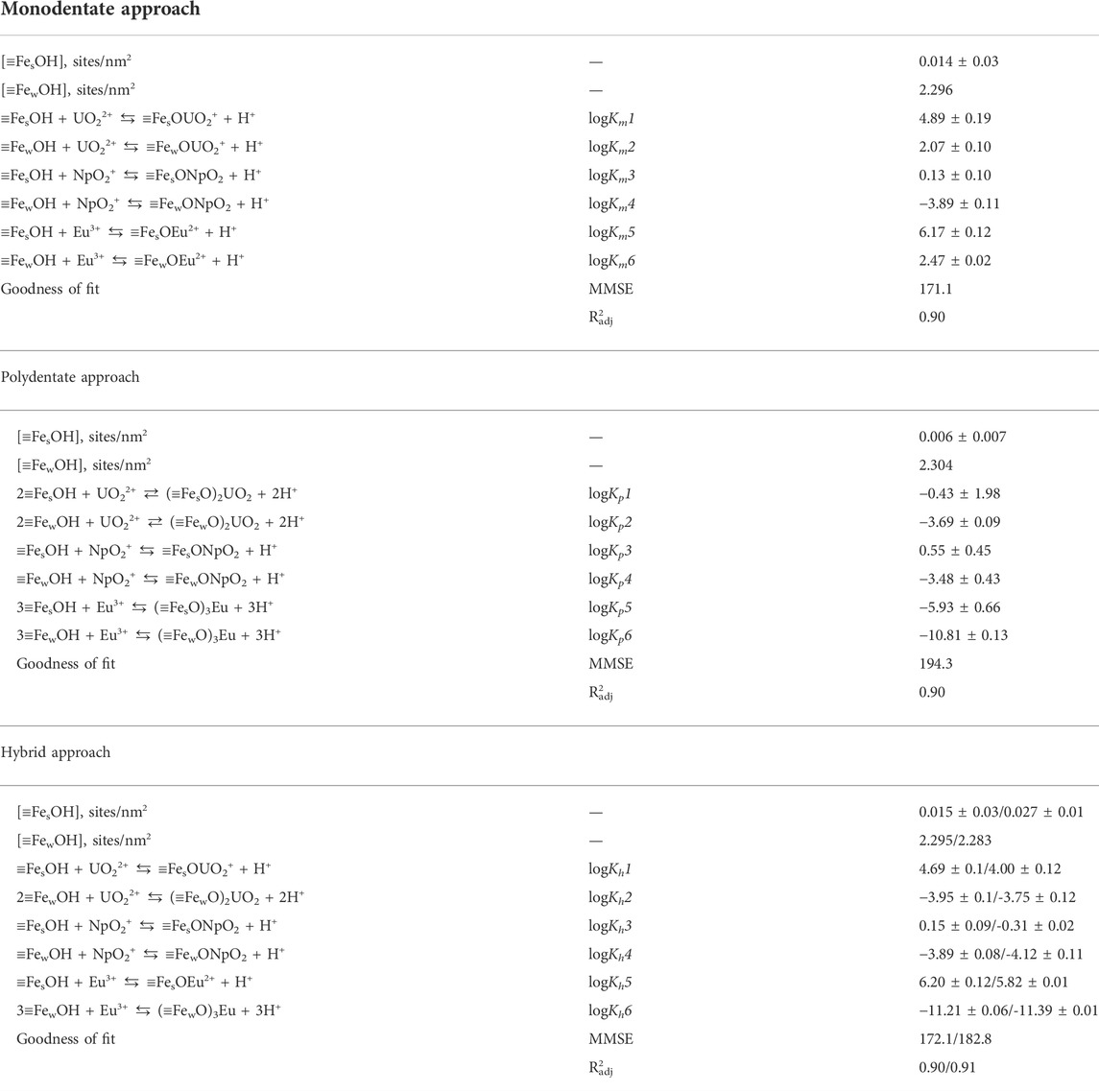
TABLE 1. Parameters of the best solutions of Eu(III), Np(V), and U(VI) sorption optimization onto goethite using different approaches in the units of sorption %.
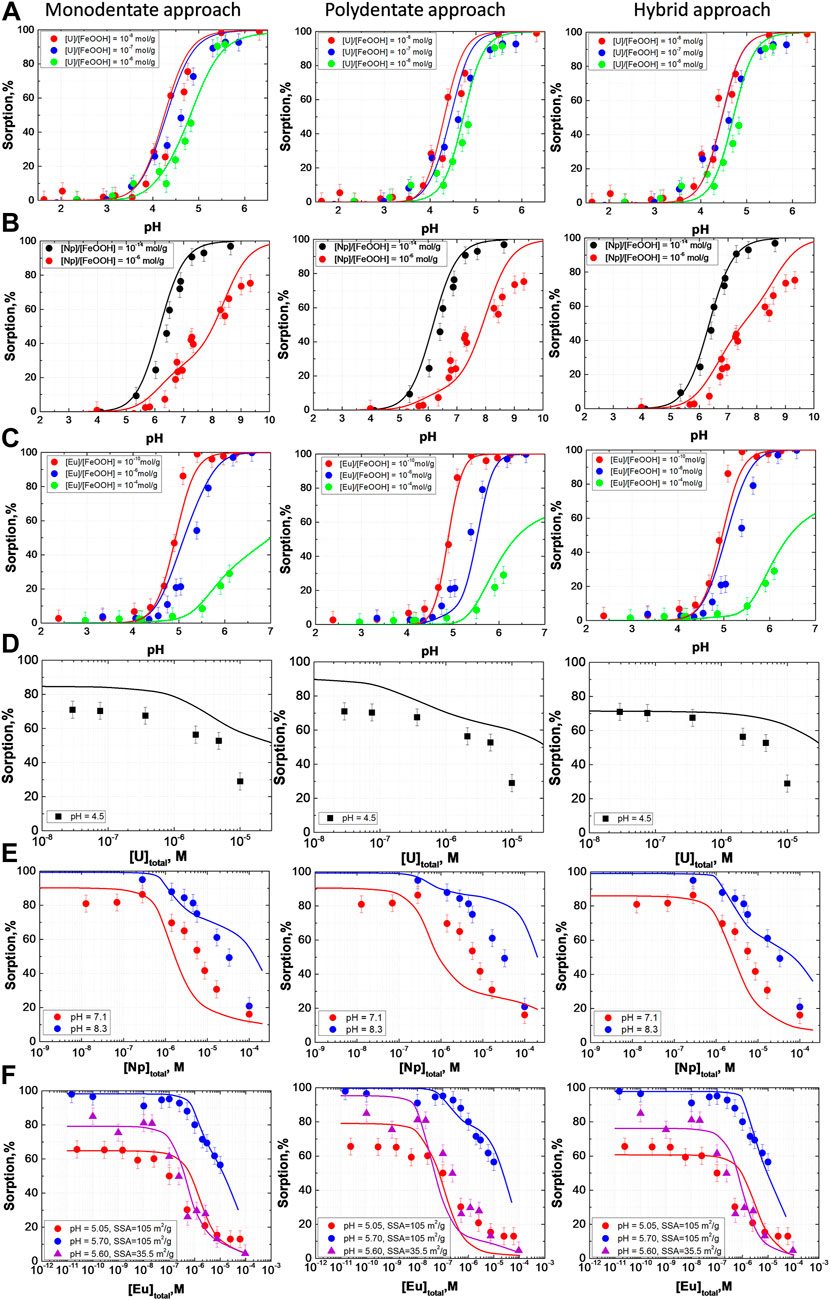
FIGURE 6. The experimental data obtained in this work together with the modeling for Monodentate, Polydentate, and Hybrid approaches Parameters of the models are presented in Table 1.
To analyze how models with obtained parameters fit the literature data, we presented the results graphically via diagonal plots featuring predicted versus observed values with 95% confidence and prediction intervals (Figure 7). The confidence interval shows how well the average experimental value can be estimated and the prediction interval demonstrates how well individual experimental values can be simulated. All used modeling approaches correctly fit most experimental literature data. However, some of the data points are apparent outliers. As mentioned above, differences in the experimental conditions (concentration, phase separation methods, CO2 presence, and other factors) may influence the determined sorption value. Supplementary Table S4 lists the specific experimental conditions from the studied literature data. When comparing pH dependence, the data from (Coutelot et al., 2018) and (Khasanova et al., 2007) differ from all other data regardless of applied approaches. In both cases, the additional filtration through filters may have led to an overestimation of the sorption value due to the partial sorption of radionuclides onto the filter surface.
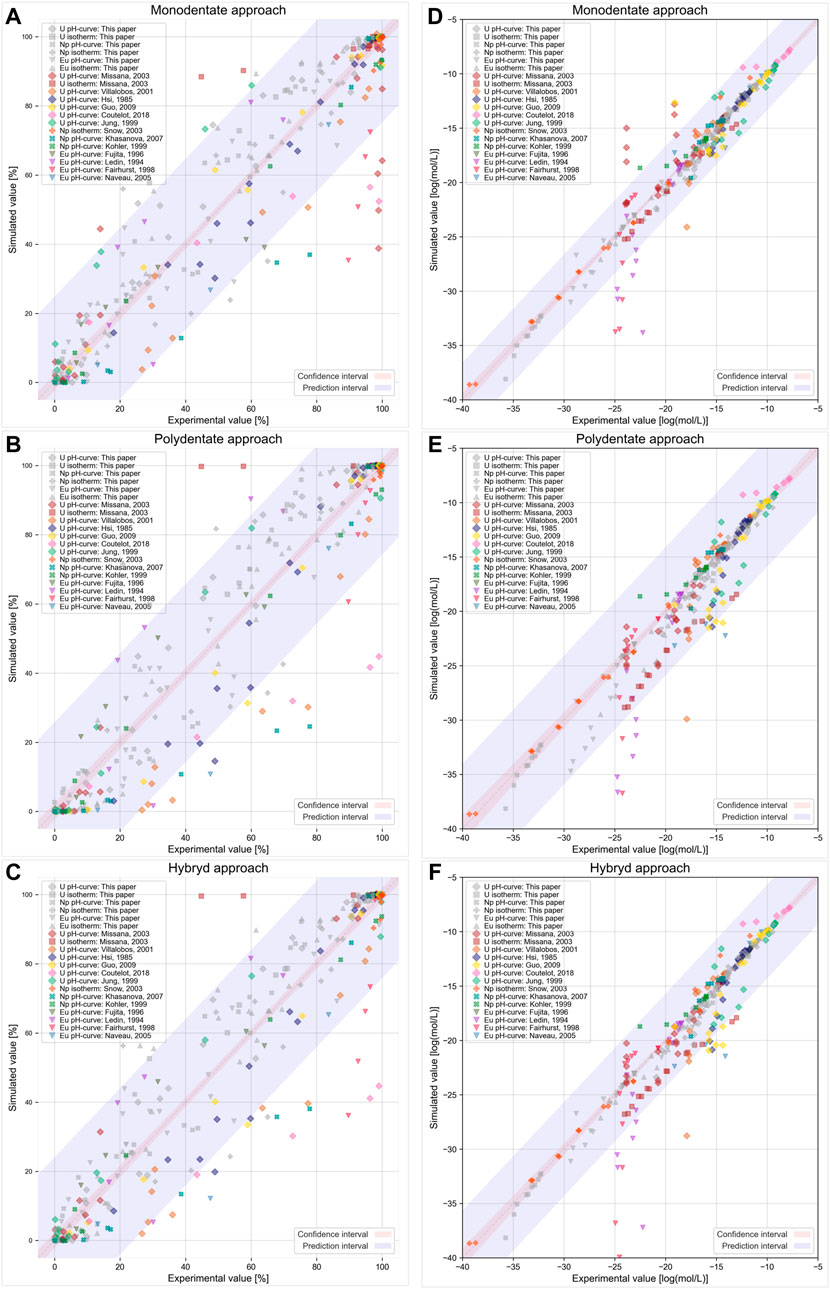
FIGURE 7. Graphical presentation of literature data vs modeling predictions for the used modeling approaches in (A,B,C) sorption % and (D,E,F) mol/L scales. Parameters of the models from Table 1 were used.
Sorption isotherms are presented in the literature less often than pH dependences. The data from Missana et al., 2003 lie beyond the prediction interval of all models in the current study. However, the pH dependences from the same paper are described much better. A possible explanation for this result is that the partial precipitation of intrinsic U phases expected at concentrations higher than 10−7 M at the studied pH values may affect the sorption isotherm. For the accounting sorption together with precipitation, another model is needed.
3.5 LFER and adding Cd and Zn
Despite the successful use of LFER as an additional condition for the choice of parameters, this assumption is insufficient for predicting other radionuclides’ sorption constants. Therefore, to increase predictive capability and to verify the adopted models, the literature data for the Zn and Cd sorption onto goethite were added to the dataset. These two cations were chosen because the hydrolysis constants values allowed equal coverage of the data points for the LFER and also on the score of literature data availability. In this part, only the hybrid approach was chosen as an example and as the most promising from our perspective approach.
Adding the Cd and Zn sorption data to the dataset slightly changed all the parameters (Table 2). The results of modeling Cd and Zn sorption data are presented in Supplementary Figure S12. The fitted curve is quite good in representing the experimental data. Thus, a developed model allows us to describe the sorption of 5 different cations.
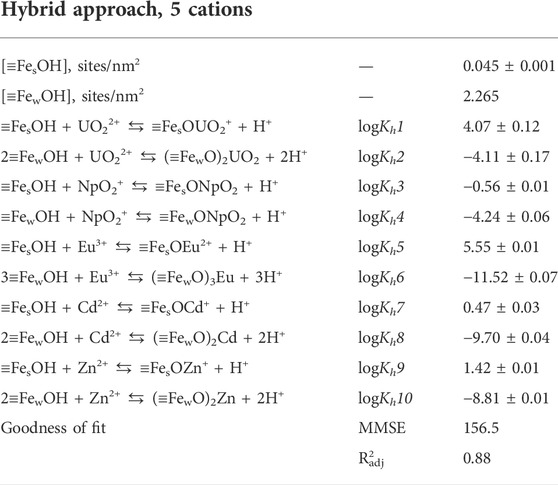
TABLE 2. Parameters Eu(III), Np(V), U(VI), Cd(II), Zn(II) sorption onto goethite optimization using the hybrid approach in the units of sorption %.
Figure 8 shows obtained LFER. It can be seen that the values of the weak site reaction constant are closer to linear dependence compared to the strong site. As was discussed above, the constants of the sorption reaction onto the weak site are determined much more reliably. The significant variation in the values for strong site reaction can be related to the complexity of determining their concentration and to the possible different nature of the binding of different cations on them. In addition, the uncertainty in the determination of the hydrolysis constant can also affect the reliability of LFER. It should also be noted that the chemical properties of the studied cations are pretty different. It is still unclear whether the “yl” cations (UO22+ and NpO2+) should be separated from the other cations (Eu3+, Cd2+, Zn2+). Nevertheless, the obtained equations can be used to predict the sorption constants for various cations with hard-to-detect sorption, such as plutonium in different oxidation states.
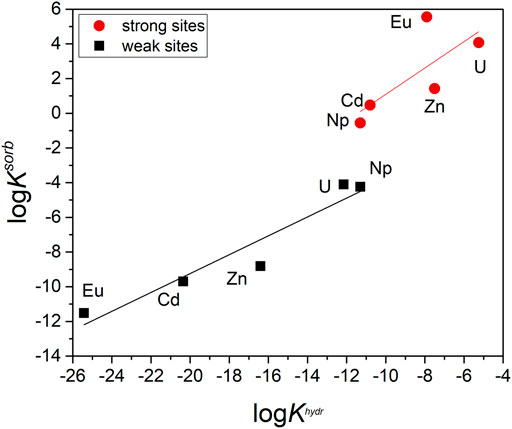
FIGURE 8. LFERs for cations sorption onto strong and weak sites of goethite. Data from Supplementary Table S5. The obtained equations: strong site logKsorb = 0.76·logKhydr + 8.69, R2 = 0.56, weak site logKsorb = 0.54·logKhydr + 1.64, R2 = 0.92.
3.6 Parameter optimization details: objective function, parameter scale, method choice, and uncertainties of the optimization results
While applying the general optimization procedure described in Section 2.3.2 to the specific problem, one faces multiple choices. Some of them such as the selection of model units and stopping criteria, and dealing with outliers were already discussed above. In this section, we wanted to highlight some other seemingly minor aspects that nevertheless could affect the practical outcome.
To start with, defining the objective function is more or less obvious when we are dealing with the single output of the simulation. In the case when the output of interest consists of multiple points or even multiple different curves, there are several issues to address. For example, it is not uncommon for experimental and simulated values to be obtained at different points, so we need to interpolate them before comparison. In our case, we applied piecewise-linear interpolation to the simulated curves.
In addition to this, the distance between experimental data and modeled results could be defined in various ways. A brief overview of goodness-of-fit measures is provided in section S8 of the supplementary material. Some general reasoning for the choice of goodness-of-fit measures can be found, for example, in Moriasi et al., 2007 and El-Khaiary and Malash, 2011. The main recommendation is to use measures that take into account the number of data points and the number of varied model parameters. Since the number of the parameters was the same in most of the comparisons during this work, the MMSE was selected as one of the simplest generalizations of the root mean square error for multiple curves with a different number of points in each of them. However, this choice could be debatable, in particular, the obvious drawback of the MMSE function is that it is not normalized which means that we could rank objective function values only by comparison with each other, not on some predefined scale. Also, to take into account the fact that values of output in mol/L units differed by several orders of magnitude, we used their logarithm during calculations of the objective function for corresponding model variants. An alternative way to balance the relevance of the wide-ranging points by assigning weighting factors based on measurement uncertainty is described in Zavarin et al., 2022. The use of weighting in general is a considerably common tool to include some additional information or expert insights into an objective function definition. The main controversial aspect of it is that in many cases the weighting process is difficult to universally formalize. In our case, we used weighting only to balance experimental curves with a different number of data points. However, analysis of the bulk optimization results indicates that if many S-shaped curves are being fitted, a decent goodness-of-fit can be reached by having a perfect fit at the beginning and end of the curve at the cost of the bend section of the curve. To correct this behavior, in further studies we consider assigning higher weights to bend points because they correspond to the main process under investigation.
And this brings us back to the discussion of the modeling units. On one hand, the downside of fitting models to data in % units is that data near 0 and 100% sorption are obscured, and for some strongly sorbing elements such as Eu(III) or Th(IV), it becomes difficult to fit curves where the majority of data are close to 100% sorbed. On the other hand, while using % as the unit of sorption, it is easier to determine the primary process, which provides a sharp inflection on the experimental curve. Additionally, sorption in the range around 0 and 100% sometimes can be affected by competing processes, such as complexation, that need to be considered in the conceptual model. Nevertheless, today there is no unambiguous answer to what units are better.
Next, considerations on the parameter ranges are relatively obvious but still important: when we are narrowing it down too much, we are missing some solutions. But when we are broadening it too much, we will slow down the optimization process and also will need to filter out a lot of technically satisfactory but unrealistic solutions at the later stages. Another related decision point is the scale of the parameters. Optimization algorithms usually implicitly assume that all insignificant parameters are excluded at the sensitivity analysis stage and the remaining parameters are commeasurable in terms of their impact on the modeling result. This assumption means that, for example, using linear increments in parameter values or agent velocities as part of the optimization algorithm would be efficient for searching through parametric space. In this study, we had two types of parameters: logarithms of reaction constants and sorption site concentrations. To ensure that all the dimensions of the parametric space are equal for the optimization routine, we applied a logarithmic transformation to the site concentrations before optimization and an inverse transformation afterward.
The next decision point is the optimization method choice. Albeit the fact that the complex discussion on the comparison and the selection of the optimization methods is clearly outside the scope of this work, we wanted to outline several aspects of this topic.
As was stated above, in this work, we used the PSO algorithm which belongs to the wide class of heuristic optimization techniques. The main idea of heuristic optimization is that natural systems behave in a way that successfully solves different kinds of real-world optimization problems, and these quasi-random behavior patterns can be efficiently reproduced for the purposes of searching for the optimum for the “black-box” model. Heuristic optimization methods are known to be efficient tools for fitting models to experimental data in various fields, including geochemical modeling (Villegas-Jiménez and Mucci, 2009; Shi et al., 2014; Abdelaziz et al., 2019; Stolze et al., 2019).
Despite the advantages of heuristic optimization methods (namely, abilities for global search of the optima for high-dimensional multimodal nondifferentiable functions) and their widespread acceptance, the previous generations of optimization methods, i.e. local methods such as Levenberg-Marquardt gradient-based algorithm or Nelder-Mead downhill simplex algorithm (Venter, 2010) are also still in use (Elo et al., 2017; Komárek et al., 2018; Morelová et al., 2020; Mosai et al., 2021). Partly this is because these old methods are fast and efficient, typically require little problem-specific tuning, and are also frequently incorporated into the well-known modeling toolboxes such as FITEQL (Herbelin and Westall, 1999), PEST (Doherty, 2015), UCODE_2005 (Poeter et al., 2005). To overcome the locality of their search through the parametric space, some modifications are often introduced, such as multiple starts from different random points in the parametric space (Bompoti et al., 2019). That, strictly speaking, transforms the initial local method into one another heuristic approach. It is noteworthy as we can see even from the current paper multiple starts could be helpful for heuristic optimization as well, but in this case to overcome the whole different layer of issues.
Coming back to the optimization technique choice it is fair to mention the main drawback of heuristic methods formulated in the «no-free-lunch theorem of optimization» (Wolpert and Macready, 1997): there is no general-purpose and universal best optimization strategy, and the only way for one heuristic algorithm to outperform another is to be adjusted to the structure of the specific problem.
Analyzing the experience of this case study, we could point out at least a couple of desired characteristics of the optimization technique that could be beneficial in connection to the adjustment optimization methods specifically for parameter optimization of surface complexation models. In particular, two types of approaches seem to be worth exploring in this context: multimodal optimization methods (Li et al., 2017) and heuristic methods for constrained optimization (Kulkarni et al., 2021). On the other hand, optimization procedures that are employing different kinds of regularization (Liu et al., 2018) should be used very carefully. That is because their main strength, namely, to obtain any satisfactory solution as fast as possible, could do a disservice in the situation when we want to explore the variability of possible solutions.
Another significant issue with global optimization procedures lies in the presentation of the confidence bounds of the optimization results. Since parameter optimization is an inseparable part of the whole process of dealing with model uncertainties (Saveleva et al., 2021), it seems odd not to mention the uncertainty of the optimization results. The matter is that the confidence assessment of optimization results for linear models obtained using local search methods is rather straightforward. Assuming that deviations between predicted and experimental data follow a normal probability distribution, the confidence region defines a hyperellipsoid in the parameter space, with the best estimate of model parameters placed at the center (Schwaab et al., 2008; Wang et al., 2015). On the other hand, when we are dealing with complex nonlinear problems with multiple optima (as in the case of surface complexation model fitting), the assumption that the confidence region is an ellipsoid is obviously very far from reality because these regions could be not only nonelliptical but even unbounded, nonconvex and composed of unconnected parts. In this case, likelihood confidence regions could be used as a more accurate representation of obtained solution uncertainty (Schwaab et al., 2008; Tolazzi et al., 2018).
In this paper, the proposed optimization procedure allowed us to address this issue from another angle. In particular, the clustering step allowed us to decompose the uncertainty of optimization results into two separate components: multiple possible solutions and the spread within each of them. Corresponding plots for the hybrid conceptual model are shown in Figure 5D and Figure 9.
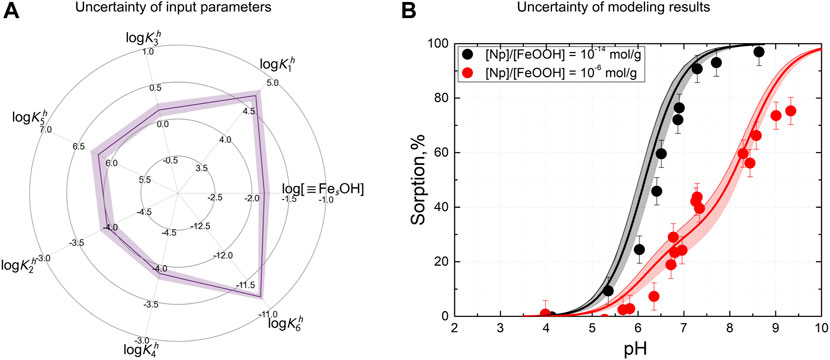
FIGURE 9. Illustration on the representation of uncertainties: (A) parameters’ range for the best cluster of solutions obtained by the hybrid approach in sorption % units and (B) corresponding spread for two simulated dependences.
The bottom line is that while developing a surface complexation model we are dealing not only with uncertainties associated with models’ parameters but also with multiple conceptual decisions, and these decisions are not always made transparently yet they could result in significantly dissimilar outcomes of the optimization. In this work, we are not in a position to recommend one and only right choice for each of them, but we attempted to identify these decisions explicitly and provide some consideration on possible options in Figure 10.
4 Conclusion
In this paper, we investigated the sorption of different radionuclides onto goethite using the surface complexation modeling approach. A wide range of sorption data with varying experimental conditions is essential for SCM parametrization. Therefore, large datasets were collected to ensure more reliable values of sorption constants. A substantial effort was undertaken both to obtain quality experimental data on U(VI), Np(V), and Eu(III) sorption over a wide range of total concentrations and to analyze the available published data.
Over the course of the model development, the concept of using two types of sorption sites (strong and weak) was approved based on both theoretical and experimental evidence. Then, in an effort to obtain a more feasible and substantiated model description of the experimental data, three modeling approaches were tested. First, the monodentate approach assumes only monodentate complex formation. The second, the polydentate approach, presumes the formation of surface species with a neutral charge as a result of sorption. And third, the hybrid approach proposed in the current work anticipates the formation of monodentate complexes with strong sites and polydentate with weak sites. Overall all three modeling approaches could produce appropriate simulation results given properly adjusted parameters. However, in the case of the monodentate approach, more parameters are required for a better description at higher pH values compared to other methods.
Parameter optimization of the proposed models was performed by the multi-start optimization procedure developed on the basis of the PSO heuristic algorithm with filtering and clustering stages. This approach made it possible not only to obtain some satisfactory set of parameters but to identify and compare different variants of parametrization for each model.
The analysis of possible modeling approaches and their parametrization raises the discussion on approaches and challenges for a unified numerical description of sorption processes. In our opinion, one of the most critical problems is the difficulty of determining the concentration of sorption sites, especially strong ones. Not least relevant is also the problem of choosing sorption reaction equations. Several conceptual decisions could affect the outcome of the parametrization process and, therefore, should be made transparently.
Finally, the developed models were tested by adding the literature data on two other cations, Cd(II) and Zn(II). It resulted in the construction of a reliable model that could adequately describe the sorption of at least five cations simultaneously and could probably be extended using the obtained LFER.
Author contributions
AIL and AYR carried out the experiment, AVE performed HRTEM characterization of the goethite samples., PDB, YMN, VSS performed optimization procedure, AYR and VSS conceived the original idea, performed data analysis and visualization, and co-wrote the manuscript, EAS, SNK supervised the project.
Funding
The sorption experiment and chemical part of the modeling were supported by the Russian Science Foundation (21-73-20083). MOUSE numerical code development is supported by State Atomic Energy Corporation “Rosatom” (contract number N.4d.241.20.22.1070). Experimental studies were partially performed on equipment acquired with funding from the Lomonosov Moscow State University Development Program.
Acknowledgments
The obtained experimental data associated with this article can be accessed at https://doi.org/10.17632/xtfnf5r3pf.1. Further inquiries can be directed to the corresponding author.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2022.969171/full#supplementary-material
References
Abdelaziz, R., Merkel, B. J., Zambrano-Bigiarini, M., and Nair, S. (2019). Particle swarm optimization for the estimation of surface complexation constants with the geochemical model PHREEQC-3.1.2. Geosci. Model Dev. 12, 167–177. doi:10.5194/gmd-12-167-2019
Amayri, S., Breckheimer, M., Drebert, J., and Reich, T. (2007). “EXAFS study of neptunium (V) sorption onto hematite,” in Speciation techniques and facilities for radioactive materials at synchrotron light sources, 163–172.
Appelo, C. A. J., and Postma, D. (1993). Geochemistry, groundwater and pollution. Rotterdam: Balkema. doi:10.1002/esp.3290200510
Atkinson, R. J., Posner, A. M., and Quirk, J. P. (1967). Adsorption of potential-determining ions at the ferric oxide-aqueous electrolyte interface. J. Phys. Chem. 71, 550–558. doi:10.1021/j100862a014
Balistrieri, L., Brewer, P. G., and Murray, J. W. (1981). Scavenging residence times of trace metals and surface chemistry of sinking particles in the deep ocean. Deep Sea Res. Part A. Oceanogr. Res. Pap. 28, 101–121. doi:10.1016/0198-0149(81)90085-6
Balistrieri, L. S., and Murray, J. W. (1982). The adsorption of Cu, Pb, Zn, and Cd on goethite from major ion seawater. Geochim. Cosmochim. Acta 46, 1253–1265. doi:10.1016/0016-7037(82)90010-2
Bargar, J. R., Reitmeyer, R., and Davis, J. A. (1999). Spectroscopic confirmation of uranium(VI)-carbonato adsorption complexes on hematite. Environ. Sci. Technol. 33, 2481–2484. doi:10.1021/es990048g
Bargar, J. R., Reitmeyer, R., Lenhart, J. J., and Davis, J. A. (2000). Characterization of U(VI)-carbonato ternary complexes on hematite: EXAFS and electrophoretic mobility measurements. Geochim. Cosmochim. Acta 64, 2737–2749. doi:10.1016/S0016-7037(00)00398-7
Bompoti, N. M., Chrysochoou, M., and Machesky, M. L. (2019). Assessment of modeling uncertainties using a multistart optimization tool for surface complexation equilibrium parameters (MUSE). ACS Earth Space Chem. 3, 473–483. doi:10.1021/acsearthspacechem.8b00125
Bouby, M., Lützenkirchen, J., Dardenne, K., Preocanin, T., Denecke, M. A., Klenze, R., et al. (2010). Sorption of Eu(III) onto titanium dioxide: Measurements and modeling. J. Colloid Interface Sci. 350, 551–561. doi:10.1016/j.jcis.2010.06.060
Bradbury, M. H., and Baeyens, B. (2005). Modelling the sorption of Mn(II), Co(II), Ni(II), Zn(II), Cd(II), Eu(III), Am(III), Sn(IV), Th(IV), Np(V) and U(VI) on montmorillonite: Linear free energy relationships and estimates of surface binding constants for some selected heavy metals and actinides. Geochim. Cosmochim. Acta 69, 875–892. doi:10.1016/j.gca.2004.07.020
Brendler, V., Vahle, A., Arnold, T., Bernhard, G., and Fanghänel, T. (2003). RES3T-Rossendorf expert system for surface and sorption thermodynamics. J. Contam. Hydrol. 61, 281–291. doi:10.1016/S0169-7722(02)00129-8
Combes, J.-M., Chlsholm-Brause, C. J., Brown, G. E., Parks, G. A., Conradson, S. D., Gary Eller, P., et al. (1992). EXAFS spectroscopic study of neptunium(V) sorption at the .alpha.-iron hydroxide oxide (.alpha.-FeOOH)/water interface. Environ. Sci. Technol. 26, 376–382. doi:10.1021/es00026a020
Cornell, R. M., and Schwertmann, U. (2003). The iron oxides: Structure, properties, reactions, occurrences and uses. Weinheim, Germany: WILEY-VCH GmbH&Co.KgaA.
Coutelot, F. M., Seaman, J. C., and Baker, M. (2018). Uranium(VI) adsorption and surface complexation modeling onto vadose sediments from the Savannah River Site. Environ. Earth Sci. 77, 148. doi:10.1007/s12665-018-7316-7
Cromieres, L., Moulin, V., Fourest, B., Guillaumont, R., and Giffaut, E. (1998). Sorption of thorium onto hematite colloids. Radiochim. Acta 88, 249–256. doi:10.1524/ract.1998.82.special-issue.249
Davis, J. A., and Kent, D. B. (1990). Surface complexation modeling in aqueous geochemistry. Rev. Mineral. Geochem. 23, 177–260.
Doherty, J. (2015). Calibration and uncertainty analysis for complex environmental models. Brisbane, Australia: Watermark Numerical Computing.
Dzombak, D. A., and Morel, F. M. M. (1990). Surface complexation modelling: Hydrous ferric oxide. New York: Wiley & Sons.
El-Khaiary, M. I., and Malash, G. F. (2011). Common data analysis errors in batch adsorption studies. Hydrometallurgy 105, 314–320. doi:10.1016/j.hydromet.2010.11.005
Elo, O., Müller, K., Ikeda-Ohno, A., Bok, F., Scheinost, A. C., Hölttä, P., et al. (2017). Batch sorption and spectroscopic speciation studies of neptunium uptake by montmorillonite and corundum. Geochim. Cosmochim. Acta 198, 168–181. doi:10.1016/j.gca.2016.10.040
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996). “A density-based algorithm for discovering clusters in large spatial databases with noise,” in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (Portland, OR: AAAI Press), 226–231.
Fairhurst, A. J., and Warwick, P. (1998). The influence of humic acid on europium-mineral interactions. Colloids Surfaces A Physicochem. Eng. Aspects 145, 229–234. doi:10.1016/S0927-7757(98)00662-1
Finck, N., Radulescu, L., Schild, D., Rothmeier, M., Huber, F., Lützenkirchen, J., et al. (2016). XAS signatures of Am(III) adsorbed onto magnetite and maghemite. J. Phys. Conf. Ser. 712, 012085–012087. doi:10.1088/1742-6596/712/1/012085
Fujita, T., and Tsukamoto, M. (1997). Influence of carbonate ions on europium sorption onto iron-oxides. MRS Proc. 465, 781–788. doi:10.1557/PROC-465-781
Fujita, T., Tsukamoto, M., Ohe, T., Nakayama, S., and Sakamoto, Y. (1995). Modeling of neptunium(V) sorption behavior onto iron-containing minerals. MRS Proc. 353, 965–972. doi:10.1557/PROC-353-965
Geckeis, H., Lu, J., Polly, R., Rabung, T., and Schmidt, M. (2013). Mineral − water interface reactions of actinides. doi:10.1021/cr300370h
Girvin, D. C., Ames, L. L., Schwab, A. P., and McGarrah, J. E. (1991). Neptunium adsorption on synthetic amorphous iron oxyhydroxide. J. Colloid Interface Sci. 141, 67–78. doi:10.1016/0021-9797(91)90303-P
Goldberg, S., Criscenti, L. J., Turner, D. R., Davis, J. A., and Cantrell, K. J. (2007). Adsorption-Desorption processes in subsurface reactive transport modeling. Vadose Zone J. 6, 407–435. doi:10.2136/vzj2006.0085
Guo, Z., Li, Y., and Wu, W. (2009). Sorption of U(VI) on goethite: Effects of pH, ionic strength, phosphate, carbonate and fulvic acid. Appl. Radiat. Isot. 67, 996–1000. doi:10.1016/j.apradiso.2009.02.001
Hachiya, K., Sasaki, M., Saruta, Y., Mikami, N., and Yasunaga, T. (1984). Static and kinetic studies of adsorption-desorption of metal ions on a .gamma.-alumina surface. 1. Static study of adsorption-desorption. J. Phys. Chem. 88, 23–27. doi:10.1021/j150645a007
Herbelin, A., and Westall, J. (1999). FITEQL. A computer program for determination constant from experimental data.
M. F. Hochella, and A. F. White (Editors). (1990). Mineral-water interface geochemistry. (Menlo Park, CA: Mineralogical Society of America), 23. doi:10.1515/9781501509131
Hoins, U., Charlet, L., and Sticher, H. (1993). Ligand effect on the adsorption of heavy metals: The sulfate – cadmium – Goethite case. Water Air Soil Pollut. 68, 241–255. doi:10.1007/BF00479406
Honeyman, B. D., and Santschi, P. H. (1991). Coupling adsorption and particle aggregation: Laboratory studies of “colloidal pumping” using iron-59-labeled hematite. Environ. Sci. Technol. 25, 1739–1747. doi:10.1021/es00022a010
Hsi, C. D., and Langmuir, D. (1985). Adsorption of uranyl onto ferric oxyhydroxides: Application of the surface complexation site-binding model. Geochim. Cosmochim. Acta 49, 1931–1941. doi:10.1016/0016-7037(85)90088-2
Huang, C. P., and Stumm, W. (1976). Interaction of Pb2+ with hydrous g-Al2O3. J. Colloid Interface Sci. 55, 281–288.
Jung, J., Hyun, S. P., Lee, J. K., Cho, Y. H., and Hahn, P. S. (1999). Adsorption of UO22+ on natural composite materials. J. Radioanal. Nucl. Chem. 242, 405–412. doi:10.1007/bf02345570
Kalmykov, S. N., Schäfer, T., Claret, F., Perminova, I. V., Petrova, A. B., Shcherbina, N. S., et al. (2008). Sorption of neptunium onto goethite in the presence of humic acids with different hydroquinone group content. Radiochim. Acta 96, 685–690. doi:10.1524/ract.2008.1554
Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN’95 - International Conference on Neural Networks, 1942–1948. doi:10.1109/ICNN.1995.488968
Kersting, A. B. (2013). Plutonium transport in the environment. Inorg. Chem. 52, 3533–3546. doi:10.1021/ic3018908
Khasanova, A. B., Kalmykov, S. N., Perminova, I. V., and Clark, S. B. (2007). Neptunium redox behavior and sorption onto goethite and hematite in the presence of humic acids with different hydroquinone content. J. Alloys Compd. 444–445, 491–494. doi:10.1016/j.jallcom.2007.02.069
Kirsch, R., Fellhauer, D., Altmaier, M., Neck, V., Rossberg, A., Fanghanel, T., et al. (2011). Oxidation state and local structure of plutonium reacted with magnetite, mackinawite, and chukanovite. Environ. Sci. Technol. 45, 7267–7274. doi:10.1021/es200645a
Kohler, M., Honeyman, B. D., and Leckie, J. O. (1999). Neptunium(V) sorption on hematite (α-Fe2O3) in aqueous suspension: The effect of CO2. Radiochim. Acta. 85, 33–48. doi:10.1524/ract.1999.85.12.33
Komárek, M., Antelo, J., Králová, M., Veselská, V., Číhalová, S., Chrastný, V., et al. (2018). Revisiting models of Cd, Cu, Pb and Zn adsorption onto Fe(III) oxides. Chem. Geol. 493, 189–198. doi:10.1016/j.chemgeo.2018.05.036
Kulkarni, A. J., Mezura-Montes, E., Wang, Y., Gandomi, A. H., and Krishnasamy, G. (2021). in Constraint handling in metaheuristics and applications. Editors A. J. Kulkarni, E. Mezura-Montes, Y. Wang, A. H. Gandomi, and G. Krishnasamy (Springer Singapore). doi:10.1007/978-981-33-6710-4
Ledin, A., Karlsson, S., Düker, A., and Allard, B. (1994). The adsorption of europium to colloidal iron oxyhydroxides and quartz – the impact of pH and an aquatic fulvic acid. Radiochim. Acta. 66/67, 213–220. doi:10.1524/ract.1994.6667.special-issue.213
Li, X., Epitropakis, M. G., Deb, K., and Engelbrecht, A. (2017). Seeking multiple solutions: An updated survey on niching methods and their applications. IEEE Trans. Evol. Comput. 21, 518–538. doi:10.1109/TEVC.2016.2638437
Linge, I. I., Utkin, S. S., Svitelman, V. S., and Deryabin, S. A. (2020). Numerical safety assessment and optimization of decisions on radioactive waste disposal and nuclear decommissioning: Trends, needs, opportunities. Radioact. Waste 2 (11), 85–98. doi:10.25283/2587-9707-2020-2-85-98
Liu, Y., Zhou, A., and Zhang, H. (2018). “Termination detection strategies in evolutionary algorithms: A survey,” in Proceedings of the Genetic and Evolutionary Computation Conference GECCO ’18, Kyoto, Japan (New York, NY: Association for Computing Machinery), 1063–1070. doi:10.1145/3205455.3205466
Livi, K. J. T., Villalobos, M., Leary, R., Varela, M., Barnard, J., Villacís-García, M., et al. (2017). Crystal face distributions and surface site densities of two synthetic goethites: Implications for adsorption capacities as a function of particle size. Langmuir 33, 8924–8932. doi:10.1021/acs.langmuir.7b01814
Lützenkirchen, J., Marsac, R., Kulik, D. A., Payne, T. E., Xue, Z., Orsetti, S., et al. (2015). Treatment of multi-dentate surface complexes and diffuse layer implementation in various speciation codes. Appl. Geochem. 55, 128–137. doi:10.1016/j.apgeochem.2014.07.006
Marmier, N., Dumonceau, J., and Fromage, F. (1997). Surface complexation modeling of Yb(III) sorption and desorption on hematite and alumina. J. Contam. Hydrol. 26, 159–167. doi:10.1016/S0169-7722(96)00065-4
Mathur, S. S., and Dzombak, D. A. (2006). “Surface complexation modelling: Goethite,” in Surface complexation modelling. Editor J. Lutzenkirchen (Elsevier), 443–468. doi:10.1016/S1573-4285(06)80060-8
Missana, T., García-Gutiérrez, M., and Maffiotte, C. (2003). Experimental and modeling study of the uranium(VI) sorption on goethite. J. Colloid Interface Sci. 260, 291–301. doi:10.1016/S0021-9797(02)00246-1
Morelová, N., Finck, N., Lützenkirchen, J., Schild, D., Dardenne, K., and Geckeis, H. (2020). Sorption of americium/europium onto magnetite under saline conditions: Batch experiments, surface complexation modelling and X-ray absorption spectroscopy study. J. Colloid Interface Sci. 561, 708–718. doi:10.1016/j.jcis.2019.11.047
Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D., and Veith, T. L. (2007). Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50, 885–900. doi:10.13031/2013.23153
Mosai, A. K., Johnson, R. H., and Tutu, H. (2021). Modelling of palladium(II) adsorption onto amine-functionalised zeolite using a generalised surface complexation approach. J. Environ. Manage. 277, 111416. doi:10.1016/j.jenvman.2020.111416
Moyes, L. N., Parkman, R. H., Charnock, J. M., Vaughan, D. J., Livens, F. R., Hughes, C. R., et al. (2000). Uranium uptake from aqueous solution by interaction with goethite, lepidocrocite, muscovite, and Mackinawite: An x-ray absorption spectroscopy study. Environ. Sci. Technol. 34, 1062–1068. doi:10.1021/es990703k
Müller, K., Gröschel, A., Rossberg, A., Bok, F., Franzen, C., Brendler, V., et al. (2015). In situ spectroscopic identification of neptunium(V) inner-sphere complexes on the hematite-water interface. Environ. Sci. Technol. 49, 2560–2567. doi:10.1021/es5051925
Naveau, A., Monteil-Rivera, F., Dumonceau, J., and Boudesocque, S. (2005). Sorption of europium on a goethite surface: Influence of background electrolyte. J. Contam. Hydrology 77, 1–16. doi:10.1016/j.jconhyd.2004.10.002
OECD/NEA (2012). Thermodynamic sorption modelling in support of radioactive waste disposal safety cases. NEA sorption project phase III. Paris, France: OECD Publishing. doi:10.1787/9789264177826-en
Parkhurst, D. L., and Appelo, C. A. J. (1999). User’s guide to PHREEQC (version 2): A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations.
Payne, T. E., Brendler, V., Ochs, M., Baeyens, B., Brown, P. L., Davis, J. A., et al. (2013). Guidelines for thermodynamic sorption modelling in the context of radioactive waste disposal. Environ. Model. Softw. 42, 143–156. doi:10.1016/j.envsoft.2013.01.002
Poeter, E. E., Hill, M. C., Banta, E. R., Mehl, S., and Christensen, S. (2005). UCODE_2005 and six other computer codes for universal sensitivity analysis, calibration, and uncertainty evaluation constructed using the JUPITER API. doi:10.3133/tm6A11
Powell, B. A., Kaplan, D. I., and Miller, T. M. (2018). Neptunium(V) sorption to vadose zone sediments: Reversible, not readily reducible, and predictable based on Fe-oxide content. Chem. Geol. 481, 53–64. doi:10.1016/j.chemgeo.2018.01.026
Puigdomenech, I. (2006). HYDRA (hydrochemical equilibrium-constant database) and MEDUSA (make equilibrium diagrams using sophisticated algorithms) programs. Sweden: Royal Institute of Technology. Available at: http://www.kemi.kth.se/medusa.
Rihs, S., Gaillard, C., Reich, T., and Kohler, S. J. (2014). Uranyl sorption onto birnessite: A surface complexation modeling and EXAFS study. Chem. Geol. 373, 59–70. doi:10.1016/j.chemgeo.2014.02.025
Romanchuk, A. Y., and Kalmykov, S. N. (2014). Actinides sorption onto hematite: Experimental data, surface complexation modeling and linear free energy relationship. Radiochim. Acta 102, 303–310. doi:10.1515/ract-2014-2108
Romanchuk, A. Y., and Kalmykov, S. N. (2020). “Function of colloidal and nanoparticles in the sorption of radionuclides,” in Behavior of radionuclides in the environment I: Function of particles in aquatic system, 151–176. doi:10.1007/978-981-15-0679-6_6
Satpathy, A., Wang, Q., Giammar, D. E., and Wang, Z. (2021). Intercomparison and refinement of surface complexation models for U(VI) adsorption onto goethite based on a metadata analysis. Environ. Sci. Technol. 55, 9352–9361. doi:10.1021/acs.est.0c07491
Saveleva, E., Svitelman, V., Blinov, P., and Valetov, D. (2021). Sensitivity analysis and model calibration as a part of the model development process in radioactive waste disposal safety assessment. Reliab. Eng. Syst. Saf. 210, 107521. doi:10.1016/j.ress.2021.107521
Schindler, P. W., and Stumm, W. (1987). “The surface chemistry of oxides, hydroxides, and oxide minerals,” in Chemical processes at the particle-water interface. Editor W. Stumm (New York: Wiley), 83–110.
Schindler, P. W., Furst, B., Dick, R., and Wolf, P. U. (1976). Ligand properties of surface silanol groups. I. surface complex formation with Fe3+, Cu2+, Cd2+, and Pb2+. J. Colloid Interface Sci. 55, 469–475. doi:10.1016/0021-9797(76)90057-6
Schwaab, M., Biscaia Evaristo Chalbaud, J., Monteiro, J. L., and Pinto, J. C. (2008). Nonlinear parameter estimation through particle swarm optimization. Chem. Eng. Sci. 63, 1542–1552. doi:10.1016/j.ces.2007.11.024
Sherman, D. M., Peacock, C. L., and Hubbard, C. G. (2008). Surface complexation of U(VI) on goethite (α-FeOOH). Geochim. Cosmochim. Acta 72, 298–310. doi:10.1016/j.gca.2007.10.023
Shi, X., Ye, M., Curtis, G. P., Miller, G. L., Meyer, P. D., Kohler, M., et al. (2014). Assessment of parametric uncertainty for groundwater reactive transport modeling. Water Resour. Res. 50, 4416–4439. doi:10.1002/2013WR013755
Shi, Y., and Eberhart, R. (1998). “A modified particle swarm optimizer,” in 1998 IEEE International Conference on Evolutionary Computation Proceedings (IEEE World Congress on Computational Intelligence), 69–73. doi:10.1109/ICEC.1998.699146
Snow, M. S., Zhao, P., Dai, Z., Kersting, A. B., and Zavarin, M. (2013). Neptunium(V) sorption to goethite at attomolar to micromolar concentrations. J. Colloid Interface Sci. 390, 176–182. doi:10.1016/j.jcis.2012.08.058
Spathariotis, E., and Kallianou, C. (2007). Adsorption of copper, zinc, and cadmium on goethite, aluminum-substituted goethite, and a system of kaolinite-goethite: Surface complexation modeling. Commun. Soil Sci. Plant Anal. 38, 611–635. doi:10.1080/00103620701216005
Stolze, L., Zhang, D., Guo, H., and Rolle, M. (2019). Surface complexation modeling of arsenic mobilization from goethite: Interpretation of an in-situ experiment. Geochim. Cosmochim. Acta 248, 274–288. doi:10.1016/j.gca.2019.01.008
Stumm, W., Huang, C. P., and Jenkins, S. R. (1970). Specific chemical interaction affecting the stability of dispersed systems. Croat. Chem. Acta 42, 223.
Swedlund, P. J., Webster, J. G., and Miskelly, G. M. (2009). Goethite adsorption of Cu(II), Pb(II), Cd(II), and Zn(II) in the presence of sulfate: Properties of the ternary complex. Geochim. Cosmochim. Acta 73, 1548–1562. doi:10.1016/j.gca.2008.12.007
Tan, X., Fan, Q., Wang, X., and Grambow, B. (2009). Eu(III) sorption to TiO2 (anatase and rutile): Batch, XPS, and EXAFS studies. Environ. Sci. Technol. 43, 3115–3121. doi:10.1021/es803431c
Tolazzi, N., Steffani, E., Barbosa-Coutinho, E., Severo Júnior, J. B., Pinto, J. C., and Schwaab, M. (2018). Adsorption equilibrium models: Computation of confidence regions of parameter estimates. Chem. Eng. Res. Des. 138, 144–157. doi:10.1016/j.cherd.2018.08.027
Ulrich, K. U., Rossberg, A., Foerstendorf, H., Zänker, H., and Scheinost, A. C. (2006). Molecular characterization of uranium(VI) sorption complexes on iron(III)-rich acid mine water colloids. Geochim. Cosmochim. Acta 70, 5469–5487. doi:10.1016/j.gca.2006.08.031
Venter, G. (2010). “Review of optimization techniques,” in Encyclopedia of aerospace engineering (American Cancer Society). doi:10.1002/9780470686652.eae495
Villalobos, M., Trotz, M. A., and Leckie, J. O. (2001). Surface complexation modeling of carbonate effects on the adsorption of Cr(VI), Pb(II), and U(VI) on goethite. Environ. Sci. Technol. 35, 3849–3856. doi:10.1021/es001748k
Villegas-Jiménez, A., and Mucci, A. (2009). Estimating intrinsic formation constants of mineral surface species using a genetic algorithm. Math. Geosci. 42, 101–127. doi:10.1007/s11004-009-9259-8
Wang, B., Shi, W., and Miao, Z. (2015). Confidence analysis of standard deviational ellipse and its extension into higher dimensional euclidean space. PLoS One 10, e0118537. doi:10.1371/journal.pone.0118537
Wang, Z., and Giammar, D. E. (2013). Mass action expressions for bidentate adsorption in surface complexation modeling: Theory and practice. Environ. Sci. Technol. 47, 3982–3996. doi:10.1021/es305180e
Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1, 67–82. doi:10.1109/4235.585893
Yusan, S., and Erenturk, S. (2011). Sorption behaviors of uranium(VI) ions on α-FeOOH. Desalination 269, 58–66. doi:10.1016/j.desal.2010.10.042
Keywords: sorption, uranium, neptunium, europium, goethite, surface complexation modeling, parameter optimization, parameters clustering
Citation: Romanchuk AY, Svitelman VS, Blinov PD, Larina AI, Nevolin IM, Egorov AV, Saveleva EA and Kalmykov SN (2022) U(VI), Np(V), Eu(III) sorption on goethite: A wide-ranging multiradionuclide dataset and uncertainty-aware parametrization of surface complexation models. Front. Nucl. Eng. 1:969171. doi: 10.3389/fnuen.2022.969171
Received: 14 June 2022; Accepted: 18 July 2022;
Published: 12 August 2022.
Edited by:
David García, Amphos 21, SpainReviewed by:
Mavrik Zavarin, Lawrence Livermore National Laboratory (DOE), United StatesFrank Bok, Helmholtz Association of German Research Centers (HZ), Germany
Copyright © 2022 Romanchuk, Svitelman, Blinov, Larina, Nevolin, Egorov, Saveleva and Kalmykov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Yu. Romanchuk, cm9tYW5jaHVrYXlAbXkubXN1LnJ1
 Anna Yu. Romanchuk
Anna Yu. Romanchuk Valentina S. Svitelman
Valentina S. Svitelman Peter D. Blinov2
Peter D. Blinov2 Elena A. Saveleva
Elena A. Saveleva Stepan N. Kalmykov
Stepan N. Kalmykov