Abstract
In the context of nuclear waste disposal, a pre-requisite to assure their long term safety is the need for safety assessment studies aided by computational simulations, in particular, radionuclide migration from the waste to the geosphere. It is established that underground repositories for nuclear waste will provide retardation barriers for radionuclides. However, the understanding of the sorption mechanisms of radionuclides onto mineral surfaces (i.e., illite, montmorillonite) is essential for modelling their migration. On the other hand, mechanistic-based radionuclide migration simulations, typically for 1 million years, poses a computational challenge. Surrogate-based simulations can be useful to enable sensitivity/uncertainty analysis that would be prohibitive otherwise. Considering the current challenges in modelling radionuclide migration and the importance of the results and implications of these simulations (i.e., for the public and nuclear waste management agencies), it is necessary to provide appropriate computational tools in a transparent and easy-to-use way. In this work, we aim to provide such tools in a framework that combines the simulation capabilities of OpenGeoSys6 for radionuclide migration and the approachable nature of Project Jupyter (i.e., JupyterLab), which provides a modular web-based environment for development, simulation and data. In this way, we aim to promote the collaborative research of radionuclide migration assessment and, at the same time, to guarantee the availability and reproducibility of the scientific outcome through the OpenGeoSys initiative.
1 Highlights
• A lightweight, highly-integrated, yet easy-to-use framework for simulating radionuclide migration is presented.
• In addition to a mechanistic model, a surrogate-based model is also presented which is more computationally efficient.
• Two radionuclide migration examples with distinct sorption behaviors are discussed to demonstrate the capability of the presented framework.
2 Introduction
The deep underground repositories planned to dispose high-level radioactive waste (HLW) produced by nuclear power plants (i.e., spent nuclear fuel, SNF) or reprocessing, contain a determined inventory of several radionuclides (Hu et al., 2010; Metz et al., 2012). Research efforts by many countries are aimed at selecting potential disposal sites, to construct underground facilities at depths below 400 m (Boulton, 1978; Ewing, 2015; Jobmann et al., 2017). The HLW is planned to be buried by relying on a multi-barrier system that will serve as containment for radionuclides release to the environment. The multi-barrier system consists of several engineered barriers of different materials (Sellin and Leupin, 2013) surrounded by a natural barrier (i.e., host-rock). Potentially suitable host rocks studied around the world are salt, claystone and crystalline rock. For instance, a multi-barrier system for high level waste (HLW) in clay rock could contain a steel canister embedded by a bentonite buffer (De Windt et al., 2004; Marty et al., 2010; Lu et al., 2011; Berner et al., 2013; Mon et al., 2017; Idiart et al., 2020; Vehmas et al., 2020) which will retard the migration of radionuclides to the geosphere (i.e., host rock and surrounding rock formations). On the other hand, the potential advantages of clay rocks as natural barrier, are their high sorption capacity to many radionuclides (Mazurek, 2010) and their low permeability (Nagra, 2002; Mazurek et al., 2011). With hydraulic conductivities ranging from 10−14 to 10−12 m s−1, the main transport mechanism in clay rocks is diffusion (Bossart et al., 2002; Bossart et al., 2018). Other characteristic of clay rocks is that the negatively charged surfaces and nano-porosity of the clay minerals produce different diffusion pathways for anionic, cationic and neutral species. All these properties of clay-rocks made that the accessible porosity, sorption and the effective diffusion coefficient depend on the geochemistry of the system and each radionuclide present in the waste (Van Loon et al., 2003; Van Loon et al., 2004; Wersin et al., 2004; Appelo et al., 2008; Soler et al., 2008; Leupin et al., 2018; Soler et al., 2019).
Long-term nuclear waste safety assessments must show evidence that a deep underground repository multi-barrier system provides sufficient containment of radionuclides after 1 million years (Hennig et al., 2020). This poses the necessity of employing simulation tools and specific conceptual models to predict the long-term behavior of radionuclides migration through the engineered barriers and the specific host rock. In this context, reactive transport codes including sorption/desorption processes and diffusion is a key tool (Steefel et al., 2005) in the safety assessment of nuclear waste repositories in clay rocks. Nowadays there is a growing need to integrate simulation tools in the form of lightweight, flexible and easy-to-use software packages that are supported by the scientific and technical community via open-source initiatives. Moreover, the ever-growing availability of platforms and operating systems make the packaging of software dependencies more challenging. On the other hand, an open-source initiative for radionuclide migration as a data and modelling framework can deal with the reproducibility of the simulation results, a version-controlled history of the changes as new data emerges, input-output and data visualization, sharing and integration, as well as reaching non-technical audiences. To alleviate such issues, the use of software containers (Bilke, 2022) can provide a highly flexible, transferable and modular framework yet robust enough, that is, reliable and can be expanded on-demand as needed. Furthermore, the adoption of software containers by numerical modelling software has gained relevance in recent years, such as dfnWorks (Hyman et al., 2015) and FEniCS (Alnæs et al., 2015). Finally, the development of new software or the extension of already existing codes should provide quality assurance process including state-of-the-art scientific knowledge, testing and benchmarking (Cao et al., 2019; Águila et al., 2021; Montoya et al., 2022).
In this work, we provide a framework to model radionuclides migration in low permeable porous media, like the clay-rocks, by combining the capabilities of OpenGeoSys (OGS-6) (Bilke et al., 2019) with the feature-rich JupyterLab (Kluyver et al., 2016) software. This tool will serve to the purposes mentioned above, as well as enabling new scientific outcome as new understanding is being gained. Ultimately, we aim to promote the scientific collaboration on the topic as well as enabling non-technical decision-makers and interested parties to access state-of-the-art simulation data of radionuclides migration. We show the relevance and potential application of our framework through two examples dealing with the long-term diffusion in a widely studied clay rock [i.e., Opalinus Clay (OPA)] of two safety relevant radionuclides (i.e., Cs-135 and U-238) which will not significantly decay in 1 million years. This is done by applying two different numerical approaches to couple the radionuclide diffusion with the specific geochemical processes affecting their retardation. On one hand, one numerical methods consider, a mechanistic approach taking into account surface complexation and cation exchange processes with a realistic composition of the porewater of the clay rock (Appelo and Wersin, 2007). Although mechanistic approaches have benefits in terms of process understanding, it does so at the cost of a significant increase in computational expense, sometimes resulting prohibitive for large-scale simulations (Appelo and Wersin, 2007; Cao et al., 2019; Águila et al., 2021; Montoya et al., 2022). Mechanistic sorption models are typically obtained from batch experiments, where the sorption behavior of one radionuclide is studied as a function of radionuclide concentration (Bradbury and Baeyens, 2005). Further, we adopt a single-species approach by leveraging the use of a generated look-up table (Huang et al., 2018; Huang et al., 2021; Águila et al., 2021) as a surrogate for the complex geochemical model to speed-up simulations significantly.
This paper is organized as follows. In Section 2 we present the basic equations for the mathematical model used to simulate the diffusion-sorption behaviour in porous media (continuum-scale). Then, in Section 3 we expand on the proposed computational workflow in OGS6@Jupyter to assess the migration of radionuclides in clay. There, we provide details about the usage of the platform in the context of radionuclides migration simulations. In Section 4 we show a demonstrative application of our computational workflow for the migration assessment of two radionuclides with distinct geochemical behavior. In this section, we estimate the long-term radionuclides migration (1 million years) in Opalinus clay using a mechanistic and a surrogate modelling approach. Furthermore, an accuracy/efficiency analysis of the surrogate models is presented. We provide the assessment of two different radionuclides (Cs and U) into the same framework to highlight the flexibility of our proposed workflow, as well as to analyze the differences between both cases. Finally, Section 5 summarizes the main conclusions and provides future directions of the presented work.
3 Mathematical Model
3.1 Mass Balance Equation
The mass balance equations for a diffusion-reaction system can be written in a compact form as: (Kirkner and Reeves, 1988; Steefel and Lasaga, 1994; Bear and Bachmat, 2012)where cTα [mol m−3] is the total concentration of the primary chemical species α, ϕ [-] is the accessible porosity, De [m2 s−1] is the non-species-specific effective diffusion coefficient, and Rα [mol m−3 s−1] is the heterogeneous reaction term which incorporates the combined effect of aqueous complexation, surface complexation and ion-exchange reactions in this work. The effective diffusion coefficient is defined as (Archie, 1942; Bear and Corapcioglu, 2012)where Dp [m2 s−1] is the pore diffusion coefficient, which takes into account the constrictivity and tortuosity of the porous media.
3.2 Chemical Processes
In what follows, only brief descriptions of aqueous complexation, surface complexation and cation exchange models are presented. These are the two major chemical processes that are considered in modelling radionuclide migration in Opalinus clay in this work. Details about the modelling of these and other chemical processes (e.g., precipitation, dissolution) can be found elsewhere (Parkhurst and Appelo, 2013) and have been explained extensively (Appelo and Postma, 2004).
3.2.1 Surface Complexation
The solute sorption onto surface sites (denoted as S-OH in the following) can be described through a set of surface complexation reactions. In this work, we adopt a surface complexation formulation that neglects the effect of the electrostatic potential in the surface (Dzombak and Morel, 1991). For instance, consider the reaction for the sorption of a particular species Mthe mass-action equation iswhere Keq,S-OH is commonly referred to as an intrinsic equilibrium constant.
In OGS6#iPHREEQC, surface sites are treated as additional species in the mass-action expressions. Thus, the sorption of surface sites, disregarding the electrostatic potential terms, is modelled by the set mass-action equationswhere Keq,i is an equilibrium constant for surface species i in Np surface sites, a are the corresponding activities for both surface species and Nα primary chemical species, and vj,i are the stoichiometric coefficients of the sorption model. Note that, usually, the total number of sites Np is used to represent a surface with a determined number of i sites.
The above means that, for the surface complexation modelling (SCM) cases approached in this work, it is assumed that a set of surface reactions, intrinsic equilibrium constants and the moles of each surface site are available. Equilibrium constants and reaction equations for the aqueous complexation are taken off-the-shelf from existing chemical thermodynamic databases.
3.2.2 Cation Exchange Process
Cation exchange is described as a set of equilibrium reactions between free cations in solution and interlayer exchangeable cations in an exchange site. For instance, consider the following reactions for the exchange occurring on site X among Na+ and fictitious cations J+ and Q+
Then, the equilibrium constants can be expressed aswhere and a are the activities of the exchange sites and the dissolved cations, respectively.
According to the Gaines-Thomas convention (Gaines and Thomas, 1953), a general expression for a cation exchange reaction based on cation S* can be represented bywhere Si represents the interlayer cation, -Si represents the exchange site occupied by the interlayer cation i and -S∗ denotes the exchange site occupied by the base cation. Symbols v∗ and vi are the charges of the base and interlayer cations, respectively. Therefore, the mass-action set of equations yieldswhere Keq,i is the equilibrium constant for the reaction involving the base and i cations. Symbols and represent the exchange site activities of the base and the i dissolved cation, respectively. Similarly, symbols a* and ai represent the activities of the base and the i dissolved cation.
3.2.3 Aqueous Speciation
Such modelling techniques require the development of consistent chemical thermodynamic databases [e.g., PSI/Nagra (Thoenen et al., 2014), ThermoChimie (Giffaut et al., 2014)] that contain aqueous reactions of complexes participating in the sorption process. These databases are updated constantly as new information becomes available. More importantly in the context of this work, however, is that surface reactions need to be explicitly described including a reaction mechanism as well as appropriate selectivity constants (i.e., log K). The activity coefficients are calculated with the Davies equation (Davies and Association, 1962) since the ionic strength of the porewater in all the simulation scenarios does not reach higher values than 0.5 mol/L. Furthermore, the aqueous complexation reactions for all the radionuclides and aqueous species are taken from the latest version of the PSI/Nagra database (Thoenen and Hummel, 2021) in PHREEQC format (Miron, 2021).
Although the latest version of the PSI/Nagra database contains available information to calculate the activity coefficients with the Specific ion Interaction Theory (SIT) aqueous model, we have chosen to use the Davies equations for the reason mentioned above. The Davies equation is a function of the ionic strength of the solution and it readswhere γi is the activity coefficient of aqueous species i, A is a temperature-dependent constant, zi is the ionic charge of aqueous species i and μ is the ionic strength of the solution. The activity coefficient is related to the molality mi of aqueous species i with ai = γimi, where ai is the activity and is used in the mass-action equations (see Eq. 5).
4 Computational Workflow
In this section, we describe the basic components of our framework (i.e., OGS-6 and Jupyter) without going into great detail about OGS-6, which can be found elsewhere (Kolditz et al., 2012). First, we present a brief introduction to OGS-6 in a general context and in the context of reactive transport modelling. Then, we show how OGS-6 and Jupyter (among other required software packages) can be deployed to users in a self-containing package using Linux container technology. Finally, code snippets of OGS-6@Jupyter are shown as an example of radionuclide migration workflow. A general OGS-6@Jupyter workflow diagram for radionuclides transport in porous media is presented in Figure 1.
FIGURE 1

Workflow diagram for radionuclide migration assessment with OGS-6@Jupyter.
4.1 OpenGeoSys
OpenGeoSys (OGS-6) is a scientific open-source initiative for the numerical simulation and development of Thermo-Hydro-Mechanical-Chemical (THMC) processes in porous and fractured media (Bilke et al., 2019). OGS-6 is written in C++ and is based on the Galerkin finite element method. The OGS-6 development hub can be found in its official DevOps platform in GitLab (https://gitlab.opengeosys.org/ogs/ogs), which provides a secure platform to develop and manage source code, access to Continuous Integration/Continuous Delivery (CI/CD), issue-tracking and development support. GitLab can also provide a reliable source of model data, where simulation inputs can be integrated into the CI/CD process to be tested against source code changes, that, in turn, improves the reliability of the source code itself.
OGS-6 has been established by its application to a wide range of problems, such as geothermal energy, contaminant hydrology, CO2 sequestration/storage and nuclear waste management. In the context of reactive transport modelling, OGS-6 has been coupled to the geochemical solver PHREEQC in a recent work by using a novel operator splitting approach (Lu et al., 2022) in which speciation calculation is performed on the integration points instead. However, previous versions of OGS have been successfully coupled to other geochemical solvers, in the form of OGS-GEMS (Kosakowski and Watanabe, 2014), OGS-ChemAPP (Li et al., 2014), and OGS-ECLIPSE (Pfeiffer et al., 2016). Furthermore, OGS has been used extensively in reactive transport modelling applications. For instance, in cement/clay interactions in nuclear waste repositories (Berner et al., 2013; Kosakowski and Berner, 2013; Shao et al., 2013; Idiart et al., 2020), multi-phase reactive transport in concrete degradation (Huang et al., 2021) and, recently, radionuclides migration assessment in clay rocks (Águila et al., 2021).
4.2 Software Packaging of OGS-6@Jupyter Using Linux Containers
Linux containers are light-weight virtual machines which provide an isolated and portable runtime environment for software. We provide pre-built container images for the container runtimes Docker and Singularity for users to get started easily. The image contains the OGS simulator and its pre-processing tools, Python packages for pre- and post-processing as well as the Jupyter Lab application. Usage information can be found on the OGS documentation1.
A modular container creation framework, the OGS Container Maker (Bilke, 2022) (ogscm), is used for generating container definitions and building the resulting image. The framework can create custom containers adapted to specific use cases, e.g., by customizing the OGS software configuration or by adding additional Python packages or Jupyter Lab extensions. See the projects documentation2 for further customization possibilities. The creation of the container image is integrated into the CI process to provide up-to-date and downloadable images for the user.
4.3 OpenGeoSys-6@Jupyter Workflow Overview
OGS-6 project files (*.prj) are used as an interface to set up models. Project files must be valid XML files before they can be used by the software. XML keywords in the “tree-like” structure are used to control different aspects of the model. A lot of information about the usage of OGS-6 project files can be found in the official website (https://www.opengeosys.org/). It is not the intention of this section to provide a complete guide on the software usage; our intention is to show a simple reference example about the OGS-6@Jupyter workflow in the context of diffusive transport of radionuclides.
To begin using OGS-6@Jupyter, a project file must be written. Several model components must be carefully designed (e.g., a computational mesh, time-stepping scheme). A general XML tree instance of an OGS-6 model is shown in Figure 2. Under the main <OpenGeoSysProject> keyword, several required keywords need to be added in order to have a functioning project file. The <meshes> keyword, for instance, is used to specify mesh files. The same applies to the remaining keywords in the project file, each containing required information about the model.
FIGURE 2

Snippet of the general structure of an OGS-6 input file in XML format.
Besides the project file, a different kind of XML file, the OpenGeoSysGLI file type is used to specify boundary conditions in the model domain. Recall that the official documentation for this file type can also be found in the OGS-6 website. We provide a snippet relevant in the context of this work in Figure 3. The XML file should have a *.gml extension. This file is not called at simulation time, it is rather used in a pre-processing step, which can be integrated into OGS-6@Jupyter, as shown later. In the snippet, the coordinates of two points are specified for the domain as an “inlet” (i.e., the source term/constant inlet for radionuclides) and an outlet (i.e., a no-flux boundary).
FIGURE 3

Snippet of the OpenGeoSys-GLI file used to specify boundary conditions in the domain.
The following code snippets are used directly in a Jupyter notebook inside the OGS-6@Jupyter container. Note that the purpose of the snippets is to serve as a general guidance; future versions of the software may require the modification of some keywords. The first few commands that can be executed in a notebook cell are shown in Figure 4A. Two OGS-specific utilities are used to pre-process the mesh file “domain.msh” (i.e., created with a third-party software like GMSH) into usable mesh files by OGS-6. The GMSH2OGS simply generates an equivalent *.vtu file from the *.msh file. The second command constructMeshesFromGeometry takes the newly created *.vtu file and the prepared *.gml file to generate point meshes to be used as boundaries by the model. Note that many other pre- and post-processing utilities are available in OGS-6 for a wide-ranging use-cases.
FIGURE 4

Sample Python snippets of the OGS-6@Jupyter workflow. (A) Snippet used to run OGS-6 pre-processing utilities. (B) Snippet used to run an OGS-6 model with ogs6py. (C) Snippet used to plot the results of an OGS-6 model with VTUinterface.
After successfully running the pre-processing steps, the OGS model can be easily executed without leaving the Jupyter interface. In a new cell, for instance, the code snippet in Figure 4B can be executed to run the project file “ogs_model.prj” using the ogs6py API (Buchwald et al., 2021). Note that many other variations of the model execution can exist. For instance, OGS models can be run in an array-like structure to perform scenario and/or sensitivity analysis. Further, a Jupyter notebook can be used as a connecting interface for multi-step simulations. This enables tremendous flexibility in terms of accommodating for specific modelling needs through the use of a general high-level programming language such as Python.
Finally, an important feature of OGS-6@Jupyter is the possibility to use popular Python libraries for visualization in the same platform where the OGS model is executed. The Python package VTUinterface (Buchwald et al., 2021) is used for this purpose, as shown in Figure 4C. This package extracts the information from the generated output by OGS in easy-to-use data arrays that can be passed to plotting functions, as with any other data structure. Python libraries Numpy and Matplotlib are used, in this case, to create a simple line plot of the concentration profile along the x axis. Note that other data and plotting packages can be made available in OGS-6@Jupyter by custom installation in the container (e.g., via pip) or by requesting the feature to the OGS developers (https://gitlab.opengeosys.org/ogs/ogs).
4.4 Surrogate-Based Modelling: OpenGeoSys-6-Look-up Table
In what follows, we present the details of the surrogate-based modelling approach used in this work. This approach leverages the use of a custom look-up table at the source-code level to perform geochemical calculations. As such, the need to call the iPHREEQC solver (or any other geochemical solver) in the operator-splitting algorithm is entirely avoided. As it will be shown, the acceleration of computation is quite significant. This is because cheap calculations (e.g., linear interpolation) are used in place of solving a non-linear system of algebraic equations (generated by the mass-action equations of the chemical system). For the radionuclides simulations presented in this work, the surrogate-based models produce results with minimal loss of accuracy when compared to the use of the geochemical solver. Note, however, that this is true for the single-species approach (i.e., single-radionuclide migration). In general, adding more variables to the look-up table will increase the computational effort and, in some cases, its use may not be justified over directly calling the geochemical solver.
4.4.1 Code Implementation
The look-up table (LT) approach has been implemented in OGS-6 following similar methodologies reported previously (Huang et al., 2018; Huang et al., 2021). A schematic representation of the code implementation is shown in Figure 5. The approach is based on a simple search of the concentration values over the discretized spatial domain inside the specified look-up table and obtaining bounding values (i.e., lower and upper bounds). Then, these values are interpolated to compute a new set of values as given in the table. After this, the new values are assigned over the spatial domain for the next time-step and the process begins again until all the time-steps have been completed. Since a linear interpolation procedure has been adopted, the number of instances (i.e., points) specified in the look-up table have a large impact on the accuracy of the method. Therefore, special care must be given to selecting an appropriate number of look-up table points. Too few points will allow faster computation but may not produce sufficient accuracy. On the other hand, a high number of points will probably produce very accurate solutions at the cost of increased computational expense.
FIGURE 5
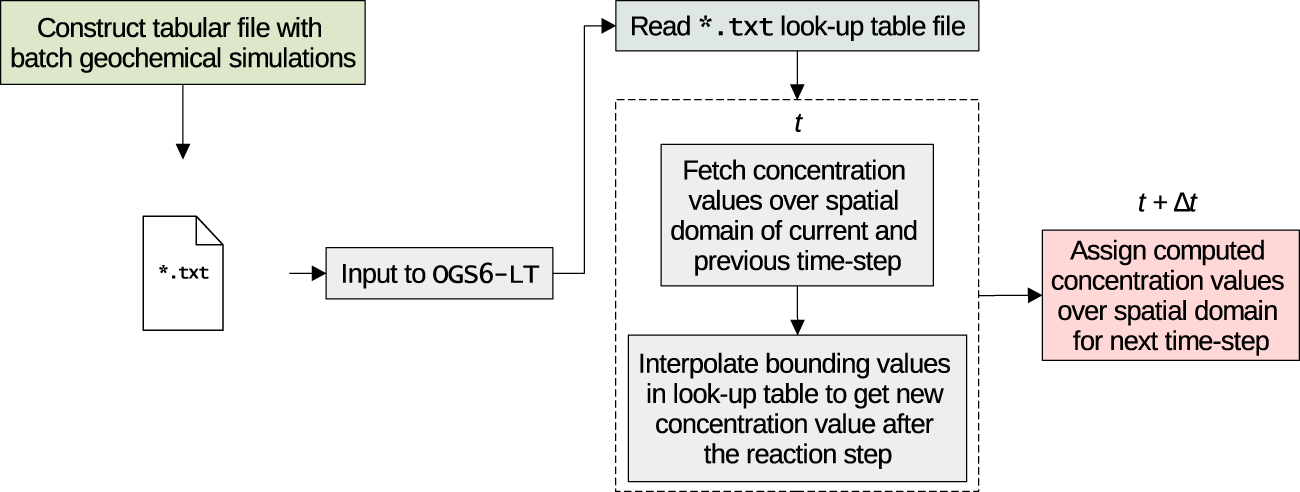
Schematic illustration of the implementation of the look-up table approach in OGS-6-LT.
4.4.2 Generating a Look-up Table From PHREEQC Batch Simulations
A general flow chart for generating a LT is shown in Figure 6. We show the general procedure for the construction of a LT with only one variable. However, note that the capabilities of OGS6-LT can be extended to any number of variables. The process starts with the definition of a sorption model (SCM or cation exchange) that describes the sorption of a radionuclide. If an OGS6#iPHREEQC simulation pre-exists, then this model can be taken directly, as it is shown in the examples of this work. Nonetheless, the purpose of the LT approach is to replace the CPU expensive geochemical calculations performed by OGS6#iPHREEQC with a much less CPU expensive alternative. Thus, a pre-existing OGS6#iPHREEQC simulation is not a prerequisite of the LT approach.
FIGURE 6
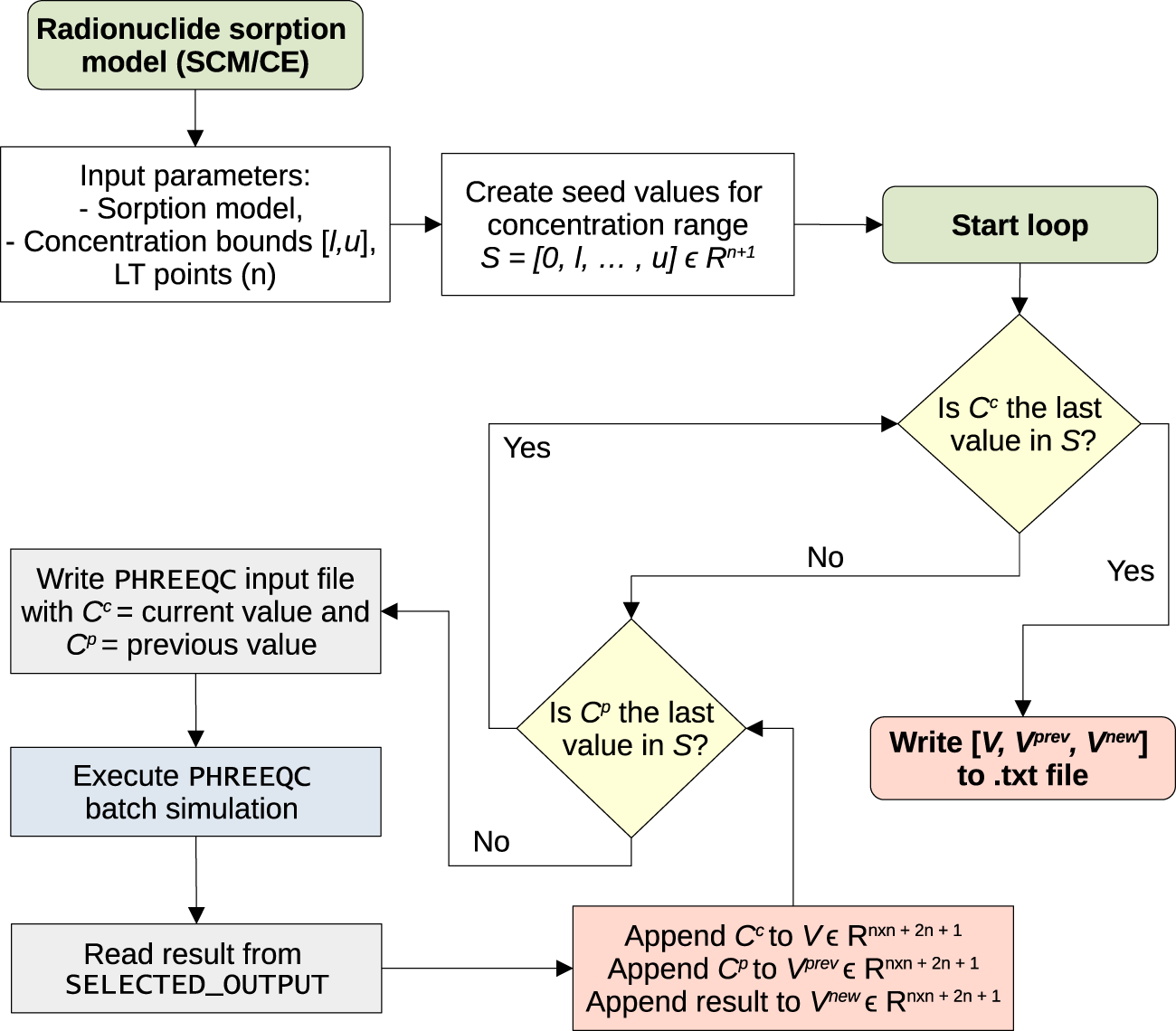
Flow chart for generating a look-up table with PHREEQC batch simulations.
After the definition of the sorption model, two additional parameters are required to generate the LT. First, adequate concentration bounds must be chosen. The lower l and upper u bounds are important parameters with major influence on the LT accuracy and performance. We have found that these bounds must be as tight as possible to the radionuclide concentration range in the medium porewater. The lower bound can be set to the background/initial concentration of the radionuclide. Whereas, because of the implementation of the numerical algorithm, the upper bound can be set slightly above the inlet concentration. This ensures that the interpolation point, when reading the LT values at higher concentrations, does not surpass the given concentration range. We have found that a value 10% larger than the initial concentration for the upper bound is sufficient in our simulations.
The second parameter is the number of discretization points for the LT. As shown later in our simulation results, these parameters will dictate the accuracy of the LT approach. Moreover, it has implications on the CPU time; the more points the more CPU is used by OGS6-LT. Therefore, the number of LT points is always a compromise between accuracy and computational efficiency. In addition, constructing a very large LT can also be computationally expensive due to the large number of PHREEQC batch calculations.
Finally, after the selection of the above parameters, the algorithm for constructing the LT can be followed. With the LT bounds [l, u] and number of points n, a vector is created. Note that the vector is always of size n + 1 because the first value is always 0, regardless of the given lower bound. The vector S is usually chosen over a log space to attain a better approximation towards the extreme values of the given range (i.e., the highest concentration gradients). Then, a nested loop sequence that iterates over the values of S computes three vectors that make up the LT. denotes the vector with the current concentration values. Vector represents the values of the previous time-step (i.e., before the reaction stage). And contains the results of the sorption calculations after the equilibration with the surface sites has occurred.
5 Radionuclides Migration Assessment
In this section, the diffusion of two strongly-sorbing radionuclides (i.e., Cs and U) in Opalinus clay is presented. On the one hand, the diffusion of Cs is evaluated by estimating its sorption with a cation exchange model (Águila et al., 2021). We adopt a constant concentration of Cs at the inlet of the clay domain by imposing Dirichlet boundary conditions. As such, we simulate the migration of Cs at low and high concentrations. We then apply our surrogate-based modelling approach by constructing a look-up table and compare the results to the mechanistic-based approach. On the other hand, we show the migration of U assuming the same physical and chemical conditions of the previous case. However, we adopt a surface complexation modelling approach which has larger number of sorption sites and distinct behaviour than the Cs case (Hennig et al., 2020). Furthermore, the U case is also abstracted into a look-up table approach and the results are compared to the mechanistic approach. OGS@JupyterLab notebooks are provided for the Cs and U simulations. There are several advantages of using the integration of OGS into the JupyterLab notebooks. First, the software packaging in Linux containers (see Section 3.2) ensures that all required software dependencies are available out-of-the-box, therefore, there is no requirement of installing additional software. This also enables seamless reproducibility. Second, all the components of the workflow (i.e., preprocessing, model preparation, visualization) can be executed without leaving the JupyterLab environment. This results in a easy-to-use interface and reduces the overall workload by avoiding manual integration with other software tools. And third, the modularity of the JupyterLab notebooks can be exploited when expanding/adapting a model as needed. We believe that this also facilitates collaboration, since notebooks can be shared and executed in a wide range of computational environments, without the need to develop platform-specific software packages. All the simulations presented in this section were carried out on a single Intel® Core® i7-10510U @ 2.6 GHz CPU.
5.1 General Model Setup
5.1.1 Physical Settings
Figure 7 shows the chosen modelling setup in our simulations. The model domain consists of 1-D line elements along the x-axis. Although the model setup is general for diffusion-controlled systems, the parameters for Opalinus clay are given in Table 1. A sufficient domain length is chosen to neglect the influence of the outlet (closed) boundary onto the concentration profiles. It has been found that 40 m of length is enough to neglect this effect for both Cs and U. Note, however, that this may not be true for other radionuclides and/or different physical and geochemical conditions. In this case, the domain length should be adjusted accordingly.
FIGURE 7

1-D modelling setup for radionuclide migration assessment.
TABLE 1
| Parameter | Description | Unit | Value |
|---|---|---|---|
| ϕ | Porosity | - | 0.15 |
| D p | Pore diffusion coefficient | m2 s−1 | 1 × 10−10 |
| D eff | Effective diffusion coefficient | m2 s−1 | 1.5 × 10−11 |
| P | Pressure | atm | 1 |
| T | Temperature | C | 25 |
Physical parameters of Opalinus clay.
Besides the domain length, the mesh discretization plays a major role in the computational effort. Therefore, a compromise between model accuracy and CPU time must be taken into account when choosing the size of the mesh elements. In our model setup, a spatial discretization of 200 line elements with Δx = 0.2 m is chosen as a best compromise between accuracy and speed. The solution accuracy with the chosen mesh resolution has been verified by using a refined mesh with 400 line elements (Δx = 0.1) for each simulation. The results do not show significant differences between the chosen mesh and the refined mesh (see Supplementary Figure S4–S6 in the Supplementary Material). The line elements are further refined towards the inlet boundary (i.e., the zone with the highest concentration gradient) producing a non-uniform mesh. The minimum element size at the boundary results in Δx = 0.04 whereas the maximum size at the outlet boundary is Δx = 0.35 m.
The time discretization is another key factor that will have a significant influence, not only in the required computational effort, but on the produced migration results. Thus, it is necessary to design a time discretization scheme, that is, acceptably accurate within affordable runtime. We adopt the von Neumann stability criterion for diffusive transport to ensure solution accuracy, which is given bywhere Δx is the element size. Since our initial discretization (without refinement) is 0.2 m, the time step size used in our simulations is Δt = 0.22/(2 × 1 × 10−10) = 2 × 108 s ≈ 6.34 years. This means that a total of 157,680 time steps are needed to simulate a time span of 1 million years. Note that both the fully coupled (calling a geochemical solver) and surrogate (using a look-up table) approaches use the same time-stepping scheme. Therefore, the CPU time speed-up gained in the surrogate approach is entirely due to avoiding the calling of the geochemical solver.
5.1.2 Geochemical Conditions
The porewater composition of Opalinus clay (Águila et al., 2021), common for all the radionuclides simulations presented in this work, is listed in Table 2. The porewater composition corresponds to measurements from Opalinus clay samples from the Mont Terri URL (Pearson et al., 2003). The Cs and U concentrations are only applied as initial values for each corresponding simulation. This means that only single-radionuclide simulations are carried out. Further, the pE value of Table 2 is set as constant throughout the spatial and temporal domains.
TABLE 2
| Species (mol/kgw) | Value |
|---|---|
| 4.659 × 10−4 | |
| Ca2+ | 2.651 × 10−2 |
| Cl− | 3.058 × 10−1 |
| K+ | 1.631 × 10−3 |
| Mg2+ | 1.733 × 10−2 |
| Na+ | 2.447 × 10−1 |
| 1.417 × 10−2 | |
| Sr2+ | 4.577 × 10−4 |
| pH | 7.6 |
| pE | −2 |
| Cs+ | 1.019 × 10−10 |
| Utotal | 2.549 × 10−9 |
Porewater composition of Opalinus clay. Cs and U values are background concentrations that are only applied for the corresponding radionuclide migration simulation.
As mentioned, the only processes affecting the geochemical composition of the Opalinus clay porewater are the sorption processes, whether via surface complexation or cation exchange, and the aqueous complexation reations. With this, we aim to focus on the main process (i.e., sorption) that affects the mobility of radionuclides. This, however, does not mean that more processes cannot be included in the model. OGS-6#iPHREEQC provides an interface to incorporate geochemical processes such as mineral dissolution/precipitation via equilibrium or kinetic reactions (Poonoosamy et al., 2022). Further, it is possible to capture the effect of changes in the pore space due to chemical reactions and its effect over the diffusion properties of the medium, which would, in turn, have a significant effect on the mobility of radionuclides (Lu et al., 2022).
5.2 Caesium
The isotope 135Cs is a long-lived radionuclide with a half-life of 2.3 × 106 years (Nagra, 2002). Because of the large half-life of 135Cs, radioactive decay is not considered. Recall that the migration assessment is typically done for one million years. The migration of Cs in Opalinus clay is simulated first with OGS#iPHREEQC using fully coupled chemistry (i.e., multi-species concept). Then, a surrogate-based simulation by adopting the single-species concept is performed. The surrogate model is implemented by replacing the expensive chemical calculations with a pre-calculated look-up table to quickly estimate the sorption behavior of Cs. The migration results for one million years are shown in Figure 8. Details about the Cs sorption model in Opalinus clay (cation exchange) can be found in (Águila et al., 2021) and the input parameters are summarized in Table 3. Note that the sorption of Cs is modeled by defining a SURFACE through the iPHREEQC module. Furthermore, the local mass imbalance error (i.e., in terms of the molar flow rate) is calculated node-by-node and shown in Supplementary Figure S1, S2 of the Supplementary Information. The calculated local mass imbalance error is negligibly small, thus ensuring that mass is locally conserved in our simulations.
FIGURE 8

Migration behavior of Cs in Opalinus clay for 1 million years using fully coupled chemistry and the look-up table approach. (A) Comparison of concentration profiles along the domain and (B) breakthrough curves for low and high concentrations at the inlet boundary.
TABLE 3
| Site name | Description | Capacity (mol/kgw) |
|---|---|---|
| Su_ | Double layer planar sites | 1.425 |
| Su_ii | Type II sites of intermediate strength | 1.38 × 10−1 |
| Su_fes | Frayed edge sites | 1.8 × 10−3 |
Sorption data for Caesium (Águila et al., 2021).
For this specific case, two Cs concentrations applied at the inlet boundary: 1) 1 × 10−7 mol kgw−1 and 2) 1 × 10−3 mol kgw−1 (i.e., low and high concentrations) to demonstrate the capabilities of the LT approach. As discussed in (Águila et al., 2021), possible high concentrations of Cs in the porewater may be poorly handled by the single-species approach, where instead, a more complex chemical model is necessary to capture the higher non-linearity of the sorption behaviour. Therefore, we verify that the LT approach handles the higher inlet concentration well, as shown in Figure 8. In general, the results using the LT approach show good agreement for both low and high inlet concentrations when compared to the full chemical model. However, it is observed that a much higher number of LT points is necessary when applying the high inlet boundary concentration. This is expected due to the higher concentration gradient produced by the increased inlet concentration.
It is expected that the higher number of LT points will increase the CPU time. This is produced by the look-up algorithm having to go through a higher number of entries in the table. However, even for a “dense” table (96 points), the CPU time is greatly reduced in comparison to the full chemistry approach. Recall that a “96 points” table is actually a tabular file with 96 × 96 + 2 × 96 + 1 = 9409 rows. However, it could be safely assumed that, even for an extremely high number of points, the LT algorithm is tractable (within memory limits). On the other hand, requiring a high number of points (e.g., > 500) may be an indication that the single species approach may not reproduce the same geochemical conditions, possibly because additional variables (e.g., dissolved species, pH, pE) may be influenced by the mobile radionuclide. In such case, more variables can be added to the look-up table, however, as mentioned earlier, this could significantly reduce the speed-up gained in comparison to the full chemistry approach.
5.3 Uranium
The sorption model for Uranium is taken from (Hennig et al., 2020). The isotope of Uranium 238U has, in particular, a long half-life of 4.5 × 109 years. Therefore, similar to the Cs migration scenario, no radioactive decay is considered in the simulations. The surface complexation model is comprised of 7 different sorption sites corresponding to distinct clay minerals present in Opalinus clay, as shown in Table 4. This SCM model is added to the selected chemical thermodynamic database (i.e., PSI/Nagra). More details about the addition of a SCM to the database can be found in the PHREEQC documentation (Parkhurst and Appelo, 2013). Then, the information of Table 4 is passed to OGS-6#iPHREEQC through the use of the <chemical_system> and <media> keywords. The input of these parameters can be found in the corresponding OGS project file in the OGS6@Jupyter notebook. Similar to the previous case, the nodal molar flow rate is calculated as shown in Supplementary Figure S3 of the Supplementary Information. The calculated molar flow rate is negligible as well.
TABLE 4
| Site name | Description | Capacity (mol/kgw) |
|---|---|---|
| Ill_wOH | Illite weak site | 6.254 × 10−1 |
| Ill_sOH | Illite strong site | 1.384 × 10−2 |
| Kln_aOH | Kaolinite Aluminol site | 7.351 × 10−2 |
| Kln_siOH | Kaolinite Silanol site | 7.351 × 10−2 |
| Mll_wOH | Montmorillonite weak site | 1.137 × 10−1 |
| Mll_sOH | Montmorillonite strong site | 2.516 × 10−3 |
| ChlOH | Chlorite | 9.414 × 10−3 |
Sorption data for Uranium (Hennig et al., 2020).
Figure 9 shows the Uranium migration results. Analogous to the Caesium case, the reactive transport model was simulated via 1) a multi-species approach with the mechanistic sorption model in OGS-6#iPHREEQC and 2) a single-species approach by replacing the geochemical calculations with a look-up table in OGS-6-LT. As it will be discussed later, several simulations of the look-up table approach were done by using tables with different numbers of discretization points. However, only the best-fitting simulation result is shown in Figure 9.
FIGURE 9
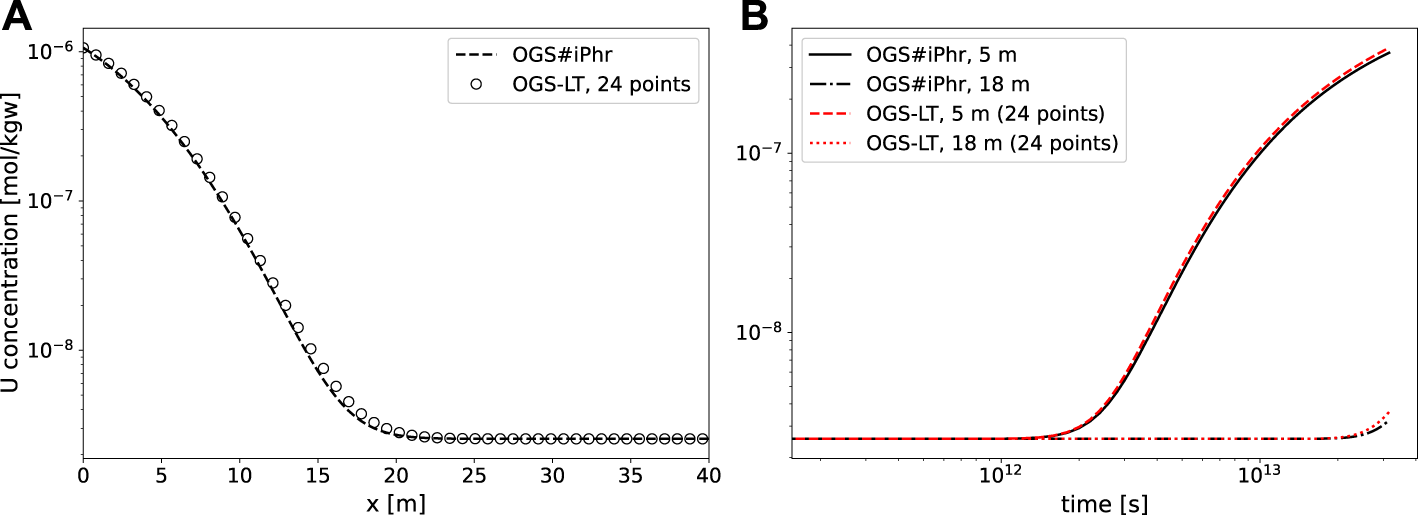
Migration behavior of U in Opalinus clay for 1 million years using fully coupled chemistry and the look-up table approach. (A) Concentration profile along the domain and (B) breakthrough curve.
The migration of Uranium shows a significant breakthrough at a distance of up to approximately 20 m. This is consistent with previously reported results (Hennig et al., 2020). After obtaining the results with the multi-species approach, the look-up table is constructed using the same sorption model. Then, OGS-6-LT can be used to simulate the migration through the single-species approach. The results shown in Figure 9 confirm a good agreement between the multi and single species approach for a look-up table with 12 discretization points. Note that a higher number of points in the table are needed for this case with respect to the Caesium migration. This could be explained by the higher inlet concentration applied in comparison with the lower concentration of Cs at the inlet boundary, as well as the more complex sorption model. CPU times of both the OGS-6#iPHREEQC and OGS-6-LT approaches are shown in Table 5.
TABLE 5
| Radionuclide | OGS-LT, 6 points | 12 | 24 | 48 | 96 | 192 | 384 |
|---|---|---|---|---|---|---|---|
| Cs | 351.9 | 322.01 | 260.62 | 201.94 | 143.55 | 62.75 | 32.06 |
| U | 521.44 | 467.91 | 385.77 | 288.2 | 207.17 | 92.81 | 46.99 |
Execution time speed-up comparison on a single core of the fully coupled and the look-up table simulations. Cs and U simulation times using the fully coupled approach are 83,400 and 123,060 s, respectively.
5.4 Performance of Surrogate-Based Models
A comparison of the CPU times, Mean Absolute Percentage Error MAPE and the Euclidean norm against the chosen points in the LT is shown in Figure 10, where A and F are the values obtained with the fully coupled and surrogate approach, respectively. It is clearly observed a strong correlation with the applied concentration at the inlet boundary and the number of LT points to achieve a low error. After 12 LT points, both the Cs (lower inlet concentration) and U show diminishing returns in lowering the error compared to the full coupling. This is not the case for Cs at a higher inlet concentration. Even at 96 LT points (i.e., a “dense” LT), the measured error is still higher than the lowest amount of points for the lower inlet concentration case. A significant difference is observed when comparing the MAPE to the Euclidean norm. In Figure 10A, the MAPE shows the mean error over the entire domain. For the U case, a counter-intuitive pattern is observed when only considering the MAPE (i.e., the error decreases from 6 to 24 LT points to then increase slightly again at 48 LT points). However, the Euclidean norm, which considers the accumulated error, shows a consistent decreasing pattern the more look-up table points are used. This is produced because, at 48 points, the error is lower at the first portion of the domain, while having a larger error near the breakthrough zone. Furthermore, note that the high MAPE for the U case at 6 LT points (143%) results from the overshooting the fully coupled profile, for which the MAPE is very sensitive. More details about each simulation using the look-up table approach can be found in Supplementary Figure S7–S9 of the supplementary material accompanying this paper.
FIGURE 10

(A) Mean Absolute Percentage Error and (B) Euclidean norm of the concentration profiles of Cs and U for increasing look-up table points used in the OGS-LT simulations against the fully coupled simulation results.
It is important to note that the much higher CPU performance of the surrogate models could enable statistical simulations, were thousands of scenarios could be simulated, which would be prohibitive with the full coupling. Thus, choosing a reasonable compromise between CPU time and accuracy is relevant. Table 5 shows the execution speed-up obtained with the fully coupled and the LT simulations. A maximum speed-up (not considering the CPU efficiency) of 521 is attained with the smallest LT (6 points) for the U simulation. This is because the fully coupled U simulation needs more CPU time due (123060 s) in comparison to the Cs simulation (83400 s) due to more computation time required by the chemical solver. Since the LT approach performs the same calculation regardless of the radionuclide, the speed-up gained in the U simulation using the LT approach is better. The LT CPU time for the cases with less table points is around 0.2% of the full coupling total time. This roughly corresponds to the time needed to the conservative simulation when the iPHREEQC module is not called at each time step.
On the other hand, recall that our simulation setup employs a 1D domain. OGS is capable of modelling reactive transport in 2D and 3D. However, the computational cost (mostly dictated by the number of elements in the mesh) can become prohibitive depending on the chosen time-space discretization. For instance, in our 1D simulations, 400 batch calculations are done per time step (one for each integration point in the 200 elements mesh). This is because OGS uses a novel integration-point operator-splitting approach (Lu et al., 2022). Each time-step needs around 0.4 s (Cs case). Therefore, each batch calculation takes around 0.001 s to compute. By neglecting the time needed for the transport stage (usually, 99% of the total CPU time is used by the chemical solver), we estimate that a 2D model with a 40 × 40 m size with a 0.2 m resolution would need roughly 146 days to simulate for 1 million years. In the 3D case, we estimate a staggering 14600 days of CPU time. This is, of course, extremely prohibitive. In such cases, a coarser time-space discretization would be necessary. On the other hand, the LT approach can help to overcome the unfeasible CPU times for the 2D and 3D cases. As we have shown in Table 5, a speed-up of 385 with an acceptable error (24 LT points) is attained for the Cs case. Therefore, a 3D case would become feasible ( ≈ 40 days) in an extremely large mesh (8 million elements), highlighting the potential application of the LT approach. Moreover, recall that our simulations have been computed on a single CPU. This means that the computational cost can be further reduced by employing HPC in a cluster system, where speed-up gains can become even more significant.
6 Conclusions and Outlook
In this work, a framework for reactive transport modelling has been implemented by integrating OGS and Jupyter into a simulation tool. Further, the computational framework has been cast in the form of a software container (i.e., OGS6@Jupyter) that guarantees that all the source code and its dependencies can be executed efficiently and reliably, independent of any computing environment. On the one hand, by employing this so-called containerization approach, we aim to provide a secure and reproducible platform for radionuclide migration assessments. On the other hand, a key advantage of our proposed framework is that OGS, the main component of the software container, is an open-source code. In this way, OGS can be integrated seamlessly into the computational framework. Moreover, the open-source nature of the framework and the availability of the OGS@Jupyter container allows for a community-based development, as well as the incorporation of additional software packages on-demand. We believe that this is relevant in the context of radionuclide migration assessments in potential nuclear waste repositories. This is because, one important aspect of such assessments, is the numerical simulation of the long-term migration of radionuclies (which is what has been demonstrated in this work). Moreover, the results of these simulations should be made available in a transparent way for both technical and non-technical audiences. In this work, we attempt to provide an environment, that is, highly efficient, easy to use, and has the potential to be expanded.
The demonstration of our framework is done by the numerical modelling of the migration behaviour of two radionuclides (Cs and U). Both cases are simulated under the same physical and geochemical conditions (i.e., Opalinus clay). The first case simulates the migration of Cs under two scenarios of low and high inlet concentrations. Diffusion of up to 12 m is observed considering the high concentration inlet scenario. However, it is likely that much lower concentrations of Cs occur in the event of release from the waste canister (Águila et al., 2021). In the case of a low inlet concentration, the observed diffusion only shows significant breakthrough at around 3 m. Furthermore, simulations are carried out by employing a multi-species (i.e., mechanistic) concept with a complex chemical system and a single-species concept by replacing the geochemical calculations with a surrogate modelling approach (i.e., look-up table). The results of the surrogate models agree well with the mechanistic approach at a highly reduced computational time (up to 500 times faster). However, for coarser surrogate models (i.e., sparse look-up tables), the approach does not capture the non-linear sorption behavior well, specially for higher concentration gradients. Therefore, a compromise between accuracy and speed when employing the look-up table approach must be considered.
The second case is devoted to the migration assessment of U. Our results confirm the migration of Uranium under similar conditions in Opalinus clay for up to 20 m after 1 million years (Hennig et al., 2020). Recall that the assumption of a constant inlet concentration of U is a simplification of both modelling approaches. However, this simplification can be interpreted as a conservative modelling choice that would produce maximum migration lengths. In a similar way as done for Cs, the model is simulated using mechanistic and single-species concepts. A minimum mean absolute error percentage of 6% is observed when using a higher-fidelity surrogate model (i.e., a high number of points in the look-up table). In contrast, a lower error of 2.6% is achieved for the surrogate model of Cs. This is an indication that the geochemical behaviour of U is distinctively different than that of Cs, even though similar modelling approaches are used. Furthermore, the differences between the cases highlight the need of a tailored modelling approach for individual radionuclides, even when surrogate models are employed.
Finally, we expect that our proposed framework can be used to incorporate the complete spectrum of radionuclides in a nuclear waste repository. Long-lived radionuclides such as radioactive isotopes of Selenium, Thorium, or Neptunium (Nagra, 2002), to name a few, can be added as more understanding of their migration on clay rocks is being gained. On the other hand, we are aware that considering a homogeneous porous medium in our modelling approach is not able to approximate more realistic conditions in a repository. As discussed, the multi-barrier disposal cell is comprised by several layers of materials with different physical and chemical properties (e.g., steel, buffer, concrete). Moreover, it is known that the properties of the multi-barrier system will be drastically affected over long-time periods due to large chemical gradients induced at different stages in their evolution. Furthermore, the non-decaying single radionuclide assessment posed in this work can be extended to consider decay chains, as well as competitive sorption of multiple radionuclides onto the available surface sites. With this work, we hope to provide a framework that can be used in a wide range of modelling scenarios to gain better understanding of radionuclies migration in the context of nuclear waste repositories.
Statements
Data availability statement
The dataset (DOI: 10.5281/zenodo.6614860) and code to reproduce the results of this work can be found at the following URL: https://zenodo.org/record/6614860#.YpzJDt-xVEY.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
We deeply acknowledge the funding of the iCROSS-Project (Integrity of nuclear waste repository systems—Cross-scale system understanding and analysis) by the Federal Ministry of Research and Education (grant number 02NUK053E, gefördert vom BMBF) and Helmholtz Association (Helmholtz-Gemeinschaft e.V.) through the Impulse and Networking Funds (grant number SO-093). This work is also contributing to the European Joint Programme on Radioactive Waste Management EURAD (grant number 847593), specially the WP for DONUT.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2022.919541/full#supplementary-material
Footnotes
1.^Container usage information: https://www.opengeosys.org/docs/userguide/basics/jupyter-notebooks
2.^OGS Container Maker README: https://gitlab.opengeosys.org/ogs/container-maker/-/blob/main/README.md
References
1
Águila J. F. Montoya V. Samper J. Montenegro L. Kosakowski G. Krejci P. et al (2021). Modeling Cesium Migration through Opalinus Clay: a Benchmark for Single- and Multi-Species Sorption-Diffusion Models. Comput. Geosci.25, 1405–1436. 10.1007/s10596-021-10050-5
2
Alnæs M. Blechta J. Hake J. Johansson A. Kehlet B. Logg A. et al (2015). The Fenics Project Version 1.5. Archive Numer. Softw.3. 10.11588/ans.2015.100.20553
3
Appelo C. A. J. Postma D. (2004). Geochemistry, Groundwater and Pollution. Boca Raton, Florida, USA: CRC Press.
4
Appelo C. A. J. Vinsot A. Mettler S. Wechner S. (2008). Obtaining the Porewater Composition of a Clay Rock by Modeling the in- and Out-Diffusion of Anions and Cations from an In-Situ Experiment. J. Contam. Hydrology101, 67–76. 10.1016/j.jconhyd.2008.07.009
5
Appelo C. A. J. Wersin P. (2007). Multicomponent Diffusion Modeling in Clay Systems with Application to the Diffusion of Tritium, Iodide, and Sodium in Opalinus Clay. Environ. Sci. Technol.41, 5002–5007. 10.1021/es0629256
6
Archie G. E. (1942). The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME146, 54–62. 10.2118/942054-g
7
Bear J. Bachmat Y. (2012). Introduction to Modeling of Transport Phenomena in Porous Media, Vol. 4. Berlin, Germany: Springer Science & Business Media.
8
Bear J. Corapcioglu M. Y. (2012). Advances in Transport Phenomena in Porous Media, Vol. 128. Berlin, Germany: Springer Science & Business Media.
9
Berner U. Kulik D. A. Kosakowski G. (2013). Geochemical Impact of a Low-Ph Cement Liner on the Near Field of a Repository for Spent Fuel and High-Level Radioactive Waste. Phys. Chem. Earth, Parts A/B/C64, 46–56. 10.1016/j.pce.2013.03.007
10
[Dataset] Bilke L. (2022). ufz/ogs-container-maker: 2.3.5 (2.3.5). Zenodo. 10.5281/zenodo.6303119
11
Bilke L. Flemisch B. Kalbacher T. Kolditz O. Helmig R. Nagel T. (2019). Development of Open-Source Porous Media Simulators: Principles and Experiences. Transp. Porous Med.130, 337–361. 10.1007/s11242-019-01310-1
12
Bossart P. Bernier F. Birkholzer J. Bruggeman C. Connolly P. Dewonck S. et al (2018). Mont Terri Rock Laboratory, 20 Years of Research: Introduction, Site Characteristics and Overview of Experiments. Mont Terri Rock Laboratory, 20 Years. Berlin, Germany: Springer, 3–22.
13
Bossart P. Meier P. M. Moeri A. Trick T. Mayor J.-C. (2002). Geological and Hydraulic Characterisation of the Excavation Disturbed Zone in the Opalinus Clay of the Mont Terri Rock Laboratory. Eng. Geol.66, 19–38. 10.1016/S0013-7952(01)00140-5
14
Boulton J. (1978). Management of Radioactive Fuel Wastes: The Canadian Disposal Program. Tech. Rep. Chalk River, Canada: Atomic Energy of Canada Ltd.
15
Bradbury M. H. Baeyens B. (2005). Experimental Measurements and Modeling of Sorption Competition on Montmorillonite. Geochimica Cosmochimica Acta69, 4187–4197. 10.1016/j.gca.2005.04.014
16
Buchwald J. Kolditz O. Nagel T. (2021). Ogs6py and Vtuinterface: Streamlining Opengeosys Workflows in python. Joss6, 3673. 10.21105/joss.03673
17
Cao X. Zheng L. Hou D. Hu L. (2019). On the Long-Term Migration of Uranyl in Bentonite Barrier for High-Level Radioactive Waste Repositories: The Effect of Different Host Rocks. Chem. Geol.525, 46–57. 10.1016/j.chemgeo.2019.07.006
18
[Dataset] Davies C. Association I. (1962). Ion Association. London: Butterworths.
19
De Windt L. Pellegrini D. Van Der Lee J. (2004). Coupled Modeling of Cement/Claystone Interactions and Radionuclide Migration. J. Contam. Hydrology68, 165–182. 10.1016/S0169-7722(03)00148-7
20
Dzombak D. A. Morel F. M. (1991). Surface Complexation Modeling: Hydrous Ferric Oxide. Hoboken, NJ, USA: John Wiley & Sons.
21
Ewing R. C. (2015). Long-Term Storage of Spent Nuclear Fuel. Nat. Mater14, 252–257. 10.1038/nmat4226
22
Gaines G. L. Jr Thomas H. C. (1953). Adsorption Studies on Clay Minerals. Ii. A Formulation of the Thermodynamics of Exchange Adsorption. J. Chem. Phys.21, 714–718. 10.1063/1.1698996
23
Giffaut E. Grivé M. Blanc P. Vieillard P. Colàs E. Gailhanou H. et al (2014). Andra Thermodynamic Database for Performance Assessment: Thermochimie. Appl. Geochem.49, 225–236. 10.1016/j.apgeochem.2014.05.007
24
Hennig T. Stockmann M. Kühn M. (2020). Simulation of Diffusive Uranium Transport and Sorption Processes in the Opalinus Clay. Appl. Geochem.123, 104777. 10.1016/j.apgeochem.2020.104777
25
Hu Q.-H. Weng J.-Q. Wang J.-S. (2010). Sources of Anthropogenic Radionuclides in the Environment: A Review. J. Environ. Radioact.101, 426–437. 10.1016/j.jenvrad.2008.08.004
26
Huang Y. Shao H. Wieland E. Kolditz O. Kosakowski G. (2018). A New Approach to Coupled Two-phase Reactive Transport Simulation for Long-Term Degradation of Concrete. Constr. Build. Mater.190, 805–829. 10.1016/j.conbuildmat.2018.09.114
27
Huang Y. Shao H. Wieland E. Kolditz O. Kosakowski G. (2021). Two-phase Transport in a Cemented Waste Package Considering Spatio-Temporal Evolution of Chemical Conditions. npj Mater Degrad.5, 4. 10.1038/s41529-021-00150-z
28
Hyman J. D. Karra S. Makedonska N. Gable C. W. Painter S. L. Viswanathan H. S. (2015). Dfnworks: A Discrete Fracture Network Framework for Modeling Subsurface Flow and Transport. Comput. Geosciences84, 10–19. 10.1016/j.cageo.2015.08.001
29
Idiart A. Laviña M. Kosakowski G. Cochepin B. Meeussen J. C. L. Samper J. et al (2020). Reactive Transport Modelling of a Low-Ph Concrete/Clay Interface. Appl. Geochem.115, 104562. 10.1016/j.apgeochem.2020.104562
30
Jobmann M. Bebiolka A. Burlaka V. Herold P. Jahn S. Lommerzheim A. et al (2017). Safety Assessment Methodology for a German High-Level Waste Repository in Clay Formations. J. Rock Mech. Geotechnical Eng.9, 856–876. 10.1016/j.jrmge.2017.05.007
31
Kirkner D. J. Reeves H. (1988). Multicomponent Mass Transport with Homogeneous and Heterogeneous Chemical Reactions: Effect of the Chemistry on the Choice of Numerical Algorithm: 1. Theory. Water Resour. Res.24, 1719–1729. 10.1029/WR024i010p01719
32
Kluyver T. Ragan-Kelley B. Pérez F. Granger B. Bussonnier M. Frederic J. et al (2016). “Jupyter Notebooks - a Publishing Format for Reproducible Computational Workflows,” in Positioning and Power in Academic Publishing: Players, Agents and Agendas. Editors Loizides,F.ScmidtB. (Amsterdam, Netherlands: IOS Press), 87–90.
33
Kolditz O. Bauer S. Bilke L. Böttcher N. Delfs J. O. Fischer T. et al (2012). Opengeosys: An Open-Source Initiative for Numerical Simulation of Thermo-Hydro-Mechanical/chemical (Thm/c) Processes in Porous Media. Environ. Earth Sci.67, 589–599. 10.1007/s12665-012-1546-x
34
Kosakowski G. Berner U. (2013). The Evolution of Clay Rock/cement Interfaces in a Cementitious Repository for Low- and Intermediate Level Radioactive Waste. Phys. Chem. Earth, Parts A/B/C64, 65–86. 10.1016/j.pce.2013.01.003
35
Kosakowski G. Watanabe N. (2014). Opengeosys-gem: a Numerical Tool for Calculating Geochemical and Porosity Changes in Saturated and Partially Saturated Media. Phys. Chem. Earth, Parts A/B/C70-71, 138–149. 10.1016/j.pce.2013.11.008
36
Leupin O. X. Van Loon L. R. Gimmi T. Wersin P. Soler J. M. (2018). Exploring Diffusion and Sorption Processes at the Mont Terri Rock Laboratory (switzerland): Lessons Learned from 20 Years of Field Research. Mont Terri Rock Laboratory, 20 Years. Berlin, Germany: Springer, 393–405. 10.1007/978-3-319-70458-6_21
37
Li D. Bauer S. Benisch K. Graupner B. Beyer C. (2014). Opengeosys-Chemapp: a Coupled Simulator for Reactive Transport in Multiphase Systems and Application to Co2 Storage Formation in Northern germany. Acta Geotech.9, 67–79. 10.1007/s11440-013-0234-7
38
Lu C. Samper J. Fritz B. Clement A. Montenegro L. (2011). Interactions of Corrosion Products and Bentonite: An Extended Multicomponent Reactive Transport Model. Phys. Chem. Earth, Parts A/B/C36, 1661–1668. 10.1016/j.pce.2011.07.013
39
Lu R. Nagel T. Poonoosamy J. Naumov D. Fischer T. Montoya V. et al (2022). A New Operator-Splitting Finite Element Scheme for Reactive Transport Modeling in Saturated Porous Media. Comput. Geosciences163, 105106. 10.1016/j.cageo.2022.105106
40
Marty N. C. M. Fritz B. Clément A. Michau N. (2010). Modelling the Long Term Alteration of the Engineered Bentonite Barrier in an Underground Radioactive Waste Repository. Appl. Clay Sci.47, 82–90. 10.1016/j.clay.2008.10.002
41
Mazurek M. Alt-Epping P. Bath A. Gimmi T. Niklaus Waber H. Buschaert S. et al (2011). Natural Tracer Profiles across Argillaceous Formations. Appl. Geochem.26, 1035–1064. 10.1016/j.apgeochem.2011.03.124
42
Mazurek M. (2010). Far-field Process Analysis and Radionuclide Transport Modelling in Geological Repository Systems. Geol. Repos. Syst. Safe Dispos. Spent Nucl. Fuels Radioact. Waste2010, 222–257. 10.1533/9781845699789.2.222
43
Metz V. Geckeis H. González-Robles E. Loida A. Bube C. Kienzler B. (2012). Radionuclide Behaviour in the Near-Field of a Geological Repository for Spent Nuclear Fuel. Radiochim. Acta100, 699–713. 10.1524/ract.2012.1967
44
Miron G. (2021). Psi Chemical Thermodynamic Database 2020 in Phreeqc Format. Villigen: Nagra
45
Mon A. Samper J. Montenegro L. Naves A. Fernández J. (2017). Long-Term Non-Isothermal Reactive Transport Model of Compacted Bentonite, Concrete and Corrosion Products in a Hlw Repository in Clay. J. Contam. Hydrology197, 1–16. 10.1016/j.jconhyd.2016.12.006
46
Montoya V. Noseck U. Mattick F. Britz S. Blechschmidt I. Schäfer T. (2022). Radionuclide Geochemistry Evolution in the Long-Term In-Situ Test (Lit) at Grimsel Test Site (switzerland). J. Hazard. Mater.424, 127733. 10.1016/j.jhazmat.2021.127733
47
[Dataset] Nagra (2002). Project Opalinus Clay - Safety Report. Nagra Technical Report, Ntb 02-05. Wettingen: Nagra
48
Parkhurst D. L. Appelo C. A. J. (2013). Description of Input and Examples for Phreeqc Version 3—a Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. U. S. Geol. Surv. Tech. methods6, 497.
49
Pearson F. Arcos D. Bath A. Boisson J. Fernández A. Gaebler H. et al (2003). Mont Terri Project - Geochemistry of Water in the Opalinus Clay Formation at the Mont Terri Rock Laboratory-Synthesis Report. Bern, Switzerland: Federal Office for Water and Geology, FOWG.
50
Pfeiffer W. Graupner B. Bauer S. (2016). The Coupled Non-isothermal, Multiphase-Multicomponent Flow and Reactive Transport Simulator Opengeosys–Eclipse for Porous Media Gas Storage. Environ. Earth Sci.75, 1–15. 10.1007/s12665-016-6168-2
51
Poonoosamy J. Lu R. Lönartz M. I. Deissmann G. Bosbach D. Yang Y. (2022). A Lab on a Chip Experiment for Upscaling Diffusivity of Evolving Porous Media. Energies15, 2160. 10.3390/en15062160
52
Sellin P. Leupin O. X. (2013). The Use of Clay as an Engineered Barrier in Radioactive-Waste Management - a Review. Clays Clay Min.61, 477–498. 10.1346/CCMN.2013.0610601
53
Shao H. Kosakowski G. Berner U. Kulik D. A. Mäder U. Kolditz O. (2013). Reactive Transport Modeling of the Clogging Process at Maqarin Natural Analogue Site. Phys. Chem. Earth, Parts A/B/C64, 21–31. 10.1016/j.pce.2013.01.002
54
Soler J. M. Samper J. Yllera A. Hernández A. Quejido A. Fernández M. et al (2008). The Di-b In Situ Diffusion Experiment at Mont Terri: Results and Modeling. Phys. Chem. Earth, Parts A/B/C33, S196–S207. 10.1016/j.pce.2008.10.010
55
Soler J. M. Steefel C. I. Gimmi T. Leupin O. X. Cloet V. (2019). Modeling the Ionic Strength Effect on Diffusion in Clay. The Dr-A Experiment at Mont Terri. ACS Earth Space Chem.3, 442–451. 10.1021/acsearthspacechem.8b00192
56
Steefel C. DePaolo D. Lichtner P. (2005). Reactive Transport Modeling: An Essential Tool and a New Research Approach for the Earth Sciences. Earth Planet. Sci. Lett.240, 539–558. 10.1016/j.epsl.2005.09.017
57
Steefel C. I. Lasaga A. C. (1994). A Coupled Model for Transport of Multiple Chemical Species and Kinetic Precipitation/dissolution Reactions with Application to Reactive Flow in Single Phase Hydrothermal Systems. Am. J. Sci.294, 529–592. 10.2475/ajs.294.5.529
58
[Dataset] Thoenen T. Hummel W. Berner U. Curti E. (2014). The Psi/nagra Chemical Thermodynamic Database 12/07. Villigen: Nagra
59
[Dataset] Thoenen T. Hummel W. (2021). The Psi Chemical Thermodynamic Database 2020. Wettingen: Nagra
60
Van Loon L. R. Soler J. M. Bradbury M. H. (2003). Diffusion of HTO, 36Cl- and 125I- in Opalinus Clay Samples from Mont Terri. Effect of Confining Pressure. J. Contam. Hydrology61, 73–83. 10.1016/S0169-7722(02)00114-6
61
Van Loon L. R. Wersin P. Soler J. M. Eikenberg J. Gimmi T. Hernán P. et al (2004). In-situ Diffusion of Hto, 22na+, Cs+ and I- in Opalinus Clay at the Mont Terri Underground Rock Laboratory. Radiochim. Acta92, 757–763. 10.1524/ract.92.9.757.54988
62
Vehmas T. Montoya V. Alonso M. C. Vašíček R. Rastrick E. Gaboreau S. et al (2020). Characterization of Cebama Low-Ph Reference Concrete and Assessment of its Alteration with Representative Waters in Radioactive Waste Repositories. Appl. Geochem.121, 104703. 10.1016/j.apgeochem.2020.104703
63
Wersin P. Van Loon L. R. Soler J. M. Yllera A. Eikenberg J. Gimmi T. et al (2004). Long-term Diffusion Experiment at Mont Terri: First Results from Field and Laboratory Data. Appl. Clay Sci.26, 123–135. 10.1016/j.clay.2003.09.007
Summary
Keywords
radionuclide diffusion, reactive transport modelling, look-up table, sorption, jupyter notebook
Citation
Garibay-Rodriguez J, Chen C, Shao H, Bilke L, Kolditz O, Montoya V and Lu R (2022) Computational Framework for Radionuclide Migration Assessment in Clay Rocks. Front. Nucl. Eng. 1:919541. doi: 10.3389/fnuen.2022.919541
Received
13 April 2022
Accepted
23 May 2022
Published
24 June 2022
Volume
1 - 2022
Edited by
David García, Amphos 21 (Spain), Spain
Reviewed by
Albert Nardi, Amphos 21 Consulting S.L., Spain
Maruti Kumar Mudunuru, Pacific Northwest National Laboratory (DOE), United States
Updates
Copyright
© 2022 Garibay-Rodriguez, Chen, Shao, Bilke, Kolditz, Montoya and Lu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jaime Garibay-Rodriguez, jaime.garibay-rodriguez@ufz.de
† Present Address: Vanessa Montoya, Engineered and Geosystems Analysis Unit, Waste & Disposal Expert Group, Institute for Environment, Health and Safety, Belgian Nuclear Research Centre (SCK CEN), Mol, Belgium
This article was submitted to Radioactive Waste Management, a section of the journal Frontiers in Nuclear Engineering
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.