A review of the oxygen vacancy ordering in surrogate structures simulating Pu-based nuclear ceramics

Advanced nuclear power systems and nuclear fuel cycles will require nuclear fuels capable of higher burnup and with higher transuranic concentrations than those previously developed for current nuclear power plants. Expensive qualification tests are required to validate the thermal and mechanical performance of fuels in normal and accident-scenario operations. Research of surrogate systems with specific properties and characteristics of advanced nuclear fuels can be an effective way to frame the problem, reduce costs, and support the technical development of future research. From this perspective, lanthanide counterparts like mixed oxides of Ce and Nd can provide replica systems for many technological properties of the actual fuels. These ceramic systems can lead to a better understanding of the fundamental irradiation processes responsible for the evolution of their microstructures, the interplay with charge and defect localisation, and the evolution of their mechanical properties. In non-stoichiometric MO_2−x binary systems (M = Ce, Pr, and Tb), there is evidence of systematic ordering of vacancies resulting in a deviation from the ideal fluorite structure and the formation of several intermediate fluorite-related phases. Substitution of the 4+ cations with 3+ cations in these systems drives the formation of oxygen vacancies as a charge compensation mechanism. By analogy with MO_2−x systems, a variety of similar intermediate phases would also be expected to form in the MO₂:Ln₂O₃ (Ln = La, Nd, Gd … etc). However, in order to achieve chemical homogeneity and charge ordering, prolonged annealing just above the charge ordering transition temperature is required, covering a time-scale determined by the chemical diffusion coefficient. Achieving these conditions with powder metallurgy techniques, commonly employed in literature, is practically impossible. This paper reviews the transport properties and structural features found in these surrogate systems which may be helpful in addressing challenges facing advanced nuclear fuels. We present results of a recent diffraction experiment investigating the structure of neodymium doped ceria synthesised using soft chemical methods. The sample shows a deviation from previous literature as the diffraction data is best described by a monoclinic Ln₆O₁₁-type structure (SG P2₁/c), often referred to as “β phase” in PrO_2−x.

1 Introduction

The design, fabrication, and performance of advanced nuclear fuels, particularly those containing a significant fraction of Pu and minor actinides, is a significant challenge that requires a fundamental understanding of the thermodynamics, transport, and chemical behavior of complex materials during processing and irradiation. An understanding of complex phenomena occurring in these systems is a requirement for building robust models of complex phenomena including transport and phase segregation. This knowledge will be a requirement for any large-scale fuel fabrication and performance calculations. Advanced fuels, waste forms, and separations technologies are highly interactive, multi-component systems. This entangled context is a challenging area in complexity, with broad implications across science and technology. Significantly, there is a substantial lack of knowledge on fundamental materials properties for unirradiated advanced actinide fuels. This situation is due to several reasons: the current experimental knowledge basis of the minor actinides is small, principally because there were no engineering needs in the past; experiments are inherently difficult because of their radiological constraints but also because the properties of these systems can change sharply with composition and experience internal decay heating; the mechanisms of radiation damage formation in ceramic fuels from elastic collisions with high-energy neutrons and from fission product recoils are not well understood. These constraints are therefore motivation for research of surrogate systems that can exhibit some of the relevant behaviours of the advanced fuels.

Like many major countries in the world trying to decarbonize their energy mix, the United Kingdom has plans to significantly accelerate the building of new nuclear reactors with a capacity of up to 25 GW by 2050 providing 25% of electricity. This has also led to the recent announcement of the building of the first new nuclear power station at Hinkley Point C in Somerset (Net Zero Strategy, 2021; British Energy Security Strategy, 2022). As part of this strategy, United Kingdom has plans to invest in High-Temperature Gas Cooled Reactors HTGR as advanced modular reactors. In addition to producing electricity from nuclear, these AMR’s are planned with the aim to clean hydrogen as well as heat that could be used by industries. The efficient operation of these new nuclear reactors requires the need to understand fuel performance as fission products and minor actinides like Pu build-up during reactor operation. In addition, energy from nuclear has always been plagued by poor public perception because of risks associated with the management of spent nuclear fuel and nuclear waste. Among various significant scientific and technological efforts made to underpin fundamental science backing these challenges, a science-based understanding of complex oxides comprising various lanthanides and actinides (including U and Pu) is key to building a new nuclear future.

Fission products produced during nuclear fission are not created equally, rather their distribution contains two peaks around Mo and Tc (A ≈ 91) and around Xe and lanthanides (A ≈ 142). Importantly many of the lanthanide elements (Pm, Sm, etc) are high-yield fission products. Solid fission products produced during fission ultimately end in one of three states within the nuclear fuel. Depending on the thermodynamic driving force for a particular reaction to occur across the range of temperatures relevant to the problem (operando conditions, storage, …), some elements quickly oxidise while others do not. Mo and Ru with minor amounts of Pd and Rh migrate to grain boundaries and form metallic phases. Other elements, including most of the lanthanide fission byproducts, have very low Gibbs energies of formation of oxides: they vigorously compete with the fuel for oxygen to form a solid solution within the oxide fuel matrix (Olander, 1976). Determining which state a species of fission product will ultimately end up in is possible by comparing the Gibbs formation energy of the fission product oxide with that of the fuel. Formation of these solid solutions has wide-ranging effects on both the structure and properties (mechanical, thermal, and transport) of the fuel and as such, it is important therefore to have a fundamental understanding of the consequences arising from the formation of these solid solutions.

Long-lived plutonium and minor actinides, although present in nuclear waste at relatively low concentrations, are associated with long-term radiotoxicity and are hazardous if released into the biosphere. These elements have a particular influence on the definition of the waste management framework (storage or longer-term disposal). In advanced nuclear fuels, the presence of these elements can represent a substantial fraction of the fuel. The behavior of these systems is also interesting for the fundamental chemical and structural properties of these elements. Materials such as Al₂O₃, MgO, CeO₂, MgAl₂O₄, Y₃Al₅O₁₂ and stabilized zirconia (ZrO₂:Y, YSZ) have been investigated in the past as host matrices for Pu and minor actinide incineration, either in solid solution or in dispersed form (Kleykamp, 1999). Indeed, YSZ and CeO₂ are some of the best candidates among the oxide-based materials considered as host matrices. Since Pu and minor actinides are highly radioactive and radiotoxic, they must be handled in glove boxes with particular care. In order to conduct fundamental research in this field, it is very important to use non-radioactive substitutes in place of these elements before carrying out actual experimentation on systems presenting radiological risks. Cerium dioxide can be used as a substitute material for plutonium oxide (Tyagi et al., 2002), while Neodymium oxide (Nd₂O₃) has been widely used as a simulant for two minor actinides, Americium (Am₂O₃) and Curium (Cm₂O₃) oxide (Williams et al., 2013). The reason for this choice is mainly attributed to the ionic radii and iso-structural crystal structures of the respective compounds in the solid state. CeO₂ was tested as an inert matrix component in the EFTTRA experiment (Konings et al., 1998). Similarly to its use as a plutonium surrogate, CeO₂ has been used as a surrogate for UO₂ in some research capacities (Sonoda et al., 2006; Stennett et al., 2013), however the situation is complicated by the ability of UO₂ to form hyperstoichiometric UO_2+x which CeO₂ cannot. Other materials used to simulate the properties of UO₂ include ZrO₂ (Kim et al., 2007) and HfO₂ (Tucker et al., 2015).

The phase stability of these complex oxides is also of interest when it comes to powering space systems using Radioisotope thermometric Generators (RTG) that utilise the decay from ²³⁸Pu. With the scarcity of ²³⁸Pu, the European Space Agency (ESA) is exploring other isotopes such as ²⁴¹Am in various fluorite-type mixed oxides phases. While the capability to handle Am-based oxides is limited, fundamental work on understanding the phase stability has heavily relied on the use of surrogates like CeO₂ and Nd₂O₃ to understand the behaviour of AmO₂ or PuO₂ and Am₂O₃ respectively (Watkinson et al., 2017; Vigier et al., 2018). Hence understanding the phase stability of complex oxides is key to various future nuclear technologies.

2 Pseudo-binary systems of cerium and lanthanide oxides

2.1 Mixed valence states of lanthanide oxides

The chemical properties of lanthanides are largely determined by their valence shell electrons. Most lanthanides are trivalent because the energy levels of 4f electrons have lower energies than those of the outer electrons, 5d6s2: typically, 4f radial functions are localized and they do not contribute actively to the bonding with other elements when an oxide is formed. This explains why most lanthanides are chemically similar, but some of them are notable exceptions: Hund’s rule states that empty, half-filled, and completely filled electronic levels are more stable configurations. Therefore, Ce⁴⁺ and Tb⁴⁺ can give up an f electron to achieve an empty and half-filled 4f level, respectively, whereas Eu²⁺ and Yb²⁺ would add an f electron to have a half-filled or completely filled 4f level, respectively. The same mechanism can explain the existence of mixed valence states involving the Pr⁴⁺ and Sm²⁺ ions, as observed for instance in compounds like Pr₆O₁₁.

2.2 Polymorphism of lanthanide oxides

All lanthanides can form a sesquioxide but, as for Ce at standard temperature and pressure, this may not be the stable equilibrium composition. There are five different polymorphs for the sesquioxide phases (Zinkevich, 2007), the phase diagram is illustrated in Figure 1: These are labeled as A, B, C, H, and X. The A-type polymorph (trigonal) exists for the light lanthanides (that also have larger ionic radii); they transform to the H-type polymorph (hezagonal) at higher temperatures, and then to the X-type (cubic) at even higher temperatures. The B-type polymorph (monoclinic) is characteristic of the middle lanthanides; they also transform to the H and X polymorph at high temperatures, near their melting point. The cubic C-type polymorph (also referred to by the corresponding mineral name, bixbyite) is encountered for heavy lanthanides. The C-type polymorph transforms to the B-type upon heating, and then to the H-type before melting. All these structures can be derived from the prototype fluorite phase (face-centered cubic) that is commonly observed in CeO₂ at room temperature and ambient oxygen partial pressure.

FIGURE 1

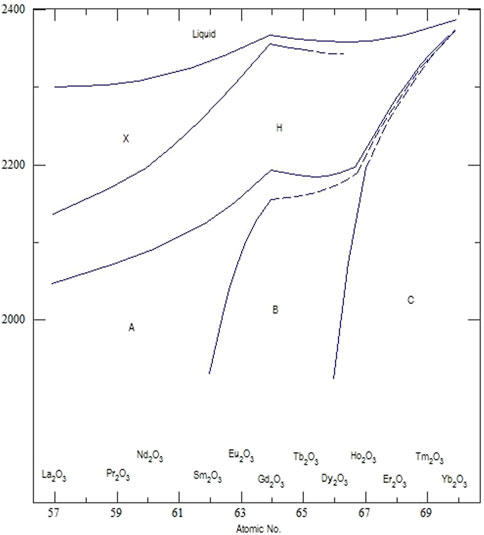
FIGURE 1. Phase diagram of the sesquioxide polymorphs with respect to the cation identity (Lopato et al., 1974). A-Type—Trigonal, B-type—Monoclinic, C-Type—Cubic, H-Type—Hexagonal and X-Type—Cubic.

At room temperature, the structure of Nd₂O₃ is typically reported as a trigonal A-type (space group $P\bar{3}m1$). However, metastable B-type or C-type structures are sometimes observed (Warshaw and Roy, 1961; Gasgnier et al., 1989). The fact that the transition from the A-type to other structures occurs near the Nd₂O₃ (Coutures et al., 1974) compounds might favour the observed metastability. Nevertheless, the A-type Nd₂O₃ polymorph is the thermodynamically stable polymorph at room temperature. At higher temperatures, Nd₂O₃ displays the same phase transition sequence observed in other light-lanthanide sesquioxides (La, Ce, and Pr).

Cerium, praseodymium, and terbium can form tetravalent or partially tetravalent oxides as CeO₂, Pr₆O₁₁, and Tb₄O₇. Since the free enthalpies of formation of the sesquioxides of these three elements are close to those of the respective higher oxides, a whole series of intermediate oxide phases is observed for these three compounds with stoichiometries LnO_x (1.5 < x < 2) that can be produced by controlling the temperature, oxygen pressure, and sometimes by quenching the sample. Further discussion of the structural features of the Ce-O phase diagram is carried out in Section 3.

2.3 Defect compensation in cerium dioxide

In any real crystal, at a sufficiently high temperature, there will be an equilibrium concentration of intrinsic (stoichiometric) defects within the crystal structure. In ionic solids, interstitial and vacancy defects are known as Frenkel and Schottky defects respectively. In fluorite structures, it is expected that the fraction of metal defects is negligible at any temperature (Catlow and Norgett, 1973). Metal Frenkel pairs, even just below the melting temperature, are typically two orders of magnitude smaller than those of anion defects. At high temperatures, though well below the melting temperature, the concentration of anion Frenkel pairs follows an Arrhenius regime, until a superionic transition occurs (Vlieg et al., 1986). As the fluorite structure is heated, it is then the anion that disorders and contributes to the increase of the ionic conductivity. Some of the oxygen ions move from their regular positions and occupy the empty octahedral positions. The redistribution of the fluorine ions with rising temperature causes an anomaly in the heat capacity.

The formation energies for each defect type in ceria are given in Table 1. From these formation energies, it can be seen that cation Frenkel defects are indeed unlikely to form in ceria, and anion Frenkel defects are the predominant mechanism for the intrinsic disorder. As a result, the cation sublattice is highly stable (Zhang and Hong, 2017). The anion Frenkel defects can be formally described by the following Kröger-Vink equation:

${\mathrm{O}}_O^X\leftrightarrow V_O^{••}+{\mathrm{O}}_i^{\prime \prime }(1)$

Where $O_O^X$ denotes an oxygen atom occupying an oxygen position in the lattice, $V_O^{••}$ an oxygen vacancy with a +2 charge (represented by ••) and $O_i^{\prime \prime }$ an oxygen interstitial with a −2 charge (represented by ′′). Between 450K and 1550K, CeO_2−x is a mixed n-type semiconductor where the conduction takes place by small-polaron transport. The ionic contribution to the total conductivity is quite low: in pure reduced ceria, at 1250K and at pO₂ ≈ 10^–6 atm, it is less than 3% of the total (Mogensen et al., 2000). In a simplified picture, the small polaron in bulk ceria is an electronic carrier, localized on the Ce atoms, that self-traps in the displacement field of the surrounding O atoms. The polaron (i.e., the electron-hole with the associated distortion field) migrates by a thermally activated hopping (Blumenthal and Panlener, 1970). Using the Kröger-Vink notation, the small polaron in CeO_2−x may thus be modeled as ${\mathrm{C}\mathrm{e}}_{Ce}^{\prime }$. It was later demonstrated by Shoko et al. (2010) that this simplified picture is not correct and that the excess electrons localize at cerium ions that are next nearest neighbors to the vacancies. The electronic conductivity of CeO_2−x shows a linear dependence on the value of x for x ≤ 0.05, then it saturates (Tuller and Nowick, 1977). With decreasing p_O2 (also by increasing temperature), oxygen vacancies form, requiring charge compensation by two electrons localized on trivalent cerium cations, the already discussed small polarons. This mecanism is effective over wide compositional range, producing a non-stoichiometric oxide CeO_2−x with 0 ≤ x < 0.5 (Reiss et al., 1988) and is described by Eq. 2:

$2{\mathrm{C}\mathrm{e}}_{Ce}^X+O_O^X\leftrightarrow 2{\mathrm{C}\mathrm{e}}_{Ce}^{\prime }+V_O^{••}+\frac{1}{2}{\mathrm{O}}_2(2)$

At lower deviations from stoichiometry, the formation of doubly charged oxygen vacancies is the dominant defect type. However, as this deviation increases and defect interactions start to occur, there is a transition to singly charged oxygen vacancies being the main defect type (Blumenthal et al., 1971; Tuller and Nowick, 1979). To summarize, much of the functional properties of ceria can be linked to the presence of oxygen vacancies, and among native defects in ceria, the oxygen vacancy is by far the most extensively studied and the most stable defect under a very broad set of conditions.

TABLE 1

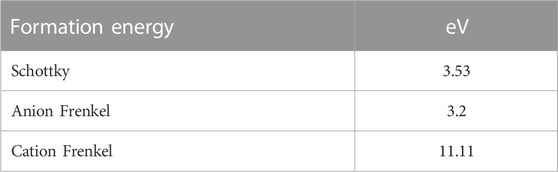
TABLE 1. Formation energies of intrinsic defects in CeO₂. Data obtained from (Minervini et al., 1999).

2.4 Charge compensation mechanisms in doped cerium dioxide

Doping CeO₂ with trivalent lanthanides, (e.g., Nd³⁺) causes Ce⁴⁺ ions to be substituted by Ln³⁺ ions. This substitution drives the formation of defects in the crystal in order to compensate for the charge difference between the ions and keep the crystal electrically neutral. Ikuma et al. (2005) investigated the predominant defects in the CeO₂-Nd₂O₃ system and through comparison of the theoretical density of cation interstitial and anion vacancy defect models against the measured density found that the anion vacancy model showed a similar trend of decreasing density with increasing Nd concentration, showing that anion vacancies are the main charge compensating defect formed when doping ceria with lower valency ions. The following quasi-chemical reaction describes the anion vacancy model in this case:

${\mathrm{N}\mathrm{d}}_2{\mathrm{O}}_3\leftrightarrow 2{\mathrm{N}\mathrm{d}}_{Ce}^{\prime }+3{\mathrm{O}}_O^X+V_O^{••}(3)$

While conductivity in undoped CeO_2−x is largely electronic due to the hopping of small polarons through the lattice, aliovalent doping with trivalent ions leads to a different situation where the conductivity becomes mainly ionic. The mechanism of ionic conduction in the system is the hopping of oxygen ions between the large concentrations of vacancies formed to compensate for the doping. One would expect the conductivity to rise monotonically with dopant concentration, as more doping creates more vacancies, which in turn allows for the easier transport of oxygen ions. However, when studying ionic conductivity in Ce_1−xSm_x${\mathrm{O}}_{2-\frac{x}{2}}$, Yahiro et al. (1988) found the ionic conductivity to rise rapidly for x < 0.1 then reaches a maximum and plateaus briefly at around x = 0.2 and then gradually decreases for x > 0.3. This behavior of increasing conductivity up to a critical dopant concentration, x_c, is observed for other rare earth elements, with the value for x_c generally falling between 0.06 < x_c < 0.2 depending on the dopant and the temperature of the system (Koettgen et al., 2018). This decrease in the ionic conductivity has been explained in terms of trapping of vacancies through defect ordering (Yamamura et al., 2007) and formation of the dopant-vacancy pair $[2{\mathrm{N}\mathrm{d}}^{\prime }:V_O^{••}]$ (Kilner, 1983) effectively removing a portion of the hopping sites for oxide ions, lowering the conductivity despite the increased concentration of vacancies introduced when doping.

2.5 Topological features of O vacancy clustering in Ln_nO_2n−2

(Ln = Ce, Tb, Pr) Tetrahedron-shaped building blocks are interesting enough by themselves, but under the right circumstances, we have discovered they do something remarkable. Under irradiation, these anion-centred building blocks demonstrate an unanticipated ability to re-arrange themselves into superstructures (Patel et al., 2020; Iwasaki et al., 2022). The changes promoted by irradiation can be understood as a first-order phase transition between two tetrahedral networks of different densities. It is interesting to observe that tetrahedra themselves are not chiral because they can be superimposed on their mirror images. The ι and C-type phases of lanthanide oxides are also non-chiral networks of tetrahedra (Figure 2).

FIGURE 2

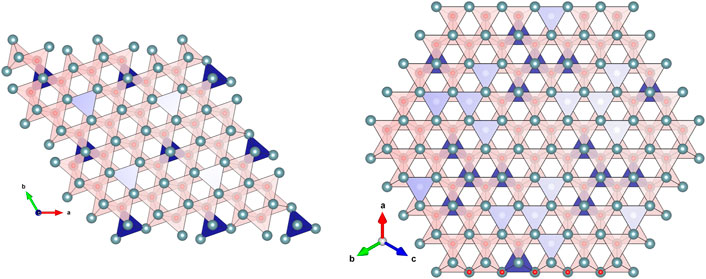
FIGURE 2. The ι phase (n = 7, Ln₇O₁₂) of mixed valence lanthanides like Ce, Pr, and Tb (left panel) is a three-dimensional stack of OLn₄ tetrahedra (red colour) linked together by 5 out of 6 edges. The blue-colour tetrahedra correspond to the positions of the O vacant sites. The C-type bixbyite phase of heavy lanthanides (n = 4, Ln₂O₃) is also a three-dimensional stack of OLn₄ tetrahedra but linked by 4 out of 6 edges. This demonstrates the two structures have identical connectivity and they can have interesting topological properties.

When these tetrahedra come together, they stack with their tips either up or down. As these blocks assemble, their corners (the metal ions) are shared. This configuration provides a dense packing compatible with the constraint of maintaining optimum cation-anion distances and leads to trigonal-domain formation. In the irradiation-induced transformation between the ι and C-type phases, the first neighbour distances are kept unchanged but a change of the tetrahedral networks takes place. From a topological perspective, this can be described as a transition between a disentangled, low-density configuration of empty tetrahedra (the isolated ones of the ι phase) and an entangled, high-density configuration of these empty tetrahedra that assemble in groups of 4, forming a more topologically complex motif.

The topological arrangement of the O vacancy clusters in the δ phase (Figure 3) is topologically equivalent to the one observed in the ι phase, though less dense and producing a stripe-like pattern that develops along the b axis of this monoclinic structure. The anisotropy of this organization of tetrahedra in stripes is nevertheless affected by the complex microdomain twinning of these phases produced by the ferroelastic nature of their relation to the parent prototype fluorite structure.

FIGURE 3

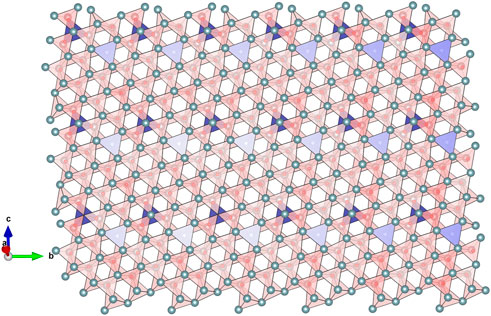
FIGURE 3. Representation of the three-dimensional stack of OLn₄ tetrahedra (red colour) in the δ phase (n = 11, Ln₁₁O₂₀ or LnO_1.818). The tetrahedra connectivity is topologically equivalent to the one observed in the ι phase (n = 7, Ln₇O₁₂) but the density of empty tetrahedra (blue colour ones) is lower. The correlation between empty tetrahedra is maintained along the b direction of Ln₁₁O₂₀ that roughly corresponds to the a direction of Ln₇O₁₂ (hexagonal setting). On the other hand, the correlation is different along the b direction of Ln₇O₁₂, forming a distinctive stripe-like pattern in Ln₁₁O₂₀.

These observations also apply to the β phase structure, where the stack of the empty tetrahedra describing the environments of the O vacancies is also anisotropic (see Figure 4).

FIGURE 4

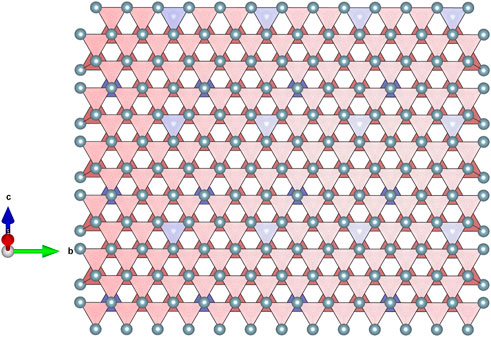
FIGURE 4. Representation of the three-dimensional stack of OLn₄ tetrahedra (red colour) in the β phase (n = 12, Ln₁₂O₂₂, or LnO_1.833). This is the first phase encountered during the reduction of LnO₂ fluorite systems. The tetrahedra connectivity is topologically equivalent to the one observed in the ι and δ phases (n = 7 and n = 11) but with a lower density. The correlation between empty tetrahedra (blue colour ones) is still more pronounced along the b direction, an anisotropic feature already observed for the δ phase.

Though the radiation stability of this structure is not well known, it forms during the irradiation of CeO₂ in the slightly reducing conditions of the secondary vacuum of the irradiation chamber (Cureton et al., 2018). This demonstrates the prominent tendency to the order of O vacancies, even in severe out-of-equilibrium conditions.

2.6 Structure metastability and kinetic effects

There is a considerable divergence in the results describing the fluorite-based phase diagrams, particularly evident in the assessment of the phase diagram of pure and aliovalent-doped zirconia. This problem is related to a variety of metastable structures and to the difficulty of reaching thermodynamic equilibrium conditions in experiments below 1500 K. While the phase stability between two competing structural organisations is driven by their free enthalpy difference, ΔG. Nevertheless, the actual free enthalpy barrier between the two phases is a factor of paramount importance when the polymorphic phase transition has martensitic or reconstructive character (for instance a change in the first sphere of coordination of the cations). The large hysteresis associated with the tetragonal to monoclinic phase transition in pure zirconia (Simeone et al., 2003) and hafnia is a clear illustration of this effect, more remarkable because these are diffusionless phase transitions.

The stabilization of a metastable organisation can be more severe in morphotropic phase transformations requiring cation diffusion because the local chemical cation composition strongly affects the local oxygen stoichiometry. In a diffusion process, the well-known relation $x=\sqrt{Dt}$ provides an estimate of the time interval t, in which the average atom travels over the distance x when D is the temperature-dependent diffusion coefficient. It is customary to suppose the temperature dependence of the diffusion coefficient for both cations and anions follows an Arrhenius law:

$D\left(T\right)=D_0\exp \left(-\frac{Q_m}{RT}\right)(4)$

The prefactor coefficient D₀ has about the same magnitude for anions and cations in fluorites (0.03–0.08 cm²s⁻¹, but, much more important, the migration enthalpy Q_m is much higher for cations (about 4 eV) than for anions (typically about 1.3 eV) (Ikuma et al., 1991).

Therefore, the diffusion rate of cations is very slow, as illustrated in Figure 5, whereas that of oxygen is so fast that most of these compounds can be used as oxygen-ion electrolytes in devices. In order to establish true phase equilibria at low temperatures in systems containing more than one cation, the production of ceramics using ordinary solid-state reactions should be avoided as it relies primarily upon atomic diffusion. In this context, the challenge is the possible existence of an ordering transition temperature for the metal ions sharing the same cation sublattice. Indeed, in some compounds, a cation selectivity for particular sites in the crystal structures is observed, an effect that also influences the final distribution of defects in the more mobile oxygen sublattice. Experimental evidence suggests this cation-ordering temperature below 1400 K (Garcia-Chain et al., 1994), well below any practical temperature where diffusion in that sublattice is effective. Therefore, the exploration of the phase diagrams of compositions involving more than one metal ion requires soft chemistry methods, where the desired homogeneity of the cation distribution over the relevant spatial scales does not rely upon diffusion but is achieved by the control at the nanoscale of the atomic distributions over the two sublattices of the structure.

FIGURE 5

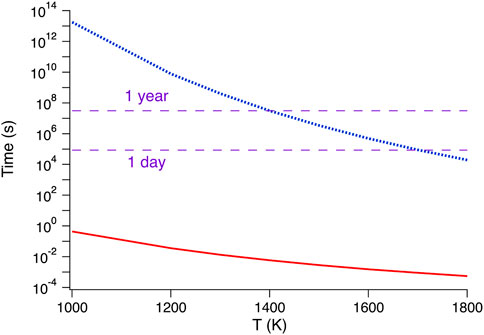
FIGURE 5. Comparison of the time interval of oxygen ions and cations required to diffuse over 1  μm at various temperatures, assuming typical values of fluorite structures: $D_0^{Ox}=0.08$ cm²s⁻¹ (red curve), $Q_m^{Ln}=1.3$ eV and $D_0^{Ox}=0.03$ cm²s⁻¹, $Q_m^{Ln}=4.0$ eV for cations (blue curve). It is worthy of notice that, at 1400 K, it takes 1 year for cations to diffuse over 1 μm, a characteristic length for functional properties; it takes about 1 day at 1700 K. Therefore, conventional annealing treatments below 1400 K cannot produce systems at thermodynamic equilibrium when the initial heterogeneity of the system is of the order of 1 μm.

Another factor preventing cation homogeneity at all scales is the effect of kinetic demixing. Kinetic demixing of a ternary solid solution oxide can occur over a few monolayers across an interface when the transport rates of the constituent oxides are different, provided that these different rates of diffusion are not limited by oxygen diffusion (Schmalzried et al., 1979). Fluorite structures where two aliovalent cations are present are therefore a typical case where the effect can be observed. Chemical demixing is driven by the existence of a stress gradient at the grain boundaries and interfaces, favouring stress-directed diffusion from regions in compression to regions in tension, until a sufficient concentration gradient builds up opposing further segregation. The effect produces a selective increase of the concentration of the trivalent metal ion that has a larger volume of the corresponding oxide in the topmost layers at the grain boundary, and the reverse effect on the monolayers immediately beneath the interface region. The spatial amplitude of this compositional fluctuation typically does not exceed the nanometer scale across the grain boundaries of the mixed oxides of lanthanides (Surble et al., 2008).

2.7 Soft chemistry processes to mitigate cation heterogeneity

Freeze drying (Shlyakhtina et al., 2004) and sol-gel syntheses (Livage and Sanchez, 1992) avoid long-range atomic diffusion processes and thus help maintain a homogeneous distribution of cations in the samples. Single crystals of mixed metal oxides with nanometric sizes can be prepared using freeze-drying methods or by sol-gel type syntheses. The nanocrystals thus obtained can have a controlled size (monodisperse), typically ranging from 2.5 to 25 nm. These sizes can be adjusted with controlled annealing of these systems. In addition, mesoporous thin films of metal oxides (these are systems consisting of a network of nanometric crystals intertwined with a network of interconnected pores characterized by sizes between 1 and 20 nm) can be synthesized using sol-gel techniques. The resulting materials generally have a structure made up of nanometric particles (10 nm in diameter typically), interconnected, and forming an open chain. The size of the pores and the particles can be adjusted via the specificities of the sol-gel synthesis, such as the choice of the template, the solvent, their respective concentrations, and the process parameters (temperature, humidity) (Baldinozzi et al., 2012). These mesoporous systems offer the possibility to study the effects of high defect concentrations with very short atomic transport distances, and therefore present exceptional conditions to analyze the cross-effects of these particular geometries with the non-equilibrium defect supersaturations produced by extreme conditions like irradiation. When synthesising these materials it is important to avoid methods that require long range diffusion, as diffusion of cations is sluggish in fluorite systems, therefore to ensure an ideal cation homogeneity wet chemical methods should be employed.

3 Structures in fluorite related oxides

Ideally, lattice parameters of solid solutions are expected to vary linearly with the concentration of the substituted ion, following the empirical Vegard’s law (Vegard, 1921). The pertinence of such law agrees with the additivity of ionic radii, as earlier suggested by Pauling and Huggins (1934), implying that atomic volumes remain constant independently of the extent of the mixing. However, diffraction techniques are based on the coherent interference generated by long-range order, therefore, the information obtained by these techniques is averaged over many unit cells. Deviations from linearity can be observed experimentally in many systems and can be attributed either to actual bond length variations or to eventual long-range ordering phenomena. The understanding of the behaviour of the lattice parameter in mixed cerium-lanthanide oxides is not only an academic problem: indeed, under changes of the oxygen partial pressure or in presence of operating gradients typical of electrolyte systems, chemical expansion can promote cracking of cerium oxide ceramics, therefore, the requirement of the knowledge of the lattice parameter behaviour to predict safe operating conditions. Moreover, an increase in lattice parameters is generally associated with a decrease in the elastic modulus, requiring additional mechanical assessment in device design. The buildup of mechanical stress is also relevant to phenomena like kinetic demixing that we have already mentioned. In pure ceria, lattice expansion arises by defect formation by the relevant reduction reaction Eq. 2. The lattice expansion is believed to result from the combined effects of the formation of defects during this reduction reaction, namely the increase in ionic radius, resulting from the decrease of the formal valence state of the cations from +4 to +3, and the formation of positively charged oxygen vacancies with subsequent electrostatic repulsion of the cation neighbours. Hong and Virkar (1995) analyzed the lattice parameter change in ceria, at room temperature in air, by partial substitution of tetravalent cerium with trivalent cations (La, Er, Yb). This empirical model explains that doping-induced expansion results from the joint contribution of an ionic radius change (the difference between Ce and the substitutional cation radii) and an effective anion radius change (from the difference between the oxygen and effective vacancy radius). The observed behaviour of the lattice parameter is compatible with the mechanism described by Eq. 3, but the linearity is observed only between 5% and 25% atomic substitutions with smaller-size dopants like Yb and Er in CeO₂, whereas the substitution effect is non-linear for the larger dopants like La (Pr and Nd). Therefore, it seems legitimate to investigate the structural effects of substitutions of the lighter lanthanides in ceria, as their behaviour is inherently more complex than the predictions of the above-mentioned empirical model, and defect correlations or associations may occur under particular conditions.

3.1 Salient structures in undoped CeO_2−x

Pure ceria crystallises in the fluorite structure (Figure 6, with atomic positions given in Table 2), a cubic structure with the space group $Fm\bar{3}m$. In the fluorite structure, cerium ions take a face-centred pattern, occupying the corners and the faces of the cubic-unit cell in eightfold coordination with the oxygen ions, which themselves form a simple cubic arrangement with the ions in fourfold coordination inside the cerium tetrahedra.

FIGURE 6

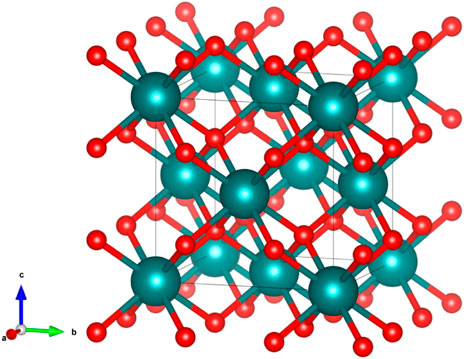
FIGURE 6. The fluorite structure. Teal spheres represent the cations while the red spheres represent the anions.

TABLE 2

TABLE 2. Atomic positions for the fluorite structure in the $Fm\bar{3}m$ space group.

The fluorite structure is known to be a stable structure, as ceria maintains this structure over a wide compositional range and temperature. Neutron diffraction data shows that CeO₂ maintains a single-phase fluorite structure over the temperature range 40–1,497°C and that at higher temperatures oxygen vacancies shift along the ⟨111⟩ directions (Yashima et al., 2006). Bevan (1955) studied the structure for various CeO_2−x samples quenched from 800–1,200°C in air and showed that the CeO₂-Ce₂O₃ system forms a range of intermediate, fluorite-related ordered structures, which can be described as a solid solution between CeO₂ and Ce₂O₃ across the compositional range, as illustrated in Figure 7. The γ, β, and δ phases were described as having rhombohedral structures, although at high temperatures the δ phase at CeO_1.698 has been shown to transition to a cubic structure (Kummerle and Heger, 1999).

FIGURE 7

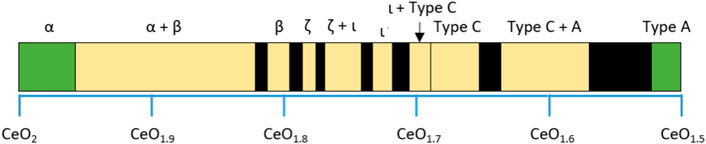
FIGURE 7. Phases present in the CeO₂—Ce₂O₃ system as identified by Bevan. The end members are highlighted in green and the intermediate phases are coloured yellow. Black regions were not reported in the study. Data were taken from (50).

3.1.1 The ι phase Ln₇O₁₂ (LnO_1.714)

Of the known phases in the Ln_nO_2n−2 series, the structure corresponding to n = 7, corresponding to the ι phase, is considered to have the highest stability and occurs across all three of the rare earth oxide systems. Originally this composition was proposed in the work by Bevan et al. (Zinkevich, 2007) who proposed structural models over the composition range CeO_{1.722−1.717} with trigonal symmetry in a hexagonal setting with lattice parameters of a = 3.921 and c = 9.637, however, no actual structural model was refined.

A study by Ray and Cox (1975) attempted to determine the crystal structure of Ce₇O₁₁ through neutron diffraction of both single crystals and powders. The powder contained both strong peaks that could be indexed as a face-centred cubic cell, like the fluorite structure, but also weak reflections which were indexed in terms of a hexagonal cell, and the structure was refined using the structural model of UY₆O₁₂. This structure of Ce₇O₁₂ is related to the parent CeO₂ by placing the oxygen vacancies in strings along the $\left[111\right]$ axis of the fluorite structure. The formation and ordering of oxygen vacancies reduce the coordination of the cations, with one-seventh found in sixfold coordination while the remaining are in a sevenfold coordinated environment (Ray and Cox, 1975), lower than the ideal eightfold coordination characteristic of the ideal fluorite structure. This string of $\left[111\right]$ vacancies is said to represent the basic building block for the family of Ln_nO_2n−2 family of phases.

Neutron diffraction studies conducted by Von Dreele et al. (1975) on the Pr₇O₁₂ system also concluded the structure to be of rhombohedral symmetry with the $R\bar{3}$ space group. The atomic positions of the structural model are given in Table 3.

TABLE 3

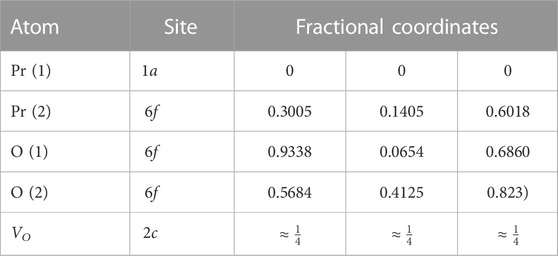
TABLE 3. Atomic parameters of the rhombohedral setting of the trigonal $R\bar{3}$ space group determined by Von Dreele et al. (1975).

They found that it is the Pr (British Energy Security Strategy, 2022) atom found in sixfold coordination while the Pr (Net Zero Strategy, 2021) atom is in sevenfold coordination, in agreement with the model above. From comparing with data from the UY₆O₁₂ and Zr₃Sc₄O₁₂ systems they concluded that if there were any selectivity for the sixfold coordination site, it would depend on the size of the cation rather than the charge, with the smaller ions preferring the sixfold site.

The same $R\bar{3}$ structure was reported in the Tb₇O₁₂ system by Zhang et al. (1993) who analysed neutron diffraction data from Tb₇O₁₂ powders. Similarly to the Pr₇O₁₂ system, the Tb (British Energy Security Strategy, 2022) atom was found in sixfold coordination with a +4 charge. The Tb (Net Zero Strategy, 2021) atom, however, was found to be in a mixed valence state between +3 and +4. Whether this was a structural feature or due to the hopping of electrons between Tb ions was not determined.

3.1.2 The β phase Ln₆O₁₁ (LnO_1.833)

The β phase of the series Ln_nO_2n−2 is that of n = 12. Similarly to the ι phase, it is considered to be a highly stable phase in the series, occurring at atmospheric oxygen pressures and at room temperature (Zhang et al., 1996a). An early study on single crystals of Pr₆O₁₁ by Lowenstein et al. (1972) showed both strong fluorite reflections and weak reflections corresponding to the β phase lattice in the diffraction pattern. These extra reflections were indexed based on a monoclinic cell with space group P2₁/n although no structure was proposed, The monoclinic cell volume was determined to be six times the volume of the fluorite cell.

Later studies by Zhang et al. (1996b) used neutron powder data to determine the structure of Pr₁₂O₂₂ through rietveld analysis of powder neutron data. The structure was found to be monoclinic, similar to the earlier study by Lowenstein et al. However the space group was determined to be P2₁/c as opposed to P2₁/n previously proposed. The most surprising finding was the absence of the oxygen vacancy pairs found in other members of the Ln_nO_2n−2 series such as Ln₇O₁₂. Instead only single oxygen vacancies were observed to be distributed in the lattice in a uniform pattern. The relationship between the monoclinic structure and fluorite lattice vectors is given by:

$\left\{\begin{array}{cc}{a}_{\beta }=\hfill & \frac{1}{2}\left(2a_F+b_F+c_F\right)\hfill \\ b_{\beta }=\hfill & \frac{3}{2}\left(b_F+c_F\right)\hfill \\ c_{\beta }=\hfill & \frac{1}{2}\left(2a_F-3b_F+3c_F\right)\hfill \end{array}\right.(5)$

In the various structures of the series Ln_nO_2n−2 there is a common defect cluster with which these intermediate structures can be built, proposed by Martin (1974). This coordination defect occurs when an oxygen atom is removed from the centre of the M4 tetrahedron located in the fluorite octant. The vacancy left behind causes relaxations of the nearby atoms due to its positive charge, such that the neighbouring cations shift away from the vacancy while the six oxygen ions surrounding relax towards the vacancy.

3.2 Notable structural features in ceria doped with Ln₂O₃

3.2.1 Global average structure

As mentioned in earlier, substitution of Ln⁺³ ions for Ce⁺⁴+ introduces oxygen vacancies in the system, which as their concentration increases has an effect on the system’s structure. Due to the similarity of charge compensation mechanisms, one would expect the binary system CeO₂:Ln₂O₃ to form the same cornucopia of intermediate phases as the undoped system.

The first and most important effect that doping ceria with trivalent ions has is that a phase change occurs once the amount of dopant reaches some critical value (x_c). The system changes from fluorite to the rare earth C-Type structure (also referred to as bixbyite), one of the polymorphs of the lanthanide sesquioxides discussed in Section 2.2.

The C-type structure (space group $Ia\bar{3}$) is closely related to the fluorite structure, and can be formed by placing eight anion-deficient fluorite octants together (Figure 8, atomic positions given in Table 4). A C-type octant is formed by taking a fluorite unit cell and shifting the origin to be halfway up the cell, creating a new cell with metal atoms at the centre of each edge and in the middle of the cell while the oxygen atoms remain in a simple cubic pattern inside the metal tetrahedra. In addition to shifting the origin, two oxygen atoms are removed along the body diagonal in one of three ways: upper right front and lower left back (type 1), lower left front and upper right back (type 2) and lower right back and upper left front (type 3) (Galasso, 1970). While cations in a fluorite structure can be found in eightfold coordination with anions and have well-defined positions, in the C-type structure they are found in sixfold coordination and the 24 days site is shifted due to repulsion with the oxygen vacancies, which unlike in the fluorite structure allows for some degrees of freedom in the atomic position of the cations in the system. Additionally, the O (1) site is ideally fully occupied whereas the occupational factor of the O (2) site is $1-x_{L{n}^{+3}}$.

FIGURE 8

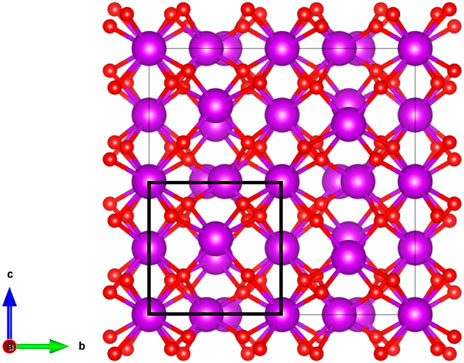
FIGURE 8. C-Type structure. Purple spheres represent the cations while the red spheres represent the anions. A fluorite octant has been highlighted.

TABLE 4

TABLE 4. Atomic positions for the rare earth C-Type structure. The value for the refined coordinate of the M (2) site is: x ≈ − 0.035, and the values for the O (1) site are: x ≈ 0.38, y ≈ 0.162 and z ≈ 0.4 respectively (Galasso, 1970).

The x_c value for the phase change has been studied for various CeO₂:Ln₂O₃ systems and shows a large variation for most dopants. In the CeO₂:Nd₂O₃ system the value of x has been reported in the range 0.30 < x_c < 0.51 (Hong and Virkar, 1995; Chavan et al., 2005; Ikuma et al., 2005; Hagiwara et al., 2009). The wide variation in the reported values for x_c is likely due to the similarity between the fluorite and the C-type structures. The diffraction patterns of fluorite and C-type differ by the appearance of small superstructure peaks between the major fluorite ones (illustrated in Figure 9), which grow in intensity with the formation of more C-type. If the data is noisy it is difficult to be able to tell the peaks apart from the background, leading to the value for x_c being overestimated. In addition to the similarity of the structures, the synthesis method used and the thermal history of the sample also have a significant effect on the stability range for the fluorite and C-type structures (Horlait et al., 2011) which adds to the observed variation in the value of x_c.

FIGURE 9

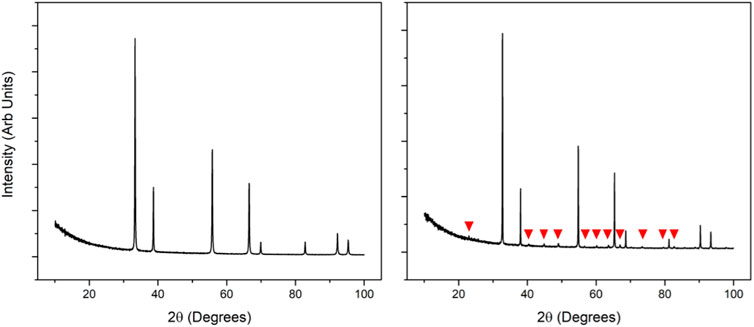
FIGURE 9. XRD patterns for fluorite (left, obtained from XRD of CeO₂) and C-Type (right, obtained from XRD of Ce_0.4Nd_0.6O_1.7), the superstructure peaks in the C-Type diffraction pattern have been labelled with red ticks. These peaks are very low intensity compared to the high intensity fluorite peaks and so can often be missed leading to an incorrect assumption on the structure.

At higher dopant concentrations the system forms a biphasic mixture between the C-type and A-type phases as the solubility limit of Nd in CeO₂ is reached. A-type is formed in the system under standard conditions, and Nd₂O₃ crystallises in this structure. The value of x for the solubility limit has been reported to vary between 0.7 < x_sol < 0.76 (McCullough, 1950; Jardim and Maple, 1993; Ikuma et al., 2005; Horlait et al., 2011).

In addition to the phase change, the other major global structural change that occurs with the doping of ceria with Nd⁺³ is a change in the lattice parameter of the system. As more neodymium is introduced the lattice parameter increases, showing a roughly linear trend in accordance with Vergard’s law as (Ikuma et al., 2005) although there are two regions with different gradients corresponding to the fluorite and the C-Type phases respectively. As the C-type structure is made up of fluorite unit cells, the lattice parameter of C-type structures will be described in regards to the lattice parameter of a fluorite octant, $a_F=\frac{1}{2}{a}_C$ such that it is easier for comparison between these phases. Changes to the lattice parameter are not limited to Nd doping as changes are seen when ceria is doped with other trivalent rare earth with the rate of change varying depending on the identity of the dopant ion. Increases to the lattice parameter are observed for Gd, La, Eu, and Sm dopants whereas shrinkage is seen for Er, Yb, and Y (McBride et al., 1994; Horlait et al., 2011) illustrated in Figure 10. The change in the lattice parameter, whether it expands or contracts, is determined by the size of the dopant ion, as the order of expansion (from largest expansion to most contraction) runs along the lanthanide series in the periodic table, following the lanthanide contraction series, a property of the lanthanide group in which the ionic radii of each species decrease along the group.

FIGURE 10

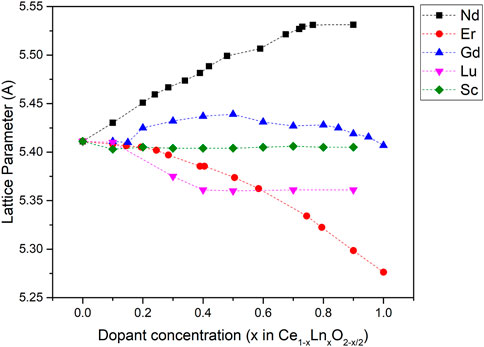
FIGURE 10. Lattice parameters of various Ce_1−xLn_xO_2−x/2 compounds as a function of dopant concentration. Eu and Nd (Horlait et al., 2011), Gd (Grover and Tyagi, 2004), Lu and Sc (Grover et al., 2008). The lattice parameters plotted are the fluorite equivalent lattice parameters, a_f = 1/2a_C.

3.2.2 Local structure of doped ceria

In the previous section, the results of XRD studies on the CeO₂:Nd₂O₃ were discussed as showing single-phase fluorite or C-type structures, however, on a local scale, this may not be the case. The behaviour of the ionic conductivity with respect to the amount of dopant added is an indication of the existence of some local disorder in these systems as the conductivity decreases after $x_{L{n}^{+3}}\approx 0.2$ despite the fact no phase changes or other long-range structural transformations occur. XRD is a valuable tool for determining the global average structure of a material, however, in order to gain a better insight into the local scale structure different techniques are required.

Nitani et al. (2004) used x-ray absorption spectroscopy (XAS) to probe the local structure of the ceria system doped with Nd, Pr, and Sm and while for the Pr-doped system the Ce-O and Pr-O interatomic distances were the same across the values of $x_{L{n}^{+3}}$ tested, it was noted that Sm and Nd doping makes the lattice expand but causes the oxygen to shift towards either the Ce or the dopant ions, giving rise to local distortions of the lattice. Another study in the Gd-Ce system showed similar results (Ohashi et al., 1998), the M-O distances decreased as dopant concentration increased. From their results, they proposed the system formed clusters composed of vacancies and dopant ions. The system initially contains (Gd′:${\mathrm{V}}_O^{••}$) pairs at low dopant concentrations and evolves to contain more (2Gd′:${\mathrm{V}}_O^{••}$) clusters at higher concentrations. The increase in the number of (2Ln′:${\mathrm{V}}_O^{••}$) clusters would result in a decrease in the ionic conductivity in these systems as previously discussed.

High-resolution electron microscopy (HRTEM) is useful when determining the structure of a substance as imaging allows local structures to be seen and pictured rather than inferred from data. The local structure of Sm and La-doped ceria was investigated by Toshiyuki et al. (2002) using HRTEM and SAED. They observed diffuse scattering in the background of electron diffraction patterns, indicating the existence of micro-domains of ordered structure within the fluorite lattice. These domains form in order to reduce the strain induced when Ce⁺⁴ ions are substituted by lower valency ions. In a later study (Morui and Drennan, 2006) on Gd and Dy doped ceria, it was observed that the size of the domains increased with dopant concentration. This observation can be used to explain the lowering of the ionic conductivity with increasing dopant concentration, as larger micro-domains would contain more ordered vacancies, removing them from being oxygen transport sites and causing the observed drop in ionic conductivity. The composition of these micro-domains was determined to have a higher dopant concentration than the surrounding fluorite matrix and a structure modelled in which the arrangement of oxygen vacancies and structure is similar to that of the C-type structure typical of the rare earth sesquioxides (Ye et al., 2007; Ou et al., 2008).

We recently reported crystallization of a compound Gd₂Ce₂O₇ in the Gd₂O₃:CeO₂ system exhibiting a bixbyite symmetry (Patel et al., 2022). However, in comparison with conventional bixbyite, in this compound half of the vacant anion sites are filled with charge compensating oxygen interstitials making this an anion excess bixbyite. Here, the topological defects linked with the anion sub-lattice play a crucial role in increasing the radiation tolerance by creating micro-domains that act as localized sinks while retaining long range periodicity of cation sublattice.

Raman spectroscopy is another technique that can be used to gain information on the local scale structure of a material such as the coordination of ions and their chemical environment. Spectroscopy carried out by McBride et al. (1994) showed the lattice constant increases with dopant concentration and the rate of expansion is determined by the ionic radius of the dopant. Additionally, the appearance of a peak at 570 cm⁻¹ which broadened with dopant concentration was attributed to the formation of oxygen vacancies in the system. The existence of domains at low dopant concentration $(x_{L{n}^{+3}}<0.2)$ is indicated by Artini et al. (2015) who observed a broad signal at 370 cm⁻¹ which becomes sharper with increasing $x_{L{n}^{+3}}$. This signal was attributed to Ln-O stretching mode for the sixfold coordination of the rare earth ion, similar to that found in the C-type structure, despite the system showing only single-phase fluorite according to the XRD data. Taniguchi et al. (2009) observed a band at 560 cm⁻¹ for samples containing 20% mol of Gd attributed to the formation of (${\mathrm{G}\mathrm{d}}^{\prime }:V_O^{••}$) and (2Gd$:V_O^{••}$) defect complexes like those observed in (Ohashi et al., 1998) high energy shift of the band position indicates an increase in the number of 2Gd complexes at higher x_Gd values over the single Gd ion complexes.

3.2.3 Structure of doped ceria synthesised by freeze drying

Many studies on the structure and properties of trivalent doped ceria employ a solid-state fabrication technique to prepare samples (Jardim and Maple, 1993; Hong and Virkar, 1995; Grover and Tyagi, 2004), due to its simplicity and ease of processing. Ball milling the reactant powders will produce a homogeneous mixture on the macro scale, however, at the nano-scale, the mixture will not be ideally homogenised and thus will require prolonged annealing to drive cation diffusion. As discussed in Section 2.6, diffusion of cations is incredibly sluggish in fluorite systems due to the high activation energy for diffusion, requiring solid-state methods to employ high temperatures (typically 1,400–1600 K) during annealing, higher than the cation-ordering temperature of below 1400 K.

In recent experiments to study the oxygen vacancy ordering in binary Ce_1−xNd_xO_2−x/2 systems, samples were synthesised employing a freeze-drying method in order to avoid kinetic demixing and annealing above cation ordering temperatures and were characterized through the use of X-Ray diffraction. The sample preparation started with diluting and mixing solutions of CeCl₃*7H₂O and NdCl₃*6H₂0 in de-ionized water (typically 0.005 mol of salts in 200 ml of de-ionized water). After freezing and primary sublimation, an anhydrous and amorphous intermediate forms which has the approximate formula (Ce,Nd)OCl. This intermediate is immediately calcined at 550°C with a dwell time of 15–30 min to allow grain growth. During calcination the intermediate products decompose to form the final oxide (Ce,Nd)O₂. Higher temperature and longer dwell times are used to accelerate the kinetic of the growth and obtain larger nanocrystals. Nanocrystal growth and particle size dispersion can be controlled through the initial dilution of the solution, calcination temperature, dwell time, and spreading and limiting the amount of the intermediate in the combustion boat.

Samples in which x_Nd < 0.4 were found to be in fluorite structure, in accordance to previously discussed studies. However, in samples with the composition x_Nd > 0.4. We observe a deviation from what has been previously observed in the literature. The XRD pattern for this sample is given in Figure 11. It was apparent that a phase change had occurred in the system, as while intense peaks corresponding to a fluorite-type lattice were present, low-intensity peaks appear at 44.8 and 52.3° 2θ, these peaks could be qualitatively indexed as the type-C rare earth polymorph, however, the peak located at 31.3° could not be attributed to this structure.

FIGURE 11

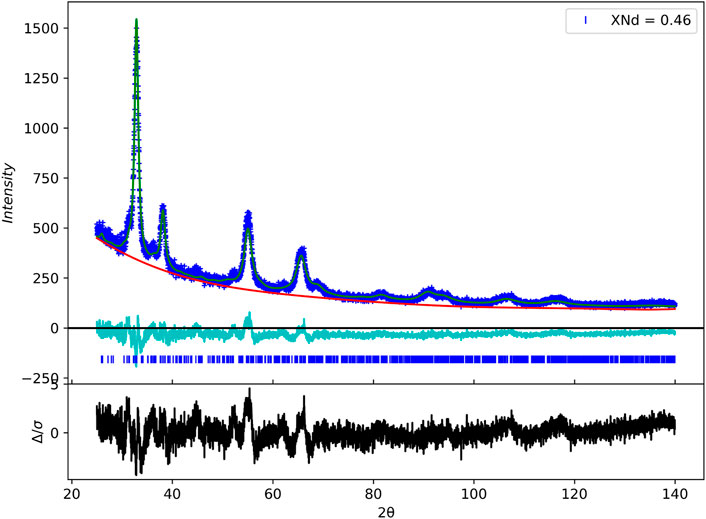
FIGURE 11. Rietveld refinement using a model derived from the β-phase for the composition Ce_0.54Nd_0.46O_1.77. Experimentally obtained data (blue line), calculated structure factor (green line), subtracted background (red line), peak positions (blue ticks) and the difference between observed and calculated XRD structure factor (Turquoise and black lines).

In order to determine the structure, structures derived from the intermediate phases of fluorite-related systems (discussed in Section 3) were chosen as initial models. It was discussed that the peak at 31.3° was due to the splitting of the [111]_F peak due to a phase change to a rhombohedral structure, and thus an initial model of the ι phase (Von Dreele et al., 1975) was tested to limited success. LeBail fitting of a rhombohedral lattice accounted for many of the low-intensity peaks but would not fit the small peak at 2θ = 36.1 and thus a new model was required.

A second model derived from the β phase was subsequently tested with much greater success than that of the ι phase. Figure 11 shows the result of Rietveld refinements after testing a single phase structure, using initial atomic positions described in (55). It can be seen that the calculated intensity fits well with the experimentally obtained diffraction pattern. The refined structural parameters and atomic positions are given in Table 5. The existence of the β phase in these samples is interesting, as while the β phase has been well documented for the PrO_2−x (Lowenstein et al., 1972; Schweda et al., 1991; Zhang et al., 1996a) and the TbO_2−x (Eyring, 1979) systems, there is debate as to whether this phase is present in the CeO_2−x system and as discussed previously, experiments on the doping ceria with trivalent RE ions show only a phase transition from fluorite to C-type structures.

TABLE 5

TABLE 5. Refinement parameters for Ce_0.54Nd_0.46O_1.77 freeze dried sample.

4 Conclusion

Nuclear fuel systems typically require decades to optimize, and even today light water reactor fuels have known difficulties associated with extended burnup. Trial and error approaches are used most successfully with simple problems: sometimes it is the last resort when no apparent rule applies. While this approach is not inherently careless, the methodical manipulation of the parameters in an attempt to sort through possibilities could result in success, but the process is inherently slow and expensive. Minor actinides seem to require a change of paradigm, because they have unique behaviors that are not fully understood, requiring a more fundamental understanding of the transport and chemical behavior of the materials during processing that affects the predictions about stoichiometry, segregation, and material microstructure. Therefore, radiation induced defect models for multi-component actinide fuel systems are needed. These model systems must capture the unconventional phase behavior and stoichiometry of these more complex and relatively in inaccessible systems, going beyond simple descriptive defect models. Surrogate systems like mixed cerium oxides can provide an interesting alternative to establish the effect of radiation damage over systems with complex microstructures, charge and defect localisation that are quite similar to those encountered in the actual actinide-based advanced fuels. As in actinide systems, the description of the structural and microstructural changes produced by irradiation is compounded by the fact that the properties of these systems can change abruptly with composition.

In this paper we have discussed defect mechanisms in fluorite oxides and the diffusion characteristics of cations and anions in fluorite-related compounds, highlighting the importance of soft chemical methods to ensure ideal cation homogeneity during synthesis. We have also reviewed the structural studies on Ce_1−xLn_xO_2−x/2 compounds and presented preliminary results from some recent experiments conducted on samples of Ce_0.54Nd_0.46O_1.77 fabricated by freeze drying, which were found to be best described by the β phase in PrO_2−x systems. This result is fascinating, as existing literature on these systems reports a change from the fluorite structure to the C or A-type Ln₂O₃ structure, and thus a possible reassessment of the equilibrium phase diagrams of many binary systems may be required.

Author contributions

HC was responsible for planning and writing the initial draft manuscript. Once the plan was made, all authors contributed equally to the manuscript. GB fabricated the samples discussed in the section and all authors contributed equally to the analysis of the data.

Funding

This work was funded by EPSRC through the Next Generation Nuclear Centre for Doctoral Training (NGN-CDT) programme.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Artini, C., Pani, M., Carnasciali, M. M., Buscaglia, M. T., Plaisier, J. R., and Costa, G. A. (2015). Structural features of Sm- and Gd-doped ceria studied by synchrotron X ray diffraction and μ Raman spectroscopy. Inorg. Chem. 54, 4126–4137. doi:10.1021/acs.inorgchem.5b00395

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldinozzi, G., Muller, G., Laberty-Robert, C., Gosset, D., Simeone, D., and Sanchez, C. (2012). Probing properties, stability, and performances of hierarchical mesoporous materials with nanoscale interfaces. J. Phys. Chem. C 116, 7658–7663. doi:10.1021/jp211872z

CrossRef Full Text | Google Scholar

Bevan, D. J. M. (1955). Ordered intermediate phases in the system CeO₂ - Ce₂O₃. J. Nucl. Inorg. Chem. 1, 49–59. doi:10.1016/0022-1902(55)80067-x

CrossRef Full Text | Google Scholar

Blumenthal, R. N., Lee, P. W., and Panlener, R. J. (1971). Studies of the defect structure of nonstoichiometric cerium dioxide. J. Electrochem. Soc. 118, 123. doi:10.1149/1.2407923

CrossRef Full Text | Google Scholar

Blumenthal, R. N., and Panlener, R. J. (1970). Electron mobility in nonstoichiometric cerium dioxide at high temperatures. J. Phys. Chem. Solids 31, 1190–1192. doi:10.1016/0022-3697(70)90329-x

CrossRef Full Text | Google Scholar

British Energy Security Strategy (2022). British energy security strategy. Available at: www.gov.uk/government/publications/british-energy-security-strategy.

Google Scholar

Catlow, C. R. A., and Norgett, M. J. (1973). Shell model calculations of the energies of formation of point defects in alkaline Earth fluorides. J. Phys. C. Solid State Phys. 6, 1325–1339.

CrossRef Full Text | Google Scholar

Chavan, S. V., Mathews, M. D., and Tyagi, A. K. (2005). Phase relations and thermal expansion studies in the CeO₂-NdO_1.5 system. Mater. Res. Bull. 40, 1558–1568. doi:10.1016/j.materresbull.2005.04.014

CrossRef Full Text | Google Scholar

Coutures, J., Verges, R., and Foex, M. (1974). Etude a haute temperature des systemes formes par le sesquioxyde de neodyme avec les sesquioxydes d’yttrium et d’ytterbium. Mat. Res. Bull. 9, 1603–1611. doi:10.1016/0025-5408(74)90150-0

CrossRef Full Text | Google Scholar

Cureton, W. F., Palomares, R. I., Walters, J., Tracy, C. L., Chen, C. H., Ewing, R. C., et al. (2018). Grain size effects on irradiated CeO₂, ThO₂, and UO₂. Acta Mater. 160, 47–56. doi:10.1016/j.actamat.2018.08.040

CrossRef Full Text | Google Scholar

Eyring, L. (1979). Chapter 27 the binary rare Earth oxides. Handb. Phys. Chem. Rare Earths 3, 337–399. doi:10.1016/S0168-1273(79)03010-5

CrossRef Full Text | Google Scholar

Galasso, F. S. (1970). “Chapter 5 - ZnS type and related structures,” in Structure and properties of inorganic materials (Pergamon: Elsevier), 90–95.

Google Scholar

Garcia-Chain, P., Rojas, R. M., Herrero, P., and Gunter, J. R. (1994). Microstructural characterization of the fluorite phase in the U-La-O system: II. Hexagonal microdomain formation in (U_1−yLa_y)O_2−x, 0.70 ≤ y ≤ 0.80. J. Solid State Chem. 108, 236–242. doi:10.1006/jssc.1994.1037

CrossRef Full Text | Google Scholar

Gasgnier, M., Schiffmacher, G., and Caro, P. (1989). Relationships between rare Earth oxide polymorphs in thin films treated with water vapour. J. Of Mater. Sci. 24, 2801–2807. doi:10.1007/bf02385629

CrossRef Full Text | Google Scholar

Grover, V., Banerji, A., Sengupta, P., and Tyagi, A. K. (2008). Raman, XRD and microscopic investigations on CeO₂–Lu₂O₃ and CeO₂–Sc₂O₃ systems: A sub-solidus phase evolution study. J. Solid State Chem. 181, 1930–1935. doi:10.1016/j.jssc.2008.04.001

CrossRef Full Text | Google Scholar

Grover, V., and Tyagi, A. K. (2004). Phase relations, lattice thermal expansion in CeO₂–Gd₂O₃ system, and stabilization of cubic gadolinia. Mater. Res. Bull. 39, 859–866. doi:10.1016/j.materresbull.2004.01.007

CrossRef Full Text | Google Scholar

Hagiwara, T., Kyo, Z., Manabe, A., Yamamura, H., and Nomura, K. (2009). formation of C-type rare Earth structures int the Ce_1−xNd_xO_2−d system: A factor for the decrease in oxide-ion conductivity. J. Ceram. Soc. Jpn. 117, 1306–1310. doi:10.2109/jcersj2.117.1306

CrossRef Full Text | Google Scholar

Hong, S. J., and Virkar, A. V. (1995). Lattice parameters and densities of rare-earth oxide doped ceria electrolytes. J. Am. Ceram. Soc. 78, 433–439. doi:10.1111/j.1151-2916.1995.tb08820.x

CrossRef Full Text | Google Scholar

Horlait, D., Claparede, L., Clavier, N., Szenknect, S., Dacheux, N., Ravaux, J., et al. (2011). Stability and structural evolution of Ce(IV)_1−xLn(III)_xO_2−x/2 solid solutions: A coupled μ-Raman/XRD approach. Inorg. Chem. 50, 7150–7161. doi:10.1021/ic200751m

PubMed Abstract | CrossRef Full Text | Google Scholar

Ikuma, Y., Shimada, E., and Okamura, N. (2005). Effect of Nd₂O₃ concentration on the defect structure of CeO₂-Nd₂O₃ solid solution. J. Am. Ceram. Soc. 88, 419–423. doi:10.1111/j.1551-2916.2005.00076.x

CrossRef Full Text | Google Scholar

Ikuma, Y., Tsubaki, Y., and Masaki, T. (1991). Oxygen diffusion in nanocrystalline yttria-stabilized zirconia: The effect of grain boundaries. J. Ceram. Soc. Jpn. 99, 101–103. doi:10.2109/jcersj.99.101

CrossRef Full Text | Google Scholar

Iwasaki, M., Kanazawa, Y., Manago, D., Patel, M. K., Baldinozzi, G., Sickafus, K. E., et al. (2022). Anomalous structural phase transformation in swift heavy ion-irradiated δ-Sc₄Hf₃O₁₂. J. Appl. Phys. 132, 075901. doi:10.1063/5.0098518

CrossRef Full Text | Google Scholar

Jardim, R., and Maple, M. B. (1993). On the formation of LnCeOy (Ln = Nd, Pr, Sm, Eu) solid solutions. Mater. Lett. 18, 5–10. doi:10.1016/0167-577x(93)90046-z

CrossRef Full Text | Google Scholar

Kilner, J. A. (1983). Fast anion transport in solids. Solid state ionics 8, 201–207. doi:10.1016/0167-2738(83)90017-6

CrossRef Full Text | Google Scholar

Kim, W. K., Cho, M. S., Lee, Y. W., Kim, W. J., Park, J. Y., Park, J. B., et al. (2007). “Measurement of the coating thickness for simulated TRISO-coated fuel particles by phase contrast X-ray radiography,” in Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, May 10-11, 2007.

Google Scholar

Kleykamp, H. (1999). Selection of materials as diluents for burning of plutonium fuels in nuclear reactors. J. Nucl. Mat. 275, 1–11. doi:10.1016/s0022-3115(99)00144-0

CrossRef Full Text | Google Scholar

Koettgen, J., Grieshammer, S., Hein, P., Grope, B. O., Nakayama, M., and Martin, M. (2018). Understanding the ionic conductivity maximum in doped ceria: Trapping and blocking. Phys. Chem. Chem. Phys. 20 (21), 14291–14321. doi:10.1039/c7cp08535d

PubMed Abstract | CrossRef Full Text | Google Scholar

Konings, R., Bakker, K., Boshoven, J., Conrad, R., and Hein, H. (1998). The influence of neutron irradiation on the microstructure of Al₂O₃, MgAl₂O₄, Y₃Al₅O₁₂ and CeO₂. J. Nucl. Mat. 254, 135–142. doi:10.1016/s0022-3115(97)00355-3

CrossRef Full Text | Google Scholar

Kummerle, E. A., and Heger, G. (1999). The Structures of C - Ce₂O_3+x, Ce₇O₁₂, and Ce₁₁O₂₀. J. solid state Chem. 147 (2), 485–500. doi:10.1006/jssc.1999.8403

CrossRef Full Text | Google Scholar

Livage, J., and Sanchez, C. (1992). Sol-gel chemistry. J. Non-Crystalline Solids 145, 11–19. doi:10.1016/s0022-3093(05)80422-3

CrossRef Full Text | Google Scholar

Lopato, L. M., Shevchenko, A. V., Kushchevskii, A. E., and Tresvyatskii, S. G. (1974). Polymorphic transitions of rare Earth oxides at high temperatures. Inorg. Mat. (USSR) Engl. Transl.) 10 (8), 1276–1281.

Google Scholar

Lowenstein, M. Z., Kihlborg, L., Lau, K. H., Haschke, J. M., and Eyring, L. (1972). Growth and X-ray studies of single crystals of higher oxides of praseodymium and terbium. Nat. Bur. Stand. (U. S.) 364, 343–351.

Google Scholar

Martin, R. L. (1974). Structural theory for non-stoicheiometry. Part I . Defect fluorite-type structures: Lanthanoid oxides MO_x with 1.7 < x < 2.0. J. Chem. Soc. Dalton Trans. 12, 1335–1350. doi:10.1039/dt9740001335

CrossRef Full Text | Google Scholar

McBride, J. R., Hass, K. C., Poindexter, B. D., and Weber, W. H. (1994). Raman and x-ray studies of Ce_1−xRE_xO_2−y where RE=La, Pr, Nd, Eu, Gd, and Tb. J. Appl. Phys. 76, 2435–2441. doi:10.1063/1.357593

CrossRef Full Text | Google Scholar

McCullough, J. D. (1950). An X-ray study of the rare-Earth oxide systems: Ce^IV—Nd^III, Cr^IV—Pr^III, Ce^IV—Pr^IV and Pr^IV—Nd^III1. J. Am. Chem. Soc. 72 (32), 1386–1390. doi:10.1021/ja01159a085

CrossRef Full Text | Google Scholar

Minervini, L., Zacate, M. O., and Grimes, R. W. (1999). Defect cluster formation in M₂O₃-doped CeO₂. Solid State Ionics 116, 339–349. doi:10.1016/s0167-2738(98)00359-2

CrossRef Full Text | Google Scholar

Mogensen, M., Sammes, N. M., and Tompsett, G. A. (2000). Physical, chemical and electrochemical properties of pure and doped ceria. Solid State Ionics 129, 63–94. doi:10.1016/s0167-2738(99)00318-5

CrossRef Full Text | Google Scholar

Morui, T., and Drennan, J. (2006). Influence of microstructure on oxide ionic conductivity in doped CeO₂ electrolytes. J. electroceramics 17, 749–757. doi:10.1007/s10832-006-6311-7

CrossRef Full Text | Google Scholar

Net Zero Strategy (2021). Net Zero strategy: Build back greener. Available at: www.gov.uk/government/publications/net-zero-strategy.

Google Scholar

Nitani, H., Takashi, N., Yamaniuchi, M., Osuki, T., Yuya, M., and Yamamoto, T. A. (2004). XAFS and XRD study of ceria doped with Pr, Nd or Sm. Mater. Lett. 58, 2076–2081. doi:10.1016/j.matlet.2004.01.005

CrossRef Full Text | Google Scholar

Ohashi, T., Yamazaki, S., Tokunaga, T., Arita, Y., Matsui, T., Harami, T., et al. (1998). EXAFS study of Ce_1−xGd_xO_2−x/2. Solid state ionics 113-115, 559–564. doi:10.1016/s0167-2738(98)00322-1

CrossRef Full Text | Google Scholar

Olander, D. R. (1976). “Chapter 12 - behaviour of solid fission products in oxide fuel elements,” in Fundamental Aspects of Nuclear Fuel Elements, Tennessee, 172–196.

Google Scholar

Ou, D. R., Toshiyuki, M., Ye, F., Zou, J., Auchterloine, G., and Drennan, J. (2008). Oxygen-vacancy ordering in lanthanide-doped ceria: Dopant-type dependence and structure model. Phys. Rev. B 77, 024108–8. doi:10.1103/physrevb.77.024108

CrossRef Full Text | Google Scholar

Patel, M., Aguiar, J., Sickafus, K., and Baldinozzi, G. (2022). Structure and radiation response of anion excess bixbyite Gd2Ce2O7. Phys. Rev. Mater 6, 013610–013619. doi:10.1103/physrevmaterials.6.013610

CrossRef Full Text | Google Scholar

Patel, M. K., Sickafus, K. E., and Baldinozzi, G. (2020). Divergent short-and long-range behavior in ion-irradiated δ-Sc₄Hf₃O₁₂. Phys. Rev. Mater. 4, 093605. doi:10.1103/physrevmaterials.4.093605

CrossRef Full Text | Google Scholar

Pauling, L., and Huggins, M. L. (1934). Covalent radii of atoms and interatomic distances in crystals containing electron-pair bonds. Z. für Kristallogr. 87, 205–238. doi:10.1524/zkri.1934.87.1.205

CrossRef Full Text | Google Scholar

Ray, S. P., and Cox, D. E. (1975). Neutron diffraction determination of the crystal structure of Ce₇O₁₂. J. Solid State Chem. 15, 333–343. doi:10.1016/0022-4596(75)90289-3

CrossRef Full Text | Google Scholar

Reiss, I., Koerner, R., Ricken, M., and Noelting, J. (1988). Nonstoichiometric phases in cerium oxide. Solid State Ionics 30, 539–541. doi:10.1016/s0167-2738(88)80098-5

CrossRef Full Text | Google Scholar

Schmalzried, H., Laqua, W., and Lin, P. L. (1979). Crystalline oxide solid solutions in oxygen potential gradients. Z. für Naturforsch. A 34, 192–199. doi:10.1515/zna-1979-0211

CrossRef Full Text | Google Scholar

Schweda, E., Bevan, D. J., and Eyring, L. (1991). On the Pr_nO_2n−2 series of oxides and the structure of Pr₂₄O₄₄: An investigation by high-resolution electron microscopy. J. Solid State Chem. 90, 109–125. doi:10.1016/0022-4596(91)90178-k

CrossRef Full Text | Google Scholar

Shlyakhtina, A. V., Shcherbakova, L. G., Knotko, A. V., and Steblevskii, A. (2004). Study of the fluorite–pyrochlore–fluorite phase transitions in Ln₂Ti₂O₇ (Ln=Lu, Yb, Tm). J. Solid State Electrochem 8, 661–667. doi:10.1007/s10008-003-0491-8

CrossRef Full Text | Google Scholar

Shoko, E., Smith, M. F., and McKenzie, R. H. (2010). Charge distribution near bulk oxygen vacancies in cerium oxides. J. Phys. Condens. Matter 22, 223201. doi:10.1088/0953-8984/22/22/223201

PubMed Abstract | CrossRef Full Text | Google Scholar

Simeone, D., Baldinozzi, G., Gosset, D., Dutheil, M., Bulou, A., and Hansen, T. (2003). Monoclinic to tetragonal semireconstructive phase transition of zirconia. Phys. Rev. B 67, 064111. doi:10.1103/physrevb.67.064111

CrossRef Full Text | Google Scholar

Sonoda, T., Kinoshita, M., Chimi, Y., Ishikawa, N., Sataka, M., and Iwase, A. (2006). Electronic excitation effects in CeO₂ under irradiations with high-energy ions of typical fission products. Nucl. Instrum. Methods Phys. Res. B 250, 254–258. doi:10.1016/j.nimb.2006.04.120

CrossRef Full Text | Google Scholar

Stennett, M. C., Corkhill, C. L., Marshall, L. A., and Hyatt, N. C. (2013). Preparation, characterisation and dissolution of a CeO₂ analogue for UO₂ nuclear fuel. J. Nucl. Mater. 432, 182–188. doi:10.1016/j.jnucmat.2012.07.038

CrossRef Full Text | Google Scholar

Surble, S., Baldinozzi, G., Dolle, M., Gosset, D., Petot, C., and Petot-Ervas, G. (2008). Defect thermodynamic and transport properties of nanocrystalline Gd-doped ceria. Ionics 14, 33–36. doi:10.1007/s11581-007-0169-9

CrossRef Full Text | Google Scholar

Taniguchi, T., Watanabe, T., Sugiyama, N., Subramani, A. K., Wagata, H., Matsushita, N., et al. (2009). Identifying defects in ceria-based nanocrystals by UV resonance Raman spectroscopy. J. Phys. Chem. 113, 19789–19793. doi:10.1021/jp9049457

CrossRef Full Text | Google Scholar

Toshiyuki, M., Drennan, J., Lee, J.-H., Li, J.-G., and Mori, T. (2002). Oxide ionic conductivity and microstructures of Sm- or La- doped CeO₂-based systems. Solid state ionics 154-155, 461–466. doi:10.1016/s0167-2738(02)00483-6

CrossRef Full Text | Google Scholar

Tucker, D. S., Connor, A. O., and Hickman, R. (2015). A methodology for producing uniform distribution of UO₂ in a tungsten matrix. J. Phys. Sci. Appl. 5 (4), 255–262.

Google Scholar

Tuller, H. L., and Nowick, A. S. (1979). Defect structure and electrical properties of nonstoichiometric CeO₂ single crystals. J. Electrochem. Soc. 126, 209–217. doi:10.1149/1.2129007

CrossRef Full Text | Google Scholar

Tuller, H. L., and Nowick, A. S. (1977). Small polaron electron transport in reduced CeO₂ single crystals. J. Phys. Chem. Solids 38, 859–867. doi:10.1016/0022-3697(77)90124-x

CrossRef Full Text | Google Scholar

Tyagi, A. K., Ambekar, B., and Mathews, M. (2002). Simulation of lattice thermal expansion behaviour of Th_1−xPu_xO₂ (0.0 ≤ x ≤ 1.0) using CeO₂ as a surrogate material for PuO₂. J. Alloys Compd. 337, 277–281. doi:10.1016/s0925-8388(01)01964-8

CrossRef Full Text | Google Scholar

Vegard, L. (1921). Die Konstitution der Mischkristalle und die Raumffillung der Atome. Z. Phys. 5, 17–26. doi:10.1007/bf01349680

CrossRef Full Text | Google Scholar

Vigier, J-F., Freis, D., Pöml, P., Prieur, D., Lajarge, P., Gardeur, S., et al. (2018). Optimization of uranium-doped americium oxide synthesis for space application. Inorg. Chem. 57, 4317–4327. doi:10.1021/acs.inorgchem.7b03148

PubMed Abstract | CrossRef Full Text | Google Scholar

Vlieg, E., Den Hartog, H. W., and Winnink, M. (1986). The superionic phase transition of fluorite-type crystals. J. Phys. Chem. Solids 47, 521–528. doi:10.1016/0022-3697(86)90052-1

CrossRef Full Text | Google Scholar

Von Dreele, R. B., Eyring, L., Bowman, A. L., and Yarnell, J. L. (1975). Refinement of the crystal structure of Pr₇O₁₂ by powder neutron diffraction. Acta Cryst. B31, 971–974. doi:10.1107/s056774087500430x

CrossRef Full Text | Google Scholar

Warshaw, I., and Roy, R. (1961). Polymorphism of the rare Earth sesquioxides¹. J. Phys. Chem. 65, 2048–2051. doi:10.1021/j100828a030

CrossRef Full Text | Google Scholar

Watkinson, E. J., Ambrosi, R. M., Williams, H. R., Sarsfield, M. J., Stephenson, K., Weston, D. P., et al. (2017). Cerium neodymium oxide solid solution synthesis as a potential analogue for substoichiometric AmO₂ for radioisotope power systems. J. Nucl. Mat. 486, 308–322. doi:10.1016/j.jnucmat.2017.01.011

CrossRef Full Text | Google Scholar

Williams, H., Ning, H., Reece, M., Ambrosi, R., Bannister, N., and Stephenson, K. (2013). Metal matrix composite fuel for space radioisotope energy sources. J. Nucl. Mat. 433, 116–123. doi:10.1016/j.jnucmat.2012.09.030

CrossRef Full Text | Google Scholar

Yahiro, H., Eguchi, Y., Eguchi, K., and Arai, H. (1988). Oxygen ion conductivity of the ceria-samarium oxide system with fluorite structure. J. Of Appl. Electrochem. 18, 527–531. doi:10.1007/bf01022246

CrossRef Full Text | Google Scholar

Yamamura, H., Takeda, S., and Kakinuma, K. (2007). Dielectric relaxations in the Ce_1−xNd_xO_2−δ system. Solid state ionics 178, 1059–1064. doi:10.1016/j.ssi.2007.05.010

CrossRef Full Text | Google Scholar

Yashima, M., Kobayashi, S., and Yasui, T. (2006). Crystal structure and the structural disorder of ceria from 40 to 1497 °C. C. Solid state ionics 177 (3), 211–215. doi:10.1016/j.ssi.2005.10.033

CrossRef Full Text | Google Scholar

Ye, F., Mori, T., Ou, D. R., Takahashi, M., Zou, J., and Drennan, J. (2007). Ionic conductivities and microstructures of ytterbium-doped ceria. J. Electrochem. Soc. 154 (2), B180–B185. doi:10.1149/1.2403084

CrossRef Full Text | Google Scholar

Zhang, J. L., and Hong, G. Y. (2017). “Nonstoichiometric compounds,” in Modern inorganic synthetic chemistry. Second Edition (Amsterdam, Netherlands: Elsevier), 329–353.

CrossRef Full Text | Google Scholar

Zhang, J., Von Dreele, R. B., and Eyring, L. (1996). Structures in the oxygen-deficient fluorite-related R_nO_2n−2 homologous series: Pr₁₂O₂₂. J. Solid State Chem. 122, 53–58. doi:10.1006/jssc.1996.0081

CrossRef Full Text | Google Scholar

Zhang, J., Von Dreele, R. B., and Eyring, L. (1993). The structures of TbO₇ and Tb₁₁O₂₀. J. Solid State Chem. 104, 21–32. doi:10.1006/jssc.1993.1138

CrossRef Full Text | Google Scholar

Zinkevich, M. (2007). Thermodynamics of rare Earth sesquioxides. Prog. Mater. Sci. 52, 597–647. doi:10.1016/j.pmatsci.2006.09.002

CrossRef Full Text | Google Scholar